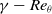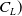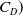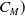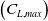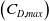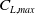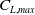Nomenclature
-
 $\alpha $
$\alpha $
-
angle-of-attack
-
 ${\alpha _m}$
${\alpha _m}$
-
mean incidence angle
-
 ${\alpha _a}$
${\alpha _a}$
-
amplitude incidence angle
-
 ${C_L}$
${C_L}$
-
lift coefficient
-
 ${C_{L,max}}$
${C_{L,max}}$
-
maximum lift coefficient
-
 ${C_D}$
${C_D}$
-
drag coefficient
-
 ${C_{D,max}}$
${C_{D,max}}$
-
maximum drag coefficient
-
 $c$
$c$
-
chord
-
 ${C_P}$
${C_P}$
-
pressure coefficient
-
 $k$
$k$
-
reduced frequency
-
 $t$
$t$
-
time
-
 ${U_\infty }$
${U_\infty }$
-
freestream velocity
- LEV
-
leading edge vortex
- TEV
-
trailing edge vortex
- DSV
-
dynamic stall vortex
- MLE
-
morphing leading edge
- MTE
-
morphing trailing edge
1.0 Introduction
The increasing demand for air transportation has heightened environmental concerns and put a strain on the aircraft sector. Due to the unpredictability of fuel costs and growing environmental concerns, fuel efficiency has become a critical element in aircraft design. In 2020, the global aviation industry was predicted to surpass 40.3 million commercial flights, a 50% increase over the previous decade. The aviation industry’s main objectives are to improve the quality and affordability of air transportation, to mitigate its environmental impact by reducing CO2, NOX, fossil fuels consumption and noise emissions, and to address safety problems [1]. These goals have resulted in an increasing demand for novel research ideas aimed at developing more efficient and environmentally friendly aircraft. Moreover, all the new studies dealing with the use of batteries for electric flight, new biofuels and hydrogen suggest the need for the increase of the aerodynamic efficiency in terms of energy to weight ratio. Aircraft configurations with higher efficiency could anticipate the batteries development level required for effective operations. Several significant collaborations have been established between industry, academia and research institutions to design, manufacture and test innovative morphing technologies with the aim of reducing emissions [Reference Frota2–Reference Papadopoulos4]. Numerous investigations at the Research Laboratory in Active Controls, Avionics, and AeroServoElasticity (LARCASE) have explored potential ways for reducing aircraft fuel consumption and increasing the aerodynamic efficiency, including experimental investigations of morphing wing models [Reference Botez5–Reference Communier, Botez and Wong11]. Figure 1 shows the Price-Païdoussis subsonic blow down wind tunnel used to carry out the LARCASE experimental studies. Different metaheuristic optimisation algorithms to improve the flight phase cost in terms of fuel burn have been studied for commercial aircraft models [Reference Murrieta Mendoza, Botez, Vucinic, Rodrigues Leta and Janardhanan12, Reference Viviani, Aldinucci, d’Ippolito, Lemeire and Vucinic13]. Some of the algorithms implemented for different optimisation strategies are genetic algorithms, the artificial bee colony and the ant colony algorithm.

Figure 1. LARCASE Price-Païdoussis subsonic blow down wind tunnel.
Morphing can increase an aircraft’s performance in terms of lift, drag and noise by removing wing surface discontinuities and gaps [Reference Arena, Chiatto, Amoroso, Pecora and de Luca14–Reference Barbarino, Pecora, Lecce, Concilio, Ameduri and De Rosa19], thus obtaining a smooth surface. Nowadays aircraft are designed to produce maximum aerodynamic performance (highest lift-to-drag ratio) within a flight envelope. Moreover, the maximum efficiency is not typically reached during the cruise because it requires a speed which is often too reduced, so that a trade-off between performances and operational needs must be defined. However, mission criteria vary continuously during flight phases, and an aircraft frequently flies in suboptimal conditions. Although typical aircraft are equipped with hinged lifting mechanisms and trailing edge surfaces to manage airflow, these aircraft may generate surface discontinuities and increase drag [Reference Kintscher, Wiedemann, Monner, Heintze and Kühn3, Reference Ameduri, Concilio, Dimino, Pecora and Ricci20]. These hinged surfaces have drawbacks in both their deployed and retracted states [Reference Li, Wang and Zhang21]. If the high lifting surface is not aligned properly, it can induce noise, turbulence and a turbulent boundary layer, thus increasing the drag. Moreover, also from a structural point of view, moving surfaces require complex mechanisms and in the case of the flaps usually only few deflection positions can be set by pilots in commercial aircraft. Many experts claim that laminarisation technology can reduce drag and prevent flow separation [Reference Abbas, De Vicente and Valero22–Reference Concilio, Dimino and Pecora24]. The morphing leading edge device is a gapless flexible droop nose that undergoes a substantial shape and camber alteration. The actuation system can lie within the aerofoil, thus avoiding the need for external mechanisms and fairings. Various advanced device concepts have been studied in detail considering both aerodynamic performance assessment and aeroelastic wing deflection effects [Reference Carossa, Ricci, De Gaspari, Liauzun, Dumont and Steinbuch25–Reference Lepage, Amosse, Brazier, Forte, Vermeersch and Liauzun27].
Unsteady aerodynamic analysis plays an important role in the process of conceptual morphing designs. Morphing optimisation has revealed that optimised lift and drag coefficients can be obtained at different flight conditions. The use of morphing wing technology as a flow control technique has resulted in efficient aerodynamic designs [Reference Dimino, Lecce and Pecora15, Reference Sinapius, Monner, Kintscher and Riemenschneider28–Reference Vu, Kelkar and Whitmer30]. Dynamic stall control is especially significant because it occurs in all aerospace applications, such as on UAVs [Reference Mathisen, Gryte, Gros and Johansen31, Reference Sekimoto, Kato, Fujii and Yoneda32], helicopter rotors [Reference Liiva33, Reference Richez34], wind turbines [Reference Larsen, Nielsen and Krenk35, Reference Zhu, Qiu and Wang36] and military aircraft [Reference Brandon37, Reference Nguyen, Lowenberg and Neild38]. The effects of unsteady parameters, such as the oscillation amplitude, reduced frequency, Reynolds number and aerofoil kinematics (deformation, variable thickness etc.) have been investigated by different researchers from the perspective of aerodynamic coefficients [Reference Zi, Daochun, Xiang and Cheng39–Reference Andersen, Gaunaa, Bak and Hansen42]. Numerical studies were used to investigate morphing wing aerodynamic stall and to explore adaptive morphing trailing-edge wings, 1% drag reduction on-design and 5% off-design were obtained [Reference Lyu and Martins43]. A hybrid RANS-LES technique was used to investigate the aerodynamic performance of an aerofoil with a downward, statically morphing trailing-edge flap (TEF). Morphing enhanced lift-to-drag by 6% [Reference Abdessemed, Yao, Bouferrouk and Narayan44, Reference Abdessemed, Bouferrouk and Yao45]. Similar results were reported for the aerodynamic and aeroacoustics responses of an aerofoil fitted with a harmonically morphing trailing edge flap [Reference Abdessemed, Bouferrouk and Yao46]. It is worth noting that a slight increase in efficiency impacts with a magnification factor the maximum take off (MTO) mass of an aircraft by reducing in a significant way the fuel consumption. Moreover, RANS numerical simulations of a NACA0012 aerofoil with a flexible trailing-edge showed that the morphing surface can delay the beginning of flow separation with the aim to achieve optimal aerodynamic performance [Reference Kamliya Jawahar, Ai and Azarpeyvand47, Reference Jawahar, Ai and Azarpeyvand48].
The dynamic stall is an aerodynamic phenomenon that occurs when the flow over the wings and aerodynamic bodies separates rapidly due to changes in relative freestream conditions. Dynamic stall is marked by increased flow-field unsteadiness, resulting in increased airframe vibration and reduced aerodynamic performance [Reference Wei, Gao and Li49, Reference Gupta and Ansell50]. A thin reversed flow region forms at the trailing edge before dynamic stall. A reverse pressure gradient moves the reversed flow area to the leading edge, while the flow remains attached. The leading edge of the vortex produces a powerful suction. A leading-edge vortex (LEV) progressively splits from the aerofoil surface to generate a dynamic stall vortex (DSV). The DSV develops near the trailing edge as the angle-of-attack increases, resulting in aerodynamic moment variations. For a higher angle-of-attack, the DSV separates from the trailing edge of the aerofoil.
Both dynamic and static stall produces significant losses in lift and large increases in drag. The dynamic stall has the added feature of generating significant negative pitching moments. These large pitching moments and the associated negative damping of the cycle cause high torsional stresses in a helicopter rotor blade, which can lead to its destruction. The dynamic stall phenomenon, which is the process of delayed flow separation brought on by a quick change in the angle-of-attack of rotating blades, significantly impacts the performance parameters of vertical axis wind turbines. Low tip speed ratios, where unstable flow separation and dynamic stall dominate the blade aerodynamics, cause the wind turbines to perform poorly in terms of power output.
Numerous flow control devices have been developed to avoid flow separation and to mitigate dynamic stall effects. They can be classified as active, or passive based on their operational properties. Vortex generators, micro-tabs, and serrated trailing edges are all examples of passive control devices. Active control mechanisms include trailing-edge flaps and synthetic jets of fluids. The use of leading-edge slats [Reference Imamura, Enomoto, Yokokawa and Yamamoto51, Reference Balaji, Bramkamp, Hesse and Ballmann52], trailing-edge flaps [Reference Gerontakos and Lee53, Reference Lee and Su54], synthetic jet/periodic excitation strategies [Reference Traub, Miller, Rediniotis, Kim, Jayasuriya and Jung55–Reference Greenblatt and Wygnanski57], plasma actuators [Reference Post and Corke58], vortex generators [Reference Heine, Mulleners, Joubert and Raffel59], and dynamically morphing leading-edge [Reference Sahin, Sankar, Chandrasekhara and Tung60] has been studied. In a wind tunnel, a morphing wing was optimised in real time to delay the flow transition to the trailing edge [Reference Popov, Grigorie, Botez, Mamou and Mébarki61]. The upper surface of the morphing rectangular finite aspect ratio wing was designed using a flexible composite material, and it was further equipped with pressure sensors and two smart memory alloy actuators. The morphing wing was obtained using several optimiaed aerofoils by controlling the two actuators’ strokes automatically. It was demonstrated in this study that the optimisation mechanism in the control software code allowed the morphing wing to optimise its shape for various flight cases.
Studies for dynamic stall reduction using flow control have been done in the literature. These studies included the use of aerofoil leading or trailing edge flaps [Reference Gerontakos and Lee53, Reference Bashir, Zonzini, Botez, Ceruti and Wong62], vortex generators [Reference Singh, Peake, Kokkalis, Khodagolian, Coton and Galbraith63], zero mass jets [Reference Ramesh, Ke, Gopalarathnam and Edwards64], flow blowing and sucking devices [Reference Kral, Donovan, Cain, Cary, Kral, Donovan, Cain and Cary65] etc. The high-frequency control techniques for dynamic stall control gave the benefits of instabilities associated with the laminar separation bubble (LSB) to delay the occurrence of a dynamic stall vortex (DSV) [Reference Visbal and Benton66, Reference Visbal and Garmann67]. The authors mentioned that the substantial negative pitching moment and its associated aerodynamic damping properties were obtained because of the trailing edge vortex. The TE flaps dynamics was investigated using the dynamic loads generated through oscillating aerofoils [Reference Visbal and Garmann67].
The use of a leading-edge slat device for dynamic stall control was investigated numerically using a two-dimensional Navier–Stokes solver for multi-element aerofoils [Reference Sahin and Sankar68]. Another option is to use suction/blowing. Blowing slots were set at 10% and 70% of the chord to conduct a dynamic-stall control test. Sun and Sheikh numerically simulated dynamic-stall control with near-leading-edge tangential blowing [Reference Seifert and Pack69].
A deployable leading edge vortex generator was used in an active dynamic stall control approach [Reference Le Pape, Costes, Richez, Joubert, David and Deluc70]. Wind tunnel studies have shown that the device delayed the static stall and reduced dynamic stall penalties. Three degrees were added to the static stall angle. The dynamic stall reduced the negative pitching moment peak by 60% [Reference Abdessemed, Bouferrouk and Yao46]. Numerical studies evaluated the impact of the synthetic jet control on the unstable dynamic stall over a rotor aerofoil [Reference Qijun, Yiyang and Guoqing71]. It was shown that the jets were most efficient when the stall was located at the flow separation point. Adjusting jet angle and momentum coefficients had similar impacts on dynamic stall characteristics. When situated near the flow separation point, a modest jet angle offered the optimum control effects on aerofoil aerodynamic forces. In the separated flow region, a medium-angle synthetic jet is more effective. Experimental investigations using plasma-based devices or other high-frequency actuation were carried out using employing high-fidelity wall-resolved large-eddy simulations [Reference Visbal and Benton66, Reference Visbal and Garmann72].
The effects of the trailing edge flap (TEF) flow control on helicopter rotor blade dynamic stall were explored in Ref. (Reference Feszty, Gillies and Vezza73). The authors found that the substantial negative pitching moments and their related negative aerodynamic damping were caused by the trailing edge vortex: and its only upward flap deflections reduced aerodynamic damping. Another study examined the outcome of the TEF and LEF on the dynamic loads generated by an oscillating aerofoil [Reference Lee and Gerontakos74, Reference Gerontakos and Lee75].
The study indicated that the downward LEF motion suppressed leading edge separation and eliminated the occurrence of the DSV, leading to a minor reduction in
![]() ${C_{L,max}}\;$
but a considerably improved post stall lift condition, compared with the baseline aerofoil. The joint upward LEF and downward TEF control produced the largest
${C_{L,max}}\;$
but a considerably improved post stall lift condition, compared with the baseline aerofoil. The joint upward LEF and downward TEF control produced the largest
![]() ${C_{L,max\;.}}$
Another investigation was carried out to study the effect of a TEF on dynamic stall of wind turbine blades [Reference Samara and Johnson76]. The TEF reduced lift and root bending moment by 26% and 24%, respectively. These results show how TEF reduced wind turbine blade loads changes. Another study analysed the flow field around a helicopter blade in forward flight [Reference Karimian, Aramian and Abdolahifar77]. The two-dimensional model incorporated forward flight speed, resulting in a time-variable aerofoil flow speed. Therefore, phenomena such as shock wave near the leading-edge of aerofoil, which is critical to dynamic stall formation, were modeled using more realistic flow conditions. This study examined aerofoil nose drooping and showed that it reduces and alleviates dynamic stall. An aerofoil can be drooped to eliminate shock wave from its leading edge, and therefore no dynamic stall will occur.
${C_{L,max\;.}}$
Another investigation was carried out to study the effect of a TEF on dynamic stall of wind turbine blades [Reference Samara and Johnson76]. The TEF reduced lift and root bending moment by 26% and 24%, respectively. These results show how TEF reduced wind turbine blade loads changes. Another study analysed the flow field around a helicopter blade in forward flight [Reference Karimian, Aramian and Abdolahifar77]. The two-dimensional model incorporated forward flight speed, resulting in a time-variable aerofoil flow speed. Therefore, phenomena such as shock wave near the leading-edge of aerofoil, which is critical to dynamic stall formation, were modeled using more realistic flow conditions. This study examined aerofoil nose drooping and showed that it reduces and alleviates dynamic stall. An aerofoil can be drooped to eliminate shock wave from its leading edge, and therefore no dynamic stall will occur.
Therefore, the literature mentioned above has proven mainly those different methods can be implemented to control the dynamic stall of the pitching aerofoil. In this paper, the attention is focused on the morphing aerofoil deformations, which are done in the frame of one of the most promising methods available to control the dynamic stall. However, dynamic aerofoil morphing phenomena imposes a significant amount of complexity in the structure and control systems of a morphing wing. Therefore, the first objective of this study is to obtain optimised aerofoils for the (MLE and the MTE to enhance the overall aerodynamic performance. The obtained optimised aerofoils are then evaluated to investigate the dynamic stall. To our knowledge, only a few numerical studies have used optimised aerofoils to model the dynamic stall phenomenon at a moderate Reynolds number turbulent flow regime. Transition SST model’s ability to predict laminar, transitional and fully turbulent flow regimes will contribute to a better understanding of the flow physics of dynamic stall and its delay. The paper is structured as follows Section 2 describes the methodology developed to optimise the aerofoil, Section 3 includes a discussion of the results obtained in Section 2. Finally, Section 4 describes the outcome of this study and future work that could be carried out to investigate the dynamic stall.
2.0 Methodolgy
2.1 Optimisation problem definition
The MLE and MTE aerofoils derived from the UAS-S45 aerodynamic shape have been obtained through an optimisation by using an intelligent and iterative approach based on user-defined aerodynamics and constraints. In the aerodynamic technique used here, an objective function formulation was coupled with a geometrical shape parameterisation model, an aerodynamic flow solver and an optimisation algorithm. All these mathematical tools have been combined together in order to find a solution. Different morphing aerofoil shapes were obtained for improving the UAV’s aerodynamic performance.
An optimisation framework was developed for this study to allow the integration of aerofoil generation via the direct manipulation of the aerofoil shape variables while respecting to geometrical limitations. Figure 2 depicts the optimisation approach structure, which includes a geometrical modelling block based on the Bezier-PARSEC (BP) parameterisation technique and an aerodynamic solver, namely the panel solver XFOIL. The Transition SST model’s results are validated using a high-fidelity solver in Ansys Fluent, based on Reynolds-Averaged Navier–Stokes (RANS) equations. A hybrid optimiser is also utilised, which combines the particle swarm optimization (PSO) method with the pattern search (PS) technique. The optimisation procedure is presented in more details [Reference Bashir, Longtin-Martel, Botez and Wong7].

Figure 2. Schematics of the optimisation procedure [Reference Bashir, Longtin-Martel, Botez and Wong7].
The ability to search and obtain the best solution is demonstrated by designing an optimised aerofoil derived from the UAS-S45 aerofoil, with the goal of maximiaing lift-to-drag ratio at cruise speed. For this design challenge, the following optimiaation function was constructed as shown in Equation (1):
such that:
where
![]() $N$
is the number of flight conditions for which the objective function is maximised, LB is the lower bound and UB is the upper bound.
$N$
is the number of flight conditions for which the objective function is maximised, LB is the lower bound and UB is the upper bound.
The geometrical parameterisation is one of the most important aspects of the aerofoil shape optimisation and design. By optimising both the geometric and aerodynamic properties, the parameterised aerofoil should have a small number of design variables. The number of design variables can be increased, which will take a long time and require high computing resources [Reference Khurana, Winarto and Sinha78]. There are numerous methods available for the shape parameterisation of aerofoils geometries. Some of the well-known methods are discrete points, Bezier or B-Spline, free-form representation and cubic spline control point representation [Reference Khurana, Winarto and Sinha78, Reference Trad, Segui and Botez79]. These methods have the disadvantages such as the method does not use aerofoil parameters as design variables, requiring a large number of design variables than those of the aerofoil parameters, and they frequently produce erroneous shapes for aerofoil’s leading and trailing edges. The main problem needed to solve is to find a mathematical description of the aerofoil based on the positions of a limited set of points, whose positions are changed by the optimisation algorithm.
The BP parameterisation was developed by Derksen and Rogalsky, and describes Bezier curves using PARSEC parameterizations [Reference Derksen and Rogalsky80]. It is classified into BP3333 and BP3434. The BP3333 uses third-order Bezier curves for the aerofoil camber and thickness, and its key advantages are of close relevance to aerofoil aerodynamic parameters, fast optimisation, continuity features low number of design variation and avoidance of abrupt leading edges. Reduced degree of freedom prevents the parameterisation of camber trailing edge aerofoils. In the BP3434, third-order Bezier curves define the camber and thickness of the aerofoil’s leading edge, whereas fourth-order Bezier curves define the trailing edge, as shown in Fig. 3. When an aerofoil’s camber is negative along its chord, the BP3434 is more efficient than BP3333, and therefore the BP3434 type is implemented in this study.

Figure 3. BP3434 parameterisation scheme defining the Bezier aerofoil curves.
It is worth noting that Bezier curves are not defined by a set of interpolating points from which the curve passes through, but by a control polygon; the shape of the curve is managed by changing the positions of the points of the control polygon. However, the BP method’s inverse design problem does not have enough potential for accelerated convergence when parameterisation is considered while determining algorithm robustness and convergence rate. In addition, higher-order Bezier curves are required for better solutions, such as BP 3434, which is more robust than BP 3333, and some of these curves will contribute in a non-linear way to the objective function.
For the UAS-S45 aerofoil optimisation, a hybrid optimiser based on the (PSO method combined with the PS algorithm was employed to improve the solution convergence and refinement. The PSO technique is based on the imitation of flock of birds or school of fish while searching for food, with solutions represented by particles that heuristically search a design space.
The hybrid optimisation approach initially uses the PSO to optimise all variables. A second optimiser is then applied to the PSO’s output due to small particles motion and their positions near optimised values or patterns. PSO is followed by PS optimisation. The PS can identify a local optimum in a confined search region; the coupled use of PSO-PS provides better results than a single optimiser. One of the problems of heuristic optimisation is the local minimum solution: such an algorithm can find a sub-optimal solution and not find the zones of the design space where the best solution lies. The optimisation procedure generates a cost for every tested configuration by use of an objective function and a penalty function with the aim to remove non-realistic or non-feasible solutions from possible optimisation results. Upper and lower bounds control the number of input variables. These bounds ensure that the search space for both the PSO and the PS remain within them. During the PSO execution, if a particle is outside the search space constraints, its value is replaced by that of the within bound.
2.2 Unsteady analysis using Computational Fluid Dynamics (CFD) solver
For the pitching aerofoil dynamic cases, the Reynolds number based on the aerofoil chord length is Re = 2.4 × 106. During dynamic simulations, the aerofoil undergoes a sinusoidal pitching motion, as shown in Equation (2):
where
![]() ${\alpha _m}$
= 11° is the mean incidence angle,
${\alpha _m}$
= 11° is the mean incidence angle,
![]() ${\alpha _a}$
= 20° is the amplitude, f is the aerofoil oscillation frequency and t is the time.
${\alpha _a}$
= 20° is the amplitude, f is the aerofoil oscillation frequency and t is the time.
The reduced frequency
![]() $k$
is defined in Equation (3):
$k$
is defined in Equation (3):
where
![]() ${U_\infty }$
is the freestream velocity, and c is the aerofoil chord length. Various reduced frequencies
${U_\infty }$
is the freestream velocity, and c is the aerofoil chord length. Various reduced frequencies
![]() $k$
were chosen for the aerofoil and the Reynolds number based on the unit chord length and free-stream velocity of 35.5 m/s was set to 2.4 × 106.
$k$
were chosen for the aerofoil and the Reynolds number based on the unit chord length and free-stream velocity of 35.5 m/s was set to 2.4 × 106.
2.2.1 Computational domain and grid
The computational domain is 20c (20 times the length of the aerofoil chord) upstream and 30c downstream of the aerofoil pitch axis, while the inner circular region is 5c in diameter and centered at 0.25c aft of the leading edge. The mesh employs sliding mesh to obtain the aerofoil pitching motion to avoid re-meshing, and to maintain cells quality. This work focusses on the pitching mode denoted by
![]() $\alpha \left( {} \right) = \;11\; + \;15{\rm{sin}}\left( {\omega t} \right)$
in which the aerofoil enters a deep dynamic stall phase with considerable flow unsteadiness. Figure 4 shows the pitching axis 0.25c downstream of the chord line’s leading edge. As already mentioned, based on the chord length and freestream velocity, the Reynolds number is 2.4 × 106.
$\alpha \left( {} \right) = \;11\; + \;15{\rm{sin}}\left( {\omega t} \right)$
in which the aerofoil enters a deep dynamic stall phase with considerable flow unsteadiness. Figure 4 shows the pitching axis 0.25c downstream of the chord line’s leading edge. As already mentioned, based on the chord length and freestream velocity, the Reynolds number is 2.4 × 106.

Figure 4. Computational domain with the pitching mode.
One of the most important aspects in numerical simulations is the discretisation of the computational domain. It is common practice to spend most of the time analysing and studying the grid generation in order to find a grid-independent solution: a good trade-off between accuracy and computational effort must be found, which is most often addressed by a trial-and-error approach in which the numerical solution is compared with experimental data or analytical solutions. The mesh sensitivity analysis conducted after the initial validation process is detailed in the next section. The selection of a correct size and shape for the computational domain are crucial factors for the results quality, and they are strongly dependent on the aerodynamic characteristics, and on the type of the problem which is faced.
A hybrid mesh made from a combination of structured and unstructured mesh was generated with ANSA, a multidisciplinary CAE pre-processor. It consists of a structured quadrilateral layer mesh around the aerofoil and an unstructured triangular mesh for the rest of the domain. Moreover, with the use of a blunt trailing edge it was possible to obtain O-shaped block layers around the aerofoil and most importantly, to prevent instabilities of the solution induced by singular points located at the sharp corners of the trailing edge.
Figure 5 models the simulation domain with two mesh regions: (i) the inner rotating grid, and (ii) the outer stationary grid. The total number of elements in the grid is 103,212, and the boundary region’s first layer height is 0.006 mm with a bias factor of 1.08. The internal region has a minimum element length of 0.001 mm, a maximum length of 0.035 mm, and a bias factor of 1.08, while the external region has a minimum length of 0.035 mm, a maximum length of 0.6 mm and a bias factor of 1.08. The use of an internal circular domain allowed the mesh to move with the pitching aerofoil without affecting the simulation’s cell quality. High-quality quadrangular elements were used to refine the grid for its numerical stability in simulations, and mesh-independent results were obtained. Sliding meshes were applied to the interfaces between the circular and external domains, thus designing non-matching nodes due to rotation, called ‘hanging nodes’: this improves the flow prediction near the walls. Since the nodes should have a constant position in their moving frame, no smoothing dynamic mesh approach was needed, and the quality remained the same.

Figure 5. Mesh structure around the aerofoil (a) mesh around the aerofoil; (b) near the leading-edge, (c) near the aerofoil, and (d) near the trailing-edge.
The simulations were performed with a commercial CFD solver, called ANSYS Fluent. All scaled residuals were expected to decrease below 1x106. The matching length of each time step was found to be below the sliding interface’s minimum cell length to limit the interpolation error.
2.3 Validation of results
Figure 6(a) shows the aerofoils unsteady motion expressed by the lift coefficients variation with time for three pitching cycles and Fig. 6(b) shows the lift coefficient vs angle-of-attack for the same timescale. As soon as the lift coefficient reaches its highest value, a sudden decrease is observed, thus depicting the beginning of the downstroke phase. The comparison of experimental with computational results was not close enough the due to large vortices on the aerofoil surface, that were predicted by the transition SST model and the flow three-dimensionality.

Figure 6. Lift coefficient variation with time for the pitch oscillating aerofoil.
Table 1 presents the properties of three different grid sizes which have been used for grid independency investigations. Figure 7 shows the lift coefficient versus the angle-of-attack for these three different grid sizes. Good correlation between each hysteresis loop is shown and the upstroke and downstroke also showed a good agreement. The lift coefficients for grid size 1 and grid size 2 are slightly different in the down-stroke phase, and the stall (the peak of the lift curve) has a slight variation. Additionally, the fluctuations in the lift coefficient for all the three grid sizes are similar in shape and magnitude. Similarly, very small discrepancies are visualised between grid size 3 and the other two grid sizes during the upstroke, while a small difference can be seen between the lift coefficients in the downstroke. The flow reattachment location for all grid sizes is the same. Therefore, grid size 2 was selected as the computational domain due to acceptable (medium size) cell count and results obtained.
Table 1. Grid properties of the three grid sizes for the grid-sensitivity analysis


Figure 7. Comparisons of the numerical results for the lift coefficient versus the angle-of-attack for three different grid sizes.
Figure 8 compares the model’s computed lift and drag coefficients to their experimental values [Reference Mcallister, Carr and Mccroskey81] and numerical data from previous literature [Reference Correa82]. The first simulation example used as a reference the experiments of McAlister et al. with Reynolds number 2.5 x106 and reduced frequency k = 0.10, from 50 to 250, with a mean incidence of 150, while the second simulation example used for benchmarking Correa et al.’s 2015 numerical data for the same settings.

Figure 8. Comparison of our numerical results with experimental results obtained from previous wind tunnel tests [Reference Kral, Donovan, Cain, Cary, Kral, Donovan, Cain and Cary65] and numerical results [Reference Visbal and Benton66]: (a) lift coefficient; (b) drag coefficient.
The
![]() $SST\;k - \omega $
turbulence model can forecast the results’ trend. The lift coefficient corresponds with its experimental value in the upstroke phase but it predicts the stall differently than the experimental results. As the unsteady analysis is often dissipative, it reduces the flow intensity and thus the kinetic energy. The numerical result is good, as it captures the load variation trend before the stall region. The ranges of differences in the peak noticed in the lift coefficient is small. The down-stroke variations are due to the extensive post-stall process, and hence discrepancy in the initial LEV prediction.
$SST\;k - \omega $
turbulence model can forecast the results’ trend. The lift coefficient corresponds with its experimental value in the upstroke phase but it predicts the stall differently than the experimental results. As the unsteady analysis is often dissipative, it reduces the flow intensity and thus the kinetic energy. The numerical result is good, as it captures the load variation trend before the stall region. The ranges of differences in the peak noticed in the lift coefficient is small. The down-stroke variations are due to the extensive post-stall process, and hence discrepancy in the initial LEV prediction.
Figure 8(b) illustrates the drag coefficient variation with angle-of-attack and a difference exists particularly when α > 12, as the deep stall causes the drag to increase. The drag coefficient with angle-of-attack in Correa’s numerical simulations is lower than the drag coefficient obtained in the other simulations. However, our numerical results of aerofoil’s maximum drag coefficient are lower than the experimental results due to large vortices on the aerofoil surface and to the flow three dimensionality. These vortices occur because of the persistent flow separations at high angles of attack, which makes it difficult to effectively describe the viscous effects near the aerofoil surface. The CFD simulations in our study also indicate a secondary LEV that contributes to the recovery of the lift and drag coefficients around the maximum angle-of-attack.
3.0 Discussion of results
The outcomes of the optimisation procedure are expressed in terms of LE and MTE aerofoil designs in the first part of this section. The findings of the unsteady flow analysis are presented in the second part of this section in order to better understand the DSV studies and the results of various aerofoil configurations.
3.1 Optimisation results
The aerodynamic optimisation was obtained for the MLE and MTE aerofoils using the methodology presented in Ref. (Reference Bashir, Longtin-Martel, Botez and Wong7). The study presents the leading edge and trailing edge optimisation results of the S45 UAS’ aerofoil and will demonstrate the overall benefits of the morphing.
Figure 9(a) indicates that the lift coefficients of the MLE aerofoil are higher than those of the reference aerofoil at Reynolds number = 2.4 × 106, where C
L
is 1.57 and 1.65 for the MLE and the reference aerofoil, respectively, thus representing a 5.09 % increase, and a static angle-of-attack increase of 3°. Figure 9(b) shows the lift-to-drag ratio of the reference aerofoil and the optimised aerofoils and reveals a 3.8 % increase for
![]() ${\left( {\frac{{{C_L}}}{{{C_D}}}} \right)_{max}}$
for MLE when compared to the reference aerofoil.
${\left( {\frac{{{C_L}}}{{{C_D}}}} \right)_{max}}$
for MLE when compared to the reference aerofoil.

Figure 9. Comparison of aerodynamic coefficients: (a) CL, (b) CL vs CD ratio and (c) CP of the MLE versus the reference aerofoil coefficients.
Figure 9(c) shows the pressure variations with the chord for MLE and reference aerofoils. The MLE aerofoil upper surface has the higher-pressure fluctuations than the reference aerofoil. The chord-wise pressure distribution shows that the MLE optimised aerofoil’s cruise performance was improved by delaying the turbulent flow towards the trailing edge.
Figure 10(a) shows that the optimised aerofoil has higher lift coefficients than the reference aerofoil. The MTE lift coefficient was improved by maximum of 8.6% over the reference aerofoil. In addition, the MTE aerofoil stall angle increased by 2° with respect to the reference aerofoil stall angle.

Figure 10. Comparison of aerodynamic coefficients: (a) CL, (b) CL vs CD ratio and (c) CP of the MLE versus the reference aerofoil coefficients.
Figure 10(b) shows the drag polar of the reference aerofoil, and the optimised MTE aerofoil. The morphing MTE aerofoil has a higher
![]() $\frac{{{C_L}}}{{{C_D}}}$
ratio than the reference aerofoil. Figure 10(c) shows the reference versus the MTE aerofoil pressure coefficients at 10° angle-of-attack. The MTE aerofoils have larger suction peaks than the reference aerofoil.
$\frac{{{C_L}}}{{{C_D}}}$
ratio than the reference aerofoil. Figure 10(c) shows the reference versus the MTE aerofoil pressure coefficients at 10° angle-of-attack. The MTE aerofoils have larger suction peaks than the reference aerofoil.
Figure 11 presents the velocity contour with streamlines depicting the separation bubble on the reference aerofoil at an angle-of-attack of 10°. The LSB can be seen over the leading edge of an aerofoil. The separation area was not visualised at lower angles of attack.

Figure 11. Velocity contour with streamlines at an angle-of-attack of 10°.
Figure 12 shows the aerofoil upper surface skin friction coefficient variation at angles of attack (AoA) of 2°, 6° and 10°. Figure 12(a) depicts the aerofoil lower surface skin friction coefficients by showing their way of increase with the incidence angle. The skin friction coefficient distribution on the upper surface of the aerofoil shows that the transition position moves towards the leading edge gradually with the increase of the angle-of-attack. The skin friction coefficient curve at α = 10° shows an irregular variation, which is a typical trend for cases when flow separation exists. Figure 12(b) shows the upper surface skin friction coefficients with their higher values at higher angles of attack by indicating the reduced shear velocity. In addition, the presence of flow separation is seen at 0.036c.

Figure 12. Skin friction coefficient variation with the chord location on the: (a) upper surface and (b) lower surface.
3.2 Unsteady aerodynamics results
Unsteady numerical simulations of a sinusoidally pitching UAS-S45 aerofoil and its morphing configurations will be studied. Aerofoil pitching occurs at the quarter chord position. To analyse the dynamic stall, we demonstrate the occurrence of LEVs over the UAS-S45 aerofoil for different morphing aerofoil configurations. Using this unsteady flow phenomena over the optimized aerofoil configurations, the dynamic stall analysis will be presented.
3.2.1 Effect of reduced frequency on the UAS-S45 aerofoil
Figure 13 presents a comparison of aerodynamic coefficients at different reduced frequencies for
![]() $\alpha \left( t \right) = \;{\alpha _m} + \;{\alpha _a}\sin \left( {\omega t} \right).\;$
The effect of the reduced frequency on the unsteady pitching aerofoil motion is investigated by plotting the
$\alpha \left( t \right) = \;{\alpha _m} + \;{\alpha _a}\sin \left( {\omega t} \right).\;$
The effect of the reduced frequency on the unsteady pitching aerofoil motion is investigated by plotting the
![]() ${C_L}$
versus the angle-of-attack for several reduced frequencies k = 0.05, 0.08, 0.12, 0.16, and 0.20 at Re = 2.4 × 106. As shown in Fig. 13,
${C_L}$
versus the angle-of-attack for several reduced frequencies k = 0.05, 0.08, 0.12, 0.16, and 0.20 at Re = 2.4 × 106. As shown in Fig. 13,
![]() ${C_{L,max}}$
increases with the reduced frequency values; from
${C_{L,max}}$
increases with the reduced frequency values; from
![]() ${C_{L,max}}$
= 2.43at k = 0.05,
${C_{L,max}}$
= 2.43at k = 0.05,
![]() ${C_{L,max}}$
= 2.49at k = 0.08,
${C_{L,max}}$
= 2.49at k = 0.08,
![]() ${C_{L,max}}$
= 2.54 at k = 0.12,
${C_{L,max}}$
= 2.54 at k = 0.12,
![]() ${C_{L,max}}$
= 2.59at k = 0.16 and 2.64 at k = 0.20. A greater k value broadens the hysteresis loops but does not affect the lift curve slope. Figure 13(b) shows a similar behaviour for the drag coefficient, but k has a mixed influence (
${C_{L,max}}$
= 2.59at k = 0.16 and 2.64 at k = 0.20. A greater k value broadens the hysteresis loops but does not affect the lift curve slope. Figure 13(b) shows a similar behaviour for the drag coefficient, but k has a mixed influence (
![]() ${C_{D,max}})$
. That is, increasing k changes
${C_{D,max}})$
. That is, increasing k changes
![]() ${C_{D,max}}\;$
from 1.17 at k = 0.05 to 1.45 at k = 0.2. Table 2 clearly shows the values of
${C_{D,max}}\;$
from 1.17 at k = 0.05 to 1.45 at k = 0.2. Table 2 clearly shows the values of
![]() ${C_{L,max}}$
and
${C_{L,max}}$
and
![]() ${C_{D,max}}$
. Different types of vortices are generated at the trailing edge, as it can be seen from the downstroke. These vortices increase the lift force from the instant in which they are produced until their separation and shedding into the downstream wake. This process continues until the vortices are no longer present.
${C_{D,max}}$
. Different types of vortices are generated at the trailing edge, as it can be seen from the downstroke. These vortices increase the lift force from the instant in which they are produced until their separation and shedding into the downstream wake. This process continues until the vortices are no longer present.

Figure 13. Aerodynamic coefficient hysteresis loops at different reduced frequencies for the variations of the (a) lift coefficient, (b) drag coefficient, and (c) pitching moment coefficient with the AoA.
The vortex patterns at various instances of a dynamic stall cycle for k = 0.05 case are shown in Fig. 14. Figure 14(a) depicts the upstroke LEVs in stall formation at four values of
![]() ${\rm{AoA}}$
. At
${\rm{AoA}}$
. At
![]() $\alpha $
= 25.5°, the formation of fully developed primary LEV is visualised, along with the beginning of a secondary LEV. This phenomena occurs as the incoming flow from the aerofoil above the stagnation point enters the vortex. The fluid bypasses the vortex and enters the boundary layer at the trailing edge. However, the primary vortex rolls up under the action of the secondary vortices, which enter in the boundary layer. As the angle-of-attack increases, more high-energy flow enters in the primary vortex, thus increasing its size. The separation point advances towards the trailing edge as the vortex increases. Secondary and tertiary vortices are visualised in the last two portions of Fig. 14(a).
$\alpha $
= 25.5°, the formation of fully developed primary LEV is visualised, along with the beginning of a secondary LEV. This phenomena occurs as the incoming flow from the aerofoil above the stagnation point enters the vortex. The fluid bypasses the vortex and enters the boundary layer at the trailing edge. However, the primary vortex rolls up under the action of the secondary vortices, which enter in the boundary layer. As the angle-of-attack increases, more high-energy flow enters in the primary vortex, thus increasing its size. The separation point advances towards the trailing edge as the vortex increases. Secondary and tertiary vortices are visualised in the last two portions of Fig. 14(a).
At
![]() $\alpha $
= 27.3°, the flow on the bottom of the aerofoil increases the size of the first trailing edge vortex. As the angle-of-attack increases to 28.8°, the separation point advances further behind the trailing edge, the mass of the fluid entering covers the entire aerofoil, and the lift coefficient reaches its maximum. A part of the fluid enters as upstream vortices along the boundary layer, while the rest of it is transported downstream into the wake. A secondary trailing edge vortex appears, and large vortices confirm the dynamic stall occurrence.
$\alpha $
= 27.3°, the flow on the bottom of the aerofoil increases the size of the first trailing edge vortex. As the angle-of-attack increases to 28.8°, the separation point advances further behind the trailing edge, the mass of the fluid entering covers the entire aerofoil, and the lift coefficient reaches its maximum. A part of the fluid enters as upstream vortices along the boundary layer, while the rest of it is transported downstream into the wake. A secondary trailing edge vortex appears, and large vortices confirm the dynamic stall occurrence.

Figure 14. Velocity contour superimposed with flow at k = 0.05: (a) up-stroke cycle and (b) down-stroke cycle.
Figure 14(b) depicts the velocity contour in the downstroke phase. At
![]() $\alpha $
= 27.92°, the separation points travel behind the trailing edge, a vortex structure covers the entire aerofoil from its leading edge to its trailing edge, and the lift coefficient increases. As the angle-of-attack reaches 20.42°, the bigger vortex reduces and starts to merge into the flow. The separation points travel upstream, and these vortices disappear at 13.91°. The vortex region is sucked into the boundary layer, and a part of it is transferred downstream into the wake. Eventually, the separation zones disappear, and the reattached flow occurs at the low angles of attack.
$\alpha $
= 27.92°, the separation points travel behind the trailing edge, a vortex structure covers the entire aerofoil from its leading edge to its trailing edge, and the lift coefficient increases. As the angle-of-attack reaches 20.42°, the bigger vortex reduces and starts to merge into the flow. The separation points travel upstream, and these vortices disappear at 13.91°. The vortex region is sucked into the boundary layer, and a part of it is transferred downstream into the wake. Eventually, the separation zones disappear, and the reattached flow occurs at the low angles of attack.
Figure 15 reveals the stall development for up-stroke and down-stroke cycles of the aerofoil for a higher reduced frequency of k = 0.16. In Fig. 15(a), at upstroke angle-of-attack of 20.3°, the flow evolves slowly and stays attached to the aerofoil; the LSB is small and starts to form without a visible vortex. At 25.5°, the LEV evolves along the leading edge and continues to grow slowly. The increase of the angle-of-attack to 27.3° makes the LEV bigger and stronger. However, the dynamic stall can be seen at similar angles of attack, as it can be seen at k = 0.05 in Fig. 14(a).
Table 2. Aerofoil performance parameters at different reduced frequencies

Note:
![]() ${C_{L,\;\;max}}$
= max dynamic lift coefficient;
${C_{L,\;\;max}}$
= max dynamic lift coefficient;
![]() ${C_{D,max}}\;$
= max drag coefficient;
${C_{D,max}}\;$
= max drag coefficient;
![]() ${\alpha _{ds}}$
= dynamic stall angle;
${\alpha _{ds}}$
= dynamic stall angle;
![]() $\Delta {C_{L,max}}$
= max lift difference from steady state results;
$\Delta {C_{L,max}}$
= max lift difference from steady state results;
![]() $\Delta {C_{D,max}}$
= max drag coefficient difference from steady state results.
$\Delta {C_{D,max}}$
= max drag coefficient difference from steady state results.

Figure 15. Velocity contour superimposed with flow at k = 0.16: (a) up-stroke cycle and (b) down-stroke cycle.
Figure 15(b) shows the downstroke flow angles; multiple vortices are located over the aerofoil at 27.92°, and the vortices merge and reduce in size at 20.42° and 13.91°. One important aspect is that the flow fails to fully reattach at higher reduced frequencies, which can also be seen in the downstroke cycle shown in Fig. 14(b).
Table 2 presents the results expressed in terms of aerodynamic parameters and stall features of an oscillating aerofoil at different reduced frequencies. The values of the stall angle-of-attack (
![]() ${\alpha _{ds}}\left[ ^\circ \right])$
reveal how reduced frequencies resulted in different dynamic stall angles. The stall angle increased from k = 0.05 to k = 0.20 by 4 degrees. It can be seen that the lift coefficient increases with the increasing reduced frequency. The lift coefficient of a pitching aerofoil is higher than that of a static aerofoil. Table 2 shows that the lift and drag coefficients variations during pitching motion at different reduced frequencies, and they increase at higher reduced frequencies.
${\alpha _{ds}}\left[ ^\circ \right])$
reveal how reduced frequencies resulted in different dynamic stall angles. The stall angle increased from k = 0.05 to k = 0.20 by 4 degrees. It can be seen that the lift coefficient increases with the increasing reduced frequency. The lift coefficient of a pitching aerofoil is higher than that of a static aerofoil. Table 2 shows that the lift and drag coefficients variations during pitching motion at different reduced frequencies, and they increase at higher reduced frequencies.
3.2.2 Effect of the MLE
Figure 16 compares the aerodynamic coefficients of the morphing leading-edge aerofoils to those of a reference aerofoil with respect to the angle-of-attack over one complete cycle. Figure 16(a) shows that morphing aerofoils have both successfully increased
![]() ${C_{L,max}}$
value from 2.49 to 3.04. It is also clear that the morphing leading edge increased
${C_{L,max}}$
value from 2.49 to 3.04. It is also clear that the morphing leading edge increased
![]() ${C_{L,max}}$
, with the stall angle-of-attack increase. The main objective of the stall study is to delay or increase the stall angle, as stall angle-of-attack delay helps to maintain the aerofoil lift coefficient even in the downstroke cycle. However, this result indicates that a strong vortex has been formed in the leading-edge of aerofoil, which later results in dynamic stall.
${C_{L,max}}$
, with the stall angle-of-attack increase. The main objective of the stall study is to delay or increase the stall angle, as stall angle-of-attack delay helps to maintain the aerofoil lift coefficient even in the downstroke cycle. However, this result indicates that a strong vortex has been formed in the leading-edge of aerofoil, which later results in dynamic stall.

Figure 16. Aerodynamic coefficient hysteresis loops at k = 0.08: (a) lift coefficient, (b) drag coefficient and (c) pitching moment coefficient.
Similarly, the drag coefficients are lower for the MLE aerofoil for AoA lower than 30°, and the
![]() ${C_{D,max}}$
increases substantially at the peak angle with respect to the reference aerofoil, as seen in Fig. 16(b). Therefore, the drag coefficient of the MLE aerofoil remains low for a large range of angles of attack. The MLE aerofoil moment coefficient shows smaller
${C_{D,max}}$
increases substantially at the peak angle with respect to the reference aerofoil, as seen in Fig. 16(b). Therefore, the drag coefficient of the MLE aerofoil remains low for a large range of angles of attack. The MLE aerofoil moment coefficient shows smaller
![]() ${C_M}$
values with respect to those of the reference aerofoil, as seen in Fig. 16(c).
${C_M}$
values with respect to those of the reference aerofoil, as seen in Fig. 16(c).
Figure 17(a) and (b) illustrate optimised MLE aerofoil streamlines and Mach number contours. Figure 17(a) depicts the flow development at different upstroke angles of attack for the reference aerofoil. The reference aerofoil’s primary LEV can be clearly seen at 25.5° angle-of-attack. The clockwise vortex can also be seen near the trailing edge. As the angle-of-attack increases, the vortex size grows accordingly. The secondary and tertiary LEVs are also formed along with the primary LEV as the attack angle increases from 25.5° to 28.8°. The AoA increase results in more flow along the boundary layer by secondary and tertiary vortices, and a bigger trailing edge vortex at 29.8°and 31°.

Figure 17. Velocity contour superimposed with flow at different values of α: (a) reference aerofoil and (b) MLE aerofoil.
In the case of an MLE aerofoil, as seen in Fig. 17(b), the flow separation phenomenon is slow at low angles of attack, such as 25.5°, as the flow remains largely attached to the aerofoil. By increasing the angle-of-attack to 28.8°, the leading-edge suction increases, and the LEV moves towards the trailing edge. The LEV also increases its size at 28.8°. This leading-edge vortex shedding is intensified by the formation of a small secondary vortex, which grows and breaks apart the main LEV. From 29.8° to 31°, the DSV is formed, which moves towards the trailing edge and increases the pitching moment coefficient.
Large-scale vortical structures arise over the aerofoil in the separated zone during the up-stroke motion by causing a ripple in the surface pressure distribution at α = 25.5°, as seen in Fig. 18(a). Figure 18(b) shows the separated flow impact on the skin friction coefficient at x/c = 0.14 at α = 25.5°. The flow reattaches at x/c = 0.24, and it remains then in its attached state. The flow acceleration around the leading-edge increases as the aerofoil pitches up at α = 29.8°, resulting in a larger peak suction and a stronger adverse pressure gradient across the laminar separation bubble. As shown in Fig. 18(c), the pressure coefficient is higher than -10 at α = 29.8°, and the LEV formation can be clearly seen in the vicinity of the leading and trailing edges. The skin friction coefficients variations with the chord in Fig. 18(d) show that the flow separation is becoming bigger and is moving towards the trailing edge, accompanied by secondary and tertiary leading-edge vortices. The occurrence of the LEV is due to the increasing adverse pressure gradient, and then the dynamic stall vortex emerges and moves towards the trailing edge. As a result of the separation bubble occurrence, the skin friction coefficients show a large flow separation on the upper surface of the aerofoil. Figure 18(e) reveals that the negative pressure of the main vortex turns the flow from the pressure side of the aerofoil at the trailing edge towards the suction side by generating a counter-rotating trailing edge vortex. As depicted in Fig. 18(f), the leading-edge vortex continues to flow along the aerofoil surface by causing vortex shedding. Due to the shedding of the main leading-edge vortex, the lift coefficient begins to decrease.

Figure 18. Computed pressure and skin friction coefficients for a MLE aerofoil.
Figure 19 illustrates the reference and optimised MLE aerofoils’ vorticity contours during one pitching cycle. Figure 19(a) shows the boundary layer attached to a shear layer at an attack angle of 25.5°. As the oscillating aerofoil’s angle-of-attack increases, reversed flow circulates from the trailing edge towards the leading edge (α = 29.8°) as seen in Fig. 19(b). It shows a LEV that moves downstream along the aerofoil surface, and results in increased vorticity forces. The vorticity sheds away from the trailing edge at α = 30.8° shown in Fig. 19(c).

Figure 19. Comparison of vorticity contours of the reference aerofoil with an MLE aerofoil at different angles of attack.
Figure 19(d) shows the MLE aerofoil’s vorticity at an angle-of-attack of 25.5°. Figure 19(e) shows that the MLE aerofoils vorticity strength is less than the reference aerofoil at an angle-of-attack of 29.8°. At the same time, a strong TEV is produced during the stall at 30.8°: this vortex is quickly replaced by a secondary LEV that spans over the chord. Throughout the downstroke, alternating LEV and TEV creation and shedding causes force coefficient changes. The MLE aerofoil also stalls, but at a smaller AoA than the reference aerofoil.
Table 3 shows the maximum aerodynamic lift and drag coefficients, and their stall angle variations values of the reference aerofoil and of the MLE aerofoil. It is worth noting that the maximum lift coefficient increased by 22.08% and the maximum drag coefficient increased by 57.31% for the MLE aerofoil with respect to the to
![]() $\;{C_L}$
of the reference aerofoil. An increased delay in the stall angle-of-attack of 14.26% was achieved with the optimised MLE aerofoil. Moreover, incremental values of
$\;{C_L}$
of the reference aerofoil. An increased delay in the stall angle-of-attack of 14.26% was achieved with the optimised MLE aerofoil. Moreover, incremental values of
![]() $\Delta {C_{L,max}}$
and
$\Delta {C_{L,max}}$
and
![]() $\Delta {C_{D,max}}$
are provided for the MLE aerofoil with respect to the static aerofoil, in which the maximum lift coefficient of the MLE aerofoil increased by 47.82% with respect to the reference aerofoil maximum lift coefficient. The main objective of delaying the stall angle-of-attack was achieved, as it was delayed by 3.81° degrees.
$\Delta {C_{D,max}}$
are provided for the MLE aerofoil with respect to the static aerofoil, in which the maximum lift coefficient of the MLE aerofoil increased by 47.82% with respect to the reference aerofoil maximum lift coefficient. The main objective of delaying the stall angle-of-attack was achieved, as it was delayed by 3.81° degrees.
Table 3. Comparison of aerofoil performance parameters of the reference aerofoil with those of the MLE aerofoil

Note:
![]() ${C_{L,\;\;x}}$
= max dynamic lift coefficient;
${C_{L,\;\;x}}$
= max dynamic lift coefficient;
![]() ${C_{D,max}}\;$
= max drag coefficient;
${C_{D,max}}\;$
= max drag coefficient;
![]() ${\alpha _{ds}}$
= dynamic stall angle;
${\alpha _{ds}}$
= dynamic stall angle;
![]() $\Delta {C_{L,max}}$
= max lift difference from steady state results;
$\Delta {C_{L,max}}$
= max lift difference from steady state results;
![]() $\;\Delta {C_{D,max}}$
= max drag coefficient difference from steady state results.
$\;\Delta {C_{D,max}}$
= max drag coefficient difference from steady state results.
3.2.3. Effect of the MTE
Figures 20(a) and (b) illustrate the velocity contours with streamlines of an optimised MTE aerofoil compared to those of the reference aerofoil. Figure 20(a) depicts the flow development over the reference aerofoil for different angles of attack. At α = 25.5°, the flow remains attached to the aerofoil with a LEV. A small clockwise vortex can also be seen near the trailing edge. Subsequently, the secondary and tertiary LEVs are produced starting from the leading edge, and the primary vortex size increases significantly as the aerofoil pitches from 25.5° to 28.8°. The leading-edge suction results in the formation of a LEV at 28.8°. This leading-edge vortex shedding is exacerbated by a tiny vortex formed at the leading edge, which increases from α = 29.8° and breaks from the main LEV. The LEV continues to increase and to spread over the aerofoil, as seen at the AoA of 31°.

Figure 20. Velocity contour superimposed with flow at different values of AoA for the (a) reference aerofoil and (b) MTE aerofoil.
Figure 20(b) shows that the MTE aerofoil at 25.5° has a small trailing edge separation area. As the angle-of-attack increases to 28.8°, the LEV increases and advances towards the trailing edge. Due to the growing pressure gradient at α = 29.8°, the LEV bursts. It is evident that the trailing edge has resulted in an earlier stall formation than that of the reference aerofoil.
Figure 21 shows how a complete cycle of angles of attack impacts the aerodynamic coefficients of aerofoils equipped with a morphing trailing edge compared to the aerodynamic coefficients of the reference aerofoil. In Figure 21(a), the
![]() ${C_{L,max}}\;$
value increases from 2.49 to 2.67, while the morphing aerofoil shows
${C_{L,max}}\;$
value increases from 2.49 to 2.67, while the morphing aerofoil shows
![]() ${C_L}$
increase throughout the full angle-of-attack cycle with respect to the reference aerofoil. However, the stall angle-of-attack of MTE aerofoil is slightly lower than that of the reference aerofoil by 0.86°. The morphing aerofoil has a lift drop similar to that of the reference aerofoil during the downstroke, as expected. Figure 21(b) and (c) display the coefficients of drag and moment, respectively, of the two aerofoils. Both
${C_L}$
increase throughout the full angle-of-attack cycle with respect to the reference aerofoil. However, the stall angle-of-attack of MTE aerofoil is slightly lower than that of the reference aerofoil by 0.86°. The morphing aerofoil has a lift drop similar to that of the reference aerofoil during the downstroke, as expected. Figure 21(b) and (c) display the coefficients of drag and moment, respectively, of the two aerofoils. Both
![]() ${C_{D,max}}\;$
and
${C_{D,max}}\;$
and
![]() ${C_{M,max}}\;$
of the morphing aerofoil are higher than those of the reference aerofoil, with a maximum
${C_{M,max}}\;$
of the morphing aerofoil are higher than those of the reference aerofoil, with a maximum
![]() ${C_D}\;$
increase of 5.42%.
${C_D}\;$
increase of 5.42%.

Figure 21. Aerodynamic coefficient hysteresis loops at k = 0.08: (a) lift coefficient, (b) drag coefficient; (c) pitching moment coefficient.
Figure 22(a) shows the pressure coefficient variations with the chord position
![]() $\frac{x}{c}$
at the angle-of-attack of 25.5°, with only very large scale vortical structures growing over the aerofoil during up-stroke motion. This phenomenon results in smooth surface pressure contours. Figure 22(b) shows the occurrence of the separated flow on the skin friction coefficient at
$\frac{x}{c}$
at the angle-of-attack of 25.5°, with only very large scale vortical structures growing over the aerofoil during up-stroke motion. This phenomenon results in smooth surface pressure contours. Figure 22(b) shows the occurrence of the separated flow on the skin friction coefficient at
![]() $\frac{x}{c} = 0.8$
for an angle-of-attack of 25.5°. When the angle-of-attack further increases to 29.8° (Fig. 22(c)), there is an increase in the leading-edge flow acceleration, resulting in a larger unfavourable pressure gradient, and resulting in a stall. Figure 22(c) shows the pressure coefficient at 29.8°, thus indicating that the pressure coefficient has a smaller value than
$\frac{x}{c} = 0.8$
for an angle-of-attack of 25.5°. When the angle-of-attack further increases to 29.8° (Fig. 22(c)), there is an increase in the leading-edge flow acceleration, resulting in a larger unfavourable pressure gradient, and resulting in a stall. Figure 22(c) shows the pressure coefficient at 29.8°, thus indicating that the pressure coefficient has a smaller value than
![]() $ - 4\;,\;$
and it clearly indicates that the LEV is at x/c = 0.6. Flow separation inflates and moves towards the trailing edge with many secondary and tertiary leading-edge vortices (see Figure 22(d)), and the bubble breaks down due to the increased adverse pressure gradient. The dynamic stall vortex is formed while moving towards the trailing edge. A significant separation of the skin friction coefficient is caused by the stall occurrence. The flow from the aerofoil’s pressure side has a motion towards the suction side near the trailing edge, due to the negative pressure of the vortex causing a counter-rotating trailing edge vortex, as shown in Fig. 22(e) for the angle-of-attack of 30°. Figure 22(f) shows vortex shedding as the leading-edge vortex moves over the aerofoil surface. The leading-edge vortex dissipation causes a lift coefficient decrease.
$ - 4\;,\;$
and it clearly indicates that the LEV is at x/c = 0.6. Flow separation inflates and moves towards the trailing edge with many secondary and tertiary leading-edge vortices (see Figure 22(d)), and the bubble breaks down due to the increased adverse pressure gradient. The dynamic stall vortex is formed while moving towards the trailing edge. A significant separation of the skin friction coefficient is caused by the stall occurrence. The flow from the aerofoil’s pressure side has a motion towards the suction side near the trailing edge, due to the negative pressure of the vortex causing a counter-rotating trailing edge vortex, as shown in Fig. 22(e) for the angle-of-attack of 30°. Figure 22(f) shows vortex shedding as the leading-edge vortex moves over the aerofoil surface. The leading-edge vortex dissipation causes a lift coefficient decrease.

Figure 22. Computed pressure coefficient and skin friction coefficient for the MTE aerofoil.
Figure 23 shows the vorticity contours at different angles of attack during a pitching cycle for both the reference and the MTE aerofoils. Figure 23(a) and (d) reveal that the boundary layer separation takes place, and that the separation is more deepened for the MTE aerofoil. The flow remains attached to the rest of the aerofoil at angle-of-attack of 25.5°. When the angle-of-attack increases while the aerofoil oscillates, a more reversed flow area occurs in the MTE aerofoil than the reference aerofoil, moving from the trailing edge towards the leading edge as visualised at
![]() $\alpha = 29.8^\circ $
.
$\alpha = 29.8^\circ $
.

Figure 23. Comparison of vorticity contours of the reference aerofoil with those of the MTE aerofoil at different angles of attack.
LEVs containing significant energy are created, and they migrate downstream on the aerofoil surface, as seen in Fig. 23(b), thus resulting in strong integral forces. These vortices structures are characterised by a stronger force coefficient curve slope, as displayed earlier in Fig. 13.
The MTE aerofoil also results in a much stronger vortex, as shown in Fig. 23(e), while a weaker TEV is produced at the critical angle-of-attack of 30.8° on the reference aerofoil, as shown in Fig. 23(c). This TEV dissipates downstream where it is replaced by a secondary LEV, which spreads over most of the aerofoil’s chord span. Both LEVs and TEVs form and shed during the downstroke, causing significant force coefficient fluctuations. Using an MTE, the aerofoil fully stalled and with a higher strength than the one observed in the reference aerofoil.
Table 4 presents the aerodynamic coefficients and stall characteristics of the reference aerofoil and the MTE aerofoil. The stall angle-of-attack was increased by1° for the MTE aerofoil with respect to that of the reference aerofoil. The maximum lift coefficient increased slightly by a maximum of 6.8%, and the maximum drag coefficient by 8.5%. The other results followed a similar trend, including the increase in maximum lift coefficient values of a pitching aerofoil compared to a static aerofoil.
Table 4. Comparison of aerofoil performance parameters of the reference aerofoil with the MTE aerofoil

Note:
![]() ${C_{L,\;\;max}}$
= max dynamic lift coefficient;
${C_{L,\;\;max}}$
= max dynamic lift coefficient;
![]() ${C_{D,max}}\;$
= max drag coefficient;
${C_{D,max}}\;$
= max drag coefficient;
![]() ${\alpha _{ds}}$
= dynamic stall angle;
${\alpha _{ds}}$
= dynamic stall angle;
![]() $\Delta {C_{L,max}}$
= max lift difference from steady state results;
$\Delta {C_{L,max}}$
= max lift difference from steady state results;
![]() $\;\Delta {C_{D,max}}$
= max drag coefficient difference from steady state results.
$\;\Delta {C_{D,max}}$
= max drag coefficient difference from steady state results.
4.0 Conclusion
This paper investigated the effect of the optimised MLE and MTE on the DSV around a pitching aerofoil through numerical simulations. Firstly, the optimisation of the UAS-S45 aerofoil was performed using a morphing optimisation framework. This framework used Bezier-PARSEC parametrisation and the PSO coupled with the PS algorithm with the aim of designing an aerodynamically efficient S-45 aerofoil. The
![]() $\gamma - R{e_\theta }$
transition turbulence model was applied to predict the laminar-turbulent flow transition region. Secondly, the study presented the unsteady analysis of the UAS-S45 aerofoil and its morphing configurations. Finally, the unsteady flow field and the aerodynamic forces were analysed at the Reynolds number of 2.4 × 106, and five different reduced frequencies. The lift (
$\gamma - R{e_\theta }$
transition turbulence model was applied to predict the laminar-turbulent flow transition region. Secondly, the study presented the unsteady analysis of the UAS-S45 aerofoil and its morphing configurations. Finally, the unsteady flow field and the aerodynamic forces were analysed at the Reynolds number of 2.4 × 106, and five different reduced frequencies. The lift (
![]() ${C_L})$
, drag (
${C_L})$
, drag (
![]() ${C_D})$
and moment (
${C_D})$
and moment (
![]() ${C_M})\;$
coefficients of the reference and the morphing aerofoils were compared. Based on this study, the following conclusions were drawn:
${C_M})\;$
coefficients of the reference and the morphing aerofoils were compared. Based on this study, the following conclusions were drawn:
The morphing aerofoils improved the overall aerodynamic performance and delayed the boundary layer separation. The lift coefficients of the MLE aerofoil compared to those of the reference aerofoil have higher values, increasing from 1.57 to 1.65, which represented a 5.09% gain, while the static angle-of-attack increased, by 3°. An increase of 3.8% in the maximum
![]() $\frac{{{C_L}}}{{{C_D}}}\;$
was obtained for an MLE aerofoil compared to the reference aerofoil.
$\frac{{{C_L}}}{{{C_D}}}\;$
was obtained for an MLE aerofoil compared to the reference aerofoil.
The optimal shapes of MTE aerofoil produced an increase of the lift coefficient with respect to the reference aerofoil of up to almost 8.6%. In addition, an increase of 2° in the static stall angle was obtained for the MTE aerofoil.
The effect of the reduced frequency on the unsteady pitching motion was investigated by plotting the
 ${C_l}\;$
versus the angle-of-attack for several reduced frequencies of k = 0.05, 0.08, 0.12, 0.16 and 0.20 at Re = 2.4 × 106. The
${C_l}\;$
versus the angle-of-attack for several reduced frequencies of k = 0.05, 0.08, 0.12, 0.16 and 0.20 at Re = 2.4 × 106. The
 ${C_{L,max}}$
increased with reduced frequency, from
${C_{L,max}}$
increased with reduced frequency, from
 ${C_{L,max}}$
= 2.43 at k = 0.05 to
${C_{L,max}}$
= 2.43 at k = 0.05 to
 ${C_{L,max}}$
= 2.64 at k = 0.12.
${C_{L,max}}$
= 2.64 at k = 0.12.The results showed a similar pattern for the drag coefficients values; however, ‘k’ had a mixed effect on the maximum drag coefficients (
 ${C_{D,max}})$
.
${C_{D,max}})$
.
 ${C_{D,max}}$
changed from 1.17 at k = 0.05 to 1.45 at k = 0.2 and from
${C_{D,max}}$
changed from 1.17 at k = 0.05 to 1.45 at k = 0.2 and from
 ${C_{D,max}}$
of 1.29 at k = 0.08 to 1.44 at k = 0.16 as ‘k’ increased. On the downstroke, numerous sorts of vortices were formed near the trailing edge. From the time of their separation and shedding into the downstream wake, these vortices increased the lift force.
${C_{D,max}}$
of 1.29 at k = 0.08 to 1.44 at k = 0.16 as ‘k’ increased. On the downstroke, numerous sorts of vortices were formed near the trailing edge. From the time of their separation and shedding into the downstream wake, these vortices increased the lift force.It was found that higher reduced frequency stabilised the LEV that provided its lift by reducing lift variation during the dynamic stall phase. High-reduced frequency LEV stabilised the flow even when the aerofoil was in the downstroke. The
 ${C_{L,max}}$
,
${C_{L,max}}$
,
 ${C_{D,max}}\;$
and stall angles of attack were calculated for all reduced frequencies.
${C_{D,max}}\;$
and stall angles of attack were calculated for all reduced frequencies.The numerical results have shown that the new radius of curvature of the MLE aerofoil can minimise the streamwise adverse pressure gradient and prevent significant flow separation by delaying the DSV occurrence. Furthermore, it was shown that the morphing aerofoil delayed the stall angle-of-attack with respect to the stall of the reference aerofoil by 14.26 %, and
 ${C_{L,max}}\;$
of the aerofoil increased from 2.49 to 3.04.
${C_{L,max}}\;$
of the aerofoil increased from 2.49 to 3.04.However, while the MTE aerofoil was found to increase the overall lift coefficient and the
 ${C_{l,max}}$
, it did not affect the dynamic stall. Vorticity behaviour during DSV generation and separation has shown that the MTE can change vortices’ evolution and increase vorticity strength from the leading-edge shear layer by increasing DSV flow.
${C_{l,max}}$
, it did not affect the dynamic stall. Vorticity behaviour during DSV generation and separation has shown that the MTE can change vortices’ evolution and increase vorticity strength from the leading-edge shear layer by increasing DSV flow.
To cause the wing to create the desired elastic deformation and to control the aircraft’s stall, it depends on the smooth deflection of leading anad trailing edge control surfaces. However, according to the analysis of the flexible wing’s aerodynamic properties, the control efficiency of the wings’ leading and trailing edges becomes complex as the speed increases. The resultant aerodynamic forces increase non-linearly with the control deflection. Therefore, it is significant to employ the appropriate control approach due to the control reverse effect phenomena brought on by the wing’s flexibility.
A control allocation technique should be proposed to solve the leading and trailing edges multi-control surfaces deflection problem, specifying maximisation of the control effectiveness of the control surfaces. Several actuation mechanisms, such as smart material-based shape-memory alloy actuators or electromechanical actuator systems, can be implemented into the wing.
Additionally, Finite Element Analysis (FEA) should be performed to evaluate the structural advantages that actuation could provide, such as the ability to control the spanwise load. The requirements for more degrees of freedom, smooth transition with resonance frequencies, mode shapes, modal damping, etc., will provide detailed results for selecting proper actuation mechanisms.
Regarding future works, the LARCASE’s Price-Padoussis subsonic wind tunnel will be used for wind tunnel studies of the MLE and MTE aerofoils. The findings are expected to clarify the flow physics and validate the results of the morphing aerofoil flow phenomena. In addition, we will use an optimised mathematical model that can govern the pitching motion (reduced frequency) along with the aerofoil deflection (deflection frequency) and the morphing starting time.
Acknowledgments
Special thanks are dues to the Natural Sciences and Engineering Research Council of Canada (NSERC) for the Canada Research Chair Tier 1 in Aircraft Modelling and Simulation Technologies grant. We would also like to thank Mrs. Odette Lacasse for her support at the ETS, as well as Hydra Technologies’ team members Mr. Carlos Ruiz, Mr. Eduardo Yakin and Mr. Alvaro Gutierrez Prado in Mexico. We would like to thank the NSERC and Prof. Jeremy Laliberte for their support within the CREATE-UTILI program.