1. INTRODUCTION
The use of the measurements from Global Positioning System (GPS) receivers and Inertial Navigation Systems (INS) provides a complementary method to absorb their advantages while overcoming their individual drawbacks (Hasan et al., Reference Hasan, Samsudin, Ramli, Azmir and Ismaeel2009). Hence, this arrangement is often the core of a modern multi-sensor integrated navigation system. A Kalman Filter (KF) is the most commonly used technique for the fusion of different types of measurements. In a GPS/INS integrated navigation system, the KF performs measurement updates by using the GPS observations. The low sampling rate of GPS receivers decreases the observability of the system state vector (Hong et al., Reference Hong, Lee, Chun, Kwon and Speyer2005) and has a negative impact on the navigation accuracy between two GPS epochs. Specifically, the Micro-Electromechanical Sensor (MEMS) Inertial Measurement Unit (IMU) endows large bias errors and poor stability. Its position error can reach metre level in one second navigation time (Brown and Lu, Reference Brown and Lu2004). A GPS receiver with high sampling rate may correct the MEMS-IMU errors in time and guarantee navigation accuracy. However, it will increase the cost of an integrated navigation system.
For the processing of a GPS-aided INS, many enhancement methods have been proposed to increase navigation accuracy and system stability. GPS/INS integrated navigation systems with other aiding sensors such as odometer, magnetometer and so on (Seo et al., Reference Seo, Lee, Lee and Park2006) can improve the observability of the state vector. Some constraints based on the vehicle's movement and environmental conditions can also be applied as additional observations, which are able to improve navigation precision when GPS partial outages are encountered (Chai et al., Reference Chai, Yang, Wang, Zhong, Ou and Yuan2011). In the odometer-aided inertial navigation system (Yan, Reference Yan2006), the horizontal position offset can be less than 25 m in 50 km or 50 min trajectory with the position fixes. The fusion of GPS-aided INS with a magnetometer can prevent the filter from diverging during GPS outages and ensure accurate attitude information (Wang and Zhang, Reference Wang and Zhang2006). Because more sensors are utilised in the integrated system, more filters were proposed. The performance of the two-dimensional (2-D) navigation solution by integrating a GPS receiver, a MEMS gyroscope and an odometer using a mixture particle filter once with the parallel cascade identification model and once with the autoregressive stochastic model was tested in a land vehicle (Georgy et al., Reference Georgy, Noureldin, Korenberg and Bayoumi2010). Under some specific kinematic conditions, part of the state variables were able to be satisfied with some specific constraints, which are the basis to construct certain virtual measurements and were often used during GPS outages (Godha and Cannon, Reference Godha and Cannon2007). The relevant research work focused on adding the virtual observation by minimising the physical property of the vehicle's motion, which can provide equivalent external velocity measurements to correct the navigation solution (Bloch et al., Reference Bloch, Reyhanoglu and McClamroch1992). However, it aimed at improving the accuracy of few state variables and was not able to increase the observability of the whole navigation system (Dissanayake et al., Reference Dissanayake, Sukkarieh, Nebot and Durrant2001). At the same time, more sensors may increase the filter complexity and decrease the system filter stability.
In order to improve the observability of the state vector and not increase the navigation system complexity, the GPS observation expansion method is proposed in this paper and applied in GPS/INS integrated navigation. The GPS observation expansion method is mainly suitable for urban land vehicles. The urban land vehicle will often be driving at low speeds. If there is traffic, the vehicle will be in one place for an extended period of time. In general, the sample frequency of INS is much higher than GPS. The sample period of INS and GPS are 0·01 s and 1 s in this paper, respectively. The INS navigation result will be updated by GPS information at the time of T. If the vehicle is at low speed or stays in one place, the INS self-navigation result of the next sample period should also be updated by the GPS information at the time of T. In theory, the INS self-navigation result of every sample period should be updated by the GPS information at the time of T until the next epoch GPS information is obtained. The INS resolution is updated by the same GPS information repeatedly during the process of observation expansion, when the vehicle is driving at low speed or stationary.
The observations of various sensors have different errors and data features and the outlier exists in observation during filtering. So the adaptive filter is often applied to resist the influence of disturbance and improve the accuracy of model parameters (Wu et al., Reference Wu, Yang and Zhang2012). It is important to construct an appropriate adaptive factor in an adaptive filter. In GPS-aided inertial integrated navigation, the adaptive factor was typically the function of the state discrepancies and the predicted residuals (Wu and Yang, Reference Wu and Yang2010). Meanwhile, the adaptive Kalman filtering by using the residual sequences to adapt the stochastic properties of the filter (Hide et al., Reference Hide, Moore and Smith2003) and two-step adaptive robust Kalman filtering (Wu et al., Reference Wu, Yang and Zhang2012) were proposed, which was able to prevent the filter diverging. Because the observations from other sensors or virtual measurements are less accurate than the GPS measurements, the adaptive factor should be constructed based on the less accurate information.
The proposed GPS observation expansion will improve the system observability but it will also increase the data uncertainty. So the uncertainty is the key of GPS observation expansion. The information entropy is introduced to describe the uncertainty of GPS observation expansion quantitatively. A new adaptive filter method is constructed based on the uncertainty information in the paper. The proposed filter method is to control the uncertainty introduced by the GPS observation expansion. Following this introduction, GPS/INS loosely coupled navigation integration is reviewed in Section 2. Section 3 describes the principle and method of the GPS observation expansion. The proposed adaptive filter method with GPS observation expansion is shown in Section 4. Section 5 reveals the land vehicle test and result analysis and conclusions are given in the last section.
2. GPS/INS LOOSELY COUPLED INTEGRATION
2.1. Dynamics Model
The system error dynamic model of integrated navigation used in the Kalman filter is designed based on the INS error equations. The insignificant terms are neglected in the process of linearization (Titterton and Weston, Reference Titterton and Weston2004). The psi-angle error equations of INS are as follows (Li et al., Reference Li, Wang, Li, Gao and Tan2014):
where
![]() $\delta {\bf r}$
,
$\delta {\bf r}$
,
![]() $\delta {\bf v}$
and
$\delta {\bf v}$
and
![]() $\delta {\bf \psi} $
are the position, velocity and orientation error vectors, respectively.
$\delta {\bf \psi} $
are the position, velocity and orientation error vectors, respectively.
![]() ${{\bf \omega} _{{\rm en}}}$
is the rate of navigation frame with respect to Earth, and
${{\bf \omega} _{{\rm en}}}$
is the rate of navigation frame with respect to Earth, and
![]() ${{\bf \omega} _{{\rm ie}}}$
is the rate of Earth with respect to inertial frame. The system error dynamics of GPS/INS integration are obtained by expanding the accelerometer bias error vector
${{\bf \omega} _{{\rm ie}}}$
is the rate of Earth with respect to inertial frame. The system error dynamics of GPS/INS integration are obtained by expanding the accelerometer bias error vector
![]() ${\bf \eta} $
and the gyro drift error vector
${\bf \eta} $
and the gyro drift error vector
![]() ${\bf \varepsilon} $
.
${\bf \varepsilon} $
.
The accelerometer bias error vector
![]() ${\bf \eta} $
and the gyro drift error vector
${\bf \eta} $
and the gyro drift error vector
![]() ${\bf \varepsilon} $
are regarded as the random walk process vectors, which are modelled as follows (Wang et al., Reference Wang, Lee, Hewitson and Lee2003):
${\bf \varepsilon} $
are regarded as the random walk process vectors, which are modelled as follows (Wang et al., Reference Wang, Lee, Hewitson and Lee2003):
where
![]() ${{\bf u}_{\rm \eta}} $
and
${{\bf u}_{\rm \eta}} $
and
![]() ${{\bf u}_{\rm \varepsilon}} $
are white Gaussian noise vectors.
${{\bf u}_{\rm \varepsilon}} $
are white Gaussian noise vectors.
Combining Equations (1) to (5), the system dynamical model becomes:
 $$\left\{ {\matrix{ {\delta {\dot {\bf r}} = - {{\bf \omega} _{{\rm en}}} \times \delta {\bf r} + \delta {\bf v}} \hfill \cr {\delta {\dot {\bf v}} = - ({{\bf \omega} _{{\rm ie}}} + {{\bf \omega} _{{\rm in}}}) \times \delta {\bf v} - \delta {\bf \psi} \times {\bf f} + {\bf \eta}} \hfill \cr {\delta {\dot {\bf \psi}} = - {{\bf \omega} _{{\rm in}}} \times \delta {\bf \psi} + {\bf \varepsilon}} \hfill \cr {{\bf \eta} = {{\bf u}_{\rm \eta}}} \hfill \cr {{\bf \varepsilon} = {{\bf u}_{\rm \varepsilon}}} \hfill \cr}} \right.$$
$$\left\{ {\matrix{ {\delta {\dot {\bf r}} = - {{\bf \omega} _{{\rm en}}} \times \delta {\bf r} + \delta {\bf v}} \hfill \cr {\delta {\dot {\bf v}} = - ({{\bf \omega} _{{\rm ie}}} + {{\bf \omega} _{{\rm in}}}) \times \delta {\bf v} - \delta {\bf \psi} \times {\bf f} + {\bf \eta}} \hfill \cr {\delta {\dot {\bf \psi}} = - {{\bf \omega} _{{\rm in}}} \times \delta {\bf \psi} + {\bf \varepsilon}} \hfill \cr {{\bf \eta} = {{\bf u}_{\rm \eta}}} \hfill \cr {{\bf \varepsilon} = {{\bf u}_{\rm \varepsilon}}} \hfill \cr}} \right.$$
which can be generalized in matrix and vector form:
where X is the error state vector,
![]() ${\bf \Phi} $
is the system transition matrix, and u is the process noise vector.
${\bf \Phi} $
is the system transition matrix, and u is the process noise vector.
2.2. Observation Model
The observation model in GPS/INS integrated navigation is composed of the position and velocity difference vector between the GPS solutions and the INS computation value (Titterton and Weston, Reference Titterton and Weston2004):
 $$\eqalign{&{Z_{\rm r}}(t) = {r_{{\rm GPS}}}(t) - {r_{{\rm INS}}}(t) \cr & \qquad = {r_{{\rm GPS}}}(t) - \left( {{r_{{\rm INS}}}(t - \Delta t) + {v_{{\rm INS}}}(t - \Delta t) \cdot \Delta t + \displaystyle{1 \over 2}\alpha (t) \cdot \Delta {t^2}} \right)} $$
$$\eqalign{&{Z_{\rm r}}(t) = {r_{{\rm GPS}}}(t) - {r_{{\rm INS}}}(t) \cr & \qquad = {r_{{\rm GPS}}}(t) - \left( {{r_{{\rm INS}}}(t - \Delta t) + {v_{{\rm INS}}}(t - \Delta t) \cdot \Delta t + \displaystyle{1 \over 2}\alpha (t) \cdot \Delta {t^2}} \right)} $$
where Z r(t) is the position error measurement vector at t time, Z v(t) is the velocity error measurement vector, r GPS(t) is the GPS position vector, r INS(t) is the INS position vector, v GPS(t) is the GPS velocity vector, v INS(t) is the INS velocity vector, α(t) is the acceleration vector determined by the INS alone and Δt is the sample time of INS.
The generic measurement equation system of the Kalman filter can be written as:
where
![]() ${{\bf B}_{\rm k}}$
is the observation matrix, and τ is the measurement noise vector, assumed to be white Gaussian noise.
${{\bf B}_{\rm k}}$
is the observation matrix, and τ is the measurement noise vector, assumed to be white Gaussian noise.
3. GPS OBSERVATION EXPANSION
In order to increase the observability of state vector X, the GPS observation expansion method is proposed. Suppose that the data sampling rate of GPS and INS are 1 Hz and 100 Hz, respectively, in a GPS/INS integrated navigation system and the system acquires the GPS observation (x T, y T) at a time instant T. Accordingly, a filter update of the integrated system can be performed using the current GPS observation (x T, y T). At the times of T + 0·01 s,T + 0·02 s…T + 0·99 s, position information can be accumulated by INS alone without real-time GPS correction. If the vehicle is at a low speed of less than 20 km/h, from T to T + 0·01 s, the travelling distance of the vehicle is 0·055 m, which is much smaller than the GPS single point position error. The position of vehicle at T + 0·01 s is close to the position at T. Therefore, we can try to filter and update the INS state variables at T + 0·01 s using the GPS observation values (x T, y T), which realizes the GPS observation expansion. In the observation expansion, the GPS observation values (x T, y T) are regarded as the input of the observation model of filter at the time of T + 0·01 s.
From the perspective of error ellipse, the Probability Density Function (PDF) of GPS observation can be written as (Wolf and Ghilani, Reference Wolf and Ghilani1997):
 $$\eqalign{f\,(x,y) & = \displaystyle{1 \over {2{\rm \pi} {\sigma _{\rm x}}{\sigma _{\rm y}}\sqrt {1 - {\rho ^2}}}} \cr & \quad \cdot \exp \left\{ {\displaystyle{{ - 1} \over {2(1 - {\rho ^2})}}\left[ {\displaystyle{{{{(x - {u_{\rm x}})}^2}} \over {\sigma _{\rm x}^2}} - 2\rho \displaystyle{{x - {u_{\rm x}}} \over {{\sigma _{\rm x}}}} \cdot \displaystyle{{y - {u_{\rm y}}} \over {{\sigma _{\rm y}}}} + \displaystyle{{{{(y - {u_{\rm y}})}^2}} \over {\sigma _{\rm y}^{\rm 2}}}} \right]} \right\}}$$
$$\eqalign{f\,(x,y) & = \displaystyle{1 \over {2{\rm \pi} {\sigma _{\rm x}}{\sigma _{\rm y}}\sqrt {1 - {\rho ^2}}}} \cr & \quad \cdot \exp \left\{ {\displaystyle{{ - 1} \over {2(1 - {\rho ^2})}}\left[ {\displaystyle{{{{(x - {u_{\rm x}})}^2}} \over {\sigma _{\rm x}^2}} - 2\rho \displaystyle{{x - {u_{\rm x}}} \over {{\sigma _{\rm x}}}} \cdot \displaystyle{{y - {u_{\rm y}}} \over {{\sigma _{\rm y}}}} + \displaystyle{{{{(y - {u_{\rm y}})}^2}} \over {\sigma _{\rm y}^{\rm 2}}}} \right]} \right\}}$$
In which u x and u y are the mathematical expectation of position in X and Y direction respectively and ρ is the correlation coefficient, which is computed:
in which σ x and σ y are the mean square error of position in the X and Y direction, respectively and σ xy is the covariance between σ x and σ y.
The mean square errors of GPS position can be assumed to be spatially homogeneous, denoted by σ. According to current studies, the errors of GPS observation in the X and Y directions do not have a significant correlation (Li et al., Reference Li, Shen and Xu2008). So the value of σ xy can be regarded as zero. At the time of T, with the mathematical expectation of the position (x T, y T), the PDF of GPS position solution can be simplified to:
 $$f\,(x,y) = \displaystyle{1 \over {2\pi {\sigma ^2}}} \cdot \exp \left\{ { - \displaystyle{1 \over 2}\left[ {\displaystyle{{{{(x - {x_{\rm T}})}^2} + {{(y - {y_{\rm T}})}^2}} \over {{\sigma ^2}}}} \right]} \right\}$$
$$f\,(x,y) = \displaystyle{1 \over {2\pi {\sigma ^2}}} \cdot \exp \left\{ { - \displaystyle{1 \over 2}\left[ {\displaystyle{{{{(x - {x_{\rm T}})}^2} + {{(y - {y_{\rm T}})}^2}} \over {{\sigma ^2}}}} \right]} \right\}$$
Under the consideration of only the horizontal GPS position, the longer the distance between the current point and its mathematical expectation is, the smaller the PDF is. Regarding the distance as an independent variable, the PDF of horizontal GPS position is a descent function. Under the conditions that x = x T and y = y T, the PDF is:
At the time of T + 0·01 s, the vehicle travels 0·055 m. If the value (x T , y T) is regarded as the mathematical expectation at T + 0·01 s, which indicates that the GPS observation (x T , y T) is regarded as input of observation model of filter at T + 0·01 s, the PDF of T + 0·01 s can be computed:
 $${\,f_{{\rm T} + 0.01{\rm s}}} = \displaystyle{1 \over {2\pi {\sigma ^2}}} \cdot \exp \left( { - \displaystyle{{{{0.055}^2}} \over {2{\sigma ^2}}}} \right)$$
$${\,f_{{\rm T} + 0.01{\rm s}}} = \displaystyle{1 \over {2\pi {\sigma ^2}}} \cdot \exp \left( { - \displaystyle{{{{0.055}^2}} \over {2{\sigma ^2}}}} \right)$$
By comparing f T with f T+0.01s, one obtains the ratio q:
 $$q = \displaystyle{{{\,f_{{\rm T} + 0.01{\rm s}}}} \over {{\,f_{\rm T}}}} = \exp \left( { - \displaystyle{{{{0.055}^2}} \over {2{\sigma ^2}}}} \right)$$
$$q = \displaystyle{{{\,f_{{\rm T} + 0.01{\rm s}}}} \over {{\,f_{\rm T}}}} = \exp \left( { - \displaystyle{{{{0.055}^2}} \over {2{\sigma ^2}}}} \right)$$
In GPS/INS integrated navigation, the mean square error of GPS position obtained by single point positioning is more than 1 m. So the ratio q is larger than 0·998. This means that the value f T+0.01s is close to f T. The probability of the single point (x T, y T) in a small integration area around the time T is similar to that around the time T + 0·01 s. When the position information (x T, y T) is as the Kalman filter input at T and T + 0·01 s, the reliability is about the same. So the method using the GPS position information (x T, y T) to filter and update the states at time T + 0·01 s, T + 0·02 s, … is feasible. The block diagram of GPS observation expansion is presented in Figure 1.

Figure 1. The GPS observation expansion.
It can be seen that the principle of the proposed GPS observation expansion is similar to the principle of the Zero Velocity Update (ZUPT) algorithm. The two methods are used to provide additional observation information according the moving condition of a vehicle. In the ZUPT method, the zero velocity point is employed to update the state parameters in the Kalman filter when the vehicle is identified to be motionless. In the proposed GPS observation expansion method, the position information is employed to update the state parameters in the Kalman filter when the vehicle is identified to be only slowly moving. When the vehicle is motionless, the GPS observation expansion method will also be employed in the filter update. From this perspective, the GPS observation expansion algorithm is an extension of the ZUPT method. A comparison between ZUPT and GPS observation expansion is shown in Table 1. Compared with the ZUPT algorithm, the proposed method is applicable in more situations. Nevertheless, the reliability of the new method is reduced because the judgment condition is slow moving, not motionless as in the ZUPT algorithm. The difference between the position used in the filter update and the real position after a small movement will cause systematic errors in the GPS observation expansion method. Therefore an adaptive Kalman filter based on the uncertainty principle is proposed and employed in the GPS observation expansion to control the influence of systematic errors.
Table 1. Comparison between ZUPT and GPS observation expansion.

4. ADAPTIVE KALMAN FILTER WITH GPS OBSERVATION EXPANSION
4.1. Kalman Filter in GPS/INS Integrated Navigation
The Kalman filter is the most common method to realise the data fusion of different sensors. The optimal estimates of the state vector from the Kalman filter can be reached through a time update and a measurement update at a time instant:
where
![]() ${{\bf G}_{\rm k}}$
is the gain matrix of Kalman filter at time k,
${{\bf G}_{\rm k}}$
is the gain matrix of Kalman filter at time k,
![]() ${{\bf P}_{\rm k}}$
is the covariance matrix of state vector at time k,
${{\bf P}_{\rm k}}$
is the covariance matrix of state vector at time k,
![]() ${{\bf R}_{\rm k}}$
is the covariance matrix of measurement noise vector at time k,
${{\bf R}_{\rm k}}$
is the covariance matrix of measurement noise vector at time k,
![]() ${{\bf Q}_{\rm k}}$
is the covariance matrix of process noise at time k, and the subscript k,k-1 represents the state and covariance estimates forward from time k-1 to time k.
${{\bf Q}_{\rm k}}$
is the covariance matrix of process noise at time k, and the subscript k,k-1 represents the state and covariance estimates forward from time k-1 to time k.
In a closed loop integration scheme, a feedback loop is used for correcting the systematic errors. In this way, the mechanisation performs a simple navigation calculation under the assumption of small errors. In this case, the error states will be reset to zero after every measurement update (Godha, Reference Godha2006). Thus, the navigation resolution is expressed by:
4.2. Uncertainty of GPS Observation Expansion
GPS observation expansion is able to increase the filter frequency, while it brings the data uncertainty to the GPS/INS integrated navigation. To control the uncertainty of GPS observation expansion, it should be described quantitatively. Although it is feasible to apply the GPS position information (x T , y T) to filter and update the states at time T + 0·01 s, T + 0·02 s, the PDF at the time T + 0·01 s, T + 0·02 s … is decreasing with respect to the PDF at time T. This indicates that the uncertainty of the expanded GPS observation of T + 0·01 s, T + 0·02 s, … increases. The uncertainty growth of the GPS positions will decrease the filter accuracy. In order to know the depth of uncertainty well, the information entropy can be used to describe the uncertainty of the expanded GPS observation.
The information entropy is used to measure how much information is in an event. The larger uncertainty a variable has, the more complex information it will contain, or it will have a larger information entropy. The information entropy can be defined as (Xu et al., Reference Xu, Ma and Su2011):
From Equations (13) and (23), the information entropy of GPS position observation is
 $$H = \left( {\ln \displaystyle{1 \over {2\pi {\sigma ^2}}} - \displaystyle{{{r^2}} \over {2{\sigma ^2}}} - 1} \right) \cdot {e^{\textstyle{{{r^2}} \over {2{\sigma ^2}}}}} - \ln \displaystyle{1 \over {2\pi {\sigma ^2}}} + 1$$
$$H = \left( {\ln \displaystyle{1 \over {2\pi {\sigma ^2}}} - \displaystyle{{{r^2}} \over {2{\sigma ^2}}} - 1} \right) \cdot {e^{\textstyle{{{r^2}} \over {2{\sigma ^2}}}}} - \ln \displaystyle{1 \over {2\pi {\sigma ^2}}} + 1$$
where
![]() $r = \sqrt {{{\left( {x - {x_{\rm T}}} \right)}^2} + {{\left( {y - {y_{\rm T}}} \right)}^2}} $
is the distance between the current position (x, y) and its mathematical expectation (x
T , y
T).
$r = \sqrt {{{\left( {x - {x_{\rm T}}} \right)}^2} + {{\left( {y - {y_{\rm T}}} \right)}^2}} $
is the distance between the current position (x, y) and its mathematical expectation (x
T , y
T).
The derivative of Equation (24) is given by
 $$H^{\prime} = - \displaystyle{r \over {{\sigma ^2}}} \cdot {e^{\textstyle{{{r^2}} \over {2{\sigma ^2}}}}}\left( {\ln \displaystyle{1 \over {2{\rm \pi} {\sigma ^2}}} - \displaystyle{{{r^2}} \over {2{\sigma ^2}}}} \right)$$
$$H^{\prime} = - \displaystyle{r \over {{\sigma ^2}}} \cdot {e^{\textstyle{{{r^2}} \over {2{\sigma ^2}}}}}\left( {\ln \displaystyle{1 \over {2{\rm \pi} {\sigma ^2}}} - \displaystyle{{{r^2}} \over {2{\sigma ^2}}}} \right)$$
if σ is larger than
![]() $1/\sqrt {2{\rm \pi}} $
, and the derivative H′ is bigger than zero. In GPS/INS integrated navigation, the σ of GPS position from single point positioning is larger than one metre, which implies that the information entropy of expanded GPS observation is the increasing function of the variable r. During the GPS observation expansion, the further the expansion of the observation is with respect to the mathematical expectation, the larger uncertainty it will have.
$1/\sqrt {2{\rm \pi}} $
, and the derivative H′ is bigger than zero. In GPS/INS integrated navigation, the σ of GPS position from single point positioning is larger than one metre, which implies that the information entropy of expanded GPS observation is the increasing function of the variable r. During the GPS observation expansion, the further the expansion of the observation is with respect to the mathematical expectation, the larger uncertainty it will have.
4.3. Adaptive Filter with GPS Observation Expansion
In order to control the influence of growing uncertainty in GPS observation expansion, the adaptive filter can be deployed. The common adaptive filter resolution is generally expressed as:
where
![]() ${{\bar {\bf G}}_{\rm k}}$
is the adaptive Kalman filter gain matrix (Yang and Gao, Reference Yang and Gao2006):
${{\bar {\bf G}}_{\rm k}}$
is the adaptive Kalman filter gain matrix (Yang and Gao, Reference Yang and Gao2006):
with a feedback loop, the adaptive filter resolution can be simplified to:
in which α k is the adaptive factor.
During GPS observation expansion, the expansion information due to the uncertainty will bring outlier disturbance. Thus,
![]() $\alpha _{\rm k}^{\rm H} $
is introduced to decrease or even eliminate the outlier disturbance. On the basis of the uncertainty of the expanded GPS position observations,
$\alpha _{\rm k}^{\rm H} $
is introduced to decrease or even eliminate the outlier disturbance. On the basis of the uncertainty of the expanded GPS position observations,
![]() $\alpha _{\rm k}^{\rm H} $
is defined by:
$\alpha _{\rm k}^{\rm H} $
is defined by:
where H is the uncertainty in current time.
Except where the adaptive factor can decrease or eliminate the abruptness of GPS observation expansion, it can also be used to inhibit the influence of gross errors on the GPS observation. Accordingly, the adaptive factor
![]() $\alpha _{\rm k}^{\rm e} $
is introduced based on predicted residual (Mohamed and Schwarz, Reference Mohamed and Schwarz1999):
$\alpha _{\rm k}^{\rm e} $
is introduced based on predicted residual (Mohamed and Schwarz, Reference Mohamed and Schwarz1999):
 $$\alpha _{\rm k}^{\rm e} = \left\{ {\matrix{ 1 & { \vert \Delta {V_{\rm k}} \vert \le {\rm c}} \cr {\displaystyle{{\rm c} \over {{\rm \vert} \Delta {V_{\rm k}}{\rm \vert}}}} & { \vert \Delta {V_{\rm k}} \vert \gt {\rm c}} \cr}} \right.$$
$$\alpha _{\rm k}^{\rm e} = \left\{ {\matrix{ 1 & { \vert \Delta {V_{\rm k}} \vert \le {\rm c}} \cr {\displaystyle{{\rm c} \over {{\rm \vert} \Delta {V_{\rm k}}{\rm \vert}}}} & { \vert \Delta {V_{\rm k}} \vert \gt {\rm c}} \cr}} \right.$$
where c is a constant between 0·85 and 1·0.
The learning statistic ΔV k is constructed as follows
 $$\Delta {V_{\rm k}} = \displaystyle{{{\bf V}_{\rm k}^{\rm T} {{\bf V}_{\rm k}}} \over {{\rm tr}({{\bf B}_{\rm k}}{{\bf P}_{{\rm k},{\rm k} - 1}}{\bf B}_{\rm k}^{\rm T} + {{\bf R}_{\rm k}})}}$$
$$\Delta {V_{\rm k}} = \displaystyle{{{\bf V}_{\rm k}^{\rm T} {{\bf V}_{\rm k}}} \over {{\rm tr}({{\bf B}_{\rm k}}{{\bf P}_{{\rm k},{\rm k} - 1}}{\bf B}_{\rm k}^{\rm T} + {{\bf R}_{\rm k}})}}$$
The following should be noted about the proposed filter method. Firstly, when the GPS observation contaminated by gross error at the time of T is used to implement the filter update as GPS observation expansion, the Kalman filter solution suffers from gross error and outlier disturbance due to observation expansion, which can easily lead to a filter divergence. Hence, the GPS observation expansion should not be performed at the time T + 0·01 s, T + 0·02 s …in the case that GPS observation is affected by gross error at the time of T. Secondly, because the vertical accuracy of a GPS position is much lower than the horizontal accuracy, GPS observation expansion only makes use of horizontal position. Thirdly, if the position at the current time is far away from the position at the time of T, the expanding observation with large uncertainty is used to perform the measurement update of the states, which may easily lead to a major outlier. In that case, the GPS observation expansion may be counter-productive. Therefore, the GPS measurement expansion with large uncertainty should be rejected by setting up a threshold β.
We schematically present a block diagram in Figure 2 to outline the fundamental mechanism of the proposed adaptive filter method. The flow of the proposed adaptive filter with GPS observation expansion can be summarised as follows:
-
1) At the time T, resolve the navigation result by the adaptive filter with the GPS observation (x T , y T) using the adaptive factor
 $\alpha _{\rm k}^{\rm e} $
(
$\alpha _{\rm k}^{\rm e} $
(
 ${\alpha _{\rm k}} = \alpha _{\rm k}^{\rm e} $
);
${\alpha _{\rm k}} = \alpha _{\rm k}^{\rm e} $
); -
2) For the further time instants from T + 0·01 s to T + 0·99 s, if
 $\alpha _{\rm k}^{\rm e} \lt 1$
at time T, the navigation results only make use of the free inertial navigation solution without observation expansion;
$\alpha _{\rm k}^{\rm e} \lt 1$
at time T, the navigation results only make use of the free inertial navigation solution without observation expansion; -
3) If
 $\alpha _{\rm k}^{\rm e} = 1$
at the time T, calculate the distance r between the current position with (x
T , y
T) and obtain the uncertainty H using Equation (16);
$\alpha _{\rm k}^{\rm e} = 1$
at the time T, calculate the distance r between the current position with (x
T , y
T) and obtain the uncertainty H using Equation (16); -
4) If H ≤ β, calculate the adaptive factor
 $\alpha _{\rm k}^{\rm H} $
and perform the adaptive filter update using the expanded GPS observation (
$\alpha _{\rm k}^{\rm H} $
and perform the adaptive filter update using the expanded GPS observation (
 ${\alpha _{\rm k}} = \alpha _{\rm k}^{\rm H} $
). Otherwise, only the inertial self-navigation is introduced;
${\alpha _{\rm k}} = \alpha _{\rm k}^{\rm H} $
). Otherwise, only the inertial self-navigation is introduced; -
5) If H > β, the integrated navigation does not perform any measurement update using GPS observation expansion, until the GPS receiver delivers the new position information, and then repeats the steps above.
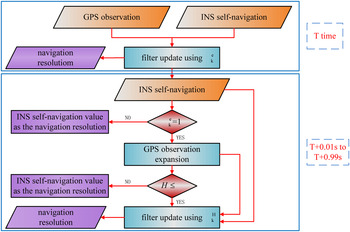
Figure 2. The proposed adaptive filter with GPS observation expansion
According to the above description, the adaptive factor
![]() $\alpha _{\rm k}^{\rm e} $
is only used at the time when the GPS observation inputs and the adaptive factor
$\alpha _{\rm k}^{\rm e} $
is only used at the time when the GPS observation inputs and the adaptive factor
![]() $\alpha _{\rm k}^{\rm H} $
is only applied during GPS observation expansion. The two kinds of factor are not used at the same time to avoid filter divergence. If one compares the adaptive filter using GPS observation expansion with the standard Kalman filtering, one can find the following: (1) GPS observation expansion increases the frequency of the observation updates for the time between two GPS observation epochs; (2) the adaptive filter with GPS observation expansion can not only control the effect of GPS measurement errors on the states, but also lessens the influence of outliers due to GPS observation expansion; (3) the proposed GPS observation expansion is based on the dynamic characteristics of a vehicle itself, which relies on the velocity of the vehicle. The Kalman filter will be processed more times in the proposed method and the corresponding amount of calculation will be increased. Not too many conditions meet the requirements of GPS observation expansion, so the overall calculation burden will not be significantly increased. On the other hand, the key of navigation work is real-time performance. So the different operations in GPS/INS integrated navigation have been set on different priorities. The GPS observation expansion algorithm is one assisting method and its priority is the lowest to make sure that it will not impact the real-time performance.
$\alpha _{\rm k}^{\rm H} $
is only applied during GPS observation expansion. The two kinds of factor are not used at the same time to avoid filter divergence. If one compares the adaptive filter using GPS observation expansion with the standard Kalman filtering, one can find the following: (1) GPS observation expansion increases the frequency of the observation updates for the time between two GPS observation epochs; (2) the adaptive filter with GPS observation expansion can not only control the effect of GPS measurement errors on the states, but also lessens the influence of outliers due to GPS observation expansion; (3) the proposed GPS observation expansion is based on the dynamic characteristics of a vehicle itself, which relies on the velocity of the vehicle. The Kalman filter will be processed more times in the proposed method and the corresponding amount of calculation will be increased. Not too many conditions meet the requirements of GPS observation expansion, so the overall calculation burden will not be significantly increased. On the other hand, the key of navigation work is real-time performance. So the different operations in GPS/INS integrated navigation have been set on different priorities. The GPS observation expansion algorithm is one assisting method and its priority is the lowest to make sure that it will not impact the real-time performance.
5. FIELD TEST AND ANALYSIS
5.1. Test One
To test the efficiency of the proposed method, a land vehicle field test was carried out. The field test was conducted in the Daxing district of Beijing. An overview of the test trajectory is given in Figure 3. The road condition is complex and diverse including city circular road, street area and bridge overpass. The whole test lasts about half an hour. The MEMS IMU ran at the data rate of 100 Hz and its technical data is shown in Table 2. The GPS receiver was used at the data rate of 1 Hz. A SPAN-CPT (Synchronous Position, Attitude and Navigation combined GNSS and INS) product by NovAtel Inc., together with the MEMS-IMU was installed in the vehicle. One GPS antenna was installed on the roof of the vehicle and another GPS receiver was set on a known point as the dynamical differential GPS reference station. The post-processed differential GPS solutions were used as the position reference value and the post-processed SPAN-CPT outputs were used as the velocity and attitude reference value and their accuracies are shown in Table 3.

Figure 3. The trajectory of test one.
Table 2. The MEMS-IMU's technical data.

Table 3. The reference value accuracy.

In the data processing, the initial parameters of the Kalman filter for the integrated navigation were determined based on experience. The initial position errors were 3 m, 3 m and 5 m and the initial velocity errors were 0·1 m/s, 0·1 m/s and 0·5 m/s in NED (North-East-Down) directions, respectively. The initial platform alignment errors were 0·01°, 0·01°, 0·1°. The initial standard deviations of gyro and accelerometer biases were 10°/h and 500 mg, respectively. The initial standard deviation of GPS position and velocity were 3·3 m and 0·1 m/s. The alignment information can be obtained with INS and GPS information in static condition. The initial position, velocity and attitude are set the same for different schemes to obtain a better comparison performance.
In order to test the efficiency of the new method, three calculation schemes are performed:
-
Scheme 1: the standard Kalman filter,
-
Scheme 2: the adaptive Kalman filter without GPS observation expansion (Yang and Gao, Reference Yang and Gao2006),
-
Scheme 3: the enhanced GPS/INS integrated navigation system with GPS observation expansion (the proposed method in this paper).
The whole analysis focuses on four road conditions: 1. High-speed (velocity ⩾ 40 km/h) and straight road, 2. High-speed and curving road, 3. Low-speed (velocity < 40 km/h) and straight road, 4. Low-speed and curving road.
Figure 4 shows the trajectory chart of the reference and three schemes. One local area of the four road conditions mentioned above was chosen and shown in Figure 5. In order to compare the error in different regions of Figure 5, the horizontal position error series of three schemes is shown in Figure 6. Whether on straight roads or on curving roads, the navigation solution of three schemes in high speed conditions was almost the same. However, the navigation result from Scheme 3 was better than the result from Scheme 1 and Scheme 2 when the vehicle was driven at low speed. This was due to the fact that the vehicle in high-speed conditions was leaving from the position at the time T in a short time span. The expanding GPS observations were very few or even non-existent, which would weaken the effect of the GPS observation expansion.

Figure 4. Trajectory comparison of different schemes.

Figure 5. Trajectory comparison of different motion regions (enlargement): (a) High-speed straights region; (b) High-speed corners region; (c) Low-speed straights region; (d) Low-speed corners region.

Figure 6. Horizontal position error comparison of different motion regions: (a) High-speed straights region; (b) High-speed corners region; (c) Low-speed straights region; (d) Low-speed corners region.
Figure 7 shows the time series of position error from three schemes vs. dynamical differential GPS solution in the NED directions. A statistical summary of the Root Mean Square errors (RMS) and maximum value for position error is presented in Table 4. From the whole trajectory, the navigation accuracy with Scheme 2 was little better than the accuracy with Scheme 1. The navigation accuracy for Scheme 3 was superior to the accuracy from Scheme 1 and Scheme 2. The adaptive filter (Scheme 2) could resist the impact of dynamics model outliers on the state estimates. The GPS observation expansion (Scheme 3) could not only increase the measurement update rate, but also inhibit the negative effect of the growing uncertainty from the expanding GPS observation, which can improve the navigation accuracy and prevent the filter from diverging. The results show that the position of Scheme 3 can achieve an accuracy of 0·852 m, 0·946 m and 0·951 m in the north, east and down coordinate components, respectively. Compared with Scheme 1, the position accuracy in the north, east and down directions is improved by 69%, 67% and 16% for Scheme 3 respectively. Compared with Scheme 2, the position accuracy in the north, east and down directions are improved by 43%, 43% and 11% for Scheme 3 respectively. Because only the horizontal coordinate is brought in the GPS observation expansion, δr N and δr E are the directly measurable variables and δr D is the indirectly measurable variable. So the accuracy improvement in the north and east directions is larger than that in the down direction.

Figure 7. The position error for different schemes: (a) position error in north; (b) position error in east; (c) position error in down.
Table 4. Comparison of three schemes in terms of position error.

Table 5 shows the velocity improvement realized by the enhanced GPS/INS integrated navigation system with GPS observation expansion proposed in the paper. Figure 8 plots the integrated system velocity errors in north, east and down directions respectively. The results show that the velocity of Scheme 3 can achieve an accuracy of 0·304 m/s, 0·304 m/s and 0·118 m/s in the north, east and down coordinate components, respectively, which is a better performance than Scheme 1 and Scheme 2. Compared to Scheme 1, the proposed enhanced GPS/INS integrated navigation system improves all the velocity errors in the north, east and down direction by 45%, 47% and 1% RMS, respectively. The velocity accuracies of three schemes are almost of the same level in the down direction. Because the velocity is very small in the north direction for land vehicles, the velocity value is set to zero at the beginning of the INS self-navigation computation period, which is one non-holonomic constraint for land vehicles.

Figure 8. The velocity error for different schemes: (a) velocity error in north; (b) velocity error in east; (c) velocity error in down.
Table 5. Comparison of three schemes in terms of velocity error.

The roll, pitch and yaw errors of Scheme 1, Scheme 2 and Scheme 3 are given in Figure 9 and Table 6. It can be seen that the attitude accuracy has been improved with Scheme 3. In terms of RMS, compared with Scheme 1 (3·763°) and Scheme 2 (3·254°), the error from Scheme 3 dropped down to 2·709°in yaw attitude. The largest attitude errors of roll, pitch and yaw angles are 0·399°, 0·261° and 6·005°, respectively, when Scheme 1 is used. By contrast, the largest attitude errors are 0·304°, 0·194° and 4·701° when the proposed approach is applied, which are considerably smaller.

Figure 9. The attitude error for different schemes: (a) attitude error in roll; (b) attitude error in pitch; (c) attitude error in yaw.
Table 6. Comparison of three schemes in terms of attitude error.

5.2. Test Two
Longer field tests were conducted to evaluate the performance of the proposed method. The test systems are the same as test one. The field test was conducted in China University of Mining and Technology of Xuzhou. An overview of the test trajectory is given in Figure 10.The whole time of the test was about two hours. The three calculation schemes of test one were performed.

Figure 10. The trajectory of test two.
Shown in Figure 11 are time series of position solution differences with respect to the reference value from different schemes. Table 7 illustrates RMS and maximum values of position error. The results of test two are similar to those of test one. The results show that the position of Scheme 3 can achieve an accuracy of 0·845 m, 0·768 m and 2·399 m in the north, east and down coordinate components, respectively. Compared with Scheme 1, the position accuracy in the north, east and down directions are improved by 62%, 56% and 51% for Scheme 3 respectively. The result shows that the enhanced GPS/INS integrated navigation system with GPS observation expansion is able to realise better performance in longer term navigation work.

Figure 11. The position error for different schemes: (a) position error in north; (b) position error in east; (c) position error in down.
Table 7. Comparison of three schemes in terms of position error.

6. CONCLUSIONS
On the basis of the PDF of random variables, the GPS observation can be expanded by being bound on the dynamics of a land vehicle. The information entropy has been deployed to describe the uncertainty of the expanded GPS observations using their PDFs. The uncertainty has been used to calculate the adaptive factor for the Kalman filter. The enhanced GPS/INS integrated navigation system with the GPS observation expansion can increase the rate of the measurement updates without other aiding sensors and inhibit the influence of the growing uncertainty on the expanding GPS observation. The results for a land vehicle have shown that the proposed method could improve the accuracy of the position, velocity and attitudes effectively, especially in the urban area where the land vehicle could be driven at varying speeds. Comparison with the standard Kalman filter and the classical adaptive filter has shown its advantages. At the same time, combining the new proposed method with other methods, such as using more sensors, the GPS/INS integrated navigation system should obtain even better performance, and this is work for the future.
FINANCIAL SUPPORT
The work is partially sponsored by the Fundamental Research Funds for the Central Universities (2014ZDPY29) and partially sponsored by A Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (SZBF2011-6-B35).




















