Impact Statement
The hydrodynamic forces and moments experienced by a pair of bodies in a free-stream flow can significantly differ from those acting on an isolated body. These hydrodynamic interactions, dependent on the relative positions and speeds of the bodies, can either enhance or impair operational performance metrics for underwater vehicles or biological swimmers. Existing research primarily concentrates on drag coefficient changes in stationary configurations. However, lateral forces and yawing moments are crucial as they determine the extent to which control systems need to intervene to maintain the bodies in their relative positions, leading to additional hydrodynamic drag overhead. These insights are even more important for overtaking manoeuvres. The findings of this study illustrate the significance of lateral forces on submerged bodies for side-by-side configurations and overtaking manoeuvres. Further, our work indicates the need for further research into viscous and three-dimensional effects on these lateral forces. Overall, the results improve our understanding of unmanned underwater vehicle formations and fish schooling dynamics.
1. Introduction
The hydrodynamic interactions between bodies moving in close formation within a fluid flow have been investigated from a variety of perspectives. The hydrodynamics of two unmanned underwater vehicles (UUVs) operating in close formation have previously been modelled using three-dimensional (3-D) Reynolds-averaged Navier–Stokes (RANS) simulations and experimental testing, revealing that UUV interactions can be either beneficial or harmful to overall drag depending on the formation (Reference Rattanasiri, Wilson and PhillipsRattanasiri, Wilson & Phillips 2014; Reference Tian, Mao, Zhao and ZhaoTian et al. 2017; Reference Zhang, Chao and PanZhang, Chao & Pan 2019a). Across these studies, echelon-like configurations were found to offer benefits for both UUVs together, with the drag decrease on the trailing body outweighing the drag increase on the leading body. Quantitative predictions on the drag reduction across these studies vary significantly, with maximum drag variations relative to an isolated body ranging from ![]() ${\pm }100\,\%$ (Reference Rattanasiri, Wilson and PhillipsRattanasiri et al. 2014) to
${\pm }100\,\%$ (Reference Rattanasiri, Wilson and PhillipsRattanasiri et al. 2014) to ![]() $+10$ % and
$+10$ % and ![]() $-30$ % (Reference Zhang, Pan, Shi, Wang and ChaoZhang et al. 2019b). In-line configurations find significant drag reductions for both UUVs as well, but in the absence of propeller wake modelling these results do not translate to realistic predictions. Formation drag reduction is also of interest in land-based applications such as cycling (Reference Blocken, Defraeye, Koninckx, Carmeliet and HespelBlocken et al. 2022) and car racing (Reference Romberg, Chianese and LajoieRomberg, Chianese & Lajoie 1971).
$-30$ % (Reference Zhang, Pan, Shi, Wang and ChaoZhang et al. 2019b). In-line configurations find significant drag reductions for both UUVs as well, but in the absence of propeller wake modelling these results do not translate to realistic predictions. Formation drag reduction is also of interest in land-based applications such as cycling (Reference Blocken, Defraeye, Koninckx, Carmeliet and HespelBlocken et al. 2022) and car racing (Reference Romberg, Chianese and LajoieRomberg, Chianese & Lajoie 1971).
Hydrodynamic interactions are prevalent in biological swimmers, where they are thought to reduce energy expenditure for one or multiple individuals in a formation. Dolphin and whale calves are hypothesized to exploit drag-advantaged swim formations (Reference Noren and EdwardsNoren & Edwards 2011; Reference Shoele and ZhuShoele & Zhu 2015). By swimming in certain positions relative to its mother, the calf experiences a decrease in hydrodynamic drag, leading to a predicted reduction in swimming effort of as much as 90 % (Reference WeihsWeihs 2004). A more complex setting is offered by fish swimming, where the hydrodynamic force interactions and benefits of schooling have been a long-standing debate in the scientific community (Reference WeihsWeihs 1973; Reference Partridge and PitcherPartridge & Pitcher 1979). The additional complexity in fish schooling over UUVs is the active body deformation that leads to complex vortical wakes, and creates a dependency between the hydrodynamic benefits of formation patterns and phase differences in the swimming kinematics of the fish in the school (Reference Li, Nagy, Graving, Bak-Coleman, Xie and CouzinLi et al. 2020; Reference Timm, Pandhare and MasoudTimm, Pandhare & Masoud 2023).
The cases mentioned above primarily consider the effects of the drag coefficient of bodies translating in various fixed formation patterns. From a practical perspective, however, the hydrodynamic lateral (sway) forces and (yaw) moments within a given formation pattern are important as well. For UUVs, active control of rudders or asymmetric thrust is required to maintain a formation, but this requires a suitable control mechanism and further comes at an additional energetic cost associated with induced drag. Similarly, for biological swimming any efforts at maintaining course and relative position will require additional muscular activations, coming at an energetic cost. It is thus important to quantify the lateral forces and yaw moment, relative to any changes in the hydrodynamic drag within a given formation.
Compared with the changes in drag force, there is significantly less existing research on the lateral forces and moments on a pair of submerged bodies moving together in a fluid flow, forcing a broader look at the existing results. An experimental study on equal-sized ellipsoidal bodies placed side by side showed that lateral forces reach up to 50 % of the total drag force (Reference Molland and UtamaMolland & Utama 2002). More results are available for lateral forces in ship–ship interactions, typically investigated using potential flow techniques (Reference Tuck and NewmanTuck & Newman 1976) or experimental analyses (Reference Vantorre, Verzhbitskaya and LaforceVantorre, Verzhbitskaya & Laforce 2002), and recently reviewed in Reference Muscat-Fenech, Sant, Zheku, Villa and MartelliMuscat-Fenech et al. (2022). Broadly, existing results state that lateral forces between two ships are attractive when the ships are moving side by side and repulsive when, roughly, the bow of one ship clears the stern of the other. These findings are qualitatively consistent with a potential flow study on submerged slender bodies of revolution (Reference WangWang 2007). Experiments found that lateral force magnitudes can be significantly larger than the drag force on the ships (Reference Vantorre, Verzhbitskaya and LaforceVantorre et al. 2002). In the context of flapping foils, Reference Kurt and MooredKurt & Moored (2018) used experiments at Reynolds numbers of ![]() $\mathcal {O}(10^4)$ of tandem pitching wings to show that the mean lift coefficient can change from repulsive (in-phase motions) to attractive (out-of-phase) depending on the relative phase of the pitching motions between the two wings.
$\mathcal {O}(10^4)$ of tandem pitching wings to show that the mean lift coefficient can change from repulsive (in-phase motions) to attractive (out-of-phase) depending on the relative phase of the pitching motions between the two wings.
Besides equal speed interactions, the effect of relative motion on all force and moment coefficients is important when considering practical scenarios where overtaking manoeuvres would be necessary. With the bodies in relative motion, close-range hydrodynamic interactions will gain a dependency on the speed ratio between the two bodies. Within the ocean engineering community this has been predominantly investigated in potential flow settings, for submerged bodies (Reference WangWang 2007) and for ship overtaking manoeuvres (Reference Skejic and FaltinsenSkejic & Faltinsen 2007; Reference Xiang and FaltinsenXiang & Faltinsen 2011; Reference Yu, Wang and YeungYu, Wang & Yeung 2019), complemented by ship–ship interaction experiments (Reference Vantorre, Verzhbitskaya and LaforceVantorre et al. 2002; Reference Muscat-Fenech, Sant, Zheku, Villa and MartelliMuscat-Fenech et al. 2022). For low overtaking speeds, the hydrodynamic interactions agree roughly with the forces found for interactions without relative motion. The model test results in Reference Vantorre, Verzhbitskaya and LaforceVantorre et al. (2002) do show significant dependency on the results for lateral forces depending on the ship types used in the experiments. Larger overtaking speeds generally amplify the trends, with the larger response to the velocity difference occurring on the slower, overtaken body, rather than the faster, overtaking body (Reference Vantorre, Verzhbitskaya and LaforceVantorre et al. 2002; Reference WangWang 2007).
From the results above, there is a lack of quantitative, high-fidelity analysis of the lateral forces on side-by-side submerged bodies without and with relative motions. Existing knowledge is predominantly concentrated around potential and very high Reynolds number flows, mostly for ships, which only provides limited insight into the fully submerged setting relevant for smaller-scale UUVs (Reference Mintchev, Donati, Marrazza and StefaniniMintchev et al. 2014; Reference Hackbarth, Kreuzer and SolowjowHackbarth, Kreuzer & Solowjow 2015), biological swimmers and relative motions in a formation. Simultaneously, the interaction between heaving and/or pitching fins is predominantly investigated at lower Reynolds numbers, but involves significantly more complexity with respect to the vortical wakes induced by the relative lateral and angular kinematics of the fins. Consequently, the base problem of two bluff bodies moving side by side in a viscous incoming flow without and with relative motion provides an open area of study, especially when considering the lateral forces and moments.
Here, we use 2-D numerical simulations to characterize the hydrodynamic interactions between 6 : 1 (length-to-width) ellipses for different configurations and relative speeds. The ellipse interactions were studied using high-fidelity simulations of an incompressible, viscous flow with chord-based Reynolds numbers ![]() $1500 \leq Re \leq 3000$. These Reynolds numbers are similar to many studies on biological interactions although much lower than many engineering applications of underwater vehicles. However, as argued above, studying the lower end of the Reynolds number range provides complementary insights into viscous and transient effects while offering high-fidelity numerical results. Further, tackling a 2-D problem offers more flexibility in exploring a wide parameter space, and complements existing results on hydrodynamic interactions between cylinders (Reference SumnerSumner 2010) and foils and swimmers (e.g. Reference Dewey, Quinn, Boschitsch and SmitsDewey et al. 2014; Reference Kelly, Pan, Menzer and DongKelly et al. 2023; Reference Timm, Pandhare and MasoudTimm et al. 2023) that extend into this Reynolds number regime.
$1500 \leq Re \leq 3000$. These Reynolds numbers are similar to many studies on biological interactions although much lower than many engineering applications of underwater vehicles. However, as argued above, studying the lower end of the Reynolds number range provides complementary insights into viscous and transient effects while offering high-fidelity numerical results. Further, tackling a 2-D problem offers more flexibility in exploring a wide parameter space, and complements existing results on hydrodynamic interactions between cylinders (Reference SumnerSumner 2010) and foils and swimmers (e.g. Reference Dewey, Quinn, Boschitsch and SmitsDewey et al. 2014; Reference Kelly, Pan, Menzer and DongKelly et al. 2023; Reference Timm, Pandhare and MasoudTimm et al. 2023) that extend into this Reynolds number regime.
The rest of this work is structured as follows. Section 2 explains the computational method and numerical parameters. Section 3 briefly states the drag coefficient found for isolated elliptical bodies across the Reynolds number regime considered here, which serves as reference to quantify the hydrodynamic interactions of ellipse pairs. The main results are presented and discussed in § 4 for two ellipses operating at the same speed, and § 5 for overtaking manoeuvres. Finally, § 6 describes the conclusions of this work.
2. Methodology and set-up
In this section, we briefly explain the details of the numerical methodology, including physical parameters and definitions used in the simulations.
2.1 Simulation methodology
All simulations in this work are performed with a direct numerical solver for the 2-D incompressible Navier–Stokes equations. We solve the equations in a conservative vorticity–velocity form
with ![]() $\omega = \boldsymbol {\nabla } \times \boldsymbol {u}$ the scalar vorticity field,
$\omega = \boldsymbol {\nabla } \times \boldsymbol {u}$ the scalar vorticity field, ![]() $\boldsymbol {u}$ the velocity field and
$\boldsymbol {u}$ the velocity field and ![]() $\nu$ the kinematic viscosity. With
$\nu$ the kinematic viscosity. With ![]() $\omega$ as primary variable, the velocity field can be recovered by solving a scalar Poisson equation
$\omega$ as primary variable, the velocity field can be recovered by solving a scalar Poisson equation
where ![]() $\psi$ is the streamfunction so that
$\psi$ is the streamfunction so that ![]() $\boldsymbol {u} = \boldsymbol {\nabla } \times \psi + \boldsymbol {U}_\infty$, with
$\boldsymbol {u} = \boldsymbol {\nabla } \times \psi + \boldsymbol {U}_\infty$, with ![]() $\boldsymbol {U}_\infty$ any irrotational, divergence-free velocity field that satisfies the far-field boundary conditions.
$\boldsymbol {U}_\infty$ any irrotational, divergence-free velocity field that satisfies the far-field boundary conditions.
Our solver discretizes these equations on a uniform Cartesian grid organized in constant-size blocks of ![]() $N_b \times N_b$ grid points where, in this work,
$N_b \times N_b$ grid points where, in this work, ![]() $N_b = 32$ grid points. The advection term on the left-hand side is discretized using a third-order conservative upwind finite-difference scheme (Reference ShuShu 1998), and the diffusion term uses a second-order centred finite-difference scheme. The Poisson equation is solved using a fast Fourier transform library (Reference Caprace, Gillis and ChatelainCaprace, Gillis & Chatelain 2021) with arbitrary combinations of free-space, periodic or symmetry/mirror boundary conditions on the domain boundaries. Finally, we use a third-order low-storage Runge–Kutta scheme for time integration, imposing a Courant–Friedrichs–Lewy-based stability constraint.
$N_b = 32$ grid points. The advection term on the left-hand side is discretized using a third-order conservative upwind finite-difference scheme (Reference ShuShu 1998), and the diffusion term uses a second-order centred finite-difference scheme. The Poisson equation is solved using a fast Fourier transform library (Reference Caprace, Gillis and ChatelainCaprace, Gillis & Chatelain 2021) with arbitrary combinations of free-space, periodic or symmetry/mirror boundary conditions on the domain boundaries. Finally, we use a third-order low-storage Runge–Kutta scheme for time integration, imposing a Courant–Friedrichs–Lewy-based stability constraint.
The no-slip boundary conditions on the immersed body(-ies) are enforced to second-order accuracy using an immersed interface method (IIM). As an embedded geometry technique, the IIM removes the need for meshes to conform to the boundary geometry, which enables the type of relative motions for side-by-side bodies presented below. Our version of the IIM imposes boundary conditions using a polynomial extrapolation of the field across immersed boundaries, taking into account any body boundary conditions, and using the extrapolated values in a standard free-space finite-difference scheme. This approach essentially injects local corrections in the finite-difference stencil to account for the presence of the boundary. We combine this approach with a low-rank correction approach to enforce a no-through boundary condition on the velocity field when solving from the vorticity. Further, the dynamic evolution of vorticity is augmented with a Thom-like wall-vorticity boundary condition which enforces the no-slip condition through the diffusion of the wall-bounded vortex layer into the flow (Reference ThomThom 1933; Reference Gillis, Marichal, Winckelmans and ChatelainGillis et al. 2019). The approach is described and validated for single and multiple stationary bodies in Reference Gabbard, Gillis, Chatelain and van ReesGabbard et al. (2022), and single and multiple moving bodies in Reference Ji, Gabbard and van ReesJi, Gabbard & van Rees (2023).
Throughout this study, we choose a simulation area as though viewed from above, with the positive ![]() $x$-axis pointing to the right, the positive
$x$-axis pointing to the right, the positive ![]() $y$-axis pointing upward and the positive
$y$-axis pointing upward and the positive ![]() $z$-axis pointing out of the page and toward the viewer. In all results below, we choose our computational frame of reference to follow the ellipse that is initially located upstream. Consequently, the left, top and bottom of the domain were treated as free-space boundaries, with no imposed restriction on the velocity or velocity gradient – instead, the velocity is solved so that it decays towards
$z$-axis pointing out of the page and toward the viewer. In all results below, we choose our computational frame of reference to follow the ellipse that is initially located upstream. Consequently, the left, top and bottom of the domain were treated as free-space boundaries, with no imposed restriction on the velocity or velocity gradient – instead, the velocity is solved so that it decays towards ![]() $U_{\infty }$ far away from the body (Reference Gabbard, Gillis, Chatelain and van ReesGabbard et al. 2022). The right domain boundary was treated as an outflow condition (Reference Chatelain, Backaert, Winckelmans and KernChatelain et al. 2013; Reference Gabbard, Gillis, Chatelain and van ReesGabbard et al. 2022). For all simulations in this work, the density of the fluid is constant and free-surface effects are ignored as the bodies are assumed to operate at large depth.
$U_{\infty }$ far away from the body (Reference Gabbard, Gillis, Chatelain and van ReesGabbard et al. 2022). The right domain boundary was treated as an outflow condition (Reference Chatelain, Backaert, Winckelmans and KernChatelain et al. 2013; Reference Gabbard, Gillis, Chatelain and van ReesGabbard et al. 2022). For all simulations in this work, the density of the fluid is constant and free-surface effects are ignored as the bodies are assumed to operate at large depth.
2.2 Physical set-up and notation
Throughout this study, we fix the aspect ratio of the ellipses as ![]() $L/D = 6$, with
$L/D = 6$, with ![]() $L$ the ellipse length and
$L$ the ellipse length and ![]() $D$ its height. This ratio is chosen because it is representative of many UUV aspect ratios and thus commonly used in biological and UUV studies featuring elliptical (2-D) and ellipsoidal (3-D) shapes.
$D$ its height. This ratio is chosen because it is representative of many UUV aspect ratios and thus commonly used in biological and UUV studies featuring elliptical (2-D) and ellipsoidal (3-D) shapes.
We study configurations of two ellipses in a free-space domain. We define ellipse 0 as the initially upstream ellipse and ellipse 1 as the initially downstream ellipse (figure 1). During the overtaking simulations, ellipse 1 moves in the negative ![]() $x$-direction to overtake ellipse 0. Denoting the centroid position of ellipse 0 as
$x$-direction to overtake ellipse 0. Denoting the centroid position of ellipse 0 as ![]() $(x_0, y_0)$ and of ellipse 1 as
$(x_0, y_0)$ and of ellipse 1 as ![]() $(x_1, y_1)$, we define the non-dimensional quantities
$(x_1, y_1)$, we define the non-dimensional quantities ![]() $x^* = (x_0 - x_1)/L$ and
$x^* = (x_0 - x_1)/L$ and ![]() $y^* = (y_0 - y_1)/L$ to denote the relative positions between the two. During overtaking manoeuvres,
$y^* = (y_0 - y_1)/L$ to denote the relative positions between the two. During overtaking manoeuvres, ![]() $x^*$ increases from its initial negative value (ellipse 1 downstream of ellipse 0) to its final positive value (ellipse 1 upstream of ellipse 0). Throughout this work
$x^*$ increases from its initial negative value (ellipse 1 downstream of ellipse 0) to its final positive value (ellipse 1 upstream of ellipse 0). Throughout this work ![]() $y^*$ remains a constant positive value set independently for each simulation.
$y^*$ remains a constant positive value set independently for each simulation.

Figure 1. Set-up and notation for the ellipse simulations, with the drawn state corresponding to ![]() $x^* = -1.5$ and
$x^* = -1.5$ and ![]() $y^*=0.3$.
$y^*=0.3$.
During overtaking, we introduce relative motion between the two ellipses. Here, for simplicity, we define ![]() $U_0 > 0$ and
$U_0 > 0$ and ![]() $U_1 > 0$ as the speeds of ellipses 0 and 1, respectively. As noted before, the simulations are performed in a frame of reference moving with ellipse 0 by introducing a left-to-right background flow velocity
$U_1 > 0$ as the speeds of ellipses 0 and 1, respectively. As noted before, the simulations are performed in a frame of reference moving with ellipse 0 by introducing a left-to-right background flow velocity ![]() $u_{\infty }$ with magnitude
$u_{\infty }$ with magnitude ![]() $u_\infty = U_0$. In this frame, the
$u_\infty = U_0$. In this frame, the ![]() $x$-component of the velocity of ellipse 0 is
$x$-component of the velocity of ellipse 0 is ![]() $u_0 = 0$ and this quantity for ellipse 1 is
$u_0 = 0$ and this quantity for ellipse 1 is ![]() $u_1 = U_0 - U_1$. However, our results below will be discussed only with reference to the positive ellipse speeds
$u_1 = U_0 - U_1$. However, our results below will be discussed only with reference to the positive ellipse speeds ![]() $U_0$ and
$U_0$ and ![]() $U_1$, and the associated length-based Reynolds numbers
$U_1$, and the associated length-based Reynolds numbers
The hydrodynamic quantities of interest in this study are the non-dimensional force and moment coefficients. Specifically, we define the drag, lift and moment coefficient for each ellipse as
 \begin{equation} \left.\begin{array}{@{}c@{}}
\displaystyle C_{D,0}(t) =
\dfrac{F_{x,0}(t)}{\dfrac{1}{2}\rho U_0^2 L} \quad
C_{D,1}(t) = \dfrac{F_{x,1}(t)}{\dfrac{1}{2}\rho U_1^2 L}\\
\displaystyle C_{L,0}(t) =
\dfrac{F_{y,0}(t)}{\dfrac{1}{2}\rho U_0^2 L}\quad
C_{L,1}(t) = {-}\dfrac{F_{y,1}(t)}{\dfrac{1}{2}\rho U_1^2
L}\\
\displaystyle C_{M,0}(t) =
{-}\dfrac{M_{z,0}(t)}{\dfrac{1}{2}\rho U_0^2 L^2}\quad
C_{M,1}(t) = \dfrac{M_{z,1}(t)}{\dfrac{1}{2}\rho U_1^2 L^2}
\end{array}\right\},
\end{equation}
\begin{equation} \left.\begin{array}{@{}c@{}}
\displaystyle C_{D,0}(t) =
\dfrac{F_{x,0}(t)}{\dfrac{1}{2}\rho U_0^2 L} \quad
C_{D,1}(t) = \dfrac{F_{x,1}(t)}{\dfrac{1}{2}\rho U_1^2 L}\\
\displaystyle C_{L,0}(t) =
\dfrac{F_{y,0}(t)}{\dfrac{1}{2}\rho U_0^2 L}\quad
C_{L,1}(t) = {-}\dfrac{F_{y,1}(t)}{\dfrac{1}{2}\rho U_1^2
L}\\
\displaystyle C_{M,0}(t) =
{-}\dfrac{M_{z,0}(t)}{\dfrac{1}{2}\rho U_0^2 L^2}\quad
C_{M,1}(t) = \dfrac{M_{z,1}(t)}{\dfrac{1}{2}\rho U_1^2 L^2}
\end{array}\right\},
\end{equation}
with ![]() $F_{(x,y)}$ the forces in the
$F_{(x,y)}$ the forces in the ![]() $(x,y)$ direction and
$(x,y)$ direction and ![]() $M_z$ the yaw moment around the centroid of the ellipse, positive counter-clockwise. We emphasize the normalization with
$M_z$ the yaw moment around the centroid of the ellipse, positive counter-clockwise. We emphasize the normalization with ![]() $U_0$ and
$U_0$ and ![]() $U_1$ for ellipse 0 and ellipse 1, respectively, as well as the opposing signs of
$U_1$ for ellipse 0 and ellipse 1, respectively, as well as the opposing signs of ![]() $C_{L}$ and
$C_{L}$ and ![]() $C_M$: the latter, together with the fact that
$C_M$: the latter, together with the fact that ![]() $y_0 \ge y_1$ throughout, implies:
$y_0 \ge y_1$ throughout, implies:
• a positive lift coefficient for either ellipse means the force points away from the other ellipse, i.e. a repulsive force; similarly a negative lift coefficient means the force points towards the other ellipse, i.e. an attractive force;
• a positive moment coefficient for either ellipse means a bow-out moment orientation; a negative moment coefficient means a bow-in moment orientation.
This choice is consistently made throughout the plots below to simplify the interpretation of the results.
These quantities depend on time, and in this study we have normalized time ![]() $t$ by the convective time scale as
$t$ by the convective time scale as
We further define time-averaged force and moment coefficients, defined for each quantity in (2.4), as
with ![]() $t_s$ and
$t_s$ and ![]() $t_f$ the start and end of the averaging window specified in the results sections below.
$t_f$ the start and end of the averaging window specified in the results sections below.
2.3 Numerical set-up
2.3.1 Initial transient
After starting each simulation, the wake behind the ellipses remains symmetric for a long time as the absence of sufficient numerical noise suppresses the vortex shedding instability. To accelerate the onset of shedding, we impose an early-time transient lateral perturbation in the free-stream velocity for all simulations discussed below. The perturbation consists of a temporary, smoothly increasing and decreasing addition of a flow in the lateral ![]() $y$-direction, described through the function
$y$-direction, described through the function
This function is shifted and scaled so that the lateral component to the free-stream velocity activates at ![]() $t^*=1$, peaks at
$t^*=1$, peaks at ![]() $t^*=2$ and vanishes again at
$t^*=2$ and vanishes again at ![]() $t^*=3$, with a peak amplitude of
$t^*=3$, with a peak amplitude of ![]() $u_\infty$.
$u_\infty$.
2.3.2 Domain size study
The upstream, top and bottom edges of our domain are free-space boundaries. Their distances from the body are solely set by the requirement to contain the vortical wake. Preliminary work found that a distance of ![]() $0.83L$ in front of the upstream ellipse, and a total domain height equal to half the total domain length, are sufficient choices to capture the vorticity field.
$0.83L$ in front of the upstream ellipse, and a total domain height equal to half the total domain length, are sufficient choices to capture the vorticity field.
The downstream edge, however, is an outflow boundary condition. In previous work (Reference Gabbard, Gillis, Chatelain and van ReesGabbard et al. 2022), we found that positioning the outflow boundary approximately 30 diameters behind a cylinder gives converged results for that flow. Here, we investigate the required distance for our ellipse configuration. To do so, we study a single ellipse and fix the resolution to ![]() $L/h = 175$. The distance from the trailing ellipse to the outflow boundary
$L/h = 175$. The distance from the trailing ellipse to the outflow boundary ![]() $L_{out}$ is expressed relative to
$L_{out}$ is expressed relative to ![]() $L$ and varied as
$L$ and varied as ![]() $L_{out}/L \in [3,5,7,8,9,11,13]$. We set the Reynolds number to the highest value used in this work so that
$L_{out}/L \in [3,5,7,8,9,11,13]$. We set the Reynolds number to the highest value used in this work so that ![]() $Re = U L/\nu = 3000$, advance the flow until
$Re = U L/\nu = 3000$, advance the flow until ![]() $t^* = 67$ and compute for each domain size the mean drag on the ellipse between
$t^* = 67$ and compute for each domain size the mean drag on the ellipse between ![]() $t^* = 40$ and
$t^* = 40$ and ![]() $t^*=60$. Comparing the mean drag with the value at
$t^*=60$. Comparing the mean drag with the value at ![]() $L_{out}/L = 13$, we find that choosing
$L_{out}/L = 13$, we find that choosing ![]() $L_{out}/L \ge 8$ keeps the difference within 1 % of the longest domain result. For the remainder of this study, we therefore ensure all our simulation domains are set up so that
$L_{out}/L \ge 8$ keeps the difference within 1 % of the longest domain result. For the remainder of this study, we therefore ensure all our simulation domains are set up so that ![]() $L_{out}/L \ge 8$, where
$L_{out}/L \ge 8$, where ![]() $L_{out}$ measures the initial distance from the most downstream ellipse to the outflow boundary.
$L_{out}$ measures the initial distance from the most downstream ellipse to the outflow boundary.
2.3.3 Grid resolution study
To determine the spatial resolution required for accurate simulation results, we perform a number of simulations at varying resolutions for both a single ellipse and a pair of ellipses. The studies are performed at the maximum considered Reynolds number ![]() $Re = 3000$ and, for the pair of ellipses, at the minimum considered centre-to-centre distance of
$Re = 3000$ and, for the pair of ellipses, at the minimum considered centre-to-centre distance of ![]() $0.3L$. We run the simulations until final times
$0.3L$. We run the simulations until final times ![]() $t^* = 67$ (single ellipse) and
$t^* = 67$ (single ellipse) and ![]() $t^*=100$ (two ellipses) and normalize the grid spacing
$t^*=100$ (two ellipses) and normalize the grid spacing ![]() $h$ with
$h$ with ![]() $L$, so that
$L$, so that ![]() $L/h$ describes the number of grid points along the length of an ellipse. For all cases, we position the ellipses so that the distance from their trailing edge to the outflow boundary is
$L/h$ describes the number of grid points along the length of an ellipse. For all cases, we position the ellipses so that the distance from their trailing edge to the outflow boundary is ![]() $8L$, in accordance with the domain study results described above.
$8L$, in accordance with the domain study results described above.
For a single ellipse, we consider resolutions ![]() $L/h \in [100, 150, 175, 200, 250]$ and record the mean drag coefficient from
$L/h \in [100, 150, 175, 200, 250]$ and record the mean drag coefficient from ![]() $t^* = 40$ to
$t^* = 40$ to ![]() $t^* = 60$ for each resolution. Our results are shown in the second and third columns of table 1, where we report both the mean drag coefficient and the relative difference at any resolution compared with the finest grid results at
$t^* = 60$ for each resolution. Our results are shown in the second and third columns of table 1, where we report both the mean drag coefficient and the relative difference at any resolution compared with the finest grid results at ![]() $L/h=250$. The results show that a resolution above
$L/h=250$. The results show that a resolution above ![]() $L/h=150$ is sufficient to obtain a mean drag value to within 1 %–2 % of the finest resolution result.
$L/h=150$ is sufficient to obtain a mean drag value to within 1 %–2 % of the finest resolution result.
Table 1. Resolution study for simulations with a single ellipse (columns 2 and 3), as well as simulations with two side-by-side ellipses with ![]() $y^*=0.3$ (columns 4 through 7). All differences are computed with respect to the finest resolution result
$y^*=0.3$ (columns 4 through 7). All differences are computed with respect to the finest resolution result ![]() $L/h=250$.
$L/h=250$.

For the ellipse pair, we consider ![]() $L/h \in [150, 175, 200, 250]$, so that the minimum number of grid points across the gap ranges from
$L/h \in [150, 175, 200, 250]$, so that the minimum number of grid points across the gap ranges from ![]() $20$ to
$20$ to ![]() $33$. We report the average mean drag and average mean lift coefficient for the ellipse pair, as well as the percentage difference in these quantities from the finest resolution result at
$33$. We report the average mean drag and average mean lift coefficient for the ellipse pair, as well as the percentage difference in these quantities from the finest resolution result at ![]() $L/h=250$. The lift coefficient is somewhat slower to converge but still a resolution of
$L/h=250$. The lift coefficient is somewhat slower to converge but still a resolution of ![]() $L/h=175$ is sufficient to find a difference under 5 % with respect to the finest grid result.
$L/h=175$ is sufficient to find a difference under 5 % with respect to the finest grid result.
We note that these simulations are run at the highest Reynolds number and, for the two ellipse case, at the closest overall distance between the bodies, and thus provide the most challenging flow configuration. With this in mind, we consider ![]() $L/h= 175$ as a sufficient resolution to proceed and use this resolution for all simulation results presented below, unless specified otherwise.
$L/h= 175$ as a sufficient resolution to proceed and use this resolution for all simulation results presented below, unless specified otherwise.
3. Drag of isolated ellipse at various speeds
To provide a reference for all results below, we simulated the time-averaged drag coefficient of an isolated ellipse in a free stream at different Reynolds numbers. These simulations were done with ![]() $L/h=175$,
$L/h=175$, ![]() $L_{out}/L=9$ and drag coefficients are averaged between
$L_{out}/L=9$ and drag coefficients are averaged between ![]() $t^*=40$ and
$t^*=40$ and ![]() $t^*=60$. Table 2 shows the results of
$t^*=60$. Table 2 shows the results of ![]() $\bar {C}_{D,{iso}}$ at the Reynolds numbers considered in this work,
$\bar {C}_{D,{iso}}$ at the Reynolds numbers considered in this work, ![]() $Re= 1500$, 1875, 2250, 2625 and 3000, showing a slight decay consistent with the drag on bluff bodies in this Reynolds number regime (Reference WieselsbergerWieselsberger 1921).
$Re= 1500$, 1875, 2250, 2625 and 3000, showing a slight decay consistent with the drag on bluff bodies in this Reynolds number regime (Reference WieselsbergerWieselsberger 1921).
Table 2. Time-averaged drag coefficients of an isolated ellipse in a free stream at the different Reynolds numbers considered in this work.

For all results below, these drag coefficient values on isolated ellipses will be used as reference to quantify the effect of hydrodynamic interactions between an ellipse pair.
4. Flow past ellipses without relative motion
To provide a reference for the overtaking cases, we investigate first the case of flow past two ellipses without relative motion. To do so, we fix ![]() $Re_0 = Re_1 = 1500$ and vary
$Re_0 = Re_1 = 1500$ and vary ![]() $0 \leq x^* \leq 1.5$ and
$0 \leq x^* \leq 1.5$ and ![]() $0.3 \leq y^* \leq 0.6$ in increments of
$0.3 \leq y^* \leq 0.6$ in increments of ![]() $1/6$ and
$1/6$ and ![]() $1/10$, respectively. For each pair
$1/10$, respectively. For each pair ![]() $(x^*,y^*)$ we run a simulation to steady state and record the time-averaged coefficients for drag, lift and moment. Using the intrinsic symmetry in the problem, we use the results from this quadrant to report the forces on both ellipses for the entire range
$(x^*,y^*)$ we run a simulation to steady state and record the time-averaged coefficients for drag, lift and moment. Using the intrinsic symmetry in the problem, we use the results from this quadrant to report the forces on both ellipses for the entire range ![]() $-1.5\leq x^* \leq 1.5$. As reported above, at this Reynolds number, the mean drag coefficient on an isolated ellipse is
$-1.5\leq x^* \leq 1.5$. As reported above, at this Reynolds number, the mean drag coefficient on an isolated ellipse is ![]() $\bar {C}_{D,{iso}} = 0.1171$, and both the mean lift coefficient
$\bar {C}_{D,{iso}} = 0.1171$, and both the mean lift coefficient ![]() $\bar {C}_{L,{iso}}$ and the mean moment coefficient
$\bar {C}_{L,{iso}}$ and the mean moment coefficient ![]() $\bar {C}_{M,{iso}}$ are zero.
$\bar {C}_{M,{iso}}$ are zero.
4.1 Results
Figure 2 shows the results of the force coefficients on ellipse 0 as a function of ![]() $(x^*,y^*)$, i.e. the relative location of ellipse 1, in a set of contour plots. As the results are symmetric with respect to the sign of
$(x^*,y^*)$, i.e. the relative location of ellipse 1, in a set of contour plots. As the results are symmetric with respect to the sign of ![]() $y^*$, each contour plot shows a different quantity in the top and bottom halves. The top-left contour plot shows a relative drag coefficient of
$y^*$, each contour plot shows a different quantity in the top and bottom halves. The top-left contour plot shows a relative drag coefficient of ![]() $\bar {C}_{D,0}/\bar {C}_{D,{iso}} - 1$, whereas the bottom-left contour plot shows the relative average drag coefficient
$\bar {C}_{D,0}/\bar {C}_{D,{iso}} - 1$, whereas the bottom-left contour plot shows the relative average drag coefficient ![]() $(\bar {C}_{D,0} + \bar {C}_{D,1})/(2\bar {C}_{D,{iso}}) - 1$. The right contour plot shows
$(\bar {C}_{D,0} + \bar {C}_{D,1})/(2\bar {C}_{D,{iso}}) - 1$. The right contour plot shows ![]() $\bar {C}_{L,0}/\bar {C}_{D,{iso}}$ in the top half, and
$\bar {C}_{L,0}/\bar {C}_{D,{iso}}$ in the top half, and ![]() $\bar {C}_{M,0}/\bar {C}_{D,{iso}}$ in the bottom.
$\bar {C}_{M,0}/\bar {C}_{D,{iso}}$ in the bottom.

Figure 2. Contour plot of drag force coefficient changes (left) and lift force/moment coefficient (right) on ellipse 0 travelling right to left (![]() $Re = 1500$) as a function of the relative location of ellipse 1 travelling at the same speed. On the left, the top half contour levels indicate
$Re = 1500$) as a function of the relative location of ellipse 1 travelling at the same speed. On the left, the top half contour levels indicate ![]() $C_{D,0}/C_{D,{iso}} - 1$, whereas the bottom half contour levels indicate
$C_{D,0}/C_{D,{iso}} - 1$, whereas the bottom half contour levels indicate ![]() $(C_{D,0}+C_{D,1})/(2C_{D,{iso}}) - 1$. On the right, the top half of the plot shows
$(C_{D,0}+C_{D,1})/(2C_{D,{iso}}) - 1$. On the right, the top half of the plot shows ![]() $C_{L,0}/C_{D,{iso}}$ and the bottom half shows
$C_{L,0}/C_{D,{iso}}$ and the bottom half shows ![]() $C_{M,0}/C_{D,{iso}}$, where the lift coefficient is defined positive when repulsive, and negative when attractive; similarly, the moment coefficient is defined positive for bow-out and negative for bow-in. In all plots, the zero contour is indicated with a solid black line, and the simulated data points by solid black circles.
$C_{M,0}/C_{D,{iso}}$, where the lift coefficient is defined positive when repulsive, and negative when attractive; similarly, the moment coefficient is defined positive for bow-out and negative for bow-in. In all plots, the zero contour is indicated with a solid black line, and the simulated data points by solid black circles.
The behaviour of the drag coefficient shows that, generally, a side-by-side configuration is equally disadvantageous for both ellipses, with a drag coefficient increase of around 24 % for the closest lateral separation of ![]() $y^*=0.3$, decaying to 5 %–10 % for
$y^*=0.3$, decaying to 5 %–10 % for ![]() $y^*=0.6$, depending on the precise value of
$y^*=0.6$, depending on the precise value of ![]() $x^*$. Staggered configurations reduce the drag only for the trailing ellipse when
$x^*$. Staggered configurations reduce the drag only for the trailing ellipse when ![]() $0.5 < |x^*| < 1.0$, and for both ellipses when
$0.5 < |x^*| < 1.0$, and for both ellipses when ![]() $|x^*| > 1.0$ – although disproportionately so for the trailing ellipse. A completely in-line configuration leads to up to 60 % drag decrease of the trailing ellipse, and approximately 5 % for the leading ellipse. Taken together, the average drag of both ellipses decreases compared with an isolated ellipse for
$|x^*| > 1.0$ – although disproportionately so for the trailing ellipse. A completely in-line configuration leads to up to 60 % drag decrease of the trailing ellipse, and approximately 5 % for the leading ellipse. Taken together, the average drag of both ellipses decreases compared with an isolated ellipse for ![]() $|x^*| > 0.6$.
$|x^*| > 0.6$.
The lift coefficient (top-right in figure 2) shows the lift coefficient on ellipse 0 as repulsive for ![]() $x^* < 0.6$, i.e. for configurations where the second ellipse is slightly in front, side by side and aft of ellipse 0. Only for
$x^* < 0.6$, i.e. for configurations where the second ellipse is slightly in front, side by side and aft of ellipse 0. Only for ![]() $x^* > 0.6$, i.e. a staggered configuration where the second ellipse is further in front of ellipse 0, does the nature of the lift coefficient on ellipse 0 change to attractive. The behaviour of the moment coefficient follows largely that of the lift coefficient. The lift and moment coefficients are normalized with
$x^* > 0.6$, i.e. a staggered configuration where the second ellipse is further in front of ellipse 0, does the nature of the lift coefficient on ellipse 0 change to attractive. The behaviour of the moment coefficient follows largely that of the lift coefficient. The lift and moment coefficients are normalized with ![]() $\bar {C}_{D,{iso}}$ to demonstrate that, by far, these effects dominate those observed on drag. Specifically, the peak mean repulsive lift coefficient is approximately four times
$\bar {C}_{D,{iso}}$ to demonstrate that, by far, these effects dominate those observed on drag. Specifically, the peak mean repulsive lift coefficient is approximately four times ![]() $\bar {C}_{D,{iso}}$ for the closest lateral separation distance
$\bar {C}_{D,{iso}}$ for the closest lateral separation distance ![]() $y^*=0.3$. With our normalization, any moment coefficient
$y^*=0.3$. With our normalization, any moment coefficient ![]() $\bar {C}_{M}$ is statically equivalent to a force couple of the same value applied to the front and aft of the ellipse. From figure 2, we observe that this force couple reaches values comparable to
$\bar {C}_{M}$ is statically equivalent to a force couple of the same value applied to the front and aft of the ellipse. From figure 2, we observe that this force couple reaches values comparable to ![]() $\bar {C}_{D,{iso}}$. These big changes in
$\bar {C}_{D,{iso}}$. These big changes in ![]() $\bar {C}_{L}$ and
$\bar {C}_{L}$ and ![]() $\bar {C}_{M}$, from their zero values for an isolated ellipse, dominate compared with the changes in
$\bar {C}_{M}$, from their zero values for an isolated ellipse, dominate compared with the changes in ![]() $\bar {C}_{D}$ for both ellipses. From a practical perspective, this means that the manoeuvring cost of maintaining a given vehicle formation will be important. Consequently, any analysis of changes in drag coefficients between different configuration is incomplete when that cost is not taken into account.
$\bar {C}_{D}$ for both ellipses. From a practical perspective, this means that the manoeuvring cost of maintaining a given vehicle formation will be important. Consequently, any analysis of changes in drag coefficients between different configuration is incomplete when that cost is not taken into account.
4.2 Discussion
A significant body of work exists on the flow-mediated interactions between two 2-D cylinders placed in various configurations, and the related effects on the drag, lift and moment coefficients (Reference HoriHori 1959; Reference ZdravkovichZdravkovich 1977; Reference SumnerSumner 2010). Notably, these studies find reduced drag for in-line configurations and mean average drag increases for side-by-side configurations, similar to our work. Further, they find repulsive lift coefficients in side-by-side configurations, and slight attractive lift forces for narrow staggered arrangements. These features are common to our results as well. The Reynolds number effect on these qualitative regimes seems to be relatively small, and our qualitative results at ![]() $Re=1500$ match well those at Reynolds numbers ten or a hundred times larger. Available results on side-by-side spheres (all in the Reynolds number range
$Re=1500$ match well those at Reynolds numbers ten or a hundred times larger. Available results on side-by-side spheres (all in the Reynolds number range ![]() $50 \le Re \le 300$) also show a repulsive lift force for the separation distances considered here (Reference Kim, Elghobashi and SirignanoKim, Elghobashi & Sirignano 1993; Reference Brydon and ThompsonBrydon & Thompson 2001; Reference Yoon and YangYoon & Yang 2007). Further, the experimental results of Reference Kurt and MooredKurt & Moored (2018) show that, for in-phase pitching motions, a pair of tandem wings also experiences a net repulsive lift force.
$50 \le Re \le 300$) also show a repulsive lift force for the separation distances considered here (Reference Kim, Elghobashi and SirignanoKim, Elghobashi & Sirignano 1993; Reference Brydon and ThompsonBrydon & Thompson 2001; Reference Yoon and YangYoon & Yang 2007). Further, the experimental results of Reference Kurt and MooredKurt & Moored (2018) show that, for in-phase pitching motions, a pair of tandem wings also experiences a net repulsive lift force.
Comparing with UUV results, the drag interactions observed in this study also qualitatively resembled those in Reference Rattanasiri, Wilson and PhillipsRattanasiri et al. (2014) and Reference Tian, Mao, Zhao and ZhaoTian et al. (2017), who characterized drag interactions between twin prolate spheroids at ![]() $Re=\mathcal {O}(10^6)$ using RANS simulations. A notable exception was that the push region identified by Reference Rattanasiri, Wilson and PhillipsRattanasiri et al. (2014) in the closest tandem configuration of
$Re=\mathcal {O}(10^6)$ using RANS simulations. A notable exception was that the push region identified by Reference Rattanasiri, Wilson and PhillipsRattanasiri et al. (2014) in the closest tandem configuration of ![]() $(x^*, y^*) = (-1.17, 0.0)$ was not observed in the results of this study. Apart from the large difference in Reynolds number (which did not otherwise affect the drag interaction regions significantly), the lack of a push region could be attributed to limitations in the chosen grid resolution between ellipses at the closest spacing, or a small difference in the flow characteristics of two dimensions versus three dimensions at this location. However, the inconsistency at this configuration is not particularly relevant to the UUV application because neither simulation accounts for propeller effects, which are expected to make a sizable difference in the flow characteristics when one UUV is positioned in the wake of the other.
$(x^*, y^*) = (-1.17, 0.0)$ was not observed in the results of this study. Apart from the large difference in Reynolds number (which did not otherwise affect the drag interaction regions significantly), the lack of a push region could be attributed to limitations in the chosen grid resolution between ellipses at the closest spacing, or a small difference in the flow characteristics of two dimensions versus three dimensions at this location. However, the inconsistency at this configuration is not particularly relevant to the UUV application because neither simulation accounts for propeller effects, which are expected to make a sizable difference in the flow characteristics when one UUV is positioned in the wake of the other.
In contrast to the largely matching trends in drag coefficients, our results on the lateral forces are very different compared with UUV results. In particular, several 3-D RANS-based studies at Reynolds numbers of ![]() $\mathcal {O}(10^6)$ show an attractive lift force between side-by-side ellipsoids and similar streamlined bodies, compared with the repulsive lift force reported in this work. Specifically, we believe that Reference Romberg, Chianese and LajoieRomberg et al. (1971), Reference Molland and UtamaMolland & Utama (2002), Reference Leong, Ranmuthugala, Penesis and NguyenLeong et al. (2015), Reference Yuan, He, Kellett, Incecik, Turan and BoulougourisYuan et al. (2015) and Reference Zhang, Chao and PanZhang et al. (2019a) all report attractive lift forces across various scenarios for side-by-side bodies of either equal or different sizes in three dimensions at high Reynolds numbers. This points towards Reynolds number, geometry and/or three-dimensionality effects on the sign of the lift coefficient between side-by-side bodies. Physically, these parameters could all affect pressure gradients on the inside of the gap, and thus the flow acceleration and boundary layer separation location. Other important factors that merit further investigation include blockage in both numerical and experimental settings, and the choice of turbulence model in RANS simulations which is known to affect results on comparable geometries in complex flow conditions (Reference Kim, Rhee and MillerKim, Rhee & Miller 2013).
$\mathcal {O}(10^6)$ show an attractive lift force between side-by-side ellipsoids and similar streamlined bodies, compared with the repulsive lift force reported in this work. Specifically, we believe that Reference Romberg, Chianese and LajoieRomberg et al. (1971), Reference Molland and UtamaMolland & Utama (2002), Reference Leong, Ranmuthugala, Penesis and NguyenLeong et al. (2015), Reference Yuan, He, Kellett, Incecik, Turan and BoulougourisYuan et al. (2015) and Reference Zhang, Chao and PanZhang et al. (2019a) all report attractive lift forces across various scenarios for side-by-side bodies of either equal or different sizes in three dimensions at high Reynolds numbers. This points towards Reynolds number, geometry and/or three-dimensionality effects on the sign of the lift coefficient between side-by-side bodies. Physically, these parameters could all affect pressure gradients on the inside of the gap, and thus the flow acceleration and boundary layer separation location. Other important factors that merit further investigation include blockage in both numerical and experimental settings, and the choice of turbulence model in RANS simulations which is known to affect results on comparable geometries in complex flow conditions (Reference Kim, Rhee and MillerKim, Rhee & Miller 2013).
5. Flow past ellipses during an overtaking manoeuvre
For the overtaking manoeuvres, ellipse 0 moves at a constant speed associated with ![]() $Re_0 = 1500$, and ellipse 1 overtakes ellipse 0 at a constant speed. The overtaking manoeuvre of ellipse 1 is defined in terms of the time-varying speed
$Re_0 = 1500$, and ellipse 1 overtakes ellipse 0 at a constant speed. The overtaking manoeuvre of ellipse 1 is defined in terms of the time-varying speed
 \begin{equation} \tilde{U}_1(t) = \begin{cases} U_0 & t < t_0, \\ U_0 + \dfrac{1}{2}\left(1-\cos\left({\rm \pi}\dfrac{t - t_0}{t_1 - t_0}\right)\right) (U_1 - U_0) & t_0 \le t \le t_1, \\ U_1 & t > t_1. \end{cases} \end{equation}
\begin{equation} \tilde{U}_1(t) = \begin{cases} U_0 & t < t_0, \\ U_0 + \dfrac{1}{2}\left(1-\cos\left({\rm \pi}\dfrac{t - t_0}{t_1 - t_0}\right)\right) (U_1 - U_0) & t_0 \le t \le t_1, \\ U_1 & t > t_1. \end{cases} \end{equation}
The initial window ![]() $t < t_0$ where ellipse 1 moves at the same speed as
$t < t_0$ where ellipse 1 moves at the same speed as ![]() $U_0$ ensures that the wake is developed prior to the start of the relative motion, whereas the transition phase from
$U_0$ ensures that the wake is developed prior to the start of the relative motion, whereas the transition phase from ![]() $t_0$ to
$t_0$ to ![]() $t_1$ is designed to smoothly change the velocity between
$t_1$ is designed to smoothly change the velocity between ![]() $U_0$ and
$U_0$ and ![]() $U_1$. Here, we set
$U_1$. Here, we set ![]() $t^*_0 = 16.7$ and
$t^*_0 = 16.7$ and ![]() $t^*_1 = 19.2$.
$t^*_1 = 19.2$.
In all overtaking simulations, we ensure that the time at which ellipse 1 reaches its ![]() $U_1$ speed coincides with a relative distance of
$U_1$ speed coincides with a relative distance of ![]() $x^*(t_1) = -1.5$, so that we can gather data in the range
$x^*(t_1) = -1.5$, so that we can gather data in the range ![]() $-1.5 \leq x^* \leq 1.5$. This is achieved by integrating equation (5.1) in time to compute the distance travelled by ellipse 1 at
$-1.5 \leq x^* \leq 1.5$. This is achieved by integrating equation (5.1) in time to compute the distance travelled by ellipse 1 at ![]() $t_1$, and then initializing
$t_1$, and then initializing ![]() $x^*(0)$ so that
$x^*(0)$ so that ![]() $x^*(t_1) = -1.5$.
$x^*(t_1) = -1.5$.
We vary the relative speed of ellipse 1 in the range ![]() $1.25 \le U_1/U_0 \le 2$, associated with Reynolds numbers in the range
$1.25 \le U_1/U_0 \le 2$, associated with Reynolds numbers in the range ![]() $1875 \le Re_1 \le 3000$. For each relative speed, we further vary the non-dimensional lateral separation distance
$1875 \le Re_1 \le 3000$. For each relative speed, we further vary the non-dimensional lateral separation distance ![]() $0.3 \le y^* \le 0.6$. We include also the results of the case with no relative motion (
$0.3 \le y^* \le 0.6$. We include also the results of the case with no relative motion (![]() $Re_1 = Re_0 = 1500$) discussed in the previous section, by concatenating the time-averaged force/moment coefficient results at each value of
$Re_1 = Re_0 = 1500$) discussed in the previous section, by concatenating the time-averaged force/moment coefficient results at each value of ![]() $x^*$ into an array, and interpreting the array as if
$x^*$ into an array, and interpreting the array as if ![]() $x^*$ were equivalent to time. In this way, the case without relative motion can be interpreted as an overtaking simulation in the limit of
$x^*$ were equivalent to time. In this way, the case without relative motion can be interpreted as an overtaking simulation in the limit of ![]() $U_1/U_0 \to 1$.
$U_1/U_0 \to 1$.
5.1 Time-varying results
Figure 3 shows how the drag, lift and moment coefficients change as a function of the non-dimensional separation distance ![]() $x^*$. The plot shows results at the smallest separation distance
$x^*$. The plot shows results at the smallest separation distance ![]() $y^* = 0.3$ and all relative velocities
$y^* = 0.3$ and all relative velocities ![]() $1.25 \le U_1/U_0 \le 2$. Further, we superimpose the integrated results from the previous section as a quasi-static approximation of the limit
$1.25 \le U_1/U_0 \le 2$. Further, we superimpose the integrated results from the previous section as a quasi-static approximation of the limit ![]() $U_1/U_0 \to 1$. Similar plots for other values of
$U_1/U_0 \to 1$. Similar plots for other values of ![]() $y^*$ are included in the Appendix.
$y^*$ are included in the Appendix.

Figure 3. Evolution of the drag (a), lift (b) and moment (c) coefficients on ellipse 0 (blue) and ellipse 1 (red) as a function of the non-dimensional separation distance ![]() $x^*$, with time progressing from right to left as indicated by the inset on the top left. The lateral separation distance is fixed at
$x^*$, with time progressing from right to left as indicated by the inset on the top left. The lateral separation distance is fixed at ![]() $y^* = 0.3$. For both ellipses, the lift coefficient is defined positive when repulsive, and negative when attractive; similarly, the moment coefficient is defined positive for bow-out and negative for bow-in. The line colour darkness increases with the Reynolds number of ellipse 1:
$y^* = 0.3$. For both ellipses, the lift coefficient is defined positive when repulsive, and negative when attractive; similarly, the moment coefficient is defined positive for bow-out and negative for bow-in. The line colour darkness increases with the Reynolds number of ellipse 1: ![]() $Re_1 \in [1875, 2250, 2625, 3000]$, and the case
$Re_1 \in [1875, 2250, 2625, 3000]$, and the case ![]() $Re_1 = Re_0 = 1500$ is indicated with a light-coloured dashed line.
$Re_1 = Re_0 = 1500$ is indicated with a light-coloured dashed line.
Starting with the drag, we observe that, at low velocity ratios, the drag of the overtaking ellipse 1 (in red) increases as it approaches ellipse 0, similar to the steady-state results of the previous section. This trend decreases, however, as the velocity ratio increases, and at ![]() $U_1/U_0 = 2$ the drag of ellipse 1 even decreases compared with its isolated value when
$U_1/U_0 = 2$ the drag of ellipse 1 even decreases compared with its isolated value when ![]() $x^* < 0$. Across all cases shown in figure 3, the peak drag on ellipse 1 is achieved when
$x^* < 0$. Across all cases shown in figure 3, the peak drag on ellipse 1 is achieved when ![]() $0 \le x^* \le 0.5$, with the drag coefficients increasing by up to 35 % compared with their values in isolation. At
$0 \le x^* \le 0.5$, with the drag coefficients increasing by up to 35 % compared with their values in isolation. At ![]() $x^* = 1.0$, when ellipse 1 has cleared ellipse 0, the drag of ellipse 1 across all relative velocities has returned to within 10 % of the respective values in isolation. The trend for the overtaken ellipse 0, even though it is always moving at
$x^* = 1.0$, when ellipse 1 has cleared ellipse 0, the drag of ellipse 1 across all relative velocities has returned to within 10 % of the respective values in isolation. The trend for the overtaken ellipse 0, even though it is always moving at ![]() $Re=1500$, is very different. As ellipse 1 approaches, ellipse 0 sees a significant increase in its drag coefficient, with a more pronounced trend for larger velocities of ellipse 1. The highest drag on ellipse 0 is achieved for
$Re=1500$, is very different. As ellipse 1 approaches, ellipse 0 sees a significant increase in its drag coefficient, with a more pronounced trend for larger velocities of ellipse 1. The highest drag on ellipse 0 is achieved for ![]() $U_1/U_0=2$, when the separation distance
$U_1/U_0=2$, when the separation distance ![]() $x^* = -0.35$, and reaches up to
$x^* = -0.35$, and reaches up to ![]() $2.5$ times the isolated drag. As ellipse 1 passes, the trend reverses and ellipse 0 gains a large drag decrease, even gaining a net thrust for the largest velocity ratios around
$2.5$ times the isolated drag. As ellipse 1 passes, the trend reverses and ellipse 0 gains a large drag decrease, even gaining a net thrust for the largest velocity ratios around ![]() $x^* = 0.6$. As ellipse 1 moves ahead of ellipse 0, the drag on ellipse 0 increases again to roughly its isolated value.
$x^* = 0.6$. As ellipse 1 moves ahead of ellipse 0, the drag on ellipse 0 increases again to roughly its isolated value.
The effect of ![]() $U_1/U_0$ on the lift and moment curves are very similar to the drag: for ellipse 1, an increase in
$U_1/U_0$ on the lift and moment curves are very similar to the drag: for ellipse 1, an increase in ![]() $U_1/U_0$ diminishes the deviations from the quasi-static trends (dashed line), whereas for ellipse 0, an increase the overtaking velocity enhances the deviations from the quasi-static trends. The lift coefficients start out attractive for the upstream ellipse 0 and repulsive for the overtaking ellipse 1, changing to repulsive for both in the range
$U_1/U_0$ diminishes the deviations from the quasi-static trends (dashed line), whereas for ellipse 0, an increase the overtaking velocity enhances the deviations from the quasi-static trends. The lift coefficients start out attractive for the upstream ellipse 0 and repulsive for the overtaking ellipse 1, changing to repulsive for both in the range ![]() $-0.5 \le x^* \le 0.7$, and then switching to attractive for ellipse 1 only. This is largely in line with the regimes shown in figure 2 for the stationary interactions. The moment coefficients behave analogously to the lift, again following figure 2. Across all three generalized force coefficients, when
$-0.5 \le x^* \le 0.7$, and then switching to attractive for ellipse 1 only. This is largely in line with the regimes shown in figure 2 for the stationary interactions. The moment coefficients behave analogously to the lift, again following figure 2. Across all three generalized force coefficients, when ![]() $x^*$ exceeds values around
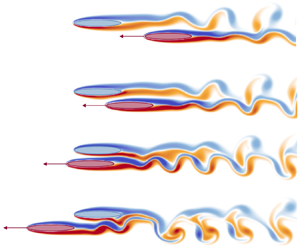
$x^*$ exceeds values around ![]() $0.5$, the curves become oscillatory, predominantly for ellipse 0. Figure 4 shows that this coincides with the unsteady vortices that developed in the wake of ellipse 1, which for
$0.5$, the curves become oscillatory, predominantly for ellipse 0. Figure 4 shows that this coincides with the unsteady vortices that developed in the wake of ellipse 1, which for ![]() $x^*$ roughly larger than
$x^*$ roughly larger than ![]() $0.5$ begin to affect the forces measured on the ellipse 0.
$0.5$ begin to affect the forces measured on the ellipse 0.

Figure 4. Vorticity field at four instances during an overtaking manoeuvre with ![]() $U_1/U_0 = 2$ and
$U_1/U_0 = 2$ and ![]() $y^*=0.3$. Time proceeds from right to left as ellipse 1 (in red) overtakes ellipse 0 (in blue).
$y^*=0.3$. Time proceeds from right to left as ellipse 1 (in red) overtakes ellipse 0 (in blue).
For the specific case of ![]() $U_1/U_0 = 1.5$ and
$U_1/U_0 = 1.5$ and ![]() $y^*=0.3$, figure 5 shows the changes in the force coefficients in a more intuitive sketch, which provides a sense of the qualitative interactions as well as the relative magnitude of the associated force changes. The top sketch confirms that the predominant effects are the lift coefficient changes, which are comparatively stronger on ellipse 0 than on ellipse 1. The bottom sketch shows in more depth the changes in drag coefficient only, demonstrating again that dominant effects occur on ellipse 0, specifically in regions 2 and 4 when ellipse 1 is diagonally behind and in front, respectively.
$y^*=0.3$, figure 5 shows the changes in the force coefficients in a more intuitive sketch, which provides a sense of the qualitative interactions as well as the relative magnitude of the associated force changes. The top sketch confirms that the predominant effects are the lift coefficient changes, which are comparatively stronger on ellipse 0 than on ellipse 1. The bottom sketch shows in more depth the changes in drag coefficient only, demonstrating again that dominant effects occur on ellipse 0, specifically in regions 2 and 4 when ellipse 1 is diagonally behind and in front, respectively.

Figure 5. Changes in drag and lift forces (a) and only drag (b) on the slower ellipse 0 (blue) and the overtaking ellipse 1 (red) during the overtaking manoeuvre (time increases from right to left), at ![]() $y^* = 0.3$ and
$y^* = 0.3$ and ![]() $U_1/U_0 = 1.5$. The force arrows are scaled relative to the drag of an isolated ellipse at the speed of the slower ellipse, with a unit-length vector shown in the top-left rectangle. For the drag (bottom), the scale is increased to better see the relative effects. The forces shown are the mean forces within five interaction regions defined as (from right to left): 1:
$U_1/U_0 = 1.5$. The force arrows are scaled relative to the drag of an isolated ellipse at the speed of the slower ellipse, with a unit-length vector shown in the top-left rectangle. For the drag (bottom), the scale is increased to better see the relative effects. The forces shown are the mean forces within five interaction regions defined as (from right to left): 1: ![]() $-1.5 \le x^* \le -0.9$; 2:
$-1.5 \le x^* \le -0.9$; 2: ![]() $-0.9 \le x^* \le -0.3$; 3:
$-0.9 \le x^* \le -0.3$; 3: ![]() $-0.3 \le x^* \le 0.3$; 4:
$-0.3 \le x^* \le 0.3$; 4: ![]() $0.3 \le x^* \le 0.9$; 5:
$0.3 \le x^* \le 0.9$; 5: ![]() $0.9 \le x^* \le 1.5$.
$0.9 \le x^* \le 1.5$.
Summarizing, we can see that the signs for all force coefficients, as a function of ![]() $x^*$, largely follow the stationary interactions of figure 2 across all values of
$x^*$, largely follow the stationary interactions of figure 2 across all values of ![]() $U_1/U_0$. The main effect of
$U_1/U_0$. The main effect of ![]() $U_1/U_0$ is on the amplitude of the force coefficients: for the overtaken ellipse 0 the amplitudes increase as
$U_1/U_0$ is on the amplitude of the force coefficients: for the overtaken ellipse 0 the amplitudes increase as ![]() $U_1$ increases; for the overtaking ellipse 1 the amplitudes decrease as
$U_1$ increases; for the overtaking ellipse 1 the amplitudes decrease as ![]() $U_1$ increases.
$U_1$ increases.
The variation of the transient force coefficients during overtaking across all various lateral separation distances ![]() $y^*$ is shown in figure 7 in the Appendix. The trends discussed above for
$y^*$ is shown in figure 7 in the Appendix. The trends discussed above for ![]() $y^*=0.3$ remain also at larger values of
$y^*=0.3$ remain also at larger values of ![]() $y^*$, although with less pronounced peak force values and variations as a function of both
$y^*$, although with less pronounced peak force values and variations as a function of both ![]() $x^*$ and
$x^*$ and ![]() $U_1/U_0$.
$U_1/U_0$.
5.2 Time-averaged results
For each combination of ![]() $y^*$ and
$y^*$ and ![]() $U_1/U_0$, we can integrate the drag, lift and moment coefficients for each ellipse between
$U_1/U_0$, we can integrate the drag, lift and moment coefficients for each ellipse between ![]() $x^* = -1.5$ and
$x^* = -1.5$ and ![]() $x^* = 1.5$. Dividing this integral by the elapsed time gives a time-averaged force coefficient, which for
$x^* = 1.5$. Dividing this integral by the elapsed time gives a time-averaged force coefficient, which for ![]() $C_D$ specifically can be interpreted as an averaged power coefficient associated with the cost of the overtaking manoeuvre
$C_D$ specifically can be interpreted as an averaged power coefficient associated with the cost of the overtaking manoeuvre
 \begin{equation} \bar{C}_{P,i} = \frac{\displaystyle \frac{1}{t_e-t_s} \int_{t_s}^{t_e} F_{x,i}(t) \tilde{U}_i(t) \, \text{d} t}{\dfrac{1}{2} \rho U_i^3 L} = \frac{\displaystyle \frac{1}{t_e-t_s} \int_{t_s}^{t_e} F_{x,i}(t) \, \text{d} t}{\dfrac{1}{2} \rho U_i^2 L} = \bar{C}_{D,i}, \end{equation}
\begin{equation} \bar{C}_{P,i} = \frac{\displaystyle \frac{1}{t_e-t_s} \int_{t_s}^{t_e} F_{x,i}(t) \tilde{U}_i(t) \, \text{d} t}{\dfrac{1}{2} \rho U_i^3 L} = \frac{\displaystyle \frac{1}{t_e-t_s} \int_{t_s}^{t_e} F_{x,i}(t) \, \text{d} t}{\dfrac{1}{2} \rho U_i^2 L} = \bar{C}_{D,i}, \end{equation}
as long as ![]() $\tilde {U}_i(t) = U_i$ (
$\tilde {U}_i(t) = U_i$ (![]() $i = 0,1$) between
$i = 0,1$) between ![]() $t_s$ and
$t_s$ and ![]() $t_e$. Here, we choose the integration window such that
$t_e$. Here, we choose the integration window such that ![]() $x^*(t_s) = -1.5$ and
$x^*(t_s) = -1.5$ and ![]() $x^*(t_e) = 1.5$, and both ellipses move at constant velocities during that time.
$x^*(t_e) = 1.5$, and both ellipses move at constant velocities during that time.
Figure 6 shows the average force and moment coefficient values as a function of the speed of the faster ellipse for the range of tested ![]() $y^*$ values. In the plot of mean drag coefficient (left), we further plot the reference drag coefficient of an isolated ellipse
$y^*$ values. In the plot of mean drag coefficient (left), we further plot the reference drag coefficient of an isolated ellipse ![]() $\bar {C}_{D,{iso}}$ at the Reynolds numbers of both ellipses associated with each
$\bar {C}_{D,{iso}}$ at the Reynolds numbers of both ellipses associated with each ![]() $U_1/U_0$ with black dashed lines.
$U_1/U_0$ with black dashed lines.

Figure 6. Average drag (a), lift (b) and moment (c) coefficients on ellipse 0 (circles) and ellipse 1 (squares) during the overtaking manoeuvre, as a function of the velocity ratio ![]() $U_1/U_0$ (
$U_1/U_0$ (![]() $Re_0 = 1500$ throughout). For both ellipses, the lift coefficient is defined positive when repulsive, and negative when attractive; similarly, the moment coefficient is defined positive for bow-out and negative for bow-in. The line colour lightness indicate the non-dimensional separation distance:
$Re_0 = 1500$ throughout). For both ellipses, the lift coefficient is defined positive when repulsive, and negative when attractive; similarly, the moment coefficient is defined positive for bow-out and negative for bow-in. The line colour lightness indicate the non-dimensional separation distance: ![]() $y^* \in [0.3, 0.4, 0.6]$ from darkest to lightest. For the drag coefficient, the black dashed lines indicate the drag coefficient of an isolated ellipse at each ellipse's Reynolds number.
$y^* \in [0.3, 0.4, 0.6]$ from darkest to lightest. For the drag coefficient, the black dashed lines indicate the drag coefficient of an isolated ellipse at each ellipse's Reynolds number.
The mean force values confirm the trends observed in the transient results. The mean drag of ellipse 1 during the overtaking manoeuvre is only slightly increased compared with the value of an isolated ellipse at equivalent Reynolds number. Consequently, the mean drag is largely unaffected by the lateral separation distance. In contrast, the mean drag of ellipse 0 increases significantly as the overtaking speed of ellipse 1 increases, with a peak value of 0.133 or an approximately 13 % increase over the reference value at ![]() $y^*=0.3$ and
$y^*=0.3$ and ![]() $U_1/U_0=2$. For
$U_1/U_0=2$. For ![]() $y^* > 0.3$ the increase appears monotonic with
$y^* > 0.3$ the increase appears monotonic with ![]() $U_1/U_0$, whereas for
$U_1/U_0$, whereas for ![]() $y^*=0.3$ the mean drag drops slightly below the reference value in the range
$y^*=0.3$ the mean drag drops slightly below the reference value in the range ![]() $1 \le U_1/U_0 \le 1.5$. This might be related to the oscillations in the transient drag curve (figure 3, left), which we attribute to the effect of ellipse 1 on the dynamic vortex shedding of ellipse 0. This would imply a possible dependency of the precise transient drag evolution on the phase difference between the start of the overtaking motion and the vortex shedding cycle, likely more pronounced for smaller values of
$1 \le U_1/U_0 \le 1.5$. This might be related to the oscillations in the transient drag curve (figure 3, left), which we attribute to the effect of ellipse 1 on the dynamic vortex shedding of ellipse 0. This would imply a possible dependency of the precise transient drag evolution on the phase difference between the start of the overtaking motion and the vortex shedding cycle, likely more pronounced for smaller values of ![]() $U_1/U_0$. Overall, these results indicate that, during an overtaking manoeuvre between two bodies moving in the same direction, the average power required for the faster-moving overtaking body is largely unchanged from its value in free space. The slower-moving body, however, requires significantly more power to maintain its speed, and this cost increases with the speed difference of the overtaking body.
$U_1/U_0$. Overall, these results indicate that, during an overtaking manoeuvre between two bodies moving in the same direction, the average power required for the faster-moving overtaking body is largely unchanged from its value in free space. The slower-moving body, however, requires significantly more power to maintain its speed, and this cost increases with the speed difference of the overtaking body.
The mean lift coefficient of both ellipses is repulsive for all velocities and lateral distances. For ellipse 0, ![]() $\bar {C}_{L}$ increases with the velocity of ellipse 1, reaching
$\bar {C}_{L}$ increases with the velocity of ellipse 1, reaching ![]() $\bar {C}_{L} = -0.425$ at
$\bar {C}_{L} = -0.425$ at ![]() $y^*=0.3$ and
$y^*=0.3$ and ![]() $U_1/U_0 = 2$, which amounts to
$U_1/U_0 = 2$, which amounts to ![]() $4.5$ times the value of
$4.5$ times the value of ![]() $\bar {C}_{D,{iso}}$ at this Reynolds number. The mean lift coefficient on the faster-moving ellipse 1 decreases with
$\bar {C}_{D,{iso}}$ at this Reynolds number. The mean lift coefficient on the faster-moving ellipse 1 decreases with ![]() $U_1/U_0$, but still reaches values comparable to
$U_1/U_0$, but still reaches values comparable to ![]() $\bar {C}_{D,{iso}}$ for
$\bar {C}_{D,{iso}}$ for ![]() $y^*=0.3$ and
$y^*=0.3$ and ![]() $U_1/U_0=2$. Across all velocity ratios, increasing the lateral distance
$U_1/U_0=2$. Across all velocity ratios, increasing the lateral distance ![]() $y^*$ decreases the magnitude of the mean lift coefficient for both ellipses.
$y^*$ decreases the magnitude of the mean lift coefficient for both ellipses.
5.3 Discussion
Compared with a potential flow study on overtaking manoeuvres of submerged bodies (Reference WangWang 2007), our transient results in viscous flow differ substantially. In Reference WangWang (2007), the lift on the overtaking body is shown to be attractive first and then repulsive, consistent with our observations of ellipse 1; however, the overtaken body experiences an initial repulsion, then strong attraction when the bodies are side by side, followed by repulsion. Our results, in contrast, show that ellipse 0 experiences repulsion during the majority of the manoeuvre. As ellipse 1 pulls ahead, the lateral force on ellipse 0 drops and switches to attraction, at least for the small speed differences. We note that the trends of Reference WangWang (2007) match also potential flow (Reference Yuan, He, Kellett, Incecik, Turan and BoulougourisYuan et al. 2015; Reference Yu, Wang and YeungYu et al. 2019; Reference Muscat-Fenech, Sant, Zheku, Villa and MartelliMuscat-Fenech et al. 2022) and experimental (Reference Vantorre, Verzhbitskaya and LaforceVantorre et al. 2002) studies on ship–ship interactions, although free-surface and/or Reynolds number effects likely play a role in those results.
Our results further show a mean drag increase over the isolated drag coefficient for all separation distances ![]() $y^* > 0.3$, as well as mean repulsive lift coefficients. Increasing the velocity of the overtaking body (ellipse 1) decreases the changes in mean drag and lift on the overtaking body, while increasing the mean forces on the overtaken body (ellipse 0). This observation is consistent with a potential flow analysis of two slender bodies of revolution translating in proximity (Reference WangWang 2007) (§ 4.3 of that work), indicating that these trends can be expected across the entire Reynolds number regime.
$y^* > 0.3$, as well as mean repulsive lift coefficients. Increasing the velocity of the overtaking body (ellipse 1) decreases the changes in mean drag and lift on the overtaking body, while increasing the mean forces on the overtaken body (ellipse 0). This observation is consistent with a potential flow analysis of two slender bodies of revolution translating in proximity (Reference WangWang 2007) (§ 4.3 of that work), indicating that these trends can be expected across the entire Reynolds number regime.
6. Conclusions
In this work we characterize the hydrodynamic interactions due to the flow past two ellipses, focusing on drag and lift forces as a function of spatial configuration and relative motion.
In the absence of relative motion, we find that, depending on the longitudinal positions of the ellipses, the drag interaction is either mutually beneficial (drafting), detrimental (parallel), benefited the trailing ellipse (echelon) or did not produce a significant change on either ellipse (low interaction). The echelon configuration led to as much as a ![]() ${\sim }20\,\%$ drag decrease for the downstream ellipse at the cost of a similar increase for the upstream ellipse. In most configurations, the lift force on both ellipses was repulsive with a significantly (up to four times) larger magnitude than the drag force, with the (bow-out) moment coefficient following a similar trend. In a practical application, this means that the lift will dominate the behaviour of the bodies, which has strong implications in terms of having to manoeuvre the ellipses to maintain their formation. All trends are repeated across the lateral separations tested, with the effect strengthening as the size of the gap between the ellipses reduces. Our results on drag and lift forces are qualitatively consistent with existing studies on cylinder–cylinder interactions at subcritical Reynolds numbers. Comparing with inviscid and high Reynolds number results of UUVs and ships, obtained from RANS simulations as well as potential flow analyses, we find similar trends in the drag coefficient. However, the lift coefficient in those results is predominantly attractive, which would imply a qualitative transition in the behaviour of the lift coefficient associated with viscous and/or 3-D effects.
${\sim }20\,\%$ drag decrease for the downstream ellipse at the cost of a similar increase for the upstream ellipse. In most configurations, the lift force on both ellipses was repulsive with a significantly (up to four times) larger magnitude than the drag force, with the (bow-out) moment coefficient following a similar trend. In a practical application, this means that the lift will dominate the behaviour of the bodies, which has strong implications in terms of having to manoeuvre the ellipses to maintain their formation. All trends are repeated across the lateral separations tested, with the effect strengthening as the size of the gap between the ellipses reduces. Our results on drag and lift forces are qualitatively consistent with existing studies on cylinder–cylinder interactions at subcritical Reynolds numbers. Comparing with inviscid and high Reynolds number results of UUVs and ships, obtained from RANS simulations as well as potential flow analyses, we find similar trends in the drag coefficient. However, the lift coefficient in those results is predominantly attractive, which would imply a qualitative transition in the behaviour of the lift coefficient associated with viscous and/or 3-D effects.
During an overtaking manoeuvre with small speed ratios, the unsteady forces experienced by both ellipses qualitatively match the stationary results at each relative position. As the speed ratio increases, the changes in the mean drag, lift and moment coefficients on the overtaken ellipse increase significantly whereas the corresponding values on the overtaking ellipse diminish slightly, consistent with existing potential flow results. Within an overtaking manoeuvre we observe large variations in the drag and lift coefficients as a function of the relative longitudinal position. While located upstream of the overtaking ellipse, the overtaken ellipse experiences a peak drag increase of up to two-and-a-half times that of an isolated ellipse. This increase is matched by a similar drag decrease in the second half of the manoeuvre. The mean lift interaction between the ellipses is repulsive, with the slower ellipse experiencing a mean lift force up to two-and-a-half times the value under zero relative motion. Transient variations in lift coefficient on the overtaken ellipse increase with relative velocity and lateral proximity.
In general, the ellipses experience high lift and moment coefficients when operating in close proximity, with peak and mean values increasing during overtaking manoeuvres especially for the overtaken ellipse. These interactions tend to increase the difficulty of manoeuvring and need to be corrected by steering, which incurs additional drag forces that diminish any gains made from favourable configuration choices. In comparison with related studies in different flow regimes, we find that the magnitude and sign of the lift and moment coefficients are especially sensitive to variations in Reynolds number and geometry. Our results can be used for modelling these additional induced drag forces, while also pointing towards the need for future research on the sensitivity of the nature of lateral forces to Reynolds number and 3-D effects.
Declaration of interests
The authors declare no conflict of interest.
Funding
P.R. gratefully acknowledges funding from an MIT Mechanical Engineering Graduate Research Fellowship.
Appendix

Figure 7. Drag, lift and moment coefficient variations on ellipse 0 (blue) and ellipse 1 (red) as a function of ![]() $x^*$ during the overtaking manoeuvre. (a–d):
$x^*$ during the overtaking manoeuvre. (a–d): ![]() $y^* = 0.3$,
$y^* = 0.3$, ![]() $y^*=0.4$,
$y^*=0.4$, ![]() $y^*=0.5$,
$y^*=0.5$, ![]() $y^*=0.6$. In each plot, for each ellipse, the line colour becomes darker as
$y^*=0.6$. In each plot, for each ellipse, the line colour becomes darker as ![]() $U_1/U_0$ increases. See figure 3 for full caption.
$U_1/U_0$ increases. See figure 3 for full caption.