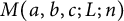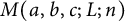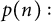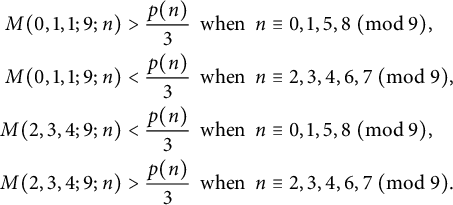Some inequalities between $M(a,b,c;L;n)$ and the partition function $p(n)$

Abstract

Let $p(n)$ and $M(m,L;n)$ be the number of partitions of n and the number of partitions of n with crank congruent to m modulo L, respectively, and let

$$ \begin{align*}M(a,b,c;L;n):= M(a,L;n) + M(b,L;n) + M(c,L;n).\end{align*} $$

In this paper, we focus on some relations between $M(m,L;n)$ and $p(n),$ which Dyson, Andrews, and Garvan etc. have studied previously. By applying a modification of the circle method to estimate the Fourier coefficients of generating functions, we establish the following inequalities between $M(a,b,c;L;n)$ and $p(n):$ for $n \geq 467$,

$$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$

In the proof of these inequalities, an inequality for the logarithm of the generating function for $p(n)$ is derived and applied. Our method reduces the last possible counterexamples to $467 \leq n \leq 22471$, and it will produce more effective estimates when proving inequalities of such types.

1 Introduction

A partition of a positive integer n is a nonincreasing sequence of positive integers whose sum equals n. Typically, $p(n)$ is used to denote the number of partitions of $n.$ The generating function for $p(n)$ is as follows:

$$ \begin{align*} \sum_{n=1}^{\infty} p(n) q^n = \frac{1}{(q;q)_{\infty}}. \end{align*} $$

Here and in what follows, $|q| < 1,$ and

$$ \begin{align*} \quad (a;q)_{\infty}: = \prod_{i=0}^{\infty} (1-aq^{i}). \end{align*} $$

In 1944, Dyson [12] defined the rank of a partition to be the largest part minus the number of parts. Let $N(m;n)$ be the number of partitions of n with rank m and $N(m,L;n)$ the number of partitions of n with rank congruent to m modulo $L.$ Dyson conjectured that

$$ \begin{align*} \begin{aligned} N(a,5;5n+4) = \frac{p(5n+4)}{5}, \\ N(a,7;7n+5) = \frac{p(5n+4)}{7}, \end{aligned} \end{align*} $$

which provide combinatorial proofs for the cases of modulo 5 and 7 in Ramanujan’s congruences. In addition, Dyson conjectured that there exists a crank function for partitions which would supply a combinatorial proof of Ramanujan’s congruences modulo 11. In 1954, Atkin and Swinnerton-Dyer [5] proved the above identities of Dyson by applying the generating function for $N(m,L;n).$

Forty years later, Andrews and Garvan [3] defined the crank function for partitions. Let $M(m;n)$ be the number of partitions of n with crank m and let $M(m,L;n)$ be the number of partitions of n with crank congruent to m modulo $L.$ Andrews and Garvan proved that

$$ \begin{align*} M(m,11;11n+6) = \frac{p(11n+6)}{11}, \quad 0\leq m \leq 10, \end{align*} $$

which provides a combinatorial proof for Ramanujan’s congruences modulo 11. Recently, many inequalities for $M(m,L;n)$ and $N(m,L;n)$ modulo 11 were deduced by Borozenets [7] and Bringmann and Pandey [8]. For inequalities between the rank counts $N(m,L;n)$ or between the crank counts $M(m,L;n),$ see, for example, [1, 10, 11, 16]. For distributions of rank and crank statistics for integer partitions, see, for example, [20, 21].

For convenience, we adopt the following notations:

$$ \begin{align*} \begin{aligned} N(a,b,c;L;n)&:= N(a,L;n) + N(b,L;n) + N(c,L;n), \\ M(a,b,c;L;n)&:= M(a,L;n) + M(b,L;n) + M(c,L;n). \end{aligned} \end{align*} $$

In [15, Theorem 4.1], Kang showed the following relationship between rank and crank:

$$ \begin{align*} \begin{aligned} \sum_{m=-\infty}^{\infty} & \sum_{n=0}^{\infty} (N(3m-1;n)+N(3m;n)+N(3m+1;n))z^m q^n \\ = & \frac{(q^3;q^3)_{\infty}}{(q;q)_{\infty}}\sum_{m=-\infty}^{\infty}\sum_{n=0}^{\infty} M(m;n)z^m q^{3n}. \end{aligned} \end{align*} $$

Inspired by this relationship, Aygin and Chan [6] provided a series of generating functions for $M(a,b,c;L;n)$ . For $L \in \{6,9,12\}$ , Aygin and Chan found generating functions of

$$ \begin{align*} \begin{aligned} N(3j-1,3j,3j+1;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1, \\ M(3j-1,3j,3j+1;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1, \\ M(3j-2,3j-1,3j;L;n), \quad \mathrm{for} ~ 0\leq j \leq L/3 - 1 \end{aligned} \end{align*} $$

and used the periodicity of the sign of the Fourier coefficients of these generating functions to prove many inequalities between $M(a,b,c;L;n)$ and the partition function $p(n).$ At the end of the paper, they proposed 18 inequalities of such type as a conjecture. In [13], Fan, Xia, and Zhao established some generating functions for $N(a,12;n)$ and $M(a,12;n)$ with $0 \leq a \leq 11$ , and used them to confirm the first 6 inequalities in the conjecture of Aygin and Chan. Later, Yao [19] proved that the remaining 12 inequalities hold for sufficiently large n. Simultaneously, at the end of their paper, Aygin and Chan said that “Additionally, the referee pointed out that the signs of theta parts of $M(0,1,1;9;n)$ , $M(2,3,4;9;n)$ , $M(0,1,2;9;n)$ , $M(3,4,5;9;n)$ , and $M(6,7,8;9;n)$ are periodic modulo 9 when $n \geq 467.$ Thus, conjectures similar to Conjecture 8.1 can be stated for $M(0,1,1;9;n)$ , $M(2,3,4;9;n)$ , $M(0,1,2;9;n)$ , $M(3,4,5;9;n)$ and $M(6,7,8;9;n)$ .” Up to now, as far as we are concerned, no inequality for $M(0,1,1;9;n)$ , $M(2,3,4;9;n)$ , $M(0,1,2;9;n)$ , $M(3,4,5;9;n)$ and $M(6,7,8;9;n),$ which is similar to [6, Conjecture 8.1], has been proposed explicitly and proved.

In this paper, we state some inequalities for $M(0,1,1;9;n)$ and $M(2,3,4;9;n)$ and prove them.

Theorem 1.1 For $n \geq 467$ , we have

$$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3}&\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$

We will employ the modification [14] of the circle method ¹ to estimate the Fourier coefficients of generating functions for $M(0,1,1;9;n)$ and $M(2,3,4;9;n)$ , obtaining information about the sign of the coefficients of $g(q)-3h(q)$ (see (3.1) and (3.2) for the definitions of $g(q)$ and $h(q)$ ), and thereby prove the inequalities in Theorem 1.1. An inequality for the logarithm of the generating function for $p(n)$ will be derived and used to reduce the last possible counterexamples to $467 \leq n \leq 22471.$ This method will produce more effective estimates when proving such types of inequalities.

2 Preliminaries

For $f(s) = \sum _{n=0}^{\infty } \alpha (n) s^n$ , we apply the residue theorem to the generating function to get

$$ \begin{align*} \alpha(n) = \frac{1}{2\pi i} \oint_{|s|=r} \frac{f(s)}{s^{n+1}} ds \end{align*} $$

with r smaller than the convergence radius.

2.1 Splitting integral intervals with Farey fractions

We set $r :=e^{-2\pi \varrho }$ with $\varrho =1/N^2$ for some $N>0$ . Let $h/k$ be a Farey fraction of order N, and let $\xi _{h,k} := [-\theta _{h,k}^{\prime },\theta _{h,k}^{\prime \prime }]$ with $\theta _{h,k}^{\prime },\theta _{h,k}^{\prime \prime }$ being the distance from $h/k$ to its neighboring mediants. If we set

$$\begin{align*}s:= r e^{2\pi i \theta} = e^{-2\pi \varrho} e^{2\pi i \theta},\end{align*}$$

and let $\theta := h/k + \varphi $ on each $\xi _{h,k}$ , then

$$\begin{align*}ds = 2\pi i e^{-2\pi \varrho} e^{2\pi i h/k} e^{2\pi i \varphi} d\varphi ,\end{align*}$$

so that

$$ \begin{align*} \alpha(n) = \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i(h/k + i\varrho + \varphi)}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{align*} $$

Set $z:=k(\varrho -i\varphi )$ and $\tau :=(h+iz)/k$ to get

(2.1) $$ \begin{align} \begin{aligned} \alpha(n) &= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i(h+iz)/k}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} f(e^{2\pi i \tau}) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{aligned} \end{align} $$

2.2 Dedekind’s eta-function

The Dedekind eta-function is defined by

$$\begin{align*}\eta(\tau):=q^{1/24}(q;q)_{\infty},\end{align*}$$

where $q=e^{2\pi i \tau }$ with $\mathrm {Im}(\tau )> 0.$ A well-known transformation formula for the Dedekind eta-function is as follows [4, p. 52].

For $\gamma = \left (\begin {matrix} a & b \\ c & d \end {matrix}\right ) \in \varGamma :=\mathrm {SL}_2(\mathbb {Z})$ , $c>0$ , we have [4, Theorem 3.4]

(2.2) $$ \begin{align} \eta(\gamma \tau) = e^{-\pi i s(d,c)} e^{\pi i (a+d)/(12c)} \sqrt{-i(c\tau + d)} \eta(\tau), \end{align} $$

where $s(d,c)$ is the Dedekind sum given by

$$ \begin{align*} s(d,c) := \sum_{n=0}^{c-1} \frac{n}{c} \left(\frac{dn}{c}-\left\lfloor \frac{dn}{c} \right\rfloor-\frac{1}{2} \right). \end{align*} $$

Set

$$ \begin{align*} F(e^{2\pi i \tau}) := \frac{1}{(q;q)_{\infty}} = \frac{e^{\pi i \tau/12}}{\eta(\tau)}. \end{align*} $$

It follows from (2.2) that

$$ \begin{align*} F(e^{2\pi i \tau}) = e^{\pi i (\tau - \gamma\tau)/12} e^{- \pi i s(d,c)} e^{\pi i (a + d)/(12c)} \sqrt{-i(c\tau + d)} F(e^{2\pi i \gamma\tau}). \end{align*} $$

For the interval $\xi _{h,k},$ if $\mathrm {gcd}(n,k)=1$ , then we choose an integer $h_n^{\prime }$ such that $nhh_n^{\prime } \equiv -1 ~ (\mathrm {mod} ~ k).$ Hence, there exists $b_n\in \mathbb {Z}$ such that $nhh_n^{\prime } - b_n k = -1.$ Set

$$ \begin{align*} \gamma_{(nh,k)} := \left(\begin{matrix} h_n^{\prime} & -b_n \\ k & -nh \end{matrix} \right) \in \varGamma. \end{align*} $$

Then,

$$ \begin{align*} \begin{aligned} \gamma_{(nh,k)} = \frac{h_n^{\prime} \frac{nh+inz}{k}-b_n}{k \frac{nh+inz}{k}-nh} = \frac{h_n^{\prime} nh - b_n k + in h_n^{\prime} z}{k i nz} = \frac{h_n^{\prime}}{k} + i\frac{1}{knz}, \end{aligned} \end{align*} $$

so that

(2.3) $$ \begin{align} \mathrm{Im}(\gamma_{(nh,k)}) = \mathrm{Re}\left(\frac{1}{knz}\right) = \frac{1}{kn} \mathrm{Re}\left(\frac{1}{z}\right), \end{align} $$

and

(2.4) $$ \begin{align} F(e^{2\pi i n \tau}) = e^{\frac{\pi}{12k}(\frac{1}{nz}-nz)}e^{\pi i s(nh,k)}\sqrt{nz} F(e^{2\pi i \gamma_{(nh,k)}(n\tau)}). \end{align} $$

2.3 Some bounds and an integral

It is obvious to observe that

$$ \begin{align*} \frac{1}{2kN} \leq \theta_{h,k}^{\prime}, \theta_{h,k}^{\prime \prime} \leq \frac{1}{kN}. \end{align*} $$

From this, we have

$$ \begin{align*} \frac{1}{kN} \leq |\xi_{h,k}| \leq \frac{2}{kN}, \end{align*} $$

and

$$ \begin{align*}|\varphi| \leq (kN)^{-1}.\end{align*} $$

Notice that $z=k(\varrho - i \varphi ).$ Then,

(2.5) $$ \begin{align} \mathrm{Re}\left(\frac{1}{z}\right) = \mathrm{Re}\left(\frac{1}{k(\varrho - i \varphi)}\right) = \frac{1}{k}\frac{\varrho}{\varrho^2 + \varphi^2} \geq \frac{1}{k}\frac{N^{-2}}{N^{-4} + k^{-2}N^{-2}} \geq \frac{k}{2}. \end{align} $$

Also, we have

(2.6) $$ \begin{align} |z|^{-1/2} = \frac{1}{k^{1/2}} \frac{1}{(\varrho^2 + \varphi^2)^{1/4}} \leq \frac{1}{(k^2\varrho^2)^{1/4}} = k^{-1/2} N. \end{align} $$

We now estimate the function $\mathrm {log}F(x)$ for $0 < x < 1.$ Since $0 < x <1$ , we have

$$ \begin{align*} mx^{m-1} \leq \frac{1-x^m}{1-x} = 1 + x + x^2 + \cdots + x^{m-1} \leq m. \end{align*} $$

From this, we deduce that

$$ \begin{align*} \frac{m(1-x)}{x} \leq \frac{1-x^m}{x^m} \leq \frac{m(1-x)}{x^m}, \end{align*} $$

so that

$$ \begin{align*} \frac{x^m}{m^2(1-x)} \leq \frac{x^m}{m(1-x^m)} \leq \frac{x}{m^2(1-x)}. \end{align*} $$

Then

(2.7) $$ \begin{align} \begin{aligned} \mathrm{log}F(x) &= \sum_{n=1}^{\infty} - \mathrm{log}(1-x^n) = \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \frac{x^{nm}}{m} = \sum_{m=1}^{\infty} \frac{x^m}{m(1-x^m)}\\ &\leq \frac{x}{1-x} \sum_{m=1}^{\infty} \frac{1}{m^2} = \frac{\pi^2}{6} \frac{x}{1-x}. \end{aligned} \end{align} $$

Let $q_m(n)$ denote the number of m-colored partitions of n into an even number of distinct parts minus the number of m-colored partitions of n into an odd number of distinct parts. Then, by [2, eq.(6.1.3)]

$$ \begin{align*} \sum_{n=0}^{\infty} q_1(n) e^{2\pi i n \tau} =\frac{1}{F(e^{2\pi i \tau})}= (q;q)_{\infty}. \end{align*} $$

Define $\hat {a}_1(n)$ (resp. $\hat {a}_2(n)$ ) as the number of partitions of n into an even (resp. odd) number of parts with distinct elements. Then, we have $q_1(n) = \hat {a}_1(n) - \hat {a}_2(n).$ Since $0 \leq \hat {a}_1(n) \leq p(n)$ , $0 \leq \hat {a}_2(n) \leq p(n)$ , we have

(2.8) $$ \begin{align} |q_1(n)| = |\hat{a}_1(n) - \hat{a}_2(n)| \leq p(n). \end{align} $$

Then,

(2.9) $$ \begin{align} \begin{aligned} \left| \frac{1}{F(e^{2\pi i \tau})} \right| &\leq \sum_{n=1}^{\infty} |q_1(n)| |e^{2\pi i n \tau}| \leq \sum_{n=1}^{\infty} p(n) |e^{2\pi i n \tau}| \\ &=F(|e^{2\pi i \tau}|) = F(e^{-2\pi \mathrm{Im}(\tau)})\\ & \leq \mathrm{exp} \left(\frac{\pi^2 e^{-2\pi \mathrm{Im}(\tau)}}{6(1-e^{-2\pi \mathrm{Im}(\tau)})}\right), \end{aligned} \end{align} $$

where the last inequality follows from (2.7).

An inequality for $F(e^{2\pi i \tau })$ is given in the following lemma.

Lemma 2.1 Let $\tau _1,\tau _2,\cdots ,\tau _n \in \mathbb {C}$ and let $m_1,m_2,\cdots ,m_n \in \mathbb {Z}\backslash \{0\}.$ Then,

(2.10) $$ \begin{align} \left|\prod_{i=1}^{n} F(e^{2\pi i \tau_i})^{m_i} - 1\right| \leq \mathrm{exp}\left(\sum_{i=1}^{n} \frac{|m_i| \pi^2 e^{-2\pi \mathrm{Im}(\tau_i)}}{6(1-e^{-2\pi \mathrm{Im}(\tau_i)})} \right) - 1. \end{align} $$

Proof Let

$$ \begin{align*} F(e^{2\pi i \tau_i})^{m_i} =: \sum_{n=1}^{\infty} c_i(n) e^{2\pi i n \tau_i}, \quad F(e^{2\pi i \tau_i})^{|m_i|} =: \sum_{n=1}^{\infty} \tilde{c}_i(n) e^{2\pi i n \tau_i}. \end{align*} $$

If $m_i \geq 0$ , then $|c_i(n)| = \tilde {c}_i(n);$ if $m_i < 0$ , then, by (2.8),

$$ \begin{align*} |c_i(n)| \leq \sum_{\substack{1 \leq j \leq |m_i| \\ \sum n_j= n}} |q_1(n_j)| \leq \sum_{\substack{1 \leq j \leq |m_i| \\ \sum n_j = n}} p(n_j) = \tilde{c}_i(n). \end{align*} $$

Hence, by (2.7),

$$ \begin{align*} \begin{aligned} \left|\prod_{i=1}^{n} F(e^{2\pi i \tau_i})^{m_i} - 1\right| &\leq \left|\sum_{k_1=0}^{\infty}\cdots \sum_{k_n=0}^{\infty}c_1(k_1)\cdots c_n(k_n)e^{2\pi i k_1 \tau_1}\cdots e^{2\pi i k_n \tau_n} - 1\right|\\ & \leq \mathop{\sum_{k_1=0}^{\infty} \cdots\sum_{k_n=0}^{\infty}}\limits_{(k_1,\cdots,k_n)\neq (0,\cdots,0)} \tilde{c}_1(k_1)\cdots \tilde{c}_n(k_n)|e^{2\pi i k_1 \tau_1}|\cdots |e^{2\pi i k_n \tau_n}|\\&= \prod_{i=1}^{n} F(|e^{2\pi i \tau_i}|)^{|m_i|} - 1\\ &\leq \mathrm{exp}\left(\sum_{i=1}^{n} \frac{|m_i| \pi^2 e^{-2\pi \mathrm{Im}(\tau_i)}}{6(1-e^{-2\pi \mathrm{Im}(\tau_i)})} \right) - 1. \end{aligned} \end{align*} $$

This completes the proof.

To facilitate certain bounds in the proof of Theorem 1.1, we examine monotonicity of a function here.

Lemma 2.2 Let $u_1,u_2,\cdots ,u_n \in \mathbb {R}_{\geq 1}$ and let $m_1,m_2,\cdots ,m_n \in \mathbb {N}.$ Then,

$$ \begin{align*} W(x) := \frac{1}{x}\left(\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) - 1\right) \end{align*} $$

is a nondecreasing function of x on $(0,1)$ .

Proof Taking derivative of $W(x)$ yields

$$ \begin{align*} \begin{aligned} W^{\prime}(x) = & -\frac{1}{x^2}\left(\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) - 1\right) \\ & + \frac{1}{x}\mathrm{exp}\left(\sum_{i=1}^{n} \frac{m_i \pi^2 x^{u_i}}{6(1-x^{u_i})}\right) \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i-1}}{(1-x^{u_i})^2}\right). \end{aligned} \end{align*} $$

Therefore, it suffices to prove

(2.11) $$ \begin{align} \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i}}{(1-x^{u_i})^2}\right) + \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right) \geq 1 \end{align} $$

for $x \in (0,1)$ . Since

$$ \begin{align*} \frac{u_ix^{u_i}}{(1-x^{u_i})^2} - \frac{x^{u_i}}{1-x^{u_i}} = \frac{(u_i-1) x^{u_i} + x^{2u_i}}{(1-x^{u_i})^2}\geq 0 \end{align*} $$

for $u_i \geq 1$ , we have

(2.12) $$ \begin{align} \begin{aligned} & \sum_{i=1}^{n}\frac{\pi^2 m_i}{6} \left(\frac{u_ix^{u_i}}{(1-x^{u_i})^2}\right) + \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right) \\ &\qquad \geq \sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}+ \mathrm{exp}\left(-\sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}\right). \end{aligned} \end{align} $$

Let

$$ \begin{align*} y := \sum_{i=1}^{n} \frac{\pi^2 m_i}{6}\frac{x^{u_i}}{1-x^{u_i}}. \end{align*} $$

Then, $y>0$ , and so $y + e^{-y} \geq 1.$ From this and (2.12), we easily obtain the inequality (2.11).

An estimate for a useful integral is given in the following form. Even though it contains the result in [9, Lemma 3.2] as a special case, its proof is similar to that of [9, Lemma 3.2], and we omit it here.

Lemma 2.3 Let $(h,k)=1$ , $b \in \mathbb {R}_{\geq 0}$ , and define

$$ \begin{align*} I := \int_{\xi_{h,k}} e^{\frac{\pi}{12k}(\frac{b}{z}-z)} z^{-\frac{1}{2}} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi. \end{align*} $$

Then,

$$ \begin{align*} I = \sqrt{\frac{2}{k(n-1/24)}} b^{1/4} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2b}{3}\left(n-\frac{1}{24}\right)} \right) + E^{(b)}(I), \end{align*} $$

where

$$ \begin{align*} |E^{(b)}(I)| \leq \sqrt{2} \pi^{-1} e^{b \pi / 3 } \frac{e^{2\pi (n-1/24) \varrho} N^{1/2}}{n-1/24}. \end{align*} $$

The following inequalities are also important in the proof of Theorem 1.1.

$$ \begin{align*} \sum_{k=1}^{N} k^n \leq \begin{cases} N^{n+1}, & \mathrm{if} ~ n\geq0, \\ \frac{1}{n+1} N^{n+1}, & \mathrm{if} ~ -1 < n<0. \end{cases} \end{align*} $$

3 Proof of Theorem 1.1

Let

(3.1) $$ \begin{align} \sum_{n=0}^{\infty} a(n) q^n := \frac{(q^9;q^9)_{\infty}^{3}}{(q;q)_{\infty}(q^{27};q^{27})_{\infty}} = \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3}=: g(q) \end{align} $$

and

(3.2) $$ \begin{align} \begin{aligned}\sum_{n=0}^{\infty} b(n) q^n &:= q^2 \frac{(q^3;q^3)_{\infty}(q^{27};q^{27})_{\infty}^2}{(q;q)_{\infty}(q^9;q^9)_{\infty}}\\ &= e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}=: h(q) \end{aligned}\end{align} $$

with $q=e^{2\pi i \tau }.$

In this section, we first employ the modification [14] of the circle method to estimate the coefficient $a(n)$ of $g(q)$ and the coefficient $b(n)$ of $h(q)$ and then obtain information about the sign of the coefficients $\{a(n) - 3b(n)\}_{n \geq 0}$ of $g(q)-3h(q).$ Finally, by [6, eqs.(2.10) and (2.11)], we know that

$$ \begin{align*} \begin{aligned} M(0,1,1;9;n) - \frac{p(n)}{3} &= \frac{2}{3}(a(n) - 3b(n) ), \\ M(2,3,4;9;n) - \frac{p(n)}{3} &= -\frac{1}{3}(a(n) - 3b(n) ). \end{aligned} \end{align*} $$

Therefore, from the sign information of the coefficients $\{a(n) - 3b(n)\}_{n \geq 0}$ , we can deduce the inequalities in Theorem 1.1.

Since $\mathrm {gcd}(k,27)=1,3,9$ or $27,$ we split each of the sums $\sum _{\substack {0 \leq h<k \leq N \\ (h,k) = 1}}$ for $a(n)$ and $b(n)$ into four parts according to the values of $\mathrm {gcd}(k,27).$

It follows from (2.1) that

(3.3) $$ \begin{align} \begin{aligned} a(n)&= \sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=\bigg(\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}}\bigg) \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \\ & \;\;\times \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=: S_1(A) + S_2(A) + S_3(A) + S_4(A) \end{aligned} \end{align} $$

with

$$ \begin{align*} A = \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} \end{align*} $$

and

$$ \begin{align*} z = k(\varrho - i\varphi), \qquad \tau = \frac{h+iz}{k}. \end{align*} $$

Similarly, we get

(3.4) $$ \begin{align} \begin{aligned} b(n)&=\sum_{\substack{0 \leq h<k \leq N \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=\bigg (\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}}\bigg) \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \\ &\;\;\times \int_{\xi_{h,k}} e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &=: S_1(B) + S_2(B) + S_3(B) + S_4(B) \end{aligned} \end{align} $$

with

$$ \begin{align*} B = e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi}. \end{align*} $$

3.1 Transformation formulas for g and h

We apply (2.4) to transform g and h according to the values of $\mathrm {gcd}(k,27).$

Case 1: $\mathrm {gcd}(k,27)=1$ . By (2.4), we have

(3.5) $$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3}\ &= \frac{1}{3 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} \\ &\quad\times e^{\pi i (s(h,k) + s(27h,k) - 3s(9h,k))} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \end{aligned} \end{align} $$

and

(3.6) $$ \begin{align} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad= \frac{1}{9 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})}{F(e^{2\pi i \gamma_{(3h,k)} (3\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})^2} \\ &\qquad\times e^{2\pi i (2h/k)} e^{\pi \frac{-48z}{12k}}e^{\pi i (s(h,k) + s(9h,k) - s(3h,k) - 2s(27h,k))} e^{\frac{\pi}{12k}(\frac{19}{27z} + 47z)} \\ &\quad= \frac{1}{9 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})}{F(e^{2\pi i \gamma_{(3h,k)} (3\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})^2} \\ &\qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,k) + s(9h,k) - s(3h,k)) - 2s(27h,k)} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)}. \end{aligned} \end{align} $$

Case 2: $\mathrm {gcd}(k,27)=3$ . Let $k = 3l_1.$ Then,

(3.7) $$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} &= \frac{1}{\sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})}{F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})^3}\\ &\quad \times e^{\pi i (s(h,3l_1) + s(9h,l_1) - 3s(3h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)} \end{aligned} \end{align} $$

and

(3.8) $$ \begin{align} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{3 \sqrt{3} \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,l_1)} (3\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})^2}\\ & \qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,3l_1) + s(3h,l_1) - s(h,l_1) - 2s(9h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)}. \end{aligned} \end{align} $$

Case 3: $\mathrm {gcd}(k,27)=9$ . Let $k = 9l_2.$ It follows that

$$ \begin{align*} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} &= \frac{\sqrt{3}}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})}{F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})^3}\\ &\quad \times e^{\pi i (s(h,9l_2) + s(3h,l_2) - 3s(h,l_2))} e^{\frac{\pi}{12k}(-\frac{23}{z} - z)} \end{aligned} \end{align*} $$

and

$$ \begin{align*} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{3 \sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2}\\ &\qquad \times e^{2\pi i (2h/k)} e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))} e^{\frac{\pi}{12k}(\frac{1}{z} - z)}. \end{aligned} \end{align*} $$

Case 4: $\mathrm {gcd}(k,27)=27$ . Let $k = 27l_3.$ We have

(3.9) $$ \begin{align} \begin{aligned} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} = & \frac{1}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,27l_3)} (\tau)})F(e^{2\pi i \gamma_{(h,l_3)} (27\tau)})}{F(e^{2\pi i \gamma_{(h,3l_3)} (9\tau)})^3} \\ & \times e^{\pi i (s(h,27l_3) + s(h,l_3) - 3s(h,3l_3))} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \end{aligned} \end{align} $$

and

$$ \begin{align*} \begin{aligned} &e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2}\\ &\quad=\frac{1}{\sqrt{z}} \frac{F(e^{2\pi i \gamma_{(h,27l_3)} (\tau)})F(e^{2\pi i \gamma_{(h,3l_3)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,9l_3)} (3\tau)})F(e^{2\pi i \gamma_{(h,l_3)} (27\tau)})^2} \\ &\qquad\times e^{2\pi i (2h/k)} e^{\pi i (s(h,27l_3) + s(h,3l_3) - s(h,9l_3) - 2s(h,l_3))} e^{\frac{\pi}{12k}(-\frac{47}{z} -z)}. \end{aligned} \end{align*} $$

From the above transformation formulas for g and h, we see that the integrands of the integrals in $S_2(A), S_2(B),S_3(A)$ , and $S_4(B)$ have factors of the forms $e^{\frac {\delta }{z}}$ with $\delta <0.$ For these integrals, we use (2.3), (2.5), (2.6), and (2.9) to give bounds. However, since the integrands of the integrals in $S_1(A), S_1(B), S_3(B)$ , and $S_4(A)$ contain factors of the forms $e^{\frac {\delta }{z}}$ with $\delta>0,$ we split these integrals into two parts and then apply Lemma 2.2, (2.3), (2.5), (2.6), and (2.10) to estimate the second parts. For the first parts, we employ Lemma 2.3 to tackle the integrals. It should be mentioned that our main term $P(n)$ (in Subsection 3.3) originates from $S_3(B).$

3.2 Bounding $S_2(A)$ , $S_2(B)$ , $S_3(A)$ , and $S_4(B)$

For $S_2(A)$ , we apply (3.7) to deduce that

$$ \begin{align*} \begin{aligned} A = & \frac{1}{\sqrt{3}} z^{-\frac{1}{2}} e^{\pi i (s(h,3l_1) + s(9h,l_1) - 3s(3h,l_1))} e^{\frac{\pi}{12k} \left(-\frac{5}{3z}-z\right)} \\ & \times \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})}{F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})^3} e^{2 \pi n \varrho} e^{-2 \pi i n \varphi} \end{aligned} \end{align*} $$

with $k=3l_1$ . Using (2.3), (2.5), (2.6), and (2.9), we find that

$$ \begin{align*} \begin{aligned} |A| \leq & \frac{1}{\sqrt{3}} F(e^{-2\pi(\frac{1}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{9z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{3z})})^3 \\ & \times e^{-\frac{5\pi}{36k}\mathrm{Re}(\frac{1}{z})} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-\frac{1}{2}} e^{2\pi n \varrho} \\ \leq & \frac{1}{\sqrt{3}} \mathrm{exp}\left(\frac{2\pi^2 e^{-\pi}}{3(1-e^{-\pi})} + \frac{\pi^2 e^{-\pi/3}}{6(1-e^{-\pi/3})}\right) \times e^{-\frac{5\pi}{72}} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \\ \leq & \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N. \end{aligned} \end{align*} $$

So we have

$$ \begin{align*} \begin{aligned} |S_2(A)| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \frac{1}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} \frac{2}{k^{\frac{3}{2}}} \\ \leq & \frac{2}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} \sum_{1 \leq k \leq N} k^{-\frac{1}{2}} \\ \leq & \frac{4}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{aligned} \end{align*} $$

For $S_2(B)$ , we apply (3.8) to give

$$ \begin{align*} \begin{aligned} B = & \frac{1}{3 \sqrt{3}} z^{-\frac{1}{2}} e^{2\pi i (2h/k)} e^{\pi i (s(h,3l_1) + s(3h,l_1) - s(h,l_1) - 2s(9h,l_1))} e^{\frac{\pi}{12k}(-\frac{5}{3z} - z)} \\ & \times \frac{F(e^{2\pi i \gamma_{(h,3l_1)} (\tau)})F(e^{2\pi i \gamma_{(3h,l_1)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,l_1)} (3\tau)})F(e^{2\pi i \gamma_{(9h,l_1)} (27\tau)})^2} e^{2 \pi n \varrho} e^{-2 \pi i n \varphi} \end{aligned} \end{align*} $$

with $k=3l_1$ . Using (2.3), (2.5), (2.6), and (2.9), we find that

$$ \begin{align*} \begin{aligned} |B| \leq & \frac{1}{3\sqrt{3}} F(e^{-2\pi(\frac{1}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{3z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{z})}) F(e^{-2\pi(\frac{3}{k})\mathrm{Re}(\frac{1}{9z})})^2 \\ & \times e^{-\frac{5\pi}{36k}\mathrm{Re}(\frac{1}{z})} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-\frac{1}{2}} e^{2\pi n \varrho} \\ \leq & \frac{1}{3\sqrt{3}} \mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{3(1-e^{-\pi})} + \frac{\pi^2 e^{-3\pi}}{6(1-e^{-3\pi})} + \frac{\pi^2 e^{-\pi/3}}{3(1-e^{-\pi/3})}\right) e^{-\frac{5\pi}{72}} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \\ \leq & \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N \end{aligned} \end{align*} $$

and

$$ \begin{align*} \begin{aligned} |S_2(B)| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} k^{-\frac{1}{2}} N d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 3}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \frac{1}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} \frac{2}{k^{\frac{3}{2}}} \\ \leq & \frac{2}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} \sum_{1 \leq k \leq N} k^{-\frac{1}{2}} \\ \leq & \frac{4}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{aligned} \end{align*} $$

Similarly, for $S_3(A)$ and $S_4(B)$ , we get

$$ \begin{align*} |S_3(A)| \leq 4\sqrt{3} e^{-2.047} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}} \end{align*} $$

and

$$ \begin{align*} |S_4(B)| \leq 4e^{-6.077} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}. \end{align*} $$

3.3 Tackling $S_1(A)$ , $S_1(B)$ , $S_3(B)$ , and $S_4(A)$

For $S_1(A)$ , set

$$ \begin{align*}\omega^{(1)}_{(h,k)} := e^{\pi i (s(h,k) + s(27h,k) - 3s(9h,k))}.\end{align*} $$

We apply (3.5) to deduce

$$ \begin{align*} S_1(A) &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \int_{\xi_{h,k}} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (27\tau)})}{F(e^{2\pi i (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \\ & \quad\times \frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag &\quad + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} \\ \notag & \quad\times \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ \notag & =: T_{1} + T_{2}. \notag \end{align*} $$

By (2.9) and (2.10), we have

$$ \begin{align*} \begin{aligned} \left| e^{\frac{\pi}{12k}\left(\frac{19}{27z}\right)} \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) \right| \leq e^{\frac{19\pi}{27\times12k}\mathrm{Re}\left(\frac{1}{z}\right)} \left( e^{f(k,z)}- 1\right), \end{aligned} \end{align*} $$

where

$$ \begin{align*}f(k,z)=\frac{\pi^2 e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{\pi^2 e^{-2\pi \frac{1}{27k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{27k} \mathrm{Re}(\frac{1}{z})})} + \frac{3\pi^2 e^{-2\pi \frac{1}{9k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{9k} \mathrm{Re}(\frac{1}{z})})} .\end{align*} $$

Let

$$ \begin{align*} x := e^{-\frac{19\pi}{27\times12k}\mathrm{Re}\left(\frac{1}{z}\right)}. \end{align*} $$

Then,

$$ \begin{align*} \begin{aligned} & \left| e^{\frac{\pi}{12k}\left(\frac{19}{27z}\right)} \left(\frac{F(e^{2\pi i \gamma_{(h,k)} (\tau)})F(e^{2\pi i \gamma_{(27h,k)} (27\tau)})}{F(e^{2\pi i \gamma_{(9h,k)} (9\tau)})^3} - 1 \right) \right| \\ &\quad \leq \frac{1}{x} \left(\mathrm{exp}\left(\frac{\pi^2 x^{\frac{648}{19}}}{6(1-x^{\frac{648}{19}})}+\frac{\pi^2 x^{\frac{24}{19}}}{6(1-x^{\frac{24}{19}})}+\frac{3\pi^2 x^{\frac{72}{19}}}{6(1-x^{\frac{72}{19}})}\right) - 1\right)=: W_1(x). \end{aligned} \end{align*} $$

By Lemma 2.2 and (2.5), we get

$$ \begin{align*} \begin{aligned} W_1(x) & \leq W_1(e^{-\frac{19\pi}{648}}) = e^{\frac{19\pi}{648}} \left(\mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{6(1-e^{-\pi})}+\frac{\pi^2 e^{-\pi/27}}{6(1-e^{-\pi/27})}+\frac{3\pi^2 e^{-\pi/9}}{6(1-e^{-\pi/9})}\right) - 1\right) \\ & \leq 9.819 \times 10^{10}. \end{aligned} \end{align*} $$

Then, by (2.6),

$$ \begin{align*} \begin{aligned} |T_{2}| \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} 1.890 \times 10^{10} e^{-\frac{\pi}{12k}\mathrm{Re}(z)} |z|^{-1/2} e^{-2\pi i n \varrho} d\varphi \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} 1.890 \times 10^{10} e^{2\pi (n - 1/24) \varrho} \frac{2}{k^{3/2}} \\ \leq & \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} 1.890 \times 10^{10} e^{2\pi (n - 1/24) \varrho} \frac{2}{k^{1/2}} \\ \leq & 7.560 \times 10^{10} e^{2\pi (n - 1/24) \varrho} N^{1/2}. \end{aligned} \end{align*} $$

Similarly, we use (3.6) to derive that

$$ \begin{align*} S_1(B)=R_{1} + R_{2}, \end{align*} $$

where

$$ \begin{align*} \begin{aligned} R_{1} := \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{9 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi, \end{aligned} \end{align*} $$

and

$$ \begin{align*} |R_{2}| \leq 1.435 \times 10^{13} e^{2\pi i (n - 1/24) \varrho} N^{1/2}. \end{align*} $$

Here, $\omega ^{(2)}_{(h,k)} := e^{\pi i (s(h,k) + s(9h,k) - s(3h,k) - 2s(27h,k))}.$

Using the software Mathematica, we find that ²

(3.10) $$ \begin{align} 4s(9h,k) - s(3h,k) -3s(27h,k) + \frac{4h}{k} \equiv 0 ~~ (\mathrm{mod} ~ 2), \end{align} $$

where $0\leq h < k \leq 17, (k,3)=1$ , and $(h,k)=1.$ From this, we have

$$ \begin{align*} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} = \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)} \end{align*} $$

with $k \leq 17$ and $\mathrm {gcd}(k,27)=1.$ Then,

$$ \begin{align*} \begin{aligned} |T_{1} - 3R_{1}| &= \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &\quad - \big. \sum_{\substack{1 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)}\\&\quad \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \bigg| \\& \leq \bigg|\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(1)}_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\bigg| \\ &\quad + \bigg|\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \omega^{(2)}_{(h,k)}\\&\quad \int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\bigg|. \end{aligned} \end{align*} $$

By Lemma 2.3, we have

$$ \begin{align*} &\sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \left|\int_{\xi_{h,k}} \frac{1}{3 \sqrt{3} \sqrt{z}} e^{\frac{\pi}{12k}(\frac{19}{27z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi\right| \\ \notag &\leq \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{\frac{2}{k(n-1/24)}} \left(\frac{19}{27}\right)^{1/4} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{19}{27}\times\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \\ &\quad+ \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{2} \pi^{-1} e^{19\pi/81} \frac{e^{2\pi (n-1/24) \varrho} N^{1/2}}{n-1/24} \\\notag &\leq \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} \sqrt{\frac{2k}{n-1/24}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \\ \notag &\; + \sum_{\substack{19 \leq k \leq N \\ (k,27) = 1}} 1.2828 \frac{e^{2\pi (n-1/24) \varrho} k N^{1/2}}{n-1/24} \\ \notag & \leq N^{3/2} \sqrt{\frac{2}{n-1/24}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) + 1.2828 \frac{e^{2\pi (n-1/24) \varrho} N^{5/2}}{n-1/24}. \notag \end{align*} $$

So we have

$$ \begin{align*} |T_{1} - 3R_{1}| \leq 2N^{3/2} \sqrt{\frac{2}{(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{18} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) + 2.5656 \frac{e^{2\pi (n-1/24) \varrho} N^{5/2}}{n-1/24}. \end{align*} $$

Setting $N:=\sqrt {2\pi (n-1/24)}$ , we obtain

$$ \begin{align*} \begin{aligned} |T_{1} - 3R_{1}| &\leq 2 (2\pi)^{3/4} \sqrt{2} (n-1/24)^{(1/4)} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1)\\ &+ 2.5656 e (2\pi)^{5/4} (n-1/24)^{(1/4)} \\ &\leq 11.225 (n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 80.601 (n-1/24)^{(1/4)}. \end{aligned} \end{align*} $$

For $S_3(B)$ , set $\Omega _{(h,k)} := e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))}$ . We apply (3.1) to conclude that

$$ \begin{align*} \begin{aligned}\! S_3(B)& = \!\sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \!\!e^{-2\pi i nh/k}\! \int_{\xi_{h,k}} \!e^{2\pi i (2\tau)} \frac{F(e^{2\pi i \tau})F(e^{2\pi i (9\tau)})}{F(e^{2\pi i (3\tau)})F(e^{2\pi i (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & = \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \\ & \quad \times \frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & \quad + \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} \frac{1}{3 \sqrt{z}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} \\ &\quad\times \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ & =:P_{1} + P_{2} \end{aligned} \end{align*} $$

with $k=9l_2$ .

For $P_2$ , by (2.10), we have

$$ \begin{align*} \begin{aligned} \left| e^{\frac{\pi}{12k}(\frac{1}{z})} \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) \right| \leq e^{\frac{\pi}{12k}\mathrm{Re}\left(\frac{1}{z}\right)} \left( e^{g(k,z)}- 1\right), \end{aligned} \end{align*} $$

where

$$ \begin{align*}g(k,z)=\frac{\pi^2 e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{1}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{\pi^2 e^{-2\pi \frac{9}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{9}{k} \mathrm{Re}(\frac{1}{z})})} + \frac{3\pi^2 e^{-2\pi \frac{3}{k} \mathrm{Re}(\frac{1}{z})}}{6(1-e^{-2\pi \frac{3}{k} \mathrm{Re}(\frac{1}{z})})}.\end{align*} $$

Let

$$ \begin{align*} x := e^{-\frac{\pi}{12k}\mathrm{Re}(\frac{1}{z})}. \end{align*} $$

Then,

$$ \begin{align*} \begin{aligned} & \left| e^{\frac{\pi}{12k}(\frac{1}{z})} \left(\frac{F(e^{2\pi i \gamma_{(h,9l_2)} (\tau)})F(e^{2\pi i \gamma_{(h,l_2)} (9\tau)})}{F(e^{2\pi i \gamma_{(h,3l_2)} (3\tau)})F(e^{2\pi i \gamma_{(3h,l_2)} (27\tau)})^2} - 1 \right) \right| \\ & \quad\leq \frac{1}{x} \left(\mathrm{exp}\left(\frac{\pi^2 x^{24}}{6(1-x^{24})}+\frac{\pi^2 x^{216}}{6(1-x^{216})}+\frac{3\pi^2 x^{72}}{6(1-x^{72})}\right) - 1\right) =: W_3(x). \end{aligned} \end{align*} $$

By Lemma 2.2 and (2.5), we have

$$ \begin{align*} \begin{aligned} W_3(x) &\leq W_3(e^{-\frac{\pi}{24}}) = e^{\frac{\pi}{24}} \left(\mathrm{exp}\left(\frac{\pi^2 e^{-\pi}}{6(1-e^{-\pi})}+\frac{\pi^2 e^{-9\pi}}{6(1-e^{-9\pi})} + \frac{\pi^2 e^{-3\pi}}{2(1-e^{-3\pi})}\right) - 1\right) \\ & \leq 0.089. \end{aligned} \end{align*} $$

Hence,

$$ \begin{align*} \begin{aligned} |P_2| &\leq 0.0297 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} |z|^{-\frac{1}{2}} e^{\frac{-\pi}{12k}\mathrm{Re}(z)} e^{2\pi n \varrho} d\varphi \\ &\leq 0.0297 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \int_{\xi_{h,k}} k^{-\frac{1}{2}} N e^{2\pi (n - 1/24) \varrho} d\varphi \\ &\leq 0.0594 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} k^{-\frac{3}{2}} e^{2\pi (n - 1/24) \varrho} \\ &\leq 0.0594 \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} k^{-\frac{1}{2}} e^{2\pi (n - 1/24) \varrho} \\&\leq 0.119 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}}.\\ \end{aligned} \end{align*} $$

For $P_1,$ applying Lemma 2.3 with $b=1$ , we establish

$$ \begin{align*} P_1 &= \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \int_{\xi_{h,k}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} z^{-\frac{1}{2}} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \notag \\ &=\frac{1}{3} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} \sqrt{\frac{2}{9(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{9} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \notag \\ & \quad+\frac{1}{3} \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right)\\ &\quad + \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} E^{(1)}(I) \\ &= \frac{1}{3} \bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \notag \\ &\quad + \frac{1}{3} \bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{-\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \notag \\ & \quad+ \frac{1}{3} \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right) \notag \\ &\quad+ \frac{1}{3} \sum_{\substack{1 \leq k \leq N \\ (k,27) = 9}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)} E^{(1)}(I) \notag \\ & =:P(n) + Q \notag \end{align*} $$

with

$$ \begin{align*} P(n) = \bigg(\frac{1}{3} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \end{align*} $$

and

$$ \begin{align*} \begin{aligned} |Q| \leq & \sum_{\substack{18 \leq k \leq N \\ (k,27) = 9}} \bigg(\frac{1}{3} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n-2)h/k} \Omega_{(h,k)}\bigg) \sqrt{\frac{2}{k(n-1/24)}} \\ & \times \left(e^{\frac{\pi}{k} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + e^{-\frac{\pi}{k} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\right) + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)}\\ \leq & \sum^{\lfloor\sqrt{2\pi(n-1/24)}/9\rfloor}_{2 \leq l_2 \leq N} \frac{\sqrt{k}}{3} \sqrt{\frac{2}{n-1/24}} \left(e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1\right)\\ & + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)} \\ \leq & \left(\frac{\sqrt{2\pi(n-1/24)}}{9}\right)^{\frac{3}{2}} \sqrt{\frac{2}{n-1/24}} \left(e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1\right) \\ & + \frac{2\sqrt{2}}{3} + 11.563 (n-1/24)^{(1/4)} \\ \leq & 0.208(n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 11.771(n-1/24)^{(1/4)} + 0.943. \end{aligned} \end{align*} $$

Similarly, applying (3.9), we deduce that

$$ \begin{align*} S_4(A)= U_{1} + U_{2}, \end{align*} $$

with

$$ \begin{align*} U_{1} = \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i nh/k} \omega^{(3)}_{(h,k)} \int_{\xi_{h,k}} z^{-\frac{1}{2}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi, \end{align*} $$

and

$$ \begin{align*} |U_{2}| \leq 0.3536 e^{2\pi (n - 1/24) \varrho} N^{1/2}. \end{align*} $$

Here, $\omega ^{(3)}_{(h,k)} := e^{\pi i (s(h,27l_3) + s(h,l_3) - 3s(h,3l_3))}.$

For $U_1$ , we have

$$ \begin{align*} \begin{aligned} |U_1| &= \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} \int_{\xi_{h,k}} z^{-\frac{1}{2}} e^{\frac{\pi}{12k}(\frac{1}{z} - z)} e^{2\pi n \varrho} e^{-2\pi i n \varphi} d\varphi \\ &\leq \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} \sqrt{\frac{2}{k(n-1/24)}} \mathrm{cosh}\left(\frac{\pi}{k} \sqrt{\frac{2}{3}\left(n-\frac{1}{24}\right)} \right)\bigg| \\ &\quad + \bigg|\sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} e^{-2\pi i (n)h/k} \omega^{(3)}_{(h,k)} E^{(1)}(I)\bigg| \\ &\leq \sum_{\substack{1 \leq k \leq N \\ (k,27) = 27}} \sum_{\substack{0 \leq h < k \\ (h,k) = 1}} \sqrt{\frac{2}{k(n-1/24)}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\ &\leq \sum^{\lfloor\sqrt{2\pi (n-1/24)}/27 \rfloor}_{l_3=1} \sqrt{\frac{54l_3}{n-1/24}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\ &\leq \left(\frac{\sqrt{2\pi (n-\frac{1}{24})}}{27}\right)^{\frac{3}{2}} \sqrt{\frac{54}{n-1/24}} (e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}+1) + 34.698 (n-1/24)^{(1/4)} \\& \leq 0.208(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 34.897(n-1/24)^{(1/4)}. \end{aligned} \end{align*} $$

3.4 Signs of the Fourier coefficients of $g(q)-3h(q)$

It follows from (3.1) and (3.2) that

$$ \begin{align*}g(q)-3h(q)=\sum_{n=1}^{\infty} (a(n) - 3b(n))q^n.\end{align*} $$

From (3.3), (3.4) and the results in Subsections 3.2 and 3.3, we derive that

$$ \begin{align*} \begin{aligned} a(n) - 3b(n)& = S_1(A) + S_2(A) + S_3(A) + S_4(A) - 3(S_1(B) + S_2(B) + S_3(B) + S_4(B)) \\ & = T_1 - 3R_1 + T_2 - 3R_2 + S_2(A) + S_3(A) - 3S_2(B) \\ &\quad - 3P(n) -3P_2 -3Q + U_1 + U_2 - 3S_4(B) \\ &=: -3P(n) + E(n) \end{aligned} \end{align*} $$

with

$$ \begin{align*} -3P(n) = -\bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}. \end{align*} $$

From Subsctions 3.2 and 3.3, we know that

$$ \begin{align*} \begin{cases} |T_1 - 3R_1| & \leq \quad 11.225 (n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 80.601 (n-1/24)^{(1/4)}, \\ |T_2| & \leq \quad 7.560 \times 10^{10} e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}} = 3.254 \times 10^{11}(n-1/24)^{(1/4)}\\ |R_2| & \leq \quad 1.435 \times 10^{13} e^{2\pi i (n - 1/24) \varrho} N^{\frac{1}{2}} = 6.176 \times 10^{13}(n-1/24)^{(1/4)}, \\ |S_2(A)| & \leq \quad \frac{4}{\sqrt{3}} e^{0.969} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}} = 26.193(n-1/24)^{(1/4)}, \\ |S_3(A)| & \leq \quad 4\sqrt{3} e^{-2.047} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}= 3.850(n-1/24)^{(1/4)}, \\ |S_2(B)| & \leq \quad \frac{4}{3\sqrt{3}} e^{1.710} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}=18.318(n-1/24)^{(1/4)}, \\ |P_2| & \leq \quad 0.119 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}}=0.513(n-1/24)^{(1/4)}, \\ |Q| & \leq \quad 0.208(n-1/24)^{(1/4)} e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 11.771(n-1/24)^{(1/4)} + 0.943, \\ |U_1| & \leq \quad 0.208(n-1/24)^{(1/4)}e^{(\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})})} + 34.897(n-1/24)^{(1/4)}, \\ |U_2| & \leq \quad 0.3536 e^{2\pi (n - 1/24) \varrho} N^{\frac{1}{2}} = 1.522(n-1/24)^{(1/4)}, \\ |S_4(B)| & \leq \quad 4e^{-6.077} e^{2\pi(n-\frac{1}{24})\varrho} N^{\frac{1}{2}}=0.040(n-1/24)^{(1/4)}, \end{cases} \end{align*} $$

so that

$$ \begin{align*} \begin{aligned} |E(n)| &\leq |T_1 - 3R_1| + |T_2| + 3|R_2| + |S_2(A)| + |S_3(A)| + 3|S_2(B)| \\ &\quad + 3|P_2| + 3|Q| + |U_1| + |U_2| + 3|S_4(B)| \\ &\leq 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 3.772 \\ &\quad + (3.254 \times 10^{11} + 3\times6.176 \times 10^{13} + 26.193 + 3.850 + 3\times 18.318 + \\ &\qquad 3\times 0.513 + 3\times 12.969 + 12.969 + 1.522 + 3\times 0.040)\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}} \\ &\leq 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1.857\times 10^{14}\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}}. \end{aligned} \end{align*} $$

It is observed that the signs of the main term $P(n)$ are determined by

$$ \begin{align*} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} \end{align*} $$

with $\Omega _{(h,9)}:= e^{\pi i (s(h,9l_2) + s(h,l_2) - s(h,3l_1) - 2s(3h,l_2))}$ . After calculations, we have

$$ \begin{align*} \begin{cases} \Omega_{(1,9)} = e^{\frac{25}{54}\pi i},\quad \Omega_{(2,9)} = e^{\frac{11}{54}\pi i}, \\ \Omega_{(4,9)} = e^{-\frac{11}{54}\pi i},\quad \Omega_{(5,9)} = e^{\frac{11}{54}\pi i}, \\ \Omega_{(7,9)} = e^{-\frac{11}{54}\pi i},\quad \Omega_{(8,9)} = e^{-\frac{25}{54}\pi i}. \end{cases} \end{align*} $$

Therefore,

$$ \begin{align*} \sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)} = \begin{cases} 2\mathrm{cos}(23\pi/54) + 4\mathrm{cos}(49\pi/54) & \mathrm{if} ~n \equiv 0 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(35\pi/54) + 4\mathrm{cos}(37\pi/54) & \mathrm{if} ~n \equiv 1 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(25\pi/54) + 4\mathrm{cos}(11\pi/54) & \mathrm{if} ~n \equiv 2 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(49\pi/54) + 4\mathrm{cos}(13\pi/54) & \mathrm{if} ~n \equiv 3 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(37\pi/54) + 4\mathrm{cos}(\pi/54) & \mathrm{if} ~n \equiv 4 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(11\pi/54) + 4\mathrm{cos}(47\pi/54) & \mathrm{if} ~n \equiv 5 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(13\pi/54) + 4\mathrm{cos}(23\pi/54) & \mathrm{if} ~n \equiv 6 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(\pi/54) + 4\mathrm{cos}(35\pi/54) & \mathrm{if} ~n \equiv 7 ~(\mathrm{mod} ~ 9) \\ 2\mathrm{cos}(47\pi/54) + 4\mathrm{cos}(25\pi/54) & \mathrm{if} ~n \equiv 8 ~(\mathrm{mod} ~ 9). \\ \end{cases} \end{align*} $$

It is easily computed that

$$ \begin{align*} \bigg|\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg|\geq 0.20142 \end{align*} $$

for $n\in \mathbb {N}.$ When $n \geq 22472$ ,

$$ \begin{align*} \begin{aligned} |-3P(n)| &= \bigg|\bigg(\sum_{\substack{0 \leq h < 9 \\ (h,9) = 1}} e^{-2\pi i (n-2)h/9} \Omega_{(h,9)}\bigg) \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}}\bigg| \\ & \geq 0.20142 \sqrt{\frac{2}{9(n-1/24)}} e^{\frac{\pi}{9} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} \\ &> 12.057(n-1/24)^{(1/4)}e^{\frac{\pi}{18} \sqrt{\frac{2}{3}(n-\frac{1}{24})}} + 1.857\times 10^{14}\bigg(n-\frac{1}{24}\bigg)^{\frac{1}{4}}\\ & \geq |E(n)|. \end{aligned} \end{align*} $$

From this, we obtain that

(3.11) $$ \begin{align} \begin{cases} a(n) - 3b(n)> 0 & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9) \\ a(n) - 3b(n) < 0 & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9) \end{cases} \end{align} $$

holds for $n\geq 22472$ . Calculating the first $22471$ coefficients of $g(q)-3h(q)$ by using the software Mathematica, we find that (3.11) is also true for $467 \leq n \leq 22471.$

3.5 Proof of Theorem 1.1

It follows from the identities in [6, eqs.(2.10) and (2.11)] that

$$ \begin{align*} \sum_{n=1}^{\infty} M(0,1,1;9;n) q^n - \frac{1}{3(q;q)_{\infty}} = \frac{2}{3}(g(q)-3h(q)), \end{align*} $$

and

$$ \begin{align*} \sum_{n=1}^{\infty} M(2,3,4;9;n) q^n - \frac{1}{3(q;q)_{\infty}} = -\frac{1}{3}(g(q)-3h(q)), \end{align*} $$

so that

$$ \begin{align*} \begin{aligned} M(0,1,1;9;n) - \frac{p(n)}{3} &= \frac{2}{3}(a(n) - 3b(n) ), \\ M(2,3,4;9;n) - \frac{p(n)}{3} &= -\frac{1}{3}(a(n) - 3b(n) ). \end{aligned} \end{align*} $$

It is known from Subsection 3.4 that (3.11) holds for $n \geq 467.$ Hence, when $n \geq 467,$

$$ \begin{align*} \begin{cases} M(0,1,1;9;n)> \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\[1ex] M(0,1,1;9;n) < \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\[1ex] M(2,3,4;9;n) < \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\[1ex] M(2,3,4;9;n)> \frac{p(n)}{3}, & \mathrm{if} ~ n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \\[1ex] \end{cases} \end{align*} $$

This finishes the proof of Theorem 1.1.