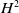Dynamical behaviour of a logarithmically sensitive chemotaxis model under time-dependent boundary conditions

Abstract

This article studies the dynamical behaviour of classical solutions of a hyperbolic system of balance laws, derived from a chemotaxis model with logarithmic sensitivity, with time-dependent boundary conditions. It is shown that under suitable assumptions on the boundary data, solutions starting in the $H^2$-space exist globally in time and the differences between the solutions and their corresponding boundary data converge to zero as time goes to infinity. There is no smallness restriction on the magnitude of the initial perturbations. Moreover, numerical simulations show that the assumptions on the boundary data are necessary for the above-mentioned results to hold true. In addition, numerical results indicate that the solutions converge asymptotically to time-periodic states if the boundary data are time-periodic.

1. Introduction

The movement of an organism or cell in response to a chemical stimulus in its local environment is termed as chemotaxis. It is the underlying mechanism of many biological processes in modern cell biology, biochemistry and clinical pathology, such as tumour angiogenesis, blood vessel formation, slime mould formation, bacterial foraging, immune response, embryonic development, tissue homeostasis, fish pigmentation patterning, primitive streak formation, wound healing, just to mention a few. Early scholarly descriptions of chemotaxis were introduced in the late 19th century by Engelmann (1881), Pfeffer (1884), Metchnikoff (1882-1886) and Jennings (1906). Later important contributions include, but are not limited to, quality control of chemotaxis assays (Harris 1953) and study of intracellular signal transduction of bacteria (Adler 1966).

Mathematical modelling of chemotaxis using continuum partial differential equations was initiated in the 1950s by Patlak [30] from a probabilistic perspective and regained popularity in the 1970s through the seminal work of Keller and Segel [17–19] using a phenomenological approach. The original Keller–Segel models contain two prototypes according to the chemotactic sensitivity function: linear sensitivity and logarithmic sensitivity. The linear sensitivity was employed in the modelling of self-aggregation of Dictyostelium discoideum in response to cyclic adenosine monophosphate (cAMP) [18], while the logarithmic sensitivity appeared in [19] to interpret J. Adler’s experimental result [1] on the formation of travelling bands in nutrient-enticed E. Coli population.

In general form, the Keller–Segel model reads as

(1.1a) \begin{align} u_{t} &=D u_{xx} - \chi \big [u\Phi (c)_x\big ]_x, \end{align}

(1.1b) \begin{align} c_{t} & =\varepsilon c_{xx} - \mu u c^m - \sigma c, \\[10pt] \nonumber \end{align}

where the unknown functions $u(x,t)$ and $c(x,t)$ denote the density of the organism or cell population and concentration of the chemical signal at position $x$ at time $t$ , respectively. The parameter $D\gt 0$ denotes the diffusion coefficient of the organism or cell population; $\chi \neq 0$ is the coefficient of chemotactic sensitivity, the sign of $\chi$ dictates whether the chemotaxis is attractive ( $\chi \gt 0$ ) or repulsive ( $\chi \lt 0$ ), with $|\chi |$ measuring the strength of the chemotactic response; $\varepsilon \ge 0$ is the diffusion coefficient of the chemical signal; $\mu \neq 0$ is the coefficient of the density-dependent production/degradation rate of the chemical signal; $\sigma \ge 0$ is the natural degradation rate of the chemical signal; and $m\ge 0$ characterises the mode of temporal growth/decay of the chemical signal. Moreover, $\Phi (c)$ denotes the chemotactic sensitivity with either $\Phi (c)=c$ or $\Phi (c)=\log (c)$ . The nonlinear term $-\chi \big [u\Phi (c)_x\big ]_x$ underlines the main feature of (1.1), advection induced by the spatial gradient of the chemical signal in the local environment.

The pioneering work of Keller and Segel inspired many of the modern studies in chemotaxis research. From the mathematical analysis perspective, there have been studies of both of the aforementioned kinds of chemotactic sensitivity. However, a search in the literature shows that there are extensive results on the model with linear sensitivity (see e.g. [3, 12, 13]), but much less is known for the model with logarithmic sensitivity, due to its possible singular nature. The authors would like to point out that the study of the logarithmic sensitivity model is of essential importance given that this sensitivity obeys the Weber–Fechner’s law, which is a fundamental principle in psychophysics and has prominent applications in biology. This article focuses on the model with logarithmic sensitivity:

(1.2a) \begin{align} u_{t} &=D u_{xx} - \chi \big [u(\log c)_x\big ]_x, \end{align}

(1.2b) \begin{align} c_{t} &=\varepsilon c_{xx} - \mu u c^m - \sigma c,\\[10pt] \nonumber \end{align}

which has been utilised in a variety of contexts to explain the underlying mechanisms of different chemotactic processes. For example, the original Keller–Segel model ( $\chi \gt 0$ , $\mu \gt 0$ , $0\le m\lt 1$ , $\sigma =0$ ) was proposed in [19] to describe the travelling bands observed in Adler’s experiment [1]. The same model with $m=1$ was employed by Levine et al [21] to interpret the dynamical interactions between vascular endothelial cells (VECs) and signalling molecules vascular endothelial growth factor (VEGF) in the onset of tumour angiogenesis. On the other hand, when $\chi \lt 0$ , $\mu \lt 0$ , $m=1$ and $\sigma \gt 0$ , the model was designed in [20, 29] to illustrate the chemotactic movement of reinforced random walkers (e.g. surface or matrix-bound adhesive molecules) that deposit non-diffusive ( $\varepsilon =0$ ) or slowly moving ( $0\lt \varepsilon \ll 1$ ) chemical signals that modify the local environment for succeeding passages.

Despite its versatility in biological modelling, the singular nature of the logarithmic sensitivity presents a significant challenge to both the numerical and analytical studies of the model. Depending on the value of the parameter $m$ , the mathematical treatment of the model differs significantly. In this article, we focus on the case when $m=1$ . In this case, the singular nature can be removed by the Cole–Hopf-type transformation: $v = \frac{c_x}{c}$ . By applying such a transformation and the rescalings: $t \to |\chi \mu |D^{-1}\,t$ , $x \to \sqrt{|\chi \mu |}\,D^{-1}\,x$ , $v \to \mathrm{sign}(\chi )\sqrt{|\chi |\,|\mu |^{-1}}\, v$ , one obtains a system of conservation laws:

(1.3a) \begin{align} u_t - (u v)_x &= u_{xx}, \end{align}

(1.3b) \begin{align} v_t - \mathrm{sign}(\chi \mu ) u_x &= \varepsilon{D}^{-1} v_{xx} + \varepsilon \chi ^{-1} (v^2)_x, \\[10pt] \nonumber \end{align}

A direct calculation shows that the eigenvalues of the Jacobian matrix associated with the flux on the left of (1.3) are given by

(1.4) \begin{align} \lambda _\pm = \frac{\left (2\varepsilon \chi ^{-1} -1\right )v \pm \sqrt{\left (2\varepsilon \chi ^{-1}+1\right )^2v^2 + 4\,\mathrm{sign}(\chi \mu ) u}}{2}, \end{align}

which indicates that when $\chi \mu \gt 0$ and $u\gt 0$ , the principle part of (1.3) is hyperbolic. This enables the adaptation of fundamental analytic tools in hyperbolic balance laws, such as entropy method, to study the qualitative behaviour of the model. Throughout this article, we focus on the case when $\chi \mu \gt 0$ . It is worth mentioning that when $\chi \mu \lt 0$ , the characteristic fields may change type, which could alter the dynamics of the model drastically. This is supported by the blowup (explicit and numerical) solutions constructed in [20].

Since the work of Levine and Sleeman [20], mathematical analysis of (1.3) has developed into an active area in chemotaxis research. To put things into perspective, we briefly survey the literature in connection with (1.3) when $\chi \mu \gt 0$ . First of all, since (1.3) satisfies the Shizuta–Kawashima condition [34], the global well-posedness and stability of classical solutions to the Cauchy problem near constant equilibria are guaranteed by some of the contemporary frameworks on hyperbolic/parabolic balance laws (cf. [40, 41]). See also [48] for a similar result on a finite interval. For large amplitude classical solutions, the global well-posedness results on finite and infinite intervals are first established in [10] and [11], respectively. In a series of recent works [22–26, 28, 32, 35, 39], the aforementioned results are upgraded by demonstrating the global stability of constant equilibrium states, which suggested that uniform distribution is a generic phenomenon in logarithmically sensitive chemoattraction with chemical consumption or chemorepulsion with chemical production. In addition to the study of global dynamics, the zero chemical diffusivity limit (i.e., as $\varepsilon \to 0$ ) and instantaneous spatial analyticity of large amplitude classical solutions have also been investigated in [14–16, 23, 24, 28, 32, 39]. Another major direction of research is concerned with the existence and stability of non-trivial patterns of (1.3). We refer the reader to [7, 8, 31] and the references therein for the studies of large-strength travel wave solutions, and to [4–6] for non-trivial steady-state solutions. In the multi-dimensional spaces, the qualitative behaviours of the model have been investigated under various smallness assumptions on the initial data. We refer the readers to [27, 33, 37] and the references therein. Moreover, the appended version of (1.3) with logistic growth is studied in [2, 44–47] where the enhanced dissipation induced by logistic damping is explored. Furthermore, the amended model with nonlinear density-dependent chemical production/consumption rate (i.e., replacing $u_x$ by $(u^\gamma )_x$ with $\gamma \gt 1$ ) has been analysed in [9, 49, 50].

Among the foregoing works, of particular relevance to this article is the study of the global dynamics of classical solutions to (1.3) and its companion with nonlinear chemical production/consumption rate on finite intervals subject to time-dependent Dirichlet boundary conditions (cf. [9, 32]). Comparing with constant valued boundary conditions, time-dependent boundary conditions are of more biological importance. For instance, nutrient availability in natural environments is often highly time-dependent. Furthermore, we note that in the previous studies, the Dirichlet boundary conditions are required to match at the endpoints of the spatial domain $I=[a,b]$ , i.e., $u(a,t)=u(b,t)$ , $v(a,t)=v(b,t)$ . Although those results are mathematically meaningful, they are less realistic from the point of view of physical/biological applications, since, in real-world circumstances, the boundary values of certain quantity under consideration may be different time by time. Hence, mathematical studies of the model subject to unmatching boundary conditions becomes relevant. This is one of the motivations of this article. Moreover, (1.3) with zero chemical diffusivity (i.e., $\varepsilon =0$ ) is a conceptually idealised model that was designed to simplify the underlying mathematical analysis [20]. Though such a model has been analysed under various types of boundary conditions, the large-time behaviour of classical solutions subject to time-dependent boundary conditions has never been examined.

Driven by the purpose of filling the above-mentioned gaps, we dedicate this article to study the dynamical behaviour of large-data classical solutions to (1.3) subject to time-dependent boundary conditions. First, we aim to generalise the rigorous mathematical results of [32] by studying the case of time-dependent Dirichlet boundary conditions that do not necessarily match at any time. Our goal is to identify a set of conditions on the boundary data, under which global classical solutions exist and stabilise in the long run. Second, because of the ubiquitous presence of time-periodic phenomena in nature (e.g. day/night, freeze/thaw, and rain/dry cycles) and in clinical research (e.g. administering drug delivery in cancer therapeutics [36]), we devote the second part of this article to investigate whether time-periodic boundary data induce time periodicity of the solution, and if so, how the period of the solution depends on the boundary period(s). The investigation is carried out through numerical simulations.

The remainder of the article is organised as follows: First, we state the main analytical results in Section 2. Then, we prove the main results in Sections 3 and 4, respectively. Numerical simulations are performed in Section 5 to verify the analytical results, show that the assumptions on the boundary data are necessary for the results to hold, and study the dynamics of the solutions subject to time-periodic boundary conditions. We finish the article with concluding remarks in Section 6.

2. Statement of results

To simplify the presentation, we take $\chi =-1,\, D=1$ , since the specific values of the parameters do not affect our qualitative analysis. Also, without loss of generality, we take the spatial interval as the unit interval, i.e., $(0,1)$ . Moreover, recall that we concentrate upon the case of $\chi \mu \gt 0$ , so $\mu \lt 0$ . Under these circumstances, the model (1.3) is written as

(2.1a) \begin{align} u_t - (u v)_x &= u_{xx}, \end{align}

(2.1b) \begin{align} v_t - u_x &= \varepsilon v_{xx} - \varepsilon (v^2)_x. \\[10pt] \nonumber \end{align}

When $\varepsilon =0$ , system (2.1) becomes

(2.2a) \begin{align} u_t-(uv)_x &=u_{xx}, \end{align}

(2.2b) \begin{align} v_t-u_x &= 0. \\[10pt] \nonumber \end{align}

Both (2.1) and (2.2) are subject to the initial condition

(2.3) \begin{equation} (u,v)(x,0)=(u_0,v_0)(x), \quad x\in [0,1]. \end{equation}

When $\varepsilon \gt 0$ , (2.1) is supplemented with the boundary conditions:

(2.4a) \begin{align} &u(0,t)=\alpha _1(t),\quad u(1,t)=\alpha _2(t), \quad t \ge 0, \end{align}

(2.4b) \begin{align} &v(0,t)=\beta _1(t),\quad v(1,t)=\beta _2(t), \quad t \ge 0. \\[10pt] \nonumber \end{align}

When $\varepsilon =0$ , only the function $u$ needs supplementary information from the boundary:

(2.5) \begin{equation} u(0,t)=\alpha _1(t),\quad u(1,t)=\alpha _2(t), \quad t \ge 0, \end{equation}

while the function $v$ does not, since otherwise the system would be over-determined.

With the initial and boundary conditions at our disposal, we are now ready to present the main results of this paper. The first one is concerned with the global nonlinear stability of large-data classical solutions to the diffusive model under unmatching dynamic boundary conditions for $v$ . This upgrades the result of [32], where the case of matching boundary data is analysed.

Theorem 2.1. Consider the initial-boundary value problem (2.1), (2.3), (2.4). Suppose the initial data satisfy $u_0\gt 0$ , $(u_0,v_0) \in [H^2((0,1))]^2$ and are compatible with the boundary conditions. Assume $\alpha _1=\alpha _2=\alpha$ , $\beta _1$ and $\beta _2$ are smooth functions on $[0,\infty )$ satisfying

(2.6) \begin{align} & \bullet \quad \alpha (t)\ge \underline{\alpha } \gt 0, \quad \forall \,t\ge 0, \quad \text{and}\quad \alpha ^{\prime} \in W^{1,1}(\mathbb{R}_+), \end{align}

(2.7) \begin{align} & \bullet \quad \beta _1-\beta _2 \in L^1(\mathbb{R}_+) \quad \text{and} \quad \beta _1^{\prime},\beta _2^{\prime} \in W^{1,1}(\mathbb{R}_+), \\[10pt] \nonumber \end{align}

where $\underline{\alpha }$ is a constant. Then, there exists a unique solution to the IBVP such that

\begin{align*} \|\tilde{u}(t)\|^2_{H^2((0,1))}+\|\tilde{v}(t)\|^2_{H^2((0,1))} + \int _0^t \big (\|\tilde{u}(\tau )\|^2_{H^3((0,1))}+\|\tilde{v}(\tau )\|^2_{H^3((0,1))}\big )\mathrm{d}\tau \le C, \end{align*}

where $\tilde{u}(x,t) = u(x,t) - \alpha (t)$ , $\tilde{v}(x,t) = v(x,t) - [\beta _2(t)-\beta _1(t)]x - \beta _1(t)$ , and the constant $C\gt 0$ is independent of $t$ . Moreover, the solution has the large-time behaviour:

\begin{align*} \|\tilde{u}(t)\|_{H^2((0,1))}+\|\tilde{v}(t)\|_{H^2((0,1))} \to 0\quad \text{as}\quad t\to \infty . \end{align*}

The second theorem addresses the dynamics of large-data classical solutions to the non-chemically-diffusive model subject to matching dynamic boundary conditions for $u$ , which has not been documented in the literature. This is a generalisation of the result of [23, 24], where the global stability of constant Dirichlet-type boundary condition is established.

Theorem 2.2. Consider the initial-boundary value problem (2.2), (2.3), (2.5). Suppose the initial data satisfy $u_0\gt 0$ , $(u_0,v_0) \in [H^2((0,1))]^2$ and are compatible with the boundary conditions. Assume $\alpha _1=\alpha _2=\alpha$ is a smooth function on $[0,\infty )$ satisfying

\begin{align*} \alpha (t) \ge \underline{\alpha } \gt 0,\quad \forall \,t\ge 0, \quad \text{and}\quad \alpha ^{\prime} \in W^{1,1}(\mathbb{R}_+), \end{align*}

where $\underline{\alpha }$ is a constant. Then, there exists a unique solution to the IBVP such that

\begin{align*} \|\tilde{u}(t)\|^2_{H^2((0,1))}+\|\tilde{v}(t)\|^2_{H^2((0,1))} + \int _0^t \big (\|\tilde{u}(\tau )\|^2_{H^3((0,1))}+\|\tilde{v}(\tau )\|^2_{H^2((0,1))}\big )\mathrm{d}\tau \le C, \end{align*}

where $\tilde{u}(x,t) = u(x,t) - \alpha (t)$ , $\tilde{v}(x,t) =v(x,t) - \int _0^1 v_0(x){\mathrm{d}x}$ , and the constant $C\gt 0$ is independent of $t$ . Moreover, the solution has the large-time behaviour:

\begin{align*} \|\tilde{u}(t)\|_{H^2((0,1))}+\|\tilde{v}(t)\|_{H^2((0,1))} \to 0\quad \text{as}\quad t\to \infty . \end{align*}

We have several remarks concerning Theorems 2.1 and 2.2.

Remark 2.1. The assumptions in Theorem 2.1 imply that the difference between $\beta _1(t)$ and $\beta _2(t)$ will converge to zero as $t\to \infty$ , i.e., the unmatching boundary data will eventually match. However, based on the assumptions, we see that the boundary functions are not necessarily equal to each other at any finite time. This generalises all of the previous results for the model under matching boundary conditions. We also expect that our results will help provide useful information for the understanding of more realistic situations involving logarithmically sensitive chemotaxis.

Remark 2.2. Since the boundary functions are smooth on $[0,\infty )$ and their first order derivatives belong to $W^{1,1}(\mathbb{R}_+)$ , it follows from the Fundamental Theorem of Calculus that the functions themselves alongside their first-order derivatives are uniformly bounded with respect to $t$ . Such information will be frequently utilized in the proof of the theorems.

Remark 2.3. It is an intriguing question to ask whether the matching boundary data of $u$ can be relaxed, i.e., $\alpha _1(t)\neq \alpha _2(t)$ . In this case, the reference profile interpolating the boundary values becomes $\alpha _1(t) + x[\alpha _2(t)-\alpha _1(t)]$ . Unfortunately, the $x$ -dependence of the profile picks up additional nonlinearities when implementing the entropy estimate, see (3.2), which cannot be handled by using the approach in this paper, due to the sub-quadraticity of the relative entropy. We leave the investigation for the future.

Remark 2.4. Theorem 2.1 suggests that the large-time behaviour of (2.1) is determined by its boundary data, while its initial information is gradually lost as time evolves. On the other hand, Theorem 2.2 indicates that both its initial and boundary information are carried by (2.2) in the long run. It is interesting to investigate whether there are mechanisms that can drive the solutions to other stationary solutions rather than those determined by the initial and/or boundary data. Among various types of modelling structures, the logistic growth may give us a definite answer. However, the analysis in this paper can not be directly carried over to the model with logistic growth, due to the quadratic nonlinearity. We will report such a result in a forthcoming paper.

Remark 2.5. Systems (2.1) and (2.2) themselves have deep mathematical interests as they serve as prototypes of general parabolic/hyperbolic balance laws. The nature of possible non-uniform dissipativity (i.e., $\varepsilon =0$ ) coupled with nonlinear flux functions, together with the non-triviality of the dynamic boundary data in this type of problems, presents significant challenges in mathematical analysis. The analysis of (2.1) and (2.2) helps to shed light on how to advance fundamental research of parabolic/hyperbolic balance laws in related topics, and we expect the study in this paper to be helpful to other parabolic/hyperbolic balance laws.

We prove Theorem2.1 and Theorem2.2 in Section 3 and Section 4, respectively. The integrability conditions of the boundary data are thoroughly examined to fit into the framework previously established for the case of matching boundary conditions. The proof of Theorem2.1 takes advantage of the fully dissipative structure of (2.1), which results in energy estimates depending on the reciprocal of the chemical diffusion coefficient. For this reason, the arguments cannot be carried over to (2.2). Instead, Theorem2.2 is proven by deriving a nonlinear damping equation for the spatial derivative of $v$ . It should be mentioned that the approach for analysing (2.2) cannot be utilised for (2.1), due to the lack of information of higher order spatial derivatives of the solution to the latter, causing integration-by-parts to be unaccessible. Thus, the energy methods for studying (2.1) and (2.2) are mutually exclusive.

Lastly, for notational convenience, throughout the rest of the article, we use $\|\cdot \|$ , $\|\cdot \|_{H^s}$ and $\|\cdot \|_\infty$ to denote the standard norms $\|\cdot \|_{L^2((0,1))}$ , $\|\cdot \|_{H^s((0,1))}$ and $\|\cdot \|_{L^\infty ((0,1))}$ , respectively. Moreover, we use $C$ to denote a generic constant which is independent of time, but may depend on the parameter $\varepsilon$ and initial and/or boundary data. The value of the constant may vary line by line according to the context.

3. Proof of Theorem2.1

The proof of Theorem2.1 is divided into five steps contained in five subsections. First of all, the local well-posedness of the IBVP under the assumptions of Theorem2.1 can be established via standard approaches, such as mollification, Galerkin approximation, energy estimate, contraction mapping principle and compactness argument. We omit most of the standard technical details for brevity, while focus on deriving the a priori estimates of the local solution, in order to extend it to a global one. The a priori estimates can be justified by standard means, which are indeed carried out on the local smooth approximate solutions obtained from the mollified initial data and contraction mapping. Moreover, according to the assumptions in Theorem2.1 and the maximum principle, the local solution $u$ is positive within its life span, say, $[0,T^*)$ for some $T^*\gt 0$ . The subsequent estimates are derived within such a time window. It will be shown that the estimates are indeed independent of $t$ . Then, the global well-posedness follows from the uniform estimates and standard continuation argument. We begin with an estimate based on the relative entropy-entropy flux pair associated with the IBVP.

3.1. Entropy estimate

Lemma 3.1. Under the assumptions of Theorem 2.1, there exists a constant $C\gt 0$ which is independent of $t$ , such that

\begin{align*} E(u,\alpha )(t)+\|(v-\beta )(t)\|^2+\int _0^t\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x\mathrm{d}\tau +\int _0^t \varepsilon \|(v_x-\beta _x)(\tau )\|^2\mathrm{d}\tau \le C, \end{align*}

where $\beta (x,t)=[\beta _2(t)-\beta _1(t)]x + \beta _1(t)$ and

\begin{align*} E(u,\alpha )\equiv \int _0^1 \left [(u\ln u-u)-(\alpha \ln \alpha -\alpha )-(u-\alpha )\ln \alpha \right ]\mathrm{d}x\ge 0 \end{align*}

denotes the relative entropy.

Proof. Step 1. By a direct calculation, we can show that

(3.1) \begin{align} (u\ln u-u)_t-(\alpha \ln \alpha -\alpha )_t-[(u-\alpha )\ln \alpha ]_t =(\ln u-\ln \alpha )u_t-(u-\alpha )\frac{\alpha ^{\prime}}{\alpha }. \end{align}

Using equation (2.1a) and noting $\alpha$ depends only on $t$ , we deduce

(3.2) \begin{align} (\ln u-\ln \alpha )u_t =[(\ln u-\ln \alpha )uv]_x+[(\ln u-\ln \alpha )u_x]_x-v\,u_x-\frac{(u_x)^2}{u}. \end{align}

Substituting (3.2) into (3.1) gives us

(3.3) \begin{align} &(u\ln u-u)_t-(\alpha \ln \alpha -\alpha )_t-[(u-\alpha )\ln \alpha ]_t \nonumber \\ =\,&[(\ln u-\ln \alpha )uv]_x+[(\ln u-\ln \alpha )u_x]_x-v u_x-\frac{(u_x)^2}{u}-(u-\alpha )\frac{\alpha ^{\prime}}{\alpha }. \end{align}

Integrating (3.3) over $[0,1]$ and using the boundary conditions, we have

(3.4) \begin{equation} \frac{\mathrm{d}}{\mathrm{d}t}E(u,\alpha )+\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x = -\int _0^1 v u_x\mathrm{d}x-\int _0^1(u-\alpha )\frac{\alpha ^{\prime}}{\alpha }\mathrm{d}x. \end{equation}

Let $\beta (x,t)=[\beta _2(t)-\beta _1(t)]x + \beta _1(t)$ . Then, we derive from equation (2.1b) that

(3.5) \begin{align} &(v-\beta )_t-u_x\nonumber \\ =\,&\varepsilon (v-\beta )_{xx}-2\varepsilon (v-\beta )(v-\beta )_x -2\varepsilon (v-\beta )\beta _x-2\varepsilon \beta (v-\beta )_x - 2\varepsilon \beta \beta _x-\beta _t. \end{align}

Taking $L^2$ inner product of (3.5) with $v-\beta$ and using the boundary conditions, we obtain

(3.6) \begin{align} &\frac 12\frac{\mathrm{d}}{\mathrm{d}t} \|v-\beta \|^2+ \varepsilon \|(v-\beta )_x\|^2\nonumber \\ = &\int _0^1(v-\beta )u_x\mathrm{d}x - \varepsilon \int _0^1(v-\beta )^2\beta _x\mathrm{d}x -2\varepsilon \int _0^1\beta \beta _x(v-\beta )\mathrm{d}x -\int _0^1(v-\beta )\beta _t\mathrm{d}x. \end{align}

Note since $\alpha$ is independent of $x$ , it holds that

\begin{align*} \int _0^1(v-\beta )u_x\mathrm{d}x =\int _0^1 v u_x\mathrm{d}x + \int _0^1 \beta _x(u-\alpha )\mathrm{d}x. \end{align*}

We then get from (3.6) that

(3.7) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t} \|v-\beta \|^2+ \varepsilon \|(v-\beta )_x\|^2 &= \int _0^1 v u_x\mathrm{d}x+ \int _0^1 \beta _x(u-\alpha )\mathrm{d}x - \varepsilon \int _0^1(v-\beta )^2\beta _x\mathrm{d}x \nonumber \\ &\quad -2\varepsilon \int _0^1\beta \beta _x(v-\beta )\mathrm{d}x -\int _0^1(v-\beta )\beta _t\mathrm{d}x. \end{align}

Adding (3.7) and (3.4), we can show that

(3.8) \begin{align} &\frac{\mathrm{d}}{\mathrm{d}t}\Big (E(u,\alpha )+\frac 12\|v-\beta \|^2\Big )+\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x+ \|(v-\beta )_x\|^2 \nonumber \\ =&\int _0^1(u-\alpha )\big (\beta _x-\frac{\alpha ^{\prime}}{\alpha }\big )\mathrm{d}x - \varepsilon \int _0^1(v-\beta )^2\beta _x\mathrm{d}x - \int _0^1 (2 \varepsilon \beta \beta _x+\beta _t)(v-\beta )\mathrm{d}x \nonumber \\ \le &\Big (\frac{|\alpha ^{\prime}|}{\alpha }+|\beta _x|\Big )\int _0^1|u-\alpha |\mathrm{d}x+\varepsilon |\beta _x|\,\|\beta -v\|^2+\int _0^1\big (2\varepsilon |\beta \beta _x|+|\beta _t|\big )|v-\beta |\mathrm{d}x. \end{align}

Step 2. Define

\begin{align*} F_\alpha (u)\equiv (u\ln u-u)-(\alpha \ln \alpha -\alpha )-(u-\alpha )\ln \alpha +(e-1)\alpha -u. \end{align*}

Then, it can be readily checked that $F_\alpha (e\alpha )=0$ , $F_\alpha ^{\prime}(e\alpha )=0$ , and $F_\alpha ^{\prime\prime}(u)=\frac{1}{u}\ge 0$ for $u\ge 0$ . These imply $F_\alpha (u)\ge 0$ for $u\ge 0$ . Hence,

\begin{align*} 0\le u \le (u\ln u-u)-(\alpha \ln \alpha -\alpha )-(u-\alpha )\ln \alpha +(e-1)\alpha, \end{align*}

which yields

(3.9) \begin{equation} 0\le \int _0^1 u(x,t)\mathrm{d}x \le E(u,\alpha )+(e-1)\alpha . \end{equation}

The triangle inequality then gives us

(3.10) \begin{align} \int _0^1|u-\alpha |\mathrm{d}x \le E(u,\alpha )+e\alpha . \end{align}

Applying (3.10) to the right-hand side of (3.8), we can show that

\begin{align*} \bullet &\quad \Big (\frac{|\alpha ^{\prime}|}{\alpha }+|\beta _x|\Big )\int _0^1|u-\alpha |\mathrm{d}x \le C\big (|\alpha ^{\prime}| + |\beta _1 - \beta _2|\big )\big [E(u,\alpha )+1\big ],\\ \bullet &\quad \varepsilon |\beta _x|\,\|\beta -v\|^2 \le \varepsilon |\beta _1-\beta _2|\,\|\beta -v\|^2,\\ \bullet &\quad \int _0^1\big (2\varepsilon |\beta \beta _x|+|\beta _t|\big )|v-\beta |\mathrm{d}x \le C\big (\varepsilon |\beta _1-\beta _2|+|\beta _1^{\prime}|+|\beta _2^{\prime}|\big )\big (\|v-\beta \|^2+1\big ), \end{align*}

where we used the uniform boundedness of $\beta$ and the Cauchy–Schwarz inequality. Using the above estimates, we update (3.8) as

(3.11) \begin{align} &\frac{\mathrm{d}}{\mathrm{d}t}\Big (E(u,\alpha )+\frac 12\|v-\beta \|^2+1\Big )+\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x+ \varepsilon \|(v-\beta )_x\|^2 \nonumber \\ \le \, &C\big (|\alpha ^{\prime}| + \varepsilon |\beta _1-\beta _2| + |\beta _1^{\prime}|+ |\beta _2^{\prime}|\big )\Big (E(u,\alpha )+\frac 12\|v-\beta \|^2+1\Big ). \end{align}

Applying Grönwall’s inequality to (3.11) and using the assumptions in Theorem2.1 give us

(3.12) \begin{equation} E(u,\alpha )(t)+\frac 12\|(v-\beta )(t)\|^2\le C. \end{equation}

Substituting (3.12) into (3.11), then integrating with respect to $t$ , we have in particular,

(3.13) \begin{equation} \int _0^t\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x\mathrm{d}\tau +\int _0^t \varepsilon \|(v_x-\beta _x)(\tau )\|^2\mathrm{d}\tau \le C, \end{equation}

where the constant is independent of $t$ . This, along with (3.12), completes the proof of Lemma 3.1.

3.2. $L^\infty _tL^2_x$ – $L^2_tH^1_x$ –estimates

We now switch to standard $L^2$ -based energy estimates. To facilitate our asymptotic analysis, we define

\begin{align*} \tilde{u}\equiv u-\alpha \quad \text{and} \quad \tilde{v}\equiv v-\beta, \end{align*}

where $(u, v)$ satisfies (2.1) and $\beta (x,t)=[\beta _2(t)-\beta _1(t)]x+\beta _1(t)$ . Then, $(\tilde{u},\tilde{v})$ satisfies

(3.14a) \begin{align} \tilde{u}_t-(\tilde{u}\tilde{v})_x&=\tilde{u}_{xx} +\alpha \tilde{v}_x + \beta \tilde{u}_x + \beta _x\tilde{u}+\alpha \beta _x-\alpha ^{\prime}, \end{align}

(3.14b) \begin{align} \tilde{v}_t-\tilde{u}_x&= \varepsilon \tilde{v}_{xx}-2 \varepsilon \tilde{v}\tilde{v}_x -2\varepsilon \beta \tilde{v}_x -2\varepsilon \tilde{v}\beta _x -2\varepsilon \beta \beta _x-\beta _t, \\[10pt] \nonumber \end{align}

(3.14c) \begin{align} (\tilde{u},\tilde{v})(x,0)&=(u_0(x)-\alpha (0),v_0(x)-\beta (x,0)), \\[10pt] \nonumber \end{align}

(3.14d) \begin{align} \tilde{u}(0,t)&=\tilde{u}(1,t)=0,\, \, \, \tilde{v}(0,t)=\tilde{v}(1,t)=0. \\[10pt] \nonumber \end{align}

Using Lemma 3.1, we can show the following:

Lemma 3.2. Under the assumptions of Theorem 2.1, there exists a constant $C\gt 0$ which is independent of $t$ , such that

\begin{align*} \|\tilde{u}(t)\|^2+\|\tilde{v}(t)\|^2+\int _0^t\|\tilde{u}_x(\tau )\|^2\mathrm{d}\tau \le C. \end{align*}

Proof. Step 1. Taking $L^2$ inner product of (3.14a) with $\tilde{u}$ , we have

(3.15) \begin{equation} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{u}\|^2+\|\tilde{u}_x\|^2=-\int _0^1 \tilde{u}\tilde{v}\tilde{u}_x\mathrm{d}x+\alpha \int _0^1 \tilde{u}\tilde{v}_x\mathrm{d}x +(\alpha \beta _x-\alpha ^{\prime})\int _0^1\tilde{u}\mathrm{d}x +\frac{\beta _x}{2}\|\tilde{u}\|^2. \end{equation}

Taking $L^2$ inner product of (3.14b) with $\tilde{v}$ yields

(3.16) \begin{equation} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{v}\|^2+\varepsilon \|\tilde{v}_x\|^2=\int _0^1 \tilde{v}\tilde{u}_x\mathrm{d}x - \varepsilon \beta _x\|\tilde{v}\|^2 -\int _0^1 (2\varepsilon \beta \beta _x+\beta _t)\tilde{v}\mathrm{d}x. \end{equation}

Multiplying (3.16) by $\alpha$ , we obtain

(3.17) \begin{equation} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\left (\alpha \|\tilde{v}\|^2\right )+\alpha \varepsilon \|\tilde{v}_x\|^2 =-\alpha \int _0^1 \tilde{u}\tilde{v}_x\mathrm{d}x +\big (\frac{\alpha ^{\prime}}{2}-\alpha \varepsilon \beta _x\big )\|\tilde{v}\|^2 - \alpha \int _0^1 (2\varepsilon \beta \beta _x+\beta _t) \tilde{v}\mathrm{d}x. \end{equation}

Adding (3.17) to (3.15) gives us

(3.18) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\left (\|\tilde{u}\|^2+\alpha \|\tilde{v}\|^2\right )+\|\tilde{u}_x\|^2 &+\alpha \varepsilon \|\tilde{v}_x\|^2 = -\int _0^1 \tilde{u}\tilde{v}\tilde{u}_x\mathrm{d}x+ (\alpha \beta _x-\alpha ^{\prime})\int _0^1\tilde{u}\mathrm{d}x + \frac{\beta _x}{2}\|\tilde{u}\|^2 \nonumber \\ & + \big (\frac{\alpha ^{\prime}}{2}-\alpha \varepsilon \beta _x\big )\|\tilde{v}\|^2 -\alpha \int _0^1 (2\varepsilon \beta \beta _x+\beta _t)\tilde{v}\mathrm{d}x \equiv \sum _{k=1}^5I_k. \end{align}

Step 2. To estimate $I_1$ , we note that

(3.19) \begin{align} |I_1| \le \frac 12\|\tilde{u}\|_{L^\infty }^2\|\tilde{v}\|^2 + \frac 12\|\tilde{u}_x\|^2 \le C\|\tilde{u}\|_{L^\infty }^2 + \frac 12\|\tilde{u}_x\|^2, \end{align}

where we used (3.12). Since $\tilde{u}(0,t)=0$ , for any $x\in [0,1]$ , it holds that

(3.20) \begin{align} |\tilde{u}(x,t)|^2=\Big |\int _0^x \tilde{u}_y(y,t)\mathrm{d}y\Big |^2 &\le \Big (\int _0^1|\tilde{u}_x|\mathrm{d}x \Big )^2 \le \Big (\int _0^1u(x,t)\mathrm{d}x\Big )\Big (\int _0^1\frac{(\tilde{u}_x)^2}{u}\mathrm{d}x\Big ), \end{align}

where $u$ denotes the solution to (2.1). Since $E(u,\alpha )$ and $\alpha$ are uniformly bounded with respect to $t$ (see (3.12)), we obtain from (3.9) and (3.20) that

(3.21) \begin{align} \|\tilde{u}(t)\|_{L^\infty }^2\le C\int _0^1\frac{(\tilde{u}_x)^2}{u}\mathrm{d}x. \end{align}

Substituting (3.21) into (3.19) gives us

(3.22) \begin{equation} \left |I_1\right |\le C\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x+\frac 12\|\tilde{u}_x\|^2. \end{equation}

The remaining terms are estimated as

\begin{align*} \bullet \quad & |I_2|\le C\big (|\beta _1-\beta _2|+|\alpha ^{\prime}| \big )\big (\|\tilde{u}\|^2+1\big ),\\ \bullet \quad & |I_5| \le C\big (\varepsilon |\beta _1-\beta _2|+|\beta _1^{\prime}|+|\beta _2^{\prime}|\big )\big (\|\tilde{v}\|^2+1\big ). \end{align*}

Then, we update (3.18) as

(3.23) \begin{align} &\, \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\left (\|\tilde{u}\|^2+\alpha \|\tilde{v}\|^2+1\right )+\frac 12\|\tilde{u}_x\|^2+\alpha \varepsilon \|\tilde{v}_x\|^2\nonumber \\ \le &\, C\big [|\alpha ^{\prime}| + (1+\varepsilon ) |\beta _1-\beta _2| + |\beta _1^{\prime}|+|\beta _2^{\prime}| \big ]\left (\|\tilde{u}\|^2+\alpha \|\tilde{v}\|^2+1\right ) + C\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x. \end{align}

Applying Grönwall’s inequality to (3.23) and using (3.13) and the assumptions in Theorem2.1, we obtain

(3.24) \begin{equation} \|\tilde{u}(t)\|^2+\alpha (t)\|\tilde{v}(t)\|^2\le C. \end{equation}

Substituting (3.24) into (3.23), then integrating the resulting inequality with respect to $t$ , we have

(3.25) \begin{equation} \int _0^t\|\tilde{u}_x(\tau )\|^2\mathrm{d}\tau \le C, \end{equation}

where the constant is independent of $t$ . We conclude the proof by noticing $0\lt \underline{\alpha }\le \alpha (t)$ .

3.3. $L^\infty _tH^1_x$ – $L^2_tH^2_x$ –estimates

Lemma 3.3. Under the assumptions of Theorem 2.1, there exists a constant $C\gt 0$ which is independent of $t$ , such that

\begin{align*} \|\tilde{u}_x(t)\|^2+\|\tilde{v}_x(t)\|^2+\int _0^t\left (\|\tilde{u}_{xx}(\tau )\|^2+\varepsilon \|\tilde{v}_{xx}(\tau )\|^2\right )\mathrm{d}\tau \le C. \end{align*}

Proof. Taking $L^2$ inner products of (3.14a) with $-\tilde{u}_{xx}$ and (3.14b) with $-\tilde{v}_{xx}$ , respectively, then adding the results, we obtain

(3.26) \begin{align} &\frac 12\frac{\mathrm{d}}{\mathrm{d}t}\left (\|\tilde{u}_x\|^2+\|\tilde{v}_x\|^2\right ) +\|\tilde{u}_{xx}\|^2 + \varepsilon \|\tilde{v}_{xx}\|^2 \nonumber \\ =&-\int _0^1\left [ (\tilde{u}\tilde{v})_x+\alpha \tilde{v}_x+(\beta \tilde{u})_x\right ]\,\tilde{u}_{xx}\mathrm{d}x -(\alpha \beta _x-\alpha ^{\prime})\int _0^1\tilde{u}_{xx}\mathrm{d}x + 2\varepsilon \int _0^1 (\tilde{v}+\beta )\tilde{v}_x\tilde{v}_{xx}\mathrm{d}x \nonumber \\ & + 2\varepsilon \beta _x\int _0^1 \tilde{v}\tilde{v}_{xx}\mathrm{d}x - \int _0^1 \tilde{u}_x\tilde{v}_{xx}\mathrm{d}x + \int _0^1 (2\varepsilon \beta \beta _x+\beta _t)\tilde{v}_{xx}\mathrm{d}x \equiv \sum _{k=1}^6 J_k. \end{align}

Since $\beta =(\beta _2-\beta _1)x+\beta _1$ and $\alpha, \beta _1,\beta _2$ are uniformly bounded (see Remark2.2), using the Cauchy–Schwarz, Sobolev and Poincaré inequalities, we can show that

\begin{align*} |J_1| &\le \frac 14\|\tilde{u}_{xx}\|^2+C\left (\|\tilde{v}\|_{L^\infty }^2\|\tilde{u}_x\|^2+\|\tilde{u}\|^2_{L^\infty }\|\tilde{v}_x\|^2+\|\tilde{v}_x\|^2+\|\tilde{u}_x\|^2+\|\tilde{u}\|^2\right )\\ &\le \frac 14\|\tilde{u}_{xx}\|^2 + C\left (\|\tilde{u}_x\|^2\|\tilde{v}_x\|^2+\|\tilde{v}_x\|^2+\|\tilde{u}_x\|^2\right ). \end{align*}

Since $\alpha ^{\prime}(t)$ is uniformly bounded (see Remark2.2), we estimate $J_2$ as

\begin{align*} |J_2| &\le \frac 14\|\tilde{u}_{xx}\|^2+ C(|\beta _1-\beta _2|^2+|\alpha ^{\prime}|^2) \le \frac 14\|\tilde{u}_{xx}\|^2+ C(|\beta _1-\beta _2|+|\alpha ^{\prime}|). \end{align*}

Similar to the estimate of $J_1$ , we can show that

\begin{align*} |J_3| \le \frac{\varepsilon }{4}\|\tilde{v}_{xx}\|^2+C\varepsilon (\|\tilde{v}_x\|^2+1)\|\tilde{v}_x\|^2. \end{align*}

By the boundedness of the boundary data and Poincaré’s inequality, we estimate the remaining terms as:

\begin{align*} |J_4|+|J_5|+|J_6| \le \frac{\varepsilon }{4}\|\tilde{v}_{xx}\|^2+C(\varepsilon, \varepsilon ^{-1})\big (\|(\tilde{v}_x,\tilde{u}_x)\|^2+|(\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime})|\big ). \end{align*}

We remark that the constant $C(\varepsilon, \varepsilon ^{-1})$ results from applying the Cauchy–Schwarz inequality to $J_5$ and $J_6$ where $\varepsilon$ does not appear. Substituting the above estimates into (3.26) gives us

(3.27) \begin{align} &\, \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\left (\|\tilde{u}_x\|^2+\|\tilde{v}_x\|^2\right )+\frac 12\|\tilde{u}_{xx}\|^2+\frac{\varepsilon }{2}\|\tilde{v}_{xx}\|^2 \nonumber \\ \le &\, C\|\tilde{v}_x\|^2(\|\tilde{u}_x\|^2+\varepsilon \|\tilde{v}_x\|^2)+C(\varepsilon, \varepsilon ^{-1})\big (\|(\tilde{v}_x,\tilde{u}_x)\|^2+|(\alpha ^{\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime})|\big ). \end{align}

Applying Grönwall’s inequality to (3.27) and using (3.13), (3.25), we obtain

(3.28) \begin{equation} \|\tilde{u}_x(t)\|^2+\|\tilde{v}_x(t)\|^2+\int _0^t\left (\|\tilde{u}_{xx}(\tau )\|^2+\varepsilon \|\tilde{v}_{xx}(\tau )\|^2\right )\mathrm{d}\tau \le C(\varepsilon, \varepsilon ^{-1}), \end{equation}

where the constant is independent of $t$ . This completes the proof of Lemma 3.3.

3.4. $L^\infty _tH^2_x$ – $L^2_tH^3_x$ –estimates

Lemma 3.4. Under the assumptions of Theorem 2.1, there exists a constant $C\gt 0$ which is independent of $t$ , such that

\begin{align*} \|\tilde{u}_{xx}(t)\|^2+\|\tilde{v}_{xx}(t)\|^2+\int _0^t\left (\|\tilde{u}_{xxx}(\tau )\|^2+ \varepsilon \|\tilde{v}_{xxx}(\tau )\|^2\right )\mathrm{d}\tau \le C. \end{align*}

Proof. Since the information of the higher order spatial derivatives of the solution is unknown at the boundary points, one cannot differentiate the equations with respect to $x$ to estimate the $L^\infty _tH^2_x$ and $L^2_tH^3_x$ norms of the solution. We turn to the estimation of the temporal derivatives and then utilize the equations to recover the spatial derivatives.

Step 1. Taking $\partial _t$ of (3.14a) and (3.14b), we obtain

(3.29a) \begin{align} \tilde{u}_{tt}-(\tilde{u}\tilde{v})_{xt} &=\tilde{u}_{xxt} +\alpha ^{\prime} \tilde{v}_x+\alpha \tilde{v}_{xt}+\beta _t\tilde{u}_x+\beta \tilde{u}_{xt}+\beta _{xt}\tilde{u}+\beta _x\tilde{u}_t+\alpha ^{\prime}\beta _x-\alpha \beta _{xt}-\alpha ^{\prime\prime}, \end{align}

(3.29b) \begin{align} \tilde{v}_{tt}-\tilde{u}_{xt} &=\varepsilon \tilde{v}_{xxt} - 2 \varepsilon \tilde{v}_t\tilde{v}_x - 2 \varepsilon \tilde{v}\tilde{v}_{xt} - 2 \varepsilon \beta _t\tilde{v}_x - 2 \varepsilon \beta \tilde{v}_{xt} - 2 \varepsilon \tilde{v}_t\beta _x - 2 \varepsilon \tilde{v}\beta _{xt} - 2 \varepsilon \beta _t\beta _x \nonumber \\ &\quad - 2 \varepsilon \beta \beta _{xt}-\beta _{tt}. \\[10pt] \nonumber \end{align}

Taking $L^2$ inner product of (3.29a) with $\tilde{u}_t$ , we have

(3.30) \begin{align} \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t} &\|\tilde{u}_t\|^2+\|\tilde{u}_{xt}\|^2 = -\int _0^1(\tilde{u}\tilde{v})_t\tilde{u}_{xt}\mathrm{d}x + \alpha ^{\prime}\int _0^1\tilde{v}_x\tilde{u}_t\mathrm{d}x -\alpha \int _0^1\tilde{v}_{t}\tilde{u}_{xt}\mathrm{d}x + \int _0^1 \beta _t\tilde{u}_{x}\tilde{u}_t\mathrm{d}x \nonumber \\ & + \int _0^1 \beta \tilde{u}_{xt}\tilde{u}_t\mathrm{d}x +\beta _{xt}\int _0^1\tilde{u}\tilde{u}_t\mathrm{d}x + \beta _x\|\tilde{u}_{t}\|^2 + (\alpha ^{\prime}\beta _x-\alpha \beta _{xt}-\alpha ^{\prime\prime})\int _0^1\tilde{u}_t\mathrm{d}x \equiv \sum _{k=1}^8 K_k. \end{align}

For $K_{1}$ , we can show that

\begin{align*} |K_{1}| \le & \frac 16 \|\tilde{u}_{xt}\|^2 + 3\big (\|\tilde{u}\|_{L^\infty }^2\|\tilde{v}_t\|^2 + \|\tilde{v}\|_{L^\infty }^2\|\tilde{u}_t\|^2\big )\\ \le & \frac 16 \|\tilde{u}_{xt}\|^2 + C\big (\|\tilde{u}\|_{H^1}^2\|\tilde{v}_t\|^2 + \|\tilde{v}\|_{H^1}^2\|\tilde{u}_t\|^2\big ) \le \frac 16 \|\tilde{u}_{xt}\|^2 + C\|(\tilde{v}_t, \tilde{u}_t)\|^2, \end{align*}

where we applied Lemmas 3.2 and 3.3. Using the boundedness of the boundary data, we have

\begin{align*} |K_{2}| + |K_{3}| + |K_{4}| + |K_{5}| +|K_6| + |K_7| \le \frac 13 \|\tilde{u}_{xt}\|^2 + C\|(\tilde{u}_x,\tilde{v}_x,\tilde{u}_t,\tilde{v}_t)\|^2, \end{align*}

where we also invoked Poincaré’s inequality. Similarly, $K_{8}$ is estimated as

\begin{align*} |K_{8}| \le & |\alpha ^{\prime\prime}|\,\|\tilde{u}_t\|^2 + C\big (|\alpha ^{\prime\prime}|+\|\tilde{u}_t\|^2+|\alpha ^{\prime}|^2|\beta _1-\beta _2|^2+|\alpha |^2(|\beta _1^{\prime}|^2+|\beta _2^{\prime}|^2)\big )\\ \le & \frac 12 |\alpha ^{\prime\prime}|\,\|\tilde{u}_t\|^2 + C\big (\|\tilde{u}_t\|^2+|(\alpha ^{\prime\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime})|\big ). \end{align*}

Substituting the above estimates into (3.30) gives us

(3.31) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{u}_t\|^2+\|\tilde{u}_{xt}\|^2 \le |\alpha ^{\prime\prime}|\,\|\tilde{u}_t\|^2+C\big (\|(\tilde{u}_t,\tilde{u}_x,\tilde{v}_t,\tilde{v}_x)\|^2 + |(\alpha ^{\prime\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime})|\big ). \end{align}

Step 2. Taking $L^2$ inner product of (3.29b) with $\tilde{v}_t$ , we obtain

(3.32) \begin{align} \frac{1}{2}\frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{v}_t\|^2+& \varepsilon \|\tilde{v}_{xt}\|^2 = -\int _0^1\tilde{u}_t\tilde{v}_{xt}\mathrm{d}x + 2 \varepsilon \int _0^1\tilde{v}\tilde{v}_t\tilde{v}_{xt}\mathrm{d}x - 2 \varepsilon \int _0^1\beta _t\tilde{v}_{x}\tilde{v}_t\mathrm{d}x - \varepsilon \beta _x\|\tilde{v}_t\|^2 \nonumber \\ &\quad -2 \varepsilon \beta _{xt} \int _0^1 \tilde{v}\tilde{v}_t\mathrm{d}x - 2 \varepsilon \beta _{x}\int _0^1\beta _t \tilde{v}_t\mathrm{d}x - 2 \varepsilon \beta _{xt}\int _0^1\beta \tilde{v}_t\mathrm{d}x-\int _0^1\beta _{tt}\tilde{v}_t\mathrm{d}x. \end{align}

Using the arguments in Step 1, we can show that

(3.33) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{v}_t\|^2+\varepsilon \|\tilde{v}_{xt}\|^2 \le |(\beta _1^{\prime\prime},\beta _2^{\prime\prime})|\,\|\tilde{v}_t\|^2+C\big (\|(\tilde{u}_t,\tilde{u}_x,\tilde{v}_t,\tilde{v}_x)\|^2 + |(\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime},\beta _1^{\prime\prime},\beta _2^{\prime\prime})|\big ). \end{align}

Note that according to the assumptions of Theorem2.1 and Lemmas 3.1–3.2, the quantities on the right-hand sides of (3.31) and (3.33), except $\|\tilde{u}_t\|^2$ and $\|\tilde{v}_t\|^2$ , are uniformly integrable with respect to $t$ . For $\|\tilde{u}_t\|^2$ and $\|\tilde{v}_t\|^2$ , based on the equations (3.14a) and (3.14b), we can show that

\begin{align*} \bullet \quad &\|\tilde{u}_t\|^2 \le C\big (\|(\tilde{u}_x, \tilde{v}_x, \tilde{u}_{xx})\|^2 + |(\alpha ^{\prime},\beta _1-\beta _2)| \big ),\\ \bullet \quad &\|\tilde{v}_t\|^2 \le C\big (\|(\tilde{u}_x, \tilde{v}_x, \tilde{v}_{xx})\|^2 + |(\beta _1-\beta _2, \beta _1^{\prime}, \beta _2^{\prime})|\big ). \end{align*}

Then we update (3.31) and (3.33) as

\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{u}_t\|^2+\|\tilde{u}_{xt}\|^2 \le |\alpha ^{\prime\prime}|\,\|\tilde{u}_t\|^2+C\big (\|(\tilde{u}_{xx}, \tilde{u}_x, \tilde{v}_{xx}, \tilde{v}_x)\|^2 +|(\alpha ^{\prime}, \alpha ^{\prime\prime}, \beta _1-\beta _2, \beta _1^{\prime}, \beta _2^{\prime})|\big ), \end{align*}

and

\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{v}_t\|^2+\varepsilon \|\tilde{v}_{xt}\|^2 \le |(\beta _1^{\prime\prime},\beta _2^{\prime\prime})|\,\|\tilde{v}_t\|^2+C\big (\|(\tilde{u}_{xx},\tilde{u}_x,\tilde{v}_{xx},\tilde{v}_x)\|^2 +|(\alpha ^{\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime},\beta _1^{\prime\prime},\beta _2^{\prime\prime})|\big ). \end{align*}

Applying Grönwall’s inequality to the above inequalities, using the assumptions of Theorem2.1 and Lemmas 3.1–3.3, we can show that

(3.34) \begin{equation} \|\tilde{u}_{t}(t)\|^2+\|\tilde{v}_{t}(t)\|^2+\int _0^t\left (\|\tilde{u}_{xt}(\tau )\|^2+ \varepsilon \|\tilde{v}_{xt}(\tau )\|^2\right )\mathrm{d}\tau \le C. \end{equation}

As a consequence, we can show by using the equations in (3.14) that

\begin{align*} \|\tilde{u}_{xx}(t)\|^2+\|\tilde{v}_{xx}(t)\|^2+\int _0^t\left (\|\tilde{u}_{xxx}(\tau )\|^2+\varepsilon \|\tilde{v}_{xxx}(\tau )\|^2\right )\mathrm{d}\tau \le C. \end{align*}

We omit the routine technical details for brevity. This completes the proof of Lemma 3.4.

Lemma 3.1–Lemma 3.4 established the desired a priori estimates of the local solution. The global well-posedness of the IBVP then follows from these estimates and standard continuation argument. To finish the proof of Theorem2.1, it remains to derive the time decay of the perturbation, which is carried out in the next subsection.

3.5. Decay estimate

Lemma 3.5. Under the assumptions of Theorem 2.1, $\|\tilde{u}(t)\|_{H^2}+\|\tilde{v}(t)\|_{H^2} \to 0$ , as $t\to \infty$ .

Proof. Step 1. From Lemma 3.1–Lemma 3.2, we know that $\|\tilde{u}_x(t)\|^2+\|\tilde{v}_x(t)\|^2 \in L^1(\mathbb{R}_+)$ , which, together with Poincaré’s inequality, implies $\|\tilde{u}(t)\|^2+\|\tilde{v}(t)\|^2 \in L^1(\mathbb{R}_+)$ . Since $0\lt \alpha (t)$ is uniformly bounded, we obtain

(3.35) \begin{align} \|\tilde{u}(t)\|^2+\alpha (t)\|\tilde{v}(t)\|^2 \in L^1(\mathbb{R}_+). \end{align}

Using the assumptions of Theorem2.1 and Lemma 3.1–Lemma 3.4, we deduce from (3.18) that

\begin{align*} \Big |\frac{\mathrm{d}}{\mathrm{d}t} \left (\|\tilde{u}\|^2+\alpha \|\tilde{v}\|^2\right ) \Big | \le C\big (\|(\tilde{u}_x,\tilde{v}_x)\|^2 + |(\beta _1-\beta _2,\alpha ^{\prime},\beta _1^{\prime},\beta _2^{\prime})|\big ), \end{align*}

where the constant is independent of $t$ . Integrating the above inequality gives us

(3.36) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \left (\|\tilde{u}(t)\|^2+\alpha (t)\|\tilde{v}(t)\|^2\right ) \in L^1(\mathbb{R}_+). \end{align}

From (3.35) and (3.36), $\|\tilde{u}(t)\|^2+\alpha (t)\|\tilde{v}(t)\|^2 \in W^{1,1}(\mathbb{R}_+)$ . Hence, $\|\tilde{u}(t)\|^2+\alpha (t)\|\tilde{v}(t)\|^2 \to 0$ , as $t\to \infty$ . Since $0\lt \underline{\alpha }\le \alpha (t)$ , we conclude $\|\tilde{u}(t)\|^2+\|\tilde{v}(t)\|^2 \to 0$ , as $t\to \infty$ .

Step 2. The decay of $\|\tilde{u}_x(t)\|^2+\|\tilde{v}_x(t)\|^2$ follows by the same idea. Indeed, from (3.26), we have

\begin{align*} \Big |\frac{\mathrm{d}}{\mathrm{d}t} \left (\|\tilde{u}_x\|^2+\|\tilde{v}_x\|^2\right ) \Big | \le C\big (\|(\tilde{u}_x,\tilde{v}_x,\tilde{u}_{xx},\tilde{v}_{xx})\|^2+ |(\alpha ^{\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime})|\big ), \end{align*}

which, together with the estimates of the solution and the assumptions of Theorem2.1, implies

\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} \left (\|\tilde{u}_x\|^2+\|\tilde{v}_x\|^2\right ) \in L^1(\mathbb{R}_+). \end{align*}

Hence, $\|\tilde{u}_x(t)\|^2+\|\tilde{v}_x(t)\|^2 \in W^{1,1}(\mathbb{R}_+)$ , which implies $\|\tilde{u}_x(t)\|^2+\|\tilde{v}_x(t)\|^2 \to 0$ , as $t\to \infty$ .

Step 3. For the second order spatial derivatives, we know from (3.34) and Poincaré’s inequality that $\|\tilde{u}_t(t)\|^2+\|\tilde{v}_t(t)\|^2 \in L^1(\mathbb{R}_+)$ . By (3.30) and (3.32), we can show that

\begin{align*} \Big | \frac{\mathrm{d}}{\mathrm{d}t} \left (\|\tilde{u}_t\|^2+\|\tilde{v}_t\|^2\right ) \Big | \le C\big (\|(\tilde{u}_t,\tilde{v}_t,\tilde{u}_{xt},\tilde{v}_{xt},\tilde{u}_x,\tilde{v}_x)\|^2 + |(\alpha ^{\prime},\alpha ^{\prime\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime},\beta _1^{\prime\prime},\beta _2^{\prime\prime})| \big ), \end{align*}

which, together with the estimates of the solution and the assumptions of Theorem2.1, implies

\begin{align*} \frac{\mathrm{d}}{\mathrm{d}t} \left (\|\tilde{u}_t(t)\|^2+\|\tilde{v}_t(t)\|^2\right ) \in L^1(\mathbb{R}_+). \end{align*}

Hence, $\|\tilde{u}_t(t)\|^2+\|\tilde{v}_t(t)\|^2 \in W^{1,1}(\mathbb{R}_+)$ , which implies $\|\tilde{u}_t(t)\|^2+\|\tilde{v}_t(t)\|^2 \to 0$ , as $t\to \infty$ . According to (3.14), we can show that

(3.37) \begin{align} \|\tilde{u}_{xx}\|^2+\|\tilde{v}_{xx}\|^2 \le C\big ( \|(\tilde{u}_t,\tilde{v}_t,\tilde{u}_x,\tilde{v}_x)\|^2 + |(\alpha ^{\prime},\beta _1-\beta _2,\beta _1^{\prime},\beta _2^{\prime})|\big ). \end{align}

Since $\alpha ^{\prime}$ , $\beta _1-\beta _2$ , $\beta _1^{\prime}$ and $\beta _2^{\prime}$ belong to $W^{1,1}(\mathbb{R}_+)$ , they all tend to zero as $t\to \infty$ . Therefore, the decay of $\|\tilde{u}_{xx}(t)\|^2+\|\tilde{v}_{xx}(t)\|^2$ follows from (3.37) and the decay of the first-order derivatives of the perturbation. This completes the proof of Lemma 3.5.

4. Proof of Theorem2.2

This section is devoted to prove Theorem2.2. Recall system (2.2):

(4.1a) \begin{align} u_t-(uv)_x &=u_{xx}, \end{align}

(4.1b) \begin{align} v_t-u_x&= 0, \\[10pt] \nonumber \end{align}

together with the initial and boundary conditions:

(4.2a) \begin{align} (u,v)(x,0) &= (u_0,v_0)(x), \quad x \in [0,1], \end{align}

(4.2b) \begin{align} u(0,t)&=u(1,t)=\alpha (t),\quad t \ge 0. \\[10pt] \nonumber \end{align}

We stress that some of the a priori estimates in the previous section cannot be carried over to (4.1). This can be seen from (3.27), in which the constant blows up when $\varepsilon \to 0$ . We adapt a different approach to estimate higher order spatial derivatives of the solution.

Step 1. First we note that (3.4) is still valid when $\varepsilon =0$ . We record it here for convenience:

(4.3) \begin{equation} \frac{\mathrm{d}}{\mathrm{d}t}E(u,\alpha )+\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x = -\int _0^1 v u_x\mathrm{d}x-\int _0^1(u-\alpha )\frac{\alpha ^{\prime}}{\alpha }\mathrm{d}x, \end{equation}

where $E(u,\alpha )$ is the same as before. Integrating (4.1b) with respect to $x$ and $t$ and using the boundary conditions for $u$ , we have

(4.4) \begin{align} \int _0^1 v(x,t){\mathrm{d}x} = \int _0^1 v(x,0){\mathrm{d}x} \equiv \overline{v}. \end{align}

Since $\overline{v}$ is a constant, we easily obtain

(4.5) \begin{align} (v-\overline{v})_t - u_x=0. \end{align}

Taking $L^2$ inner product of (4.5) with $(v-\overline{v})$ , we obtain

(4.6) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t} \|v-\overline{v}\|^2 = \int _0^1 u_x(v-\overline{v}){\mathrm{d}x} = \int _0^1 u_x v{\mathrm{d}x}, \end{align}

where the integral of $u_x\overline{v}$ is zero, since $\overline{v}$ is a constant and the boundary values of $u$ match at the endpoints. Taking the sum of (4.3) and (4.6) gives us

(4.7) \begin{equation} \frac{\mathrm{d}}{\mathrm{d}t} \Big (E(u,\alpha ) + \frac 12\|v-\overline{v}\|^2\Big ) +\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x = -\int _0^1(u-\alpha )\frac{\alpha ^{\prime}}{\alpha }\mathrm{d}x. \end{equation}

Similar to Step 2 of the proof of Lemma 3.1, we can show that

(4.8) \begin{equation} \frac{\mathrm{d}}{\mathrm{d}t} \Big (E(u,\alpha ) + \frac 12\|v-\overline{v}\|^2\Big ) +\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x \le \frac{|\alpha ^{\prime}|}{\underline{\alpha }}E(u,\alpha ) + e|\alpha ^{\prime}|. \end{equation}

Applying Grönwall’s inequality and using the assumptions for $\alpha$ , we obtain

(4.9) \begin{align} E(u,\alpha )(t)+\|(v-\overline{v})(t)\|^2+\int _0^t\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x\mathrm{d}\tau \le C, \end{align}

where the constant on the right-hand side is independent of $t$ .

Step 2. Again, we define the perturbed variables: ${\tilde u}(x,t) = u(x,t) - \alpha (t)$ , ${\tilde v}(x,t) = v(x,t) - \overline{v}$ . Similar to (3.14), we have

(4.10a) \begin{align} \tilde{u}_t-(\tilde{u}\tilde{v})_x &=\tilde{u}_{xx} + \alpha \tilde{v}_x + \overline{v}\tilde{u}_x - \alpha ^{\prime}, \end{align}

(4.10b) \begin{align} \tilde{v}_t-\tilde{u}_x &= 0. \\[10pt] \nonumber \end{align}

Taking $L^2$ inner product of (4.10a) with $\tilde u$ , we have

(4.11) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t} \|{\tilde u}\|^2 + \|{\tilde u}_x\|^2 = -\int _0^1{\tilde u}{\tilde v}{\tilde u}_x{\mathrm{d}x} + \alpha \int _0^1{\tilde v}_x{\tilde u}{\mathrm{d}x} - \alpha ^{\prime}\int _0^1{\tilde u}{\mathrm{d}x}. \end{align}

Taking $L^2$ inner product of (4.10b) with $\alpha{\tilde v}$ , we obtain

(4.12) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\big (\alpha \|{\tilde v}\|^2\big ) = \alpha \int _0^1{\tilde u}_x{\tilde v}{\mathrm{d}x} + \frac{\alpha ^{\prime}}{2}\|{\tilde v}\|^2. \end{align}

Taking the sum of (4.11) and (4.12) gives us

(4.13) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t} \big (\|{\tilde u}\|^2 +\alpha \|{\tilde v}\|^2\big ) + \|{\tilde u}_x\|^2 = -\int _0^1{\tilde u}{\tilde v}{\tilde u}_x{\mathrm{d}x} - \alpha ^{\prime}\int _0^1{\tilde u}{\mathrm{d}x} + \frac{\alpha ^{\prime}}{2}\|{\tilde v}\|^2. \end{align}

The estimate of the first integral on the right-hand side of (4.13) is identical to (3.23), which is recorded here for convenience:

(4.14) \begin{equation} \int _0^1{\tilde u}{\tilde v}{\tilde u}_x{\mathrm{d}x} \le C\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x+\frac 12\|\tilde{u}_x\|^2. \end{equation}

The second integral on the right-hand side of (4.13) is estimated as

(4.15) \begin{align} \alpha ^{\prime}\int _0^1{\tilde u}{\mathrm{d}x} \le |\alpha ^{\prime}|\,\|{\tilde u}\| \le \frac{|\alpha ^{\prime}|}{2}\|{\tilde u}\|^2 + \frac{|\alpha ^{\prime}|}{2}. \end{align}

Substituting (4.14) and (4.15) into (4.13), we obtain

(4.16) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \big (\|{\tilde u}\|^2 +\alpha \|{\tilde v}\|^2\big ) + \|{\tilde u}_x\|^2 \le C|\alpha ^{\prime}|\big (\|{\tilde u}\|^2 +\alpha \|{\tilde v}\|^2\big ) + C\Big (\int _0^1\frac{(u_x)^2}{u}\mathrm{d}x + |\alpha ^{\prime}|\Big ), \end{align}

where we utilised the strictly positive lower bound of $\alpha$ for the third term on the right-hand side of (4.13). Applying Grönwall’s inequality and using the assumptions for $\alpha$ , we can show that

(4.17) \begin{align} \|{\tilde u}(t)\|^2 + \|{\tilde v}(t)\|^2 + \int _0^t\|{\tilde u}_x(\tau )\|^2\mathrm{d}\tau \le C, \end{align}

where (4.9) is applied and the constant $C$ is independent of $t$ .

Step 3. This step is the major difference between the proof of Theorems2.1 and 2.2. The following equation, obtained by substituting ${\tilde u}_{xx}={\tilde v}_{xt}$ into (4.10a),

(4.18) \begin{align} {\tilde v}_{xt} + \alpha \tilde{v}_x = \tilde{u}_t-(\tilde{u}\tilde{v})_x - \overline{v}\tilde{u}_x + \alpha ^{\prime}, \end{align}

serves as the ground for the time integrability of ${\tilde v}_x$ . Taking $L^2$ inner product of (4.18) with ${\tilde v}_x$ , we have

(4.19) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t} \|{\tilde v}_x\|^2 + \alpha \|{\tilde v}_x\|^2 = \int _0^1{\tilde u}_t{\tilde v}_x{\mathrm{d}x} - \int _0^1 ({\tilde u}{\tilde v})_x{\tilde v}_x{\mathrm{d}x} - \overline{v}\int _0^1{\tilde u}_x{\tilde v}_x{\mathrm{d}x} + \alpha ^{\prime}\int _0^1{\tilde v}_x{\mathrm{d}x}. \end{align}

Using (4.10b), we rewrite the first integral on the right-hand side of (4.19) as

(4.20) \begin{align} \int _0^1{\tilde u}_t{\tilde v}_x{\mathrm{d}x} = \frac{\mathrm{d}}{\mathrm{d}t}\int _0^1{\tilde u}{\tilde v}_x{\mathrm{d}x} - \int _0^1{\tilde u}{\tilde v}_{xt}{\mathrm{d}x} = \frac{\mathrm{d}}{\mathrm{d}t}\int _0^1{\tilde u}{\tilde v}_x{\mathrm{d}x} + \|{\tilde u}_x\|^2. \end{align}

Substituting (4.20) into (4.19), we obtain

(4.21) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \Big (\frac 12\|{\tilde v}_x\|^2 -\int _0^1{\tilde u}{\tilde v}_x{\mathrm{d}x}\Big ) + \alpha \|{\tilde v}_x\|^2 = \|{\tilde u}_x\|^2 - \int _0^1 \left [ ({\tilde u}{\tilde v})_x+ \overline{v}{\tilde u}_x - \alpha ^{\prime}\right ]{\tilde v}_x{\mathrm{d}x}. \end{align}

The three pieces in the integral on the right-hand side of (4.21) are estimated as

\begin{align*} \bullet \quad &\int _0^1 ({\tilde u}{\tilde v})_x{\tilde v}_x{\mathrm{d}x} \le C\|{\tilde u}_x\| \|{\tilde v}_x\| \|{\tilde v}_x\| \le \frac{\alpha }{6}\|{\tilde v}_x\|^2 + \frac{C}{\alpha }\|{\tilde u}_x\|^2\|{\tilde v}_x\|^2, \\ \bullet \quad &\overline{v}\int _0^1{\tilde u}_x{\tilde v}_x{\mathrm{d}x} \le C\|{\tilde u}_x\| \|{\tilde v}_x\| \le \frac{\alpha }{6}\|{\tilde v}_x\|^2 + \frac{C}{\alpha }\|{\tilde u}_x\|^2, \\ \bullet \quad &\alpha ^{\prime}\int _0^1{\tilde v}_x{\mathrm{d}x} \le |\alpha ^{\prime}| \|{\tilde v}_x\| \le \frac{\alpha }{6}\|{\tilde v}_x\|^2 + \frac{C}{\alpha }|\alpha ^{\prime}|^2. \end{align*}

Substituting these estimates into (4.21) gives us

(4.22) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \Big (\frac 12\|{\tilde v}_x\|^2 -\int _0^1{\tilde u}{\tilde v}_x{\mathrm{d}x}\Big ) + \frac{\alpha }{2}\|{\tilde v}_x\|^2 \le C\|{\tilde u}_x\|^2\|{\tilde v}_x\|^2 + C\big ( \|{\tilde u}_x\|^2 +|\alpha ^{\prime}|\big ), \end{align}

where we used the information that $\alpha (t)\ge \underline{\alpha }\gt 0$ and that $|\alpha ^{\prime}|$ is uniformly bounded. According to (4.17), there is a constant, denoted by $\overline{U}_1$ , such that $\|{\tilde u}\|^2 \le \overline{U}_1$ . Since

\begin{align*} \Big | \int _0^1{\tilde u}{\tilde v}_x{\mathrm{d}x} \Big | &\le \|{\tilde u}\|^2 + \frac 14\|{\tilde v}_x\|^2 \le \overline{U}_1 + \frac 14\|{\tilde v}_x\|^2, \end{align*}

we know that

(4.23) \begin{align} E_1(t) := \frac 12\|{\tilde v}_x\|^2 -\int _0^1{\tilde u}{\tilde v}_x{\mathrm{d}x} + \overline{U}_1 \ge \frac 14\|{\tilde v}_x\|^2. \end{align}

Then we update (4.22) as

(4.24) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} E_1(t) + \frac{\alpha }{2}\|{\tilde v}_x\|^2 \le C\|{\tilde u}_x\|^2 E_1(t) + C\big ( \|{\tilde u}_x\|^2 +|\alpha ^{\prime}|\big ). \end{align}

Applying Grönwall’s inequality, using (4.17) and the assumptions for $\alpha$ , we can show that

(4.25) \begin{align} \|{\tilde v}_x(t)\|^2 + \int _0^t \|{\tilde v}_x(\tau )\|^2\mathrm{d}\tau \le C, \end{align}

where (4.23) is applied and the constant on the right-hand side is independent of $t$ .

Step 4. Taking $L^2$ inner product of (4.10a) with $-{\tilde u}_{xx}$ , we have

(4.26) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t} \|{\tilde u}_x\|^2 + \|{\tilde u}_{xx}\|^2 = -\int _0^1 \left [ ({\tilde u}{\tilde v})_x + \alpha{\tilde v}_x + \overline{v}{\tilde u}_x - \alpha ^{\prime}\right ]{\tilde u}_{xx}{\mathrm{d}x}. \end{align}

The integral on the right-hand side of (4.26) is estimated as

\begin{align*} \int _0^1 \left [ ({\tilde u}{\tilde v})_x + \alpha{\tilde v}_x + \overline{v}{\tilde u}_x - \alpha ^{\prime}\right ]{\tilde u}_{xx}{\mathrm{d}x} \le C\big (\|{\tilde u}_x\|\|{\tilde v}_x\| +\|{\tilde v}_x\| + \|{\tilde u}_x\| + |\alpha ^{\prime}|\big ) \|{\tilde u}_{xx}\|. \end{align*}

Substituting the above into (4.26) and applying the Cauchy–Schwarz inequality, we obtain

(4.27) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t} \|{\tilde u}_x\|^2 + \|{\tilde u}_{xx}\|^2 \le C\|{\tilde u}_x\|^2\|{\tilde v}_x\|^2 + C\big (\|{\tilde u}_x\|^2 + \|{\tilde v}_x\|^2 + |\alpha ^{\prime}|\big ), \end{align}

where the uniform boundedness of $|\alpha ^{\prime}|$ is used. Applying Grönwall’s inequality to (4.27), using (4.17), (4.25) and the assumptions for $\alpha$ , we can show that

(4.28) \begin{align} \|{\tilde u}_x(t)\|^2 + \int _0^t\|{\tilde u}_{xx}(\tau )\|^2\mathrm{d}\tau \le C, \end{align}

where the constant on the right-hand side is independent of $t$ .

Step 5. Differentiating (4.10a) with respect to $t$ , we have

(4.29) \begin{align} \tilde{u}_{tt}-(\tilde{u}\tilde{v})_{xt}=\tilde{u}_{xxt} + (\alpha \tilde{v})_{xt} + \overline{v}\tilde{u}_{xt} - \alpha ^{\prime\prime}. \end{align}

Taking $L^2$ inner product of (4.29) with ${\tilde u}_t$ and integrating by parts, we obtain

(4.30) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{u}_t\|^2 + \|{\tilde u}_{xt}\|^2 = -\int _0^1 (\tilde{u}\tilde{v})_{t}{\tilde u}_{xt}{\mathrm{d}x} - \int _0^1 (\alpha \tilde{v})_{t}{\tilde u}_{xt}{\mathrm{d}x} - \alpha ^{\prime\prime} \int _0^1{\tilde u}_t{\mathrm{d}x}. \end{align}

The integrals on the right-hand side of (4.30) are estimated as

\begin{align*} \bullet \quad &\int _0^1 (\tilde{u}\tilde{v})_{t}{\tilde u}_{xt}{\mathrm{d}x} \le C\big (\|{\tilde u}_x\|\|{\tilde v}_t\| + \|{\tilde v}_x\| \|{\tilde u}_t\|\big )\|{\tilde u}_{xt}\|, \\ \bullet \quad &\int _0^1 (\alpha \tilde{v})_{t}{\tilde u}_{xt}{\mathrm{d}x} \le \big (|\alpha ^{\prime}|\|{\tilde v}\| + |\alpha | \|{\tilde v}_t\|\big ) \|{\tilde u}_{xt}\|, \\ \bullet \quad &\alpha ^{\prime\prime} \int _0^1{\tilde u}_t{\mathrm{d}x} \le \frac{|\alpha ^{\prime\prime}|}{2} + \frac{|\alpha ^{\prime\prime}|}{2}\|{\tilde u}_t\|^2. \end{align*}

Using these estimates and the Cauchy-Schwarz inequality, we update (4.30) as

(4.31) \begin{align} \frac{\mathrm{d}}{\mathrm{d}t}\|\tilde{u}_t\|^2 + \|{\tilde u}_{xt}\|^2 \le &\,C\big (\|{\tilde v}_x\|^2+|\alpha ^{\prime\prime}|\big ) \|{\tilde u}_t\|^2 + C\big (\|{\tilde u}_x\|^2\|{\tilde v}_t\|^2 + \|{\tilde v}\|^2 + \|{\tilde v}_t\|^2 + |\alpha ^{\prime\prime}|\big ) \nonumber \\ \le &\,C\big (\|{\tilde v}_x\|^2+|\alpha ^{\prime\prime}|\big ) \|{\tilde u}_t\|^2 + C\big (\|{\tilde u}_x\|^2 + \|{\tilde v}_x\|^2 + |\alpha ^{\prime\prime}|\big ), \end{align}

where we replaced ${\tilde v}_t$ by ${\tilde u}_x$ and utilised (4.28) and the uniform boundedness of $|\alpha ^{\prime}|$ and $|\alpha |$ , together with Poincaré’s inequality for $\tilde v$ (since it is mean free). Applying Grönwall’s inequality gives us

(4.32) \begin{align} \|\tilde{u}_t(t)\|^2 + \int _0^t \|{\tilde u}_{xt}(\tau )\|^2\mathrm{d}\tau \le C. \end{align}

As a consequence of (4.32), (4.10a) and previous estimates, we have

(4.33) \begin{align} \|{\tilde u}_{xx}(t)\|^2 \le C\big (\|{\tilde u}_t\|^2 + \|{\tilde u}_x\|^2\|{\tilde v}_x\|^2 + \|{\tilde v}_x\|^2 + \|{\tilde u}_x\|^2 + |\alpha ^{\prime}|^2\big ) \le C, \end{align}

where the constant $C$ is independent of $t$ .

Step 6. Taking $\partial _x$ of (4.18) gives us

(4.34) \begin{align} {\tilde v}_{xxt} + \alpha \tilde{v}_{xx} = \tilde{u}_{xt}-(\tilde{u}\tilde{v})_{xx} - \overline{v}\tilde{u}_{xx}. \end{align}

Taking $L^2$ inner product of (4.34) with ${\tilde v}_{xx}$ , we have

(4.35) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\|{\tilde v}_{xx}\|^2 + \alpha \|\tilde{v}_{xx}\| = \int _0^1 \tilde{u}_{xt}{\tilde v}_{xx}{\mathrm{d}x} -\int _0^1 (\tilde{u}\tilde{v})_{xx}{\tilde v}_{xx}{\mathrm{d}x} - \overline{v} \int _0^1 \tilde{u}_{xx}{\tilde v}_{xx}{\mathrm{d}x}. \end{align}

The integrals on the right-hand side are estimated as:

\begin{align*} \bullet \quad &\int _0^1 \tilde{u}_{xt}{\tilde v}_{xx}{\mathrm{d}x} \le C\|{\tilde u}_{xt}\|^2 + \frac{\alpha }{6}\|{\tilde v}_{xx}\|^2, \\ \bullet \quad &\int _0^1 (\tilde{u}\tilde{v})_{xx}{\tilde v}_{xx}{\mathrm{d}x} \le C\big (\|{\tilde v}_x\|^2\|{\tilde u}_{xx}\|^2 + \|{\tilde u}_x\|^2\|{\tilde v}_{xx}\|^2\big ) + \frac{\alpha }{6}\|{\tilde v}_{xx}\|^2, \\ \bullet \quad &\overline{v} \int _0^1 \tilde{u}_{xx}{\tilde v}_{xx}{\mathrm{d}x} \le C\|{\tilde u}_{xx}\|^2 + \frac{\alpha }{6}\|{\tilde v}_{xx}\|^2. \end{align*}

Then we update (4.35) as

(4.36) \begin{align} \frac 12\frac{\mathrm{d}}{\mathrm{d}t}\|{\tilde v}_{xx}\|^2 + \frac{\alpha }{2} \|\tilde{v}_{xx}\| \le C\|{\tilde u}_x\|^2\|{\tilde v}_{xx}\|^2 + C\big (\|{\tilde u}_{xt}\|^2 + \|{\tilde u}_{xx}\|^2\big ), \end{align}

where we used (4.25) for the estimate of $\|{\tilde v}_x(t)\|$ . Applying Grönwall’s inequality, we obtain

(4.37) \begin{align} \|{\tilde v}_{xx}(t)\|^2 + \int _0^t \|{\tilde v}_{xx}(\tau )\|^2\mathrm{d}\tau \le C. \end{align}

As a consequence of (4.37), (4.10a) and previous estimates, we can show that

(4.38) \begin{align} \int _0^t \|{\tilde u}_{xxx}(\tau )\|^2\mathrm{d}\tau \le C, \end{align}

where the constant on the right-hand side is independent of $t$ . The routine technical details are omitted for brevity. This completes the proof of the a priori estimates of the solution, as stated in Theorem2.2. Moreover, the time decay of the perturbation follows from the same spirit in the previous section. The proof of Theorem2.2 is thus complete.

5. Numerical studies

In this section, we carry out numerical tests to study the dynamical properties of solutions to (2.1), and those of (2.2). In particular, we 1) provide numerical confirmation of the rigorous qualitative results established in Theorems2.1-2.2, 2) explore the steady states of the solutions when relaxing some of the assumptions in the theorems and 3) determine whether the solutions converge to time-periodic states when the boundary data are periodic in time.

In order to study the dynamical behavior of the solutions subject to time-periodic boundary conditions, we introduce the following definition.

Definition 5.1. We say that a function $g(x,t)$ defined in $\Omega \times [0,\infty )$ converges to a time-periodic state if there exists $T\gt 0$ such that for any $\epsilon \gt 0$ , there exists $t^*\gt 0$ , such that

\begin{align*} |g(x,t+T)-g(x,t)|\leq \epsilon \end{align*}

for any $(x,t)\in \Omega \times [t^*,\infty )$

For the simulations in this section, we make use of an explicit finite-difference scheme to solve (2.1) and (2.2) with a second-order approximation of spatial derivatives with a temporal mesh, $\Delta t= \frac{(\Delta x)^2}2$ , and a spatial mesh, $\Delta x\lt \sqrt{\frac{\varepsilon }{10}}$ , similar to what would be chosen for the heat equation in order to avoid that the numerical diffusion dominates the chemical diffusion. The domain for the system is the unit interval $[0,1]$ with time-dependent boundary data $\alpha _1, \alpha _2$ and $\beta _1, \beta _2$ . For the following results, we have used initial data $u(x,0)=0.3+0.1 \sin ^2(2\pi x)$ and $v(x,0)=0.2 \sin ^2(2\pi x)$ . We would like to point out that the large–time behaviors of the solutions do not vary for similar kinds of initial data. For consistency, we use the same initial conditions and $N=200$ throughout the computations in this section.

We define $A (x,t)= (\alpha _2-\alpha _1)x+ \alpha _1$ and $B (x,t)= (\beta _2-\beta _1)x+ \beta _1$ , the linear interpolation of the boundary data, $\tilde u=u-A$ and $\tilde v=v-B$ . Moreover, throughout this section, the letters with overhead bar denote real constants.

5.1. Solutions of (2.1) with converging boundary data

We study the existence of steady states of solutions to (2.1) with different converging conditions on the boundary data. For these computations, we use $\varepsilon =0.7$ .

Case 1: $\boxed{\alpha _1=\alpha _2\to \bar{\alpha }, \, \, \beta _1\neq \beta _2,\, \, \beta _1\to \bar \beta \gets \beta _2}$

The solution $(u,v)$ converges to the steady state $(\bar \alpha, \bar \beta )$ as proved in Theorem2.1.

Figure 1. Solution of (2.1) with $\alpha _1=\alpha _2\to \bar \alpha, \, \, \beta _1\neq \beta _2,\, \, \beta _1\to \bar \beta \gets \beta _2$ .

In this case, we plot $u,v, A, B$ with $\alpha _1=0.7+\exp ({-}200000t)=\alpha _2$ , $\beta _1=0.3+1/(1+10000t)$ and $\beta _2= 0.3+1/(4+1000t)$ . Figure 1a plots the solution $(u,v)$ and the linear interpolation $(A,B)$ at time $t=0.168$ , with $\alpha _1=0.7=\alpha _2$ , $\beta _1=0.301, \beta _2=0.306$ . Figure 1b plots $(u,v,A,B)$ at time $t=49.9$ , with $\alpha _1=0.7=\alpha _2$ , $\beta _1=0.3002, \beta _2=0.3018$ . In particular, we observe that the solution reaches the steady state $(\bar \alpha, \bar \beta )=(0.7,0.3)$ , as $t\to \infty$ .

Case 2: $\boxed{\alpha _1\neq \alpha _2, \, \, \alpha _1\to \bar \alpha \gets \alpha _2,\, \, \beta _1\neq \beta _2,\, \, \beta _1\to \bar \beta \gets \beta _2}$

The solution $(u,v)$ converges to the steady state $(\bar \alpha, \bar \beta )$ .

Figure 2. Solution of (2.1) with $\alpha _1\neq \alpha _2, \, \, \alpha _1\to \bar \alpha \gets \alpha _2,\, \, \beta _1\neq \beta _2,\, \, \beta _1\to \bar \beta \gets \beta _2$ .

In this case, we plot $u,v, A, B$ with $\alpha _1=0.7+\exp ({-}200000t)$ , $\alpha _2=0.7+\exp ({-}20t)$ , $\beta _1=0.3+1/(1+10000t)$ and $\beta _2= 0.3+1/(4+1000t)$ . Figure 2a plots the solution $(u,v)$ and the linear interpolation $(A,B)$ at time $t=0.1440$ , with $\alpha _1=0.7$ , $\alpha _2=0.756$ , $\beta _1=0.300,\, \beta _2=0.306$ . Figure 2b plots $(u,v,A,B)$ at time $t=49.99$ , with $\alpha _1=0.7=\alpha _2$ , $\beta _1=0.3, \beta _2=0.3002$ . In particular, we observe that the solution reaches the steady state $(\bar \alpha, \bar \beta )=(0.7,0.3)$ as in Case 1.

Case 3: $\boxed{\alpha _1=\alpha _2\to \bar \alpha, \, \, \beta _1\to \bar \beta _1\neq \bar \beta _2\gets \beta _2}$

The solution $(u,v)$ has a steady state different from $\big (\bar \alpha, (\bar \beta _2-\bar \beta _1)x+\bar \beta _1\big )$ .

Figure 3. Solution of (2.1) with $\alpha _1=\alpha _2\to \bar \alpha, \, \, \beta _1\to \bar \beta _1\neq \bar \beta _2\gets \beta _2.$ .

In this case, we plot $u,v, A, B$ with $\alpha _1=0.7+\exp ({-}200000t)=\alpha _2$ , $\beta _1=0.5+1/(1+10000t)$ and $\beta _2= 0.3+1/(4+1000t)$ . Figure 3a plots the solution $(u,v)$ and the linear interpolation $(A,B)$ at time $t=0.168$ , with $\alpha _1=0.7=\alpha _2$ , $\beta _1=0.301, \beta _2=0.306$ . Figure 3b shows $(u,v,A,B)$ at time $t=49.9$ , with $\alpha _1=0.7=\alpha _2$ , $\beta _1=0.500, \beta _2=0.300$ . In particular, we observe that the solution reaches a steady state different from $\big (\bar \alpha, (\bar \beta _2-\bar \beta _1)x+\bar \beta _1\big )=\big (0.7,-0.2x+0.5\big )$ .

Case 4: $\boxed{\alpha _1\to \bar \alpha _1\neq \bar \alpha _2\gets \alpha _2,\, \, \beta _1\to \bar \beta _1\neq \bar \beta _2\gets \beta _2}$

The solution $(u,v)$ has a steady state different from $\big ((\bar \alpha _2-\bar \alpha _1)x+\bar \alpha _1,(\bar \beta _2-\bar \beta _1)x+\bar \beta _1\big )$ .

Figure 4. Solution of (2.1) with $\alpha _1\to \bar \alpha _1\neq \bar \alpha _2\gets \alpha _2,\, \, \beta _1\to \bar \beta _1\neq \bar \beta _2\gets \beta _2$ .

In this case, we plot $u,v, A, B$ with $\alpha _1=0.7+\exp ({-}200000t)$ , $\alpha _2=0.4+\exp ({-}200000t)$ , $\beta _1=0.5+1/(1+10000t)$ and $\beta _2= 0.3+1/(4+1000t)$ . Figure 4a plots the solution $(u,v)$ and the linear interpolation $(A,B)$ at time $t=8.7$ , with $\alpha _1=0.7, \alpha _2=0.4$ , $\beta _1=0.500, \beta _2=0.300$ . Figure 4b plots $(u,v,A,B)$ at time $t=49.9$ , with $\alpha _1=0.7, \alpha _2=0.4$ , $\beta _1=0.500, \beta _2=0.300$ . In particular, we observe that the solution reaches a steady state different from $\big ((\bar \alpha _2-\bar \alpha _1)x+\bar \alpha _1,(\bar \beta _2-\bar \beta _1)x+\bar \beta _1\big )=\big ({-}0.3x+0.7,-0.2x+0.5\big )$ .

5.2 Solutions of (2.2) with converging boundary data

This section contains numerical studies of steady state solutions of (2.2) with different converging boundary conditions. For simulations in this section, we use the boundary data $\alpha _1, \alpha _2$ for $u$ , but notice that the boundary conditions for $v$ cannot be imposed. In this case, they are implicit by (2.2b). Numerically, this presents a challenge that we have overcome by computing explicitly the values at the boundary at each step using (2.2b). Throughout these computations $\varepsilon =0$ , we observe the following.

Case 1: $\boxed{\alpha _1=\alpha _2\to \bar \alpha }$

The solution $(u, v)$ converges to the steady state $(\bar \alpha, \bar v)$ as proved in Theorem2.2.

Figure 5. Solution of (2.2) with $\alpha _1=\alpha _2\to \bar \alpha$ .

In this case, we plot $u,v, A$ with $\alpha _1=0.3+\exp ({-}200000t)=\alpha _2$ . Notice that the average of $v_0$ , $\bar v=0.1$ . Figure 5 shows the evolution in time of the solution $(u,v)$ and the linear interpolation $A$ at times $t=0.036$ , $t=1.2$ , $t=8.4$ and $t=49.99$ . In particular, we observe that the solution approaches the steady state $(A,\bar v)=(0.3,0.1)$ , as $t\to \infty$ . Notice that even if the chemical diffusion coefficient is zero, the function $v$ still smooths up and converges to its initial average, as predicted in Theorem2.2.

Case 2: $\boxed{\alpha _1\neq \alpha _2,\, \, \alpha _1\to \bar \alpha \gets \alpha _2}$

In this case, $u$ converges to $\bar \alpha$ and $v$ converges to a steady–state different from $\bar v$ .

Figure 6. Solution of (2.2) with $\alpha _1\neq \alpha _2$ , $\alpha _1\to \bar \alpha \gets \alpha _2$ .

We plot $u,v, A$ with $\alpha _1=0.3-\exp ({-}200000t)$ and $\alpha _2=0.3+1/(1+200t)$ . Figure 6 shows the evolution in time of the solution $(u,v)$ at times $t=0.036$ , $t=0.168$ , $t=3.576$ , and $t=49.92$ . In particular, we observe that $u$ converges to the steady state $\bar \alpha =0.3$ , but $v$ converges to a steady–state different from $\bar v=0.1$ . This shows that the assumptions in Theorem2.2 are in fact necessary.

Case 3: $\boxed{\alpha _1\to \bar \alpha _1\neq \bar \alpha _2\gets \alpha _2}$

The solution $u$ converges to a steady state different from $(\bar \alpha _2-\bar \alpha _1)x+\bar \alpha _1$ , but $v$ keeps growing or decaying depending on $\alpha _2-\alpha _1$ being negative or positive respectively.

Figure 7. Solution of (2.2) with $\alpha _1\to \bar \alpha _1\neq \bar \alpha _2\gets \alpha _2$ .

In this case, we plot $u,v, A$ with $\alpha _1=0.7+\exp ({-}200000t)$ and $\alpha _2=0.3+\exp ({-}200000t)$ . Figure 7 shows the evolution in time of the solution $(u,v)$ at times $t=0.072$ , $t=0.372$ , $t=0.612$ and $t=49.99$ . In particular, we observe that $u$ reaches a steady state different from $(\bar \alpha _2-\bar \alpha _1)x+\bar \alpha _1=-0.4x+0.7$ , and that $v$ diverges driven by (2.2b).

5.3. Convergence to time-periodic states

We study the dynamical behaviour of the solution with time-periodic boundary conditions for the following cases.

Case 1: $\boxed{\alpha _1= \alpha _2, \beta _1=\beta _2, \varepsilon \gt 0}$

We observe that the solution converges to a time-periodic state with the same exact period as the one of the boundary data.

Figure 8. Induced time-periodic state on solution of (2.1) with $T=1/10$ for $\alpha _1= \alpha _2, \beta _1=\beta _2, \varepsilon \gt 0$ .

For the simulations in Figure 8, we have chosen $\alpha _1=0.3+0.1\sin (20\pi t)=\alpha _2$ and $\beta _1=0.7+0.1\sin (20\pi t)=\beta _2$ . We have used $\varepsilon =0.7$ . We observe that the time periodicity of the boundary data ( $T=1/10$ ) is induced in the stable time-periodic state with the same period.

Case 2: $\boxed{\alpha _1\neq \alpha _2, \beta _1\neq \beta _2, \varepsilon \gt 0}$

We observe that the solution converges to a time-periodic state whose period is the least common multiple of the periods of the boundary data.

Figure 9. Induced time-periodic state on solution of (2.1) with $T=1/10$ for $\alpha _1\neq \alpha _2, \beta _1\neq \beta _2, \varepsilon \gt 0$ .

Figure 10. Induced time-periodic state on solution of (2.1) with $T=6$ for $\alpha _1\neq \alpha _2, \beta _1\neq \beta _2, \varepsilon \gt 0$ .

For the simulations in Figure 9, we have chosen $\alpha _1=0.3+0.1\sin (20\pi t), \alpha _2=0.3+0.1\sin (40\pi t)$ and $\beta _1=0.7+0.1\sin (20\pi t), \beta _2=0.7+0.1\sin (40\pi t)$ , and for the ones in Figure 10 we have chosen $\alpha _1=0.3+0.1\sin (\pi t), \alpha _2=0.3+0.1\sin (\frac 23\pi t)$ and $\beta _1=0.7+0.1\sin (\pi t), \beta _2=0.7+0.1\sin (\frac 23\pi t)$ . In both cases, we use $\varepsilon =0.7$ for the chemical diffusivity coefficient. We observe that the solution converges to a time-periodic state whose period is the least common multiple of the periods of the boundary data ( $T=1/10$ for the first one and $T=6$ for the second one). Figures 9a and 9b, and 10a and 10b show the evolution of both $u$ and $v$ over space and time for both cases.

Case 3: $\boxed{\alpha _1= \alpha _2, \varepsilon =0}$

We observe that the solution converges to a time-periodic state with the same period as that of the boundary data.

Figure 11. Induced time-periodic state on solution of (2.1) with $T=1/10$ for $\alpha _1 = \alpha _2, \varepsilon =0$ .

For the simulations in Figure 11, we have chosen $\alpha _1=0.3+0.1\sin (20\pi t)=\alpha _2$ . We observe that the time periodicity ( $T=1/10$ ) of the boundary data is induced in the time-periodic state. However, the solution $v$ , in contrast with Case 1 in this section, takes a longer time to converge to the time-periodic state (see Figure 8b and Figures 11b–11c).

Case 4: $\boxed{\alpha _1\neq \alpha _2, \varepsilon =0}$

We observe that the time periodicity of the boundary data induces a time-periodic state of the solution $u$ . When the periods of the boundary data are different, the solution picks up the least common multiple of the periods of the boundary data. Solution $v$ will converge to a time-periodic state if the non-periodic parts of $\alpha _1$ and $\alpha _2$ are equal. However, in any other case, $v$ will diverge as in Section 5.2, Case 3.

Figure 12. Induced time-periodic state on solution of (2.2) with $T=1/10$ for $\alpha _1\neq \alpha _2, \varepsilon =0$ .

For the simulations in Figure 12, we have chosen $\alpha _1=0.3+0.1\sin (20\pi t)$ and $ \alpha _2=0.3+0.1\sin (40\pi t)$ . Figure 12a shows the induced time-periodic state of the solution $u$ from the boundary data. In this case, the period induced ( $T=1/10$ ) is the least common multiple of the periods of the boundary data. Again, comparing Figures 12b–12c with Figure 9b, we see that it take solution $v$ a longer time to converge to the time-periodic state.

6. Conclusion

We have studied the dynamical behaviour of classical solutions to the system of balance laws (1.3) with $\chi \mu \gt 0$ , derived from the Keller–Segel type model of chemotaxis with logarithmic sensitivity (1.2), on a finite interval subject to time-dependent Dirichlet-type boundary conditions. For the model with $\varepsilon \gt 0$ , it is shown that under the assumptions (2.6) and (2.7), classical solutions are globally well-posed and the perturbations around the reference profiles interpolating the boundary data converge to zero as time goes to infinity. There is no smallness restriction on the strength of the initial perturbations (see Theorem2.1). This result generalises previous ones in the sense that the values of the function $v$ at the endpoints of the spatial interval are allowed to be different at any time. When $\varepsilon =0$ , similar results are obtained, except in this case, the steady state of $v$ is given by its initial average over the spatial interval (see Theorem2.2).

Numerically, we have seen that by keeping the asymptotic convergence of the boundary data while relaxing the assumptions of Theorems2.1 and 2.2, the solutions still converge to steady states, except in the case of zero chemical diffusion and unequal end-states of the boundary data for $u$ , in which $v$ diverges. For convergent solutions, when the end-states of the boundary data of $u$ and/or $v$ are different, the steady states of the solutions are non-trivial functions of $x$ and are different from the linear profiles interpolating the corresponding end-states of the boundary data. On the other hand, when the boundary data are periodic in time, the periodicity of the boundary functions will induce time-periodic states of the solutions, except when there is no chemical diffusivity and the non-periodic parts of $\alpha _1$ and $\alpha _2$ are different. When the solutions converge to time-periodic states, the time-periodic states pick up the least common multiple of the periods of the boundary data.

The model considered in this article has been utilised to examine the role of protease inhibitors in the initiation of angiogenesis [21], which can be potentially linked to cancer treatments, such as chemotherapy. This work investigates how the dynamic input on the boundary of the spatial domain affects the behaviour of the solution in the interior of the domain. Given the time-dependent nature of cancer therapy, such as drug delivery, we believe that when this work can be verified experimentally, it will help provide meaningful insights into the design of effective therapeutic strategies for cancer patients. For example, our numerical simulations indicate that the time periodicity of the boundary data can be induced into the solution, and that the solution picks up the least common multiple of the boundary periods. This suggests that when a drug or chemical is periodically injected into the surrounding of a tumour near its boundary, one could make quantitative predictions (with a certain degree of confidence) of the time-periodic nature of the key quantities (e.g. cancer cells, drug concentration) inside of the tumour tissue, whose measurements are usually technically unfeasible. The predictions then could be combined with clinical data to evaluate the efficiency of drug delivery systems.

On the other hand, several of the numerical results observed in this article still remain to be proved analytically. For example, whether the matching boundary conditions for the function $u$ can be relaxed so that similar results as Theorems2.1 and 2.2 can be obtained (see Remark2.3). Another direction of future exploration is the dynamical behaviour of the appended model with logistic growth in the $u$ -equation. Because of the enhanced dissipation mechanism induced by logistic damping, the chemotaxis growth model may give us a definite answer to the preceding question.