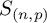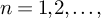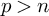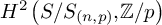1 Introduction
The purpose of this paper is to study the p-Zassenhaus filtration of a free profinite group S and its cohomology by means of the combinatorics of words. Here p is a fixed prime number, and we recall that the p-Zassenhaus filtration of a profinite group G is given by
![]() $G_{\left (n,p\right )}=\prod _{ip^j\geq n}\left (G^{(i)}\right )^{p^j}$
,
$G_{\left (n,p\right )}=\prod _{ip^j\geq n}\left (G^{(i)}\right )^{p^j}$
,
![]() $n=1,2,\dotsc $
– that is,
$n=1,2,\dotsc $
– that is,
![]() $G_{\left (n,p\right )}$
is generated as a profinite group by all
$G_{\left (n,p\right )}$
is generated as a profinite group by all
![]() $p^j$
-powers of elements of the ith term of the (profinite) lower central filtration
$p^j$
-powers of elements of the ith term of the (profinite) lower central filtration
![]() $G^{(i)}$
of G for
$G^{(i)}$
of G for
![]() $ip^j\geq n$
.
$ip^j\geq n$
.
This filtration was introduced by Zassenhaus [Reference Zassenhaus39] for discrete groups (under the name dimension subgroups modulo p) as a tool to study free Lie algebras in characteristic p. It proved itself to be a powerful tool in a variety of group-theoretic and arithmetic problems: the Golod–Shafarevich solution to the class field tower problem ([Reference Koch20], [Reference Koch21, §7.7], [Reference Zelmanov40], [Reference Ershov13]), the structure of finitely generated pro-p groups of finite rank [Reference Dixon, Du Sautoy, Mann and Segal5, Ch. 11], mild groups [Reference Labute24] and one-relator pro-p groups [Reference Gärtner15, §2.4], multiple residue symbols and their knot-theory analogues ([Reference Morishita29], [Reference Morishita30, Ch. 8], [Reference Vogel37]), and more.
In the Galois-theory context, where
![]() $G=G_F$
is the absolute Galois group of a field F containing a root of unity of order p, it was shown in [Reference Efrat and Mináč12] that the quotient
$G=G_F$
is the absolute Galois group of a field F containing a root of unity of order p, it was shown in [Reference Efrat and Mináč12] that the quotient
![]() $G/G_{\left (3,p\right )}$
determines the full cohomology ring
$G/G_{\left (3,p\right )}$
determines the full cohomology ring
![]() $H^*(G)=\bigoplus _{i\geq 0}H^i(G)$
with the cup product. Here and in the sequel we abbreviate
$H^*(G)=\bigoplus _{i\geq 0}H^i(G)$
with the cup product. Here and in the sequel we abbreviate
![]() $H^i(G)=H^i(G,\mathbb {Z}/p)$
for the profinite cohomology group of G with its trivial action on
$H^i(G)=H^i(G,\mathbb {Z}/p)$
for the profinite cohomology group of G with its trivial action on
![]() $\mathbb {Z}/p$
. Moreover,
$\mathbb {Z}/p$
. Moreover,
![]() $G/G_{\left (3,p\right )}$
is the smallest Galois group of F with this property (see also [Reference Chebolu, Efrat and Mináč3]).
$G/G_{\left (3,p\right )}$
is the smallest Galois group of F with this property (see also [Reference Chebolu, Efrat and Mináč3]).
In the present paper we focus on the cohomology group
![]() $H^2\left (G/G_{\left (n,p\right )}\right )$
for a profinite group G and
$H^2\left (G/G_{\left (n,p\right )}\right )$
for a profinite group G and
![]() $n\geq 2$
. Its importance is that it controls the relator structure in the pro-p group
$n\geq 2$
. Its importance is that it controls the relator structure in the pro-p group
![]() $G/G_{(n,p)}$
, whereas its generators are captured by the group
$G/G_{(n,p)}$
, whereas its generators are captured by the group
![]() $H^1(G/G_{\left (n,p\right )})$
, which is well understood [Reference Neukirch, Schmidt and Wingberg31, §3.9].
$H^1(G/G_{\left (n,p\right )})$
, which is well understood [Reference Neukirch, Schmidt and Wingberg31, §3.9].
Our main result gives, for a free profinite group S on a basis X, an explicit description of
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
in terms of the combinatorics of words. Namely, we consider X as an alphabet with a fixed total order, and let
$H^2\left (S/S_{\left (n,p\right )}\right )$
in terms of the combinatorics of words. Namely, we consider X as an alphabet with a fixed total order, and let
![]() $X^*$
be the monoid of words in X. For every
$X^*$
be the monoid of words in X. For every
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $\mathbb {Z}\langle X\rangle _n$
be the free
$\mathbb {Z}\langle X\rangle _n$
be the free
![]() $\mathbb {Z}$
-module generated by all words in
$\mathbb {Z}$
-module generated by all words in
![]() $X^*$
of length n. Let
$X^*$
of length n. Let
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}$
be its quotient by the submodule generated by all shuffle products
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}$
be its quotient by the submodule generated by all shuffle products
, where
![]() $u,v$
are nonempty words in
$u,v$
are nonempty words in
![]() $X^*$
with
$X^*$
with
![]() $\lvert u\rvert +\lvert v\rvert =n$
. We recall that for words
$\lvert u\rvert +\lvert v\rvert =n$
. We recall that for words
![]() $u=(x_1\dotsm x_r)$
and
$u=(x_1\dotsm x_r)$
and
![]() $v=(x_{r+1}\dotsm x_{r+s})$
in
$v=(x_{r+1}\dotsm x_{r+s})$
in
![]() $X^*$
, one defines
$X^*$
, one defines
where
![]() $\sigma $
ranges over all permutations of
$\sigma $
ranges over all permutations of
![]() $\{1,2,\dotsc , r+s\}$
such that
$\{1,2,\dotsc , r+s\}$
such that
![]() $\sigma (1)<\dotsb <\sigma (r)$
and
$\sigma (1)<\dotsb <\sigma (r)$
and
![]() $\sigma (r+1)<\dotsb < \sigma (r+t)$
. Thus
$\sigma (r+1)<\dotsb < \sigma (r+t)$
. Thus
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}$
is the nth homogenous component of the indecomposable quotient of the shuffle algebra
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}$
is the nth homogenous component of the indecomposable quotient of the shuffle algebra
![]() $\operatorname {\mathrm {Sh}}(X)$
in the sense of [Reference Efrat9, §5] (see §9). We prove the following word-combinatorial description of
$\operatorname {\mathrm {Sh}}(X)$
in the sense of [Reference Efrat9, §5] (see §9). We prove the following word-combinatorial description of
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
for p sufficiently large:
$H^2\left (S/S_{\left (n,p\right )}\right )$
for p sufficiently large:
Main Theorem. Suppose that
![]() $n<p$
. There is a canonical isomorphism of
$n<p$
. There is a canonical isomorphism of
![]() $\mathbb {F}_p$
-linear spaces
$\mathbb {F}_p$
-linear spaces
 $$ \begin{align*} \left(\bigoplus_{x\in X}\mathbb{Z}/p\right)\oplus\left(\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},n}\otimes(\mathbb{Z}/p)\right)\xrightarrow{\sim} H^2\left(S/S_{\left(n,p\right)}\right). \end{align*} $$
$$ \begin{align*} \left(\bigoplus_{x\in X}\mathbb{Z}/p\right)\oplus\left(\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},n}\otimes(\mathbb{Z}/p)\right)\xrightarrow{\sim} H^2\left(S/S_{\left(n,p\right)}\right). \end{align*} $$
When
![]() $p\leq n$
we have a similar result, in the form of a canonical epimorphism.
$p\leq n$
we have a similar result, in the form of a canonical epimorphism.
More specifically, to any word w in
![]() $X^*$
of length
$X^*$
of length
![]() $1\leq \lvert w\rvert \leq n$
we associate a canonical cohomology element
$1\leq \lvert w\rvert \leq n$
we associate a canonical cohomology element
![]() $\alpha _{w,n}\in H^2\left (S/S_{\left (n,p\right )}\right )$
. Then the isomorphism in the Main Theorem is induced by the map
$\alpha _{w,n}\in H^2\left (S/S_{\left (n,p\right )}\right )$
. Then the isomorphism in the Main Theorem is induced by the map
![]() $w\mapsto \alpha _{w,n}$
, where w is either a single-letter word or a word of length n. In these cases,
$w\mapsto \alpha _{w,n}$
, where w is either a single-letter word or a word of length n. In these cases,
![]() $\alpha _{w,n}$
turns out to be a Bockstein element or an element of an n-fold Massey product, respectively (see Examples 7.1–7.2 and the remarks below). The construction of
$\alpha _{w,n}$
turns out to be a Bockstein element or an element of an n-fold Massey product, respectively (see Examples 7.1–7.2 and the remarks below). The construction of
![]() $\alpha _{w,n}$
is based on a representation of
$\alpha _{w,n}$
is based on a representation of
![]() $S/S_{\left (n,p\right )}$
in a group of unitriangular (i.e., unipotent upper-triangular) matrices, which we derive from the Magnus map – see §5 and §7 for details.
$S/S_{\left (n,p\right )}$
in a group of unitriangular (i.e., unipotent upper-triangular) matrices, which we derive from the Magnus map – see §5 and §7 for details.
A main ingredient of the proof, of independent importance, is the construction of a canonical
![]() $\mathbb {F}_p$
-linear basis of
$\mathbb {F}_p$
-linear basis of
![]() $H^2\left (S/S_{(n,p)}\right )$
, which we call the Lyndon basis. Recall that a nonempty word w in
$H^2\left (S/S_{(n,p)}\right )$
, which we call the Lyndon basis. Recall that a nonempty word w in
![]() $X^*$
is called a Lyndon word if it is smaller in the alphabetic order (induced by the fixed total order on X) than all its nontrivial right factors (i.e., suffixes). The Lyndon basis then consists of all cohomology elements
$X^*$
is called a Lyndon word if it is smaller in the alphabetic order (induced by the fixed total order on X) than all its nontrivial right factors (i.e., suffixes). The Lyndon basis then consists of all cohomology elements
![]() $\alpha _{w,n}$
, where w is a Lyndon word of length
$\alpha _{w,n}$
, where w is a Lyndon word of length
![]() $\left \lceil n/p^k\right \rceil $
for some
$\left \lceil n/p^k\right \rceil $
for some
![]() $k\geq 0$
. When
$k\geq 0$
. When
![]() $n\leq p$
the possible lengths are only
$n\leq p$
the possible lengths are only
![]() $1$
and n, leading to the two direct summands in the left-hand side of the Main Theorem.
$1$
and n, leading to the two direct summands in the left-hand side of the Main Theorem.
We further use Lyndon words to give a canonical basis of the
![]() $\mathbb {F}_p$
-linear space
$\mathbb {F}_p$
-linear space
![]() $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
, and prove a duality (in a unitriangular sense) between the Lyndon basis of
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
, and prove a duality (in a unitriangular sense) between the Lyndon basis of
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
and this latter basis (Corollary 8.2). In the smallest case,
$H^2\left (S/S_{\left (n,p\right )}\right )$
and this latter basis (Corollary 8.2). In the smallest case,
![]() $n=2$
, this recovers classical duality results between Bockstein elements/cup products and p-powers/commutators, respectively, proved by Labute in his classical work on Demuškin groups ([Reference Labute22, Prop. 8], [Reference Serre34], [Reference Neukirch, Schmidt and Wingberg31, Ch. III, §9], [Reference Serre34]). In the case
$n=2$
, this recovers classical duality results between Bockstein elements/cup products and p-powers/commutators, respectively, proved by Labute in his classical work on Demuškin groups ([Reference Labute22, Prop. 8], [Reference Serre34], [Reference Neukirch, Schmidt and Wingberg31, Ch. III, §9], [Reference Serre34]). In the case
![]() $n=3$
, it refines results by Vogel [Reference Vogel37, §2].
$n=3$
, it refines results by Vogel [Reference Vogel37, §2].
The paper builds upon our earlier work [Reference Efrat8], supplemented by [Reference Efrat9], where we proved analogous results for the lower p-central filtration, defined inductively by
![]() $G^{\left (1,p\right )}=G$
and
$G^{\left (1,p\right )}=G$
and
![]() $G^{\left (n,p\right )}=\left (G^{\left (n-1,p\right )}\right )^p\left [G,G^{\left (n-1,p\right )}\right ]$
for
$G^{\left (n,p\right )}=\left (G^{\left (n-1,p\right )}\right )^p\left [G,G^{\left (n-1,p\right )}\right ]$
for
![]() $n\geq 2$
. In many respects, this filtration and the p-Zassenhaus filtration are the opposite extremes among the filtrations related to mod-p cohomology.
$n\geq 2$
. In many respects, this filtration and the p-Zassenhaus filtration are the opposite extremes among the filtrations related to mod-p cohomology.
While we follow the general philosophy of [Reference Efrat8] and [Reference Efrat9], their methods fall short when applied to the p-Zassenhaus filtration. Therefore we modify these methods in several aspects: mainly, whereas in the lower p-central case one should consider words w of arbitrary lengths, in the case of Zassenhaus filtration we need to restrict to words of lengths
![]() $\left \lceil n/p^k\right \rceil $
,
$\left \lceil n/p^k\right \rceil $
,
![]() $k\geq 0$
, as above. These ‘jumps’ arise when we analyze the filtration for the group
$k\geq 0$
, as above. These ‘jumps’ arise when we analyze the filtration for the group
![]() $\mathbb {U}_i\left (\mathbb {Z}/p^j\right )$
of unitriangular
$\mathbb {U}_i\left (\mathbb {Z}/p^j\right )$
of unitriangular
![]() $(i+1)\times (i+1)$
-matrices over
$(i+1)\times (i+1)$
-matrices over
![]() $\mathbb {Z}/p^j$
. They turn out to have crucial, and quite nonobvious, properties, which are in particular needed for handling the dual
$\mathbb {Z}/p^j$
. They turn out to have crucial, and quite nonobvious, properties, which are in particular needed for handling the dual
![]() $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
of
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
of
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
. Here commutator identities due to Shalev [Reference Shalev36] also play a key role. By contrast, the corresponding quotient in the lower p-central case is
$H^2\left (S/S_{\left (n,p\right )}\right )$
. Here commutator identities due to Shalev [Reference Shalev36] also play a key role. By contrast, the corresponding quotient in the lower p-central case is
![]() $S^{\left (n,p\right )}/S^{\left (n+1,p\right )}$
, which is considerably more tractable. In addition, the analysis for the lower p-central filtration in [Reference Efrat8] is based on (mixed) Lie-algebra computations. In the case of Zassenhaus filtration we instead apply the theory of free p-restricted Lie algebra, following [Reference Lazard25] and [Reference Gärtner15].
$S^{\left (n,p\right )}/S^{\left (n+1,p\right )}$
, which is considerably more tractable. In addition, the analysis for the lower p-central filtration in [Reference Efrat8] is based on (mixed) Lie-algebra computations. In the case of Zassenhaus filtration we instead apply the theory of free p-restricted Lie algebra, following [Reference Lazard25] and [Reference Gärtner15].
The correspondence in the Main Theorem demonstrates deep connections between the p-Zassenhaus filtration and its cohomology and the n-fold Massey product
![]() $H^1(G)^n\to H^2(G)$
. In fact, it was shown in [Reference Efrat7] that when S is a free profinite group,
$H^1(G)^n\to H^2(G)$
. In fact, it was shown in [Reference Efrat7] that when S is a free profinite group,
![]() $S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
is dual to the subgroup of
$S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
is dual to the subgroup of
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
generated by all such products. Moreover, the latter subgroup is the kernel of the inflation map
$H^2\left (S/S_{\left (n,p\right )}\right )$
generated by all such products. Moreover, the latter subgroup is the kernel of the inflation map
![]() $H^2\left (S/S_{\left (n,p\right )}\right )\to H^2\left (S/S_{\left (n+1,p\right )}\right )$
. The size of
$H^2\left (S/S_{\left (n,p\right )}\right )\to H^2\left (S/S_{\left (n+1,p\right )}\right )$
. The size of
![]() $S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
was computed in [Reference Mináč, Rogelstad and Tân26]. The behavior of Massey products for absolute Galois groups
$S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
was computed in [Reference Mináč, Rogelstad and Tân26]. The behavior of Massey products for absolute Galois groups
![]() $G=G_F$
has been the focus of extensive research in recent years, where the p-Zassenhaus filtration has played an important role (see, e.g., [Reference Efrat and Matzri10], [Reference Guillot, Mináč, Topaz and Wittenberg16], [Reference Harpaz and Wittenberg17], [Reference Hopkins and Wickelgren18], [Reference Mináč and Tân27], [Reference Mináč and Tân28] and the references therein).
$G=G_F$
has been the focus of extensive research in recent years, where the p-Zassenhaus filtration has played an important role (see, e.g., [Reference Efrat and Matzri10], [Reference Guillot, Mináč, Topaz and Wittenberg16], [Reference Harpaz and Wittenberg17], [Reference Hopkins and Wickelgren18], [Reference Mináč and Tân27], [Reference Mináč and Tân28] and the references therein).
2 Hall sets
Let X be a nonempty set, considered as an alphabet. Let again
![]() $X^*$
be the free monoid on X. We consider its elements as associative words. It is equipped with the binary operation
$X^*$
be the free monoid on X. We consider its elements as associative words. It is equipped with the binary operation
![]() $(u,v)\mapsto uv$
of associative concatenation. Let
$(u,v)\mapsto uv$
of associative concatenation. Let
![]() $\mathcal {M}_X$
be the free magma on X (see [Reference Serre35, Part I, Ch. IV, §1], [Reference Efrat8, §2]). Thus the elements of
$\mathcal {M}_X$
be the free magma on X (see [Reference Serre35, Part I, Ch. IV, §1], [Reference Efrat8, §2]). Thus the elements of
![]() $\mathcal {M}_X$
are the nonempty nonassociative words in the alphabet X, and it is equipped with the binary operation
$\mathcal {M}_X$
are the nonempty nonassociative words in the alphabet X, and it is equipped with the binary operation
![]() $(u,v)\mapsto (uv)$
of nonassociative concatenation. There is a natural foliage (brackets-dropping) map
$(u,v)\mapsto (uv)$
of nonassociative concatenation. There is a natural foliage (brackets-dropping) map
![]() $f\colon \mathcal {M}_X\to X^*$
, which is the identity on X (considered as a subset of both
$f\colon \mathcal {M}_X\to X^*$
, which is the identity on X (considered as a subset of both
![]() $\mathcal {M}_X$
and
$\mathcal {M}_X$
and
![]() $X^*$
) and which commutes with the concatenation maps.
$X^*$
) and which commutes with the concatenation maps.
We fix a total order on X. It induces on
![]() $X^*$
the alphabetic order
$X^*$
the alphabetic order
![]() $\leq _{\text {alp}}$
, which is also total. We denote the length of a word
$\leq _{\text {alp}}$
, which is also total. We denote the length of a word
![]() $w\in X^*$
by
$w\in X^*$
by
![]() $\lvert w\rvert $
.
$\lvert w\rvert $
.
Let
![]() $\mathcal {H}$
be a subset of words in
$\mathcal {H}$
be a subset of words in
![]() $\mathcal {M}_X$
and
$\mathcal {M}_X$
and
![]() $\leq $
any total order on
$\leq $
any total order on
![]() $\mathcal {H}$
. We say that
$\mathcal {H}$
. We say that
![]() $(\mathcal {H},\leq )$
is a Hall set in
$(\mathcal {H},\leq )$
is a Hall set in
![]() $\mathcal {M}_X$
if the following conditions hold [Reference Reutenauer33, §4.1]:
$\mathcal {M}_X$
if the following conditions hold [Reference Reutenauer33, §4.1]:
-
(1)
 $X\subseteq \mathcal {H}$
as ordered sets.
$X\subseteq \mathcal {H}$
as ordered sets. -
(2) If
 $h=(h'h")\in \mathcal {H}\setminus X$
, then
$h=(h'h")\in \mathcal {H}\setminus X$
, then
 $h"\in \mathcal {H}$
and
$h"\in \mathcal {H}$
and
 $h<h"$
.
$h<h"$
. -
(3) For
 $h=(h'h")\in \mathcal {M}_X \setminus X$
, one has
$h=(h'h")\in \mathcal {M}_X \setminus X$
, one has
 $h\in \mathcal {H}$
if and only if
$h\in \mathcal {H}$
if and only if-
•
 $h',h"\in \mathcal {H}$
and
$h',h"\in \mathcal {H}$
and
 $h'<h"$
, and
$h'<h"$
, and -
• either
 $h'\in X$
or
$h'\in X$
or
 $h'=(h_1h_2)$
with
$h'=(h_1h_2)$
with
 $h_2\geq h"$
.
$h_2\geq h"$
.
-
In this case we say that
![]() $H=f(\mathcal {H})$
is a Hall set in
$H=f(\mathcal {H})$
is a Hall set in
![]() $X^*$
.
$X^*$
.
Every
![]() $w\in H$
can be written as
$w\in H$
can be written as
![]() $w=f(h)$
for a unique
$w=f(h)$
for a unique
![]() $h\in \mathcal {H}$
[Reference Reutenauer33, Cor. 4.5]. If
$h\in \mathcal {H}$
[Reference Reutenauer33, Cor. 4.5]. If
![]() $w\in H\setminus X$
, then we can uniquely write
$w\in H\setminus X$
, then we can uniquely write
![]() $h=(h'h")$
with
$h=(h'h")$
with
![]() $h',h"\in \mathcal {H}$
[Reference Reutenauer33, p. 89]. Setting
$h',h"\in \mathcal {H}$
[Reference Reutenauer33, p. 89]. Setting
![]() $w'=f(h'),w"=f(h")\in H$
, we call
$w'=f(h'),w"=f(h")\in H$
, we call
![]() $w=w'w"$
the standard factorization of w.
$w=w'w"$
the standard factorization of w.
Example 2.1. The set of all Lyndon words in
![]() $X^*$
(see the Introduction) is a Hall set with respect to
$X^*$
(see the Introduction) is a Hall set with respect to
![]() $\leq _{\text {alp}}$
[Reference Reutenauer33, Th. 5.1].
$\leq _{\text {alp}}$
[Reference Reutenauer33, Th. 5.1].
The standard factorization of Lyndon words is explicitly given as follows:
Lemma 2.2. Let
![]() $w,u,v\in X^*$
be nonempty words such that
$w,u,v\in X^*$
be nonempty words such that
![]() $w=uv$
and w is Lyndon. The following conditions are equivalent:
$w=uv$
and w is Lyndon. The following conditions are equivalent:
-
(a)
 $w=uv$
is the standard factorization of w in the set of Lyndon words.
$w=uv$
is the standard factorization of w in the set of Lyndon words. -
(b) v is the
 $\leq _{\text {alp}}$
-minimal nontrivial right factor of w which is Lyndon.
$\leq _{\text {alp}}$
-minimal nontrivial right factor of w which is Lyndon. -
(c) v is the longest nontrivial right factor of w which is Lyndon.
Proof. (a)
![]() $\Leftrightarrow $
(b): This is shown in the proof of [Reference Reutenauer33, Th. 5.1].
$\Leftrightarrow $
(b): This is shown in the proof of [Reference Reutenauer33, Th. 5.1].
(b)
![]() $\Rightarrow $
(c): Let
$\Rightarrow $
(c): Let
![]() $v'$
by a nontrivial Lyndon right factor of w. By (b),
$v'$
by a nontrivial Lyndon right factor of w. By (b),
![]() $v\leq _{\text {alp}} v'$
. Since
$v\leq _{\text {alp}} v'$
. Since
![]() $v'$
is Lyndon, v cannot be a nontrivial right factor of
$v'$
is Lyndon, v cannot be a nontrivial right factor of
![]() $v'$
. Hence
$v'$
. Hence
![]() $v'$
is a right factor of v, so
$v'$
is a right factor of v, so
![]() $\lvert v'\rvert \leq \lvert v\rvert $
.
$\lvert v'\rvert \leq \lvert v\rvert $
.
(c)
![]() $\Rightarrow $
(b): Let
$\Rightarrow $
(b): Let
![]() $v'$
be a nontrivial Lyndon right factor of w. By (c), it is a right factor of v. Since v is Lyndon,
$v'$
be a nontrivial Lyndon right factor of w. By (c), it is a right factor of v. Since v is Lyndon,
![]() $v\leq _{\text {alp}}v'$
.
$v\leq _{\text {alp}}v'$
.
We order
![]() $\mathbb {Z}_{\geq 0}\times X^*$
lexicographically with respect to the usual order on
$\mathbb {Z}_{\geq 0}\times X^*$
lexicographically with respect to the usual order on
![]() $\mathbb {Z}_{\geq 0}$
and
$\mathbb {Z}_{\geq 0}$
and
![]() $\leq _{\textrm {alp}}$
. We then define a second total order
$\leq _{\textrm {alp}}$
. We then define a second total order
![]() $\preceq $
on
$\preceq $
on
![]() $X^*$
by setting
$X^*$
by setting
with respect to the latter order on
![]() $\mathbb {Z}_{\geq 0}\times X^*$
.
$\mathbb {Z}_{\geq 0}\times X^*$
.
3 Lie algebras
Let R be a unital commutative ring. We write
![]() $R\langle X\rangle $
for the free associative R-algebra over the set X. We view its elements as polynomials in the set X of noncommuting variables and with coefficients in R. Alternatively, it is the free R-module on the basis
$R\langle X\rangle $
for the free associative R-algebra over the set X. We view its elements as polynomials in the set X of noncommuting variables and with coefficients in R. Alternatively, it is the free R-module on the basis
![]() $X^*$
with multiplication induced by concatenation. The algebra
$X^*$
with multiplication induced by concatenation. The algebra
![]() $R\langle X\rangle $
is graded with respect to total degree.
$R\langle X\rangle $
is graded with respect to total degree.
We write
![]() $R\langle \langle X\rangle \rangle $
for the R-algebra of formal power series in the set X of noncommuting variables and with coefficients in R.
$R\langle \langle X\rangle \rangle $
for the R-algebra of formal power series in the set X of noncommuting variables and with coefficients in R.
Let k be a field. For an associative k-algebra A, let
![]() $A_{\text {Lie}}$
be the Lie algebra on A with Lie bracket
$A_{\text {Lie}}$
be the Lie algebra on A with Lie bracket
![]() $[a,b]=ab-ba$
.
$[a,b]=ab-ba$
.
We now assume that X is a nonempty totally ordered set, and fix a Hall set H in
![]() $X^*$
.
$X^*$
.
Let
![]() $L(X)$
be the free Lie k-algebra on the set X. The universal enveloping algebra of
$L(X)$
be the free Lie k-algebra on the set X. The universal enveloping algebra of
![]() $L(X)$
is
$L(X)$
is
![]() $k\langle X\rangle $
[Reference Serre35, Part I, Ch. IV, Th. 4.2].
$k\langle X\rangle $
[Reference Serre35, Part I, Ch. IV, Th. 4.2].
Let L be a Lie k-algebra containing X. Define a map
![]() $P_L=P_L^H\colon H\to L$
by
$P_L=P_L^H\colon H\to L$
by
![]() $P_L(x)=x$
for
$P_L(x)=x$
for
![]() $x\in X$
, and
$x\in X$
, and
![]() $P_L(w)=[P_L(u),P_L(v)]$
, if
$P_L(w)=[P_L(u),P_L(v)]$
, if
![]() $w=uv$
is the standard factorization of w, as in §2. This construction is functorial in L in the natural sense.
$w=uv$
is the standard factorization of w, as in §2. This construction is functorial in L in the natural sense.
Proposition 3.1.
-
(a) When
 $L=L(X)$
, the images
$L=L(X)$
, the images
 $P_L(w)$
, where
$P_L(w)$
, where
 $w\in H$
, form a k-linear basis of
$w\in H$
, form a k-linear basis of
 $L(X)$
.
$L(X)$
. -
(b) Let L be a Lie k-algebra containing X. Then the image of
 $P_L\, k$
-linearly spans the Lie k-subalgebra of L generated by X.
$P_L\, k$
-linearly spans the Lie k-subalgebra of L generated by X.
Proof. (a) See [Reference Reutenauer33, Th. 4.9(i)].
(b) This follows from (a), the universal property of
![]() $L(X)$
, and the functoriality of
$L(X)$
, and the functoriality of
![]() $P_L$
.
$P_L$
.
By Proposition 3.1(a) and the Poincaré–Birkhoff–Witt theorem [Reference Serre35, Part I, Ch. III, §4], the products
![]() $\prod _{i=1}^mP_{L(X)}(w_i)$
, with
$\prod _{i=1}^mP_{L(X)}(w_i)$
, with
![]() $w_1\geq _{\text {alp}}\dotsb \geq _{\text {alp}}w_m$
in H, form a k-linear basis of the universal enveloping algebra
$w_1\geq _{\text {alp}}\dotsb \geq _{\text {alp}}w_m$
in H, form a k-linear basis of the universal enveloping algebra
![]() $k\langle X\rangle $
of
$k\langle X\rangle $
of
![]() $L(X)$
.
$L(X)$
.
Next assume that
![]() $\operatorname {\mathrm {char}}\,k=p>0$
. A restricted Lie k-algebra L is a Lie k-algebra with an additional unary operation
$\operatorname {\mathrm {char}}\,k=p>0$
. A restricted Lie k-algebra L is a Lie k-algebra with an additional unary operation
![]() $a\mapsto a^{[p]}$
for which there is an associative k-algebra A and a Lie k-algebra monomorphism
$a\mapsto a^{[p]}$
for which there is an associative k-algebra A and a Lie k-algebra monomorphism
![]() $\theta \colon L\to A_{\text {Lie}}$
such that
$\theta \colon L\to A_{\text {Lie}}$
such that
![]() $\theta \left (a^{[p]}\right )=\theta (a)^p$
for every
$\theta \left (a^{[p]}\right )=\theta (a)^p$
for every
![]() $a\in L$
([Reference Dixon, Du Sautoy, Mann and Segal5, §12.1]; see also [Reference Jacobson19] for an alternative equivalent definition). A morphism of restricted Lie k-algebras is a morphism of Lie k-algebras which commutes with the
$a\in L$
([Reference Dixon, Du Sautoy, Mann and Segal5, §12.1]; see also [Reference Jacobson19] for an alternative equivalent definition). A morphism of restricted Lie k-algebras is a morphism of Lie k-algebras which commutes with the
![]() $(\cdot )^{[p]}$
-maps.
$(\cdot )^{[p]}$
-maps.
Every associative k-algebra A is endowed with the structure of a restricted Lie algebra
![]() $A_{\text {res.Lie}}$
, where we set
$A_{\text {res.Lie}}$
, where we set
![]() $[a,b]=ab-ba$
and
$[a,b]=ab-ba$
and
![]() $a^{[p]}=a^p$
. Every restricted Lie k-algebra L has a unique restricted universal enveloping algebra
$a^{[p]}=a^p$
. Every restricted Lie k-algebra L has a unique restricted universal enveloping algebra
![]() $\mathcal {U}_{\text {res}}(L)$
. This means that
$\mathcal {U}_{\text {res}}(L)$
. This means that
![]() $\mathcal {U}_{\text {res}}(L)$
is an associative k-algebra, and the functor
$\mathcal {U}_{\text {res}}(L)$
is an associative k-algebra, and the functor
![]() $A\mapsto A_{\text {res.Lie}}$
from the category of associative k-algebras to the category of restricted Lie k-algebras and the functor
$A\mapsto A_{\text {res.Lie}}$
from the category of associative k-algebras to the category of restricted Lie k-algebras and the functor
![]() $L\mapsto \mathcal {U}_{\text {res}}(L)$
from the category of restricted Lie k-algebras to the category of associative k-algebras are adjoint ([Reference Dixon, Du Sautoy, Mann and Segal5, §12.1], [Reference Jacobson19, Ch. V, Th. 12]).
$L\mapsto \mathcal {U}_{\text {res}}(L)$
from the category of restricted Lie k-algebras to the category of associative k-algebras are adjoint ([Reference Dixon, Du Sautoy, Mann and Segal5, §12.1], [Reference Jacobson19, Ch. V, Th. 12]).
Given a restricted Lie k-algebra L containing X, we define a map
![]() $\widehat {P}_L=\widehat {P}_L^H\colon \mathbb {Z}_{\geq 0}\times H\to L$
by
$\widehat {P}_L=\widehat {P}_L^H\colon \mathbb {Z}_{\geq 0}\times H\to L$
by
![]() $\widehat {P}_L(j,w)=P_L(w)^{[p]^j}$
, where
$\widehat {P}_L(j,w)=P_L(w)^{[p]^j}$
, where
![]() $(\cdot )^{[p]^j}$
denotes applying j times the operation
$(\cdot )^{[p]^j}$
denotes applying j times the operation
![]() $(\cdot )^{[p]}$
. In analogy with Proposition 3.1(b) we have the following:
$(\cdot )^{[p]}$
. In analogy with Proposition 3.1(b) we have the following:
Proposition 3.2. The image of
![]() $\widehat {P}_L\, k$
-linearly spans the restricted Lie k-subalgebra of L generated by X.
$\widehat {P}_L\, k$
-linearly spans the restricted Lie k-subalgebra of L generated by X.
Proof. Let
![]() $\widehat {L}_0$
be the k-linear subspace of L spanned by
$\widehat {L}_0$
be the k-linear subspace of L spanned by
![]() $\operatorname {\mathrm {Im}}\left (\widehat {P}_L\right )$
. Let
$\operatorname {\mathrm {Im}}\left (\widehat {P}_L\right )$
. Let
![]() $L_0$
be the k-linear subspace of L spanned by
$L_0$
be the k-linear subspace of L spanned by
![]() $\operatorname {\mathrm {Im}}(P_L)$
. Clearly,
$\operatorname {\mathrm {Im}}(P_L)$
. Clearly,
![]() $X\subseteq L_0\subseteq \widehat {L}_0$
. By Proposition 3.1(b),
$X\subseteq L_0\subseteq \widehat {L}_0$
. By Proposition 3.1(b),
![]() $L_0$
is the Lie k-subalgebra of L generated by X.
$L_0$
is the Lie k-subalgebra of L generated by X.
Since
![]() $\operatorname {\mathrm {char}}\,k=p$
, the binomial formula implies that the subspace
$\operatorname {\mathrm {char}}\,k=p$
, the binomial formula implies that the subspace
![]() $\widehat {L}_0$
is closed under
$\widehat {L}_0$
is closed under
![]() $(\cdot )^{[p]}$
.
$(\cdot )^{[p]}$
.
If
![]() $w,u\in H$
, then
$w,u\in H$
, then
![]() $[P_L(w),P_L(u)]\in L_0$
. It follows from the k-bilinearity of the Lie bracket that for every
$[P_L(w),P_L(u)]\in L_0$
. It follows from the k-bilinearity of the Lie bracket that for every
![]() $\alpha ,\beta \in L_0$
, also
$\alpha ,\beta \in L_0$
, also
![]() $[\alpha ,\beta ]\in L_0$
. By induction on
$[\alpha ,\beta ]\in L_0$
. By induction on
![]() $m\geq 1$
, the m-times iterated Lie brackets
$m\geq 1$
, the m-times iterated Lie brackets
are also contained in
![]() $L_0$
. Using the identities
$L_0$
. Using the identities
![]() $\left [\alpha ,\beta ^{[p]}\right ]=\left [\alpha ,_p,\beta \right ]$
and
$\left [\alpha ,\beta ^{[p]}\right ]=\left [\alpha ,_p,\beta \right ]$
and
![]() $\left [\alpha ^{[p]},\beta \right ]=\left [\alpha ,\beta ,_p\right ]$
(see [Reference Dixon, Du Sautoy, Mann and Segal5, p. 297]), we deduce that
$\left [\alpha ^{[p]},\beta \right ]=\left [\alpha ,\beta ,_p\right ]$
(see [Reference Dixon, Du Sautoy, Mann and Segal5, p. 297]), we deduce that
![]() $\left [\alpha ^{[p]^j},\beta ^{[p]^r}\right ]\in L_0$
for every
$\left [\alpha ^{[p]^j},\beta ^{[p]^r}\right ]\in L_0$
for every
![]() $j,r\geq 0$
. By the bilinearity again,
$j,r\geq 0$
. By the bilinearity again,
![]() $\widehat {L}_0$
is therefore closed under the Lie bracket.
$\widehat {L}_0$
is therefore closed under the Lie bracket.
Hence
![]() $\widehat {L}_0$
is the restricted Lie k-subalgebra of L generated by X.
$\widehat {L}_0$
is the restricted Lie k-subalgebra of L generated by X.
There is a free restricted k-algebra
![]() $\widehat {L}(X)$
on the generating set X, with the standard universal property. It is the restricted Lie k-subalgebra of
$\widehat {L}(X)$
on the generating set X, with the standard universal property. It is the restricted Lie k-subalgebra of
![]() $k\langle X\rangle _{\text {res.Lie}}$
generated by X, and its restricted universal enveloping algebra is
$k\langle X\rangle _{\text {res.Lie}}$
generated by X, and its restricted universal enveloping algebra is
![]() $k\langle X\rangle $
[Reference Gärtner15, Prop. 1.2.7]. We note that in the algebra
$k\langle X\rangle $
[Reference Gärtner15, Prop. 1.2.7]. We note that in the algebra
![]() $k\langle X\rangle $
one has
$k\langle X\rangle $
one has
for every
![]() $j\geq 0$
and
$j\geq 0$
and
![]() $w\in H$
. The following analogue of Proposition 3.1(a) generalizes a result of Gärtner [Reference Gärtner15, Th. 1.2.11] (who considers a specific Hall family H):
$w\in H$
. The following analogue of Proposition 3.1(a) generalizes a result of Gärtner [Reference Gärtner15, Th. 1.2.11] (who considers a specific Hall family H):
Corollary 3.3. The polynomials
![]() $\widehat {P}_{\widehat {L}(X)}(j,w)$
, where
$\widehat {P}_{\widehat {L}(X)}(j,w)$
, where
![]() $j\geq 0$
and
$j\geq 0$
and
![]() $w\in H$
, form a k-linear basis of
$w\in H$
, form a k-linear basis of
![]() $\widehat {L}(X)$
.
$\widehat {L}(X)$
.
Proof. We consider
![]() $\widehat {L}(X)$
as a k-linear subspace of
$\widehat {L}(X)$
as a k-linear subspace of
![]() $k\langle X\rangle $
. By Proposition 3.2, it is spanned by the powers
$k\langle X\rangle $
. By Proposition 3.2, it is spanned by the powers
![]() $\widehat {P}_{\widehat {L}(X)}(j,w)$
, where
$\widehat {P}_{\widehat {L}(X)}(j,w)$
, where
![]() $j\geq 0$
and
$j\geq 0$
and
![]() $w\in H$
. As already observed, the products
$w\in H$
. As already observed, the products
![]() $\prod _{i=1}^mP_{L(X)}(w_i)$
, with
$\prod _{i=1}^mP_{L(X)}(w_i)$
, with
![]() $w_1\geq _{\text {alp}}\dotsb \geq _{\text {alp}}w_m$
in H, form a k-linear basis of
$w_1\geq _{\text {alp}}\dotsb \geq _{\text {alp}}w_m$
in H, form a k-linear basis of
![]() $k\langle X\rangle $
. In particular, the powers
$k\langle X\rangle $
. In particular, the powers
![]() $\widehat {P}_{\widehat {L}(X)}(j,w)=P_{L(X)}(w)^{p^j}$
are k-linearly independent. Hence they form a k-linear basis of
$\widehat {P}_{\widehat {L}(X)}(j,w)=P_{L(X)}(w)^{p^j}$
are k-linearly independent. Hence they form a k-linear basis of
![]() $L(X)_{\text {res}}$
.
$L(X)_{\text {res}}$
.
We grade
![]() $L(X)$
and
$L(X)$
and
![]() $\widehat {L}(X)$
by total degree, and write
$\widehat {L}(X)$
by total degree, and write
![]() $L(X)_n$
,
$L(X)_n$
,
![]() $\widehat {L}(X)_n$
for their homogenous components of degree n.
$\widehat {L}(X)_n$
for their homogenous components of degree n.
Corollary 3.4. Let n be a positive integer.
-
(a) The
 $P_{L(X)}(w)$
, with
$P_{L(X)}(w)$
, with
 $w\in H$
and
$w\in H$
and
 $\lvert w\rvert =n$
, form a k-linear basis of
$\lvert w\rvert =n$
, form a k-linear basis of
 $L(X)_n$
.
$L(X)_n$
. -
(b) The
 $\widehat {P}_{\widehat {L}(X)}(j,w)$
, with
$\widehat {P}_{\widehat {L}(X)}(j,w)$
, with
 $j\geq 0$
and
$j\geq 0$
and
 $w\in H$
satisfying
$w\in H$
satisfying
 $n=\lvert w\rvert p^j$
, form a k-linear basis of
$n=\lvert w\rvert p^j$
, form a k-linear basis of
 $\widehat {L}(X)_n$
.
$\widehat {L}(X)_n$
.
4 The p-Zassenhaus filtration
We fix as before a prime number p. For an integer
![]() $1\leq i \leq n$
, let
$1\leq i \leq n$
, let
![]() $j_n(i)=\lceil \log _p(n/i)\rceil $
– that is,
$j_n(i)=\lceil \log _p(n/i)\rceil $
– that is,
![]() $j_n(i)$
is the least integer j such that
$j_n(i)$
is the least integer j such that
![]() $ip^j\geq n$
.
$ip^j\geq n$
.
Lemma 4.1. The following conditions on
![]() $1\leq i\leq n$
are equivalent:
$1\leq i\leq n$
are equivalent:
-
(a)
 $i'p^{j_n\left (i'\right )}\geq ip^{j_n(i)}$
for every
$i'p^{j_n\left (i'\right )}\geq ip^{j_n(i)}$
for every
 $1\leq i'\leq i$
.
$1\leq i'\leq i$
. -
(b)
 $i=\left \lceil n/p^k\right \rceil $
for some
$i=\left \lceil n/p^k\right \rceil $
for some
 $k\geq 0$
.
$k\geq 0$
.
Proof. Set
![]() $i_k=\left \lceil n/p^k\right \rceil $
. Thus
$i_k=\left \lceil n/p^k\right \rceil $
. Thus
![]() $i_0=n$
, and the sequence
$i_0=n$
, and the sequence
![]() $i_k$
is weakly decreasing to
$i_k$
is weakly decreasing to
![]() $1$
. We may restrict ourselves to k such that
$1$
. We may restrict ourselves to k such that
![]() $p^k\leq n$
. Then
$p^k\leq n$
. Then
![]() $\left (n/p^k\right )+1\leq n/p^{k-1}$
, so
$\left (n/p^k\right )+1\leq n/p^{k-1}$
, so
![]() $n/p^k\leq i_k<n/p^{k-1}$
. Thus
$n/p^k\leq i_k<n/p^{k-1}$
. Thus
![]() $j_n(i_k)=k$
.
$j_n(i_k)=k$
.
Since
![]() $n/p^k\leq \left \lceil n/p^{k+1}\right \rceil p$
, one has
$n/p^k\leq \left \lceil n/p^{k+1}\right \rceil p$
, one has
![]() $i_kp^k\leq i_{k+1}p^{k+1}$
– that is, the sequence
$i_kp^k\leq i_{k+1}p^{k+1}$
– that is, the sequence
![]() $i_kp^{j_n\left (i_k\right )}$
is weakly increasing in the above range.
$i_kp^{j_n\left (i_k\right )}$
is weakly increasing in the above range.
We also observe that if
![]() $i< i_{k-1}$
, then
$i< i_{k-1}$
, then
![]() $i<n/p^{k-1}$
– that is,
$i<n/p^{k-1}$
– that is,
![]() $j_n(i)\geq k$
.
$j_n(i)\geq k$
.
(a)
![]() $\Rightarrow $
(b): Since (b) certainly holds for
$\Rightarrow $
(b): Since (b) certainly holds for
![]() $i=n$
, we may assume that
$i=n$
, we may assume that
![]() $i< n$
, so there is k in the above range such that
$i< n$
, so there is k in the above range such that
![]() $i_k\leq i< i_{k-1}$
. By the previous observation,
$i_k\leq i< i_{k-1}$
. By the previous observation,
![]() $j_n(i)\geq k$
. We take in (a)
$j_n(i)\geq k$
. We take in (a)
![]() $i'=i_k$
to obtain
$i'=i_k$
to obtain
Hence
![]() $i=i_k$
.
$i=i_k$
.
(b)
![]() $\Rightarrow $
(a): Suppose that
$\Rightarrow $
(a): Suppose that
![]() $1\leq i'<i_k$
. There exists l in the above range such that
$1\leq i'<i_k$
. There exists l in the above range such that
![]() $i_l\leq i'<i_{l-1}$
. Necessarily,
$i_l\leq i'<i_{l-1}$
. Necessarily,
![]() $l>k$
, so
$l>k$
, so
![]() $i_lp^l\geq i_kp^k$
. As we have observed,
$i_lp^l\geq i_kp^k$
. As we have observed,
![]() $j_n(i')\geq l$
. Hence
$j_n(i')\geq l$
. Hence
We define
![]() $J(n)$
to be the set of all
$J(n)$
to be the set of all
![]() $1\leq i\leq n$
such that the equivalent conditions of Lemma 4.1 hold.
$1\leq i\leq n$
such that the equivalent conditions of Lemma 4.1 hold.
Remark 4.2.
-
(1) When
 $n\leq p$
, one has
$n\leq p$
, one has
 $J(n)=\{1,n\}$
.
$J(n)=\{1,n\}$
. -
(2) Let
 $1\neq i\in J(n)$
and take k such that
$1\neq i\in J(n)$
and take k such that
 $i=\left \lceil n/p^k\right \rceil $
. By the first paragraph of the proof of Lemma 4.1,
$i=\left \lceil n/p^k\right \rceil $
. By the first paragraph of the proof of Lemma 4.1,
 $j_n(i)=k$
.
$j_n(i)=k$
.
Now let G be a profinite group. Given closed subgroups
![]() $K,K'$
of G and a positive integer m, we write
$K,K'$
of G and a positive integer m, we write
![]() $[K,K']$
(resp.,
$[K,K']$
(resp.,
![]() $K^m$
) for the closed subgroup of G generated by all commutators
$K^m$
) for the closed subgroup of G generated by all commutators
![]() $[k,k']=k^{-1} (k')^{-1} kk'$
(resp., powers
$[k,k']=k^{-1} (k')^{-1} kk'$
(resp., powers
![]() $k^m$
) with
$k^m$
) with
![]() $k\in K$
and
$k\in K$
and
![]() $k'\in K'$
.
$k'\in K'$
.
Recall that the (profinite) lower central series
![]() $G^{(i)}$
,
$G^{(i)}$
,
![]() $i=1,2,\dotsc ,$
of
$i=1,2,\dotsc ,$
of
![]() $G$
is defined inductively by
$G$
is defined inductively by
![]() $G^{(1)}=G$
,
$G^{(1)}=G$
,
![]() $G^{(i+1)}=\left [G,G^{(i)}\right ]$
. As in the Introduction, we denote the p-Zassenhaus filtration of G by
$G^{(i+1)}=\left [G,G^{(i)}\right ]$
. As in the Introduction, we denote the p-Zassenhaus filtration of G by
![]() $G_{\left (n,p\right )}$
,
$G_{\left (n,p\right )}$
,
![]() $n=1,2,\dotsc $
. Since
$n=1,2,\dotsc $
. Since
![]() $G^{(i)}\leq G^{(n)}$
for
$G^{(i)}\leq G^{(n)}$
for
![]() $i>n$
,
$i>n$
,
 $$ \begin{align*} G_{\left(n,p\right)}=\prod_{ip^j\geq n}\left(G^{(i)}\right)^{p^j}=\prod_{i=1}^n\left(G^{(i)}\right)^{p^{j_n(i)}}. \end{align*} $$
$$ \begin{align*} G_{\left(n,p\right)}=\prod_{ip^j\geq n}\left(G^{(i)}\right)^{p^j}=\prod_{i=1}^n\left(G^{(i)}\right)^{p^{j_n(i)}}. \end{align*} $$
The subgroups
![]() $G_{\left (n,p\right )}$
of G are characteristic, hence normal. We note that
$G_{\left (n,p\right )}$
of G are characteristic, hence normal. We note that
![]() $G^{(n)}\leq G_{\left (n,p\right )}$
.
$G^{(n)}\leq G_{\left (n,p\right )}$
.
The Zassenhaus filtration can also be defined inductively by
for
![]() $n\geq 2$
. Indeed, this follows from a theorem of Lazard in the case of discrete groups ([Reference Dixon, Du Sautoy, Mann and Segal5, Th. 11.2], [Reference Lazard25, p. 209, Equation (3.14.5)]), and the profinite analog follows by a density argument. It follows from definition (4.1) that for
$n\geq 2$
. Indeed, this follows from a theorem of Lazard in the case of discrete groups ([Reference Dixon, Du Sautoy, Mann and Segal5, Th. 11.2], [Reference Lazard25, p. 209, Equation (3.14.5)]), and the profinite analog follows by a density argument. It follows from definition (4.1) that for
![]() $n\geq 2$
,
$n\geq 2$
,
Let
![]() $r\geq 0$
. The following identity was proved in the discrete case by Shalev [Reference Shalev36, Prop. 1.2]; the profinite analog follows again by a density argument:
$r\geq 0$
. The following identity was proved in the discrete case by Shalev [Reference Shalev36, Prop. 1.2]; the profinite analog follows again by a density argument:
 $$ \begin{align*} \prod_{ip^j\geq n}\left(G^{(i+r+1)}\right)^{p^j}=\left[G,\prod_{ip^j\geq n}\left(G^{(i+r)}\right)^{p^j}\right]. \end{align*} $$
$$ \begin{align*} \prod_{ip^j\geq n}\left(G^{(i+r+1)}\right)^{p^j}=\left[G,\prod_{ip^j\geq n}\left(G^{(i+r)}\right)^{p^j}\right]. \end{align*} $$
In particular,
 $$ \begin{align} \prod_{ip^j\geq n}\left(G^{(i+1)}\right)^{p^j}=\left[G,G_{\left(n,p\right)}\right]. \end{align} $$
$$ \begin{align} \prod_{ip^j\geq n}\left(G^{(i+1)}\right)^{p^j}=\left[G,G_{\left(n,p\right)}\right]. \end{align} $$
Proposition 4.3. Let
![]() $1\leq i\leq n$
be an integer such that
$1\leq i\leq n$
be an integer such that
![]() $i\not \in J(n)$
. Then
$i\not \in J(n)$
. Then
Proof. As
![]() $i\not \in J(n)$
, there exists
$i\not \in J(n)$
, there exists
![]() $1\leq i'<i$
such that
$1\leq i'<i$
such that
![]() $ip^{j_n(i)}>i'p^{j_n\left (i'\right )}$
. We abbreviate
$ip^{j_n(i)}>i'p^{j_n\left (i'\right )}$
. We abbreviate
![]() $j=j_n(i)$
and
$j=j_n(i)$
and
![]() $j'=j_n(i')$
, so
$j'=j_n(i')$
, so
![]() $ip^j,i'p^{j'}\geq n$
.
$ip^j,i'p^{j'}\geq n$
.
If
![]() $j>j'$
, then
$j>j'$
, then
 $$ \begin{align*} \left(G^{(i)}\right)^{p^j}\leq\left(\left(G^{\left(i'\right)}\right)^{p^{j'}}\right)^{p^{j-j'}}\leq \left(G_{\left(n,p\right)}\right)^p. \end{align*} $$
$$ \begin{align*} \left(G^{(i)}\right)^{p^j}\leq\left(\left(G^{\left(i'\right)}\right)^{p^{j'}}\right)^{p^{j-j'}}\leq \left(G_{\left(n,p\right)}\right)^p. \end{align*} $$
If
![]() $j\leq j'$
, then the inequality
$j\leq j'$
, then the inequality
![]() $i>i'p^{j'-j}$
and equation (4.3) give
$i>i'p^{j'-j}$
and equation (4.3) give
 $$ \begin{align*} \left(G^{(i)}\right)^{p^j}\leq \left(G^{\left(i'p^{j'-j}+1\right)}\right)^{p^j}\leq \left[G,G_{\left(n,p\right)}\right]. \\[-40pt]\end{align*} $$
$$ \begin{align*} \left(G^{(i)}\right)^{p^j}\leq \left(G^{\left(i'p^{j'-j}+1\right)}\right)^{p^j}\leq \left[G,G_{\left(n,p\right)}\right]. \\[-40pt]\end{align*} $$
It follows from definition (4.1) that for every n the quotient
![]() $G_{\left (n,p\right )}/G_{\left (n+1,p\right )}$
is abelian of exponent dividing p. Consider the graded
$G_{\left (n,p\right )}/G_{\left (n+1,p\right )}$
is abelian of exponent dividing p. Consider the graded
![]() $\mathbb {F}_p$
-module
$\mathbb {F}_p$
-module
The commutator map and the p-power map induce on
![]() $\mathrm {gr} G$
the structure of a p-restricted Lie
$\mathrm {gr} G$
the structure of a p-restricted Lie
![]() $\mathbb {F}_p$
-algebra (see [Reference Dixon, Du Sautoy, Mann and Segal5, §12.2], [Reference Gärtner15, Prop. 1.2.14]).
$\mathbb {F}_p$
-algebra (see [Reference Dixon, Du Sautoy, Mann and Segal5, §12.2], [Reference Gärtner15, Prop. 1.2.14]).
We now specialize to the case where S is a free profinite group on the basis X, in the sense of [Reference Fried and Jarden14, §17.4]. It is the inverse limit of the free profinite groups on finite subsets of X [Reference Fried and Jarden14, Lemma 17.4.9], so in our following results one may assume whenever convenient that X is actually finite, and use limit arguments for the general case.
By [Reference Gärtner15, Th. 1.3.8], there is a well-defined isomorphism
![]() $\mathrm {gr} S\xrightarrow {\sim }\widehat {L}(X)$
of graded restricted Lie algebras. Specifically, the coset of
$\mathrm {gr} S\xrightarrow {\sim }\widehat {L}(X)$
of graded restricted Lie algebras. Specifically, the coset of
![]() $x\in X$
in
$x\in X$
in
![]() $\mathrm {gr}_1 S=S/S_{\left (2,p\right )}$
maps to x.
$\mathrm {gr}_1 S=S/S_{\left (2,p\right )}$
maps to x.
Let H be, as before, a fixed Hall set in
![]() $X^*$
. For every word
$X^*$
. For every word
![]() $w\in H$
we associate an element
$w\in H$
we associate an element
![]() $\tau _w\in S$
as in [Reference Efrat8]. Thus
$\tau _w\in S$
as in [Reference Efrat8]. Thus
![]() $\tau _{(x)}=x$
for
$\tau _{(x)}=x$
for
![]() $x\in X$
, and for a word
$x\in X$
, and for a word
![]() $w\in H$
of length
$w\in H$
of length
![]() $i>1$
with standard factorization
$i>1$
with standard factorization
![]() $w=uv$
, where
$w=uv$
, where
![]() $u,v\in H$
(see §2), we set
$u,v\in H$
(see §2), we set
![]() $\tau _w=[\tau _u,\tau _v]$
. Then
$\tau _w=[\tau _u,\tau _v]$
. Then
![]() $\tau _w\in S^{(i)}$
. Hence if
$\tau _w\in S^{(i)}$
. Hence if
![]() $ip^j\geq n$
, then
$ip^j\geq n$
, then
![]() $\tau _w^{p^j}\in \left (S^{(i)}\right )^{p^j}\leq S_{\left (n,p\right )}$
.
$\tau _w^{p^j}\in \left (S^{(i)}\right )^{p^j}\leq S_{\left (n,p\right )}$
.
Proposition 4.4. Let
![]() $n\geq 1$
. The cosets of the powers
$n\geq 1$
. The cosets of the powers
![]() $\tau _w^{p^j}$
, with
$\tau _w^{p^j}$
, with
![]() $w\in H$
and
$w\in H$
and
![]() $n=\lvert w\rvert p^j$
, form an
$n=\lvert w\rvert p^j$
, form an
![]() $\mathbb {F}_p$
-linear basis of
$\mathbb {F}_p$
-linear basis of
![]() $S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
.
$S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
.
Proof. We use the terminology of §3 with the ground field
![]() $k=\mathbb {F}_p$
. By induction on the structure of w, the isomorphism
$k=\mathbb {F}_p$
. By induction on the structure of w, the isomorphism
![]() $\mathrm {gr} S\xrightarrow {\sim }\widehat {L}(X)$
of restricted Lie
$\mathrm {gr} S\xrightarrow {\sim }\widehat {L}(X)$
of restricted Lie
![]() $\mathbb {F}_p$
-algebras maps the coset of
$\mathbb {F}_p$
-algebras maps the coset of
![]() $\tau _w$
to
$\tau _w$
to
![]() $P_{L(X)}(w)$
. Therefore it maps the coset of
$P_{L(X)}(w)$
. Therefore it maps the coset of
![]() $\tau _w^{p^j}$
to
$\tau _w^{p^j}$
to
![]() $\widehat {P}_{\widehat {L}(X)}(j,w)=P_{L(X)}(w)^{p^j}$
considered as polynomials in
$\widehat {P}_{\widehat {L}(X)}(j,w)=P_{L(X)}(w)^{p^j}$
considered as polynomials in
![]() $\mathbb {F}_p\langle X\rangle $
. The assertion now follows from Corollary 3.4(b).
$\mathbb {F}_p\langle X\rangle $
. The assertion now follows from Corollary 3.4(b).
Remark 4.5. Vogel [Reference Vogel37, Ch. I, §3] uses a specific Hall set H to give
![]() $\mathbb {F}_p$
-linear bases of
$\mathbb {F}_p$
-linear bases of
![]() $S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
for
$S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
for
![]() $n=2,3$
, as well as generating sets for arbitrary n. Namely, for similarly defined basic commutators
$n=2,3$
, as well as generating sets for arbitrary n. Namely, for similarly defined basic commutators
![]() $c_w\in S^{(i)}$
of words
$c_w\in S^{(i)}$
of words
![]() $w\in H$
with
$w\in H$
with
![]() $\lvert w\rvert =i$
, the generating set consists of all
$\lvert w\rvert =i$
, the generating set consists of all
![]() $c_w^{p^j}$
with
$c_w^{p^j}$
with
![]() $n=ip^j$
. Furthermore, according to [Reference Mináč, Rogelstad and Tân26, Cor. 3.12] the set of all such powers forms a basis of
$n=ip^j$
. Furthermore, according to [Reference Mináč, Rogelstad and Tân26, Cor. 3.12] the set of all such powers forms a basis of
![]() $S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
, but the proof lacks details. I thank J. Mináč for a correspondence on the latter reference.
$S_{\left (n,p\right )}/S_{\left (n+1,p\right )}$
, but the proof lacks details. I thank J. Mináč for a correspondence on the latter reference.
Let
![]() $n\geq 1$
. For a word
$n\geq 1$
. For a word
![]() $w\in H$
of length
$w\in H$
of length
![]() $1\leq i\leq n$
we abbreviate
$1\leq i\leq n$
we abbreviate
Thus
![]() $\sigma _w\in S_{\left (n,p\right )}$
.
$\sigma _w\in S_{\left (n,p\right )}$
.
Theorem 4.6. The cosets of
![]() $\sigma _w$
, where
$\sigma _w$
, where
![]() $w\in H$
has length
$w\in H$
has length
![]() $i\in J(n)$
, generate
$i\in J(n)$
, generate
![]() $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
.
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
.
Proof. Proposition 4.4 implies, by induction on
![]() $r\geq 1$
, that
$r\geq 1$
, that
![]() $S_{\left (n,p\right )}/S_{\left (n+r,p\right )}$
is generated by the cosets of
$S_{\left (n,p\right )}/S_{\left (n+r,p\right )}$
is generated by the cosets of
![]() $\tau _w^{p^j}$
, where
$\tau _w^{p^j}$
, where
![]() $w\in H$
has length i, and
$w\in H$
has length i, and
![]() $n\leq ip^j<n+r$
. We apply this for
$n\leq ip^j<n+r$
. We apply this for
![]() $n+r=np$
. By the inclusion (4.2),
$n+r=np$
. By the inclusion (4.2),
![]() $S_{\left (np,p\right )}\leq \left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
, and we deduce that
$S_{\left (np,p\right )}\leq \left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
, and we deduce that
![]() $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
is generated by the cosets of
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
is generated by the cosets of
![]() $\tau _w^{p^j}$
, where
$\tau _w^{p^j}$
, where
![]() $w\in H$
has length i and
$w\in H$
has length i and
![]() $n\leq ip^j<np$
. Moreover, it suffices to take such powers with
$n\leq ip^j<np$
. Moreover, it suffices to take such powers with
![]() $j=j_n(i)$
, since otherwise
$j=j_n(i)$
, since otherwise
![]() $\tau _w^{p^j}\in \left (S_{\left (n,p\right )}\right )^p$
. Finally, by Proposition 4.3, if
$\tau _w^{p^j}\in \left (S_{\left (n,p\right )}\right )^p$
. Finally, by Proposition 4.3, if
![]() $i\not \in J(n)$
then the coset of
$i\not \in J(n)$
then the coset of
![]() $\sigma _w=\tau _w^{p^{j_n(i)}}$
is trivial. We are therefore left with the generators
$\sigma _w=\tau _w^{p^{j_n(i)}}$
is trivial. We are therefore left with the generators
![]() $\sigma _w$
, as in the assertion.
$\sigma _w$
, as in the assertion.
5 The fundamental matrix
For a profinite ring R, let
![]() $R\langle \langle X\rangle \rangle ^\times $
be the group of invertible elements in
$R\langle \langle X\rangle \rangle ^\times $
be the group of invertible elements in
![]() $R\langle \langle X\rangle \rangle $
(see §3). As before, let S be the free profinite group over the basis X. The continuous Magnus homomorphism
$R\langle \langle X\rangle \rangle $
(see §3). As before, let S be the free profinite group over the basis X. The continuous Magnus homomorphism
is defined on the (profinite) generators
![]() $x\in X$
of S by
$x\in X$
of S by
![]() $\Lambda (x)=1+x$
(see [Reference Efrat7, §5] for details, and note that
$\Lambda (x)=1+x$
(see [Reference Efrat7, §5] for details, and note that
![]() $1+x$
is invertible by the geometric progression formula). For an arbitrary
$1+x$
is invertible by the geometric progression formula). For an arbitrary
![]() $\sigma \in S$
we write
$\sigma \in S$
we write
with
![]() $\epsilon _{w,R}(\sigma )\in R$
. The map
$\epsilon _{w,R}(\sigma )\in R$
. The map
![]() $\epsilon _{w,R}\colon S\to R$
is continuous, and
$\epsilon _{w,R}\colon S\to R$
is continuous, and
![]() $\epsilon _{\emptyset ,R}(\sigma )=1$
for every
$\epsilon _{\emptyset ,R}(\sigma )=1$
for every
![]() $\sigma $
(where
$\sigma $
(where
![]() $\emptyset $
denotes the empty word).
$\emptyset $
denotes the empty word).
Let
![]() $\mathbb {U}_i(R)$
be the profinite group of all unitriangular
$\mathbb {U}_i(R)$
be the profinite group of all unitriangular
![]() $(i+1)\times (i+1)$
-matrices over R. Given a word
$(i+1)\times (i+1)$
-matrices over R. Given a word
![]() $w=(x_1\dotsm x_i)\in X^*$
of length i, we define a continuous map
$w=(x_1\dotsm x_i)\in X^*$
of length i, we define a continuous map
![]() $\rho _w\colon S\to \mathbb {U}_i(R)$
by
$\rho _w\colon S\to \mathbb {U}_i(R)$
by
The fact that
![]() $\Lambda $
is a homomorphism implies that
$\Lambda $
is a homomorphism implies that
![]() $\rho _w$
is a homomorphism of profinite groups [Reference Efrat7, Lemma 7.5]. We call it the Magnus representation of S corresponding to w.
$\rho _w$
is a homomorphism of profinite groups [Reference Efrat7, Lemma 7.5]. We call it the Magnus representation of S corresponding to w.
The subgroup
![]() $S^{(n)}$
of S is characterized in terms of the Magnus map as the set of all
$S^{(n)}$
of S is characterized in terms of the Magnus map as the set of all
![]() $\sigma \in S$
such that
$\sigma \in S$
such that
![]() $\epsilon _{w,\mathbb {Z}_p}(\sigma )=0$
for every word w of length
$\epsilon _{w,\mathbb {Z}_p}(\sigma )=0$
for every word w of length
![]() $1\leq i<n$
[Reference Efrat8, Prop. 4.1(a)]. The following result gives similar restrictions on the Magnus coefficients of elements of
$1\leq i<n$
[Reference Efrat8, Prop. 4.1(a)]. The following result gives similar restrictions on the Magnus coefficients of elements of
![]() $S_{\left (n,p\right )}$
. In the discrete case it was proved in [Reference Chapman and Efrat2, Example 4.6], where it was further shown that these restrictions in fact characterize
$S_{\left (n,p\right )}$
. In the discrete case it was proved in [Reference Chapman and Efrat2, Example 4.6], where it was further shown that these restrictions in fact characterize
![]() $S_{\left (n,p\right )}$
. While it is possible to derive the proposition from the discrete case using a density argument, we provide a direct proof.
$S_{\left (n,p\right )}$
. While it is possible to derive the proposition from the discrete case using a density argument, we provide a direct proof.
Proposition 5.1. If
![]() $\sigma \in S_{\left (n,p\right )}$
, then
$\sigma \in S_{\left (n,p\right )}$
, then
![]() $\epsilon _{w,\mathbb {Z}_p}(\sigma )\in p^{j_n(i)}\mathbb {Z}_p$
for every word
$\epsilon _{w,\mathbb {Z}_p}(\sigma )\in p^{j_n(i)}\mathbb {Z}_p$
for every word
![]() $w\in X^*$
of length
$w\in X^*$
of length
![]() $i\geq 1$
.
$i\geq 1$
.
Proof. Consider the subset
 $$ \begin{align*} I=\sum_{i\geq1}\sum_{\lvert w\rvert=i}p^{j_n(i)}\mathbb{Z}_pw =\sum_{1\leq i\leq n}\sum_{\lvert w\rvert=i}p^{j_n(i)}\mathbb{Z}_pw+\sum_{i>n}\sum_{\lvert w\rvert=i}\mathbb{Z}_pw \end{align*} $$
$$ \begin{align*} I=\sum_{i\geq1}\sum_{\lvert w\rvert=i}p^{j_n(i)}\mathbb{Z}_pw =\sum_{1\leq i\leq n}\sum_{\lvert w\rvert=i}p^{j_n(i)}\mathbb{Z}_pw+\sum_{i>n}\sum_{\lvert w\rvert=i}\mathbb{Z}_pw \end{align*} $$
of
![]() $\mathbb {Z}_p\langle \langle X\rangle \rangle $
. It is an ideal in
$\mathbb {Z}_p\langle \langle X\rangle \rangle $
. It is an ideal in
![]() $\mathbb {Z}_p\langle \langle X\rangle \rangle $
, and therefore
$\mathbb {Z}_p\langle \langle X\rangle \rangle $
, and therefore
![]() $1+I$
is closed under multiplication. Moreover, the identity
$1+I$
is closed under multiplication. Moreover, the identity
![]() $\alpha ^{-1}=1-\alpha ^{-1}(\alpha -1)$
shows that
$\alpha ^{-1}=1-\alpha ^{-1}(\alpha -1)$
shows that
![]() $1+I$
is in fact a subgroup of
$1+I$
is in fact a subgroup of
![]() $\mathbb {Z}_p\langle \langle X\rangle \rangle ^\times $
.
$\mathbb {Z}_p\langle \langle X\rangle \rangle ^\times $
.
As
![]() $S_{\left (n,p\right )}=\prod _{i=1}^n\left (S^{(i)}\right )^{p^{j_n(i)}}$
, it therefore suffices to show that
$S_{\left (n,p\right )}=\prod _{i=1}^n\left (S^{(i)}\right )^{p^{j_n(i)}}$
, it therefore suffices to show that
![]() $\Lambda _{\mathbb {Z}_p}\left (\tau ^{p^{j_n(i)}}\right )\in 1+I$
for every
$\Lambda _{\mathbb {Z}_p}\left (\tau ^{p^{j_n(i)}}\right )\in 1+I$
for every
![]() $\tau \in S^{(i)}$
with
$\tau \in S^{(i)}$
with
![]() $1\leq i\leq n$
. We abbreviate
$1\leq i\leq n$
. We abbreviate
![]() $j=j_n(i)$
. Then
$j=j_n(i)$
. Then
![]() $\Lambda _{\mathbb {Z}_p}(\tau )=1+\sum _{\lvert w\rvert \geq i}\epsilon _{w,\mathbb {Z}_p}(\tau )w$
, by [Reference Efrat8, Prop. 4.1(a)]. For every
$\Lambda _{\mathbb {Z}_p}(\tau )=1+\sum _{\lvert w\rvert \geq i}\epsilon _{w,\mathbb {Z}_p}(\tau )w$
, by [Reference Efrat8, Prop. 4.1(a)]. For every
![]() $1\leq l\leq p^j$
such that
$1\leq l\leq p^j$
such that
![]() $il\leq n$
, one has
$il\leq n$
, one has
![]() $p^{j_n(il)}\mid \binom {p^j}l$
[Reference Chapman and Efrat2, Example 3.9]. Hence
$p^{j_n(il)}\mid \binom {p^j}l$
[Reference Chapman and Efrat2, Example 3.9]. Hence
 $$ \begin{align*} \Lambda_{\mathbb{Z}_p}\left(\tau^{p^j}\right)&=\sum_{0\leq l\leq p^j}\binom{p^j}l\left(\sum_{\lvert w\rvert\geq i}\epsilon_{w,\mathbb{Z}_p}(\tau)w\right)^l \subseteq 1+\sum_{1\leq l\leq p^j}\binom{p^j}l\left(\sum_{\lvert w\rvert\geq i}\mathbb{Z}_pw\right)^l\\ & \quad\subseteq 1+\sum_{1\leq l\leq p^j, il\leq n}p^{j_n(il)}\left(\sum_{\lvert w\rvert\geq i}\mathbb{Z}_pw\right)^l+\sum_{1\leq l\leq p^j, il>n}\left(\sum_{\lvert w\rvert\geq i}\mathbb{Z}_pw\right)^l \\ & \quad\subseteq1+I, \end{align*} $$
$$ \begin{align*} \Lambda_{\mathbb{Z}_p}\left(\tau^{p^j}\right)&=\sum_{0\leq l\leq p^j}\binom{p^j}l\left(\sum_{\lvert w\rvert\geq i}\epsilon_{w,\mathbb{Z}_p}(\tau)w\right)^l \subseteq 1+\sum_{1\leq l\leq p^j}\binom{p^j}l\left(\sum_{\lvert w\rvert\geq i}\mathbb{Z}_pw\right)^l\\ & \quad\subseteq 1+\sum_{1\leq l\leq p^j, il\leq n}p^{j_n(il)}\left(\sum_{\lvert w\rvert\geq i}\mathbb{Z}_pw\right)^l+\sum_{1\leq l\leq p^j, il>n}\left(\sum_{\lvert w\rvert\geq i}\mathbb{Z}_pw\right)^l \\ & \quad\subseteq1+I, \end{align*} $$
as desired.
As before, let H be a Hall set in
![]() $X^*$
.
$X^*$
.
Corollary 5.2. Let
![]() $w,w'$
be nonempty words in
$w,w'$
be nonempty words in
![]() $X^*$
of lengths
$X^*$
of lengths
![]() $1\leq i, i'\leq n$
, respectively, with
$1\leq i, i'\leq n$
, respectively, with
![]() $w'\in H$
. Then
$w'\in H$
. Then
![]() $\epsilon _{w,\mathbb {Z}_p}\left (\sigma _{w'}\right )\in p^{j_n(i)}\mathbb {Z}_p$
.
$\epsilon _{w,\mathbb {Z}_p}\left (\sigma _{w'}\right )\in p^{j_n(i)}\mathbb {Z}_p$
.
For an integer
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
be the natural epimorphism. For words
![]() $w,w'$
of lengths i,
$w,w'$
of lengths i,
![]() $i'$
, respectively, with
$i'$
, respectively, with
![]() $w'\in H$
, we define
$w'\in H$
, we define
By Corollary 5.2,
![]() $\langle w,w'\rangle _n\in p^{j_n(i)}\mathbb {Z}_p/p^{j_n(i)+1}\mathbb {Z}_p$
. We identify the latter group with
$\langle w,w'\rangle _n\in p^{j_n(i)}\mathbb {Z}_p/p^{j_n(i)+1}\mathbb {Z}_p$
. We identify the latter group with
![]() $\mathbb {Z}/p$
, and thus view
$\mathbb {Z}/p$
, and thus view
![]() $\langle w,w'\rangle _n$
as an element of
$\langle w,w'\rangle _n$
as an element of
![]() $\mathbb {Z}/p$
.
$\mathbb {Z}/p$
.
Consider the (possibly infinite) transposed matrix
over
![]() $\mathbb {Z}/p$
, where
$\mathbb {Z}/p$
, where
![]() $w,w'$
range over all words in H of lengths in
$w,w'$
range over all words in H of lengths in
![]() $J(n)$
, and indexed with respect to the total order
$J(n)$
, and indexed with respect to the total order
![]() $\preceq $
on
$\preceq $
on
![]() $X^*$
defined in §2. We call it the fundamental matrix of level n of H.
$X^*$
defined in §2. We call it the fundamental matrix of level n of H.
We now focus on the Hall set of Lyndon words (see the Introduction). We record the following fundamental triangularity property of H [Reference Reutenauer33, Th. 5.1]: For every Lyndon word
![]() $w\in X^*$
, one has
$w\in X^*$
, one has
Proposition 5.3. Let H be the Hall set of all Lyndon words in
![]() $X^*$
. The fundamental matrix of H of level n is unitriangular (i.e., unipotent and upper-triangular).
$X^*$
. The fundamental matrix of H of level n is unitriangular (i.e., unipotent and upper-triangular).
Proof. Let w be a Lyndon word of length
![]() $i\leq n$
. By (5.1),
$i\leq n$
. By (5.1),
where the remaining terms are multiples of words strictly larger than w in
![]() $\preceq $
. Therefore
$\preceq $
. Therefore
![]() $\langle w,w\rangle _n=\pi _i\left (p^{j_n(i)}\right )=1$
in
$\langle w,w\rangle _n=\pi _i\left (p^{j_n(i)}\right )=1$
in
![]() $\mathbb {Z}/p$
.
$\mathbb {Z}/p$
.
Furthermore, for Lyndon words
![]() $w\prec w'$
we get
$w\prec w'$
we get
![]() $\epsilon _{w,\mathbb {Z}_p}\left (\sigma _{w'}\right )=0$
, whence
$\epsilon _{w,\mathbb {Z}_p}\left (\sigma _{w'}\right )=0$
, whence
![]() $\langle w,w'\rangle _n=0$
(note that the empty word is not Lyndon).
$\langle w,w'\rangle _n=0$
(note that the empty word is not Lyndon).
Consequently, the matrix
![]() $[\langle w,w'\rangle _n]_{w,w'}$
is unipotent lower-triangular, and therefore its transpose is unitriangular.
$[\langle w,w'\rangle _n]_{w,w'}$
is unipotent lower-triangular, and therefore its transpose is unitriangular.
Example 5.4. Suppose that
![]() $n=2$
. Then
$n=2$
. Then
![]() $J(n)=\{1,2\}$
.
$J(n)=\{1,2\}$
.
The Lyndon words of length
![]() $\leq 2$
are the words
$\leq 2$
are the words
![]() $w=(x)$
and
$w=(x)$
and
![]() $w=(xy)$
, with
$w=(xy)$
, with
![]() $x,y\in X$
,
$x,y\in X$
,
![]() $x<y$
. Then
$x<y$
. Then
![]() $\sigma _w$
is
$\sigma _w$
is
![]() $\tau _w^{p^{j_2(1)}}=x^p$
and
$\tau _w^{p^{j_2(1)}}=x^p$
and
![]() $\tau _w^{p^{j_2(2)}}=[x,y]$
, respectively. In [Reference Efrat8, §10] it is shown that the value of
$\tau _w^{p^{j_2(2)}}=[x,y]$
, respectively. In [Reference Efrat8, §10] it is shown that the value of
![]() $\langle w,w'\rangle $
, where
$\langle w,w'\rangle $
, where
![]() $w,w'$
are Lyndon words of lengths
$w,w'$
are Lyndon words of lengths
![]() $\leq 2$
, is
$\leq 2$
, is
![]() $1$
if
$1$
if
![]() $w=w'$
and is
$w=w'$
and is
![]() $0$
otherwise. Thus the fundamental matrix of level
$0$
otherwise. Thus the fundamental matrix of level
![]() $2$
for the Lyndon words is the identity matrix.
$2$
for the Lyndon words is the identity matrix.
Example 5.5. Suppose that
![]() $n=3$
. Then
$n=3$
. Then
![]() $J(n)=\{1,3\}$
for
$J(n)=\{1,3\}$
for
![]() $p\geq 3$
and
$p\geq 3$
and
![]() $J(3)=\{1,2,3\}$
for
$J(3)=\{1,2,3\}$
for
![]() $p=2$
.
$p=2$
.
The Lyndon words w of length
![]() $3$
are of the forms
$3$
are of the forms
where
![]() $x,y,z\in X$
and
$x,y,z\in X$
and
![]() $x<y<z$
. For these words we have
$x<y<z$
. For these words we have
respectively. We recall that
![]() $\langle w,w\rangle _3=1$
for every w, and
$\langle w,w\rangle _3=1$
for every w, and
![]() $\langle w,w'\rangle _3=0$
when
$\langle w,w'\rangle _3=0$
when
![]() $w\prec w'$
. It remains to compute
$w\prec w'$
. It remains to compute
![]() $\langle w,w'\rangle _3$
when
$\langle w,w'\rangle _3$
when
![]() $w'\prec w$
.
$w'\prec w$
.
If
![]() $\lvert w\rvert ,\lvert w'\rvert \leq 2$
, then by Example 5.4,
$\lvert w\rvert ,\lvert w'\rvert \leq 2$
, then by Example 5.4,
![]() $\langle w,w'\rangle _3=0$
. We may therefore assume that
$\langle w,w'\rangle _3=0$
. We may therefore assume that
![]() $\lvert w'\rvert \leq \lvert w\rvert =3$
.
$\lvert w'\rvert \leq \lvert w\rvert =3$
.
If w contains a letter which does not appear in
![]() $w'$
, then
$w'$
, then
![]() $\epsilon _{w,\mathbb {Z}_p}\left (\sigma _{w'}\right )=0$
, whence
$\epsilon _{w,\mathbb {Z}_p}\left (\sigma _{w'}\right )=0$
, whence
![]() $\langle w,w'\rangle _3=0$
. Thus we may assume that every letter in w appears in
$\langle w,w'\rangle _3=0$
. Thus we may assume that every letter in w appears in
![]() $w'$
.
$w'$
.
When
![]() $w=(xyy)$
and
$w=(xyy)$
and
![]() $w'=(xxy)$
, where
$w'=(xxy)$
, where
![]() $x<y$
, the proof of [Reference Efrat8, Prop. 11.2] gives
$x<y$
, the proof of [Reference Efrat8, Prop. 11.2] gives
Similarly, when
![]() $w=(xzy)$
and
$w=(xzy)$
and
![]() $w'=(xyz)$
, where
$w'=(xyz)$
, where
![]() $x<y<z$
, the proof of [Reference Efrat8, Prop. 11.2] gives
$x<y<z$
, the proof of [Reference Efrat8, Prop. 11.2] gives
This covers all possible cases when
![]() $p\geq 3$
. When
$p\geq 3$
. When
![]() $p=2$
we also need to consider Lyndon words
$p=2$
we also need to consider Lyndon words
![]() $w'=(xy)$
of length
$w'=(xy)$
of length
![]() $2$
, where
$2$
, where
![]() $x<y$
. Then
$x<y$
. Then
![]() $w=(xxy)$
or
$w=(xxy)$
or
![]() $w=(xyy)$
. An explicit computation gives
$w=(xyy)$
. An explicit computation gives
where the remaining terms are of degree
![]() $\geq 4$
. The square of this series has no terms
$\geq 4$
. The square of this series has no terms
![]() $(xxy)$
and
$(xxy)$
and
![]() $(xyy)$
, so
$(xyy)$
, so
![]() $\epsilon _{(xxy),\mathbb {Z}_2}\left ([x,y]^2\right )=\epsilon _{(xyy),\mathbb {Z}_2}\left ([x,y]^2\right )=0$
. Therefore
$\epsilon _{(xxy),\mathbb {Z}_2}\left ([x,y]^2\right )=\epsilon _{(xyy),\mathbb {Z}_2}\left ([x,y]^2\right )=0$
. Therefore
![]() $\langle (xxy),(xy)\rangle _3=\langle (xyy),(xy)\rangle _3=0$
.
$\langle (xxy),(xy)\rangle _3=\langle (xyy),(xy)\rangle _3=0$
.
Altogether, we have shown that
 $$ \begin{align*} \langle w,w'\rangle_3= \begin{cases} 1 & \text{if } w=w',\\ -1& \text{if}\ w=(xzy), w'=(xyz), \text{ where } x,y,z\in X, \ x<y<z,\\ 0& \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \langle w,w'\rangle_3= \begin{cases} 1 & \text{if } w=w',\\ -1& \text{if}\ w=(xzy), w'=(xyz), \text{ where } x,y,z\in X, \ x<y<z,\\ 0& \text{otherwise}. \end{cases} \end{align*} $$
In particular, the fundamental matrix need not be the identity matrix.
6 Unitriangular matrices
Let
![]() $i\geq 1$
and
$i\geq 1$
and
![]() $j\geq 0$
be integers and consider the ring
$j\geq 0$
be integers and consider the ring
![]() $R=\mathbb {Z}/p^{j+1}$
. In this section we study the p-Zassenhaus filtration of the group
$R=\mathbb {Z}/p^{j+1}$
. In this section we study the p-Zassenhaus filtration of the group
![]() $\mathbb {U}=\mathbb {U}_i(R)$
of all unitriangular
$\mathbb {U}=\mathbb {U}_i(R)$
of all unitriangular
![]() $(i+1)\times (i+1)$
-matrices over R, and in particular characterize the values of
$(i+1)\times (i+1)$
-matrices over R, and in particular characterize the values of
![]() $i,j$
for which
$i,j$
for which
![]() $\mathbb {U}_{\left (n,p\right )}\cong \mathbb {Z}/p$
(see §5 for the notation).
$\mathbb {U}_{\left (n,p\right )}\cong \mathbb {Z}/p$
(see §5 for the notation).
We denote the unit matrix in
![]() $\mathbb {U}$
by I, and write
$\mathbb {U}$
by I, and write
![]() $E_{1,i+1}$
for the matrix which is
$E_{1,i+1}$
for the matrix which is
![]() $1$
at entry
$1$
at entry
![]() $(1,i+1)$
and is
$(1,i+1)$
and is
![]() $0$
elsewhere. For
$0$
elsewhere. For
![]() $i'\geq 1$
, the subgroup
$i'\geq 1$
, the subgroup
![]() $\mathbb {U}^{\left (i'\right )}$
of
$\mathbb {U}^{\left (i'\right )}$
of
![]() $\mathbb {U}$
consists of all matrices in
$\mathbb {U}$
consists of all matrices in
![]() $\mathbb {U}$
which are zero on the first
$\mathbb {U}$
which are zero on the first
![]() $i'-1$
diagonals above the main diagonal [Reference Bier and Hołubowski1, Th. 1.5(i)].
$i'-1$
diagonals above the main diagonal [Reference Bier and Hołubowski1, Th. 1.5(i)].
We record the following fact about binomial coefficients:
Lemma 6.1. Let
![]() $t,j'$
be positive integers such that
$t,j'$
be positive integers such that
![]() $1\leq t\leq p^{j'}$
. The following conditions are equivalent:
$1\leq t\leq p^{j'}$
. The following conditions are equivalent:
-
(a)
 $p^j\mid \binom {p^{j'}}l$
,
$p^j\mid \binom {p^{j'}}l$
,
 $l=1,2,\dotsc , t$
.
$l=1,2,\dotsc , t$
. -
(b)
 $p^j\mid \binom {p^{j'}}l$
for
$p^j\mid \binom {p^{j'}}l$
for
 $l=p^{\left \lfloor \log _pt\right \rfloor }$
.
$l=p^{\left \lfloor \log _pt\right \rfloor }$
. -
(c)
 $j'\geq j+\left \lfloor \log _pt\right \rfloor $
.
$j'\geq j+\left \lfloor \log _pt\right \rfloor $
.
Proof. (a)
![]() $\Rightarrow $
(b) is trivial. For (a)
$\Rightarrow $
(b) is trivial. For (a)
![]() $\Rightarrow $
(c) and (b)
$\Rightarrow $
(c) and (b)
![]() $\Rightarrow $
(c) see [Reference Efrat9, Prop. 2.2(c)] and its proof.
$\Rightarrow $
(c) see [Reference Efrat9, Prop. 2.2(c)] and its proof.
Proposition 6.2. Let
![]() $1\leq i'\leq i$
and
$1\leq i'\leq i$
and
![]() $j'\geq 0$
.
$j'\geq 0$
.
-
(a) One has
 $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=\{I\}$
if and only if
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=\{I\}$
if and only if
 $j'\geq j+1+\left \lfloor \log _p(i/i')\right \rfloor $
.
$j'\geq j+1+\left \lfloor \log _p(i/i')\right \rfloor $
. -
(b) One has
 $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+p^j\mathbb {Z} E_{1,i+1}$
if and only if
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+p^j\mathbb {Z} E_{1,i+1}$
if and only if
 $j'=j+\log _p(i/i')$
(in particular,
$j'=j+\log _p(i/i')$
(in particular,
 $i/i'$
is a p-power).
$i/i'$
is a p-power). -
(c) One has
 $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}\leq I+p^j\mathbb {Z} E_{1,i+1}$
if and only if
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}\leq I+p^j\mathbb {Z} E_{1,i+1}$
if and only if
 $j'\geq j+\log _p (i/i')$
.
$j'\geq j+\log _p (i/i')$
.
Proof. Let N be an
![]() $(i+1)\times (i+1)$
-matrix over
$(i+1)\times (i+1)$
-matrix over
![]() $\mathbb {Z}/p^{j+1}$
such that
$\mathbb {Z}/p^{j+1}$
such that
![]() $I+N\in \mathbb {U}^{\left (i'\right )}$
. Then
$I+N\in \mathbb {U}^{\left (i'\right )}$
. Then
![]() $N^l=0$
for every integer l with
$N^l=0$
for every integer l with
![]() $i/i'<l$
. Hence
$i/i'<l$
. Hence
 $$ \begin{align*} (I+N)^{p^{j'}}=\sum_{l=0}^{p^{j'}}\binom{p^{j'}}lN^l =\sum_{l=0}^{\min\left(p^{j'},\lfloor i/i'\rfloor\right)}\binom{p^{j'}}lN^l. \end{align*} $$
$$ \begin{align*} (I+N)^{p^{j'}}=\sum_{l=0}^{p^{j'}}\binom{p^{j'}}lN^l =\sum_{l=0}^{\min\left(p^{j'},\lfloor i/i'\rfloor\right)}\binom{p^{j'}}lN^l. \end{align*} $$
Further, if
![]() $i'\mid i$
, then
$i'\mid i$
, then
![]() $N^{i/i'}\in \mathbb {Z} E_{1,i+1}$
.
$N^{i/i'}\in \mathbb {Z} E_{1,i+1}$
.
In particular, let M be the
![]() $(i+1)\times (i+1)$
-matrix over
$(i+1)\times (i+1)$
-matrix over
![]() $\mathbb {Z}/p^{j+1}$
which is
$\mathbb {Z}/p^{j+1}$
which is
![]() $1$
on the (first) super-diagonal and is
$1$
on the (first) super-diagonal and is
![]() $0$
elsewhere. Then the matrix
$0$
elsewhere. Then the matrix
![]() $M^{i'l}$
is
$M^{i'l}$
is
![]() $1$
on the
$1$
on the
![]() $i'l$
th diagonal above the main one and is
$i'l$
th diagonal above the main one and is
![]() $0$
elsewhere. In particular,
$0$
elsewhere. In particular,
![]() $I+M^{i'}\in \mathbb {U}^{\left (i'\right )}$
. By what we have justed noted,
$I+M^{i'}\in \mathbb {U}^{\left (i'\right )}$
. By what we have justed noted,
 $$ \begin{align*} \left(1+M^{i'}\right)^{p^{j'}}=\sum_{l=0}^{\min\left(p^{j'}, \lfloor i/i'\rfloor\right)}\binom{p^{j'}}lM^{i'l}. \end{align*} $$
$$ \begin{align*} \left(1+M^{i'}\right)^{p^{j'}}=\sum_{l=0}^{\min\left(p^{j'}, \lfloor i/i'\rfloor\right)}\binom{p^{j'}}lM^{i'l}. \end{align*} $$
This matrix is
![]() $\binom {p^{j'}}l$
on the
$\binom {p^{j'}}l$
on the
![]() $i'l$
th diagonals above the main one and is
$i'l$
th diagonals above the main one and is
![]() $0$
elsewhere.
$0$
elsewhere.
(a) By the previous observations,
![]() $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=\{I\}$
holds if and only if
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=\{I\}$
holds if and only if
 $$ \begin{align*} p^{j+1}\mid\binom{p^{j'}}l, \quad l=1,2,\dotsc,\min\left(p^{j'},\lfloor i/i'\rfloor\right). \end{align*} $$
$$ \begin{align*} p^{j+1}\mid\binom{p^{j'}}l, \quad l=1,2,\dotsc,\min\left(p^{j'},\lfloor i/i'\rfloor\right). \end{align*} $$
In light of Lemma 6.1, this is equivalent to
![]() $j'\geq j+1+\min \left (j',\left \lfloor \log _p\lfloor i/i'\rfloor \right \rfloor \right )$
, and it remains to note that
$j'\geq j+1+\min \left (j',\left \lfloor \log _p\lfloor i/i'\rfloor \right \rfloor \right )$
, and it remains to note that
![]() $\left \lfloor \log _p\lfloor i/i'\rfloor \right \rfloor =\left \lfloor \log _p(i/i')\right \rfloor $
.
$\left \lfloor \log _p\lfloor i/i'\rfloor \right \rfloor =\left \lfloor \log _p(i/i')\right \rfloor $
.
(b) First assume that
![]() $i=i'$
. Then
$i=i'$
. Then
![]() $\mathbb {U}^{\left (i'\right )}=I+\mathbb {Z} E_{1,i+1}$
. Hence
$\mathbb {U}^{\left (i'\right )}=I+\mathbb {Z} E_{1,i+1}$
. Hence
![]() $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+\mathbb {Z} p^{j'}E_{1,i+1}$
, and the equality
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+\mathbb {Z} p^{j'}E_{1,i+1}$
, and the equality
![]() $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+\mathbb {Z} p^jE_{1,i+1}$
means that
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+\mathbb {Z} p^jE_{1,i+1}$
means that
![]() $j'=j$
, as desired.
$j'=j$
, as desired.
Next we assume that
![]() $i>i'$
. By the previous observations,
$i>i'$
. By the previous observations,
![]() $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+\mathbb {Z} p^jE_{1,i+1}$
holds if and only if the following conditions hold:
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j'}}=I+\mathbb {Z} p^jE_{1,i+1}$
holds if and only if the following conditions hold:
-
(i)
 $i/i'$
is an integer
$i/i'$
is an integer
 $\leq p^{j'}$
;
$\leq p^{j'}$
; -
(ii)
 $p^{j+1}\mid \binom {p^{j'}}l$
,
$p^{j+1}\mid \binom {p^{j'}}l$
,
 $l=1,2,\dotsc , (i/i')-1$
;
$l=1,2,\dotsc , (i/i')-1$
; -
(iii)
 $p^j\mid \binom {p^{j'}}{i/i'}$
,
$p^j\mid \binom {p^{j'}}{i/i'}$
,
 $p^{j+1}{\,\not |\,}\binom {p^{j'}}{i/i'}$
.
$p^{j+1}{\,\not |\,}\binom {p^{j'}}{i/i'}$
.
By Lemma 6.1 again, (i)–(iii) mean that
![]() $i/i'$
is an integer
$i/i'$
is an integer
![]() $\leq p^{j'}$
, and
$\leq p^{j'}$
, and
 $$ \begin{align*} j'&\geq j+1+\left\lfloor\log_p((i/i')-1)\right\rfloor\\ j'&\geq j+\left\lfloor\log_p(i/i')\right\rfloor\\ j'&<j+1+\left\lfloor\log_p(i/i'))\right\rfloor. \end{align*} $$
$$ \begin{align*} j'&\geq j+1+\left\lfloor\log_p((i/i')-1)\right\rfloor\\ j'&\geq j+\left\lfloor\log_p(i/i')\right\rfloor\\ j'&<j+1+\left\lfloor\log_p(i/i'))\right\rfloor. \end{align*} $$
This amounts to saying that
![]() $j'=j+\log _p(i/i')$
.
$j'=j+\log _p(i/i')$
.
(c) This follows from (a) and (b).
The case
![]() $i'=1$
of Proposition 6.2(a) was shown by Sawin (see [Reference Efrat9, Prop. 2.3]).
$i'=1$
of Proposition 6.2(a) was shown by Sawin (see [Reference Efrat9, Prop. 2.3]).
The following corollary stands behind our definition of the sets
![]() $J(n)$
. In the case
$J(n)$
. In the case
![]() $i=n$
it was proved by Mináč, Rogelstad and Tân [Reference Mináč, Rogelstad and Tân26, Cor. 3.7].
$i=n$
it was proved by Mináč, Rogelstad and Tân [Reference Mináč, Rogelstad and Tân26, Cor. 3.7].
Corollary 6.3. Suppose that
![]() $1\leq i\leq n$
and
$1\leq i\leq n$
and
![]() $j=j_n(i)$
. One has
$j=j_n(i)$
. One has
![]() $\mathbb {U}_{\left (n,p\right )}=I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
if and only if
$\mathbb {U}_{\left (n,p\right )}=I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
if and only if
![]() $i\in J(n)$
.
$i\in J(n)$
.
Proof. Recall that
![]() $\mathbb {U}_{\left (n,p\right )}=\prod _{i'=1}^n\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j_n\left (i'\right )}}$
.
$\mathbb {U}_{\left (n,p\right )}=\prod _{i'=1}^n\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j_n\left (i'\right )}}$
.
If
![]() $i'>i$
, then
$i'>i$
, then
![]() $\mathbb {U}^{\left (i'\right )}=\{I\}$
, whence
$\mathbb {U}^{\left (i'\right )}=\{I\}$
, whence
![]() $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j_n\left (i'\right )}}=\{I\}$
.
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j_n\left (i'\right )}}=\{I\}$
.
Taking in Proposition 6.2(b),
![]() $i'=i$
, and
$i'=i$
, and
![]() $j'=j=j_n(i)$
, we obtain that
$j'=j=j_n(i)$
, we obtain that
![]() $\left (\mathbb {U}^{(i)}\right )^{p^{j_n(i)}}=I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
.
$\left (\mathbb {U}^{(i)}\right )^{p^{j_n(i)}}=I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
.
Therefore,
![]() $\mathbb {U}_{\left (n,p\right )}=I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
holds if and only if for every
$\mathbb {U}_{\left (n,p\right )}=I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
holds if and only if for every
![]() $1\leq i'\leq i$
one has
$1\leq i'\leq i$
one has
![]() $\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j_n\left (i'\right )}}\leq I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
. By Proposition 6.2(c), this inclusion is equivalent to
$\left (\mathbb {U}^{\left (i'\right )}\right )^{p^{j_n\left (i'\right )}}\leq I+p^{j_n(i)}\mathbb {Z} E_{1,i+1}$
. By Proposition 6.2(c), this inclusion is equivalent to
![]() $i'p^{j_n\left (i'\right )}\geq ip^{j_n(i)}$
.
$i'p^{j_n\left (i'\right )}\geq ip^{j_n(i)}$
.
Thus, for
![]() $i\in J(n)$
and
$i\in J(n)$
and
![]() $\mathbb {U}=\mathbb {U}_i\left (\mathbb {Z}/p^{j_n(i)+1}\right )$
there is a central extension
$\mathbb {U}=\mathbb {U}_i\left (\mathbb {Z}/p^{j_n(i)+1}\right )$
there is a central extension
where the isomorphism is the projection on the
![]() $(1,i+1)$
-entry composed with the isomorphism
$(1,i+1)$
-entry composed with the isomorphism
![]() $p^{j(i)}\mathbb {Z}/p^{j(i)+1}\mathbb {Z}\cong \mathbb {Z}/p$
.
$p^{j(i)}\mathbb {Z}/p^{j(i)+1}\mathbb {Z}\cong \mathbb {Z}/p$
.
7 The cohomology elements
 $\alpha _{w,n}$
$\alpha _{w,n}$
Let S be again a free profinite group on the basis X, and let
![]() $n\geq 2$
. Consider the transgression homomorphism
$n\geq 2$
. Consider the transgression homomorphism
![]() $\operatorname {\mathrm {trg}}\colon H^1\left (S_{\left (n,p\right )}\right )^S\to H^2\left (S/S_{\left (n,p\right )}\right )$
(recall that the cohomology groups are with respect to the coefficient module
$\operatorname {\mathrm {trg}}\colon H^1\left (S_{\left (n,p\right )}\right )^S\to H^2\left (S/S_{\left (n,p\right )}\right )$
(recall that the cohomology groups are with respect to the coefficient module
![]() $\mathbb {Z}/p$
with trivial action). It is the differential
$\mathbb {Z}/p$
with trivial action). It is the differential
![]() $d_2^{01}$
in the Lyndon–Hochschild–Serre spectral sequence corresponding to the closed normal subgroup
$d_2^{01}$
in the Lyndon–Hochschild–Serre spectral sequence corresponding to the closed normal subgroup
![]() $S_{\left (n,p\right )}$
of S [Reference Neukirch, Schmidt and Wingberg31, Th. 2.4.3]. From the five-term sequence in profinite cohomology [Reference Neukirch, Schmidt and Wingberg31, Prop. 1.6.7] and the fact that S has cohomological dimension
$S_{\left (n,p\right )}$
of S [Reference Neukirch, Schmidt and Wingberg31, Th. 2.4.3]. From the five-term sequence in profinite cohomology [Reference Neukirch, Schmidt and Wingberg31, Prop. 1.6.7] and the fact that S has cohomological dimension
![]() $1$
, it follows that
$1$
, it follows that
![]() $\operatorname {\mathrm {trg}}$
is an isomorphism.
$\operatorname {\mathrm {trg}}$
is an isomorphism.
Now consider a word w of length
![]() $i\in J(n)$
. Consider the ring
$i\in J(n)$
. Consider the ring
![]() $R_i=\mathbb {Z}/p^{j_n(i)+1}$
, and set
$R_i=\mathbb {Z}/p^{j_n(i)+1}$
, and set
![]() $\mathbb {U}=\mathbb {U}_i(R_i)$
. As before, let
$\mathbb {U}=\mathbb {U}_i(R_i)$
. As before, let
![]() $\overline {\mathbb {U}}=\mathbb {U}/\mathbb {U}_{\left (n,p\right )}$
. By Corollary 6.3, the projection on the
$\overline {\mathbb {U}}=\mathbb {U}/\mathbb {U}_{\left (n,p\right )}$
. By Corollary 6.3, the projection on the
![]() $(1,i+1)$
-entry gives an isomorphism
$(1,i+1)$
-entry gives an isomorphism
The Magnus representation
![]() $\rho =\rho _w\colon S\to \mathbb {U}$
induces continuous homomorphisms
$\rho =\rho _w\colon S\to \mathbb {U}$
induces continuous homomorphisms
Let
![]() $\bar \rho _w^*\colon H^2\left (\overline {\mathbb {U}}\right )\to H^2\left (S/S_{\left (n,p\right )}\right )$
be the pullback of
$\bar \rho _w^*\colon H^2\left (\overline {\mathbb {U}}\right )\to H^2\left (S/S_{\left (n,p\right )}\right )$
be the pullback of
![]() $\bar \rho _w$
.
$\bar \rho _w$
.
Let
![]() $\gamma =\gamma _{n,R_i}\in H^2\left (\overline {\mathbb {U}}\right )$
correspond to the extension (6.1) under the Schreier correspondence [Reference Neukirch, Schmidt and Wingberg31, Th. 1.2.4]. We set
$\gamma =\gamma _{n,R_i}\in H^2\left (\overline {\mathbb {U}}\right )$
correspond to the extension (6.1) under the Schreier correspondence [Reference Neukirch, Schmidt and Wingberg31, Th. 1.2.4]. We set
Example 7.1
![]() $\alpha _{w,n}$
for a word
$\alpha _{w,n}$
for a word
![]() $w=(x)$
of length 1. Let
$w=(x)$
of length 1. Let
![]() $j=j_n(1)=\lceil \log _pn\rceil $
, so
$j=j_n(1)=\lceil \log _pn\rceil $
, so
![]() $\mathbb {U}=\mathbb {U}_1\left (\mathbb {Z}/p^{j+1}\right )\cong \mathbb {Z}/p^{j+1}$
. As
$\mathbb {U}=\mathbb {U}_1\left (\mathbb {Z}/p^{j+1}\right )\cong \mathbb {Z}/p^{j+1}$
. As
![]() $1\in J(n)$
, we have
$1\in J(n)$
, we have
![]() $\mathbb {U}_{\left (n,p\right )}\cong \mathbb {Z}/p$
, and the central extension (6.1) becomes
$\mathbb {U}_{\left (n,p\right )}\cong \mathbb {Z}/p$
, and the central extension (6.1) becomes
We consider this extension as a sequence of trivial
![]() $S/S_{\left (n,p\right )}$
-modules. The Bockstein homomorphism
$S/S_{\left (n,p\right )}$
-modules. The Bockstein homomorphism
is the associated connecting homomorphism.
We may identify
![]() $\rho _{(x)}\colon S\to \mathbb {U}$
with
$\rho _{(x)}\colon S\to \mathbb {U}$
with
![]() $\epsilon _{(x),\mathbb {Z}/p^{j+1}}\colon S\to \mathbb {Z}/p^{j+1}$
, and
$\epsilon _{(x),\mathbb {Z}/p^{j+1}}\colon S\to \mathbb {Z}/p^{j+1}$
, and
![]() $\bar \rho _{(x)}\colon S/S_{\left (n,p\right )}\to \overline {\mathbb {U}}$
with
$\bar \rho _{(x)}\colon S/S_{\left (n,p\right )}\to \overline {\mathbb {U}}$
with
![]() $\epsilon _{(x),\mathbb {Z}/p^j}\colon S/S_{\left (n,p\right )}\to \mathbb {Z}/p^j$
, which are both continuous homomorphisms. Thus
$\epsilon _{(x),\mathbb {Z}/p^j}\colon S/S_{\left (n,p\right )}\to \mathbb {Z}/p^j$
, which are both continuous homomorphisms. Thus
![]() $\alpha _{(x),n}$
corresponds to the pullback of the extension (7.1) under
$\alpha _{(x),n}$
corresponds to the pullback of the extension (7.1) under
![]() $\epsilon _{(x),\mathbb {Z}/p^j}$
. By [Reference Efrat8, Remark 7.3],
$\epsilon _{(x),\mathbb {Z}/p^j}$
. By [Reference Efrat8, Remark 7.3],
For the next Example, we first recall a few facts about Massey products. While these products are defined in the general context of differential graded algebras, in the special case of the n-fold Massey product
![]() $H^1(G,R)^n\to H^2(G,R)$
in profinite (or discrete) group cohomology it can be alternatively described in terms of unitriangular representations. This was discovered by Dwyer [Reference Dwyer6] in the discrete case, and we refer to [Reference Efrat7, §8] for the profinite case, which is considered here. We assume as before that
$H^1(G,R)^n\to H^2(G,R)$
in profinite (or discrete) group cohomology it can be alternatively described in terms of unitriangular representations. This was discovered by Dwyer [Reference Dwyer6] in the discrete case, and we refer to [Reference Efrat7, §8] for the profinite case, which is considered here. We assume as before that
![]() $n\geq 2$
and R is a finite commutative ring on which G acts trivially (see [Reference Wickelgren38] for the case of a nontrivial action).
$n\geq 2$
and R is a finite commutative ring on which G acts trivially (see [Reference Wickelgren38] for the case of a nontrivial action).
Specifically, let
![]() $\mathbb {U}=\mathbb {U}_n(R)$
and let
$\mathbb {U}=\mathbb {U}_n(R)$
and let
![]() $\overline {\mathbb {U}}$
be again the quotient of
$\overline {\mathbb {U}}$
be again the quotient of
![]() $\mathbb {U}$
by the central subgroup
$\mathbb {U}$
by the central subgroup
![]() $I+R E_{1,n+1}\left (\cong R^+\right )$
. The central extension
$I+R E_{1,n+1}\left (\cong R^+\right )$
. The central extension
of trivial G-modules corresponds to a cohomology element
![]() $\gamma _R\in H^2(G,R^+)$
. Given
$\gamma _R\in H^2(G,R^+)$
. Given
![]() $\psi _1,\dotsc ,\psi _n\in H^1(G,R^+)$
, we consider the continuous homomorphisms
$\psi _1,\dotsc ,\psi _n\in H^1(G,R^+)$
, we consider the continuous homomorphisms
![]() $\bar \rho \colon G\to \overline {\mathbb {U}}$
whose projection
$\bar \rho \colon G\to \overline {\mathbb {U}}$
whose projection
![]() $\bar \rho _{k,k+1}\colon G\to R$
on the
$\bar \rho _{k,k+1}\colon G\to R$
on the
![]() $(k,k+1)$
-entry is
$(k,k+1)$
-entry is
![]() $\psi _k$
, for
$\psi _k$
, for
![]() $k=1,2,\dotsc , n$
. As before, let
$k=1,2,\dotsc , n$
. As before, let
![]() $\bar \rho ^*\colon H^2\left (\overline {\mathbb {U}},R^+\right )\to H^2(G,R^+)$
be the pullback of
$\bar \rho ^*\colon H^2\left (\overline {\mathbb {U}},R^+\right )\to H^2(G,R^+)$
be the pullback of
![]() $\bar \rho $
. Then
$\bar \rho $
. Then
![]() $\bar \rho ^*(\gamma _R)$
corresponds to the central extension
$\bar \rho ^*(\gamma _R)$
corresponds to the central extension
where the fiber product is with respect to the natural projection
![]() $\mathbb {U}\to \overline {\mathbb {U}}$
and to
$\mathbb {U}\to \overline {\mathbb {U}}$
and to
![]() $\bar \rho $
. The n-fold Massey product
$\bar \rho $
. The n-fold Massey product
![]() $\langle \psi _1,\dotsc ,\psi _n\rangle $
is the subset of
$\langle \psi _1,\dotsc ,\psi _n\rangle $
is the subset of
![]() $H^2(G,R^+)$
consisting of all pullbacks
$H^2(G,R^+)$
consisting of all pullbacks
![]() $\bar \rho ^*(\gamma _R)$
[Reference Efrat7, Prop. 8.3]. Thus the n-fold Massey product
$\bar \rho ^*(\gamma _R)$
[Reference Efrat7, Prop. 8.3]. Thus the n-fold Massey product
![]() $\langle \cdot ,\dotsc ,\cdot \rangle \colon H^1(G,R^+)^n\to H^2(G,R^+)$
is a multivalued map. In the special case
$\langle \cdot ,\dotsc ,\cdot \rangle \colon H^1(G,R^+)^n\to H^2(G,R^+)$
is a multivalued map. In the special case
![]() $n=2$
, one has
$n=2$
, one has
![]() $\langle \psi _1,\psi _2\rangle =\{\psi _1\cup \psi _2\}$
.
$\langle \psi _1,\psi _2\rangle =\{\psi _1\cup \psi _2\}$
.
Example 7.2
![]() $\alpha _{w,n}$
for a word w of length
$\alpha _{w,n}$
for a word w of length
![]() $n\geq 2$
. Since
$n\geq 2$
. Since
![]() $j_n(n)=0$
we have
$j_n(n)=0$
we have
![]() $R_n=\mathbb {Z}/p$
, so
$R_n=\mathbb {Z}/p$
, so
![]() $\mathbb {U}=\mathbb {U}_n(\mathbb {Z}/p)$
. As
$\mathbb {U}=\mathbb {U}_n(\mathbb {Z}/p)$
. As
![]() $n\in J(n)$
, Corollary 6.3 shows that
$n\in J(n)$
, Corollary 6.3 shows that
![]() $\mathbb {U}_{\left (n,p\right )}=I+\mathbb {Z} E_{1,n+1}\cong \mathbb {Z}/p$
. Thus the extension (7.2) (for
$\mathbb {U}_{\left (n,p\right )}=I+\mathbb {Z} E_{1,n+1}\cong \mathbb {Z}/p$
. Thus the extension (7.2) (for
![]() $R=\mathbb {Z}/p$
) coincides with the extension (6.1) with
$R=\mathbb {Z}/p$
) coincides with the extension (6.1) with
![]() $i=n$
.
$i=n$
.
Now take a word
![]() $w=(x_1\dotsm x_n)\in X^*$
of length n. Let
$w=(x_1\dotsm x_n)\in X^*$
of length n. Let
![]() $\bar \rho =\bar \rho _w\colon S/S_{\left (n,p\right )}\to \overline {\mathbb {U}}$
and let
$\bar \rho =\bar \rho _w\colon S/S_{\left (n,p\right )}\to \overline {\mathbb {U}}$
and let
![]() $\bar \rho _{k,k+1}$
be homomorphisms as before. By its definition as the pullback of the extension (6.1),
$\bar \rho _{k,k+1}$
be homomorphisms as before. By its definition as the pullback of the extension (6.1),
![]() $\alpha _{w,n}$
is an element of the n-fold Massey product
$\alpha _{w,n}$
is an element of the n-fold Massey product
![]() $\langle \rho _{12},\rho _{23},\dotsc ,\rho _{n,n+1}\rangle $
in
$\langle \rho _{12},\rho _{23},\dotsc ,\rho _{n,n+1}\rangle $
in
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
. Note that
$H^2\left (S/S_{\left (n,p\right )}\right )$
. Note that
![]() $\bar \rho _{k,k+1}$
is given by
$\bar \rho _{k,k+1}$
is given by
![]() $\bar \rho _{k,k+1}(x_l)=\delta _{kl}$
for every
$\bar \rho _{k,k+1}(x_l)=\delta _{kl}$
for every
![]() $1\leq k,l\leq n$
.
$1\leq k,l\leq n$
.
8 The Lyndon bases
We continue with the setup of §7. Identifying
![]() $H^1\left (S_{\left (n,p\right )}\right )=\operatorname {\mathrm {Hom}}\left (S_{\left (n,p\right )},\mathbb {Z}/p\right )$
, we obtain a nondegenerate bilinear map
$H^1\left (S_{\left (n,p\right )}\right )=\operatorname {\mathrm {Hom}}\left (S_{\left (n,p\right )},\mathbb {Z}/p\right )$
, we obtain a nondegenerate bilinear map
[Reference Efrat and Mináč11, Cor. 2.2]. It gives rise to the bilinear transgression pairing
 $$ \begin{align} \begin{gathered} (\cdot,\cdot)_n\colon S_{\left(n,p\right)}/\left(S_{\left(n,p\right)}\right)^p\left[S,S_{\left(n,p\right)}\right]\times H^2\left(S/S_{\left(n,p\right)}\right)\to\mathbb{Z}/p, \\ (\bar\sigma,\alpha)_n=-\left(\operatorname{\mathrm{trg}}^{-1}\alpha\right)(\sigma), \end{gathered} \end{align} $$
$$ \begin{align} \begin{gathered} (\cdot,\cdot)_n\colon S_{\left(n,p\right)}/\left(S_{\left(n,p\right)}\right)^p\left[S,S_{\left(n,p\right)}\right]\times H^2\left(S/S_{\left(n,p\right)}\right)\to\mathbb{Z}/p, \\ (\bar\sigma,\alpha)_n=-\left(\operatorname{\mathrm{trg}}^{-1}\alpha\right)(\sigma), \end{gathered} \end{align} $$
where
![]() $\bar \sigma $
denotes the coset of
$\bar \sigma $
denotes the coset of
![]() $\sigma \in S_{\left (n,p\right )}$
. It is therefore also nondegenerate.
$\sigma \in S_{\left (n,p\right )}$
. It is therefore also nondegenerate.
By Proposition 5.1 and Corollary 6.3, for a word w of length
![]() $i\in J(n)$
there is a commutative diagram
$i\in J(n)$
there is a commutative diagram

where, as before,
![]() $\pi _i\colon {\mathbb {Z}}_p\to {\mathbb {Z}}/p^{j_n(i)+1}$
is the natural projection, and the lower isomorphism is the projection on the
$\pi _i\colon {\mathbb {Z}}_p\to {\mathbb {Z}}/p^{j_n(i)+1}$
is the natural projection, and the lower isomorphism is the projection on the
![]() $(1,i+1)$
-entry. We deduce the following link between cohomology and the Magnus map. As before, we identify
$(1,i+1)$
-entry. We deduce the following link between cohomology and the Magnus map. As before, we identify
![]() $p^{j_n(i)}\mathbb {Z}/p^{j_n(i)+1}\mathbb {Z}$
with
$p^{j_n(i)}\mathbb {Z}/p^{j_n(i)+1}\mathbb {Z}$
with
![]() $\mathbb {Z}/p$
.
$\mathbb {Z}/p$
.
Proposition 8.1. For
![]() $\sigma \in S_{\left (n,p\right )}$
and a word
$\sigma \in S_{\left (n,p\right )}$
and a word
![]() $w\in X^*$
of length
$w\in X^*$
of length
![]() $i\in J(n)$
, one has
$i\in J(n)$
, one has
![]() $\left (\bar {\sigma },\alpha _{w,n}\right )_n=\pi _i\left (\epsilon _{w,\mathbb {Z}_p}(\sigma )\right )$
.
$\left (\bar {\sigma },\alpha _{w,n}\right )_n=\pi _i\left (\epsilon _{w,\mathbb {Z}_p}(\sigma )\right )$
.
Proof. The central extension (6.1) gives rise to a transgression homomorphism
![]() $\operatorname {\mathrm {trg}}\colon H^1\left (\mathbb {U}^{\left (n,p\right )}\right )^{\mathbb {U}}\to H^2\left (\overline {\mathbb {U}}\right )$
. Let
$\operatorname {\mathrm {trg}}\colon H^1\left (\mathbb {U}^{\left (n,p\right )}\right )^{\mathbb {U}}\to H^2\left (\overline {\mathbb {U}}\right )$
. Let
![]() $\iota \colon \mathbb {U}_{\left (n,p\right )}\xrightarrow {\sim }\mathbb {Z}/p$
be the composition of the lower row in diagram (8.2) with the isomorphism
$\iota \colon \mathbb {U}_{\left (n,p\right )}\xrightarrow {\sim }\mathbb {Z}/p$
be the composition of the lower row in diagram (8.2) with the isomorphism
![]() $p^{j_n(i)}\mathbb {Z}/p^{j_n(i)+1}\mathbb {Z}\cong \mathbb {Z}/p$
. By the results of [Reference Efrat8, §7],
$p^{j_n(i)}\mathbb {Z}/p^{j_n(i)+1}\mathbb {Z}\cong \mathbb {Z}/p$
. By the results of [Reference Efrat8, §7],
The functoriality of transgression gives a commutative square

As
![]() $\sigma \in S_{(n,p)}$
, this square and diagram (8.2) give
$\sigma \in S_{(n,p)}$
, this square and diagram (8.2) give
 $$ \begin{align*} \left(\bar\sigma,\alpha_{w,n}\right)_n&=\left(\bar\sigma,\bar\rho_w^*(\gamma)\right)_n =-\left(\bar\sigma,\bar\rho_w^*(\operatorname{\mathrm{trg}}(\iota))\right)_n =-\left(\bar\sigma,\operatorname{\mathrm{trg}}\left(\left(\rho_w^0\right)^*(\iota)\right)\right)_n \\ &=\left(\left(\rho_w^0\right)^*(\iota)\right)(\sigma) =\iota\left(\rho_w^0(\sigma)\right) =\pi_i\left(\epsilon_{w,\mathbb{Z}_p}(\sigma)\right). \\[-35pt] \end{align*} $$
$$ \begin{align*} \left(\bar\sigma,\alpha_{w,n}\right)_n&=\left(\bar\sigma,\bar\rho_w^*(\gamma)\right)_n =-\left(\bar\sigma,\bar\rho_w^*(\operatorname{\mathrm{trg}}(\iota))\right)_n =-\left(\bar\sigma,\operatorname{\mathrm{trg}}\left(\left(\rho_w^0\right)^*(\iota)\right)\right)_n \\ &=\left(\left(\rho_w^0\right)^*(\iota)\right)(\sigma) =\iota\left(\rho_w^0(\sigma)\right) =\pi_i\left(\epsilon_{w,\mathbb{Z}_p}(\sigma)\right). \\[-35pt] \end{align*} $$
Now consider words
![]() $w,w'\in X^*$
of lengths
$w,w'\in X^*$
of lengths
![]() $i,i'\in J(n)$
, respectively, with
$i,i'\in J(n)$
, respectively, with
![]() $w'$
Lyndon. We deduce from Proposition 8.1 that
$w'$
Lyndon. We deduce from Proposition 8.1 that
We can therefore restate Proposition 5.3 cohomologically:
Corollary 8.2. The transposed matrix
![]() $\bigl [\left (\bar \sigma _{w'},\alpha _{w,n}\right )_n\bigr ]_{w,w'}^T$
, where
$\bigl [\left (\bar \sigma _{w'},\alpha _{w,n}\right )_n\bigr ]_{w,w'}^T$
, where
![]() $w,w'$
range over all Lyndon words in
$w,w'$
range over all Lyndon words in
![]() $X^*$
of lengths
$X^*$
of lengths
![]() $i,i'$
, respectively, in
$i,i'$
, respectively, in
![]() $J(n)$
, and totally ordered by
$J(n)$
, and totally ordered by
![]() $\preceq $
, coincides with the fundamental matrix of level n of the Lyndon words. In particular, it is unitriangular, whence invertible.
$\preceq $
, coincides with the fundamental matrix of level n of the Lyndon words. In particular, it is unitriangular, whence invertible.
Example 8.3. Let
![]() $n=2$
. Then
$n=2$
. Then
![]() $J(n)=\{1,2\}$
. For every
$J(n)=\{1,2\}$
. For every
![]() $x\in X$
let
$x\in X$
let
![]() $\epsilon _x\in H^1\left (S/S_{\left (2,p\right )}\right )$
be the homomorphism induced by
$\epsilon _x\in H^1\left (S/S_{\left (2,p\right )}\right )$
be the homomorphism induced by
![]() $\epsilon _{(x),\mathbb {Z}/p}$
. It is
$\epsilon _{(x),\mathbb {Z}/p}$
. It is
![]() $1$
on the coset of x and is
$1$
on the coset of x and is
![]() $0$
on the coset of any
$0$
on the coset of any
![]() $x'\in X$
,
$x'\in X$
,
![]() $x'\neq x$
.
$x'\neq x$
.
For a one-letter word
![]() $w=(x)$
(which is always Lyndon) we have
$w=(x)$
(which is always Lyndon) we have
![]() $\sigma _w=\tau _w^p=x^p$
and
$\sigma _w=\tau _w^p=x^p$
and
![]() $\alpha _{w,2}=\mathrm {Bock}_{p,S/S_{\left (2,p\right )}}(\epsilon _x)$
(Example 7.1).
$\alpha _{w,2}=\mathrm {Bock}_{p,S/S_{\left (2,p\right )}}(\epsilon _x)$
(Example 7.1).
For a two-letter Lyndon word
![]() $w=(xy)$
,
$w=(xy)$
,
![]() $x<y$
, the projections of the representation
$x<y$
, the projections of the representation
![]() $\bar \rho _w$
on the
$\bar \rho _w$
on the
![]() $(1,2)$
- and
$(1,2)$
- and
![]() $(2,3)$
-entries are
$(2,3)$
-entries are
![]() $\bar \rho _{12}=\epsilon _x$
and
$\bar \rho _{12}=\epsilon _x$
and
![]() $\bar \rho _{23}=\epsilon _y$
. Thus
$\bar \rho _{23}=\epsilon _y$
. Thus
![]() $\sigma _w=\tau _w=[x,y]$
, and
$\sigma _w=\tau _w=[x,y]$
, and
![]() $\alpha _{w,2}=\epsilon _x\cup \epsilon _y$
(Example 7.2).
$\alpha _{w,2}=\epsilon _x\cup \epsilon _y$
(Example 7.2).
Recall that the fundamental matrix for Lyndon words and for
![]() $n=2$
is the identity matrix (Example 5.4). Thus we recover the fundamental duality, discovered by Labute, between Bockstein elements/cup products and pth powers/commutators, respectively ([Reference Labute22, Prop. 8], [Reference Labute23, §2], [Reference Neukirch, Schmidt and Wingberg31, Ch. III, §9]).
$n=2$
is the identity matrix (Example 5.4). Thus we recover the fundamental duality, discovered by Labute, between Bockstein elements/cup products and pth powers/commutators, respectively ([Reference Labute22, Prop. 8], [Reference Labute23, §2], [Reference Neukirch, Schmidt and Wingberg31, Ch. III, §9]).
We will need the following elementary fact in linear algebra [Reference Efrat8, Lemma 8.4]:
Lemma 8.4. Let R be a commutative ring and let
![]() $(\cdot ,\cdot )\colon A\times B\to R$
be a nondegenerate bilinear map of R-modules. Let
$(\cdot ,\cdot )\colon A\times B\to R$
be a nondegenerate bilinear map of R-modules. Let
![]() $(I,\leq )$
be a finite totally ordered set, and for every
$(I,\leq )$
be a finite totally ordered set, and for every
![]() $w\in I$
let
$w\in I$
let
![]() $a_w\in A$
,
$a_w\in A$
,
![]() $b_w\in B$
. Suppose that the matrix
$b_w\in B$
. Suppose that the matrix
![]() $\bigl [\left (a_w,b_{w'}\right )\bigr ]_{w,w'\in I}$
is invertible, and that
$\bigl [\left (a_w,b_{w'}\right )\bigr ]_{w,w'\in I}$
is invertible, and that
![]() $a_w$
,
$a_w$
,
![]() $w\in I$
, generate A. Then
$w\in I$
, generate A. Then
![]() $a_w$
,
$a_w$
,
![]() $w\in I$
, is an R-linear basis of A, and
$w\in I$
, is an R-linear basis of A, and
![]() $b_w$
,
$b_w$
,
![]() $w\in I$
, is an R-linear basis of B.
$w\in I$
, is an R-linear basis of B.
We now deduce our first main result. Note that part (a) of the theorem strengthens Theorem 4.6 in the special case where H is the Hall set of Lyndon words.
Theorem 8.5.
-
(a) The
 $\mathbb {F}_p$
-linear space
$\mathbb {F}_p$
-linear space
 $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
has a basis consisting of the cosets
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
has a basis consisting of the cosets
 $\bar \sigma _w$
of
$\bar \sigma _w$
of
 $\sigma _w$
, where w is a Lyndon word in
$\sigma _w$
, where w is a Lyndon word in
 $X^*$
of length
$X^*$
of length
 $i\in J(n)$
.
$i\in J(n)$
. -
(b) The
 $\mathbb {F}_p$
-linear space
$\mathbb {F}_p$
-linear space
 $H^2\left (S/S_{\left (n,p\right )}\right )$
has a basis consisting of all
$H^2\left (S/S_{\left (n,p\right )}\right )$
has a basis consisting of all
 $\alpha _{w,n}$
, where w is a Lyndon word in
$\alpha _{w,n}$
, where w is a Lyndon word in
 $X^*$
of length
$X^*$
of length
 $i\in J(n)$
.
$i\in J(n)$
.
Proof. First assume that X is finite. By Theorem 4.6, the cosets in (a) generate
![]() $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
. Furthermore, the bilinear map
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
. Furthermore, the bilinear map
![]() $(\cdot ,\cdot )_n$
of (8.1) is nondegenerate, and the fundamental matrix
$(\cdot ,\cdot )_n$
of (8.1) is nondegenerate, and the fundamental matrix
![]() $\bigl [\left (\bar \sigma _{w'},\alpha _{w,n}\right )_n\bigr ]_{w,w'}$
is invertible, by Corollary 8.2. Therefore Lemma 8.4 implies both assertions.
$\bigl [\left (\bar \sigma _{w'},\alpha _{w,n}\right )_n\bigr ]_{w,w'}$
is invertible, by Corollary 8.2. Therefore Lemma 8.4 implies both assertions.
The case of general X follows from the finite case by a standard limit argument (see [Reference Neukirch, Schmidt and Wingberg31, Prop. 1.2.5]).
When
![]() $2\leq n\leq p$
we have
$2\leq n\leq p$
we have
![]() $J(n)=\{1,n\}$
(Remark 4.2(1)),
$J(n)=\{1,n\}$
(Remark 4.2(1)),
![]() $j_n(1)=1$
, and
$j_n(1)=1$
, and
![]() $j_n(n)=0$
. In view of Examples 7.1 and 7.2, we deduce the following:
$j_n(n)=0$
. In view of Examples 7.1 and 7.2, we deduce the following:
Corollary 8.6. Suppose that
![]() $2\leq n\leq p$
.
$2\leq n\leq p$
.
-
(a) The
 $\mathbb {F}_p$
-linear space
$\mathbb {F}_p$
-linear space
 $S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
has a basis consisting of:
$S_{\left (n,p\right )}/\left (S_{\left (n,p\right )}\right )^p\left [S,S_{\left (n,p\right )}\right ]$
has a basis consisting of:-
(i) the cosets of
 $x^p$
,
$x^p$
,
 $x\in X$
, and
$x\in X$
, and -
(ii) the cosets of
 $\tau _w$
, where w is a Lyndon word in
$\tau _w$
, where w is a Lyndon word in
 $X^*$
of length n.
$X^*$
of length n.
-
-
(b) The
 $\mathbb {F}_p$
-linear space
$\mathbb {F}_p$
-linear space
 $H^2\left (S/S_{\left (n,p\right )}\right )$
has a basis consisting of:
$H^2\left (S/S_{\left (n,p\right )}\right )$
has a basis consisting of:-
(i) the Bockstein elements
 $\mathrm {Bock}_{p,S/S_{\left (n,p\right )}}\left (\epsilon _{(x),\mathbb {Z}/p}\right )=\alpha _{(x),n}$
,
$\mathrm {Bock}_{p,S/S_{\left (n,p\right )}}\left (\epsilon _{(x),\mathbb {Z}/p}\right )=\alpha _{(x),n}$
,
 $x\in X$
, and
$x\in X$
, and -
(ii) the n-fold Massey product elements
 $\alpha _{w,n}$
, where w is a Lyndon word in
$\alpha _{w,n}$
, where w is a Lyndon word in
 $X^*$
of length n.
$X^*$
of length n.
-
The number of words of a given length in a Hall set H can be expressed in terms of Witt’s necklace function, defined for integers
![]() $i,m\geq 1$
by
$i,m\geq 1$
by
 $$ \begin{align*} \varphi_i(m)=\frac1i\sum_{d\mid i}\mu(d)m^{i/d}. \end{align*} $$
$$ \begin{align*} \varphi_i(m)=\frac1i\sum_{d\mid i}\mu(d)m^{i/d}. \end{align*} $$
Here
![]() $\mu $
is the Möbius function – that is,
$\mu $
is the Möbius function – that is,
![]() $\mu (d)=(-1)^k$
if d is a product of k distinct prime numbers, and
$\mu (d)=(-1)^k$
if d is a product of k distinct prime numbers, and
![]() $\mu (d)=0$
otherwise. We also set
$\mu (d)=0$
otherwise. We also set
![]() $\varphi _i(\infty )=\infty $
. Then the number of words of length i in H is
$\varphi _i(\infty )=\infty $
. Then the number of words of length i in H is
![]() $\varphi _i(\lvert X\rvert )$
[Reference Reutenauer33, Cor. 4.14]. We deduce the following:
$\varphi _i(\lvert X\rvert )$
[Reference Reutenauer33, Cor. 4.14]. We deduce the following:
Corollary 8.7.
-
(a) For every
 $n\geq 2$
, one has
$n\geq 2$
, one has  $$ \begin{align*} \dim_{\mathbb{F}_p}H^2\left(S/S_{\left(n,p\right)}\right)=\sum_{i\in J(n)}\varphi_i(\lvert X\rvert). \end{align*} $$
$$ \begin{align*} \dim_{\mathbb{F}_p}H^2\left(S/S_{\left(n,p\right)}\right)=\sum_{i\in J(n)}\varphi_i(\lvert X\rvert). \end{align*} $$
-
(b) If
 $2\leq n\leq p$
, then
$2\leq n\leq p$
, then
 $\dim _{\mathbb {F}_p}H^2\left (S/S_{\left (n,p\right )}\right )=\lvert X\rvert +\varphi _n(\lvert X\rvert )$
.
$\dim _{\mathbb {F}_p}H^2\left (S/S_{\left (n,p\right )}\right )=\lvert X\rvert +\varphi _n(\lvert X\rvert )$
.
9 Shuffle relations
Recall that the shuffle product
![]() of words u, v was defined in the Introduction. It extends naturally to a bilinear, commutative, and associative product map
of words u, v was defined in the Introduction. It extends naturally to a bilinear, commutative, and associative product map
![]() . The shuffle algebra
. The shuffle algebra
![]() $\operatorname {\mathrm {Sh}}(X)$
on X is the graded
$\operatorname {\mathrm {Sh}}(X)$
on X is the graded
![]() $\mathbb {Z}$
-algebra whose underlying module is the free module on
$\mathbb {Z}$
-algebra whose underlying module is the free module on
![]() $X^*$
(graded by the length of words), and its multiplication is
$X^*$
(graded by the length of words), and its multiplication is
![]() .
.
We define the infiltration product
![]() $u\downarrow v$
of words
$u\downarrow v$
of words
![]() $u=(x_1\dotsm x_r)$
,
$u=(x_1\dotsm x_r)$
,
![]() $v=(x_{r+1}\dotsm x_{r+t})$
in
$v=(x_{r+1}\dotsm x_{r+t})$
in
![]() $X^*$
as follows (see [Reference Chen, Fox and Lyndon4], [Reference Reutenauer33, pp. 134–135]). Consider all maps
$X^*$
as follows (see [Reference Chen, Fox and Lyndon4], [Reference Reutenauer33, pp. 134–135]). Consider all maps
![]() $\sigma \colon \{1,2,\dotsc , r+t\}\to \{1,2,\dotsc , r+t\}$
with
$\sigma \colon \{1,2,\dotsc , r+t\}\to \{1,2,\dotsc , r+t\}$
with
![]() $\sigma (1)<\dotsb <\sigma (r)$
and
$\sigma (1)<\dotsb <\sigma (r)$
and
![]() $\sigma (r+1)<\dotsb <\sigma (r+t)$
, and which satisfy the following weak form of injectivity: If
$\sigma (r+1)<\dotsb <\sigma (r+t)$
, and which satisfy the following weak form of injectivity: If
![]() $\sigma (i)=\sigma (j)$
, then
$\sigma (i)=\sigma (j)$
, then
![]() $x_i=x_j$
. Let the image of
$x_i=x_j$
. Let the image of
![]() $\sigma $
consist of
$\sigma $
consist of
![]() $l_1<\dotsb <l_{m(\sigma )}$
. Then we set
$l_1<\dotsb <l_{m(\sigma )}$
. Then we set
By our assumption,
![]() $x_{\sigma ^{-1}\left (l_i\right )}$
does not depend on the choice of the preimages
$x_{\sigma ^{-1}\left (l_i\right )}$
does not depend on the choice of the preimages
![]() $\sigma ^{-1}(l_i)$
of
$\sigma ^{-1}(l_i)$
of
![]() $l_i$
. We also write
$l_i$
. We also write
![]() $\operatorname {\mathrm {Infil}}(u,v)$
for the set of all such words
$\operatorname {\mathrm {Infil}}(u,v)$
for the set of all such words
![]() $\left (x_{\sigma ^{-1}\left (l_1\right )}\dotsm x_{\sigma ^{-1}\left (l_{m(\sigma )}\right )}\right )$
. Thus
$\left (x_{\sigma ^{-1}\left (l_1\right )}\dotsm x_{\sigma ^{-1}\left (l_{m(\sigma )}\right )}\right )$
. Thus
![]() is the part of
is the part of
![]() $u\downarrow v$
of degree
$u\downarrow v$
of degree
![]() $r+t$
– that is, the partial sum corresponding to all such maps
$r+t$
– that is, the partial sum corresponding to all such maps
![]() $\sigma $
which in addition are bijective. The product
$\sigma $
which in addition are bijective. The product
![]() $\downarrow $
on words extends by linearity to an associative and commutative bilinear map on
$\downarrow $
on words extends by linearity to an associative and commutative bilinear map on
![]() $\mathbb {Z}\langle X\rangle $
.
$\mathbb {Z}\langle X\rangle $
.
There is a well-defined
![]() $\mathbb {Z}_p$
-bilinear map
$\mathbb {Z}_p$
-bilinear map
where
![]() $f_w,g_w$
are the coefficients of f, g, respectively, at w [Reference Reutenauer33, p. 17].
$f_w,g_w$
are the coefficients of f, g, respectively, at w [Reference Reutenauer33, p. 17].
The following connection between the Magnus representation and the infiltration product is proved in the discrete case in [Reference Chen, Fox and Lyndon4, Th. 3.6]. We refer to [Reference Vogel37, Prop. 2.25] and [Reference Morishita30, Prop. 8.16] for the profinite case. Here we view the infiltration and shuffle products as elements of
![]() $\mathbb {Z}\langle X\rangle \subseteq \mathbb {Z}_p\langle X\rangle $
.
$\mathbb {Z}\langle X\rangle \subseteq \mathbb {Z}_p\langle X\rangle $
.
Proposition 9.1. For every
![]() $\emptyset \neq u,v\in X^*$
and every
$\emptyset \neq u,v\in X^*$
and every
![]() $\sigma \in S$
, one has
$\sigma \in S$
, one has
Corollary 9.2. Let
![]() $u,v$
be nonempty words in
$u,v$
be nonempty words in
![]() $X^*$
with
$X^*$
with
![]() $i=\lvert u\rvert +\lvert v\rvert \leq n$
. For every
$i=\lvert u\rvert +\lvert v\rvert \leq n$
. For every
![]() $\sigma \in S_{\left (n,p\right )}$
, one has
$\sigma \in S_{\left (n,p\right )}$
, one has
![]() .
.
Proof. Let w be a word of length
![]() $1\leq k\leq i-1$
. Then
$1\leq k\leq i-1$
. Then
![]() $j_n(k)\geq j_n(i-1)$
, so by Proposition 5.1,
$j_n(k)\geq j_n(i-1)$
, so by Proposition 5.1,
![]() $\epsilon _{w,\mathbb {Z}_p}(\sigma )\in p^{j_n(k)}\mathbb {Z}_p\subseteq p^{j_n(i-1)}\mathbb {Z}_p$
. In particular, this is the case for
$\epsilon _{w,\mathbb {Z}_p}(\sigma )\in p^{j_n(k)}\mathbb {Z}_p\subseteq p^{j_n(i-1)}\mathbb {Z}_p$
. In particular, this is the case for
![]() $w=u$
,
$w=u$
,
![]() $w=v$
, and for
$w=v$
, and for
![]() $w\in \operatorname {\mathrm {Infil}}(u,v)$
of length smaller than i. Since
$w\in \operatorname {\mathrm {Infil}}(u,v)$
of length smaller than i. Since
![]() is the part of
is the part of
![]() $u\downarrow v$
consisting of summands of maximal length i, Proposition 9.1 implies that
$u\downarrow v$
consisting of summands of maximal length i, Proposition 9.1 implies that
![]() .
.
We obtain the following shuffle relations. Here
![]() $X^i$
stands for the set of words in
$X^i$
stands for the set of words in
![]() $X^*$
of length i.
$X^*$
of length i.
Theorem 9.3. Let
![]() $\emptyset \neq u,v\in X^*$
with
$\emptyset \neq u,v\in X^*$
with
![]() $i=\lvert u\rvert +\lvert v\rvert \in J(n)$
. Then
$i=\lvert u\rvert +\lvert v\rvert \in J(n)$
. Then
Proof. As
![]() $2\leq i\in J(n)$
, we have
$2\leq i\in J(n)$
, we have
![]() $(i-1)p^{j_n(i-1)}\geq ip^{j_n(i)}$
, whence
$(i-1)p^{j_n(i-1)}\geq ip^{j_n(i)}$
, whence
![]() $j_n(i-1)>j_n(i)$
.
$j_n(i-1)>j_n(i)$
.
We recall that
is homogenous of degree i. For
![]() $\sigma \in S_{\left (n,p\right )}$
, Corollary 9.2 gives
$\sigma \in S_{\left (n,p\right )}$
, Corollary 9.2 gives

Therefore, by Proposition 8.1,

Now use the fact that
![]() $(\cdot ,\cdot )_n$
is nondegenerate.
$(\cdot ,\cdot )_n$
is nondegenerate.
Given a graded R-algebra
![]() $A=\bigoplus _{i\geq 0} A_i$
, we denote
$A=\bigoplus _{i\geq 0} A_i$
, we denote
![]() $A_+=\bigoplus _{i\geq 1} A_i$
. Let
$A_+=\bigoplus _{i\geq 1} A_i$
. Let
![]() $\text {WD}(A)$
be the R-submodule of A generated by all products
$\text {WD}(A)$
be the R-submodule of A generated by all products
![]() $aa'$
, where
$aa'$
, where
![]() $a,a'\in A_+$
. We call
$a,a'\in A_+$
. We call
![]() $\text {WD}(A)$
the submodule of weakly decomposable elements of A. It is also generated by all products
$\text {WD}(A)$
the submodule of weakly decomposable elements of A. It is also generated by all products
![]() $aa'$
, where
$aa'$
, where
![]() $a,a'\in A_+$
are homogenous. Hence the quotient
$a,a'\in A_+$
are homogenous. Hence the quotient
![]() $A_{\mathrm {indec}}=A/\text {WD}(A)$
has the structure of a graded R-module, which we call the indecomposable quotient of A.
$A_{\mathrm {indec}}=A/\text {WD}(A)$
has the structure of a graded R-module, which we call the indecomposable quotient of A.
Note that
![]() $\text {WD}(A)_0=\text {WD}(A)_1=\{0\}$
, so the graded module morphism
$\text {WD}(A)_0=\text {WD}(A)_1=\{0\}$
, so the graded module morphism
![]() $A\to A_{{\mathrm {indec}}}$
is an isomorphism in degrees
$A\to A_{{\mathrm {indec}}}$
is an isomorphism in degrees
![]() $0$
and
$0$
and
![]() $1$
. For example, when
$1$
. For example, when
![]() $A=R\langle X\rangle $
, one has
$A=R\langle X\rangle $
, one has
![]() $A_{{\mathrm {indec}},0}=R$
,
$A_{{\mathrm {indec}},0}=R$
,
![]() $A_{{\mathrm {indec}},1}$
is the free R-module on the basis X, and
$A_{{\mathrm {indec}},1}$
is the free R-module on the basis X, and
![]() $A_{{\mathrm {indec}},i}=0$
for all
$A_{{\mathrm {indec}},i}=0$
for all
![]() $i\geq 2$
.
$i\geq 2$
.
When
![]() $A=\operatorname {\mathrm {Sh}}(X)$
is the shuffle algebra, we recover the module
$A=\operatorname {\mathrm {Sh}}(X)$
is the shuffle algebra, we recover the module
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}$
as defined in the Introduction. The following key fact was proved in [Reference Efrat9, Prop. 6.3]. It is based on a construction by Radford [Reference Radford32] and Perrin and Viennot of a basis of
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}$
as defined in the Introduction. The following key fact was proved in [Reference Efrat9, Prop. 6.3]. It is based on a construction by Radford [Reference Radford32] and Perrin and Viennot of a basis of
![]() $\mathbb {Z}\langle X\rangle $
, which arises from the decomposition of words in
$\mathbb {Z}\langle X\rangle $
, which arises from the decomposition of words in
![]() $X^*$
into Lyndon words.
$X^*$
into Lyndon words.
Proposition 9.4. Suppose that
![]() $1\leq n<p$
. Then the images of the Lyndon words of length n span
$1\leq n<p$
. Then the images of the Lyndon words of length n span
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}\otimes (\mathbb {Z}/p)$
as an
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}\otimes (\mathbb {Z}/p)$
as an
![]() $\mathbb {F}_p$
-linear space.
$\mathbb {F}_p$
-linear space.
In fact, in [Reference Efrat9, Th. 7.3(b)] it is proved that these images form a linear basis of
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}\otimes (\mathbb {Z}/p)$
, but we shall not use this stronger result.
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}\otimes (\mathbb {Z}/p)$
, but we shall not use this stronger result.
Theorem 9.5. Suppose that
![]() $n\geq 2$
. The map
$n\geq 2$
. The map
![]() $w\mapsto \alpha _{w,n}$
induces an epimorphism of
$w\mapsto \alpha _{w,n}$
induces an epimorphism of
![]() $\mathbb {F}_p$
-linear spaces
$\mathbb {F}_p$
-linear spaces
 $$ \begin{align*} \left(\bigoplus_{i\in J(n)}\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},i}\right)\otimes(\mathbb{Z}/p)\to H^2\left(S/S_{\left(n,p\right)}\right). \end{align*} $$
$$ \begin{align*} \left(\bigoplus_{i\in J(n)}\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},i}\right)\otimes(\mathbb{Z}/p)\to H^2\left(S/S_{\left(n,p\right)}\right). \end{align*} $$
Proof. For
![]() $i\in J(n)$
, the map
$i\in J(n)$
, the map
![]() $X^i\to H^2\left (S/S_{\left (n,p\right )}\right )$
,
$X^i\to H^2\left (S/S_{\left (n,p\right )}\right )$
,
![]() $w\mapsto \alpha _{w,n}$
, extends by linearity to a
$w\mapsto \alpha _{w,n}$
, extends by linearity to a
![]() $\mathbb {Z}$
-module homomorphism
$\mathbb {Z}$
-module homomorphism
By Theorem 9.3,
![]() for any nonempty words
for any nonempty words
![]() $u,v\in X^*$
with
$u,v\in X^*$
with
![]() $i=\lvert u\rvert +\lvert v\rvert $
. Consequently,
$i=\lvert u\rvert +\lvert v\rvert $
. Consequently,
![]() $\Phi _i$
factors via
$\Phi _i$
factors via
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},i}$
, and induces an
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},i}$
, and induces an
![]() $\mathbb {F}_p$
-linear map
$\mathbb {F}_p$
-linear map
where
![]() $\bar \Phi _i(\bar w)=\alpha _{w,n}$
for
$\bar \Phi _i(\bar w)=\alpha _{w,n}$
for
![]() $w\in X^i$
. Since the
$w\in X^i$
. Since the
![]() $\alpha _{w,n}$
, where w ranges over all Lyndon words of an arbitrary length
$\alpha _{w,n}$
, where w ranges over all Lyndon words of an arbitrary length
![]() $i\in J(n)$
, form an
$i\in J(n)$
, form an
![]() $\mathbb {F}_p$
-linear basis of
$\mathbb {F}_p$
-linear basis of
![]() $H^2\left (S/S_{\left (n,p\right )}\right )$
(Theorem 8.5(b)), we obtain an epimorphism
$H^2\left (S/S_{\left (n,p\right )}\right )$
(Theorem 8.5(b)), we obtain an epimorphism
 $$ \begin{align*} \bigoplus_{i\in J(n)}\bar\Phi_i\colon\left(\bigoplus_{i\in J(n)}\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},i}\right)\otimes(\mathbb{Z}/p)\to H^2\left(S/S_{\left(n,p\right)}\right). \\[-40pt]\end{align*} $$
$$ \begin{align*} \bigoplus_{i\in J(n)}\bar\Phi_i\colon\left(\bigoplus_{i\in J(n)}\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},i}\right)\otimes(\mathbb{Z}/p)\to H^2\left(S/S_{\left(n,p\right)}\right). \\[-40pt]\end{align*} $$
We now obtain the Main Theorem from the Introduction:
Theorem 9.6. Suppose that
![]() $2\leq n<p$
. Then there is an isomorphism of
$2\leq n<p$
. Then there is an isomorphism of
![]() $\mathbb {F}_p$
-linear spaces
$\mathbb {F}_p$
-linear spaces
 $$ \begin{align} \left(\bigoplus_{x\in X}\mathbb{Z}/p\right)\oplus\Bigl(\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},n}\otimes(\mathbb{Z}/p)\Bigr)\xrightarrow{\sim} H^2\left(S/S_{\left(n,p\right)}\right). \end{align} $$
$$ \begin{align} \left(\bigoplus_{x\in X}\mathbb{Z}/p\right)\oplus\Bigl(\operatorname{\mathrm{Sh}}(X)_{{\mathrm{indec}},n}\otimes(\mathbb{Z}/p)\Bigr)\xrightarrow{\sim} H^2\left(S/S_{\left(n,p\right)}\right). \end{align} $$
Specifically, this isomorphism maps a generator
![]() $1_x$
of the
$1_x$
of the
![]() $\mathbb {Z}/p$
-summand at
$\mathbb {Z}/p$
-summand at
![]() $x\in X$
to
$x\in X$
to
![]() $\mathrm {Bock}_{p,S/S_{\left (n,p\right )}}\left (\epsilon _{(x),\mathbb {Z}/p}\right )$
, and maps the image
$\mathrm {Bock}_{p,S/S_{\left (n,p\right )}}\left (\epsilon _{(x),\mathbb {Z}/p}\right )$
, and maps the image
![]() $\bar w$
of a word
$\bar w$
of a word
![]() $w\in X^*$
of length n to the n-fold Massey product element
$w\in X^*$
of length n to the n-fold Massey product element
![]() $\alpha _{w,n}$
.
$\alpha _{w,n}$
.
Proof. By Remark 4.2(1),
![]() $J(n)=\{1,n\}$
. Therefore, Theorem 9.5 gives an epimorphism as in (9.2). The generators
$J(n)=\{1,n\}$
. Therefore, Theorem 9.5 gives an epimorphism as in (9.2). The generators
![]() $1_x$
and the images
$1_x$
and the images
![]() $\bar w$
of words w of length n are mapped as specified, by Examples 7.1 and 7.2.
$\bar w$
of words w of length n are mapped as specified, by Examples 7.1 and 7.2.
The generators
![]() $1_x$
,
$1_x$
,
![]() $x\in X$
, clearly span
$x\in X$
, clearly span
![]() $\bigoplus _{x\in X}\mathbb {Z}/p$
, and by Proposition 9.4, the images
$\bigoplus _{x\in X}\mathbb {Z}/p$
, and by Proposition 9.4, the images
![]() $\bar w$
of the Lyndon words w in
$\bar w$
of the Lyndon words w in
![]() $X^*$
of length n span
$X^*$
of length n span
![]() $\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}\otimes (\mathbb {Z}/p)$
. Together they form a spanning set of the left-hand side of the epimorphism (9.2), which is mapped to a linear basis of the right-hand side (Corollary 8.6). It follows that this spanning set is a linear basis, and the map (9.2) is an isomorphism.
$\operatorname {\mathrm {Sh}}(X)_{{\mathrm {indec}},n}\otimes (\mathbb {Z}/p)$
. Together they form a spanning set of the left-hand side of the epimorphism (9.2), which is mapped to a linear basis of the right-hand side (Corollary 8.6). It follows that this spanning set is a linear basis, and the map (9.2) is an isomorphism.
Acknowledgments
I thank the referee for his/her comments and helpful suggestions. This research was supported by the Israel Science Foundation (grant 569/21).
Competing Interest
None.