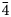Theuerdankite, Ag₃AsO₄, a new mineral from the Alter Theuerdank Mine, St. Andreasberg, Germany

Abstract

The new mineral theuerdankite, ideally Ag₃AsO₄, was found in the Alter Theuerdank Mine, Beerberg, St. Andreasberg, Goslar District, Lower Saxony, Germany. Theuerdankite occurs as aggregates of anhedral grains up to 3 mm in size, growing in cavities of strongly supergene-weathered material consisting of native silver and chlorargyrite (but with calcite present). It is dark violet, changing to reddish and black when exposed to the air and light. It has a grey to violet grey streak; when readily fresh, its streak is brownish-red. The Mohs hardness is ~2. It is brittle with no observable cleavage or parting and with a conchoidal fracture. The calculated density is 6.620 g⋅cm^–3. In reflected light, theuerdankite is dark grey with a pinkish tint, with no observable bireflectance, pleochroism, or anisotropy. It shows dark red internal reflections. The reflectance values for wavelengths recommended by the Commission on Ore Mineralogy of the International Mineralogical Association are (R, %): 13.3 (470 nm), 12.8 (546 nm), 12.7 (589 nm) and 12.5 (650 nm). The empirical formula (based on 4 apfu) is Ag_3.00As_1.00O₄. Theuerdankite is cubic, space group P$\bar{4}$3n, a = 6.144(2) Å, V = 231.93(13) ų and Z = 2. The six strongest powder X-ray diffraction lines are [d_obs in Å, (I) hkl]: 3.0736, (22) 200; 2.7502, (100) 210; 2.5106, (55) 211; 1.7050, (36) 320; 1.6249, (44) 321; and 1.3412, (17) 421. The crystal structure of theuerdankite (R₁ = 1.69% for 519 reflections having I > 3σ(I)), is isotypic to those of synthetic Ag₃AsO₄ and Ag₃PO₄. The Gram–Charlier development describing the higher-order tensors representing the atomic displacement parameters of the silver atom was implemented, documenting that silver tends to behave anharmonically in the theuerdankite structure at room temperature.

Introduction

Theuerdankite, ideally Ag₃AsO₄, is a new silver mineral from the famous historic mining region of St. Andreasberg in Lower Saxony, Germany. It is named after the type locality, the Alter Theuerdank Mine. The new mineral and its name (symbol Td) have been approved by the Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2023–009, Plášil et al., 2023). The holotype specimen (polished section) of theuerdankite is deposited in the collections of the Department of Mineralogy and Petrology, National Museum in Prague, Cirkusová 1740, 193 00 Prague 9, Czech Republic under the catalogue number P1P 59/2022. Here, we report on its description, including crystal structure refinement using a Gram–Charlier development describing the thermal movement of the silver atom in the crystal structure, which vibrates anharmonically around its equilibrium position. We also append a discussion on the proper handling of the diffraction data and the refinement.

Occurrence

Theuerdankite was found on a single specimen originating from the Alter Theuerdank Mine, Beerberg, St Andreasberg, Braunlage, Goslar District, Lower Saxony, Germany (51°42' 29''N, 10°31'41''E). This mine is among the important mines in the St. Andreasberg mining district and it is famous for the rich findings of the so-called ‘buttermilch-erz’ = ore consisting of chlorargyrite. We refer to the paper by Schnorrer et al. (2009) for details on the occurrence and geology. Associated minerals within the specimen studied are chlorargyrite, native silver and calcite. Theuerdankite is most probably of supergene origin but could also be late hydrothermal if these fluids were oxidising enough to convert As in the primary minerals to arsenates.

Physical and optical properties

Theuerdankite occurs as irregular aggregates up to 3 mm in size (Fig. 1), growing in cavities of strongly supergene-weathered material consisting of native silver and chlorargyrite. Its colour is dark violet, changing to reddish and black when exposed to the air. It darkens when exposed to light. It has a grey to violet grey streak; when fresh, its streak is brownish-red. It is non-fluorescent in SW and LW ultraviolet light. The Mohs hardness is estimated at ~2 based on scratch tests. Theuerdankite is brittle; no cleavage and no parting were observed. The fracture is conchoidal. The calculated density (Z = 2), based on the empirical formula and the unit-cell parameters refined from single-crystal X-ray diffraction data, is 6.620 g⋅cm^–3. Theuerdankite is dark grey with pinkish tints in reflected light with no visible bireflectance and no pleochroism; no anisotropy has been observed. There are dark red internal reflections, visible around fractures, and inclusions of native silver (Fig. 2). Reflectance values measured in air using a spectrophotometer MSP400 Tidas at Leica microscope, with a 20× objective, are given in Table 1 and shown in Fig. 3.

Figure 1. Theuerdankite (1) from the type locality associated with native silver (2) and chlorargyrite (3) in the cavity of strongly supergene-weathered material; Field of view: 3.6 mm; holotype specimen (P1P 59/2022); photo M. Gross.

Figure 2. Dark-red internal reflections in theuerdankite visible especially around fractures and inclusions of native silver (white); field of view: 700 μm; photo in reflected light (partly crossed polars) by J. Sejkora.

Table 1. Reflectance data for theuerdankite*.

* The reference wavelengths required by the Commission on Ore Mineralogy (COM) are given in bold.

Figure 3. Reflectivity curve for theuerdankite from the Alter Theuerdank Mine, St Andreasberg, Germany.

Chemical composition

Quantitative chemical analyses were carried out using a Cameca SX100 electron microprobe (WDS mode, 15 kV, 5 nA and 10 μm beam diameter) at the National Museum Prague, Czech Republic. The following standards and X-ray lines were used to minimise line overlaps: Ag (AgLα), chalcopyrite (CuKα), clinoclase (AsLα) and fluorapatite (PKα). Peak counting times were 20 s for all elements and 10 s for each background. The results obtained (average of 16 spot analyses) are given in Table 2. Contents of other elements with atomic numbers higher than that of C (Z = 6) are below detection limits. Matrix correction by PAP software (Pouchou and Pichoir, 1985) was applied to the data. The calculated empirical formula of theuerdankite based on 4 atoms per formula unit and 4 O atoms is Ag_3.00As_1.00O₄. The ideal formula for theuerdankite is Ag₃AsO₄, which requires Ag₂O 75.15 and As₂O₅ 24.85, a total of 100.00 wt.%. It is soluble in a 25% ammonia solution and decomposes when heated up in a melting point tube without the evolution of H₂O.

Table 2. Chemical composition (n = 12) (in wt.%) of theuerdankite.

S.D. – standard deviation

Raman spectroscopy

The Raman spectra of theuerdankite were collected in the range 50–4000 cm^–1 using a DXR dispersive Raman Spectrometer (Thermo Scientific) mounted on a confocal Olympus microscope. The Raman signal was excited by an unpolarised green 532 nm solid state, diode-pumped laser and detected by a CCD detector. The experimental parameters were: 100× objective, 10 s exposure time, 100 exposures, 50 μm slit spectrograph aperture and 1 mW laser power level. The eventual thermal damage of the measured points was excluded by visual inspection of the excited surface after measurement, observation of possible decay of spectral features at the start of excitation, and checking for a thermal downshift of Raman lines. The instrument was set up using a software-controlled calibration procedure using multiple neon emission lines (wavelength calibration), multiple polystyrene Raman bands (laser frequency calibration), and standardised white-light sources (intensity calibration). Spectral manipulations were performed using the Omnic 9 software (Thermo Scientific).

The Raman spectrum of theuerdankite is given in Fig. 4. The main bands observed are (in wavenumbers): 816, 787, 408, 337 and 82 cm^–1. The most prominent very strong Raman band at 787 cm^–1 with a shoulder at 816 cm^–1 is attributed to overlapping ν₁ (AsO₄)^3– symmetric stretching and ν₃ (AsO₄)^3– antisymmetric stretching vibrations. The Raman band at 408 cm^–1 is attributed to the ν₄ (AsO₄)^3– bending vibration. The Raman band at 337 cm^–1 is related to the ν₂ (AsO₄)^3– bending vibrations and those below 200 cm^–1 to lattice modes (Vansant et al., 1973; Nakamoto, 2009; Frost et al., 2010; Čejka et al., 2011). The observed bands are comparable to those in the infrared absorption spectrum of the synthetic Ag₃AsO₄ — 825, 785, 405 and 330 cm^–1 (Hájek et al., 1979; Muck et al., 1980).

Figure 4. Raman spectrum of theuerdankite.

X-ray crystallography and structure refinement

Powder X-ray diffraction (XRD) data of theuerdankite were obtained using a pseudo-Gandolfi scan on a XtaLAB Synergy R, DW system equipped with the HyPix-Arc150 detector, using monochromatic MoKα radiation from the microfocus rotating anode. The positions and intensities of the diffraction peaks were found and refined using the Pearson VII profile-shape function of the ZDS program package (Ondruš, 1993). The unit-cell parameters were refined by the least-squares program of Burnham (1962). The powder X-ray diffraction data of theuerdankite are given in Table 3. The refined unit-cell parameter (for the space group P $\bar{4}$3n) is a = 6.1448(3) Å, with V = 231.01(2) ų and Z = 2.

Table 3. Powder X-ray diffraction data (d in Å) for theuerdankite; the six strongest diffractions are reported in bold.

*I_calc.; *d_calc. – Intensity and d _hkl (in Å) calculated using the software PowderCell2.3 (Kraus and Nolze, 1996) on the basis of the structural model given in Tables 4 and 5. Only reflections with I _calc > 0.5 are listed.

Table 4. Summary of data collection and refinements (harmonic/anharmonic) for theuerdankite.

Table 5. Atom positions, equivalent displacement parameters (in Ų) and bond-valence sums (BVS; in valence units) for theuerdankite.

Single-crystal XRD data for theuerdankite were collected on an XtaLAB Synergy, DW system equipped with the HyPix-Arc150 detector, using monochromatic MoKα radiation from the microfocus rotating anode from the same crystal as powder XRD data were collected. A fragment of the single crystal with approximate dimensions 85 × 48 × 28 μm was mounted on a glass fibre and analysed. The complete data set (100% to the resolution of 0.4 Å) of the high-redundancy (>6) was collected using ω-scans (frame width of 0.5° and a counting time of 4 seconds per frame). Data reduction was performed using CrysAlisPro Version 1.171.43.111 (Rigaku, 2024). The data were corrected for Lorentz factor and absorption (multi-scan, ABSPACK scaling algorithm; Rigaku, 2024).

The structure of theuerdankite was solved from the intensity data using the intrinsic phasing by the SHELXT program (Sheldrick, 2015) and refined using the software Jana2020 (Petříček et al., 2023). The structure was refined as an inversion twin, and extinction (isotropic; Becker and Coppens, 1974) was also refined during the final stages of the refinement (Table 4). We used a Wilson modification to the least-square routine (weights) to avoid the statistical bias (Wilson, 1976). We employed the third-order anharmonic Gram–Charlier development (see for instance Volkov et al., 2023) to describe the Debye–Waller factors for the Ag atoms, which improved the refinement considerably (see the Discussion). Refinement details are given in Table 4, atomic parameters (including atomic displacement parameters (ADP) and bond-valence sums calculated using parameters reported by Gagné and Hawthorne, 2015) are given in Table 5 and Table 6; the coefficients of the third-order Gram–Charlier development are given in the Supplementary crystallographic information file (cif, see below); selected interatomic distances are reported in Table 7. The Vesta program (Momma and Izumi, 2011) was used to plot the electron density and the isosurface for ADPs of silver atoms.

Table 6. Anisotropic displacement parameters (in Ų) for atoms in the theuerdankite structure.

Table 7. Selected interatomic distances (in Å) in theuerdankite.

The structure of theuerdankite contains AsO₄ tetrahedra (Table 5) whose centres lie on lattice points of a b.c.c. lattice. The Ag1 atom occupies the 6c Wyckoff position, surrounded by four O atoms at a distance of 2.372(2) Å. The displacement of the Ag atom is slightly anisotropic with the general direction of vibration perpendicular to a plane formed approximately by four symmetrically related O1 atoms and assumes a pear-like shape (Fig. 6).

Related minerals and structures

The structure of theuerdankite is isotypic to that of synthetic Ag₃PO₄ (Ng et al., 1978) and synthetic Ag₃AsO₄ (Weil, 2003). The electronic structure of the synthetic analogue of theuerdankite has been investigated (e.g. Reunchan et al., 2016; Li and Chen, 2017) due to its promising photocatalytic properties.

As a chemically related mineral, tetragonal tillmannsite, (Ag₃Hg)(V,As)O₄ (Sarp et al., 2003) could be considered. However, theuerdankite is structurally wholly distinctive. Tillmannsite contains isolated (V,As)O₄ tetrahedra and (Ag₃Hg) tetrahedral clusters. Clusters are specific for the disordered distribution of Ag and Hg atoms, which is a distinctive feature over chemically related synthetic compounds AgHg₂PO₄ and AgHg₂AsO₄ (Masse et al., 1978) where Ag and Hg atoms are completely ordered and form the dimers O₂Ag–AgO₂ and O₃Hg–HgO₃. In tillmannsite, each (Ag,Hg) metallic atom is coordinated by three metallic neighbours and by three oxygens.

Also, cubic rudabányaite, (Ag₂Hg₂)(AsO₄)Cl (Effenberger et al., 2019) can be viewed as a related mineral species but is structurally completely different. Its crystal structure is a framework based on by two crystallographically different [M ₄]⁴⁺ cluster cations forming tetrahedra (M = (Ag,Hg) with a ratio Ag:Hg ~ 1:1), with no evidence for ordering between the Ag and Hg atoms. Small amounts of the M atoms are displaced by ~0.5 Å. Topologically, the barycentres of the [M ₄]⁴⁺ clusters and the As atom positions of the crystal structure of rudabányaite form a cubic primitive lattice with a’ = 1/2a = 8.68 Å; half of the voids are occupied by Cl atoms.

Discussion

Harmonic vs. anharmonic refinement and adequate data handling

Initially, the structure of theuerdankite was refined using a harmonic approach to the displacement parameters of all atoms, thus described by the thermal ellipsoids. The final refinement converged smoothly (including isotropic extinction and inversion twin) to somewhat acceptable R-factors (comparison of harmonic and anharmonic refinement given in Table 4). However, one may suggest that the goodness-of-fit (GoF) from the harmonic refinement (GoF = 2.83 for all reflections) is rather high for a correct model and a reliable refinement. Nevertheless, these issues warrant further discussion. The standard approach to the goodness-of-fit and, consequently, a weighting scheme for the refinement is somewhat misleadingly applied by many users. The most widely used program for the structure refinement from the single-crystal X-ray data, SHELXL (Sheldrick, 2008), forces (if not changed by the user) the refinement to achieve a GoF value close to unity, namely by changing (refining) the weights. In contrast to this approach, the program Jana2020 (Petříček et al., 2023) does not refine the weighting scheme but bases it purely on the experimental expectations (see _refine_ls_weighting_details in the cif) that does not force GoF to be one. Therefore, in general, the GoF values obtained by Jana are usually larger than most of those reported by the SHELX program. The GoF values in Jana, however, do have a physical meaning. For example, if the final reported GoF is >2.0, it does not automatically mean that the model is incorrect or entirely wrong. It just means that there are some features within a given dataset that the current model 1) does not describe/fit data well enough, or 2) there are systematic errors inherent to the diffraction data (from the measurement, for instance). Such undescribed features can include disorder (both positional or occupational), hidden twinning, modulation, or deformation of electron density (charge-density studies). Therefore, this approach also requires a careful and meaningful handling and evaluation of the diffraction data. In Jana, there are several ways of data handling, including different schemes and approaches to averaging the reflection file for refinement (for details, see Petříček et al., 2014, 2023). Here, we used the refinement file obtained by averaging measured reflections using Poisson statistics. We used a refined instability factor value (= 0.010409), close to the most typical value of instability factor tested over the years of the Jana program development, which is 0.01 for the ‘non problematic’ datasets. The actual value of the instability factor for the given diffraction dataset is deduced during the merging of reflections. The instability factor corrects the sigma values of individual/merged reflections obtained from the experimental reflection file provided by the diffractometer/data reduction program, such as they are fitted to the values obtained from merging statistics (Poisson). We recommend using the refined value of the instability factor for highly redundant datasets with expected reliable merging statistics. For comparison, we present here difference-Fourier maps obtained from the harmonic refinements with different weights (Fig. 5a–c). It is apparent how the choice of the ‘proper’ weights affects the results of the refinement (and in the worst case, the wrong choice of the weights can lead to biased refinement and interpretation). Finally, we relied on a refined value of the instability factor (corresponding map displayed in Fig. 5b) and used it for the final refinement of the structure with an anharmonic approach to the atomic displacement parameters of silver (using a Gram–Charlier development). The final refinement converged to R ₁ = 1.69% for 519 observed reflections and GoF of 1.54. The final difference-Fourier map is provided in Fig. 6a; the highest residual density is located around the silver atom (Fig. 6b). For comparison, the refinement with instability coefficient = 0.08 (overestimated!) would lead, in the case of anharmonic refinement, to R ₁ = 2.31% for 519 observed reflections and a (alarming!) goodness-of-fit = 0.76 with corresponding difference-Fourier electron density of 0.56 and –0.6 e^–/ų.

Figure 5. Difference-Fourier maps from the crystal structure refinements of theuerdankite using distinct weights (given) and harmonic approach to the ADP of silver. Colour scheme: Ag = pale blue, As = green, O = red; solid lines = positive contours, dashed lines = negative contours; numbers (pale blue) = highest electron density (e ^–/ų). (a) Refinement relying on statistics only returned a rather ‘noisy’ difference map with too many features. (b) Refinement using a refined value of the instability factor provides a less noisy and more ‘useful’ difference-Fourier map. (c) Refinement with overestimated weights returns unrealistically ‘nearly clean’ Fourier map and, accordingly, a low GoF. The selected weights for the final refinement were those used in (b).

Figure 6. Difference-Fourier map from the final refinement of theuerdankite structure using an anharmonic approach to the ADP of silver. The colour scheme is the same as in the previous figure; the highest electron density is given in e ^–/ų. (a) The Difference-Fourier map from the final refinement and (b) its 3D representation was done in the Vesta program (Momma and Izumi, 2011). Thermal ellipsoids given at the 75% probability level. Residual positive electron density is displayed in yellow colour (isosurface).

Silver atoms seem to vibrate somewhat anharmonically (Fig. 7) in the theuerdankite structure at room temperature, based on currently obtained high-resolution X-ray diffraction data. Investigating the silver behaviour as a function of temperature would be thus very interesting. Nevertheless, this is beyond the scope of this paper and shall be subject to further studies.

Figure 7. Representation of the anharmonic behaviour of the ADP of silver at room temperature in the crystal structure of theuerdankite as obtained from the non-harmonic refinement of the displacement parameters using JPDF maps.

The conditions of formation

The assemblage of native silver, chlorargyrite, calcite and theuerdankite provides only limited clues about the conditions of the formation of the new mineral. Assuming that these minerals formed together, the presence of silver and chlorargyrite suggests that the redox conditions were near the Ag⁰/Ag⁺ redox boundary. The presence of calcite suggests that the solutions were near-neutral.

As chlorargyrite is a fairly common secondary silver mineral, it can be asked if theuerdankite is indeed rare or if it is simply overlooked. In the absence of arsenates other than theuerdankite, no information about the activity of As(V) species in the aqueous solution can be extracted. The solubility of Ca arsenates (e.g. haidingerite) is too high and they are not a part of the observed mineral assemblage.

Thermodynamic properties of the synthetic Ag₃AsO₄ are known. Wagman et al. (1982) list Δ_fG^o = –542.6 kJ/mol without references to the original source. Using the appropriate auxiliary data, the solubility constant log K _sp for Ag₃AsO₄ is

$${\rm A}{\rm g}_3{\rm As}{\rm O}_4\to 3{\rm A}{\rm g}^ + { + } {\rm As}{\rm O}_4^{3\ndash } , \;{\rm log}\;K_{{\rm sp}} = \ndash 22.13$$

Wagman et al. (1982) also provided Δ_fG^o values for Ag₃PO₄, Ag₂SO₄, and AgCl. Inserting all these data into the thermodynamic database of the PHREEQC code (Parkhurst and Appelo, 1999), some information can be extracted from available data on mine-drainage (MD) waters. Because Ag is rarely analysed, only 20 analyses from almost 1200 analyses in our collection of MD waters yielded saturation indices for the Ag phases. Figure 8a shows that the saturation indices (SI) for theuerdankite are consistently much lower than those of chlorargyrite. The difference is caused by the abundance of Cl^– as an anion in most waters. In fact, it is interesting that the SI values for chlorargyrite scatter around 0, meaning that this mineral controls Ag concentrations in the oxidised portions of ore bodies. From these limited data, it seems that theuerdankite can only form if the solutions initially contain Ag in excess of Cl (in molar proportions), such that the Cl concentrations are significantly depressed by the precipitation of AgCl. Hence, theuerdankite can be expected in secondary ores with abundant chlorargyrite and with some source of arsenate. Reduction of Ag⁺ from the solution and precipitation of secondary native silver will not favour the formation of theuerdankite because it removes Ag, not Cl, from the solution.

Figure 8. (a) Saturation indices for chlorargyrite (diamonds) and theuerdankite (circles) in a range of pH values in mine-drainage waters. (b) Box-and-whiskers diagrams that compare saturation indices of four Ag phases in mine-drainage waters. Boxes show the first and third quartile, the horizontal line the median, and the whiskers the total data range. Data in both (a) and (b) calculated with PHREEQC (Parkhurst and Appelo, 1999), for details see text.

Calculation of the saturation indices of the other phases (Fig. 8b) shows that the occurrence of Ag₃PO₄ is even less probable than that of Ag₃AsO₄. The saturation indices are even lower, and such a potentially new mineral could only form in environments rich in chlorargyrite but unusually poor in arsenate. On the other hand, the saturation indices of Ag₂SO₄ are quite high but the availability of sulfate can be easily limited by precipitation of common secondary sulfates such as gypsum.