Near-wall hydrodynamic slip triggers swimming state transition of micro-organisms

Abstract

The interaction of motile micro-organisms with a nearby solid substrate is a well-studied phenomenon. However, the effects of hydrodynamic slippage on the substrate have received little attention. In the present study, within the framework of the squirmer model, we impose a tangential velocity at the swimmer surface as a representation of the ciliary propulsion, and subsequently obtain an exact solution of the Stokes equation based on a combined analytical–numerical approach. We illustrate how the near-wall swimming velocities are non-trivially altered by the interaction of wall slip and hydrodynamic forces. We report a characteristic transition of swimming trajectories for both puller- and pusher-type microswimmers by hydrodynamic slippage if the wall slip length crosses a critical value. In the case of puller microswimmers that are propelled by a breaststroke-like action of their swimming apparatus ahead of their cell body, the wall slip can cause wall-bound trapping swimming states, as either periodic or damped periodic oscillations, which would otherwise escape from a no-slip wall. The associated critical slip length has a non-monotonic dependence on the initial orientation of the swimmer, which is represented by novel phase diagrams. Pushers, which get their propulsive thrust from posterior flagellar action, also show similar swimming state transitions, but in this case the wall-slip-mediated reorientation dynamics and the swimming modes compete in a different fashion from that of the pullers. Although neutral swimmers lack a sufficient reorientation torque to exhibit any wall-bound trajectory, their detention time near the substrate can be significantly increased by tailoring the extent of hydrodynamic slippage at the nearby wall. The present results pave the way for understanding the motion characteristic of biological microswimmers near confinements with hydrophobic walls or strategize the design of microfluidic devices used for sorting and motion rectification of artificial swimmers by tailoring their surface wettability.

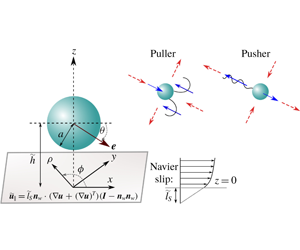
1 Introduction

Microswimmers encountering a confining geometry are common occurrences in a plethora of biological scenarios, such as the marine ecosystem, animal bodies as well as in controlled microfluidic lab-on-a-chip devices (Denissenko et al. 2012; Bechinger et al. 2016). One of the most important practical applications of the surface–micro-organism interaction is bacterial entrapment near surfaces, which is regarded as an essential step during biofilm formation (Costerton et al. 1987). In addition, a confining surface has been found to cause a host of intriguing phenomena, ranging from directional circular motion of motile cells near a solid surface or an air–liquid interface (Lauga et al. 2006; Lemelle et al. 2010; Di Leonardo et al. 2011), scattering of Chlamydomonas algae cells (Molaei et al. 2014), suppression of the tumbling motion of bacteria Escherichia coli (Kantsler et al. 2013) to pairwise dancing of Volvox (Drescher et al. 2011), etc. Such elemental near-surface behaviour of motile cells is found to affect various biophysical activities, such as guidance of sperm cells through the female oviduct (Guidobaldi et al. 2015; Ishimoto & Gaffney 2015), and also crucially affects the process of bacterial infection (Harkes, Dankert & Feijen 1992). With recent advancement of microfluidics techniques, different artificial microswimmers have been successfully fabricated with promising applications, ranging from biochemical sensing, targeted drug delivery to environmental remediation (Duan et al. 2015; Campuzano et al. 2017; Richard, Simmchen & Eychmüller 2018; Poddar, Bandopadhyay & Chakraborty 2019). The interfacial properties of the microfluidic chips can be exploited to gain control over the design of such synthetic microswimmers (Das et al. 2015; Simmchen et al. 2016). In a recent experimental study, Ketzetzi et al. (2020) observed an enhanced swimming speed of spherical self-diffusiophoretic swimmers near hydrophobic substrates.

Inspired by their fascinating trends of near-surface swimming, different theoretical models of microswimmers have been proposed to physically describe their kinematics of motion (Berke et al. 2008; Or & Murray 2009; Zargar, Najafi & Miri 2009; Shum, Gaffney & Smith 2010; Crowdy 2011; Spagnolie & Lauga 2012; Ishimoto & Gaffney 2013; Li & Ardekani 2014; Spagnolie et al. 2015; Mathijssen et al. 2016; Pimponi et al. 2016; Daddi-Moussa-Ider et al. 2018; Desai, Shaik & Ardekani 2018; Kuron et al. 2019; Walker et al. 2019). Employing a force-dipole swimmer model, Berke et al. (2008) was able to explain the high concentration of bacteria E. coli near glass surfaces as a consequence of hydrodynamic attraction and wall-parallel reorientation of the swimmer by its image. Although hydrodynamic attraction enhances accumulation of pushers near walls, simulations and experiments reported in the literature revealed that different microswimmers adhere to the surface even in the absence of hydrodynamics (Li & Tang 2009; Tailleur & Cates 2009; Li et al. 2011; Elgeti & Gompper 2013; Kantsler et al. 2013). Motile micro-organisms such as Opalina, Volvox and Paramecium have been widely modelled by considering a deformable spherical cell body with external appendages such as cilia or flagella on them performing small-amplitude periodic beating and causing a bulk streaming of their cell surface. In the absence of inertial effects, these organisms show a force-free swimming (Lauga & Powers 2009). These model microswimmers, popularly known as ‘squirmers’ (Lighthill 1952; Blake 1971), have been used to understand a variety of physical phenomena, which include but are not limited to hydrodynamic interaction of two microswimmers (Ishikawa, Simmonds & Pedley 2006), diffusion and suspension rheology (Ishikawa & Pedley 2007), nutrient uptake (Magar & Pedley 2005), rheotaxis (Uspal et al. 2015a ) and density stratification of the suspending medium on the vertical motion of the microswimmer (Doostmohammadi, Stocker & Ardekani 2012). Spherical squirmers and their variants have also been used to analyse the microswimmer behaviour near confinements (Spagnolie & Lauga 2012; Ishimoto & Gaffney 2013; Li & Ardekani 2014; Yazdi & Borhan 2017).

The wettability of the confining substrate can severely influence the near-wall flow and the interfacial friction of the fluid, leading to interesting consequences at the micro- and nanoscale (Chakraborty 2008; Pati, Som & Chakraborty 2013; Bakli & Chakraborty 2015, 2019; Das et al. 2015; Maduar et al. 2015; Bandyopadhyay et al. 2019; Dey, Saha & Chakraborty 2020). This is characterized by slip length, defined as the extrapolation distance below the surface where the tangential fluid velocity would vanish. Hydrophilic surfaces, in contact with aqueous solutions, give rise to a negligible hydrodynamic slippage, while the slip length lies in the range of a few tens of nanometres for smooth hydrophobic surfaces (Huang et al. 2008; Bocquet & Charlaix 2010). On the other hand, the presence of depleted, low-viscosity, wall-adjacent regions in bacterial polymeric solutions or surface chemistry modification, usually by coating of self-assembled monolayers of hydrophobic molecules, often lead to an augmented partial slip, with the slip length in the range of micrometres (Tretheway & Meinhart 2002, 2004; Lauga, Brenner & Stone 2007). Moreover, in the case of specially treated nano- or microstructured surfaces, air bubbles get trapped in their asperities. Hence the fluid experiences patches of solid wall that can be modelled as no-slip or partial-slip boundaries. The air–liquid interfaces can be modelled as free-slip or partial-slip boundaries with high slip length. The effective hydrodynamic boundary condition at the fluid–solid interface can then be modelled as a uniform partial slippage with high slip length in micrometres (Choi & Kim 2006; Joseph et al. 2006; Lee & Choi 2008; Asmolov et al. 2013; Nizkaya et al. 2015). The value of this apparent slip length can be fine-tuned according to the relevant surface properties, as reported in the relevant literature (Ybert et al. 2007; Asmolov et al. 2013).

Most of the previous studies related to the locomotion of microswimmers near confinements were based on the no-slip walls or air–liquid interface characterized by an infinite fluid slip. However, the consequences of a partial-slip boundary have received less attention in the past (Lemelle et al. 2013; Lopez & Lauga 2014; Hu et al. 2015). In their experimental investigation, Lemelle et al. (2013) observed a reversal of circular wall-parallel trajectories of E. coli with addition of polymeric inclusions in the swimming medium and attributed the phenomenon as an effect of enhanced slip. Subsequently, the results of the mesoscopic simulations of Hu et al. (2015) showed a similar shift of clockwise to anticlockwise rotation of E. coli in a plane parallel to the surface. In addition, they showed that a patterned surface with different slip lengths can be used to direct bacterial motion. The far-field analysis of Lopez & Lauga (2014) employed an image singularity solution applied to a force dipole swimmer, which predicted that a partial-slip condition at the nearby surface will impart a wall-faced rotation and will always attract a pusher-type swimmer. Even within the far-field analysis, they did not consider the contributions from the higher-order singularities arising from a finite-size cell body or the fore–aft asymmetry of the swimmer, which were found to have a profound effect on the motion characteristics near a no-slip wall (Spagnolie & Lauga 2012). Also, an overestimation of the near-field hydrodynamic interactions by the far-field analysis (Lopez & Lauga 2014) was revealed in the numerical simulations of Hu et al. (2015).

The orientation dynamics of a microswimmer taking place in close proximity to a wall has been reported to exhibit diverse trajectory characteristics, ranging from wall escape to wall-induced stable trapping (Ishimoto & Gaffney 2013; Li & Ardekani 2014; Lintuvuori et al. 2016; Ishimoto 2017). Beyond a far-field prediction based on fundamental singularities of Stokes flow, a more detailed account of the near-wall hydrodynamic effects is necessary to explore the resulting trajectory as the microswimmer approaches a wall (Ishimoto & Gaffney 2013; Li & Ardekani 2014; Bechinger et al. 2016). In the present work we employ the squirmer model for spherical cell-bodied swimmers, and within the realm of Stokes flow we obtain an exact solution of the governing equations under interfacial slip, by exploiting a combined analytical–numerical method based on eigenfunction expansion in bispherical coordinates. The results indicate that wall slip beyond a stipulated strength can cause intense characteristic modifications in the swimmer trajectories of different types of microswimmer. In this, it is noteworthy that periodic and damped oscillatory trajectories have been reported by previous numerical simulations (Lintuvuori et al. 2016; Ishimoto 2017), where the wall is repulsive in nature, albeit with no hydrodynamic slippage. In sharp contrast, the exclusiveness of the present study lies in identifying and characterizing different swimming states in the presence of wall slip and how the enhancement in slip modulates different swimming aspects observed near a no-slip wall.

2 Mathematical description

2.1 Problem formulation

We consider the quasi-steady motion of a microswimmer in a Newtonian fluid near a solid surface, along which the no-slip condition of fluid velocity is violated and hydrodynamic slippage takes place. The schematic description of the problem geometry is presented in figure 1(a). The spherical cell body of the model microswimmer has a radius $a$ and its centre is at a distance $\tilde{h}$ from the adjacent slippery wall. The size of the microswimmer is small enough to neglect the inertial effects and at the same time not small enough that Brownian effects become dominant. The swimmer thrust is along $\boldsymbol{e}$ , which is at a pitching angle $\unicode[STIX]{x1D703}$ relative to the wall. The azimuthal angle $\unicode[STIX]{x1D719}$ is the angle made by the horizontal projection of $\boldsymbol{e}$ with the $x$ axis. Thus the director vector can be expressed in the fixed frame as follows: $\boldsymbol{e}=\cos (\unicode[STIX]{x1D703})\cos (\unicode[STIX]{x1D719})\,\boldsymbol{i}_{x}+\cos (\unicode[STIX]{x1D703})\sin (\unicode[STIX]{x1D719})\,\boldsymbol{i}_{y}-\sin (\unicode[STIX]{x1D703})\,\boldsymbol{i}_{z}$ . However, in the presence of only axisymmetric squirming velocity at the microswimmer surface, we have $\unicode[STIX]{x1D719}=0$ throughout the problem. The clockwise rotation along the $y$ axis is taken as positive. Here $\tilde{l}_{S}$ is the slip length denoting the extrapolation distance below the surface where the tangential fluid velocity would vanish. Here we assume that the fluid slippage is uniform over the plane wall and the effect of surface texture does not affect the microswimming characteristics.

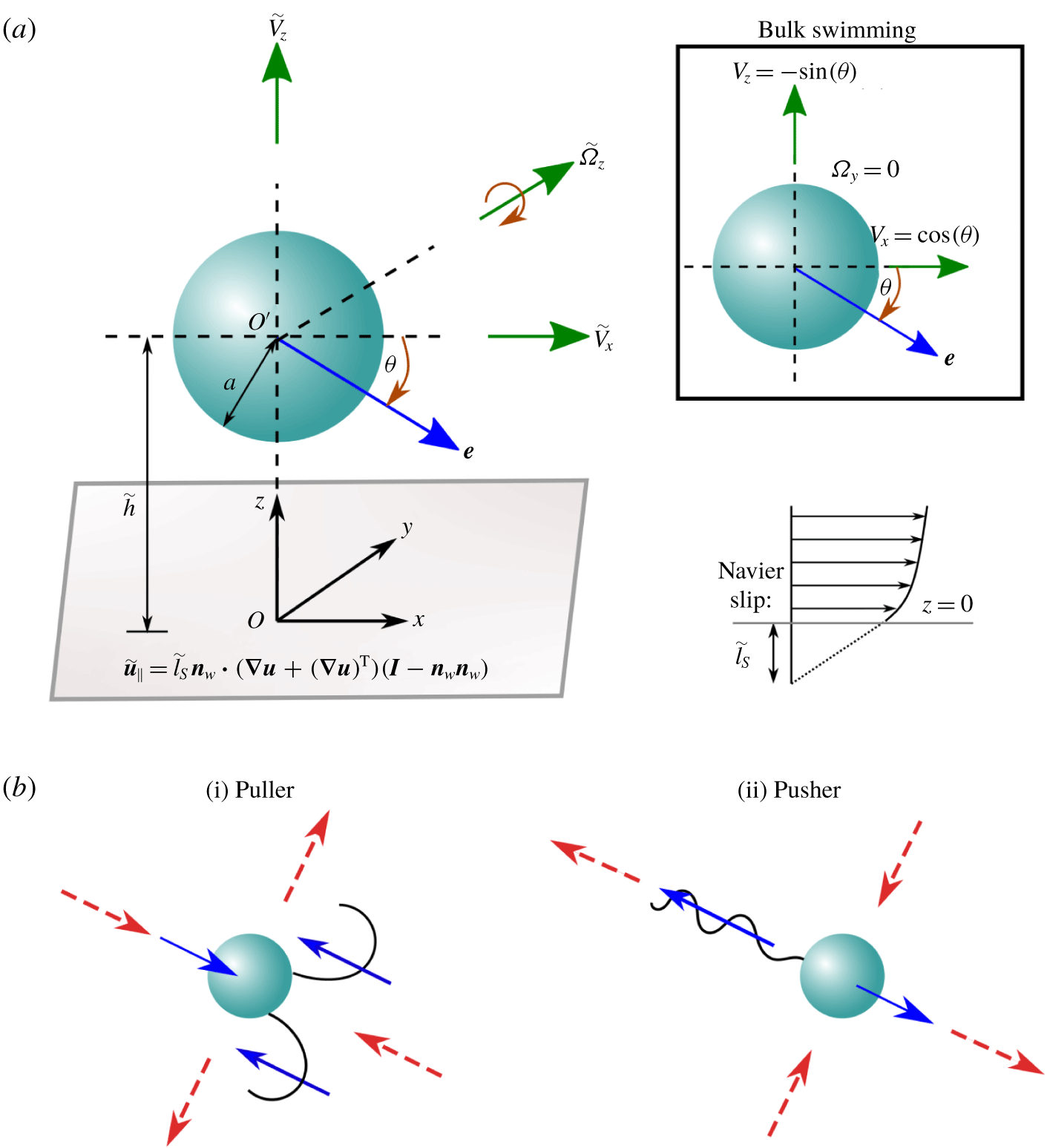
Figure 1. Schematic representation of a model microswimmer near a slippery flat surface obeying the Navier slip condition. (a) The microswimmer has a spherical cell body with radius $a$ . The direction of swimmer thrust or the director vector is indicated by $\boldsymbol{e}$ . The angle $\unicode[STIX]{x1D703}$ is the pitching angle of the director relative to the wall. The adjacent flat surface has a slip length of $\tilde{l}_{S}$ . The inset describes the corresponding situation when the microswimmer is far from the wall. The dimensionless swimming velocity components are also highlighted. (b) Puller and pusher swimmers having two different propulsion mechanisms are schematically shown in an unbounded domain. Red dashed arrows show surrounding fluid flow, while blue arrows indicate local forcing directions of the microswimmer to the fluid when viewed from the laboratory frame.

Neglecting the inertial effects, the flow field around the swimmer can be described by the incompressibility condition and Stokes equation as

(2.1a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\tilde{\boldsymbol{v}}=0\quad \text{and}\quad -\unicode[STIX]{x1D735}\tilde{p}+\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FB}^{2}\tilde{\boldsymbol{v}}=0.\end{eqnarray}$$

The hydrodynamic slippage at the confining wall is characterized by the Navier slip boundary condition (Navier 1823), where the surface slip velocity has a linear variation with the shear rate at the plane surface, given as

(2.2) $$\begin{eqnarray}\tilde{\boldsymbol{u}}_{\Vert }=\tilde{l}_{S}\boldsymbol{n}_{w}\boldsymbol{\cdot }(\unicode[STIX]{x1D735}\boldsymbol{u}+(\unicode[STIX]{x1D735}\boldsymbol{u})^{\text{T}})(\unicode[STIX]{x1D644}-\boldsymbol{n}_{w}\boldsymbol{n}_{w}),\end{eqnarray}$$

where $\boldsymbol{n}_{w}$ is the unit normal at the plane wall pointing into the fluid and $\boldsymbol{u}_{\Vert }$ is the velocity component tangential to the plane wall. The microswimmer gains motility from the surface distortions generated by their swimming appendages. Following the ‘squirmer’ model by Lighthill (1952) and Blake (1971), we impose a tangential velocity on a particle surface, which mimics the locomotion of microbes due to ciliary beating on their surface. The tangential surface velocity of a squirmer has the form

(2.3) $$\begin{eqnarray}\tilde{\boldsymbol{u}}^{s}=\left(\frac{\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{r}}{|\boldsymbol{r}|}\frac{\boldsymbol{r}}{|\boldsymbol{r}|}-\boldsymbol{e}\right)\mathop{\sum }_{n=1}^{\infty }\frac{2}{n(n+1)}B_{n}P_{n}^{\prime }\left(\frac{\boldsymbol{e}\boldsymbol{\cdot }\boldsymbol{r}}{|\boldsymbol{r}|}\right),\end{eqnarray}$$

where $\boldsymbol{e}$ is the orientation vector of the director of the swimmer, $\boldsymbol{r}$ is the position vector of an arbitrary point on the swimmer surface with respect to the particle centre, $B_{n}$ denotes the $n$ th squirming mode amplitude and $P_{n}^{\prime }$ is the derivative of the Legendre polynomial, $P_{n}$ . The tangential velocity is assumed to be time-independent and represents an average over numerous beating cycles.

Following earlier studies (Ishikawa et al. 2006; Li & Ardekani 2014; Shaik & Ardekani 2017; Yazdi & Borhan 2017; Shen, Würger & Lintuvuori 2018), we consider only the first two squirming modes. Depending on the ratio of the first two squirming mode amplitudes, we define a squirmer parameter, $\unicode[STIX]{x1D6FD}=B_{2}/B_{1}$ , which characterizes the intensity of the stresslet exerted by the swimmer. Pusher-type swimmers, e.g. bacteria or sperm cells, which have the flagella behind the main cell body, correspond to $\unicode[STIX]{x1D6FD}>0$ ; while, in contrast, pullers have their flagella in the front, e.g. Chlamydomonas. The distinct propulsion mechanisms of these swimmers are shown schematically in figure 1(b). Also, $\unicode[STIX]{x1D6FD}=0$ denotes the class of swimmers generating a symmetric flow field and which are designated as neutral swimmers, e.g. Volvox. We non-dimensionalize the lengths by the swimmer radius $a$ , velocity by $U_{ref}=2B_{1}/3$ (so that the unbounded-medium squirming velocity becomes unity as shown in the inset of figure 1 a), time by $a/U_{ref}$ and pressure by $\unicode[STIX]{x1D707}U_{ref}/a$ . Hereafter, the normalized variables will be denoted without the $\,\tilde{~}\,$ symbol.

If the microswimmer has a translational velocity of $\boldsymbol{V}$ and a rotational velocity of $\unicode[STIX]{x1D734}$ , then, in the laboratory frame, the boundary condition for the fluid velocity at the surface of the swimmer can be written as

(2.4) $$\begin{eqnarray}\boldsymbol{u}_{s}=\boldsymbol{V}+\unicode[STIX]{x1D734}\times \boldsymbol{r}+\boldsymbol{u}^{s}.\end{eqnarray}$$

In addition, since the swimmer is assumed to be neutrally buoyant in the suspending fluid, it experiences zero net force and zero net torque about its centre, i.e.

(2.5a,b ) $$\begin{eqnarray}\boldsymbol{F}=\iint _{S_{p}}\unicode[STIX]{x1D748}\boldsymbol{\cdot }\boldsymbol{n}_{p}\,\text{d}S=0\quad \text{and}\quad \boldsymbol{L}=\iint _{S_{p}}\boldsymbol{r}\times (\unicode[STIX]{x1D748}\boldsymbol{\cdot }\boldsymbol{n}_{p})\,\text{d}S=0,\end{eqnarray}$$

where $\unicode[STIX]{x1D748}$ is the stress tensor and $\boldsymbol{n}_{p}$ is the unit outward normal to the swimmer surface $S_{p}$ . Now, solving (2.1) along with the boundary conditions (2.2) and (2.4), one can obtain $\boldsymbol{V}$ and $\unicode[STIX]{x1D734}$ by satisfying (2.5).

Owing to the axisymmetric squirmer surface velocity in the present model (2.3), the director $\boldsymbol{e}$ of the swimmer is confined in the $x{-}z$ plane. Also, it will rotate around an axis directed along $\boldsymbol{n}_{w}\times \boldsymbol{e}$ . For the chosen coordinate system, this lies along the $y$ axis. Hence, the locomotion of the microswimmer can be described by $\{\boldsymbol{V},\unicode[STIX]{x1D734}\}=\{V_{x}\boldsymbol{i}_{x}+V_{z}\boldsymbol{i}_{z},\unicode[STIX]{x1D6FA}_{y}\boldsymbol{i}_{y}\}$ .

2.2 Exact solution using bispherical coordinates

The Stokes equation, coupled with the pertinent boundary conditions, including interfacial slip, is solved in terms of the eigensolutions for bispherical coordinates $(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702},\unicode[STIX]{x1D719})$ . The velocity components are evaluated in a cylindrical coordinate system $(\unicode[STIX]{x1D70C},z,\unicode[STIX]{x1D719})$ having its origin at the plane wall, the $z$ axis being normal to the wall and passing through the centre of the spherical swimmer body. The bispherical and cylindrical coordinates are related as (Happel & Brenner 1981)

(2.6a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D70C}=c\frac{\sin (\unicode[STIX]{x1D702})}{\cosh (\unicode[STIX]{x1D709})-\cos (\unicode[STIX]{x1D702})}\quad \text{and}\quad z=c\frac{\sinh (\unicode[STIX]{x1D709})}{\cosh (\unicode[STIX]{x1D709})-\cos (\unicode[STIX]{x1D702})},\end{eqnarray}$$

where $c$ is a positive scale factor. Here $\unicode[STIX]{x1D709}=0$ represents the plane wall and $\unicode[STIX]{x1D709}=\unicode[STIX]{x1D709}_{0}$ (where $\unicode[STIX]{x1D709}_{0}>0$ ) denotes the surface of the sphere, which has its centre at $z=c\coth (\unicode[STIX]{x1D709}_{0})$ and has a radius of $c/\sinh (\unicode[STIX]{x1D709}_{0})$ . A schematic diagram describing the relation between the bispherical and a related cylindrical system has been provided in appendix A.

The general solution of the flow field was given by Lee & Leal (1980) with the help of seven unknown constants ( $A_{n}^{m},B_{n}^{m},C_{n}^{m},E_{n}^{m},F_{n}^{m},G_{n}^{m},H_{m}^{n}$ ) and associated Legendre polynomial, $P_{n}^{m}=P_{n}^{m}(\cos (\unicode[STIX]{x1D702}))$ . Using the same general solution, researchers have solved the flow fields due to squirming microswimmer problems near a two-fluid interface (Shaik & Ardekani 2017; Yazdi & Borhan 2017) or the problem of a diffusiophoretic swimmer near a no-slip plane wall (Mozaffari et al. 2016). In sharp contrast, here, the situation is more complex, since both the squirmer boundary condition at the swimmer surface, equation (2.4), as well as the Navier slip condition at the plane wall, equation (2.2), are to be satisfied while obtaining the arbitrary constants. In the cylindrical coordinates, the slip boundary condition at the plane wall reads

(2.7a,b ) $$\begin{eqnarray}u_{\unicode[STIX]{x1D70C}}=l_{S}\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D70C}z}\quad \text{and}\quad u_{\unicode[STIX]{x1D719}}=l_{S}\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D719}z}\quad \text{at }z=0.\end{eqnarray}$$

Using the no-penetration condition of fluid at this surface, the above equations get simplified to

(2.8) $$\begin{eqnarray}u_{\unicode[STIX]{x1D70C}}=l_{S}\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D70C}}}{\unicode[STIX]{x2202}z}\quad \text{and}\quad u_{\unicode[STIX]{x1D719}}=l_{S}\frac{\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D719}}}{\unicode[STIX]{x2202}z}\quad \text{at }z=0.\end{eqnarray}$$

It is noteworthy to observe that, although acting in a regime of low-Reynolds-number flow, the wall slip effects are not obtained as a trivial extension to previously researched studies on a microswimmer near a no-slip wall. Also, the present approach differs from the asymptotic perturbation approach in terms of a small slip length as a perturbation parameter, which has been employed previously for unbounded particles with inhomogeneous surface slip (Swan & Khair 2008; Willmott 2008; Ramachandran & Khair 2009). In effect, our results demonstrate that the effects of the fluid slip at the wall, manifested through the dimensionless slip length $l_{S}$ , modify the velocity field in a rather intriguing and non-trivial manner. Further details regarding the solution procedure have been provided in appendix B. The exact solution approach deployed by us, using bispherical coordinates, can incorporate any separation distance from the wall and any degree of wall slip (Lee & Leal 1980; Kezirian 1992; Loussaief, Pasol & Feuillebois 2015). Thus it stands as a unified approach that circumvents the necessity of two different analysis tools in different regimes, i.e. an image-singularity-based far-field analysis (Spagnolie & Lauga 2012; Lopez & Lauga 2014) and a singular perturbation analysis in the lubrication regime (Ishikawa et al. 2006).

The complete swimming problem is decomposed into a thrust problem (considering the case when the swimmer is held fixed and experiencing only a tangential surface velocity) and a drag problem (when it undergoes a rigid-body motion with $\{\boldsymbol{V},\unicode[STIX]{x1D734}\}$ and experiences hydrodynamic drag). In the $z$ direction, the force-free condition (2.5) reduces to

(2.9a ) $$\begin{eqnarray}\displaystyle & \displaystyle F_{z,T}^{(Drag)}+F_{z}^{(Thrust)}=0, & \displaystyle\end{eqnarray}$$

(2.9b ) $$\begin{eqnarray}\displaystyle & \displaystyle F_{x,T}^{(Drag)}+F_{x,R}^{(Drag)}+F_{x}^{(Thrust)}=0, & \displaystyle\end{eqnarray}$$

(2.9c ) $$\begin{eqnarray}\displaystyle & \displaystyle L_{y,T}^{(Drag)}+L_{y,R}^{(Drag)}+L_{y}^{(Thrust)}=0. & \displaystyle\end{eqnarray}$$

Here, various hydrodynamic forces (torques) and velocity (angular velocity) components are linearly related through various resistance coefficients (denoted with ‘ $f$ ’) as $F_{z,T}^{(Drag)}=f_{z,T}V_{z}$ , $F_{x,T}^{(Drag)}=f_{x,T}V_{x}$ , $F_{x,R}^{(Drag)}=f_{x,R}\unicode[STIX]{x1D6FA}_{y}$ , $L_{y,T}^{(Drag)}=f_{y,T}V_{x}$ and $L_{y,R}^{(Drag)}=f_{y,R}\unicode[STIX]{x1D6FA}_{y}$ . In these expressions, the first subscript represents the direction of the force or torque while the second subscript tells whether a particular drag force or torque is developed due to translation without rotation $(T)$ or rotation without translation $(R)$ . The hydrodynamic resistance coefficients are functions of only the distance of the microswimmer from the wall $(h)$ and the slip length $(l_{S})$ , while the thrust force and torque are also dependent on the squirmer variables $\unicode[STIX]{x1D6FD}$ and $\unicode[STIX]{x1D703}$ . Once the solution of a particular ‘fundamental problem’ (see appendix C for details) is found, the resistance coefficients, the thrust force and the torque can be determined by series summations in terms of the constants in the eigenfunction expansions (see (C 1)–(C 8) for details). Hence, the velocity components $V_{x}$ , $V_{z}$ and $\unicode[STIX]{x1D6FA}_{y}$ are easily obtained by solving (2.9a )–(2.9c ).

It is noteworthy that the propulsive force and torque on the microswimmer can be alternatively determined without solving the Stokes equation by utilizing the Reynolds reciprocal theorem. The details of this approach applicable for the present problem is provided in appendix D.

3 Results and discussions

Towards investigating the microswimmer trajectories, we solve the following dynamic system:

(3.1a-c ) $$\begin{eqnarray}\frac{\text{d}x(t)}{\text{d}t}=V_{x},\quad \frac{\text{d}h(t)}{\text{d}t}=V_{z},\quad \frac{\text{d}\unicode[STIX]{x1D703}(t)}{\text{d}t}=\unicode[STIX]{x1D6FA}_{y}.\end{eqnarray}$$

Here we do not consider any stochastic motion due to translational or rotational diffusion, and the trajectories are computed based on deterministic forces only. The close approach of a microswimmer towards the wall often leads to the swimmer crashing against the wall and the subsequent motion becomes untraceable. To overcome this problem, we employ an additional short-range repulsive force of the form (Spagnolie & Lauga 2012) $\boldsymbol{F}_{rep}=[(\unicode[STIX]{x1D6FC}_{1}\exp (-\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FF}))/(1-\exp (-\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FF}))]\boldsymbol{i}_{z}$ . Following Spagnolie & Lauga (2012) the parameter values $\unicode[STIX]{x1D6FC}_{1}=100$ and $\unicode[STIX]{x1D6FC}_{2}=100$ are chosen to prevent the swimmer coming closer than a distance of ${\sim}0.01$ times the swimmer radius from the wall. Such forces originate from the nanoscale interaction between the swimmer body and the wall surface, especially in physiological conditions (Klein, Clapp & Dickinson 2003). Diverse forms of repulsive forces have been employed in the literature (Li & Ardekani 2014; Hu et al. 2015; Katuri et al. 2018; Walker et al. 2019). It is to be noted that the use of a short-range repulsive force at the wall destroys the puller–pusher duality during time reversal (Ishimoto 2017; Walker et al. 2019).

First we illustrate the wall-slip-mediated alterations in the translational and rotational velocity components of different types of squirmers having a spherical cell body. Subsequently, the resulting trajectories are elucidated and different phase transitions of swimming states are discussed. Considering a typical microswimmer radius in the range of $1{-}100~\unicode[STIX]{x03BC}\text{m}$ and in view of the experimentally observed dimensional slip lengths (Zhu & Granick 2001; Tretheway & Meinhart 2002; Huang et al. 2008), we take the dimensionless slip length $(l_{S})$ in the range of 0 to 10.

3.1 Swimming velocity alterations

Figure 2 portrays the effects of slip length $(l_{S})$ on the velocity components $(V_{z},V_{x},\unicode[STIX]{x1D6FA}_{y})$ at different separation distances of the microswimmer from the wall $(\unicode[STIX]{x1D6FF})$ . In many situations the said effects turn out to be different in nature, if not opposite, for the puller- and pusher-type microswimmers. To understand the physical origin of the same, we first look into the fundamental differences in the propulsion mechanisms and surrounding flow patterns associated with these two types of swimmers in an unbounded domain.

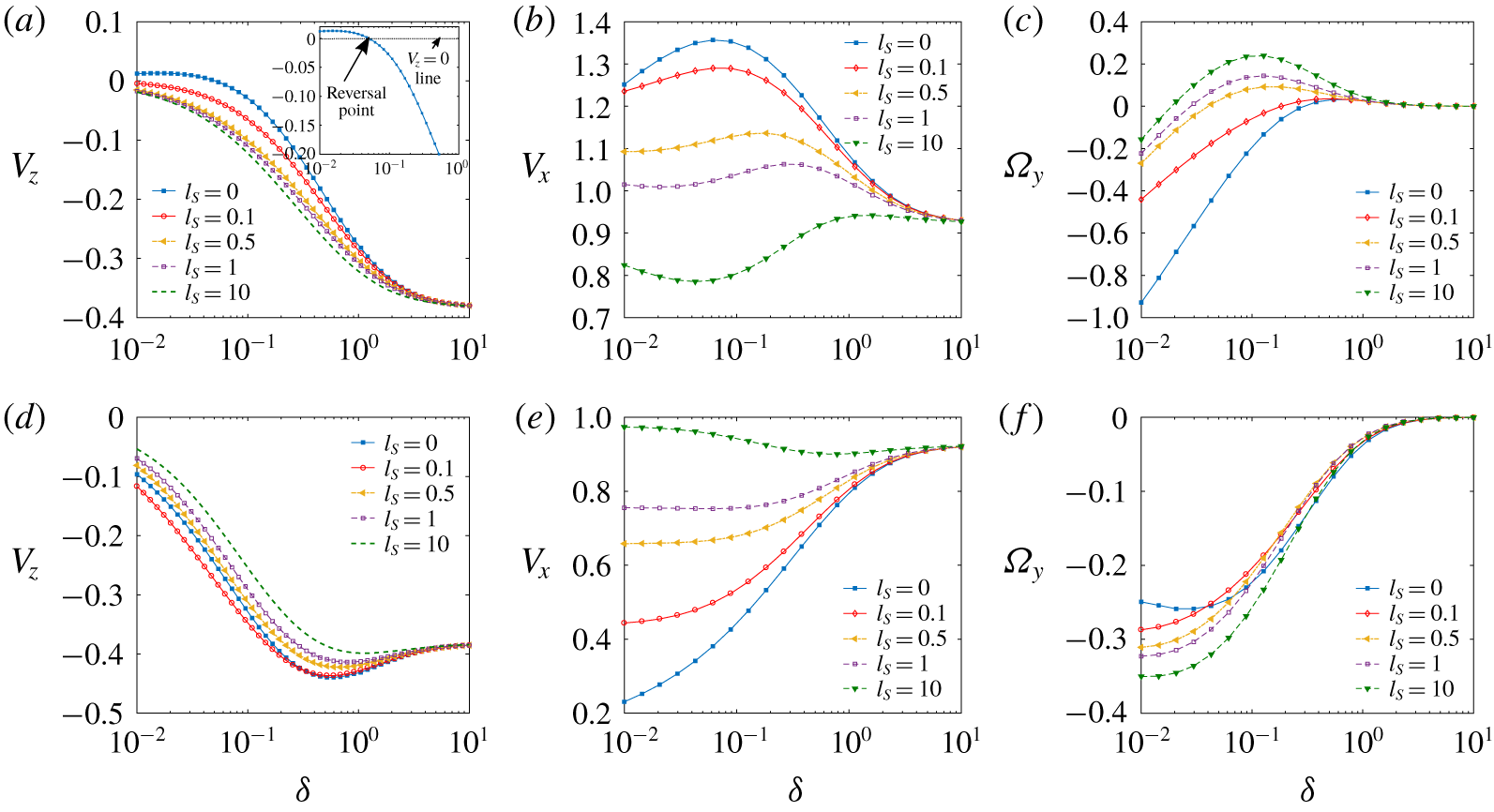
Figure 2. Velocity components of a microswimmer versus smallest separation distance from the wall $(\unicode[STIX]{x1D6FF}=h-1)$ for different slip lengths $(l_{S})$ . Panels (a–c) are for a puller and (d–f) are for a pusher, all having a squirmer parameter value $|\unicode[STIX]{x1D6FD}|=4$ and angular orientation $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/8$ . In the inset of (a), a magnified view of the no-slip case is shown.

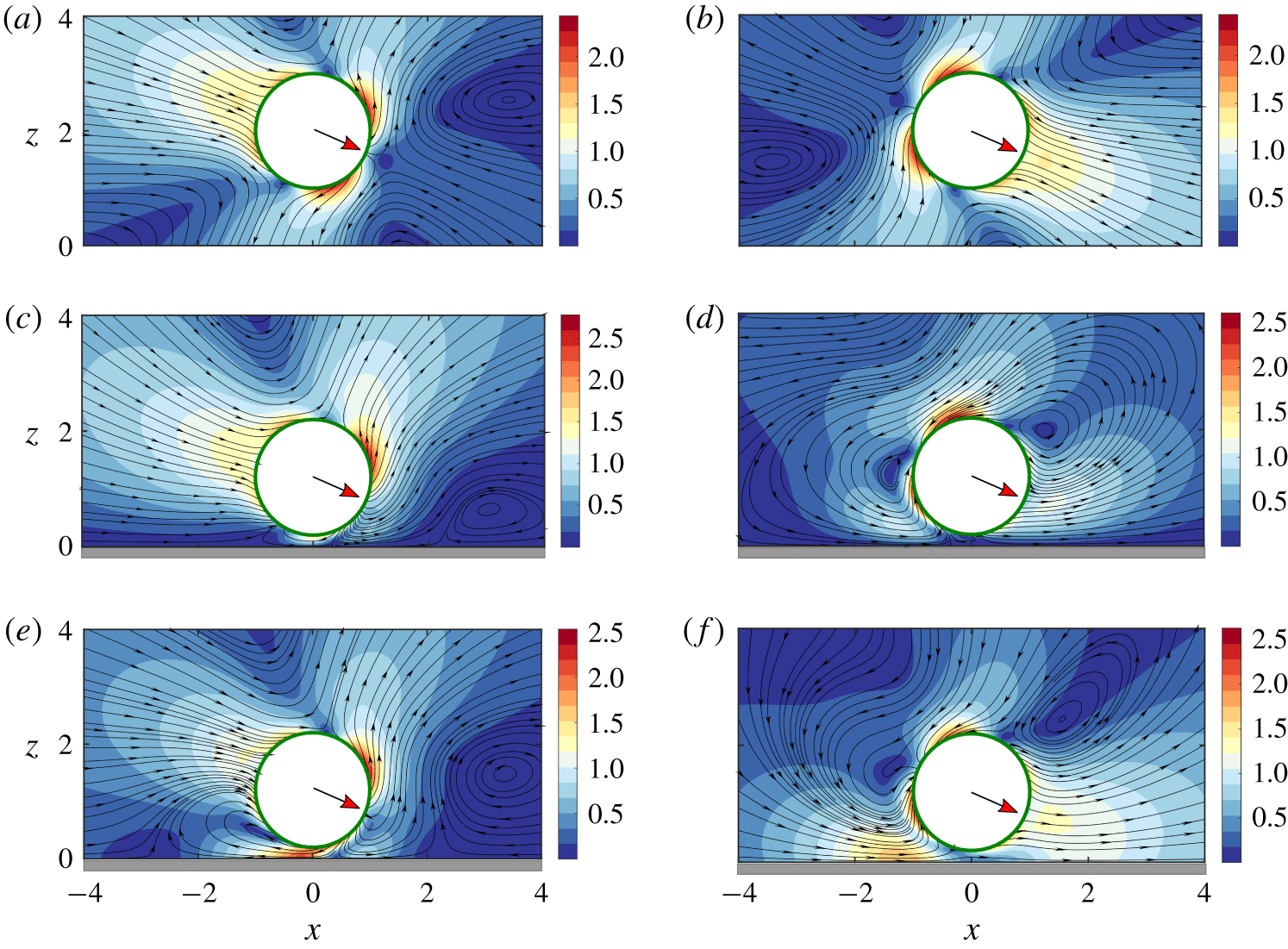
Figure 3. Velocity field around both puller-type (a,c,e) and pusher-type (b,d,f) microswimmers in the $x$ – $z$ plane for pitching angle $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/8$ and $|\unicode[STIX]{x1D6FD}|=4$ . The rows (from top to bottom) correspond to the situations of an unbounded microswimmer, a microswimmer near a no-slip surface and near a slippery surface $(l_{S}=5)$ , respectively. Distance from the wall is taken as $\unicode[STIX]{x1D6FF}=0.2$ . The colour scale depicts the fluid velocity magnitude and the streamlines are shown in the laboratory frame.

Pullers have their flagella ahead of their cell body and the thrust generated by the flagella is cancelled by the cell body at the back. Thus, at large length scales, a moving puller squirmer gives rise to a contractile dipolar flow in the surroundings (figure 1 bi). In contrast, pushers have their flagella at the back and the thrust is generated from behind, thereby mimicking a extensile dipolar flow at large length scales (figure 1 bii). Also, beyond a sufficient stirring action created due to the second squirming mode $(|\unicode[STIX]{x1D6FD}|>1)$ , a pair of circulation rolls, symmetric about the direction of motion, is observed from a comoving frame, but at different locations, behind the cell body for a puller but ahead of the cell body for a pusher (Magar, Goto & Pedley 2003; De Corato, Greco & Maffettone 2015).

The flow field around the squirmer and the wall can be visualized from figure 3. Considering the illustrated situation, when swimmers of both types are pointing towards the wall, the effect of wall-reflected flow is first sensed by their flagella in the case of a puller and the thrust created by their breaststroke action gets affected due to a confinement. In contrast, the frontal cell body of the pusher will be the first to experience the distorted flow, which must be adjusted by a modified pushing action by their posterior flagella. Evidently, the stress distribution around the swimmer will also face modifications based on the relative position of the cell body and the flagella and the corresponding flow adjustments created by them. The presence of wall slip further complicates the scenario by allowing a non-zero tangential fluid velocity at the plane wall. Consequently, the pattern and intensity of the micro-vortices around the squirmer get adjusted differently as demonstrated in figure 3(e,f). This not only creates alterations in the propulsive action of the swimmer and but also modifies the hydrodynamic resistance to a finite-size cell body moving near the wall.

In figure 2(a) the effect of wall slip on the wall-normal velocity component $V_{z}$ is shown for a puller microswimmer with locations ranging from very close to far away separations from the plane wall. The spherical cell body faces different extents of surface stresses due to a near-wall movement. The narrow gap between the swimmer body and the wall generates large velocity gradients, which result in enhanced surface stress in the lower half of the sphere in comparison to the upper half, which does not encounter the wall directly. Hocking (1973) showed that the presence of wall slip results in a logarithmic increase in $f_{z,T}$ with $\unicode[STIX]{x1D6FF}$ and it becomes inversely proportional to the slip length $(l_{S})$ . While considering the behaviour of microswimmer velocity $V_{z}$ , we also have to examine the thrust force variations shown in figure 4. Figure 4(a) demonstrates that a puller-type microswimmer experiences a decreasing thrust force when the wall is slip-free and it becomes negative after the separation exceeds a certain value. This is responsible for velocity reversal in figure 2(a). With increasing slip length, this reversal in $V_{z}$ ceases to occur and it indicates a wall-approaching trend of the microswimmer for all separation distances, consistent with the thrust force variations.

Figure 4. Variation of thrust force and torque components $(F_{z}^{(Thrust)},F_{x}^{(Thrust)},L_{y}^{(Thrust)})$ with wall separation distance $(\unicode[STIX]{x1D6FF})$ for different slip lengths $(l_{S})$ . The parameters correspond to those of figure 2.

Figure 2(d) depicts that, for a pusher-type swimmer, the variations in $V_{z}$ are non-monotonic in both $\unicode[STIX]{x1D6FF}$ and $l_{S}$ , although the thrust force is monotonic (figure 4 d). Observing figure 5 we find that at very low wall separations $(0.01\lesssim \unicode[STIX]{x1D6FF}\lesssim 0.1)$ there exists an intermediate slip length $l_{S}\sim 0.1$ for which the wall-bound velocity becomes maximum in magnitude. This again indicates a considerable importance of hydrodynamic drag force variations on the swimmer velocity. Notably, the above observations for a pusher are in sharp contrast to the characteristics of a force dipole pusher, which, in the far-field analysis, always tends to get attracted to the wall with increasing slip length (Lopez & Lauga 2014). Such disagreement arises from the fact that, in a force dipole model, the contributions from the higher-order singularities arising from a finite-size cell body or the fore–aft asymmetry of the swimmer are not taken into account (Spagnolie & Lauga 2012). In addition to these far-field effects, in the present case, the near-field hydrodynamic interaction also plays its role in modifying the swimmer velocity.

Figure 5. Variation of wall-normal velocity $V_{z}$ of a pusher swimmer $(\unicode[STIX]{x1D6FD}=-4)$ with slip length for various wall separation distances $(\unicode[STIX]{x1D6FF})$ . Here microswimmer orientation, $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/8$ .

Figure 2(b) shows that the wall-parallel velocity $(V_{x})$ remains higher than the unbounded-medium velocity, i.e.  $(V_{x}\rightarrow \cos (\unicode[STIX]{x1D703}))$ for all wall separations, until the slip length becomes high enough (e.g.  $l_{S}=10$ ) to cause $V_{x}$ to fall below the unbounded-medium velocity. A fall in swimming velocity with increasing $l_{S}$ is in contrast to intuition, since a spherical particle translating parallel to the wall experiences lower hydrodynamic resistance in the presence of slip (Davis, Kezirian & Brenner 1994; Loussaief et al. 2015). To address this apparent anomaly, we consider the fact that the microswimmer velocity is dependent on a coupled effect of the hydrodynamic resistances to the simultaneous translational and rotational movement parallel to the wall as well as on the thrust generated due to the propulsive action. Both the propulsive thrust force $(F_{x}^{(Thrust)})$ and torque $(L_{y}^{(Thrust)})$ are affected by wall slip as shown in figures 4(b) and 4(c), respectively. It is observed that the increase in $F_{x}^{(Thrust)}$ with reducing swimmer–wall distances in the no-slip case is now slowed down by the wall slip effect. In addition, the wall slip acts to reduce the propulsive torque away from the wall and even makes it act in the reverse direction for extremely high slip lengths, but only for an intermediate range of wall separations (see figure 4 c). A propulsive torque towards the wall also contributes in reducing $V_{x}$ , which can be confirmed from the final expression of $V_{x}$ in (3.2a ).

The sign of the angular velocity of a microswimmer near a wall $(\unicode[STIX]{x1D6FA}_{y})$ is determined by two main opposing physical mechanisms arising from the propulsive action: the torque whose direction depends on the direction of the slip flow at the surface of the swimmer, and the torque that always acts towards the wall due to the wall-parallel forward movement. The force-free conditions in (2.9) provide the following final expressions of $V_{x}$ and $\unicode[STIX]{x1D6FA}_{y}$ :

(3.2a,b ) $$\begin{eqnarray}V_{x}={\displaystyle \frac{F_{x}^{(Thrust)}f_{y,R}-L_{y}^{(Thrust)}f_{x,R}}{f_{x,R}\,f_{y,T}-f_{x,T}f_{y,R}}}\quad \text{and}\quad \unicode[STIX]{x1D6FA}_{y}={\displaystyle \frac{\overbrace{L_{y}^{(Thrust)}f_{x,T}}^{T_{1}}-\overbrace{F_{x}^{(Thrust)}f_{y,T}}^{T_{2}}}{\underbrace{f_{x,R}\,f_{y,T}-f_{x,T}f_{y,R}}_{T_{3}}}}.\end{eqnarray}$$

They suggest that the hydrodynamic resistance factors are intrinsically coupled with the thrust force and torque and take part in deciding the resultant rotation direction. The effect of wall slip on the various terms contributing to the rotation rate are shown in figure 6. This shows that increasing wall slip drastically alters $T_{1}$ and $T_{3}$ , while changes in $T_{2}$ are not significant. In effect, for a puller swimmer the wall slip exerts a strong opposing torque to the swimmer rotation away from the wall $(\unicode[STIX]{x1D6FA}_{y}<0)$ , which for high slip lengths causes it to rotate towards the wall $(\unicode[STIX]{x1D6FA}_{y}>0)$ , before reaching the bulk zero-rotation state (refer to the inset of figure 1 a) at a distance of nearly one radius away from the wall, as demonstrated in figure 2(c).

Figure 6. Three different terms $(T_{1},T_{2},T_{3})$ controlling the effective rotation rate of a (a) puller and (b) pusher, as shown in (3.2b ). The parameters are the same as in figure 2.

Variation of the thrust force $(F_{x}^{(Thrust)})$ for a pusher (see figure 4 e) is highly complex and non-monotonic in nature. However, the corresponding wall-parallel velocity component $(V_{x})$ shows a trend of getting escalated with slip length (see figure 2 e), a phenomenon that is exactly opposite to that of a puller. The negative thrust torque on the microswimmer gets reduced by the wall slip for all separations (see figure 4 f). Again, this fixed trend is not followed by the rotation rate $\unicode[STIX]{x1D6FA}_{y}$ . Figure 2(f) demonstrates that, for a pusher swimmer located very close to the wall $(\unicode[STIX]{x1D6FF}\lesssim 0.04)$ , the wall slip forces it to rotate away from the wall. However, beyond this distance, the slip-induced rotation gets either escalated or suppressed, depending on a subtle interplay between slip and wall separation. This is again in contradiction to the previously studied far-field behaviour of a force dipole swimmer (Lopez & Lauga 2014), due to the similar reasons discussed for  $V_{z}$ .

3.2 Modulations in near-wall swimming trajectories

3.2.1 Neutral squirmer

A neutral squirmer, which is characterized by $\unicode[STIX]{x1D6FD}=0$ , gives rise to a quadrupolar flow field around the swimmer in an unbounded domain and thus vorticity is absent in the velocity field (Zhu et al. 2011; Zhu, Lauga & Brandt 2012). In the absence of the wall slip, for an initial orientation away from the wall or even with a small tilt towards the wall, a neutral swimmer does not show any tendency to move towards the wall and escapes from the wall along a straight line with the final orientation angle reaching an asymptotic constant value $(\unicode[STIX]{x1D703}_{f})$ . The scenario changes for moderate values of the initial orientation angles towards the wall. As it moves towards the wall, its director gradually points away from the wall due to a net anticlockwise torque arising from the near-field hydrodynamic effect, which subsequently forces the swimmer to attain a negative orientation angle $\unicode[STIX]{x1D703}_{0}<0$ . In effect, the normal velocity component becomes positive $(V_{z}>0)$ , leading to the escape of the swimmer away from wall. Beyond a critical initial orientation, $\unicode[STIX]{x1D703}_{0,cr}$ , the swimmer eventually collides with the wall, remains in the wall-adjacent region for some time, and finally escapes with a final orientation equal to its initial one, $\unicode[STIX]{x1D703}_{f}\approx \unicode[STIX]{x1D703}_{0}$ . When the swimmer has an initial height of $h_{0}=2$ , this critical angle for descending to a height below $h=1.05$ has been reported to be ${\sim}0.4$ by Spagnolie & Lauga (2012). We show in figure 7(a) that the critical angle for the transition of a scattering trajectory to a colliding one (with a cutoff distance for collision as $h=1.01$ ) shows a drastic decrease from the no-slip case ( $l_{S}=0$ , $\unicode[STIX]{x1D703}_{0,cr}=0.59$ ) to $\unicode[STIX]{x1D703}_{0,cr}=0.38$ for $l_{S}=1$ and finally reaches an asymptote of $\unicode[STIX]{x1D703}_{0,cr}\rightarrow 0.36$ for higher values of the wall slip length.

Here we define the wall-bound detention time of a microswimmer $(T_{det})$ by the time interval during which the microswimmer remains below a distance of one-tenth of its diameter. For a typical microswimmer diameter of $10$ to $30~\unicode[STIX]{x03BC}\text{m}$ , this cutoff distance remains consistent with the experimental evidence of E. coli cells remaining at a distance of ${<}1{-}3~\unicode[STIX]{x03BC}\text{m}$ near a wall (Drescher et al. 2011) for an extended time. Figure 7(b) shows that, although the escaping nature of the microswimmer motion is preserved even with a very high slip length, the detention time for a neutral swimmer gets increased significantly with the slip length $(l_{S})$ (see the inset of figure 7 b). Interestingly, for small tilt angles towards the wall (e.g.  $\unicode[STIX]{x1D703}_{0}=0.05\unicode[STIX]{x03C0}$ ), where the detention time is negligible near a no-slip wall, the increasing slip length beyond a critical value is found to impart a high detention time.

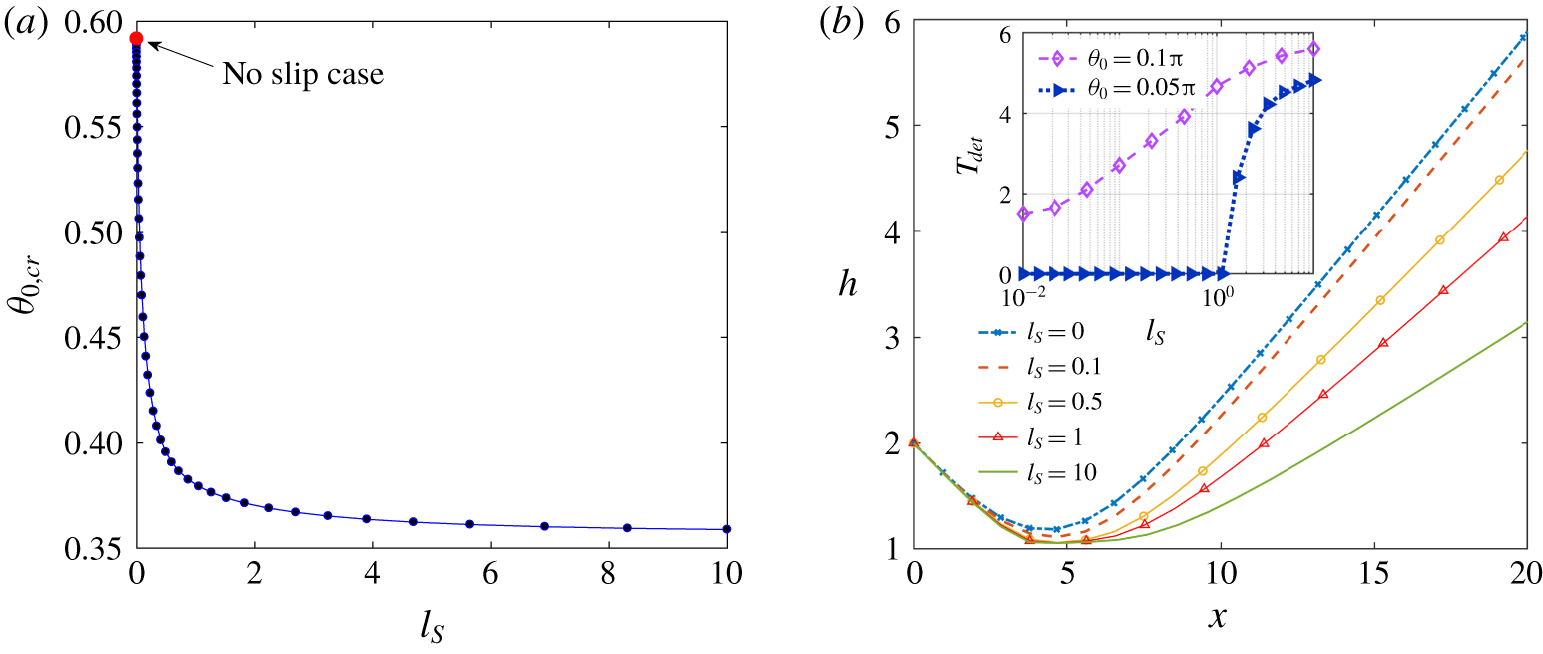
Figure 7. (a) Critical initial orientation $(\unicode[STIX]{x1D703}_{0,cr})$ versus slip length $(l_{S})$ . (b) Trajectory with initial orientation, $\unicode[STIX]{x1D703}_{0}=0.1\unicode[STIX]{x03C0}$ . In the inset the variation of dimensionless detention time with slip length is shown. In both panels the initial height, $h_{0}=2$ is taken.

3.2.2 Puller squirmer

While swimming near a no-slip wall, the director $(\boldsymbol{e})$ does not face a hydrodynamic rotation relative to the wall if the strength of the vorticity generation term $(\propto \unicode[STIX]{x1D6FD})$ in the squirmer surface velocity is not sufficiently high (Ishimoto & Gaffney 2013). As $\unicode[STIX]{x1D6FD}$ crosses a critical value, the hydrodynamic torque imparts an extra rotation of the puller towards the wall and a stable swimming state parallel to the boundary takes place favoured by an initial tilt towards the wall, i.e.  $\unicode[STIX]{x1D703}_{0}>0$ , while the wall effects are negligible for $\unicode[STIX]{x1D703}_{0}<0$ (Li & Ardekani 2014). We found that, even in the presence of wall slip, the wall-bound attraction of the swimmer is non-existent for small values of the squirmer parameter $\unicode[STIX]{x1D6FD}\lesssim 2.75$ with any initial director orientation. Similar to the neutral squirmers, we observe that the escaping nature is affected in the sense that the minimum height reached by the swimmer gets reduced and the detention time near the wall is increased with rising slip lengths.

Figure 8. Phase maps of the final swimming states of puller microswimmers in the $(l_{S},\unicode[STIX]{x1D703}_{0})$ plane. Panels (a–c) correspond to squirmer parameters $\unicode[STIX]{x1D6FD}=3$ , 4.5 and 5, respectively. The ‘blue’ circles and ‘red’ crosses correspond to the escaping and trapping states, respectively. In all the presented cases, the $l_{S}=0.01$ case gives a swimming state similar to a no-slip wall. The illustrations are with an initial launching height of $h_{0}=2$ .

The scenario changes as $\unicode[STIX]{x1D6FD}$ crosses this limiting value and the wall slip triggers a transition of swimming states from wall escape to wall entrapment, as summarized in the phase diagrams of figure 8(a–c). Phase diagrams depicting diverse trajectory characteristics of squirmers (Uspal et al. 2015a ) as well as three-sphere microswimmers (Daddi-Moussa-Ider et al. 2018) near a no-slip surface have been constructed previously on the basis of the release height and orientation. In stark contrast, in the present study we represent unique phase diagrams elucidating the immense contribution of hydrodynamic slip length in deciding the resulting trajectory. All the escaping trajectories have been confirmed from long-time simulations with a cutoff distance of $h_{escape}=15$ (Ishimoto & Gaffney 2013). The trajectories starting from a launch angle $\unicode[STIX]{x1D703}_{0}\sim \unicode[STIX]{x03C0}/2$ , which cause direct impact (Spagnolie & Lauga 2012) and become computationally demanding, have been excluded from computation by limiting the initial orientation angle in the range $\unicode[STIX]{x1D703}_{0}\leqslant 0.95\times \unicode[STIX]{x03C0}/2$ . The presence of wall slip severely modifies the near-field hydrodynamic interaction, as observed during the discussions of velocity components in § 3.1. As a consequence, low values of the initial tilt angle, which do not lead to any trapping state near a no-slip wall, are found to be sufficient for the swimmer to attain that extra rotation towards the wall which favours a state transition from escaping to wall-bound trapping, in the form of either periodic oscillations or steady-state sliding.

We would like to draw the attention of the reader to the fact that, in the no-slip case itself, previous studies have reported wall entrapment where the wall is equipped with a repulsive force of different forms (Lintuvuori et al. 2016; Ishimoto 2017). As a verification of the fact that the swimming state transitions are exclusively caused by hydrodynamic slippage and not due to the sole effect of short-range repulsive forces $\boldsymbol{F}_{rep}$ , we have carefully examined the trajectories of the microswimmer where the microswimmer escapes from the wall without coming too close to the wall $(\unicode[STIX]{x1D6FF}<0.01)$ and thus not getting affected by $\boldsymbol{F}_{rep}$ . A typical case is presented later in figure 18. It is observed that here only an interfacial slip length beyond a certain limit $(l_{S,cr})$ is necessary to impart the required reorientation for swimming state transition.

Figure 9. Different characteristics of the slip-induced swimming state transitions for different squirming parameters for puller swimmers $(\unicode[STIX]{x1D6FD}>0)$ . The corresponding parameters are shown above each panel. The insets of panels (a) and (b) correspond to the trajectory in the phase space, while the inset of panel (c) depicts the variation’s maximum attained height $(h_{max})$ and final steady-state sliding height $(h_{f})$ with slip length $(l_{S})$ .

For moderate values of $\unicode[STIX]{x1D6FD}$ (i.e.  $2.75\lesssim \unicode[STIX]{x1D6FD}\lesssim 3.75$ ), as the initial swimmer orientation departs slightly from the wall-parallel direction $(\unicode[STIX]{x1D703}_{0}=0)$ , the transition phenomenon occurs sharply at a fixed value of the slip length $(l_{S,cr})$ , without showing any non-monotonic dependence on $\unicode[STIX]{x1D703}_{0}$ . In this case, as the swimmer collides with the wall, the short-range repulsive force imparts an upward velocity component $(V_{z}>0)$ and at the same time the swimmer continues to rotate away $(\unicode[STIX]{x1D6FA}_{y}<0)$ from the wall. Gradually the effect of $\boldsymbol{F}_{rep}$ is overcome. At a certain height and configuration, again the clockwise torque and the downward force dominate, causing the sign reversal of both $\unicode[STIX]{x1D6FA}_{y}$ and $V_{z}$ (refer to figure 2(a,c) and their corresponding discussions in § 3.1 for a depiction on the physical origin of similar critical conditions). Thus, the microswimmer again moves towards the wall. Upon subsequent repetition of this motion behaviour, finally a periodic oscillatory trajectory results (see figure 9(a) for representative scenarios) and limit cycles emerge in the phase plane of the dynamic system. We also observe that the amplitudes of the present periodic oscillations get decreased with enhancing slip lengths.

With further increase in $\unicode[STIX]{x1D6FD}$ , i.e.  $\unicode[STIX]{x1D6FD}\gtrsim 3.75$ , the trapping states become damped oscillatory in nature beyond a critical slip length, as portrayed in figure 9(b,c) and eventually steady-state stable swimming takes place with a fixed height and orientation $(h_{f},\unicode[STIX]{x1D703}_{f})$ . These final swimming states give rise to fixed points in the phase map of the dynamic system of $({\dot{h}},\dot{\unicode[STIX]{x1D703}})$ . The transition of periodic to damped-amplitude trapping with increase in $\unicode[STIX]{x1D6FD}$ suggests that, during the combined influence of the torques due to hydrodynamic slip and that due to the circulating flow pattern emerging from the propulsive action, if the former one is more dominant than the other, damping of swimmer oscillations is less prominent. This condition further arises in specific cases of pusher swimmer characteristics to be discussed subsequently.

As observed in figure 9(c), for a high value of $\unicode[STIX]{x1D6FD}$ (e.g.  $\unicode[STIX]{x1D6FD}=5.5$ ), the swimmer initially moves away from the wall much above the initial height but gets attracted towards the wall due to the high reorientation torque imparted by the pronounced contribution of the stresslet term in the swimmer surface velocity and shows some small-amplitude oscillations in height before getting trapped. Additionally, the maximum height reached during the first bouncing motion $(h_{max})$ and the final sliding height $h_{f}$ both get reduced due to wall slip. Also the longitudinal distance travelled before coming too close to the wall gets decreased. This effectively portrays the wall slip effect as a strong influencing parameter to cause trajectory transition even if the swimmer reaches a height much above the wall.

Interestingly, with increase in $\unicode[STIX]{x1D6FD}$ (see figure 8 b,c) for a band of low $\unicode[STIX]{x1D703}_{0}$ values, the swimming state transition occurs even with zero wall slip. However, beyond a critical high value of the slip length, only stable trapping states exist for all the initial tilt angles considered and the non-monotonicity with $\unicode[STIX]{x1D703}_{0}$ vanishes. This renders the critical slip length dependent on the initial launching angle, i.e.  $l_{S,cr}=l_{S,cr}(\unicode[STIX]{x1D703}_{0})$ . Some illustrative trajectories are shown in figure 10(a). It depicts that, for some initial orientations in the intermediate range $0.05\unicode[STIX]{x03C0}\lesssim \unicode[STIX]{x1D703}_{0}\lesssim 0.16\unicode[STIX]{x03C0}$ , the swimmer travels a maximum vertical distance almost as high as the initial height, $h_{0}=2$ , but thereafter, sensing the slip in the wall, it follows a damped-amplitude oscillatory motion and finally slides parallel to the wall at a fixed height, $h_{f}=1.464$ , and positive angle (see figure 10 b), $\unicode[STIX]{x1D703}_{f}=0.266$ . Beyond this $\unicode[STIX]{x1D703}_{0}$ , the swimmer bounces on the wall, thereafter travels to height $h>h_{0}$ , which is beyond the reach of the reorientation torque of the slippery wall, and finally escapes away from the wall.

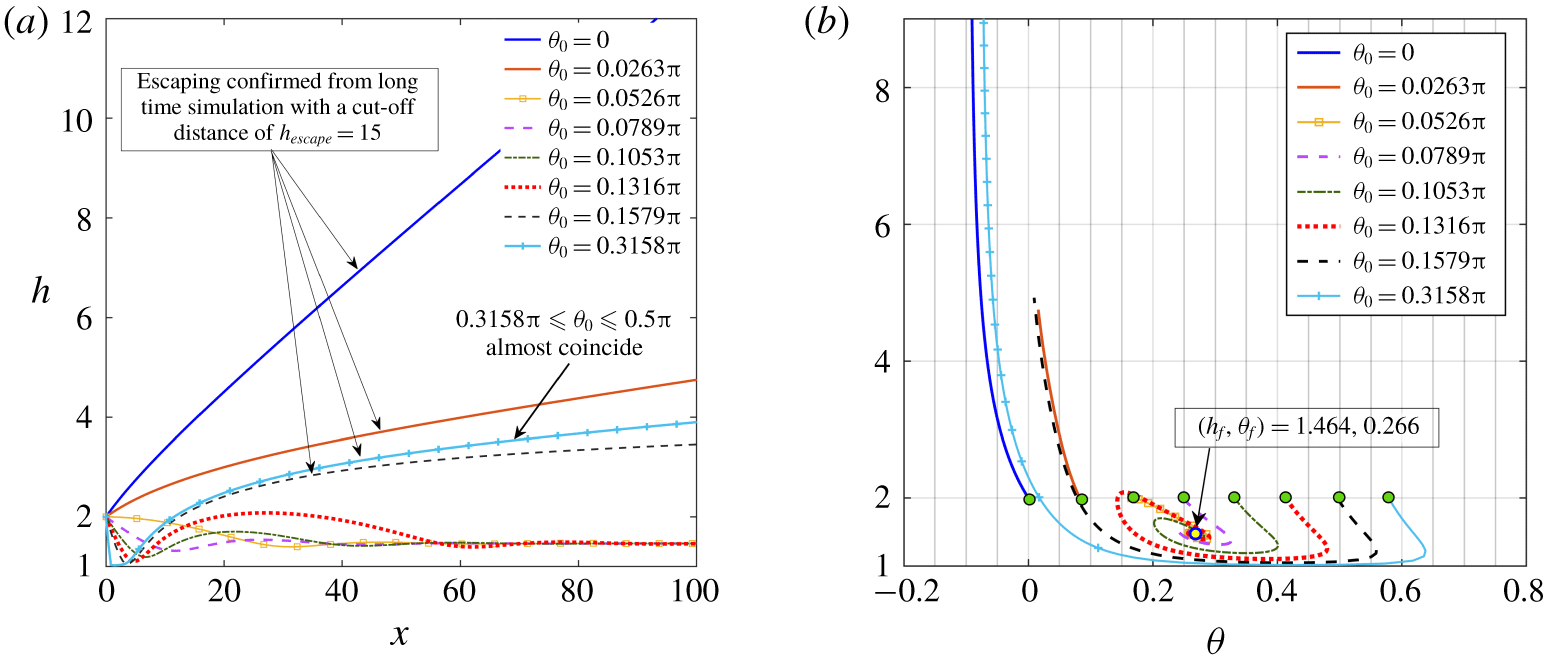
Figure 10. Trajectory of a puller squirmer with $\unicode[STIX]{x1D6FD}=5$ and a wall slip length $l_{S}=0.03$ for various initial orientations $(\unicode[STIX]{x1D703}_{0})$ . (a) Trajectory in the $(x,h)$ plane and (b) phase plane dynamics, $h$ versus $\unicode[STIX]{x1D703}$ . In (b), the green circles represent the initial states while the final fixed point for the trapping instances is shown with a black circle.

Figure 11. Increase in detention time for a puller swimmer with $\unicode[STIX]{x1D6FD}=3,\unicode[STIX]{x1D703}_{0}=0.1\unicode[STIX]{x03C0}$ .

Before a full transition of escape to trapping occurs, rising wall slip affects the trajectories by increasing the wall-bound detention time $(T_{det})$ for both pullers and pushers, similar to the previously discussed case of a neutral one. A representative behaviour with $\unicode[STIX]{x1D6FD}=3$ is described in figure 11. In these cases, even after the collision with the wall, the torque on the swimmer is not sufficient to impart a sliding-type motion near the wall. Rather, the swimmer escapes the wall-adjacent region after gliding along the wall for a finite detention time. Thus, the wall-bound detention time of the neutral and puller microswimmers can be controlled by suitably tuning the wall slip length, thus facilitating the formation of bio-aggregates such as biofilms near a wall (Watnick & Kolter 2000).

3.2.3 Pusher squirmer

The swimming states of a pusher swimmer also show wall-bound trapping nature beyond a critical slip length $(l_{s,cr})$ . However, in contrast to pullers, here we find that these stable trapped states exist even for small initial tilt away from the wall, but a further increase of tilt away from the wall results in escaping states only (see figure 12 for an example). In this context, the colliding-escape maps in Shum et al. (2010) and Pimponi et al. (2016) give us information about the trajectories of an E. coli bacterium having properties of a pusher microswimmer (Berke et al. 2008) near a no-slip and perfect-slip surface. The present results bear resemblance with the reported ones in terms of predicting escaping states for $\unicode[STIX]{x1D703}_{0}\lesssim 0$ . However, their prediction of colliding trajectories for both surface types with $\unicode[STIX]{x1D703}_{0}\gtrsim 0$ and the absence of stable swimming states for a perfect-slip surface cannot be readily compared with the present results since we have used an additional repulsive force $(\boldsymbol{F}_{rep})$ near the wall to prevent crashing, a strategy that is also common among others (Spagnolie & Lauga 2012; Li & Ardekani 2014; Lintuvuori et al. 2016) for predicting the motion of the microswimmer after collision.

Figure 12. Transition of swimming states for a pusher $(\unicode[STIX]{x1D6FD}=-5)$ near a no-slip and slippery wall with $\unicode[STIX]{x1D703}_{0}=-0.165$ . In the inset, the escaping states corresponding a more negative angle, $\unicode[STIX]{x1D703}_{0}=-0.248$ , are also shown.

Figure 13. Critical slip length $(l_{s,cr})$ versus squirmer parameter $(\unicode[STIX]{x1D6FD})$ for pusher-type swimmers with initial conditions $(h_{0},\unicode[STIX]{x1D703}_{0})=(2,0)$ . In the insets (a,b) the transition behaviours are highlighted for $\unicode[STIX]{x1D6FD}=-5$ and $-2$ , respectively, while the inset (c) describes the characteristic changes in the periodic oscillations with increasing slip length for $\unicode[STIX]{x1D6FD}=-10$ . The onset of transition takes place for $\unicode[STIX]{x1D6FD}\sim -1.6$ and is denoted by a ‘blue’ marker.

The non-monotonicity of this critical slip length with initial angular orientations (as shown in figure 8) has not been observed in the case of pushers. Beyond this critical slip length, the swimmer slides along the wall for any initial orientations in the range of $\unicode[STIX]{x1D703}_{0}$ , as discussed above. Figure 13 depicts the consolidated effect of the wall slip on the pusher swimmers for a range of squirmer parameter $-10\leqslant \unicode[STIX]{x1D6FD}\leqslant -2$ . The onset of transition from an escaping to a damped-amplitude oscillation takes place for $|\unicode[STIX]{x1D6FD}|\sim 1.6$ with a high value of slip length $(l_{S})$ . The oscillations become periodic in nature for $|\unicode[STIX]{x1D6FD}|\gtrsim 5$ . This is again opposite to the trend of puller microswimmers, which exhibit periodic and damped-amplitude oscillations for low and high values of the same parameter, respectively. This difference can be related to the contrast in the near-field hydrodynamic effects brought in by the fluid slip at the wall, as discussed in § 3.1. Realization of slip-mediated trapping for pushers with low $|\unicode[STIX]{x1D6FD}|$ is of utmost importance in view of their non-existence near a no-slip wall.

For a significantly high strength of $|\unicode[STIX]{x1D6FD}|$ , the periodic oscillations are present even in the absence of wall slip, as illustrated for $\unicode[STIX]{x1D6FD}=-10$ in the inset (c) of figure 13. Here also, the slip has an important role to play in the form of increasing the frequency of oscillatory height and reducing their amplitudes. This, in turn, allows the swimmer to slide along the wall, maintaining a minimal wall separation as dictated by the balance of the wall repulsive force and the hydrodynamic force for a high slip length.

Starting from the same initial orientation, during the final states of a damped cyclic swimming, the puller swimmers point towards the wall (quantified by a positive angle) while pushers show the opposite trend (please refer to figure 14 a). This difference in sign (but not exactly opposite in magnitude) can be attributed to the differences in the physical mechanisms providing the reorientation torque during the trapping states and deciding the actual orientation angle at a particular height, which was also shown to give rise to different rotation rates for the two types of swimmers, as described in figure 2(c,f). It may be counter-intuitive to observe that a pusher swimmer is attracted towards the wall during the oscillations even though it points its director away from the wall $(\unicode[STIX]{x1D703}<0)$ (in figure 14 a). An analogous scenario was reported by Lintuvuori et al. (2016) for a pusher near a no-slip wall. Figure 14(b) depicts the flow field at the end state location of the pusher trajectory. The distortion in the flow field around the microswimmer is observed to be severely altered in the presence of a slippery wall. As a consequence, figure 14(c) shows that, even for negative pitch angles, there exist situations where the thrust force remains negative, i.e. the swimmer gets attracted towards the wall. With subsequent decaying of the amplitudes of oscillation, the microswimmer finally reaches a critical location $(h,\unicode[STIX]{x1D703})\approx (1.110,-0.267)$ where the thrust force $(F_{z}^{(Thrust)})$ becomes zero and it does not move further in the vertical direction.

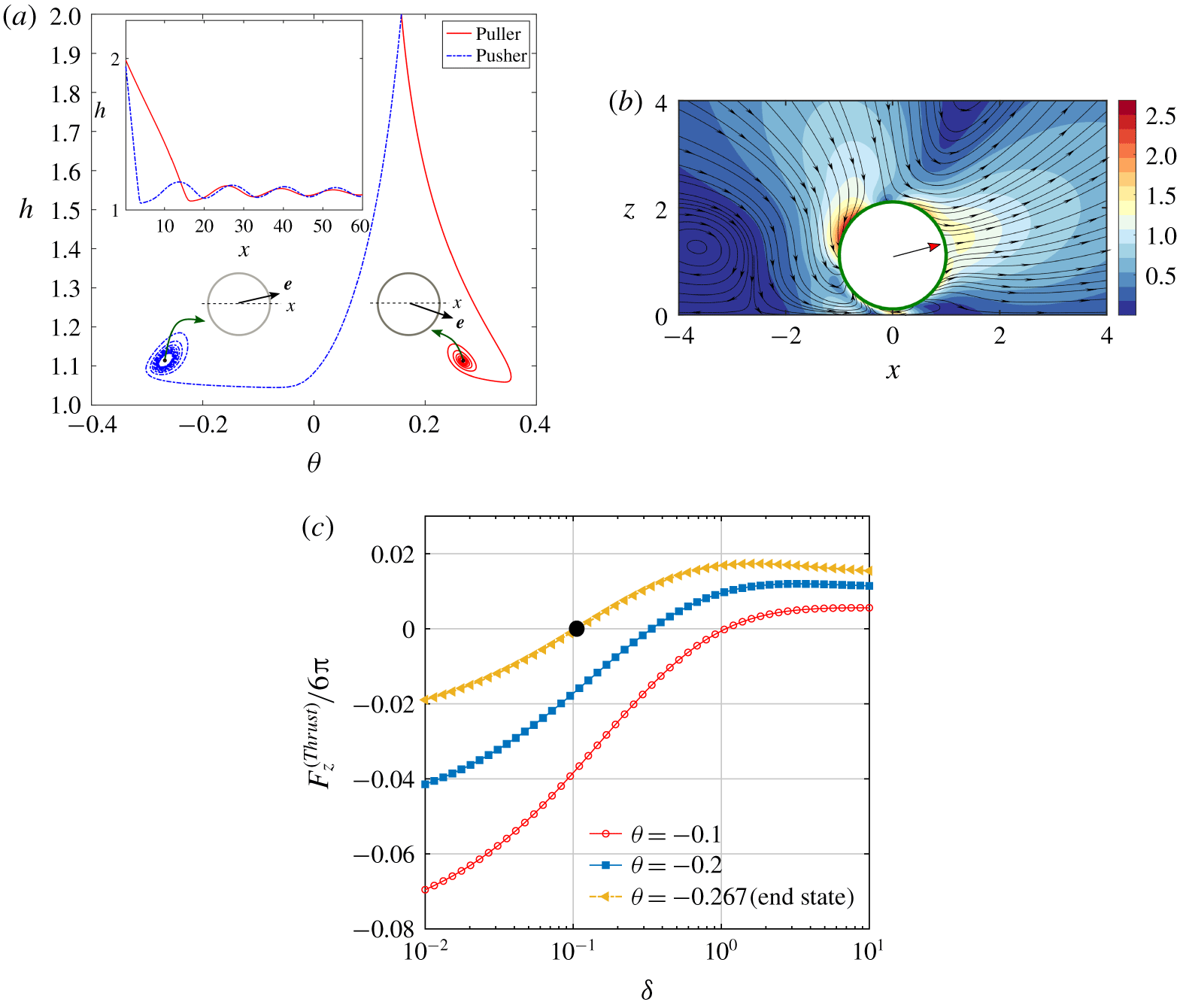
Figure 14. (a) Phase-space trajectory comparison for puller and pusher microswimmers. The parameters are $\unicode[STIX]{x1D6FF}_{0}=1$ , $\unicode[STIX]{x1D703}_{0}=0.05\unicode[STIX]{x03C0}$ , $l_{S}=0.55$ and $|\unicode[STIX]{x1D6FD}|=4$ . In the inset, the trajectories are compared in the $(x,h)$ plane. Swimmer orientations during the final steady-state swimming are also described schematically. (b) The laboratory-frame flow field around the pusher at this end state point in the trajectory. (c) Vertical thrust force variation with distance from the wall at different negative pitch angles attained by the pusher in the trajectory of panel (a). The black filled circle indicates the end state point in the trajectory.

The slip-modulated wall-bound motion of squirmers shares a characteristic feature with the recent experimental investigation of Ketzetzi et al. (2020), who found a prominent tendency of diffusiophoretic Janus colloids to self-propel adjacent to hydrophobic surfaces having high slip lengths and to occasionally leave the surface followed by a steady swimming in wall proximity. In view of the similarity of the surrounding flow patterns in an unbounded domain, the behaviour of such chemically active synthetic particles has been previously mapped onto the squirmer model (Michelin & Lauga 2014). However, near a confinement, the distribution of the chemical species around a self-diffusiophoretic particle gets modified, which in turn affects the slip velocity at the particle surface (Uspal et al. 2015b ; Mozaffari et al. 2016), in contrast to the squirmers, which have a prescribed surface velocity. Thus a qualitative matching of the respective swimming states calls for an explicit account of the dependence of hydrodynamics interaction and chemical species distribution (Popescu et al. 2018).

4 Conclusions and remarks

To summarize, we have adopted a ‘squirmer’ model to mathematically describe the swimming characteristics of micro-organisms near a plane wall with hydrodynamic slippage. In the low-Reynolds-number regime, the governing fluid flow equations are solved by employing an exact solution technique in the bispherical coordinate system and the hydrodynamic slippage at the wall has been modelled using the Navier slip boundary condition. This provided a unified platform to investigate the translational–rotational velocities of a microswimmer in the far-field domain as well as in the near-surface lubrication region.

The results reveal that hydrodynamic slippage mediates the competitive effects of the near-field hydrodynamic drag and propulsive forces. Consequently, the translational and rotational velocities are both altered, sometimes even showing changes in sign, in contrast to the previous theoretical model of the far-field characteristics of a force-dipole swimmer (Lopez & Lauga 2014). The pattern and intensity of the slip-induced changes in the swimming kinematics are critically dependent on the squirming modes and the distance of the microswimmer from the wall.

In comparison to the case of a no-slip wall, near-wall slip reduces the critical value of the dimensionless strength of the second squirming mode required to exert a sufficient hydrodynamic torque enabling a transformation of an escaping microswimmer trajectory to a wall trapping one. Thus wall slip triggers a robust trapping nature of near-surface swimming states. Interestingly, depending upon the launching orientation angle and the strength of the swimming gait, the slip-induced trapping can become either a periodic oscillation or a damped-amplitude oscillations with a final fixed height and orientation. However, in contrast to pullers, for which the critical slip length non-monotonically depends on the initial orientation angle, the critical slip length for pushers is independent of the initial orientation angle. In addition, the maximum attained height, the average height of the periodic oscillations and the final stable height, all get decreased with enhanced slip length.

We have identified that neutral swimmers do not show any tendency to get entrapped near a slippery wall; however, their detention time faces a significant enhancement with increasing wall slip, and their minimum wall separation distance gets reduced before the wall escape takes place. Additionally, as the slip length increases, the critical release orientation of the swimmer director for the transition from scattering to wall collision becomes more pointed away from the wall and finally reaches an asymptotic value.

The present results may turn out to be elemental in providing a theoretical understanding of the complex behaviour either of natural microswimmers near a confinement boundary in a biophysical environment or of artificial swimmers in a controlled lab-on-a-chip device. The above analysis based on uniform surface slip is immediately applicable for conditions where the substrate has a coating of self-assembled monolayers of hydrophobic molecules on atomically smooth surfaces and the sliding of the first layers of molecules takes place giving rise to a phenomenon called ‘intrinsic slippage’ (Huang et al. 2008; Sega et al. 2013; Gentili et al. 2014).

However, it is worth mentioning that the present results with high slip length in the micrometre scale are to be used with caution when the characteristic length of the surface asperities of a nano-engineered surface $(\tilde{l}_{a})$ also span over the identical regime, i.e.  $\tilde{l}_{a}\sim \tilde{l}_{S}$ (Choi & Kim 2006; Joseph et al. 2006). In that case an elaborate consideration of the slip length variation along the wall may become inevitable (Ybert et al. 2007; Asmolov et al. 2013), especially when the microswimmer goes very close to the wall, i.e.  $\unicode[STIX]{x1D6FF}<l_{S}$ . Researchers have found the significant role of the actual features of a superhydrophobic wall in influencing the motion of particles, both passive or self-propelled, when the particle is very close to the wall (Pimponi et al. 2014; Hu et al. 2015; Nizkaya et al. 2015, 2020). On the other hand, molecular simulations have predicted that specially structured surfaces with nanometre scale roughness can also lead to superhydrophobicity (Lundgren, Allan & Cosgrove 2007; Yang, Tartaglino & Persson 2008; Koishi et al. 2009; Daub et al. 2010), a situation that broadens the applicability of the present research. Experimental verification of the present results can be truly intriguing. A major challenge, however, is to realize a pre-designed pattern of wall slip and probe the near-wall dynamics of micro-organisms under the influence of the same by high-resolution microscopy. This may be taken up as a novel research agenda in this field.

Moreover, beyond the presently adopted spherical squirmer model of micro-organisms, the inclusion of higher-order squirming modes (Pak & Lauga 2014) will be of interest to the community. It may also be stimulating research directions to additionally inspect the various aspects of microswimming, such as elongated shape of micro-organisms (Shum et al. 2010; Ishimoto & Gaffney 2013), direct flagellar contact dynamics (Kantsler et al. 2013) or the existence of thermal noise (Li & Tang 2009; Drescher et al. 2011; Schaar, Zöttl & Stark 2015).