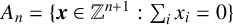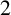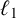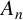1 Introduction
Let
![]() $ G $
be a finite Abelian group of order
$ G $
be a finite Abelian group of order
![]() $ |G| = v $
, written additively. A subset
$ |G| = v $
, written additively. A subset
![]() $ D \subseteq G $
of cardinality
$ D \subseteq G $
of cardinality
![]() $ k $
is said to be a
$ k $
is said to be a
![]() $ (v, k, \lambda ) $
-difference set [Reference Beth, Jungnickel and Lenz2] if every nonzero element of
$ (v, k, \lambda ) $
-difference set [Reference Beth, Jungnickel and Lenz2] if every nonzero element of
![]() $ G $
can be expressed as a difference
$ G $
can be expressed as a difference
![]() $ d_i - d_j $
of two elements from
$ d_i - d_j $
of two elements from
![]() $ D $
in exactly
$ D $
in exactly
![]() $ \lambda $
ways. The parameters
$ \lambda $
ways. The parameters
![]() $ v, k, \lambda $
then necessarily satisfy the identity
$ v, k, \lambda $
then necessarily satisfy the identity
![]() $ \lambda (v-1) = k(k-1) $
. Difference sets with parameter
$ \lambda (v-1) = k(k-1) $
. Difference sets with parameter
![]() $ \lambda = 1 $
are called planar. These objects appeared first in the work of Singer [Reference Singer8] and have attracted the interest of mathematicians ever since. The ensuing research has produced numerous beautiful results at the crossroads of algebra, combinatorics and geometry [Reference Beth, Jungnickel and Lenz2, Reference Moore and Pollatsek7], and has also found several applications, for example in coding theory [Reference Ding4]. The purpose of this note is to contribute to this line of work by providing another geometric and combinatorial interpretation of difference sets, more precisely, by showing that difference sets can be represented in a simple and natural way as sublattices of
$ \lambda = 1 $
are called planar. These objects appeared first in the work of Singer [Reference Singer8] and have attracted the interest of mathematicians ever since. The ensuing research has produced numerous beautiful results at the crossroads of algebra, combinatorics and geometry [Reference Beth, Jungnickel and Lenz2, Reference Moore and Pollatsek7], and has also found several applications, for example in coding theory [Reference Ding4]. The purpose of this note is to contribute to this line of work by providing another geometric and combinatorial interpretation of difference sets, more precisely, by showing that difference sets can be represented in a simple and natural way as sublattices of
![]() $ \mathbb {Z} ^n $
having certain packing/covering/tiling properties. Consequently, many statements involving difference sets, in particular those dealing with existence questions, can be reformulated in purely geometric terms.
$ \mathbb {Z} ^n $
having certain packing/covering/tiling properties. Consequently, many statements involving difference sets, in particular those dealing with existence questions, can be reformulated in purely geometric terms.
The
![]() $ {\boldsymbol{A}}_{\boldsymbol{n}} $
lattice under the
$ {\boldsymbol{A}}_{\boldsymbol{n}} $
lattice under the
![]() $ \mathbf {\ell _1} $
metric. A lattice in
$ \mathbf {\ell _1} $
metric. A lattice in
![]() $ \mathbb {R}^n $
is a discrete subgroup of
$ \mathbb {R}^n $
is a discrete subgroup of
![]() $ (\mathbb {R}^n, +) $
. The
$ (\mathbb {R}^n, +) $
. The
![]() $ A_n $
lattice is
$ A_n $
lattice is
 $$ \begin{align*} A_n = \bigg\{ (x_0, x_1, \ldots, x_n) \in \mathbb{Z} ^{n+1} \; : \; \sum_{i=0}^n x_i = 0 \bigg\}, \end{align*} $$
$$ \begin{align*} A_n = \bigg\{ (x_0, x_1, \ldots, x_n) \in \mathbb{Z} ^{n+1} \; : \; \sum_{i=0}^n x_i = 0 \bigg\}, \end{align*} $$
where
![]() $ \mathbb {Z} $
denotes the integers, as usual. In particular,
$ \mathbb {Z} $
denotes the integers, as usual. In particular,
![]() $ A_1 $
is equivalent to
$ A_1 $
is equivalent to
![]() $ \mathbb {Z} $
,
$ \mathbb {Z} $
,
![]() $ A_2 $
to the hexagonal lattice and
$ A_2 $
to the hexagonal lattice and
![]() $ A_3 $
to the face-centred cubic lattice [Reference Conway and Sloane3].
$ A_3 $
to the face-centred cubic lattice [Reference Conway and Sloane3].

Figure 1 Ball of radius
![]() $ 1 $
in
$ 1 $
in
![]() $ (A_2, d) $
(hexagon) and in
$ (A_2, d) $
(hexagon) and in
![]() $ (A_3, d) $
(cuboctahedron).
$ (A_3, d) $
(cuboctahedron).
The metric on
![]() $ A_n $
that we consider is essentially the
$ A_n $
that we consider is essentially the
![]() $ \ell _1 $
(also termed Manhattan or taxi) distance,
$ \ell _1 $
(also termed Manhattan or taxi) distance,
 $$ \begin{align*} d( \boldsymbol {x}, \boldsymbol {y}) = \frac{1}{2} {\lVert \boldsymbol {x} - \boldsymbol {y} \rVert}_{1} = \frac{1}{2} \sum_{i = 0}^n | x_i - y_i | , \end{align*} $$
$$ \begin{align*} d( \boldsymbol {x}, \boldsymbol {y}) = \frac{1}{2} {\lVert \boldsymbol {x} - \boldsymbol {y} \rVert}_{1} = \frac{1}{2} \sum_{i = 0}^n | x_i - y_i | , \end{align*} $$
where
![]() $ \boldsymbol {x} = ( x_0, x_1, \ldots , x_n ) $
,
$ \boldsymbol {x} = ( x_0, x_1, \ldots , x_n ) $
,
![]() $ \boldsymbol {y} = ( y_0, y_1, \ldots , y_n ) $
; the constant
$ \boldsymbol {y} = ( y_0, y_1, \ldots , y_n ) $
; the constant
![]() $ 1/2 $
is adopted for convenience because
$ 1/2 $
is adopted for convenience because
![]() $ {\lVert \boldsymbol {x} - \boldsymbol {y} \rVert }_{1} $
is always even for
$ {\lVert \boldsymbol {x} - \boldsymbol {y} \rVert }_{1} $
is always even for
![]() $ \boldsymbol {x}, \boldsymbol {y} \in A_n $
. The metric
$ \boldsymbol {x}, \boldsymbol {y} \in A_n $
. The metric
![]() $ d $
also represents the graph distance in
$ d $
also represents the graph distance in
![]() $ A_n $
. If
$ A_n $
. If
![]() $ \Gamma (A_n) $
is a graph with the vertex set
$ \Gamma (A_n) $
is a graph with the vertex set
![]() $ A_n $
and with edges joining neighbouring points (points at distance
$ A_n $
and with edges joining neighbouring points (points at distance
![]() $ 1 $
under
$ 1 $
under
![]() $ d $
), then
$ d $
), then
![]() $ d( \boldsymbol {x}, \boldsymbol {y}) $
is the length of the shortest path between
$ d( \boldsymbol {x}, \boldsymbol {y}) $
is the length of the shortest path between
![]() $ \boldsymbol {x} $
and
$ \boldsymbol {x} $
and
![]() $ \boldsymbol {y} $
in
$ \boldsymbol {y} $
in
![]() $ \Gamma (A_n) $
. The ball of radius
$ \Gamma (A_n) $
. The ball of radius
![]() $ 1 $
around
$ 1 $
around
![]() $ \boldsymbol {x} \in A_n $
contains
$ \boldsymbol {x} \in A_n $
contains
![]() $ 2 {n+1 \choose 2} + 1 = n^2 + n + 1 $
points of the form
$ 2 {n+1 \choose 2} + 1 = n^2 + n + 1 $
points of the form
![]() $ \boldsymbol {x} + \boldsymbol {f}_{i,j} $
, where
$ \boldsymbol {x} + \boldsymbol {f}_{i,j} $
, where
![]() $ \boldsymbol {f}_{i,j} $
is the vector having
$ \boldsymbol {f}_{i,j} $
is the vector having
![]() $ 1 $
at the
$ 1 $
at the
![]() $ i $
th coordinate,
$ i $
th coordinate,
![]() $ -1 $
at the
$ -1 $
at the
![]() $ j $
th coordinate and zeros elsewhere (by convention,
$ j $
th coordinate and zeros elsewhere (by convention,
![]() $ \boldsymbol {f}_{i,i} = \textbf {0} $
) (see Figure 1). The convex interior of the points in this ball forms a highly symmetrical polytope with the property that the distance between any vertex and the centre is equal to the distance between any two neighbouring vertices.
$ \boldsymbol {f}_{i,i} = \textbf {0} $
) (see Figure 1). The convex interior of the points in this ball forms a highly symmetrical polytope with the property that the distance between any vertex and the centre is equal to the distance between any two neighbouring vertices.
Remark 1.1. For the purpose of studying packing and covering problems, it is sometimes more convenient to visualise
![]() $ \mathbb {Z}^n $
instead of an arbitrary lattice. In our case, there is a simple mapping that makes the transition to
$ \mathbb {Z}^n $
instead of an arbitrary lattice. In our case, there is a simple mapping that makes the transition to
![]() $ \mathbb {Z}^n $
and back very easy, namely
$ \mathbb {Z}^n $
and back very easy, namely
![]() $ \boldsymbol {x} = (x_0, x_1, \ldots , x_n) \mapsto \boldsymbol {x}' = (x_1, \ldots , x_n) $
. If we define the following metric on
$ \boldsymbol {x} = (x_0, x_1, \ldots , x_n) \mapsto \boldsymbol {x}' = (x_1, \ldots , x_n) $
. If we define the following metric on
![]() $ \mathbb {Z} ^n $
:
$ \mathbb {Z} ^n $
:
 $$ \begin{align*} d^+ ( \boldsymbol {x}', \boldsymbol {y}') = \max \bigg\{ \sum_{\substack{ i = 1 \\ x_i> y_i}}^n (x_i - y_i) , \sum_{\substack{ i = 1 \\ x_i < y_i}}^n (y_i - x_i) \bigg\} , \end{align*} $$
$$ \begin{align*} d^+ ( \boldsymbol {x}', \boldsymbol {y}') = \max \bigg\{ \sum_{\substack{ i = 1 \\ x_i> y_i}}^n (x_i - y_i) , \sum_{\substack{ i = 1 \\ x_i < y_i}}^n (y_i - x_i) \bigg\} , \end{align*} $$
then it is not difficult to show that the above mapping is an isometry between
![]() $ (A_n, d) $
and
$ (A_n, d) $
and
![]() $ (\mathbb {Z}^n, d^+ ) $
[Reference Kovačević and Tan6, Theorem 4]. Consequently, packing and similar problems in
$ (\mathbb {Z}^n, d^+ ) $
[Reference Kovačević and Tan6, Theorem 4]. Consequently, packing and similar problems in
![]() $ (A_n, d) $
are equivalent to those in
$ (A_n, d) $
are equivalent to those in
![]() $ (\mathbb {Z}^n, d^+ ) $
.
$ (\mathbb {Z}^n, d^+ ) $
.
2
 $ (v, k, \lambda ) $
-difference sets and coverings of
$ (v, k, \lambda ) $
-difference sets and coverings of
 $ A_n $
$ A_n $
In the following, when using notions from graph theory in our setting, we have in mind the graph representation
![]() $ \Gamma (A_n) $
of
$ \Gamma (A_n) $
of
![]() $ A_n $
, as introduced in Section 1. An
$ A_n $
, as introduced in Section 1. An
![]() $ (r, i, j) $
-cover in a graph
$ (r, i, j) $
-cover in a graph
![]() $ \Gamma = (V, E) $
[Reference Axenovich1] is a set of its vertices
$ \Gamma = (V, E) $
[Reference Axenovich1] is a set of its vertices
![]() $ S \subseteq V $
having the property that every element of
$ S \subseteq V $
having the property that every element of
![]() $ S $
, respectively
$ S $
, respectively
![]() $ V \setminus S $
, is covered by exactly
$ V \setminus S $
, is covered by exactly
![]() $ i $
, respectively
$ i $
, respectively
![]() $ j $
, balls of radius r centred at elements of
$ j $
, balls of radius r centred at elements of
![]() $ S $
. Special cases of such sets, namely
$ S $
. Special cases of such sets, namely
![]() $ (1, i, j) $
covers, have also been studied in the context of domination in graphs [Reference Telle10]. Note also that an
$ (1, i, j) $
covers, have also been studied in the context of domination in graphs [Reference Telle10]. Note also that an
![]() $ (r, 1, 1) $
-cover is a tiling of
$ (r, 1, 1) $
-cover is a tiling of
![]() $ V $
with balls of radius
$ V $
with balls of radius
![]() $ r $
(in coding theory, this is known as an
$ r $
(in coding theory, this is known as an
![]() $ r $
-perfect code). An independent set in a graph
$ r $
-perfect code). An independent set in a graph
![]() $ \Gamma = (V, E) $
is a subset of its vertices
$ \Gamma = (V, E) $
is a subset of its vertices
![]() $ I \subseteq V $
, no two of which are adjacent in
$ I \subseteq V $
, no two of which are adjacent in
![]() $ \Gamma $
.
$ \Gamma $
.
We now state our main result. The proof is a generalisation of the connection between lattice packing/tiling and so-called group splitting [Reference Stein and Szabó9].
Theorem 2.1. There exists an Abelian
![]() $ (v, n+1, \lambda ) $
-difference set if and only if the lattice
$ (v, n+1, \lambda ) $
-difference set if and only if the lattice
![]() $ A_{n} $
contains a
$ A_{n} $
contains a
![]() $ (1, 1, \lambda ) $
-covering sublattice.
$ (1, 1, \lambda ) $
-covering sublattice.
Proof. Suppose that
![]() $ D = \{ d_0, d_1, \ldots , d_{n} \} $
is a
$ D = \{ d_0, d_1, \ldots , d_{n} \} $
is a
![]() $ (v, n+1, \lambda ) $
-difference set in an Abelian group
$ (v, n+1, \lambda ) $
-difference set in an Abelian group
![]() $ G $
and consider the sublattice
$ G $
and consider the sublattice
 $$ \begin{align} {\mathcal L}_D = \bigg\{ \boldsymbol {x} \in A_{n} : \sum_{i=0}^{n} x_i d_i = 0 \bigg\} , \end{align} $$
$$ \begin{align} {\mathcal L}_D = \bigg\{ \boldsymbol {x} \in A_{n} : \sum_{i=0}^{n} x_i d_i = 0 \bigg\} , \end{align} $$
where
![]() $ x_i d_i $
denotes the sum in
$ x_i d_i $
denotes the sum in
![]() $ G $
of
$ G $
of
![]() $ |x_i| $
copies of
$ |x_i| $
copies of
![]() $ d_i $
, respectively
$ d_i $
, respectively
![]() $ -d_i $
, if
$ -d_i $
, if
![]() $ x_i> 0 $
, respectively
$ x_i> 0 $
, respectively
![]() $ x_i < 0 $
. Let us show that
$ x_i < 0 $
. Let us show that
![]() $ {\mathcal L}_D $
is a
$ {\mathcal L}_D $
is a
![]() $ (1, 1, \lambda ) $
-cover of
$ (1, 1, \lambda ) $
-cover of
![]() $ A_{n} $
. Consider a point
$ A_{n} $
. Consider a point
![]() $ \boldsymbol {y} = (y_0, y_1, \ldots , y_{n}) \notin {\mathcal L}_D $
, meaning that
$ \boldsymbol {y} = (y_0, y_1, \ldots , y_{n}) \notin {\mathcal L}_D $
, meaning that
![]() $ \sum _{i=0}^n y_i d_i = a \in G $
,
$ \sum _{i=0}^n y_i d_i = a \in G $
,
![]() $ a \neq 0 $
. The neighbours of
$ a \neq 0 $
. The neighbours of
![]() $ \boldsymbol {y} $
are of the form
$ \boldsymbol {y} $
are of the form
![]() $ \boldsymbol {y} + \boldsymbol {f}_{i,j} $
,
$ \boldsymbol {y} + \boldsymbol {f}_{i,j} $
,
![]() $ i \neq j $
(recall that
$ i \neq j $
(recall that
![]() $ \boldsymbol {f}_{i,j} $
denotes the vector having
$ \boldsymbol {f}_{i,j} $
denotes the vector having
![]() $ 1 $
at the
$ 1 $
at the
![]() $ i $
th coordinate,
$ i $
th coordinate,
![]() $ -1 $
at the
$ -1 $
at the
![]() $ j $
th coordinate and zeros elsewhere). Because
$ j $
th coordinate and zeros elsewhere). Because
![]() $ D $
is a difference set,
$ D $
is a difference set,
![]() $ -a \in G $
can be written as a difference of two elements from
$ -a \in G $
can be written as a difference of two elements from
![]() $ D $
in exactly
$ D $
in exactly
![]() $ \lambda $
ways, meaning that there are
$ \lambda $
ways, meaning that there are
![]() $ \lambda $
different pairs
$ \lambda $
different pairs
![]() $ (s,t) $
for which
$ (s,t) $
for which
![]() $ d_s - d_t = -a $
,
$ d_s - d_t = -a $
,
![]() $ d_s, d_t \in D $
. For every such pair, consider the point
$ d_s, d_t \in D $
. For every such pair, consider the point
![]() $ \boldsymbol {z}_{s,t} = \boldsymbol {y} + \boldsymbol {f}_{s,t} $
. Note that
$ \boldsymbol {z}_{s,t} = \boldsymbol {y} + \boldsymbol {f}_{s,t} $
. Note that
![]() $ \boldsymbol {z}_{s,t} \in {\mathcal L}_D $
because
$ \boldsymbol {z}_{s,t} \in {\mathcal L}_D $
because
![]() $ \sum _{i=0}^n z_i d_i = \sum _{i=0}^n y_i d_i + d_s - d_t = a - a = 0 $
. Therefore, there are exactly
$ \sum _{i=0}^n z_i d_i = \sum _{i=0}^n y_i d_i + d_s - d_t = a - a = 0 $
. Therefore, there are exactly
![]() $ \lambda $
points in the lattice
$ \lambda $
points in the lattice
![]() $ {\mathcal L}_D $
that are adjacent to
$ {\mathcal L}_D $
that are adjacent to
![]() $ \boldsymbol {y} $
, that is, such that balls of radius
$ \boldsymbol {y} $
, that is, such that balls of radius
![]() $ 1 $
around them cover
$ 1 $
around them cover
![]() $ \boldsymbol {y} $
. To show that the elements of
$ \boldsymbol {y} $
. To show that the elements of
![]() $ {\mathcal L}_D $
are covered only by the balls around themselves (that is,
$ {\mathcal L}_D $
are covered only by the balls around themselves (that is,
![]() $ {\mathcal L}_D $
is an independent set in
$ {\mathcal L}_D $
is an independent set in
![]() $ \Gamma (A_n) $
), note that if there were two points at distance
$ \Gamma (A_n) $
), note that if there were two points at distance
![]() $ 1 $
in
$ 1 $
in
![]() $ {\mathcal L}_D $
, then, by the same argument as above, we would obtain
$ {\mathcal L}_D $
, then, by the same argument as above, we would obtain
![]() $ d_s - d_t = 0 $
, that is,
$ d_s - d_t = 0 $
, that is,
![]() $ d_s = d_t $
for some
$ d_s = d_t $
for some
![]() $ s \neq t $
, which is not possible if
$ s \neq t $
, which is not possible if
![]() $ | D | = n + 1 $
.
$ | D | = n + 1 $
.
For the other direction, assume that
![]() $ {\mathcal L} $
is a
$ {\mathcal L} $
is a
![]() $ (1, 1, \lambda ) $
-covering sublattice of
$ (1, 1, \lambda ) $
-covering sublattice of
![]() $ A_{n} $
. Consider the quotient group
$ A_{n} $
. Consider the quotient group
![]() $ G = A_{n} / {\mathcal L} $
and take
$ G = A_{n} / {\mathcal L} $
and take
![]() $ D_{\mathcal L} = \{ d_0, d_1, \ldots , d_{n} \} \subseteq G $
, where
$ D_{\mathcal L} = \{ d_0, d_1, \ldots , d_{n} \} \subseteq G $
, where
![]() $ d_i = [\kern2pt \boldsymbol {f}_{i,0}] \equiv \boldsymbol {f}_{i,0} + {\mathcal L} $
are cosets (elements of
$ d_i = [\kern2pt \boldsymbol {f}_{i,0}] \equiv \boldsymbol {f}_{i,0} + {\mathcal L} $
are cosets (elements of
![]() $ G $
). Let us first check that all the
$ G $
). Let us first check that all the
![]() $ d_i $
terms are distinct. Suppose that
$ d_i $
terms are distinct. Suppose that
![]() $ d_s = d_t $
for some
$ d_s = d_t $
for some
![]() $ s \neq t $
. This implies that
$ s \neq t $
. This implies that
![]() ${ d_s - d_t = [\kern2pt \boldsymbol {f}_{s,t}] = [ \boldsymbol {0}] }$
, which means that
${ d_s - d_t = [\kern2pt \boldsymbol {f}_{s,t}] = [ \boldsymbol {0}] }$
, which means that
![]() $ \boldsymbol {f}_{s,t} \in {\mathcal L} $
. However, because
$ \boldsymbol {f}_{s,t} \in {\mathcal L} $
. However, because
![]() $ \boldsymbol {0} \in {\mathcal L} $
and
$ \boldsymbol {0} \in {\mathcal L} $
and
![]() $ \boldsymbol {0} $
and
$ \boldsymbol {0} $
and
![]() $ \boldsymbol {f}_{s,t} $
are at distance
$ \boldsymbol {f}_{s,t} $
are at distance
![]() $ 1 $
, this would contradict the fact that
$ 1 $
, this would contradict the fact that
![]() $ {\mathcal L} $
is an independent set in
$ {\mathcal L} $
is an independent set in
![]() $ \Gamma (A_n) $
. Hence,
$ \Gamma (A_n) $
. Hence,
![]() $ | D_{\mathcal L} | = n + 1 $
. Now take any nonzero element of
$ | D_{\mathcal L} | = n + 1 $
. Now take any nonzero element of
![]() $ G $
, say
$ G $
, say
![]() $ [ \kern2pt\boldsymbol {y}] $
,
$ [ \kern2pt\boldsymbol {y}] $
,
![]() $ \boldsymbol {y} \notin {\mathcal L} $
. By assumption,
$ \boldsymbol {y} \notin {\mathcal L} $
. By assumption,
![]() $ \boldsymbol {y} $
is covered by exactly
$ \boldsymbol {y} $
is covered by exactly
![]() $ \lambda $
elements of
$ \lambda $
elements of
![]() $ {\mathcal L} $
, that is,
$ {\mathcal L} $
, that is,
![]() $ \boldsymbol {y} + \boldsymbol {f}_{s,t} \in {\mathcal L} $
for exactly
$ \boldsymbol {y} + \boldsymbol {f}_{s,t} \in {\mathcal L} $
for exactly
![]() $ \lambda $
vectors
$ \lambda $
vectors
![]() $ \boldsymbol {f}_{s,t} $
. Because
$ \boldsymbol {f}_{s,t} $
. Because
![]() $ \boldsymbol {f}_{s,t} = \boldsymbol {f}_{s,0} - \boldsymbol {f}_{t,0} $
, this means that
$ \boldsymbol {f}_{s,t} = \boldsymbol {f}_{s,0} - \boldsymbol {f}_{t,0} $
, this means that
![]() $ d_t - d_s = [\kern2pt \boldsymbol {f}_{t,0}] - [\kern2pt \boldsymbol {f}_{s,0}] = [ \kern2pt\boldsymbol {y}] $
for exactly
$ d_t - d_s = [\kern2pt \boldsymbol {f}_{t,0}] - [\kern2pt \boldsymbol {f}_{s,0}] = [ \kern2pt\boldsymbol {y}] $
for exactly
![]() $ \lambda $
pairs
$ \lambda $
pairs
![]() $ (s,t) $
. Therefore,
$ (s,t) $
. Therefore,
![]() $ D_{\mathcal L} $
is a
$ D_{\mathcal L} $
is a
![]() $ (v, n + 1, \lambda ) $
-difference set.
$ (v, n + 1, \lambda ) $
-difference set.
Note that we have not specified the order of the elements of
![]() $ D $
when defining the corresponding lattice
$ D $
when defining the corresponding lattice
![]() $ {\mathcal L}_D $
in (2.1) because it would only affect it in an insignificant way. Note also that if we write
$ {\mathcal L}_D $
in (2.1) because it would only affect it in an insignificant way. Note also that if we write
![]() $ d_i' = zd_i + g $
instead of
$ d_i' = zd_i + g $
instead of
![]() $ d_i $
in (2.1), where
$ d_i $
in (2.1), where
![]() $ z $
is a fixed integer coprime with
$ z $
is a fixed integer coprime with
![]() $ v $
and
$ v $
and
![]() $ g $
is a fixed element of
$ g $
is a fixed element of
![]() $ G $
, the same lattice is obtained because
$ G $
, the same lattice is obtained because
 $$ \begin{align*} \sum_{i=0}^{n} x_i d_i = 0 \quad \Leftrightarrow \quad \sum_{i=0}^{n} x_i d_i' = 0 , \end{align*} $$
$$ \begin{align*} \sum_{i=0}^{n} x_i d_i = 0 \quad \Leftrightarrow \quad \sum_{i=0}^{n} x_i d_i' = 0 , \end{align*} $$
which follows from
![]() $ \sum _{i=0}^{n} x_i = 0 $
and
$ \sum _{i=0}^{n} x_i = 0 $
and
![]() $ \operatorname {gcd}(z, v) = 1 $
. (Recall that two difference sets
$ \operatorname {gcd}(z, v) = 1 $
. (Recall that two difference sets
![]() $ D $
and
$ D $
and
![]() $ D' $
in an Abelian group
$ D' $
in an Abelian group
![]() $ G $
are said to be equivalent [Reference Beth, Jungnickel and Lenz2, Remark 1.11, page 302] if
$ G $
are said to be equivalent [Reference Beth, Jungnickel and Lenz2, Remark 1.11, page 302] if
![]() $ D' = \{ zd + g: d \in D \} $
, for some
$ D' = \{ zd + g: d \in D \} $
, for some
![]() $ z \in \mathbb {Z} $
coprime with
$ z \in \mathbb {Z} $
coprime with
![]() $ v = |G| $
and some
$ v = |G| $
and some
![]() $ g \in G $
.)
$ g \in G $
.)

Figure 2 A
![]() $ (1, 1, 2) $
-covering sublattice of
$ (1, 1, 2) $
-covering sublattice of
![]() $ A_2 $
, representing the difference set
$ A_2 $
, representing the difference set
![]() $ D = \{ 0, 1, 2 \} \subset \mathbb {Z}_4 $
.
$ D = \{ 0, 1, 2 \} \subset \mathbb {Z}_4 $
.
Geometrically, the theorem states that balls of radius
![]() $ 1 $
around the points of the sublattice
$ 1 $
around the points of the sublattice
![]() $ {\mathcal L}_D $
overlap in such a way that every point that does not belong to
$ {\mathcal L}_D $
overlap in such a way that every point that does not belong to
![]() $ {\mathcal L}_D $
is covered by exactly
$ {\mathcal L}_D $
is covered by exactly
![]() $ \lambda $
balls. (The points in
$ \lambda $
balls. (The points in
![]() $ {\mathcal L}_D $
(centres of the balls) are covered by one ball only, and hence this notion is different from multitiling [Reference Gravin, Robins and Shiryaev5].) Note that increasing
$ {\mathcal L}_D $
(centres of the balls) are covered by one ball only, and hence this notion is different from multitiling [Reference Gravin, Robins and Shiryaev5].) Note that increasing
![]() $ \lambda $
increases the density of the lattice
$ \lambda $
increases the density of the lattice
![]() $ {\mathcal L}_D $
in
$ {\mathcal L}_D $
in
![]() $ A_{n} $
. The densest such lattice is therefore obtained for
$ A_{n} $
. The densest such lattice is therefore obtained for
![]() $ \lambda = n + 1 $
(which is the maximum value because
$ \lambda = n + 1 $
(which is the maximum value because
![]() $ \lambda (v-1) = n(n+1) $
and
$ \lambda (v-1) = n(n+1) $
and
![]() ${n \leq v - 1}$
). It corresponds to the trivial
${n \leq v - 1}$
). It corresponds to the trivial
![]() $ (v,v,v) $
-difference set
$ (v,v,v) $
-difference set
![]() $ D = G $
in an arbitrary Abelian group
$ D = G $
in an arbitrary Abelian group
![]() $ G $
.
$ G $
.
Example 2.2.
![]() $ D = \{ 0, 1, 2 \} $
is a
$ D = \{ 0, 1, 2 \} $
is a
![]() $ (4, 3, 2) $
-difference set in the cyclic group
$ (4, 3, 2) $
-difference set in the cyclic group
![]() $ \mathbb {Z}_4 $
. A
$ \mathbb {Z}_4 $
. A
![]() $ (1, 1, 2) $
-covering sublattice
$ (1, 1, 2) $
-covering sublattice
![]() $ {\mathcal L}_D \subset A_2 $
corresponding to this difference set (see (2.1)) is illustrated in Figure 2. Points in
$ {\mathcal L}_D \subset A_2 $
corresponding to this difference set (see (2.1)) is illustrated in Figure 2. Points in
![]() $ {\mathcal L}_D $
are depicted as black and those in
$ {\mathcal L}_D $
are depicted as black and those in
![]() $ A_2\setminus {\mathcal L}_D $
as white dots. For illustration, Figure 3 shows an example of a
$ A_2\setminus {\mathcal L}_D $
as white dots. For illustration, Figure 3 shows an example of a
![]() $ (1, \boldsymbol {3}, 2) $
-covering sublattice of
$ (1, \boldsymbol {3}, 2) $
-covering sublattice of
![]() $ A_2 $
, which does not represent any difference set.
$ A_2 $
, which does not represent any difference set.

Figure 3 A
![]() $ (1, 3, 2) $
-covering sublattice of
$ (1, 3, 2) $
-covering sublattice of
![]() $ A_2 $
.
$ A_2 $
.
3 Planar difference sets and tilings of
 $ A_n $
$ A_n $
A
![]() $ (v, k, 1) $
-difference set
$ (v, k, 1) $
-difference set
![]() $ D \subseteq G $
is called planar (or simple). The condition
$ D \subseteq G $
is called planar (or simple). The condition
![]() $ \lambda = 1 $
means that every nonzero element of the group
$ \lambda = 1 $
means that every nonzero element of the group
![]() $ G $
can be expressed as a difference of two elements from
$ G $
can be expressed as a difference of two elements from
![]() $ D $
in a unique way. In this case, we necessarily have
$ D $
in a unique way. In this case, we necessarily have
![]() $ v = |G| = k^2 - k + 1 $
. The order of a planar difference set
$ v = |G| = k^2 - k + 1 $
. The order of a planar difference set
![]() $ D $
of cardinality
$ D $
of cardinality
![]() $ k $
is defined as
$ k $
is defined as
![]() $ k - 1 $
. These objects are very well-studied, and a large body of literature is devoted to their constructions and investigation of their properties [Reference Beth, Jungnickel and Lenz2]. One of the most well-known problems in the area concerning the existence of planar difference sets for specific sets of parameters is the so-called prime power conjecture [Reference Beth, Jungnickel and Lenz2, Conjecture 7.5, page 346], which states that a planar difference set of order
$ k - 1 $
. These objects are very well-studied, and a large body of literature is devoted to their constructions and investigation of their properties [Reference Beth, Jungnickel and Lenz2]. One of the most well-known problems in the area concerning the existence of planar difference sets for specific sets of parameters is the so-called prime power conjecture [Reference Beth, Jungnickel and Lenz2, Conjecture 7.5, page 346], which states that a planar difference set of order
![]() $ n $
exists if and only if
$ n $
exists if and only if
![]() $ n $
is a prime power (counting
$ n $
is a prime power (counting
![]() $ n = 1 $
as a prime power). Existence of such sets for
$ n = 1 $
as a prime power). Existence of such sets for
![]() $ n = p^m $
,
$ n = p^m $
,
![]() $ p $
prime,
$ p $
prime,
![]() $ m \in \mathbb {N} $
, was demonstrated by Singer [Reference Singer8], but the necessity of this condition remains an open problem for over eight decades.
$ m \in \mathbb {N} $
, was demonstrated by Singer [Reference Singer8], but the necessity of this condition remains an open problem for over eight decades.
As we noted earlier, a
![]() $ (1, 1, 1) $
-cover of
$ (1, 1, 1) $
-cover of
![]() $ A_n $
is in fact a tiling of
$ A_n $
is in fact a tiling of
![]() $ (A_n, d) $
with balls of radius
$ (A_n, d) $
with balls of radius
![]() $ 1 $
, meaning that every point in
$ 1 $
, meaning that every point in
![]() $ A_n $
is covered by exactly one ball. If the centres of the balls form a sublattice of
$ A_n $
is covered by exactly one ball. If the centres of the balls form a sublattice of
![]() $ A_n $
, then this is said to be a lattice tiling. We can now state what Theorem 2.1 reduces to in the special case
$ A_n $
, then this is said to be a lattice tiling. We can now state what Theorem 2.1 reduces to in the special case
![]() $ \lambda = 1 $
.
$ \lambda = 1 $
.
Corollary 3.1. There exists an Abelian planar difference set of order
![]() $ n $
if and only if the space
$ n $
if and only if the space
![]() $ (A_n, d) $
admits a lattice tiling with balls of radius
$ (A_n, d) $
admits a lattice tiling with balls of radius
![]() $ 1 $
.
$ 1 $
.
Existence of such tilings when
![]() $ n $
is a prime power follows from the existence of the corresponding planar difference sets [Reference Singer8], but the necessity of this condition is open and is equivalent to the prime power conjecture.
$ n $
is a prime power follows from the existence of the corresponding planar difference sets [Reference Singer8], but the necessity of this condition is open and is equivalent to the prime power conjecture.
Conjecture 3.2 (Prime power conjecture).
The space
![]() $ (A_n, d) $
admits a lattice tiling with balls of radius
$ (A_n, d) $
admits a lattice tiling with balls of radius
![]() $ 1 $
if and only if the dimension
$ 1 $
if and only if the dimension
![]() $ n $
is a prime power.
$ n $
is a prime power.
A stronger conjecture would claim the above even for nonlattice tilings.
Example 3.3. Consider a planar difference set
![]() $ D = \{0, 1, 3, 9\} \subset \mathbb {Z}_{13} $
. The corresponding lattice tiling of
$ D = \{0, 1, 3, 9\} \subset \mathbb {Z}_{13} $
. The corresponding lattice tiling of
![]() $ (A_3, d) $
is illustrated in Figure 4(a). The figure shows the intersection of
$ (A_3, d) $
is illustrated in Figure 4(a). The figure shows the intersection of
![]() $ A_3 $
with the plane
$ A_3 $
with the plane
![]() $ x_0 = 0 $
; the intersections of a ball of radius
$ x_0 = 0 $
; the intersections of a ball of radius
![]() $ 1 $
in
$ 1 $
in
![]() $ (A_3, d) $
with the planes
$ (A_3, d) $
with the planes
![]() $ x_0 = \text {const.} $
are shown in Figure 4(b) as a clarification.
$ x_0 = \text {const.} $
are shown in Figure 4(b) as a clarification.

Figure 4 Lattice tiling of
![]() $ (A_3, d) $
corresponding to the difference set
$ (A_3, d) $
corresponding to the difference set
![]() $ D = \{0, 1, 3, 9\} \subset \mathbb {Z}_{13} $
.
$ D = \{0, 1, 3, 9\} \subset \mathbb {Z}_{13} $
.
Corollary 3.1 and Example 3.3 were also stated in [Reference Kovačević and Tan6] by using coding theoretic terminology.
Another important unsolved problem in the field is the following: all Abelian planar difference sets live in cyclic groups [Reference Beth, Jungnickel and Lenz2, Conjecture 7.7, page 346]. Because the group
![]() $ G $
containing a difference set
$ G $
containing a difference set
![]() $ D $
which defines a lattice
$ D $
which defines a lattice
![]() $ {\mathcal L}_D $
is isomorphic to
$ {\mathcal L}_D $
is isomorphic to
![]() $ A_n/{\mathcal L}_D $
, the statement that
$ A_n/{\mathcal L}_D $
, the statement that
![]() $ G $
is cyclic, that is, that it has a generator, is equivalent to the following statement.
$ G $
is cyclic, that is, that it has a generator, is equivalent to the following statement.
Conjecture 3.4 (All Abelian planar difference sets are cyclic).
Suppose a lattice
![]() $ \mathcal L \subset A_n $
defines a lattice tiling of
$ \mathcal L \subset A_n $
defines a lattice tiling of
![]() $ (A_n, d) $
with balls of radius
$ (A_n, d) $
with balls of radius
![]() $ 1 $
. Then the period of
$ 1 $
. Then the period of
![]() $ \mathcal L $
in
$ \mathcal L $
in
![]() $ A_n $
along the direction
$ A_n $
along the direction
![]() $ \boldsymbol {f}_{i,j} $
is equal to
$ \boldsymbol {f}_{i,j} $
is equal to
![]() $ n^2 + n + 1 $
for at least one vector
$ n^2 + n + 1 $
for at least one vector
![]() $ \boldsymbol {f}_{i,j} $
,
$ \boldsymbol {f}_{i,j} $
,
![]() $ (i,j) \in \{0, 1, \ldots , n\}^2 $
.
$ (i,j) \in \{0, 1, \ldots , n\}^2 $
.
The cyclic case. To conclude the paper, let us consider briefly the case of cyclic planar difference sets of order
![]() $ n $
, where it is assumed that the group we are working with is
$ n $
, where it is assumed that the group we are working with is
![]() $ \mathbb {Z}_v $
,
$ \mathbb {Z}_v $
,
![]() $ v = n^2 + n + 1 $
. As mentioned above, the restriction to cyclic groups might not be a restriction at all. So let
$ v = n^2 + n + 1 $
. As mentioned above, the restriction to cyclic groups might not be a restriction at all. So let
![]() $ D = \{ d_0, d_1, \ldots , d_n \} \subset \mathbb {Z}_v $
be a difference set and assume that
$ D = \{ d_0, d_1, \ldots , d_n \} \subset \mathbb {Z}_v $
be a difference set and assume that
![]() $ d_0 = 0 $
,
$ d_0 = 0 $
,
![]() $ d_1 = 1 $
. (This is not a loss in generality because if
$ d_1 = 1 $
. (This is not a loss in generality because if
![]() $ D $
is a difference set, then there exist two elements, say
$ D $
is a difference set, then there exist two elements, say
![]() $ d_0, d_1 \in D $
, such that
$ d_0, d_1 \in D $
, such that
![]() $ d_1 - d_0 = 1 $
, so one can instead consider the equivalent difference set
$ d_1 - d_0 = 1 $
, so one can instead consider the equivalent difference set
![]() $ D' = \{ d_i - d_0 : d_i \in D \} $
which obviously contains
$ D' = \{ d_i - d_0 : d_i \in D \} $
which obviously contains
![]() $ 0 $
and
$ 0 $
and
![]() $ 1 $
.) Let
$ 1 $
.) Let
![]() $ {\mathcal L}_D \subset \mathbb {Z} ^n $
be the lattice defined as in (2.1), but with the
$ {\mathcal L}_D \subset \mathbb {Z} ^n $
be the lattice defined as in (2.1), but with the
![]() $ 0 $
-coordinate of all vectors left out (the latter is done for convenience, because
$ 0 $
-coordinate of all vectors left out (the latter is done for convenience, because
![]() $ d_0 = 0 $
). Leaving out the
$ d_0 = 0 $
). Leaving out the
![]() $ 0 $
-coordinate essentially transforms the space
$ 0 $
-coordinate essentially transforms the space
![]() $ (A_n, d) $
to
$ (A_n, d) $
to
![]() $ (\mathbb {Z}^n, d^+ ) $
(see Remark 1.1). The generator matrix of the lattice
$ (\mathbb {Z}^n, d^+ ) $
(see Remark 1.1). The generator matrix of the lattice
![]() $ {\mathcal L}_D $
can then be written in the following simple and explicit form:
$ {\mathcal L}_D $
can then be written in the following simple and explicit form:
 $$ \begin{align*} B({\mathcal L}_D) = \begin{pmatrix} v & 0 & 0 & \cdots & 0 \\ -d_2 & 1 & 0 & \cdots & 0 \\ -d_3 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -d_n & 0 & 0 & \cdots & 1 \end{pmatrix} , \end{align*} $$
$$ \begin{align*} B({\mathcal L}_D) = \begin{pmatrix} v & 0 & 0 & \cdots & 0 \\ -d_2 & 1 & 0 & \cdots & 0 \\ -d_3 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -d_n & 0 & 0 & \cdots & 1 \end{pmatrix} , \end{align*} $$
that is, the elements of the lattice are the vectors
![]() $ \boldsymbol {x} = \boldsymbol {\xi } \cdot B({\mathcal L}_D) $
,
$ \boldsymbol {x} = \boldsymbol {\xi } \cdot B({\mathcal L}_D) $
,
![]() $ \boldsymbol {\xi } \in \mathbb {Z}^n $
. The generator matrix of the dual lattice
$ \boldsymbol {\xi } \in \mathbb {Z}^n $
. The generator matrix of the dual lattice
![]() $ {\mathcal L}_D^* $
is
$ {\mathcal L}_D^* $
is
 $$ \begin{align*} B({\mathcal L}_D^*) = B({\mathcal L}_D)^{-{T}} = \begin{pmatrix} {1}/{v} & {d_2}/{v} & {d_3}/{v} & \cdots & {d_n}/{v} \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} B({\mathcal L}_D^*) = B({\mathcal L}_D)^{-{T}} = \begin{pmatrix} {1}/{v} & {d_2}/{v} & {d_3}/{v} & \cdots & {d_n}/{v} \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end{pmatrix}. \end{align*} $$