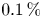Global stochastic optimization of stellarator coil configurations

Abstract

In the construction of a stellarator, the manufacturing and assembling of the coil system is a dominant cost. These coils need to satisfy strict engineering tolerances, and if those are not met the project could be cancelled as in the case of the National Compact Stellarator Experiment (NCSX) project (R.L. Orbach, 2008, https://ncsx.pppl.gov/DOE_NCSX_052208.pdf). Therefore, our goal is to find coil configurations that increase construction tolerances without compromising the performance of the magnetic field. In this paper, we develop a gradient-based stochastic optimization model which seeks robust stellarator coil configurations in high dimensions. In particular, we design a two-step method: first, we perform an approximate global search by a sample efficient trust-region Bayesian optimization; second, we refine the minima found in step one with a stochastic local optimizer. To this end, we introduce two stochastic local optimizers: BFGS applied to the sample average approximation; and Adam, equipped with a control variate for variance reduction. Numerical simulations performed on a W7-X-like coil configuration demonstrate that our global optimization approach finds a variety of promising local solutions at less than $0.1\,\%$ of the cost of previous work, which considered solely local stochastic optimization.

1. Introduction

The design process of finding promising stellarator coil configurations is traditionally split into two steps. First, one aims to find the optimal plasma shape with respect to performance criteria such as, for example, the magnetohydrodynamic stability or alpha particle confinement. For the second step – the coil design – one tries to reproduce the target magnetic field confining the plasma. Construction and placement of these coils are difficult tasks since minor errors in the fabrication or alignment can lead to major modifications of the magnetic field and thus poor particle confinement (Andreeva et al. 2009; Lobsien, Drevlak & Pedersen 2018).

To be able to guarantee good confinement when the stellarator is in operation, stringent engineering tolerances on the coils are required during the stellarator fabrication and assembly process. Unfortunately, such stringent tolerances can increase the cost and production timeline of a stellarator, which is what led to the cancellation of the National Compact Stellarator Experiment (NCSX) project (Orbach 2008). During the Columbia Non-neutral Torus (CNT) design, a stochastic perturbation analysis was used to identify the robustness of coil-induced magnetic fields to coil alignment errors (Kremer 2007). This allowed the reduction of engineering coil tolerances significantly (Kremer et al. 2003). Furthermore, recent work has shown that stochastic optimization is a promising method to improve the robustness of the generated magnetic field to fabrication and alignment errors in the associated coils (Lobsien et al. 2020; Wechsung et al. 2021). However, all aforementioned approaches do not globally explore the coil design space. Indeed, design engineers are usually interested in having not only one, but multiple designs to choose from. In addition to the magnetic field, engineers care about other physical properties such as specific aspect ratio and rotational transforms; see figure 1 for an example of different coils. Thus, there is a need for efficient stochastic methods for global exploration in order to provide multiple coil configurations in the design process.

Figure 1. Variety of stochastic minima derived with DTuRBO and AdamCV (D-ACV).

In this work, we develop an algorithm for the efficient global stochastic optimization of stellarator coil configurations. We seek a coil set that is robust to random errors in the coils in expectation,

(1.1a)\begin{align} \min_{\boldsymbol{x} \in \mathbb{R}^{N}}& \quad \mathbb{E}[f_\text{stoc}(\boldsymbol{x}+\boldsymbol{U})] + f_{\text{reg}}(\boldsymbol{x}) \end{align}

(1.1b)\begin{align} & \quad c_i(\boldsymbol{x}) \ge \epsilon_i \quad i=1,\ldots,N_C-1, \end{align}

where $\boldsymbol {x}\in \mathbb {R}^{N}$ defines the geometry of the coil set; $\boldsymbol {U}$ is a random error to the coils; $\mathbb {E}$ is the expectation over $\boldsymbol {U}$; $N_C$ is the number of coils in a single field period; $\epsilon \in \mathbb {R}$ is a constraint value; and the functions $f_\text {stoc}, f_{\text {reg}}, c_i:\mathbb {R}^{N} \rightarrow \mathbb {R}$ measure the quality of the coils and induced magnetic field. We define the components of the optimization model precisely in § 3. Similarly to Lobsien et al. (2020), we consider fabrication errors to be spatially correlated Gaussian perturbations to the coils. In order to optimize (1.1), we present a two-step global-to-local algorithm for stochastic optimization. In the first step, we perform a global exploration of the stochastic optimization model given in (1.1) using a trust-region Bayesian optimization (BO) method based on (Eriksson et al. 2019). This global stage finds multiple approximate minima which, in the second step, are resolved by local stochastic optimizers. To perform local stochastic optimization we apply the BFGS optimizer (Nocedal & Wright 2006) to the sample average approximation (SAA) (Shapiro 2001) of (1.1) as well as the Adam optimizer (Kingma & Ba 2014) enhanced by a control variate for variance reduction. Finally, we arrive at multiple local stochastic minima from which one can choose the most promising configuration.

From a stellarator optimization point of view, the main new ingredients of our optimization routine are (to the best of our knowledge) the following.

1. (i) A method for efficient stochastic global exploration of the design space.

2. (ii) A local stochastic optimization with Adam enhanced with novel control variate.

Moreover, this is the first work to perform stochastic optimization using the coil optimization code FOCUS (Zhu et al. 2017).

This paper is organized as follows. We briefly describe FOCUS and the internal representation of the coils in § 2. In § 3, we introduce the formulation of the stochastic optimization model. Subsequently in § 4, we describe our global-to-local stochastic optimization algorithm. Numerical results on a W7-X configuration are presented in § 5. We conclude with a summary and ideas for future work in § 6.

2. FOCUS

For the second design stage of a stellarator, multiple codes are available to optimize for coil configurations which replicate a target magnetic field. Well known examples are NESCOIL (Merkel 1987), REGCOIL (Landreman 2017), ONSET (Drevlak 1998), COILOPT (Strickler, Berry & Hirshman 2002), COILOPT++ (Brown et al. 2015) and FOCUS (Zhu et al. 2017). In order to perform stochastic optimization, we decided to use FOCUS for two reasons: first, it allows coils to move freely in space whereas the other aforementioned coil optimization codes restrict to a so-called winding surface; and second, FOCUS provides analytic first-order derivatives which improve efficiency in the optimization process.

In FOCUS, the coils are described by a three-dimensional Fourier representation. As input, FOCUS takes a vector of Fourier coefficients $\boldsymbol {x} = (\boldsymbol {x}^{1}, \ldots, \boldsymbol {x}^{N_C} ) \in \mathbb {R}^{N}$ describing the geometry of $N_C$ filamentous coils. From the Fourier coefficients $\boldsymbol {x}^{i} = (x^{i}_{c,0},\ldots, x^{i}_{s,N_F}, y^{i}_{c,0},\ldots, y^{i}_{s,N_F}, z^{i}_{c,0}, \ldots, z^{i}_{s,N_F})^{{\rm T}}$ for the $i$-th coil, FOCUS constructs coils as a parameterized curve with $x$-coordinate

(2.1)\begin{equation} x^{i}(\boldsymbol{x}^{i},t) = x^{i}_{c,0} + \sum_{n=1}^{N_F} [x^{i}_{c,n}\cos(nt) + x^{i}_{s,n}\sin(nt)], \quad t \in [0,2{\rm \pi}), \end{equation}

with $N_F$ being the number of Fourier modes and analogous forms for the $y$-, $z$-coordinates $y^{i}(\boldsymbol {x},t),z^{i}(\boldsymbol {x},t)$.¹ By $\boldsymbol {X}^{i}(\boldsymbol {x},t) = (x^{i}(\boldsymbol {x},t),y^{i}(\boldsymbol {x},t),z^{i}(\boldsymbol {x},t))^{{\rm T}}$ we denote the parametric representation of the $i$-th coil filament with $t\in [0,2{\rm \pi} )$. The number of parameters per coil is given by $3(2N_F +1)$ such that the total number of parameters results in $N:= 3N_C(2N_F +1).$ Note that FOCUS only requires the description of a single field period of coils, constructing the other coils through reflection and rotation around the stellarator.

With the Fourier representation FOCUS can, among other things, efficiently compute coil metrics related to coil curvature, coil length, normal magnetic field, quasisymmetry, magnetic island width and their respective gradients with respect to the Fourier coefficients (Zhu et al. 2019). In this study, we only make use of the normal component of the magnetic field $f_{B}$ and length metric $f_{L}$, which we describe in the following.

The metric $f_{B}$ addresses deviations in the magnetic field produced by a coil set $\boldsymbol {x}$ compared with a target magnetic field $\boldsymbol {B}$. Given a target plasma boundary $S$ and a target magnetic field $\boldsymbol {B}$ the normal field error $f_B$ is given by

(2.2)\begin{equation} f_B(\boldsymbol{\boldsymbol{x}}) = \int_S \frac{1}{2} (\boldsymbol{B}\boldsymbol{\cdot}\boldsymbol{n})^{2}\,{\rm d}s, \end{equation}

where $\boldsymbol {n}$ is the unit normal on the target plasma boundary. Typically the target plasma boundary is provided as an output of the first design stage of a stellarator. This first design stage usually involves a magnetohydrodynamic equilibrium solver such as, for example, VMEC (Hirshman & Whitson 1983) or SPEC (Hudson et al. 2012).

The metric $f_L$ is introduced to influence the length of the coils such that they are not prohibitively long. For the $i$-th coil with length $L_i(\boldsymbol {x}) \in \mathbb {R}$ and user-specified target length $L_{i}^{\text {target}}$, FOCUS computes the length metric

(2.3)\begin{equation} f_L(\boldsymbol{\boldsymbol{x}}) = \frac{1}{N_C} \sum_{i=1}^{N_C}\frac{1}{2}\frac{(L_i(\boldsymbol{x}) - L_{i}^{\text{target}})^{2}}{\left(L_{i}^{\text{target}}\right)^{2}}. \end{equation}

In the next section, we detail how we design our stochastic optimization model using the introduced FOCUS metrics.

3. Optimization model formulation

In this section we describe our stochastic optimization model for finding a set of coils which generate a target magnetic field and simultaneously hedge against errors in the coil fabrication. The decision variables $\boldsymbol {x}\in \mathbb {R}^{N}$ for our problem are the $N = 3N_C(2N_F +1)$ Fourier coefficients defining the geometry of the $N_C$ coils, see § 2. The stochasticity is motivated by fabrication errors in the coils and modelled as spatially correlated Gaussian perturbations as described in § 3.1. In § 3.2 we detail the stochastic and non-stochastic parts of the objective function. We design a coil-to-coil separation constraint and formulate the final optimization problem used in the numerical simulations in § 3.3.

3.1. Coil fabrication uncertainty

Errors during coil fabrication can alter the shape of the coil and in turn lead to modifications of the magnetic field. Mathematically, we model coil fabrication errors as spatially correlated Gaussian perturbations. Numerically, the perturbations are independent of the coil discretization by considering additive perturbations modelled by Gaussian processes (GPs), with a periodic kernel. Similar approaches to model coil perturbations for stellarators have been presented in Lobsien et al. (2020) and Wechsung et al. (2021). As in Wechsung et al. (2021), the perturbation of the coils is independent from the discretization of the coils. Moreover, the perturbations themself do not need to preserve stellarator symmetry – but for simplicity we restricted the simulations to the stellarator symmetry-preserving case. Preserving the stellarator symmetries leads to systematic errors in the stellarator design, as the error is assumed to be the same for each coil identical in construction. Breaking the stellarator symmetry would lead to statistical errors, as for each coil, the error would be modelled separately. For the ease of notation, we omit the dependency on $i$ as the $i$-th coil in this subsection as without loss of generality we consider the derivation for one coil.

Let $\boldsymbol {X}(\boldsymbol {x},t)= (x(\boldsymbol {x},t),y(\boldsymbol {x},t),z(\boldsymbol {x},t))^{{\rm T}}$ be a parametric representation of a coil filament with $t\in [0,2{\rm \pi} )$. We consider the distribution of the fabrication's errors to be smooth along the entirety of the coil. As such we model them by zero-mean Gaussian random variables that affect every point on the coil. Equivalently, the coil filament $\boldsymbol {X}(\boldsymbol {x},t)$ is perturbed by a zero-mean GP,

(3.1)\begin{equation} (g_x(t),g_y(t),g_z(t))^{{\rm T}}=:\boldsymbol{g}(t)\sim{{\mathcal{G} \mathcal{P}}}(\boldsymbol{0},\kappa_{\text{per}}(t, t')), \quad t,t' \in [0,2{\rm \pi}), \end{equation}

with a $2{\rm \pi}$-periodic kernel $\kappa _{\text {per}}$. We assume that $\boldsymbol {g}(t)$ is an isotropic GP, i.e. the kernel $\kappa _{\text {per}}$ is only a function of distance of $t,t'$, and that $g_x(t),g_y(t),g_z(t)$ are independent of each other. Then the perturbed coil filament $\boldsymbol {X}_P(\boldsymbol {x},t)$ is again a GP with mean $\boldsymbol {X}(\boldsymbol {x},t)$,

(3.2)\begin{equation} \boldsymbol{X}_{P}(\boldsymbol{x},t) :=\boldsymbol{X}(\boldsymbol{x},t) + \boldsymbol{g}(t) \sim{{\mathcal{G} \mathcal{P}}}(\boldsymbol{X}(\boldsymbol{x},t), \kappa_{\text{per}}(t,t')), \quad t,t' \in [0,2{\rm \pi}). \end{equation}

To compute relevant properties of the perturbed coil $\boldsymbol {X}_{P}(\boldsymbol {x},t)$ in FOCUS, we need a Fourier representation $\boldsymbol {x}_P(t)$ of $\boldsymbol {X}_P(\boldsymbol {x},t)$. As we already know the Fourier representation of $\boldsymbol {X}(\boldsymbol {x},t)$, we only need to calculate the Fourier representation of $\boldsymbol {g}(t)$. The $k$-th cosine and sine Fourier coefficients of the $x$-coordinate of the GP $g_x(t)$, are denoted $\hat {x}_{ck},\hat {x}_{sk}$, and can be calculated with

(3.3a,b)\begin{equation} \hat{x}_{ck} = \frac{1}{\rm \pi}\int_0^{2{\rm \pi}}g_x(t)\cos(kt)\,{\rm d}t, \quad \hat{x}_{sk} = \frac{1}{\rm \pi}\int_0^{2{\rm \pi}}g_x(t)\sin(kt)\,{\rm d}t, \end{equation}

with analogous forms for the $y$-, $z$-coordinates using $g_y(t),g_z(t)$. We collect these Fourier coefficients into the vector $\boldsymbol {U}$. As $\boldsymbol {g}(t)$ is a GP and integration is a linear operation, it follows that $\boldsymbol {U}$ is a normally distributed random vector, see Parzen (1999). The mean of $\boldsymbol {U}$ is zero, i.e. $\mathbb {E}[\boldsymbol {U}] = 0$ and the covariance can be written in terms of the Fourier coefficients of the GP kernel $\kappa _{\text {per}}$, Parzen (1999), i.e.

(3.4)\begin{equation} \text{Cov}[\hat{x}_{ck},\hat{x}_{sj}] = \frac{1}{{\rm \pi}^{2}} \int_0^{2{\rm \pi}}\int_{0}^{2{\rm \pi}} \kappa_{per}(s,t)\cos(kt)\sin(js)\,{\rm d}s\,{\rm d}t. \end{equation}

From the assumption that the $g_x(t),g_y(t),g_z(t)$ are independent of each other, it follows that their Fourier coefficients are independent as well. Thus, the covariance matrix $\boldsymbol {C}$ of the perturbation Fourier coefficients $\boldsymbol {U}$ is block diagonal, where each diagonal block has entries from (3.4). Due to (3.2), a randomly perturbed coil can then be described in FOCUS’ Fourier representation by $\boldsymbol {x}_P = \boldsymbol {x} + \boldsymbol {U}$, where $\boldsymbol {\boldsymbol {U}}\sim \mathcal {N}(\boldsymbol {0},\boldsymbol {C})$.

3.1.1. The kernel and hyperparameters

To ensure the GP perturbations are periodic, we use the exponential sine squared kernel (also known as the periodic kernel) with $2{\rm \pi}$ periodicity

(3.5)\begin{equation} \kappa_{\text{per}}(t,t') = h\exp\left(-\dfrac{2\sin^{2}\left(\dfrac{|t-t'|}{2}\right)}{\ell^{2}}\right), \quad t,t' \in [0,2{\rm \pi}), \end{equation}

where $h>0$ denotes the size of the perturbations and $\ell >0$ is the length scale of the GP. While other choices of periodic kernels are available, this periodic analogue of the squared exponential kernel ensures smoothness and rapidly decaying correlations. We set the hyperparameters $h, \ell$ such that at any point the mean norm squared of the multioutput GP equals the desired mean perturbation size $p$ squared, i.e. $\mathbb {E}[||\boldsymbol {g}(t)||_2^{2}] = p^{2}$. As $g_x(t),g_y(t),g_z(t)$ all have identical moments and a first moment of zero we simplify the equality to $3\text {Var}[g_x(t)] = p^{2}$ which yields $h = p^{2}/3$.

The length scale $\ell$ determines the frequency of the perturbations, as depicted in figure 2. If data on manufacturing errors is available, the length scale $\ell$ can be selected by fitting the error model to the data. In the absence of data we manually selected $\ell$, finding $\ell =0.5$ to balance high-frequency perturbations and low-frequency translational and rotational perturbations. As shown in figure 2, a length scale of $\ell =0.1$ would not be an interesting case as the perturbations are realized as ‘small wiggles’ which may not significantly affect the magnetic field. In contrast, the case $\ell =1.0$ seemed to capture larger translational and rotational perturbations which we would expect for an assembly error, which we do not take into account here. Thus, $\ell =0.5$ seems most appropriate for our study, and is used in our numerical simulations.

Figure 2. Random perturbations of a circular coil generated from a GP with length scale $\ell =0.1$ (a), $\ell =0.5$ (b) and $\ell =1.0$ (c). Note that perturbations generated from a GP with a larger length scale have lower frequency oscillations.

Note that due to the non-uniqueness of the Fourier representation of coils, the GP perturbations to the coil do not necessarily have a fixed speed $\|({{\rm d}}/{{\rm d}t})\boldsymbol {g}(t)\|$. Thus the perturbation length scale $\ell$ may be distorted along the length of the coil. Nonetheless, figure 2 still provides a reliable depiction of the perturbations and can be used to estimate a desirable value for $\ell$.

3.2. Objectives

The primary goal of the second stage of stellarator optimization is to find a set of coils which reproduce a target magnetic field while satisfying engineering targets, such as reasonable coil length and separation between coils. To this end, we chose our objective function $f$ to penalize the normal component of the magnetic field produced by the coils $f_B$ (2.2) and regularize the coil length $f_L$ (2.3) to discourage excessively long coils. We find that adding a simple penalty $f_L$ to the objective is sufficient to regularize coil length. While additional coil regularization functions such as curvature are available in FOCUS, using a length regularization proved to be sufficient.

Not only do we seek a set of coils which generates the target magnetic field $\boldsymbol {B}$, we simultaneously want to hedge against errors in the coil fabrication. To this end, we formulate the following stochastic objective:

(3.6)\begin{equation} f(\boldsymbol{x}) = \mathbb{E}[\omega_B f_B(\boldsymbol{x}+\boldsymbol{U})] + \omega_L f_L(\boldsymbol{x}), \quad \boldsymbol{x} \in \mathbb{R}^{N}, \end{equation}

where $\omega _B, \omega _L \in \mathbb {R}$ are weights of the respective objective, $\boldsymbol {U}\sim \mathcal {N}(\boldsymbol {0},\boldsymbol {C})$ is a multivariate normal random variable described in § 3.1 and $\mathbb {E}$ denotes the expectation over $\boldsymbol {U}$. Referring to (1.1), we set the stochastic and the regularizing part of the objective to

(3.7a,b)\begin{equation} f_\text{stoc}(\boldsymbol{x}) := \omega_B f_B(\boldsymbol{x}), \quad f_\text{reg}(\boldsymbol{x}):= \omega_L f_L(\boldsymbol{x}). \end{equation}

Note that we only penalize perturbations in the magnetic field penalty and not perturbations in the length penalty as fabrication errors that minorly increase coil length are not necessarily problematic from an engineering perspective.

3.3. Coil-to-coil separation constraint

Engineering requirements state that a reasonable configuration must have sufficient spacing between all pairs of coils, see for example Beidler et al. (1990). In order to ensure that this condition is satisfied we include it as a constraint in our optimization model. The implication is that the coil-to-coil distance for adjacent coils is now bounded from below, but any larger distance is allowed and will not add unnecessary penalties to the optimization model. We find that without enforcing this constraint coils come too close during numerical simulations. This constraint is particularly important as FOCUS models coils as infinitely thin filaments, which may not intersect even when their finite width counterparts do. We model the minimum distance between coils $i$ and $i+1$ by

(3.8)\begin{equation} c_i(\boldsymbol{x}) = \min_{s,t \in[0,2{\rm \pi}]^{2}} \|\boldsymbol{X}^{i}(\boldsymbol{x},s) - \boldsymbol{X}^{i+1}(\boldsymbol{x},t) \|_2^{2}. \end{equation}

Thus, for our optimization model in (1.1), we enforce the constraint

(3.9)\begin{equation} \min_{s,t \in[0,2{\rm \pi}]^{2}} \|\boldsymbol{X}^{i}(\boldsymbol{x},s) - \boldsymbol{X}^{i+1}(\boldsymbol{x},t) \|_2^{2} \geq \epsilon_c^{2} \quad i \in\{1,\ldots,N_C -1\}. \end{equation}

To handle the constraints (3.9) we discretize our coils into $N_{\text {seg}}$ segments and compute the minimum across a total of $N_{\text {seg}}^{2}$ discrete points for any adjacent coil pairs. Moreover, as we are constraining the minimum distance between adjacent coils, it might happen, that, for example, coil $i$ and $i+3$ get too close to each other. We did not encounter such a behaviour in our numerical simulations, but additional constraints of the same type could easily be added to prevent this scenario.

In order to continue to use derivative-based optimization techniques we calculate the minimum distance and the derivative between a pair of coils with a smooth approximation to the minimum function, the so-called $\alpha$-quasimax function, see Lange et al. (2014) (also known as LogSumExp function). The $\alpha$-quasimax function approximates the minimum $\min (x_1, \ldots, x_n), \ x_i \in \mathbb {R}, i=1, \ldots, n$, by

(3.10)\begin{equation} \mathcal{Q}_{\alpha}(x_1, \ldots, x_n) := \frac{1}{-\alpha} \log \left( \sum_{i=1}^{n} \exp\left(-\alpha x_i\right) \right), \end{equation}

with $\alpha >0$. Therefore, in the limit $\mathcal {Q}_{\alpha }(x_1, \ldots, x_n) \rightarrow \min (x_1, \ldots, x_n)$ for $\alpha \rightarrow \infty$ and the following bound holds:

(3.11)\begin{equation} \min(x_1, \ldots, x_n) - \frac{\log(n)}{\alpha} \le \mathcal{Q}_{\alpha}(x_1, \ldots, x_n) < \min(x_1, \ldots, x_n). \end{equation}

Thus, we arrive at the final optimization model considered in this paper: we seek $\boldsymbol {x} \in \mathbb {R}^{N}$ such that

(3.12a)\begin{align} \min_{\boldsymbol{x} \in \mathbb{R}^{N}} & \quad \mathbb{E}[ \omega_B f_B(\boldsymbol{x}+\boldsymbol{U})] + \omega_L f_L(\boldsymbol{x}), \end{align}

(3.12b)\begin{align} \min_{s,t \in[0,2{\rm \pi}]^{2}} & \quad \|\boldsymbol{X}^{i}(\boldsymbol{x},s) - \boldsymbol{X}^{i+1}(\boldsymbol{x},t) \|_2^{2} \geq \epsilon_c^{2}, \quad i=\{1,\ldots,N_{c}-1\}. \end{align}

In the next section, we present our efficient global optimization algorithm for the stochastic optimization of (3.12). In order to continue to use derivative-based optimization techniques we calculate the minimum distance between coils with a smooth approximation to the minimum function, the LogSumExp function $Q_\alpha$ (Lange et al. 2014).

4. Two-stage global stochastic optimization

In this section, we introduce our global-to-local stochastic optimization algorithm for solving (3.12). To this end, we modify two methods, the global trust-region BO TuRBO (Eriksson et al. 2019) method and the Adam (Kingma & Ba 2014) algorithm. The Bayesian derivative-free optimization routine TuRBO is designed to efficiently globally optimize a nonlinear function in a high-dimensional bound constrained space. As FOCUS provides derivative information we use DTuRBO (Padidar et al. 2021), which is a further development of TuRBO incorporating derivative information. To prioritize efficient exploration, DTuRBO does not resolve minima to high orders of accuracy. Therefore, we apply a stochastic local optimization starting from the points we get from the final stage of DTuRBO. Thus our approach can be summarized in two stages:

1. (i) perform an approximate global optimization with DTuRBO and select a set of promising solution points;

2. (ii) resolve these solution points locally utilizing a stochastic optimizer.

In order to provide choices for prospective future users of this two-stage approach, we introduce two options for a local stochastic optimizer, the SAA method and the Adam algorithm enhanced with a novel control variate (AdamCV) for variance reduction. This two-stage approach makes efficient use of the computational budget as the local optimizer will resolve the minima much more efficiently than DTuRBO. We start by describing the global optimization.

4.1. Stage 1: efficient global exploration of design space

In this section, we detail the global optimization by first describing TuRBO and subsequently commenting on the modifications made to arrive at DTuRBO.

The TuRBO algorithm is a derivative-free method for global optimization of a nonlinear function across a high-dimensional hypercube $\varOmega =[\text {lb},\text {ub}]^{N}$ with $\text {lb}, \text {ub} \in \mathbb {R}^{N}$ being a vector of lower and upper bounds for the design space variables. The TuRBO algorithm starts by performing a Latin hypercube sampling on $\varOmega$ receiving a sample $X_{\text {init}}=[\boldsymbol {x}_1, \ldots, \boldsymbol {x}_{n_{\text {sample}}}]$ of size $n_{\text {sample}}\in \mathbb {N}$ and then evaluates the objective function $f$ for each $\boldsymbol {x} \in X_{\text {init}}$. Subsequently, $M$ local BO runs are started at the $M$ best points from $X_{\text {init}}$ by building local GPs within $M$ distinct rectangular trust-regions. At each iteration Thompson sampling (see Thompson (1933)) is performed within each trust region to generate a set of candidate points. A batch of the most promising of these candidate points is evaluated by the function $f$ and these function values are used to update the GP surrogates. Note, that the batch of evaluations is chosen from the union of candidate points across the trust regions. Therefore, the evaluations are distributed to each trust region by the region's predicted success through Thompson sampling. The trust regions are centred around the best point found in the evaluation history, and are expanded or contracted by a factor of $2$ depending on consecutive successes/failures of decreasing the function value. A local BO will terminate after the trust region reaches a minimum size. This indicates that the local BO is no longer making an improvement and is near an optima. Precisely these approximate minima are gathered and passed on to the second stage of our approach for further refinement with the local optimizer. Then, a new Latin hypercube sampling of $\varOmega$ is performed and a local BO is again started at the best point. The algorithm terminates when the computational budget, i.e. the maximum number of function evaluations, is reached.

The success of TuRBO in high dimensions is found in its ability to leverage multiple local surrogates and simultaneously efficiently distribute the computational budget across the local BO runs. While the common BO can only be used up to approximately 20 dimensions (see e.g. Frazier (2018)), TuRBO is designed for significantly higher-dimensional problems. Also, DTuRBO further improves on TuRBO by equipping it with a scalable method of incorporating derivatives into the GP models, which yields several advantages. For example, gradients encode the local descent direction ensuring that the surrogate is locally accurate and a decreasing direction can be found more easily. Internally DTuRBO uses a stochastic variational GP (Hensman, Matthews & Ghahramani 2015; Jankowiak, Pleiss & Gardner 2020) to scalably incorporate the high-dimensional gradient data by approximating it with a low-dimensional representation, see Padidar et al. (2021). For practical use, DTuRBO takes in a pair of noisy function and gradient evaluations rather than only noisy function evaluations of $f$. The approximate minima gathered from DTuRBO are passed as starting points for the local stochastic optimizers to be resolved further.

4.2. Stage 2: local stochastic optimization

Approximate minima found in stage one by the DTuRBO algorithm can further be refined by local stochastic optimizers. The benefit of using local stochastic optimization techniques is that they will converge to the minima faster than global optimizers as their main focus is on exploitation rather than exploration. Additionally, some of those methods provide convergence guarantees. Common choices for first-order techniques are variants of the stochastic gradient method (Spall 2005) or the application of non-stochastic optimizers within the SAA method, which has also been used in Lobsien et al. (2020) and Wechsung et al. (2021). The SAA approximation determines a fixed-accuracy approximation to the true stochastic objective, where the error in the approximation decays with the square root of the number of samples. However, this approximation can be optimized in a relatively small number of steps of an algorithm like BFGS. In contrast, stochastic gradient descent methods, including our AdamCV approach, converge to the optimum of the true stochastic objective using a large number of relatively inexpensive steps. Which method is most appropriate depends strongly on how accurately the stochastic optimization problem should be solved.

In the following, we give an introduction to the Adam algorithm used in this work for the stochastic local optimization. Subsequently, we enhance Adam with a novel control variate, which is a variance reduction technique to improve convergence. Additionally, we give a brief overview over the SAA method.

4.2.1. Adam algorithm

In order to efficiently arrive at a well-refined solution, we use a variant of the Adam algorithm (Kingma & Ba 2014). The Adam algorithm is a popular stochastic optimization method in machine learning due to its improved performance over traditional stochastic gradient methods. The success of Adam is largely due to the inclusion of a raw second moment estimator $\boldsymbol {v}_k$ of the stochastic gradient. At each iteration Adam evaluates a small number $N_A$ (also called batchsize) of gradients and averages to form a gradient estimator,

(4.1)\begin{equation} \boldsymbol{g}_k = \dfrac{1}{N_A}\sum_{i=1}^{N_A} \boldsymbol{\nabla} f(\boldsymbol{x}_k+{\boldsymbol{u}}_{k,i}), \quad k=1, \ldots, N_{\text{max}}, \end{equation}

where $N_{\text {max}}$ is the maximum number of iterations and $\boldsymbol {u}_{k,i}$ are $N_A$ realizations of the random variable $\boldsymbol {U}$. To stabilize gradient estimates, Adam employs exponential moving averages of the first and second raw moments of the stochastic gradient $\boldsymbol {m}_k, \boldsymbol {v}_k\in \mathbb {R}^{N}$ in each step $k$,

(4.2)\begin{align} \boldsymbol{m}_k & = \beta_1 \boldsymbol{m}_k + (1-\beta_1)\boldsymbol{g}_k, \quad k=1, \ldots, N_{\text{max}}, \end{align}

(4.3)\begin{align} \boldsymbol{v}_k & = \beta_2 \boldsymbol{v}_k + (1-\beta_2) \boldsymbol{g}_k^{2}, \quad k=1, \ldots, N_{\text{max}}, \end{align}

where the parameters $\beta _1, \beta _2 \in [0,1]$ are usually set close to unity. The first and second moments estimators $\boldsymbol {m}_k, \boldsymbol {v}_k$ are biased as they are initialized as the vector of all zeros. To correct the bias, the estimators $\boldsymbol {m}_k,\boldsymbol {v}_k$ are divided by $(1-\beta _1^{k})$ and $(1-\beta _2^{k})$ to create the bias corrected estimators $\hat {\boldsymbol {m}}_k,\hat {\boldsymbol {v}}_k \in \mathbb {R}^{N}$, as follows:

(4.4a,b)\begin{equation} \hat{\boldsymbol{m}}_k = \frac{\boldsymbol{m}_k}{(1-\beta_1^{k})}, \quad \hat{\boldsymbol{v}}_k = \frac{\boldsymbol{v}_k}{(1-\beta_2^{k})}, \quad k=1, \ldots, N_{\text{max}}, \end{equation}

where with $\beta _1^{k}$, $\beta _2^{k}$ we denote $\beta _1$, $\beta _2$ to the power of $k$. Utilizing these estimators Adam converges to a local minima of (3.12) with the following step sequence:

(4.5)\begin{equation} \boldsymbol{x}_{k+1} = \boldsymbol{x}_k - \eta_k \hat{\boldsymbol{m}}_k/(\sqrt{\hat{\boldsymbol{v}}_k}+\epsilon_A), \end{equation}

where $\epsilon _A \in \mathbb {R}^{+}$ is a small parameter to improve conditioning. To improve the convergence rate we use the decreasing step size sequence $\eta _k = \eta /(1+\sqrt {k}\gamma )$ where $\eta,\gamma$ are tunable parameters. It is essential that the learning rates for Adam are well-tuned for good convergence.

4.2.2. AdamCV

When the variance of the perturbations $\boldsymbol {U}$ becomes large it is beneficial to use variance reduction techniques to reduce the variance of the gradient estimate $\boldsymbol {g}_k$. We follow Wang et al. (2013) in developing such a variance estimator for $\boldsymbol {g}_k$ with control variates. By using a Taylor expansion of the FOCUS objective function we can derive an approximate stochastic gradient to $f$ with moments that are easy to calculate. This approximate gradient can be combined with the true gradient to create an unbiased estimator for $\boldsymbol {g}_k$ with a reduced variance. The first-order Taylor expansion of $\boldsymbol {\nabla } f$ is $\boldsymbol {\nabla } f(\boldsymbol {z}) \approx \boldsymbol {\nabla } f(\boldsymbol {x}) + \boldsymbol {H}(\boldsymbol {z}-\boldsymbol {x})$ where $\boldsymbol {H}$ denotes the Hessian matrix of $f$. Evaluating the Taylor expansion at $\boldsymbol {z} = \boldsymbol {x}+\boldsymbol {U}$ yields the control variate $\tilde {{g}}(\boldsymbol {x})$, as follows:

(4.6)\begin{equation} \tilde{{g}}(\boldsymbol{x})= \boldsymbol{\nabla} f(\boldsymbol{x}) + \boldsymbol{H}\boldsymbol{U}, \end{equation}

which is an estimator for $\mathbb {E}[\tilde {{g}}(\boldsymbol {x})] = \boldsymbol {\nabla } f(\boldsymbol {x})$, which can be found using linearity of the expectation and $\mathbb {E}[\boldsymbol {U}] = 0$. Combining the estimator $\tilde {{g}}$ (4.6) with our original gradient estimator $\boldsymbol {g}_k$ (4.1) leads us to an unbiased gradient estimator with lower variance,

(4.7)\begin{equation} g(\boldsymbol{x}) = \boldsymbol{\nabla} f(\boldsymbol{x}+\boldsymbol{U}) + \boldsymbol{A}(\tilde{{g}}(\boldsymbol{x}) - \mathbb{E}[\tilde{{g}}(\boldsymbol{x})]), \end{equation}

where the choice of the diagonal matrix $\boldsymbol {A}\in \mathbb {R}^{N \times N}$ is detailed in the following. This unbiased gradient estimator with lower variance can be applied to (4.1) as a replacement for $\boldsymbol {\nabla } f(\boldsymbol {x}+\boldsymbol {U})$ to accelerate the convergence of the Adam routine. By following this approach, we ensure that the control variate is highly correlated with $\boldsymbol {\nabla } f(\boldsymbol {x}+\boldsymbol {U})$, such that we obtain the variance reduction with respect to the gradient estimates.

As shown in Wang et al. (2013), the optimal diagonal matrix $\boldsymbol {A}\in \mathbb {R}^{N\times N}$ is chosen in order to minimize the trace of the variance of $g(\boldsymbol {x})$, i.e.

(4.8)\begin{equation} \boldsymbol{A} = \frac{\text{diag}\left(\text{Cov}(\boldsymbol{H}\boldsymbol{U},\boldsymbol{\nabla} f(\boldsymbol{x}+\boldsymbol{U})) + \text{Cov}(\boldsymbol{\nabla} f(\boldsymbol{x}+\boldsymbol{U}),\boldsymbol{H}\boldsymbol{U})\right)}{2 \text{diag}\left(\boldsymbol{H}\boldsymbol{C}\boldsymbol{H}^{\rm T}\right)}, \end{equation}

where we use diag to indicate the diagonal entries of a matrix. By using the optimal $\boldsymbol {A}$ in (4.7) we arrive at a reduced variance for $\tilde {{g}}(\boldsymbol {x}_k)$ given by

(4.9)\begin{equation} \text{Var}[{\tilde{\boldsymbol{g}}(\boldsymbol{x}_k)}] = (1-\boldsymbol{\rho}^{2})\text{Var}[{g}_k], \end{equation}

where $\boldsymbol {\rho }\in \mathbb {R}^{N}$ has entries $\boldsymbol {\rho }_i = \text {Corr}(\partial _{\boldsymbol {x}_i} f(\boldsymbol {x}+\boldsymbol {U}),\tilde {\boldsymbol {g}}(\boldsymbol {x}_k)_i ),\ i = 1, \ldots, N$. As the analytic Hessian $\boldsymbol {H}$ of $f$ is not available in FOCUS we use an approximate Hessian $\boldsymbol {H}_k$ in optimization step $k$ according to the BFGS Hessian approximation (Nocedal & Wright 2006)

(4.10)\begin{gather} \boldsymbol{y}_{k-1} := \boldsymbol{\nabla} f(\boldsymbol{x}_{k}) - \boldsymbol{\nabla} f(\boldsymbol{x}_{k-1}), \end{gather}

(4.11)\begin{gather}\boldsymbol{s}_{k-1} := \boldsymbol{x}_{k}-\boldsymbol{x}_{k-1}, \end{gather}

(4.12)\begin{gather}\boldsymbol{H}_{k} = \boldsymbol{H}_{k-1} + \frac{\boldsymbol{y}_{k-1}\boldsymbol{y}_{k-1}^{\rm T}}{\boldsymbol{y}_{k-1}^{\rm T}\boldsymbol{H}_{k-1}\boldsymbol{s}_{k-1}} - \frac{\boldsymbol{H}_{k-1}\boldsymbol{s}_{k-1}(\boldsymbol{H}_{k-1}\boldsymbol{s}_{k-1})^{\rm T}}{\boldsymbol{s}_{k-1}^{\rm T}\boldsymbol{H}_{k-1}\boldsymbol{s}_{k-1}}, \end{gather}

with $\boldsymbol {H}_0$ initialized as the $N \times N$ identity matrix. We find that equipping Adam with the control variate approach leads to rapid convergence rates in practice, particularly when warm-starting our optimization from a solution from stage one. We call the combination of the Adam algorithm enhanced with the control variate ‘AdamCV’.

4.2.3. SAA

The SAA method (see Shapiro (2001), Kim, Pasupathy & Henderson (2015) and Kleywegt, Shapiro & Homem-de Mello (2002)), is a method of forming a non-stochastic approximation to a stochastic problem by using the Monte Carlo method. For instance, in order to approximate the stochastic component

(4.13)\begin{equation} \mathbb{E}[f_{\text{stoc}}(\boldsymbol{x} + \boldsymbol{U})], \end{equation}

of the objective (3.12) with $f_\text {stoc}$ given as in (3.7a,b), we draw $N_{\text {SAA}}\in \mathbb {N}$ independent realizations of the random variable $\boldsymbol {U}$, i.e. $\{\boldsymbol {u}_i\}_{i=1}^{N_{\text {SAA}}}$. These realizations $\{\boldsymbol {u}_i\}_{i=1}^{N_{\text {SAA}}}$ are taken to form the approximation

(4.14)\begin{equation} f_{\text{SAA}}(\boldsymbol{x}) = \frac{1}{N_{\text{SAA}}}\sum_{i=1}^{N_{\text{SAA}}} f_{\text{stoc}}(\boldsymbol{x} + \boldsymbol{u}_i), \end{equation}

with analogous form for the gradient approximation. This objective is straightforward to implement and can be minimized efficiently with standard non-stochastic optimizers such as BFGS (Nocedal & Wright 2006) since the samples $\boldsymbol {u}_i$ are kept fixed.² Solving the SAA comes with large sample size guarantees. In the limit as the sample size $N_{\text {SAA}}$ approaches infinity, the order of convergence is $O(1/\sqrt {N_{\text {SAA}}})$ as for standard Monte Carlo methods. For a finite batchsize $N_{\text {SAA}}$, the minima of the SAA may not converge to minima of the stochastic problem. So it is recommended that any minima to the SAA is re-evaluated under the stochastic objective to estimate the ‘out-of-sample’ performance, i.e. draw values $\boldsymbol {u}_i$ different from the ones used in the optimization and re-evaluate (4.14).

5. Numerical results

In this section, we present numerical results for a W7-X configuration. In the following, we detail our model data and perform the global-to-local stochastic optimization described in § 4 to find multiple stochastic minima. To better differentiate between the global and the local optimizer, we perform a comparison of the local optimizers SAA and AdamCV initialized at equispaced circular coils in § 5.2. Then, in § 5.3, we use our two-step global optimization method to find multiple promising stochastic minima.

5.1. Model data

We perform simulations on a W7-X configuration, see e.g. Klinger et al. (2019) for a description of W7-X. In particular, we use the same high-mirror configuration as in Lobsien et al. (2020), which is detailed in Nührenberg (1996). A half-module of W7-X consists of five distinct modular coils, such that after applying the stellarator symmetry, i.e. making use of the point symmetry of each module and the five-fold symmetry of W7-X, we arrive at a total of 50 coils. For this study, we find $N_F=6$ Fourier modes to be sufficient for both describing sufficiently complex coils and capturing the perturbation distribution. To ensure six modes did not truncate the effects of the perturbations, we verified that the mean $\mathbb {E}[f_{{\rm stoc}}(\boldsymbol {x}+\boldsymbol {U})]$ is only altered by a relative error of $4.3\times 10^{-4}$ when increasing the number of Fourier modes to 12 and when $\boldsymbol {x}$ is the $1.5$ m circular coils (FOCUS’ default initialization). Using $N_F=6$ modes results in a state dimension of $N = 195$. The weights used in our simulations as well as other optimization parameters for FOCUS can be found in table 1. Heuristically, we found that these weights struck a nice balance between minimizing the field error and finding smooth coils. Moreover, we used $N_{\text {seg}}=64$ segments per coil as well as $N_{\text {theta}}=N_{\text {zeta}} = 64$ nodes in either discretization direction of the plasma boundary. In order to enforce a reasonable coil-to-coil constraint for all pairs of adjacent coils, we have to take a minimum distance and the width of the coils into account. The latter is crucial as FOCUS models coils as infinitely thin filaments. Therefore, we motivate the value of $\epsilon _c$ by coil separation distances for the W7-X candidate configurations HS-5-7 and HS-5-8 given in Beidler et al. (1990). The minimum distance between the coils for the candidate configurations were $0.06$ m and $0.04$ m, respectively. The average lateral coil width of the coils was $0.18$ m, such that we chose the coil-to-coil separation to be at least $\epsilon _c = 0.23 = \tfrac {1}{2}(0.04+0.06) +0.18$ m in all of our simulations. The coil-to-coil separation constraints were included in the model via a quadratic penalty method, see Nocedal & Wright (2006). Thus all optimizations were performed on the penalty objective with $\lambda \in \mathbb {R}^{+}$:

(5.1)\begin{equation} f_\text{pen}(\boldsymbol{x}) := f(\boldsymbol{x}) + \lambda\sum_{i=1}^{N_C - 1} \min[c_i(\boldsymbol{x}) - \epsilon_c^{2},0]^{2}, \end{equation}

with $f(\boldsymbol {x})$ given in (3.6) and $c_i(\boldsymbol {x})$ (3.8). A $\lambda$ value of $100$ was found to be sufficient in consistently achieving constraint satisfaction. Moreover, we set $\alpha =10\,000$ for the $\alpha$-quasimax function in (3.10).

Table 1. Optimization parameter used in numerical simulations: weights in FOCUS objective function $\omega _B, \omega _L$; target length $L_{i}^{\text {target}}$; coil-to-coil separation width $\epsilon _c$; and length scale $\ell$.

5.2. Numerical results for local optimization

We compare the AdamCV algorithm described in § 4.2.2 with the BFGS algorithm applied to SAA § 4.2.3. We initialized the local optimization of (3.12) from a configuration of equispaced circular coils using the perturbation size $p=10$ mm for all simulations in this section. We ran this experiment for the different perturbation sizes $p =2$ mm, $p= 5$ mm, $p=20$ mm and made similar observations.

In order to compare the two algorithms as fairly as possible, we set the number of gradient evaluations per step to 10 and the maximum number of gradient evaluations to 50 000. The remaining parameters of AdamCV are set to $\eta =0.04$, $\gamma =0.1$, $\beta _1=\beta _2=0.95$, $\epsilon _{A}=10^{-10}$. The SAA approximation was optimized with the deterministic SciPy optimizer BFGS (Virtanen et al. 2020) and was restarted with new sample values $\boldsymbol {u}_i$ once a minimum for a fixed sample set had been reached. Due to the restarting, we find that a sample size of $10$ is indeed enough for the SAA algorithm, as we find very similar values, for example, batchsize $100$. We plot the final coil sets found by SAA and AdamCV in figure 3 and find the coils to be similar. Additionally, the BFGS needs to evaluate the objective function as many times as the gradient such that we have an additional 50 000 function evaluations adding to the cost.

Figure 3. Final coil configuration of local stochastic optimization: optimized with (a) SAA $p=10$ mm and (b) with AdamCV $p=10$ mm.

We measure the quality of the coil sets by looking at three measures: the stochastic objective function $f(\boldsymbol {x})$ (3.12a); the normal field error $f_B(\boldsymbol {x})$ (2.2); and the stochastic normal field error $\mathbb {E}[f_B(\boldsymbol {x}+\boldsymbol {U})]$. We provide an overview of our findings in table 2. We find that when optimizing with the AdamCV algorithm we arrive at a similar stochastic function value, with the AdamCV algorithm providing a $0.4\,\%$ smaller value than the SAA. When we evaluate the stochastic component of the objective function, i.e. the stochastic normal field error, AdamCV finds a $2.1\,\%$ smaller stochastic field error value than SAA.

Table 2. Values of stochastic objective function (3.12a), normal field error (2.2) and stochastic normal field error $\mathbb {E}[f_B(\boldsymbol {x}+\boldsymbol {U})]$ for W7-X. The stochastic values are computed using perturbation size $p=10$ mm and we are averaging over 1000 realizations of $\boldsymbol {U}$. For the stochastic values we include the 95 % confidence interval after the function value.

We find that AdamCV arrives at slightly lower stochastic function values/field error, at an improved computational expense as it does not need to evaluate the function values additionally to the gradient evaluations. This success is in part due to proper selection of the learning rate parameters $\eta,\gamma$, which we find through a grid search across the parameters on short duration runs. The SAA procedure performs similarly well, is easy to implement, and works well with only having to choose the sample size. We recommend restarting the SAA optimization with a new batch of samples after a run converges, as we see an improvement throughout the subsequent runs. In our experience, both methods can work well in the local refinement step of our two-stage approach. We choose to use the AdamCV algorithm due to the ability to converge to the true minimum and the incorporation of randomness in every step over the SAA approach.

5.3. Numerical results for global optimization

In this section, we describe the global stochastic optimization of a W7-X configuration with model data given in § 5.1. We first describe the global optimization results and then provide an analysis of the optimized magnetic fields.

5.3.1. Global optimization

For our two-stage approach detailed in § 4, we use the pair D-ACV for the efficient global search and local refinement steps, respectively. In our numerical simulations, we set the average perturbations amplitudes to $p = 5$ mm and $p = 10$ mm. The global exploration algorithm DTuRBO was given a maximum number of 100 000 evaluations, a batchsize of $100$ and $200$ initial evaluations.

The bounding boxes for DTuRBO should be set large enough such that there is enough flexibility in the design space, while not so large as to capture poor regions of the design space. As the design variables are Fourier coefficients the box constraints should get narrower for higher-order Fourier modes. To this end, the lower and upper bounds were computed using the variance of the perturbations as an approximate length scale. We set the bounding boxes for DTuRBO to be centred around $\boldsymbol {x}_0$, which denotes circular coils of radius $1.5$ m, resulting in $\text {lb},\text {ub} = \boldsymbol {x}_0 \pm \delta \text {Var}[\boldsymbol {U}]$. The scalar $\delta = {1.5}/{2\text {Var}[U_0]}$ resizes the box width such that the translational modes have perturbations bounded by $1.5/2$ m, where $\text {Var}[U_0]$ is the perturbation variance to the translational mode.

Using this optimization setting, DTuRBO finds around 15 approximate stochastic minima, which were subsequently resolved with the minimizer AdamCV with a maximum number of $2000$ iterations with a batchsize of $10$ and parameters $\eta =0.001$, $\gamma =0.01$, $\beta _1=\beta _2=0.95$, $\epsilon _{A}=10^{-10}$. Using this optimization setting, on average, the combined optimization routine D-ACV found eight approximate minima within 116 000 evaluations, which had low enough stochastic objective value/field error to use them for further study of physical properties.³ We monitored the change in objective value over iterations of the optimization, towards the end of which the change in objective value was at least two to three points past the first significant digit, less than the standard deviation of $f(\boldsymbol {x} + \boldsymbol {U})$. In other words, a typical perturbation will more negatively affect a solution than an optimization step can improve. The final configurations arrived at a relative gradient tolerance of $10^{-3}$ for all but one run, which had a gradient tolerance of the order of $10^{-2}$, resulting in a reduction of at least three orders of magnitude. Using the relative gradient tolerance $\|\boldsymbol {\nabla } f(x)\|/(w_B+w_L)$ rather than an absolute tolerance reduces the effect that the weights in the objective have on rescaling the gradient, i.e. increasing the weights by a factor of 10 will increase the norm of the gradient by a factor of 10 as well. In figure 4, we show three final coil sets found by the global optimization for the different perturbation sizes. Although it seems like the coils are close in the plots, the minimum distance is satisfied in all configurations. All of these coil sets achieved a low normal field error $f_B(\boldsymbol {x})$ and stochastic normal field error $\mathbb {E}[f_B(\boldsymbol {x} +\boldsymbol {U})]$, as seen in table 3. We also compute the 95 % confidence interval of each coil configuration and find the size to be at least a magnitude smaller than the respective value, varying slightly with respect to the coil configuration.

Figure 4. Final coil sets for the optimization with D-ACV: (a) $p=5$ mm; (b) $p=10$ mm. Corresponding field error can be found in table 3. For each plot, we sorted and coloured the coils according to their stochastic objective value with respect to table 3: low (red); medium (blue); high (black). In panel (a), the two rightmost blue coils appear to be very close. This is deceptive as the rightmost coil extends outward while the other passes behind it.

Table 3. Values of stochastic objective function (3.12a), normal field error (2.2) and stochastic normal field error $\mathbb {E}[f_B(\boldsymbol {x}+\boldsymbol {U})]$ for six different coil configurations for W7-X shown in figure 4. The stochastic values are computed using the respective perturbation size, and averaged over 1000 realizations of $\boldsymbol {U}$. For the stochastic values we include the 95 % confidence interval after the function value. The colour adjacent to the coil configuration denotes the corresponding coloured coil set in figure 4. All coils have been optimized with D-ACV and the number in the coil configuration indicates the perturbation size.

Comparing with the available literature we find that our total costs for arriving at an approximate stochastic global minimum is less than $0.1\,\%$ compared with the evaluation budget in Lobsien et al. (2020), where solely local stochastic optimization has been used. Here, we assume that function evaluations in the respective codes take a similar amount of time/resources and we use a 5-to-1 conversion factor to convert the time for gradient evaluations to the time for function evaluations.⁴ We attribute this improvement in efficiency to a judicious choice of algorithms and the availability of gradients in FOCUS.

Remark 5.1 (The need for global exploration)

The global exploration stage of the optimization routine is critical to finding many distinct local minima. To gauge the value, we randomly initialized ten stochastic optimization runs per perturbation size ($p=5,10$ mm) by randomly perturbing the default starting point (circular coils), i.e. $\boldsymbol {x}_{\text {init}}:= \boldsymbol {x}_0 + \boldsymbol {U}, \boldsymbol {\boldsymbol {U}}\sim \mathcal {N}(\boldsymbol {0},\boldsymbol {C})$. We then compared the result with a stochastic optimization initialized directly from the default starting point. All 11 runs for each perturbation size converged to the same local minimum, thus lacking the benefits of global exploration. One could, of course, extend this local search by running more randomly initialized stochastic runs per perturbation size – or – increasing the magnitude of the resulting perturbation after a fixed number of ‘unsuccessful’ runs. This would lead to higher (and potentially very large) computational costs. Therefore, we employ our efficient surrogate-based global exploration in the first step to find promising regions at low computational cost.

5.3.2. Analysis of magnetic field

In this section, we provide an analysis of the magnetic field of configurations optimized through our two-stage approach. We perform a perturbation analysis to showcase the resilience of the optimized configurations’ magnetic fields in 5.3.1 to perturbations in in the coils for the $5$ mm case.⁵ Additionally, we provide a Poincaré plot of one configuration to show the magnetic surfaces.

For the perturbation analysis, we followed the setting in Lobsien et al. (2020), where each coil configuration is perturbed $200\,000$ times. A histogram of the field error is presented in figure 5. The colour of the respective histogram is consistent with the coloured coil set in figure 4 and with the name convention in table 3. Despite having a lower stochastic function value than D-ACV-5 (black), the coil configuration D-ACV-5 (blue) has a slightly higher field error on average. We observe that all field error histograms have a small standard deviation and hence small tails, verifying that the stochastic optimization found three solutions that are robust to errors in the coils.

Figure 5. Perturbation analysis for the three D-ACV-5 coil configurations of W7-X in figure 4(a) and values in table 3. The colour of the field error histogram is consistent with the colour of the coil in figure 4(a). All coil sets were perturbed 200 000 times with a perturbation size of $5$ mm.

To show the quality of the magnetic field, we include a Poincaré plot of the best coil configuration in the $10$ mm case, i.e. D-ACV-10 (red), and compare it with an approximated target magnetic field⁶ in figure 6. To create the Poincaré plots, field lines are followed for multiple times around the stellarator and a point is set whenever the field line intersects with a fixed plane. For the Poincaré plots in figure 6(a), we follow $25$ field lines for $3000$ rotations and chose the toroidal angle $\phi =0$. For a better comparison, we plot the upper half of the approximated target magnetic field in blue and the stochastic optimized magnetic field in the lower half in red. We observe that both, the magnetic field of the approximated target configuration and the stochastic minimum, have nested flux surfaces. In the outer part, we see the characteristic W7-X island chain with five islands. The inner surfaces of the Poincaré plots align well and the outer surfaces have minor differences. In addition, we compare the rotational transform profile $\iota$ for both configurations, where we assume the rotational transform profile for the approximated target magnetic field yields a good approximation to the true target rotational transform profile. For a quantitive comparison, we compute the maximum and average deviation for the rotational transform profile from the stochastic minimum to the approximated target rotational transform profile. The maximum deviation yields $4.2\,\%$, and the average deviation is $1.0\,\%$, such that the rotational transform profile of the stochastic minimum yields a good approximation to the approximated target configuration, despite this was not an optimization target.

Figure 6. (a) Poincaré plot for the best (with respect to stochastic field error) D-ACV-10 coil configuration (red, lower half) of W7-X in figure 4(b) (red) and values in table 3 compared with the Poincaré plot of the approximated target magnetic field (blue,upper half). (b) Rotational transform $\iota$ profile for the best D-ACV-10 coil configuration (red) and for approximated target magnetic field (blue).

Thus, we conclude that our optimization arrives at a good magnetic field in the sense that it is close to the (approximated) target magnetic field, resembles the known characteristics of the W7-X magnetic field, has nested flux surfaces and approximates the target rotational transform profile.

6. Conclusion and future work

In this paper we develop a stochastic optimization model for stellarator coil configurations in order to hedge against fabrication errors in the construction. Our model considers the effects of normally distributed coil fabrication uncertainties on the normal field error, a length regularization and a coil-to-coil separation distance constraint. Our novel global-to-local approach leverages the efficient high-dimensional derivative-based Bayesian optimizer DTuRBO, as well as SAA and the Adam algorithm equipped with control variates to perform an efficient global exploration. In our numerical simulations for a W7-X-like configuration, we found many satisfactory minima at a low computational expense, approximately less than $0.1\,\%$ of previous work. Note, that previous work only addresses local stochastic optimization, whereas we perform global stochastic optimization.

Possible further directions for work include the investigation of other objective functions which show high sensitivity to coil errors. For instance, Andreeva et al. (2015) and Kremer (2007) showed the magnetic island width to be a quantity highly affected by errors in the coils. Another direction might be to perform this global-to-local approach with, for example, different physical properties such as rotational transform, alpha particle confinement, etc. using different codes such as SIMSOPT (Landreman et al. 2021) or PyPlasmaOpt (Wechsung et al. 2021). Both of these codes include derivative information, which has been indispensable in this work. Furthermore, the model posed here only considers fabrication uncertainties whereas coil placement and alignment uncertainties, considered in Kremer (2007), are yet another source of error with a distinct distribution. Future work could investigate the distributional assumptions of the models.