No CrossRef data available.
Published online by Cambridge University Press: 27 November 2024
The goal of this paper is to show that the theory of curvature invariant, as introduced by Arveson, admits a natural extension to the framework of 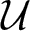 ${\mathcal U}$-twisted polyballs
${\mathcal U}$-twisted polyballs 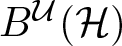 $B^{\mathcal U}({\mathcal H})$ which consist of k-tuples
$B^{\mathcal U}({\mathcal H})$ which consist of k-tuples  $(A_1,\ldots, A_k)$ of row contractions
$(A_1,\ldots, A_k)$ of row contractions 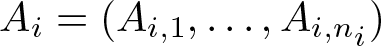 $A_i=(A_{i,1},\ldots, A_{i,n_i})$ satisfying certain
$A_i=(A_{i,1},\ldots, A_{i,n_i})$ satisfying certain 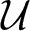 ${\mathcal U}$-commutation relations with respect to a set
${\mathcal U}$-commutation relations with respect to a set 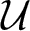 ${\mathcal U}$ of unitary commuting operators on a Hilbert space
${\mathcal U}$ of unitary commuting operators on a Hilbert space 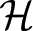 ${\mathcal H}$. Throughout this paper, we will be concerned with the curvature of the elements
${\mathcal H}$. Throughout this paper, we will be concerned with the curvature of the elements 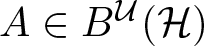 $A\in B^{\mathcal U}({\mathcal H})$ with positive trace class defect operator
$A\in B^{\mathcal U}({\mathcal H})$ with positive trace class defect operator 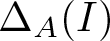 $\Delta_A(I)$. We prove the existence of the curvature invariant and present some of its basic properties. A distinguished role as a universal model among the pure elements in
$\Delta_A(I)$. We prove the existence of the curvature invariant and present some of its basic properties. A distinguished role as a universal model among the pure elements in 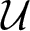 ${\mathcal U}$-twisted polyballs is played by the standard
${\mathcal U}$-twisted polyballs is played by the standard  $I\otimes{\mathcal U}$-twisted multi-shift S acting on
$I\otimes{\mathcal U}$-twisted multi-shift S acting on  $\ell^2({\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. The curvature invariant
$\ell^2({\mathbb F}_{n_1}^+\times\cdots\times {\mathbb F}_{n_k}^+)\otimes {\mathcal H}$. The curvature invariant 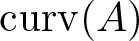 $\mathrm{curv} (A)$ can be any non-negative real number and measures the amount by which A deviates from the universal model S. Special attention is given to the
$\mathrm{curv} (A)$ can be any non-negative real number and measures the amount by which A deviates from the universal model S. Special attention is given to the  $I\otimes {\mathcal U}$-twisted multi-shift S and the invariant subspaces (co-invariant) under S and
$I\otimes {\mathcal U}$-twisted multi-shift S and the invariant subspaces (co-invariant) under S and  $I\otimes {\mathcal U}$, due to the fact that any pure element
$I\otimes {\mathcal U}$, due to the fact that any pure element 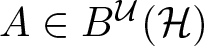 $A\in B^{\mathcal U}({\mathcal H})$ with
$A\in B^{\mathcal U}({\mathcal H})$ with 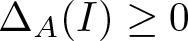 $\Delta_A(I)\geq 0$ is the compression of S to such a co-invariant subspace.
$\Delta_A(I)\geq 0$ is the compression of S to such a co-invariant subspace.