Bayesian B-spline mapping for dynamic quantitative traits

JUN XING; JIAHAN LI; RUNQING YANG; XIAOJING ZHOU; SHIZHONG XU

doi:10.1017/S0016672312000249

Bayesian B-spline mapping for dynamic quantitative traits

Published online by Cambridge University Press: 25 May 2012

JUN XING ,

JIAHAN LI ,

RUNQING YANG ,

XIAOJING ZHOU and

SHIZHONG XU

Show author details

JUN XING: Affiliation:
Department of Gastroenterology, Tumor Hospital of Harbin Medical University, Harbin 150086, People's Republic of China
JIAHAN LI: Affiliation:
Department of Applied and Computational Mathematics and Statistics, University of Notre Dame, Notre Dame, IN 46556, USA
RUNQING YANG*: Affiliation:
Animal Science and Veterinary Medicine, Heilongjiang Bayi Agricultural University, Daqing, 163319, People's Republic of China School of Agriculture and Biology, Shanghai Jiaotong University, Shanghai 200240, People's Republic of China
XIAOJING ZHOU: Affiliation:
Department of Mathematics, Heilongjiang Bayi Agricultural University, Daqing, 163319, People's Republic of China
SHIZHONG XU: Affiliation:
Department of Botany and Plant Science, University of California, Riverside, CA 92521, USA
*: *Corresponding author: School of Agriculture and Biology, Shanghai Jiaotong University, Shanghai 200240, People's Republic of China. Tel: (8621) 34206146. Fax: (8621) 34206146. E-mail: [email protected]

Article contents

Summary
Introduction
Methods
Simulation
Example
Discussion
References

Rights & Permissions

Summary

Owing to their ability and flexibility to describe individual gene expression at different time points, random regression (RR) analyses have become a popular procedure for the genetic analysis of dynamic traits whose phenotypes are collected over time. Specifically, when modelling the dynamic patterns of gene expressions in the RR framework, B-splines have been proved successful as an alternative to orthogonal polynomials. In the so-called Bayesian B-spline quantitative trait locus (QTL) mapping, B-splines are used to characterize the patterns of QTL effects and individual-specific time-dependent environmental errors over time, and the Bayesian shrinkage estimation method is employed to estimate model parameters. Extensive simulations demonstrate that (1) in terms of statistical power, Bayesian B-spline mapping outperforms the interval mapping based on the maximum likelihood; (2) for the simulated dataset with complicated growth curve simulated by B-splines, Legendre polynomial-based Bayesian mapping is not capable of identifying the designed QTLs accurately, even when higher-order Legendre polynomials are considered and (3) for the simulated dataset using Legendre polynomials, the Bayesian B-spline mapping can find the same QTLs as those identified by Legendre polynomial analysis. All simulation results support the necessity and flexibility of B-spline in Bayesian mapping of dynamic traits. The proposed method is also applied to a real dataset, where QTLs controlling the growth trajectory of stem diameters in Populus are located.

Type: Research Papers
Information: Genetics Research , Volume 94 , Issue 2 , April 2012 , pp. 85 - 95

DOI: https://doi.org/10.1017/S0016672312000249 [Opens in a new window]
Copyright: Copyright © Cambridge University Press 2012

1. Introduction

Dynamic traits are those that change over time in the developmental process of life or other quantitative factors (e.g. environmental condition). These traits are often observed in the fields of biology and medicine, such as growth and developmental traits, milk production, egg production and drug response. Any development in plant and animal experiences both systematic and individual-specific processes, and quantitative trait loci (QTLs) are genes across the whole genome that control the systematic component of this developmental process. Mapping QTL of dynamic traits can be conducted in various ways: the simplest approach consists of performing single-trait analysis at each time point, this is the least restrictive approach in the sense that no parametric restrictions are imposed on the curve shape that is formulated by observed data points. However, the single-trait approach may not be efficient because the inference of QTL effects at each time point does not benefit from ‘borrowing’ information from other time points. A natural alternative is to conduct a multiple-trait analysis in which measurements at each time point are regarded as different traits. Although the multiple-trait method takes into account the correlations among measurements, it can only identify the QTL for the measured time points. If too many measuring points exist, the solution to multivariate analysis will be infeasible. In contrast, random regression (RR) analysis (e.g. Henderson, Reference Henderson1982; Jamrozik et al., Reference Jamrozik, Schaeffer and Dekkers1997; Schaeffer, Reference Schaeffer2004) fits the dynamic pattern of the genetic effect for each QTL, which can not only detect the QTL-controlled dynamic trajectories but also infer QTL at arbitrary time points (Macgregor et al., Reference Macgregor, Knott, White and Visscher2005; Yang et al., Reference Yang, Tian and Xu2006, Reference Yang, Gao, Wang, Zhang, Zeng and Wu2007; Yang & Xu, Reference Yang and Xu2007). Along with these ideas, Wu and his colleagues (Ma et al., Reference Ma, Casella and Wu2002; Wu et al., Reference Wu, Ma, Littell, Wu, Yin, Huang, Wang and Casella2002, Reference Wu, Ma, Zhao and Casella2003, Reference Wu, Ma, Lin, Wang and George2004) have developed a functional-mapping strategy that uses some structured models to fit residuals (Jin et al., Reference Jin, Li, Guo, Zhou, Yang and Wu2010). But in RR analysis, fitting time-dependent residuals by polynomials can take advantages of the many well-developed inference methods available in linear model literature.

In order to map QTL for traits with dynamic patterns, both parametric and non-parametric models are used to describe the change of genotypic effects over time. Emphasizing on the interpretability of mapping results, earlier functional mapping (Ma et al., Reference Ma, Casella and Wu2002; Wu et al., Reference Wu, Ma, Littell, Wu, Yin, Huang, Wang and Casella2002, Reference Wu, Ma, Zhao and Casella2003, Reference Wu, Ma, Lin, Wang and George2004) fits QTL phenotypic effects by biologically meaningful mathematical functions. However, its applicability is limited due to non-linearity and the pool of candidate mathematical functions (Yang et al., Reference Yang, Tian and Xu2006, Reference Yang, Gao, Wang, Zhang, Zeng and Wu2007, Reference Yang, Wu and Casella2009; Yang & Xu, Reference Yang and Xu2007). In contrast, Legendre polynomials have been widely used for mapping dynamic traits. In addition to the flexibility of fitting biological curves with arbitrary shapes, the Legendre polynomial is a linear model, and thus theories and algorithms that developed in linear models could be applied directly to estimate QTL parameters. However, although higher-order polynomials are capable of modelling changes in means and variances along a continuous scale, such polynomials often overemphasize on observations at the extremes and may result in Runge's phenomenon. That is, the goodness of fit to curve decreases with the order of polynomials, due to oscillations at two extremes of the curve (de Boor, Reference de Boor2001). Alternatively, the splines that construct curves from pieces of lower-degree polynomials smoothed at selected pointed (knots) are more commonly used in non-parametric data analysis. As a particular type of spline curve, B-splines yield the same fit as splines based on truncated power functions, but have better numerical properties (Ruppert et al., Reference Ruppert, Wand and Carroll2003). The applications of the B-splines to mapping QTL for dynamic traits have been firstly discussed by Yang et al. (Reference Yang, Wu and Casella2006) and introduced by Yang et al. (Reference Yang, Wu and Casella2009), respectively.

Frameworks for mapping dynamic trait loci have been developed from the interval-mapping procedure under maximum likelihood to the Bayesian-mapping method. Compared to interval mapping that detects one QTL at a time based on a single QTL model, Bayesian mapping based on a multiple QTL model can simultaneously identify multiple QTLs across the entire genome, which greatly enhances the statistical power of QTL detection. In this paper, using B-spline to model the dynamics of population mean, QTL effects and individual-specific time-dependent environmental errors, we establish a multiple QTL model for mapping dynamic trait loci and estimate QTL parameters using the Bayesian shrinkage method. Through computer simulations, we compare the performance of Bayesian-mapping and interval-mapping methods, as well as the flexibilities of B-splines and Legendre polynomials in the QTL mapping of dynamic quantitative traits.

2. Methods

(i) Genetic model of dynamic traits

We now use a backcross design as an example to describe the genetic model for dynamic traits. Based on Mendel's law of inheritance, there are two possible genotypes in a backcross population at any given locus, denoted by Qq and qq, respectively, with equal frequencies. Let y_i (t) be the phenotypic value of individual i measured at time t, which can be described by the following linear model:

(1)

$y_{i} \lpar t\rpar \equals \mu \lpar t\rpar \plus \mathop\sum\limits_{j \equals \setnum{1}}^{q} {x_{ij} \alpha _{j} \lpar t\rpar } \plus \beta _{i} \lpar t\rpar \plus \varepsilon _{i} \comma$

for i=1, 2, … , n, where n is the number of individuals, q is the maximum number of QTLs evaluated in the genome, μ(t) is the population mean at time t, x_ij is the genotype indicator variable (defined as 1 for one genotype and −1 for the alternative genotype) for the ith individual at the jth locus, α _j (t) (j=1, 2, …, q) is the genetic value of the jth QTL at time t, β _i (t) is an individual-specific time-dependent environmental error with an i.i.d. N[0, σ_β²(t)] distribution and ∊ _i is an individual-specific time-independent environmental error with an i.i.d. N(0, σ_∊²) distribution. This is a mixed effects model with μ(t) and α _j (t) being the fixed effects and β _i (t) being the random effect. The purpose of the QTL mapping is to estimate α _j (t), the time-dependent functional genetic effect of locus j, for j=1, 2, …, q.

All the model parameters, except σ_∊², are functions of time. The functional relationships between parameters and time may be described by B-splines. Define ψ(t)=[ψ_{0, p}(t) ψ_{1, p}(t) … ψ_{r, p}(t)] as a covariable of the B-splines with k knots and p-order polynomial, where r=k−p−2 (see Appendix A). Also define μ=[μ₀ μ₁ … μ _r ]^T as a vector of population means, which is time independent. The time-dependent population mean μ(t) may be described as a linear combination of μ weighted by the basis of the B-splines, i.e. μ(t)=ψ(t)μ. Similarly, we can describe other parameters using the same B-splines, e.g. α _j (t)=ψ(t)α_j , where α _j =[α _j ₀ α _j ₁ … α _jr ]^T for j=1, 2, …, q and β _i (t)=ψ(t)β_i , where β _i =[β _i ₀ β _i ₁ … β _ir ]^T for i=1, 2, …, n. Since β_i is treated as an RR effect, we assume that β_i is i.i.d. N(0, Σ_β ) with Σ_β being the covariance matrix of RR effect for individual-specific time-dependent environmental errors.

With the B-spline reparameterization, model (1) is now rewritten as a linear function of the time-independent parameters:

(2)

$y_{i} \lpar t\rpar \equals {\bimpsi }\lpar t\rpar {\bimmu } \plus \mathop\sum\limits_{j \equals \setnum{1}}^{q} {x_{ij} {\bimpsi }\lpar t\rpar {\bimalpha }_{j} } \plus {\bimpsi }\lpar t\rpar {\bimbeta }_{i} \plus \bimepsi _{i} \comma$

The phenotypic values for each individual are collected at m+1 fixed time points, t ₀, t ₁, …, t_m , denoted by a vector y_i =[y_i (t ₀) y_i (t ₁) … y_i (t_m )]^T . Define

${\bimpsi } \equals \lsqb \matrix{ {{\bimpsi }^{\rm T} \lpar t_{\setnum{0}} \rpar } \tab {{\bimpsi }^{\rm T} \lpar t_{\setnum{1}} \rpar } \, \cdots \, {{\bimpsi }^{\rm T} \lpar t_{m} \rpar } \cr} \rsqb$

as an (r+1)×(m+1) matrix. In matrix notation, the linear model for y_i is

(3)

${\bi y}_{i} \equals {\bimpsi }^{\rm T} {\bimmu } \plus \mathop\sum\limits_{j \equals \setnum{1}}^{p} {x_{ij} {\bimpsi }^{\rm T} {\bimalpha }_{j} } \plus {\bimpsi }^{\rm T} {\bimbeta }_{i} \plus {\bimepsi }_{i} \comma$

where ${\bimepsi }_{i} \equals \lsqb \matrix{ {\varepsilon _{it_{\setnum{0}} } } \, \cdots \, {\varepsilon _{it_{m} } } \cr} \rsqb ^{\rm T}$ is an (m+1)×1 vector for the residual effects assumed ∊ _i ~N(0, Iσ_∊ ²). The expectation of model (3) is

${\rm E\lpar }{\bf y}_{i} \left\vert {{\bimmu }\comma } \right.{\bimalpha }_{j} \rpar \equals {\bf U}_{i} \equals {\bimpsi }^{\rm T} {\bimmu } \plus \mathop\sum\limits_{j \equals \setnum{1}}^{p} {x_{ij} {\bimpsi }^{\rm T} {\bimalpha }_{j} }$

and the covariance matrix is

${\rm Var\lpar }{\bf y}_{i} \left\vert {{\bimmu }\comma } \right.{\bimalpha }_{j} \rpar \equals {\bf V} \equals {\bimpsi }^{\rm T} {\bmSigma }_{\bimbeta } {\bimpsi } \plus {\bf I}\sigma _{\varepsilon }^{\setnum{2}}.$

(ii) Bayesian B-spline mapping

In Bayesian mapping analysis for dynamic traits, the observed data are phenotypes y={y_i} for i=1, 2, …, n and marker information M={M_j} for i=1, 2, …, n. Parameters θ include population mean μ, QTL regression effects α={α_j} for j=1, 2, …, q, RR effect for individual-specific time-dependent environmental errors β={β_i} for i=1, 2, …, n, QTL positions λ={λ _j } for j=1, 2, …, q, the QTL genotype indicator variable x={x_ij } for i=1, 2, …, n and j=1, 2, …, q, prior covariance matrice of QTL regression effects A={A_j } for j=1, 2, …, q, covariance matrix of RR effects for individual-specific time-dependent environmental error Σ_β and residual variance σ_∊².

(a) Likelihoods

Given unknown parameters, the observed data are conditionally independent (Sen & Churchill, Reference Sen and Churchill2001; Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005) so that

$p\lpar {\bf y}\comma {\bf M}\vert {\bimtheta }\rpar \equals p\lpar {\bf y}\vert {\bf M}\comma {\bimtheta }\rpar p\lpar {\bf M}\vert {\bimtheta }\rpar \comma$

where we have the likelihood based on the model (3)

(4)

$p\lpar {\bf y}\vert {\bf M}\comma {\bimtheta }\rpar \equals \prod\limits_{i \equals \setnum{1}}^{n} {p\lpar {\bf y}_{i} \vert {\bf M}\comma {\bimtheta }\rpar } \propto \;\vert {\bf V}\vert ^{ \minus n\lpar m \plus \setnum{1}\rpar \sol \setnum{2}} {\rm exp}\left[ {\mathop\sum\limits_{i \equals \setnum{1}}^{n} {{\rm \lpar }{\bf y}_{i} \minus {\bf U}_{i} \rpar ^{\rm T} {\bf V}^{ \minus \setnum{1}} {\rm \lpar }{\bf y}_{i} \minus {\bf U}_{i} \rpar } } \right]$

and

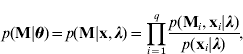
$p\lpar {\bf M}\left\vert {\bimtheta } \right.\rpar \equals p\lpar {\bf M}\left\vert {{\bf x\comma }{\bimlambda }} \right.\rpar \equals \prod\limits_{i \equals \setnum{1}}^{q} {{{p\lpar {\bf M}_{i} \comma {\bf x}_{i} \left\vert {\bimlambda } \right.\rpar } \over {p\lpar {\bf x}_{i} \left\vert {\bimlambda } \right.\rpar }}} \comma$

which is derived from a Markov model under the assumption of no segregation interference (Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005).

(b) Prior specification

In the Bayesian shrinkage analysis for QTL mapping, the number of QTLs, q, is treated as a constant (see Wang et al. Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005 and Yang et al. Reference Yang, Gao, Wang, Zhang, Zeng and Wu2007 for justification). The prior distribution for μ is uniform. The prior distribution for each of the genetic effects is multivariate normal, i.e. p(α_j |A_j)=N(0, A_j ) for all j=1, 2, …, q, where A_j has its own prior, p(A_j )=IW(b ₀, Γ _A ), an inverse Wishart distribution with b ₀ and Γ_A being hyperparameters. The prior distribution for Σ_β is also inverse Wishart, i.e. Σ_β ~IW(d ₀, Γ_β ), where d ₀ and Γ_β are hyperparameters. The prior for σ_∊² is inverted chi-square distribution IC(v_e , (v_eS_e )⁻ ¹) with v_e and S_e being hyperparameters, and p(λ _j )=1/l_j for j=1, 2, …, q, where l_j is the distance between the two neighbouring QTLs (Sillanpää & Arjas, Reference Sillanpää and Arjas1998, Reference Sillanpää and Arjas1999; Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005). The joint prior distribution of all the parameters is

(5)

$p\lpar {\bimtheta }\rpar \equals p\lpar {\bimmu }\rpar p\lpar {\bmSigma }_{\bimbeta } \rpar p\lpar \rmsigma _{\varepsilon }^{\setnum{2}} \rpar \prod\limits_{j \equals \setnum{1}}^{q} {p\lpar {\bimalpha }_{j} \vert {\bf A}_{j} \rpar } p\lpar {\bf A}_{j} \rpar .$

Combining the conditional density of the data with the prior distribution of parameters, we obtain the joint distribution of the data and parameters, which is proportional to the joint posterior distribution of the parameters,

(6)

$p\lpar {\bimtheta }\vert {\bf y}\comma {\bf M}\rpar \propto p\lpar {\bf y}\comma {\bf M}\vert {\bimtheta }\rpar p\lpar {\bimtheta }\rpar .$

(c) Markov chain Monte Carlo (MCMC) sampling for QTL parameters

This joint posterior distribution is the target distribution from which parameters are sampled. Due to analytically intractable joint posterior distribution, the MCMC methods such as Gibbs sampler (Gelman et al., Reference Gelman, Carlin, Stern and Rubin1995) and Metropolis–Hastings algorithm (Metropolis et al., Reference Metropolis, Rosenbluth, Rosenbluth, Teller and Teller1953; Hastings, Reference Hastings1970) are used to sample each parameter conditional on all other parameters. Except for QTL genotypes without the closed form of conditional posterior distribution, other unknown parameters can be drawn by Gibbs samplers from their conditional posterior distributions (see Appendix B for details of derivation).

Considering that the genotype of QTL closely depends on the QTL position, we adopt Metropolis–Hastings algorithm to sample jointly the QTL position and relative genotype for one locus at a time. Each locus is drawn from a variable interval whose boundaries are the positions of adjoining QTLs (Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005; Zhang & Xu, Reference Zhang and Xu2005).

Genotypes of missing markers were generated randomly in each iteration on the basis of the probability inferred jointly from the nearest non-missing flanking markers and the phenotypes (Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005). The probability of missing marker genotype estimated by the flanking markers is treated as the prior probability. After incorporating the marker (QTL) effects through the phenotype, the probability becomes the posterior probability, which is used to generate the missing marker genotype.

In summary, the MCMC algorithm is described in the following steps:

(1) Initialize all variables with values sampled from their prior distributions.
(2) Update the population means with a sample from a multivariate normal with mean (B.1) and covariance matrix (B.2) in Appendix B.
(3) Update the genetic effects for each QTL with sample from a multivariate normal with mean (B.3) and covariance matrix (B.4) in Appendix B.
(4) Update the covariance matrix for each QTL with a sample from the inverse Wishart (B.5) of Appendix B.
(5) Update the RR effects for individual-specific time-dependent environmental errors with a sample from a multivariate normal with mean (B.6) and covariance matrix (B.7) in Appendix B.
(6) Update the covariance matrix of RR effects for individual-specific time-dependent environmental errors with a sample from the inverse Wishart (B.8) of Appendix B.
(7) Update the residual variance with a sample from a scaled inverse chi-square (B.9) of Appendix B.
(8) Update the QTL position for each marker interval.
(9) Update the genotypes for each QTL.
(10) Impute the genotypes of missing markers.
(11) Repeat steps (2)–(10) until the Markov chain reaches a desirable length.

(d) Post-Bayesian analysis

In conventional Bayesian mapping, the marginal posterior distribution of the QTL position can be shown by plotting the number of hits by the QTL in a short interval against the genome location (Sillanpää & Arjas, Reference Sillanpää and Arjas1998, Reference Sillanpää and Arjas1999; Yi & Xu, Reference Yi and Xu2000a, Reference Yi and Xub; Wang et al., Reference Wang, Zhang, Li, Masinde, Mohan, Baylink and Xu2005). The curve is called QTL intensity profile. If an interval contains a QTL, we expect that the QTL intensity profile within the interval shows a peak. Otherwise, the intensity profile appears flat (uniform). The intensity profile only provides us a signal of ‘peak’ at possible QTL, but it is unable to answer whether the effects of the QTL with higher intensity are statistically significant or not. To address this problem, we used a Wald test to determine statistical significance from a frequentist perspective (see Yang et al. Reference Yang, Gao, Wang, Zhang, Zeng and Wu2007 for theoretical justification). Let us denote the QTL intensity profile by f(λ), which is a function of the genome location, and the test statistic of the overall QTL effect by T ²(λ), which is

(7)

$T^{\setnum{2}} \lpar \lambda \rpar \equals \left\{ {\matrix{ {{\bimalpha }^{\rm T} \lpar \lambda \rpar {\bf S}_{\bimalpha }^{ \minus \setnum{1}} \lpar \lambda \rpar {\bimalpha }\lpar \lambda \rpar \comma } \hfill \tab {f\lpar \lambda \rpar \gt f_{\setnum{0}} \comma } \hfill \cr {0\comma } \hfill \tab {f\lpar \lambda \rpar \les f_{\setnum{0}\comma } } \hfill \cr} } \right.$

where T ²(λ) is the Wald test statistic, α(λ) is the vector for posterior means of the QTL regression effects, S _α (λ) is the estimated posterior sample covariance matrix for the QTL regression effects and the f ₀ is the flat intensity in the interval without the peak. Under the null hypothesis, i.e. there is no QTL at position λ, T ²(λ) will have an asymptotic chi-square distribution with r degrees of freedom. Therefore, a critical value of chi-square distribution may be used to declare statistical significance at position λ. Generally, there are higher intensity and larger genetic effect at the position where QTL exists. Using the statistic T ²(λ) profile to indicate the locations of the QTL, most of the intervals will have T ²(λ) of zeros due to the lower intensities and thus only the intervals with possible significant QTL effects and higher intensities will show clear peaks.

3. Simulation

To evaluate the efficiency of Bayesian B-spline mapping for dynamic traits and the flexibility of B-spline in this framework, we conduct three simulations: (1) comparing the statistical power of QTL detection between the proposed method and the interval-mapping method (Yang et al., Reference Yang, Tian and Xu2006); (2) fitting the simulated data generated by B-spline using the Legendre polynomial-based approach and (3) fitting the simulated data generated by the Legendre polynomials using B-spline based Bayesian mapping approach for dynamic traits.

For the first two scenarios, we simulate a backcross population including 150 segregating individuals. The 61 co-dominant markers are evenly spaced on the chromosome fragment of 600 cM long. We put ten QTLs governing the trajectory of a dynamic trait along the genome. Assume that changes in phenotype of the trait and QTL additive effects over time follow B-splines with four knots and polynomial segments of order 2. The array of measurement time points for each individual was designated as 10, 20, 30, 40, 50, 60, 70, 80, 90 and 100, from which four knot points were chosen at 10, 40, 70 and 100. The regression coefficients for overall mean were set to

${\bimmu } \equals \left( {\matrix{ {8{\cdot}13} \tab {25{\cdot}14} \tab {12{\cdot}27} \tab {0{\cdot}83} \tab {24{\cdot}71} \cr} } \right)^{\rm T} .$

The covariance matrix of RR effects for individual-specific time-dependent environmental errors was

${\bmSigma }_{\bimbeta } \equals \left[ {\matrix{ {1{\cdot}04} \tab {\hskip9pt 0{\cdot}171} \tab { \minus 0{\cdot}315} \tab {0{\cdot}100} \tab {0{\cdot}280} \cr {\hskip5pt 0{\cdot}171} \tab {\hskip9pt 1{\cdot}586} \tab { \minus 0{\cdot}035} \tab {0{\cdot}041} \tab {0{\cdot}410} \cr { \hskip-6pt\minus 0{\cdot}315} \tab { \minus 0{\cdot}035} \tab {\hskip9pt 1{\cdot}736} \tab {0{\cdot}287} \tab {0{\cdot}050} \cr {\hskip4pt 0{\cdot}100} \tab {\hskip9pt 0{\cdot}041} \tab {\hskip9pt 0{\cdot}287} \tab {0{\cdot}772} \tab {0{\cdot}320} \cr {\hskip4pt 0{\cdot}280} \tab {\hskip9pt 0{\cdot}410} \tab {\hskip9pt 0{\cdot}050} \tab {0{\cdot}320} \tab {1{\cdot}250} \cr} } \right]\comma$

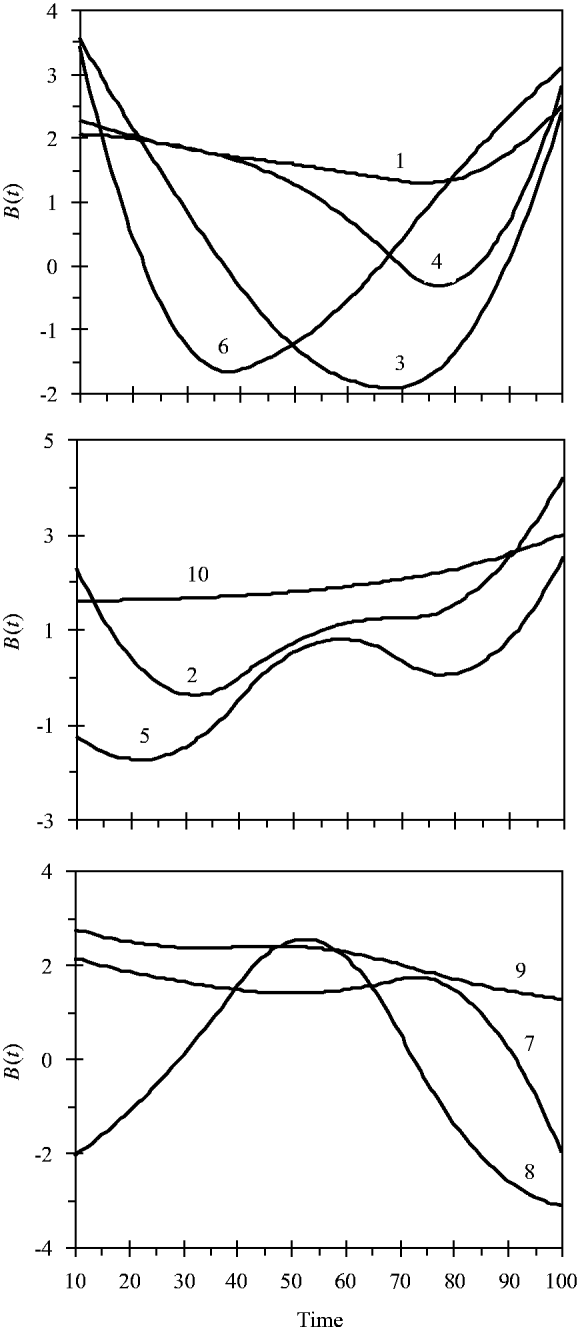
and the variance for random experimental error was σ_∊²=2·0. The locations of the ten simulated QTLs and their regression genetic effects are shown in Table 1. The cumulative proportion of phenotypic variance from measurement time point 10–100 contributed by an individual QTL ranged from 0·026 to 0·157, as calculated in Yang et al. (Reference Yang, Tian and Xu2006), the total genetic variance contributed by all ten QTLs was 0·903. The trajectories for each QTL are shown in Fig. 1. They are categorized into three groups according to the shape of curves.

Based on the simulated parameters above, a vector of the phenotypic values for individual was randomly generated by ${\bf y}_{i} \equals {\bimpsi }^{\rm T} \left( {{\bimmu } \plus \sum\nolimits_{j \equals \setnum{1}}^{\setnum{10}} {{\bimalpha }_{j} \plus {\bimbeta }_{i} } } \right) \plus {\bimepsi }_{i}$ , where β_i and ∊_i were the vectors of random numbers sampled from N(0, Σ_β ) and N(0, Iσ_∊ ²), respectively. The simulated data were analysed using both the Bayesian B-spline-mapping method and the interval-mapping method based on maximum likelihood (Yang et al., Reference Yang, Tian and Xu2006).

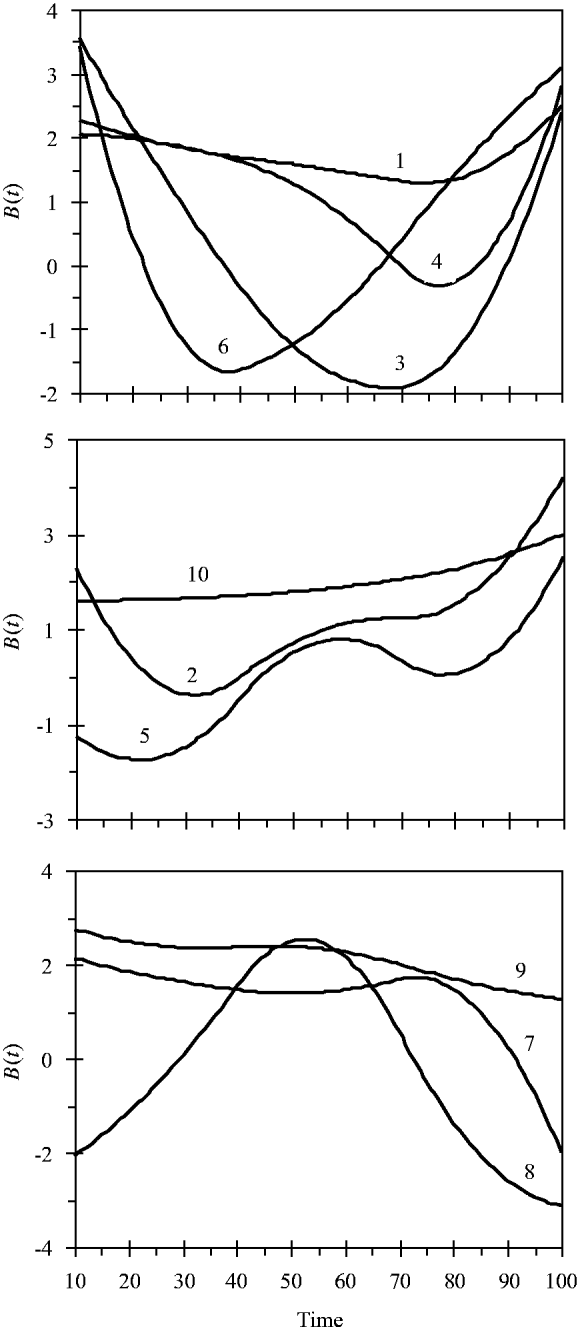
Fig. 1. Changes in genetic effects for ten simulated QTLs with time.

Table 1. QTL regression effects for B-splines used in simulation

In the MCMC-implemented Bayesian analysis with the moving interval approach, we include only 20 QTLs in the working model. By fitting the phenotypic B-spline of each individual, the initial value of the overall mean (μ) is determined as population mean for regression coefficients, the covariance matrix of RR effects for individual-specific time-dependent environmental error (Σ_β ) is initialized with population covariance matrix for regression coefficients, and residual variance (σ_∊²) starts with population mean for residual error variances of phenotypic B-splines. The regression coefficients for genetic effects of all QTLs (α) are initialized as zero. Both the hyperparameters b ₀ and d ₀ are taken to be 5 and the prior covariance Γ _A and Γ_β were assigned to be the identity matrix I and 0·5I, respectively. The initial value of λ _j takes the middle point of the interval where the jth QTL resides. The initial value of genotype indicator x_ij is sampled from the probability of x_ij conditional on the flanking markers. The Gibbs sampler was run for 30 000 cycles after discarding the first 6000 cycles as the burn-in period. The chain was thinned to reduce serial correlation by saving one observation in every 30 cycles and thus the posterior sample contained 1000 samples for post-MCMC analysis. The simulation experiment was replicated five times. Herein, we only report the result of one replicate because there is very little variation in the mapping result among the replicates.

Figure 2 shows the profiles for QTL intensity and T ² statistic estimated with Bayesian analysis along with the true locations of simulated QTL, where the critical value of T ² is 11·05, that is, the critical value of chi-square distribution with 5 degree of freedom at the significance level of 5%. It can be seen that either the QTL intensity or test statistic profile in Bayesian analysis was able to detect nine simulated QTLs clearly. In contrast, interval-mapping analysis only detected seven simulated QTLs (see Fig. 3). Although the two analyses have no power to separate closely linked QTL within the same interval of markers, such as the QTL3 and QTL4, the Bayesian analysis easily detected the linked closely QTL that located in different marker intervals, such as QTL6 and QTL7.

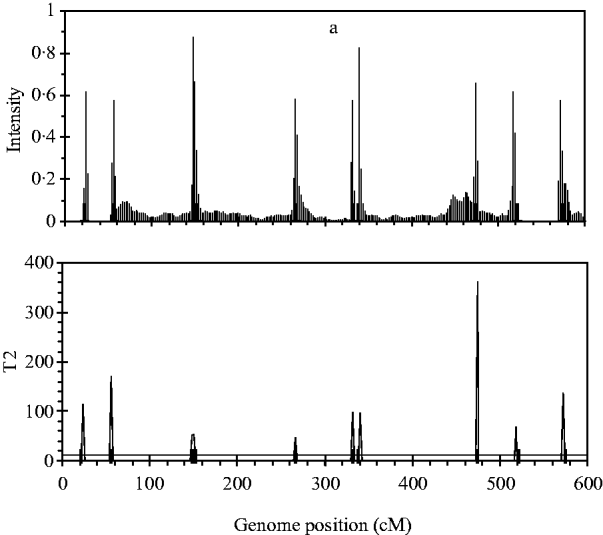
Fig. 2. The QTL intensity profile (above) and T ² test statistic profile (below) over the entire genome obtained with Bayesian B-spline mapping. The true positions of the simulated QTL are represented by black needles. In T ² test statistic plot, the horizontal line indicates the empirical critical value of 11·05 when the type I error rate was 5%.

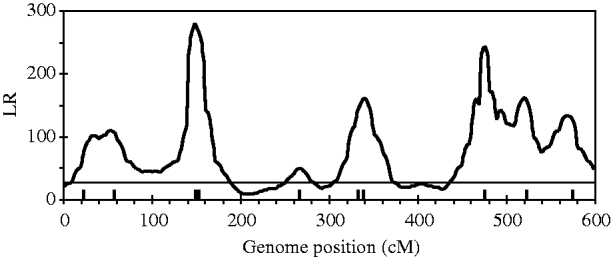
Fig. 3. The likelihood ratio statistic profiles estimated with interval-mapping analysis for the entire genome. The horizontal line indicates the empirical critical value of 25·01 when the type I error rate was 5%, which is estimated from 500 permutation tests.

The estimated QTL locations and effects obtained from Bayesian analysis are summarized in Table 2 along with the true parameters. Clearly, Bayesian analysis is capable of accurately estimating the QTL locations and effects. The posterior means (standard deviations) for population mean and covariance matrix of RR effects for individual-specific time-dependent environmental errors are estimated as

${\hat{\bimmu }} \equals \left[ {\matrix{ {8{\cdot}08\lpar 0{\cdot}17\rpar } \tab {24{\cdot}87\lpar 0{\cdot}20\rpar } \tab {12{\cdot}56\lpar 0{\cdot}18\rpar } \tab {0{\cdot}93\lpar 0{\cdot}19\rpar } \tab {24{\cdot}69\lpar 0{\cdot}15\rpar } \cr} } \right]^{\rm T}$

and

${{\bm \hats \Sigma }}_{\bimbeta } \equals \hskip-3pt\left[ {\matrix{ \hskip6pt {0{\cdot}789\lpar 0{\cdot}368\rpar } \tab \hskip-2pt { \minus 0{\cdot}245\lpar 0{\cdot}282\rpar } \tab \hskip-4pt { \minus 0{\cdot}135\lpar 0{\cdot}265\rpar } \tab { \minus 0{\cdot}224\lpar 0{\cdot}251\rpar } \tab {0{\cdot}096\lpar 0{\cdot}220\rpar } \cr \hskip-4pt { \minus 0{\cdot}245\lpar 0{\cdot}282\rpar } \tab {\hskip9pt 0{\cdot}769\lpar 0{\cdot}391\rpar } \tab {\hskip7pt 0{\cdot}317\lpar 0{\cdot}248\rpar } \tab {\hskip9pt 0{\cdot}250\lpar 0{\cdot}240\rpar } \tab {0{\cdot}272\lpar 0{\cdot}215\rpar } \cr { \minus 0{\cdot}135\lpar 0{\cdot}265\rpar } \tab {\hskip9pt 0{\cdot}317\lpar 0{\cdot}248\rpar } \tab {\hskip7pt 1{\cdot}065\lpar 0{\cdot}423\rpar } \tab {\hskip9pt 0{\cdot}404\lpar 0{\cdot}220\rpar } \tab {0{\cdot}472\lpar 0{\cdot}235\rpar } \cr { \minus 0{\cdot}224\lpar 0{\cdot}251\rpar } \tab {\hskip9pt 0{\cdot}250\lpar 0{\cdot}240\rpar } \tab {\hskip7pt 0{\cdot}404\lpar 0{\cdot}220\rpar } \tab {\hskip9pt 0{\cdot}616\lpar 0{\cdot}291\rpar } \tab {0{\cdot}179\lpar 0{\cdot}206\rpar } \cr {\hskip9pt 0{\cdot}096\lpar 0{\cdot}220\rpar } \tab {\hskip9pt 0{\cdot}272\lpar 0{\cdot}215\rpar } \tab {\hskip7pt 0{\cdot}472\lpar 0{\cdot}235\rpar } \tab {\hskip9pt 0{\cdot}179\lpar 0{\cdot}206\rpar } \tab {0{\cdot}657\lpar 0{\cdot}257\rpar } \cr} } \right]\comma$

respectively. The posterior mean (standard deviation) of residual variance is $\hat{\bimsigma }_{\varepsilon }^{\setnum{2}}$ =1·985 (0·098). Although there are relatively large estimated errors for the covariance matrix of RR effects for individual-specific time-dependent environmental errors, nine detected QTLs collectively contribute 0·891 of the total accumulative phenotypic variance calculated by ${\bf \hats{V}} \equals {\bimpsi }^{\rm T} {\bm \hats\Sigma }_{\bimbeta } {\bimpsi } \plus {\bf I}\hat{\sigma }_{\varepsilon }^{\setnum{2}}$ , which is very close to the true value used in the simulation. In contrast, the interval-mapping analysis overestimated the effects of detected QTLs (see Table 3) and is unable to estimate the total accumulative proportion of phenotypic variance contributed by the detected QTL, since in this framework there are no unique and accurate estimates of Σ_β and σ_∊².

For the simulated dataset, we replace the B-spline with Legendre polynomials of orders 4, 5 and 6, respectively, to identify ten simulated QTLs. Legendre polynomials of order 4 and the B-spline mentioned above have the same number of regression coefficients. Meanwhile, we expect that polynomials of orders 5 and 6 yield higher goodness of fit to the simulated dataset than that of order 4. Fitting results indicate that although QTL intensity profiles for the three polynomials (not shown) all arise clear signal at each simulated locus, significant loci identified with these three polynomials are less than those with Bayesian B-spline mapping. As expected, polynomials of higher order may find more QTLs than those of low orders (Figure 4).

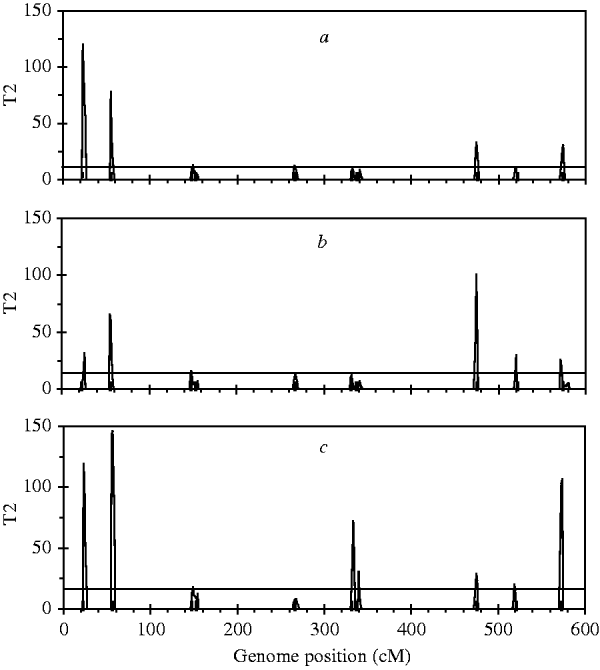
Fig. 4. The T ² statistic profiles for the entire genome obtained with Bayesian mapping based on Legendre polynomials of 4 (a), 5 (b) and 6 (c) order. The true positions of the simulated QTL are represented by black needles. The horizontal lines indicate the empirical critical values when the type I error rate was 5%, which are 11·07 for (a), 12·59 for (b) and 14·07 for (c), respectively.

Table 2. The estimated posterior means (posterior standard deviations) for QTL positions and regression effects for B-spines obtained with Bayesian B-spline mapping

– indicates that the position or regression effect cannot be estimated by the Bayesian B-spline mapping.

Table 3. The estimated posterior means (standard deviations) of QTL regression effects for B-spline obtained with interval mapping

– indicates that the position or regression effect cannot be estimated by the interval mapping.

Next, we generate the simulated data with Legendre polynomials and take a look at the detecting result with Bayesian B-spline mapping. For the same design of experiment implemented above, we describe changes in population mean, QTL genetic effects and individual-specific time-dependent environmental errors with Legendre polynomial of order 3. The regression effects for ten simulated QTLs are listed in Table 4. The population mean is μ=[45 44 −1 −7]^T , the covariance matrix of RR effects for individual-specific time-dependent environmental errors is

${\bmSigma }_{\bimbeta } \equals \left[ {\matrix{ {\hskip8pt 1{\cdot}042} \tab {0{\cdot}171} \tab { \minus 0{\cdot}035} \tab {0{\cdot}100} \cr {\hskip8pt 0{\cdot}171} \tab {0{\cdot}086} \tab {\hskip8pt 0{\cdot}041} \tab {0{\cdot}032} \cr { \minus 0{\cdot}035} \tab {0{\cdot}041} \tab {\hskip8pt 0{\cdot}087} \tab {0{\cdot}052} \cr {\hskip8pt 0{\cdot}100} \tab {0{\cdot}032} \tab {\hskip8pt 0{\cdot}052} \tab {0{\cdot}076} \cr} } \right]\comma$

and the residual variance is σ_∊²=2·0. Note that measuring time points are assigned as 5, 8, 13, 21, 26, 32 and 39.

Table 4. QTL regression effects for Legendre polynomials used in the simulation experiment

Yang & Xu (Reference Yang and Xu2007) have analysed the simulated data with Bayesian shrinkage estimation based on Legendre polynomials and identified nine of these simulated QTLs. For the same simulated dataset, Bayesian B-spline mapping also has the ability to obtain the same mapping result as Legendre polynomial analysis for the simulated data (results not shown). Herein, the knot points are chosen as 5, 20 and 39 in the used B-spline.

4. Example

The data published by Ma et al. (Reference Ma, Casella and Wu2002) are used to demonstrate the application of the proposed method to real data from dynamic traits. The analysed trait is the growth of the stem diameter of Populus trees measured annually in 11 years. The mapping population consists of 78 progeny of pseudo-backcross derived from the triple hybridization of Populus. A genetic linkage map has been constructed using 90 markers distributed on 23 linkage groups. Since the growth of the stem diameter follows the S-shaped curve, Ma et al. (Reference Ma, Casella and Wu2002) fit change of QTL genotypic value by Logistic curve within the interval-mapping framework. Subsequently, Yang et al. (Reference Yang, Tian and Xu2006, Reference Yang, Wu and Casella2009) replaced Logistic curve with Legendre polynomials and B-splines, respectively, and obtained good results.

In the Bayesian mapping procedure used here, the maximum number of QTLs is set to 100. Initial values of all unknown parameters and all the hyperparameters are determined according to the method used in the simulation. The algorithm used in this analysis is the same as that used in the analysis of simulated data. The B-spline with three knots and polynomial segments of order 2 is used to model the dynamic of population mean and genetic effect for each QTL in model (1). When the knots are chosen as 1, 6 and 11 years, the proposed method detects seven QTLs on linkage group D3-1, D4, D9, D10, D15 and D17 that control the growth trajectory of stem diameter of Populus. Parameter estimates of detectable QTLs are listed in Table 5. As a comparison, we also choose polynomials of orders 3, 4 and 5 and find only the polynomials of order 4 identifies the same QTLs as what we have from the B-spline approach (results not shown), demonstrating the capability of B-spline to replace polynomial in Bayesian mapping for dynamic quantitative traits. Moreover, in the B-spline, if internal knot points are taken as 5 and 7 years, respectively, mapping results are almost the same for either the Bayesian-mapping method or the interval-mapping method. This implies that the efficiency of the proposed method strongly depends on the choice of internal knots. For the real dataset, interval mapping based on model (1) with a single QTL only locates two QTLs on linkage group D10 and D17. However, functional mapping developed by Ma et al. (Reference Ma, Casella and Wu2002) only find QTLs on linkage group D10. Yang et al. (Reference Yang, Wu and Casella2009) also detect seven QTLs with B-spline-based interval mapping, but only two QTLs on linkage group D4 and D10 are consistent with our findings in this paper. This difference may be due to different mapping methods and the covariance structure specification for residuals.

Table 5. Parameter estimates of QTLs obtained from Bayesian B-spline mapping for stem diameters in Populus

5. Discussion

We successfully extended the Bayesian shrinkage method to mapping multiple QTLs for dynamic traits, and demonstrated by the simulated data analysis that Bayesian mapping is able to effectively and accurately detect QTL governing dynamic traits. The Bayesian-mapping analysis of dynamic traits was based on RR model, in which B-spline was chosen to simultaneously describe the dynamics of population means, genetic effects of multiple QTL and other environmental factors over time. This overcomes the disadvantages of Logistic curve used in traditional functional mapping, due to its non-additivity. Our model can be considered as a general framework for mapping QTL, for instance, which could be reduced to repeatability model for multiple traits when the order of B-spline was set to 0, and could be reduced to a single-trait model when all the covariates of measuring time were 1.

As illustrated in simulations and real data analysis, B-spline can capture complicated patterns but it is highly sensitive to the choice of knots. Therefore, the choice of knots should be the key elements of model specification in Bayesian B-spline mapping. Theoretically, too many knots lead to the over-fitting of the data, while too few knots lead to under-fitting. Some authors have proposed automatic schemes for optimizing the number and the positions of the knots (Friedman & Silverman, Reference Friedman and Silverman1989; Kooperberg & Stone, Reference Kooperberg and Stone1991, Reference Kooperberg and Stone1992). In particular, the choice of knots can be easily dealt with by using penalized or Bayesian estimation methods (e.g. Whaba, Reference Wahba1990; Rupert et al., Reference Ruppert, Wand and Carroll2003). Due to many different B-splines nested for each QTL and individual-specific environmental effects, however, Bayesian shrinkage analysis with the choice of a large number of knots will become computationally expensive and thus difficult to map dynamic trait loci. If only those positions with significant genetic effects are drawn with Bayesian model choice (Yi et al., Reference Yi, Yandell, Churchill, Allison, Eisen and Pomp2005; Min & Czado, Reference Min and Czado2011), the computational time can be greatly reduced. Here, we use the same B-spline to fit the changes in population means, genetic effects of multiple QTLs and other environmental factors over time, according to the averages fit of phenotypic values at different measurement points. Apparently, this choice for B-spline may not be optimal.

Since regression coefficients of B-spline determine the shape of dynamic trajectory, Bayesian B-spline mapping proposed here infers the QTL controlling the dynamic trajectory of dynamic quantitative traits by the Wald test statistic derived from posterior samples for QTL regression effects. By substituting each group of posterior sampling values for QTL regression effects into B-spline, we can obtain posterior sample for QTL effects at any dynamic point or within changing process of interest and by which infer the QTLs controlling any dynamic point or changing process of dynamic traits. According to the relationship between QTL regression effects and the parameters in biological meaningful model such as logistic curve, as derived in Yang & Xu (Reference Yang and Xu2007), we can also infer those QTLs controlling the biological meaningful characters. Therefore, it is easy to answer the criticism on the polynomial approach when applied to any curve is the interpretability of the polynomial regression coefficients in mapping QTL for dynamic traits.

6. Acknowledgment

The research was partially supported by the National Natural Science Foundation of China (30972077 and 31110103065) to R. Y.

Appendix A. The B-spline

Given k knots with t ₀⩽t ₁⩽…⩽t_k− ₁, B-spline of degree p is a parametric curve composed of a linear combination of basis B-splines ψ _i,p (t):

$B\lpar t\rpar \equals \mathop\sum\limits_{i \equals \setnum{0}}^{k \minus p \minus \setnum{2}} {b_{i} } \psi _{i\comma p} \lpar t\rpar \comma$

where b_i are called control points or de Boor points.

The k−p−1 basis B-splines of degree p can be defined, for p=0, 1, …, k−2, using the Cox–de Boor recursion formula. Basis functions of degree p=0 have values of unity for all points in a given interval, and zero otherwise. For the jth interval given by knots t_j and t_j ₊₁ with t_j<t_j ₊₁,

$\psi _{j\comma \setnum{0}} \lpar t\rpar \equals \left\{ {\matrix{ {1\comma } \tab {{\rm if}\,t_{j} \lt t \lt t_{j \plus \setnum{1}} } \cr {0\comma } \tab {{\rm otherwise\comma }} \cr} } \right.\quad {\rm for}\,j \equals 0\comma 1\comma \ldots\comma k \minus 2.$

Higher-degree basis functions ψ _{i, p} (t) for p>0, are then determined recursively from the values of the lower degree basis functions and the width of the adjoining intervals between knots. The general relationship is

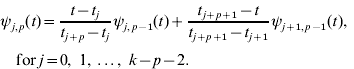
$\psi _{j\comma p} \lpar t\rpar \equals {{t \minus t_{j} } \over {t_{j \plus p} \minus t_{j} }}\psi _{j\comma p \minus \setnum{1}} \lpar t\rpar \plus {{t_{j \plus p \plus \setnum{1}} \minus t} \over {t_{j \plus p \plus \setnum{1}} \minus t_{j \plus \setnum{1}} }}\psi _{j \plus \setnum{1}\comma p \minus \setnum{1}} \lpar t\rpar \comma \quad {\rm for}\,j \equals 0\comma \;1\comma \ldots \comma \;k \minus p \minus 2.$

Obviously, there are a limited number of non-zero basis functions of lower order for each p.

Appendix B. Conditional posterior densities used for Gibbs samplers

The conditional posterior distribution for each unknown parameter can be derived from the joint posterior distribution density by fixing other parameters.

The conditional posterior distribution of μ is multivariate normal with mean

(B1)

${\rm E}\lpar {\bimmu }\vert \ldots\rpar \equals \lpar n{\bimpsi }{\bf V}^{ \minus \setnum{1}} {\bimpsi }^{\rm T} \rpar ^{ \minus \setnum{1}} {\bimpsi }{\bf V}^{ \minus \setnum{1}} \mathop\sum\limits_{i \equals \setnum{1}}^{n} {\left( {{\bf y}_{i}^{} \minus \mathop\sum\limits_{j \equals \setnum{1}}^{q} {x_{ij} {\bimpsi }^{\rm T} {\bimalpha }_{j} } } \right)}$

and covariance matrix

(B2)

${\rm Var}\lpar {\bimmu }\vert \ldots\rpar \equals \lpar n{\bimpsi }{\bf V}^{ \minus \setnum{1}} {\bimpsi }^{\rm T} \rpar ^{ \minus \setnum{1}} \comma$

where the μ| … notation is a short expression for conditional variable μ given all the data and other variables. Note that all variables appearing on the right-hand side of eqn (B1) are actual values sampled in a previous iteration.

The conditional posterior distribution of the jth QTL effects is multivariate normal with mean

(B3)

${\rm E}\lpar {\bimalpha }_{j} \vert \ldots\rpar \equals \mathop\sum\limits_{i \equals \setnum{1}}^{n} {{\bf A}_{j} {\bimpsi }} \lpar {\bf V} \plus x_{ij}^{\setnum{2}} {\bimpsi }^{\rm T} {\bf A}_{j} {\bimpsi }\rpar ^{ \minus \setnum{1}} x_{ij} \left( {{\bf y}_{i}^{} \minus {\bimpsi }^{\rm T} {\bimmu } \minus \mathop\sum\limits_{j\prime \ne j}^{q} {x_{ij\prime} {\bimpsi }^{\rm T} {\bimalpha }_{j\prime} } } \right)\comma$

and covariance matrix

(B4)

${\rm Var}\lpar {\bimalpha }_{j} \vert \ldots\rpar \equals {\bf A}_{j} \minus \mathop\sum\limits_{i \equals \setnum{1}}^{n} {x_{ij}^{\setnum{2}} {\bf A}_{j} {\bimpsi }} \lpar {\bf V} \plus x_{ij}^{\setnum{2}} {\bimpsi }^{\rm T} {\bf A}_{j} {\bimpsi }\rpar ^{ \minus \setnum{1}} {\bimpsi }^{\rm T} {\bf A}_{j} .$

The conditional posterior distribution of A_j is inverse Wishart with degrees of freedom b ₀+1 and covariance matrix (α _j α _j^T +Γ_A ⁻¹)⁻¹, i.e.

(B5)

${\bf A}_{j} \sim{\rm IW}\left[ {b_{\setnum{0}} \plus 1\comma \ \lpar {\bimalpha }_{j}^{} {\bimalpha }_{j}^{\rm T} \plus {\bmGamma }_{\bf A}^{{\bf - \setnum{1}}} \rpar ^{ \minus \setnum{1}} } \right].$

The conditional posterior distribution of the individual-specific β_i is a multivariate normal distribution with mean

(B6)

${\rm E}\lpar {\bimbeta }_{i} \vert \ldots\rpar \equals {\bmSigma }_{\bimbeta } {\bimpsi }{\bf V}^{ \minus \setnum{1}} \lpar {\bf y}_{i}^{} \minus {\bf U}_{i} \rpar$

and covariance matrix

(B7)

${\rm Var}\lpar {\bimbeta }_{i} \vert \ldots\rpar \equals {\bmSigma }_{\bimbeta } \minus {\bmSigma }_{\bimbeta } {\bimpsi }{\bf V}^{ \minus \setnum{1}} {\bimpsi }^{\rm T} {\bmSigma }_{\bimbeta } .$

The conditional posterior distribution of Σ_β is inverse Wishart, i.e.

(B8)

${\bmSigma }_{\bimbeta } \sim{\rm IW}\left[ {d_{\setnum{0}} \plus n\comma \left( {\mathop\sum\limits_{i \equals \setnum{1}}^{n} {{\bimbeta }_{i} {\bimbeta }_{i}^{\rm T} } \plus {\bmGamma }_{\bimbeta }^{ \minus \setnum{1}} } \right)^{ \minus \setnum{1}} } \right]$

The conditional posterior distribution for residual variance σ_∊² is a scaled inverse chi-square with parameters n(m+1)+v_e and $h_{e} S_{e} \plus \left( {\sum\nolimits_{i \equals \setnum{1}}^{n} {{\bimepsi }_{i}^{\rm T} {\bimepsi }_{i} } } \right)^{ \minus \setnum{1}}$ , where h_e =v_e +n(m+1) and

(B9)

${\bimepsi }_{i} \equals {\bf y}_{i} \minus {\bf U}_{i} \minus {\bimpsi }^{\rm T} {\bimbeta }_{i} .$

References

de Boor, C. (2001). A Practical Guide to Splines, Vol. 27, 2nd edn. New York: Springer-Verlag.Google Scholar

Friedman, J. H. & Silverman, B. W. (1989). Flexible parsimonious smoothing and additive modeling. Technometrics 31, 3–21.CrossRef Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S. & Rubin, D. B. (1995). Bayesian Data Analysis. New York: Chapman & Hall.CrossRef Google Scholar

Hastings, W. K. (1970). Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109.CrossRef Google Scholar

Henderson, C. R. (1982). Analysis of covariance in the mixed model: higher-level, nonhomogeneous, and random regressions. Biometrics 38, 623–640.CrossRef Google Scholar PubMed

Jamrozik, J., Schaeffer, L. R. & Dekkers, J. C. M. (1997). Genetic evaluation of dairy cattle using test day yields and random regression model. Journal of Dairy Science 80, 1217–1226.CrossRef Google Scholar PubMed

Jin, T., Li, J., Guo, Y., Zhou, X., Yang, R. & Wu, R. (2010). An optimal strategy for functional mapping of dynamic trait loci. Genetical Research 3, 1–8.Google Scholar

Kooperberg, C. & Stone, C. J. (1991). A study of logspline density estimation. Computational Statistics and Data Analysis 12, 327–348.CrossRef Google Scholar

Kooperberg, C. & Stone, C. J. (1992). Logspline density estimation for censored data. Journal of Computational and Graphical Statistics 1, 301–328.Google Scholar

Ma, C. X., Casella, G. & Wu, R. (2002). Functional mapping of quantitative trait loci underlying the character process: a theoretical framework. Genetics 161, 1751–1762.CrossRef Google Scholar PubMed

Macgregor, S., Knott, S. A., White, I. & Visscher, P. M. (2005). Quantitative trait locus analysis of longitudinal quantitative trait data in complex pedigrees. Genetics 171, 1365–1376.CrossRef Google Scholar PubMed

Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. (1953). Equation of state calculations by fast computing machines. Journal of Chemical Physics 21, 1087–1092.CrossRef Google Scholar

Min, A. & Czado, C. (2011). Bayesian model selection for D-vine pair-copula constructions. Canadian Journal of Statistics 2, 239–258.CrossRef Google Scholar

Ruppert, D., Wand, M. P. & Carroll, R. J. (2003). Semiparametric Regression. New York: Cambridge University Press.CrossRef Google Scholar

Schaeffer, L. R. (2004). Application of random regression models in animal breeding. Livestock Production Science 86, 35–45.CrossRef Google Scholar

Sen, Ś. & Churchill, G. A. (2001). A statistical framework for quantitative trait mapping. Genetics 159, 371–387.CrossRef Google Scholar PubMed

Sillanpää, M. J. & Arjas, E. (1998). Bayesian mapping of multiple quantitative trait loci from incomplete inbred line cross data. Genetics 148, 1373–1388.CrossRef Google Scholar PubMed

Sillanpää, M. J. & Arjas, E. (1999). Bayesian mapping of multiple quantitative trait loci from incomplete outbred offspring data. Genetics 151, 1605–1619.CrossRef Google Scholar PubMed

Wang, H., Zhang, Y. M., Li, X., Masinde, G. L., Mohan, S., Baylink, D. J. & Xu, S. (2005). Bayesian shrinkage estimation of quantitative trait loci parameters. Genetics 170, 465–480.CrossRef Google Scholar PubMed

Wahba, G. (1990). Spline Models for Observational Data. CBMS-NSF Regional Conference Series in Applied Mathematics 59. Philadelphia, PA: SIAM.CrossRef Google Scholar

Wu, R., Ma, C. X., Littell, R. C., Wu, S. S., Yin, T., Huang, M., Wang, M. & Casella, G. (2002). A logistic mixture model for characterizing genetic determinants causing differentiation in growth trajectories. Genetical Research 79, 235–245.CrossRef Google Scholar PubMed

Wu, R. L., Ma, C. X., Lin, M., Wang, Z. H. & George, C. (2004). Functional mapping of quantitative trait loci underlying growth trajectories using a transform-both-sides logistic model. Biometrics 60, 729–738.CrossRef Google Scholar PubMed

Wu, R., Ma, C. X., Zhao, W. & Casella, G. (2003). Functional mapping for quantitative trait loci governing growth rates: a parametric model. Physiological Genomics 14, 241–249.CrossRef Google Scholar

Yang, J., Wu, R. & Casella, G. (2009). Nonparametric functional mapping of quantitative trait loci. Biometrics 65, 30–39.CrossRef Google Scholar PubMed

Yang, R., Gao, H., Wang, X., Zhang, J., Zeng, Z. B. & Wu, R. (2007). A semiparametric approach for composite functional mapping of dynamic quantitative traits. Genetics 177, 1859–1870.CrossRef Google Scholar PubMed

Yang, R., Tian, Q. & Xu, S. (2006). Mapping quantitative trait loci for longitudinal traits in line crosses. Genetics 173, 2339–2356.CrossRef Google Scholar PubMed

Yang, R. & Xu, S. (2007). Bayesian shrinkage analysis of quantitative trait loci for dynamic traits. Genetics 176, 1169–1185.CrossRef Google Scholar PubMed

Yi, N. & Xu, S. (2000 a). Bayesian mapping of quantitative trait loci for complex binary traits. Genetics 155, 1391–1403.CrossRef Google Scholar PubMed

Yi, N. & Xu, S. (2000 b). Bayesian mapping of quantitative trait loci under the identity-by-descent-based variance component model. Genetics 156, 411–422.CrossRef Google Scholar PubMed

Yi, N., Yandell, B. S., Churchill, G. A., Allison, D. B., Eisen, E. J. & Pomp, D. (2005). Bayesian model selection for genome-wide epistatic quantitative trait loci analysis. Genetics 170, 1333–1344.CrossRef Google Scholar PubMed

Zhang, Y. M. & Xu, S. (2005). Advanced statistical methods for detecting multiple quantitative trait loci. Recent Research Developments in Genetics and Breeding 2, 1–23.Google Scholar

Fig. 1. Changes in genetic effects for ten simulated QTLs with time.

Table 1. QTL regression effects for B-splines used in simulation

Fig. 2. The QTL intensity profile (above) and T2 test statistic profile (below) over the entire genome obtained with Bayesian B-spline mapping. The true positions of the simulated QTL are represented by black needles. In T2 test statistic plot, the horizontal line indicates the empirical critical value of 11·05 when the type I error rate was 5%.

Fig. 4. The T2 statistic profiles for the entire genome obtained with Bayesian mapping based on Legendre polynomials of 4 (a), 5 (b) and 6 (c) order. The true positions of the simulated QTL are represented by black needles. The horizontal lines indicate the empirical critical values when the type I error rate was 5%, which are 11·07 for (a), 12·59 for (b) and 14·07 for (c), respectively.

Table 2. The estimated posterior means (posterior standard deviations) for QTL positions and regression effects for B-spines obtained with Bayesian B-spline mapping

Table 3. The estimated posterior means (standard deviations) of QTL regression effects for B-spline obtained with interval mapping

Table 4. QTL regression effects for Legendre polynomials used in the simulation experiment

Table 5. Parameter estimates of QTLs obtained from Bayesian B-spline mapping for stem diameters in Populus

Article contents

Bayesian B-spline mapping for dynamic quantitative traits

Summary

1. Introduction

2. Methods

(i) Genetic model of dynamic traits

(ii) Bayesian B-spline mapping

(a) Likelihoods

(b) Prior specification

(c) Markov chain Monte Carlo (MCMC) sampling for QTL parameters

(d) Post-Bayesian analysis

3. Simulation

4. Example

5. Discussion

6. Acknowledgment

Appendix A. The B-spline

Appendix B. Conditional posterior densities used for Gibbs samplers

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests