The Competition of Beverage Products in Current Market: A Composite Demand Analysis

Abstract

The beverage sector plays an important role in consumers' daily diet. Recent declines in fruit beverage and soft drink consumption may be a reflection of changing consumers' lifestyles and perceptions. This study uses recent scanner data to develop a demand analysis to examine the competition of various beverages. To obtain reliable demand and elasticity estimates, we test for valid aggregations using the generalized composite commodity theorem. Results suggest that while consumers substitute refrigerated juice with low calorie drinks, a larger proportion of consumers substitute regular soft drinks with fruit drinks.

The sales of nonalcoholic beverages in the United States, including milk, juice, soft drinks, bottled water, energy drinks, coffee, and tea, have increased moderately since 2008, reaching $131 billion in 2013, and are expected to continue growing to $164 billion by 2018 (Mintel 2014). While the overall beverage market grew in the past decade, different types of beverage products have had different growth rates. According to the Beverage Marketing Corporation (2015), bottled water, ready-to-drink coffee/tea, and energy drinks grew rapidly in 2014, while traditional carbonated soft drinks continued to lose both volume and market share. Compared to 2013, fruit beverages (including juice and drinks) lost 2.8 percent in sales volume, even though 100 percent fruit juice is a recommended part of the Dietary Guidelines for Americans. Given the ongoing changes in the sector, analysis of consumer demand and price competition among nonalcoholic beverage products will provide useful information for both private and public sectors, particularly for those associated with traditional industries experiencing difficulties.

Scanner data, considered a reliable source for demand analysis and consumers' real purchase choices in the markets, capture consumers' dynamic behavior by recording their purchases over time. However, using scanner data is not without cost, and one issue is data aggregation in demand analysis. As disaggregated data used in demand analysis may lead to difficulties such as degrees of freedom and computational limitations (Capps and Love 2002), aggregation over food products is important for demand analysis. However, to aggregate groups, appropriate tests are needed to determine if the products should be aggregated. Two of the most common justifications for aggregation are separable preferences and the Hicks-Leontief composite commodity theorem (CCT). Separable preferences restrict the patterns of expenditures and test how consumers allocate their expenditures over groups of products, while CCT restricts price movements and requires relative prices within a group to be constant over time. Previous studies have shown that both conditions tend to be violated in empirical work (Eales and Unnevehr 1988, Nayga and Capps 1994, Reed, Levedahl, and Hallahan 2005, Schulz, Schroeder, and Xia 2012). A more recent substitute approach for justifying data aggregation is the generalized composite commodity theorem (GCCT) proposed by Lewbel (1996), which showed that aggregation can be justified by relaxing the strict conditions of CCT. GCCT only requires that relative prices be statistically independent of group prices rather than be constant over time. This approach has been applied in various studies investigating the valid aggregation of both consumer goods and agricultural supplies. For example, Davis, Lin, and Shumway (2000) applied GCCT to test for consistent aggregation for U.S. and Mexican agricultural outputs. Schulz, Schroeder, and Xia (2012) tested for valid aggregation of ground beef by lean percentage and brand types. Reed, Levedahl, and Hallahan (2005), who tested 19 food categories, proposed 5 at-home food composites (cereal and bakery products, meat, dairy, fruit and vegetables, and other food-at-home), of which they showed that nonalcoholic beverages could be aggregated into the other food-at-home composite. Another study considering beverage products was conducted by Capps and Love (2002); in this study, they tested for valid aggregation of chilled and shelf-stable fruit juice and drink products by brands. More importantly, they concluded that aggregation based on GCCT not only reduced elements to be considered in a demand system, but also only marginally affected parameter estimates of non-aggregated products. Unlike previous studies, we examined beverage competition among various categories to shed light on recent changes in the consumption of traditional beverages, especially fruit beverages and soft drinks.

Several researchers have studied the beverage market using scanner data, with demand analysis being implemented at some level of aggregation (Yen et al. 2004, Zheng and Kaiser 2008, Smith, Yin, and Lee 2010), mostly based on traditional groupings or research purposes rather than on empirical tests. For example, aggregating 100-percent fruit juice and fruit drinks as fruit beverages, and aggregating regular and diet carbonated soft drinks as soft drinks is commonly used in studies. Capps and Love (2002) tested for aggregation on chilled and shelf-stable drinks by brands but not for aggregation on fruit juice and fruit drinks. With changes in consumers' lifestyles and perceptions, questions can be raised regarding the validation of such traditional aggregations. One factor that drives current beverage sales is consumers' perceptions of the health benefits of various types of beverages. For example, consumers are increasingly concerned about overweight and obesity, and many consumers are avoiding regular soft drinks to reduce sugar and calorie intake from beverage consumption, while trends in diet soft drink consumption might be different because of the lack of sugar content, indicating that regular and diet soft drinks could be classified as two separate categories. Similarly, fruit juice is 100-percent juice and naturally sweet, while fruit drinks contain less than 100-percent fruit juice and have extra sugar added, indicating that these two types of beverages could be classified as two separate categories. Although a few studies have separated regular and diet soft drinks or fruit juice and fruit drinks into individual or different categories (i.e., Dharmasena and Capps 2009, Smith, Yin, and Lee 2010), we are unaware of any studies that have tested their aggregation. Therefore, our study contributes to the literature by testing conventional aggregations and revealing valid aggregation using GCCT and recent scanner data. Moreover, if the aggregation is valid, we further estimate price elasticities of demand and investigate price competition among these beverage composites in the current market.

The objectives of our study are (1) to apply GCCT to the beverage market data to determine valid aggregation strategies, and (2) to estimate price elasticities of demand for beverage composites. We use ACNielsen retail scanner data of beverage sales for April 2013 through April 2015. Fifteen beverage products are used in this study, including ready-to-drink (RTD) coffee, RTD tea, milk, flavored milk, refrigerated orange juice, shelf-stable orange juice, refrigerated apple juice, shelf-stable apple juice, refrigerated other fruit juice, shelf-stable other fruit juice, refrigerated fruit drinks, shelf-stable fruit drinks, regular soft drinks, diet soft drinks, and bottled water.¹ A Rotterdam model is used to estimate price and expenditure elasticities. Our study provides useful and timely information to understand current consumers' demand for beverage products and the price competition in the market.

Methods and Data

This section describes the empirical procedure as follows. First, fifteen beverage products are tested for valid demand composites based on the GCCT. Second, if the aggregation is valid, we conduct demand analysis for composites using a Rotterdam model.

Testing

Following Lewbel (1996) and Reed, Levedahl, and Hallahan (2005), we define p _i as the price of good i and P _I as the Laspeyres price index of group I that contains good i. Letting γ _i = ln(p _i) and R _I = ln(P _I), the ith relative price, ρ _i, can be presented as

(1)$$\rho _i = \gamma _i - R_I\; $$

According to Lewbel (1996), a valid aggregation requires that ρ _i is independent of R _I. Therefore, testing whether or not GCCT holds is equivalent to testing whether or not ρ _i and R _I are independent of each other. Following Lewbel (1996), tests depend on the time series properties of the data. The procedure can be described as two steps: (1) determine the stationarity of each ρ _i and R _I using unit root tests and (2) based on the results of step 1, test the independences between ρ _i and R _I. Three possible results can be specified from the first step: if both ρ _i and R _I are stationary, a correlation test will be conducted to test independence; if ρ _i and R _I are both nonstationary, a cointegration test will be conducted to test independence; and if ρ _i is stationary and R _I is nonstationary, or R _I is stationary and ρ _i is nonstationary, then no test is required because two series cannot be cointegrated when one is stationary and the other is not, which is a direct result of the algebra of cointegration (Granger and Hallman 1988).

Following Reed, Levedahl, and Hallahan (2005) and Schulz, Schroeder, and Xia (2012), both the Augmented Dickey-Fuller (ADF) test (Dickey and Fuller 1979) and Kwaitkowski, Phillips, Schmidt, and Shin (KPSS) test (Kwaikowski et al. 1992) are conducted for relative prices and composite group price indices. The ADF test has a null hypothesis of nonstationarity, while the KPSS test has a null hypothesis of stationarity. When results from two tests are conflicted, inferences based on the joint confirmation hypothesis (JCH) of a unit root are used (Carrion-i-Silvestre, Sanso-i-Rossello, and M.A. Ortuno, 2001). The Engle-Granger test is used to test for cointegration when both the composite price index (R _I) and relative price (ρ _i) are nonstationary, with a null hypothesis that the two series are not cointegrated. The Spearman's rank test is used to test for correlation when both the two series are stationary, with a null hypothesis that two series are not correlated.

Rotterdam Model

The Rotterdam model is used to estimate the composite demand systems implied by GCCT tests. The Rotterdam model, introduced by Theil (1965), is widely used in demand system estimation using scanner data. The absolute value version of the Rotterdam model is specified as follows:

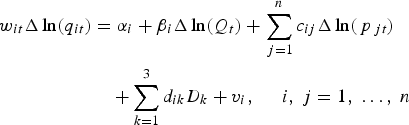(2)$$\eqalign{w_{it}\Delta \ln \lpar{q_{it}} \rpar& = \alpha _i + \beta _i\Delta \ln \lpar{Q_t} \rpar+ \mathop \sum \limits_{\,j = 1}^n c_{ij}\Delta \ln \lpar{\,p_{\,jt}} \rpar\cr & \quad + \mathop \sum \limits_{k = 1}^3 d_{ik}D_k + v_i\comma \; \; \; \; \; i\comma \; j = 1\comma \; \ldots\comma \; n} $$

where w _it is the budget share of the ith product in time t; Δ is the first difference operator; q _it is consumption of ith product in time t; Δln(Q _t) is the Divisia volume index $\Delta \ln \left({Q_t} \right)= \mathop \sum \nolimits_{j = 1}^n w_i\Delta {\rm ln}\left({q_{it}} \right)$; p _jt is the price of the jth product in time t; D _k is a quarterly dummy variable to capture seasonality; v _i is a random error term; and α _i, β _i, c _ij, and d _ik are coefficients to be estimated. The intercept α _i is used to capture any structure changes or trends that not captured by other variables (Taylor and Tonsor 2013).

The adding-up, homogeneity, and symmetry restrictions are imposed to ensure the demand model is consistent with economic theory. The adding-up restrictions are $\mathop \sum \nolimits_{i = 1}^n \beta _i = 1\semicolon \; \; \mathop \sum \nolimits_{i = 1}^n c_{ij} = 0$; the homogeneity and symmetry restrictions are $\mathop \sum \nolimits_{j = 1}^n c_{ij} = 0\semicolon \; \; c_{ij} = c_{ji}$. The own- and cross-price compensated demand elasticities, and the expenditure elasticity can be calculated by $e_{ij} = \displaystyle{{c_{ij}} \over {w_i}}\semicolon \; \; e_i = \displaystyle{{\beta _i} \over {w_i}}$. To avoid singularity of the covariance matrix, the equation for bottled water is dropped. A delta method is used to estimate the variance of each elasticity, and t-values are computed to test for statistical significance.

Data

The nationwide aggregated weekly sales on major beverage products (i.e., refrigerated orange juice and regular carbonated cola) from April 2013 through April 2015 were provided by ACNielsen, and the sales on each product from different brands, channels, and regions have been combined. For each product, ACNielsen recorded information on dollar sales and equivalent unit from U.S. grocery stores with $2 million or more in annual sales and from Walmart. Because a beverage product can be sold in single bottles, cans, or packs varying in size, equivalent units can be used to account for differences in packaging sizes. The unit price is computed by dividing the dollar sales by the equivalent unit. For simplification purposes, beverages were aggregated into fifteen categories: RTD coffee, RTD tea, milk, flavored milk, refrigerated fruit drinks, shelf-stable fruit drinks (usually pasteurized and packaged using various techniques for storage in sealed containers without refrigeration for longer shelf life), refrigerated apple juice, shelf-stable apple juice, refrigerated orange juice, shelf-stable orange juice, refrigerated other juice, shelf-stable other juice, regular soft drinks, diet soft drinks, and bottled water.

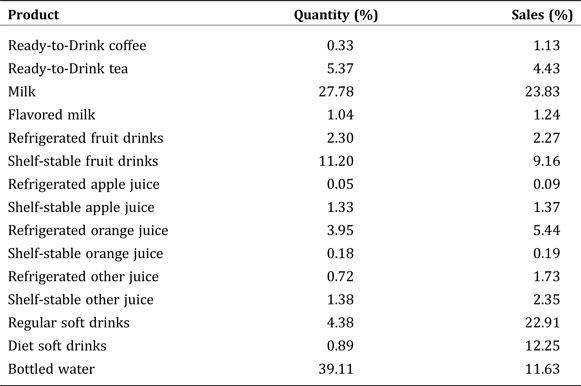
Percentage shares of quantity and sales for each product are calculated and reported in Table 1.² In this dataset, milk accounts for the largest share of sales dollar with nearly 24 percent, followed by regular soft drinks with about 23 percent share of sales. Diet soft drinks and bottled water have shares of sales of 12.3 percent and 11.6 percent, respectively. Refrigerated apple juice and shelf-stable orange juice have the lowest percentage shares of sales dollar with less than 1 percent (0.08 percent and 0.19 percent, respectively).

Table 1. Average Percentage Share of Quantity and Sales

Results

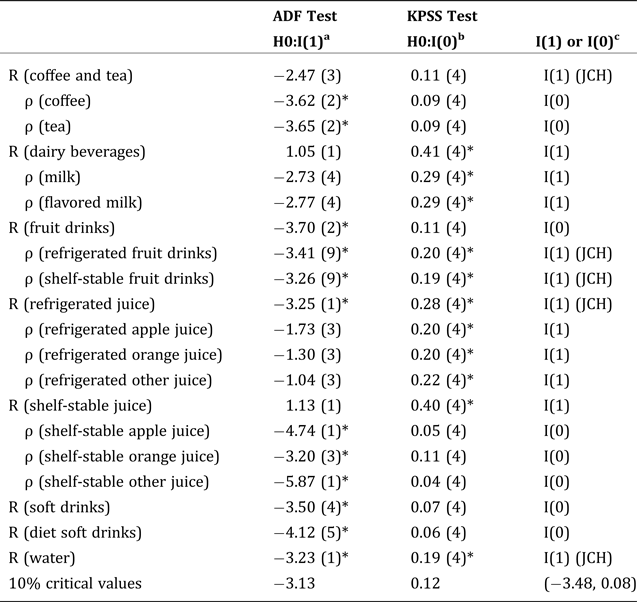
GCCT results for the valid aggregation are summarized in Tables 2 and 3. The stochastic nature of the GCCT may support numerous aggregation schemes (Reed, Levedahl, and Hallahan 2005), and we have tested several conventional groupings that were not supported. For example, the aggregation of regular soft drinks with diet soft drinks is unsupported by GCCT. Both ADF and KPSS tests show that both the relative and composite prices of regular and diet soft drinks are stationary. The Spearman's rank test was then conducted to test for independence between the individual relative price and the composite price. The null hypothesis of no correlation was rejected for both the relative price of regular soft drinks (r = −0.49, pvalue = 0.00) and the relative price of diet soft drinks (r = 0.49, pvalue = 0.00). Because the results indicated that both relative prices are not independent of the composite price index, we treated them separately in this study. Similarly, we also rejected the aggregation of refrigerated fruit drinks with fruit juice, and shelf-stable fruit drinks with fruit juice, as well as refrigerated fruit juice and shelf-stable juice. Such results indicate that aggregations need to be tested to obtain reliable information from demand system analysis. We propose to aggregate the fifteen beverage products into eight composites. The coffee and tea composite includes RTD coffee and RTD tea; the dairy beverage composite includes milk and flavored milk; the fruit drink composite includes refrigerated fruit drinks and shelf-stable fruit drinks; the refrigerated juice composite includes refrigerated apple juice, refrigerated orange juice, and refrigerated other juice; and the shelf-stable juice composite includes shelf-stable apple juice, shelf-stable orange juice, and shelf-stable other juice. Regular soft drinks, diet soft drinks, and bottled water are treated as valid separate composites.

Table 2. Unit Root Test Results

Note: * denotes rejection of the null at the 10-percent significant level.

^aThe test statistics of the null hypothesis of I(1) are the ADF t-statistics of the lagged level variable in the regression of the first-differences on a constant, a time trend, the lagged level and lagged-differences of variables appended to the regression. The number of lags of first-differences is reported in parentheses and determined by R statistical software.

^bThe test statistics of the null hypothesis of I(0) are the KPSS t-statistics. The t-statistics are the sum of the squared partial sums of residuals divided by an error variance estimator. The residuals are computed from a model in which the series is regressed on a constant and a time trend. For the correction of the error term a Bartlett window with four lags was used to ensure the variance matrix was well behaved.

^cInferences based on the joint confirmation hypothesis (JCH) of a unit root are used when the ADF and KPSS tests conflict. The joint critical values of (−3.48, 0.08) represent the mid-point of critical values for 100 and 150 observations for the ADF and KPSS tests with trend. They are interpreted as follows. If the value of ADF statistic is less (greater) than -3.48, and the value of the KPSS statistic is less (greater) than 0.08, then the series is considered (at the 10-percent level) stationary (nonstationary). Otherwise, the series cannot be confirmed to be a unit root and is therefore considered stationary.

Table 3. Generalized Composite Commodity Test Results

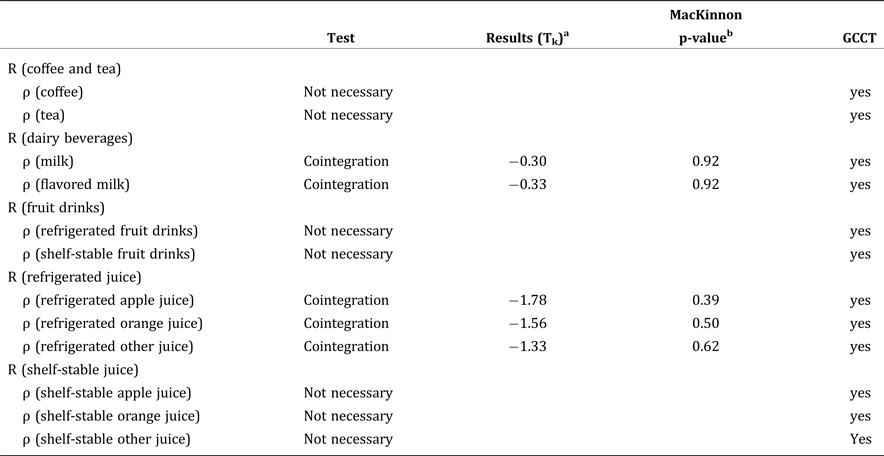
^aThe test statistics are the Engel-Granger tests of the null hypothesis that the kth relative price and the vector of composite group prices are not cointegrated. The entries are ADF tests of I(1) residuals formed from regressing the kth relative price on each of the integrated group price indices.

^bThe p-values are based on MacKinnon's t-statistics (with a constant in the cointegrating vector) and 104 observations (MacKinnon 1996).

Unit root tests on twelve relative prices and eight composite prices are reported in Table 2. Results show that the composite price index for coffee and tea, dairy beverages, refrigerated juice, shelf-stable juice, and bottled water follow unit root, while the composite price index for fruit drinks, regular soft drinks, and diet soft drinks are stationary. Relative prices of both products within the dairy beverage composite (milk and flavored milk), both products within the fruit drink composite (refrigerated and shelf-stable fruit drinks), and all products within the refrigerated juice composite (refrigerated apple juice, orange juice, and other juice) are nonstationary, while relative prices of coffee and tea, and products within the shelf-stable juice composite, including shelf-stable apple juice, orange juice, and other juice, are considered to be stationary. The Engle-Granger test results are summarized in Table 3. Because the tests failed to reject the null that the composite price index and relative price are not cointegrated, the series are independent of each other, indicating GCCT holds, and the proposed aggregation is valid.

The price and expenditure elasticities were estimated with the Rotterdam model, using SAS 9.4 software. The estimated results are presented in Table 4. All the own-price elasticities are negative and statistically significant at the 5-percent level, with the estimated price elasticities ranging from –0.64 to –2.07. Although numerous factors influence the determination of price elasticity, closeness of substitute products is an important factor. Because a beverage product is easily substitutable, the own-price elasticity of the product is high. The dairy beverage composite is price inelastic with an own-price elasticity value of 0.64, indicating that when the dairy beverage composite price increases by 1 percent, the demand for dairy beverages decreases by less than 1 percent. However, the own-price elasticities of other beverage composites are elastic, implying that demand for these beverages is very sensitive to price changes. The diet soft drink composite is the most price sensitive with an elasticity value of 2.07, followed by the fruit drink composite with an elasticity value of 2.00, and the fruit juice composite with elasticity values of 1.76 for refrigerated and 1.70 for shelf-stable juice. Andreyeva, Long, and Brownell (2010), who reviewed previously estimated price elasticity of demand for major food categories, reported the value of price elasticity for soft drinks ranged between 0.13 and 3.18, juice price elasticity ranged between 0.33 and 1.77, and dairy beverage (milk) price elasticity ranged between 0.02 and 1.68. Compared to previous studies, our elasticity estimates are at the high end of the range. For example, Zheng and Kaiser (2008) reported the value of price elasticity for bottled water was 0.50. Zheng and Kaiser (2008) and Yen et al. (2004) found the value of price elasticity for milk ranged between 0.15 and 0.59, followed by soft drinks that ranged between 0.15 and 0.52, juice that ranged between 0.17 and 0.35, and coffee and tea that ranged between 0.08 and 0.47. However, these studies aggregated products into only four or five categories. Dharmasena and Capps (2009) used household panel data from 1998–2003 to study ten categories. They reported consistently higher values of price elasticities compared to previous studies, and found that regular and diet soft drinks were the most price sensitive, behind sports drinks, followed by fruit juices. They found that only sports drinks and soft drinks were price elastic, while other beverages were inelastic or not statistically significant. These differences in elasticity estimates might be due to different products, time spans, and aggregation and estimation methods.

Table 4. Estimated Composite Compensated Price and Expenditure Elasticities (Standard Error)

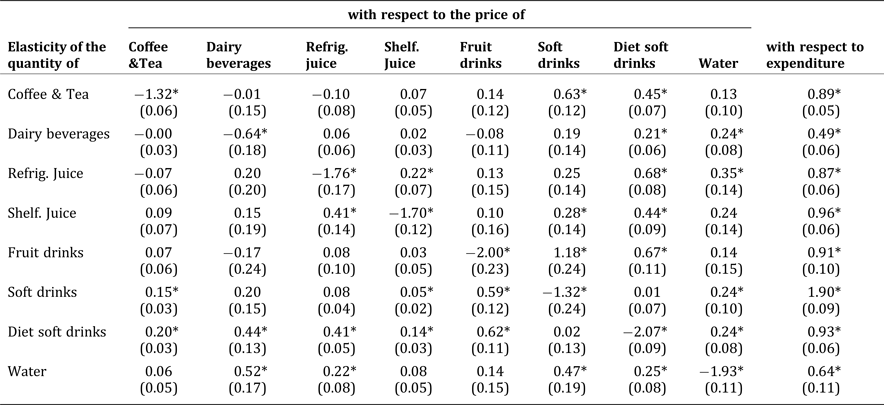
Note: * denotes statistically significance at the 5-percent level.

Estimated cross-price elasticities provide the demand relationship among composites. The composite for coffee and tea is a substitute for regular and diet soft drinks. The composite for dairy beverages is a substitute for diet soft drinks and bottled water. The composite for refrigerated juice is a substitute for shelf-stable juice, diet soft drinks, and water, while the composite for shelf-stable juice is a substitute for refrigerated juice, and regular and diet soft drinks. Based on the magnitude, more consumers would switch to refrigerated juice when the price of shelf-stable juice increases than those who would switch to shelf-stable juice when the price of refrigerated juice increases. Previous studies usually found that milk, juice, coffee, and tea were complements (Yen et al. 2004, Dharmassena and Capps 2009, Smith, Yin, and Lee 2010), possibly because they are often consumed together during breakfast (Dharmassena and Capps 2009). The different relationships found in our results may indicate that consumers' choices and perceptions for breakfast beverages have changed. Our results also show that the fruit drink composite is a substitute for regular and diet soft drinks. The substitution effect between fruit drinks and regular soft drinks is much larger than for other pairs, which implies that when regular soft drinks become more expensive, a large portion of consumers would substitute with fruit drinks, another type of sugary beverage. Unlike Dharmassena and Capps (2009), who reported a net substitution relationship, our study does not show fruit drinks to be a statistically significant substitute for fruit juice products. This could be because of changes in consumers' perceptions of beverages. Regular soft drinks are a substitute for coffee and tea, shelf-stable juice, fruit drinks, and water. Diet soft drinks are a substitute for all beverage composites except regular soft drinks (Dharmassena and Capps 2009). Such results indicate that consumers who purchase regular soft drinks and those who purchase diet soft drinks are two different consumer segments. Bottled water can substitute for dairy beverages, refrigerated juice, regular soft drinks, and diet soft drinks.

All expenditure elasticities are statistically significant, ranging from 0.49 for dairy beverages to 1.90 for soft drinks. The positive expenditure elasticities indicate demand for beverages increases with income. Soft drinks have an expenditure elasticity greater than one, indicating demand for soft drinks is sensitive to income changes. The expenditure elasticity is slightly smaller than one for fruit juice and fruit drinks, indicating fruit beverages are relatively sensitive to total expenditure changes.

Conclusions

Just as consumers' lifestyles and health perceptions have dramatically changed in recent years, so have sales of traditional nonalcoholic beverages such as soft drinks and fruit beverages. Our analysis of consumer demand and price competition among beverage products based on recent data can provide information for both private and public sectors associated with this industry.

We apply GCCT to nationwide scanner data to test for valid commodity aggregation to obtain reliable information from price and demand analysis. The empirical results show that some conventional aggregations are not supported by GCCT, confirming that aggregations must be justified prior to implementation. Our results support aggregation of coffee and tea, dairy beverages, refrigerated juice, shelf-stable juice, fruit drinks, regular soft drinks, diet soft drinks, and bottled water.

Demand analysis shows that consumers substitute coffee and tea with regular and diet soft drinks, possibly due to caffeine content. Dairy beverages and refrigerated juice are substituted with diet soft drinks and water, which consumers consider healthier or low-calorie beverages. The composite for shelf-stable juice substitutes for refrigerated juice, and regular and diet soft drinks, which may indicate that shelf-stable juice is not considered low calorie. More consumers switch to refrigerated juice when the price of shelf-stable juice increases than those who switch to shelf-stable juice when refrigerated juice price increases, which may indicate that refrigerated juice is perceived as a higher quality or healthier product. Fruit drinks are not a statistically significant substitute for fruit juice, possibly because consumers do not consider fruit drinks as healthy as fruit juice. Moreover, fruit drinks are a closer substitute with regular soft drinks, indicating a large proportion of consumers would switch to another high-calorie beverage even if regular soft drinks become more expensive. Bottled water substitutes with other beverages on a higher hydration index (Maughan et al. 2016), including dairy beverages, refrigerated juice, and regular and diet soft drinks.

Our study sheds light on the competition of fruit beverages and soft drinks based on current consumers' perceptions and tastes. Our study suggests that consumption of fruit beverages and diet soft drinks is very sensitive to prices, while consumption of regular soft drinks is relatively less price sensitive. Because consumers distinguish differences between fruit juice and fruit drinks, the two types of fruit beverages are not competing for the same consumers. Similarly, regular and diet soft drinks target different consumer groups. Refrigerated fruit juice and diet soft drinks appear to be perceived as healthier or low-calorie beverages. We found that fruit drink is a major substitution for soft drinks, suggesting that both types of products compete for consumers likely to choose sweet beverages. In addition, Zhen et al. (2013) predicted that increasing the prices of sugar-sweetened beverages will increase consumption of other high-calorie food. Our results raise concerns that policies such as the soda tax might cause consumers to switch to other high-calorie beverages.