The regression coefficient estimates, standard errors, and measures of fit given in Tables 1 and 2 in the published version of this article are incorrect, as are the textual statements that relied on their numerical values, because the observational ordering of the data-frames and spatial weights matrices were not properly matched. Consequently, the strength of spatial dependence was underestimated in all of the regression models that estimated it. Only the “Empirical Reanalyses” section is affected by these corrections. No substantive points made or conclusions drawn in the article are altered by these corrections; in fact, the results supporting those points and conclusions are generally made quantitatively stronger/greater in magnitude by the corrections. We have updated our APSR Dataverse and Replication files.
CHANGES
1. The original Table 1 in the published article is incorrect, the corrected estimates are reported below in the revised Table 1.
Table 1. Reanalysis of Development and Democracy in Acemoglu et al. (Reference Acemoglu, Johnson, Robinson and Yared2008)

Note:
![]() $ {}^{\ast }p<0.10{,}^{\hskip2pt \ast \ast }p<0.05{,}^{\hskip2pt \ast \ast \ast }p<0.01 $
.
$ {}^{\ast }p<0.10{,}^{\hskip2pt \ast \ast }p<0.05{,}^{\hskip2pt \ast \ast \ast }p<0.01 $
.
2. The two sentences about the column (2) model would read: “Since democracy trends globally over the sample period, this addition improves model fit: log-likelihood increases 11% (−141.84 to −125.88), but BIC increases from 310.69 to 332.76, reflecting little purchase from the 8 degrees of freedom consumed. The
![]() $ \hat{\rho} $
estimate declines by about
$ \hat{\rho} $
estimate declines by about
![]() $ \frac{1}{3} $
(and the RGDPpc coefficient-estimate compensatorily increases slightly: about
$ \frac{1}{3} $
(and the RGDPpc coefficient-estimate compensatorily increases slightly: about
![]() $ 7\% $
), but remains highly significant.”
$ 7\% $
), but remains highly significant.”
3. The following sentences regarding the column (3) and column (4) models would read: “The spatial-lag coefficient becomes less, but still quite, significant in column (3), with the country fixed-effects apparently absorbing noticeable time-invariant spatial clustering in both RGDPpc and democracy. The impact on model fit, however, is less clear. LL improves greatly, but the BIC fit statistic, which penalizes for over-parameterizing the model and over-fitting the sample, gets much worse, increasing 40% (332.76 to 467.05).”
4. The following sentences about the preferred column (5) model and its comparison to the column (3) model are modified to these: “The final column (5) presents results from the model with by far the best BIC (−412.81) and LL close to model (3) despite 132 fewer estimated parameters. The Likelihood Ratio test of model (5), which includes both temporal and spatial lag, and period fixed-effects, versus model (3) yields a Chi-Squared statistic of 11.14, which with 132 degrees of freedom overwhelmingly fails to reject:
![]() $ p\approx 1.0 $
.”
$ p\approx 1.0 $
.”
5. The sentence comparing the application’s estimated spatial-lag coefficients in models with and without temporal lag also included to that ratio in the simulations would read: “In the simulations, the SAR model
![]() $ \hat{\rho} $
averaged about twice the true STADL
$ \hat{\rho} $
averaged about twice the true STADL
![]() $ \rho $
; similarly here,
$ \rho $
; similarly here,
![]() $ \hat{\rho} $
from model (5) is 0.115, whereas model (2)
$ \hat{\rho} $
from model (5) is 0.115, whereas model (2)
![]() $ \hat{\rho} $
is roughly 1.7 times larger at 0.197.”
$ \hat{\rho} $
is roughly 1.7 times larger at 0.197.”
6. The sentences about the effects of development on democracy would read: “Using model (5) coefficient-estimates, a one-unit single-country shock to RGDPpc has contemporaneous ADE of +0.037 on democracy in that same country, AIE of +0.005 on democracy in other countries, for a combined ATE of +0.042. The respective long-run cumulative estimates are LRSS ADE=+0.144, LRSS AIE=+0.018, LRSS ATE=+0.162. These differ considerably from model (2), where the estimated effects have no temporal dynamics and are instead instantaneous at ADE=+0.200, AIE=+0.048, and ATE=+0.248. These latter static SAR-model estimated effects might seem dissimilar enough from the long-run effects from spatiotemporally dynamic STADL model (5)—differences of ADE +.056
![]() $ \approx $
39%, AIE +.030
$ \approx $
39%, AIE +.030
![]() $ \approx $
167%, and ATE=+.086
$ \approx $
167%, and ATE=+.086
![]() $ \approx $
53%—but the effects from model (2) incur immediately and fully, so the same-country, same-period effects from a change in development on democracy is ADE=+0.037 in model (5) versus ADE=+0.200 in model (2), more than a four-fold (
$ \approx $
53%—but the effects from model (2) incur immediately and fully, so the same-country, same-period effects from a change in development on democracy is ADE=+0.037 in model (5) versus ADE=+0.200 in model (2), more than a four-fold (
![]() $ \approx $
+441%) difference.
$ \approx $
+441%) difference.
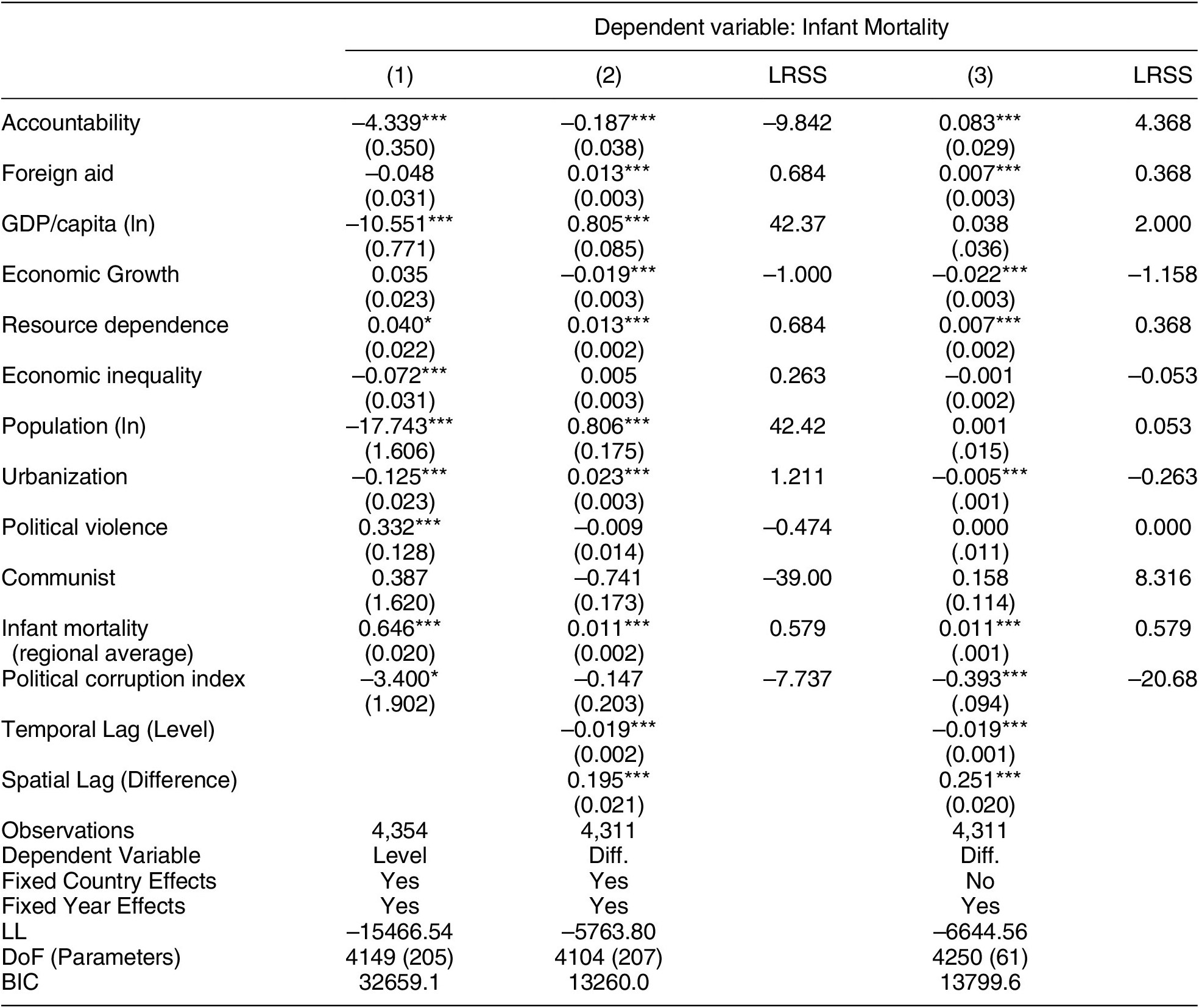
7. The original Table 2 in the published article is incorrect, the corrected estimates are reported in the revised Table 2.
Table 2. Reanalysis of the Accountability/Infant Mortality Regression in Lührmann, Marquardt, and Mechkova (Reference Lührmann, Marquardt and Mechkova2020)
Note:
![]() $ {}^{\ast }p<0.10{,}^{\hskip2pt \ast \ast }p<0.05{,}^{\hskip2pt \ast \ast \ast }p<0.01 $
.
$ {}^{\ast }p<0.10{,}^{\hskip2pt \ast \ast }p<0.05{,}^{\hskip2pt \ast \ast \ast }p<0.01 $
.
8. Using the correct estimates, the paragraph describing Table 2 would read: “Comparing the implicit spatial steady-state implied by the regional-average variable in the original regression, which ignores temporal (autoregressive) dynamics, with our estimate of the spatial steady-state effect, we estimate that the former overstates the extent of spatial dependence by nearly 12% in this comparison. More simply and starkly, comparing the first and third columns, we estimate that the spatiotemporal LRSS effect of Lührmann et al.’s (Reference Lührmann, Marquardt and Mechkova2020) political accountability on infant mortality rates (
![]() $ -9.842 $
) is more than double the ‘effect’ they reported (
$ -9.842 $
) is more than double the ‘effect’ they reported (
![]() $ \hat{\beta}=-4.339 $
), which mostly ignores these important spatial and temporal dynamic dependencies. In column 4 (model 3), we drop the country dummies from model 2. In contrast with the analysis in Table 1, we find that the inclusion of country fixed-effects here leads to unambiguous improvement in model-fit by either LL or BIC. Model 2 is clearly the preferred model among this set.”
$ \hat{\beta}=-4.339 $
), which mostly ignores these important spatial and temporal dynamic dependencies. In column 4 (model 3), we drop the country dummies from model 2. In contrast with the analysis in Table 1, we find that the inclusion of country fixed-effects here leads to unambiguous improvement in model-fit by either LL or BIC. Model 2 is clearly the preferred model among this set.”





Comments
No Comments have been published for this article.