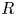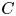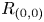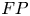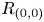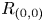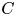Part I. Finite domination over strongly $\mathbb {Z}^2$![]() -graded rings
-graded rings
1. Introduction
Let $L$![]() be a unital ring, and let $K$
be a unital ring, and let $K$![]() be a subring of $L$
be a subring of $L$![]() . A bounded chain complex $C$
. A bounded chain complex $C$![]() of (right) $L$
of (right) $L$![]() -modules is $K$
-modules is $K$![]() -finitely dominated if $C$
-finitely dominated if $C$![]() , considered as a complex of $K$
, considered as a complex of $K$![]() -modules, is a retract up to homotopy of a bounded complex of finitely generated free $K$
-modules, is a retract up to homotopy of a bounded complex of finitely generated free $K$![]() -modules; this happens if and only if $C$
-modules; this happens if and only if $C$![]() is homotopy equivalent, as a $K$
is homotopy equivalent, as a $K$![]() -module complex, to a bounded complex of finitely generated projective $K$
-module complex, to a bounded complex of finitely generated projective $K$![]() -modules [Reference Ranicki7, Proposition 3.2. (ii)]. The following result of Ranicki gives a complete homological characterization of finite domination in an important special case:
-modules [Reference Ranicki7, Proposition 3.2. (ii)]. The following result of Ranicki gives a complete homological characterization of finite domination in an important special case:
Theorem 1.1 Ranicki [Reference Ranicki8, Theorem 2]
Let $K$![]() be a unital ring, and let $K[t,t^{-1} ]$
be a unital ring, and let $K[t,t^{-1} ]$![]() denote the Laurent polynomial ring in the indeterminate $t$
denote the Laurent polynomial ring in the indeterminate $t$![]() . Let $C$
. Let $C$![]() be a bounded chain complex of finitely generated free $K[t,t^{-1} ]$
be a bounded chain complex of finitely generated free $K[t,t^{-1} ]$![]() -modules. The complex $C$
-modules. The complex $C$![]() is $K$
is $K$![]() -finitely dominated if and only if both
-finitely dominated if and only if both
have vanishing homology in all degrees. Here we use the notation $K(\kern -1.7pt ( {t})\kern -1.7pt ) = K[\kern -1pt [{t}] \kern -1pt ][t^{-1} ]$![]() for the ring of formal Laurent series in $t$
for the ring of formal Laurent series in $t$![]() , and similarly $K(\kern -1.7pt ( {t^{-1}})\kern -1.7pt ) = K[\kern -1pt [{t^{-1}}] \kern -1pt ][t]$
, and similarly $K(\kern -1.7pt ( {t^{-1}})\kern -1.7pt ) = K[\kern -1pt [{t^{-1}}] \kern -1pt ][t]$![]() stands for the ring of formal Laurent series in $t^{-1}$
stands for the ring of formal Laurent series in $t^{-1}$![]() .
.
The cited paper [Reference Ranicki8] also contains a discussion of the relevance of finite domination in topology. The rings $K(\kern -1.7pt ( {t})\kern -1.7pt )$![]() and $K(\kern -1.7pt ( {t^{-1}})\kern -1.7pt )$
and $K(\kern -1.7pt ( {t^{-1}})\kern -1.7pt )$![]() are known as Novikov rings. The theorem can be formulated more succinctly: The chain complex $C$
are known as Novikov rings. The theorem can be formulated more succinctly: The chain complex $C$![]() is $K$
is $K$![]() -finitely dominated if and only if it has trivial Novikov homology.
-finitely dominated if and only if it has trivial Novikov homology.
This result was extended by Quinn and the first author to Laurent polynomial rings in two variables; contrary to appearance, this is not a straight-forward modification of the original result, introducing additional levels of complication in homological algebra.
Theorem 1.2 Hüttemann and Quinn [Reference Hüttemann and Quinn3, Theorem I.1.2]
Let $C$![]() be a bounded chain complex of finitely generated free $L$
be a bounded chain complex of finitely generated free $L$![]() -modules, where $L = K[x,x^{-1}, y, y^{-1}]$
-modules, where $L = K[x,x^{-1}, y, y^{-1}]$![]() is a Laurent polynomial ring in two variables over the unital ring $K$
is a Laurent polynomial ring in two variables over the unital ring $K$![]() . The following two statements are equivalent:
. The following two statements are equivalent:
(1) The complex $C$
 is $K$
is $K$ -finitely dominated, i.e., $C$
-finitely dominated, i.e., $C$ is homotopy equivalent, as an $K$
is homotopy equivalent, as an $K$ -module chain complex, to a bounded chain complex of finitely generated projective $K$
-module chain complex, to a bounded chain complex of finitely generated projective $K$ -modules.
-modules.(2) The eight chain complexes listed below are acyclic (all tensor products are taken over $L$
 ):
(1.1a)\begin{align} & \left.\begin{aligned} & C \mathop{\otimes} K[x,\, x^{{-}1}](\kern -1.7pt ( {y})\kern-1.7pt ) \ , & & C \mathop{\otimes} K[x,\, x^{{-}1}](\kern -1.7pt ( {y^{{-}1}})\kern-1.7pt ) \\ & C \mathop{\otimes} K[y,\, y^{{-}1}](\kern -1.7pt ( {x})\kern-1.7pt ) \ , & & C \mathop{\otimes} K[y,\, y^{{-}1}](\kern -1.7pt ( {x^{{-}1}})\kern-1.7pt ) \end{aligned}\right\} \end{align}
):
(1.1a)\begin{align} & \left.\begin{aligned} & C \mathop{\otimes} K[x,\, x^{{-}1}](\kern -1.7pt ( {y})\kern-1.7pt ) \ , & & C \mathop{\otimes} K[x,\, x^{{-}1}](\kern -1.7pt ( {y^{{-}1}})\kern-1.7pt ) \\ & C \mathop{\otimes} K[y,\, y^{{-}1}](\kern -1.7pt ( {x})\kern-1.7pt ) \ , & & C \mathop{\otimes} K[y,\, y^{{-}1}](\kern -1.7pt ( {x^{{-}1}})\kern-1.7pt ) \end{aligned}\right\} \end{align} (1.1b)\begin{align} \left.\begin{aligned} & C \mathop{\otimes} K(\kern -1.7pt ( {x,\, y})\kern-1.7pt ) \ , & & C \mathop{\otimes} K(\kern -1.7pt ( {x^{{-}1},\, y^{{-}1}})\kern-1.7pt ) \\ & C \mathop{\otimes} K(\kern -1.7pt ( {x,\, y^{{-}1}})\kern-1.7pt ) \ , & & C \mathop{\otimes} K(\kern -1.7pt ( {x^{{-}1},\, y})\kern-1.7pt ) \end{aligned}\right\} \end{align}Here $K(\kern -1.7pt ( {x,y})\kern -1.7pt ) = K[\kern -1pt [{x,y}] \kern -1pt ][1/xy]$
(1.1b)\begin{align} \left.\begin{aligned} & C \mathop{\otimes} K(\kern -1.7pt ( {x,\, y})\kern-1.7pt ) \ , & & C \mathop{\otimes} K(\kern -1.7pt ( {x^{{-}1},\, y^{{-}1}})\kern-1.7pt ) \\ & C \mathop{\otimes} K(\kern -1.7pt ( {x,\, y^{{-}1}})\kern-1.7pt ) \ , & & C \mathop{\otimes} K(\kern -1.7pt ( {x^{{-}1},\, y})\kern-1.7pt ) \end{aligned}\right\} \end{align}Here $K(\kern -1.7pt ( {x,y})\kern -1.7pt ) = K[\kern -1pt [{x,y}] \kern -1pt ][1/xy]$
 is a localization of the ring of formal power series in $x$
is a localization of the ring of formal power series in $x$ and $y$
and $y$ , and the other rings are defined analogously.
, and the other rings are defined analogously.
The authors of the present paper generalized theorem 1.1 in an entirely different direction, exhibiting the graded structure of Laurent polynomial rings as the crucial property for setting up the theory.
Theorem 1.3 Hüttemann and Steers [Reference Hüttemann and Steers4, Theorem 1.3]
Let $R_*[t,t^{-1} ] = \bigoplus _{k \in \mathbb {Z}} R_{k}$![]() be a strongly $\mathbb {Z}$
be a strongly $\mathbb {Z}$![]() -graded ring, and let $C$
-graded ring, and let $C$![]() be a bounded chain complex of finitely generated free $R_*[t,t^{-1} ]$
be a bounded chain complex of finitely generated free $R_*[t,t^{-1} ]$![]() -modules. The complex $C$
-modules. The complex $C$![]() is $R_{0}$
is $R_{0}$![]() -finitely dominated if and only if both
-finitely dominated if and only if both
have vanishing homology in all degrees. Here the rings
are used as formal analogues of the usual Novikov rings.
The notion of a strongly graded ring will be discussed in detail below. In the first instance, $R = \bigoplus _{k \in \mathbb {Z}} R_{k}$![]() is a $\mathbb {Z}$
is a $\mathbb {Z}$![]() -graded ring. The (usual) Laurent polynomial ring $R[t,t^{-1}]$
-graded ring. The (usual) Laurent polynomial ring $R[t,t^{-1}]$![]() has a $\mathbb {Z}$
has a $\mathbb {Z}$![]() -graded subring $R_*[t,t^{-1}]$
-graded subring $R_*[t,t^{-1}]$![]() with $k$
with $k$![]() th component the set of monomials $r_{k} t^{k}$
th component the set of monomials $r_{k} t^{k}$![]() with $r_{k} \in R_{k}$
with $r_{k} \in R_{k}$![]() . In fact, we may identify $R_* [t,t^{-1}]$
. In fact, we may identify $R_* [t,t^{-1}]$![]() with $R$
with $R$![]() itself. In a similar spirit, the Novikov rings $R (\kern -1.7pt ( {t^{-1}})\kern -1.7pt )$
itself. In a similar spirit, the Novikov rings $R (\kern -1.7pt ( {t^{-1}})\kern -1.7pt )$![]() and $R (\kern -1.7pt ( {t})\kern -1.7pt )$
and $R (\kern -1.7pt ( {t})\kern -1.7pt )$![]() have subrings $R_* (\kern -1.7pt ( {t^{-1}})\kern -1.7pt )$
have subrings $R_* (\kern -1.7pt ( {t^{-1}})\kern -1.7pt )$![]() and $R_* (\kern -1.7pt ( {t})\kern -1.7pt )$
and $R_* (\kern -1.7pt ( {t})\kern -1.7pt )$![]() determined by the condition that the coefficient of $t^{k}$
determined by the condition that the coefficient of $t^{k}$![]() be an element of $R_{k}$
be an element of $R_{k}$![]() , for any $k \in \mathbb {Z}$
, for any $k \in \mathbb {Z}$![]() . It may be worth pointing out that these subrings do not contain the indeterminate $t$
. It may be worth pointing out that these subrings do not contain the indeterminate $t$![]() , which should be considered a purely notational device.
, which should be considered a purely notational device.
2. The main theorem
In the present paper, we take the step to strongly $\mathbb {Z}^2$![]() -graded rings, combining ideas from both of the aforementioned publications [Reference Hüttemann and Quinn3] and [Reference Hüttemann and Steers4]. Roughly speaking, a bounded chain complex $C$
-graded rings, combining ideas from both of the aforementioned publications [Reference Hüttemann and Quinn3] and [Reference Hüttemann and Steers4]. Roughly speaking, a bounded chain complex $C$![]() of finitely generated free modules over a strongly $\mathbb {Z}^2$
of finitely generated free modules over a strongly $\mathbb {Z}^2$![]() -graded ring is finitely dominated over the degree-$0$
-graded ring is finitely dominated over the degree-$0$![]() subring if and only if certain eight complexes induced from $C$
subring if and only if certain eight complexes induced from $C$![]() are acyclic. Indeed, from a $\mathbb {Z}^{2}$
are acyclic. Indeed, from a $\mathbb {Z}^{2}$![]() -graded ring $R = \bigoplus _{\sigma \in \mathbb {Z}^{2}} R_{\sigma }$
-graded ring $R = \bigoplus _{\sigma \in \mathbb {Z}^{2}} R_{\sigma }$![]() we construct the following eight Novikov-type rings:
we construct the following eight Novikov-type rings:

Similar to notation used earlier, the symbols $x$![]() and $y$
and $y$![]() do not stand for actual indeterminates; they are purely notational devices, emphasizing a formal similarity with Laurent polynomial rings and their associated Novikov rings. The ring $R_*[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$
do not stand for actual indeterminates; they are purely notational devices, emphasizing a formal similarity with Laurent polynomial rings and their associated Novikov rings. The ring $R_*[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$![]() is the subring of $R[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$
is the subring of $R[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$![]() with elements $\sum _{(a,b) \in \mathbb {Z}^2} r_{a,b} x^a y^b$
with elements $\sum _{(a,b) \in \mathbb {Z}^2} r_{a,b} x^a y^b$![]() such that $r_{a,b} \in R_{(a,b)}$
such that $r_{a,b} \in R_{(a,b)}$![]() , and similar for the other seven cases. With this notational camouflage, we obtain a perfect analogue of theorem 1.2:
, and similar for the other seven cases. With this notational camouflage, we obtain a perfect analogue of theorem 1.2:
Theorem 2.1 Let $R=\bigoplus _{k\in \mathbb {Z}^2}R_k$![]() be a strongly $\mathbb {Z}^2$
be a strongly $\mathbb {Z}^2$![]() -graded ring, and let $C$
-graded ring, and let $C$![]() be a bounded chain complex of finitely generated free $R$
be a bounded chain complex of finitely generated free $R$![]() -modules. The complex $C$
-modules. The complex $C$![]() is $R_{(0,0)}$
is $R_{(0,0)}$![]() -finitely dominated if and only if all of the eight complexes
-finitely dominated if and only if all of the eight complexes

and

have vanishing homology in all degrees.
Applications in $\Sigma$ -invariant theory
-invariant theory
Let $G$![]() be a group. Every character $\chi \colon G \longrightarrow \mathbb {R}$
be a group. Every character $\chi \colon G \longrightarrow \mathbb {R}$![]() to the additive group of the reals determines a monoid $G_\chi = \{g \in G \,|\, \chi (g) \geq 0\}$
to the additive group of the reals determines a monoid $G_\chi = \{g \in G \,|\, \chi (g) \geq 0\}$![]() . Now suppose $C$
. Now suppose $C$![]() is a non-negatively indexed chain complex of $\mathbb {Z}[G]$
is a non-negatively indexed chain complex of $\mathbb {Z}[G]$![]() -modules. Then $C$
-modules. Then $C$![]() has, by restriction of scalars, the structure of a $\mathbb {Z}[G_\chi ]$
has, by restriction of scalars, the structure of a $\mathbb {Z}[G_\chi ]$![]() -module chain complex. Following Farber et.al. one defines [Reference Farber, Geĭgan and Shyutts2, Definition 9] the $m$
-module chain complex. Following Farber et.al. one defines [Reference Farber, Geĭgan and Shyutts2, Definition 9] the $m$![]() th $\Sigma$
th $\Sigma$![]() -invariant of $C$
-invariant of $C$![]() as
as
that is, $\Sigma ^m (C)$![]() is a quotient of the set of those non-trivial $\chi$
is a quotient of the set of those non-trivial $\chi$![]() for which there is a chain complex $C^\prime$
for which there is a chain complex $C^\prime$![]() consisting of finitely generated projective $\mathbb {Z}[G_\chi ]$
consisting of finitely generated projective $\mathbb {Z}[G_\chi ]$![]() -modules, and a $\mathbb {Z}[G_\chi ]$
-modules, and a $\mathbb {Z}[G_\chi ]$![]() -linear chain map $f \colon C^\prime \longrightarrow C$
-linear chain map $f \colon C^\prime \longrightarrow C$![]() with $f_i \colon H_i (C^\prime ) \longrightarrow H_i (C)$
with $f_i \colon H_i (C^\prime ) \longrightarrow H_i (C)$![]() an isomorphism for $i< m$
an isomorphism for $i< m$![]() and an epimorphism for $i=m$
and an epimorphism for $i=m$![]() . Two different characters are identified in the quotient precisely when they are positive real multiples of each other. The set $\Sigma ^m(C)$
. Two different characters are identified in the quotient precisely when they are positive real multiples of each other. The set $\Sigma ^m(C)$![]() can be used to detect whether $C$
can be used to detect whether $C$![]() is $\mathbb {Z}[N]$
is $\mathbb {Z}[N]$![]() -finitely dominated:
-finitely dominated:
Theorem 2.2 [Reference Farber, Geĭgan and Shyutts2, Corollary 4]
Suppose that $C$![]() consists of finitely generated free $\mathbb {Z}[G]$
consists of finitely generated free $\mathbb {Z}[G]$![]() -modules, and is such that $C_i = 0$
-modules, and is such that $C_i = 0$![]() whenever $i>m$
whenever $i>m$![]() . Let $N$
. Let $N$![]() be a normal subgroup of $G$
be a normal subgroup of $G$![]() with abelian quotient $G/N$
with abelian quotient $G/N$![]() . Then the $\mathbb {Z}[N]$
. Then the $\mathbb {Z}[N]$![]() -module complex $C$
-module complex $C$![]() is chain homotopy equivalent to a bounded chain complex of finitely generated projective $\mathbb {Z}[N]$
is chain homotopy equivalent to a bounded chain complex of finitely generated projective $\mathbb {Z}[N]$![]() -modules concentrated in degrees $\leq m$
-modules concentrated in degrees $\leq m$![]() if and only if the set $\Sigma ^m(C)$
if and only if the set $\Sigma ^m(C)$![]() contains the equivalence class of every non-trivial character of $G$
contains the equivalence class of every non-trivial character of $G$![]() that factorizes through $G/N$
that factorizes through $G/N$![]() (i.e., whose kernel contains $N$
(i.e., whose kernel contains $N$![]() ).
).
For $K$![]() a unital ring and a character $\chi \colon G \longrightarrow \mathbb {R}$
a unital ring and a character $\chi \colon G \longrightarrow \mathbb {R}$![]() we define the Novikov ring
we define the Novikov ring
where $\mathrm {supp}(f) = f^{-1} (K \setminus \{0\} )$![]() , with multiplication given by the usual involution product. Note that $K[G]$
, with multiplication given by the usual involution product. Note that $K[G]$![]() is a subring of $\widehat {K G_\chi }$
is a subring of $\widehat {K G_\chi }$![]() . Vanishing of Novikov homology, that is, vanishing of homology with coefficients in the rings $\widehat {K G_\chi }$
. Vanishing of Novikov homology, that is, vanishing of homology with coefficients in the rings $\widehat {K G_\chi }$![]() , characterizes whether $C$
, characterizes whether $C$![]() is finitely dominated over $K[N]$
is finitely dominated over $K[N]$![]() , provided $G/N$
, provided $G/N$![]() is free abelian of finite rank:
is free abelian of finite rank:
Theorem 2.3 Schütz [Reference Schütz10, Theorem 4.7]
Let $C$![]() be a bounded chain complex of finitely generated free $K[G]$
be a bounded chain complex of finitely generated free $K[G]$![]() -modules. Suppose that $N$
-modules. Suppose that $N$![]() is a normal subgroup of $G$
is a normal subgroup of $G$![]() with quotient $G/N \cong \mathbb {Z}^k$
with quotient $G/N \cong \mathbb {Z}^k$![]() a free abelian group of finite rank. The complex $C$
a free abelian group of finite rank. The complex $C$![]() is $K[N]$
is $K[N]$![]() -finitely dominated if and only if for every non-zero character $\chi \colon G \longrightarrow \mathbb {R}$
-finitely dominated if and only if for every non-zero character $\chi \colon G \longrightarrow \mathbb {R}$![]() which is trivial on $N$
which is trivial on $N$![]() the complex $C \mathop {\otimes }_{K[G]} \widehat {K G_\chi }$
the complex $C \mathop {\otimes }_{K[G]} \widehat {K G_\chi }$![]() is acyclic.
is acyclic.
The non-zero characters which are trivial on $N$![]() correspond bijectively to non-zero homomorphisms $\mathbb {Z}^{k} \cong G/N \to \mathbb {R}$
correspond bijectively to non-zero homomorphisms $\mathbb {Z}^{k} \cong G/N \to \mathbb {R}$![]() , which in turn correspond bijectively to elements of $\mathbb {R}^{k} \setminus \{0\}$
, which in turn correspond bijectively to elements of $\mathbb {R}^{k} \setminus \{0\}$![]() ; the set of equivalence classes of such characters thus forms a sphere $S^{k-1} \cong \big ( \mathbb {R}^{k} \setminus \{0\} \big ) / \mathbb {R}_+$
; the set of equivalence classes of such characters thus forms a sphere $S^{k-1} \cong \big ( \mathbb {R}^{k} \setminus \{0\} \big ) / \mathbb {R}_+$![]() of dimension $k-1$
of dimension $k-1$![]() . With this identification, the $\Sigma$
. With this identification, the $\Sigma$![]() -invariants $\Sigma ^m(C)$
-invariants $\Sigma ^m(C)$![]() and their analogues
and their analogues
are subsets of $S^{k-1}$![]() . The two theorems assert that $C$
. The two theorems assert that $C$![]() is $K[N]$
is $K[N]$![]() -finitely dominated, with the equivalent finite type complex concentrated in chain degrees $\leq m$
-finitely dominated, with the equivalent finite type complex concentrated in chain degrees $\leq m$![]() in case of the first theorem, if and only if $\Sigma ^m(C) = S^{k-1}$
in case of the first theorem, if and only if $\Sigma ^m(C) = S^{k-1}$![]() or $\Sigma '(C) = S^{k-1}$
or $\Sigma '(C) = S^{k-1}$![]() , respectively. Even for $k=2$
, respectively. Even for $k=2$![]() , computation of $\Sigma ^m(C)$
, computation of $\Sigma ^m(C)$![]() and $\Sigma '(C)$
and $\Sigma '(C)$![]() a priori involves infinitely many Novikov rings.
a priori involves infinitely many Novikov rings.
Fixing a choice of isomorphism $G/N \cong \mathbb {Z}^{k}$![]() gives a group epimorphism $\pi \colon G \to \mathbb {Z}^{k}$
gives a group epimorphism $\pi \colon G \to \mathbb {Z}^{k}$![]() with kernel $N$
with kernel $N$![]() , which can be used to equip the group ring $K[G] = \bigoplus _{p \in \mathbb {Z}^{k}} K\big [ \pi ^{-1}(p) \big ]$
, which can be used to equip the group ring $K[G] = \bigoplus _{p \in \mathbb {Z}^{k}} K\big [ \pi ^{-1}(p) \big ]$![]() with the structure of a strongly $\mathbb {Z}^{k}$
with the structure of a strongly $\mathbb {Z}^{k}$![]() -graded ring as indicated. The subring of degree 0 elements is precisely $K[N]$
-graded ring as indicated. The subring of degree 0 elements is precisely $K[N]$![]() . For $k=2$
. For $k=2$![]() , this gives a large and natural class of strongly $\mathbb {Z}^2$
, this gives a large and natural class of strongly $\mathbb {Z}^2$![]() -graded rings to which our main theorem 2.1 applies, providing a characterization of $K[N]$
-graded rings to which our main theorem 2.1 applies, providing a characterization of $K[N]$![]() -finite domination of $K[G]$
-finite domination of $K[G]$![]() -module complexes involving eight Novikov rings only. The four conditions (2.2a) occur already in theorem 2.3 (the ring $R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$
-module complexes involving eight Novikov rings only. The four conditions (2.2a) occur already in theorem 2.3 (the ring $R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$![]() , for example, arising as $\widehat {K G_\chi }$
, for example, arising as $\widehat {K G_\chi }$![]() for the character $\xi$
for the character $\xi$![]() corresponding to the point $(1,0) \in S^1$
corresponding to the point $(1,0) \in S^1$![]() ), but the four conditions (2.2b) are of a new type. The special case of a product group $G = N \times \mathbb {Z}^{2}$
), but the four conditions (2.2b) are of a new type. The special case of a product group $G = N \times \mathbb {Z}^{2}$![]() , with $K[G] \cong K[N][x,\, x^{-1},\, y,\, y^{-1}]$
, with $K[G] \cong K[N][x,\, x^{-1},\, y,\, y^{-1}]$![]() a Laurent polynomial ring in two indeterminates, is the remit of the paper [Reference Hüttemann and Quinn3] where the reader can find additional discussion and examples.
a Laurent polynomial ring in two indeterminates, is the remit of the paper [Reference Hüttemann and Quinn3] where the reader can find additional discussion and examples.
Applications in topology
A topological space $Z$![]() is finite up to homotopy if and only if (i) it is finitely dominated in the sense of being a retract up to homotopy of a finite CW complex, and (ii) a certain $K$
is finite up to homotopy if and only if (i) it is finitely dominated in the sense of being a retract up to homotopy of a finite CW complex, and (ii) a certain $K$![]() -theoretical obstruction vanishes, see theorem 2.5. The obstruction is only defined if condition (i) is met. The results of [Reference Hüttemann and Steers4] and of the present paper yield algebraic criteria to verify condition (i) for important classes of topological spaces, including regular covering spaces with deck transformation group $\mathbb {Z}$
-theoretical obstruction vanishes, see theorem 2.5. The obstruction is only defined if condition (i) is met. The results of [Reference Hüttemann and Steers4] and of the present paper yield algebraic criteria to verify condition (i) for important classes of topological spaces, including regular covering spaces with deck transformation group $\mathbb {Z}$![]() or $\mathbb {Z}^2$
or $\mathbb {Z}^2$![]() .
.
Apart from their intrinsic interest, finiteness results of this type have manifold applications in topology themselves. For example, for a closed manifold $M$![]() to fibre over $S^1$
to fibre over $S^1$![]() it is necessary (but not sufficient) that its infinite cyclic covering $\bar M$
it is necessary (but not sufficient) that its infinite cyclic covering $\bar M$![]() is finitely dominated, cf. [Reference Ranicki9, §15]. Moreover, if $\bar M$
is finitely dominated, cf. [Reference Ranicki9, §15]. Moreover, if $\bar M$![]() is finitely dominated and $M$
is finitely dominated and $M$![]() has dimension at least 6, a given 1-dimensional cohomology class $\xi \in H^1(M, \mathbb {R})$
has dimension at least 6, a given 1-dimensional cohomology class $\xi \in H^1(M, \mathbb {R})$![]() is represented by a non-singular closed 1-form provided its Latour obstruction $\tau (M, \xi )$
is represented by a non-singular closed 1-form provided its Latour obstruction $\tau (M, \xi )$![]() , which is defined if $\bar M$
, which is defined if $\bar M$![]() is finitely dominated, vanishes, cf. [Reference Schütz10].
is finitely dominated, vanishes, cf. [Reference Schütz10].
Homotopy finiteness and finite domination of topological spaces
A connected CW-complex $X$![]() is homotopy finite if it is homotopy equivalent to a finite CW-complex. We say that $X$
is homotopy finite if it is homotopy equivalent to a finite CW-complex. We say that $X$![]() is finitely dominated if it is a retract up to homotopy of a finite connected CW-complex, that is, if and only if there exist maps $s \colon X \to K$
is finitely dominated if it is a retract up to homotopy of a finite connected CW-complex, that is, if and only if there exist maps $s \colon X \to K$![]() and $r \colon K \to X$
and $r \colon K \to X$![]() with $K$
with $K$![]() a finite connected CW-complex such that $r \circ s$
a finite connected CW-complex such that $r \circ s$![]() is homotopic to $\mathrm {id}_{X}$
is homotopic to $\mathrm {id}_{X}$![]() . (This is condition (i) from above.)
. (This is condition (i) from above.)
Any homotopy finite space is finitely dominated, and any finitely dominated space has a finitely presented fundamental group. The following two theorems, going back to the work of Wall, are fundamental (see [Reference Ranicki8, §3] for a discussion):
Theorem 2.4 A connected CW complex $Z$![]() is finitely dominated if and only if
is finitely dominated if and only if
• the fundamental group $\pi = \pi _1(Z)$
 is finitely presented, and
is finitely presented, and• the cellular chain complex $C(\tilde Z)$
 of the universal covering $\tilde Z$
of the universal covering $\tilde Z$ of $Z$
of $Z$ (a complex of free $\mathbb {Z}[\pi ]$
(a complex of free $\mathbb {Z}[\pi ]$ -modules) is $\mathbb {Z}[\pi ]$
-modules) is $\mathbb {Z}[\pi ]$ -finitely dominated, that is, is chain homotopy equivalent to a bounded complex $D$
-finitely dominated, that is, is chain homotopy equivalent to a bounded complex $D$ of finitely generated projective $\mathbb {Z}[\pi ]$
of finitely generated projective $\mathbb {Z}[\pi ]$ -modules.
-modules.
Theorem 2.5 Let $Z$![]() be a finitely dominated CW-complex, and let $D$
be a finitely dominated CW-complex, and let $D$![]() be a bounded chain complex of finitely generated projective $\mathbb {Z}[\pi ]$
be a bounded chain complex of finitely generated projective $\mathbb {Z}[\pi ]$![]() -modules homotopy equivalent to $C(\tilde Z)$
-modules homotopy equivalent to $C(\tilde Z)$![]() , as described in theorem 2.4. Let $[Z] = \sum _{k \in \mathbb {Z}} (-1)^k [D_k]$
, as described in theorem 2.4. Let $[Z] = \sum _{k \in \mathbb {Z}} (-1)^k [D_k]$![]() denote the class of $D$
denote the class of $D$![]() in $\tilde K_0 \big ( \mathbb {Z}[\pi ] \big )$
in $\tilde K_0 \big ( \mathbb {Z}[\pi ] \big )$![]() . The class $[Z]$
. The class $[Z]$![]() does not depend on the choice of $D,$
does not depend on the choice of $D,$![]() and is a finiteness obstruction in the sense that $Z$
and is a finiteness obstruction in the sense that $Z$![]() is homotopy finite if and only if $[Z] = 0$
is homotopy finite if and only if $[Z] = 0$![]() .
.
This latter theorem is precisely condition (ii) from above.
Fundamental groups mapping surjectively onto $\mathbb {Z}$
Let $X$![]() now be a finite connected CW-complex with fundamental group $G = \pi _1(X)$
now be a finite connected CW-complex with fundamental group $G = \pi _1(X)$![]() , and suppose there is a surjective group homomorphism $h \colon G \to \mathbb {Z}$
, and suppose there is a surjective group homomorphism $h \colon G \to \mathbb {Z}$![]() with kernel $\pi$
with kernel $\pi$![]() . Then $G$
. Then $G$![]() is a semi-direct product $G = \pi \rtimes \mathbb {Z}$
is a semi-direct product $G = \pi \rtimes \mathbb {Z}$![]() since $h$
since $h$![]() has a section. Let $\bar X$
has a section. Let $\bar X$![]() be the covering space of $X$
be the covering space of $X$![]() determined by $\pi$
determined by $\pi$![]() ; it has fundamental group $\pi$
; it has fundamental group $\pi$![]() . The universal covering space of $\bar X$
. The universal covering space of $\bar X$![]() is the universal cover $\tilde X$
is the universal cover $\tilde X$![]() of $X$
of $X$![]() . We can apply the previous theorem to $Z = \bar X$
. We can apply the previous theorem to $Z = \bar X$![]() and $\tilde Z = \tilde X$
and $\tilde Z = \tilde X$![]() to conclude that the space $\bar X$
to conclude that the space $\bar X$![]() is finitely dominated if and only if $\pi$
is finitely dominated if and only if $\pi$![]() is finitely presented, and the chain complex $C(\tilde X)$
is finitely presented, and the chain complex $C(\tilde X)$![]() is $\mathbb {Z}[\pi ]$
is $\mathbb {Z}[\pi ]$![]() -finitely dominated.
-finitely dominated.
As a first remark, we note that $G = \pi \rtimes \mathbb {Z}$![]() is a finitely presented group in this situation since $X$
is a finitely presented group in this situation since $X$![]() is a finite CW-complex. If $G = \pi \times \mathbb {Z}$
is a finite CW-complex. If $G = \pi \times \mathbb {Z}$![]() is a direct product, then $\pi$
is a direct product, then $\pi$![]() is a retract of $G$
is a retract of $G$![]() in the category of groups and hence is finitely presented itself. This, however, does not hold in general for a semi-direct product $G = \pi \rtimes \mathbb {Z}$
in the category of groups and hence is finitely presented itself. This, however, does not hold in general for a semi-direct product $G = \pi \rtimes \mathbb {Z}$![]() . For an explicit example, consider $\pi = \mathbb {Z}[\frac 12]$
. For an explicit example, consider $\pi = \mathbb {Z}[\frac 12]$![]() with $\mathbb {Z}$
with $\mathbb {Z}$![]() acting on $\pi$
acting on $\pi$![]() as ${}^k x = 2^k \cdot x$
as ${}^k x = 2^k \cdot x$![]() whence
whence
is finitely presented, while $\pi$![]() is not even finitely generated. This can be topologically realized by taking $X$
is not even finitely generated. This can be topologically realized by taking $X$![]() to be the mapping torus of the self map $z \mapsto z^2$
to be the mapping torus of the self map $z \mapsto z^2$![]() of $S^1 \subset \mathbb {C}$
of $S^1 \subset \mathbb {C}$![]() with $\bar X$
with $\bar X$![]() the canonical infinite cyclic cover, the dyadic solenoid [Reference Ranicki9, Remark 3.5 (ii)].
the canonical infinite cyclic cover, the dyadic solenoid [Reference Ranicki9, Remark 3.5 (ii)].
More in the spirit of the present paper is the observation that $\mathbb {Z}[G]$![]() is a strongly $\mathbb {Z}$
is a strongly $\mathbb {Z}$![]() -graded ring, with degree $k$
-graded ring, with degree $k$![]() component the free abelian group with set of generators $h^{-1}(k) \subseteq G$
component the free abelian group with set of generators $h^{-1}(k) \subseteq G$![]() . Thus, we can detect finite domination homologically, by combining the above discussion with the main result of [Reference Hüttemann and Steers4] (Theorem 1.3) as follows.
. Thus, we can detect finite domination homologically, by combining the above discussion with the main result of [Reference Hüttemann and Steers4] (Theorem 1.3) as follows.
We write $R_*[t,t^{-1}]$![]() for the strongly $\mathbb {Z}$
for the strongly $\mathbb {Z}$![]() -graded ring $\mathbb {Z}[G]$
-graded ring $\mathbb {Z}[G]$![]() , and write $H_* \big (X,\, R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt ) \big )$
, and write $H_* \big (X,\, R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt ) \big )$![]() for the Novikov homology of $X$
for the Novikov homology of $X$![]() , the homology of the chain complex $C(\tilde X) \mathop {\otimes }_{R_*[t,t^{-1}]} R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt )$
, the homology of the chain complex $C(\tilde X) \mathop {\otimes }_{R_*[t,t^{-1}]} R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt )$![]() .
.
Theorem 2.6 Let $X$![]() be a finite connected CW-complex with fundamental group $G$
be a finite connected CW-complex with fundamental group $G$![]() . Suppose there exists a surjective group homomorphism $h \colon G \to \mathbb {Z}$
. Suppose there exists a surjective group homomorphism $h \colon G \to \mathbb {Z}$![]() . Let $\bar X$
. Let $\bar X$![]() denote the covering space of $X$
denote the covering space of $X$![]() determined by $\ker (h),$
determined by $\ker (h),$![]() and let $R_*[t,t^{-1}]$
and let $R_*[t,t^{-1}]$![]() denote the ring $\mathbb {Z}[G]$
denote the ring $\mathbb {Z}[G]$![]() equipped with the strong $\mathbb {Z}$
equipped with the strong $\mathbb {Z}$![]() -grading induced by $h$
-grading induced by $h$![]() .
.
(1) The space $\bar X$
 is finitely dominated if and only if
is finitely dominated if and only if
• the group $\ker (h)$
 is finitely presented, and
is finitely presented, and• $X$
 has trivial NOVIKOV homology, $H_* \big (X,\, R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt ) \big ) = \{0\}$
has trivial NOVIKOV homology, $H_* \big (X,\, R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt ) \big ) = \{0\}$ .
.
(2) Suppose in addition that $G = \ker (h) \times \mathbb {Z},$
 and that $h$
and that $h$ is the projection map $h = \mathrm {pr}_2 \colon G = \ker (h) \times \mathbb {Z} \to \mathbb {Z}$
is the projection map $h = \mathrm {pr}_2 \colon G = \ker (h) \times \mathbb {Z} \to \mathbb {Z}$ . In this case, $\ker (h)$
. In this case, $\ker (h)$ is finitely presented, and the space $\bar X$
is finitely presented, and the space $\bar X$ is finitely dominated if and only if $H_* \big (X,\, R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt ) \big )$
is finitely dominated if and only if $H_* \big (X,\, R_*(\kern -1.7pt ( {t^{\pm 1}})\kern -1.7pt ) \big )$ is trivial.
is trivial.
Note that the group ring $\mathbb {Z}[G]$![]() is isomorphic, as a $\mathbb {Z}[\ker (h)]$
is isomorphic, as a $\mathbb {Z}[\ker (h)]$![]() -ring, to a skew Laurent polynomial ring $\mathbb {Z}[\ker (h)]_{\alpha }[t,t^{-1}]$
-ring, to a skew Laurent polynomial ring $\mathbb {Z}[\ker (h)]_{\alpha }[t,t^{-1}]$![]() , with $t$
, with $t$![]() corresponding to $1 \in \mathbb {Z} \subseteq \ker (h) \rtimes \mathbb {Z}$
corresponding to $1 \in \mathbb {Z} \subseteq \ker (h) \rtimes \mathbb {Z}$![]() and $\alpha$
and $\alpha$![]() determined by the action of $\mathbb {Z}$
determined by the action of $\mathbb {Z}$![]() on $\ker (h)$
on $\ker (h)$![]() . If $G = \ker (h) \times \mathbb {Z}$
. If $G = \ker (h) \times \mathbb {Z}$![]() then $\mathbb {Z}[G] = \mathbb {Z}[\ker (h)][t,t^{-1}]$
then $\mathbb {Z}[G] = \mathbb {Z}[\ker (h)][t,t^{-1}]$![]() is a Laurent polynomial ring in the usual sense.
is a Laurent polynomial ring in the usual sense.
Fundamental groups mapping surjectively onto $\mathbb {Z}^2$
Let $X$![]() be a finite connected CW-complex with fundamental group $G = \pi _1(X)$
be a finite connected CW-complex with fundamental group $G = \pi _1(X)$![]() , and suppose there is a surjective group homomorphism $h \colon G \to \mathbb {Z}^2$
, and suppose there is a surjective group homomorphism $h \colon G \to \mathbb {Z}^2$![]() with kernel $\pi$
with kernel $\pi$![]() . If $h$
. If $h$![]() has a section, then $G = \pi \rtimes \mathbb {Z}^{2}$
has a section, then $G = \pi \rtimes \mathbb {Z}^{2}$![]() is a semi-direct product, but in general $G$
is a semi-direct product, but in general $G$![]() may have a more complicated structure. Note that $G$
may have a more complicated structure. Note that $G$![]() is finitely presented but $\pi$
is finitely presented but $\pi$![]() may not be. If $G = \pi \times \mathbb {Z}^2$
may not be. If $G = \pi \times \mathbb {Z}^2$![]() is a direct product (with $h$
is a direct product (with $h$![]() being the projection map), then $\pi$
being the projection map), then $\pi$![]() is finitely presented as well. On the other hand, if $G$
is finitely presented as well. On the other hand, if $G$![]() is a free group on two generators $a$
is a free group on two generators $a$![]() and $b$
and $b$![]() , and $h \colon G \to \mathbb {Z}^2$
, and $h \colon G \to \mathbb {Z}^2$![]() is the obvious surjection, $\pi = \ker (h)$
is the obvious surjection, $\pi = \ker (h)$![]() is freely generated by the (infinitely many) commutators $[a^m, b^n]$
is freely generated by the (infinitely many) commutators $[a^m, b^n]$![]() for non-zero exponents $m$
for non-zero exponents $m$![]() and $n$
and $n$![]() ; of course $G$
; of course $G$![]() can be realized topologically by the figure-8 space $X = S^1 \vee S^1$
can be realized topologically by the figure-8 space $X = S^1 \vee S^1$![]() .
.
Let $\bar X$![]() be the covering space of $X$
be the covering space of $X$![]() determined by $\pi$
determined by $\pi$![]() . The universal covering space of $\bar X$
. The universal covering space of $\bar X$![]() is the universal cover $\tilde X$
is the universal cover $\tilde X$![]() of $X$
of $X$![]() , and its cellular chain complex $C(\tilde X)$
, and its cellular chain complex $C(\tilde X)$![]() is a bounded complex of finitely generated free $\mathbb {Z}[G]$
is a bounded complex of finitely generated free $\mathbb {Z}[G]$![]() -modules.
-modules.
The homomorphism $h$![]() endows $\mathbb {Z}[G]$
endows $\mathbb {Z}[G]$![]() with the structure of a strongly $\mathbb {Z}^2$
with the structure of a strongly $\mathbb {Z}^2$![]() -graded ring which we denote by $R = R_*[x,x^{-1},y,y^{-1}]$
-graded ring which we denote by $R = R_*[x,x^{-1},y,y^{-1}]$![]() . Thus, the eight Novikov rings listed in (2.1) are at our disposal. If $S$
. Thus, the eight Novikov rings listed in (2.1) are at our disposal. If $S$![]() is any of these rings, we write $H_*(X, S)$
is any of these rings, we write $H_*(X, S)$![]() for the homology of the chain complex $C(\tilde X) \mathop {\otimes }_{R} S$
for the homology of the chain complex $C(\tilde X) \mathop {\otimes }_{R} S$![]() . Using the main result of the present paper, theorem 2.1, we obtain the following characterization of finite domination of the covering space determined by $\ker (h)$
. Using the main result of the present paper, theorem 2.1, we obtain the following characterization of finite domination of the covering space determined by $\ker (h)$![]() :
:
Theorem 2.7 Let $X$![]() be a finite connected CW-complex with fundamental group $G$
be a finite connected CW-complex with fundamental group $G$![]() . Suppose there exists a surjective group homomorphism $h \colon G \to \mathbb {Z}^2$
. Suppose there exists a surjective group homomorphism $h \colon G \to \mathbb {Z}^2$![]() . Let $\bar X$
. Let $\bar X$![]() denote the covering space of $X$
denote the covering space of $X$![]() determined by $\ker (h),$
determined by $\ker (h),$![]() and let $R = R_*[x,x^{-1},y,y^{-1}]$
and let $R = R_*[x,x^{-1},y,y^{-1}]$![]() denote the integral group ring $\mathbb {Z}[G]$
denote the integral group ring $\mathbb {Z}[G]$![]() of $G$
of $G$![]() equipped with the strong $\mathbb {Z}^2$
equipped with the strong $\mathbb {Z}^2$![]() -grading induced by $h$
-grading induced by $h$![]() .
.
(1) The space $\bar X$
 is finitely dominated if and only if
is finitely dominated if and only if
• the group $\ker (h)$
 is finitely presented, and
is finitely presented, and• $X$
 has trivial NOVIKOV homology:
(2.3)\begin{equation} \left. \begin{aligned} H_* \big(X,\, R[x,\,x^{{-}1}] (\kern -1.7pt ( {y^{{\pm} 1}})\kern-1.7pt ) \big) & = \{0\},\, \\ H_* \big(X,\, R[y,\,y^{{-}1}] (\kern -1.7pt ( {x^{{\pm} 1}})\kern-1.7pt ) \big) & = \{0\},\, \\ H_* \big(X,\, R(\kern -1.7pt ( {x^{{\pm} 1},\, y^{{\pm} 1}})\kern-1.7pt ) \big) & = \{0\}. \end{aligned} \right\} \end{equation}
has trivial NOVIKOV homology:
(2.3)\begin{equation} \left. \begin{aligned} H_* \big(X,\, R[x,\,x^{{-}1}] (\kern -1.7pt ( {y^{{\pm} 1}})\kern-1.7pt ) \big) & = \{0\},\, \\ H_* \big(X,\, R[y,\,y^{{-}1}] (\kern -1.7pt ( {x^{{\pm} 1}})\kern-1.7pt ) \big) & = \{0\},\, \\ H_* \big(X,\, R(\kern -1.7pt ( {x^{{\pm} 1},\, y^{{\pm} 1}})\kern-1.7pt ) \big) & = \{0\}. \end{aligned} \right\} \end{equation}
(2) Suppose in addition that $G = \ker (h) \times \mathbb {Z}^2,$
 and that $h$
and that $h$ is the projection map $h = \mathrm {pr}_2 \colon G = \ker (h) \times \mathbb {Z}^2 \to \mathbb {Z}^2$
is the projection map $h = \mathrm {pr}_2 \colon G = \ker (h) \times \mathbb {Z}^2 \to \mathbb {Z}^2$ . In this case, $\ker (h)$
. In this case, $\ker (h)$ is finitely presented, and the space $\bar X$
is finitely presented, and the space $\bar X$ is finitely dominated if and only if $X$
is finitely dominated if and only if $X$ has trivial NOVIKOV homology as in (2.3).
has trivial NOVIKOV homology as in (2.3).
Note that provided $h$![]() has a section, the group ring $\mathbb {Z}[G]$
has a section, the group ring $\mathbb {Z}[G]$![]() is isomorphic, as a $\mathbb {Z}[\ker (h)]$
is isomorphic, as a $\mathbb {Z}[\ker (h)]$![]() -ring, to a skew Laurent polynomial ring of the form $\mathbb {Z}[\ker (h)]_{\alpha }[x,x^{-1}, y, y^{-1}]$
-ring, to a skew Laurent polynomial ring of the form $\mathbb {Z}[\ker (h)]_{\alpha }[x,x^{-1}, y, y^{-1}]$![]() , with $x$
, with $x$![]() and $y$
and $y$![]() corresponding to the generators of $\mathbb {Z}^2$
corresponding to the generators of $\mathbb {Z}^2$![]() and $\alpha$
and $\alpha$![]() determined by the action of $\mathbb {Z}^2$
determined by the action of $\mathbb {Z}^2$![]() on $\ker (h)$
on $\ker (h)$![]() . If $G = \ker (h) \times \mathbb {Z}^2$
. If $G = \ker (h) \times \mathbb {Z}^2$![]() , then $\mathbb {Z}[G] = \mathbb {Z} [\ker (h)][x,x^{-1}, y, y^{-1}]$
, then $\mathbb {Z}[G] = \mathbb {Z} [\ker (h)][x,x^{-1}, y, y^{-1}]$![]() is a Laurent polynomial ring in the usual sense. In general, however, $\mathbb {Z}[G]$
is a Laurent polynomial ring in the usual sense. In general, however, $\mathbb {Z}[G]$![]() is not a skew Laurent polynomial ring.
is not a skew Laurent polynomial ring.
An explicit algebraic example
The applications discussed so far feature strongly graded rings that are in fact group rings, and hence specific examples of crossed products which are graded rings having homogeneous units of all degrees. However, theorem 2.1 does not rely on this feature. To illustrate the extent of the generalization achieved in this paper, we describe a strongly $\mathbb {Z}^2$![]() -graded ring $\hat {K}$
-graded ring $\hat {K}$![]() that is not a crossed product (and in particular not a Laurent polynomial ring), and a complex of finitely generated free $\hat K$
that is not a crossed product (and in particular not a Laurent polynomial ring), and a complex of finitely generated free $\hat K$![]() -modules that is $\hat {K}_{(0,0)}$
-modules that is $\hat {K}_{(0,0)}$![]() -finitely dominated by the above criterion.
-finitely dominated by the above criterion.
Let $\overline K = K[a, b, c, d] / ab+cd-1$![]() ; this is a strongly $\mathbb {Z}$
; this is a strongly $\mathbb {Z}$![]() -graded ring if we let $a, c$
-graded ring if we let $a, c$![]() have degree $1$
have degree $1$![]() and $b, d$
and $b, d$![]() have degree $-1$
have degree $-1$![]() . It is not a Laurent polynomial ring, in fact not a crossed product, since the only units in $\overline {K}$
. It is not a Laurent polynomial ring, in fact not a crossed product, since the only units in $\overline {K}$![]() are the elements of $K^\times$
are the elements of $K^\times$![]() in degree $0$
in degree $0$![]() , as can be shown using ideas from Gröbner basis theory. In particular, there is no unit in ${\overline K}_{1}$
, as can be shown using ideas from Gröbner basis theory. In particular, there is no unit in ${\overline K}_{1}$![]() .
.
The $\mathbb {Z}^2$![]() -graded ring $\hat K = \overline K \mathop {\otimes }_{{\overline K}_0} \overline K$
-graded ring $\hat K = \overline K \mathop {\otimes }_{{\overline K}_0} \overline K$![]() , where $\hat K_{(k,\ell )} = {\overline K}_k \mathop {\otimes }_{{\overline K}_0} {\overline K}_\ell$
, where $\hat K_{(k,\ell )} = {\overline K}_k \mathop {\otimes }_{{\overline K}_0} {\overline K}_\ell$![]() , can be seen to be strongly graded as the necessary partitions of unity are present as in point $(3)$
, can be seen to be strongly graded as the necessary partitions of unity are present as in point $(3)$![]() of proposition 4.5. It is not a crossed product since, for example, there is no unit in $\hat {K}_{(1,0)} = {\overline K}_{1}$
of proposition 4.5. It is not a crossed product since, for example, there is no unit in $\hat {K}_{(1,0)} = {\overline K}_{1}$![]() .
.
We will define a fourfold chain complex $V$![]() concentrated in degrees $(\epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4) \in \mathbb {Z}^4$
concentrated in degrees $(\epsilon _1, \epsilon _2, \epsilon _3, \epsilon _4) \in \mathbb {Z}^4$![]() with $\epsilon _j = 0,1$
with $\epsilon _j = 0,1$![]() . The entries are $\hat {K}$
. The entries are $\hat {K}$![]() , a free $\hat {K}$
, a free $\hat {K}$![]() -module of rank 1; the non-trivial differentials are multiplication by
-module of rank 1; the non-trivial differentials are multiplication by

That is, the map from position $(1,\epsilon _2, \epsilon _3, \epsilon _4)$![]() to position $(0,\epsilon _2, \epsilon _3, \epsilon _4)$
to position $(0,\epsilon _2, \epsilon _3, \epsilon _4)$![]() is multiplication by $1 - a \mathop {\otimes } 1$
is multiplication by $1 - a \mathop {\otimes } 1$![]() , the map from position $(\epsilon _1, 1, \epsilon _3, \epsilon _4)$
, the map from position $(\epsilon _1, 1, \epsilon _3, \epsilon _4)$![]() to position $(\epsilon _1, 0, \epsilon _3, \epsilon _4)$
to position $(\epsilon _1, 0, \epsilon _3, \epsilon _4)$![]() is multiplication by $1 - 1 \mathop {\otimes } c$
is multiplication by $1 - 1 \mathop {\otimes } c$![]() , and so on.
, and so on.
The totalization $C$![]() of $V$
of $V$![]() can be obtained by taking ‘iterated mapping cones’, and up to isomorphism it does not matter in which order we choose the different directions. Now the map $1 - a \mathop {\otimes } 1$
can be obtained by taking ‘iterated mapping cones’, and up to isomorphism it does not matter in which order we choose the different directions. Now the map $1 - a \mathop {\otimes } 1$![]() is an isomorphism with inverse
is an isomorphism with inverse
over the rings $\hat {K}_* [y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$![]() and $\hat {K}_* (\kern -1.7pt ( {x, y^{\pm 1}})\kern -1.7pt )$
and $\hat {K}_* (\kern -1.7pt ( {x, y^{\pm 1}})\kern -1.7pt )$![]() , by the usual telescoping sum argument familiar from the geometric series. Note that the series defines an element in each of these rings since $a^k \mathop {\otimes } 1 = (a \mathop {\otimes } 1)^k$
, by the usual telescoping sum argument familiar from the geometric series. Note that the series defines an element in each of these rings since $a^k \mathop {\otimes } 1 = (a \mathop {\otimes } 1)^k$![]() has degree $(k,0)$
has degree $(k,0)$![]() . Thus, after tensoring $V$
. Thus, after tensoring $V$![]() with one of these rings, the mapping cones in 1-direction will be acyclic, hence the tensor product of $C$
with one of these rings, the mapping cones in 1-direction will be acyclic, hence the tensor product of $C$![]() with one of these rings will be acyclic.
with one of these rings will be acyclic.
Similarly, the map $1 - 1 \mathop {\otimes } bcd$![]() is an isomorphism over $\hat {K}_* [x, x^{-1}](\kern -1.7pt ( {y^{-1}})\kern -1.7pt )$
is an isomorphism over $\hat {K}_* [x, x^{-1}](\kern -1.7pt ( {y^{-1}})\kern -1.7pt )$![]() and $\hat {K}_* (\kern -1.7pt ( {x^{\pm 1}, y^{-1}})\kern -1.7pt )$
and $\hat {K}_* (\kern -1.7pt ( {x^{\pm 1}, y^{-1}})\kern -1.7pt )$![]() , with inverse
, with inverse
this is an element of the rings in question since the degree of $1 \mathop {\otimes } (bcd)^k$![]() is $(0,-k)$
is $(0,-k)$![]() . Consequently, after tensoring $V$
. Consequently, after tensoring $V$![]() with one of these rings the mapping cones in 4-direction will be acyclic, hence the tensor product of $C$
with one of these rings the mapping cones in 4-direction will be acyclic, hence the tensor product of $C$![]() with one of these rings will be acyclic. The cases of $1 - 1 \mathop {\otimes } c$
with one of these rings will be acyclic. The cases of $1 - 1 \mathop {\otimes } c$![]() and $1 - d \mathop {\otimes } 1$
and $1 - d \mathop {\otimes } 1$![]() are similar, involving the rings $\hat {K}_* [x, x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$
are similar, involving the rings $\hat {K}_* [x, x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$![]() and $\hat {K}_* (\kern -1.7pt ( {x^{\pm 1}, y})\kern -1.7pt )$
and $\hat {K}_* (\kern -1.7pt ( {x^{\pm 1}, y})\kern -1.7pt )$![]() in the former case, the rings $\hat {K}_* [y, y^{-1}](\kern -1.7pt ( {x^{-1}})\kern -1.7pt )$
in the former case, the rings $\hat {K}_* [y, y^{-1}](\kern -1.7pt ( {x^{-1}})\kern -1.7pt )$![]() and $\hat {K}_* (\kern -1.7pt ( {x^{-1}, y^{\pm 1}})\kern -1.7pt )$
and $\hat {K}_* (\kern -1.7pt ( {x^{-1}, y^{\pm 1}})\kern -1.7pt )$![]() in the latter.
in the latter.
Structure of the paper
The paper can be seen as an amalgamation of the two publications [Reference Hüttemann and Quinn3] and [Reference Hüttemann and Steers4], combining the graded viewpoint of the latter with the elaborate homological algebra of the former. Replacing central indeterminates by inherently non-commutative structures is a non-trivial task, and it is rather surprising that with the right set-up the overall pattern of proof remains virtually unchanged.
We start with recalling basic concepts from the theory of strongly graded rings. The ‘if’ implication of the main theorem is verified in part II, building on [Reference Hüttemann and Steers4] and [Reference Hüttemann and Quinn3]; the main point is to relate the given chain complex with a complex of diagrams which are the analogues of well-known line bundles on the scheme $\mathbb {P}^1 \times \mathbb {P}^1$![]() . Part III focuses on the ‘only if’ implication. The main technical device is the algebraic torus (a ‘two-dimensional’ version of the algebraic mapping torus), and the Mather trick which allows to replace the complex $C$
. Part III focuses on the ‘only if’ implication. The main technical device is the algebraic torus (a ‘two-dimensional’ version of the algebraic mapping torus), and the Mather trick which allows to replace the complex $C$![]() with an algebraic torus of a complex $D$
with an algebraic torus of a complex $D$![]() consisting of finitely generated projective $R_{(0,0)}$
consisting of finitely generated projective $R_{(0,0)}$![]() -modules.
-modules.
3. Graded rings and Novikov rings
Definition 3.1 A $\mathbb {Z}^2$![]() -graded ring is a (unital) ring $L$
-graded ring is a (unital) ring $L$![]() equipped with a direct sum decomposition into additive subgroups $L=\bigoplus _{\sigma\in {\mathbb {Z}}^2} L_\sigma$
equipped with a direct sum decomposition into additive subgroups $L=\bigoplus _{\sigma\in {\mathbb {Z}}^2} L_\sigma$![]() such that $L_\sigma L_\tau \subseteq L_{\sigma+\tau }$
such that $L_\sigma L_\tau \subseteq L_{\sigma+\tau }$![]() for all $\sigma,\tau \in {\mathbb {Z}}^2$
for all $\sigma,\tau \in {\mathbb {Z}}^2$![]() , where $L_\sigma L_\tau$
, where $L_\sigma L_\tau$![]() consists of the finite sums of ring products $xy$
consists of the finite sums of ring products $xy$![]() with $x \in L_\sigma$
with $x \in L_\sigma$![]() and $y \in L_\tau$
and $y \in L_\tau$![]() . The summands $L_{\sigma}$
. The summands $L_{\sigma}$![]() are called the (homogeneous) components of $L$
are called the (homogeneous) components of $L$![]() ; elements of $L_{\sigma}$
; elements of $L_{\sigma}$![]() are called homogeneous of degree $\sigma$
are called homogeneous of degree $\sigma$![]() .
.
Relevant examples are the polynomial ring $K[x,y]$![]() and the Laurent polynomial ring $R = K[x,x^{-1},y,y^{-1}]$
and the Laurent polynomial ring $R = K[x,x^{-1},y,y^{-1}]$![]() in two variables, equipped with the usual $\mathbb {Z}^{2}$
in two variables, equipped with the usual $\mathbb {Z}^{2}$![]() -grading by the exponents of $x$
-grading by the exponents of $x$![]() and $y$
and $y$![]() , respectively; here $K$
, respectively; here $K$![]() may be any unital ring. The main difference between these examples, from the point of view taken in this paper, is that the latter is strongly $\mathbb {Z}^2$
may be any unital ring. The main difference between these examples, from the point of view taken in this paper, is that the latter is strongly $\mathbb {Z}^2$![]() -graded (definition 4.4) but the former is not.
-graded (definition 4.4) but the former is not.
From a unital ring $R$![]() , for the moment not equipped with a grading, we can construct various ‘Novikov rings’ of formal Laurent series as follows:
, for the moment not equipped with a grading, we can construct various ‘Novikov rings’ of formal Laurent series as follows:

Here $x$![]() and $y$
and $y$![]() are central indeterminates which commute with each other, and with the elements of $R$
are central indeterminates which commute with each other, and with the elements of $R$![]() . The slightly informal notation $S [\kern -1pt [{x}] \kern -1pt ] [x^{-1}]$
. The slightly informal notation $S [\kern -1pt [{x}] \kern -1pt ] [x^{-1}]$![]() is meant to denote the ring of formal power series in the indeterminate $x$
is meant to denote the ring of formal power series in the indeterminate $x$![]() with coefficients in $S$
with coefficients in $S$![]() , localized at the multiplicative system $\{x^k \,|\, k \geq 0\}$
, localized at the multiplicative system $\{x^k \,|\, k \geq 0\}$![]() .
.
Returning to the case of a $\mathbb {Z}^{2}$![]() -graded ring $R$
-graded ring $R$![]() , we can introduce subrings of rings of formal power or Laurent series, denoted by adding the decoration ‘$*$
, we can introduce subrings of rings of formal power or Laurent series, denoted by adding the decoration ‘$*$![]() ’ as a subscript to the ring $R$
’ as a subscript to the ring $R$![]() , consisting of those elements such that the coefficient of $x^{s} y^{t}$
, consisting of those elements such that the coefficient of $x^{s} y^{t}$![]() is an element of $R_{(s,t)}$
is an element of $R_{(s,t)}$![]() . The resulting unital subrings will not contain the elements $x$
. The resulting unital subrings will not contain the elements $x$![]() and $y$
and $y$![]() as, for example, $x = 1 \cdot x$
as, for example, $x = 1 \cdot x$![]() has coefficient $1 \in R_{(0,0)}$
has coefficient $1 \in R_{(0,0)}$![]() , whereas the monomial $x$
, whereas the monomial $x$![]() has degree $(1,0)$
has degree $(1,0)$![]() . At this point, we may treat the ‘variables’ as a purely notational device keeping track of degrees of various elements. As an illustration, we put forward the ring $R_*[x,x^{-1},y,y^{-1}]$
. At this point, we may treat the ‘variables’ as a purely notational device keeping track of degrees of various elements. As an illustration, we put forward the ring $R_*[x,x^{-1},y,y^{-1}]$![]() which has elements the finite sums of terms $r_{s,t} x^{s} y^{t}$
which has elements the finite sums of terms $r_{s,t} x^{s} y^{t}$![]() , with $s,t \in \mathbb {Z}$
, with $s,t \in \mathbb {Z}$![]() and $r_{s,t} \in R_{(s,t)}$
and $r_{s,t} \in R_{(s,t)}$![]() . We may in fact identify this ring with the (graded) ring $R$
. We may in fact identify this ring with the (graded) ring $R$![]() itself. When applied to the Novikov rings listed above, we arrive at the identifications listed in (2.1).
itself. When applied to the Novikov rings listed above, we arrive at the identifications listed in (2.1).
4. Partitions of unity and strongly graded rings
Definition 4.1 Let $S = \bigoplus _{\sigma \in \mathbb {Z}^{2}} S_{\sigma }$![]() be a $\mathbb {Z}^2$
be a $\mathbb {Z}^2$![]() -graded unital ring. For $\rho \in \mathbb {Z}^2$
-graded unital ring. For $\rho \in \mathbb {Z}^2$![]() , an finite sum expression of the form $1=\sum _{j} {u_j}{v_j}$
, an finite sum expression of the form $1=\sum _{j} {u_j}{v_j}$![]() with $u_j\in S_{\rho }$
with $u_j\in S_{\rho }$![]() and $v_j\in S_{-\rho }$
and $v_j\in S_{-\rho }$![]() is called a partition of unity of type $(\rho,-\rho )$
is called a partition of unity of type $(\rho,-\rho )$![]() .
.
By a straightforward computation, one can show:
Lemma 4.2 For $\rho, \rho ' \in \mathbb {Z}^2$![]() let $1=\sum _{j} u_jv_j$
let $1=\sum _{j} u_jv_j$![]() and $1=\sum _{k} u'_kv'_k$
and $1=\sum _{k} u'_kv'_k$![]() be partitions of unity of type $\rho$
be partitions of unity of type $\rho$![]() and $\rho ',$
and $\rho ',$![]() respectively. Then
respectively. Then
is a partition of unity of type $\rho + \rho '$![]() .
.
If $S_{\rho } S_{-\rho } = S_{(0,0)}$![]() then, since $1 \in S_{(0,0)}$
then, since $1 \in S_{(0,0)}$![]() , there exists a partition of unity of type $(\rho,-\rho )$
, there exists a partition of unity of type $(\rho,-\rho )$![]() . Conversely, if a partition of unity of type $(\rho,-\rho )$
. Conversely, if a partition of unity of type $(\rho,-\rho )$![]() exists, then $1 \in S_{\rho } S_{-\rho }$
exists, then $1 \in S_{\rho } S_{-\rho }$![]() and thus $S_{(0,0)} \subseteq S_{\rho } S_{-\rho }$
and thus $S_{(0,0)} \subseteq S_{\rho } S_{-\rho }$![]() so that $S_{(0,0)} = S_{\rho } S_{-\rho }$
so that $S_{(0,0)} = S_{\rho } S_{-\rho }$![]() ; this implies moreover
; this implies moreover
so that $S_{\sigma } = S_{\sigma +\rho } S_{-\rho }$![]() for any $\sigma \in \mathbb {Z}^{2}$
for any $\sigma \in \mathbb {Z}^{2}$![]() , and similarly $S_{\sigma } = S_{\rho } S_{\sigma - \rho }$
, and similarly $S_{\sigma } = S_{\rho } S_{\sigma - \rho }$![]() .
.
Proposition 4.3 Let $R$![]() be a $\mathbb {Z}^{2}$
be a $\mathbb {Z}^{2}$![]() -graded ring. Let $\lambda, \rho \in \mathbb {Z}^{2}$
-graded ring. Let $\lambda, \rho \in \mathbb {Z}^{2}$![]() be such that there exists a partition of unity $1 = \sum _{j} \alpha _{j} \beta _{j}$
be such that there exists a partition of unity $1 = \sum _{j} \alpha _{j} \beta _{j}$![]() of type $(\lambda, -\lambda )$
of type $(\lambda, -\lambda )$![]() . The multiplication map
. The multiplication map
is an isomorphism of $R_{(0,0)}$![]() -bimodules; its inverse can be written as
-bimodules; its inverse can be written as
The map $\mu _{\lambda, \rho }$![]() does not depend on the choice of partition of unity.
does not depend on the choice of partition of unity.
Proof. The map $\pi _{\lambda,\rho }$![]() is an $R_{(0,0)}$
is an $R_{(0,0)}$![]() -balanced, thus well-defined, $R_{(0,0)}$
-balanced, thus well-defined, $R_{(0,0)}$![]() -bimodule homomorphism. Hence, it is enough to show that $\mu _{\lambda,\rho }$
-bimodule homomorphism. Hence, it is enough to show that $\mu _{\lambda,\rho }$![]() , considered as a homomorphism of right $R_{(0,0)}$
, considered as a homomorphism of right $R_{(0,0)}$![]() -modules, is its inverse. For $z \in R_{\lambda +\rho }$
-modules, is its inverse. For $z \in R_{\lambda +\rho }$![]() , we calculate
, we calculate
so that $\pi _{\lambda,\rho } \circ \mu _{\lambda,\rho }$![]() is the identity map. Similarly, for $x \in R_{\lambda }$
is the identity map. Similarly, for $x \in R_{\lambda }$![]() and $y \in R_{\rho }$
and $y \in R_{\rho }$![]() , we have
, we have
(since $\beta _{j} x \in R_{(0,0)}$![]() ) so that $\mu _{\lambda,\rho } \circ \pi _{\lambda,\rho }$
) so that $\mu _{\lambda,\rho } \circ \pi _{\lambda,\rho }$![]() is the identity map.
is the identity map.
Definition 4.4 Dade [Reference Dade1, §1]:
A $\mathbb {Z}^2$![]() -graded ring $L = \bigoplus _{\rho \in \mathbb {Z}^{2}} L_{\rho }$
-graded ring $L = \bigoplus _{\rho \in \mathbb {Z}^{2}} L_{\rho }$![]() is called a strongly ${\mathbb {Z}}^2$
is called a strongly ${\mathbb {Z}}^2$![]() -graded ring if $L_{\kappa } L_{\lambda } = L_{\kappa +\lambda }$
-graded ring if $L_{\kappa } L_{\lambda } = L_{\kappa +\lambda }$![]() for all $\kappa, \lambda \in \mathbb {Z}^{2}$
for all $\kappa, \lambda \in \mathbb {Z}^{2}$![]() .
.
The establishing example is the Laurent polynomial ring in two variables, $R = K[x,x^{-1},y,y^{-1}]$![]() . This is a strongly ${\mathbb {Z}}^2$
. This is a strongly ${\mathbb {Z}}^2$![]() -graded ring when $x$
-graded ring when $x$![]() and $y$
and $y$![]() are given degrees $(1,0)$
are given degrees $(1,0)$![]() and $(0,1)$
and $(0,1)$![]() , respectively.
, respectively.
Using [Reference Dade1, Proposition 1.6] and lemma 4.2, one obtains the following characterization of strongly $\mathbb {Z}^{2}$![]() -graded rings:
-graded rings:
Proposition 4.5 Let $R$![]() be a $\mathbb {Z}^2$
be a $\mathbb {Z}^2$![]() -graded ring. The following statements are equivalent:
-graded ring. The following statements are equivalent:
(1) The ring $R$
 is strongly graded.
is strongly graded.(2) For every $\rho \in {\mathbb {Z}}^2$
 , there is at least one partition of unity of type $(\rho,-\rho )$
, there is at least one partition of unity of type $(\rho,-\rho )$ .
.(3) There is at least one partition of unity of each of the types
• $((1,0),(-1,0))$
 and $((-1,0),(1,0))$
and $((-1,0),(1,0))$ ,
,• $((0,1),(0,-1))$
 and $((0,-1),(0,1))$
and $((0,-1),(0,1))$ .
.
(4) For every $\rho \in \mathbb {Z}^{2}$
 , we have $L_{\rho } L_{-\rho } = L_{(0,0)}$
, we have $L_{\rho } L_{-\rho } = L_{(0,0)}$ .
.
Corollary 4.6 If $L = \bigoplus _{\kappa \in \mathbb {Z}^2} L_{\kappa }$![]() is strongly graded, then all $L_{\kappa }$
is strongly graded, then all $L_{\kappa }$![]() are invertible $L_{(0,0)}$
are invertible $L_{(0,0)}$![]() -bimodules. In particular, the $L_{\kappa }$
-bimodules. In particular, the $L_{\kappa }$![]() are finitely generated projective as right and as left $L_{(0,0)}$
are finitely generated projective as right and as left $L_{(0,0)}$![]() -modules.
-modules.
Part II. Contractibility of Novikov homology implies finite domination
5. Rings and modules associated to faces of a square
We denote by the symbol $\mathfrak {S}$![]() the set of non-empty faces of the polytope $S = [-1,1] \times [-1,1] \subset \mathbb {R}^{2}$
the set of non-empty faces of the polytope $S = [-1,1] \times [-1,1] \subset \mathbb {R}^{2}$![]() , partially ordered by inclusion. In figure 1, we show our chosen labelling and orientation of the faces (the orientations will be used later to define incidence numbers).
, partially ordered by inclusion. In figure 1, we show our chosen labelling and orientation of the faces (the orientations will be used later to define incidence numbers).

Figure 1. Labelling and orientation of the faces of the square $S$![]() .
.
With each face $F \in \mathfrak {S}$![]() , we associate its barrier cone
, we associate its barrier cone
where $\mathrm {cone}\,(X)$![]() denotes the set of finite linear combinations of elements of $X$
denotes the set of finite linear combinations of elements of $X$![]() with non-negative real coefficients. For example, $T_{v_{bl}}$
with non-negative real coefficients. For example, $T_{v_{bl}}$![]() is the first quadrant and $T_{e_r}$
is the first quadrant and $T_{e_r}$![]() is the left half-plane. Given a $\mathbb {Z}^{2}$
is the left half-plane. Given a $\mathbb {Z}^{2}$![]() -graded ring $R = \bigoplus _{\rho \in \mathbb {Z}^{2}} R_{\rho }$
-graded ring $R = \bigoplus _{\rho \in \mathbb {Z}^{2}} R_{\rho }$![]() , we let $A_F = R_*[T_F]$
, we let $A_F = R_*[T_F]$![]() denote the subring of $R = R_*[x, x^{-1}, y, y^{-1}]$
denote the subring of $R = R_*[x, x^{-1}, y, y^{-1}]$![]() consisting of elements with support in $T_F$
consisting of elements with support in $T_F$![]() ; explicitly,
; explicitly,
Thus, for example,

For $k \in \mathbb {Z}$![]() , we introduce the $R_*[T_{F}]$
, we introduce the $R_*[T_{F}]$![]() -bimodules
-bimodules
where $kF + T_{F} = \{ kx + y \,|\, x \in F \textrm { and } y \in T_{F} \}$![]() . In different notation,
. In different notation,

As a final bit of notation for now, we let $p_{F} \in F \cap \mathbb {Z}^{2}$![]() denote the barycentre of $F$
denote the barycentre of $F$![]() . For example, $p_{e_{t}} = (0,1)$
. For example, $p_{e_{t}} = (0,1)$![]() and $p_{S} = (0,0)$
and $p_{S} = (0,0)$![]() . Then $kF+T_{F} = kp_{F} + T_{F}$
. Then $kF+T_{F} = kp_{F} + T_{F}$![]() , and every element $\sigma$
, and every element $\sigma$![]() of $kF+T_{F}$
of $kF+T_{F}$![]() can in fact be written in the form $kp_{F} + \tau$
can in fact be written in the form $kp_{F} + \tau$![]() for some $\tau \in T_{F}$
for some $\tau \in T_{F}$![]() . Also, given faces $F \subseteq G$
. Also, given faces $F \subseteq G$![]() , the barrier cones satisfy $T_{G} = T_{F} + \mathbb {R} \cdot (p_{G} - p_{F})$
, the barrier cones satisfy $T_{G} = T_{F} + \mathbb {R} \cdot (p_{G} - p_{F})$![]() so that, in particular, $k(p_{G}-p_{F}) \in T_{G}$
so that, in particular, $k(p_{G}-p_{F}) \in T_{G}$![]() .
.
Lemma 5.1 Let $R$![]() be a strongly $\mathbb {Z}^{2}$
be a strongly $\mathbb {Z}^{2}$![]() -graded ring. For all $k \in \mathbb {Z}$
-graded ring. For all $k \in \mathbb {Z}$![]() and for all $F,G \in \mathfrak {S}$
and for all $F,G \in \mathfrak {S}$![]() with $F \subseteq G,$
with $F \subseteq G,$![]() the $R_*[T_{F}]$
the $R_*[T_{F}]$![]() -linear inclusion map $\alpha _{F,G} \colon R_*[kF + T_{F}] \longrightarrow R_*[kG + T_{G}]$
-linear inclusion map $\alpha _{F,G} \colon R_*[kF + T_{F}] \longrightarrow R_*[kG + T_{G}]$![]() is such that its adjoint map
is such that its adjoint map
is an isomorphism.
Proof. Choose a partition of unity of type $(kp_{F},-kp_{F})$![]() , say $1= \sum _{j} u_jv_j$
, say $1= \sum _{j} u_jv_j$![]() with $u_j\in R_{kp_{F}}$
with $u_j\in R_{kp_{F}}$![]() and $v_j\in R_{-kp_{F}}$
and $v_j\in R_{-kp_{F}}$![]() . The map
. The map
is well-defined. First, $u_{j}$![]() has degree $kp_{F} \in kF \subseteq kF + T_{F}$
has degree $kp_{F} \in kF \subseteq kF + T_{F}$![]() whence $u_{j} \in R_* [kF + T_{F}]$
whence $u_{j} \in R_* [kF + T_{F}]$![]() . Second, every element $\sigma$
. Second, every element $\sigma$![]() of $(kG + T_{G}) \cap \mathbb {Z}^{2}$
of $(kG + T_{G}) \cap \mathbb {Z}^{2}$![]() can be written in the form $kp_{G} + \tau$
can be written in the form $kp_{G} + \tau$![]() , with $\tau \in T_{G} \cap \mathbb {Z}^{2}$
, with $\tau \in T_{G} \cap \mathbb {Z}^{2}$![]() . Thus,
. Thus,
It follows that for $x \in R_*[kG + T_{G}]$![]() , the product $v_{j} x$
, the product $v_{j} x$![]() is an element of $R_*[T_{G}]$
is an element of $R_*[T_{G}]$![]() . The map $\beta _{F,G}$
. The map $\beta _{F,G}$![]() is $R_*[T_{G}]$
is $R_*[T_{G}]$![]() -linear and satisfies $\alpha _{F,G}^{\sharp } \circ \beta _{F,G} = \mathrm {id}$
-linear and satisfies $\alpha _{F,G}^{\sharp } \circ \beta _{F,G} = \mathrm {id}$![]() by direct calculation, using $1= \sum _{j} u_jv_j$
by direct calculation, using $1= \sum _{j} u_jv_j$![]() . We also have
. We also have
where the equality labelled $(*)$![]() is true since $v_{j} r \in R_*[T_{F}]$
is true since $v_{j} r \in R_*[T_{F}]$![]() for any $r \in R_*[kF + T_{F}]$
for any $r \in R_*[kF + T_{F}]$![]() , whence $\beta _{F,G} \circ \alpha _{F,G}^{\sharp } = \mathrm {id}$
, whence $\beta _{F,G} \circ \alpha _{F,G}^{\sharp } = \mathrm {id}$![]() .
.
6. Čech complexes
Incidence numbers and Čech complexes
Suppose $P$![]() is a poset equipped with a strictly increasing ‘rank’ function
is a poset equipped with a strictly increasing ‘rank’ function
and with a notion of ‘incidence numbers’
satisfying the following conditions:
(DI1) $[x\colon y] = 0$
 unless $x>y$
unless $x>y$ and $\mathrm {rk}(y) = \mathrm {rk}(x) - 1$
and $\mathrm {rk}(y) = \mathrm {rk}(x) - 1$ .
.(DI2) For all $z< x$
 with $\mathrm {rk}(z) = \mathrm {rk}(x) - 2$
with $\mathrm {rk}(z) = \mathrm {rk}(x) - 2$ , the set
\[ P(z< x) = \{y\in P \,|\, z< y< x\} \]is finite, and
, the set
\[ P(z< x) = \{y\in P \,|\, z< y< x\} \]is finite, and \[ \sum_{y\in P( z< x)} [x \colon y] \cdot [y \colon z] = 0 . \]
\[ \sum_{y\in P( z< x)} [x \colon y] \cdot [y \colon z] = 0 . \]
(DI3) For $x \in P$
 with $\mathrm {rk}(x)=1$
with $\mathrm {rk}(x)=1$ , the set
\[ P({<}x) = \{y\in P \,|\, y< x\} \]is finite, and
, the set
\[ P({<}x) = \{y\in P \,|\, y< x\} \]is finite, and \[ \sum_{y \in P({<}x)}[x \colon y] = 0. \]
\[ \sum_{y \in P({<}x)}[x \colon y] = 0. \]
We can then associate a ‘Čech complex’ with a diagram of $K$![]() -modules ($K$
-modules ($K$![]() a unital ring) indexed by $P$
a unital ring) indexed by $P$![]() :
:
Definition 6.1 Given diagram $\Phi \colon P \longrightarrow K\textrm {-}\mathrm {Mod}$![]() with structure maps $\varphi _{x,y}\colon \Phi _y\longrightarrow \Phi _x$
with structure maps $\varphi _{x,y}\colon \Phi _y\longrightarrow \Phi _x$![]() , define its Čech complex $\Gamma (\Phi ) = \Gamma _{P} (\Phi )$
, define its Čech complex $\Gamma (\Phi ) = \Gamma _{P} (\Phi )$![]() to be the chain complex concentrated in non-positive degrees with chain modules
to be the chain complex concentrated in non-positive degrees with chain modules
with differential induced by $[x:y] \varphi _{x,y}$![]() for $x>y$
for $x>y$![]() .
.
It is easy to check that by virtue of (DI1) and (DI2), this is indeed a chain complex. Condition (DI3) ensures that a cone $M \xrightarrow{.} \Phi$![]() on $\Phi$
on $\Phi$![]() , that is, a collection of $K$
, that is, a collection of $K$![]() -module maps $\kappa _{x} \colon M \longrightarrow \Phi _x$
-module maps $\kappa _{x} \colon M \longrightarrow \Phi _x$![]() satisfying the compatibility condition $\kappa _{x}= \varphi _{x,y} \circ \kappa _{y}$
satisfying the compatibility condition $\kappa _{x}= \varphi _{x,y} \circ \kappa _{y}$![]() , yields a chain complex
, yields a chain complex
with co-augmentation $\kappa$![]() induced by the maps $\kappa _{x}$
induced by the maps $\kappa _{x}$![]() for $x \in \mathrm {rk}^{-1}(0)$
for $x \in \mathrm {rk}^{-1}(0)$![]() .
.
Čech complexes of diagrams of chain complexes
The assignment $\Phi \mapsto \Gamma _{P} (\Phi )$![]() is in fact an exact functor from the category of $P$
is in fact an exact functor from the category of $P$![]() -indexed diagrams of $K$
-indexed diagrams of $K$![]() -modules to the category of chain complexes of $K$
-modules to the category of chain complexes of $K$![]() -modules. Hence, it can be prolongated, by levelwise application, to a functor $\Gamma _{P}$
-modules. Hence, it can be prolongated, by levelwise application, to a functor $\Gamma _{P}$![]() from the category of $P$
from the category of $P$![]() -indexed diagrams of $K$
-indexed diagrams of $K$![]() -module chain complexes to the category of double chain complexes of $K$
-module chain complexes to the category of double chain complexes of $K$![]() -modules. The resulting double complexes have rows $\Gamma _{P}(C_{t})$
-modules. The resulting double complexes have rows $\Gamma _{P}(C_{t})$![]() , that is, $\Gamma _{P}(C)_{s,t} = \Gamma _{P}(C_{t})_{s}$
, that is, $\Gamma _{P}(C)_{s,t} = \Gamma _{P}(C_{t})_{s}$![]() , and commuting differentials. By construction, $\Gamma _{P}(C)_{s,t} = 0$
, and commuting differentials. By construction, $\Gamma _{P}(C)_{s,t} = 0$![]() for $s > 0$
for $s > 0$![]() . Passage to Čech complexes is homotopy invariant in the following sense:
. Passage to Čech complexes is homotopy invariant in the following sense:
Lemma 6.2 Let $\chi \colon \Phi \longrightarrow \Psi$![]() be a natural transformation of functors $\Phi,\Psi \colon P\longrightarrow \textsf {Ch}\,(K\textrm {-}\mathrm {Mod})$
be a natural transformation of functors $\Phi,\Psi \colon P\longrightarrow \textsf {Ch}\,(K\textrm {-}\mathrm {Mod})$![]() . Suppose that for each $p\in P$
. Suppose that for each $p\in P$![]() the component $\chi _{p} \colon \Phi _{p} \longrightarrow \Psi _{p}$
the component $\chi _{p} \colon \Phi _{p} \longrightarrow \Psi _{p}$![]() is a quasi-isomorphism. Suppose also that the rank function is bounded above. Then the induced map of chain complexes
is a quasi-isomorphism. Suppose also that the rank function is bounded above. Then the induced map of chain complexes
is also a quasi-isomorphism.
Proof. This is a standard result, we include an elementary proof for convenience. For $p \geq 0$![]() let $\Gamma ^{p}$
let $\Gamma ^{p}$![]() , denote the horizontal truncation at $-p$
, denote the horizontal truncation at $-p$![]() of $\Gamma$
of $\Gamma$![]() . That is, $\Gamma ^{p} (\Phi )$
. That is, $\Gamma ^{p} (\Phi )$![]() is defined to be the double chain complex that agrees with $\Gamma (\Phi )$
is defined to be the double chain complex that agrees with $\Gamma (\Phi )$![]() in columns $-p, - p+1,\, \cdots,\, 0$
in columns $-p, - p+1,\, \cdots,\, 0$![]() , and is trivial otherwise. As the rank function is bounded above, $\Gamma ^{p} = \Gamma$
, and is trivial otherwise. As the rank function is bounded above, $\Gamma ^{p} = \Gamma$![]() for sufficiently large $p$
for sufficiently large $p$![]() .
.
The obvious surjection $\Gamma ^{p+1}(\Phi ) \longrightarrow \Gamma ^{p} (\Phi )$![]() , given by identity maps in horizontal degrees $-p$
, given by identity maps in horizontal degrees $-p$![]() and higher, has kernel the vertical chain complex
and higher, has kernel the vertical chain complex
considered as a double chain complex concentrated in column $-(p+1)$![]() . Its totalization is then the shift suspension $K_{p+1}(\Phi )[-p-1]$
. Its totalization is then the shift suspension $K_{p+1}(\Phi )[-p-1]$![]() of the chain complex $K$
of the chain complex $K$![]() . By induction on $p \geq 0$
. By induction on $p \geq 0$![]() , using the five lemma for ladder diagrams of long exact homology sequences induced by the diagram of short exact sequences below,
, using the five lemma for ladder diagrams of long exact homology sequences induced by the diagram of short exact sequences below,

the induced maps $\mathrm {Tot} \Gamma ^{p} (\chi ) \colon \mathrm {Tot} \Gamma ^{p} (\Phi ) \longrightarrow \mathrm {Tot} \Gamma ^{p} (\Psi )$![]() are seen to be quasi-isomorphisms for all $p \in \mathbb {N}$
are seen to be quasi-isomorphisms for all $p \in \mathbb {N}$![]() .
.
7. Quasi-coherent diagrams
As before, we denote by the symbol $\mathfrak {S}$![]() the poset of non-empty faces of the square $S = [-1,1] \times [-1,1]$
the poset of non-empty faces of the square $S = [-1,1] \times [-1,1]$![]() . For the purpose of taking Čech complexes, we equip $\mathfrak {S}$
. For the purpose of taking Čech complexes, we equip $\mathfrak {S}$![]() with the rank function $\mathrm {rk}(F) = \dim (F)$
with the rank function $\mathrm {rk}(F) = \dim (F)$![]() , and the usual incidence numbers coming from the orientations indicated in figure 1. For example, $[e_{r} : v_{tr}] = 1$
, and the usual incidence numbers coming from the orientations indicated in figure 1. For example, $[e_{r} : v_{tr}] = 1$![]() and $[e_{r} : v_{br}] = -1$
and $[e_{r} : v_{br}] = -1$![]() , and $[S : e_?] = 1$
, and $[S : e_?] = 1$![]() for any decoration $? \in \{t,l,b,r\}$
for any decoration $? \in \{t,l,b,r\}$![]() . Let $R$
. Let $R$![]() be a $\mathbb {Z}^2$
be a $\mathbb {Z}^2$![]() -graded ring.
-graded ring.
Definition 7.1 A quasi-coherent diagram of modules is a functor
as depicted in figure 2. In addition, for each $F$![]() , the entry $M^F$
, the entry $M^F$![]() is to be equipped with a specified structure of an $R_*[T_{F}]$
is to be equipped with a specified structure of an $R_*[T_{F}]$![]() -module, extending the given $R_{(0,0)}$
-module, extending the given $R_{(0,0)}$![]() -module structure. For an inclusion of faces $F \subseteq G$
-module structure. For an inclusion of faces $F \subseteq G$![]() , we require the structure map $\alpha ^{F,G} \colon M^{F} \longrightarrow M^{G}$
, we require the structure map $\alpha ^{F,G} \colon M^{F} \longrightarrow M^{G}$![]() to be $R_*[T_{F}]$
to be $R_*[T_{F}]$![]() -linear, such that the adjoint map
-linear, such that the adjoint map
is an isomorphism of $R_*[T_{G}]$![]() -modules. A quasi-coherent diagram of chain complexes is a chain complex of quasi-coherent diagrams of modules.
-modules. A quasi-coherent diagram of chain complexes is a chain complex of quasi-coherent diagrams of modules.

Figure 2. Quasi-coherent diagram.
We remark that a quasi-coherent diagram of chain complexes can be considered as a functor defined on $\mathfrak {S}$![]() with values in the category of chain complexes of $R_{(0,0)}$
with values in the category of chain complexes of $R_{(0,0)}$![]() -modules, subject to conditions as above specified levelwise. Moreover, any quasi-coherent diagram of modules can be considered as a quasi-coherent diagram of complexes concentrated in chain degree $0$
-modules, subject to conditions as above specified levelwise. Moreover, any quasi-coherent diagram of modules can be considered as a quasi-coherent diagram of complexes concentrated in chain degree $0$![]() .
.
In case $R$![]() is a Laurent polynomial ring in two variables with coefficients in a commutative ring $K$
is a Laurent polynomial ring in two variables with coefficients in a commutative ring $K$![]() , a quasi-coherent diagram of modules is nothing but a quasi-coherent sheaf of modules on the product $\mathbb {P}^{1}_{K} \times \mathbb {P}^{1}_{K}$
, a quasi-coherent diagram of modules is nothing but a quasi-coherent sheaf of modules on the product $\mathbb {P}^{1}_{K} \times \mathbb {P}^{1}_{K}$![]() of the projective line over $R_{K}$
of the projective line over $R_{K}$![]() with itself.
with itself.
Given a $\mathbb {Z}^2$![]() -graded ring $R$
-graded ring $R$![]() and $k \in \mathbb {Z}$
and $k \in \mathbb {Z}$![]() , we denote by $D(k)$
, we denote by $D(k)$![]() the diagram depicted in figure 3.
the diagram depicted in figure 3.

Figure 3. The quasi-coherent diagram $D(k)$![]() .
.
The arrows are inclusion maps. For a strongly $\mathbb {Z}^{2}$![]() -graded ring, this diagram is quasi-coherent as the adjoint maps are isomorphisms in light of lemma 5.1. These diagrams will play a central role later on. They are the analogues of certain line bundles on $\mathbb {P}^{1}_{R_{(0,0)}} \times \mathbb {P}^{1}_{R_{(0,0)}}$
-graded ring, this diagram is quasi-coherent as the adjoint maps are isomorphisms in light of lemma 5.1. These diagrams will play a central role later on. They are the analogues of certain line bundles on $\mathbb {P}^{1}_{R_{(0,0)}} \times \mathbb {P}^{1}_{R_{(0,0)}}$![]() , viz., the external tensor square of $\mathcal {O}(k)$
, viz., the external tensor square of $\mathcal {O}(k)$![]() . We thus are led to expect the following calculation of its ‘global sections’ and (trivial) ‘higher cohomology’ (note $H_{-n} \Gamma _{\mathfrak {S}} \cong \lim ^{n}$
. We thus are led to expect the following calculation of its ‘global sections’ and (trivial) ‘higher cohomology’ (note $H_{-n} \Gamma _{\mathfrak {S}} \cong \lim ^{n}$![]() as shown, e.g., in [Reference Hüttemann5, Corollary 2.19]):
as shown, e.g., in [Reference Hüttemann5, Corollary 2.19]):
Proposition 7.2 For $k \geq 0$![]() , the complex
, the complex

is exact, where $\iota$![]() is the diagonal embedding, induced from the inclusions of its source into $D(k)^{v}$
is the diagonal embedding, induced from the inclusions of its source into $D(k)^{v}$![]() with $v$
with $v$![]() a vertex of $S$
a vertex of $S$![]() .
.
More explicitly, the sequence

is exact.
Proof. The complex consists of $\mathbb {Z}^{2}$![]() -graded $R_{(0,0)}$
-graded $R_{(0,0)}$![]() -modules and degree-preserving maps, so exactness can be checked in each degree separately. In degree $(x,y) \in [-k,k]^2$
-modules and degree-preserving maps, so exactness can be checked in each degree separately. In degree $(x,y) \in [-k,k]^2$![]() , the complex is the dual of the augmented cellular chain complex of the square (equipped with its obvious cellular structure), which is contractible, tensored with $R_{(x,y)}$
, the complex is the dual of the augmented cellular chain complex of the square (equipped with its obvious cellular structure), which is contractible, tensored with $R_{(x,y)}$![]() . For all other degrees $(x,y)$
. For all other degrees $(x,y)$![]() , we see the dual of the cellular complex associated to the complement of a visibility subcomplex of the boundary of $S$
, we see the dual of the cellular complex associated to the complement of a visibility subcomplex of the boundary of $S$![]() . In either case, the resulting complex is acyclic. More details on the computation can be found in the appendix of §2.5 in [Reference Hüttemann6], for example.
. In either case, the resulting complex is acyclic. More details on the computation can be found in the appendix of §2.5 in [Reference Hüttemann6], for example.
8. Extending chain complexes of modules to quasi-coherent diagrams of chain complexes
Suppose that $M$![]() is a finitely generated free module over the $\mathbb {Z}^{2}$
is a finitely generated free module over the $\mathbb {Z}^{2}$![]() -graded ring $R$
-graded ring $R$![]() . Then there exists a quasi-coherent diagram which has $M$
. Then there exists a quasi-coherent diagram which has $M$![]() as its middle entry. More precisely, we fix an isomorphism between $M$
as its middle entry. More precisely, we fix an isomorphism between $M$![]() and $R^{n}$
and $R^{n}$![]() , for some $n \geq 0$
, for some $n \geq 0$![]() , and have $( \bigoplus _{n} D(k) )^{S} \cong M$
, and have $( \bigoplus _{n} D(k) )^{S} \cong M$![]() for any $k \in \mathbb {Z}$
for any $k \in \mathbb {Z}$![]() . This shows that finitely generated free $R$
. This shows that finitely generated free $R$![]() -modules can be extended to quasi-coherent diagrams. We need the following chain complex version of this fact:
-modules can be extended to quasi-coherent diagrams. We need the following chain complex version of this fact:
Proposition 8.1 Let $R$![]() be a $\mathbb {Z}^{2}$
be a $\mathbb {Z}^{2}$![]() -graded ring, and let $C$
-graded ring, and let $C$![]() be a bounded above chain complex of finitely generated free $R$
be a bounded above chain complex of finitely generated free $R$![]() -modules. Then there exists a complex $\mathcal {Y}$
-modules. Then there exists a complex $\mathcal {Y}$![]() of diagrams of the form $\bigoplus _{r} D(k),$
of diagrams of the form $\bigoplus _{r} D(k),$![]() for various $r \geq 0,$
for various $r \geq 0,$![]() such that $C \cong \mathcal {Y}^{S}$
such that $C \cong \mathcal {Y}^{S}$![]() as $R$
as $R$![]() -module complexes. More precisely, suppose that $C$
-module complexes. More precisely, suppose that $C$![]() is concentrated in degrees $\leq t$
is concentrated in degrees $\leq t$![]() . There are numbers
. There are numbers
and numbers $r_{n} \geq 0$![]() , with $r_{n} = 0$
, with $r_{n} = 0$![]() whenever $C_{n} = 0$
whenever $C_{n} = 0$![]() , such that we can choose $\mathcal {Y}_{n} = \bigoplus _{r_{n}} D(k_{n})$
, such that we can choose $\mathcal {Y}_{n} = \bigoplus _{r_{n}} D(k_{n})$![]() . If $C$
. If $C$![]() is bounded, then so is $\mathcal {Y}$
is bounded, then so is $\mathcal {Y}$![]() . If the ring $R$
. If the ring $R$![]() is strongly $\mathbb {Z}^{2}$
is strongly $\mathbb {Z}^{2}$![]() -graded, then $\mathcal {Y}$
-graded, then $\mathcal {Y}$![]() consists of quasi-coherent diagrams.
consists of quasi-coherent diagrams.
Proof. We identify the chain module $C_{n}$![]() with $R^{r_{n}}$
with $R^{r_{n}}$![]() , for suitable numbers $r_{n} \geq 0$
, for suitable numbers $r_{n} \geq 0$![]() , where $r_{n} = 0$
, where $r_{n} = 0$![]() if and only if $C_{n} = 0$
if and only if $C_{n} = 0$![]() ; this amounts to choosing basis elements for the free modules $C_{n}$
; this amounts to choosing basis elements for the free modules $C_{n}$![]() . The action of the differential $C_{n} \longrightarrow C_{n-1}$
. The action of the differential $C_{n} \longrightarrow C_{n-1}$![]() is then given by left multiplication by a matrix $D_{n}$
is then given by left multiplication by a matrix $D_{n}$![]() of size $r_{n-1} \times r_{n}$
of size $r_{n-1} \times r_{n}$![]() , with entries in $R$
, with entries in $R$![]() .
.
Given a homogeneous non-zero element $x \in R_{(s,t)}$![]() , we write $a(x) = \max ( |s|, |t| )$
, we write $a(x) = \max ( |s|, |t| )$![]() ; we also agree $a(0) = 0$
; we also agree $a(0) = 0$![]() . For a general element $x \in R$
. For a general element $x \in R$![]() , let $a(x)$
, let $a(x)$![]() denote the maximum of the values $a(x_i)$
denote the maximum of the values $a(x_i)$![]() , where the $x_i$
, where the $x_i$![]() are the homogeneous components of $x$
are the homogeneous components of $x$![]() . We denote by $a_{n}$
. We denote by $a_{n}$![]() the maximum of the values $a(x)$
the maximum of the values $a(x)$![]() where $x$
where $x$![]() varies over the entries of the matrix $D_{n}$
varies over the entries of the matrix $D_{n}$![]() , with the convention that $a_{n} = 0$
, with the convention that $a_{n} = 0$![]() if $D_{n}$
if $D_{n}$![]() is the empty matrix (i.e., if $r_{n} = 0$
is the empty matrix (i.e., if $r_{n} = 0$![]() or $r_{n-1} = 0$
or $r_{n-1} = 0$![]() ).
).
Suppose that $C$![]() is concentrated in chain degrees $\leq t$
is concentrated in chain degrees $\leq t$![]() . We set $k_{n} = 0$
. We set $k_{n} = 0$![]() for $n \geq t$
for $n \geq t$![]() , and
, and

for $k < t$![]() . We then define the chain complex $\mathcal {Y}$
. We then define the chain complex $\mathcal {Y}$![]() of quasi-coherent diagrams by setting $\mathcal {Y}_{n} = \bigoplus _{r_{n}} D(k_{n})$
of quasi-coherent diagrams by setting $\mathcal {Y}_{n} = \bigoplus _{r_{n}} D(k_{n})$![]() ; the differentials $d_{n} \colon \mathcal {Y}_{n} \longrightarrow \mathcal {Y}_{n-1}$
; the differentials $d_{n} \colon \mathcal {Y}_{n} \longrightarrow \mathcal {Y}_{n-1}$![]() are given by left multiplication by the matrix $D_{n}$
are given by left multiplication by the matrix $D_{n}$![]() in each component, so that
in each component, so that
(This is well defined: The numbers $k_{n}$![]() are chosen precisely to ensure that $d_{n}^{F}$
are chosen precisely to ensure that $d_{n}^{F}$![]() maps $\mathcal {Y}_{n}^{F}$
maps $\mathcal {Y}_{n}^{F}$![]() to $\mathcal {Y}_{n-1}^{F}$
to $\mathcal {Y}_{n-1}^{F}$![]() .) As $D_{n-1} \cdot D_{n} = 0$
.) As $D_{n-1} \cdot D_{n} = 0$![]() , we have $d_{n-1} \circ d_{n} = 0$
, we have $d_{n-1} \circ d_{n} = 0$![]() , and $C = \mathcal {Y}^{S}$
, and $C = \mathcal {Y}^{S}$![]() by construction.
by construction.
It was observed before that the diagrams $D(k)$![]() are quasi-coherent if $R$
are quasi-coherent if $R$![]() is strongly $\mathbb {Z}^{2}$
is strongly $\mathbb {Z}^{2}$![]() -graded (this follows from lemma 5.1); hence $\mathcal {Y}$
-graded (this follows from lemma 5.1); hence $\mathcal {Y}$![]() consists of quasi-coherent diagrams in this case.
consists of quasi-coherent diagrams in this case.
Corollary 8.2 Let $R$![]() , $C,$
, $C,$![]() $\mathcal {Y},$
$\mathcal {Y},$![]() $r_{n}$
$r_{n}$![]() and $k_{n}$
and $k_{n}$![]() be as in proposition 8.1, with $C$
be as in proposition 8.1, with $C$![]() bounded. Then $D = \lim \mathcal {Y}$
bounded. Then $D = \lim \mathcal {Y}$![]() is a bounded complex of $R_{(0,0)}$
is a bounded complex of $R_{(0,0)}$![]() -modules with chain modules
-modules with chain modules

If $R$![]() is strongly $\mathbb {Z}^{2}$
is strongly $\mathbb {Z}^{2}$![]() -graded, these $R_{(0,0)}$
-graded, these $R_{(0,0)}$![]() -modules are finitely generated projective. The natural map $D \longrightarrow \mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$
-modules are finitely generated projective. The natural map $D \longrightarrow \mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$![]() is a homotopy equivalence of $R_{(0,0)}$
is a homotopy equivalence of $R_{(0,0)}$![]() -module complexes so that $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$
-module complexes so that $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$![]() is $R_{(0,0)}$
is $R_{(0,0)}$![]() -finitely dominated.
-finitely dominated.
Proof. Consider the double complex concentrated in columns $-2$![]() , $-1$
, $-1$![]() , $0$
, $0$![]() and $1$
and $1$![]() with $n$
with $n$![]() th row given by
th row given by

Column 1 is the chain complex $\lim \, \mathcal {Y}$![]() , see proposition 7.2, which consists of finitely generated projective $R_{(0,0)}$
, see proposition 7.2, which consists of finitely generated projective $R_{(0,0)}$![]() -modules if $R$
-modules if $R$![]() is strongly graded by corollary 4.6. As the rows are exact (by proposition 7.2 again), standard homological algebra asserts that the natural map $\lim \mathcal {Y} \longrightarrow \mathrm {Tot} \, \Gamma (\mathcal {Y})$
is strongly graded by corollary 4.6. As the rows are exact (by proposition 7.2 again), standard homological algebra asserts that the natural map $\lim \mathcal {Y} \longrightarrow \mathrm {Tot} \, \Gamma (\mathcal {Y})$![]() is a quasi-isomorphism. In the strongly graded case, this is a homotopy equivalence (all complexes are bounded below and consist of projective $R_{(0,0)}$
is a quasi-isomorphism. In the strongly graded case, this is a homotopy equivalence (all complexes are bounded below and consist of projective $R_{(0,0)}$![]() -modules) so that $\mathrm {Tot} \, \Gamma (\mathcal {Y})$
-modules) so that $\mathrm {Tot} \, \Gamma (\mathcal {Y})$![]() is $R_{(0,0)}$
is $R_{(0,0)}$![]() -finitely dominated.
-finitely dominated.
9. Flags and stars, and their associated rings
Definition 9.1 For $F \in \mathfrak {S}$![]() , define the star of $F$
, define the star of $F$![]() , denoted $\mathrm {st}(F)$
, denoted $\mathrm {st}(F)$![]() , as the set of faces of $S$
, as the set of faces of $S$![]() that contain $F$
that contain $F$![]() ; this is a sub-poset of $\mathfrak {S}$
; this is a sub-poset of $\mathfrak {S}$![]() . Let $\mathcal {N}_{F}$
. Let $\mathcal {N}_{F}$![]() be the set of flags in $\mathrm {st}(F)$
be the set of flags in $\mathrm {st}(F)$![]() ; an element $\tau = \langle P_0,\, P_1,\, \cdots,\, P_k \rangle$
; an element $\tau = \langle P_0,\, P_1,\, \cdots,\, P_k \rangle$![]() of $\mathcal {N}_{F}$
of $\mathcal {N}_{F}$![]() is a strictly increasing sequence $P_0\subset P_1 \subset \ldots \subset P_k$
is a strictly increasing sequence $P_0\subset P_1 \subset \ldots \subset P_k$![]() of faces of $S$
of faces of $S$![]() with $F \subseteq P_{0}$
with $F \subseteq P_{0}$![]() . We consider $\mathcal {N}_{F}$
. We consider $\mathcal {N}_{F}$![]() as a poset with order given by inclusion (or refinement) of flags, the smaller flag in the partial order having fewer elements.
as a poset with order given by inclusion (or refinement) of flags, the smaller flag in the partial order having fewer elements.
For each $F \in \mathfrak {S}$![]() , we equip $\mathcal {N}_{F}$
, we equip $\mathcal {N}_{F}$![]() with the rank function
with the rank function
and with standard simplicial incidence numbers: $[\tau :\sigma ] = 0$![]() unless the flag $\sigma$
unless the flag $\sigma$![]() is obtained from $\tau = \langle P_0,\, P_1,\, \cdots,\, P_k \rangle$
is obtained from $\tau = \langle P_0,\, P_1,\, \cdots,\, P_k \rangle$![]() by omitting the entry $P_{j}$
by omitting the entry $P_{j}$![]() , in which case $[\tau :\sigma ] = (-1)^j$
, in which case $[\tau :\sigma ] = (-1)^j$![]() . Whenever we form a Čech complex of a diagram indexed by $\mathcal {N}_{F}$
. Whenever we form a Čech complex of a diagram indexed by $\mathcal {N}_{F}$![]() , we will use these data.
, we will use these data.
We now attach a ring $A\langle P_0,\, P_1,\, \cdots,\, P_k \rangle$![]() to each flag $\langle P_0,\, P_1,\, \cdots,\, P_k \rangle$
to each flag $\langle P_0,\, P_1,\, \cdots,\, P_k \rangle$![]() of faces in $\mathfrak {S}$
of faces in $\mathfrak {S}$![]() , as follows:
, as follows:

The effect of replacing ‘left’ by ‘right’ (i.e., replacing the subscript ‘$l$![]() ’ by ‘$r$
’ by ‘$r$![]() ’ throughout) is to replace $x$
’ throughout) is to replace $x$![]() by $x^{-1}$
by $x^{-1}$![]() , while replacing ‘bottom’ by ‘top’ (i.e., replacing the subscript ‘$b$
, while replacing ‘bottom’ by ‘top’ (i.e., replacing the subscript ‘$b$![]() ’ by ‘$t$
’ by ‘$t$![]() ’ throughout) means replacing $y$
’ throughout) means replacing $y$![]() by $y^{-1}$
by $y^{-1}$![]() . Swapping ‘bottom’ and ‘left’ amounts to swapping $x$
. Swapping ‘bottom’ and ‘left’ amounts to swapping $x$![]() with $y$
with $y$![]() , and swapping ‘top’ and ‘right’ results in $x^{-1}$
, and swapping ‘top’ and ‘right’ results in $x^{-1}$![]() and $y^{-1}$
and $y^{-1}$![]() swapping places. Thus, for example,
swapping places. Thus, for example,
By direct inspection, this collection of rings is seen to have the following properties:
(1) If $\sigma \subseteq \tau$
 , then $A \langle \sigma \rangle \subseteq A \langle \tau \rangle$
, then $A \langle \sigma \rangle \subseteq A \langle \tau \rangle$ . In particular, if $S \in \tau$
. In particular, if $S \in \tau$ , then $R = R_*[x,x^{-1}, y,y^{-1}] = A \langle S \rangle$
, then $R = R_*[x,x^{-1}, y,y^{-1}] = A \langle S \rangle$ is a subring of $A \langle \tau \rangle$
is a subring of $A \langle \tau \rangle$ .
.(2) If $\tau \in \mathcal {N}_{F}$
 (i.e., if all faces in $\tau$
(i.e., if all faces in $\tau$ contain $F$
contain $F$ ), then $A_{F} \subseteq A \langle \tau \rangle$
), then $A_{F} \subseteq A \langle \tau \rangle$ .
.
Fix $F \in \mathfrak {S}$![]() . The rings $A \langle \tau \rangle$
. The rings $A \langle \tau \rangle$![]() defined above fit into a commutative diagram
defined above fit into a commutative diagram
of $A_{F}$![]() -modules with structure maps given by inclusions. For $F = S$
-modules with structure maps given by inclusions. For $F = S$![]() , the diagram $E_{S}$
, the diagram $E_{S}$![]() has a single entry indexed by the flag $\langle S \rangle$
has a single entry indexed by the flag $\langle S \rangle$![]() , and takes value $A \langle S \rangle = R$
, and takes value $A \langle S \rangle = R$![]() there. For $F = e_{l}$
there. For $F = e_{l}$![]() , the left-hand edge of $S$
, the left-hand edge of $S$![]() , the diagram $E_{e_{l}}$
, the diagram $E_{e_{l}}$![]() looks like this:
looks like this:
And finally, for $F = v_{bl}$![]() the bottom left vertex of $S$
the bottom left vertex of $S$![]() , the diagram $E_{v_{bl}}$
, the diagram $E_{v_{bl}}$![]() is depicted in figure 4.
is depicted in figure 4.

Figure 4. The diagram $E_{v_{bl}}$![]() .
.
We let $\Gamma _{\mathcal {N}_{F}} (E_{F})$![]() denote the Čech complex of $E_{F}$
denote the Čech complex of $E_{F}$![]() . Considering $A_{F}$
. Considering $A_{F}$![]() as a chain complex concentrated in chain level $0$
as a chain complex concentrated in chain level $0$![]() , we have a chain map
, we have a chain map
given by the diagonal embedding $A_{F} \longrightarrow \bigoplus _{G \supseteq F} A \langle G \rangle$![]() . This is indeed a chain map thanks to property (DI3) of incidence numbers.
. This is indeed a chain map thanks to property (DI3) of incidence numbers.
Lemma 9.2 The map $\xi ^{F}$![]() is a quasi-isomorphism of chain complexes of $A_{F}$
is a quasi-isomorphism of chain complexes of $A_{F}$![]() -modules.
-modules.
Proof. Note that for $F = S$![]() , there is actually nothing to show as the category $\mathcal {N}_{S}$
, there is actually nothing to show as the category $\mathcal {N}_{S}$![]() has a single object; for $F = e_{l}$
has a single object; for $F = e_{l}$![]() , the claim is equivalent to saying that the sequence
, the claim is equivalent to saying that the sequence

is exact, and it is not too hard to see that it is actually split exactly as a sequence of $R_{(0,0)}$![]() -modules. The case of $F = v_?$
-modules. The case of $F = v_?$![]() a vertex is somewhat more demanding in terms of book-keeping. Full details are worked out in the proof of Lemma 4.5.1 in [Reference Hüttemann and Quinn3], writing $R_*[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$
a vertex is somewhat more demanding in terms of book-keeping. Full details are worked out in the proof of Lemma 4.5.1 in [Reference Hüttemann and Quinn3], writing $R_*[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$![]() in place of $R[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$
in place of $R[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$![]() (and similar for the other rings); the proof carries over mutatis mutandis since the claim can be checked in each degree separately.
(and similar for the other rings); the proof carries over mutatis mutandis since the claim can be checked in each degree separately.
For faces $G \supsetneqq F$![]() , let $E_{F}^{G}$
, let $E_{F}^{G}$![]() denote the $\mathcal {N}_{F}$
denote the $\mathcal {N}_{F}$![]() -indexed diagram which agrees with $E_{G}$
-indexed diagram which agrees with $E_{G}$![]() on $\mathcal {N}_{G}$
on $\mathcal {N}_{G}$![]() , and is zero everywhere else. The obvious map of diagrams $E_{F} \longrightarrow E_{F}^{G}$
, and is zero everywhere else. The obvious map of diagrams $E_{F} \longrightarrow E_{F}^{G}$![]() , given by identities where possible, results in a map of chain complexes
, given by identities where possible, results in a map of chain complexes
given by projecting away from all those summands in the source which involve flags in $\mathcal {N}_{F} \setminus \mathcal {N}_{G}$![]() . These maps are functorial on the poset $\mathfrak {S}$
. These maps are functorial on the poset $\mathfrak {S}$![]() so that there results a commutative diagram
so that there results a commutative diagram
Proposition 9.3 The maps $\xi ^{F}$![]() constructed above assemble to a natural transformation
constructed above assemble to a natural transformation
Its components $\xi ^{F} \colon A_{F} \longrightarrow \Gamma _{\mathcal {N}_{F}} (E_{F})$![]() are quasi-isomorphisms of complexes of $A_{F}$
are quasi-isomorphisms of complexes of $A_{F}$![]() -modules.
-modules.
Proof. This is the content of lemma 9.2, together with the observation that the maps $\xi ^{F}$![]() are natural in $F$
are natural in $F$![]() with respect to the structure maps in $E$
with respect to the structure maps in $E$![]() .
.
Given a flat $A_{F}$![]() -module $M_{F}$
-module $M_{F}$![]() , we thus obtain a quasi-isomorphism
, we thus obtain a quasi-isomorphism
here $M_{F} \mathop {\otimes }_{A_{F}} E_{F}$![]() stands for the pointwise tensor product of the module $M_{F}$
stands for the pointwise tensor product of the module $M_{F}$![]() with the entries of the diagram $E_{F}$
with the entries of the diagram $E_{F}$![]() . In other words, the sequence
. In other words, the sequence

is exact.
For $M$![]() an arbitrary quasi-coherent diagram, we obtain a natural transformation
an arbitrary quasi-coherent diagram, we obtain a natural transformation
where the target $M'$![]() is the diagram of chain complexes
is the diagram of chain complexes
$M \mathop {\otimes }_{D(0)} D(0)$![]() denotes the pointwise tensor product
denotes the pointwise tensor product
and $M \mathop {\otimes }_{D(0)} E$![]() stands similarly for the pointwise tensor product of the diagrams $M$
stands similarly for the pointwise tensor product of the diagrams $M$![]() and $E$
and $E$![]() . If moreover $M$
. If moreover $M$![]() is such that the entry $M_{F}$
is such that the entry $M_{F}$![]() is a flat $A_{F}$
is a flat $A_{F}$![]() -module, the components of $\chi$
-module, the components of $\chi$![]() are quasi-isomorphisms.
are quasi-isomorphisms.
10. From trivial Novikov homology to finite domination
We will now prove the ‘if’ implication of theorem 2.1. So let $R$![]() be a strongly $\mathbb {Z}^{2}$
be a strongly $\mathbb {Z}^{2}$![]() -graded ring. Suppose that $C$
-graded ring. Suppose that $C$![]() is a bounded complex of finitely generated free $R$
is a bounded complex of finitely generated free $R$![]() -modules, and further that the complexes listed in (2.2a) and (2.2b) are acyclic. In view of the assumed freeness of $C$
-modules, and further that the complexes listed in (2.2a) and (2.2b) are acyclic. In view of the assumed freeness of $C$![]() , these eight complexes are then actually contractible. They are of the form
, these eight complexes are then actually contractible. They are of the form
where $e$![]() and $v$
and $v$![]() denote an edge and a vertex of $S$
denote an edge and a vertex of $S$![]() , respectively. As tensor products preserve contractions, it follows that for all eight maximal flags $\langle v,\, e,\, S \rangle$
, respectively. As tensor products preserve contractions, it follows that for all eight maximal flags $\langle v,\, e,\, S \rangle$![]() , for $v$
, for $v$![]() a vertex of $S$
a vertex of $S$![]() and $e$
and $e$![]() an edge incident to $v$
an edge incident to $v$![]() , the complex
, the complex
is contractible (and hence acyclic) as well.
Extend the complex $C$![]() to a complex of sheaves $\mathcal {Y} \colon F \mapsto \mathcal {Y}_{F}$
to a complex of sheaves $\mathcal {Y} \colon F \mapsto \mathcal {Y}_{F}$![]() , which can be done by proposition 8.1. In more detail, this means that we find a complex of sheaves such that $C$
, which can be done by proposition 8.1. In more detail, this means that we find a complex of sheaves such that $C$![]() is identified with $\mathcal {Y}^{S}$
is identified with $\mathcal {Y}^{S}$![]() , and such that there is a quasi-isomorphism $\lim \mathcal {Y} \longrightarrow \mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$
, and such that there is a quasi-isomorphism $\lim \mathcal {Y} \longrightarrow \mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$![]() with $R_{(0,0)}$
with $R_{(0,0)}$![]() -finitely dominated source (corollary 8.2).
-finitely dominated source (corollary 8.2).
Let, for the moment, $F \neq \emptyset$![]() denote a fixed face of $S$
denote a fixed face of $S$![]() . We observe that if $F \neq S$
. We observe that if $F \neq S$![]() ,
,
The isomorphism labelled (${\dagger}$![]() ) combines two facts: first, the entries of the complex $\mathcal {Y}$
) combines two facts: first, the entries of the complex $\mathcal {Y}$![]() are quasi-coherent diagrams (proposition 8.1) so that $\mathcal {Y}_{F} \mathop {\otimes }_{A_F} A_{S} \cong \mathcal {Y}^{S}$
are quasi-coherent diagrams (proposition 8.1) so that $\mathcal {Y}_{F} \mathop {\otimes }_{A_F} A_{S} \cong \mathcal {Y}^{S}$![]() ; second, by construction of $\mathcal {Y}$
; second, by construction of $\mathcal {Y}$![]() there is an identification of $\mathcal {Y}^{S}$
there is an identification of $\mathcal {Y}^{S}$![]() with $C$
with $C$![]() .
.
If $F = v$![]() is a vertex and $e \supseteq v$
is a vertex and $e \supseteq v$![]() an edge incident to $e$
an edge incident to $e$![]() , we make use of (10.1) to conclude similarly
, we make use of (10.1) to conclude similarly
For arbitrary $F \neq \emptyset$![]() , exactness of the sequence (9.2) implies that the double complex
, exactness of the sequence (9.2) implies that the double complex
has exact rows (using the fact that $\mathcal {Y}_{F}$![]() consists of projective $A_{F}$
consists of projective $A_{F}$![]() -modules), so there results a quasi-isomorphism
-modules), so there results a quasi-isomorphism
We will now make use of the fact that some entries of the diagram $\mathcal {Y}_{F} \mathop {\otimes }_{A_{F}} E_{F}$![]() are known to be acyclic. Let $Z_{F}$
are known to be acyclic. Let $Z_{F}$![]() denote the $\mathcal {N}_{F}$
denote the $\mathcal {N}_{F}$![]() -indexed diagram which agrees with $\mathcal {Y}_{F} \mathop {\otimes }_{A_{F}} E_{F}$
-indexed diagram which agrees with $\mathcal {Y}_{F} \mathop {\otimes }_{A_{F}} E_{F}$![]() on those flags not containing $S$
on those flags not containing $S$![]() , and is zero elsewhere. Let $K_{F}$
, and is zero elsewhere. Let $K_{F}$![]() denote the diagram which takes the value $C$
denote the diagram which takes the value $C$![]() at $\{S\}$
at $\{S\}$![]() , and is zero otherwise. The obvious surjective map $\mathcal {Y}_{F} \mathop {\otimes }_{A_{F}} E_{F} \longrightarrow Z_{F} \oplus K_{F}$
, and is zero otherwise. The obvious surjective map $\mathcal {Y}_{F} \mathop {\otimes }_{A_{F}} E_{F} \longrightarrow Z_{F} \oplus K_{F}$![]() is a pointwise quasi-isomorphism, by (10.2) and (10.3), and hence induces a quasi-isomorphism
is a pointwise quasi-isomorphism, by (10.2) and (10.3), and hence induces a quasi-isomorphism
We compute further that the target of this map is
In total, this yields a quasi-isomorphism
Allowing $F$![]() to vary again, and making use of the naturality of the constructions above, we see that we obtain a natural quasi-isomorphism of diagrams
to vary again, and making use of the naturality of the constructions above, we see that we obtain a natural quasi-isomorphism of diagrams
with the $\mathfrak {S}$![]() -indexed diagram
-indexed diagram
and the constant diagram
It follows that $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$![]() , which is an $R_{(0,0)}$
, which is an $R_{(0,0)}$![]() -finitely dominated by corollary 8.2, is quasi-isomorphic to
-finitely dominated by corollary 8.2, is quasi-isomorphic to
The second summand is, in turn, quasi-isomorphic to $C$![]() . (In effect, this is true since the nerve of $\mathfrak {S}$
. (In effect, this is true since the nerve of $\mathfrak {S}$![]() is contractible; for a more explicit argument, observe that the double complex
is contractible; for a more explicit argument, observe that the double complex
concentrated in columns $-2$![]() , $-1$
, $-1$![]() , $0$
, $0$![]() and $1$
and $1$![]() has acyclic rows so that its totalization is acyclic. But the totalization is, up to isomorphism, the mapping cone of the map $C \longrightarrow \mathrm {Tot} \, \Gamma _{\mathfrak {S}} \big ( \mathrm {con}\,(C) \big )$
has acyclic rows so that its totalization is acyclic. But the totalization is, up to isomorphism, the mapping cone of the map $C \longrightarrow \mathrm {Tot} \, \Gamma _{\mathfrak {S}} \big ( \mathrm {con}\,(C) \big )$![]() which is thus a weak equivalence. See also [Reference Hüttemann and Quinn3, Lemma 4.6.4].)
which is thus a weak equivalence. See also [Reference Hüttemann and Quinn3, Lemma 4.6.4].)
Thus in the derived category of the ring $R_{(0,0)}$![]() , the complex $C$
, the complex $C$![]() is a retract of $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$
is a retract of $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$![]() , and as both complexes are bounded and consist of projective $R_{(0,0)}$
, and as both complexes are bounded and consist of projective $R_{(0,0)}$![]() -modules, this makes $C$
-modules, this makes $C$![]() a retract up to homotopy of $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$
a retract up to homotopy of $\mathrm {Tot} \, \Gamma _{\mathfrak {S}} (\mathcal {Y})$![]() . As the latter is $R_{(0,0)}$
. As the latter is $R_{(0,0)}$![]() -finitely dominated so is $C$
-finitely dominated so is $C$![]() , as was to be shown.
, as was to be shown.
Part III. Finite domination implies triviality of Novikov homology
11. Algebraic tori
Definition 11.1 Let $R = \bigoplus _{\sigma \in \mathbb {Z}^{2}} R_{\sigma }$![]() be a strongly $\mathbb {Z}^2$
be a strongly $\mathbb {Z}^2$![]() -graded unital ring. Given an $R$
-graded unital ring. Given an $R$![]() -module $M$
-module $M$![]() and an element $\rho \in \mathbb {Z}^2$
and an element $\rho \in \mathbb {Z}^2$![]() , we define the map of right $R$
, we define the map of right $R$![]() -modules
-modules
where $1 = \sum _{j} u_{j} v_{j}$![]() is any partition of unity of type $(-\rho, \rho )$
is any partition of unity of type $(-\rho, \rho )$![]() .
.
The map $\chi _\rho$![]() is $R_{(0,0)}$
is $R_{(0,0)}$![]() -balanced and independent of the choice of partition of unity as its restriction to $M \mathop {\otimes }_{R_{(0,0)}} R_{\sigma }$
-balanced and independent of the choice of partition of unity as its restriction to $M \mathop {\otimes }_{R_{(0,0)}} R_{\sigma }$![]() can be re-written as
can be re-written as
with $\mu _{-\rho, \sigma +\rho }$![]() the $R_{(0,0)}$
the $R_{(0,0)}$![]() -bimodule isomorphism from proposition 4.3, and with $\omega (m \mathop {\otimes } x \mathop {\otimes } y) = (mx) \mathop {\otimes } y$
-bimodule isomorphism from proposition 4.3, and with $\omega (m \mathop {\otimes } x \mathop {\otimes } y) = (mx) \mathop {\otimes } y$![]() . In case $M=R$
. In case $M=R$![]() , the map $\chi _{\rho }$
, the map $\chi _{\rho }$![]() is an $R$
is an $R$![]() -bimodule homomorphism.
-bimodule homomorphism.
Of course $\chi _{(0,0)} = \mathrm {id}$![]() . As $\chi _{\rho }$
. As $\chi _{\rho }$![]() does not depend on the choice of partition of unity, lemma 4.2 implies:
does not depend on the choice of partition of unity, lemma 4.2 implies:
Corollary 11.2 For all $\rho, \sigma \in \mathbb {Z}^{2}$![]() , there are equalities of maps $\chi _\rho \chi _\sigma = \chi _{\rho +\sigma } = \chi _{\sigma } \chi _{\rho }$
, there are equalities of maps $\chi _\rho \chi _\sigma = \chi _{\rho +\sigma } = \chi _{\sigma } \chi _{\rho }$![]() . The maps $\chi _{\rho }$
. The maps $\chi _{\rho }$![]() are isomorphisms of $R$
are isomorphisms of $R$![]() -modules with $\chi _{\rho }^{-1} = \chi _{-\rho }$
-modules with $\chi _{\rho }^{-1} = \chi _{-\rho }$![]() .
.
We can consider
as a $\mathbb {Z}^2$![]() -graded $R$
-graded $R$![]() -module. With respect to this grading, we observe:
-module. With respect to this grading, we observe:
Lemma 11.3 The map $\chi _{\rho }$![]() maps homogeneous elements of degree $\sigma$
maps homogeneous elements of degree $\sigma$![]() to homogeneous elements of degree $\rho + \sigma$
to homogeneous elements of degree $\rho + \sigma$![]() . For the homogeneous element $m \mathop {\otimes } r$
. For the homogeneous element $m \mathop {\otimes } r$![]() of degree $-\rho,$
of degree $-\rho,$![]() the formula $\chi _{\rho } (m \mathop {\otimes } r) = mr \mathop {\otimes } 1$
the formula $\chi _{\rho } (m \mathop {\otimes } r) = mr \mathop {\otimes } 1$![]() holds.
holds.
Let $C$![]() be a chain complex of $R$
be a chain complex of $R$![]() -modules. Then $\chi _{\rho }$
-modules. Then $\chi _{\rho }$![]() , applied in each chain level, defines a chain map
, applied in each chain level, defines a chain map
Let $D$![]() be an additional $R_{(0,0)}$
be an additional $R_{(0,0)}$![]() -chain complex, let $\alpha \colon C \longrightarrow D$
-chain complex, let $\alpha \colon C \longrightarrow D$![]() and $\beta \colon D\longrightarrow C$
and $\beta \colon D\longrightarrow C$![]() be $R_{(0,0)}$
be $R_{(0,0)}$![]() -linear chain maps, and let $H\colon \mathrm {id}_C\simeq \beta \alpha$
-linear chain maps, and let $H\colon \mathrm {id}_C\simeq \beta \alpha$![]() be a homotopy from $\beta \alpha$
be a homotopy from $\beta \alpha$![]() to $\mathrm {id}$
to $\mathrm {id}$![]() such that $dH+Hd=\beta \alpha -\mathrm {id}_C$
such that $dH+Hd=\beta \alpha -\mathrm {id}_C$![]() . Then the outer square in the diagram
. Then the outer square in the diagram ![]() $T(\alpha, \beta ; H)$
$T(\alpha, \beta ; H)$

(writing $f^* = f \mathop {\otimes } \mathrm {id}$![]() , for any map $f$
, for any map $f$![]() ) is homotopy commutative, with the diagonal arrow recording a preferred homotopy of the two possible compositions. Note that if $\beta \alpha = \mathrm {id}_C$
) is homotopy commutative, with the diagonal arrow recording a preferred homotopy of the two possible compositions. Note that if $\beta \alpha = \mathrm {id}_C$![]() , we can choose $H=0$
, we can choose $H=0$![]() and in this case the outer squares of $T(\alpha, \beta ; 0)$
and in this case the outer squares of $T(\alpha, \beta ; 0)$![]() commute by corollary 11.2.
commute by corollary 11.2.
Definition 11.4 The algebraic torus ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$![]() is defined as the totalization of the homotopy commutative diagram $T(\alpha, \beta ; H)$
is defined as the totalization of the homotopy commutative diagram $T(\alpha, \beta ; H)$![]() . That is, ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$
. That is, ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$![]() is the complex with chain modules
is the complex with chain modules

and boundary $d_{{\mathfrak {T}({{{\alpha },{\beta };{H}}})}}$![]() given by the following matrix:
given by the following matrix:

12. Canonical resolutions
Let $C$![]() be a chain complex of $R$
be a chain complex of $R$![]() -modules. The commutative diagram
-modules. The commutative diagram

gives rise, via totalization, to the algebraic torus ${\mathfrak {T}({{{\mathrm {id}_{C}},{\mathrm {id}_{C}};{0}}})}$![]() . The $R$
. The $R$![]() -module structure map $\gamma \colon (x,r) \mapsto xr$
-module structure map $\gamma \colon (x,r) \mapsto xr$![]() induces a map of $R$
induces a map of $R$![]() -module chain complexes
-module chain complexes
Proposition 12.1 Canonical resolution
The map $\kappa$![]() is a quasi-isomorphism. If $C$
is a quasi-isomorphism. If $C$![]() is a bounded below complex of projective $R$
is a bounded below complex of projective $R$![]() -modules, then $\kappa$
-modules, then $\kappa$![]() is a chain homotopy equivalence.
is a chain homotopy equivalence.
In preparation of the proof, we note that ${\mathfrak {T}({{{\mathrm {id}_{C}},{\mathrm {id}_{C}};{0}}})}$![]() can be described as the totalization (in the usual sense) of a double complex of the form
can be described as the totalization (in the usual sense) of a double complex of the form
The $R$![]() -module structure map $\gamma \colon (x,r) \mapsto xr$
-module structure map $\gamma \colon (x,r) \mapsto xr$![]() of $C$
of $C$![]() can be used to augment this to the $R$
can be used to augment this to the $R$![]() -module double complex
-module double complex
We will consider a single row of this double complex, that is, a sequence of the form
where $M$![]() is a right $R$
is a right $R$![]() -module. Here the maps $\alpha$
-module. Here the maps $\alpha$![]() and $\beta$
and $\beta$![]() are given by the matrices
are given by the matrices
Lemma 12.2 The complex (12.3) is exact.
Proof. We allow $M$![]() to be an arbitrary $R_{(0,0)}$
to be an arbitrary $R_{(0,0)}$![]() -module initially. We have the direct sum decomposition $M \mathop {\otimes }_{R_{(0,0)}} R = \bigoplus _{(i,j)} M \mathop {\otimes }_{R_{(0,0)}} R_{(i,j)}$
-module initially. We have the direct sum decomposition $M \mathop {\otimes }_{R_{(0,0)}} R = \bigoplus _{(i,j)} M \mathop {\otimes }_{R_{(0,0)}} R_{(i,j)}$![]() ; in fact, $M \mathop {\otimes }_{R_{(0,0)}} R$
; in fact, $M \mathop {\otimes }_{R_{(0,0)}} R$![]() is a $\mathbb {Z}^2$
is a $\mathbb {Z}^2$![]() -graded $R$
-graded $R$![]() -module in this way. Any element $z \in M \mathop {\otimes }_{R_{(0,0)}} R$
-module in this way. Any element $z \in M \mathop {\otimes }_{R_{(0,0)}} R$![]() can be expressed uniquely in the form
can be expressed uniquely in the form
such that $m_{i,j} = 0$![]() for almost all pairs $(i,j)$
for almost all pairs $(i,j)$![]() . We say that $z$
. We say that $z$![]() has $x$
has $x$![]() -amplitude in the interval $[a,b]$
-amplitude in the interval $[a,b]$![]() if $m_{i,j} =0$
if $m_{i,j} =0$![]() for $i \notin [a,b]$
for $i \notin [a,b]$![]() . The support of $z$
. The support of $z$![]() is the (finite) set of all pairs $(i,j)$
is the (finite) set of all pairs $(i,j)$![]() with $m_{i,j} \neq 0$
with $m_{i,j} \neq 0$![]() .
.
After these initial comments, we proceed to verify exactness of the sequence. We remark first that $\gamma$![]() is surjective since $\gamma (p \otimes 1)=p$
is surjective since $\gamma (p \otimes 1)=p$![]() . As a matter of fact, $\sigma (p) = p \otimes 1$
. As a matter of fact, $\sigma (p) = p \otimes 1$![]() defines an $R_{(0,0)}$
defines an $R_{(0,0)}$![]() -linear section $\sigma$
-linear section $\sigma$![]() of $\gamma$
of $\gamma$![]() .
.
Next, we show that $\alpha$![]() is injective. Let $z=\sum _{i,j \in \mathbb {Z}} m_{i,j}$
is injective. Let $z=\sum _{i,j \in \mathbb {Z}} m_{i,j}$![]() be an element of $\ker (\alpha )$
be an element of $\ker (\alpha )$![]() . Since $\chi _{e_2}(m_{i,j}) \in M \mathop {\otimes }_{R_{(0,0)}} R_{(i,j+1)}$
. Since $\chi _{e_2}(m_{i,j}) \in M \mathop {\otimes }_{R_{(0,0)}} R_{(i,j+1)}$![]() , the equality
, the equality

implies, by considering the homogeneous component of degree $(i,j)$![]() of the second entry, that $m_{i,j} - \chi _{e_2} (m_{i,j-1}) = 0$
of the second entry, that $m_{i,j} - \chi _{e_2} (m_{i,j-1}) = 0$![]() . If $z \neq 0$
. If $z \neq 0$![]() , there exists $(i,j)$
, there exists $(i,j)$![]() in the support of $z$
in the support of $z$![]() such that $m_{i,j-1} = 0$
such that $m_{i,j-1} = 0$![]() . For these indices, we have $m_{i,j} = \chi _{e_2} (m_{i,j-1}) = \chi _{e_2}(0) = 0$
. For these indices, we have $m_{i,j} = \chi _{e_2} (m_{i,j-1}) = \chi _{e_2}(0) = 0$![]() , a contradiction. This enforces $z=0$
, a contradiction. This enforces $z=0$![]() whence $\alpha$
whence $\alpha$![]() is injective.
is injective.
To show that $\mathrm {im}\,\alpha = \ker \beta$![]() , we will take an element $(z_1,z_2)$
, we will take an element $(z_1,z_2)$![]() of $\ker \beta$
of $\ker \beta$![]() and show that it can be reduced to $0$
and show that it can be reduced to $0$![]() by subtracting a sequence of elements of $\mathrm {im}\,\alpha \subseteq \ker \beta$
by subtracting a sequence of elements of $\mathrm {im}\,\alpha \subseteq \ker \beta$![]() . This clearly implies that $(z_1,z_2) \in \mathrm {im}\,\alpha$
. This clearly implies that $(z_1,z_2) \in \mathrm {im}\,\alpha$![]() as required.
as required.
So let $(z_1,z_2) \in \ker \beta$![]() , where
, where
Choose integers $a$![]() , $b$
, $b$![]() and $k$
and $k$![]() such that $z_1$
such that $z_1$![]() has $x$
has $x$![]() -amplitude in $[a,k]$
-amplitude in $[a,k]$![]() and $z_2$
and $z_2$![]() has $x$
has $x$![]() -amplitude in $[a,b]$
-amplitude in $[a,b]$![]() . If $k > a$
. If $k > a$![]() , we define
, we define
and set $(z_1',z_2') = (z_1,z_2) - \alpha (u)$![]() . The $(k,j)$
. The $(k,j)$![]() -homogeneous component of $z_1'$
-homogeneous component of $z_1'$![]() vanishes by construction of $u$
vanishes by construction of $u$![]() and corollary 11.2, so that $z_1'$
and corollary 11.2, so that $z_1'$![]() has $x$
has $x$![]() -amplitude in $[a,k-1]$
-amplitude in $[a,k-1]$![]() while the $x$
while the $x$![]() -amplitude of $z_2$
-amplitude of $z_2$![]() remains in $[a,b]$
remains in $[a,b]$![]() . The element $(z_1',z_2')$
. The element $(z_1',z_2')$![]() will be in $\mathrm {im}\,\alpha$
will be in $\mathrm {im}\,\alpha$![]() if and only if $(z_1,z_2) \in \mathrm {im}\,\alpha$
if and only if $(z_1,z_2) \in \mathrm {im}\,\alpha$![]() .
.
By iteration, we may thus assume that our initial pair $(z_1,z_2)$![]() is such that the $x$
is such that the $x$![]() -amplitude of $z_1$
-amplitude of $z_1$![]() is in $\{a\} = [a,a]$
is in $\{a\} = [a,a]$![]() . This actually necessitates $z_2=0$
. This actually necessitates $z_2=0$![]() . To see this, assume $z_2 \neq 0$
. To see this, assume $z_2 \neq 0$![]() . We can then choose $(i,j)$
. We can then choose $(i,j)$![]() in the support of $z_2$
in the support of $z_2$![]() (so that in particular $i \geq a$
(so that in particular $i \geq a$![]() ) such that $(i+1,j)$
) such that $(i+1,j)$![]() is not in the support of $z_2$
is not in the support of $z_2$![]() , i.e., such that $n_{i+1,j} = 0$
, i.e., such that $n_{i+1,j} = 0$![]() . Since $\beta (z_1,z_2) = 0$
. Since $\beta (z_1,z_2) = 0$![]() we have, by considering the homogeneous component of degree $(i+1,j)$
we have, by considering the homogeneous component of degree $(i+1,j)$![]() , the equality
, the equality
But the first three terms vanish, by choice of $i$![]() and our hypothesis on $z_1$
and our hypothesis on $z_1$![]() , so that $\chi _{e_1} (n_{i,j}) = 0$
, so that $\chi _{e_1} (n_{i,j}) = 0$![]() whence $n_{i,j} = 0$
whence $n_{i,j} = 0$![]() , contradicting the choice of $i$
, contradicting the choice of $i$![]() .
.
Thus, $z_2=0$![]() . This in turn implies that $\beta (z_1,0) = 0$
. This in turn implies that $\beta (z_1,0) = 0$![]() so that $m_{a,\ell } - \chi _{e_2} (m_{a,\ell -1}) \!=\! 0$
so that $m_{a,\ell } - \chi _{e_2} (m_{a,\ell -1}) \!=\! 0$![]() for any $\ell$
for any $\ell$![]() . If $z_1$
. If $z_1$![]() is non-zero, we let $\ell$
is non-zero, we let $\ell$![]() be minimal with $m_{a, \ell } \neq 0$
be minimal with $m_{a, \ell } \neq 0$![]() . Then $m_{a,\ell } = \chi _{e_2}(m_{a, \ell -1}) = \chi _{e_2}(0) = 0$
. Then $m_{a,\ell } = \chi _{e_2}(m_{a, \ell -1}) = \chi _{e_2}(0) = 0$![]() , a contradiction. We conclude that $(z_1,z_2) = 0 \in \mathrm {im}\,\alpha$
, a contradiction. We conclude that $(z_1,z_2) = 0 \in \mathrm {im}\,\alpha$![]() as required.
as required.
To show $\mathrm {im}\,\beta = \ker \gamma$![]() , it is enough to produce an $R_{(0,0)}$
, it is enough to produce an $R_{(0,0)}$![]() -linear map
-linear map
such that $\beta \varphi + \sigma \gamma = \mathrm {id}$![]() , where $\sigma$
, where $\sigma$![]() is the section of $\gamma$
is the section of $\gamma$![]() given by $\sigma (p) = p \mathop {\otimes } 1$
given by $\sigma (p) = p \mathop {\otimes } 1$![]() . It is enough to define $\varphi$
. It is enough to define $\varphi$![]() on homogeneous primitive tensors $x = m \mathop {\otimes } r$
on homogeneous primitive tensors $x = m \mathop {\otimes } r$![]() with $r \in R_{\rho }$
with $r \in R_{\rho }$![]() , for the various $\rho \in \mathbb {Z}^2$
, for the various $\rho \in \mathbb {Z}^2$![]() .
.
• If $a,b \geq 0$
 :
\[ \varphi(x) = \Big( - \sum_{k=1}^{b} \chi_{(0,-k)} (x) \qquad \sum_{\ell=1}^{a} \chi_{(-\ell, -b)} (x) \Big) \]
:
\[ \varphi(x) = \Big( - \sum_{k=1}^{b} \chi_{(0,-k)} (x) \qquad \sum_{\ell=1}^{a} \chi_{(-\ell, -b)} (x) \Big) \]
• If $a,b < 0$
 :
\[ \varphi(x) = \Big( \sum_{k=0}^{|b|-1} \chi_{(0,k)} (x) \qquad - \sum_{\ell=0}^{|a|-1} \chi_{(\ell, |b|)} (x) \Big) \]
:
\[ \varphi(x) = \Big( \sum_{k=0}^{|b|-1} \chi_{(0,k)} (x) \qquad - \sum_{\ell=0}^{|a|-1} \chi_{(\ell, |b|)} (x) \Big) \]
• If $a< 0$
 and $b \geq 0$
and $b \geq 0$ :
\[ \varphi(x) = \Big( - \sum_{k=1}^{b} \chi_{(0,-k)} (x) \qquad - \sum_{\ell=0}^{|a|-1} \chi_{(\ell, |b|)} (x) \Big) \]
:
\[ \varphi(x) = \Big( - \sum_{k=1}^{b} \chi_{(0,-k)} (x) \qquad - \sum_{\ell=0}^{|a|-1} \chi_{(\ell, |b|)} (x) \Big) \]
• If $a \geq 0$
 and $b < 0$
and $b < 0$ :
\[ \varphi(x) = \Big( \sum_{k=0}^{|b|-1} \chi_{(0,k)} (x) \qquad \sum_{\ell=1}^{a} \chi_{(-\ell, -b)} (x) \Big) \]
:
\[ \varphi(x) = \Big( \sum_{k=0}^{|b|-1} \chi_{(0,k)} (x) \qquad \sum_{\ell=1}^{a} \chi_{(-\ell, -b)} (x) \Big) \]
In view of corollary 11.2, computing $\beta \varphi (m \mathop {\otimes } r)$![]() , for $r \in R$
, for $r \in R$![]() a homogeneous element of degree $\rho$
a homogeneous element of degree $\rho$![]() , results in a telescoping sum simplifying to $m \mathop {\otimes } r - \chi _{-\rho } (m \mathop {\otimes } r)$
, results in a telescoping sum simplifying to $m \mathop {\otimes } r - \chi _{-\rho } (m \mathop {\otimes } r)$![]() . But $\chi _{-\rho } (m \mathop {\otimes } r) = mr \mathop {\otimes } 1$
. But $\chi _{-\rho } (m \mathop {\otimes } r) = mr \mathop {\otimes } 1$![]() by lemma 11.3 whence $\chi _{-\rho } (m \mathop {\otimes } r) = \sigma \gamma (m \mathop {\otimes } r)$
by lemma 11.3 whence $\chi _{-\rho } (m \mathop {\otimes } r) = \sigma \gamma (m \mathop {\otimes } r)$![]() so $\beta \varphi + \sigma \gamma = \mathrm {id}$
so $\beta \varphi + \sigma \gamma = \mathrm {id}$![]() as required.
as required.
Proof of proposition 12.1. The map $\kappa$![]() is a quasi-isomorphism if and only if its mapping cone is acyclic. But this mapping cone is precisely the totalization of the double complex (12.2). As it is concentrated in a finite vertical strip, and as its rows are acyclic by lemma 12.2, the totalization is acyclic by standard results for double complexes.
is a quasi-isomorphism if and only if its mapping cone is acyclic. But this mapping cone is precisely the totalization of the double complex (12.2). As it is concentrated in a finite vertical strip, and as its rows are acyclic by lemma 12.2, the totalization is acyclic by standard results for double complexes.
13. The Mather trick
Let $C$![]() be a chain complex of $R$
be a chain complex of $R$![]() -modules, and let $D$
-modules, and let $D$![]() be a chain complex of $R_{(0,0)}$
be a chain complex of $R_{(0,0)}$![]() -modules. Suppose we have $R_{(0,0)}$
-modules. Suppose we have $R_{(0,0)}$![]() -linear chain maps $\alpha \colon C \longrightarrow D$
-linear chain maps $\alpha \colon C \longrightarrow D$![]() and $\beta \colon D \longrightarrow C$
and $\beta \colon D \longrightarrow C$![]() and a chain homotopy $H \colon \mathrm {id}_C \simeq \beta \alpha$
and a chain homotopy $H \colon \mathrm {id}_C \simeq \beta \alpha$![]() such that $dH+Hd=\beta \alpha -\mathrm {id}_C$
such that $dH+Hd=\beta \alpha -\mathrm {id}_C$![]() . A calculation shows:
. A calculation shows:
Lemma 13.1 The matrix

where we abbreviate
defines a chain map of algebraic tori
Theorem 13.2 Mather trick
If the map $\alpha$![]() is a quasi-isomorphism, then $C$
is a quasi-isomorphism, then $C$![]() is quasi-isomorphic to ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$
is quasi-isomorphic to ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$![]() . More precisely, the maps
. More precisely, the maps
are quasi-isomorphism.
Proof. The map $\kappa$![]() is a quasi-isomorphism by lemma 12.1. The map $\lambda$
is a quasi-isomorphism by lemma 12.1. The map $\lambda$![]() , defined in lemma 13.1, is a quasi-isomorphism if $\alpha$
, defined in lemma 13.1, is a quasi-isomorphism if $\alpha$![]() is since the representing matrix of $\lambda$
is since the representing matrix of $\lambda$![]() is lower triangular with diagonal terms $\alpha ^*$
is lower triangular with diagonal terms $\alpha ^*$![]() . Note that $\alpha ^* = \alpha \mathop {\otimes } \mathrm {id}_R$
. Note that $\alpha ^* = \alpha \mathop {\otimes } \mathrm {id}_R$![]() is a quasi-isomorphism since $R$
is a quasi-isomorphism since $R$![]() is strongly graded and hence is a projective $R_{(0,0)}$
is strongly graded and hence is a projective $R_{(0,0)}$![]() -module.
-module.
14. Novikov homology
Let $K$![]() be a $\mathbb {Z}^2$
be a $\mathbb {Z}^2$![]() -graded $R$
-graded $R$![]() -module, with $R$
-module, with $R$![]() a $\mathbb {Z}^2$
a $\mathbb {Z}^2$![]() -graded ring as usual. In analogy to (2.1), we can define
-graded ring as usual. In analogy to (2.1), we can define
which is an $R_*[x,x^{-1}](\kern -1.7pt ( {y})\kern -1.7pt )$![]() -module in a natural way; similarly, we can define
-module in a natural way; similarly, we can define
which is an $R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() -module in a natural way; and so on.
-module in a natural way; and so on.
For $R$![]() -modules of the form $K = M \mathop {\otimes }_{R_{(0,0)}} R$
-modules of the form $K = M \mathop {\otimes }_{R_{(0,0)}} R$![]() , with $M$
, with $M$![]() an $R_{(0,0)}$
an $R_{(0,0)}$![]() -module, these constructions are close to the usual induction functors; for example:
-module, these constructions are close to the usual induction functors; for example:
Proposition 14.1 Let $M$![]() be a right $R_{(0,0)}$
be a right $R_{(0,0)}$![]() -module. There is a natural map
-module. There is a natural map

which is an isomorphism if $M$![]() is finitely presented.
is finitely presented.
Proof. This can be verified by standard techniques: establish the result for $M = R_{(0,0)}$![]() first (in which case it is trivial),��� extend to the case $M = R_{(0,0)}^n$
first (in which case it is trivial),��� extend to the case $M = R_{(0,0)}^n$![]() and then treat the general case using a finite presentation of $M$
and then treat the general case using a finite presentation of $M$![]() .
.
From now on, assume that $C$![]() is a bounded below complex of finitely generated projective $R$
is a bounded below complex of finitely generated projective $R$![]() -modules which is $R_{(0,0)}$
-modules which is $R_{(0,0)}$![]() -finitely dominated. Thus, we choose, once and for all, a bounded complex of finitely generated projective $R_{(0,0)}$
-finitely dominated. Thus, we choose, once and for all, a bounded complex of finitely generated projective $R_{(0,0)}$![]() -modules $D$
-modules $D$![]() and mutually inverse chain homotopy equivalences $\alpha \colon C \longrightarrow D$
and mutually inverse chain homotopy equivalences $\alpha \colon C \longrightarrow D$![]() and $\beta \colon D \longrightarrow C$
and $\beta \colon D \longrightarrow C$![]() , and a chain homotopy $H \colon \mathrm {id}_C \simeq \beta \alpha$
, and a chain homotopy $H \colon \mathrm {id}_C \simeq \beta \alpha$![]() so that $dH+Hd = \beta \alpha - \mathrm {id}_C$
so that $dH+Hd = \beta \alpha - \mathrm {id}_C$![]() .
.
The Mather trick 13.2 guarantees that $C$![]() and ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$
and ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$![]() are quasi-isomorphic; as both $R$
are quasi-isomorphic; as both $R$![]() -module complexes are bounded below and consist of projective $R$
-module complexes are bounded below and consist of projective $R$![]() -modules, they are in fact chain homotopy equivalent.
-modules, they are in fact chain homotopy equivalent.
Lemma 14.2 The chain complex $C \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() is contractible.
is contractible.
Proof. By the previous remarks, it is enough to show that the chain complex ${\mathfrak {T}({{{\alpha },{\beta };{H}}})} \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() is acyclic. Recall that ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$
is acyclic. Recall that ${\mathfrak {T}({{{\alpha },{\beta };{H}}})}$![]() is obtained from the diagram $T (\alpha, \beta, H)$
is obtained from the diagram $T (\alpha, \beta, H)$![]() by a totalization process, which commutes with induction. Thus, we can realize ${\mathfrak {T}({{{\alpha },{\beta };{H}}})} \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$
by a totalization process, which commutes with induction. Thus, we can realize ${\mathfrak {T}({{{\alpha },{\beta };{H}}})} \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() by totalizing the following diagram:
by totalizing the following diagram:

(We have used implicitly that the two functors $\,\textrm {-} \, \mathop {\otimes }_{R_{(0,0)}} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() and $\,\textrm {-} \, \mathop {\otimes }_{R_{(0,0)}} R \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$
and $\,\textrm {-} \, \mathop {\otimes }_{R_{(0,0)}} R \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() are naturally isomorphic.) By lemma
are naturally isomorphic.) By lemma
, we can re-write this further as the totalization of the diagram

with maps suitably interpreted. To wit, an element $z$![]() of $D_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$
of $D_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() (in some fixed chain level) has the form $z = \sum _{x,y \geq a} z_{x,y}$
(in some fixed chain level) has the form $z = \sum _{x,y \geq a} z_{x,y}$![]() for some $a \in \mathbb {Z}$
for some $a \in \mathbb {Z}$![]() and certain $z_{x,y} \in D \mathop {\otimes }_{R_{(0,0)}} R_{x,y}$
and certain $z_{x,y} \in D \mathop {\otimes }_{R_{(0,0)}} R_{x,y}$![]() , and
, and
see lemma 11.3; similar formulæ can be written out for the other maps.
The point is that the self-map $\mathrm {id}^*-\alpha ^*\chi _{e_1}\beta ^*$![]() of $D_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$
of $D_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() is an isomorphism with inverse given by the ‘geometric series’
is an isomorphism with inverse given by the ‘geometric series’

This follows immediately from the usual telescoping sum argument, once it is understood that the series actually defines a well-defined self-map of $D_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() . But this is the case because $\alpha ^* \chi _{e_1} \beta ^*$
. But this is the case because $\alpha ^* \chi _{e_1} \beta ^*$![]() maps an element of degree $(x,y)$
maps an element of degree $(x,y)$![]() to an element of degree $(x+1,y)$
to an element of degree $(x+1,y)$![]() .
.
It is now a matter of computation to verify that the matrix

almost defines a contraction of the totalization of (14.1), in the sense that $dp + pd$![]() is an automorphism $q$
is an automorphism $q$![]() (in each chain level)—in fact, $q$
(in each chain level)—in fact, $q$![]() is given by a triagonal matrix with identity diagonal entries—where $d$
is given by a triagonal matrix with identity diagonal entries—where $d$![]() denotes the boundary map of the totalization. It follows that $q^{-1} p$
denotes the boundary map of the totalization. It follows that $q^{-1} p$![]() is a chain contraction as required.
is a chain contraction as required.
Lemma 14.3 The complex $C \mathop {\otimes }_{R} R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$![]() is contractible.
is contractible.
Proof. This is shown just like the previous lemma. It is enough to demonstrate that the chain complex ${\mathfrak {T}({{{\alpha },{\beta };{H}}})} \mathop {\otimes }_{R} R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$![]() is acyclic; this complex can be written, using a variant of lemma 14.1, as the totalization of the following diagram:
is acyclic; this complex can be written, using a variant of lemma 14.1, as the totalization of the following diagram:

The self-map $\mathrm {id}^*-\alpha ^*\chi _{e_1}\beta ^*$![]() of $D_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$
of $D_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$![]() is an isomorphism with inverse $P(z) = \sum _{k \geq 0} \big ( \alpha ^* \chi _{e_1} \beta ^* \big )^{k} (z)$
is an isomorphism with inverse $P(z) = \sum _{k \geq 0} \big ( \alpha ^* \chi _{e_1} \beta ^* \big )^{k} (z)$![]() ; the matrix $p$
; the matrix $p$![]() from (14.2) is such that $dp + pd$
from (14.2) is such that $dp + pd$![]() is an automorphism $q$
is an automorphism $q$![]() (in each chain level), where $d$
(in each chain level), where $d$![]() denotes the boundary map of the totalization. Consequently, $q^{-1} p$
denotes the boundary map of the totalization. Consequently, $q^{-1} p$![]() is a chain contraction.
is a chain contraction.
Proof of only if in theorem 2.1. By lemma 14.2, the complex $C \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x,y})\kern -1.7pt )$![]() is acyclic. Replacing $R$
is acyclic. Replacing $R$![]() by the strongly $\mathbb {Z}^2$
by the strongly $\mathbb {Z}^2$![]() -graded ring $\bar R$
-graded ring $\bar R$![]() with $\bar R_{(x,y)} = R_{(-x,y)}$
with $\bar R_{(x,y)} = R_{(-x,y)}$![]() , effectively substituting $x^{-1}$
, effectively substituting $x^{-1}$![]() for $x$
for $x$![]() , gives that $C \mathop {\otimes }_{\bar R} \bar R_*(\kern -1.7pt ( {x,y})\kern -1.7pt ) = C \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x^{-1},y})\kern -1.7pt )$
, gives that $C \mathop {\otimes }_{\bar R} \bar R_*(\kern -1.7pt ( {x,y})\kern -1.7pt ) = C \mathop {\otimes }_{R} R_*(\kern -1.7pt ( {x^{-1},y})\kern -1.7pt )$![]() is acyclic. The remaining cases of (1.1b) are dealt with by similar re-indexing.
is acyclic. The remaining cases of (1.1b) are dealt with by similar re-indexing.
By lemma 14.3, the complex $C \mathop {\otimes }_{R} R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt )$![]() is acyclic. Replacing $R$
is acyclic. Replacing $R$![]() by the strongly $\mathbb {Z}^2$
by the strongly $\mathbb {Z}^2$![]() -graded ring $\bar R$
-graded ring $\bar R$![]() with $\bar R_{(x,y)} = R_{(-x,y)}$
with $\bar R_{(x,y)} = R_{(-x,y)}$![]() gives that $C \mathop {\otimes }_{\bar R} \bar R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt ) = C \mathop {\otimes }_{R} R_*[y,y^{-1}](\kern -1.7pt ( {x^{-1}})\kern -1.7pt )$
gives that $C \mathop {\otimes }_{\bar R} \bar R_*[y,y^{-1}](\kern -1.7pt ( {x})\kern -1.7pt ) = C \mathop {\otimes }_{R} R_*[y,y^{-1}](\kern -1.7pt ( {x^{-1}})\kern -1.7pt )$![]() is acyclic. The other cases of (1.1a) are dealt with by using $\bar R_{(x,y)} = R_{(y,x)}$
is acyclic. The other cases of (1.1a) are dealt with by using $\bar R_{(x,y)} = R_{(y,x)}$![]() and $\bar R_{(x,y)} = R_{(-y,x)}$
and $\bar R_{(x,y)} = R_{(-y,x)}$![]() , respectively.
, respectively.