Published online by Cambridge University Press: 27 January 2022
Erdős space
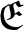 $\mathfrak {E}$
and complete Erdős space
$\mathfrak {E}$
and complete Erdős space
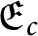 $\mathfrak {E}_{c}$
have been previously shown to have topological characterizations. In this paper, we provide a topological characterization of the topological space
$\mathfrak {E}_{c}$
have been previously shown to have topological characterizations. In this paper, we provide a topological characterization of the topological space
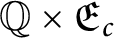 $\mathbb {Q}\times \mathfrak {E}_{c}$
, where
$\mathbb {Q}\times \mathfrak {E}_{c}$
, where
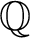 $\mathbb {Q}$
is the space of rational numbers. As a corollary, we show that the Vietoris hyperspace of finite sets
$\mathbb {Q}$
is the space of rational numbers. As a corollary, we show that the Vietoris hyperspace of finite sets
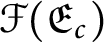 $\mathcal {F}(\mathfrak {E}_{c})$
is homeomorphic to
$\mathcal {F}(\mathfrak {E}_{c})$
is homeomorphic to
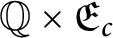 $\mathbb {Q}\times \mathfrak {E}_{c}$
. We also characterize the factors of
$\mathbb {Q}\times \mathfrak {E}_{c}$
. We also characterize the factors of
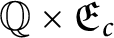 $\mathbb {Q}\times \mathfrak {E}_{c}$
. An interesting open question that is left open is whether
$\mathbb {Q}\times \mathfrak {E}_{c}$
. An interesting open question that is left open is whether
 $\sigma \mathfrak {E}_{c}^{\omega }$
, the
$\sigma \mathfrak {E}_{c}^{\omega }$
, the
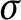 $\sigma $
-product of countably many copies of
$\sigma $
-product of countably many copies of
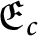 $\mathfrak {E}_{c}$
, is homeomorphic to
$\mathfrak {E}_{c}$
, is homeomorphic to
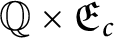 $\mathbb {Q}\times \mathfrak {E}_{c}$
.
$\mathbb {Q}\times \mathfrak {E}_{c}$
.
This work is part of the doctoral work of the second-named author at UNAM, Mexico City, under the direction of the first-named author. This research was supported by a CONACyT doctoral scholarship with number 696239.