Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gan, Longzhi
Li, Wen
Hanzelka, Miroslav
Ma, Qianli
Albert, Jay M.
and
Artemyev, Anton V.
2023.
Electron precipitation caused by intense whistler-mode waves: combined effects of anomalous scattering and phase bunching.
Frontiers in Astronomy and Space Sciences,
Vol. 10,
Issue. ,
Lukin, A. S.
Artemyev, A. V.
Zhang, X.‐J.
Vasko, I. Y.
and
Petrukovich, A. A.
2023.
On the Role of Kinetic Alfven Waves in the Magnetosheath Ion Thermalization Around the Night‐Side Magnetopause.
Journal of Geophysical Research: Space Physics,
Vol. 128,
Issue. 5,
Tonoian, David S.
Shi, Xiaofei
Artemyev, Anton V.
Zhang, Xiao-Jia
and
Angelopoulos, Vassilis
2023.
Electron resonant interaction with whistler-mode waves around the Earth's bow shock. II: The mapping technique.
Physics of Plasmas,
Vol. 30,
Issue. 12,
Vargas, Alexander D.
Artemyev, Anton V.
Zhang, Xiao-Jia
and
Albert, Jay
2023.
Role of “positive phase bunching” effect for long-term electron flux dynamics due to resonances with whistler-mode waves.
Physics of Plasmas,
Vol. 30,
Issue. 11,
Shi, Xiaofei
Tonoian, David S.
Artemyev, Anton V.
Zhang, Xiao-Jia
and
Angelopoulos, Vassilis
2023.
Electron resonant interaction with whistler-mode waves around the Earth's bow shock I: The probabilistic approach.
Physics of Plasmas,
Vol. 30,
Issue. 12,
Tsai, Ethan
Artemyev, Anton
Ma, Qianli
Mourenas, Didier
Agapitov, Oleksiy
Zhang, Xiao‐Jia
and
Angelopoulos, Vassilis
2024.
Key Factors Determining Nightside Energetic Electron Losses Driven by Whistler‐Mode Waves.
Journal of Geophysical Research: Space Physics,
Vol. 129,
Issue. 3,
Lukin, A. S.
Artemyev, A. V.
Zhang, X.‐J.
Allanson, O.
and
Tao, X.
2024.
On the Two Approaches to Incorporate Wave‐Particle Resonant Effects Into Global Test Particle Simulations.
Journal of Geophysical Research: Space Physics,
Vol. 129,
Issue. 2,
Artemyev, Anton
An, Xin
Vainchtein, Dmitri
Rankin, Robert
Zhou, Xuzhi
Li, Li
and
Zhang, Xiao‐Jia
2024.
Electron Resonant Interaction With Coherent ULF Waves: Hamiltonian Approach.
Journal of Geophysical Research: Space Physics,
Vol. 129,
Issue. 4,
Kondrashov, D.
Drozdov, A. Y.
and
Shprits, Y.
2024.
Nonlinear Wave‐Particle Interaction Effects on Radiation Belt Electron Dynamics in 9 October 2012 Storm.
Journal of Geophysical Research: Space Physics,
Vol. 129,
Issue. 9,
Ling, W.
Jing, C.
Wan, J.
Mao, A.
Xiao, Q.
Guan, J.
Cheng, J.
Liu, C.
and
E, P.
2024.
Design and construction of the near-earth space plasma simulation system of the Space Plasma Environment Research Facility.
Journal of Plasma Physics,
Vol. 90,
Issue. 1,
Allanson, Oliver
Ma, Donglai
Osmane, Adnane
Albert, Jay M.
Bortnik, Jacob
Watt, Clare E. J.
Chapman, Sandra C.
Spencer, Joseph
Ratliff, Daniel J.
Meredith, Nigel P.
Elsden, Thomas
Neukirch, Thomas
Hartley, David P.
Black, Rachel
Watkins, Nicholas W.
and
Elvidge, Sean
2024.
The challenge to understand the zoo of particle transport regimes during resonant wave-particle interactions for given survey-mode wave spectra.
Frontiers in Astronomy and Space Sciences,
Vol. 11,
Issue. ,
Artemyev, A. V.
Mourenas, D.
Zhang, X.-J.
Agapitov, O.
Neishtadt, A. I.
Vainchtein, D. L.
Vasiliev, A. A.
Zhang, X.
Ma, Q.
Bortnik, J.
and
Krasnoselskikh, V. V.
2025.
Nonlinear Resonant Interactions of Radiation Belt Electrons with Intense Whistler-Mode Waves.
Space Science Reviews,
Vol. 221,
Issue. 1,
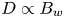 , in contrast to the quasi-linear diffusion scaling $D_{QL}\propto B_w^2$
, in contrast to the quasi-linear diffusion scaling $D_{QL}\propto B_w^2$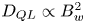 . Using observed wave amplitude distributions, we demonstrate that the quasi-linear diffusion model significantly overestimates electron scattering by incoherent, but intense whistler-mode waves. We discuss the results obtained in the context of simulations of long-term electron flux dynamics in space plasma systems.
. Using observed wave amplitude distributions, we demonstrate that the quasi-linear diffusion model significantly overestimates electron scattering by incoherent, but intense whistler-mode waves. We discuss the results obtained in the context of simulations of long-term electron flux dynamics in space plasma systems.