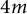1 Introduction
Let
![]() $(X, \omega )$
be a symplectic manifold. A submanifold
$(X, \omega )$
be a symplectic manifold. A submanifold
![]() $L\subset X$
is called Lagrangian if
$L\subset X$
is called Lagrangian if
![]() $\omega |_L\equiv 0$
and
$\omega |_L\equiv 0$
and
![]() $\dim L=\frac {1}{2}\dim X$
. See the textbook and papers [Reference Audin, Lalonde and Polterovich1, Reference McDuff and Salamon12, Reference Weinstein16] for basic properties, general backgrounds, and developments in the study of Lagrangian submanifolds. One question is to understand topological obstructions of embedding manifolds into symplectic manifolds as Lagrangian submanifolds, which has been intensively studied (cf. [Reference Audin, Lalonde and Polterovich1, Reference Biran3, Reference Biran and Cieliebak4, Reference Cieliebak and Mohnke6, Reference Kharlamov11, Reference Seidel13, Reference Viterbo14, Reference Welschinger17, Reference Zhang18]).
$\dim L=\frac {1}{2}\dim X$
. See the textbook and papers [Reference Audin, Lalonde and Polterovich1, Reference McDuff and Salamon12, Reference Weinstein16] for basic properties, general backgrounds, and developments in the study of Lagrangian submanifolds. One question is to understand topological obstructions of embedding manifolds into symplectic manifolds as Lagrangian submanifolds, which has been intensively studied (cf. [Reference Audin, Lalonde and Polterovich1, Reference Biran3, Reference Biran and Cieliebak4, Reference Cieliebak and Mohnke6, Reference Kharlamov11, Reference Seidel13, Reference Viterbo14, Reference Welschinger17, Reference Zhang18]).
In [Reference Zhang19], a phenomenon has been noticed while searching for obstructions of the existence of positive scalar curvature Riemannian metrics on symplectic 4-manifolds. More precisely, Theorem 2.3 of [Reference Zhang19] should be interpreted as a simple topological consequence of the presence of certain Lagrangian submanifolds in symplectic 4-manifolds, and this topological constraint is a well-known obstruction of positive scalar curvature metrics by quoting Taubes’ theorem on the Seiberg–Witten invariant. The goal of this paper is to reformulate this result in a more suitable context, and to generalize it to the case of
![]() $4m$
-dimensional symplectic manifolds, which might have some independent interests.
$4m$
-dimensional symplectic manifolds, which might have some independent interests.
If X is a compact oriented
![]() $4m$
-dimensional manifold, the intersection pairing is the symmetric nondegenerated quadratic form
$4m$
-dimensional manifold, the intersection pairing is the symmetric nondegenerated quadratic form
which is represented by the diagonal matrix diag
![]() $(1,\ldots ,1,-1,\ldots ,-1)$
under a suitable basis. Denote
$(1,\ldots ,1,-1,\ldots ,-1)$
under a suitable basis. Denote
![]() $b_{2m}^+(X)$
the number of plus ones in the matrix, and
$b_{2m}^+(X)$
the number of plus ones in the matrix, and
![]() $b_{2m}^-(X)$
the number of minus ones. Both of
$b_{2m}^-(X)$
the number of minus ones. Both of
![]() $b_{2m}^\pm (X)$
are topological invariants, and the
$b_{2m}^\pm (X)$
are topological invariants, and the
![]() $2m$
-Betti number
$2m$
-Betti number
![]() $b_{2m}(X)=b_{2m}^+(X)+b_{2m}^-(X)$
. If X admits a symplectic form
$b_{2m}(X)=b_{2m}^+(X)+b_{2m}^-(X)$
. If X admits a symplectic form
![]() $\omega $
, then
$\omega $
, then
![]() $[\omega ^m]\in H^{2m}(X, \mathbb {R})$
, and
$[\omega ^m]\in H^{2m}(X, \mathbb {R})$
, and
which implies
The main theorem asserts that
![]() $ b_{2m}^\pm (X)$
provides some constraints of the existence of certain Lagrangian submanifolds.
$ b_{2m}^\pm (X)$
provides some constraints of the existence of certain Lagrangian submanifolds.
Theorem 1.1 Let
![]() $(X, \omega )$
be a compact symplectic manifold of dimension
$(X, \omega )$
be a compact symplectic manifold of dimension
![]() $4m$
,
$4m$
,
![]() $m\geq 1$
,
$m\geq 1$
,
![]() $ m\in \mathbb {Z}$
, and let L be an orientable Lagrangian submanifold in X.
$ m\in \mathbb {Z}$
, and let L be an orientable Lagrangian submanifold in X.
-
(i) If the Euler characteristic
 $\chi (L)$
of L satisfies
$\chi (L)$
of L satisfies  $$ \begin{align*}(-1)^{m}\chi(L)> 0, \ \ \ \ \ \ \ {then} \ \ \ \ \ \ \ \ \ b_{2m}^+(X)\geq 2.\end{align*} $$
$$ \begin{align*}(-1)^{m}\chi(L)> 0, \ \ \ \ \ \ \ {then} \ \ \ \ \ \ \ \ \ b_{2m}^+(X)\geq 2.\end{align*} $$
-
(ii) If L represents a nontrivial homology class, i.e.,
 $$ \begin{align*}0\neq [L]\in H_{2m}(X, \mathbb{R}), \ \ \ {and} \ \ \ \chi(L) =0,\end{align*} $$
$$ \begin{align*}0\neq [L]\in H_{2m}(X, \mathbb{R}), \ \ \ {and} \ \ \ \chi(L) =0,\end{align*} $$
 $$ \begin{align*}{then} \ \ \ \ \ \ \ \ \ b_{2m}^+(X)\geq 2, \ \ \ \ {and} \ \ \ \ \ b_{2m}^-(X)\geq1.\end{align*} $$
$$ \begin{align*}{then} \ \ \ \ \ \ \ \ \ b_{2m}^+(X)\geq 2, \ \ \ \ {and} \ \ \ \ \ b_{2m}^-(X)\geq1.\end{align*} $$
-
(iii) If
 $$ \begin{align*}(-1)^{m}\chi(L)< 0, \ \ \ \ \ \ \ {then} \ \ \ \ \ \ \ \ \ b_{2m}^-(X)\geq 1.\end{align*} $$
$$ \begin{align*}(-1)^{m}\chi(L)< 0, \ \ \ \ \ \ \ {then} \ \ \ \ \ \ \ \ \ b_{2m}^-(X)\geq 1.\end{align*} $$
-
(iv) If the
 $2m$
-Betti number
$2m$
-Betti number
 $b_{2m}(X)=1$
, then
$b_{2m}(X)=1$
, then  $$ \begin{align*}\chi(L)=0, \ \ \ {and} \ \ \ 0= [L]\in H_{2m}(X, \mathbb{R}).\end{align*} $$
$$ \begin{align*}\chi(L)=0, \ \ \ {and} \ \ \ 0= [L]\in H_{2m}(X, \mathbb{R}).\end{align*} $$
When X is four-dimensional, this theorem is known to experts (Proposition 2.17 of [Reference Zhang18]), and (i) and (ii) have appeared in the proof of Theorem 2.3 of [Reference Zhang19]. There are some immediate applications of Theorem 1.1 that are surely known to experts (cf. [Reference Biran3, Reference Biran and Cieliebak4, Reference Cieliebak and Mohnke6, Reference Eliashberg, Givental and Hofer7, Reference Seidel13, Reference Viterbo14]):
-
(i) Neither
 $\mathbb {CP}^{m}$
nor
$\mathbb {CP}^{m}$
nor
 $S^{2m}$
can be embedded in
$S^{2m}$
can be embedded in
 $\mathbb {CP}^{2m}$
as a Lagrangian submanifold.
$\mathbb {CP}^{2m}$
as a Lagrangian submanifold. -
(ii) Only possible orientable Lagrangian submanifolds in
 $\mathbb {CP}^{2}$
are 2-tori
$\mathbb {CP}^{2}$
are 2-tori
 $T^2$
. Orientable Lagrangian submanifolds in
$T^2$
. Orientable Lagrangian submanifolds in
 $\mathbb {CP}^{1}\times \mathbb {CP}^{1}$
are either tori
$\mathbb {CP}^{1}\times \mathbb {CP}^{1}$
are either tori
 $T^2$
or spheres
$T^2$
or spheres
 $S^2$
by
$S^2$
by
 $ b_2^+(\mathbb {CP}^{1}\times \mathbb {CP}^{1})=1$
.
$ b_2^+(\mathbb {CP}^{1}\times \mathbb {CP}^{1})=1$
. -
(iii) There is no Lagrangian sphere
 $S^{4m}$
in
$S^{4m}$
in
 $\mathbb {CP}^{4m-1}\times \Sigma $
, where
$\mathbb {CP}^{4m-1}\times \Sigma $
, where
 $\Sigma $
is a compact Riemann surface, since
$\Sigma $
is a compact Riemann surface, since
 $ b_{4m}^+(\mathbb {CP}^{4m-1}\times \Sigma )=1$
.
$ b_{4m}^+(\mathbb {CP}^{4m-1}\times \Sigma )=1$
.
Theorems in [Reference Cieliebak and Mohnke6, Reference Eliashberg, Givental and Hofer7, Reference Viterbo14] assert that Riemannian manifolds with negative sectional curvature do not admit any Lagrangian embedding into uniruled symplectic manifolds. As a corollary, we show certain constraints of the existence of special metrics on Lagrangian submanifolds.
Corollary 1.2 Let
![]() $(X, \omega )$
be a compact symplectic
$(X, \omega )$
be a compact symplectic
![]() $4m$
-dimensional manifold with
$4m$
-dimensional manifold with
-
(i) A compact orientable
 $2m$
-manifold Y admitting a hyperbolic metric, i.e., a Riemannian metric with sectional curvature
$2m$
-manifold Y admitting a hyperbolic metric, i.e., a Riemannian metric with sectional curvature
 $-1$
, cannot be embedded into X as a Lagrangian submanifold.
$-1$
, cannot be embedded into X as a Lagrangian submanifold. -
(ii) If
 $m=2$
, and L is an orientable Lagrangian submanifold in X admitting an Einstein metric g, i.e., the Ricci tensor for a constant
$m=2$
, and L is an orientable Lagrangian submanifold in X admitting an Einstein metric g, i.e., the Ricci tensor for a constant $$ \begin{align*}\mathrm{ Ric}(g)=\lambda g\end{align*} $$
$$ \begin{align*}\mathrm{ Ric}(g)=\lambda g\end{align*} $$
 $\lambda \in \mathbb {R}$
, then a finite covering of L is the 4-torus
$\lambda \in \mathbb {R}$
, then a finite covering of L is the 4-torus
 $T^4$
.
$T^4$
.
We remark that the condition
![]() $b_{2m}^+(X)=1$
is necessary for Corollary 1.2(ii). For example, any symplectic 4-manifold
$b_{2m}^+(X)=1$
is necessary for Corollary 1.2(ii). For example, any symplectic 4-manifold
![]() $(X, \omega )$
admitting an Einstein metric could be diagonally embedded into the symplectic 8-manifold
$(X, \omega )$
admitting an Einstein metric could be diagonally embedded into the symplectic 8-manifold
![]() $(X, \omega )\times (X, -\omega )$
as a Lagrangian.
$(X, \omega )\times (X, -\omega )$
as a Lagrangian.
We prove Theorem 1.1 and Corollary 1.2 by using classical differential topology/geometry techniques in the next section.
2 Proofs
First, we recall basic relevant facts, and provide the detailed proofs for the completeness. Let
![]() $(X, \omega )$
be a compact symplectic
$(X, \omega )$
be a compact symplectic
![]() $4m$
-dimensional manifold, and let L be an orientable Lagrangian submanifold in X. The symplectic form
$4m$
-dimensional manifold, and let L be an orientable Lagrangian submanifold in X. The symplectic form
![]() $\omega $
induces a natural orientation of X, i.e., given by
$\omega $
induces a natural orientation of X, i.e., given by
![]() $\omega ^{2m}$
. We fix an orientation on L.
$\omega ^{2m}$
. We fix an orientation on L.
Lemma 2.1
where
![]() $[L]^2$
is the self-intersection number of L in X. Consequently, if
$[L]^2$
is the self-intersection number of L in X. Consequently, if
![]() $\chi (L) \neq 0$
, then
$\chi (L) \neq 0$
, then
![]() $[L]^2\neq 0$
, and
$[L]^2\neq 0$
, and
Proof The Weinstein neighborhood theorem (cf. [Reference Weinstein16, Reference McDuff and Salamon12]) asserts that there is a tubular neighborhood U of L in X diffeomorphic to a neighborhood of the zero section in the cotangent bundle
![]() $T^*L$
, and the restriction of
$T^*L$
, and the restriction of
![]() $\omega $
on U is the canonical symplectic form on
$\omega $
on U is the canonical symplectic form on
![]() $T^*L$
under the identification. More precisely, if
$T^*L$
under the identification. More precisely, if
![]() $x_1, \ldots , x_{2m}$
are local coordinates on L, then the symplectic form
$x_1, \ldots , x_{2m}$
are local coordinates on L, then the symplectic form
 $$ \begin{align*}\omega=\sum_{i=1}^{2m} dx_i\wedge dp_i,\end{align*} $$
$$ \begin{align*}\omega=\sum_{i=1}^{2m} dx_i\wedge dp_i,\end{align*} $$
where
![]() $p_1, \ldots , p_{2m}$
are coordinates on fibers induced by
$p_1, \ldots , p_{2m}$
are coordinates on fibers induced by
![]() $dx_j$
, i.e., any 1-form
$dx_j$
, i.e., any 1-form
![]() $\sum \limits _{i=1}^{2m} p_idx_i$
is given by the numbers
$\sum \limits _{i=1}^{2m} p_idx_i$
is given by the numbers
![]() $p_j$
. We regard L as the zero section of
$p_j$
. We regard L as the zero section of
![]() $T^*L$
, and assume that
$T^*L$
, and assume that
![]() $dx_1\wedge \cdots \wedge dx_{2m}$
gives the orientation of L.
$dx_1\wedge \cdots \wedge dx_{2m}$
gives the orientation of L.
If we denote
![]() $\varpi _i= dx_i\wedge dp_i$
,
$\varpi _i= dx_i\wedge dp_i$
,
![]() $i=1, \ldots , 2m $
, then the algebraic relationships are
$i=1, \ldots , 2m $
, then the algebraic relationships are
The orientation inherited from the symplectic manifold is given by
The orientation on L induces an orientation on
![]() $T^*L$
given by
$T^*L$
given by
If
![]() $L'$
is a small deformation of L intersecting with L transversally, the intersection number
$L'$
is a small deformation of L intersecting with L transversally, the intersection number
![]() $L\cdot L'$
with respect to the orientation given by
$L\cdot L'$
with respect to the orientation given by
![]() $\omega ^{2m}$
is the self-intersection number of L in X, i.e.,
$\omega ^{2m}$
is the self-intersection number of L in X, i.e.,
![]() $L\cdot L'=[L]^2$
. The Euler characteristic of L equals to the intersection number
$L\cdot L'=[L]^2$
. The Euler characteristic of L equals to the intersection number
![]() $L\tilde {\cdot } L'$
with respect to the orientation defined by
$L\tilde {\cdot } L'$
with respect to the orientation defined by
![]() $dx_1\wedge \cdots \wedge dx_{2m}\wedge dp_1\wedge \cdots \wedge dp_{2m}$
(cf. [Reference Bott and Tu5]), i.e.,
$dx_1\wedge \cdots \wedge dx_{2m}\wedge dp_1\wedge \cdots \wedge dp_{2m}$
(cf. [Reference Bott and Tu5]), i.e.,
![]() $L\tilde {\cdot } L'= \chi (L)$
, where we identify the tangent bundle
$L\tilde {\cdot } L'= \chi (L)$
, where we identify the tangent bundle
![]() $TL$
with
$TL$
with
![]() $T^*L$
via a Riemannian metric. Since
$T^*L$
via a Riemannian metric. Since
![]() $ L\cdot L'=(-1)^mL\tilde {\cdot } L' $
, we obtain
$ L\cdot L'=(-1)^mL\tilde {\cdot } L' $
, we obtain
![]() $ [L]^2= (-1)^m \chi (L)$
.
$ [L]^2= (-1)^m \chi (L)$
.
There are analogous formulae in more general contexts (see, e.g., [Reference Webster15]).
Let g be a Riemannian metric compatible with
![]() $\omega $
, i.e.,
$\omega $
, i.e.,
![]() $g(\cdot , \cdot )=\omega (\cdot , J \cdot )$
for an almost complex structure J compatible with
$g(\cdot , \cdot )=\omega (\cdot , J \cdot )$
for an almost complex structure J compatible with
![]() $\omega $
, and let
$\omega $
, and let
![]() $\ast $
be the Hodge star operator of g. The volume form
$\ast $
be the Hodge star operator of g. The volume form
![]() $dv_g$
of g is the symplectic volume form, i.e.,
$dv_g$
of g is the symplectic volume form, i.e.,
![]() $dv_g= \frac {1}{(2m)!}\omega ^{2m} $
. When
$dv_g= \frac {1}{(2m)!}\omega ^{2m} $
. When
![]() $\ast $
acts on
$\ast $
acts on
![]() $\wedge ^{2m}T^*X$
,
$\wedge ^{2m}T^*X$
,
![]() $\ast ^2=$
Id holds.
$\ast ^2=$
Id holds.
![]() $H^{2m}(X, \mathbb {R})$
is isomorphic to the space of harmonic
$H^{2m}(X, \mathbb {R})$
is isomorphic to the space of harmonic
![]() $2m$
-forms by the Hodge theory (cf. [Reference Griffith and Harris8]). Thus,
$2m$
-forms by the Hodge theory (cf. [Reference Griffith and Harris8]). Thus,
![]() $H^{2m}(X, \mathbb {R})$
admits the self-dual/anti-self-dual decomposition
$H^{2m}(X, \mathbb {R})$
admits the self-dual/anti-self-dual decomposition
Note that
![]() $b_{2m}^\pm (X)=\dim \mathcal {H}_{\pm }(X).$
$b_{2m}^\pm (X)=\dim \mathcal {H}_{\pm }(X).$
Lemma 2.2
Proof Since
![]() $d\omega ^m=0$
, we only need to verify that
$d\omega ^m=0$
, we only need to verify that
![]() $\omega ^m$
is self-dual, i.e.,
$\omega ^m$
is self-dual, i.e.,
![]() $\ast \omega ^m=\omega ^m$
, which is a pointwise condition. For any point
$\ast \omega ^m=\omega ^m$
, which is a pointwise condition. For any point
![]() $x\in X$
, we choose coordinates
$x\in X$
, we choose coordinates
![]() $x_1, \ldots , x_{2m},p_1, \ldots , p_{2m}$
on a neighborhood of x such that on the tangent space
$x_1, \ldots , x_{2m},p_1, \ldots , p_{2m}$
on a neighborhood of x such that on the tangent space
![]() $T_xX$
,
$T_xX$
,
 $$ \begin{align*}\omega=\sum_{i=1}^{2m} dx_i\wedge dp_i, \ \ \ \mathrm{and} \ \ \ g=\sum_{i=1}^{2m} (dx_i^2+dp_i^2).\end{align*} $$
$$ \begin{align*}\omega=\sum_{i=1}^{2m} dx_i\wedge dp_i, \ \ \ \mathrm{and} \ \ \ g=\sum_{i=1}^{2m} (dx_i^2+dp_i^2).\end{align*} $$
The calculation is the same as those in the Kähler case (cf. [Reference Griffith and Harris8]) because of the locality. If we still write
![]() $\varpi _i= dx_i\wedge dp_i$
,
$\varpi _i= dx_i\wedge dp_i$
,
![]() $i=1, \ldots , 2m $
, then the volume form
$i=1, \ldots , 2m $
, then the volume form
![]() $dv_g=\varpi _1\wedge \cdots \wedge \varpi _{2m}.$
Denote the multi-index sets
$dv_g=\varpi _1\wedge \cdots \wedge \varpi _{2m}.$
Denote the multi-index sets
![]() $I=\{i_1, \ldots , i_m\}$
,
$I=\{i_1, \ldots , i_m\}$
,
![]() $i_1 < \cdots < i_m$
, and the complement
$i_1 < \cdots < i_m$
, and the complement
![]() $I^c=\{1, \ldots , 2m\}\backslash I$
. Note that
$I^c=\{1, \ldots , 2m\}\backslash I$
. Note that
By
![]() $ \varpi _I\wedge \ast \varpi _I= dv_g= \varpi _I\wedge \varpi _{I^c}$
, we obtain
$ \varpi _I\wedge \ast \varpi _I= dv_g= \varpi _I\wedge \varpi _{I^c}$
, we obtain
![]() $\ast \varpi _I= \varpi _{I^c}$
. Hence,
$\ast \varpi _I= \varpi _{I^c}$
. Hence,
![]() $\ast \omega ^m=\omega ^m$
.
$\ast \omega ^m=\omega ^m$
.
Now, we are ready to prove the results.
Proof (Theorem 1.1)
Note that the assumptions imply
![]() $0\neq [L]\in H_{2m}(X, \mathbb {R})$
in the cases (i)–(iii). If
$0\neq [L]\in H_{2m}(X, \mathbb {R})$
in the cases (i)–(iii). If
![]() $PU(L)\in H^{2m}(X, \mathbb {R})$
is the Poincaré dual of
$PU(L)\in H^{2m}(X, \mathbb {R})$
is the Poincaré dual of
![]() $[L]$
, then
$[L]$
, then
Since
![]() $\int _X \alpha _+\wedge \alpha _- =0$
,
$\int _X \alpha _+\wedge \alpha _- =0$
,
If
![]() $(-1)^m \chi (L) \geq 0$
, then
$(-1)^m \chi (L) \geq 0$
, then
If
![]() $\alpha _+ =0$
, then
$\alpha _+ =0$
, then
![]() $\alpha _-=0$
and
$\alpha _-=0$
and
![]() $PU(L)=0$
, which is a contradiction. Thus,
$PU(L)=0$
, which is a contradiction. Thus,
![]() $\alpha _+\neq 0$
, and
$\alpha _+\neq 0$
, and
Since
![]() $\omega ^m $
and
$\omega ^m $
and
![]() $\alpha _+$
are linearly independent in
$\alpha _+$
are linearly independent in
![]() $\mathcal {H}_{+}(X)$
. Therefore, we obtain
$\mathcal {H}_{+}(X)$
. Therefore, we obtain
![]() $b_{2m}^+(X)\geq 2$
.
$b_{2m}^+(X)\geq 2$
.
If
![]() $\chi (L)=0$
, then
$\chi (L)=0$
, then
Thus,
![]() $\alpha _-\neq 0$
and
$\alpha _-\neq 0$
and
![]() $b_{2m}^-(X)\geq 1$
.
$b_{2m}^-(X)\geq 1$
.
If we assume
![]() $(-1)^m \chi (L) <0$
, then
$(-1)^m \chi (L) <0$
, then
We obtain the conclusion
![]() $b_{2m}^-(X)\geq 1$
.
$b_{2m}^-(X)\geq 1$
.
If
![]() $b_{2m}(X)=1$
, then
$b_{2m}(X)=1$
, then
![]() $b_{2m}^+(X)=1$
,
$b_{2m}^+(X)=1$
,
![]() $b_{2m}^-(X)=0$
, and
$b_{2m}^-(X)=0$
, and
![]() $H^{2m}(X, \mathbb {R})\cong \mathcal {H}_{+}(X)$
. Hence,
$H^{2m}(X, \mathbb {R})\cong \mathcal {H}_{+}(X)$
. Hence,
![]() $\chi (L)=0$
and
$\chi (L)=0$
and
![]() $[L]=0$
.
$[L]=0$
.
Proof (Corollary 1.2)
Let Y be an orientable compact
![]() $2m$
-manifold, and let h be a hyperbolic metric on Y. By the Gauss–Bonnet formula of hyperbolic manifolds (cf. [Reference Hopf9, Reference Kellerhals and Zehrt10]),
$2m$
-manifold, and let h be a hyperbolic metric on Y. By the Gauss–Bonnet formula of hyperbolic manifolds (cf. [Reference Hopf9, Reference Kellerhals and Zehrt10]),
where
![]() $\varepsilon _{2m}>0$
is a constant depending only on m, and
$\varepsilon _{2m}>0$
is a constant depending only on m, and
![]() $\mathrm {Vol}_h(Y)$
is the volume of the hyperbolic metric. Theorem 1.1 implies (i).
$\mathrm {Vol}_h(Y)$
is the volume of the hyperbolic metric. Theorem 1.1 implies (i).
Now, we assume that
![]() $m=2$
. If g is a Riemannian metric on L, then the Gauss–Bonnet–Chern formula for 4-manifolds reads
$m=2$
. If g is a Riemannian metric on L, then the Gauss–Bonnet–Chern formula for 4-manifolds reads
 $$ \begin{align*}\chi(L)= \frac{1}{8\pi^2}\int_{L}\bigg(\frac{R^2}{24}+|W^+|_g^2+|W^-|_g^2-\frac{1}{2}|\mathrm{Ric}^o|_g^2\bigg)dv_g,\end{align*} $$
$$ \begin{align*}\chi(L)= \frac{1}{8\pi^2}\int_{L}\bigg(\frac{R^2}{24}+|W^+|_g^2+|W^-|_g^2-\frac{1}{2}|\mathrm{Ric}^o|_g^2\bigg)dv_g,\end{align*} $$
where R is the scalar curvature,
![]() $W^\pm $
denotes the self-dual/anti-self-dual Weyl curvature of g, and
$W^\pm $
denotes the self-dual/anti-self-dual Weyl curvature of g, and
![]() $\mathrm {Ric}^o=\mathrm {Ric}-\frac {R}{4}g$
is the Einstein tensor (cf. [Reference Besse2]). If g is Einstein, then
$\mathrm {Ric}^o=\mathrm {Ric}-\frac {R}{4}g$
is the Einstein tensor (cf. [Reference Besse2]). If g is Einstein, then
![]() $\mathrm {Ric}^o\equiv 0$
and thus
$\mathrm {Ric}^o\equiv 0$
and thus
![]() $\chi (L) \geq 0$
. By Theorem 1.1, either
$\chi (L) \geq 0$
. By Theorem 1.1, either
![]() $\chi (L)<0$
, or
$\chi (L)<0$
, or
![]() $\chi (L)=0$
and
$\chi (L)=0$
and
![]() $[L]=0$
in
$[L]=0$
in
![]() $H^{4}(X, \mathbb {R})$
since
$H^{4}(X, \mathbb {R})$
since
![]() $b_{4}^+(X)=1 $
. Therefore,
$b_{4}^+(X)=1 $
. Therefore,
![]() $\chi (L)=0$
, which implies that
$\chi (L)=0$
, which implies that
The curvature tensor of g vanishes, i.e., g is a flat metric. Thus, a finite covering is the torus
![]() $T^4$
.
$T^4$
.
A An alternative proof
by Anonymous Referee
Proposition 2.17 of [Reference Zhang18] gives a very simple argument using the light cone lemma (which is a version of the Cauchy–Schwartz inequality) to eventually prove Theorem 1.1(i) and (ii), the harder parts, for
![]() $m = 1$
. In fact, using the light cone lemma to give topological restriction on Lagrangians is not new (cf. [Reference Kharlamov11, Reference Welschinger17]). This argument is easily generalized to prove the whole Theorem 1.1 for arbitrary m as follows.
$m = 1$
. In fact, using the light cone lemma to give topological restriction on Lagrangians is not new (cf. [Reference Kharlamov11, Reference Welschinger17]). This argument is easily generalized to prove the whole Theorem 1.1 for arbitrary m as follows.
The light cone lemma asserts that for the light cone
![]() $ \mathcal {C}$
of signature
$ \mathcal {C}$
of signature
![]() $(1, n)$
(
$(1, n)$
(
![]() $n> 0$
),
$n> 0$
),
![]() $ \mathcal {C} \subset \mathbb {R}^{1,n} $
, any two elements in the forward cone
$ \mathcal {C} \subset \mathbb {R}^{1,n} $
, any two elements in the forward cone
![]() $\mathcal {C}_+ $
have a nonnegative inner product. Especially, if the inner product is zero, then the two elements are proportional to each other. Note that
$\mathcal {C}_+ $
have a nonnegative inner product. Especially, if the inner product is zero, then the two elements are proportional to each other. Note that
![]() $ \mathcal {C}\backslash \{0\}$
has two connected components. One is the forward cone
$ \mathcal {C}\backslash \{0\}$
has two connected components. One is the forward cone
![]() $\mathcal {C}_+ $
, and the other is the backward cone
$\mathcal {C}_+ $
, and the other is the backward cone
![]() $\mathcal {C}_- $
. Furthermore,
$\mathcal {C}_- $
. Furthermore,
![]() $ \mathcal {C}_+=-\mathcal {C}_-$
.
$ \mathcal {C}_+=-\mathcal {C}_-$
.
Now, we follow Proposition 2.17 of [Reference Zhang18] to prove Theorem 1.1 instead. If
![]() $ (-1)^m \chi (L)\geq 0$
, we have
$ (-1)^m \chi (L)\geq 0$
, we have
If we assume
![]() $[L]\neq 0$
and
$[L]\neq 0$
and
![]() $b_{2m}^+(X)=1$
, both classes
$b_{2m}^+(X)=1$
, both classes
![]() $PU(L)$
and
$PU(L)$
and
![]() $[\omega ^m] \in H^{2m}(X, \mathbb {R})$
are in the forward cone by choosing a suitable orientation of L. Then the light cone lemma implies that this is a contradiction. That is, if
$[\omega ^m] \in H^{2m}(X, \mathbb {R})$
are in the forward cone by choosing a suitable orientation of L. Then the light cone lemma implies that this is a contradiction. That is, if
![]() $b_{2m}^+(X)=1$
, then
$b_{2m}^+(X)=1$
, then
![]() $ (-1)^m \chi (L)<0$
, and if
$ (-1)^m \chi (L)<0$
, and if
![]() $\chi (L)=0$
, then
$\chi (L)=0$
, then
![]() $[L]=0\in H_{2m}(X, \mathbb {R})$
. Other parts of Theorem 1.1 can be similarly argued and are easier (without using Riemannian metrics and self-dual/anti-self-dual decompositions).
$[L]=0\in H_{2m}(X, \mathbb {R})$
. Other parts of Theorem 1.1 can be similarly argued and are easier (without using Riemannian metrics and self-dual/anti-self-dual decompositions).
Finally, the same argument of Corollary 1.2(i) also works to show that a manifold admitting a complex hyperbolic metric,
![]() $X\cong \mathbb {CH}^m/\Gamma $
, cannot be embedded as a Lagrangian since
$X\cong \mathbb {CH}^m/\Gamma $
, cannot be embedded as a Lagrangian since
by the traditional Gauss–Bonnet theorem. This in particular implies that fake projective planes cannot be embedded as Lagrangians of eight-dimensional symplectic manifolds with
![]() $ b_4^+=1$
.
$ b_4^+=1$
.
Acknowledgment
The author thanks the referee for many helpful suggestions.