Article contents
Tenacious wall states in thermal convection in rapidly rotating containers
Published online by Cambridge University Press: 24 June 2020
Abstract
Convection in a container, heated from below, cooled from above and rapidly rotated around a vertical axis, starts from its sidewall. When the imposed vertical temperature gradient is not sufficiently large for bulk modes to set in, thermal convection can start in the form of wall modes, which are observed near the sidewall as pairs of hot ascending and cold descending plumes that drift along the wall. With increasing temperature gradient, different wall and bulk modes occur and interact, leading finally to turbulence. A recent numerical study by Favier & Knobloch (J. Fluid Mech., 895, 2020, R1) reveals an extreme robustness of the wall states. They persist above the onset of bulk modes and turbulence, thereby relating them to the recently discovered boundary zonal flows in highly turbulent rotating thermal convection. More exciting is that the wall modes can be thought of as topologically protected states, as they are robust with respect to the sidewall shape. They stubbornly drift along the wall, following its contour, independent of geometric obstacles.
- Type
- Focus on Fluids
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
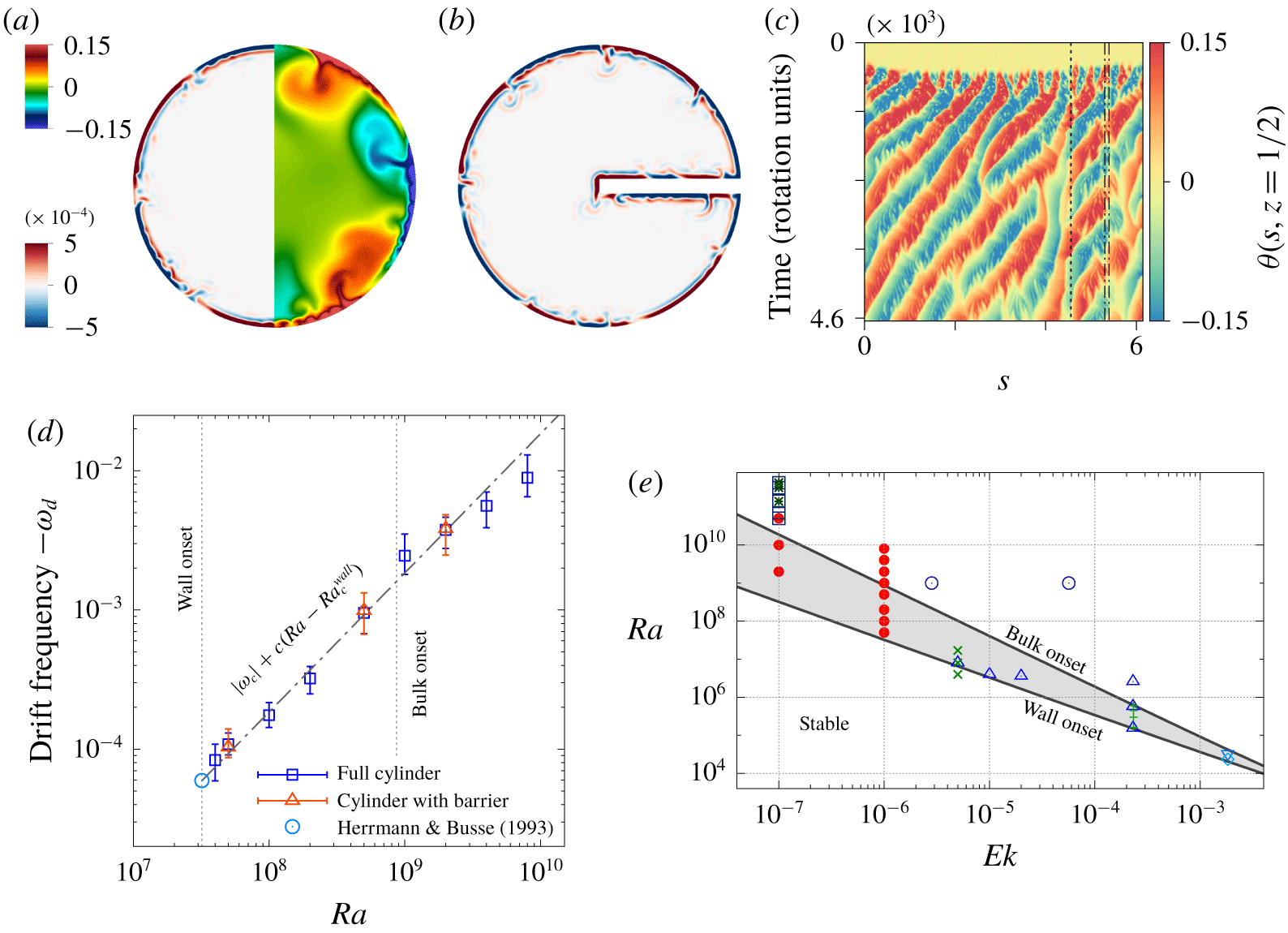
Figure 1. For panels (a–d)  $Ek=10^{-6}$,
$Ek=10^{-6}$,  $Pr=1$,
$Pr=1$,  $\unicode[STIX]{x1D6E4}=1.5$, the cylinder mid-height, and for panels (a–c)
$\unicode[STIX]{x1D6E4}=1.5$, the cylinder mid-height, and for panels (a–c)  $Ra=5\times 10^{8}$. (a) Instantaneous vertical velocity (left) and temperature (right) in a full cylinder; (b) vertical velocity; and (c) temporal evolution of the temperature along the arclength
$Ra=5\times 10^{8}$. (a) Instantaneous vertical velocity (left) and temperature (right) in a full cylinder; (b) vertical velocity; and (c) temporal evolution of the temperature along the arclength  $s$ at a distance
$s$ at a distance  $10^{-2}H$ from the wall in a cylinder with a barrier, whose corners are shown with vertical lines. (d) Drift frequency,
$10^{-2}H$ from the wall in a cylinder with a barrier, whose corners are shown with vertical lines. (d) Drift frequency,  $-\unicode[STIX]{x1D714}_{d}\equiv \unicode[STIX]{x1D714}/(2\unicode[STIX]{x1D6FA})$, as a function of
$-\unicode[STIX]{x1D714}_{d}\equiv \unicode[STIX]{x1D714}/(2\unicode[STIX]{x1D6FA})$, as a function of  $Ra$, in a full cylinder (blue squares) and in a cylinder with a barrier (red triangles), together with the frequency
$Ra$, in a full cylinder (blue squares) and in a cylinder with a barrier (red triangles), together with the frequency  $\unicode[STIX]{x1D714}_{d}=\unicode[STIX]{x1D714}_{c}\approx -59Ek/Pr$ (Herrmann & Busse 1993) for the onset of the instability (blue circle). (e) Onsets of the wall (Zhang & Liao 2009) and bulk (Chandrasekhar 1961) modes with the parameter range studied by Favier & Knobloch (2020) (filled red circles), Zhang et al. (2020) (blue circles), de Wit et al. (2020) (black squares and stars) and others. Figures adopted from Favier & Knobloch (2020).
$\unicode[STIX]{x1D714}_{d}=\unicode[STIX]{x1D714}_{c}\approx -59Ek/Pr$ (Herrmann & Busse 1993) for the onset of the instability (blue circle). (e) Onsets of the wall (Zhang & Liao 2009) and bulk (Chandrasekhar 1961) modes with the parameter range studied by Favier & Knobloch (2020) (filled red circles), Zhang et al. (2020) (blue circles), de Wit et al. (2020) (black squares and stars) and others. Figures adopted from Favier & Knobloch (2020).
- 17
- Cited by



1 Introduction
Thermally induced buoyancy, constrained by rapid rotation, governs many astro- and geophysical processes. Examples are thermal convection in the atmosphere, ocean and liquid-metal core of the Earth and convection on the surface of the Sun. A paradigmatic system to study these processes in the laboratory is rotating Rayleigh–Bénard convection (RBC; Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009) in an upright cylinder with height $H$, diameter-to-height aspect ratio
$H$, diameter-to-height aspect ratio  $\unicode[STIX]{x1D6E4}$ and temperature difference
$\unicode[STIX]{x1D6E4}$ and temperature difference  $\unicode[STIX]{x1D6E5}$ from the bottom to the top, filled with a fluid of Prandtl number
$\unicode[STIX]{x1D6E5}$ from the bottom to the top, filled with a fluid of Prandtl number  $Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$ and rotated uniformly about its axis at rate
$Pr=\unicode[STIX]{x1D708}/\unicode[STIX]{x1D705}$ and rotated uniformly about its axis at rate  $\unicode[STIX]{x1D6FA}$. The strengths of buoyancy and rotation are determined by the Rayleigh number
$\unicode[STIX]{x1D6FA}$. The strengths of buoyancy and rotation are determined by the Rayleigh number  $Ra\equiv \unicode[STIX]{x1D6FC}gH^{3}\unicode[STIX]{x1D6E5}/(\unicode[STIX]{x1D705}\unicode[STIX]{x1D708})$ and the Ekman number
$Ra\equiv \unicode[STIX]{x1D6FC}gH^{3}\unicode[STIX]{x1D6E5}/(\unicode[STIX]{x1D705}\unicode[STIX]{x1D708})$ and the Ekman number  $Ek\equiv \unicode[STIX]{x1D708}/(2\unicode[STIX]{x1D6FA}H^{2})$, where
$Ek\equiv \unicode[STIX]{x1D708}/(2\unicode[STIX]{x1D6FA}H^{2})$, where  $g$ is the gravitational acceleration and
$g$ is the gravitational acceleration and  $\unicode[STIX]{x1D708}$,
$\unicode[STIX]{x1D708}$,  $\unicode[STIX]{x1D705}$ and
$\unicode[STIX]{x1D705}$ and  $\unicode[STIX]{x1D6FC}$ are, respectively, the viscosity, thermal diffusivity and isobaric expansion coefficients.
$\unicode[STIX]{x1D6FC}$ are, respectively, the viscosity, thermal diffusivity and isobaric expansion coefficients.
In a laterally unbounded, rotating fluid layer, convection sets in as oscillatory (for small $Pr$) or steady motions, when
$Pr$) or steady motions, when  $Ra$ exceeds a critical value
$Ra$ exceeds a critical value  $Ra_{c}^{bulk}$ that scales as
$Ra_{c}^{bulk}$ that scales as ${\sim}Ek^{-4/3}$ in the limit
${\sim}Ek^{-4/3}$ in the limit  $Ek\rightarrow 0$ (Chandrasekhar Reference Chandrasekhar1961). Experiments in confined containers show, however, that convection can occur for
$Ek\rightarrow 0$ (Chandrasekhar Reference Chandrasekhar1961). Experiments in confined containers show, however, that convection can occur for  $Ra<Ra_{c}^{bulk}$ (Rossby Reference Rossby1969), which means that, in contrast to the non-rotating case, the sidewalls play a destabilizing role in rapidly rotating RBC. The wall modes have the form of
$Ra<Ra_{c}^{bulk}$ (Rossby Reference Rossby1969), which means that, in contrast to the non-rotating case, the sidewalls play a destabilizing role in rapidly rotating RBC. The wall modes have the form of  $m$ pairs of hot ascending and cold descending plumes that drift in a retrograde direction along the sidewall (Zhong, Ecke & Steinberg Reference Zhong, Ecke and Steinberg1991). Asymptotic analysis gives a critical
$m$ pairs of hot ascending and cold descending plumes that drift in a retrograde direction along the sidewall (Zhong, Ecke & Steinberg Reference Zhong, Ecke and Steinberg1991). Asymptotic analysis gives a critical  $Ra$ for the onset of the wall modes, namely,
$Ra$ for the onset of the wall modes, namely,  $Ra_{c}^{wall}\approx \unicode[STIX]{x03C0}^{2}\sqrt{6\sqrt{3}}\,Ek^{-1}+46.5\,Ek^{-2/3}$, and the corresponding onset drift frequency
$Ra_{c}^{wall}\approx \unicode[STIX]{x03C0}^{2}\sqrt{6\sqrt{3}}\,Ek^{-1}+46.5\,Ek^{-2/3}$, and the corresponding onset drift frequency  $\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}\approx Ek\,Pr^{-1}(4\unicode[STIX]{x03C0}^{2}\sqrt{6+3\sqrt{3}}-1464.5\,Ek^{1/3})$ and mode number
$\unicode[STIX]{x1D714}_{c}/\unicode[STIX]{x1D6FA}\approx Ek\,Pr^{-1}(4\unicode[STIX]{x03C0}^{2}\sqrt{6+3\sqrt{3}}-1464.5\,Ek^{1/3})$ and mode number  $m/\unicode[STIX]{x1D6E4}\approx (\unicode[STIX]{x03C0}/2)\sqrt{2+\sqrt{3}}-17.5\,E^{1/3}$ (Zhang & Liao Reference Zhang and Liao2009). The leading terms here were calculated first by Herrmann & Busse (Reference Herrmann and Busse1993). The linear dependences on
$m/\unicode[STIX]{x1D6E4}\approx (\unicode[STIX]{x03C0}/2)\sqrt{2+\sqrt{3}}-17.5\,E^{1/3}$ (Zhang & Liao Reference Zhang and Liao2009). The leading terms here were calculated first by Herrmann & Busse (Reference Herrmann and Busse1993). The linear dependences on  $Ra$ of the drift frequency and mean vertical heat transport in the system (Nusselt number
$Ra$ of the drift frequency and mean vertical heat transport in the system (Nusselt number  $Nu$), near the wall mode onset, indicate a supercritical Hopf bifurcation from the conductive case (Ecke, Zhong & Knobloch Reference Ecke, Zhong and Knobloch1992). With increasing
$Nu$), near the wall mode onset, indicate a supercritical Hopf bifurcation from the conductive case (Ecke, Zhong & Knobloch Reference Ecke, Zhong and Knobloch1992). With increasing  $Ra$, additional wall modes with different
$Ra$, additional wall modes with different  $m$ occur and may be subjected to modulational merging instabilities (Liu & Ecke Reference Liu and Ecke1999). The wall modes can further interact with the bulk modes, leading to a very complex nonlinear dynamics (Zhong, Ecke & Steinberg Reference Zhong, Ecke and Steinberg1993; Bodenschatz, Pesch & Ahlers Reference Bodenschatz, Pesch and Ahlers2000; Horn & Schmid Reference Horn and Schmid2017).
$m$ occur and may be subjected to modulational merging instabilities (Liu & Ecke Reference Liu and Ecke1999). The wall modes can further interact with the bulk modes, leading to a very complex nonlinear dynamics (Zhong, Ecke & Steinberg Reference Zhong, Ecke and Steinberg1993; Bodenschatz, Pesch & Ahlers Reference Bodenschatz, Pesch and Ahlers2000; Horn & Schmid Reference Horn and Schmid2017).
2 The exciting findings by Favier & Knobloch (Reference Favier and Knobloch2020)
Figure 1. For panels (a–d) $Ek=10^{-6}$,
$Ek=10^{-6}$,  $Pr=1$,
$Pr=1$,  $\unicode[STIX]{x1D6E4}=1.5$, the cylinder mid-height, and for panels (a–c)
$\unicode[STIX]{x1D6E4}=1.5$, the cylinder mid-height, and for panels (a–c)  $Ra=5\times 10^{8}$. (a) Instantaneous vertical velocity (left) and temperature (right) in a full cylinder; (b) vertical velocity; and (c) temporal evolution of the temperature along the arclength
$Ra=5\times 10^{8}$. (a) Instantaneous vertical velocity (left) and temperature (right) in a full cylinder; (b) vertical velocity; and (c) temporal evolution of the temperature along the arclength  $s$ at a distance
$s$ at a distance  $10^{-2}H$ from the wall in a cylinder with a barrier, whose corners are shown with vertical lines. (d) Drift frequency,
$10^{-2}H$ from the wall in a cylinder with a barrier, whose corners are shown with vertical lines. (d) Drift frequency,  $-\unicode[STIX]{x1D714}_{d}\equiv \unicode[STIX]{x1D714}/(2\unicode[STIX]{x1D6FA})$, as a function of
$-\unicode[STIX]{x1D714}_{d}\equiv \unicode[STIX]{x1D714}/(2\unicode[STIX]{x1D6FA})$, as a function of  $Ra$, in a full cylinder (blue squares) and in a cylinder with a barrier (red triangles), together with the frequency
$Ra$, in a full cylinder (blue squares) and in a cylinder with a barrier (red triangles), together with the frequency  $\unicode[STIX]{x1D714}_{d}=\unicode[STIX]{x1D714}_{c}\approx -59Ek/Pr$ (Herrmann & Busse Reference Herrmann and Busse1993) for the onset of the instability (blue circle). (e) Onsets of the wall (Zhang & Liao Reference Zhang and Liao2009) and bulk (Chandrasekhar Reference Chandrasekhar1961) modes with the parameter range studied by Favier & Knobloch (Reference Favier and Knobloch2020) (filled red circles), Zhang et al. (Reference Zhang, van Gils, Horn, Wedi, Zwirner, Ahlers, Ecke, Weiss, Bodenschatz and Shishkina2020) (blue circles), de Wit et al. (Reference de Wit, Guzman, Madonia, Cheng, Clercx and Kunnen2020) (black squares and stars) and others. Figures adopted from Favier & Knobloch (Reference Favier and Knobloch2020).
$\unicode[STIX]{x1D714}_{d}=\unicode[STIX]{x1D714}_{c}\approx -59Ek/Pr$ (Herrmann & Busse Reference Herrmann and Busse1993) for the onset of the instability (blue circle). (e) Onsets of the wall (Zhang & Liao Reference Zhang and Liao2009) and bulk (Chandrasekhar Reference Chandrasekhar1961) modes with the parameter range studied by Favier & Knobloch (Reference Favier and Knobloch2020) (filled red circles), Zhang et al. (Reference Zhang, van Gils, Horn, Wedi, Zwirner, Ahlers, Ecke, Weiss, Bodenschatz and Shishkina2020) (blue circles), de Wit et al. (Reference de Wit, Guzman, Madonia, Cheng, Clercx and Kunnen2020) (black squares and stars) and others. Figures adopted from Favier & Knobloch (Reference Favier and Knobloch2020).
The onset of wall modes has been studied in detail (Goldstein et al. Reference Goldstein, Knobloch, Mercader and Net1993), but important questions remained unanswered: How robust are they? Do they appear only in specific regular geometries? The recent study by Favier & Knobloch (Reference Favier and Knobloch2020) provides evidence of the robustness of the wall modes: the introduction of an extreme radial barrier into the cylinder (cf. figure 1a,b) has basically no effect on the wall mode properties. Warm uprising and cold downwelling thermal plumes drift with the same frequency (figure 1c,d) along the sidewall, no matter what particular shape it has. They just follow any provided geometry. The drift frequency remains linearly dependent on $Ra$ throughout the whole purely wall-mode regime (grey region in figure 1e), which in the case of
$Ra$ throughout the whole purely wall-mode regime (grey region in figure 1e), which in the case of  $Ek=10^{-6}$ is approximately two decades of
$Ek=10^{-6}$ is approximately two decades of  $Ra$.
$Ra$.
Favier & Knobloch (Reference Favier and Knobloch2020) also show that the wall modes (already slightly above their onset, at lower $Ra$) have many qualitatively similar features with the boundary zonal flows (BZF), recently discovered in measurements and simulations of highly turbulent (high-
$Ra$) have many qualitatively similar features with the boundary zonal flows (BZF), recently discovered in measurements and simulations of highly turbulent (high- $Ra$) rotating RBC (see Zhang et al. (Reference Zhang, van Gils, Horn, Wedi, Zwirner, Ahlers, Ecke, Weiss, Bodenschatz and Shishkina2020) and de Wit et al. (Reference de Wit, Guzman, Madonia, Cheng, Clercx and Kunnen2020), and figure 1e in this paper). In particular, the flow patterns near the sidewall in both cases drift anticyclonically, while the mean azimuthal flows there are cyclonic. Although the characteristics (e.g. drift speeds, the scalings of the heat and momentum transport and layer thicknesses associated with the zonal flows, etc.) of the wall modes near their onset and of the BZF in turbulent regimes are quantitatively different, the study by Favier & Knobloch (Reference Favier and Knobloch2020) provides a clear link between these two important wall states, assuming a complex nonlinear transformation between them.
$Ra$) rotating RBC (see Zhang et al. (Reference Zhang, van Gils, Horn, Wedi, Zwirner, Ahlers, Ecke, Weiss, Bodenschatz and Shishkina2020) and de Wit et al. (Reference de Wit, Guzman, Madonia, Cheng, Clercx and Kunnen2020), and figure 1e in this paper). In particular, the flow patterns near the sidewall in both cases drift anticyclonically, while the mean azimuthal flows there are cyclonic. Although the characteristics (e.g. drift speeds, the scalings of the heat and momentum transport and layer thicknesses associated with the zonal flows, etc.) of the wall modes near their onset and of the BZF in turbulent regimes are quantitatively different, the study by Favier & Knobloch (Reference Favier and Knobloch2020) provides a clear link between these two important wall states, assuming a complex nonlinear transformation between them.
3 Future
Thanks to Favier & Knobloch (Reference Favier and Knobloch2020), we now know that the wall states are very robust and this gives rise to further questions, motivating further investigations of these tenacious wall states. As the authors speculate, the wall modes can be interpreted as topologically protected states due to their robustness with respect to the shape of the container sidewall. Can one identify similar states in other three-dimensional dissipative nonlinear systems? How exactly do the different wall and turbulent bulk modes interact and evolve with growing $Ra$? What is the role of the sidewall zonal flow in transitional and turbulent regimes? What is its contribution to the global heat transport (Zhong et al. Reference Zhong, Stevens, Clercx, Verzicco, Lohse and Ahlers2009), energy balances (Horn & Shishkina Reference Horn and Shishkina2015) and reorganization of the global flow structure (Kunnen et al. Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011; Weiss & Ahlers Reference Weiss and Ahlers2011)? Can one predict the BZF properties, for any given
$Ra$? What is the role of the sidewall zonal flow in transitional and turbulent regimes? What is its contribution to the global heat transport (Zhong et al. Reference Zhong, Stevens, Clercx, Verzicco, Lohse and Ahlers2009), energy balances (Horn & Shishkina Reference Horn and Shishkina2015) and reorganization of the global flow structure (Kunnen et al. Reference Kunnen, Stevens, Overkamp, Sun, van Heijst and Clercx2011; Weiss & Ahlers Reference Weiss and Ahlers2011)? Can one predict the BZF properties, for any given  $Ra$,
$Ra$,  $Ek$,
$Ek$,  $Pr$ and
$Pr$ and  $\unicode[STIX]{x1D6E4}$?
$\unicode[STIX]{x1D6E4}$?
The relationship between the wall modes at their onset and the turbulent BZF in the rotating system is similar to that between the bulk modes at their onset and the turbulent large-scale circulation (LSC) in the problem with no rotation. The BZF can also be interpreted as the remains of the LSC that is suppressed by rotation and confined to the near-sidewall region, or as the superstructure that substitutes the LSC in turbulent, rapidly rotating RBC. Deeper investigations of these relationships are desired. Further questions are related to the geostrophic regime, which is probably the most relevant in geo- and astrophysical studies (Cheng et al. Reference Cheng, Aurnou, Julien and Kunnen2018). Measurements and simulations for very fast rotation (low $Ek$) and strong thermal driving (high
$Ek$) and strong thermal driving (high  $Ra$) show that the heat transport in the system is highly influenced by the BZF (Zhang et al. Reference Zhang, van Gils, Horn, Wedi, Zwirner, Ahlers, Ecke, Weiss, Bodenschatz and Shishkina2020). If the wall states are that robust and their role is that important, then how should modern experiments be designed, to gain the relevant knowledge on geo- and astrophysical flows in the laboratory?
$Ra$) show that the heat transport in the system is highly influenced by the BZF (Zhang et al. Reference Zhang, van Gils, Horn, Wedi, Zwirner, Ahlers, Ecke, Weiss, Bodenschatz and Shishkina2020). If the wall states are that robust and their role is that important, then how should modern experiments be designed, to gain the relevant knowledge on geo- and astrophysical flows in the laboratory?
Declaration of interests
The author reports no conflict of interest.