No CrossRef data available.
Published online by Cambridge University Press: 23 December 2024
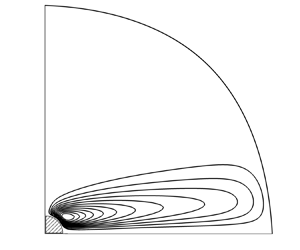
Convective flows near a cylindrical solid inclusion in a fluid-saturated porous medium heated from above are studied using the Darcy–Boussinesq equations. The impermeability condition is imposed on the inclusion surface. Two-dimensional convective flows uniform in the direction of the cylinder axis are considered. An Oseen-like approximation is implemented, however, different from the conventional Oseen approximation, quasilinearization is applied to the nonlinear terms in the energy equation and not in the momentum equation. It is shown that, when the thermal conductivity of the inclusion is higher than that of the fluid, the convective flow at a distance from the inclusion larger than the inclusion size takes the form of horizontal vortices directed away from the inclusion. In the case of low thermal conductivity of the inclusion, the direction of convective circulation is opposite: in the horizontal plane passing through the cylinder axis, the fluid is leaking to the inclusion.