1 Introduction
Following the findings of Nikuradse (Reference Nikuradse1926) on the existence of secondary currents in square duct turbulent flow, further experimental studies (Hoagland Reference Hoagland1960; Brundrett & Baines Reference Brundrett and Baines1964; Launder & Ying Reference Launder and Ying1972; Melling & Whitelaw Reference Melling and Whitelaw1976) have been conducted to obtain a better understanding of the phenomenon, which came to be known as ‘Prandtl’s secondary flow of the second kind’. These studies, which focused mainly on turbulent flow at relatively high Reynolds numbers (
![]() $Re>35\,000$
;
$Re>35\,000$
;
![]() $Re=U_{b}h/{\it\nu}$
where
$Re=U_{b}h/{\it\nu}$
where
![]() $U_{b}$
,
$U_{b}$
,
![]() $h$
and
$h$
and
![]() ${\it\nu}$
represent the bulk velocity, duct half height and kinematic viscosity, respectively) have shown that secondary flow, though weak in magnitude, has a considerable impact on the primary flow. Developments in computational fluid dynamics have made possible the direct numerical simulation (DNS) of such flows to complement experimental results and provide more insight into the turbulence structure. However computational restrictions currently limit DNS to low Reynolds numbers (
${\it\nu}$
represent the bulk velocity, duct half height and kinematic viscosity, respectively) have shown that secondary flow, though weak in magnitude, has a considerable impact on the primary flow. Developments in computational fluid dynamics have made possible the direct numerical simulation (DNS) of such flows to complement experimental results and provide more insight into the turbulence structure. However computational restrictions currently limit DNS to low Reynolds numbers (
![]() $Re<5000$
), hence comparisons between experiments and simulations have mostly been qualitative. At such Reynolds numbers, the turbulent flow field has been found to behave differently from what is observed experimentally at much higher Reynolds numbers.
$Re<5000$
), hence comparisons between experiments and simulations have mostly been qualitative. At such Reynolds numbers, the turbulent flow field has been found to behave differently from what is observed experimentally at much higher Reynolds numbers.
One of the earliest DNS of square duct turbulent flow was conducted by Gavrilakis (Reference Gavrilakis1992) at
![]() $Re=2205$
. His results show good qualitative agreement with experimental findings with regards to bulging of the contour of mean streamwise velocity towards the duct corners and an eight-vortex secondary flow pattern. However, the wall shear stress
$Re=2205$
. His results show good qualitative agreement with experimental findings with regards to bulging of the contour of mean streamwise velocity towards the duct corners and an eight-vortex secondary flow pattern. However, the wall shear stress
![]() $({\it\tau}_{w})$
was found to be non-uniformly distributed across the duct due to the secondary flow field. Specifically, three peaks were observed on each wall; one at the midpoint and the other two close to the corners. Another key finding from the simulation, which is a consequence of these wall shear stress gradients, was that the streamwise velocity profile along the wall bisector exhibited an overshoot from the well-known logarithmic law (
$({\it\tau}_{w})$
was found to be non-uniformly distributed across the duct due to the secondary flow field. Specifically, three peaks were observed on each wall; one at the midpoint and the other two close to the corners. Another key finding from the simulation, which is a consequence of these wall shear stress gradients, was that the streamwise velocity profile along the wall bisector exhibited an overshoot from the well-known logarithmic law (
![]() $u^{+}=2.5\ln y^{+}+5.5$
) in the overlap layer when normalised by the average (across the duct perimeter) rather than local friction velocity,
$u^{+}=2.5\ln y^{+}+5.5$
) in the overlap layer when normalised by the average (across the duct perimeter) rather than local friction velocity,
![]() $u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
, where
$u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
, where
![]() ${\it\rho}$
is the density. Other researchers who have conducted DNS of square duct turbulent flow and obtained similar results include Huser & Biringen (Reference Huser and Biringen1993) and Joung, Choi & Choi (Reference Joung, Choi and Choi2007).
${\it\rho}$
is the density. Other researchers who have conducted DNS of square duct turbulent flow and obtained similar results include Huser & Biringen (Reference Huser and Biringen1993) and Joung, Choi & Choi (Reference Joung, Choi and Choi2007).
A pertinent research question which, until recently, has received little attention in the literature is the determination of the mechanism for transition to turbulence in square duct flow and the flow field characteristics at the edge of turbulence. Like pipe flow, square duct flow is linearly stable at all Reynolds numbers (Tatsumi & Yoshimura Reference Tatsumi and Yoshimura1990). However, occurrence of exact coherent structures such as travelling waves is believed to signal the beginning of chaos. Travelling wave solutions have been discovered by Wedin, Bottaro & Nagata (Reference Wedin, Bottaro and Nagata2009), Okino et al. (Reference Okino, Nagata, Wedin and Bottaro2010) and Uhlmann, Kawahara & Pinelli (Reference Uhlmann, Kawahara and Pinelli2010) at
![]() $Re=598.2$
, 332 and 471 respectively.
$Re=598.2$
, 332 and 471 respectively.
Numerical simulations reveal that the limiting value of Reynolds number for the onset of self-sustaining turbulence in periodic square-duct flow ranges between
![]() $Re=865$
(
$Re=865$
(
![]() $Re_{{\it\tau}}=65$
) and
$Re_{{\it\tau}}=65$
) and
![]() $Re=1077$
(
$Re=1077$
(
![]() $Re_{{\it\tau}}=80$
), where
$Re_{{\it\tau}}=80$
), where
![]() $Re_{{\it\tau}}$
is the Reynolds number based on friction velocity and duct half-height (Biau & Bottaro Reference Biau and Bottaro2009; Uhlmann et al.
Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007). The DNS results of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) are particularly fascinating. So-called marginally turbulent flow was found to be characterised by two flow states each of which contained a four-vortex secondary flow field rather than the conventional pattern of eight vortices. The vortex pairs, which were associated with a pair of opposite walls, alternated between two different orientations, the eight-vortex secondary flow pattern being a composite of these two as reproduced in figure 1. This switching of the flow field between two states in the marginally turbulent regime has not previously been observed in experiments. This different secondary flow pattern was attributed to buffer layer coherent structures (streaks), whose preferential positioning over the duct walls matched those of the vortices.
$Re_{{\it\tau}}$
is the Reynolds number based on friction velocity and duct half-height (Biau & Bottaro Reference Biau and Bottaro2009; Uhlmann et al.
Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007). The DNS results of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) are particularly fascinating. So-called marginally turbulent flow was found to be characterised by two flow states each of which contained a four-vortex secondary flow field rather than the conventional pattern of eight vortices. The vortex pairs, which were associated with a pair of opposite walls, alternated between two different orientations, the eight-vortex secondary flow pattern being a composite of these two as reproduced in figure 1. This switching of the flow field between two states in the marginally turbulent regime has not previously been observed in experiments. This different secondary flow pattern was attributed to buffer layer coherent structures (streaks), whose preferential positioning over the duct walls matched those of the vortices.

Figure 1. The two flow states of marginally turbulent flow (a,b) and the conventional eight-vortex pattern (c). Adapted from figure 3 of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007). Contour lines show the primary mean flow
![]() $\langle U\rangle$
and vectors show the secondary mean flow
$\langle U\rangle$
and vectors show the secondary mean flow
![]() $\langle V\rangle$
,
$\langle V\rangle$
,
![]() $\langle W\rangle$
for
$\langle W\rangle$
for
![]() $Re=1205$
: (a) averaging interval
$Re=1205$
: (a) averaging interval
![]() $771h/U_{b}$
; (b) a different interval with length
$771h/U_{b}$
; (b) a different interval with length
![]() $482h/U_{b};$
(c) long-time integration including both previous intervals (
$482h/U_{b};$
(c) long-time integration including both previous intervals (
![]() $1639h/U_{b}$
). The wall bisector is indicated by dashed blue lines.
$1639h/U_{b}$
). The wall bisector is indicated by dashed blue lines.

Figure 2. Experimental set-up. (a) Schematic of the flow loop (not to scale). (b) Axes system employed;
![]() $y$
is the wall-normal direction measured from the nearest wall. The streamwise/axial direction,
$y$
is the wall-normal direction measured from the nearest wall. The streamwise/axial direction,
![]() $x$
, is into the page.
$x$
, is into the page.
In two follow-up papers, changes to the flow field as fully turbulent flow is approached were investigated (Sekimoto et al. Reference Sekimoto, Pinelli, Uhlmann, Kawahara and Eckhardt2009; Pinelli et al. Reference Pinelli, Uhlmann, Sekimoto and Kawahara2010). The distribution of wall shear stress was found to be correlated to the number and positioning of buffer layer streaks (which increased with Reynolds number), the high-speed streaks always being preferentially located in the corner region, leading to local maxima in the wall shear stress distribution. On the other hand, low-speed streaks were associated with the occurrence of local minima. This explains the two peaked wall shear stress distribution observed in DNS of marginally turbulent flows. Again, there is lack of experimental data for comparison.
It is the aim of this study, therefore, to provide experimental data on turbulent flow in a square duct at relatively low Reynolds numbers in order to investigate these marginally turbulent states and provide validation data for DNS.
2 Experimental set-up
The experimental rig used for this study is a modified version of that employed by Escudier & Smith (Reference Escudier and Smith2001). The working section (as shown in figure 2
a) consists of eight square duct modules made of stainless steel, each of length 1.2 m and cross-sectional dimensions of 80 mm
![]() $\times$
80 mm (
$\times$
80 mm (
![]() $2h\times 2h$
), followed by a transparent section 150 mm in length, constructed from Perspex and another stainless steel module, 1.2 m long, bringing the total length to 10.95 m. With this arrangement, there is a distance of about
$2h\times 2h$
), followed by a transparent section 150 mm in length, constructed from Perspex and another stainless steel module, 1.2 m long, bringing the total length to 10.95 m. With this arrangement, there is a distance of about
![]() $240h$
before the transparent section, where laser Doppler velocimetry (LDV) measurements were taken, which is enough for both fully developed laminar and turbulent flow at the Reynolds numbers studied.
$240h$
before the transparent section, where laser Doppler velocimetry (LDV) measurements were taken, which is enough for both fully developed laminar and turbulent flow at the Reynolds numbers studied.
A progressive cavity Mono pump fed by the working fluid stored in a stainless steel tank drives the flow. The pump and tank are connected to the working section using a flexible corrugated pipe, 5 m in length, which serves as a pulsation damper. This is followed by a short section that provides a gradual transition from a circular to square cross-section, which includes a honeycomb flow straightener and an additional fine mesh to remove any disturbances from the pump and inlet. The fluid is recirculated through the rig via a return loop consisting of polyvinyl chloride pipes. The mass flow rate as well as fluid temperature and density were measured using an Endress and Hauser Promass I Coriolis flow meter installed in the return loop.
Velocity measurements were taken using a two-dimensional (2D) Dantec fibreflow LDV system operated in forward scatter mode. This system consisted of a
![]() $60\times 10$
probe,
$60\times 10$
probe,
![]() $55\times 12$
beam expander and an argon-ion laser source which supplied lights of wavelengths 515.5 nm (green) and 488 nm (blue) for resolving the velocity components in the streamwise and wall-normal directions (respectively
$55\times 12$
beam expander and an argon-ion laser source which supplied lights of wavelengths 515.5 nm (green) and 488 nm (blue) for resolving the velocity components in the streamwise and wall-normal directions (respectively
![]() $x$
and
$x$
and
![]() $y$
as defined in figure 2
b). The front lens of the laser probe had a focal length of 160 mm and a beam separation distance of 51.5 mm, resulting in a measuring volume of diameter
$y$
as defined in figure 2
b). The front lens of the laser probe had a focal length of 160 mm and a beam separation distance of 51.5 mm, resulting in a measuring volume of diameter
![]() $24~{\rm\mu}\text{m}$
and length
$24~{\rm\mu}\text{m}$
and length
![]() $150~{\rm\mu}\text{m}$
in air. With this configuration, the typical data rates were around 100 Hz in non-coincidence mode and 20 Hz in coincidence mode. At each wall-normal location, data was collected for typically 30 min in the laminar and fully turbulent regimes and for up to 1 h in the marginally turbulent state. The region below 8 mm from the duct wall was not accessible to the laser beams in the wall-normal plane; hence, data on wall-normal velocity components in that area could not be collected. Signal processing was carried out using a Dantec Burst Spectrum analyser (model F50) while data acquisition and processing was done using the Dantec BSA flow software (version 2.12.00.15). The fluids used were either water (
$150~{\rm\mu}\text{m}$
in air. With this configuration, the typical data rates were around 100 Hz in non-coincidence mode and 20 Hz in coincidence mode. At each wall-normal location, data was collected for typically 30 min in the laminar and fully turbulent regimes and for up to 1 h in the marginally turbulent state. The region below 8 mm from the duct wall was not accessible to the laser beams in the wall-normal plane; hence, data on wall-normal velocity components in that area could not be collected. Signal processing was carried out using a Dantec Burst Spectrum analyser (model F50) while data acquisition and processing was done using the Dantec BSA flow software (version 2.12.00.15). The fluids used were either water (
![]() ${\it\nu}\approx 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
) or 50 % glycerol/water solution (
${\it\nu}\approx 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
) or 50 % glycerol/water solution (
![]() ${\it\nu}\approx 6\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
) depending on the Reynolds number of interest. The local wall shear stress was determined by taking measurements of the velocity profile in the viscous sublayer, obtaining the gradient of the resulting linear plot and applying the expression:
${\it\nu}\approx 6\times 10^{-6}~\text{m}^{2}~\text{s}^{-1}$
) depending on the Reynolds number of interest. The local wall shear stress was determined by taking measurements of the velocity profile in the viscous sublayer, obtaining the gradient of the resulting linear plot and applying the expression:
![]() ${\it\tau}_{w}={\it\mu}(\text{d}\langle U\rangle /\text{d}y)$
, where
${\it\tau}_{w}={\it\mu}(\text{d}\langle U\rangle /\text{d}y)$
, where
![]() $\langle U\rangle$
is the mean streamwise velocity. The local friction velocity (
$\langle U\rangle$
is the mean streamwise velocity. The local friction velocity (
![]() $u_{{\it\tau}}$
) was subsequently estimated from this value of wall shear stress. Unlike in hot-wire anemometry, this technique is free from the so-called wall effect since LDV is non-intrusive. The very small measuring volume minimises any potential errors due to velocity gradient broadening. A detailed discussion on wall shear stress determination using the near-wall velocity gradient method is given by Hutchins & Choi (Reference Hutchins and Choi2002).
$u_{{\it\tau}}$
) was subsequently estimated from this value of wall shear stress. Unlike in hot-wire anemometry, this technique is free from the so-called wall effect since LDV is non-intrusive. The very small measuring volume minimises any potential errors due to velocity gradient broadening. A detailed discussion on wall shear stress determination using the near-wall velocity gradient method is given by Hutchins & Choi (Reference Hutchins and Choi2002).
3 Transition to turbulence
3.1 Experimental studies
It is well known that a turbulent flow field can be split into a mean and fluctuating component. Steady laminar flow is characterised by no fluctuations, hence an increase in intensity of the fluctuating velocity component is a good measure for detecting the onset of transition to turbulence in ducts. Figure 3(a,b) shows the variation of mean streamwise velocities,
![]() $\langle U\rangle$
, normalised by the bulk velocity,
$\langle U\rangle$
, normalised by the bulk velocity,
![]() $U_{b}$
, and the root mean square of the fluctuations,
$U_{b}$
, and the root mean square of the fluctuations,
![]() $u_{rms}$
, with Reynolds number at the duct centreline (
$u_{rms}$
, with Reynolds number at the duct centreline (
![]() $y/h=1.0$
). The data have been obtained using water.
$y/h=1.0$
). The data have been obtained using water.

Figure 3. Onset criteria for square duct turbulent flow (
![]() $Ek\approx 1,y/h=1$
). (a) Variation of
$Ek\approx 1,y/h=1$
). (a) Variation of
![]() $\langle U\rangle /U_{b}$
with Reynolds number. (b) Variation of
$\langle U\rangle /U_{b}$
with Reynolds number. (b) Variation of
![]() $u_{rms}/\langle U\rangle$
with Reynolds number. ——, laminar flow analytical solution at
$u_{rms}/\langle U\rangle$
with Reynolds number. ——, laminar flow analytical solution at
![]() $y/h=1$
; ♢ (red), DNS of Gavrilakis (Reference Gavrilakis1992); – ⋅ – ⋅ – (red), numerical simulation of laminar flow at
$y/h=1$
; ♢ (red), DNS of Gavrilakis (Reference Gavrilakis1992); – ⋅ – ⋅ – (red), numerical simulation of laminar flow at
![]() $Ek=1$
.
$Ek=1$
.
In figure 3(a), a drop off in the values of
![]() $\langle U\rangle /U_{b}$
from the laminar flow analytical solution (White Reference White2006, p. 113) can be observed for
$\langle U\rangle /U_{b}$
from the laminar flow analytical solution (White Reference White2006, p. 113) can be observed for
![]() $Re<1000$
. This deviation from the analytical solution is surprising as the velocity fluctuations remain very low (about 2 %), indicating that the flow is laminar (see figure 3(b); the fluctuations, which ideally should be zero, can be attributed to the measurement noise of the LDV system). We believe this deviation of the observed
$Re<1000$
. This deviation from the analytical solution is surprising as the velocity fluctuations remain very low (about 2 %), indicating that the flow is laminar (see figure 3(b); the fluctuations, which ideally should be zero, can be attributed to the measurement noise of the LDV system). We believe this deviation of the observed
![]() $\langle U\rangle /U_{b}$
from the analytical solution can be ascribed to Coriolis effects due to the Earth’s rotation as has been observed previously in pipe flows by Draad & Nieuwstadt (Reference Draad and Nieuwstadt1998). They showed that the effect of rotation on a fully developed laminar flow can be estimated using the Ekman number, a ratio of viscous to Coriolis forces:
$\langle U\rangle /U_{b}$
from the analytical solution can be ascribed to Coriolis effects due to the Earth’s rotation as has been observed previously in pipe flows by Draad & Nieuwstadt (Reference Draad and Nieuwstadt1998). They showed that the effect of rotation on a fully developed laminar flow can be estimated using the Ekman number, a ratio of viscous to Coriolis forces:
where
![]() ${\it\Omega}$
is the angular velocity of the Earth (
${\it\Omega}$
is the angular velocity of the Earth (
![]() $7.272\times 10^{-5}~\text{s}^{-1}$
),
$7.272\times 10^{-5}~\text{s}^{-1}$
),
![]() $D$
is the duct width (0.08 m) and
$D$
is the duct width (0.08 m) and
![]() ${\it\alpha}$
the angle between the duct axis and the Earth’s rotation axis (
${\it\alpha}$
the angle between the duct axis and the Earth’s rotation axis (
![]() ${\approx}69^{\circ }$
). In our case, we obtain
${\approx}69^{\circ }$
). In our case, we obtain
![]() $Ek\approx 1$
for water, hence Coriolis effects cannot be ignored in the laminar regime for this fluid. The Coriolis force brings about a distortion in the laminar flow velocity profile, which should normally be parabolic and symmetrical about the wall bisector, by introducing acceleration components in the wall-normal directions.
$Ek\approx 1$
for water, hence Coriolis effects cannot be ignored in the laminar regime for this fluid. The Coriolis force brings about a distortion in the laminar flow velocity profile, which should normally be parabolic and symmetrical about the wall bisector, by introducing acceleration components in the wall-normal directions.
Transition can be said to take place at
![]() $Re\approx 1050$
as evidenced by a significant drop in the value of
$Re\approx 1050$
as evidenced by a significant drop in the value of
![]() $\langle U\rangle /U_{b}$
from those of laminar flow. At this point, turbulence bursts are introduced into the laminar flow, hence the apparently large fluctuation levels recorded in figure 3(b). As the Reynolds number is increased,
$\langle U\rangle /U_{b}$
from those of laminar flow. At this point, turbulence bursts are introduced into the laminar flow, hence the apparently large fluctuation levels recorded in figure 3(b). As the Reynolds number is increased,
![]() $u_{rms}/\langle U\rangle$
settles down to about 5 %, the turbulence having become self-sustaining, and
$u_{rms}/\langle U\rangle$
settles down to about 5 %, the turbulence having become self-sustaining, and
![]() $\langle U\rangle /U_{b}$
gradually approaches the fully turbulent value obtained from the DNS of Gavrilakis (Reference Gavrilakis1992). In turbulent flow, inertial forces dominate and Coriolis effect becomes negligible.
$\langle U\rangle /U_{b}$
gradually approaches the fully turbulent value obtained from the DNS of Gavrilakis (Reference Gavrilakis1992). In turbulent flow, inertial forces dominate and Coriolis effect becomes negligible.
To reduce the effect of Coriolis force in the laminar regime, we make use of a more viscous liquid (50 % glycerol/water solution) resulting in
![]() $Ek\approx 7$
. This fluid is employed for all subsequent experiments. Figure 4(a,b) show the variation of
$Ek\approx 7$
. This fluid is employed for all subsequent experiments. Figure 4(a,b) show the variation of
![]() $\langle U\rangle /U_{b}$
and
$\langle U\rangle /U_{b}$
and
![]() $u_{rms}/\langle U\rangle$
with Reynolds number. The experimental data for
$u_{rms}/\langle U\rangle$
with Reynolds number. The experimental data for
![]() $\langle U\rangle /U_{b}$
at
$\langle U\rangle /U_{b}$
at
![]() $y/h=1$
can be observed to agree well with the laminar flow analytical solution until
$y/h=1$
can be observed to agree well with the laminar flow analytical solution until
![]() $Re\approx 800$
where there is a drop off once again due to the Coriolis effect. This is in agreement with the findings of Escudier et al. (Reference Escudier, Poole, Presti, Dales, Nouar, Desaubry, Graham and Pullum2005) who obtained laminar velocity profiles in pipe flow which were slightly asymmetric for
$Re\approx 800$
where there is a drop off once again due to the Coriolis effect. This is in agreement with the findings of Escudier et al. (Reference Escudier, Poole, Presti, Dales, Nouar, Desaubry, Graham and Pullum2005) who obtained laminar velocity profiles in pipe flow which were slightly asymmetric for
![]() $Re$
as low as 540 for
$Re$
as low as 540 for
![]() $Ek\approx 5$
. Transition to turbulence can be observed to take place at
$Ek\approx 5$
. Transition to turbulence can be observed to take place at
![]() $Re\approx 1250$
as indicated by an increase in velocity fluctuation levels as well as a significant drop in
$Re\approx 1250$
as indicated by an increase in velocity fluctuation levels as well as a significant drop in
![]() $\langle U\rangle /U_{b}$
from the laminar flow analytical solution. The difference in transition Reynolds number between water and 50 % glycerol/water solution can be attributed to their dissimilar laminar base profiles prior to transition.
$\langle U\rangle /U_{b}$
from the laminar flow analytical solution. The difference in transition Reynolds number between water and 50 % glycerol/water solution can be attributed to their dissimilar laminar base profiles prior to transition.

Figure 4. Onset criteria for square duct turbulent flow (
![]() $Ek\approx 7$
). (a) Variation of
$Ek\approx 7$
). (a) Variation of
![]() $\langle U\rangle /U_{b}$
with Reynolds number. (b) Variation of
$\langle U\rangle /U_{b}$
with Reynolds number. (b) Variation of
![]() $u_{rms}/\langle U\rangle$
with Reynolds number. Open symbols,
$u_{rms}/\langle U\rangle$
with Reynolds number. Open symbols,
![]() $y/h=1$
; closed symbols,
$y/h=1$
; closed symbols,
![]() $y/h=0.3$
; ▫, trip rod introduced upstream; ○ (green), no trip rod upstream; ——, laminar flow analytical solution at
$y/h=0.3$
; ▫, trip rod introduced upstream; ○ (green), no trip rod upstream; ——, laminar flow analytical solution at
![]() $y/h=1$
;
$y/h=1$
;
![]() $\cdots \cdots$
, laminar flow analytical solution at
$\cdots \cdots$
, laminar flow analytical solution at
![]() $y/h=0.3$
; ♢ (red), DNS of Gavrilakis (Reference Gavrilakis1992); – ⋅ – ⋅ – (red), numerical simulation of laminar flow at
$y/h=0.3$
; ♢ (red), DNS of Gavrilakis (Reference Gavrilakis1992); – ⋅ – ⋅ – (red), numerical simulation of laminar flow at
![]() $Ek=7$
.
$Ek=7$
.
To determine the lowest Reynolds number for the onset of sustained turbulence, we introduce a trip rod upstream (about
![]() $238h$
from the measurement section). In this instance transition can be observed to take place at
$238h$
from the measurement section). In this instance transition can be observed to take place at
![]() $Re\approx 940$
. This value of
$Re\approx 940$
. This value of
![]() $Re$
is within the range given by Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) and Biau & Bottaro (Reference Biau and Bottaro2009):
$Re$
is within the range given by Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) and Biau & Bottaro (Reference Biau and Bottaro2009):
![]() $Re=1077$
and 865, respectively. It is however higher than those where previous studies have shown the emergence of travelling wave solutions, which are known to be precursors to fully developed turbulence. At
$Re=1077$
and 865, respectively. It is however higher than those where previous studies have shown the emergence of travelling wave solutions, which are known to be precursors to fully developed turbulence. At
![]() $y/h=0.3$
, the streamwise velocity, normalised by the bulk velocity can be observed to be roughly constant in the laminar regime. It however drops off during transition before approaching the fully turbulent value given by Gavrilakis (Reference Gavrilakis1992) which, coincidentally, is close to the laminar flow value. The velocity fluctuations at
$y/h=0.3$
, the streamwise velocity, normalised by the bulk velocity can be observed to be roughly constant in the laminar regime. It however drops off during transition before approaching the fully turbulent value given by Gavrilakis (Reference Gavrilakis1992) which, coincidentally, is close to the laminar flow value. The velocity fluctuations at
![]() $y/h=0.3$
after transition are much higher than those at the duct centre and attain that of fully turbulent flow more slowly (see figure 4
b). This lends credence to the idea that the important structures that govern the dynamics of transition in square duct flow are primarily located in (and around) the buffer layer.
$y/h=0.3$
after transition are much higher than those at the duct centre and attain that of fully turbulent flow more slowly (see figure 4
b). This lends credence to the idea that the important structures that govern the dynamics of transition in square duct flow are primarily located in (and around) the buffer layer.
3.2 Numerical simulation of square duct laminar flow under the influence of Coriolis force
Following the approach of Draad & Nieuwstadt (Reference Draad and Nieuwstadt1998), we carry out a numerical simulation of fully developed laminar square duct flow, including the effect of the Earth’s rotation in order to confirm our hypothesis that these effects cannot be neglected. The governing Navier–Stokes equations for the flow are as follows:
where
![]() $U_{i}$
and
$U_{i}$
and
![]() $f_{i}$
denote the velocity field and Coriolis force per unit mass, respectively, and
$f_{i}$
denote the velocity field and Coriolis force per unit mass, respectively, and
![]() $p$
is the pressure term accounting for centrifugal forces. Considering the axis system of figure 2(b), and a unidirectional flow vector
$p$
is the pressure term accounting for centrifugal forces. Considering the axis system of figure 2(b), and a unidirectional flow vector
![]() $[U(x,y,z),0,0]$
, The Coriolis force per unit mass is given by
$[U(x,y,z),0,0]$
, The Coriolis force per unit mass is given by
![]() $\boldsymbol{f}=-2{\it\bf\Omega}\times \boldsymbol{U}$
, where
$\boldsymbol{f}=-2{\it\bf\Omega}\times \boldsymbol{U}$
, where
![]() ${\it\bf\Omega}$
is the Earth’s angular velocity vector given by
${\it\bf\Omega}$
is the Earth’s angular velocity vector given by
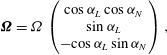 $$\begin{eqnarray}{\it\bf\Omega}={\it\Omega}\left(\begin{array}{@{}c@{}}\cos {\it\alpha}_{L}\cos {\it\alpha}_{N}\\ \sin {\it\alpha}_{L}\\ -\text{cos}\,{\it\alpha}_{L}\sin {\it\alpha}_{N}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}{\it\bf\Omega}={\it\Omega}\left(\begin{array}{@{}c@{}}\cos {\it\alpha}_{L}\cos {\it\alpha}_{N}\\ \sin {\it\alpha}_{L}\\ -\text{cos}\,{\it\alpha}_{L}\sin {\it\alpha}_{N}\end{array}\right),\end{eqnarray}$$
![]() ${\it\alpha}_{L}$
and
${\it\alpha}_{L}$
and
![]() ${\it\alpha}_{N}$
being the latitude (
${\it\alpha}_{N}$
being the latitude (
![]() $53^{\circ }$
in our case) and the angle between the direction of true north and the duct axis (
$53^{\circ }$
in our case) and the angle between the direction of true north and the duct axis (
![]() $100^{\circ }$
), respectively. Hence,
$100^{\circ }$
), respectively. Hence,
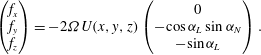 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}f_{x}\\ f_{y}\\ f_{z}\end{array}\right)=-2{\it\Omega}U(x,y,z)\left(\begin{array}{@{}c@{}}0\\ -\text{cos}\,{\it\alpha}_{L}\sin {\it\alpha}_{N}\\ -\text{sin}\,{\it\alpha}_{L}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}f_{x}\\ f_{y}\\ f_{z}\end{array}\right)=-2{\it\Omega}U(x,y,z)\left(\begin{array}{@{}c@{}}0\\ -\text{cos}\,{\it\alpha}_{L}\sin {\it\alpha}_{N}\\ -\text{sin}\,{\it\alpha}_{L}\end{array}\right).\end{eqnarray}$$
We solve the Navier–Stokes equations using the commercial software, ANSYS Fluent, for a domain:
![]() $D\times D\times 110D$
with
$D\times D\times 110D$
with
![]() $50\times 50\times 2160$
grid points (uniform in the cross-sectional plane, but non-uniform in the streamwise direction such that the ratio of the largest/first to the smallest/last cell is 7.5), using a pressure-based coupled solver. This software makes use of the finite volume approach. Spatial discretisation of pressure, gradient and momentum were carried out using the least-squares cell-based, standard and second-order upwind schemes, respectively.
$50\times 50\times 2160$
grid points (uniform in the cross-sectional plane, but non-uniform in the streamwise direction such that the ratio of the largest/first to the smallest/last cell is 7.5), using a pressure-based coupled solver. This software makes use of the finite volume approach. Spatial discretisation of pressure, gradient and momentum were carried out using the least-squares cell-based, standard and second-order upwind schemes, respectively.
Numerical simulation results at
![]() $y/h=1$
for
$y/h=1$
for
![]() $Ek=1$
and 7 are shown as dot-dashed lines in figures 3(a) and 4(a) respectively. The results show good agreement with the experimental data. The deviation of
$Ek=1$
and 7 are shown as dot-dashed lines in figures 3(a) and 4(a) respectively. The results show good agreement with the experimental data. The deviation of
![]() $\langle U\rangle /U_{b}$
from the laminar flow analytical solution can be observed to increase with Reynolds number. This is due to an increase in laminar velocity profile asymmetry, the level of distortion being higher for
$\langle U\rangle /U_{b}$
from the laminar flow analytical solution can be observed to increase with Reynolds number. This is due to an increase in laminar velocity profile asymmetry, the level of distortion being higher for
![]() $Ek=1$
. Given the previous results of Draad & Nieuwstadt (Reference Draad and Nieuwstadt1998) and the excellent agreement between experiment and simulation here for two different Ekman numbers, we conclude that Coriolis forces can be significant in fully developed laminar square duct flow, especially for water. As a consequence, all of the data which follows is for 50 % glycerol/water solution (
$Ek=1$
. Given the previous results of Draad & Nieuwstadt (Reference Draad and Nieuwstadt1998) and the excellent agreement between experiment and simulation here for two different Ekman numbers, we conclude that Coriolis forces can be significant in fully developed laminar square duct flow, especially for water. As a consequence, all of the data which follows is for 50 % glycerol/water solution (
![]() $Ek\approx 7$
).
$Ek\approx 7$
).
4 Characteristics of low-Reynolds-number turbulent flows
4.1 Mean streamwise velocity measurements
Figure 5(a) shows the profile of streamwise velocity normalised by the bulk velocity, along the wall bisector, for both marginally turbulent
![]() $(Re=1203,Re_{{\it\tau}}=81)$
and fully turbulent
$(Re=1203,Re_{{\it\tau}}=81)$
and fully turbulent
![]() $(Re=2230,Re_{{\it\tau}}=161)$
flow. The DNS results of Gavrilakis (Reference Gavrilakis1992) at a Reynolds number of 2205
$(Re=2230,Re_{{\it\tau}}=161)$
flow. The DNS results of Gavrilakis (Reference Gavrilakis1992) at a Reynolds number of 2205
![]() $(Re_{{\it\tau}}=162)$
and Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) at a Reynolds number of 1205
$(Re_{{\it\tau}}=162)$
and Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) at a Reynolds number of 1205
![]() $(Re_{{\it\tau}}=84)$
as well as the laminar flow analytical solution (White Reference White2006) are also presented for the purpose of comparison. The flow was found to be symmetric, hence only the data from the lower half of the duct along the vertical bisector is presented,
$(Re_{{\it\tau}}=84)$
as well as the laminar flow analytical solution (White Reference White2006) are also presented for the purpose of comparison. The flow was found to be symmetric, hence only the data from the lower half of the duct along the vertical bisector is presented,
![]() $y$
being the distance from the bottom wall as shown in figure 2(b).
$y$
being the distance from the bottom wall as shown in figure 2(b).

Figure 5. Axial velocity profiles along the wall bisector. (a) In outer units. (b) In wall units. ○, experiment at
![]() $Re=1203$
(
$Re=1203$
(
![]() $Re_{{\it\tau}}=81$
); ▵, experiment at
$Re_{{\it\tau}}=81$
); ▵, experiment at
![]() $Re=2230$
(
$Re=2230$
(
![]() $Re_{{\it\tau}}=161$
);
$Re_{{\it\tau}}=161$
);
![]() $\cdots \cdots$
, DNS of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) at
$\cdots \cdots$
, DNS of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) at
![]() $Re=1205$
; —— (red), DNS of Gavrilakis (Reference Gavrilakis1992) at
$Re=1205$
; —— (red), DNS of Gavrilakis (Reference Gavrilakis1992) at
![]() $Re=2205$
(
$Re=2205$
(
![]() $Re_{{\it\tau}}=162$
); ——, laminar flow analytical solution (White Reference White2006). – – – –,
$Re_{{\it\tau}}=162$
); ——, laminar flow analytical solution (White Reference White2006). – – – –,
![]() $u^{+}=2.5\ln y^{+}+5.5$
; – ⋅ – ⋅ –, (blue),
$u^{+}=2.5\ln y^{+}+5.5$
; – ⋅ – ⋅ –, (blue),
![]() $u^{+}=y^{+}$
.
$u^{+}=y^{+}$
.
The experimental results show good agreement with DNS. It is interesting to note that the velocity gradient at the wall at
![]() $Re=1203$
is very similar to that of laminar flow. However, beyond
$Re=1203$
is very similar to that of laminar flow. However, beyond
![]() $y/h\approx 0.3$
, the mean flow becomes markedly different from the laminar case. The values of
$y/h\approx 0.3$
, the mean flow becomes markedly different from the laminar case. The values of
![]() $\langle U\rangle /U_{b}$
at the duct centre are 1.40 and 1.31 for marginally and fully turbulent flow, respectively.
$\langle U\rangle /U_{b}$
at the duct centre are 1.40 and 1.31 for marginally and fully turbulent flow, respectively.
In figure 5(b), the same data is plotted in wall units, indicated by the superscript
![]() $+$
, where the velocities have been normalised by local friction velocity
$+$
, where the velocities have been normalised by local friction velocity
![]() $(u_{{\it\tau}})$
. Again, data at
$(u_{{\it\tau}})$
. Again, data at
![]() $Re_{{\it\tau}}=161$
show excellent agreement with the DNS of Gavrilakis (Reference Gavrilakis1992). A large overshoot from the logarithmic law can be observed in the data for
$Re_{{\it\tau}}=161$
show excellent agreement with the DNS of Gavrilakis (Reference Gavrilakis1992). A large overshoot from the logarithmic law can be observed in the data for
![]() $Re_{{\it\tau}}=81$
, confirming that the wall shear stress distribution is characterised by a local minimum rather than maximum at the duct midpoint in marginally turbulent flows, as shown by Pinelli et al. (Reference Pinelli, Uhlmann, Sekimoto and Kawahara2010).
$Re_{{\it\tau}}=81$
, confirming that the wall shear stress distribution is characterised by a local minimum rather than maximum at the duct midpoint in marginally turbulent flows, as shown by Pinelli et al. (Reference Pinelli, Uhlmann, Sekimoto and Kawahara2010).
4.2 Instantaneous velocity measurements
The probability density functions (p.d.f.s) of instantaneous streamwise velocity,
![]() $U$
, normalised by either local mean,
$U$
, normalised by either local mean,
![]() $\langle U\rangle$
or bulk velocity,
$\langle U\rangle$
or bulk velocity,
![]() $U_{b}$
, for both marginally and fully turbulent flow are presented in figure 6. At
$U_{b}$
, for both marginally and fully turbulent flow are presented in figure 6. At
![]() $Re=1207$
(figure 6
a), switching of the flow field between two states is confirmed by the p.d.f. at
$Re=1207$
(figure 6
a), switching of the flow field between two states is confirmed by the p.d.f. at
![]() $y/h=0.3$
being bimodal. The point
$y/h=0.3$
being bimodal. The point
![]() $y/h=0.3$
has been chosen as it is where the largest difference between the two flow states can be observed in the DNS data of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007). The data were collected over a period of
$y/h=0.3$
has been chosen as it is where the largest difference between the two flow states can be observed in the DNS data of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007). The data were collected over a period of
![]() $12\,843h/U_{b}$
(3600 s), sufficiently long to capture many switches between states. The p.d.f. could be viewed as a combination of two p.d.f.s, one for each flow state; but separating the two is not a trivial task as there is a significant overlap. It can be partially achieved by plotting a p.d.f. of modal velocities (dotted line in figure 6
a). Each modal velocity is taken from a sample of data of the order of
$12\,843h/U_{b}$
(3600 s), sufficiently long to capture many switches between states. The p.d.f. could be viewed as a combination of two p.d.f.s, one for each flow state; but separating the two is not a trivial task as there is a significant overlap. It can be partially achieved by plotting a p.d.f. of modal velocities (dotted line in figure 6
a). Each modal velocity is taken from a sample of data of the order of
![]() $43h/U_{b}$
. The resulting p.d.f. shows the bimodal form created by the two flow states more clearly, although there is still overlap. The values of
$43h/U_{b}$
. The resulting p.d.f. shows the bimodal form created by the two flow states more clearly, although there is still overlap. The values of
![]() $U/\langle U\rangle$
at the peaks correspond very well to those extracted from the time averages of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) as shown by the dashed vertical lines in figure 6(a).
$U/\langle U\rangle$
at the peaks correspond very well to those extracted from the time averages of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) as shown by the dashed vertical lines in figure 6(a).

Figure 6. Probability density functions of
![]() $U/U_{b}$
: (a)
$U/U_{b}$
: (a)
![]() $Re=1207$
and
$Re=1207$
and
![]() $y/h=0.3$
; dotted line is the p.d.f. of modal velocities and dashed lines correspond to short time averages for each state from the DNS data of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007); (b)
$y/h=0.3$
; dotted line is the p.d.f. of modal velocities and dashed lines correspond to short time averages for each state from the DNS data of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007); (b)
![]() $Re=1203$
: ○,
$Re=1203$
: ○,
![]() $y/h=0.2$
; ▫,
$y/h=0.2$
; ▫,
![]() $y/h=0.3$
; ♢,
$y/h=0.3$
; ♢,
![]() $y/h=0.4$
;
$y/h=0.4$
;
![]() $+$
,
$+$
,
![]() $y/h=0.5$
;
$y/h=0.5$
;
![]() $\times$
,
$\times$
,
![]() $y/h=0.6$
; *,
$y/h=0.6$
; *,
![]() $y/h=1$
; (c)
$y/h=1$
; (c)
![]() $y/h=0.3$
: ○,
$y/h=0.3$
: ○,
![]() $Re=1097$
; ▫,
$Re=1097$
; ▫,
![]() $Re=1125$
; ♢,
$Re=1125$
; ♢,
![]() $Re=1207$
;
$Re=1207$
;
![]() $\times$
,
$\times$
,
![]() $Re=1290$
;
$Re=1290$
;
![]() $+$
,
$+$
,
![]() $Re=1370$
; △,
$Re=1370$
; △,
![]() $Re=1596$
; *,
$Re=1596$
; *,
![]() $Re=2234$
.
$Re=2234$
.

Figure 7. Joint p.d.f. at
![]() $y/h=0.3$
and
$y/h=0.3$
and
![]() $Re=1290$
. Data were collected over a period of
$Re=1290$
. Data were collected over a period of
![]() $7004h/U_{b}$
.
$7004h/U_{b}$
.
A bimodal p.d.f. also occurs at
![]() $y/h=0.2$
but beyond
$y/h=0.2$
but beyond
![]() $y/h=0.4$
, this dual-peak feature fades away at higher distances from the wall as the two flow states become increasingly similar (see figure 6
b). In contrast, the p.d.f. for fully turbulent flow at
$y/h=0.4$
, this dual-peak feature fades away at higher distances from the wall as the two flow states become increasingly similar (see figure 6
b). In contrast, the p.d.f. for fully turbulent flow at
![]() $Re=2234$
and
$Re=2234$
and
![]() $y/h=0.3$
(figure 6
c) is unimodal, indicating that the flow exists in only one state. In this study, bimodal p.d.f.s at
$y/h=0.3$
(figure 6
c) is unimodal, indicating that the flow exists in only one state. In this study, bimodal p.d.f.s at
![]() $y/h=0.3$
were observed between
$y/h=0.3$
were observed between
![]() $Re=1097$
and
$Re=1097$
and
![]() $Re=1370$
as shown in figure 6(c). The two peaks are mostly of different heights, indicating that the flow spends more time in one state than in the other, the largest peak gradually shifting from left to right as the Reynolds number is increased (see figure 6
c).
$Re=1370$
as shown in figure 6(c). The two peaks are mostly of different heights, indicating that the flow spends more time in one state than in the other, the largest peak gradually shifting from left to right as the Reynolds number is increased (see figure 6
c).
The joint p.d.f. of streamwise and wall-normal velocities at
![]() $Re=1290$
for data collected over a period of
$Re=1290$
for data collected over a period of
![]() $7004h/U_{b}$
is shown in figure 7. A dual peak can be clearly seen, corresponding to two flow states, A and B. In state A, streamwise velocities lower than the long-term mean (indicated as a dotted line) are highly probable to occur alongside wall-normal velocities which are higher than the long term mean (shown as a solid black line). In state B, streamwise velocities higher than the long-term average have a higher probability of occurring together with essentially zero wall-normal velocities at this measurement location. This behaviour is consistent with the findings of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) with regard to the streak-vortex arrangement for any given pair of opposite walls during marginally turbulent flow. The flow alternating between periods of high turbulence activity, characterised by a low-velocity streak at the wall bisector flanked by vortices (corresponding to state A), and more quiescent periods where there are no streaks and the flow is essentially unidirectional at the measurement location (state B).
$7004h/U_{b}$
is shown in figure 7. A dual peak can be clearly seen, corresponding to two flow states, A and B. In state A, streamwise velocities lower than the long-term mean (indicated as a dotted line) are highly probable to occur alongside wall-normal velocities which are higher than the long term mean (shown as a solid black line). In state B, streamwise velocities higher than the long-term average have a higher probability of occurring together with essentially zero wall-normal velocities at this measurement location. This behaviour is consistent with the findings of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) with regard to the streak-vortex arrangement for any given pair of opposite walls during marginally turbulent flow. The flow alternating between periods of high turbulence activity, characterised by a low-velocity streak at the wall bisector flanked by vortices (corresponding to state A), and more quiescent periods where there are no streaks and the flow is essentially unidirectional at the measurement location (state B).
Variation of streamwise velocity skewness with distance from the duct wall is shown in figure 8(a). The data for
![]() $Re=2230$
show excellent agreement with the DNS of Gavrilakis (Reference Gavrilakis1992), having positive values very close to the wall and becoming negative beyond
$Re=2230$
show excellent agreement with the DNS of Gavrilakis (Reference Gavrilakis1992), having positive values very close to the wall and becoming negative beyond
![]() $y/h\approx 0.075$
. For
$y/h\approx 0.075$
. For
![]() $Re=1203$
, the velocities are more positively skewed in the near-wall region up to
$Re=1203$
, the velocities are more positively skewed in the near-wall region up to
![]() $y/h\approx 0.7$
, this is due to the presence of the two flow states at the marginally turbulent Reynolds number as shown by the p.d.f.s in figure 6. Beyond
$y/h\approx 0.7$
, this is due to the presence of the two flow states at the marginally turbulent Reynolds number as shown by the p.d.f.s in figure 6. Beyond
![]() $y/h\approx 0.7$
, similar values of skewness are observed in both flows.
$y/h\approx 0.7$
, similar values of skewness are observed in both flows.

Figure 8. (a) Axial velocity skewness along the wall bisector: ○ experiment at
![]() $Re=1203$
; ▵, experiment at
$Re=1203$
; ▵, experiment at
![]() $Re=2230$
; ——, DNS of Gavrilakis (Reference Gavrilakis1992) at
$Re=2230$
; ——, DNS of Gavrilakis (Reference Gavrilakis1992) at
![]() $Re=2205$
. (b) Streamwise velocity autocorrelation at
$Re=2205$
. (b) Streamwise velocity autocorrelation at
![]() $y/h=0.3$
: – – – (red),
$y/h=0.3$
: – – – (red),
![]() $Re=1207$
; —— (blue),
$Re=1207$
; —— (blue),
![]() $Re=2234$
;
$Re=2234$
;
![]() ${\rm\Delta}t$
is the time lag.
${\rm\Delta}t$
is the time lag.
Streamwise velocity autocorrelation functions
![]() $(R_{uu})$
for both marginally and fully turbulent flows at
$(R_{uu})$
for both marginally and fully turbulent flows at
![]() $y/h=0.3$
are shown in figure 8(b). The marginally turbulent flow is correlated over a larger time period reinforcing the evidence that the flow remains in a particular state for a significant period of time. The integral time scales have been computed by integrating the autocorrelation functions up to the first zero crossing. The integral time scale for marginally turbulent flow
$y/h=0.3$
are shown in figure 8(b). The marginally turbulent flow is correlated over a larger time period reinforcing the evidence that the flow remains in a particular state for a significant period of time. The integral time scales have been computed by integrating the autocorrelation functions up to the first zero crossing. The integral time scale for marginally turbulent flow
![]() $(2.24h/U_{b})$
is significantly larger than fully turbulent flow
$(2.24h/U_{b})$
is significantly larger than fully turbulent flow
![]() $(0.89h/U_{b})$
. Given this evidence for the persistence of each of the two states it is a valid approximation to use Taylor’s hypothesis of frozen flow to convert our time-series data into a pseudo-spatial streamwise dimension using an appropriate convection velocity (Taylor Reference Taylor1938; Dennis & Nickels Reference Dennis and Nickels2008). It is reasonable to use the bulk velocity as an approximate convection velocity and as such the non-dimensional streamwise extent becomes,
$(0.89h/U_{b})$
. Given this evidence for the persistence of each of the two states it is a valid approximation to use Taylor’s hypothesis of frozen flow to convert our time-series data into a pseudo-spatial streamwise dimension using an appropriate convection velocity (Taylor Reference Taylor1938; Dennis & Nickels Reference Dennis and Nickels2008). It is reasonable to use the bulk velocity as an approximate convection velocity and as such the non-dimensional streamwise extent becomes,
![]() ${\rm\Delta}x={\rm\Delta}tU_{b}/h$
. Therefore figure 8(b) can be viewed as a statistical measure of the increased streamwise correlation in marginally turbulent flow. We hypothesise that this is as a result of each of the two states having a significant streamwise distance, and hence there is a spatial switching between the two states along the length of the duct. This is distinct from the temporal switching observed in the axially minimal flow unit in the DNS of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007).
${\rm\Delta}x={\rm\Delta}tU_{b}/h$
. Therefore figure 8(b) can be viewed as a statistical measure of the increased streamwise correlation in marginally turbulent flow. We hypothesise that this is as a result of each of the two states having a significant streamwise distance, and hence there is a spatial switching between the two states along the length of the duct. This is distinct from the temporal switching observed in the axially minimal flow unit in the DNS of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007).
4.3 Turbulence intensity and Reynolds stress measurements
The streamwise and wall-normal turbulence intensities at
![]() $Re_{{\it\tau}}=81$
(
$Re_{{\it\tau}}=81$
(
![]() $Re=1203$
) and
$Re=1203$
) and
![]() $Re_{{\it\tau}}=161$
(
$Re_{{\it\tau}}=161$
(
![]() $Re=2230$
) as a function of distance from the duct wall along the bisector, in outer units, are shown in figure 9(a). It can be observed that
$Re=2230$
) as a function of distance from the duct wall along the bisector, in outer units, are shown in figure 9(a). It can be observed that
![]() $u_{rms}/U_{b}$
for fully turbulent flow shows good agreement with the DNS of Gavrilakis (Reference Gavrilakis1992), attaining a peak at
$u_{rms}/U_{b}$
for fully turbulent flow shows good agreement with the DNS of Gavrilakis (Reference Gavrilakis1992), attaining a peak at
![]() $y/h\approx 0.1$
. This peak value is however slightly higher than the DNS result. In the marginally turbulent case, there appears to be a shift in the location of the maximum value of
$y/h\approx 0.1$
. This peak value is however slightly higher than the DNS result. In the marginally turbulent case, there appears to be a shift in the location of the maximum value of
![]() $u_{rms}/U_{b}$
away from the wall to
$u_{rms}/U_{b}$
away from the wall to
![]() $y/h\approx 0.3$
. Close to the duct wall, the streamwise velocity fluctuations are lower than in fully turbulent flow but become larger as the peak value is approached and remains so across the remaining portion of the duct, creating an impression that the turbulence level is higher. Figure 9(b) shows the same data plotted as a function of distance along the bisector in wall units. In this case, the streamwise turbulence intensities,
$y/h\approx 0.3$
. Close to the duct wall, the streamwise velocity fluctuations are lower than in fully turbulent flow but become larger as the peak value is approached and remains so across the remaining portion of the duct, creating an impression that the turbulence level is higher. Figure 9(b) shows the same data plotted as a function of distance along the bisector in wall units. In this case, the streamwise turbulence intensities,
![]() $u_{rms}^{+}$
are very similar in both flows, with
$u_{rms}^{+}$
are very similar in both flows, with
![]() $u_{rms}^{+}$
at
$u_{rms}^{+}$
at
![]() $Re_{{\it\tau}}=81$
becoming lower than the fully turbulent values beyond
$Re_{{\it\tau}}=81$
becoming lower than the fully turbulent values beyond
![]() $y^{+}$
of 63.
$y^{+}$
of 63.

Figure 9. Turbulence intensities along the wall bisector: (a) as a function of
![]() $y/h$
; (b) as a function of
$y/h$
; (b) as a function of
![]() $y^{+}$
; ○, experiment at
$y^{+}$
; ○, experiment at
![]() $Re_{{\it\tau}}=81$
; ▵, experiment at
$Re_{{\it\tau}}=81$
; ▵, experiment at
![]() $Re_{{\it\tau}}=161$
; ——, DNS of Gavrilakis (Reference Gavrilakis1992) at
$Re_{{\it\tau}}=161$
; ——, DNS of Gavrilakis (Reference Gavrilakis1992) at
![]() $Re_{{\it\tau}}=162$
. Open and closed symbols represent streamwise and wall-normal turbulence intensities, respectively.
$Re_{{\it\tau}}=162$
. Open and closed symbols represent streamwise and wall-normal turbulence intensities, respectively.
The wall-normal turbulence intensities, which are significantly smaller, are almost constant across the duct and no distinct maxima can be identified. The wall-normal turbulence intensities at
![]() $Re_{{\it\tau}}=161$
show good agreement with DNS data, they are however a little higher than the simulation values towards the duct centre and larger than those at
$Re_{{\it\tau}}=161$
show good agreement with DNS data, they are however a little higher than the simulation values towards the duct centre and larger than those at
![]() $Re_{{\it\tau}}=81$
. The results indicate that near the centre of the duct, the turbulence is nearly isotropic, as shown by the closeness of
$Re_{{\it\tau}}=81$
. The results indicate that near the centre of the duct, the turbulence is nearly isotropic, as shown by the closeness of
![]() $u_{rms}^{+}$
and
$u_{rms}^{+}$
and
![]() $v_{rms}^{+}$
values at high
$v_{rms}^{+}$
values at high
![]() $y^{+}$
.
$y^{+}$
.
Figure 10 shows the variation of Reynolds shear stress along the wall bisector. The data have been normalised by the square of the bulk velocity. Since only the value of local friction velocity
![]() $(u_{{\it\tau}})$
at the wall midpoint is available in this experiment, normalising by
$(u_{{\it\tau}})$
at the wall midpoint is available in this experiment, normalising by
![]() $u_{{\it\tau}}^{2}$
will not provide a true picture of Reynolds shear stress distribution. The data for
$u_{{\it\tau}}^{2}$
will not provide a true picture of Reynolds shear stress distribution. The data for
![]() $Re=2230$
is in good agreement with DNS. At
$Re=2230$
is in good agreement with DNS. At
![]() $Re=1203$
, Reynolds shear stress can be observed to be lower for
$Re=1203$
, Reynolds shear stress can be observed to be lower for
![]() $y/h<0.4$
. There is also a shift in location of the maximum away from the duct wall. As the duct centre is approached, Reynolds shear stress drops to zero for both flows as it must due to symmetry.
$y/h<0.4$
. There is also a shift in location of the maximum away from the duct wall. As the duct centre is approached, Reynolds shear stress drops to zero for both flows as it must due to symmetry.
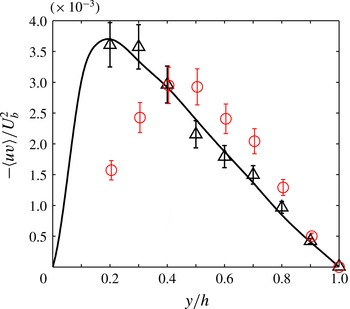
Figure 10. Variation of Reynolds shear stress along the wall bisector: ○ (red) experiment at
![]() $Re=1203$
; ▵, experiment at
$Re=1203$
; ▵, experiment at
![]() $Re=2230$
; ——, DNS of Gavrilakis (Reference Gavrilakis1992) at
$Re=2230$
; ——, DNS of Gavrilakis (Reference Gavrilakis1992) at
![]() $Re=2205$
.
$Re=2205$
.
5 Conclusion
The behaviour of turbulent flow in a square duct at relatively low Reynolds numbers has been studied. The results for both marginally turbulent flow at
![]() $Re_{{\it\tau}}=81$
and fully turbulent flow at
$Re_{{\it\tau}}=81$
and fully turbulent flow at
![]() $Re_{{\it\tau}}=161$
show good agreement with the DNS data of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) and Gavrilakis (Reference Gavrilakis1992), respectively. It has been shown that the onset of turbulence can be significantly affected by Coriolis effects due to the Earth’s rotation. This is as a result of differences in the laminar base flow velocity profiles at different values of Ekman number prior to transition. A limiting Reynolds number of about 940 for transition was observed at
$Re_{{\it\tau}}=161$
show good agreement with the DNS data of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007) and Gavrilakis (Reference Gavrilakis1992), respectively. It has been shown that the onset of turbulence can be significantly affected by Coriolis effects due to the Earth’s rotation. This is as a result of differences in the laminar base flow velocity profiles at different values of Ekman number prior to transition. A limiting Reynolds number of about 940 for transition was observed at
![]() $Ek\approx 7$
. This value is within the range obtained in previous numerical studies.
$Ek\approx 7$
. This value is within the range obtained in previous numerical studies.
In marginally turbulent flow a mean flow very similar to laminar flow has been observed in the vicinity of the duct wall, as well as a large overshoot from the logarithmic law nearer the centre. Switching between two flow states, originally predicted by the DNS of Uhlmann et al. (Reference Uhlmann, Pinelli, Kawahara and Sekimoto2007), is confirmed by bimodal p.d.f.s of streamwise velocity at certain distances from the duct wall and a joint p.d.f. of streamwise and wall-normal velocity which features two peaks corresponding to each of the two states: one essentially unidirectional (
![]() $v^{+}\approx 0$
) at the measurement location and the other containing a significant secondary flow component (
$v^{+}\approx 0$
) at the measurement location and the other containing a significant secondary flow component (
![]() $V/\langle U\rangle \approx 0.03$
).
$V/\langle U\rangle \approx 0.03$
).
It has been shown that marginally turbulent flow is more correlated than a fully turbulent flow as indicated by its longer integral time scale. Similar levels of
![]() $u_{rms}^{+}$
have been observed in both flows at different
$u_{rms}^{+}$
have been observed in both flows at different
![]() $y^{+}$
. The Reynolds stresses in the near-wall region are however lower in the former but become very similar to those of fully turbulent flow as the duct centre is approached.
$y^{+}$
. The Reynolds stresses in the near-wall region are however lower in the former but become very similar to those of fully turbulent flow as the duct centre is approached.
Acknowledgements
The authors wish to thank Professor Uhlmann of the Institute of Hydromechanics, University of Karlsruhe, Germany for providing data from their DNS for comparison with our experiments. R.J.P. acknowledges funding for a ‘Fellowship in Complex Fluids and Rheology’ from the Engineering and Physical Sciences Research Council (EPSRC, UK) under grant number EP/M025187/1.













