Introduction
Moraines of the Younger Dryas ˚Egesen Stadial" are conspicuous features in many parts of the Alps. The abundant geomorphological record from this period of time is a valuable terrestrial palaeoclimatic archive, because it is sufficiently extensive to allow a detailed and accurate reconstruction of the former glacier topographies. In this paper we offer some perspectives from quantitative palaeo-glaciologic and palaeoclimatic interpretation of that record using simple statistical and glacial-meteorological glacier-climate models. This work continues that of Reference KerschnerKerschner (1981, Reference Kerschner1985), Reference KuhnKuhn (1981b) and Maisch and Reference HaeberliHaeberli (1982), using a much larger database. Depressions of the equilibrium-line altitude (ELA) and timberline (TL) are the principal input data. The main focus will be on early Younger Dryas precipitation patterns in the northern and central Alps. These may serve as a check for the results from atmospheric general circulation models (AGCMs) for the Younger Dryas (Reference Isarin, Renssen and KosterIsarin and others, 1997; Reference RenssenRenssen, 1997), because regional precipitation patterns in the Alps are closely linked to synoptic-scale airflow patterns (Reference Fliri and SchueppFliri and Schuepp, 1983).
Methods
The Late-glacial moraine sequence ("stadials") has been extensively mapped in both the Austrian and Swiss Alps (e.g. Reference HeubergerHeuberger, 1966; Reference Mayr, Heuberger and RichmondMayr and Heuberger, 1968; Reference KerschnerKerschner 1978; Reference Furrer, Burga, Gamper, Holzhauser and MaischFurrer and others, 1987 and references therein). The moraines of the ˚Egesen Stadial" are the most marked and widespread of the series. In many valleys, three and sometimes four distinct sets of moraines can be found (Egesen-I to Egesen-III, Kromer/Kartell), representing the last cold event prior to the many advances of Holocene age, which characteristically reached only the Little Ice Age (LIA) extent (e.g. Reference Patzelt and BortenschlagerPatzelt and Bortenschlager, 1973; Reference HolzhauserHolzhauser, 1984). Basal radiocarbon dates from peat bogs and the results from pollen analysis in the tongue areas of Egesen moraines are in the late Younger Dryas-early Preboreal time range (e.g. Reference PatzeltPatzelt, 1972; Reference Müller, Kerschner and KuttelMüller and others, 1981; Reference BortenschlagerBortenschlager, 1984; Reference Furrer, Burga, Gamper, Holzhauser and MaischFurrer and others, 1987; Reference Burga and PerretBurga and Perret, 1998). Surface exposure ages of an Egesen-I moraine at Julier pass, Switzerland, show that it was deposited a few centuries after the onset of the Younger Dryas (Reference Ivy-Ochs, Schluchter, Kubik and BeerIvy-Ochs and others, 1995,Reference Ivy-Ochs, Schluchter, Kubik, Synal, Beer and Kerschner1996).
ELAs are determined using an accumulation-area ratio of 0.67 and are normally considered reliable within ±20 m. For practical reasons, ELA depressions (ΔELAs) are calculated relative to the weighted mean of the Little Ice Age (1850) ELA in the respective catchments (Reference Groß, Kerschner and PatzeltGroB and others, 1977). For a comparison with modern (1931–60) climatic data, it is assumed that the ˚modern" (mid-20th-century) ELA is 100 m higher. For the purpose of this paper, this seems to be a reasonable mean value for average-sized glaciers in the Alps (Reference GroßGroB, 1987; Reference MaischMaisch, 1992). The ΔELA values of the Egesen-I advance used in this paper were taken from our own fieldwork and from the literature (see Appendix). They show a characteristic spatial pattern with highest values (–400 to –500 m vs modern values) at the northern and western margins of the eastern Alps (e.g. western Silvretta mountains, Zugspitze and the Karwendel massif), and lowest values (–300 to –280 m) in the well-sheltered central valleys of the Alps (e.g. western Otztal mountains, upper Engadine). The gradient from areas with large ΔELA values to those with smaller ΔEL As is usually strong where the mountain chains form a barrier for precipitation associated with westerly and northwesterly airflow.
Information on theTL depression (ΔTL) comes from the palynological literature. Summaries are given by Reference BortenschlagerBortenschlager (1984) and Reference Burga and PerretBurga and Perret (1998). The necessary temperature data were taken from Reference FliriFliri (1974, Reference Fliri1975). They refer to the standard climatic period 1931–60 and are carefully homogenized. For modern precipitation data from high altitudes, we finally relied upon the results of the (P,T) model of Reference Ohmura, Kasser and FunkOhmura and others (1992; see below). These are assumed to be more ˚realistic" than precipitation figures from actual measurements due to the well-known measurement problems at high altitudes (e.g. Reference Frei and ScharFrei and Schar, 1998).
Through a complicated biological process, summer temperature determines the TL altitude (Reference TranquilliniTranquillini, 1979). Therefore, TL fluctuations are excellent parameters for summer temperature fluctuations. During the Younger Dryas, the alpine TL was 400–500 m lower than today. As it was lowered at the Allerød-Younger Dryas boundary, we can safely assume that its altitude during the Younger Dryas was determined by climate and not by the development of the alpine forest belt during the Late glacial (Reference Patzelt, Bortenschlager and FrenzelPatzelt and Bortenschlager, 1976; Reference BortenschlagerBortenschlager, 1984; Reference Burga and PerretBurga and Perret, 1998). For our calculations, we used a ΔTL value of –500 m (Reference Burga and PerretBurga and Perret, 1998). If we assume that summer temperature at theTL remains constant, the depression of summer temperature (ΔTs) can be calculated as ΔTs = ― Δ TL (∂T/∂z). With a temperature lapse rate (∂T/∂z) of –0.007 K m–1, a TL depression of –500 m is equivalent to a summer temperature depression of –3.5 K.
The ELA is determined by the climatic conditions which govern ablation and accumulation. Hence, a vertical shift of the ELA can be caused by changes in both ablation and accumulation. In many statistical glacier-climate models, ablation is parameterized by ˚summer temperature" at the ELA (Ts), and accumulation by ˚precipitation" (P). In this paper, we chose the statistical (P, T) relation of Reference Ohmura, Kasser and FunkOhmura and others (1992) and compare the results with those derived from the glacial-meteorological model of Reference KuhnKuhn (1981a). For convenience, the models are referred to below as ˚OKF model" and ˚Kuhn model".
Reference Ohmura, Kasser and FunkOhmura and others (1992, p. 401) found a non-linear relationship between the free-air summer (June-August) temperature and annual precipitation sums at the ELA, which has the form
with a standard error of the estimate of ±200 mm. Summer temperature at the modern ELA (TSm) is calculated in a first step from the standard temperature data provided by Reference FliriFliri (1974,Reference Fliri1975). Comparison of the standard climatological temperature data with the free-air temperature data used by Reference Ohmura, Kasser and FunkOhmura and others (1992) shows that the former must be augmented by 0.7 K in the central part of the Alps (high ELA) to achieve a comparable dataset, whereas they are more or less similar at the northern slope of the Alps (low ELA). Then precipitation at the modern ELA (Pm) is calculated with Equation (1). Pm is used as a reference for all subsequent calculations.
Summer temperature at the Egesen-I ELA (TSE) is calculated as
Precipitation at the Egesen-I ELA (PE) is also calculated with Equation (1). Precipitation change Δ P at the modern ELA can then be calculated as
where ∂P/∂z is the vertical precipitation gradient. For our calculations we chose ∂P/∂z as 0.33 mm nT1, which is slightly higher than the figure given by Reference FliriFliri (1975).
For comparison, precipitation change was also calculated with the glacial-meteorological model of Reference KuhnKuhn (1981a), which relates energy and mass balance at the equilibrium line. Details can be found in Reference KuhnKuhn (1981a, Reference Kuhnb, Reference Kuhn and Oerlemans1989). For our purpose, the model is first used to calculate accumulation changes. If Ac denotes the change of accumulation, it can be calculated as
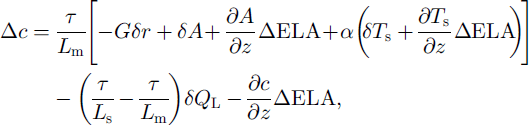
where τ is the duration of the ablation period (100 d), Lm and Ls are the latent heat of fusion (0.335 MJ kg–1) and of sublimation (2.835 MJ kg–1), respectively, G is the global radiation (20 MJ m–2d–1), τ is the albedo, A is the atmospheric longwave radiation, a is the turbulent heat-exchange coefficent (1.5 MJ m–2 d–1), Ts is the air temperature of the ablation period, Q.L is the latent-heat flux and ∂c/∂z is the vertical accumulation gradient (1 kgm–2m–1 ) . All changes not incorporated in Equation (4) are considered as zero.
Following Reference KuhnKuhn (1981a), the change in longwave atmospheric radiation is linearized as
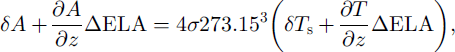
where a is the Stefan-Boltzmann constant (4.9 × l0–9 MJ K–4 d–1). The change in the latent-heat flux δQL can be calculated as δQl=δs–(Lsτ), where SS is the change in sublimation (kg m–2 a–1). Finally, the change in precipitation is calculated as ΔP = Δc/1.5 under the assumption that accumulation is 50% larger than precipitation at the ELA.
Discussion
The results of our calculations are summarized in Figures 1 and 2. The solid lines in Figure 1 show different scenarios for the Kuhn model (Equation (4)). The data points of the OKF model are close to the Kuhn model, with no changes in albedo and sublimation in those areas where the depression of the ELA is on the order of –300 m. Closer to the northern slope of the Alps, where ΔELA is in the order of –450 to 500 m, the results of the OKF model suggest that albedo and/or sublimation were slightly higher than can be expected today.
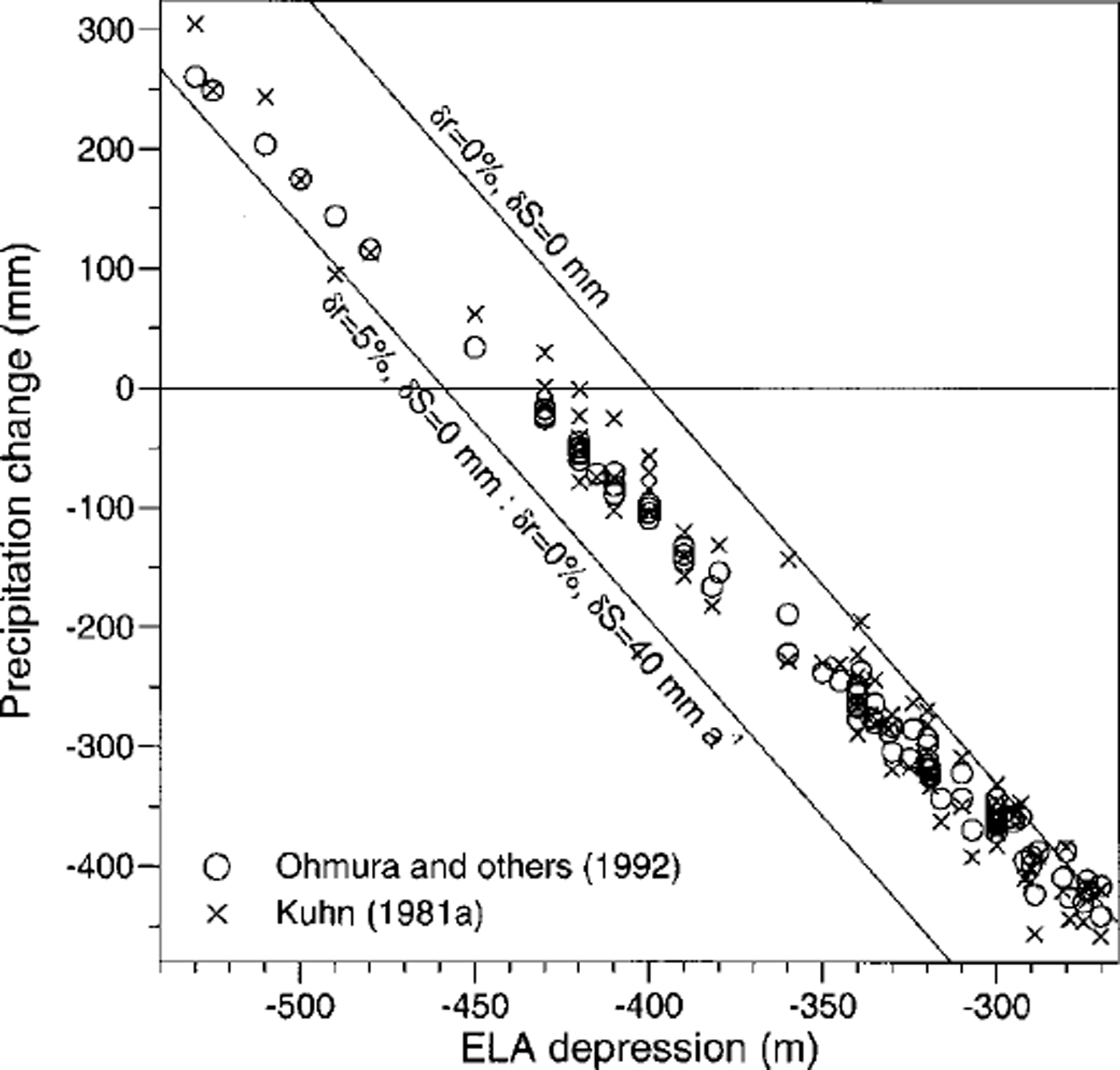
Fig. 1. Relation between early Younger Dryas (Egesen-I) ELA depression and precipitation change (mm a–11).
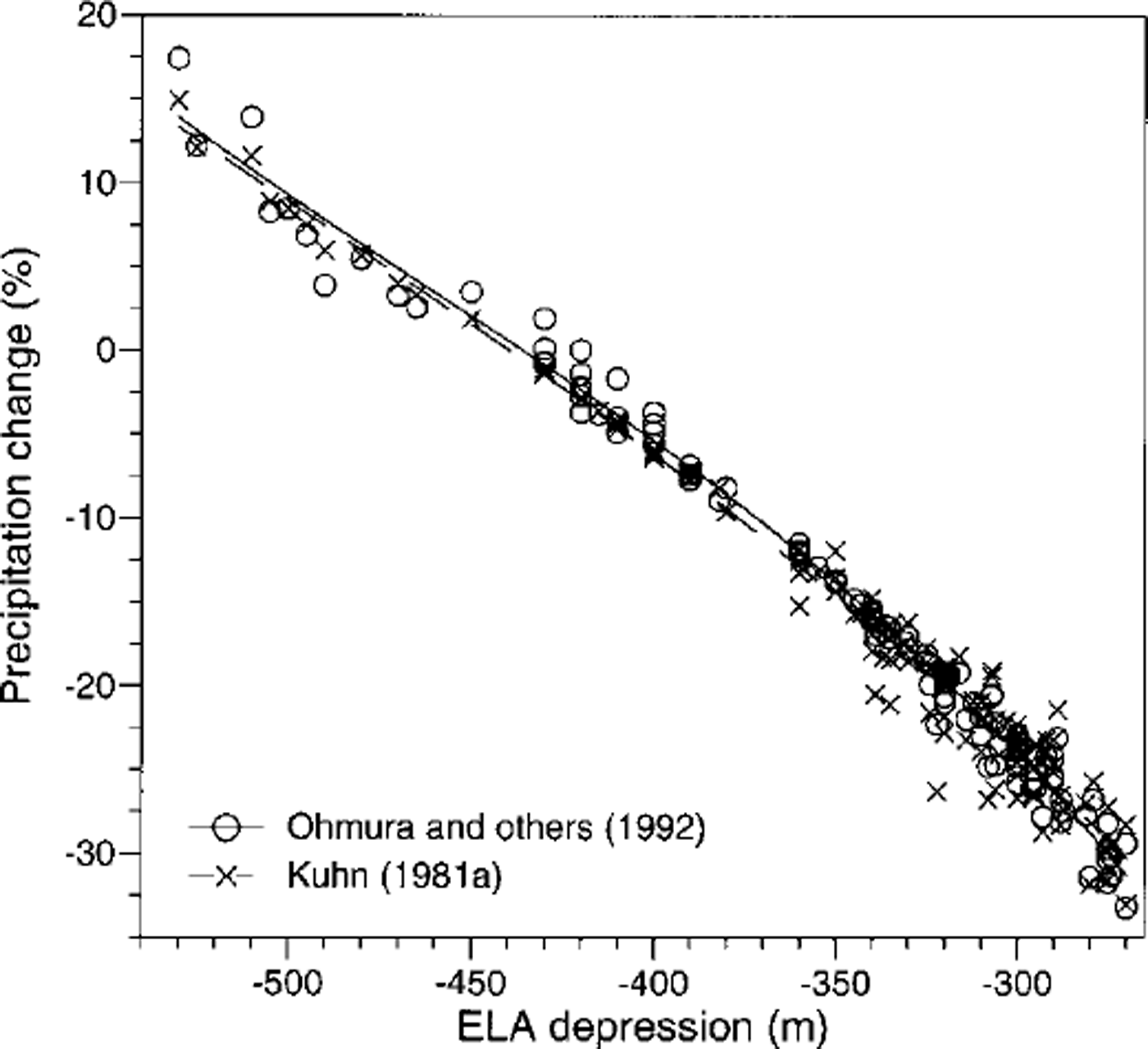
Fig. 2. Relation between early Younger Dryas (Egesen-I) ELA depression and precipitation change (%).
The best correlation between the OKF model and the Kuhn model is achieved if albedo values are gradually increased towards the northern margin of the Alps. We assume that albedo remained unchanged (Sr = 0) in the central part of the Alps (high ELA) and increased by 5% towards the northern margin (low ELA; Sr = 0.05), which is equivalent to an increase in evaporation from the glacier surface by 40 mm a"1. In that case, the correlation coefficient of precipitation change between the two models is 0.995 (Fig. 3).
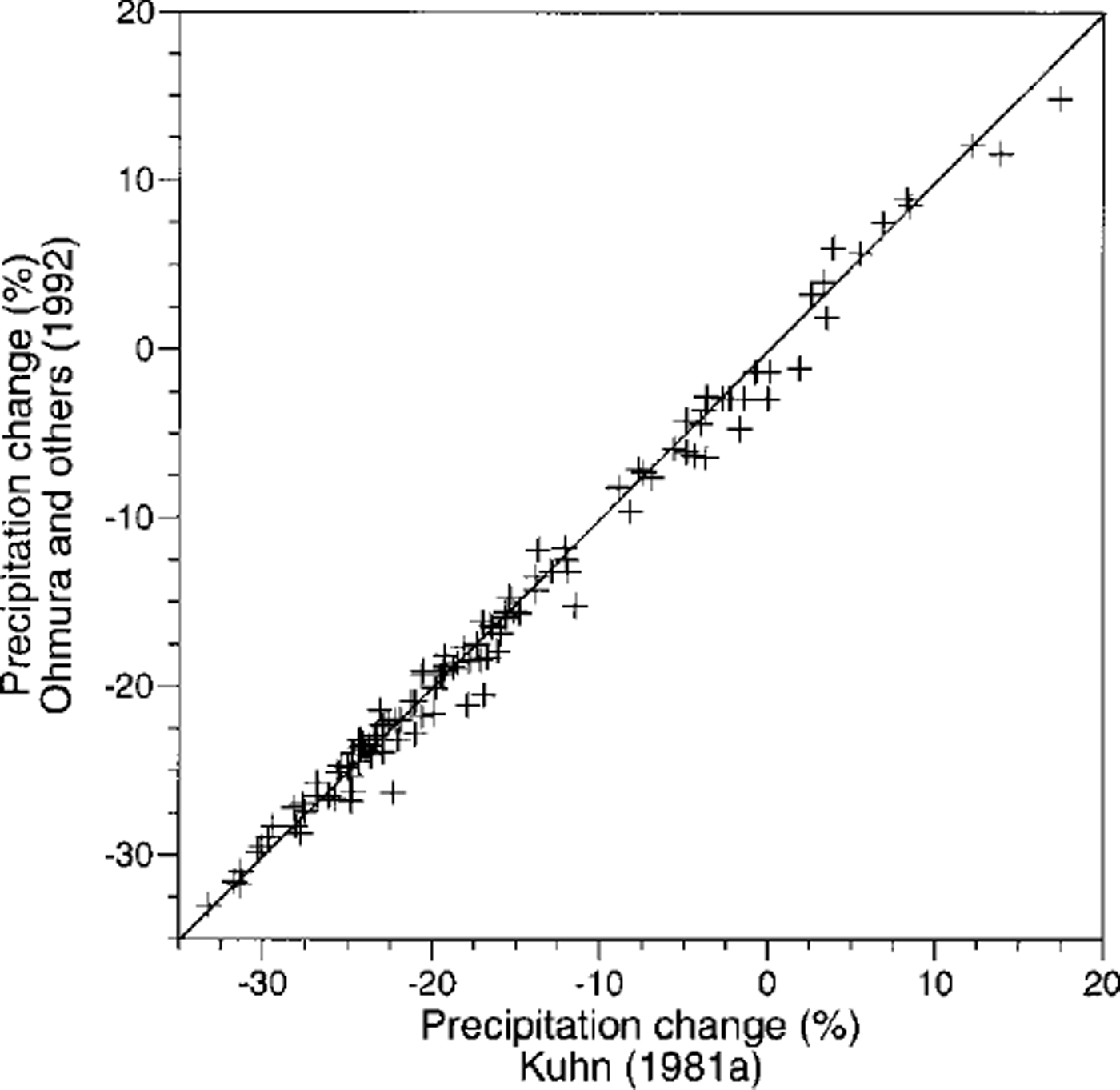
Fig. 3. Correlation between results from the models by Reference Ohmura, Kasser and FunkOhmura and others (1992) and Reference KuhnKuhn (1981a).
Figures 1 and 2 show a clear correlation between ΔELA and precipitation change. Under the assumptions made above, AP ranges between –450 mm a"1 (ΔELA = –270 m) and +250 mm a"1 (ΔELA = 520 m) or –30 to ― 3 5% and + 12%, respectively. The central, well-shielded valleys of the Alps were obviously drier than today, whereas areas exposed to westerly and northwesterly airflow seem to have been slightly more humid than today (Fig. 4). The results are broadly similar to those from earlier studies on Younger Dryas precipitation patterns in the Alps, which were based on a different methodology (Reference KerschnerKerschner, 1981,Reference Kerschner1985). They are at least partially supported by the results from permafrost-glacier studies (Reference HaeberliHaeberli 1982; Reference Sailer and KerschnerSailer and Kerschner, 1999) and the palaeoclimatic interpretation of other glaciological parameters from Late-glacial glaciers in the Alps (Maisch and Reference HaeberliHaeberli, 1982). They also agree well with the qualitative results from palaeobotanical studies (cf Reference Burga and PerretBurga and Perret, 1998). The spatial pattern of ELA depressions and precipitation change is surprisingly similar to the present-day precipitation pattern, as it is caused by cyclonic westerly and northwesterly airflow (Reference Fliri and SchueppFliri and Schuepp, 1983). This supports the results from AGCMs of the Younger Dryas (Reference Isarin, Renssen and KosterIsarin and others, 1997; Reference RenssenRenssen, 1997) which suggest a more zonal circulation over northwestern and western Europe during the Younger Dryas.
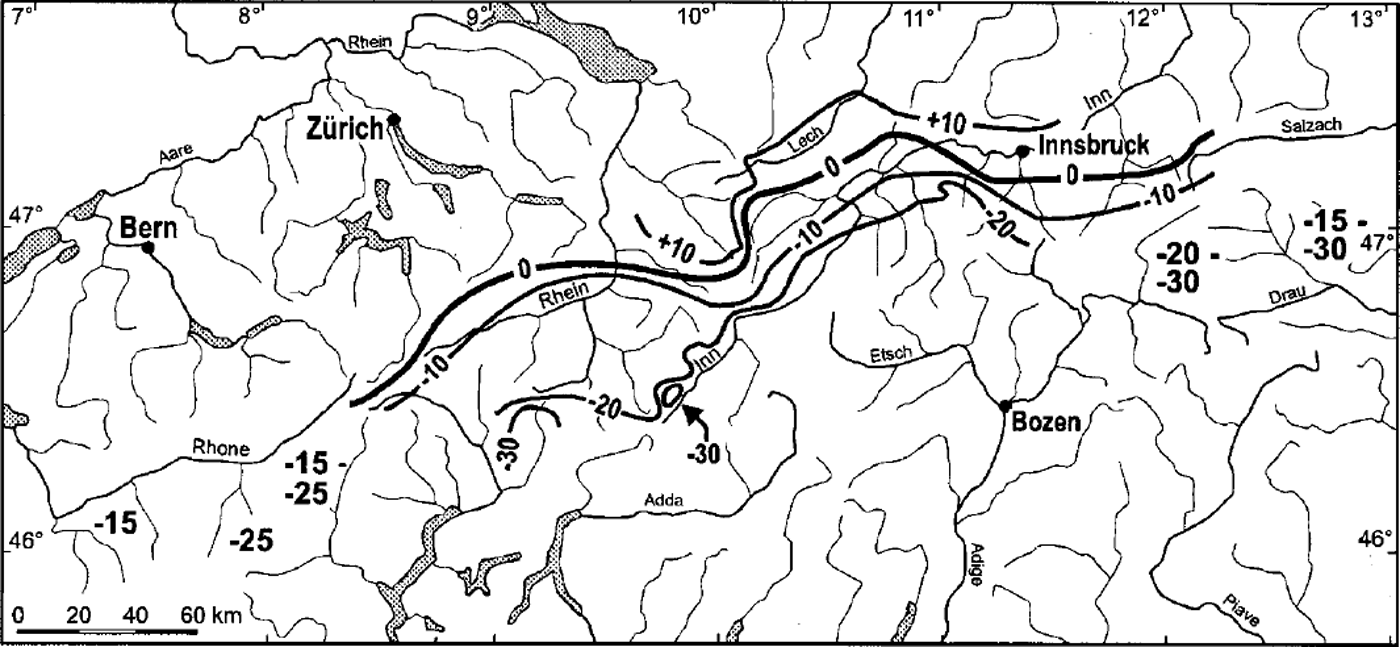
Fig. 4. Tentative map of early Younger Dryas (Egesen-I) precipitation change (%)in the Alps between Rhone valley to the west and Hohe Tauern mountains to the east.
Some possible error sources should be mentioned. One of them is the possible misinterpretation of the glacial-geomorphological record. This can be overcome only by an increase in the number of absolutely dated moraines. However, present results suggest that the assignment of moraines to the Egesen Stadial with field methods is broadly correct. From a more climatological point of view, all comparisons between past and present precipitation patterns suffer from our lack of knowledge of the present-day precipitation above TL in the Alps. Therefore, the modern precipitation at the ELA, as calculated from the OKF model, is used as reference. A further source of uncertainties is the assumption of a spatially constant TL depression and hence summer temperature depression. If we assumed that ΔTL was –500 m (ΔTs = –3.5 K) in the north and only –400 m in the central Alps (ΔTs = –2.8 K), precipitation change along the northern slope would remain the same as above, but only on the order of –10 to –15% in the central valleys. It should also be kept in mind that spatially constant vertical lapse rates of precipitation (OKF model) and accumulation (Kuhn model) are only first approximations. In reality, vertical and horizontal precipitation gradients in the Alps are inseparably linked to each other and strongly influenced by the precipitation regime and synoptic-scale airflow (e.g. Reference FliriFliri, 1975; Reference Frei and ScharFrei and Schar, 1998). The influence of precipitation change on the inferred figures is, however, difficult to quantify. Some cautious experiments with different scenarios showed that the possible error in precipitation change should be in the order of ±50 mm a"1 in the central Alps and ±100 mm a"1 along the northern slope, which is less than the standard error of the OKF model.
Conclusions
The results of our calculations show that the statistical glacier-climate model of Reference Ohmura, Kasser and FunkOhmura and others (1992) and the glacial-meteorological model of Reference KuhnKuhn (1981a) lead to similar results. They are useful tools for the inference of palaeo-precipitation patterns from ELA depressions, if independent data for summer temperature depression are available. In the case of the Younger Dryas in the Alps, TL depression as provided by palynology seems to be a reliable input variable for the calculation of summer temperature change.
The regional pattern of precipitation change shows that the contrast between the northern margin of the Alps and the central, more shielded valleys was stronger during the early Younger Dryas than today. In particular, those areas which are well exposed to westerly-to-northwesterly airflow seem to have received more precipitation than today. This suggests a higher frequency of westerly and northwesterly airflow patterns in the Alps during the early Younger Dryas. Our present results support those from AGCMs, which point towards a more zonal circulation pattern over western and northwestern Europe during the Younger Dryas.
There are still considerable gaps in our knowledge of Younger Dryas ELA depressions in wide areas of the Alps, particularly in the western and southern Alps. Future fieldwork should concentrate on areas closer to the Po plain in northern Italy and to the Mediterranean Sea.
Acknowledgements
This study was partly supported by the Austrian ˚Fonds zur Forderung der wissenschafthchen Forschung" under grant P12600–GEO We gratefully acknowledge the help of A. Hertl of Universität Innsbruck, who supplied unpublished ELA depression data from his fieldwork in the Silvretta mountains.
Appendix
Additional Sources
Aeschlimann, H. 1983. Zur Gletschergeschichte des italienischen Mont Blanc Gebiets:ValVeni — Val Ferret — Ruitor. (Inaug. Diss., Universitat Zurich.)
Bless, R. 1984. Beitrage zur spat-und postglazialen Geschichte der Gletscher im nordostlichen Mont Blanc Gebiet. Zurich, Universitat Zurich. Geographisches Institut. (Physische Geographie 15.)
Buchenauer, H. W. 1990. Gletscher- und Blockgletschergeschichte der westlichen Schobergruppe (Osttirol). Marburg. Geogr. Schr. 117.
Damm, B. 1996. Gletscher-, Landschafts- und Klimaentwicklung in der Rieserfernergruppe (Tirol) seit dem Spdtglazial. Gottingen, Universitat Gottingen. Geographisches Institut. (Gbttinger Geographische Abhandlungen 104.)
Hirtlreiter, G. 1992. Spat- und postglaziale Gletscherschwankungen im Wettersteingebirge und seiner Umgebung. (Ph.D. thesis, Universitat Milnchen.)
Kerschner, H. 1979. Spatglaziale Gletscherstande im inneren Kaunertal (Otztaler Alpen). Innsbruck. Geogr. Stud. 6, 235-247.
Kerschner, H. 1993. Spateiszeitliche Gletscherstande im siidlichen Karwendel bei Innsbruck, Tirol. Innsbruck. Geogr. Stud. 20,47-55.
Kerschner, H. and E. Berktold. 1982. Spatglaziale Gletscherstande und Schuttformen im Senderstal, nordliche Stubaier Alpen, Tirol. £ Gletscherkd. Glazialgeol, 17(2), 1981,125-134.
Maisch, M. 1981. Glazialmorphologische undgletschergeschichtliche Untersuchungen im Gebiet zwischen Landwasser- und Albulatal (Kt. Graubiinden, Schweiz). Zurich, Universitat Zurich. Geographisches Institut. (Physische Geographie 3.)
Miiller, H.N. 1984. Spatglaziale Gletscherschwankungen in den westlichen Schweizer Alpen (Simplon-Siid und Val de Nandaz, Wallis) und im nordisldndischen Trb’llaskagi- Gebirge (Skidadalur). Nafels, Kilng.
Patzelt, G. 1983. Die spatglazialen Gletscherstande im Bereich des Mieselkopfes und im Arztal, TuxerVoralpen, Tirol. Innsbruck. Geogr. Stud. 8, 35-44.
Renner, F 1982. Beitrage zur Gletschergeschichte des Gotthardgebietes und dendroklimatologische Analysen an fossilen Hb'lzern. Zurich, Universitat Zurich. Geographisches Institut. (Physische Geographie 8.)
Suter, J. 1981. Gletschergeschichte des Oberengadins: Untersuchungen von Gletscherschwankungen in der Err-Julier-Gruppe. Zurich, Universitat Zurich. Geographisches Institut. (Physische Geographie 2.)
Suter, J. and B. Gamper-Schollenberger. 1982. Gletscher-, Vegetations- und Klimageschichte im Oberengadin. In Maisch, M. and J. Suter, eds. Exkursionsfuhrer, Teil A: Ostschweiz ( Hauptversammlung DEUQUA 2jlrich). Zurich, Universitat Zurich. Geographisches Institut, 14-30. (Physische Geographie 6.)
Vogele, A. 1984. Untersuchungen zur Geomorphologie und jungquartaren Talgeschichte des Dischma (Davos, Kt. Graubiinden). Zurich, Universitat Zurich. Geographisches Institut. (Physische Geographie 14.)
Vuagneux, R. 1983. Glazialmorphologische und gletschergeschichtliche Untersuchungen im Gebiet des Fliielapass (Kt. Graubiinden, Schweiz). Zurich, Universitat Zurich. Geographisches Institut. (Physische Geographie 10.)






