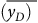Introduction
Charged particle therapy (CPT) with proton and carbon ions has been extensively used to treat various types of cancerous tumours [Reference Okada, Kamada and Tsuji1,Reference Suit, DeLaney and Goldberg2]. Charged particles deposit the major part of their energy at the end of their range when penetrating water medium. This physical characteristic of the Bragg peak allows highly localised particle beams to deposit most of the energy on the tumour while minimising residual dose to surrounding normal tissues. Heavier ions such as carbon and oxygen ions have further advantages in treating deep-seated tumours compared with protons thanks to higher relative biological effectiveness (RBE) [Reference Schulz-Ertner and Tsujii3,Reference Amaldi and Kraft4].
Proton and carbon ions are widely used in CPT worldwide. However, oxygen ions have recently gained more attention to be used in CPT [Reference Tommasino, Scifoni and Durante5]. Oxygen ions offer higher RBE, higher linear energy transfer (LET) and higher peak-to-entrance ratio compared to carbon ions. These characteristics are especially useful in treating hypoxic tumours [Reference Tommasino, Scifoni and Durante5–Reference Bassler, Toftegaard and Lühr8]. The RBE of charged particles is not constant along their penetration depth. The RBE increases drastically at the Bragg peak position, but the maximum RBE value does not occur at the same depth as the maximum physical dose [Reference Tran, Bolst and Guatelli9,Reference Kraft10]. The evaluation of the RBE in the biological medium, especially around the Bragg peak, is crucial to deliver the required biological dose to the tumour.
Many types of microdosimeters can be used to measure microdosimetric and derive RBE using radiobiological models. Tissue equivalent proportional counters (TEPC) are the most common type of microdosimetry detectors, for measuring microdosimetric quantities to derive their RBE in CPT. Unfortunately, this technology has drawbacks which include, a low spatial resolution, which does not allow high spatial resolution microdosimetry measurements within the narrow region of the Bragg peak. Silicon-on-insulator (SOI) microdosimeters developed by the Centre for Medical Radiation Physics (CMRP) of the University of Wollongong in Australia were introduced to overcome the limitations of TEPCs. The large size of TEPCs is not ideal for the sharp dose profiles at the distal edge of Bragg peak and spatial resolution is limited. The SOI microdosimeter can measure the energy deposited by a mixed radiation field with high spatial resolution [Reference Rosenfeld11].
Monte Carlo simulation modelling particle transport in matter is widely used to characterise and improve radiation detectors. In this study, the Bridge SOI microdosimeter [Reference Rosenfeld11] was simulated using Tool for Particle Simulation (TOPAS) [Reference Perl, Shin, Schümann, Faddegon and Paganetti12,Reference Faddegon, Ramos-Méndez and Schuemann13]. TOPAS is based on the Geant4 simulation toolkit [Reference Agostinelli, Allison and Amako14]. It provides pre-built components (e.g. nozzles, geometry, dosimetry and imaging components) for users to simulate a wide variety of radiation beams and dosimeters with no required extensive knowledge of C++ programming language. In this study, the TOPAS microdosimetric extension was used [Reference Zhu, Chen and Sung15]. Pre-built geometry of the Bridge SOI microdosimeter is defined in the TOPAS microdosimetry extension, and the parameters necessary for the lineal energy scorer such as the sensitive volume radius, tissues-equivalent radius, position of the sensitive volume and mean path length were specified. The pre-built lineal energy scorer recorded the energy deposition of both the primary and secondary particles in the SVs of the detector. A detailed description of the lineal energy scorer can be found in Ref. [Reference Zhu, Chen and Sung15].
To date, CPT has been extensively used to treat cancerous tumours. However, there has been limited discussion regarding microdosimetric quantities resulting from secondary fragments due to nuclear interactions and their biological effects, as well as the accurate prediction of RBE, particularly for novel oxygen ion species. Therefore, the study can play an important role in understanding the RBE values and accurate RBE prediction of oxygen ions and commissioning of RBE values used in treatment planning system and quality assurance.
TOPAS microdosimetric extension can simulate total and secondary fragment’ microdosimetric spectra, calculate microdosimetric parameters (e.g. frequency-mean lineal energy, dose-mean lineal energy) and determine the RBE10 with the microdosimetric kinetic model (MKM). The simulation configuration of the TOPAS microdosimetric extension could adequately reproduce the experimental microdosimetric spectra of proton beams [Reference Zhu, Chen and Sung15,Reference Tran, Chartier and Bolst16].
This work simulated and compared the microdosimetry spectra and evaluated RBE10 produced in a water phantom by an oxygen ion beams with respect to a carbon ion beams. The results were compared to the experimental results available in literature, providing new understanding of RBE for carbon and oxygen ions, as well as the relationship between physical doses and RBE. This work also presents a possible, fast and reliable approach to evaluate RBE10 value of carbon and oxygen ions using a Bridge SOI microdosimeter by means of TOPAS simulation.
Materials and Method
Microdosimetric quantities and RBE10 calculation
Microdosimetric spectra are given in terms of the stochastic quantity, lineal energy, y, which is the fundamental microdosimetric quantity. The definitions of the microdosimetry quantities can be found in the International Commission on Radiation Units and Measurements (ICRU) Report 36 [17] and more details of the microdosimetry theory are described in the literature [Reference Kase, Kanai and Matsumoto18–Reference Rossi and Zaider20]. y is the energy deposited in a single event in a micron-size sensitive volume (SV) per average chord length, given by:
where ε is the energy deposited for a single event in an SV with an average chord length <l>.
The mean path length <I path> is used instead of the mean chord length in the TOPAS microdosimetric extension. The concept of <I path> was proposed by Bolst et al. [Reference Bolst, Guatelli and Tran21] to suit the design of the Bridge SOI microdosimeter.
In this study, <l Path> with a value of 10 μm was used to represent the thickness of the silicon layer, considering the mean path of the charged particles when traversing the SV. The energy depositions in the SV have to be converted to tissue-equivalent SV by using the conversion factor of 0·58 to get the equivalent energy deposition in tissues [Reference Bolst, Guatelli and Tran21,Reference Bolst, Tran and Chartier22]. The frequency lineal energy spectrum, f(y), for the generated primary and secondary charged particles, can be derived from the deposited energy spectrum. The dose lineal energy spectrum d(y) is given by:
where
![]() $\overline {{y_F}} = \!\mathop {\int \nolimits _{_0} ^{\infty }} yf\left( y \right)dy$
is the frequency-mean lineal energy. After obtaining the dose lineal energy d(y), the dose-mean lineal energy
$\overline {{y_F}} = \!\mathop {\int \nolimits _{_0} ^{\infty }} yf\left( y \right)dy$
is the frequency-mean lineal energy. After obtaining the dose lineal energy d(y), the dose-mean lineal energy
![]() $\overline {{y_D}} $
can be calculated
$\overline {{y_D}} $
can be calculated
![]() $\overline {{y_D}} = \!\mathop {\int \nolimits _{_0}^{\infty }}yd\left( y \right)dy$
.
$\overline {{y_D}} = \!\mathop {\int \nolimits _{_0}^{\infty }}yd\left( y \right)dy$
.
In this study, the modified MKM introduced by Kase et al. [Reference Kase, Kanai and Matsumoto18,Reference Kase, Yamashita and Matsufuji19] was used to calculate the RBE, as previously done by Tran et al. [Reference Tran, Chartier and Bolst23]. This method is described as follows. The value of
![]() $\overline {{y_D}} $
is used to determine the α parameter in the Linear Quadratic Model (LQM), which describes the cell survival fraction in the radiation field of interest as:
$\overline {{y_D}} $
is used to determine the α parameter in the Linear Quadratic Model (LQM), which describes the cell survival fraction in the radiation field of interest as:
where
![]() $\alpha = \;{\alpha _{0\;}} + \;{\beta \over {\rho \pi r_d^2}}\;{y^{\rm{*}}}$
, β is a parameter of the LQM survival curve (which assumes LET independence),
$\alpha = \;{\alpha _{0\;}} + \;{\beta \over {\rho \pi r_d^2}}\;{y^{\rm{*}}}$
, β is a parameter of the LQM survival curve (which assumes LET independence),
![]() $\rho $
is the density of cell medium and can be assumed as water (
$\rho $
is the density of cell medium and can be assumed as water (
![]() $\rho $
= 1 g/cm2) and rd is the radius of subcellular domain in the MKM.
$\rho $
= 1 g/cm2) and rd is the radius of subcellular domain in the MKM.
![]() ${y^*}$
, shown in Equation (4), is the saturation-corrected dose-mean lineal energy that takes into account the overkilling effect of excessive local energy deposition [Reference Rossi and Zaider20]:
${y^*}$
, shown in Equation (4), is the saturation-corrected dose-mean lineal energy that takes into account the overkilling effect of excessive local energy deposition [Reference Rossi and Zaider20]:
The MKM parameters,
![]() ${y_{0\;}}$
= 150 keV/μm,
${y_{0\;}}$
= 150 keV/μm,
![]() ${\alpha _{0\;}}$
= 0·13 Gy-1,
${\alpha _{0\;}}$
= 0·13 Gy-1,
![]() $\beta $
= 0·05 Gy-2 and rd= 0·42 μm, used in this study were the same as those adopted by Kase et al. [Reference Kase, Yamashita and Matsufuji19], corresponding to the case of a human salivary gland tumour cell line. The RBE is defined as the ratio of the dose delivered with the reference radiation (200 kVp X-rays) to the dose that has to be delivered by the tested beam to obtain the same biological endpoint, e.g., the same cell survival S. The RBE for a 10% cell survival (RBE10) is expressed as:
$\beta $
= 0·05 Gy-2 and rd= 0·42 μm, used in this study were the same as those adopted by Kase et al. [Reference Kase, Yamashita and Matsufuji19], corresponding to the case of a human salivary gland tumour cell line. The RBE is defined as the ratio of the dose delivered with the reference radiation (200 kVp X-rays) to the dose that has to be delivered by the tested beam to obtain the same biological endpoint, e.g., the same cell survival S. The RBE for a 10% cell survival (RBE10) is expressed as:
where D10,ref (5 Gy) is the required dose by 200 kVp X-rays for a 10% cell survival.
The Bridge SOI microdosimeter
In this study, the Monte Carlo simulation toolkit was used to model the Bridge SOI microdosimeter developed by CMRP [Reference Bradley, Rosenfeld, Lee, Jamieson, Heiser and Satoh24–Reference Tran, Chartier and Prokopovich26]. The device is an array of 4,248 silicon sensitive volumes (SVs), organised in 59 rows and 72 columns, connected by bridging volumes of 15 × 20 × 10 μm3 each. An individual SV’s volume is 30 × 30 × 10 μm3. Bridging volumes have the same silicon characteristic of the SVs. The geometry of the detector is shown in Fig. 1. A more detailed description of the Bridge SOI microdosimeter can be found in literatures [Reference Zhu, Chen and Sung15,Reference Tran, Chartier and Bolst23,Reference Tran, Chartier and Prokopovich26]. The device was characterised in detail and successfully tested with incident carbon, oxygen and nitrogen ions at Heavy Ion Medial Accelerator in Chiba (HIMAC), Japan by experiments and simulations using the Geant4 Monte Carlo simulation toolkit [Reference Tran, Bolst and Guatelli9,Reference Tran, Chartier and Bolst16,Reference Tran, Chartier and Bolst23,Reference Tran, Chartier and Prokopovich26].

Figure 1. The geometry of the silicon-on-insulator detector (Source: Zhu et al. [Reference Zhu, Chen and Sung15])
TOPAS simulation
The Bridge SOI microdosimeter was modelled in TOPAS version 3.6.0 (based on Geant4 10.06.p03), with its microdosimetry extension. Carbon ion beams were generated with an energy of 290 MeV/u, as this is the typical energy used in carbon ion therapy at HIMAC [Reference Torikoshi, Minohara and Kanematsu27]. The energy distribution was considered Gaussian with an energy spread σ of 0·86 %. The beam spot size was simulated with σ = 11 mm. The Bridge SOI microdosimeter was positioned at various depths (entrance of the phantom, at the Bragg peak, distal edge and tail regions) along the beam direction in the water phantom. The energy depositions of the primary particle and all its correlated secondary particles are scored. At the end of simulation of each run, the energy deposition event scores are processed by analysis toolkit and the micrososimetric spectra are obtained.
Since the SVs in Bridge SOI microdosimeter are made of silicon materials, a tissue-equivalent conversion factor of 0·58 is needed to convert the simulated energy in the SVs to a tissue-equivalent material [Reference Bolst, Guatelli and Tran21,Reference Bolst, Tran and Chartier22]. The tissue-equivalent conversion factor was obtained by simulating the silicon microdosimeter and by irradiating it with 290 MeV/u 12C beam at different depths in a water phantom. The silicon microdosimeter was then replaced with tissue-equivalent material (straited muscle) at the same depth as the silicon micrososimeter, simulating the tissues-equivalent material with same energy. However, the size of the tissue SV was varied to obtain the same energy deposition spectrum as the silicon SV. In this case, the tissue-equivalent conversion factor is defined as the ratio of the length of the silicon SV to the length of the tissue SV.
Study by Bolst et al. [Reference Bolst, Tran and Chartier22] shows that the calculated correction factors can determine RBE10 with good agreement based on TEPC measurements. The maximum difference was about 5% when comparing the simulated silicon cylinder SV’s response to the simulated tissue sphere SV’s response. More detail on the conversion factor calculation can be found in Bolst et al. [Reference Bolst, Guatelli and Tran21,Reference Bolst, Tran and Chartier22]. As suggested by Zhu et al. [Reference Zhu, Chen and Sung15] the lower threshold linear energy was set to 0·5 keV/μm considering the detection threshold of the detector was 0·3–0·4 KeV/µm and 12C experimental spectra starting from about 0·5 KeV/µm at the entrance of the phantom. The depth dose distribution in a water phantom was also simulated; the dose distribution was scored along the beam axis in a cylinder of 2·5 cm diameter and 30 cm depth.
The simulations were repeated using an oxygen ion beam with energy of 345 MeV/u. This corresponds to a range of approximately 160 mm in water which is similar to the case of the carbon ion beam under investigation. All simulations were performed with 106 track histories [Reference Arce, Bolst and Bordage28,Reference Parisi, Schettino and Romano29] while 107 track histories were simulated at the distal tail of the Bragg peak. The G4HadronPhysicsQGSP_BIC_HP and G4HadronElasticPhysicsHP were used to describe the inelastic and elastic interactions, the G4EmStandardPhysics_Option_4 described electromagnetic interactions, the G4IonBinarCascedePhysics described hadronic interactions of ions. For optimal simulation time but not sacrificing the accuracy of simulation results, the CutsPerRigion functionality was used, to avoid the tracking of secondary electrons, which cannot reach and deposit energy in the detector. The electron production cut was set to 1 um in the region surrounding the microdosimeter. Outside this region, the default cut value in the water phantom was set equal to 2 mm.
To further investigate the RBE10 distribution by means of TOPAS simulation, the cylindrical mini-Tissue Equivalent Proportional Counter (mini-TEPC) developed by Istituto Nazionale di Fisica Nucleare (INFN) was also simulated. This mini-TEPC has a cylindrical SV of 0·9 mm diameter, surrounded by 0·35 mm thick A-150-cathod wall and insulator with 0·2 mm thick aluminium sleeve. The mini-TEPC was able to collect accurate data in Bragg peak region due to its small size [Reference Rollet, Colautti and Grosswendt30]. The geometry of the mini-TEPC is shown in Fig. 2. and more details can be found in the Ref. [Reference Conte, Agosteo and Bianchi31]. To compare RBE10 distributions between mini-TEPC and Bridge SOI microdosimeter, the simulations were repeated and the Bridge SOI microsoimeter was substituted with mini-TEPC. These adopted the same simulation configurations and energies.

Figure 2. The geometry of the mini-tissue equivalent proportional counters (Source: Zhu et al. [Reference Zhu, Chen and Sung15])
Results and Discussion
Dose-mean lineal energy and RBE10
Fig. 3 shows the relative absorbed dose in the water phantom for both 290 MeV/u 12C and 345 MeV/u 16O beams, normalised to per incident particle. At the entrance, at 2 mm depth from the surface of the phantom, the dose deposition for the 16O ion beam was about 60% higher than the case of 12C ions. Both 16O and 12C ions deposited their maximum dose approximately at 160 mm depth from the surface of the phantom, i.e., at the Bragg peak. At the Bragg peak, the 16O ion beam produces approximately 56% higher dose deposition than the 12C ion beam. At the distal part of the Bragg peak (2 mm beyond the Bragg peak), the 16O ion beam still produces 45% higher dose deposition than the 12C ion beam. The dose at the distal edge should be taken into consideration because organs-at-risk may be located at the distal edge.

Figure 3. Relative absorbed dose profile in water phantom per incident particle for 290 MeV/u 12C (red) and 345 MeV/u 16O (blue) ion beams
Fig. 4 shows the simulated microdosimetric, yd(y), spectra plotted as a function of lineal energy, y, obtained with the modelling of the Bridge SOI microdosimeter for 12C ions, at depths of 20, 80, 120, 158, 159, 160, 161, 162 and 165 mm in a water phantom. Fig. 5 shows the microdosimetric spectra at the distal part of the Bragg peak at 200, 250, 260 and 280 mm.

Figure 4. Simulated microdosimetric spectra for a 290 MeV/u 12C beam at 20, 80, 120, 158, 159, 160, 161 162 and 165 mm depth in water

Figure 5. Simulated microdosimetric spectra for a 290 MeV/u 12C beam at 200, 250, 260 and 280 mm depth in water
The highest simulated yd(y) value of 2·57 can be observed at a lineal energy of approximately 21 keV/µm, at a depth of 120 mm. As expected, lineal energy values are observed to increase when the beam penetrates deeper into the water, this is because of increased LET of incident ions and also contribution from secondary fragmentations generated along the penetration depth.
Fig. 6 shows the simulated microdosimetric spectra obtained with the modelling of the Bridge SOI microdosimeter for 16O ions, at depths of 20, 80, 120, 158, 159, 160, 161 and 162 mm. Fig. 7 shows the microdosimetric spectra at the distal part of the Bragg peak, at 163, 164, 165, 180, 200 and 250 mm. Similar to the case of 12C ions, the highest yd(y) value of 2·84 can be observed at a lineal energy of approximately 34 keV/µm, at a depth of 120 mm. The lineal energy values are observed to increase also after the Bragg peak at the downstream region between 163 and 165 mm.

Figure 6. Simulated microdosimetric spectra for a 345 MeV/u 16O beam at 20, 80, 120, 158, 159, 160, 161 and 162 mm depth in water

Figure 7. Simulated microdosimetric spectra for a 345 MeV/u 16O beam at 163, 164, 165, 180, 200 and 250 mm depth in water
It could be observed that Figs. 5 and 7 has a higher uncertainty due to its location at the distal part of the Bragg peak. This is because only secondary particles contributed to the energy depositions, originating from nuclear interactions that, being rare events but high-energy deposition, have a negative impact on uncertainty and strong impact the value of
![]() $\overline {{y_D}} $
[Reference Parisi, Schettino and Romano29].
$\overline {{y_D}} $
[Reference Parisi, Schettino and Romano29].
Fig. 8a and 8b show the dose-mean lineal energy values,
![]() $\overline {{y_D}\;} $
, obtained with the simulated Bridge SOI microdosimeter in a water phantom for 12C and 16O, respectively. The
$\overline {{y_D}\;} $
, obtained with the simulated Bridge SOI microdosimeter in a water phantom for 12C and 16O, respectively. The
![]() $\overline {{y_D}} $
values for 12C were approximately 17 keV/µm at the entrance, 75 keV/µm at 2 mm before the Bragg peak and increasing to approximately 110 keV/µm right at the Bragg peak. The maximum
$\overline {{y_D}} $
values for 12C were approximately 17 keV/µm at the entrance, 75 keV/µm at 2 mm before the Bragg peak and increasing to approximately 110 keV/µm right at the Bragg peak. The maximum
![]() $\overline {{y_D}} \;$
value was approximately 180 keV/µm and occurred 5 mm beyond the maximum dose at the Bragg peak, then decreasing to approximately 7 keV/µm in the tail region, at 250 mm depth. These values, obtained with TOPAS-based simulations, are compared to the measurement values by Tran et al. [Reference Tran, Bolst and Guatelli9], performed in Gunma University heavy-ion medical centre using a 290 MeV/u 12C by using percentage difference, PD, as defined in Equation (6), where Exp is the quantity value from measurement and Sim in the value from simulation.
$\overline {{y_D}} \;$
value was approximately 180 keV/µm and occurred 5 mm beyond the maximum dose at the Bragg peak, then decreasing to approximately 7 keV/µm in the tail region, at 250 mm depth. These values, obtained with TOPAS-based simulations, are compared to the measurement values by Tran et al. [Reference Tran, Bolst and Guatelli9], performed in Gunma University heavy-ion medical centre using a 290 MeV/u 12C by using percentage difference, PD, as defined in Equation (6), where Exp is the quantity value from measurement and Sim in the value from simulation.

Figure 8. Simulated
![]() $\overline {{y_D}} $
profile obtained with the Bridge SOI microdosimeter for (a) 290 MeV/u 12C and (b) 345 MeV/u 16O ion beam
$\overline {{y_D}} $
profile obtained with the Bridge SOI microdosimeter for (a) 290 MeV/u 12C and (b) 345 MeV/u 16O ion beam
Table 1 shows the comparison between the
![]() $\overline {{y_D}} \;$
values measured by Tran et al. [Reference Tran, Bolst and Guatelli9] and
$\overline {{y_D}} \;$
values measured by Tran et al. [Reference Tran, Bolst and Guatelli9] and
![]() $\overline {{y_D}} $
values in this study for 12C. The differences observed between simulations and measurements could be explained by the fact that the LET increases rapidly at the end of a carbon ion’s range, with a sharp dose gradient. This implies a very small change in depth can change the
$\overline {{y_D}} $
values in this study for 12C. The differences observed between simulations and measurements could be explained by the fact that the LET increases rapidly at the end of a carbon ion’s range, with a sharp dose gradient. This implies a very small change in depth can change the
![]() $\overline {{y_D}} \;$
value drastically. Further, while a pristine mono-energetic beam was simulated, a ripple filter was used to broaden the range of the measured carbon ions beam. Please take into consideration that these simulations were not meant to model the experimental scanning beamline in Gunma University. Thus, the comparison shown in the Table 1 is just meant to provide a general idea of the capabilities of the TOPAS-based simulations and not to provide a direct comparison with the measurement values.
$\overline {{y_D}} \;$
value drastically. Further, while a pristine mono-energetic beam was simulated, a ripple filter was used to broaden the range of the measured carbon ions beam. Please take into consideration that these simulations were not meant to model the experimental scanning beamline in Gunma University. Thus, the comparison shown in the Table 1 is just meant to provide a general idea of the capabilities of the TOPAS-based simulations and not to provide a direct comparison with the measurement values.
Table 1. Comparison of the entrance
![]() $\overline {{{\rm{y}}_{\rm{D}}}} {\rm{\;}}$
value and maximum
$\overline {{{\rm{y}}_{\rm{D}}}} {\rm{\;}}$
value and maximum
![]() $\overline {{{\rm{y}}_{\rm{D}}}} {\rm{\;}}$
value for 12C between measurement by Tran et al. [Reference Tran, Bolst and Guatelli9] and simulation in this study
$\overline {{{\rm{y}}_{\rm{D}}}} {\rm{\;}}$
value for 12C between measurement by Tran et al. [Reference Tran, Bolst and Guatelli9] and simulation in this study

The
![]() $\overline {{y_D}} $
values for 16O were approximately 34 keV/µm at the entrance, which is twice greater than 12C. The
$\overline {{y_D}} $
values for 16O were approximately 34 keV/µm at the entrance, which is twice greater than 12C. The
![]() $\overline {{y_D}} $
value increases to approximately 114 keV/µm at 158 mm depth and approximately 168 keV/µm at the Bragg peak. Similar to 12C ions, the maximum
$\overline {{y_D}} $
value increases to approximately 114 keV/µm at 158 mm depth and approximately 168 keV/µm at the Bragg peak. Similar to 12C ions, the maximum
![]() $\overline {{y_D}} $
value of 237 keV/µm for 16O ions can be observed at the distal part of the Bragg peak, specifically at a depth of 164 mm, which is slightly behind the Bragg peak. The
$\overline {{y_D}} $
value of 237 keV/µm for 16O ions can be observed at the distal part of the Bragg peak, specifically at a depth of 164 mm, which is slightly behind the Bragg peak. The
![]() $\overline {{y_D}} $
value then decreases to approximately 11 keV/µm in the tail region, at 250 mm depth in the water phantom.
$\overline {{y_D}} $
value then decreases to approximately 11 keV/µm in the tail region, at 250 mm depth in the water phantom.
RBE10 calculation with MKM
Table 2 shows the derived RBE10 values for 12C and 16O ions and Fig. 9a and 9b show the derived RBE10 distribution in the water phantom, obtained through simulations using the Bridge SOI microdosimeter for 12C and 16O ions, respectively. The RBE10 value for 12C ions at the entrance is approximately 1·25 (at 20 mm), increasing to 2·53 at the Bragg peak (depth 160 mm). The maximum RBE10 value of approximately 2·75 occurs at 164 mm, which is 4 mm after the maximum dose at the Bragg peak. The position of the maximum RBE10 obtained for 12C ions in this study is different from the one obtained experimentally by Tran et al. [Reference Tran, Bolst and Guatelli9], who reported the maximum RBE10 value at Bragg peak. In the tail region, at 250 mm depth in water, the RBE10 value decreases to approximately 1·1.
Table 2. Comparison of relative biological effectiveness values for 12C and 16O ions


Figure 9. Simulated RBE10 distribution obtained with the Bridge SOI microdosimeter for (a) 290 MeV/u 12C and (b) 345 MeV/u 16O ion beam
The RBE10 value for 16O ions at the entrance is 1·35 (at 20 mm), and the maximum RBE10 value is 2·81 at 161 mm, which is 1 mm after the maximum dose at the Bragg peak. At the distal part of the Bragg peak, the RBE10 value decreases slightly to 2·70 at 163 mm. In the tail region (250 mm depth in the water), similarly to the case of 12C ions, the RBE10 value of 16O decreases to approximately 1·1.
Fig. 10 shows the comparison of simulated RBE10 between 12C and 16O ion beams along the penetration depths in the water phantom obtained simulating the Bridge SOI microdosimeter. Overall, the RBE10 values for 16O ions were higher than the case of 12C ions at the entrance, before the Bragg peak and in the distal part of the Bragg peak. The maximum RBE10 value of 12C and 16O was 2·75 and 2·81, respectively. The maximum RBE10 value for 16O was reached earlier in depth (161 mm) than in the case of 12C (164 mm). At the tail region 250 mm, both 12C and 16O have approximately the same RBE10 value of 1·1.

Figure 10. Comparison of simulated RBE10 profile obtained with the Bridge SOI microdosimeter for 290 MeV/u 12C and 345 MeV/u 16O ion beams
Fig. 11a and 11b show the comparison of RBE10 profile obtained simulating the Bridge SOI microdosimeter and the mini-TEPC for 290 MeV/u 12C ion beam and 345 MeV/u 16O ion beam, respectively. Overall, the RBE10 values obtained simulating the mini-TEPC were slightly higher than the case of Bridge SOI microdosimeter at the entrance, before the Bragg peak and in the distal part of the Bragg peak. The discrepancy could be due to the difference in geometry of the SVs in the two detectors, and the additional events caused by the delta rays produced in the structural materials of the mini-TEPC. The Bridge SOI microdosimeter has advantages due to its small sensitive volume size allowing it to calculate microdosimetric quantities with high spatial resolution. It also does not require gas flow as a mini-TEPC does.

Figure 11. Simulated RBE10 distribution obtained with the Bridge SOI microdosimeter and mini-TEPC for (a) 290 MeV/u 12C and (b) 345 MeV/u 16O ion beam
The highest RBE10 value of 12C ion beam was 2·8 obtained with mini-TEPC at 161 mm (Bragg peak region), which is 1 mm after the maximum dose at the Bragg peak. In comparison with the Bridge SOI microdosimeter, which is 4 mm after the maximum dose at the Bragg peak with the RBE10 value of 2·7. The highest RBE10 value of 16 O ion beam obtained simulating the mini-TEPC was 2·9, which occurred at 158 mm (Bragg peak region), which is 2 mm before the maximum dose at the Bragg peak. In comparison with the Bridge SOI microdosimeter at 161 mm, which is 1 mm after the maximum dose at the Bragg peak with the RBE10 value of 2·8.
Contribution of secondary fragments to the microdosimetric spectra
Figs. 12–14 show the different secondary fragments contributing to the microdosimetric spectra obtained with the Bridge SOI microdosimeter for 290 MeV/u 12C ion beam at 20, 160 and 250 mm depth in a water phantom, in logarithmic scale and semi-logarithmic scale plots, calculated by means of TOPAS. At the entrance at 20 mm, the main contribution to the spectrum was mainly due to carbon ion (96·3%), followed by electron (1·7%) at lineal energy range of 10–100 keV/μm. Contributions from other secondary fragments were almost negligible. Their presence in the semi-log plot shown in Fig. 12b, indeed, could barely be noticed.

Figure 12. Secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI micrpdosimeter for 290 MeV/u 12C ion beam set at 20 mm depth (a) log-log scale (b) semi-log scale

Figure 13. Secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI micrpdosimeter for 290 MeV/u 12C ion beam set at 160 mm depth (a) log-log scale (b) semi-log scale

Figure 14. Secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI micrpdosimeter for 290 MeV/u 12C ion beam set at 250 mm depth (a) log-log scale (b) semi-log scale
At the Bragg peak at 160 mm, the main contribution to the spectrum was due to carbon ion (95·8%), followed by secondary fragments with Z > 6 (2·8%) and boron (0·6%) at the higher lineal energy range of 100–1,000 keV/μm. Contribution from lighter fragments dominated at the lower lineal energy range of 1–10 KeV/μm, which is helium (62·8%), followed by hydrogen (21·8%), secondary fragments with Z > 6 (8·1%), electron (3·4%) and lithium (2·9%). Contribution from beryllium, boron and carbon could be observed with less than 1%.
At the tail region at 250 mm, the microdosimetric spectrum was produced by the secondary mixed radiation field only, mainly dominated by helium (63·2%), followed by secondary fragments with Z > 6 (14·3%), hydrogen (11·3%) and lithium (7·4%) at lineal energy range of 1–100 keV/μm. Contribution from secondary electrons and beryllium could also be observed. The contribution from boron and carbon was not observed.
Fig. 15–17 show different secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI microdosimeter for 345 MeV/u 16O ion beam at 20, 160 and 250 mm depth in a water phantom, calculated by means of TOPAS. At the entrance at 20 mm depth in the water phantom, the main contribution to the spectrum was due to secondary fragments with Z > 6 (97%), followed by secondary electrons (1·8%), carbon (0·5%), helium (0·3%) and hydrogen (0·3%) at lineal energy range of 10–00 keV/μm.

Figure 15. Secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI micrpdosimeter for 345 MeV/u 16O ion beam set at 20 mm depth (a) log-log scale (b) semi-log scale

Figure 16. Secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI micrpdosimeter for 345 MeV/u 16O ion beam set at 160 mm depth (a) log-log scale (b) semi-log scale

Figure 17. Secondary fragments contributing to the microdosimetric spectrum obtained with the Bridge SOI micrpdosimeter for 345 MeV/u 16O ion beam set at 50 mm depth (a) log-log scale (b) semi-log scale
At the Bragg peak region at 160 mm depth in the water phantom, the main contribution to the spectrum was only due to secondary fragments with Z > 6 (99%) at the lineal range of 100–1,000 keV/μm. The contribution from electron, hydrogen, lithium, beryllium, helium, carbon and boron fragments was less than 1% and could only be observed in the log-log scale representation in Fig. 16a.
At the tail region, the microdosimetric spectrum is similar to the 12C beam with helium fragments as the main contribution to the spectrum (45·3%), followed by other secondaries were all fragments with Z > 6 (24·4%), boron (11·3%), hydrogen (9·9%), beryllium (4·5%), lithium (2·6%), electron, (1·9%) and carbon (0·1%) at lineal energy range of 1–100 KeV/μm.
Conclusion
Monte Carlo simulations have been widely used to study the various ion beams' mixed radiation field and to model microdosimeter detectors when irradiated with ion beams. This work presented a comparison of the RBE10 and dose-mean lineal energy (
![]() $\overline {{y_D}} $
) produced by oxygen ions and by carbon ions in a water phantom. This study was carried out using TOPAS, a Geant4-based Monte Carlo simulation toolkit. Oxygen ions are currently considered a potential alternative to carbon ions because oxygen ions have less lateral scattering and higher LET associated with higher RBE, which translates to better treatment effectiveness. Therefore, oxygen ions have been proposed as an alternative to carbon ions in charged particle therapy for treatment of hypoxic tumours [Reference Tommasino, Scifoni and Durante5–Reference Bassler, Toftegaard and Lühr8].
$\overline {{y_D}} $
) produced by oxygen ions and by carbon ions in a water phantom. This study was carried out using TOPAS, a Geant4-based Monte Carlo simulation toolkit. Oxygen ions are currently considered a potential alternative to carbon ions because oxygen ions have less lateral scattering and higher LET associated with higher RBE, which translates to better treatment effectiveness. Therefore, oxygen ions have been proposed as an alternative to carbon ions in charged particle therapy for treatment of hypoxic tumours [Reference Tommasino, Scifoni and Durante5–Reference Bassler, Toftegaard and Lühr8].
This work showed that
![]() $\overline {{y_D}} $
values at the entrance for carbon and oxygen ion beams are about and 34 keV/µm, respectively. The maximum
$\overline {{y_D}} $
values at the entrance for carbon and oxygen ion beams are about and 34 keV/µm, respectively. The maximum
![]() $\overline {{y_D}} $
values for both carbon ions and oxygen ions, respectively 180 and 237 keV/µm, occurred slightly behind the maximum physical dose. The simulated maximum RBE10 value of carbon ions also occurred slightly after the maximum physical dose. This result is slightly different from the measurement value found in the literature though, occurring at the same position as maximum physical dose [Reference Tran, Bolst and Guatelli9]. On the other hand, the simulated maximum RBE10 values of oxygen ions occurred at the same position as the maximum dose at the Bragg peak. This result was also slightly different from the measurement value in the literature, which occurred just before the maximum physical dose. This might be due to the fragmentation model accuracy in TOPAS simulation. Future improvement and verification are needed because of the importance of these quantities for accurate biological dose prediction.
$\overline {{y_D}} $
values for both carbon ions and oxygen ions, respectively 180 and 237 keV/µm, occurred slightly behind the maximum physical dose. The simulated maximum RBE10 value of carbon ions also occurred slightly after the maximum physical dose. This result is slightly different from the measurement value found in the literature though, occurring at the same position as maximum physical dose [Reference Tran, Bolst and Guatelli9]. On the other hand, the simulated maximum RBE10 values of oxygen ions occurred at the same position as the maximum dose at the Bragg peak. This result was also slightly different from the measurement value in the literature, which occurred just before the maximum physical dose. This might be due to the fragmentation model accuracy in TOPAS simulation. Future improvement and verification are needed because of the importance of these quantities for accurate biological dose prediction.
With respect to carbon ions, oxygen ions produce higher nuclear fragmentations. Secondary fragments have a significant impact on the RBE, especially beyond the Bragg peak and out-of-field. The accuracy of fragmentation in the physical models used in CPT simulation is therefore of high importance. Further verification with experimental data of the physical models available in the Geant4 TOPAS is required.
These results also demonstrate that oxygen beams may have the advantage for cancer treatment because oxygen ions provide higher RBE10 values and have the same positions with the maximum dose at the Bragg peak compared to carbon beams. These findings provide important information for accurate biological dose prediction, especially when targeting the tumours near organs at risk. The RBE10 of oxygen ions is higher than carbon ions in this work. These results are similar to the study by Tommasino et al. [Reference Tommasino, Scifoni and Durante5] using research treatment planning system and Tran et al. [Reference Tran, Bolst and Guatelli9] using both Monte Carlo simulation and microdosimetry measurement performed at the Gunma University heavy-ion medical centre. This is because oxygen ions with higher Z numbers carrying higher charges would deposit higher doses than carbon ions and are translated into higher RBE10.
However, the higher RBE values for oxygen ions at the entrance and in the distal part of the Bragg peak also result in higher toxicity for healthy tissues. Even though the RBE of oxygen ions is higher than the RBE of carbon ions around the Bragg Peak, where the tumour is located, the advantages and disadvantages of using oxygen ions are controversial issues. The study also presented a fast and reliable radiation field characterisation and RBE prediction tool in CPT for heavy-ion beams using TOPAS-based simulations toolkit. The results of the study could support the commissioning of RBE used in treatment planning system and quality assurance.
Acknowledgement
This work was supported by Ministry of Higher Education Malaysia for Fundamental Research Grant Scheme (FRGS) with Project Code: FRGS/1/2019/STG02/USM/02/7. The author would like to thank Prof Anatoly Rosenfeld from Centre of Medical Radiation Physics, University of Wollongong for his guidance and support for the study.