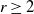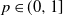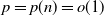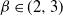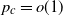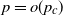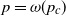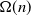Bootstrap percolation in inhomogeneous random graphs

Abstract

A bootstrap percolation process on a graph with n vertices is an ‘infection’ process evolving in rounds. Let $r \ge 2$ be fixed. Initially, there is a subset of infected vertices. In each subsequent round, every uninfected vertex that has at least r infected neighbors becomes infected as well and remains so forever.

We consider this process in the case where the underlying graph is an inhomogeneous random graph whose kernel is of rank one. Assuming that initially every vertex is infected independently with probability $p \in (0,1]$, we provide a law of large numbers for the size of the set of vertices that are infected by the end of the process. Moreover, we investigate the case $p = p(n) = o(1)$, and we focus on the important case of inhomogeneous random graphs exhibiting a power-law degree distribution with exponent $\beta \in (2,3)$. The first two authors have shown in this setting the existence of a critical $p_c =o(1)$ such that, with high probability, if $p =o(p_c)$, then the process does not evolve at all, whereas if $p = \omega(p_c)$, then the final set of infected vertices has size $\Omega(n)$. In this work we determine the asymptotic fraction of vertices that will eventually be infected and show that it also satisfies a law of large numbers.

1. Introduction

A bootstrap percolation process with activation threshold an integer $r\geq 2$ on a graph $G=G(V,E)$ is a deterministic process evolving in rounds. Every vertex has two states: it is either infected or uninfected (sometimes also referred to as active or inactive, respectively). Initially, there is a subset $\mathcal{A}_0 \subseteq V$ that consists of infected vertices, whereas every other vertex is uninfected. Subsequently, in each round, if an uninfected vertex has at least r of its neighbors infected, then it also becomes infected and remains so forever. The process stops when no more vertices become infected, and we denote the final infected set by $\mathcal{A}_f$ .

The bootstrap percolation process was introduced by Chalupa, Leath and Reich [16] in 1979 in the context of magnetic disordered systems. This process (as well as numerous variations of it) has been used as a model to describe several complex phenomena in diverse areas, from jamming transitions [35] and magnetic systems [31] to neuronal activity [4, 34] and spread of defaults in banking systems [5, 7]. Bootstrap percolation also has connections to the dynamics of the Ising model at zero temperature [23, 29]. A short survey of applications can be found in [1].

Several qualitative characteristics of bootstrap percolation, and in particular the dependence of the initial set $\mathcal{A}_0$ on the final infected set $\mathcal{A}_f$ , have been studied on a variety of graphs, such as trees [12, 22], grids [10, 15, 24], lattices on the hyperbolic plane [32], and hypercubes [9], as well as on many models of random graphs [3, 13, 26]. In particular, consider the case where $r = 2$ and G is the two-dimensional grid with $V = [n]^2=\{1, \dots, n\}^2$ (i.e., a vertex becomes infected if at least two of its neighbors are already infected). Then, for $\mathcal{A}_0 \subseteq V$ whose elements are chosen independently at random, each with probability $p=p(n)$ , the following sharp threshold was determined by Holroyd [24]. The probability I(n, p) that the entire square is eventually infected satisfies $I(n,p) \rightarrow 1$ if $\liminf_{n \rightarrow \infty} p(n) \log n > \pi^2/18$ , and $I(n,p) \rightarrow 0$ if $\limsup_{n \rightarrow \infty} p(n) \log n < \pi^2/18$ . A generalization of this result to the higher-dimensional case was proved by Balogh, Bollobás and Morris [11] (when G is the three-dimensional grid on $[n]^3$ and $r=3$ ) and by Balogh, Bollobás, Duminil-Copin and Morris [10] (in general).

In this paper we study the bootstrap percolation process on inhomogeneous random graphs. Informally, these random graphs are defined through a sequence of weights that are assigned to the vertices, which in turn determine the probability that two vertices are adjacent. More specifically, we are interested in the case where this probability is proportional to the product of the weights of these vertices. In particular, pairs of vertices such that at least one of them has a high weight are more likely to appear as edges.

A special case of our setting is the G(n, p) model of random graphs, where every edge on a set of n vertices is present independently with probability p. Here every vertex has the same weight. Janson, Łuczak, Turova and Vallier [26] presented a complete analysis of the bootstrap percolation process for various ranges of p. We focus on their findings regarding the range where $p = d/n$ and $d>0$ is fixed, as these are most relevant for the setting studied in this paper. In [26] a law of large numbers for $|\mathcal{A}_f|$ was shown when the density of $\mathcal{A}_0$ is positive, that is, when $|\mathcal{A}_0| = \theta n$ , where $\theta \in (0,1)$ . It was further shown that when $|\mathcal{A}_0| = o(n)$ , typically no evolution occurs. In other words, the density of the initially infected vertices must be positive in order for the density of the finally infected vertices to increase. This fact had been pointed out earlier by Balogh and Bollobás; cf. [13]. A similar behavior was observed in the case of random regular graphs [13], as well as in random graphs with given vertex degrees. These were studied by the first author in [3], in the case where the sum of the squares of the degrees scales linearly with n. As we shall see shortly, the random graph model we consider here is essentially a random graph with given expected degrees. Finally, more recently the bootstrap process was considered in another type of inhomogeneous random graph, namely the stochastic block model [36].

The main result of this paper provides a law of large numbers for $|\mathcal{A}_f|$ given $|\mathcal{A}_0|$ for weight sequences that satisfy fairly general and natural regularity conditions. We then consider weight sequences that follow a power-law distribution, i.e., where the proportion of vertices with weight w scales like $w^{-\beta}$ for some $\beta > 2$ , with a particular focus on the case where $\beta \in (2,3)$ . The parameter $\beta$ is called the exponent of the power law. Note that although in this case the weight sequence has a bounded average weight, its second moment grows with the number of vertices. Power laws emerge in several contexts, ranging from ecology and economics to social networks (see e.g. the survey of Mitzenmacher [28]). Already in the late 19th century, Pareto observed a power law in the distribution of wealth within populations [30]. In a completely different context, in 1926 Lotka [27] observed a power-law distribution on the frequencies of scientists whose works had been cited a certain number of times in Chemical Abstracts during the period 1910–1916. The article of Albert and Barabási [2] provides several examples of networks that exhibit power-law degree distributions. In fact, most of these examples exhibit power laws that have exponents between 2 and 3. This range of exponents is also associated with ultra-small worlds. Chung and Lu [18] showed that for the model which we will consider in this paper, the average distance between two vertices in the largest (giant) component scales like $\log \log n$ .

The methods of our paper have also been applied in the context of directed inhomogeneous random graphs [20]. Furthermore, they have found application in the analysis of bootstrap-like processes which model cascading phenomena between financial institutions [21].

In this work we extend a theorem proved by the first two authors in [6], which gives a threshold function $a_c (n)= o(n)$ such that if a(n) grows slower than $a_c (n)$ , then with high probability no evolution occurs, but if a(n) grows faster than $a_c (n)$ , then even if $a(n)=o(n)$ , the final set contains a positive fraction of the vertices. Here we determine this fraction exactly, and we show that as long as $a(n) = o(n)$ , it does not depend on a(n) itself. In the rest of this section we provide the definition of the random graph model that we consider and the statements of our theorems.

Notation. For non-negative sequences $x_n$ and $y_n$ , we write $x_n = O(y_n)$ if there exist $N \in \mathbb{N}$ and $C > 0$ such that $x_n \leq C y_n$ for all $n \geq N$ , and we write $x_n = o(y_n)$ if $x_n/ y_n \rightarrow 0$ as $n \rightarrow \infty$ . We also sometimes write $x_n \ll y_n$ for $x_n = o(y_n)$ .

Let $\{ X_n \}_{n \in \mathbb{N}}$ be a sequence of real-valued random variables on a sequence of probability spaces $\{ (\Omega_n, \mathbb{P}_n)\}_{n \in \mathbb{N}, \mathcal{F}_n}$ . If $c \in \mathbb{R}$ is a constant, we write $X_n \stackrel{p}{\rightarrow} c$ to denote that $X_n$ converges in probability to c, that is, for any $\varepsilon >0$ we have $\mathbb{P}_n (|X_n - c|>\varepsilon) \rightarrow 0$ as $n \rightarrow \infty$ . Moreover, let $\{ a_n \}_{n \in \mathbb{N}}$ be a sequence of real numbers that tends to infinity as $n \rightarrow \infty$ . We write $X_n = o_p (a_n)$ if $|X_n|/a_n$ converges to 0 in probability. If $\mathcal{E}_n$ is a measurable subset of $\Omega_n$ for any $n \in \mathbb{N}$ , we say that the sequence $\{ \mathcal{E}_n \}_{n \in \mathbb{N}}$ occurs asymptotically almost surely or with high probability (w.h.p.) if $\mathbb{P}_n (\mathcal{E}_n) = 1-o(1)$ as $n\rightarrow \infty$ .

2. Models and results

The random graph model that we consider is an extension of a model considered by Chung and Lu [18], and is a special case of the so-called inhomogeneous random graph, which was introduced by Söderberg [33] and defined in full generality by Bollobás, Janson and Riordan in [14].

2.1. Inhomogeneous random graphs with rank-1 kernel

Let $n\in\mathbb{N}$ and consider the vertex set $[n] \,:\!=\, \{1, \dots, n\}$ . Each vertex i is assigned a positive weight $w_i(n)$ , and we will write $\textbf{w}=\textbf{w}(n) = (w_1(n), \dots, w_n(n))$ . We will often suppress the dependence on n, whenever it is obvious from the context. For convenience, we will assume that $w_1 \leq w_2 \leq \cdots \leq w_n$ . For any $S \subseteq [n]$ , set

\[ W_S(\textbf{w}) \,:\!=\, \sum_{i\in S} w_i.\]

In our random graph model, the event of including the edge $\{i,j\}$ in the resulting graph is independent of the inclusion of any other edge, and its probability equals

(1) \begin{equation} p_{ij}(\textbf{w}) = \min\left\{\frac{w_iw_j}{W_{[n]}(\textbf{w})},1\right\}.\end{equation}

This model was studied by Chung and Lu in a series of papers [17–19] for fairly general choices of $\textbf{w}$ . Chung and Lu studied several typical properties of the resulting graphs, such as the average distance between two randomly chosen vertices that belong to the same component, and the component size distribution. Their model was defined under the additional assumption that $\max_{i \in [n]} w_i^2 < W_{[n]}$ . We drop this assumption and use (1) instead. We will refer to this model as the Chung–Lu model, and we shall write $CL(\textbf{w})$ for a random graph in which each possible edge $\{i,j\}$ is included independently with probability as in (1). Moreover, we will suppress the dependence on $\textbf{w}$ if it is clear from the context which sequence of weights we are referring to.

Note that in a Chung–Lu random graph the weights (essentially) control the expected degrees of the vertices. Indeed, if we ignore the minimization in (1), and also allow a loop at vertex i, then the expected degree of that vertex is $\sum_{j=1}^n w_iw_j/W_{[n]} = w_i$ .

2.2. Regular weight sequences

Following van der Hofstad [37], for any $n\in \mathbb{N}$ and any sequence of weights $\textbf{w}(n)$ , let

\[ F_n(x) = n^{-1} \sum_{i=1}^n \textbf{1}[w_i(n) \leq x] \qquad\forall x\in [0,\infty)\]

be the empirical distribution function of the weight of a vertex chosen uniformly at random. We will assume that $F_n$ has a certain structure.

Definition 1. We say that $(\textbf{w}(n))_{n \ge 1}$ is regular if it has the following properties:

• Weak convergence of weight: There is a distribution function $F\,:\,[0,\infty)\to [0,1]$ such that for all x at which F is continuous, $\lim_{n\to\infty}F_n(x) = F(x)$ .

• Convergence of average weight: Let $W_n$ be a random variable with distribution function $F_n$ , and let $W_F$ be a random variable with distribution function F. Then $\lim_{n\to\infty}\mathbb{E} \left( W_n\right) = \mathbb{E} \left( W_F\right) < \infty$ .

• Non-degeneracy: There is an $x_0 \in \mathbb{R}^+$ such that $F_n(x) = 0$ for all $x \in [0,x_0)$ and $n \in \mathbb{N}$ . (That is, the weights are bounded from below by $x_0$ .)

The regularity of $(\textbf{w}(n))_{n\ge 1}$ guarantees two important properties. First, the weight of a random vertex is approximately distributed as a random variable that follows a certain distribution. Second, this variable has finite mean, and it is easy to see that the associated Chung–Lu random graph has bounded average degree w.h.p. The third property in Definition 1 is a minor restriction guaranteeing that no vertex has a vanishing expected degree; it is added for convenience in order to simplify several of our technical considerations.

At many points in our arguments it will be important to select vertices randomly according to their weight, i.e. so that the probability of choosing $i \in [n]$ equals $w_i / W_{[n]}(\textbf{w})$ . This is the so-called size-biased distribution, and we denote by $W_{F_n}^*$ a random variable with this distribution. A straightforward calculation shows that for every bounded continuous function f,

(2) \begin{equation} \mathbb{E} \left( f\left(W_{F_n}^*\right)\right) = \frac{\mathbb{E} \left( W_{F_n} f\left(W_{F_n}\right)\right) }{ \mathbb{E} \left( W_{F_n}\right)}.\end{equation}

2.3. Results

The main theorem of this paper gives a law of large numbers for the size of $\mathcal{A}_f$ when $\mathcal{A}_0$ has positive density, in the case where the underlying random graph is a Chung–Lu random graph with a regular weight sequence. Let $\psi_r (x)$ for $x \geq 0$ be equal to the probability that a Poisson-distributed random variable with parameter x is at least r, i.e.,

$$\psi_r (x)\,:\!=\, \mathbb{P} \left[\mathsf{Po}(x)\geq r\right] =e^{-x} \sum_{j \ge r} {x^j}/{j!}.$$

Let X be a non-negative random variable and $p \in [0,1]$ . For any $r\geq 1$ and $y \in \mathbb{R}^+$ set

$$ f_r \left(y;\, X,p\right) = (1-p) \mathbb{E} \left[\psi_r (Xy)\right] + p - y.$$

Theorem 1. Let $(\textbf{w}(n))_{n \geq 1}$ be regular with limiting distribution function F. Consider the bootstrap percolation process on $CL(\textbf{w})$ with activation threshold $r\geq 2$ , where $\mathcal{A}_0 \subseteq [n]$ includes any vertex independently with fixed probability $p \in (0,1)$ . Let $\hat{y}$ be the smallest positive solution of

(3) \begin{equation}f_r\left(y;\,W_F^*,p\right) = 0.\end{equation}

Assume also that $f^{\prime}_r(\hat{y};\,W_F^*,p) < 0$ . Then

(4) \begin{equation}n^{-1}{|\mathcal{A}_f|} \stackrel{p}{\rightarrow} (1-p)\mathbb{E} \left[\psi_r \left(W_F\hat{y}\right)\right]+p \quad \mbox{as $n \rightarrow \infty $}.\end{equation}

We remark that a solution $\hat{y}$ to (3) always exists, because $f_r(y;\,W_F^*,p)$ is continuous, $f_r(0;\,W_F^*,p) > 0$ , and $f_r(1;\,W_F^*,p) \leq 0$ . Note that the conclusion of our results is valid only if $f^{\prime}_r(\hat{y};\,W_F^*,p) < 0$ . This fails to happen only if

$$\mathbb{E}\left[\frac{e^{-\hat{y}W_F^*}\left(W_F^*\hat{y}\right)^r}{r!}\right] = \frac{\hat{y}}{(1-p)r},$$

and for such (rather exceptional) weight sequences we expect a different behavior. Moreover, we show (cf. Lemma 6) that if the weight sequence has a power-law distribution with exponent between 2 and 3, this case will not happen (i.e., we always have $f^{\prime}_r(\hat{y};\,W_F^*,p) < 0$ ).

Intuitively, the quantity $\hat{y}$ represents the limit of the probability that infection is passed through a random neighbor of a vertex. The fixed-point equation $f_r(y;\,W_F^*,p) = 0$ , whose solution is $\hat{y}$ , effectively says that a vertex is infected if either it is initially infected (which occurs with probability p) or (if not, which occurs with probability $1-p$ ) it has at least r infected neighbors. The latter is a Poisson-distributed random variable with parameter equal to $W_F^* \hat{y}$ . The first factor essentially states the fact that a vertex becomes some other vertex’s neighbor with probability proportional to the latter’s weight, whereas it is infected with probability approximately $\hat{y}$ .

We will now see an extension of the above theorem to the case where p is no longer bounded away from 0. Under certain conditions the above theorem can be transferred to this case simply by setting $p=0$ . These conditions ensure that a positive but rather small fraction of the vertices become infected, and this effectively corresponds to taking a p that is in fact bounded away from 0 but small.

2.4. Power-law weight sequences

Our second result focuses on an important special case of weight sequences, namely those following a power-law distribution. This is described by the following condition.

Definition 2. We say that a regular sequence $( \textbf{w}(n) )_{n \ge 1}$ follows a power law with exponent $\beta$ if there are $0< c_1< c_2$ , $c_3, x_0 >0$ , and $0 < \zeta \leq {1/(\beta -1)} $ such that for all $x_0 \le x < c_3 \cdot n^{\zeta}$ ,

\[ c_1 x^{-\beta + 1}\le 1 - F_n(x) \le c_2 x^{-\beta + 1},\]

while $F_n(x) = 0$ for $x < x_0$ and $F_n(x) = 1$ for $x \geq c_3 \cdot n^{\zeta}$ . Moreover, for any $x > x_0$ , we have for some $c>0$ that

$$ \lim_{n \to \infty} F_n(x) = F(x) = 1 - c x^{-\beta + 1}. $$

We say that such a sequence belongs to the class $PL(\beta, \zeta)$ .

In the above definition, the maximum weight of a vertex is close to $c_3 \cdot n^\zeta$ for any n sufficiently large. Furthermore, if $\zeta = 1/(\beta -1)$ , then $c_3 \leq c_2^{1/(\beta-1)}$ .

A particular example of a power-law weight sequence is given in [18], where the authors choose $w_i = d ({n}/{(i + i_0)})^{1/(\beta - 1)}$ for some $d>0$ . This typically results in a graph with a power-law degree sequence with exponent $\beta$ , average degree O(d), and maximum degree proportional to $({n}/{i_0})^{1/(\beta - 1)}$ ; see also [37] for a detailed discussion. When $\beta \in (2,3)$ , these random graphs are also characterized as ultra-small worlds, because of the fact that the typical distance between two vertices that belong to the same component is $O(\log \log n)$ ; see [18, 37].

Theorem 1 addresses the case where the initial set $\mathcal{A}_0$ has positive density. Our second result is complementary and considers the setting where $p = p(n) = o(1)$ , with a particular focus on the case where the exponent of the power law is in (2,3). Assume that $\mathcal{A}_0$ has density $a(n)/n$ . In [6] the first two authors determined a function $a_c(n)$ (which we also give in the statement of the next theorem) such that, for $\zeta$ satisfying

$$\frac{r-1 }{ 2r - \beta + 1} < \zeta \leq \frac{1}{ \beta -1},$$

if $a(n) = o (a_c (n))$ , then w.h.p. $|\mathcal{A}_0| = |\mathcal{A}_f|$ , whereas if $a(n) = \omega(a_c(n))$ but $a(n) = o(n)$ , then w.h.p. $|\mathcal{A}_f| > \varepsilon n$ , for some $\varepsilon >0$ . However, for

$$\zeta \leq \frac{r-1 }{ 2r - \beta + 1}$$

they showed a weaker result and identified two functions $a_c^{-}(n) \ll a_c^{+}(n) = o(n)$ such that if $a(n) \gg a_c^+(n)$ , then $|\mathcal{A}_f| > \varepsilon n$ for some $\varepsilon >0$ , but if $a(n) \ll a_c^- (n)$ , then w.h.p. $|\mathcal{A}_0|= |\mathcal{A}_f|$ . $\Big($ In particular, $a_c^- (n) = a_c (n)$ and $a_c^{+} (n) = n^{1- \zeta \frac{r- \beta +2}{r-1}}$ . $\Big)$ We refine this result using the proof of Theorem 1 and determine the fraction of vertices that belong to $\mathcal{A}_f$ .

Theorem 2. Let $(\textbf{w}(n))_{n \geq 1} \in PL(\beta,\zeta)$ for some $\beta\in(2,3)$ . Consider the bootstrap percolation process on $CL (\textbf{w})$ with activation threshold $r\geq 2$ . Let

$$a_c (n) = n^{(r(1-\zeta) + \zeta (\beta -1)-1)/ r}$$

and

$$a_c^+ (n) = n^{1- \zeta \frac{r- \beta +2}{r-1}}.$$

Assume that $\mathcal{A}_0$ is a random subset of $[n]$ where each vertex is included independently with probability $a(n)/n$ . If $a(n) =o(n)$ and $a(n) = \omega(a_c (n))$ $\Big($ for $\frac{r-1}{2r - \beta + 1} < \zeta \leq \frac{1}{\beta -1}\Big)$ and $a(n) = \omega (a_c^+(n))$ $\Big($ for $ \zeta \leq \frac{r-1}{2r - \beta + 1}\Big)$ , then

$$ n^{-1}{|\mathcal{A}_f|} \stackrel{p}{\rightarrow} \mathbb{E} \left[\psi_r \left(W_F \hat{y}\right)\right] \quad \mbox{as $n \rightarrow \infty $}, $$

where $\hat{y}$ is the smallest positive solution of

$$ y = \mathbb{E} \left[\psi_r \left(W_F^* y\right)\right].$$

When $\beta > 3$ , the regularity assumptions of Theorem 1 are satisfied, and the asymptotics of the size of the final set is given by this. When $\beta = 3$ , these assumptions are no longer satisfied. Consequently, the techniques that are used for the proof of Theorem 2 in Section 3.2 do not apply immediately but need significant refinement.

Let us remark here that the (rescaled) size of the final set does not depend on $|\mathcal{A}_0|$ .

More generally, the above theorem holds as long as the initial density is such that, asymptotically almost surely, most vertices of weight exceeding some large constant become infected.

2.5. Outline

The proofs of Theorems 1 and 2 are based on a finitary approximation of the weight sequence $\textbf{w} (n)$ . In the following section we construct a sequence of weight sequences having only a finite number of weights and that ‘approximate’ the initial sequence in a certain well-defined sense. Thereafter, we show the analogue of Theorem 1 for finitary sequences; this is Theorem 3, stated below. The proof of Theorem 3 is based on the so-called differential equation method, which was developed by Wormald [38, 39] and is used to keep track of the evolution of the bootstrap percolation process through the exposure of the neighbors of each infected vertex. Such an exposure algorithm has also been applied in the homogeneous setting [26]. Of course, the inhomogeneous setting imposes significant obstacles. We close the paper with the proofs of some rather technical results, which transfer the condition on the derivative that appears in the statement of Theorem 1 to the finitary setting.

3. Finitary weight sequences

In this section we will consider so-called finitary weight sequences on [n] that are suitable approximations of an arbitrary weight sequence $\textbf{w}(n)$ . As a first step we are going to ‘remove’ all weights from $\textbf{w}$ that are too large in the following sense. Suppose that $\textbf{w} (n)$ is regular and that the corresponding sequence of empirical distributions converges to F. Let $(c_j)_{j\in \mathbb{N}}$ be an increasing sequence of points of continuity of F with the following properties:

1. 1. $\lim_{j\to \infty} c_j = \infty$ .

2. 2. $2c_j$ is also a point of continuity.

For $\gamma > 0$ let

$$C_\gamma = C_\gamma (F) \,:\!=\, \min \left\{ c_j \,:\, F\left(c_j\right) \geq 1-\gamma \right\}.$$

Then, as $n \rightarrow \infty$ , the following facts are immediate consequences. Let $\mathsf{C}_{\gamma} = \mathsf{C}_{\gamma}(n,F)$ be the set of vertices in [n] with weight at least $C_\gamma(F)$ . Then the following hold:

1. 1. With $h_F (\gamma) \,:\!=\, 1- F(C_\gamma) \leq \gamma$ , we have $|\mathsf{C}_{\gamma}(n,F)|/n \rightarrow h_F(\gamma)$ .

2. 2. $ n^{-1}{W_{\mathsf{C}_{\gamma}(n,F)} (\textbf{w}(n)) } \rightarrow \int_{C_{\gamma}}^{\infty} x dF(x) \,=\!:\,W_{\gamma}(F), $ where the latter is the Lebesgue–Stieltjes integral with respect to F.

3. 3. The assumption $\mathbb{E} \left[W_F\right] = d < \infty$ implies that $\mathbb{P}\left[W_F > x \right] = o(1/x)$ as $x \rightarrow \infty$ . Thus

   (5) \begin{equation}C_\gamma(F) \mathbb{P}\left[W_F > C_\gamma(F)\right] \rightarrow 0, \ \mbox{as $\gamma \downarrow 0$}.\end{equation}
   Also, $W_\gamma (F)/C_\gamma (F) \to 0$ as $\gamma \downarrow 0$ . We will be using this observation in several places in our proofs.

We will approximate a regular weight sequence $(\textbf{w}(n))_{n \ge 1}$ by a sequence where most vertices have weights within a finite set of values, and moreover the weights are bounded by $2C_\gamma(F)$ (cf. [37] where a similar approach is followed in a different context).

Definition 3. Let $\ell \in \mathbb{N}$ and $\gamma \in (0,1)$ .

For a function $n^{\prime}=n^{\prime}(n) \in \mathbb{N}$ with $n^{\prime}\geq n-|\mathsf{C}_\gamma (F)|$ , we say that a regular weight sequence

\[ \left(\textbf{W}^{(\ell, \gamma)}\left({n^{\prime}}\right)\right)_{n \ge 1 } = \left(W_1^{(\ell, \gamma)}\left({n^{\prime}}\right),\dots, W_{n^{\prime}}^{(\ell, \gamma)}\left({n^{\prime}}\right)\right)_{n \ge 1}\]

is an $(\ell, \gamma)$ -discretization of a regular weight sequence $(\textbf{w}(n))_{n \ge 1}$ with limiting distribution function F if the following conditions are satisfied. There are an increasing sequence of natural numbers $(p_\ell)_{\ell \in \mathbb{N}}$ and positive constants $\gamma_1, \dots, \gamma_{p(\ell)} \in (0,1)$ such that $\sum_{i=1}^{p_\ell} \gamma_i = 1 - h_F (\gamma )$ , and there are real weights $0< W_0 < W_1 < \dots < W_{p_\ell} \leq C_\gamma(F)$ which satisfy the following properties. There is a partition of $[n]\setminus \mathsf{C}_{\gamma}(F)$ into $p_\ell$ parts, denoted by $\mathsf{C}_1(n),\ldots, \mathsf{C}_{p_\ell}(n)$ , such that the following hold:

1. 1. For all $1 \le i \le p_\ell$ and for all $j \in \mathsf{C}_i(n)$ we have $W_j^{({\ell}, \gamma)}(n^{\prime}) = W_i$ .

2. 2. Let $\mathsf{C}^{\prime}_\gamma(n) \,:\!=\, [n^{\prime}]\setminus \cup_{i=1}^{p_\ell} \mathsf{C}_i(n)$ . Then $C_{\gamma}(F) \leq W_j^{(\ell, \gamma )}(n^{\prime}) \leq 2 C_{\gamma}(F)$ for all $j \in \mathsf{C}^{\prime}_\gamma(n)$ .

Moreover, as $n \to\infty$ , the following hold:

1. 3. For all $1\le i \le p_\ell$ , $n^{-1}|\mathsf{C}_i(n)| \to \gamma_i$ .

2. 4. There is an $h_F(\gamma) \le \gamma^{\prime} < h_F(\gamma) + 2W_\gamma(F)/C_\gamma(F)$ such that $ n^{-1}{|\mathsf{C}^{\prime}_\gamma(n)|} \rightarrow \gamma^{\prime} . $

3. 5. There is a $0 \le W^{\prime}_\gamma \le 4 W_\gamma(F)$ such that $n^{-1}{W_{\mathsf{C}^{\prime}_\gamma(n)}(\textbf{W}^{(\ell,\gamma)}({n^{\prime}}))} \rightarrow W^{\prime}_\gamma.$

4. 6. The weight sequence $\textbf{W}^{(\ell, \gamma)}(n)$ gives rise to a sequence of the corresponding empirical distributions which we denote by $F^{(\ell, \gamma)}_{n}$ , and we assume that they converge weakly to a limiting distribution $F^{(\ell,\gamma)}$ .

The upper bounds in Items 4 and 5 are tailored to the proof of Theorem 1. Note that in the previous definition no assumption is made on the $W_i$ , and thus $\textbf{W}^{(\ell,\gamma)}$ might look very different from $\textbf{w}$ . The next definition quantifies when an $(\ell,\gamma)$ -discretization is ‘close’ to a given regular $(\textbf{w}(n))_{n \ge 1}$ with limiting distribution function F. For a cumulative distribution function G, let $G^{*}$ denote the distribution function of the size-biased version of a G-distributed random variable.

Definition 4. Let $(\textbf{w}(n))_{n \ge 1}$ be regular and let F be its limiting distribution function. A family $\big( \big(\textbf{W}^{(\ell, \gamma)}(n^{\prime})\big)_{n \ge 1} \big)_{\ell \in \mathbb{N}, \gamma \in (0,1)}$ of $(\ell,\gamma)$ -discretizations of $(\textbf{w}(n))_{n \ge 1}$ with limiting distribution functions $F^{(\ell,\gamma)}$ is called F-convergent if the following hold:

1. 1. For every $x \in \mathbb{R}$ that is a point of continuity of F, we have

   $$ \lim_{\gamma \downarrow 0} \lim_{\ell \to \infty} F^{(\ell,\gamma)}(x) = F(x),\ \lim_{\gamma \downarrow 0} \lim_{\ell \to \infty} F^{*(\ell,\gamma)}(x) = F^*(x). $$

2. 2. We have

\begin{align*}&\lim_{\gamma \downarrow 0} \lim_{\ell \to \infty} \left| \int_0^{\infty} x d F^{(\ell, \gamma)} (x) - \mathbb{E} (W_F) \right|=0,\\ &\lim_{\gamma \downarrow 0} \lim_{\ell \to \infty} \left| \int_0^{C_\gamma} x d F^{(\ell,\gamma)} (x) - \mathbb{E} (W_F) \right|=0.\end{align*}

Let $U^{(\ell,\gamma)}$ $\big($ resp. $U^{*(\ell,\gamma)}$ $\big)$ be a random variable whose distribution function is $F^{(\ell,\gamma)}$ $\big($ resp. $F^{*(\ell,\gamma)}\big)$ . Let us observe that

$$ \mathbb{P}\big[U^{*(\ell,\gamma)} > C_\gamma\big] = \frac{\mathbb{E} \left[U^{(\ell,\gamma)} \textbf{1}_{U^{(\ell,\gamma)}> C_\gamma} \right]}{\mathbb{E} \left[U^{(\ell,\gamma)}\right]}\leq 2/W_0 \cdot \mathbb{E} \left[U^{(\ell,\gamma)} \textbf{1}_{U^{(\ell,\gamma)}> C_\gamma}\right],$$

since $\mathbb{E} \left[U^{(\ell,\gamma)}\right] \geq W_0/2$ for any $\gamma$ and any $\ell$ sufficiently large. By Part 2 of Definition 4, we have

$$\lim_{\gamma \downarrow 0} \lim_{\ell\to \infty} \mathbb{E} \left[U^{(\ell,\gamma)} \textbf{1}_{U^{(\ell,\gamma)}> C_\gamma}\right]=0.$$

We can thus deduce the following lemma, which will be used later.

Lemma 1. If $f\,:\,\mathbb{R} \to \mathbb{R}$ is a bounded function, then

$$\lim_{\gamma \downarrow 0} \lim_{\ell\to \infty}\left| \mathbb{E} \left( f(U^{*(\ell,\gamma)}) \textbf{1}_{U^{*(\ell,\gamma)}> C_\gamma}\right)\right|=0.$$

For technical reasons we consider a slightly different definition of the random graph model that we denote by $CL^{\prime} \big( \textbf{W}^{(\ell, \gamma)} \big)$ . In this modified model the edge probabilities are proportional to the product of the weights of the vertices, except that the normalizing factor is equal not to the sum of the weights in $\textbf{W}^{(\ell, \gamma)}$ , but rather to $W_{[n]}(\textbf{w}(n))$ ; that is, the edge $\{i,j\}$ is contained in $CL^{\prime} \big( \textbf{W}^{(\ell, \gamma)} \big)$ with probability

\[ p_{ij}\big(\textbf{W}^{(\ell, \gamma)}({n^{\prime}}), \textbf{w}(n)\big) = \min\left\{ \frac{W_i^{(\ell,\gamma)} {W_j^{(\ell,\gamma)}}}{W_{[n]}(\textbf{w})} ,1\right\}.\]

The next theorem quantifies the number of finally infected vertices when the weight sequence is a discretization of a given regular $(\textbf{w}(n))_{n \ge 1}$ . It is general enough to be used in the proof of Theorem 2 as well.

Theorem 3. Let $(\textbf{w}(n))_{n \ge 1}$ be regular and let F be its limiting distribution function. Let $\big( \big(\textbf{W}^{(\ell, \gamma)}({n^{\prime}})\big)_{n\ge 1}\big)_{\ell \in \mathbb{N},\gamma \in (0,1)}$ be a family of $(\ell,\gamma)$ -discretizations of $(\textbf{w}(n))_{n\geq 1}$ which is F-convergent. Moreover, assume that $f^{\prime}_r(\hat{y};W_F^*,p) <0$ (cf. Theorem 1).

Let $r \geq 2$ . Assume that initially all vertices of $CL^{\prime} (\textbf{W}^{(\ell, \gamma)})$ that belong to $\mathsf{C}^{\prime}_{\gamma}(n)$ are infected, whereas each vertex in $\mathsf{C}_i(n)$ is infected independently with probability $p\in [0,1)$ , for each $i=1,\ldots, p_\ell$ . Let $\mathcal{A}_f^{(\ell,\gamma)}$ denote the set of vertices in $[n^{\prime}] \setminus \mathsf{C}^{\prime}_{\gamma}(n)$ that eventually become infected during a bootstrap percolation process with activation threshold r. There exists $c >0$ for which the following holds: for $\gamma \in(0,c)$ and for any $\delta \in (0,1)$ , there is a subsequence $\mathcal{S} \,:\!=\,\{\ell_k\}_{k\in \mathbb{N}}$ such that for any $\ell \in \mathcal{S}$ , with probability at least $1-o(1)$ ,

$$ n^{-1}{\big|\mathcal{A}_f^{(\ell,\gamma)}\big| } = (1\pm \delta) \left( (1-p) \mathbb{E} \left[{\psi_r(W_F \hat{y})}\right] + p \right). $$

3.1. Proof of Theorem 1

Given a regular $(\textbf{w}(n))_{n \ge 1}$ , Theorem 1 follows from Theorem 3 by constructing an F-convergent family $( (\textbf{W}^{(\ell, \gamma)}(n^{\prime}))_{n\ge 1})_{\ell \in \mathbb{N},\gamma \in (0,1)}$ for a certain function $n^{\prime}\,:\, \mathbb{N} \to \mathbb{N}$ . We first describe our construction and prove some properties of it, and then proceed with the proofs of our main results.

3.1.1. The construction of approximating weight sequences

Let $(\textbf{w}(n))_{n \ge 1}$ be regular and consider the limiting distribution function F. For $\gamma \in (0,1)$ , recall that $F(C_{\gamma}) \geq 1 - \gamma$ . Recall also that from Definition 1 there is a positive real number $x_0$ such that $F(x) = 0$ for $x < x_0$ .

We define a set of intervals $\mathcal{P}_\ell$ whose union is a superset of $[x_0,C_\gamma)$ as follows. Let $\varepsilon_\ell = 1/\ell$ . First, for $i\geq 0$ , we set

$$x_{i+1} = \sup \{x \in (x_i,C_\gamma) \,:\, F(x) - F(x_i) < \varepsilon_\ell \}.$$

Set $t_\ell = \min \{ i \,:\, x_i = C_\gamma \}$ and $x_{-1}=0$ . For each $i=0,\ldots, {t_\ell}$ , let $y_{2i}, y_{2i+1}$ be such that

1. (1) $\max \big\{ \frac{1}{2} (x_{i-1}+x_i), x_i -\varepsilon_\ell \big\} < y_{2i} < x_i$ ;

2. (2) $x_i < y_{2i+1} < \min \big\{ \frac{1}{2}(x_i +x_{i+1}), x_i+ \varepsilon_\ell \big\}$ or $y_{2i+1}= C_\gamma$ , if $i=t_\ell$ ;

3. (3) $y_{2i}, y_{2i+1}$ are points of continuity of F.

Now, we set $\mathcal{P}_\ell \,:\!=\, \{ [y_0 ,y_1), \ldots, [y_{2 t_\ell}, C_\gamma) \}$ . With $p_\ell = 2 t_\ell+1$ , for $i=1,\ldots, p_\ell$ , we set $I_i = [y_{i-1}, y_{i} )$ .

Given this partition and the weight sequence $\textbf{w} (n)$ , for each $n \geq 1$ we define two finitary weight sequences $\textbf{W}^{(\ell, \gamma)+} ({n^{\prime}})$ and $\textbf{W}^{(\ell,\gamma)-} ({n^{\prime\prime}})$ on the sets [n ^′] and [n ^′′], respectively, as follows. The partition $\mathcal{P}_\ell$ gives rise to a partition of $[n] \setminus \mathsf{C}_{\gamma}$ , where for each $i =1,\ldots, p_\ell$ we have $\mathsf{C}_i = \{j \,:\, w_j(n) \in I_i \}$ . We denote this partition by $\mathcal{P}_{n,\ell,\gamma}$ , and we let this be the associated partition of $\textbf{W}^{(\ell,\gamma)+} (n)$ and $\textbf{W}^{(\ell, \gamma)-} (n)$ .

In particular, consider the random subset of $\mathsf{C}_\gamma$ in which every element of $\mathsf{C}_\gamma$ is included independently with probability p. An application of the Chernoff bounds implies that w.h.p. this has size at least $\lfloor p|\mathsf{C}_\gamma| - n^{2/3} \rfloor\,=\!:\,k_-$ . Consider a set of vertices $\mathsf{C}_\gamma^-=\{ v_1,\ldots, v_{k_-} \}$ which is disjoint from [n]. We identify with [n ^′′] the set $\left( \cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \mathsf{C}_\gamma^-$ , through a bijective mapping $\varphi^- \,:\, \left( \cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \mathsf{C}_\gamma^- \to [n^{\prime\prime}]$ . It follows that $n^{\prime\prime} = (1-{h_F(\gamma)} + p{h_F(\gamma)})n (1+o(1))$ .

For any vertex $j \in \mathsf{C}_\gamma$ such that $w_j(n) \geq 2 C_\gamma$ , we consider $c_j\,:\!=\,2 \big\lfloor \frac{w_j(n)}{C_\gamma}\big\rfloor$ copies of this vertex each having weight $2C_\gamma$ , which we label as $v_{j1},\ldots, v_{jc_j}$ . For each such j we let

$$\varepsilon_j(n)= \frac{w_j(n)}{C_\gamma} - \Big\lfloor \frac{w_j (n)}{C_\gamma} \Big\rfloor,$$

and we set

$$R = \Big\lceil 2 \sum_{j \,:\, w_j(n) \geq 2 C_\gamma} \varepsilon_j (n) \Big\rceil.$$

If $j \in \mathsf{C}_\gamma$ is such that $C_\gamma \leq w_j(n) < 2 C_\gamma$ , then we introduce a single copy $v_{j1}$ having weight equal to $w_j$ (in other words $c_j=1$ ).

We let $\mathsf{C}_\gamma^+$ be the set that is the union of these copies together with a set of R vertices which we denote by $\mathcal{R}$ (disjoint from the aforementioned sets) each having weight $2 C_\gamma$ :

$$ \mathsf{C}_\gamma^+ \,:\!=\, \mathcal{R} \cup \bigcup_{j \in \mathsf{C}_\gamma} \big\{v_{j1},\ldots, v_{jc_j} \big\}. $$

Let $n^{\prime} = \left| \left( \cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \mathsf{C}_\gamma^+ \right|$ , and identify the set [n ^′] with the vertices in $\left( \cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \mathsf{C}_\gamma^+$ , through a bijection $\varphi^+ \,:\, \left( \cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \mathsf{C}_\gamma^+ \to[n^{\prime}]$ . We will use the symbol $\mathsf{C}_\gamma^+$ to denote the set $[n^{\prime}] \setminus\varphi^+\left( \left( \cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \right)$ . In other words, the set $\mathsf{C}_\gamma^+$ consists of the replicas of the vertices in $\mathsf{C}_\gamma$ , as these were defined above, together with the set of vertices corresponding to $\mathcal{R}$ . This completes the definition of $\textbf{W}^{(\ell, \gamma)+} (n)$ .

For each $i = 1,\ldots, p_\ell$ , we set $W_i^- = y_{2(i-1)}$ and $W_i^+ = y_{2i-1}$ ; for each $j \in \mathsf{C}_i$ , we set

$$W_{{\varphi^-(j)}}^{(\ell, \gamma)-} (n) \,:\!=\, W_i^- \quad \mbox{and} \quad W_{{\varphi^+(j)}}^{(\ell, \gamma)+} (n) \,:\!=\, W_i^+.$$

For any $j \in [n^{\prime\prime}] \setminus \varphi^- \left(\cup_{i=1}^{p_\ell} \mathsf{C}_i\right)$ we set $W_j^{(\ell, \gamma)-} (n) \,:\!=\, C_\gamma$ . Note that

$$\lim_{n \rightarrow \infty} \frac{|\mathsf{C}_\gamma^-|}{n} = p h_F(\gamma),$$

and if $W_{\mathsf{C}_\gamma^-} \big(\textbf{W}^{(\ell,\gamma)-}\big)$ denotes the total weight of these vertices, then this satisfies

$$\lim_{n \rightarrow \infty} \frac{W_{\mathsf{C}_\gamma^-} \big(\textbf{W}^{(\ell,\gamma)-}\big)}{n} = ph_F(\gamma) C_\gamma \,=\!:\,W_\gamma^-< W_\gamma < 4W_\gamma.$$

Furthermore,

\begin{equation*}\begin{split}|\mathsf{C}_\gamma^+| &=\sum_{j \,:\, C_\gamma \leq w_j < 2C_\gamma} 1 + \sum_{j \,:\, w_j \geq 2C_\gamma }2 \lfloor \frac{w_j}{C_\gamma} \rfloor + R \\&= \sum_{j \,:\, C_\gamma \leq w_j < 2C_\gamma} 1 + 2 \sum_{j \,:\, w_j \geq 2C_\gamma } \frac{w_j}{C_\gamma} + e(n),\end{split}\end{equation*}

with $0\leq e(n) < 1$ . By the weak convergence of $F_n$ to F and since $\mathbb{E} \left[W_n\right] \to \mathbb{E} \left[W_F\right] < \infty$ , it follows that

(6) \begin{equation} \lim_{n \to \infty} \frac{|\mathsf{C}_\gamma^+|}{n} = \mathbb{P}\left[C_\gamma \leq W_F \leq 2C_\gamma\right] + 2 \frac{\mathbb{E} \left[\textbf{1}_{\{ W_F \geq 2C_\gamma \}}W_F\right]}{C_\gamma}\,=\!:\,\gamma^+,\end{equation}

where $\gamma^+ \downarrow 0$ as $\gamma \downarrow 0$ . So $n^{\prime}/n \to 1- h_{F}(\gamma) + \gamma^+$ as $n\to \infty$ . Moreover,

(7) \begin{equation} \lim_{\gamma \downarrow 0} \gamma^+ C_\gamma = \lim_{\gamma \downarrow 0}\big(C_\gamma \mathbb{P}\left[C_\gamma \leq W_F \leq 2C_\gamma\right] + 2 \mathbb{E} \left[\textbf{1}_{\{ W_F \geq 2C_\gamma \}}W_F\right]\big)\stackrel{5}{=} 0.\end{equation}

Also, the total weight of the vertices in $\mathsf{C}_\gamma^+$ can be bounded as follows:

\begin{equation*} \begin{split} W_{\mathsf{C}_\gamma^+} \big(\textbf{W}^{(\ell,\gamma)+}\big) &= \sum_{j \,:\, C_\gamma \leq w_j < 2C_\gamma} w_j + \sum_{j \,:\, w_j \geq 2C_\gamma } 2 \big\lfloor \frac{w_j}{C_\gamma} \big\rfloor (2 C_\gamma) \\ &\leq {\sum_{j \,:\, C_\gamma \leq w_j < 2C_\gamma} w_j}+ 4 \sum_{j \,:\, w_j \geq 2C_\gamma } w_j. \end{split} \end{equation*}

Hence, as $n \rightarrow \infty$ ,

(8) \begin{equation} \begin{split}\frac{W_{\mathsf{C}_\gamma^+} \big(\textbf{W}^{(\ell,\gamma)+}\big)}{n} \rightarrow& \mathbb{E} \left[\textbf{1}_{\big\{ C_\gamma \leq W_F < 2C_\gamma \big\}}W_F\right] + 4 \mathbb{E} \left[\textbf{1}_{ \{ W_F \geq 2C_\gamma \} }W_F\right]\,=\!:\,W_\gamma^+ {\leq} 4 W_\gamma.\end{split}\end{equation}

We denote by $U_{n}^{(\ell,\gamma)+}$ and $U_{n}^{(\ell, \gamma)-}$ the weight in $\textbf{W}^{(\ell,\gamma)+} (n^{\prime})$ and $\textbf{W}^{(\ell, \gamma)-} (n^{\prime\prime})$ of a uniformly chosen vertex from [n ^′] and [n ^′′], respectively. Also, we let $F_n^{(\ell, \gamma)-}, F_{n}^{(\ell, \gamma)+}$ denote their distribution functions. Note that both $F_n^{(\ell, \gamma)-}$ and $F_{n}^{(\ell, \gamma)+}$ converge pointwise, as $n\rightarrow \infty$ , to the functions $F^{(\ell, \gamma)-}$ and $F^{(\ell, \gamma)+}$ , respectively, where

• for each $i = 0,\ldots, p_\ell$ and for each $x \in I_i$ we set

  $$F^{(\ell, \gamma)-} (x) \,:\!=\, \frac{{F(W_i^+)}}{1-{h_F(\gamma)} + p {h_F(\gamma)}} \quad \mbox{and} \quad F^{(\ell, \gamma)+} (x) = \frac{{F(W_i^-)}}{1- {h_F(\gamma)} + \gamma^+}; $$

• for any $x\geq C_\gamma$ we have $F^{(\ell,\gamma)-}(x) = 1$ , and for any $x< y_0$ we have $F^{(\ell,\gamma)-}(x)=0$ , $F^{(\ell,\gamma)+}(x) =0$ ;

• for any $C_\gamma \leq x < 2C_\gamma$ we have

  (9) \begin{equation} F^{(\ell,\gamma)+}(x) = \frac{F( x )}{1-{h_F(\gamma)} + \gamma^+},\end{equation}
  whereas for $x\geq 2 C_\gamma$ we have $F^{(\ell,\gamma)+}(x) = 1$ .

We will now prove that both families

$$\big\{\textbf{W}^{(\ell,\gamma)+} ({n^{\prime}})\big\}_{\gamma\in (0,1), \ell \in \mathbb{N}} \quad\text{and} \quad\big\{ \textbf{W}^{(\ell, \gamma)-} ({n^{\prime\prime}}) \big\}_{\gamma\in (0,1), \ell \in \mathbb{N}}$$

are F-convergent. Thus, we will verify that they satisfy both parts of Definition 4.

Part 1 of Definition 4. It will be convenient to define a probability distribution function which will be the pointwise limit of $F^{(\ell,\gamma)+}$ and $F^{(\ell,\gamma)-}$ as $\ell \to \infty$ . For any $x\in [0,C_\gamma)$ we set

$$F^{(\gamma)+} (x) =\frac{F( x )}{1-{h_F(\gamma)} + \gamma^+} $$

and

$$F^{(\gamma)-}(x) =\frac{F(x)}{1-{h_F(\gamma)} + p h_F(\gamma)},$$

whereas $F^{(\gamma)+} (x) = F^{(\gamma)-} (x) = 0$ for $x<0$ , and $F^{(\gamma)+} (x) = F^{(\gamma)-} (x) = 1$ for $x \geq C_\gamma$ . Note first that for any point $x < C_\gamma$ that is a point of continuity of F (and therefore of $F^{(\gamma)+}$ and $F^{(\gamma)-}$ as well), we have

$$ \lim_{\ell \to \infty} F^{(\ell,\gamma)+} (x) = F^{(\gamma)+} (x)$$

and

$$ \lim_{\ell \to \infty} F^{(\ell,\gamma)-} (x) = F^{(\gamma)-} (x).$$

Moreover, note that for any $x >0$ we have

$$\lim_{\gamma \downarrow 0} F^{(\gamma)+} (x), F^{(\gamma)-} (x) = F(x).$$

We will now turn to the size-biased versions of these distributions. Let $U^{(\gamma)+}$ and $U^{(\gamma)-}$ denote two random variables with probability distribution functions $F^{(\gamma)+}$ and $F^{(\gamma)-}$ , respectively. Thus, as $\ell \to \infty$ ,

(10) \begin{equation} U^{(\ell, \gamma)+} \stackrel{d}{\rightarrow} U^{(\gamma)+} \quad \mbox{and} \quad U^{(\ell, \gamma)-} \stackrel{d}{\rightarrow} U^{(\gamma)-},\end{equation}

whereas as $\gamma \downarrow 0$ we have

(11) \begin{equation} U^{(\gamma)+}, U^{(\gamma)-} \stackrel{d}{\rightarrow} W_F.\end{equation}

Claim 4. Let $(X_n)_{n\in \mathbb{N}}$ be a sequence of non-negative random variables. Suppose that W is a random variable such that $X_n \stackrel{d}{\rightarrow} W$ as $n\to \infty$ . For every $x>0$ which is a point of continuity of the cumulative distribution function of W, we have

$$\lim_{n\to \infty} \mathbb{E} (X_n \textbf{1}_{X_n \leq x}) = \mathbb{E} (W \textbf{1}_{W\leq x}). $$

Proof. First note that $X_n \textbf{1}_{X_n \leq x} \stackrel{d}{\to}W \textbf{1}_{W\leq x}$ as $n\to \infty$ . By the Skorokhod representation theorem, there is a coupling of these random variables such that $X_n \textbf{1}_{X_n \leq x} \to W \textbf{1}_{W\leq x}$ almost surely as $n\to \infty$ . The claim now follows from the bounded convergence theorem.

This claim implies that for any $\gamma \in (0,1)$ , as $\ell \to \infty$ ,

(12) \begin{equation}F^{*(\ell,\gamma)+}(x)= \frac{ \mathbb{E} \big(U^{(\ell,\gamma)+} \textbf{1}_{U^{(\ell,\gamma)+} \leq x}\big)}{\mathbb{E} \Big(U^{(\ell,\gamma)+}\big)} \to \frac{\mathbb{E} \big(U^{(\gamma)+} \textbf{1}_{U^{(\gamma)+} \leq x}\big)}{\mathbb{E} \big(U^{(\gamma)+} \big)}\end{equation}

and

(13) \begin{equation} F^{*(\ell,\gamma)-}(x)= \frac{ \mathbb{E} \left(U^{(\ell,\gamma)-} \textbf{1}_{U^{(\ell,\gamma)-} \leq x}\right)}{\mathbb{E} \left(U^{(\ell,\gamma)-}\right)} \to \frac{\mathbb{E} \left(U^{(\gamma)-} \textbf{1}_{U^{(\gamma)-} \leq x}\right)}{\mathbb{E} \left(U^{(\gamma)-} \right)}.\end{equation}

Furthermore, we will show the following.

Lemma 2. We have $\lim_{\gamma \downarrow 0} \mathbb{E} \big(U^{(\gamma)+} \big) = \lim_{\gamma \downarrow 0} \mathbb{E} (U^{(\gamma)-} ) = \mathbb{E}(W_F)$ .

Proof. The proof is identical for both $U^{(\gamma)+}$ and $U^{(\gamma)-}$ , so we will denote these by $U^{(\gamma)\pm}$ . For $\delta>0$ , let ${\bar{C}_\delta}$ be a continuity point of F such that

(14) \begin{equation} \mathbb{E}\left(W_F \textbf{1}_{W_F > {\bar{C}_\delta}}\right) <\delta/3.\end{equation}

By Claim 4 we deduce that for any $\gamma$ sufficiently small,

(15) \begin{equation} | \mathbb{E} \left(U^{(\gamma)\pm} \textbf{1}_{U^{(\gamma)\pm} \leq {\bar{C}_\delta}}\right) - \mathbb{E} \left(W_{F} \textbf{1}_{W_{F} \leq {\bar{C}_\delta}}\right) | < \delta /3.\end{equation}

Let us bound $\mathbb{E} (U^{(\gamma)\pm} \textbf{1}_{U^{(\gamma)\pm} > {\bar{C}_\delta}})$ . Note that if $\gamma$ is small enough, then

$$\mathbb{E} \big(U^{(\gamma)\pm} \textbf{1}_{U^{(\gamma)\pm} > {\bar{C}_\delta}}\big)= \mathbb{E} \big(U^{(\gamma)\pm} \textbf{1}_{C_\gamma \geq U^{(\gamma)\pm} > {\bar{C}_\delta}}\big).$$

So it suffices to bound the latter term.

Claim 5. For any $\delta >0$ , if $\gamma$ is sufficiently small, then

$$\left|\mathbb{E} \left(U^{(\gamma)\pm} \textbf{1}_{C_\gamma \geq U^{(\gamma)\pm} > {\bar{C}_\delta}}\right) - \mathbb{E} \left(W_F \textbf{1}_{C_\gamma \geq W_F > {\bar{C}_\delta}}\right) \right| <\delta /3. $$

Proof. For ${\bar{C}_\delta} < x < C_\gamma$ , we have $F^{(\gamma)\pm} (x) = \lambda^{\pm} (\gamma) \cdot F(x)$ , where $\lambda^{\pm} (\gamma) \to 1$ as $\gamma\downarrow 0$ . Furthermore, $F^{(\gamma)^\pm} (C_\gamma) - F(C_\gamma) = 1 - (1- h_F(\gamma)) = h_F(\gamma)$ . For some integer $T> 0$ , consider a partition of $[0, C_\gamma]$ given by $p_0 =0 < p_1 < \cdots < p_T = C_\gamma$ , which are points of continuity of F. Taking $f(x) = x \textbf{1}_{{\bar{C}_\delta} < x \leq C\gamma}$ , we write

The second term on the right-hand side is

$$ \sum_{1\leq i<T} f(p_i) \Big(F^{(\gamma)^\pm} (p_i) - F^{(\gamma)^\pm} (p_{i-1})\Big) = \lambda^{\pm} (\gamma) \cdot \sum_{1\leq i<T} f(p_i) (F (p_i) - F (p_{i-1})).$$

The first term can be written as

\begin{align*}&f(p_T) \Big(F^{(\gamma)^\pm} (p_T) - F^{(\gamma)^\pm} (p_{T-1}) \Big) \\ &=f(p_T) \Big( F^{(\gamma)^\pm} (p_T) + F(p_T) - F(p_T)- F(p_{T-1}) + F(p_{T-1}) - F^{(\gamma)^\pm} (p_{T-1})\Big)\\ &= f(p_T) (F (p_T) - F (p_{T-1}) ) \\ & \hspace{2cm} + f(p_T) \Big(\Big(F^{(\gamma)^\pm} (p_T) - F(p_T) \Big)- \Big(F^{(\gamma)^\pm} (p_{T-1}) - F(p_{T-1}) \Big)\Big)\\ &\stackrel{p_T=C_\gamma}{=} f(p_T) (F (p_T) - F (p_{T-1}) ) \\ & \hspace{2cm} + f(p_T) \left((F^{(\gamma)^\pm} (C_\gamma) - F(C_\gamma) )- F(p_{T-1})(\lambda^{\pm} (\gamma) - 1) \right)\\ &\stackrel{F^{(\gamma)^\pm} (C_\gamma)=1, h_F(\gamma)=1-F(C_\gamma)}{=} f(p_T) (F (p_T) - F (p_{T-1}) ) \\ & \hspace{2cm} + f(p_T)\Big( h_F(\gamma) - F(p_{T-1})\Big(\lambda^{\pm} (\gamma) - 1 \Big)\Big)\\ &= \lambda^{\pm} (\gamma) f(p_T) (F (p_T) - F (p_{T-1}) ) + (1-\lambda^{\pm} (\gamma)) f(C_\gamma) (F (p_T) - F (p_{T-1}) ) \\ & \hspace{2cm}+ f(C_\gamma) h_F(\gamma) - f(C_\gamma)F(p_{T-1})\left(\lambda^{\pm} (\gamma) - 1 \right).\end{align*}

These two calculations imply that

Taking the limit of a sequence of partitions whose mesh tends to 0, we have $p_{T-1} \uparrow p_T = C_\gamma$ . Since $C_\gamma$ is a point of continuity for F, we obtain

By (5) we have that $C_\gamma h_F(\gamma) \downarrow 0$ as $\gamma \downarrow 0$ . Since $ |\lambda^{\pm} (\gamma) - 1| = O(\gamma^+ + h_F(C_\gamma))$ , by (7) we also have $C_\gamma |\lambda^{\pm} (\gamma) - 1| \downarrow 0$ as $\gamma \downarrow 0$ .

Combining Claim 5 with (14) and (15), we finally deduce that given $\delta >0$ , for any $\gamma$ that is sufficiently small, we have the following bound:

\begin{align*}\big|\mathbb{E} \big(U^{(\gamma)\pm}\big) - \mathbb{E} (W_F)\big| \leq & \big| \mathbb{E} \big(U^{(\gamma)\pm} \textbf{1}_{U^{(\gamma)\pm} \leq {\bar{C}_\delta}}\big) - \mathbb{E} \big(W_{F} \textbf{1}_{W_{F} \leq {\bar{C}_\delta}}\big) \big| \\&+ \Big| \mathbb{E} \Big(U^{(\gamma)\pm} \textbf{1}_{{\bar{C}_\delta} < U^{(\gamma)\pm} \leq C_\gamma}\Big) - \mathbb{E} \Big(W_{F} \textbf{1}_{{\bar{C}_\delta} < W_{F} \leq C_\gamma}\Big) \Big| \\&+ \mathbb{E}\big(W_F \textbf{1}_{W_F > C_\gamma}\big) < \delta.\end{align*}

Claim 4 also implies that for every $x >0$ which is a point of continuity of F, we have as $\gamma \downarrow 0$

(16) \begin{equation} |\mathbb{E} \big(U^{(\gamma)\pm} \textbf{1}_{U^{(\gamma)\pm} \leq x}\big) - \mathbb{E} \big(W_F \textbf{1}_{W_F \leq x}\big)| \downarrow 0 .\end{equation}

So from Lemma 2, (16), and (12)–(13) we deduce that for any continuity point $x \in \mathbb{R}$ and any $\delta >0$ there exists $\gamma_0 = \gamma_0 (\delta, x)$ with the property that for any $0< \gamma < \gamma_0$ there exists $\ell_0$ such that for any $\ell > \ell_0$ we have

(17) \begin{equation} \big| F^{*(\ell,\gamma)}(x) - F^{*}(x) \big| < \delta.\end{equation}

The above can now be translated into the next lemma.

Lemma 3. For any bounded and continuous function $f\,:\, \mathbb{R} \to \mathbb{R}$ the following holds: there exists a function $\gamma_f\,:\, \mathbb{R}_+ \to \mathbb{R}_+$ such that $\gamma_f(x) \downarrow 0$ as $x\downarrow 0$ , and moreover, for any $\delta >0$ and any $0< \gamma < \gamma_f (\delta )$ there exists $\ell_0$ with the property that for any $\ell > \ell_0$

$$ |\mathbb{E} \big(f\big(U^{*\pm (\ell,\gamma)}\big)\big) - \mathbb{E} \big(f\big(W_F^*\big)\big)| < \delta.$$

Although this is a straightforward restatement of weak convergence, we give it more explicitly as $U^{*\pm (\ell,\gamma)}$ depends on two parameters $\ell$ and $\gamma$ . It is for the sake of clarity that we state explicitly how these depend upon each other when taking the double limit.

This completes the first part of Definition 4. We now turn to the second part.

Part 2 of Definition 4. Since $F^{(\ell,\gamma)+}$ and $F^{(\ell,\gamma)-}$ are both constant (and equal to 1), for $x \geq 2 C_\gamma$ we have

\begin{equation*}\begin{split} \mathbb{E} \big( U^{(\ell,\gamma)\pm}\big) = \mathbb{E} \left( U^{(\ell,\gamma)\pm} \textbf{1}_{U^{(\ell,\gamma)\pm} \leq 2 C_\gamma}\right). \end{split}\end{equation*}

Furthermore,

\begin{equation*}\begin{split} \mathbb{E} \left[W_F\right] &= \mathbb{E} \left( W_F \textbf{1}_{W_F \leq 2C_\gamma}\right) +\mathbb{E} \left( W_F \textbf{1}_{W_F > 2 C_\gamma}\right).\end{split}\end{equation*}

Therefore,

(18)

The last term converges to 0 as $\gamma \downarrow 0$ since $\mathbb{E} \left( W_F\right) < \infty$ .

We will now bound the first term on the right-hand side in (18). We write $F^{(\ell,\gamma)\pm}$ for either of $F^{(\ell,\gamma)+}$ and $F^{(\ell,\gamma)-}$ . Using the integration-by-parts formula for the Lebesgue–Stieltjes integral, we can write

(19) \begin{equation} \begin{split}\mathbb{E} \left( U^{(\ell,\gamma)\pm} \textbf{1}_{U^{(\ell,\gamma)\pm} \leq 2 C_\gamma}\right) &= 2C_\gamma F^{(\ell,\gamma)\pm}(2C_\gamma+) -\int_{0}^{2C_\gamma} F^{(\ell,\gamma)\pm}(x)dx \\& = 2C_{\gamma} - \int_{0}^{2C_\gamma} F^{(\ell,\gamma )\pm}(x)dx.\end{split}\end{equation}

Using integration by parts, we also get

(20) \begin{equation} \begin{split} \mathbb{E} \left( W_F \textbf{1}_{W_F\leq 2C_\gamma}\right) &= 2C_\gamma \cdot F(2C_\gamma+) - 0\cdot F(0-) - \int_{0}^{2C_\gamma} F(x) dx \\&=2 C_\gamma \cdot (1- \mathbb{P}\left[W_F > 2C_\gamma\right]) - \int_{0}^{2C_\gamma} F (x) dx.\end{split}\end{equation}

Therefore,

(21) \begin{eqnarray}&& \left| \mathbb{E} \left( U^{(\ell,\gamma)\pm} \textbf{1}_{U^{(\ell,\gamma)\pm} \leq 2 C_\gamma}\right)- \mathbb{E} \left( W_F \textbf{1}_{W_F\leq 2C_\gamma}\right) \right| \leq \nonumber \\&&2 C_\gamma \mathbb{P}\left[W_F > 2C_\gamma\right]+ \int_0^{C_\gamma} |F^{(\ell,\gamma)\pm} (x) - F(x)| dx + \int_{C_\gamma}^{2C_\gamma} |F^{(\ell,\gamma)\pm} (x) - F(x)| dx.\nonumber \\ \end{eqnarray}

We will bound $\int_0^{C_\gamma} |F^{(\ell,\gamma)+} (x) - F(x)| dx$ . First, we write

\begin{eqnarray*}&&\int_{0}^{C_\gamma} |F^{(\ell,\gamma)+} (x) -F(x)| dx = {\sum_{i=0}^{p_\ell-1}}\int_{y_{i}}^{y_{i+1}} |F^{(\ell,\gamma)+} (x) -F(x)| dx \\&&= \sum_{i=0}^{t_\ell}\int_{y_{2i}}^{y_{2i+1}} |F^{(\ell,\gamma)+} (x) -F(x)| d x +\sum_{i=0}^{t_\ell-1}\int_{y_{2i+1}}^{y_{2(i+1)}} |F^{(\ell,\gamma)+} (x) -F(x)| dx.\end{eqnarray*}

For the first sum of integrals, note that for any $x\in [y_{2i},y_{2i+1})$ we have $|F(W_{2i}^-) - F(x)| \leq F(W_{2i}^+) - F(W_{2i}^-)$ . Therefore, each integrand is bounded as follows:

(22) \begin{align}|F^{(\ell,\gamma)+} (x) -F(x)| =& \left| \frac{F(W_{2i}^-)}{1-h_F(\gamma) +\gamma^+} - F(x)\right| =\left|\frac{F(W_{2i}^-) - F(x) (1-h_F(\gamma) + \gamma^+)}{1-h_F(\gamma) +\gamma^+} \right| \nonumber \\\leq& \frac{|F (W_{2i}^-) - F(x)|}{1-h_F(\gamma) +\gamma^+}+ F(x) \frac{|h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+} \nonumber \\\leq& \frac{ F(W_{2i}^+) - F(W_{2i}^-)}{1-h_F(\gamma) +\gamma^+} + \frac{|h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+}. \end{align}

Using this bound, we get

But $ \int_{y_{2i}}^{y_{2i+1}} dx = y_{2i+1} - y_{2i} \leq 2\varepsilon_\ell $ . So

$$ \sum_{i=0}^{t_\ell} \left( (F(W_i^+) - F(W_i^-)) \cdot \int_{y_{2i}}^{y_{2i+1}} dx \right) \leq2\varepsilon_\ell \cdot \sum_{i=0}^{t_\ell} \left( (F(W_i^+) - F(W_i^-)) \right)\leq 2 \varepsilon_\ell.$$

Furthermore,

$$ |h_F(\gamma) - \gamma^+\Big|\sum_{i=0}^{t_\ell} \int_{y_{2i}}^{y_{2i+1}} dx \leq C_\gamma \cdot |h_F(\gamma) - \gamma^+\Big| \leq C_\gamma \cdot |h_F(\gamma) - \gamma^+| .$$

We thus deduce that

$$ \sum_{i=0}^{t_\ell} \int_{y_{2i}}^{y_{2i+1}} |F^{(\ell,\gamma)+} (x) -F(x)| dx \leq \frac{2\varepsilon_\ell + C_\gamma |h_F(\gamma) - \gamma^+|}{1- h_F(\gamma) +\gamma^+}.$$

For the second integral, note that for $x\in [y_{2i+1},y_{2(i+1)})$ we have

$$\big|F \big(W_{2i+1}^-\big) - F(x)\big| \leq \varepsilon_\ell.$$

Arguing as in (22), we deduce that

$$ \big|F^{(\ell,\gamma)+} (x) -F(x)\big| \leq \frac{\varepsilon_\ell + |h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+}.$$

Therefore,

$$\sum_{i=0}^{t_\ell-1}\int_{y_{2i+1}}^{y_{2(i+1)}} |F^{(\ell,\gamma)+} (x) -F(x)| d x \leq\frac{C_\gamma (\varepsilon_\ell + |h_F(\gamma) - \gamma^+|)}{1-h_F(\gamma) + \gamma^+}.$$

We thus conclude that

(23) \begin{eqnarray}&&\int_{0}^{C_\gamma} |F^{(\ell,\gamma)+} (x) -F(x)| d x \leq \frac{\varepsilon_\ell (C_\gamma+2)+{2}C_\gamma |h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+} \,=\!:\, \hat{\rho}^+(\ell,\gamma). \end{eqnarray}

One can similarly show that

(24) \begin{eqnarray}\int_{0}^{C_\gamma} |F^{(\ell,\gamma)-} (x) -F(x)| d x &\leq&\frac{\varepsilon_\ell (C_\gamma+2)+{2} C_\gamma h_F(\gamma)}{1-h_F(\gamma) + p h_F(\gamma )} \,=\!:\, \hat{\rho}^- (\ell,\gamma). \end{eqnarray}

Note that $\lim_{\gamma \downarrow 0} \lim_{\ell \to \infty} \hat{\rho}^{\pm} (\ell,\gamma) =0$ .

Finally, we will consider $\int_{C_\gamma}^{2C_\gamma} |F^{(\ell,\gamma)+} (x) - F(x)| d x$ . For any $x \in [C_\gamma, 2C_\gamma]$ that is a point of continuity we have

\begin{eqnarray*}|F^{(\ell,\gamma)+} (x) -F(x)| &=& \left| \frac{F(x)}{1-h_F(\gamma) +\gamma^+} - F(x)\right| =\left|\frac{F(x) - F(x) (1-h_F(\gamma) + \gamma^+)}{1-h_F(\gamma) +\gamma^+} \right| \nonumber \\&\leq& F(x) \frac{|h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+}\leq\frac{|h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+}.\end{eqnarray*}

Therefore,

(25) \begin{equation} \begin{split}&\left|\int_{C_\gamma}^{2C_\gamma} (F^{(\ell,\gamma)+}(x) - F(x))dx \right| \leq \int_{C_\gamma}^{2C_\gamma}| F^{(\ell,\gamma)+}(x) - F(x)|dx \leq\\&\leq \frac{|h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+} \cdot (2C_\gamma -C_\gamma) = C_\gamma \cdot \frac{|h_F(\gamma) - \gamma^+|}{1-h_F(\gamma) + \gamma^+} \leq \hat{\rho}^+ (\ell,\gamma).\end{split}\end{equation}

Also,

(26) \begin{eqnarray}&&\int_{C_\gamma}^{2C_\gamma} \left| F^{(\ell,\gamma)-}(x)- F(x) \right| dx = \int_{C_\gamma}^{2C_\gamma} \left| 1- F(x) \right| dx = \int_{C_\gamma}^{2C_\gamma} \mathbb{P}\left[W_F > x\right]dx \nonumber \\&\leq& \int_{C_\gamma}^{\infty} \mathbb{P}\left[W_F \geq x\right] dx = \mathbb{E} \left( W_F \textbf{1}_{W_F \geq C_\gamma}\right).\end{eqnarray}

The latter $\downarrow 0$ as $\gamma \downarrow 0$ .

Now, substituting the bounds of (23), (24), (25), and (26) into (21), we get

(27) \begin{eqnarray}&& \left| \mathbb{E} \left( U^{(\ell,\gamma)\pm} \textbf{1}_{U^{(\ell,\gamma)\pm} \leq 2 C_\gamma}\right)- \mathbb{E} \left( W_F \textbf{1}_{W_F\leq 2C_\gamma}\right) \right| \leq \nonumber \\&& \hspace{4.5cm} 2 C_\gamma \mathbb{P}\left[W_F > 2C_\gamma\right] + {2}\hat{\rho}^{\pm} (\ell,\gamma) + \mathbb{E} \left( W_F \textbf{1}_{W_F \geq C_\gamma}\right). \nonumber\\ \end{eqnarray}

Using the upper bound of (27) in (18), and using the fact that $\mathbb{E} \left( W_F \textbf{1}_{W_F > 2C_\gamma}\right) \leq \mathbb{E} \left( W_F \textbf{1}_{W_F \geq C_\gamma}\right)$ , we finally get

(28) \begin{eqnarray}\left| \mathbb{E} \left( U^{(\ell,\gamma)\pm}\right) - \mathbb{E} \left( W_F\right) \right| &\leq& 2 C_\gamma \mathbb{P}\left[W_F > 2C_\gamma\right] +{2} \hat{\rho}^{\pm} (\ell,\gamma) + 2\mathbb{E} \left( W_F \textbf{1}_{W_F \geq C_\gamma}\right) \nonumber \\&\leq& {2 \hat{\rho}^{\pm} (\ell,\gamma) + 3\mathbb{E} \left( W_F \textbf{1}_{W_F \geq C_\gamma}\right)}.\end{eqnarray}

Another useful bound which can be deduced from (19) and (20), replacing $2C_\gamma$ with $C_\gamma$ , is

But note that $\mathbb{P}\left[U^{(\ell,\gamma)-}\leq C_\gamma\right] =1$ , whereas

$$\mathbb{P}\left[U^{(\ell,\gamma)+}\leq C_\gamma\right] = \frac{F(C_\gamma)}{1-h_F(\gamma)+\gamma^+}.$$

So

$$\left| \mathbb{P}\left[U^{(\ell,\gamma)+}\leq C_\gamma\right]- \mathbb{P}\left[W_F\leq C_\gamma\right] \right| =\frac{F(C_\gamma) |h_F(\gamma) - \gamma^+|}{1-h_F(\gamma)+\gamma^+}$$

and

$$\left| \mathbb{P}\left[U^{(\ell,\gamma)-}\leq C_\gamma\right]- \mathbb{P}\left[W_F\leq C_\gamma\right] \right| = \mathbb{P}\left[W_F> C_\gamma\right].$$

Thus,

(29)

whereas

(30) \begin{eqnarray}\left| \mathbb{E} \left( U^{(\ell,\gamma)+} \textbf{1}_{U^{(\ell,\gamma)\pm}\leq C_\gamma}\right)- \mathbb{E} \left( W_F\right) \right|&\leq& C_\gamma \mathbb{P}\left[W_F >C_\gamma\right]+ \hat{\rho}^{\pm} (\ell,\gamma) \nonumber \\&&+ \mathbb{E} \left( W_F \textbf{1}_{W_F > C_\gamma}\right). \end{eqnarray}

We conclude that (28), together with (5), (29), and (30), completes Part 2 of Definition 4.

3.1.2. Bounds on $|\mathcal{A}_f|$

For a subset $S \subseteq [n]$ , let $\mathcal{A}_f (S)$ denote the final set of infected vertices in $CL (\textbf{w})$ assuming that $\mathcal{A}_0 = S$ . With this notation, we have of course that $\mathcal{A}_f = \mathcal{A}_f (\mathcal{A}_0)$ . We also set $\mathcal{A}_f^-(S)$ to be the set of infected vertices in $CL^{\prime} \big(\textbf{W}^{(\ell,\gamma)-}\big)$ , assuming that the initial set is $\varphi^-(S \cap \cup_{i=1}^{p_\ell}\mathsf{C}_i) $ . Finally, for a subset $S \subseteq [n^{\prime}]$ , let $\mathcal{A}_f^+(S)$ be the final set of infected vertices on $CL^{\prime} \big(\textbf{W}^{(\ell,\gamma)+}\big)$ . We will show the following.

Claim 6. Let $p\in(0,1)$ . Assume that $\mathcal{A}_0$ is a random subset of [n] where each vertex is included with probability p independently of any other vertex. Then there is a coupling space on which, w.h.p.,

(31) \begin{equation}\big|\mathcal{A}_f^- \big(\mathcal{A}_0 \cup \mathsf{C}_\gamma^- \big)\big|\leq |\mathcal{A}_f| \leq \big|\mathcal{A}_f^+ \big(\mathcal{A}_0 \cup \mathsf{C}_\gamma^+\big)\big|.\end{equation}

In the proof of Claim 6 and elsewhere, we write that the probability that two vertices k and j, with $w_j(n) \leq C_\gamma$ , are adjacent is equal to $w_k(n) w_j(n)/W_{[n]}$ ; in other words, when we apply (1) we tacitly assume that n is sufficiently large so that this ratio is less than 1.

Proof of Claim 6. As $\mathcal{A}_0$ is formed by including every vertex in [n] independently with probability p, it follows that w.h.p. at least $k_-$ elements of $\mathsf{C}_\gamma$ become initially infected. We identify exactly $k_-$ of them with the set $\mathsf{C}_\gamma^-$ . Recall that for each $k \in \cup_{i=1}^{p_\ell}{ \mathsf{C}_i}$ we have $W_{\varphi^-(k)}^{(\ell,\gamma)-}(n) \leq w_k (n)$ . This implies that for each pair $k,k^{\prime} \in [n] \setminus \mathsf{C}_\gamma$ of distinct vertices, the probability that $\varphi^-(k)$ and $\varphi^- (k^{\prime})$ are adjacent in $CL^{\prime}\big(\textbf{W}^{(\ell,\gamma)-}\big)$ is smaller than the corresponding probability for k and k ^′ in $CL (\textbf{w})$ . Hence, there is a coupling space on which

$$ CL^{\prime}\big(\textbf{W}^{(\ell,\gamma)-}\big) \subseteq CL(\textbf{w}), $$

and the first inequality in (31) follows. The second inequality follows from a slightly more involved argument. Let $j \in \mathsf{C}_\gamma$ be such that $w_j (n) \geq 2C_\gamma$ , and let $k \in \cup_{i=1}^{p_\ell} \mathsf{C}_i $ . The probability that k is adjacent to j in $CL(\textbf{w})$ is equal to $w_k w_j / W_{[n]}$ . Also, the probability that k is adjacent to at least one of the copies of j in [n ^′] in the random graph $CL^{\prime}\big(\textbf{W}^{(\ell,\gamma)+}\big)$ is

$$ 1 - \left( 1- \frac{2W^{(\ell,\gamma)+}_{\varphi^+(k)} C_\gamma}{W_{[n]}} \right)^{2 \lfloor {w_j / C_\gamma}\rfloor}. $$

Assume we have shown that for n sufficiently large we have that for any $k \in \cup_{i=1}^{p_\ell} \mathsf{C}_i $ and any $j \in \mathsf{C}_\gamma$ ,

(32) \begin{equation} \frac{w_k w_j}{W_{[n]}} \leq 1 - \left( 1- \frac{2W^{(\ell,\gamma)+}_{\varphi^+(k)} C_\gamma}{W_{[n]}} \right)^{2 \lfloor {w_j / C_\gamma}\rfloor}.\end{equation}

Moreover, assume that every vertex in $\mathsf{C}^{\prime}_\gamma$ is among those vertices that are initially infected. Now, observe that there is a coupling space in which we have

(33) \begin{equation} CL(\textbf{w})\big[\cup_{i=1}^{p_\ell}\mathsf{C}_i\big] \subseteq CL^{\prime}\big(\textbf{W}^{(\ell,\gamma)+}\big)\big[\cup_{i=1}^{p_\ell}\mathsf{C}_i\big].\end{equation}

This is the case because for any $k \in \cup_{i=1}^{p_\ell}\mathsf{C}_i$ we have $w_k \leq W_{\varphi^+(k)}^{(\ell,\gamma)+}$ . Consider a vertex $k \in \cup_{i=1}^{p_\ell}\mathsf{C}_i$ and now let $j \in \mathsf{C}_\gamma$ . Then the inequality (32) implies that the probability that k is adjacent to j in $CL(\textbf{w})$ is at most the probability that $\varphi^+(k)$ is adjacent to at least one of the copies of j in [n ^′] within $CL^{\prime}\big(\textbf{W}^{(\ell,\gamma)+}\big)$ . Therefore, it follows that the number of neighbors of k in $\mathsf{C}_\gamma$ in the random graph $CL(\textbf{w})$ is stochastically dominated by the size of the neighborhood of k in $\mathsf{C}^{\prime}_\gamma$ in the random graph $CL^{\prime}\big(\textbf{W}^{(\ell,\gamma)+}\big)$ . This observation, together with (33), implies that

$$ \big|\mathcal{A}_f \big(\mathcal{A}_0 \cup \mathsf{C}_\gamma\big)\big| \leq_{st} \big|\mathcal{A}_f^+\big(\mathcal{A}_0 \cup \mathsf{C}_\gamma^+\big)\big|.$$

But also,

\begin{equation*} |\mathcal{A}_f| \leq_{st} |\mathcal{A}_f (\mathcal{A}_0 \cup \mathsf{C}_\gamma)|.\end{equation*}

The second stochastic inequality of the claim follows from the above two inequalities. It remains to show (32). Let us abbreviate $W_{\varphi^+(k)}^{(\ell,\gamma)+}\,=\!:\,W_k$ . Using the Bonferroni inequalities we have

(34) \begin{equation} \begin{split} &1 - \left( 1- \frac{2 W_k C_\gamma}{W_{[n]}} \right)^{2 \lfloor {w_j / C_\gamma}\rfloor} \geq 2 \Big\lfloor \frac{w_j}{C_\gamma}\Big\rfloor \frac{2 W_k C_\gamma}{W_{[n]}} - 2 \left( {w_j / C_\gamma} \right)^2 \,\frac{4 W_k^2 C_\gamma^2}{W_{[n]}^2}.\end{split}\end{equation}

But

$$ 2 \Big\lfloor \frac{w_j}{C_\gamma}\Big\rfloor \frac{2 W_k C_\gamma}{W_{[n]}} \geq2 \left(\frac{w_j}{C_\gamma} -1 \right) \frac{2 W_k C_\gamma}{W_{[n]}}= 2 \frac{w_j}{C_\gamma} \left( 1- \frac{C_\gamma}{w_j} \right) \frac{2 W_k C_\gamma}{W_{[n]}}\stackrel{w_j /C_\gamma \geq 2}{\geq}\frac{2 W_k w_j}{W_{[n]}}.$$

Substituting this lower bound into (34), we obtain

\begin{eqnarray*}1 - \left( 1- \frac{2 W_k C_\gamma}{W_{[n]}} \right)^{2 \lfloor \frac{w_j}{C_\gamma}\rfloor} &\geq&\frac{2 W_k w_j}{W_{[n]}} - \frac{8 W_k^2 w_j^2}{W_{[n]}^2} = \frac{2 W_k w_j}{W_{[n]}} \left(1 - \frac{4 W_k w_j}{W_{[n]}} \right) \\ &>& \frac{W_k w_j}{W_{[n]}}\geq \frac{w_k w_j}{W_{[n]}},\end{eqnarray*}

for n sufficiently large, as $w_k < C_\gamma$ and $w_j = w_j(n) = o(n)$ (uniformly for all j) but $W_{[n]} = \Theta (n)$ .

We will now apply Theorem 3 to the random variables that bound $|\mathcal{A}_f|$ in Claim 6. Theorem 3 implies that there exists $\gamma_2 >0$ satisfying the following: for any $\gamma < \gamma_2$ and any $\delta \in (0,1)$ there exists an infinite set of natural numbers $\mathcal{S}^1$ such that for every $\ell \in \mathcal{S}^1$ , with probability $1-o(1)$ ,

(35) \begin{equation} \begin{split}n^{-1}{\big|\mathcal{A}_f^{+} \big(\mathcal{A}_0 \cup \mathsf{C}_\gamma^+\big) \big|} \leq (1+ \delta) ((1-p) \mathbb{E} \left[ \psi_r( W_F \hat{y})\right] + p),\end{split}\end{equation}

and there exists an infinite set of natural numbers $\mathcal{S}^2$ such that for every $\ell \in \mathcal{S}^2$ , with probability $1-o(1)$ ,

(36) \begin{equation} \begin{split}n^{-1}{\big|\mathcal{A}_f^- \big(\mathcal{A}_0 \cup \mathsf{C}_\gamma^- \big) \big|} \geq (1-\delta) ((1-p) \mathbb{E} \left[ \psi_r(W_F \hat{y})\right] + p).\end{split}\end{equation}

Hence, Claim 6 together with (35) and (36) imply the following w.h.p. bounds on the size of $\mathcal{A}_f$ :

\begin{equation*}\begin{split}n^{-1} {|\mathcal{A}_f| } = (1\pm \delta) ((1-p) \mathbb{E} \left[ \psi_r (W_F \hat{y})\right] + p),\end{split}\end{equation*}

from which Theorem 1 follows.

3.2. Proof of Theorem 2

Let us assume that $\mathcal{A}_0$ is randomly selected, including each vertex independently with probability $a(n)/n$ , where $a(n) \gg a_c (n)$ but $a(n) = o(n)$ (cf. Theorem 2. for the definition of the function $a_c(n)$ ). For $\varepsilon \in (0,1)$ let $\mathcal{A}_0^{(\varepsilon)}$ denote a random subset of [n] where each vertex is included independently with probability $\varepsilon$ . If n is large enough, then $\mathcal{A}_0$ can be coupled with $\mathcal{A}_0^{(\varepsilon)}$ , that is, there is a coupling space in which $\mathcal{A}_0 \subseteq \mathcal{A}_0^{(\varepsilon)}$ . The following stochastic upper bound can be deduced as in Claim 6.

Claim 7. For any $\varepsilon \in (0,1)$ and any $\gamma >0$ , if n is large enough, then

\begin{equation*}|\mathcal{A}_f| \leq_{st} \big|\mathcal{A}_f \big(\mathcal{A}_0^{(\varepsilon)} \cup \mathsf{C}_\gamma \big)\big| \leq_{st} \big|\mathcal{A}_f^+ \big(\mathcal{A}_0^{(\varepsilon)} \cup \mathsf{C}_\gamma^+ \big)\big|.\end{equation*}

We will now deduce a stochastic lower bound on $|\mathcal{A}_f|$ . For $C>0$ , let $\mathcal{K}_C$ denote the set of vertices having weight at least C in ${\textbf w}$ . In [6] the first two authors prove that if $\varepsilon \in (0,1)$ is sufficiently small and $\mathcal{A}_0$ is selected as above, then at least a $(1-\varepsilon)$ -fraction of the vertices of $\mathcal{K}_C$ become infected if we consider a bootstrap percolation process on $CL(\textbf{w})$ with activation threshold r where the vertices in $[n] \setminus \mathcal{K}_C$ are assumed to be ‘frozen’; that is, they never get infected.

Lemma 4. ([6, Proposition 3.7].) There exists an $\varepsilon_0 = \varepsilon_0 (\beta, c_1, c_2) >0$ such that for any positive $\varepsilon < \varepsilon_0$ there exists $C=C( c_1, c_2, \beta, \varepsilon, r) >0$ for which the following holds. Assume that $\mathcal{A}_0$ is as above, and consider a bootstrap percolation process on $CL(\textbf{w})$ with activation threshold $r\geq 2$ and the set $\mathcal{A}_0$ as the initial set, with the restriction that the vertices in $[n] \setminus \{ \mathcal{K}_C \cup \mathcal{A}_0\}$ never become infected. Then at least $(1- \varepsilon) |\mathcal{K}_C|$ vertices of $\mathcal{K}_C$ become infected with probability $1-o(1)$ .

Lemma 4 implies that for any $\varepsilon >0$ that is sufficiently small, there exists $C = C( c_1, c_2, \beta, \varepsilon, r) >0$ such that with probability $1-o(1)$ at least $(1-\varepsilon) |\mathcal{K}_C|$ vertices of $\mathcal{K}_C$ will be infected in $CL(\textbf{w} )$ , assuming that the vertices in $[n] \setminus \{\mathcal{K}_C \cup \mathcal{A}_0 \}$ never become infected. Let $\mathcal{E}_{C,\varepsilon, n}$ denote this event; if it is realized, we let $\mathcal{K}_{C,\varepsilon}$ denote a subset of $\lfloor (1-\varepsilon)|\mathcal{K}_{C}| \rfloor\,=\!:\,k$ vertices in $\mathcal{K}_C$ that become infected, chosen in some particular way (for example, the k lexicographically smallest vertices). Then the following holds.

Claim 8. For any $C>0$ and any $\varepsilon \in (0,1)$ , there is a coupling such that if $\mathcal{E}_{C, \varepsilon, n}$ is realized, then we have

Let $\gamma \in F([0,\infty) )$ be such that $C_\gamma = C$ , where $C = C (\varepsilon)$ is as in Lemma 4. (Under the assumptions of Theorem 2, F is continuous (cf. Definition 2), and therefore $h_F(\gamma)=\gamma$ .)

Consider a set of vertices $\{v_1,\ldots, v_k\}$ which is disjoint from [n]. We define a sequence $\tilde{\textbf{W}}^{(\ell, \gamma)-}$ on $\left(\cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \{v_1,\ldots, v_k \}$ as follows. For every $j \in \mathsf{C}_i$ , with $i=1,\ldots, p_\ell$ , we have $\tilde{W}^{(\ell, \gamma)-}_j=W_j^{(\ell, \gamma)-}$ , whereas for every $j=1,\ldots, k$ we let $\tilde{W}^{(\ell, \gamma)-}_{v_j} = C_\gamma$ . We let $n_-$ be the number of vertices of the sequence $\tilde{\textbf{W}}^{(\ell,\gamma)-}$ , that is, the size of $\left(\cup_{i=1}^{p_\ell} \mathsf{C}_i \right) \bigcup \{v_1,\ldots, v_k \}$ . Since $k = (1-\varepsilon) \gamma n (1+o(1))$ , this satisfies $n_- =( (1-\gamma) + \gamma(1-\varepsilon) )n (1+o(1)) = (1-\gamma\varepsilon) n(1+o(1))$ . Hence, for large n we have $n_- < n$ . We identify the vertices in $\{ v_1,\ldots, v_k \}$ with the k lexicographically first vertices in $\mathsf{C}_\gamma$ , and we denote both subsets by $\mathsf{C}_{\gamma, k}$ . Setting $\tilde{W}_\gamma^- \,:\!=\, (1-\varepsilon) \gamma C_\gamma $ , the weight of these vertices is $n\tilde{W}_\gamma^- (1+o(1))$ , since each of them has weight equal to $C_\gamma$ .

The weight sequence $\tilde{\textbf{W}}^{(\ell,\gamma)-}$ gives rise to a probability distribution which is the limiting probability distribution of the weight of a uniformly chosen vertex from $[n_-]$ . We let $\tilde{U}^{(\ell,\gamma)-}$ be a random variable which follows this distribution and let $\tilde{W}_F^{(\ell,\gamma)-}$ denote a random variable which follows the $\tilde{U}^{(\ell,\gamma)-}$ size-biased distribution. The definition of $\tilde{\textbf{W}}^{(\ell,\gamma)-}$ yields

$$ \mathbb{P}\left[\tilde{U}^{(\ell,\gamma)-} = W_i^{(\ell,\gamma)-}\right] = \frac{\gamma_i}{1- \gamma \varepsilon},\ \mbox{and} \ \mathbb{P}\left[\tilde{U}^{(\ell,\gamma)-} = C_\gamma\right] = \frac{(1- \varepsilon ) \gamma}{1-\gamma \varepsilon}. $$

As we did in Section 3.1.1 for the sequence $\{ \textbf{W}^{(\ell, \gamma)-} (n_-) \}_{\gamma\in (0,1), \ell \in \mathbb{N}}$ , one can show that $\tilde{\textbf{W}}^{(\ell,\gamma)-}$ is an F-convergent weight sequence. We omit the proof.

Let $\hat{\mathcal{A}_f} ( \mathsf{C}_{\gamma,k} )$ be the final set of infected vertices in $CL (\textbf{w} )$ assuming that the initial set is $\mathsf{C}_{\gamma,k}$ and moreover no vertices in $\mathsf{C}_{\gamma} \setminus \mathsf{C}_{\gamma, k}$ ever become infected. Hence, on the event $\mathcal{E}_{C_\gamma, \varepsilon, n}$ we have

$$ \big|\hat{\mathcal{A}_f} \big( \mathsf{C}_{\gamma,k} \big)\big| \leq_{st} |\mathcal{A}_f ( \mathcal{K}_{C_\gamma, \varepsilon} )|.$$

(The symbol $\leq_{st}$ denotes stochastic domination.) But the assumption that no vertices in $\mathsf{C}_{\gamma} \setminus \mathsf{C}_{\gamma, k}$ ever become active amounts to a bootstrap percolation process on $CL^{\prime} \big(\tilde{\textbf{W}}^{(\ell,\gamma)-}\big)$ with activation threshold equal to r. Let $\tilde{\mathcal{A}_f} (S)$ denote the final set under the assumption that the initial set is $S \subseteq [n^{\prime}]$ . Since $CL^{\prime} \big(\tilde{\textbf{W}}^{(\ell,\gamma)-}\big) \subseteq CL (\textbf{w} )$ on a certain coupling space we have

$$ \big|\tilde{\mathcal{A}_f} \big( \mathsf{C}_{\gamma,k} \big)\big| \leq_{st} \big|\hat{\mathcal{A}_f} \big(\mathsf{C}_{\gamma,k} \big)\big|. $$

Therefore

$$\big|\tilde{\mathcal{A}_f} \big(\mathsf{C}_{\gamma,k} \big)\big| \leq_{st} \big| \mathcal{A}_f \big( \mathcal{K}_{C_\gamma, \varepsilon} \big)\big|. $$

This together with Claim 8 implies the following stochastic lower bound on $|\mathcal{A}_f|$ .

Claim 9. For any $\gamma, \varepsilon \in (0,1)$ , if $\mathcal{E}_{C_{\gamma},\varepsilon, n}$ is realized, then

\begin{equation*}\big|\tilde{\mathcal{A}_f} \big( \mathsf{C}_{\gamma,k} \big) \big| \leq_{st} |\mathcal{A}_f|.\end{equation*}

We will now apply Theorem 3 to the random variables that bound $|\mathcal{A}_f|$ in Claims 7 and 9. Let $\hat{y}_\varepsilon^+,\hat{y}$ be the smallest positive solutions of

$$y = (1-\varepsilon)\,\mathbb{E} \left[ \psi_r \left(W_F^* y\right) \right] + \varepsilon $$

and

$$y = \mathbb{E} \left[ \psi_r \left(W_F^* y\right) \right],$$

respectively.

For $\varepsilon < \varepsilon_0$ let C be as in Lemma 4 and let $\gamma < \gamma_2$ (cf. Theorem 3) be such that $C = C_\gamma$ . Theorem 3 implies that for any $\delta \in (0,1)$ there exists an infinite set of natural numbers $\mathcal{S}^1$ such that for every $\ell \in \mathcal{S}^1$ , with probability $1-o(1)$ ,

(37) \begin{equation} \begin{split}\frac{\big|\mathcal{A}_f^+ \big(\mathcal{A}_0^{(\varepsilon)} \cup \mathsf{C}_\gamma^+ \big)\big|}{n} \leq (1+ \delta) \big((1-\varepsilon ) \mathbb{E} \left[\psi_r\big(W_F \hat{y}_\varepsilon^+\big)\right] + \varepsilon\big),\end{split} \end{equation}

and an infinite set of natural numbers $\mathcal{S}^2$ such that for every $\ell \in \mathcal{S}^2$ , with probability $1-o(1)$ ,

(38) \begin{equation} \frac{\big|\tilde{\mathcal{A}_f} \big( \mathsf{C}_{\gamma, k} \big) \big|}{n} \geq (1-\delta) \mathbb{E} \left[\psi_r (W_F \hat{y})\right].\end{equation}

Hence, Claims 7 and 9 together with (37) and (38) imply that w.h.p.

$$ \frac{|\mathcal{A}_f|}{n} \leq (1+ \delta) ((1-\varepsilon ) \mathbb{E} \left[\psi_r \big(W_F \hat{y}_\varepsilon^+\big)\right] + \varepsilon) $$

and

$$ \frac{|\mathcal{A}_f|}{n} \geq (1- \delta) \mathbb{E} \left[\psi_r(W_F \hat{y})\right]. $$

But $y_\varepsilon^+ \rightarrow \hat{y}$ as $\varepsilon \rightarrow 0$ , and Theorem 2 follows.

4. Proof of Theorem 3

In this section we will give the proof of Theorem 3. At the moment our analysis does not depend on the parameters $\ell, \gamma$ , so, to simplify notation, we will drop the superscript $(\ell,\gamma)$ . For $j=0,\ldots, r-1$ , we denote by $\mathsf{C}_{i,j}$ the subset of $\mathsf{C}_i$ which consists of those vertices of $\mathsf{C}_i$ which have j infected neighbors. We also denote by $\mathsf{C}_{i,r}$ the subset of $\mathsf{C}_i$ containing all those vertices that are infected; that is, they have at least r infected neighbors or are initially infected.

We will determine the size of the final set of infected vertices by exposing sequentially the neighbors of each infected vertex and keeping track of the number of infected neighbors that an uninfected vertex has. In other words, we will be keeping track of the size of the sets $\mathsf{C}_{i,j}$ . This method of exposure has also been applied in the analysis in [26]. However, the inhomogeneity in the present context introduces additional difficulties, as the evolutions of the sets $\mathsf{C}_{i,j}$ are interdependent.

The sequential exposure proceeds as follows. For $i=1,\ldots, p_\ell$ and $j=0,\ldots, r-1$ , let $\mathsf{C}_{i,j}(t)$ denote the set of vertices which have j infected neighbors after the execution of the tth step. We also denote by $\mathsf{C}_{i,r} (t)$ the set of all those vertices that have at least r infected neighbors after the tth step.

Here $\mathsf{C}_{i,j}(0)$ denotes the set $\mathsf{C}_{i,j}$ before the beginning of the execution. Furthermore, let $\mathsf{U} (t)$ denote the set of infected unexposed vertices after the execution of the tth step, with $\mathsf{U}(0)$ denoting the set of infected vertices before the beginning of the process.

At step $t\geq 1$ , if $\mathsf{U}(t-1)$ is non-empty,

1. (i) choose a vertex v uniformly at random from $\mathsf{U}(t-1)$ ;

2. (ii) expose the neighbors v in the set $\bigcup_{i=1}^{p_\ell} \cup_{j=0}^{r-1} \mathsf{C}_{i,j}(t-1)$ ;

3. (iii) set $\mathsf{U}(t) \,:\!=\, \mathsf{U}(t-1) \setminus \{ v\}$ .

The above set of steps is repeated for as long as the set $\mathsf{U}$ is non-empty. The exposure of the neighbors of v can alternatively be thought of as a random assignment of a mark to each vertex of $\bigcup_{i=1}^{p_\ell} \cup_{j=0}^{r-1} \mathsf{C}_{i,j}(t-1)$ independently of every other vertex; if a vertex in $\mathsf{C}_{i,j}(t-1)$ receives such a mark, then it is moved to $\mathsf{C}_{i,j+1} (t)$ . Hence, during the execution of the tth step, each vertex in $\mathsf{C}_{i,j}(t-1)$ either remains a member of $\mathsf{C}_{i,j}(t)$ or is moved to $\mathsf{C}_{i,j+1}(t)$ .

4.1. Conditional expected evolution

Let $c_{i,j}$ denote the size of the set $\mathsf{C}_{i,j}$ for all $i=1,\ldots, p_\ell$ and $j=0,\ldots, r-1$ . Our equations will also incorporate the size of $\mathsf{U}$ at time $t-1$ , which we denote by $u (t-1)$ , as well as the total weight of vertices in $\mathsf{U}(t-1)$ , which we denote by $w_{\mathsf{U}} (t-1)$ . For these values of i and j we let $\textbf{c} (t) = \left( u(t), w_{\mathsf{U}} (t), ( c_{i,j}(t) )_{i,j}\right)$ . This vector determines the state of the process after step t. We will now give the expected change of $c_{i,j}$ during the execution of step t, conditional on $\textbf{c} (t-1)$ . If step t is to be executed, it is necessary to have $u(t-1)>0$ , which we will assume to be the case. We begin with $c_{i,0}$ , for $i=1,\ldots, p_\ell$ , having

(39) \begin{equation} \begin{split}\mathbb{E} \left[c_{i,0} (t) - c_{i,0} (t-1) \ | \ \textbf{c} (t-1)\right] &= -c_{i,0} (t-1) \sum_{v \in \mathsf{U} (t-1)} \frac{ W_i w_v}{W_{[n]}}\,\frac{1}{u (t-1)} \\& = -c_{i,0} (t-1)\,\frac{ W_i}{W_{[n]}}\,\frac{w_{\mathsf{U}} (t-1)}{u (t-1)}.\end{split}\end{equation}

The evolution of $c_{i,j}$ for $0< j < r$ involves a term that accounts for the ‘losses’ from the set $c_{i,j}$ as well as a term which describes the expected ‘gain’ from the set $c_{i,j-1}$ .

For $i= 1,\ldots, p_\ell$ and $0< j < r$ we have

(40) \begin{equation} \begin{split} &\mathbb{E} \left[ c_{i,j} (t) - c_{i,j} (t-1) \ | \ \textbf{c} (t-1)\right] \\= & c_{i,j-1}(t-1) \sum_{v \in \mathsf{U} (t-1)} \frac{ W_i w_v}{W_{[n]}}\,\frac{1}{u (t-1)}- c_{i,j} (t-1) \sum_{v \in \mathsf{U} (t-1)} \frac{ W_i w_v}{W_{[n]}}\,\frac{1}{ u (t-1)} \\=& (c_{i,j-1} (t-1) - c_{i,j} (t-1))\,\frac{ W_i}{W_{[n]}}\,\frac{w_{\mathsf{U}} (t-1)}{u (t-1)}.\end{split}\end{equation}

Finally, we will need to describe the expected change in the size of $\mathsf{U}$ during step t. In this case, one vertex is removed from $\mathsf{U} (t -1)$ , but additional vertices may arrive from the sets $\mathsf{C}_{i,r-1} (t-1)$ . More specifically, we write

(41) \begin{equation} \begin{split}\mathbb{E} \left[u (t) - u (t-1) \ | \ \textbf{c} (t-1)\right] &= - 1 + \sum_{i=1}^{p_\ell} c_{i,r-1} (t-1)\,\sum_{v \in \mathsf{U} (t-1)} \frac{ W_i w_v}{W_{[n]}}\,\frac{1}{u (t-1)}\\& = -1 + \frac{w_{\mathsf{U}} (t-1)}{u (t-1)} \sum_{i=1}^{p_\ell} \frac{W_i}{W_{[n]}}\,c_{i,r-1} (t-1).\end{split}\end{equation}

Similarly, the expected change in the weight of $\mathsf{U}$ during step t is as follows:

(42) \begin{equation} \begin{split}& \mathbb{E} \left[w_{\mathsf{U}} (t) - w_{\mathsf{U}} (t-1) \ | \ \textbf{c} (t-1)\right] \\= & - \frac{w_{\mathsf{U}} (t-1)}{u (t-1)} + \sum_{i=1}^{p_\ell} W_i c_{i,r-1} (t-1)\,\sum_{v \in \mathsf{U} (t-1)} \frac{ W_i w_v}{W_{[n]}}\,\frac{1}{u (t-1)} \\= & -\frac{w_{\mathsf{U}} (t-1)}{u (t-1)} + \frac{w_{\mathsf{U}} (t-1)}{u (t-1)} \sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}}\,c_{i,r-1} (t-1).\end{split}\end{equation}

4.2. Continuous approximation

The above quantities will be approximated by the solution of a system of ordinary differential equations. We will consider a collection of continuous differentiable functions $\gamma_{i,j}\,:\, [0,\infty) \rightarrow \mathbb{R}$ , for all $i=1,\ldots, p_\ell$ and $j=0,\ldots, r-1$ , through which we will approximate the quantities $c_{i,j}$ . To be more precise, $\gamma_{i,j}$ will be shown to be close to $c_{i,j}/n$ . Moreover, u and $w_{\mathsf{U}}$ will be approximated through the continuous differentiable functions $\nu, \mu_{\mathsf{U}} \,:\, [0,\infty) \rightarrow \mathbb{R}$ in a similar way. We will also use another continuous function, $G\,:\, [0,\infty) \rightarrow \mathbb{R}$ , which will approximate the ratio $w_{\mathsf{U}} / u$ ; note that this is the average weight of the set of infected unexposed vertices.

The system of differential equations that determines the functions $\gamma_{i,j}$ is as follows:

(43) \begin{equation}\begin{split}\frac{d \gamma_{i,0}}{d\tau} &= - \gamma_{i,0} (\tau) \frac{W_i}{d} G (\tau), \\\frac{d \gamma_{i,j}}{d\tau} &= \left(\gamma_{i,j-1} (\tau) - \gamma_{i,j} (\tau) \right) \frac{W_i}{d} G (\tau), \quad\mbox{ $1 \le j \le r-1$}.\end{split}\end{equation}

The continuous counterparts of (41) and (42) are

(44) \begin{equation} \frac{d \nu}{d \tau} = -1 + G (\tau) \sum_{i=1}^{p_\ell} \frac{W_i}{d}\,\gamma_{i,r-1} (\tau)\end{equation}

and

(45) \begin{equation} \frac{d \mu_{\mathsf{U}}}{d\tau} = - G (\tau) + G (\tau) \sum_{i=1}^{p_\ell} \frac{W_i^2}{d}\,\gamma_{i,r-1} (\tau).\end{equation}

The initial conditions are

(46)

In the following proposition, we will express the formal solution of the above system in terms of $\gamma_{i,0} (\tau)$ .

Proposition 1. With $I(\tau) = \int_0^{\tau} G(s) ds$ , we have

$$ \gamma_{i,0}(\tau) = \gamma_{i,0} (0) \exp \left( - {W_i } I(\tau ) / d\right) .$$

Moreover, for $1\le j \le r-1$ ,

$$ \gamma_{i,j} (\tau) = \frac{\gamma_{i,0}(\tau)}{j!} \log^j \left( \frac{\gamma_{i,0} (0)}{\gamma_{i,0} (\tau)} \right). $$

Proof. The expression for $\gamma_{i,0} (\tau)$ can be obtained through separation of variables—we omit the details. The remaining expressions will be obtained by induction. Let us consider the differential equation for $\gamma_{i,j}$ , where $0< j < r$ , assuming that we have derived the expression for $\gamma_{i,j-1}$ . This differential equation is a first-order ordinary differential equation of the form $y^{\prime}(\tau) = a(\tau )y(\tau ) + b(\tau)$ with initial condition $y(0)=0$ . Its general solution is equal to

$$ y(\tau) = \exp \left( \int_0^{\tau} a(s) ds \right) \cdot \int_0^{\tau} b(s) \exp \left( - \int_0^{s} a(\rho) d\rho \right) ds. $$

Here, we have

$$ a(\tau) = - \frac{W_i}{d} G(\tau ), \ b(\tau) = \gamma_{i,j-1}(\tau ) \frac{W_i}{d} G(\tau ) =\frac{W_i}{d}\,\frac{\gamma_{i,0}(\tau)}{(j-1)!}\,\log^{j-1} \left( \frac{\gamma_{i,0} (0)}{\gamma_{i,0} (\tau)} \right) G(\tau ),$$

by the induction hypothesis. Therefore, and using the expression for $\gamma_{i,0}$ , we obtain

(47) \begin{equation} \exp \left( \int_0^{s} a(\rho) d\rho \right)= \frac{\gamma_{i,0} (s )}{\gamma_{i,0} (0)}.\end{equation}

Hence

(48)

For $j=1$ , the last integral equals $\log (\gamma_{i,0}(0)/\gamma_{i,0}(\tau))$ . For $j\geq 2$ , it can be calculated using integration by parts:

\begin{equation*}\int \frac{\log^{j-1} (x)}{x} dx = \int \left( \log (x) \right)^{\prime} \log^{j-1}(x) dx = \log^j (x) - (j-1) \int \frac{\log^{j-1}(x)}{x}dx,\end{equation*}

which yields

\begin{equation*}\int \frac{\log^{j-1}(x)}{x}dx = \frac{\log^j (x)}{j}.\end{equation*}

Therefore, the last integral in (48) is

\begin{equation*}\int_{\gamma_{i,0}(\tau)/\gamma_{i,0}(0)}^1 \frac{\log^{j-1} (x)}{x} dx = - \frac{1}{j}\, \log^j \left(\frac{\gamma_{i,0}(\tau)}{\gamma_{i,0}(0)} \right) = \frac{(-1)^{j+1}}{j}\,\log^j \left( \frac{\gamma_{i,0}(0)}{\gamma_{i,0}(\tau)} \right).\end{equation*}

Substituting this into (48), we obtain

(49) \begin{equation} \int_0^{\tau} b(s) \exp \left( - \int_0^{s} a(\rho) d\rho \right) ds =\frac{\gamma_{i,0} (0)}{j!}\,\log^j \left( \frac{\gamma_{i,0}(0)}{\gamma_{i,0}(\tau)} \right).\end{equation}

Combining (47) and (49), we have

$$ \gamma_{i,j} (\tau) = \frac{\gamma_{i,0} (\tau )}{j!}\,\log^j \left( \frac{\gamma_{i,0}(0)}{\gamma_{i,0}(\tau)} \right).$$

In the sequel we will use the expressions for $\gamma_{i,r-1}$ , where $1 \le i \le p_\ell$ , and integrate (44) in order to deduce the expressions for $\nu$ and $\mu_{\mathsf{U}}$ .

Proposition 2. We have

\begin{equation*}\nu (\tau) = p\,(1-h_F(\gamma) ) +\gamma^{\prime} - \tau + (1-p) \sum_{i=1}^{p_\ell} \gamma_i \mathbb{P}\left[\mathsf{Po} \left( \frac{W_i}{d} I(\tau) \right) \geq r\right] \end{equation*}

and

\begin{equation*}\mu_{\mathsf{U}} (\tau ) = W^{\prime}_{\gamma} +p \sum_{i=1}^{p_\ell} W_i \gamma_i - I(\tau )+ (1-p) \sum_{i=1}^{p_\ell} W_i \gamma_i \mathbb{P}\left[\mathsf{Po} \left( \frac{W_i}{d} I(\tau) \right) \geq r\right].\end{equation*}

Proof. Applying Proposition 1 to (44) yields

\begin{equation*}\frac{d \nu}{d \tau} = -1 + G (\tau) \sum_{i=1}^{p_{\ell}} \frac{W_i}{d}\,\frac{\gamma_{i,0}(\tau)}{(r-1)!} \log^{r-1} \left( \frac{\gamma_{i,0} (0)}{\gamma_{i,0} (\tau)} \right).\end{equation*}

By integrating this expression we obtain

(50) \begin{equation} \begin{split}\nu (\tau ) &= \nu (0) - \tau + \frac{1}{(r-1)!}\sum_{i=1}^{p_\ell} \int_0^{\tau} \frac{W_i}{d}\,\gamma_{i,0}(s) G(s) \log^{r-1} \left( \frac{\gamma_{i,0} (0)}{\gamma_{i,0} (s)} \right) ds \\& \stackrel{(43)}{=}\nu (0) - \tau - \frac{1}{(r-1)!}\sum_{i=1}^{p_\ell} \int_0^{\tau}\left(\frac{d \gamma_{i,0}}{ds}\right) \, \log^{r-1} \left( \frac{\gamma_{i,0} (0)}{\gamma_{i,0} (s)} \right) ds \\&= \nu (0) - \tau - \frac{1}{(r-1)!}\sum_{i=1}^{p_\ell} \gamma_{i,0}(0) \int_1^{\gamma_{i,0}(\tau)/\gamma_{i,0}(0)}\log^{r-1} \left( \frac{1}{x}\right) dx.\end{split}\end{equation}

We calculate the last integral substituting y for $1/x$ and using integration by parts. We have

\begin{equation*}\begin{split}\int \log^{r-1} \left( \frac{1}{x} \right) dx &= - \int \frac{\log^{r-1} (y)}{y^2 } dy = \int \left(\frac{1}{y} \right)^{\prime} \log^{r-1} (y) dy \\& = \frac{ \log^{r-1} (y)}{y} - (r-1) \int \frac{\log^{r-2} (y)}{y^2} dy.\end{split}\end{equation*}

As $\int \frac{1}{y^2} dy = - \frac{1}{y}$ , dividing and multiplying by $(r-1)!$ , we obtain

$$ \int \log^{r-1} \left( \frac{1}{x} \right) dx = \frac{(r-1)!}{y}\, \sum_{i=0}^{r-1} \frac{\log^i (y)}{i!},$$

where $y=1/x$ . Therefore, for all $i=1,\ldots, p_\ell$ we have

\begin{equation*}\begin{split}\int_1^{\gamma_{i,0}(\tau)/\gamma_{i,0}(0)} \log^{r-1} \left( \frac{1}{x}\right) dx =(r-1)! \left( \frac{\gamma_{i,0}(\tau )}{\gamma_{i,0}(0 )}\,\sum_{i=0}^{r-1}\frac{1}{i!}\log^i \left(\frac{\gamma_{i,0}(0)}{\gamma_{i,0}(\tau)} \right) - 1\right).\end{split}\end{equation*}

Substituting the above into (50), we obtain

$$\nu (\tau) = \nu (0) - \tau + \sum_{i=1}^{p_\ell} \gamma_{i,0}(0)\, \left(1- \frac{\gamma_{i,0}(\tau )}{\gamma_{i,0}(0 )}\,\sum_{j=0}^{r-1}\frac{1}{j!} \log^j \left(\frac{\gamma_{i,0}(0)}{\gamma_{i,0}(\tau)} \right) \right).$$

Observe now that the expression in brackets is equal to the probability that a Poisson-distributed random variable with parameter $\log \left( \gamma_{i,0}( 0) / \gamma_{i,0}(\tau) \right)$ is at least r. But by Proposition 1, we have

$$\log \left( \frac{\gamma_{i,0}( 0)}{\gamma_{i,0}(\tau)} \right) = \frac{W_i}{d} I(\tau). $$

Also recall that by (46), $\gamma_{i,0} (0) = (1-p) \gamma_i$ , for each $i=1,\ldots, p_\ell$ , and $\nu (0) = p\,( 1- \gamma )+\gamma^{\prime}$ . Hence

\begin{equation*}\nu (\tau) = p\,(1-\gamma ) + \gamma^{\prime} - \tau + (1-p) \sum_{i=1}^\ell \gamma_i \mathbb{P}\left[\mathsf{Po} \left( \frac{W_i}{d} I(\tau) \right) \geq r\right]. \end{equation*}

The expression for $\mu_{\mathsf{U}}$ is obtained along the same lines, and we omit its proof.

4.3. Wormald’s theorem

We summarize here the method introduced by Wormald in [38, 39] for the analysis of a discrete random process using differential equations. Recall that a function $f(u_1, \ldots, u_{b+1})$ satisfies a Lipschitz condition in a domain $D \subseteq \mathbb{R}^{b+1}$ if there is a constant $L > 0$ such that

$$|f(u_1, \ldots, u_{b+1})-f(v_1, \ldots, v_{b+1})| \leq L \max _{1\leq i \leq b+1}|u_i-v_i|$$

for all $(u_1, \ldots, u_{b+1}), (v_1, \ldots, v_{b+1}) \in D$ . For variables $Y_1, \ldots, Y_b$ , the stopping time $T_D(Y_1, \ldots, Y_b)$ is defined to be the minimum t such that

$$(t/n;\, Y_1(t)/n, \ldots, Y_b(t)/n) \notin D.$$

This is written as $T_D$ when $Y_1, \ldots, Y_b$ are understood from the context.

Theorem 10. ([38].) Let $b,n \in \mathbb{N}$ . For $1 \leq j \leq b$ , suppose that $Y^{(n)}_j(t)$ is a sequence of real-valued random variables such that $0 \leq Y^{(n)}_j \leq C n$ for some constant $C > 0$ . Let $H_t$ be the history up to time t, i.e., the sequence $\{Y^{(n)}_j(k), \ 0 \leq j \leq b, \ 0 \leq k \leq t\}$ . Suppose also that for some bounded connected open set $D \subseteq \mathbb{R}^{b+1}$ containing the intersection of $\{(t,z_1,\ldots,z_b)\,:\, t\geq 0\}$ with some neighborhood of

$$\left\{(0,z_1,\ldots,z_b)\,:\,\mathbb{P} \left[Y^{(n)}_j(0)=z_j n, 1\leq j\leq b\right] \neq 0\ for\ some\ n \right\},$$

the following three conditions are satisfied:

1. 1. (Boundedness.) For some function $\omega=\omega(n)$ and $\lambda=\lambda(n)$ with $\lambda^4\log n < \omega < n^{2/3}/\lambda$ and $\lambda\to \infty$ as $n\to \infty$ , for all $l\leq b$ and uniformly for all $t<T_D$ ,

   $$\mathbb{P} \left(|Y^{(n)}_l(t+1)-Y^{(n)}_l(t)|>\frac{\sqrt{\omega}}{\lambda^2\sqrt{\log n}}\mid H_t\right) = o(n^{-3}).$$

2. 2. (Trend.) For all $l \leq b$ and uniformly over all $t<T_D$ ,

   $$\mathbb{E}[Y^{(n)}_l(t+1)-Y^{(n)}_l(t)|H_{t}] = f_l(t/n,Y_1^{(n)}(t)/n,\ldots,Y_b^{(n)}(t)/n) + o(1).$$

3. 3. (Lipschitz.) For each l, the function $f_l$ is continuous and satisfies a Lipschitz condition on D, with all Lipschitz constants uniformly bounded.

Then the following hold:

1. (a) For $(0,\hat{z}_1,\ldots,\hat{z}_b) \in D$ , the system of differential equations

   $$\frac{dz_l}{ds}=f_l(s,z_1,\ldots,z_l), \qquad l=1,\ldots,b ,$$
   has a unique solution in D, $z_l\,:\,\mathbb{R} \rightarrow \mathbb{R}$ for $l=1,\dots,b$ , which passes through $z_l(0)=\hat{z}_l,$ $l=1,\dots,b$ , and which extends to points arbitrarily close to the boundary of D.

2. (b) We have

   $$Y_l^{(n)}(t)=n z_l(t/n) + o_p(n)$$
   uniformly for $0 \leq t \leq \min\{\sigma n,T_{D}\}$ and for each l. Here $z_l(t)$ is the solution in (a) with $\hat{z}_l = Y^{(n)}_l(0)/n$ , and $\sigma = \sigma_D(n)$ is the supremum of those s to which the solution can be extended.

4.4. Proof of Theorem 3

We will apply Theorem 10 to show that the trajectory of

$$\{u(t), w_{\mathsf{U}}(t), ( c_{i,j}(t) )_{1\le i \le p_\ell, 0 \le j \le r-1}\}$$

throughout the algorithm is w.h.p. close to the solution of the deterministic equations suggested by these equations, i.e., $\{\nu, \mu_{\mathsf{U}}, ( \gamma_{i,j} )_{i=1,\dots,p_\ell, j=0,\dots,r-1}\}$ .

We set $b=r p_\ell + 2$ . For $\epsilon >0$ , we define

\begin{align*}D_{\epsilon} = \Bigg\{ (\tau, \nu, \mu_{\mathsf{U}}, (\gamma_{i,j})_{i,j}) \in \mathbb{R}^{b+1} \mid & -\epsilon<\tau<1, \ 0 < \frac{\mu_{\mathsf{U}}}{\nu} < 2 C_\gamma, \ -\epsilon< \gamma_{i,j}< \gamma_i+\epsilon, \\ \epsilon < \mu_{\mathsf{U}} < W^{\prime}_{\gamma} + \sum_{i=1}^{p_\ell} W_i \gamma_i \Bigg\}.\end{align*}

We now apply the last part (b) of Theorem 10. Note that the boundedness and trend hypotheses are verified for $t < T_{D_{\epsilon}}$ . More specifically, the boundedness hypothesis follows since the changes in the quantities $u(t), w_{\mathsf{U}}(t), c_{i,j}(t)$ are bounded by a constant multiple of the maximum degree of the random graph. But since the maximum weight is bounded, we may choose, for example, $\lambda = n^{1/8}$ and $\omega = n^{25/48}$ , and show that the maximum degree is bounded by $\sqrt{\omega} / ( \lambda^2 \log n)= n^{1/96}/\log n$ with probability $1-o(n^{-3})$ . The trend hypothesis is verified by (39)–(42). By the assumption that $0 < \frac{\mu_{\mathsf{U}}}{\nu}<2C_{\gamma}$ , the Lipschitz condition is also verified. Hence, for $0 \leq t \leq \min\{\sigma_{D} n,T_{D_{\epsilon}}\}$ , we have

(51) \begin{align} u(t) & = n \nu(t/n) + o_p(n), \nonumber \\w_{\mathsf{U}}(t) &= n \mu_{\mathsf{U}}(t/n) + o_p(n),\\c_{i,j}(t) &= n \gamma_{i,j}(t/n) + o_p(n), \ \text{for all} \ i=1,\dots,p_\ell, \ j=0,\dots,r-1.\nonumber\end{align}

This gives us the convergence up to the point where the solution leaves $D_{\epsilon}$ . Observe that the definition of the domain $D_{\epsilon}$ , together with the fact that the maximum weight is bounded by $2C_\gamma$ , implies that at round $T_{D_\epsilon}$ we have $w_{\mathsf{U}}(T_{D_\epsilon})/n \leq \epsilon$ , but $w_{\mathsf{U}}(T_{D_\epsilon} -1)/n > \epsilon$ .

First, we will bound $|\mathcal{A}_f (T_{D_\epsilon})|$ . Observe that $T_{D_{\epsilon}} = |\mathcal{A}_f (T_{D_\epsilon})|$ , as exactly one vertex is removed at each step. Also, as we noted above, $ w_{\mathsf{U}} (T_{D_{\epsilon}})/n < \epsilon$ , but $ w_{\mathsf{U}} (T_{D_{\epsilon}}-1)/n \geq \epsilon$ . Since the maximum degree is $o_p(n)$ and the weights are bounded, w.h.p. we have

$$\epsilon \leq w_{\mathsf{U}} (T_{D_{\epsilon}}-1)/n \leq 1.5\epsilon. $$

Hence, by (51), w.h.p.

(52) \begin{equation} \mu_{\mathsf{U}} \left( \frac{T_{D_{\epsilon}}-1 }{n} \right) < 2 \epsilon.\end{equation}

Also, as the minimum weight is bounded from below by $W_0$ , the bound on $w_{\mathsf{U}}$ implies that

(53) \begin{equation} u\left(T_{D_{\epsilon}}-1\right) /n \leq \frac{1.5 \epsilon}{W_0}.\end{equation}

Therefore, (51) again implies that w.h.p.

$$ \nu \left(\frac{T_{D_{\epsilon}}-1}{n} \right) \leq \frac{2\epsilon}{W_0}. $$

Let

$$\alpha (y ) \,:\!=\, p\,(1-{h_F(\gamma )} ) +\gamma^{\prime} + (1-p) \sum_{i=1}^{p_\ell} \gamma_i \psi_r \left( W_i y \right). $$

The first part of Proposition 2 implies that

(54) \begin{equation} \left| \frac{T_{D_{\epsilon}}-1}{n} -\alpha \left(\frac{1}{d} I\left( \frac{T_{D_{\epsilon}}-1}{n}\right) \right)\right| \leq \frac{2\epsilon}{W_0}.\end{equation}

Let $\hat{\tau}^{(\ell, \gamma)}$ denote the minimum $\tau >0$ such that $\mu_{\mathsf{U}} (\tau) = 0$ . By Lemma 5 below, there exists $c_1>0$ with the property that for any $\gamma < c_1$ and any $\delta \in (0,1)$ , there exists an infinite set of positive integers $\mathcal{S}$ such that when $\ell \in \mathcal{S}$ , it holds that

(55) \begin{equation} \left|\alpha (\hat{y}_{\ell,\gamma }) - \left(p + (1-p)\mathbb{E}(\psi_r (W_F \hat{y})) \right) \right| < \delta,\end{equation}

where $\hat{y}_{\ell,\gamma}$ is the smallest positive root of

$$ y = \frac{W^{\prime}_\gamma}{d} + p \frac{1}{d} \sum_{i=1}^{p_\ell} W_i \gamma_i+ (1-p) \sum_{i=1}^{p_\ell} \frac{W_i \gamma_i}{d} \psi_r (W_i y) .$$

Its existence is implied by the continuity of $I(\tau)$ and $\alpha (y)$ . By (52), from the continuity of the function $\mu_{\mathsf{U}}$ , we deduce that there exists $\delta_1 = \delta_1 (\epsilon)>0$ such that, for n large enough,

(56) \begin{equation} \left| \frac{T_{D_{\epsilon}}-1}{n} -\hat{\tau}^{(\ell,\gamma)}\right|< \delta_1. \end{equation}

Now, let $I\left( \hat{\tau}^{(\ell,\gamma)} \right) = \lim_{\tau \uparrow \hat{\tau}^{(\ell,\gamma)}} I(\tau)$ . The continuity of I and $\alpha$ implies that there exists an increasing function $f\,:\, (0,1) \rightarrow (0,1)$ (depending on $\ell$ and $\gamma$ ) such that $f(x) \downarrow 0$ as $x \downarrow 0$ and

(57) \begin{equation} \left| \alpha \left( \frac{1}{d} I\left( \hat{\tau}^{(\ell,\gamma)} \right) \right) -\alpha \left( \frac{1}{d}I\left( \frac{T_{D_{\epsilon}}-1}{n} \right) \right) \right| < f (\delta_1) .\end{equation}

Let us set $x=x (\tau) = I(\tau) /d$ . Since $\mu_{\mathsf{U}} \big(\hat{\tau}^{(\ell,\gamma )}\big) = 0$ , this implies that

\begin{equation*}\begin{split}\frac{ I\big(\hat{\tau}^{(\ell,\gamma )}\big)}{d} &= \frac{W^{\prime}_{\gamma}}{d} +p\,\frac{1}{d}\sum_{i=1}^{p_\ell} W_i \gamma_i+ (1-p) \sum_{i=1}^{p_\ell} \frac{W_i \gamma_i}{d} \mathbb{P}\left[\mathsf{Po} \left( \frac{W_i}{d} I\big( \hat{\tau}^{(\ell,\gamma )}\big) \right) \geq r\right] \\& = \frac{W^{\prime}_{\gamma}}{d} +p\,\frac{1}{d}\sum_{i=1}^{p_\ell} W_i \gamma_i+ (1-p) \sum_{i=1}^{p_\ell} \frac{W_i \gamma_i}{d} \psi_r \left( \frac{W_i}{d} I\big( \hat{\tau}^{(\ell,\gamma )}\big) \right),\end{split}\end{equation*}

whereby $\hat{y}_{\ell, \gamma} = \lim_{\tau \uparrow \hat{\tau}^{(\ell,\gamma )}} x (\tau)$ . Thus the triangle inequality together with (54), (55), and (57) implies that for any $\gamma < c_1$ , any $\delta \in (0,1)$ , and any $\ell \in \mathcal{S}$ , w.h.p.

\begin{equation*}\begin{split}\left| n^{-1}{|\mathcal{A}_f (T_{D_\epsilon})|} - \alpha \big(\hat{y}_{\ell,\gamma}\big) \right| < \frac{\epsilon}{C_\gamma} +\delta + f(\delta_1 ).\end{split}\end{equation*}

Recall that $f(\delta_1)$ can become arbitrarily small if we make $\epsilon$ small enough. Therefore, the right-hand side of the above can become as small as we please. The proof of Theorem 3 will be complete if we show that the process will finish soon after $T_{D_\epsilon}$ .

4.4.1. The end of the process

We will show that w.h.p. only a small fraction of vertices are added after $T_{D_\epsilon}$ . From now on, we start exposing the edges incident to all vertices of $\mathsf{U}$ simultaneously. Hence, we change the time scaling. Informally, each round will be approximated by a generation of a multi-type branching process which is subcritical. The subcriticality is encompassed by the following: there exists $\kappa_0 < 1$ such that with probability $1-o(1)$ ,

(58) \begin{equation} \sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}}c_{i, r-1}\left( \frac{T_{D_{\epsilon}}-1}{n} \right) < \kappa_0 < 1.\end{equation}

We start this section by proving this. First, let us observe that using the expression for $\mu_{\mathsf{U}}$ from Proposition 2 and the chain rule, for any $\tau < T_{D_\epsilon}$ we can write

$$\mu^{\prime}_{\mathsf{U}} (\tau) = G(\tau ) f_r^{(\ell,\gamma)\prime} (I(\tau)/d),$$

where

$$f_r^{(\ell,\gamma)} (x)=\frac{W^{\prime}_{\gamma}}{d} +p\, \frac{1}{d}\sum_{i=1}^{p_\ell} W_i \gamma_i -x +(1-p)\,\frac{1}{d} \sum_{i=1}^{p_\ell} W_i \gamma_i \mathbb{P}\left[\mathsf{Po} \left( W_i x \right) \geq r\right].$$

But also by (45) we can write

$$ \mu^{\prime}_{\mathsf{U}}(\tau) = G(\tau) \left( -1 +\sum_{i=1}^{p_\ell} \frac{W_i^2}{d}\gamma_{i, r-1}\left( \tau \right) \right).$$

So in particular, for $\tau = (T_{D_\epsilon} -1)/n$ , we have $G((T_{D_\epsilon} -1)/n) >0$ and therefore (with $x(\tau) = I(\tau)/d$ )

$$ f_r^{(\ell,\gamma)\prime} \left(x\left(\frac{T_{D_\epsilon} -1}{n} \right)\right) = -1 +\sum_{i=1}^{p_\ell} \frac{W_i^2}{d} \gamma_{i, r-1}\left( \frac{T_{D_\epsilon} -1}{n} \right). $$

But by Lemma 5 and Proposition 4 below, for any $\delta \in (0,1)$ there exists $c_1>0$ with the property that for any $\gamma < c_1$ there exists an infinite set of positive integers $\mathcal{S}$ such that when $\ell \in \mathcal{S}$ , it holds that

\begin{equation*}f_r^{(\ell, \gamma)\prime} \big(\hat{y}_{\ell,\gamma}\big) < f^{\prime}_r (\hat{y};\,W_F^*,p) +\delta,\end{equation*}

and, moreover, $\hat{y}_{\ell,\gamma} <1$ . (Note that $\hat{y} <1$ by its definition.) By Claim 15 below, the family $\big\{ f_r^{(\ell, \gamma)\prime} (x)\big\}_{\ell \geq \ell^{\prime}_1}$ restricted to [0,1] for $\ell^{\prime}_1 = \ell^{\prime}_1(\gamma)$ is equicontinuous provided that $\gamma < c^{\prime}_4$ . Hence, for any $\gamma < c_1 \wedge c^{\prime}_4$ and any $\ell$ sufficiently large in $\mathcal{S}$ , using (56), we conclude that if $\varepsilon$ is sufficiently small we have

$$ f_r^{(\ell,\gamma)\prime} \left(x\left(\frac{T_{D_\epsilon} -1}{n} \right)\right) < f^{\prime}_r (\hat{y};\,W_F^*,p) +2\delta.$$

We select $\delta$ small enough so that the right-hand side of the above is negative. This and (51) imply that there exists $\kappa_0 < 1$ such that (58) holds with probability $1-o(1)$ .

From step $T_{D_\epsilon}$ onward, we will provide a stochastic upper bound on $\mathsf{U}$ by a set $\widehat{\mathsf{U}}$ , whose size is an essentially subcritical multi-type branching process. In particular, the expression in (58) will dominate the principal eigenvalue of the expected progeny matrix of this branching process. In this process, rather than exposing the vertices of $\widehat{\mathsf{U}}$ one at a time, we will expose all of their neighbors simultaneously in each round. We let $\widehat{\mathsf{U}}(s)$ be the set $\widehat{\mathsf{U}}$ after s rounds.

Hence, $\widehat{\mathsf{U}}(s)$ will be the sth generation of this process, which resembles a multi-type branching process. We will keep track of the size of $\widehat{\mathsf{U}}$ through a functional which is well known in the theory of multi-type branching processes to give rise to a supermartingale. Let us proceed with the details of this argument.

We set $t_0\,:\!=\,T_{D_{\epsilon}}-1$ . Let $\widehat{\mathsf{U}} (0) = \mathsf{U}(t_0)$ , $\widehat{\mathsf{C}}_{i,r-1}(0)=\mathsf{C}_{i,r-1}(t_0)$ , and $\widehat{\mathsf{C}}_{i,<r-1}(0) = \cup_{k=2}^r \mathsf{C}_{i,r-k}(t_0)$ , for all $i=1,\ldots,p_\ell$ . Let $\widehat{\mathsf{U}}_i (s)$ denote the subset of $\widehat{\mathsf{U}} (s)$ which consists of those vertices that have weight $W_i$ , and let $u_i(s)\,:\!=\, |\widehat{\mathsf{U}}_i(s)|$ —we say that these vertices are of type i. We set $\hat{c}_{i,<r-1}(s)=|\widehat{\mathsf{C}}_{i, <r-1}(s)|$ and $\hat{c}_{i,r-1}(s) = |\widehat{\mathsf{C}}_{i,r-1}(s)|$ . Let $\overline{u}_s= [u_1(s),\ldots, u_{p_\ell}(s)]^T$ be the vector whose coordinates are the sizes of the sets $\widehat{\mathsf{U}}_i (s)$ . A vertex $v \in\widehat{\mathsf{U}}_j(s)$ (for $j\in\{1,\ldots,p_\ell\}$ ) can ‘give birth’ to vertices of type i (i.e., of weight $W_i$ ). These may be vertices from the set $\widehat{\mathsf{C}}_{i,r-1}(s)$ or from the set $\widehat{\mathsf{C}}_{i,<r-1}(s)$ . If v becomes adjacent to a vertex in $\widehat{\mathsf{C}}_{i,r-1}(s)$ , then a child of v is produced. Similarly, we say that a vertex in $\widehat{\mathsf{C}}_{i,<r-1}(s)$ produces a child of v if it is adjacent to v and to some other vertex in $\widehat{\mathsf{U}}(s)$ . In that sense, a vertex in $\widehat{\mathsf{C}}_{i,r-1} \cup \widehat{\mathsf{C}}_{i,<r-1}$ may be responsible for the birth of a child of more than one vertex in $\widehat{\mathsf{U}}(s)$ .

Furthermore, if a vertex in $\widehat{\mathsf{C}}_{i,<r-1}(s)$ is adjacent to exactly one vertex in $\widehat{\mathsf{U}}(s)$ , then a vertex is moved into $\widehat{\mathsf{C}}_{i,r-1}$ . In this process the set $\widehat{\mathsf{C}}_{i,r-1}$ can only gain, not lose, vertices. Clearly, $|\widehat{\mathsf{U}}(s)|$ is a stochastic upper bound on $\mathsf{U}$ .

If a vertex is a child of more than one vertex, we assume that it is born only once (it could be a child of any adjacent vertex in $\widehat{\mathsf{U}}(s)$ ); hence it is included in $\widehat{\mathsf{U}}(s+1)$ only once. In fact, the former case is much more likely than the latter. The expected number of those children that are born out of $\mathsf{C}_{i,r-1}(s)$ is bounded by $\frac{W_j W_i}{W_{[n]}} c_{i,r-1} (s)$ . The expected number of vertices of type i that originate from $\widehat{\mathsf{C}}_{i,<r-1}$ is bounded by $\hat{c}_{i,<r-1}(s)\frac{W_j W_i}{W_{[n]}} \left( |\widehat{\mathsf{U}}(s)| (2 C_\gamma)^2/W_{[n]} \right)$ . This is the case because the factor $|\widehat{\mathsf{U}}(s)| (2 C_\gamma)^2/W_{[n]}$ bounds from above the probability that a given vertex in $\widehat{\mathsf{C}}_{i,<r-1}(s)$ is adjacent to some other vertex in $\widehat{\mathsf{U}}(s)$ .

Now, if we let $A_s$ be the $p_\ell \times p_\ell$ matrix whose ij entry is the expected number of children of type i that a vertex of type j has, then $\mathbb{E} \left( \overline{u}_{s+1}^{T} | \mathcal{H}_s\right) \leq \overline{u}_s^{T} A_s$ (the inequality is meant to be pointwise), where $\mathcal{H}_s$ is the sub- $\sigma$ -algebra generated by the history of the process up to round s. One can view the matrix $A_s$ as the expected progeny matrix of a multi-type branching process, where the expected number of children of type j that a vertex of type i gives birth to is at most

$$A_s [i,j]\,:\!=\,\frac{W_iW_j}{W_{[n]}}a_j(s), \ \mbox{where} \ a_j(s)\,:\!=\,\hat{c}_{j,r-1}(s) +\hat{u}(s) \frac{4 C_\gamma^2}{W_{[n]}}\hat{c}_{j,<r-1} (s). $$

Throughout this section, we will be working with this upper bound, which comes from a stochastic upper bound on the process. It is not hard to see that the vector $[W_1,\ldots, W_{p_\ell}]^T$ is a right eigenvector of $A_s$ , with

$$\sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}} a_i(s)\,=\!:\,\rho_s$$

being the corresponding eigenvalue. In fact, this is the unique positive eigenvalue of $A_s$ . Since $\hat{c}_{j,r-1}(s)$ does not decrease, we have $\hat{c}_{j,r-1} (s) \geq \hat{c}_{j,r-1}(0) =c_{i, r-1}\left( \frac{T_{D_{\epsilon}}-1}{n} \right) $ . Thus for $s>0$ we have

$$\rho_s \geq \sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}}c_{i, r-1}\left( \frac{T_{D_{\epsilon}}-1}{n} \right) >\kappa^{\prime}_0 >0,$$

for some constant $\kappa^{\prime}_0$ and for any n sufficiently large.

Note also that since $\hat{c}_{j,r-1}(s),\hat{u}(s)$ , $\hat{c}_{j,<r-1} (s)\leq n$ , and $W_{[n]} = \Theta (n)$ , we have the bound $\rho_s \leq D$ for some $D>0$ , which depends on $\gamma$ , and for all $s\geq 0$ .

For $s=0$ , it is not hard to see that $\rho_{0}$ is less than and bounded away from 1, if we choose $\epsilon$ small enough. Indeed, by (53),

$$ \hat{u}(0) \frac{4 C_\gamma^2}{W_{[n]}}\hat{c}_{j,<r-1} (0) \leq\hat{u}(0) \frac{4 C_\gamma^2}{W_{[n]}} n < \hat{u} (0) \frac{5 C_\gamma^2}{d n} n \stackrel{(53)}{\leq } \epsilon \frac{15 C_\gamma^2}{2d} n.$$

Hence, combining this with (58), we deduce that if $\epsilon$ is small enough, then $\rho_{0}$ is smaller than 1 and in fact is bounded away from 1.

Let $\lambda_i\,:\!=\, W_i /\sum_j W_j$ and set $\xi\,:\!=\,[\lambda_1,\ldots, \lambda_{p_\ell}]^T$ . Clearly, this is also a right eigenvector of $A_t$ . Consider now the random variable $Z_s = (\xi, \overline{u}_s)$ , where $(\cdot ,\cdot)$ is the usual dot product. Therefore,

$$ \mathbb{E} \left( Z_{s+1} | \mathcal{H}_s\right) \leq \rho_s Z_s. $$

Claim 11. Conditional on $\mathcal{H}_s$ , with probability at least $1-1/n^2$ , we have $Z_s=0$ or

(59) \begin{align}Z_{s+1} \leq \rho_s Z_s + Z_s^{1/2}\log^{3/2} n.\end{align}

Proof. In the following we condition on $\mathcal{H}_s$ , which is suppressed from the notation. Assume that $Z_s >0$ . Note that $Z_{s+1}$ is a weighted sum of Bernoulli-distributed random variables, where the weights are bounded. More specifically,

$$Z_{s+1} = \sum_{j=1}^{p_\ell} \lambda_{j}\left( \sum_{v \in \widehat{\mathsf{C}}_{j,r-1}(s)}\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 1} + \sum_{v \in \widehat{\mathsf{C}}_{j,<r-1}(s)}\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 2} \right).$$

This expansion also shows that $Z_s >0$ implies that $Z_s >c$ , for some $c> 0$ which does not depend on s (or n).

We will appeal to Talagrand’s inequality (see for example Theorem 2.29 in [25]).

Theorem 12. Let $Z_1,\ldots, Z_N$ be independent random variables taking values in some sets $\Lambda_1,\ldots, \Lambda_N$ , respectively. Suppose that $X=f(Z_1,\ldots, Z_N)$ , where $f\,:\, \Lambda_1 \times \cdots \times \Lambda_N \to \mathbb{R}$ is a function which satisfies the following conditions:

1. (i) There are constants $c_k$ , for $k=1,\ldots, N$ , such that if $z,z^{\prime} \in \Lambda_1 \times \cdots \times \Lambda_N$ differ only in their kth coordinates, $z_k$ and $z^{\prime}_k$ respectively, then $|f(z) - f(z^{\prime})| \leq c_k$ .

2. (ii) There exists a function $\psi\,:\,\mathbb{R} \to \mathbb{R}$ such that if $z \in \Lambda_1 \times \cdots \times \Lambda_N$ satisfies $f(z)\geq r$ , then there is a witness set $J \subseteq \{1,\ldots, N \}$ with $\sum_{k\in J }c_k^2 \leq \psi (r)$ such that any $y \in \Lambda_1 \times \cdots \times \Lambda_N$ with $y_k=z_k$ , for $k \in J$ , also has $f(y)\geq r$ .

If m is a median of X, then for every $t\geq 0$ ,

$$ \mathbb{P} (X \leq m - t) \leq 2 e^{-t^2/4 \psi (m)}$$

and

$$ \mathbb{P} (X \geq m + t) \leq 2 e^{-t^2/4 \psi (m+t)}.$$

We will apply Theorem 12 to the random variable $Z_{s+1}$ . First, note that $Z_{s+1}$ is a function of independent Bernoulli random variables, which correspond to the (potential) edges that are incident to $\widehat{\mathsf{U}}(s)$ . Let us write the random variable $Z_{s+1}$ more explicitly as a function on the sample space which consists of all subsets of $\cup_{j=1}^{p_\ell} \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right) \times \widehat{\mathsf{U}} (s)$ . More specifically, for any subset

$$E \subseteq \cup_{j=1}^{p_\ell} \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right) \times \widehat{\mathsf{U}} (s)$$

we can write

$$ Z_{s+1} (E)= \sum_{j=1}^{p_\ell} \lambda_{j}\left( \sum_{v \in \widehat{\mathsf{C}}_{j,r-1}(s)}\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 1}(E) + \sum_{v \in \widehat{\mathsf{C}}_{j,<r-1}(s)}\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 2}(E) \right),$$

where the $\textbf{1}_{\mathcal{E}}(E)$ denotes the indicator function of the event $\{E \,:\, E \in \mathcal{E}\}$ . For $v \in \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s) $ , if we change any pair of vertices between v and $\widehat{\mathsf{U}}(s)$ (add it if it is not an edge, or remove it if it is), then $Z_{s+1}$ may change by at most $\lambda_j$ .

Now, for any subset of edges $E \subseteq \cup_{j=1}^{p_\ell} \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right) \times \widehat{\mathsf{U}} (s)$ and a subset $J \subseteq \cup_{j=1}^{p_\ell} \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right)$ , let

$$Z_{s+1}^{J} (E) = \sum_{j=1}^{p_\ell} \lambda_{j}\left( \sum_{v \in \widehat{\mathsf{C}}_{j,r-1}(s) \cap J}\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 1} (E) + \sum_{v \in \widehat{\mathsf{C}}_{j,<r-1}(s)\cap J}\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 2}(E) \right).$$

Suppose that $Z_{s+1}(E)\geq x$ . Let $J^* = J^*(E) \subseteq \cup_{j=1}^{p_\ell} \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right)$ be a minimal subset which is also a minimizer of $Z_{s+1}^J (E)$ subject to $Z_{s+1}^J(E)\geq x$ . (Note that a minimizer may not be minimal, as it may include a vertex v such that $\textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 1} (E),\ \textbf{1}_{d_{\widehat{\mathsf{U}}(s)}(v) \geq 2} (E)=0$ .) Observe that the minimality of $J^*$ implies that $Z_{s+1}^{J^*}(E) < x + \lambda_{max}$ , where $\lambda_{\max} = \max \{\lambda_j\}_{j=1,\ldots, p_\ell}$ .

We select a set of edges $E_{J^*}\subseteq E$ as follows: for any $v \in \widehat{\mathsf{C}}_{j,r-1}(s) \cap J^*$ , we add to $E_{J^*}$ one of the edges in E that are incident to v, if there are any such; for any $v \in \widehat{\mathsf{C}}_{j,<r-1}(s) \cap J^*$ , we add to $E_{J^*}$ two of the edges in E that are incident to v, if there are at least two such edges. Hence, any subset of edges $E^{\prime} \subseteq \cup_{j=1}^{p_\ell} \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right) \times \widehat{\mathsf{U}} (s)$ such that $E_{J^*} \subseteq E^{\prime}$ also satisfies $Z_{s+1}(E^{\prime})\geq x$ .

For any $e\in \left( \widehat{\mathsf{C}}_{j,r-1}(s) \cup \widehat{\mathsf{C}}_{j,<r-1}(s)\right) \times \widehat{\mathsf{U}} (s)$ , we set $\lambda_e = \lambda_j$ . Consider now $\sum_{e \in E_{J^*}} \lambda_e^2$ . Since $\lambda_e \leq 1$ , we have the bound

\begin{eqnarray*}\sum_{e \in E_{J^*}} \lambda_e^2 &\leq& \sum_{j=1}^{p_\ell} \left(\sum_{e \in \left( \widehat{\mathsf{C}}_{j,r-1}(s) \times \widehat{\mathsf{U}} (s) \right) \cap E_{J^*}} \lambda_e +\sum_{e \in \left( \widehat{\mathsf{C}}_{j,<r-1}(s) \times \widehat{\mathsf{U}} (s) \right) \cap E_{J^*}} \lambda_e \right) \\&=&\sum_{j=1}^{p_\ell} \left(\sum_{e \in \left( \widehat{\mathsf{C}}_{j,r-1}(s) \times \widehat{\mathsf{U}} (s) \right) \cap E_{J^*}} \lambda_j +\sum_{e \in \left( \widehat{\mathsf{C}}_{j,<r-1}(s) \times \widehat{\mathsf{U}} (s) \right) \cap E_{J^*}} \lambda_j \right) \\&=& \sum_{j=1}^{p_\ell} \left(\sum_{v \in \widehat{\mathsf{C}}_{j,r-1}(s) \cap J^*} \lambda_j +2\sum_{v \in \widehat{\mathsf{C}}_{j,<r-1}(s) \cap J^*} \lambda_j \right) \\&\leq &2 Z_{s+1}^{J^*} \leq 2 (x+ \lambda_{\max}).\end{eqnarray*}

Hence, we can apply Theorem 12, taking $\psi (x) = 2(x+\lambda_{\max})$ (conditional on $\mathcal{H}_s$ which we suppress). With $m(Z_{s+1})$ being a median of $Z_{s+1}$ , Talagrand’s inequality yields

(60) \begin{equation} \mathbb{P} \left[Z_{s+1} \geq m(Z_{s+1}) + \frac{1}{2}Z_s^{1/2}\log^{3/2} n\right] \leq 2 e^{-\frac{Z_s \log^3 n}{32\bigl(m (Z_{s+1})+\frac{1}{2} Z_s^{1/2}\log^{3/2} n+\lambda_{\max}\bigr)}}.\end{equation}

Since $\psi (x)$ is increasing with respect to x and $Z_{s+1}$ takes only non-negative values, using an argument similar to that of [25, pp. 41–42] we have

\begin{align*} &|\mathbb{E} \left( Z_{s+1}\right) - m(Z_{s+1}) | \leq \mathbb{E} \left( |Z_{s+1} - m(Z_{s+1})|\right) =\int_0^\infty \mathbb{P} \left[|Z_{s+1} - m(Z_{s+1})|>t\right] dt \\ &\leq \int_0^{m(Z_{s+1})} 4 e^{-\frac{t^2}{4 \psi (2m(Z_{s+1}))}}dt + \int_{m(Z_{s+1})}^{\infty} 2 e^{-\frac{t^2}{4 \psi (m(Z_{s+1})+t)}}dt \\ &\leq \int_0^{m(Z_{s+1})} 4 e^{-\frac{t^2}{16m(Z_{s+1})+8 \lambda_{\max}}}dt + \int_{m(Z_{s+1})}^{\infty} 2 e^{-\frac{t^2}{16t+8\lambda_{\max}}}dt \\ &\leq 8\sqrt{\pi(m(Z_{s+1})+\lambda_{\max})} + 32, \end{align*}

and using that $m(Z_{s+1}) \leq 2 m(Z_{s+1}) \mathbb{P} \left[Z_{s+1}\geq m(Z_{s+1})\right] \leq 2\mathbb{E} \left( Z_{s+1}\right)$ , we obtain

$$ |\mathbb{E} \left( Z_{s+1}\right) - m(Z_{s+1}) | = O(\mathbb{E} \left( Z_{s+1}\right)^{1/2}). $$

Hence, for n large enough, using that $\mathbb{E} \left( Z_{s+1}\right)\leq \rho_s Z_{s}$ , we have

\begin{equation*}\begin{split}&\mathbb{P} \left[Z_{s+1} \geq \mathbb{E} \left( Z_{s+1}\right) + Z_s^{1/2}\log^{3/2} n\right] \\& \leq\mathbb{P} \left[Z_{s+1} \geq m(Z_{s+1}) - O(\mathbb{E} \left( Z_{s+1}\right)^{1/2}) + Z_s^{1/2}\log^{3/2} n\right] \\& \leq \mathbb{P} \left[Z_{s+1} \geq m(Z_{s+1}) + \frac{1}{2}Z_s^{1/2}\log^{3/2} n\right].\end{split}\end{equation*}

So by (60) we conclude (using that $m(Z_{s+1}) \leq 2 \mathbb{E} \left( Z_{s+1}\right)\leq 2 \rho_s Z_{s}$ ) that

since $\rho_s$ and $\lambda_{\max}$ are bounded uniformly over all s and $Z_s$ is bounded away from 0, if $Z_s >0$ .

We denote the above event ( $Z_s=0$ or (59) holds) by $\mathcal{E}_s$ . If $Z_s > \log^6 n$ and $\mathcal{E}_s$ is realized, we have

(61) \begin{equation} \begin{split}Z_{s+1} &\leq \rho_s Z_s \left( 1 + \frac{Z_s^{1/2} \log^{3/2} n}{\rho_s Z_s} \right) \stackrel{\rho_s \geq \kappa^{\prime}_{0}}{\leq} \rho_s Z_s\left( 1 + \frac{\log^{3/2} n}{\kappa^{\prime}_{0} Z_s^{1/2}} \right) \\ &\stackrel{Z_s > \log^6 n}{\leq}\rho_s Z_s \left( 1 + \frac{\log^{3/2} n}{\kappa^{\prime}_{0} \log^3 n} \right) = \rho_s Z_s \left( 1 + \frac{1}{\kappa^{\prime}_{0} \log^{3/2} n} \right) .\end{split}\end{equation}

In a multi-type branching process, the variable $Z_s/\rho^s$ , where $\rho$ is the largest positive eigenvalue of the progeny matrix, is a martingale (see for example Theorem 4 in Chapter V.6 of [8]). Here we use this fact only approximately, since the progeny matrix changes as the process evolves. Nevertheless, it does not change immensely, and we are able to control the increase of the eigenvalue $\rho_s$ . Let us now make this precise.

By (58), the largest positive eigenvalue of $A_{0}$ is bounded by a constant $\rho_0 <1$ , with probability $1-o(1)$ . We set $\lambda_{\min}=\min \{ \lambda_i\}_{i=1,\ldots , p_\ell}$ . For any $s \geq 0$ , let

$$\mathcal{D}_s \,:\!=\,\left\{ \sum_{j=1}^{p_\ell} \sum_{v \in \widehat{\mathsf{U}}(s)} d_{\widehat{\mathsf{C}}_{j,<r-1} (s)}(v) <\max \left\{ \frac{10 C_\gamma^2}{\lambda_{\min} d} Z_s ,\log^6 n\right\} \right\}. $$

Claim 13. For any $s \geq 0$ we have $\mathbb{P} \left[\mathcal{D}_s\right] = 1-o(1/ n^2)$ .

Proof of Claim 13. The random variable

$$\sum_{j=1}^{p_\ell} \sum_{v \in \widehat{\mathsf{U}}(s)} d_{\widehat{\mathsf{C}}_{j,<r-1} (s)}(v)$$

is stochastically bounded from above by $\sum_{v \in \widehat{\mathsf{U}}(s)} X_v$ , where the $X_v$ are independent and identically distributed random variables that are distributed as $\text{Bin} (n,(2C_\gamma)^2 / W_{[n]})$ . The expected value of this sum is bounded by $\frac{5 C_\gamma^2}{d} u(t)$ for large n. Also, $u(s) \leq Z_s/\lambda_{\min}$ , as $Z_s = (\xi, \overline{u}_{s}) = \sum_{i} \lambda_i u_i(s) \geq \lambda_{\min} \sum_i u_i(s)$ . So the expectation is at most $\frac{5 C_\gamma^2}{\lambda_{\min} d} Z_s$ . The claim follows from a standard Chernoff bound on the binomial distribution (as the sum of binomial is itself binomially distributed).

Let $B_s\,:\!=\, \max \left\{ \frac{10 C_\gamma^2}{\lambda_{\min} d} Z_s ,\log^6 n \right\}$ .

On the event $\mathcal{D}_s$ , the total degree of the vertices in $\widehat{\mathsf{U}} (s)$ into the set $\widehat{\mathsf{C}}_{i,<r-1} (s)$ bounds the number of vertices that enter into the set $\widehat{\mathsf{C}}_{i,r-1}$ . Hence, on the event $\mathcal{D}_s$ , we have

$$\hat{c}_{i, r-1}(s+1) \leq\hat{c}_{i,r-1}(s) + B_s.$$

Furthermore, for large n,

$$u(s+1) \frac{4 C_\gamma^2}{W_{[n]}}\hat{c}_{i,<r-1} (s+1) \leq u(s+1) \frac{4 C_\gamma^2}{W_{[n]}} n \leq u(s+1) \frac{5 C_\gamma^2}{dn}n = u(s+1) \frac{5 C_\gamma^2}{d}\leq Z_{s+1} \frac{5 C_\gamma^2}{\lambda_{\min} d}.$$

Also, on $\mathcal{E}_s$ we have $Z_{s+1} \leq \beta_1 Z_s$ , for some constant $\beta_1 >0$ , if

$$\frac{10 C_\gamma^2}{\lambda_{\min} d} Z_s \geq \log^6 n;$$

otherwise, since $\rho_s$ is uniformly bounded by some constant over all $s>0$ , we have $Z_{s+1}\leq \beta_2 \log^6 n$ for some constant $\beta_2 >0$ . Therefore, on $\mathcal{D}_s \cap \mathcal{E}_s$ we have

\begin{eqnarray}\sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}} a_i ( s +1) &\leq& \sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}} \left( \hat{c}_{i, r-1}( s ) + B_s + Z_{s+1} \frac{5 C_\gamma^2}{\lambda_{\min} d}\right) \nonumber \\& \leq&\sum_{i=1}^{p_\ell} \frac{W_i^2}{W_{[n]}} \hat{c}_{i, r-1}( s ) + \beta \frac{B_s}{n} + \beta^{\prime} \frac{Z_{s+1}}{n} \nonumber \\&\leq & \rho_{s} + \beta \frac{B_s}{n} + \beta^{\prime} \frac{Z_{s+1}}{n}, \nonumber\end{eqnarray}

for some constants $\beta, \beta^{\prime}>0$ and any n. Furthermore, for some other constant $\beta^{\prime\prime}>0$ ,

$$B_s \leq \beta^{\prime\prime} (Z_s + \log^6 n ). $$

Therefore, for some $\gamma > 0$ , we finally obtain

(62) \begin{equation} \rho_{s+1} \leq \rho_s +\frac{1}{n} \left( \gamma (Z_s + Z_{s+1}) + \beta^{\prime\prime} \log^6 n\right) .\end{equation}

Let $\lambda_n = 1 + \frac{1}{\kappa^{\prime}_0 \log^2 n}$ and $T_0 = 2 \lceil \log_{1/\tau} n\rceil$ . We use induction to show that for every $\delta >0$ there exists $\varepsilon>0$ such that if $Z_0/n < \varepsilon$ , then for all $s\leq T_0$

(63) \begin{equation} \rho_s \leq \rho_0 + \gamma \frac{Z_0}{n} \left(2 \sum_{k=0}^{s-1} (\rho_0 +\delta)^k \lambda_n^k +(\rho_0 +\delta)^s \lambda_n^s\right) + (4 \gamma \gamma^{\prime} + \beta^{\prime\prime}) \frac{\log^6 n}{n} \sum_{k=1}^{s-1} k + 2 \gamma \gamma^{\prime} \frac{\log^6 n}{n} s.\end{equation}

Now, observe that for n sufficiently large $(\rho_0 +\delta) \lambda_n < \rho^{\prime}_0 <1 $ . From this inequality, we deduce that for every $s \leq T_0$ , we have

(64) \begin{eqnarray}\rho_s &\leq& \rho_0 + \frac{2\gamma Z_0}{n} \sum_{k=0}^\infty {\rho^{\prime}}_0^k + O\left( \frac{\log^8 n}{n}\right)=\rho_0 + \frac{2\gamma Z_0}{n}\,\frac{1}{1-\rho^{\prime}_0} + O\left( \frac{\log^8 n}{n}\right)\nonumber \\ &\stackrel{Z_0/n < \varepsilon}{\leq}& \rho_0 + 2\gamma \varepsilon\,\frac{1}{1-\rho^{\prime}_0} + O\left( \frac{\log^8 n}{n}\right) < \rho_0+\delta < 1, \end{eqnarray}

provided that $\varepsilon>0$ is small enough.

By (61), on the event $\cap_{s^{\prime}=1}^{T_0} \{ \mathcal{E}_{s^{\prime}} \cap \mathcal{D}_{s^{\prime}} \}$ , for any $s < T_0$ we have

$$Z_s \leq \rho_s Z_{s-1} \lambda_n + \gamma^{\prime} \log^6 n$$

for some constant $\gamma^{\prime} >0$ . Repeating this, we get

\begin{eqnarray}Z_s &\leq& \rho_{s-1} \rho_{s-2} Z_{s-2} \lambda_n^2 +\gamma^{\prime} (\lambda_n + 1) \log^6 n \nonumber \\& & \vdots \nonumber \\&\leq & Z_0 \lambda_n^s \prod_{i=1}^{s-1} \rho_{s-i} + \gamma^{\prime} \log^6 n \sum_{i=0}^{s-1} \lambda_n^i \nonumber \\&\leq&Z_0 \lambda_n^s\prod_{i=0}^{s-1} \rho_{s-i} + 2s \gamma^{\prime} \log^6 n, \nonumber\end{eqnarray}

where in the last inequality we used $\lambda_n^{i} \leq 2$ for n sufficiently large, uniformly over $i\leq T_0$ . By the inductive hypothesis, $\rho_{s-i} \leq \rho_0 + \delta$ for all $i\leq s$ . We thus deduce that

(65) \begin{equation} Z_s \leq Z_0 (\rho_0 +\delta )^{s} \lambda_n^s + 2s \gamma^{\prime} \log^6 n.\end{equation}

Substituting (63) into (62) and using (65), we obtain

\begin{eqnarray*}\rho_{s+1} &\leq& \rho_0 +\frac{\gamma Z_0}{n} \left(2 \sum_{k=0}^{s-1} (\rho_0 +\delta)^k \lambda_n^k +(\rho_0 +\delta)^s \lambda_n^s\right) + (4\gamma \gamma^{\prime} + \beta^{\prime\prime}) \frac{\log^6 n}{n} \sum_{k=1}^{s-1} k \\& & + 2 \gamma \gamma^{\prime} \frac{\log^6 n}{n} s + \beta^{\prime\prime} \frac{\log^6 n}{n} \\&&+\frac{1}{n} \gamma \left(Z_0 (\rho_0 +\delta )^{s} \lambda_n^s + 2s \gamma^{\prime} \log^6 n+Z_0 (\rho_0 +\delta )^{s+1} \lambda_n^{s+1} + 2(s+1) \gamma^{\prime} \log^6 n \right) \\&\leq& \rho_0 +\frac{\gamma Z_0}{n} \left(2 \sum_{k=0}^{s} (\rho_0 +\delta)^k \lambda_n^k +(\rho_0 +\delta)^{s+1} \lambda_n^{s+1}\right) + (4 \gamma \gamma^{\prime} + \beta^{\prime\prime}) \frac{\log^6 n}{n}\sum_{k=1}^{s} k \\& & + 2 \gamma \gamma^{\prime} \frac{\log^6 n}{n} (s+1),\end{eqnarray*}

where in the last inequality we used that

$$\beta^{\prime\prime} \frac{\log^6 n}{n} \leq \beta^{\prime\prime} \frac{\log^6 n}{n}s.$$

Set $\tau = \rho_0 +\delta$ and recall that $T_0 = 2 \lceil \log_{1/\tau} n\rceil$ . Claims 11 and 13 imply that

(66) \begin{equation} \mathbb{P} \left[\cap_{s\leq T_0} \{\mathcal{E}_s \cap \mathcal{D}_s \}\right] = 1 -{O(\log n/n^2)}.\end{equation}

For any $S \in \mathbb{N}$ , we let $\mathcal{S}_S = \cap_{s\leq S} \{\mathcal{E}_s \cap \mathcal{D}_s \}$ and note that if $S < S^{\prime}$ , then $\mathcal{S}_{S^{\prime}} \subset \mathcal{S}_S$ .

Using the tower property of the conditional expectation, we write

\begin{equation*}\mathbb{E} \left( Z_{T_0}\right) = \mathbb{E} \left( \mathbb{E} \left( Z_{T_0} \mid \mathcal{H}_{T_0-1}\right)\right) = \mathbb{E} \left( \mathbb{E} \left( Z_{T_0} \mid \mathcal{H}_{T_0-1}\right) \big(\textbf{1}_{\mathcal{S}_{T_0-1}} + \textbf{1}_{\mathcal{S}_{T_0-1}^c} \big)\right). \end{equation*}

But $Z_{T_0} = O(n)$ , whereby

$$ \mathbb{E} \left( \mathbb{E} \left( Z_{T_0} \mid \mathcal{H}_{T_0-1}\right) \textbf{1}_{\mathcal{S}_{T_0-1}^c}\right) = O(n)\mathbb{E} \left( \textbf{1}_{\mathcal{S}_{T_0-1}^c}\right) = {O(\log n/n)}.$$

Therefore,

\begin{eqnarray*} \mathbb{E} \left( Z_{T_0}\right) &\leq&\mathbb{E} \left( \mathbb{E} \left( Z_{T_0} \mid \mathcal{H}_{T_0-1}\right) \textbf{1}_{\mathcal{S}_{T_0-1}} \right) + {O(\log n/n)} \\&\stackrel{(64)}{\leq}& \mathbb{E} \left( (\rho_0 +\delta) Z_{T_0-1}\right) + {O(\log n /n)}.\end{eqnarray*}

Repeating this, we get

(67) \begin{equation} \mathbb{E} \left( Z_{T_0}\right) \leq (\rho_0 +\delta)^{T_0} \mathbb{E} \left( Z_0\right) +{ O(T_0 \log n /n)} \stackrel{\mathbb{E} \left( Z_0\right) = O(n)}{\leq} O(1/n + T_0/n) = o(1).\end{equation}

Therefore, $\mathbb{P} \left[\widehat{\mathsf{U}} (T_0) \not = \varnothing\right] = o(1)$ .

4.5. Auxiliary lemmas

Recall that $\hat{\tau}^{(\ell, \gamma)}$ denotes the minimum $\tau >0$ such that $\mu_{\mathsf{U}} (\tau) = 0$ . Recall also that $\hat{y}$ is the smallest positive solution of $f_r(y;\,W_F^*,p)=0$ and that we have assumed that $f^{\prime}_r(\hat{y};\,W_F^*,p) < 0$ . Recall that for $\gamma \in (0,1)$ and $\ell \in \mathbb{N}$ we set

$$f_r^{(\ell,\gamma)} (x )=\frac{W^{\prime}_{\gamma}}{d} +p\, \frac{1}{d}\sum_{i=1}^{p_\ell} W_i \gamma_i -x +(1-p)\,\frac{1}{d} \sum_{i=1}^{p_\ell} W_i \gamma_i \mathbb{P}\left[\mathsf{Po} \left( W_i x \right) \geq r\right].$$

Also, recall that

$$ \alpha (y ) \,:\!=\, p\,(1-{h_F(\gamma)} ) +\gamma^{\prime} + (1-p)\sum_{i=1}^{p_\ell} \gamma_i \psi_r \left( W_i y \right).$$

The following lemma shows that if $\gamma$ is taken small enough and $\ell$ is a large positive integer, then $\alpha \big(\hat{y}_{\ell,\gamma}\big)$ and $f_r^{(\ell,\gamma)} \big(\hat{y}_{\ell,\gamma}\big)$ can be approximated by the corresponding functions of $\hat{y}$ .

Lemma 5. For any $\delta >0$ , there exists $c_1$ such that for any $\gamma < c_1$ , there exists a subsequence $\{ \ell_k \}_{k \in \mathbb{N}}$ with the property that for every $\ell \in \{ \ell_k \}_{k \in \mathbb{N}}$ ,

1. (1) $f_r^{(\ell,\gamma)\prime} \big(\hat{y}_{\ell,\gamma}\big) < f^{\prime}_r (\hat{y};\,W_F^*,p)+\delta$ , and

2. (2) $\left|\alpha (\hat{y}_{\ell,\gamma }) - \left(p + (1-p)\mathbb{E}(\psi_r (W_F \hat{y})) \right) \right| < \delta$ .

Proof. Using Definition 3, we can express the $\gamma_i$ in terms of the $\gamma^{\prime}_i$ : $\gamma_i = (1-h_F(\gamma) +\gamma^{\prime})\gamma^{\prime}_i$ . The expression for $f_r^{(\ell,\gamma)}$ yields the following:

(68) \begin{equation} \begin{split}&f_r^{(\ell,\gamma)} (x ) = \frac{W^{\prime}_{\gamma}}{d} +p\, \frac{1}{d}\sum_{i=1}^{p_\ell} W_i \gamma_i -x +(1-p)\,\frac{1}{d} \sum_{i=1}^{p_\ell} W_i \gamma_i \mathbb{P}\left[\mathsf{Po} \left( W_i x \right) \geq r\right] \\&= \frac{W^{\prime}_{\gamma}}{d} +(1-h_F(\gamma ) + \gamma^{\prime} ) \left( p\, \frac{\hat{d}^{(\ell,\gamma )}}{d} +(1-p)\,\frac{d^{(\ell,\gamma)}}{d} \sum_{i=1}^{p_\ell} \frac{W_i \gamma^{\prime}_i}{d^{(\ell,\gamma)}} \mathbb{P}\left[\mathsf{Po} \left( W_i x \right) \geq r\right]\right) -x,\end{split}\end{equation}

where $d^{(\ell,\gamma)} = \int_{0}^{\infty} x dF^{(\ell,\gamma)}(x)$ and $\hat{d}^{(\ell,\gamma)} = \int_{0}^{C_\gamma} x dF^{(\ell,\gamma)}(x)= \sum_{i=1}^{p_\ell} W_i \gamma^{\prime}_i$ . Hence, the second sum in the above expression can be rewritten as

\begin{equation*} \sum_{i=1}^{p_\ell} \frac{W_i \gamma^{\prime}_i}{d^{(\ell,\gamma)}} \mathbb{P}\left[\mathsf{Po} \left( W_i x \right) \geq r\right] =\int_{0}^{C_\gamma} \psi_r \left( y x \right) dF^{*(\ell,\gamma)}(y),\end{equation*}

where $F^{*(\ell, \gamma)}$ is the distribution function of the $U^{(\ell,\gamma)}$ size-biased distribution.

We set $c(\gamma) = 1 -h_F(\gamma ) +\gamma^{\prime}$ and write $p^{(\ell,\gamma)} = \frac{W^{\prime}_{\gamma}}{d c(\gamma)} +p\, \frac{\hat{d}^{(\ell,\gamma)}}{d}$ . The expression in (68) becomes

\begin{equation*} f_r^{(\ell,\gamma)} (x ) = c(\gamma) \left( p^{(\ell,\gamma)} + (1-p)\,\frac{d^{(\ell,\gamma)}}{d}\,\int_{0}^{C_\gamma} \psi_r \left( y x \right) dF^{*(\ell,\gamma)}(y) \right) - x.\end{equation*}

Hence, the derivative of $f_r^{(\ell,\gamma)} (x)$ with respect to x is

(69) \begin{equation} \begin{split}f_r^{(\ell,\gamma)\prime} (x ) &= -1 + c(\gamma ) (1-p)\,\frac{d^{(\ell,\gamma)}}{d}\,\int_{0}^{C_\gamma} y e^{-y x}\frac{\left( y x \right)^{r-1}}{(r-1)!} dF^{*(\ell,\gamma)} (y) \\&= -1 + c(\gamma) (1-p)\,\frac{d^{(\ell,\gamma )}}{d}\,\frac{r}{x}\,\int_{0}^{C_\gamma} e^{-y x}\frac{\left( y x \right)^r}{r!} dF^{*(\ell,\gamma)}(y).\end{split}\end{equation}

Similarly, we can write

(70) \begin{equation} \alpha ( x ) = p (1-h_F(\gamma) ) +\gamma^{\prime} + c(\gamma ) (1-p)\int_{0}^{C_\gamma}\psi_r \left( y x \right) dF^{(\ell,\gamma)} (y).\end{equation}

For real numbers y and $\delta >0$ , let $B(y;\,\delta)$ denote the open ball of radius $\delta$ around y. We show the following result.

Proposition 3. Let $f \,:\, [0,\infty) \rightarrow [0,\infty)$ be a bounded function which is everywhere differentiable. Also, let $y_1 \in \mathbb{R}$ . For any $\delta>0$ there exists $c_2 = c_2 (\delta)$ with the property that for any $\gamma < c_2$ , there exist $\ell_0 = \ell_0(\delta, \gamma) >0$ and $\delta^{\prime} = \delta^{\prime} (\delta, \gamma)$ such that for any $\ell > \ell_0$ and any $y_2 \in B(y_1;\,\delta^{\prime})$ ,

\begin{equation*}\left| \int_{0}^{C_\gamma} f(y y_2) dF^{*(\ell,\gamma)}(y) - \mathbb{E} \left( f(W_F^* y_1) \right)\right| < \delta\end{equation*}

and

\begin{equation*}\left| \int_{0}^{C_\gamma} f(y y_2) dF^{(\ell,\gamma)}(y) - \mathbb{E} \left( f(W_F y_1) \right)\right| < \delta.\end{equation*}

We will further show that $\hat{y}_{\ell,\gamma}$ is close to $\hat{y}$ over a subsequence $\{\ell_k \}_{k\in \mathbb{N}}$ .

Proposition 4. There exists a $c_3>0$ such that for all $\gamma < c_3$ and any $\delta^{\prime} > 0$ , there exists a subsequence $\{\ell_k \}_{k \in \mathbb{N}}$ such that $\hat{y}_{\ell_k,\gamma} \in B(\hat{y};\,\delta^{\prime}).$

The above two propositions yield the following.

Corollary 1. Let $f\,:\,[0,\infty) \rightarrow [0,\infty)$ be a bounded function which is everywhere differentiable. For any $\delta>0$ and any $\gamma < c_2 \wedge c_3$ , there exists a subsequence $\{ \ell_k \}_{k \in \mathbb{N}}$ such that

\begin{equation*}\left|\int_{0}^{C_\gamma} f(y \hat{y}_{\ell_k, \gamma}) dF^{*(\ell_k,\gamma)}(y) - \mathbb{E} \left( f(W_F^* \hat{y}) \right)\right| < \delta\end{equation*}

and

\begin{equation*}\left|\int_{0}^{C_\gamma} f(y \hat{y}_{\ell_k, \gamma}) dF^{(\ell_k,\gamma)}(y) - \mathbb{E} \left( f(W_F \hat{y}) \right)\right| < \delta.\end{equation*}

The two statements of the lemma can be deduced from (69) and (70), if we let f(x) be $\psi_r (x)$ in the former case, and $e^{-x}\frac{x^{r}}{r!}$ in the latter. Note that the choice of the subsequence is determined through Proposition 4 and can be the same for both choices of f(x). Observe that both functions are bounded (by 1), they are differentiable everywhere in $\mathbb{R}$ , and they have bounded derivatives.

By the second part of Definition 4 and the fact that $c(\gamma ) \rightarrow 1$ as $\gamma \downarrow 0$ , we have

(71) \begin{equation} c(\gamma) \left|\frac{d^{(\ell, \gamma)}}{d} -1 \right| < \delta\end{equation}

for any $\gamma$ that is small enough and any $\ell$ that is large enough. We will show now that $p^{(\ell,\gamma)}$ is close to p. We will need the following claim, which is a direct consequence of the second part of Definition 4.

Claim 14. There is a function $r\,:\, (0,1) \rightarrow (0,1)$ such that $r(\gamma ) \rightarrow 0$ as $\gamma \downarrow 0$ , with the following property: for any $\gamma \in (0,1)$ , there exists $\ell_1 (\gamma)$ such that for any $\ell > \ell_1 (\gamma)$ ,

\begin{equation*}\big| \hat{d}^{(\ell,\gamma)} - d \big| < r(\gamma ).\end{equation*}

The above claim together with the fact that $W^{\prime}_{\gamma} \rightarrow 0$ as $\gamma \rightarrow 0$ implies that if $\gamma$ is small enough and $\ell$ is large enough, we have

(72) \begin{equation} \left|p^{(\ell,\gamma)} - p \right|< \delta \quad \mbox{and} \quad\left| p (1-h_F(\gamma)) + \gamma^{\prime} - p \right| < \delta.\end{equation}

Both parts of the lemma now follow from Corollary 1 together with (71) and (72). We now proceed with the proofs of Propositions 3 and 4.

Proof of Proposition 3. The proof of this proposition will proceed in two steps. First we will show that for any $\gamma < 1$ there exist $\delta^{\prime} = \delta^{\prime}(\delta, \gamma)$ and $\ell^{\prime}_0= \ell^{\prime}_0 (\delta , \gamma)$ such that for any $y_2 \in B(y_1;\,\delta^{\prime})$ and $\ell > \ell^{\prime}_0$ we have

(73) \begin{equation} \left| \int_{0}^{C_\gamma} f(y y_2) dF^{*(\ell,\gamma)}(y) -\int_{0}^{C_\gamma} f(y y_1) dF^{*}(y) \right| < \delta /2.\end{equation}

The proposition will follow if we show that there exists $c^{\prime}_2 = c^{\prime}_2 (\delta)$ such that for any $\gamma < c^{\prime}_2$ it holds that

(74) \begin{equation} \left| \int_{C_\gamma}^{\infty} f(y y_1) dF^{*}(y) \right| < \delta /2.\end{equation}

Having proved these inequalities, we deduce that

\begin{equation*}\begin{split}& \left| \int_{0}^{C_\gamma} f(y y_2) dF^{*(\ell,\gamma)}(y)- \mathbb{E} \left[f(W_F^*y_1)\right] \right| \\\le &\left| \int_{0}^{C_\gamma} f(y y_2) dF^{*(\ell,\gamma)}(y) -\int_{0}^{C_\gamma} f(y y_1) dF^{*}(y) \right| + \left| \int_{C_\gamma}^{\infty} f(y y_1) dF^{*}(y) \right| \stackrel{(73), (74)}{<} \delta.\end{split}\end{equation*}

The proof for the case of $F^{(\ell,\gamma)}$ proceeds along the same lines. We can show that for any $\gamma < 1$ there exist $\delta^{\prime} = \delta^{\prime}(\delta, \gamma)$ and $\ell^{\prime\prime}_0 = \ell^{\prime\prime}_0 (\delta , \gamma)$ such that for any $y_2 \in B(y_1;\,\delta^{\prime})$ and $\ell > \ell^{\prime\prime}_0 $ we have

(75) \begin{equation} \left| \int_{0}^{C_\gamma} f(y y_2) dF^{(\ell,\gamma)} (y) -\int_{0}^{C_\gamma} f(y y_1) dF(y) \right| < \delta /2.\end{equation}

Then we show that there exists $c^{\prime\prime}_2 = c^{\prime\prime}_2 (\delta)$ such that for any $\gamma < c^{\prime\prime}_2$ it holds that

(76) \begin{equation} \left| \int_{C_\gamma}^{\infty} f(y y_1) dF(y) \right| < \delta /2.\end{equation}

As before, from (75) and (76) we deduce

\begin{equation*}\begin{split}& \left| \int_{0}^{C_\gamma} f(y y_2) dF^{(\ell,\gamma)} (y) - \mathbb{E} \left[f(W_F y_1)\right] \right| \\\le & \left| \int_{0}^{C_\gamma} f(y y_2) dF^{(\ell,\gamma)} (y) -\int_{0}^{C_\gamma} f(y y_1) dF(y) \right| + \left| \int_{C_\gamma}^{\infty} f(y y_1) dF(y) \right| \stackrel{(75), (76)}{<} \delta.\end{split}\end{equation*}

We proceed with the proofs of (73) and (74)—the proofs of (75) and (76) are very similar (in fact, simpler) and are omitted. The lemma will follow if we take $c_2 = c^{\prime}_2 \wedge c^{\prime\prime}_2$ and $\ell_0 = \ell^{\prime}_0 \vee \ell^{\prime\prime}_0$ .

Proof of (73). We begin with the specification of $\delta^{\prime}$ . We let $\delta^{\prime}$ be such that whenever $|y_1 - y_2 | < \delta^{\prime}$ , we have

(77) \begin{equation} \left| f(x y_1) - f(x y_2) \right| < \delta/4\end{equation}

for any $x \in [0,C_\gamma]$ . This choice of $\delta^{\prime}$ is possible since f is continuous and therefore uniformly continuous in any closed interval. Consider $y_2 \in B(y_1;\,\delta^{\prime})$ . We then have

(78) \begin{equation} \begin{split}& \left| \int_{0}^{C_\gamma} f(x y_2) d F^{*(\ell,\gamma)} (x) -\int_{0}^{C_\gamma} f(x y_1) d F^*(x) \right|\\\leq & \int_{0}^{C_\gamma} |f(xy_2) - f(xy_1)| dF^{*(\ell,\gamma)} (x) \\& \hspace{2.5cm}+ \left|\int_{0}^{C_\gamma} f(x y_1) d F^{*(\ell,\gamma)} (x) -\int_{0}^{C_\gamma} f(x y_1) d F^*(x)\right| \\\stackrel{(77)}{\leq} & \delta/4 +\left|\int_{0}^{C_\gamma} f(x y_1) d F^{*(\ell,\gamma)} (x) -\int_{0}^{C_\gamma} f(x y_1) d F^*(x)\right|.\end{split}\end{equation}

We will argue that the second expression is also bounded from above by $\delta/4$ when $\gamma$ is small enough and $\ell$ is large enough. This follows from (17), as the latter implies that $F^{*(\ell,\gamma)}$ converges weakly to $F^*$ as $\gamma\downarrow 0$ and $\ell \to \infty$ . Since f has been assumed to be bounded and continuous, by Lemma 3 there exists $c_1$ such that for any $0< \gamma < c_1$ and any $\ell > \ell_1(\gamma)$ we have

$$ \left|\int_{0}^{\infty} f(x y_1) d F^{*(\ell,\gamma)} (x) -\mathbb{E} (f(W_F^* y_1)) \right| < \delta/8.$$

Furthermore, by (74), if $\gamma$ is sufficiently small we have

$$\left|\mathbb{E} (f(W_F^* y_1) \textbf{1}_{W_F^* \geq C_\gamma})\right| < \delta/8. $$

Also, by Lemma 1, for any $\gamma$ sufficiently small and any $\ell$ sufficiently large,

$$ \left|\int_{C_\gamma}^{\infty} f(x y_1) d F^{*(\ell,\gamma)} (x)\right| < \delta/8. $$

Therefore, for any such $\gamma$ and any $\ell$ sufficiently large we get

$$\left| \int_{0}^{C_\gamma} f(x y_1) d F^{*(\ell,\gamma)} (x) - \mathbb{E} (f(W_F^* y_1) \textbf{1}_{W_F^* < C_\gamma})\right| < \delta/4. $$

Substituting this bound into (78), we can deduce (73).

We now proceed with the proof of (74)

Proof of (74). Assume that $|f(x)| < b$ for any $x \in \mathbb{R}$ . Hence we have

(79) \begin{equation}\left| \int_{C_\gamma}^{\infty} f(y y_1) dF^{*}(y) \right| < b \mathbb{E} \left[\textbf{1}_{W_F^{*} \geq C_\gamma}\right].\end{equation}

Now, observe that

$$ \mathbb{E} \left[\textbf{1}_{W_F^{*} \geq C_\gamma}\right] = \frac{\mathbb{E} \left[W_F \textbf{1}_{W_F\geq C_\gamma} \right]}{\mathbb{E} \left[W_F\right]}.$$

Since $\mathbb{E} \left[W_F\right] <\infty$ , the latter is at most $\delta /(2b)$ , if $\gamma >0$ is small enough.

Therefore,

$$ \mathbb{E} \left[\textbf{1}_{W_F^{*} \geq C_\gamma}\right] \leq \frac{\delta}{2 b}, $$

and (74) follows from (79).

Proof of Proposition 4. We consider the functions $f_r^{(\ell,\gamma)} (x)$ restricted to the unit interval [0,1].

Claim 15. There exists $c_4>0$ such that for any $\gamma < c_4$ , the family

$$\left\{ f_r^{(\ell,\gamma)} (x) \right\}_{\ell > \ell_1},$$

for some $\ell_1 = \ell_1 (\gamma)$ , is equicontinuous. The analogous statement also holds for

$$\left\{ f_r^{(\ell,\gamma)\prime} (x) \right\}_{\ell > \ell^{\prime}_1},$$

for some $\ell^{\prime}_1 = \ell^{\prime}_1 (\gamma)$ and some other constant $c^{\prime}_4>0$ (this is used in Section 4.4.1 ).

Proof of Claim 15. Let $\varepsilon \in (0,1)$ , and let $c_4$ be such that for any $\gamma < c_4$ we have $1/C_\gamma < \varepsilon /2$ . Recall that $\{ \textbf{W}^{(\ell, \gamma)} \}_{\gamma \in (0,1), \ell \in \mathbb{N}}$ is F-convergent (cf. Definition 4). So there exists a function $\rho\,:\, (0,1)\to (0,1)$ satisfying $\rho(\gamma)\downarrow 0$ as $\gamma\downarrow 0$ , such that for any $\gamma$ and for any $\ell$ sufficiently large (cf. Definition 4, Part 2),

(80) \begin{equation} \left| \frac{d^{(\ell, \gamma)}}{d} - 1 \right| < \rho (\gamma) /d. \end{equation}

The function $\psi_r (y)$ is uniformly continuous on the closed interval $[0,C_\gamma]$ . Hence there exists $\delta \in (0,1)$ such that for any $x_1, x_2 \in [0,1]$ with $|x_1-x_2| < \delta / C_\gamma$ we have $|\psi_r (w x_1) - \psi_r (w x_2)| < d \varepsilon/(2\rho)$ . Thus,

(81) \begin{equation} \left| \int_{0}^{C_\gamma} \psi_r \left( y x_1\right) dF^{*(\ell,\gamma)} (y) -\int_{0}^{C_\gamma} \psi_r \left( y x_2\right) dF^{*(\ell,\gamma)} (y) \right| < \frac{d \varepsilon}{2 \rho}.\end{equation}

Therefore, for any $\gamma < c_4$ and $\ell$ sufficiently large, if $x_1, x_2 \in [0,1]$ are such that $|x_1-x_2| < \delta /C_\gamma$ , then

\begin{equation*}\begin{split}&|f_r^{(\ell,\gamma)}(x_1) - f_r^{(\ell, \gamma)}(x_2)| \\& \leq \left|x_1 - x_2 \right| + \frac{d^{(\ell,\gamma)}}{d} \left| \int_{0}^{C_\gamma} \psi_r \left( y x_1\right) dF^{*(\ell,\gamma)(y)} -\int_{0}^{C_\gamma} \psi_r \left( y x_2\right) dF^{*(\ell,\gamma)(y)} \right| \\& \stackrel{(80), (81)}{\leq}\frac{\delta}{C_\gamma} + \frac{d\varepsilon}{2\rho}\,\frac{\rho}{d} \leq \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \leq \varepsilon.\end{split}\end{equation*}

The proof for the family $\left\{ f_r^{(\ell,\gamma)\prime} (x) \right\}$ is similar, and we omit it.

By the Arzelà–Ascoli theorem, there exists a subsequence $\{ \ell_k\}_{k \in \mathbb{N}}$ such that

$$ \left\{ f_r^{(\ell_k,\gamma)} (x) \right\}_{k \in \mathbb{N}}$$

is convergent in the $L_\infty$ -norm on the space of all continuous real-valued functions on [0,1].

Now, recall that $\hat{y}$ is the smallest positive root of $f_r (y;\, W_F^*,p)=0$ and, moreover, $f^{\prime}_r(\hat{y};\,W_F^*,p) <0$ . Also, $\hat{y} < 1$ , since, by its definition, $\hat{y} = (1-p) \mathbb{E} [\psi_r (W_F^* \hat{y})] + p < 1$ . Hence, there exists $\delta_0 >0$ such that $\hat{y}+\delta_0<1$ and, furthermore,

\begin{equation*}\begin{split}&f_r (\hat{y} +\delta_0;\,W_F^*,p) < 0 \quad \mbox{and} \\& f_r (\hat{y} -\delta_0;\,W_F^*,p) > 0.\end{split}\end{equation*}

By the $L_\infty$ -convergence of the family

$$ \left\{ f_r^{(\ell_k,\gamma)} (x) \right\}_{k \in \mathbb{N}}$$

restricted to [0,1], we deduce that there exists $\ell_1 = \ell_1 (\delta_0,\gamma)$ with the property that for any k such that $\ell_k > \ell_1$ we have

\begin{equation*}\begin{split}&f_r^{(\ell_k,\gamma)} (\hat{y} +\delta_0) < 0 \quad \mbox{and} \\& f_r^{(\ell_k,\gamma)} (\hat{y} -\delta_0) > 0.\end{split}\end{equation*}

In turn, this implies that for any such k there exists a root of $f_r^{(\ell_k,\gamma)} (x)$ in $B(\hat{y};\,\delta_0)$ .

To conclude the proof of the proposition, we need to show that for all but finitely many values of k, there is no positive root of $f_r^{(\ell_k,\gamma)}$ in the interval $[0,\hat{y}-\delta_0]$ . Assume, for the sake of contradiction, that there exists a sub-subsequence $\{\ell_{k_i} \}_{i \in \mathbb{N}}$ such that $\hat{y}_{\ell_{k_i},\gamma} \in [0,\hat{y}- \delta_0]$ . By the sequential compactness of this interval, we deduce that there is a further sub-subsequence $\{ \ell_{k_j} \}_{j \in \mathbb{N}}$ over which

$$ \hat{y}_{\ell_{k_j},\gamma} \rightarrow \hat{y}_\gamma, $$

as $j \rightarrow \infty$ , for some $\hat{y}_\gamma \in [0,\hat{y}-\delta_0]$ .

Let $\delta \in (0,1)$ and let $c_2 = c_2 (\delta)$ be as in Proposition 3. Consider $\gamma < c_2$ . Then there exists $j_0$ such that for $j > j_0$ we have

(82) \begin{equation} \left|\int_{0}^{C_\gamma} \psi_r (y \hat{y}_{\ell_{k_j},\gamma}) dF^{*(\ell_{k_j},\gamma)}(y)- \mathbb{E} \left( \psi_r (W_F^* \hat{y}_\gamma) \right)\right| < \delta/3.\end{equation}

Assume that $\gamma$ is small enough so that

$$ |c(\gamma ) - 1|, \ \rho (\gamma ) /d, \ r(\gamma ) /d < \delta /9. $$

Moreover, assume that $j_0$ is large enough so that for $j > j_0$ we have

\begin{equation*}\left| \frac{d^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| < \rho (\gamma ) /d \quad \mbox{and} \quad \left| \frac{\hat{d}^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| < r(\gamma ) /d,\end{equation*}

by Part 2 of Definition 4 and by Claim 14. Hence

(83) \begin{equation}\begin{split}\left|c(\gamma )\frac{\hat{d}^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| &\leq\left| c(\gamma ) - 1\right|\frac{d^{(\ell_{k_j}, \gamma)}}{d}+ \left| \frac{\hat{d}^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| \\&\leq \left| c(\gamma ) - 1\right| + \left| c(\gamma ) - 1\right| \left| \frac{d^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| +\left| \frac{\hat{d}^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| \leq 3 \delta /9 = \delta /3.\end{split}\end{equation}

Similarly, we can show that for $\gamma$ small enough and j large enough,

(84) \begin{equation}\begin{split}\left|c(\gamma )\frac{d^{(\ell_{k_j}, \gamma)}}{d} - 1 \right| \leq \frac{\delta}{3}.\end{split}\end{equation}

Now, consider the function $\hat{f}_r (x) \,:\!=\, f_r (x;\,W_F^*,p) + W^{\prime}_{\gamma}/d$ . Since $f_r^{(\ell_{k_j},\gamma)} (\hat{y}_{\ell_{k_j},\gamma})=0$ , we can write

\begin{equation*}\begin{split}\hat{f}_r & (\hat{y}_\gamma) = \hat{f}_r (\hat{y}_\gamma) - f_r^{(\ell_{k_j},\gamma)} (\hat{y}_{\ell_{k_j},\gamma}) \\& \leq p \left| c(\gamma ) \frac{\hat{d}^{(\ell_{k_j},\gamma)}}{d} - 1 \right| \\&\hspace{1cm}+ (1-p) \left| c(\gamma ) \frac{d^{(\ell_{k_j},\gamma)}}{d}\int_{0}^{C_\gamma} \psi_r (y \hat{y}_{\ell_{k_j},\gamma}) dF^{*(\ell_{k_j},\gamma)}(y)- \mathbb{E} \left( \psi_r (W_F^* \hat{y}_\gamma) \right) \right| \\&\leq p \left| c(\gamma ) \frac{\hat{d}^{(\ell_{k_j},\gamma)}}{d } - 1 \right|+ (1-p) \left| \left( c(\gamma ) \frac{d^{(\ell_{k_j},\gamma)}}{d} - 1 \right)\int_{0}^{C_\gamma} \psi_r (y \hat{y}_{\ell_{k_j},\gamma}) dF^{*(\ell_{k_j},\gamma)}(y) \right| \\&\hspace{1cm}+(1-p) \left|\int_{0}^{C_\gamma} \psi_r (y \hat{y}_{\ell_{k_j},\gamma}) dF^{*(\ell_{k_j},\gamma)}(y)- \mathbb{E} \left( \psi_r (W_F^* \hat{y}_\gamma) \right) \right| \\&\stackrel{(83), (84), (82)}{\leq} \frac{\delta}{3} + \frac{\delta}{3}+ \frac{\delta}{3} = \delta.\end{split}\end{equation*}

Since $\delta$ is arbitrary, it follows that

$$\hat{f}_r (\hat{y}_\gamma) \,:\!=\, f_r (\hat{y}_\gamma;\,W_F^*,p) + W^{\prime}_{\gamma} = 0, $$

whereby $f_r (\hat{y}_\gamma;\,W_F^*,p) < 0$ . Recall also that $f_r (\hat{y} -\delta_0;\,W_F^*,p) > 0$ . The continuity of $f_r$ implies that there is a root in $(0,\hat{y}-\delta_0)$ . But this leads to a contradiction, as $\hat{y}$ is the smallest positive root of $f_r (x;\,W_F^*,p) = 0$ .

The following lemma shows that if the weight sequence has a power-law distribution with exponent between 2 and 3, then the condition on the derivative of $f_r(x;\,W_F^*,p)$ that appears in the statement of Theorem 1 is always satisfied.

Lemma 6. Assume that $(\textbf{w} (n))_{n \geq 1}$ follows a power law with exponent $\beta \in (2,3)$ . Then $f^{\prime}_r(\hat{y};\,W_F^*,p) < 0.$

Proof. From the definition of f we obtain that

\begin{equation*}\begin{split}f^{\prime}_r (x;\, W_F^*,p)= -1 + (1-p)\frac{r}{x} \mathbb{E} \left[e^{-W_F^* x}\frac{\left( W_F^* x \right)^r}{r!} \right].\end{split}\end{equation*}

To prove the claim it is thus sufficient to argue that

$$ (1-p)r \mathbb{E} \left[e^{-W_F^* \hat{y}}\frac{\left( W_F^* \hat{y} \right)^r}{r!} \right] < \hat{y} = p + (1-p) \mathbb{E} \left[\psi_r (W_F^* \hat{y})\right].$$

In turn, it suffices to prove that

(85) \begin{equation}r \mathbb{E} \left[e^{-W_F^* \hat{y}}\frac{\left( W_F^* \hat{y} \right)^r}{r!} \right] < \mathbb{E} \left[\psi_r (W_F^* \hat{y})\right].\end{equation}

We set $p_r (x) = e^{-x}x^r/r!$ . Furthermore, we set $g(x)\,:\!=\,\mathbb{E} \left[ p_r( W_F^* x) \right]$ and $f(x)\,:\!=\,\mathbb{E} \left[ \psi_r \left( W_F^* x \right)\right]$ . Then we claim that

$$f(x) > r g(x) \quad \text{for any } x\in(0,1],$$

which is equivalent to (85). To see the claim, we will consider the difference $f(x) - rg(x)$ and show that it is increasing with respect to x; the statement then follows from $f(0) - rg(0) = 0$ . The derivative with respect to x is

\begin{equation*}\begin{split}(f(x)-r g(x))^{\prime} &= \mathbb{E} \left[W_F^* p_{r-1}\left( W_F^* x \right)\right] + r\left( \mathbb{E} \left[ W_F^* p_{r}\left( W_F^* x \right)\right]- \mathbb{E} \left[ W_F^* p_{r-1}\left( W_F^* x \right)\right] \right) \\&= -\frac{r(r-1)}{x}\,\mathbb{E} \left[p_r\left( W_F^* x \right)\right] + \frac{r(r+1)}{x}\,\mathbb{E} \left[p_{r+1} \left( W_F^* x \right)\right] \\&= \frac{r}{x}\, \left( -(r-1)\,\mathbb{E} \left[p_r\left( W_F^* x \right)\right] + (r+1)\,\mathbb{E} \left[p_{r+1} \left( W_F^* x \right)\right]\right).\end{split}\end{equation*}

Hence, it suffices to show that

$$ (r+1)\,\mathbb{E} \left[p_{r+1} \left( W_F^* x \right)\right] > (r-1)\,\mathbb{E} \left[p_r\left( W_F^* x \right)\right], $$

for $x \in (0,1]$ . Note that the probability density function of $W_F^*$ is $(\beta - 1) c w^{-\beta + 1}$ for $w > x_0$ ; otherwise it is equal to 0. So we obtain, for $j \in \{r,r+1\}$ ,

\begin{equation*} \begin{split}\mathbb{E} \left[p_j\left( W_F^* x \right)\right] &= (\beta - 1) c \int_{x_0}^{\infty} e^{-wx}\,\frac{(wx)^j}{j!}\,w^{-\beta + 1} dw \\&\stackrel{(z=wx)}{=} (\beta - 1)\frac{x^{\beta - 2}}{j!}c \int_{x_0}^{\infty} e^{-z} z^{j-\beta + 1} dz.\end{split}\end{equation*}

Therefore, it suffices to show that

$$ \int_{x_0}^{\infty} e^{-z} z^{r-\beta + 2} dz > (r-1) \int_{x_0}^{\infty} e^{-z} z^{r-\beta + 1} dz. $$

Applying integration by parts to the integral of the left-hand side, we obtain

\begin{equation*} \begin{split}\int_{x_0}^{\infty} e^{-z} z^{r-\beta + 2} dz &= e^{-x_0} x_0^{r-\beta + 2} + (r-\beta + 2)\int_{x_0}^{\infty} e^{-z} z^{r-\beta + 1} dz \\ >& (r-\beta + 2) \int_{x_0 }^{\infty} e^{-z} z^{r-\beta + 1} dz \stackrel{(\beta < 3)}{>} (r-1)\int_{x_0}^{\infty} e^{-z} z^{r-\beta + 1} dz.\end{split}\end{equation*}