I. INTRODUCTION
A major challenge in video analytics is to efficiently detect regions within video frames that contain objects of interest. Such objects may have a large variety of properties. They can be, e.g., big or small, rigid or nonrigid, and moving or stationary. In many cases, the objects of interest are only moving objects, which makes them clearly distinguishable from the background. Applications in which moving objects are to be detected are, for instance, access control systems or traffic control systems. Or, more general, within any application scenario to solve vision tasks.
Since moving objects are usually clearly separable from the background, moving object detection methods often start with a foreground/background segmentation. Thereby, the regions that contain the foreground, or rather the moving objects, are separated from the static or only slightly moving background. Subsequent steps applied to these extracted regions could, for instance, be object recognition or tracking techniques. The algorithm presented in this paper performs a foreground/background segmentation of video streams that have been encoded according to the H.264/AVC (Advanced Video Coding) standard [1,2].
This standard describes a compression scheme for videos. The used scheme is either more or less relevant for the analysis algorithm, depending on the approach the algorithm follows. There are two approaches for creating a video analysis method, as diagramed in Fig. 1.

Fig. 1. Two video analysis approaches for different domains. Working in the compressed domain enables analysis algorithms to replace the video decoder and the frame buffer by a simple syntax parser. (a) Pixel domain video analysis. (b) Compressed domain video analysis.
The traditional approach for analyzing videos is to initially decode the received stream to gain access to each single pixel within a video frame. These raw pixel data have to be stored in a frame buffer to be able to access it during the pixel domain analysis. A corresponding processing chain is depicted in Fig. 1(a). In this approach, the used compression scheme is less important for the actual analysis. The encoded video frames are completely decoded after the transmission over the network and only raw data are analyzed according to, e.g., luminance, color, or texture information.
A more recent approach is to eliminate the computationally costly step of decoding and to just parse the syntax of the compression scheme instead. This obviously requires to be aware of the used scheme and to adapt the analysis algorithm to be able to evaluate the related syntax elements. Since in this approach the compressed bit stream is directly analyzed, its representatives operate in the so-called compressed domain. As can be seen in Fig. 1(b), the video decoder and the frame buffer have been replaced by a syntax parser, which only performs simple parsing operations and omits complex decoding steps like motion compensation. This permits compressed domain analysis methods to be less complex and to perform very fast. Additionally, the whole system benefits from less complex compressed domain algorithms, compared with their pixel domain counterparts.
H.264/AVC is still widely used in many application like those in the target domains of our algorithm. The most obvious domain is thereby visual surveillance but the algorithm can be deployed in any domain in which a large number of parallel streams should be efficiently and quickly analyzed. Generally, the purpose of a compressed domain analysis is to be able to make a fast decision for each stream whether further analysis steps should be triggered.
Our algorithm is designed to efficiently detect regions within video frames that contain moving objects. Thereto, it extracts and parses several H.264/AVC syntax elements. Namely these elements are (sub-)macroblock types, (sub-) macroblock partition modes, and quantization parameters (QPs). Furthermore, the algorithm can operate in different modes. Either a single-step spatiotemporal analysis or a two-step analysis that is starting with a spatial analysis of each frame, followed by a temporal analysis of several frames.
The remainder of this paper is organized as follows. Section II presents recently published compressed domain detection algorithms and the demarcation between them and our algorithm. The subsequent Section III introduces structures and syntax elements defined by the H.264/AVC standard, before Section IV describes how these elements are used by our moving object detection algorithm and its different operating modes. Section V shows some of our experimental results and comparisons with other algorithms for several video sequences. Finally, we conclude this paper with a summary and ideas for the future in Section VI.
II. RELATED WORK
Compressed domain analysis methods all have in common that they parse and analyze syntax elements of a specific compression scheme. Depending on the scheme and the task to be completed, different syntax elements are evaluated. So, there exist several compressed domain analysis algorithms that provide a variety of solutions for solving different problems. Some of these algorithms are presented in this section.
Probably the most basic method of analyzing compressed video bit streams is to perform an analysis without any decoding or parsing of syntax elements at all. This obviously just enables very basic problems to be solved since only very few information about the video content is available. A sample task that can be handled by such methods is global change detection, which means detecting any change within an otherwise mainly static scene.
In our previous work in [Reference Laumer, Amon, Hutter and Kaup3] we presented an algorithm that is able to detect changes in video streams that are transmitted by using the Real-time Transport Protocol (RTP) [Reference Schulzrinne, Casner, Frederick and Jacobson4]. Thereto, we just extract RTP timestamps for assigning packets to video frames and RTP packet sizes. According to the number of packets per frame and their sizes we calculate different indicators that show whether a frame contains a content change. This does not require any decoding but only simple byte-reading operations.
Schöberl et al. [Reference Schöberl, Bruns, Fößel, Bloss and Kaup5] introduced a change detection algorithm for images compressed with JPEG 2000 [6]. In contrast to H.264/AVC, JPEG 2000 has not been designed to jointly encode several frames of a video sequence but to compress still images by using a discrete wavelet transform. However, the Motion JPEG 2000 [7] extension defines a container format for storing several JPEG 2000-compliant images of a sequence. Schöberl et al. calculate the local data rate of any pixel of an image without performing the reverse wavelet transform and thus without decoding image data. Comparing these local data rates of two images enables their algorithm to detect regions with changing content.
As soon as a compressed video stream is parsed and certain syntax elements become accessible, more sophisticated problems can be solved in the compressed domain. For instance, scene change detection [Reference Jie, Aiai and Yaowu8], object tracking [Reference Khatoonabadi and Bajić9,Reference Maekawa and Goto10], or even face detection [Reference Fonseca and Nesvadba11]. However, in many scenarios the most important task is to be able to distinguish between foreground and background. Thereby, foreground is usually defined as regions with content of interest and in most cases the interest is on regions with moving content. That is the reason why moving object detection is an important task in many video applications, specifically in visual surveillance scenarios.
Maybe the most obvious and basic approach for detecting moving objects in the compressed domain has again been described by Kapotas and Skodras in [Reference Kapotas and Skodras12]. They extract the motion vectors from a H.264/AVC-compressed video stream and calculate an adaptive threshold per frame to determine foreground and background blocks. Thereby, the threshold is simply set to the average length of all available motion vectors of the current frame. Blocks with a corresponding motion vector whose length is above this threshold are considered as foreground, all other blocks are labeled as background. The foreground/background masks of three consecutive frames are then merged to get the final mask for the current frame. Although it can be assumed that this approach will only work for a limited set of video sequences, it shows that compressed domain video analysis has usually a very low complexity and is therefore able to perform very fast.
Like Schöberl et al., Poppe et al. [Reference Poppe, De Bruyne, Paridaens, Lambert and Van de Walle13] presented an algorithm that is based on analyzing the amount of data in bits. Their algorithm performs moving object detection on H.264/AVC video streams by evaluating the data size that has been required to represent a single macroblock within the stream. Thereto, they determine the maximum size of background macroblocks in an initial training phase. Each macroblock whose size exceeds this determined size is regarded as a foreground block. A post-processing step further checks the remaining background blocks and decides whether they should however be labeled foreground. In a final step, the robustness of the foreground labels is double-checked with the aid of macroblocks of the two directly neighboring frames.
While Poppe et al. are modeling the background by taking the data size, Vacavant et al. [Reference Vacavant, Robinault, Miguet, Poppe and Van de Walle14] applied and evaluated several common background modeling techniques. They reported that background modeling by using Gaussian Mixture Models (GMM) achieves the highest detection rates. Beside the background modeling process they perform the same spatial and temporal filtering steps as described by Poppe et al. in [Reference Poppe, De Bruyne, Paridaens, Lambert and Van de Walle13].
In [Reference Verstockt, De Bruyne, Poppe, Lambert and Van de Walle15], Verstockt et al. introduced a moving object detection algorithm suitable for multi-view camera scenarios. Their compressed domain algorithm is able to locate moving objects on a ground plane by evaluating the video content of several cameras that are capturing the same scene. However, this method is still comparable with other algorithms since the first step is to detect the objects in each view separately. Thereto, they extract and analyze the partition sizes of macroblocks. This results in binary images that indicate the fore- and background of each frame. Further spatial and temporal filtering processes, applied on foreground macroblocks, then consider neighboring blocks and frames, respectively, to make this segmentation more robust.
Another method for detecting objects in the compressed domain is to find their edges and boundaries. Tom and Babu [Reference Tom and Babu16] described a method that evaluates the gradients of the QPs on macroblock level. All macroblocks whose QP exceeds a threshold are regarded as containing object edges. Temporal accumulation of the results of several frames then permits to label boundary and internal macroblocks as such. The boundaries are further processed on sub-macroblock level to increase their accuracy. Thereto, blocks within the boundaries are analyzed with respect to their sizes in bits. Once the boundaries are determined, the regions that contain moving objects are extracted.
Sabirin and Kim introduced a method that evaluates the motion data created by an H.264/AVC encoder, or rather the motion vectors, and the residual data to detect and track moving objects in [Reference Sabirin and Kim17]. They assume that it is likely that moving objects either have non-zero motion vectors and/or non-zero residuals. Hence, they select all 4×4 blocks fulfilling this assumption and construct graphs out of them, in which the blocks are the nodes and the neighborhood relations are the edges. One graph is created per frame and the moving object candidates form the sub-graphs within the global graph. These spatial graphs are then used to construct spatiotemporal graphs that describe the graph relations of five consecutive frames. By further processing the spatiotemporal graphs they identify and even track – by matching sub-graphs of consecutive frames – moving objects. Although the authors present good detection results, the method appears relatively complex because of several graph-based processing steps. They state that half of the processing time is required to construct the graphs, which obviously even further increases with the number of moving objects. Due to the fact that the motion vectors do not always represent real motion, a graph pruning process to eliminate false detections is required, which also increases the complexity and hence the processing time.
We previously worked on compressed domain moving object detection as well. In [Reference Laumer, Amon, Hutter and Kaup18], we presented a frame-based algorithm that analyzes slice and macroblock types for determining the fore- and background of a single frame. Thereto, we extract all macroblock types of all slices of a frame and group similar types to several categories. These categories thereby roughly indicate the assumed probability of the corresponding macroblocks contain moving objects, which is expressed by a certain weight assigned to each category. The actual algorithm processes each macroblock by considering the weight of the current macroblock itself and of its 24 neighbors. As a result, we get one map per frame that indicates the probability for moving objects on macroblock level. After applying a threshold to these maps and an optional box filtering process, we obtain binary images that show the fore- and background.
As already mentioned, compressed domain analysis algorithms are usually intended for being used as pre-processing step to make a pre-selection for subsequent algorithms. Therefore, we presented a person detection framework [Reference Wojaczek, Laumer, Amon, Hutter and Kaup19] whose initial step is the just described algorithm. The binary images are used to initialize search regions for the Implicit Shape Model (ISM), which detects objects in the pixel domain for which it was previously trained offline. Concatenating these two algorithms permits a significant reduction in processing time without decreasing the detection rates, because of the ISM is not required to search within the whole frame but only in the pre-selected region.
An algorithm that also combines pixel and compressed domain analysis has been published by Käs et al. in [Reference Käs, Brulin, Nicolas and Maillet20]. It is intended for being used in traffic surveillance scenarios, in which mainly two opposing directions for moving objects are present: the two driving directions of roads. Their algorithm uses an additional compressed domain analysis to aid the pixel domain processing steps, which enables a significant reduction of the complexity. In an initial training phase, the algorithm performs compressed domain and pixel domain analysis at the same time. Thereby, each I frame is analyzed in the pixel domain by a GMM algorithm, which results in a background model that is further updated by analyzing each incoming I frame. Within the compressed domain training part, the motion vectors of P and/or B frames are analyzed to determine the main directions of the vehicles. Furthermore, the resulting motion vector field is used to perform Global Motion Estimation (GME), which enables to detect camera motion due to pans or zooms. The GME process is also used to roughly detect moving objects after the training phase, since the outliers of the GME usually indicate moving objects. But, during the detection phase, mainly I frames are analyzed in the pixel domain to identify moving vehicles by considering the generated background model. The compressed domain results from the GME process are used to track the vehicles in P and B frames, i.e., between two I frames.
In [Reference Laumer, Amon, Hutter and Kaup21], we recently presented some enhancements for our frame-based object detection algorithm. All the above described methods have in common that they either do not consider temporal dependencies of consecutive frames or only in a post-processing step after the actual segmentation. The enhanced algorithm in [Reference Laumer, Amon, Hutter and Kaup21] overcomes this early decision problem, in which precious information is lost prematurely, by moving the decision process whether a block belongs to the fore- or background to the very end of the processing chain. Similar to its frame-based counterpart, the first step of this algorithm is to categorize blocks with similar properties. Thereby, the macroblock types, the macroblock partition modes, the sub-macroblock types, and the sub-macroblock partition modes that are available in the H.264/AVC Baseline profile (BP) are evaluated and get assigned weights that indicate the probability of containing moving objects. A general rule is the smaller the partitions the higher is this probability and thus the weight. The next steps perform spatial and temporal processing of neighboring blocks. Since the method described in this paper is based on the algorithm presented in [Reference Laumer, Amon, Hutter and Kaup21], the detailed description of the spatial and temporal weighting processes is given in Section IV.C. The final step in which the adaptive threshold is applied is explained in Section IV.D.
In addition to the algorithm in [Reference Laumer, Amon, Hutter and Kaup21] in this paper we present a single-step mode that calculates the final weights directly by considering three dimensions, an extension that enables processing of H.264/AVC streams that have been compressed according to the High profile (HP), and experimental results for an extended test set.
III. STRUCTURE AND SYNTAX OF H.264/AVC
The international standard H.264/AVC [1,2] describes the syntax and its semantics and the decoding process of a video compression scheme. It has been jointly developed by the Moving Picture Experts Group (MPEG), which is subordinated to the International Organization for Standardization/International Electrotechnical Commission (ISO/IEC), and the Video Coding Experts Group (VCEG), which belongs to the standardization sector of the International Telecommunication Union (ITU-T). The first version of H.264/AVC has been published in 2003 and although its successor standard High Efficiency Video Coding (HEVC) [22,23] has been completed in 2013, H.264/AVC is still maintained, extended and also widely used in many applications. This section gives a brief overview of the structures and syntax of H.264/AVC, mainly of the syntax elements that are analyzed in our algorithm. A complete description can be found in the standardization documents [1,2] or in the overview paper from Wiegand et al. [Reference Wiegand, Sullivan, Bjøntegaard and Luthra24].
A) Partitioning into blocks
H.264/AVC belongs to the category of block-based hybrid video compression schemes. That means that a coded picture, as it is called in the standard, is not encoded in a whole but split into smaller structures that are then encoded separately. Please note that since we do not consider interlacing, we will use the terms coded picture and frame interchangeably. The structures defined by the standard are illustrated in Fig. 2.
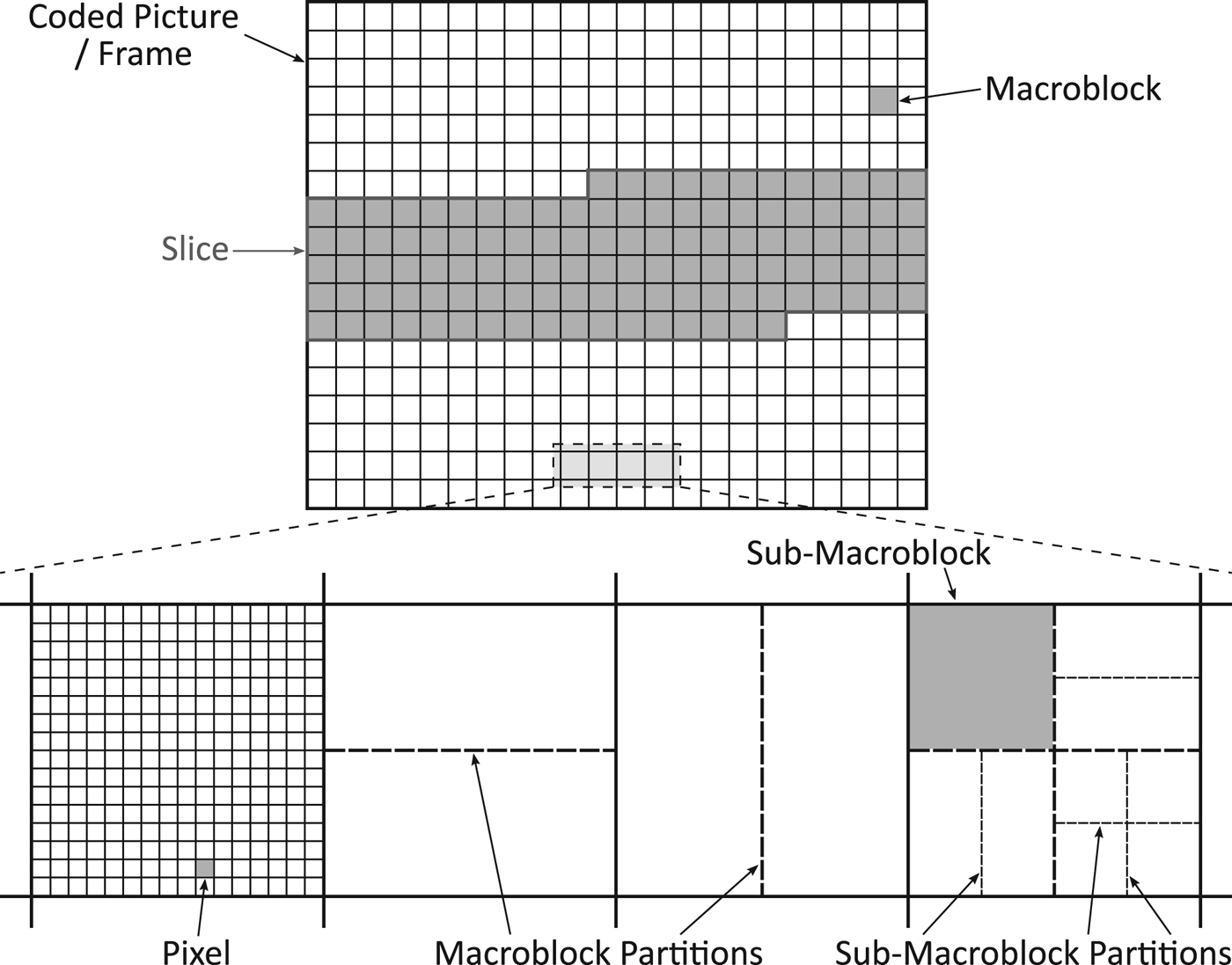
Fig. 2. Structures defined by the H.264/AVC standard. A frame consists of disjoint macroblocks that have a size of 16×16 pixels. Several macroblocks can be grouped to disjoint slices. A macroblock can be divided into four sub-macroblocks with a size of 8×8 pixels. Macroblocks and sub-macroblocks can be partitioned into rectangles or squares for motion compensation.
Each frame of a video sequence is divided into so-called macroblocks that have a size of 16×16 pixels. Thereby, the macroblocks are disjoint and arranged in a grid, as can be seen in the upper part of Fig. 2. Furthermore, H.264/AVC defines so-called slices, which are formed by grouping several macroblocks. Slices are also disjoint, i.e., a certain macroblock only belongs to exactly one slice. In the example in Fig. 2, the three slices consist of macroblocks that are connected.
The lower part of Fig. 2 shows how macroblocks are divided into sub-macroblocks and how the blocks can be partitioned for motion compensation, which is used for inter-frame prediction. A macroblock can either not be further divided or be partitioned into two 16×8 blocks, two 8×16 blocks, or four 8×8 blocks. In the case partitioning to 8×8 blocks is selected, these smaller blocks are called sub-macroblocks, which can then also be further partitioned according to the same patterns defined for macroblocks. As a result, the smallest available blocks have a size of 4×4 pixels.
Each macroblock gets assigned a macroblock type that corresponds to the selected partitioning mode. This type is directly extractable from a compressed bit stream, the corresponding syntax element is called mb_type. In the case a macroblock is split into sub-macroblocks, additional syntax elements are added to the bit stream. The element sub_mb_type represents the sub-macroblock type and indicates, similar to mb_type, how this block has been partitioned and predicted.
B) Intra- and inter-frame prediction
As already mentioned, blocks are predicted and only the residual is encoded. There are several methods and modes for the prediction process and not all modes are permitted at any constellation. Similar to mb_type and sub_mb_type, such a type element also exists for slices. The syntax element slice_type defines which macroblock types are permitted within the current slice. Please note that SI and SP slices are not considered here, because they are very rarely used in practice.
If slice_type indicates a so-called I slice, only intra-frame predicted macroblocks, or rather I macroblocks, are allowed. I macroblocks are thereby either directly predicted or split into 4×4 blocks for predicting these partitions separately. The two slice types P and B indicate that inter-frame predicted, or rather P and B macroblocks, are also permitted, in addition to the aforementioned I macroblocks. Furthermore, these slice types permit the encoder to split macroblocks into sub-macroblocks. So, it is possible that a P macroblock has up to 16 motion vectors, in the case all sub-macroblocks have been partitioned into 4×4 blocks. The concept for B macroblocks is similar to that for P macroblocks. The only difference is that these blocks are bidirectionally predicted. Bidirectional prediction further allows another 16 motion vectors per macroblock. Hence, B macroblocks may have up to 32 motion vectors.
The created motion vectors for inter-frame predicted blocks have to be transmitted to the decoder, together with the corresponding frame indices. The frame indices for each block are directly available within the bit stream. Depending on the used list of reference frames, which are called list 0 and list 1, the related syntax elements are ref_idx_l0 and ref_idx_l1, respectively. The motion vectors are not directly included in the bit stream, they are also predicted first. Thereby, the predictor creation is based on already determined neighboring motion vectors. The difference between the actual motion vector and the predictor is then included in the bit stream. The corresponding syntax elements are mvd_l0 and mvd_l1, depending on the used list of reference frames.
C) Transform and quantization
The residuals resulting from intra- or inter-frame prediction are not transferred directly but further processed first. Initially, the residuals are transformed to the frequency domain by a separable integer transform, which has been designed with similar properties as the well-known Discrete Cosine Transform (DCT). The following, important step is the quantization of the transform coefficients. Thereby, a linear quantizer is applied that is controlled by a so-called QP. It can take values from 0 to 51, at which an increasing value yields to increasing quantization step sizes, i.e., a stronger quantization.
The transform and hence the quantization is applied to 4×4 blocks, but the QP is not necessarily the same for all blocks. H.264/AVC defines some metadata structures that are valid for several components. For instance, the Picture Parameter Set (PPS) sets common parameters for several frames. One of these parameters is the initial QP value, which is indicated by the syntax element pic_init_qp_minus26. This QP value is used to quantize all blocks, unless further adaptation is signaled in the bit stream.
For adapting the initial QP value, H.264/AVC defines two additional syntax elements. The first element is slice_qp_delta, which is included in every slice header. If this element is unequal to 0, at this stage, the adapted QP value is valid for all blocks within this slice. However, the finally used QP value can be further changed on macroblock level. The syntax element mb_qp_delta, if included in the bit stream, is used to change the QP value for all blocks within this macroblock.
IV. MOVING OBJECT DETECTION
A) Coordinates and vectors
Before we describe the actual algorithm and its modes, we need to define how to address certain blocks. Thereto, we first define a Cartesian coordinate system, whose point of origin lies at the upper left corner of the first frame of the sequence, in display order. To be more precise, the point of origin is equal to the coordinates of the first 4×4 block of the first frame, which also means that the basis for the system is in 4×4 block precision. Within one frame, blocks are first counted from left to right, and then the rows of blocks are counted from top to bottom.
To address a single block, we either use two-dimensional (2D) or three-dimensional (3D) vectors, depending on the mode in which the algorithm is operating. When using 3D vectors, they are defined by
where
![]() ${\open N}$
includes 0. Thereby, k indicates the current frame and hence the temporal direction. As already mentioned, k=0 means the first frame of a sequence in display order. The coordinates x
1 and x
2 indicate the block position within the image plane of frame k. For instance, vector (k, 0, 0) describes the position of the first 4×4 block in frame k.
${\open N}$
includes 0. Thereby, k indicates the current frame and hence the temporal direction. As already mentioned, k=0 means the first frame of a sequence in display order. The coordinates x
1 and x
2 indicate the block position within the image plane of frame k. For instance, vector (k, 0, 0) describes the position of the first 4×4 block in frame k.
The 2D case defines similar vectors for the image planes. The difference is that the first coordinate k is separated from the vector and used beside it. Hence, the frames are still addressed with k but the vector x is now defined by a 2D vector as
Beside the vectors
![]() ${\bf x}^{\rm 2D}$
and
${\bf x}^{\rm 2D}$
and
![]() ${\bf x}^{\rm 3D}$
, which indicate absolute positions, we need to define displacement vectors. They are basically defined analogously, but their coordinates can take negative values as well. As a consequence, displacement vectors are defined by
${\bf x}^{\rm 3D}$
, which indicate absolute positions, we need to define displacement vectors. They are basically defined analogously, but their coordinates can take negative values as well. As a consequence, displacement vectors are defined by
and
Furthermore, arithmetic operations on displacement vectors are required to establish the algorithm. Thereto, the 2D and 3D Euclidean norms are defined as usual by
and
respectively.
B) Initial block weighting
The first step in our moving object detection algorithm is assigning a specific weight to each 4×4 block of an incoming frame. These weights reflect the assumed probability of motion within such a block. For determining the weight that should be assigned to a certain block, we analyze the type of the macroblock to which this block belongs to and the used partition mode in case of a P or B macroblock. The reason for this procedure is that the encoder already had to analyze the actual image content to be able to select the most efficient block types and modes. Hence, it is possible to estimate the amount of motion within a block when evaluating the corresponding macroblock type and partition mode.
Since H.264/AVC defines 32 different macroblock types and additionally four sub-macroblock types for the BP and even 58 macroblock and 17 sub-macroblock types for the HP, we group similar types in certain categories at first. Thereby, the categories differ in prediction modes and partition sizes of the contained blocks. An overview of the defined categories is given in Table 1. This table also states the defined initial weights w init for each category. They have been chosen to express the assumed probability of motion for the specific category. In general, the weight increases with the assumed probability of motion.
Table 1. Categories and initial weights w init defined according to block types and partition modes of H.264/AVC. All weights depend on a base weight w base.

All weights depend on a base weight w base, which defines the weight for the categories with lowest assumed motion. Those are the categories P_SKIP and B_SKIP, i.e., P or B macroblocks that have assigned the special macroblock type SKIP. SKIP mode means that beside the indication for the mode no further information is transmitted for such an inter-frame predicted block, i.e., no residual, no motion vector, and no reference frame index. Instead, the predictor of the block is directly used to reconstruct its content.
Furthermore, the assumption for inter-frame predicted macroblocks is that the finer the partitioning is the higher should be the assumed probability of motion. Hence, the weight for not further divided macroblocks (16×16) is two times the base weight, up to six times the base weight for 4×4 blocks, as can be seen in Table 1. Blocks within intra-frame predicted macroblocks, which are indicated by I_ALL in Table 1, get always assigned the maximum weight of six times the base weight. The reason is that the encoder usually only selects I macroblocks when the block could not predicted with less costly modes, which is valid for blocks containing content that has no counterpart in neighboring frames. This means that this content usually appears the first time in the scene or that an occluded region is visible again. In both cases, this region is to be considered as moving.
It is obvious that this categorization is only valid for P and B slices, since I slices only consist of I macroblocks. Hence, our algorithm just processes inter-frame predicted slices and I slices or frames are interpolated from the results of neighboring frames.
After performing the initial block weighting for a frame, we obtain a map that roughly indicates the probability of containing moving objects for each 4×4 block. Since these maps do not yet enable the extraction of clearly separable regions with moving objects, further processing is required. Hence, the initial weight maps are the input for the algorithm described in the next section.
C) Spatial, temporal, and spatiotemporal weighting
The main part of our algorithm is another weighting step that processes the initial weight maps that have been created as described in the previous section. Thereby, the algorithm is able to operate in two different modes, which can be selected by the user.
In the first mode, a predefined number of frames, including the current frame, is processed in three dimensions in a single step. Thereto, the 3D vectors described in the previous section are used to address single 4×4 blocks. Since neighboring blocks in the spatial and temporal direction are analyzed at the same time, this method can be seen as a spatiotemporal weighting process.
The second mode separates the temporal weighting from the spatial weighting. That means that in a first step incoming frames are spatially processed by weighting the initial weights of the blocks, which are addressed by using the 2D vectors introduced in the previous section. The results of a selected set of frames are then temporally processed by another weighting operation. The benefit of this separation is that a couple of calculations can be omitted and that yields to a significant gain in processing speed.
The two modes are described in detail in the following subsections.
Single-step mode
The single-step mode of our algorithm analyzes several 4×4 blocks of several frames in one equation. To calculate the final weight of a block that indicates the probability of motion within this block, we analyze the initial weights of a certain number of neighboring blocks within the same frame and the same number of blocks in neighboring frames. So, the final weight
![]() $w({\bf x}^{\rm 3D})$
of a block at position
$w({\bf x}^{\rm 3D})$
of a block at position
![]() ${\bf x}^{\rm 3D}$
is calculated by
${\bf x}^{\rm 3D}$
is calculated by
 $$\eqalign{w \lpar {\bf x}^{\rm 3D} \rpar = w_{{\rm init}} \lpar {\bf x}^{\rm 3D} \rpar + {1 \over d_1} \cdot \sum_{{\bf y}^{\rm 3D} \in M^{\rm 3D}} {w_{{\rm init}}\lpar {\bf x}^{\rm 3D} + {\bf y}^{\rm 3D}\rpar \over \Vert {\bf y}^{\rm 3D}\Vert },}$$
$$\eqalign{w \lpar {\bf x}^{\rm 3D} \rpar = w_{{\rm init}} \lpar {\bf x}^{\rm 3D} \rpar + {1 \over d_1} \cdot \sum_{{\bf y}^{\rm 3D} \in M^{\rm 3D}} {w_{{\rm init}}\lpar {\bf x}^{\rm 3D} + {\bf y}^{\rm 3D}\rpar \over \Vert {\bf y}^{\rm 3D}\Vert },}$$
where d 1>0 is a positive constant and set M 3D is defined by
where a, b>0 and
![]() $n_{\rm p}, n_{{\rm s}}\in {\open N}$
are constant values.
$n_{\rm p}, n_{{\rm s}}\in {\open N}$
are constant values.
The first summand in (1) represents the initial weight of the current block itself, which hence directly influences the final weight. The second term in (1) is a sum of initial weights of spatially and temporally neighboring blocks that are again weighted with their Euclidean distance to the current block. The influence of this distance can additionally be adapted by parameter d 1. In general, it is essential that the smaller the distance of the neighboring block to the current block is, the higher is the influence of its initial weight.
The number and positions of the blocks that are considered during the calculation are defined by the set M
3D. Since the current block itself is already considered by the first term in (1), the displacement vector
![]() ${\bf y}^{\rm 3D}$
may not be equal to (0, 0, 0), as indicated by (2). The constant values n
p and n
s in (3) stand for the number of considered preceding and subsequent frames to the current frame, respectively. That means that only blocks whose position's first coordinate j lies within the range of indicated frames are considered. Thereby, j ≡ 0 is valid and indicates the frame the current block belongs to.
${\bf y}^{\rm 3D}$
may not be equal to (0, 0, 0), as indicated by (2). The constant values n
p and n
s in (3) stand for the number of considered preceding and subsequent frames to the current frame, respectively. That means that only blocks whose position's first coordinate j lies within the range of indicated frames are considered. Thereby, j ≡ 0 is valid and indicates the frame the current block belongs to.
The last condition for set M 3D in (4) defines a region surrounding the current block. According to this definition, the region is 2D with an elliptic shape, whose size is given by the constant values a and b. The center of this ellipse is the current block and all neighboring blocks whose center point lies within this ellipse are considered during the calculation. This is not only valid for the current frame but for all neighboring frames as well. For those, the ellipse is virtually moved to the co-located position within the neighboring frame, i.e., the center point of the ellipse lies on the block with the same Cartesian coordinates x 1 and x 2 as for the current block.
Geometrically interpreted the whole region across all considered frames looks like a hose with elliptic profile. This is illustrated in Fig. 3. The current block at a position (k, x 1, x 2) for which the final weight should be calculated is marked in dark gray. In this example, n p=1 and n s=1, so that three frames are evaluated in total: k−1, k, and k+1. The blocks marked in light gray result from the size and shape of the ellipse, whose semi-axes have been set to a=3.5 and b=2.5 in this example. The ellipse is virtually displaced from frame k to the neighboring frames to determine the blocks to be considered. During the actual calculation all initial weights w init of considered blocks, which are indicated by the numbers in Fig. 3, are weighted by their Euclidean distance to the current block.

Fig. 3. Illustration of the weighting process. The current block is marked in dark gray and all blocks considered during the calculation are marked in light gray. Numbers within blocks indicate initial weights w init. Constant values: n p=n s=1, a=3.5, b=2.5, and w base=1.
Two-step mode
The two-step mode is actually very similar to the single-step mode. The only but important difference is that the initial weights are not weighted according to their Euclidean distance in a 3D space but the weighting process takes place in two separate steps. The first step is to calculate an intermediate sum of initial weights for all considered blocks in each involved frame. The considered blocks are thereby all blocks within the defined ellipse, which is still virtually displaced to neighboring frames, but now the sums are determined for each frame separately. This means for the example in Fig. 3 that the three ellipse are individually processed at first.
This sum of initial weights
![]() $w_{\rm sum} \lpar k, {\bf x}^{\rm 2D} \rpar $
of a block at position
$w_{\rm sum} \lpar k, {\bf x}^{\rm 2D} \rpar $
of a block at position
![]() ${\bf x}^{\rm 2D}$
within frame k is mathematically defined by
${\bf x}^{\rm 2D}$
within frame k is mathematically defined by
 $$\eqalign{w_{\rm sum} \lpar k, {\bf x}^{\rm 2D} \rpar &= w_{\rm init} \lpar k, {\bf x}^{\rm 2D} \rpar \cr &\quad + {1 \over d_1} \cdot \sum_{{\bf y}^{\rm 2D} \in M^{\rm 2D}} {w_{\rm init} \lpar k, {\bf x}^{\rm 2D} + {\bf y}^{\rm 2D} \rpar \over \vert {\bf y}^{\rm 2D} \vert},}$$
$$\eqalign{w_{\rm sum} \lpar k, {\bf x}^{\rm 2D} \rpar &= w_{\rm init} \lpar k, {\bf x}^{\rm 2D} \rpar \cr &\quad + {1 \over d_1} \cdot \sum_{{\bf y}^{\rm 2D} \in M^{\rm 2D}} {w_{\rm init} \lpar k, {\bf x}^{\rm 2D} + {\bf y}^{\rm 2D} \rpar \over \vert {\bf y}^{\rm 2D} \vert},}$$
where d 1>0 is a positive constant. The set M 2D is defined by
where a>0 and b>0 are positive constants.
In the two-step mode, the initial weights are hence weighted with the 2D Euclidean distance from the corresponding block to the current block. Thereby, the influence of the distance can be adjusted by the parameter d 1. The set M 2D is defined analogously to set M 3D, though the conditions for the temporal direction have been removed.
The second step involves the temporal direction in the calculation. Thereto, the final weight
![]() $w(k,{\bf x}^{\rm 2D})$
of a block at position
$w(k,{\bf x}^{\rm 2D})$
of a block at position
![]() ${\bf x}^{\rm 2D}$
within frame k is calculated by
${\bf x}^{\rm 2D}$
within frame k is calculated by
 $$\eqalign{w \lpar k,{\bf x}^{\rm 2D} \rpar & = w_{\rm sum} \lpar k,{\bf x}^{\rm 2D} \rpar \cr &\quad + {1 \over d_2} \cdot \sum_{{j = - n_{\rm p}}\atop{j\neq 0}}^{n_{\rm s}} {w_{\rm sum} \lpar k + j, {\bf x}^{\rm 2D} \rpar \over \vert j \vert },}$$
$$\eqalign{w \lpar k,{\bf x}^{\rm 2D} \rpar & = w_{\rm sum} \lpar k,{\bf x}^{\rm 2D} \rpar \cr &\quad + {1 \over d_2} \cdot \sum_{{j = - n_{\rm p}}\atop{j\neq 0}}^{n_{\rm s}} {w_{\rm sum} \lpar k + j, {\bf x}^{\rm 2D} \rpar \over \vert j \vert },}$$
where d
2>0 and
![]() $n_{\rm p}, n_{\rm s} \in {\open N}$
are positive constants.
$n_{\rm p}, n_{\rm s} \in {\open N}$
are positive constants.
The number of neighboring frames is again given according to the parameters n p and n s. This time the sums of initial weights are summed up and thereby the value is weighted by the distance |j| between the corresponding frame and the current frame. The parameter d 2 can be used to adjust the influence of this distance.
The main benefit of the separation of the spatial and temporal weighting process is that several calculations can be omitted. For instance, the sums of initial weights are pre-calculated and can be reused. The single-step mode requires to calculate the weights for each Euclidean distance in each iteration separately. On the other hand, the distance of a block to the current block is determined less accurately than in single-step mode. These pros and cons will also be reflected in the results presented in Section V.
D) Post-processing and segmentation
After creating the final weight maps according to either the single-step or the two-step mode, we additionally apply a 2D discrete N×N Gaussian filter. Thereby, we adopt the filter from our previous work described in [Reference Laumer, Amon, Hutter and Kaup21]. The width N of this filter depends on the standard deviation σ>0 as follows:
where
![]() $\lceil \cdot \rceil$
indicates the ceiling function.
$\lceil \cdot \rceil$
indicates the ceiling function.
It is possible in some cases that there are high differences between the final weights of neighboring blocks and this could result in a patchy segmentation after the final thresholding process. The purpose of the filtering is to smoothen the maps before the actual segmentation.
The only hard decision within our algorithm is the final thresholding process to obtain the segmented binary images. A block at position
![]() ${\bf x}^{\rm 2D}$
within frame k is labeled foreground if the following equation becomes true, otherwise the block belongs to the background:
${\bf x}^{\rm 2D}$
within frame k is labeled foreground if the following equation becomes true, otherwise the block belongs to the background:
with
where c 1≥1 and c 2≥0 are constant values.
For the 3D case
![]() $w({\bf x}^{\rm 3D})$
is analogously defined by
$w({\bf x}^{\rm 3D})$
is analogously defined by
with
In both cases, the base threshold t base is defined by
Thereby, t base represents the minimum threshold valid for ellipses in which all blocks have initial weights of w base. This base threshold can be adjusted by the parameter c 1.
The second term in (11) and (13) depends on the QP of the corresponding block. In fact, QP Δ represents the delta between the slice QP and the QP of the corresponding block. That means in cases were the QP has been adjusted on macroblock level, the threshold for these blocks is adjusted, too. As a result of the final thresholding process, each frame is segmented to foreground and background with an accuracy of 4×4 pixels.
V. EXPERIMENTAL RESULTS
A) Performance measures
Before the results of the algorithm can be measured, it is necessary to define a meaningful measurement system. To be comparable and by the reason of using measures everyone is familiar with, the performance of our algorithm is measured by using precision, recall, F score, and receiver operating characteristic (ROC) curves. For the sake of convenience, the measures are briefly described in the following. A more detailed description and a good discussion of the relationship between precision and recall and ROC curves can be found in [Reference Davis and Goadrich25].
Precision and recall compare true positives (TP) with false positives (FP) or false negatives (FN), respectively. So, precision Pr is defined by
and recall Re is defined by
That roughly means for detecting an object that recall indicates how much of the object could be detected and that precision indicates how accurate this detection thereby was.
The F score is related or more precisely based on precision and recall. It has been introduced to get a single measure for the performance of an algorithm that can be compared easier. The general F score F β is defined by
where β>0 is a factor for weighting either recall higher than precision or vice versa. Since our compressed domain algorithm is intended for being used as a pre-processing step, high recall values are more important than a good precision. Therefore, we provide the F 2 score that weights recall higher than precision.
Finally, we use ROC curves for determining the optimum parameters. A ROC diagram plots the true positive rate (TPR) against the false positive rate (FPR) of a system at varying settings. The TPR is thereby equally defined as recall by
The FPR is defined by
where TN indicates true negatives.
How true/false positives/negatives are counted is a matter of definition. In our case, we simply count pixels by comparing them to manually labeled ground truth in pixel accuracy. This, however, is not advantageous for measuring the performance of our algorithm, since the resulting binary images are in 4×4 pixel accuracy. Comparing these results to ground truth in pixel accuracy will always show a lower precision than comparing them to ground truth that has 4×4 pixel accuracy as well. But to provide a fair comparison with other algorithms, all measures are always based on pixel accuracy in this work.
B) Test setup
We used two different datasets for our experimental tests. The first dataset is the Multi-camera Pedestrian Videos dataset, which has been created by the CVLAB from the EPFL [Reference Berclaz, Fleuret, Türetken and Fua26] and we therefore denote as CVLAB dataset. It contains different scenarios in which the scenes have been captured with several cameras. Since our algorithm is intended for being used in single-view scenarios, we created pixel-wise ground truth for six independent sequences from this dataset: campus4-c0, campus7-c1, laboratory4p-c0, laboratory6p-c1, terrace1-c0, and terrace2-c1. Thereby, the ground truth is available for every tenth frame of the first 1000 frames, respectively.
The second dataset is the Pedestrian Detection Dataset from changedetection.net [Reference Wang, Jodoin, Porikli, Konrad, Benezeth and Ishwar27], which we denote as CDNET dataset. It is a subset of their Dataset2014 dataset and contains ten different sequences: backdoor, busStation, copyMachine, cubicle, office, pedestrians, peopleInShade, PETS2006, skating, and sofa. They provide manually labeled pixel-wise ground truth for each sequence. However, they define temporal regions of interest (ROI) for the sequences, i.e., the ground truth is only available for a subset of frames, respectively. Furthermore, for sequence backdoor there is additionally defined a spatial ROI, i.e., only pedestrians inside of this ROI should be detected. The spatial and temporal ROI are also considered in our evaluation.
All test sequences have been encoded with FFmpeg 2.7.4 (libavcodec 56.41.100) [28] by using the included libx264 [29] library. Thereby, mainly default parameters have been used, except for the following parameters:
-
– Profile: Baseline (BP), High (HP)
-
– Level: 4.0
-
– Group of Pictures (GOP) size: 50
-
– Quantization Parameter (QP): 15, 20, 25, 30, 35
As a result, all 16 test sequences have been encoded with ten different configurations and therefore our test set contains 160 sequences.
C) Parameter optimization
As described in Section IV, our algorithm has several adjustable parameters. For finding optimized parameters for the given scenarios, we adopt the procedure described in our previous work in [Reference Laumer, Amon, Hutter and Kaup21]. There we used the c0 sequences from the CVLAB dataset and created 1944 test cases for each sequence. Only one parameter changed from test case to test case, which therefore covered all possible parameter combinations. The optimized parameters, as resulted from this analysis, have been the following:
![]() $w_{\rm base} = 1.0$
, d
1=1.0, d
2=1.0, a=2.5, b=2.5, n
p=2, n
s=2, σ=1.0, c
1=1.0, and c
2=1.0.
$w_{\rm base} = 1.0$
, d
1=1.0, d
2=1.0, a=2.5, b=2.5, n
p=2, n
s=2, σ=1.0, c
1=1.0, and c
2=1.0.
In this work, we repeat a part of this analysis. Thereby, we are changing the values of three parameters: σ∈{ off, 1.0, 2.0}, c 1∈ {1.0, 1.5, 2.0}, and c 2∈ {0.0, 1.0, 2.0}. All other parameters are fixed and set to the values mentioned above. As a difference to the previous procedure, we test all CVLAB sequences, including both profiles and all QP values, respectively. Furthermore, we test the single-step and the two-step modes. This results in 27 test cases for each sequence-profile-QP-mode combination and hence in 540 test cases for a single sequence.
Figure 4 shows ROC curves for some of the results of this analysis. Since each curve is composed of only 27 supporting points, they appear not very smooth. However, the figures show that our algorithm is able to achieve a high TPR while keeping the FPR low. The upper diagrams 4(a) and 4(b) show ROC curves of all CVLAB sequences tested with single-step and two-step mode, respectively. For the sake of clarity, only the results of the sequences encoded with QP=30 are shown. It can be seen that high TPR are achieved for all sequences. The only exception is sequence campus4-c0, in which several persons stop moving for several frames. Since these persons are then labeled as background, the TPR/recall drops for these frames. The lower diagrams 4(c) and 4(d) depict the results for sequence campus7-c1, including all encoder configurations. What stands out is that the algorithm basically works for every configuration, only low QP values let the FPR increase. This observation is discussed in the next subsection in detail.

Fig. 4. ROC curves of CVLAB test sequences. (BP: Baseline profile; HP: High profile; QP: quantization parameter). (a) CVLAB, single-step mode, QP 30. (b) CVLAB, two-step mode, QP 30. (c) campus7-c1, single-step mode. (d) campus7-c1, two-step mode.
The main result of this analysis is that the previously determined parameter values are already a good choice. Just the standard deviation of the Gaussian filter should be changed to σ=2.0 to obtain the optimum performance. For the sake of completeness, all possible parameter values are again depicted in Table 2. The finally selected parameter values are bold-faced.
Table 2. Adjustable parameters and their possible values. Finally selected values are bold-faced. Source: [Reference Laumer, Amon, Hutter and Kaup21].

D) Results and discussion
Overview
For the determination of the detection performance of our algorithm, we rely on the measures precision, recall, and F 2 score, as already mentioned above. Figures 5 and 6 show all three measures against the respective QP of the current configuration, for CVLAB and CDNET sequences, respectively. Furthermore, Tables 3 and 4 summarize the results for sequences encoded with QP=30, as an example.

Fig. 5. Precision, recall, and F 2 score against QP for CVLAB test sequences. (BP: Baseline profile; HP: High profile; QP: quantization parameter). (a) Precision, single-step mode. (b) Precision, two-step mode. (c) Recall, single-step mode. (d) Recall, two-step mode. (e) F 2 score, single-step mode. (f) F 2 score, two-step mode.

Fig. 6. Precision, recall, and F 2 score against QP for CDNET test sequences. (BP: Baseline profile; HP: High profile; QP: quantization parameter). (a) Precision, single-step mode. (b) Precision, two-step mode. (c) Recall, single-step mode. (d) Recall, two-step mode. (e) F 2 score, single-step mode. (f) F 2 score, two-step mode.
Table 3. Summary of detection results for CVLAB test sequences encoded with QP=30. Shown are the results of our algorithm in single- and two-step modes, respectively, and the results of the OpenCV [Reference Bradski30] algorithms MOG and MOG2. The first column also indicates the frame size and the number of frames of the respective sequence.

BP, Baseline profile; HP, High profile; Pr, precision; Re, recall; F 2, F 2 score; FPS, frames per second.
Table 4. Summary of detection results for CDNET test sequences encoded with QP=30. Shown are the results of our algorithm in single- and two-step modes, respectively, and the results of the OpenCV [Reference Bradski30] algorithms MOG and MOG2. The first column also indicates the frame size and the number of frames of the respective sequence.

BP, baseline profile; HP, High profile; Pr, precision; Re, recall; F 2, F 2 score; FPS, frames per second.
The tables additionally provide the results of two pixel-domain object detection algorithms for comparison. Implementations of these two algorithms have been made publicly available by OpenCV 2.4.11 [Reference Bradski30] and are therefore used for comparing our algorithm with the state of the art. Both OpenCV algorithms apply background subtraction methods and rely thereby on modeling the background by using a technique that is called Mixture of Gaussians (MOG). The methods have been proposed by KaewTraKulPong and Bowden [Reference KaewTraKulPong and Bowden31] and by Zivkovic [Reference Zivkovic32] and are called MOG and MOG2 within OpenCV, respectively. We applied both in default configuration; however, the object shadows detected by MOG2 are labeled background in the binary output images.
Figures 5 and 6 again show that our algorithm is able to achieve a high recall. Furthermore, they depict that the performance is highly depending on the stream properties or, more precisely, on the selected QP. Low QP values cause the algorithm to label almost the whole frame as foreground, which indeed results in a recall near 1.0, but the precision drops to almost 0.0. The reason for this is that setting small QP values permits the encoder to spend a large number of bits for each encoded block. As a result, the encoder mainly selects macroblock types with small block partitions or even I macroblocks. Macroblocks in SKIP mode become very rare, which is crucial for our algorithm.
An increasing QP does not only mean an increasing quantization step size, but also that the encoder tries to select low-cost block types wherever applicable. As a consequence, the chosen block types and partition modes reveal more information about the content and therefore promote our algorithm. Having regard to the F 2 scores, Figs. 5 and 6 show that QP=30 seems to be a good choice with an appropriate trade-off between precision and recall.
Figures 5 and 6, and Tables 3 and 4 as well, additionally allow a comparison between the BP and the HP. For most sequences, using BP or HP does not make a huge difference. However, using the HP almost always achieves a slightly better performance. This effect increases for noisy sequences like laboratory4p-c0 and laboratory6p-c1. Table 3 shows that the precision could be increased from 0.36 to 0.57 or 0.24 to 0.45, respectively. This can be explained by the use of B macroblocks that are more suitable to represent temporal dependencies between frames.
Although using the single-step mode of our algorithm instead of the two-step mode slightly increases the precision as well, this effect is not significant. The reason for this increase is the weighting of, mainly the temporal, neighboring blocks. Since this weighting is performed in a single step and therefore more accurate than in its counterpart, the influence of neighboring blocks is also represented more precisely. The main difference between the single-step and the two-step mode is the processing speed, which is described in Section V.E.
CVLAB sequences
It is obvious that the algorithm's performance depends on the actual video content. Figure 5 shows that the results of some CVLAB sequences differ from the others. Although the precision increases with increasing QP, the advance in precision is less significant for sequences laboratory4p-c0 and laboratory6p-c1. These sequences are noisier than the others and this directly influences the precision negatively. Another example is sequence campus4-c0. The achieved recall for this sequence is significantly lower than for the other sequences. The reason for this is that our algorithm has some difficulties with objects that stop moving. In this case, it is likely that the encoder selects block types that are closer to those of background blocks. So, these blocks would be labeled background although they contain an object. In sequence campus4-c0 three persons are moving around and then one after the other stops, which results in dropping recall values for affected frames.
Figure 7 shows examples of the results of the tested algorithms for sequence campus7-c1. Both the single-step mode and the two-step mode are able to detect the moving person adequately. This results in a recall of 0.92 or even 0.95 for the whole sequence, if encoded with the HP, respectively. Furthermore, our algorithm is able to achieve a high precision by keeping FP low. They mainly only occur near the head or the feet of the person, which is clearly visible in Figs. 7(b) or 7(c), respectively. Hence, the achieved precision for this sequence is 0.74 in single-step mode and 0.71 in two-step mode.

Fig. 7. Sample segmentation of frame 135 of sequence campus7-c1, encoded with HP and QP=30. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Original. (b) Single-step mode. (c) Two-step mode. (d) MOG [31]. (e) MOG2 [32]
The MOG algorithm seems to have some problems with such sequences. While the precision is always close to or even 1.0, the algorithm is not able to achieve high recall values. This means not only that the background is very well detected, but also that several parts of the moving objects are labeled as background as well. This can be for instance seen in Fig. 7(d). Only a small region in the middle of the person is detected as foreground. One reason is that the background model could not be updated adequately or rather not accurately enough. The pants as well as the pullover of the person have similar color to the background in this image. Hence, the algorithm also labels those foreground parts as background.
The behavior of the MOG2 algorithm is more or less the other way round. Having regard to Fig. 7(e), the person is accurately detected, although there are some missing parts at the legs for the same reason, but the algorithm falsely detects several parts of the background as foreground. As a consequence, the precision drops, in this case only 0.19 could be achieved for the whole sequence.
CDNET sequences
The precision and recall values for CDNET sequences have a higher variance compared with those of CVLAB sequences, as can be seen in Fig. 6. The reason is that these sequences significantly differ in content, mainly in the size and speed of the moving objects. Furthermore, some sequences are more challenging because of difficult scenarios, like for instance standing/stopping or sitting persons (busStation, copyMachine, office, PETS2006, sofa) or abandoned baggage (PETS2006, sofa), which is labeled foreground in the ground truth but obviously not moving and therefore undetectable. Other challenging scenarios that are also included in this dataset are changing camera focus or brightness (copyMachine, peopleInShade), prominent shadows (pedestrians, peopleInShade), and bad weather conditions like snow (skating). Some of those challenging conditions are discussed in the subsequent section.
The sequence backdoor is a good example for sequences from the visual surveillance domain, for which our algorithm is intended for. The scene has a mainly static background and is crossed by moving objects, as can be seen in Fig. 8(a). Furthermore, a spatial ROI is defined, i.e., only the content inside of a certain region is important and everything outside of this region is ignored, which is also frequently used in visual surveillance scenarios. As can be seen in Fig. 6 and also in Table 4, the numerical results for sequence backdoor are very good.

Fig. 8. Sample segmentation of frame 1858 of sequence backdoor, encoded with HP and QP=30. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Original. (b) Single-step mode. (c) Two-step mode. (d) MOG [31]. (e) MOG2 [32].
Visual examples for this sequence for all tested segmentation algorithms are depicted in Fig. 8. Our algorithm is able to detect the persons almost completely, so the respective recall is 1.0 for the two-step mode and 0.99 for the single-step mode. Since FP only occur around the objects themselves, which is mainly because of the lower accuracy of 4×4 pixels or larger, the achieved precision is satisfying as well. When using the two-step mode, the precision is 0.65 and the single-step mode even reaches 0.71.
As before, it seems that MOG and MOG2 have some difficulties in updating their background model at this sequence. While in this example FP almost not occur when using MOG, several parts of the persons are not detected but falsely labeled background. For instance, the pullover of the woman on the right has a color close to the color of the wall in the background. The result is that the pattern of the fence becomes visible in the segmented image, because the pullover is easily distinguishable from the black fence but not from the lighter wall.
The recall achieved by MOG2 is much higher than by MOG, so the persons are detected well. The precision on the other hand is only 0.08 for sequence backdoor. A reason for this can be seen in Fig. 8(e), in which the lighter parts of the ground, i.e., regions without shadows, are falsely detected as foreground. This increases the FP and hence decreases the precision.
Challenging conditions
As already mentioned, the CDNET dataset contains several sequences with challenging conditions. Generally, the most analysis algorithms are challenged by a changing camera focus, automatically adapted brightness, fast moving objects, prominent object shadows, and bad weather conditions. Such scenarios are also included in the CDNET dataset.
Figure 9 shows three sample images from CDNET sequences with their corresponding segmentation of our algorithm in two-step mode. Thereby, Fig. 9(a) illustrates that prominent shadows will be detected by the algorithm as well. This is obvious because the shadows are moving in conjunction with the object itself and it is not possible to distinguish between the object and the shadow at this stage. The creators of the ground truth of the CDNET sequences hence also labeled prominent shadows as foreground in most of the sequences, as can be seen in the lower image of Fig. 9(a).

Fig. 9. Sample segmentation of some sequences with challenging conditions, encoded with HP and QP=30. The upper row shows the original frames, the lower row the results from our algorithm in two-step mode. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) peopleInShade, frame 296. (b) pedestrians, frame 474. (c) skating, frame 902.
This is different in Fig. 9(b). The shadow of the cyclist is indeed again detected but it is not labeled as foreground in the ground truth this time. Hence, this region (below the person on the right) is marked red in the lower image of Fig. 9(b). Another observation at this result image is that a relatively large region behind the cyclist in wrongly detected by the algorithm. This occurs when objects are moving very fast compared with the frame rate. In this case, the displacement of the object's position is significant between two consecutive frames. And this results in FP behind the object because of the temporal analysis of several frames.
Finally, a worst case scenario is depicted in Fig. 9(c). As can bee seen, the number of FP is very high in this case. The reason for this is the heavy snowfall in front of the camera. However, these false detections mainly only occur in regions in which the contrast between the white snow and the darker background is high. The lower parts of the persons are generally detected satisfactorily.
In addition to the challenging scenarios mentioned above, Fig. 10 shows a scenario with stopping objects, including an abandoned bag, which is also challenging for our algorithm, since it is intended to detect moving regions within a video sequence. The first segmentation result in Fig. 10(a) shows that all persons are detected as intended due to the fact that they are moving. In the next image in Fig. 10(b), the person in the center of the scene stopped moving, which results in only a partial detection. Some frames later (cf. Fig. 10(c)), the person drops its backpack, which is again detected because the person is moving by doing so. Figure 10(d) again shows that both, the person and the backpack, are not detected by the algorithm when none of them is moving. In this case, in which the persons stands still for several frames, it is obvious that the encoder selected the SKIP mode for encoding the corresponding macroblocks. Finally, it can be seen in Fig. 10(e) that the person is detected again when it starts moving again. Since the backpack is left behind, it is still not detectable.

Fig. 10. Sample segmentation of frames 411, 522, 902, 1050, and 1126 of sequence PETS2006, encoded with HP and QP=30. The upper row shows the original frames, the lower row the results from our algorithm in two-step mode. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Frame 411. (b) Frame 522. (c) Frame 902. (d) Frame 1050. (e) Frame 1126.
All those examples show, even in challenging scenarios, moving objects are detected as intended by our algorithm. In some scenarios, applying the method results in increased FP and hence a decreased precision on pixel level. But in terms of detecting objects, no object is missed, which is the most important task for compressed domain algorithms that are used to preselect certain regions for further analysis. An exception are stopping objects, which are not detectable anymore due to the characteristics of our algorithm. But since such objects will definitely have been detected in the moment they entered the scene, they can also be considered as not missed. Additional segmentation results can also be found in Figs. 11–14.

Fig. 11. Sample segmentation of frame 935 of sequence laboratory4p-c0, encoded with HP and QP=30. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Original. (b) Single-step mode. (c) Two-step mode. (d) MOG [31]. (e) MOG2 [32].

Fig. 12. Sample segmentation of frame 615 of sequence terrace1-c0, encoded with HP and QP=30. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Original. (b) Single-step mode. (c) Two-step mode. (d) MOG [31]. (e) MOG2 [32].

Fig. 13. Sample segmentation of frame 2463 of sequence cubicle, encoded with HP and QP=30. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Original, (b) Single-step mode (c) Two-step mode (d) MOG [31] (e) MOG2 [32].

Fig. 14. Sample segmentation of frame 1051 of sequence busStation, encoded with HP and QP=30. (Black pixels: TN, green pixels: TP, white pixels: FN, red pixels: FP). (a) Original. (b) Single-step mode. (c) Two-step mode. (d) MOG [31]. (e) MOG2 [32].
E) Processing speed
Compressed domain algorithms are known to be less complex than their pixel domain counterparts, mainly for two reasons. First, the costly step of decoding is replaced by simple syntax parsing operations and, second, the algorithms themselves are low-complex because they usually do not have to process all pixels. However, it is not always an easy task to directly compare different algorithms with regard to their processing speeds, especially in cases where these algorithms have been implemented supremely different.
In our implementation, we incorporated the reference implementation of the H.264/AVC standard, the JM software (JM-18.6) [33], for parsing the required syntax elements. Since the purpose of this software is not to be implemented highly optimized, it can be assumed that the decoder used by OpenCV, which is part of FFmpeg, performs much faster. Furthermore, our test implementation of the actual algorithm is also not optimized. So, in some cases, the software loops up to ten times over all 4×4 blocks of a single frame, including initializations and conversions between container formats. The OpenCV implementations, on the other hand, are usually highly optimized towards a low complexity.
Nevertheless, we measured the execution times of all tested algorithms, because we think it is important to provide this information. Tables 3 and 4 provide the processing speeds, in terms of frames per second, for the stated test sequences. Thereby, the time that has been required for parsing the syntax elements as well as the time for the actual algorithm has been measured for our algorithm. Correspondingly, the processing time for MOG and MOG2 includes the decoding and the analysis time. Furthermore, the given values are average values determined by executing each test ten times. The reason for averaging several results is that the processing speeds of MOG and MOG2 are highly fluctuating – the speed of our algorithm is almost not varying when performing the same test several times – and an average is more significant for the comparison. The tests have been performed on a relatively old desktop computer: Intel Core 2 Duo E8400 CPU @ 3.0 GHz, 8 GB DDR2 RAM, Windows 10 Pro 64-Bit. Because of the dual-core architecture, two tests have been performed in parallel.
It can be seen that the algorithm in two-step mode operates much faster than in single-step mode. For instance, the two-step mode is able to analyze about 133 frames per second in average for CVLAB sequences, while the single-step mode only achieves about 40. The reasons for this are the omitted calculations in two-step mode, as already explained in Section IV. Furthermore, it is obvious that the processing speed directly depends on the frame size, since a larger frame size means more blocks to be processed. So, for instance, only 37 frames of sequence PETS2006 could be processed per second.
Although the MOG algorithm is a pixel domain algorithm, it performs very fast. And because of the missing optimizations in our algorithm, it even operates faster than our compressed domain algorithm. The drawback is that our algorithm achieves better detection results for almost all our test sequences. Compared to the MOG2 algorithm, the proposed algorithm in two-step mode always runs just as fast or faster, even without optimizations.
As already mentioned, our algorithm uses the JM software [33] for the syntax parsing. Parsing the 1010 frames of a single CVLAB sequence that has been encoded with
![]() ${QP} = 30$
and the HP takes about 3 seconds. Performing our two-step analysis algorithm then takes another 5.2 seconds. This results in about 123 frames per second, as also stated in Table 3. So, above 36% of the overall processing time is required by the JM software to parse the syntax elements. This could be significantly decreased by incorporating a more efficient decoder, or rather parser. The implementation of the actual algorithm is also not optimized but is able to process 1010 frames of a CVLAB sequence in about 5.2 seconds, which results in about 194 frames per second. This could be increased as well by optimizing the test implementation. And even parallel processing is imaginable, for instance, the initial block weighting process for several frames could be performed in parallel, which would increase the processable number of frames even further.
${QP} = 30$
and the HP takes about 3 seconds. Performing our two-step analysis algorithm then takes another 5.2 seconds. This results in about 123 frames per second, as also stated in Table 3. So, above 36% of the overall processing time is required by the JM software to parse the syntax elements. This could be significantly decreased by incorporating a more efficient decoder, or rather parser. The implementation of the actual algorithm is also not optimized but is able to process 1010 frames of a CVLAB sequence in about 5.2 seconds, which results in about 194 frames per second. This could be increased as well by optimizing the test implementation. And even parallel processing is imaginable, for instance, the initial block weighting process for several frames could be performed in parallel, which would increase the processable number of frames even further.
VI. CONCLUSIONS
In this paper, we presented a moving object detection algorithm that operates in the compressed domain. It is based on the extraction and analysis of H.264/AVC syntax elements, mainly the macroblock and sub-macroblock types. Each type gets assigned a specific weight and a proper combination of the weights indicates regions within a video frame in which moving objects are present. The introduced algorithm has been developed for H.264/AVC but may generally be applied to any video stream that has been compressed according to a block-based hybrid video coding scheme using inter-frame prediction. The basis of the method is to exploit the results of the inter-frame prediction process and hence the algorithm is not applicable to streams that have been compressed with still image coding schemes or codecs configured to apply intra-frame prediction only.
The presented algorithm is able to work in two different modes, a single-step mode and a two-step mode. The single-step mode analyzes several frames and weights neighboring blocks by using a 3D space. The two-step mode also exploits temporal dependencies between frames but analyzes each frame separately in an initial step. In order to avoid losing precious information at a premature state, both modes avoid early thresholding operations by shifting the only binary decision to the very end. Experimental results could demonstrate that the method is able to reliably detect regions with moving objects in case of using reasonable configurations for the intended target domain. Thereby, the single-step mode achieves a slightly better detection performance than the two-step mode. However, a drawback of the spatiotemporal analysis of the single-step mode is that it significantly runs slower than the two-step mode, which separates the spatial from the temporal analysis step. As a consequence, it appears that the two-step mode should be preferred in most cases. It provides higher recall values than its single-step counterpart and performs significantly faster. Only when an increased precision is a requirement and/or the processing speed is less important, the single-step mode should be taken into consideration. However, since compressed domain analysis algorithms are usually intended for being used for taking a fast decision whether additional analysis steps should be triggered, such scenarios should not occur frequently.
Currently, we focus on additionally analyzing motion vectors to increase the precision. Furthermore, we will work on a method that is able to detect stopping objects as well. We are currently also extending the concept to be able to process video streams that have been encoded according to the HEVC standard. Finally, we will try to optimize our implementation in terms of processing speed.
Marcus Laumer received his diploma (Dipl.-Ing.) degree in Information and Communication Technology from the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Germany, in 2009, where he specialized in transmission technology and mobile communication. Since 2009 he has been working toward the Dr.-Ing. degree at the Chair of Multimedia Communications and Signal Processing at FAU. His research includes compressed domain video analysis and future Internet technologies and is supported by Siemens Corporate Technology, Munich, Germany. In these areas, he published several papers and was actively involved in the European research project FIWARE.
Peter Amon received his diploma (Dipl.-Ing.) degree in Electrical Engineering from Friedrich-Alexander- Universität Erlangen-Nürnberg (FAU), Germany, in 2001, where he specialized in communications and signal processing. In 2001, he joined Siemens Corporate Technology, Munich, Germany, where he is currently working as a Senior Research Scientist in the Sensing and Industrial Imaging Department. His research interests include video coding and transmission, image/video processing and analytics, and future Internet technologies. In these areas, he published several conference and journal papers. Since 2003, he actively contributes to the standardization at ISO/IEC MPEG, where he worked on scalable video coding and the respective storage format as well as High Efficiency Video Coding (HEVC). He has been actively involved (e.g., as work package leader) in several European research projects. He also serves as reviewer and member of the technical program committee for several conferences and journals in his field.
Andreas Hutter (M’95) received his diploma and Dr.-Ing. degrees in Communications Engineering from the Technische Universität München (TUM) in 1993 and 1999, respectively. From 1993 to 1999 he worked as a research assistant at the Institute for Integrated Circuits at TUM where he researched on algorithms for video coding and on the implementation of multimedia systems for mobile terminals. He joined Siemens Corporate Technology, Munich, Germany, in 1999, where he is currently leading a research group in the Sensing and Industrial Imaging Department. He was an active member of MPEG from 1995 to 2006 where he contributed to the MPEG-4, the MPEG-7 and the MPEG-21 standards and acted as HoD (Head of Delegation) of the German National Body at MPEG. His research interests include image and video coding, transmission and visualization as well as video analytics.
André Kaup (M’96–SM’99–F’13) received the Dipl.-Ing. and Dr.-Ing. degrees in Electrical Engineering from Rheinisch-Westfälische Technische Hochschule (RWTH) Aachen University, Aachen, Germany, in 1989 and 1995, respectively. He was with the Institute for Communication Engineering, RWTH Aachen University, from 1989 to 1995. He joined the Networks and Multimedia Communications Department, Siemens Corporate Technology, Munich, Germany, in 1995 and became the Head of the Mobile Applications and Services Group in 1999. Since 2001 he has been a Full Professor and the Head of the Chair of Multimedia Communications and Signal Processing, University of Erlangen-Nuremberg, Erlangen, Germany. From 1997 to 2001 he was the Head of the German MPEG delegation. From 2005 to 2007 he was a Vice Speaker of the DFG Collaborative Research Center 603. Since 2015 he serves as Head of the Department of Electrical Engineering and Vice Dean of the Faculty of Engineering. He has authored more than 300 journal and conference papers and has over 50 patents granted and patent applications published. His research interests include image and video signal processing and coding, and multimedia communication.
Dr. Kaup is a member of the IEEE Multimedia Signal Processing Technical Committee, a member of the Scientific Advisory Board of the German VDE/ITG, and a Fellow of the IEEE. He serves as an Associate Editor for IEEE Transactions on Circuits and Systems for Video Technology and was a Guest Editor for IEEE Journal of selected Topics in Signal Processing. From 1998 to 2001 he served as an Adjunct Professor with the Technical University of Munich, Munich. He was a Siemens Inventor of the Year 1998 and received the 1999 ITG Award. He has received several best paper awards, including the Paul Dan Cristea Special Award from the International Conference on Systems, Signals, and Image Processing in 2013. His group won the Grand Video Compression Challenge at the Picture Coding Symposium 2013 and he received the teaching award of the Faculty of Engineering in 2015.




















