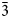Introduction
Lead–Bi-chalcogenides of the aleksite series, with the general chemical formula PbnBi4Te4Sn +2 (Cook et al., Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a, Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019; Yao et al., Reference Yao, Ciobanu, Cook and Ehrig2023) occur as accessory phases in several gold-bearing ore deposits. The aleksite series is a prime example of mixed layer compounds built by accretional homology principles. Series members are structurally derived from the same tetradymite archetype and are related to the tetradymite group of bismuth chalcogenides (Cook et al., Reference Cook, Ciobanu, Wagner and Stanley2007b; Ciobanu et al. Reference Ciobanu, Pring, Cook, Self, Jefferson, Dima and Melnikov2009, Reference Ciobanu, Slattery, Cook, Wade and Ehrig2021; Yao et al., Reference Yao, Ciobanu, Cook, Ehrig, Dima and Steinle-Neumann2024). The three named minerals in the series prior to the acceptance of clogauite are aleksite (PbBi2Te2S2; Lipovetskiy et al., Reference Lipovetskiy, Borodaev and Zav'yalov1979), saddlebackite (Pb2Bi2Te2S3; Clarke, Reference Clarke1997) and hitachiite (Pb5Bi2Te2S6; Kuribayashi et al., Reference Kuribayashi, Nagase, Nozaki, Ishibashi, Shimada, Shimizu and Momma2019) (Fig. 1a).

Figure 1. (a) Reflected light image of clogauite lamella on which all analytical data was collected. (b) Composition of previously named minerals in the aleksite series in terms of the ratios Pb/(Pb+Bi) vs. Te/(Te+S+Se). (c) EPMA data for clogauite plotted on a reduced portion of the same diagram including data from Cook et al., Reference Cook, Ciobanu, Wagner and Stanley2007b and Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019.
Clogauite, PbBi4Te4S3, is the fourth member of the series to be named and corresponds to ‘Phase C' of Lipovetskiy et al. (Reference Lipovetskiy, Borodaev and Zav'yalov1978). It also corresponds to ‘Phase D' synthesised experimentally at 500°C by Liu and Chang (Reference Liu and Chang1994). An unnamed phase with the same composition was previously reported by Bevins and Stanley (Reference Bevins and Stanley1990), Clarke (Reference Clarke1997) and Cook et al. (Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a), whereas Bonev and Neykov (Reference Bonev and Neykov1990) reported ‘lead tetradymite’, an analogous phase to clogauite of similar composition, with Pb-content between the compositions of tetradymite and aleksite. In all cases, clogauite co-exists with, or is observed in the same samples as aleksite.
Clogauite has been approved by the Commission on New Minerals, Nomenclature and Classification of the International Mineralogical Association (IMA2023–062 Cook et al., Reference Cook, Ciobanu, Yao, Stanley, Liu, Slattery and Wade2024). Preliminary optical and compositional characterisation of PbBi4Te4S3 was given by Cook et al. (Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a). Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019) presented results of a nanoscale study using high-angle annular dark-field scanning transmission electron microscope (HAADF STEM) imaging and STEM energy-dispersive X-ray spectrometry (EDS) analysis that confirmed the existence of three distinct polytypes: 57, 557.559 and 5559, after the arrangement of layer stacks. Each polytype has a total number of atoms in the layer stacks, 12, 24 and 36, which is divisible by three. Therefore, the trigonal space group $P\bar{3}m1$![]() was considered instead of $R\bar{3}m$
was considered instead of $R\bar{3}m$![]() , in agreement with the symmetry considerations of Imamov and Semiletov (Reference Imamov and Semiletov1971). The notation H (hexagonal) of Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990) was adopted for all polytypes.
, in agreement with the symmetry considerations of Imamov and Semiletov (Reference Imamov and Semiletov1971). The notation H (hexagonal) of Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990) was adopted for all polytypes.
Clogauite is named for the Clogau gold mine, Dolgellau Gold belt, Gwynedd, North Wales, United Kingdom (52°45'42''N, 3°58'5''W), where type material was found. The proposed abbreviation symbol for clogauite (Warr, Reference Warr2021) is Clg. The holotype is represented by specimen E.1309 from the collection of the Natural History Museum, United Kingdom, corresponding to Amgueddfa Cymru – National Museum Wales specimen number NMW 90.37 G.M1 and M2a and b (Bevins and Stanley, Reference Bevins and Stanley1990).
Occurrence
Clogauite type material is a specimen representative of high-grade gold veins in the Clogau deposit (Bevins and Stanley, Reference Bevins and Stanley1990). Background information on the locality is given by Dominy and Platten (Reference Dominy and Platten2012). The specimen contains lamellar intergrowths of clogauite, aleksite, galena, tellurobismuthite, and minor chalcopyrite, with traces of native gold. A complete description of the sample, including reflected light images and electron probe microanalytical data, is provided in Cook et al. (Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a) and Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). Back-scatter electron (BSE) imaging at high-magnification emphasises that many of the coarser lamellae in the specimen feature fine-scale, partially disordered intergrowths of multiple Pb–Bi-chalcogenides of both the aleksite series and tetradymite group (tellurobismuthite and tetradymite). Clogauite is defined from analysis of a single lamella, ~160 μm across, that appeared compositionally homogeneous on BSE images and electron microprobe element-distribution maps.
Optical and physical properties
Clogauite occurs as fine lamellae, exceptionally up to 160 μm in width. Colour (macroscopic), streak, lustre, hardness, cleavage, fracture and parting: could not be directly observed due to the size of the mineral. Streak can, however, be inferred from the black colour of the fine powder used for an X-ray diffraction (XRD) investigation by one of us (C.J.S.) early in the study. Lustre, hardness, and other physical properties can be expected to closely resemble those of tetradymite (e.g. metallic lustre). Calculated densities are 7.3724, 7.3738 and 7.3691 g/cm3 for clogauite-12H, -24H and -36H, respectively, based on the empirical formula. Density could not be measured because of insufficient material. Clogauite is non-magnetic and twinning is not observed.
Clogauite is opaque. Its colour in reflected light is pale grey, with reflectance higher than tetradymite and galena (Fig. 1a). Bireflectance and pleochroism are both distinct, anisotropy is strong. Internal reflections are not observed. Full reflectance data for the phase now named as clogauite were provided by Cook et al. (Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a). Reflectance values (%R 0, R e’, imR 0 and imR e’) at λ = 470 nm are: 52.7, 52.5, 38.8 and 36.8; 53.7, 51.6, 39.4 and 37.3 at 546 nm; 53.8, 51.7, 39.4 and 37.4 at 589 nm; and 53.75, 51.6, 39.2 and 37.2 at 650 nm.
Chemical composition
Quantitative mineral compositional data and electron probe microanalysis (EPMA) measurement conditions were given by Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). The mean composition based on measurement of 57 points is (in wt.%) Pb 12.56, Bi 49.45, Te 30.62, S 6.42, Se 0.12, total 99.18. The empirical formula is Pb0.98Bi3.84Te3.89(S3.26S0.02)3.28 based on a total of 12 atoms. This composition defines a small field on a plot of Pb/(Pb+Bi) vs. (Te+Se)/(Te+Se+S) (Fig. 1b, c). The simplified formula corresponds to the ideal formula PbBi4Te4S3, which requires (in wt.%) Pb 12.58, Bi 50.76, Te 30.99 and S 5.84, total 100.00. A confirmation of chemical homogeneity was afforded by EPMA element-distribution maps (Cook et al., Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). The combination of spot analysis and element distribution mapping served as a basis to identify suitable areas of the lamella to extract by focused ion beam (FIB)-scanning electron microscope methods for subsequent transmission electron microscope study.
Crystal structure
Work on synthetic PbBi4Te4S3 gave cell dimensions of a = 4.24 Å and c = 23.12 Å (Liu and Chang, Reference Liu and Chang1994). Unpublished X-ray diffraction data on PbBi4Te4S3 in Clogau material by one of us (C.J.S.) in the early 1990s (reported in Cook et al., Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a), gave cell dimensions of a = 4.25 Å and c = 69.71 Å. The discrepancy in c dimensions was later explained (Cook et al., Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019) through observation of distinct layer arrangements (polytypes) yet the same composition. The synthetic PbBi4Te4S3 of Liu and Chang corresponds to clogauite-12H, and the aforementioned earlier X-ray diffraction to clogauite-36H.
The co-existence of all three polytypes in the same holotype was confirmed by HAADF STEM imaging and STEM EDS mapping of the structures to show the internal arrangement of component atoms (Cook et al., Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). All HAADF STEM imaging and energy-dispersive X-ray spectrometry (EDS)-STEM mapping was performed using an ultra-high resolution, probe-corrected, FEI Titan Themis S/TEM housed at Adelaide Microscopy, The University of Adelaide, and operated at 200 kV. Further details of instrumentation are provided in Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). TIA and Velox software were used for image acquisition, including drift-corrected frame integration package (DCFI), and EDS data acquisition and processing. Various filters (Radial Wiener, High-pass, Average and Gaussian blur) were used to eliminate noise. Indexing of diffraction patterns was conducted with WinWulff© (JCrystalSoft) Crystal structure models were generated in CrystalMaker® and image simulations using STEM for xHREM TM software.
A foil extracted from chemically homogenous lamella in Fig. 1a shows the three distinct polytypes are intergrown with one another as distinct stacking sequences along the c axis, but with intervals of regular repeats of at least ~150 nm (Fig. 2a,b). In the example shown in Fig. 2, the polytype with the simplest (5.7) stack is the most common and occurs as repeats across distances as large as 350 nm. The polytype with the longest (557.559) stack is second most common, as repeats across ~100–200 nm. The third polytype, sequence 555.9, is the scarcest of the three. An interval of 41 stacks of the sequence 5.7 (simplest polytype) is shown on the images in Fig. 2c.

Figure 2. (a) Low-magnification view of entire thinned foil showing the distribution of the three polytypes as marked. (b) HAADF STEM images of clogauite showing a longer ~350 nm-long interval of polytype (57) (yellow arrows) and shorter, ~100–200 nm nm-long intervals (green arrows) of the (557.559) polytype interspersed with more disordered stacking sequences. Yellow circle shows the approximate area (diameter ~150 nm), for selected area electron diffractions acquisition. Note intervals marked for the 36H polytype indicating 17 (118 nm) and 27 (192 nm) unit cells. (c) Sequence of 41 consecutive stacks of the (57) polytype. Images (a) and (b) are modified from Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019).
The three polytypes, shown as high-resolution HAADF STEM images with specimen tilted on [$2\bar{1}\bar{1}0$![]() ] zone axis (Fig. 3), are interpreted in terms of the following respective arrangements: (i) polytype (57) with regular combinations of 5-atom (Te–Bi–S–Bi–Te) and 7-atom (Te–Bi–S–Pb–S–Bi–Te) layers, 12H (Fig. 3a); (ii) polytype (5559) with regular combinations of three 5-atom and one 9-atom (Te–Bi–S–Pb–S–Pb–S–Bi–Te) layers, 24H (Fig. 3b); and (iii) (557.559) with ordered combinations of two groups of layer stacks: two 5-atom and one 7-atom layers (557) followed by two 5-atom and one 9-atom layers (559), 36H (Fig. 3c).
] zone axis (Fig. 3), are interpreted in terms of the following respective arrangements: (i) polytype (57) with regular combinations of 5-atom (Te–Bi–S–Bi–Te) and 7-atom (Te–Bi–S–Pb–S–Bi–Te) layers, 12H (Fig. 3a); (ii) polytype (5559) with regular combinations of three 5-atom and one 9-atom (Te–Bi–S–Pb–S–Pb–S–Bi–Te) layers, 24H (Fig. 3b); and (iii) (557.559) with ordered combinations of two groups of layer stacks: two 5-atom and one 7-atom layers (557) followed by two 5-atom and one 9-atom layers (559), 36H (Fig. 3c).

Figure 3. HAADF STEM images with specimen tilted on the [$2\bar{1}\bar{1}0$![]() ] zone axis showing longer stacks representing the three polytypes of clogauite as labelled. A single unit cell of each repeat sequences, i.e. (57), (5559) and (557.559), is marked in a rectangle on each panel (a, b, c), and enlarged on the right to emphasise the contained atoms.
] zone axis showing longer stacks representing the three polytypes of clogauite as labelled. A single unit cell of each repeat sequences, i.e. (57), (5559) and (557.559), is marked in a rectangle on each panel (a, b, c), and enlarged on the right to emphasise the contained atoms.
Van der Waals bonds (often called gaps in the earlier literature) occur between Te atoms at the edge of neighbouring units (dark lines on HAADF STEM images), so that the individual layers (5, 7, 9) are well separated from one another. The c parameter corresponds to the length of a single stack sequence and is directly measurable from images, i.e. c ≈ 24 Å, 47 Å and 70 Å for 12H, 24H and 36H, respectively (Fig. 3).
In HAADF STEM imaging mode, the signal intensity (I) is dependent upon the atomic number (Z) of the chemical element, i.e. I ≈ Z 2. On the images in Fig. 3, the brighter dots represent Bi (Z = 83) and Pb (Z = 82) atoms, whereas the less bright dots on the margins of each module correspond to Te atoms (Z = 52). Light sulfur atoms (Z = 16) are not depicted on these images. The 5-, 7- and 9-atom layers show 2, 3 and 4 bright dots, respectively, accounting for Bi and Pb atoms. The number of lighter atoms (Te and S) are 3, 4 and 5. HAADF signal profiles across sequences comprising the three types of layers show a decrease in signal for Pb relative to Bi across 7- and 9-atom layers, whereas Te is marked by shoulders on the signal for Bi, and S is not depicted (Fig. 4). The position of Pb in the middle of 7- and 9-atom layers indicated by the profiles in Fig. 4b is also shown on high-resolution EDS STEM element distribution maps (Fig. 4c). Positions of the chalcogen atoms, Te and S, relative to Bi and Pb are concordant with the atom sequences marked on Fig. 3a–c.

Figure 4. (a) HAADF STEM image showing two profiles, each comprising three layer stacks as labelled. (b) HAADF signal intensity (black line) across the two profiles depicting the sequences and their contained atoms, i.e. double, triple and quadruple peaks for the five-, seven- and nine-atom units. Note that Bi atoms are picked out by highest intensity, followed by Pb. Sulfur atoms have the lowest intensity signals. (c) HAADF STEM image and STEM EDS element distribution maps, as marked, showing arrangement of atoms across a (5559) stack.
Selected area electron diffraction (SAED) patterns on [$2\bar{1}\bar{1}0$![]() ] zone axis for each polytype show common features such as modulation along c*, with strongest reflections defining the interlayer interval d* of comparable length (d = 1/d* in the range 1.9 and 1.98 Å for each polytype; see table 4 in Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). Measurements of d a are in the range 3.7–3.5 Å, giving parameters for a between 4.27 Å and 4.5 Å when using the formula: a = da/cos30°. The smaller value is close to a = 4.24 Å obtained for the synthetic analogue of clogauite (Liu and Chang, Reference Liu and Chang1994). We note that ($01\bar{1}0$
] zone axis for each polytype show common features such as modulation along c*, with strongest reflections defining the interlayer interval d* of comparable length (d = 1/d* in the range 1.9 and 1.98 Å for each polytype; see table 4 in Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). Measurements of d a are in the range 3.7–3.5 Å, giving parameters for a between 4.27 Å and 4.5 Å when using the formula: a = da/cos30°. The smaller value is close to a = 4.24 Å obtained for the synthetic analogue of clogauite (Liu and Chang, Reference Liu and Chang1994). We note that ($01\bar{1}0$![]() ) and ($02\bar{2}0$
) and ($02\bar{2}0$![]() ) reflections are present on SAEDs (e.g. Fig. 5a) which is indicative of space group $P\bar{3}m1$
) reflections are present on SAEDs (e.g. Fig. 5a) which is indicative of space group $P\bar{3}m1$![]() .
.

Figure 5. (a–c) Selected area electron diffraction (SAED) for each polytype with specimen tilted on [$2\bar{1}\bar{1}0$![]() ] zone axis. The d* ≈ 2 Å interval marked on the SAED patterns represents the d*subcell for each polytype. Arrows indicate the satellite reflections depicted by γ modulation along c*. (d) Schematic showing that the three polytypes are N superstructures of the d*subcell (explanations to the right). The equal divisions defined by the satellite reflections (yellow lines) and their intensity variation across d* (crop from each SAED pattern) are well defined. The number of divisions within the central part of d* (between the brightest two reflections) corresponding to the modulation vector qF are visible on the SAED patterns. The distances between two satellite reflections is dN (example d12) and represents the c parameter for H phases.
] zone axis. The d* ≈ 2 Å interval marked on the SAED patterns represents the d*subcell for each polytype. Arrows indicate the satellite reflections depicted by γ modulation along c*. (d) Schematic showing that the three polytypes are N superstructures of the d*subcell (explanations to the right). The equal divisions defined by the satellite reflections (yellow lines) and their intensity variation across d* (crop from each SAED pattern) are well defined. The number of divisions within the central part of d* (between the brightest two reflections) corresponding to the modulation vector qF are visible on the SAED patterns. The distances between two satellite reflections is dN (example d12) and represents the c parameter for H phases.
Clogauite polytypes can, however, be differentiated by (a) number of satellite reflections and their intensity along the d* interval defining 12, 24 and 36 equal divisions corresponding to total number of layers (N) for each polytype, i.e. 12H, 24H and 36H, and (b) the number of divisions in the central part of d* (between the pair of satellites of strongest intensity by the middle of d*), i.e. 2, 4 and 6 for polytypes with sequences 57, 555.9 and 557.559, respectively (Fig. 5).
The measured crystal structures identified in Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019) were further constrained from ab initio total energy calculations and structure relaxation based on density functional theory (DFT). Calculations were performed with the Vienna ab initio simulation package (VASP; Kresse and Furthmüller, Reference Kresse and Furthmüller1996), using the projector augmented wave (PAW) method. A plane wave basis set with energy cut-off of 600 eV was employed for all calculations. The electronic exchange and correlation energy were estimated by the generalised gradient approximation (GGA) with revised parameters of Perdew et al. (Reference Perdew, Ruzsinszky, Csonka, Vydrov, Scuseria, Constantin, Zhou and Burke2008). The calculations incorporated the van der Waals interactions between atoms of the same type (Te–Te) using the method of Grimme et al. (Reference Grimme, Antony, Ehrlich and Krieg2010), which adds a small dispersion energy correction to the total energy in the system. The Brillouin zone (BZ) was sampled at Γ-centred dense k-point grids based on the Monkhorst-Pack scheme. Further experimental details are given in Tables 1 and 2.
Table 1. Number of atoms and chemical formula units applied in each simulation box and KPOINTS grids for the three clogauite structures.

Table 2. Equation of state parameters fitted from the energy volume relation for the three PbBi4Te4S3 structures. V 0 represents the equilibrium volume for each simulation cell, K 0 and K 0′ are the bulk modulus and its derivative. The elastic properties are compared with experimental and previously published calculations. See also Fig. 8.

Volumes from the input file were considered as V i. Unit-cell parameters (a, c) were subsequently scaled in the range 95 to 101% to obtain a series of volume values. Total energy calculations and structural optimisation for the atomic positions and the two cell parameters were carried out with energy tolerance <10–7 eV between two ionic steps and force <0.02 eV/Å per atom. After volume relaxation, a static calculation is performed to obtain the total energy. Figure 6 is a plot of V/atom vs. E0/atom for the three structures.

Figure 6. Plot of V/atom vs. E0/atom for the three structures.
The relaxed crystal structures for the three polytypes of clogauite were modelled and assessed using CrystalMaker software and Findsym was used to generate the three crystallographic information files (cif) (available as Supplementary material, see below). Electron diffractions and STEM image simulation were performed using STEM for xHREM TM software for structure visualisation.
Clogauite crystallises in the trigonal crystal system (space group P $\bar{3}$![]() m1, # 164). Modelling results show that values for a are the same for the three polytypes. Cell dimensions and volumes are as follows: Clogauite-12H (57): a = 4.277(4) Å, c = 23.46(14) Å, V = 371.598 Å3, Z = 1; clogauite-24H (5559), a = 4.278(4) Å, c = 46.88(31) Å, V = 743.053 Å3, Z = 2; and clogauite-36H (557.559), a = 4.278(4) Å, c = 70.36(32) Å, V = 1115.283 Å3 and Z = 3.
m1, # 164). Modelling results show that values for a are the same for the three polytypes. Cell dimensions and volumes are as follows: Clogauite-12H (57): a = 4.277(4) Å, c = 23.46(14) Å, V = 371.598 Å3, Z = 1; clogauite-24H (5559), a = 4.278(4) Å, c = 46.88(31) Å, V = 743.053 Å3, Z = 2; and clogauite-36H (557.559), a = 4.278(4) Å, c = 70.36(32) Å, V = 1115.283 Å3 and Z = 3.
Atom coordinates and Wyckoff positions for the three polytypes are in Table 3. Respective bond distances are given in Table 4. The structures of the three polytypes and the bonds within the asymmetric unit cell as constructed using CrystalMaker are in Figs 7 and 8. STEM and electron diffraction simulations (Fig. 9) based on the crystallographic information data obtained from the DFT calculations show an excellent match to analytical data (Figs. 3, 5) and as given by Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). Two equivalent zone axes were chosen, [$2\bar{1}\bar{1}0$![]() ] and $[ 11\bar{2}0$
] and $[ 11\bar{2}0$![]() ], for analytical and simulations, respectively.
], for analytical and simulations, respectively.
Table 3. Atom coordinates and Wyckoff positions for clogauite-12H, clogauite-24H and clogauite-36H.

Table 4. Bond distances (Å) for clogauite-12H, clogauite-24H and clogauite-36H.


Figure 7. Crystal models plotted on [11$\bar{2}$![]() 0] zone axis as ball and stick representations showing the structures of the three clogauite polytypes as labelled.
0] zone axis as ball and stick representations showing the structures of the three clogauite polytypes as labelled.

Figure 8. Bond types and lengths for the relaxed structures of the three clogauite polytypes plotted on [$11\bar{2}0$![]() ] zone axis. Red = Bi; blue = Te; yellow = sulfur; and green = Pb.
] zone axis. Red = Bi; blue = Te; yellow = sulfur; and green = Pb.

Figure 9. STEM simulations (left) and electron diffraction (right) on [11$\bar{2}$![]() 0] zone axis using the crystallographic information data obtained by DFT calculations. This zone axis is equivalent to [$2\bar{1}\bar{1}0$
0] zone axis using the crystallographic information data obtained by DFT calculations. This zone axis is equivalent to [$2\bar{1}\bar{1}0$![]() ] used in Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). Insets on the three images (yellow boxes) show the same structures but using Se instead of S to highlight the presence and location of the chalcogen atoms. The d* interval beneath each STEM simulation shows the number of reflections (nr). The number of divisions within the two brighter reflections by the middle of d* (2, 4, and 6) corresponds to the number of building modules in each polytype.
] used in Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). Insets on the three images (yellow boxes) show the same structures but using Se instead of S to highlight the presence and location of the chalcogen atoms. The d* interval beneath each STEM simulation shows the number of reflections (nr). The number of divisions within the two brighter reflections by the middle of d* (2, 4, and 6) corresponds to the number of building modules in each polytype.
Discussion
Modularity across what has been informally referred to as the aleksite series after the first named mineral, aleksite, is depicted from the building modules formed by incremental addition of nPbS layers and leading to a homologous series with the formula: PbnBi4Te4Sn +2, where n represents homologue number (Cook et al., Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a). Compositions where n = 2k, where k is an integer value, correspond to single-layer structures, e.g. aleksite (n = 2), saddlebackite (n = 4), and hitachiite (n = 10), whereas those with n = 2k + 1 integer values are formed by combinations of modules as in clogauite (n = 1).
The generic formula for the series was revised as Pb(n–1)Bi2Xn +2 (n = homologue number, X = chalcogen) (Moëlo et al., Reference Moëlo, Makovicky, Mozgova, Jambor, Cook, Pring, Paar, Nickel, Graeser, Karup-Møller, Balic-Žunic, Mumme, Vurro, Topa, Bindi, Bente and Shimizu2008). Cook et al. (Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a) postulated the existence of a hierarchical series of Pb–Bi-tellurosulfides that can be expanded from the archetypal 5-atom tetradymite unit to larger 7-, 9-, 11-atom units, whereas Moëlo et al. (Reference Moëlo, Makovicky, Mozgova, Jambor, Cook, Pring, Paar, Nickel, Graeser, Karup-Møller, Balic-Žunic, Mumme, Vurro, Topa, Bindi, Bente and Shimizu2008) considered the tetradymite (Bi2Te2S) archetype as a link to layered sulfosalts. The same approach was taken by Kuribayashi et al. (Reference Kuribayashi, Nagase, Nozaki, Ishibashi, Shimada, Shimizu and Momma2019) when describing hitachiite as n = 6 according to the formula of Moëlo et al. (Reference Moëlo, Makovicky, Mozgova, Jambor, Cook, Pring, Paar, Nickel, Graeser, Karup-Møller, Balic-Žunic, Mumme, Vurro, Topa, Bindi, Bente and Shimizu2008).
Relationships between the aleksite and tetradymite series of mixed layer compounds
Yao et al. (Reference Yao, Ciobanu, Cook and Ehrig2023) used DFT to obtain structural data for the aleksite series, including two polytypes each of aleksite (aleksite-21R and -42R) and saddlebackite (saddlebackite-9H and -18H), hitachiite, and the n = 6, n = 8 and n = 12 homologues not yet observed in natural specimens (Pb6Bi4Te4S8, Pb8Bi4Te4S10 and Pb12Bi4Te4S14). This study followed the mixed-layer compound concept for series of Bi-chalcogenides whereby modulation vectors along c* defined from diffractions patterns underpin chemical variation in a predictable and quantifiable manner (Amelinckx et al., Reference Amelinckx, Van Tendeloo, Van Dyck and Van Landuyt1989; Frangis et al., Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990; Ciobanu et al., Reference Ciobanu, Pring, Cook, Self, Jefferson, Dima and Melnikov2009).
Prior to such TEM studies, a model for the derivation of rhombohedral crystal structures from the system Bi–Te (and comparable Bi–Se and Sb–Te systems) was proposed from basic principles of chemistry and crystallography (Imamov and Semiletov, Reference Imamov and Semiletov1971, and references therein). This model postulated (i) two fixed-width modules with stacks: Te–Bi–Te–Bi–Te (notation 5) and Bi–Bi (notation 2), which are combined in different proportions to facilitate chemical variation within the series; and (ii) calculation of lattice parameters using those known for Bi2Te3 and Bi. The 5- and 2-stack model was later formalised as nBi2.mBi2Te3, where n and m are integers, for homologous series of layered tetradymite-like compounds (Shelimova et al., Reference Shelimova, Karpinskii, Zemskov and Konstantinov2000).
Criticism of this model came from Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990) that showed an alternative derivation of modules from Bi2Te3, as the initial basic structure, to account for chemical variation of compounds in the range Bi2+δTe3 (δ<1), e.g. addition of Te–Bi instead of Bi–Bi to the same Te–Bi–Te–Bi–Te stack. Therefore, there are two module types of 7-atom layers, which are structurally identical with one another yet have different Bi and Te configurations, symmetrical and asymmetrical, and different compositions (Bi3Te4 and Bi4Te3, respectively). Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990) defined a modulation vector (qF-notation from Ciobanu et al., Reference Ciobanu, Pring, Cook, Self, Jefferson, Dima and Melnikov2009) that relates the 7- and 9-atom building modules in the derived structures to basic structures (BS), e.g. 5 as BS for 7, 7 as BS for 9, and so on, via the fractional shift method of Van Landuyt et al. (Reference Van Landuyt, De Ridder, Gevers and Amelinckx1970).
Ciobanu et al. (Reference Ciobanu, Pring, Cook, Self, Jefferson, Dima and Melnikov2009) used the mixed layer compounds approach to interpret the modularity of natural phases from the tetradymite series in the range Bi2Te3–Bi8Te3 studied by HR-TEM. The authors provided a homology formula, S′(Bi2kX3) L′[Bi2(k+1)X3], where X = chalcogen, and S′ and L′ are the number of short and long modules with asymmetric Bi and Te arrangements, respectively. This is different to the homology using modules of fixed width (Shelimova et al., Reference Shelimova, Karpinskii, Zemskov and Konstantinov2000). The model also differs that of Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990), which uses symmetrical modules, yet shares the same accretional building principle, i.e. modules of incremental rather than fixed widths.
The revised model of Ciobanu et al. (Reference Ciobanu, Pring, Cook, Self, Jefferson, Dima and Melnikov2009) was validated by electron diffraction patterns that showed all phases are N-fold superstructures (N = number of layers in the stacking sequence) of a rhombohedral subcell with c/3 = d 1 ≈ 0.2 nm, positioning of the two brightest reflections about the middle of d 1*, and a monotonic decrease of two modulations with increasing Bi content. The qF modulation of Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990) was adapted to incorporate the homology for S′, L′ modules underpinned by k as: qF = γF⋅c sub*; qF = (i/N)d 1* = i⋅d N*, i = S′ + L′, relating changes in module size and number to displacements in a basic substructure. The displacements are quantifiable by fractional shifts between reflections in the derived and basic structures. A second modulation, q = γcsub* (q ≈ homoatomic interval; γ = 1.8–1.64 for the Bi2Te3–Bi8Te3 analytical range; c sub ≈ 3d 1), based on the displacive modulation between chalcogen and Bi atoms was adapted from Lind and Lidin (Reference Lind and Lidin2003). A DFT and STEM simulations study of the tetradymite series in the same range of compositions (Bi2Te3–Bi8Te3) has confirmed the mixed-layer compound model (Yao et al., Reference Yao, Ciobanu, Cook, Ehrig, Dima and Steinle-Neumann2024).
Ciobanu et al. (Reference Ciobanu, Pring, Cook, Self, Jefferson, Dima and Melnikov2009) also stipulated that compounds with symmetrical modules discussed by Frangis et al. (Reference Frangis, Kuypers, Manolikas, Van Tendeloo, Van Landuyt and Amelinckx1990), obtained by addition of n(M–X; M = metal; X = chalcogen, Te, Se and S) layers form a chalcogen-rich isoseries with the tetradymite series postulated to exhibit comparable modulations vectors along c*. HAADF STEM imaging has shown the differences between the asymmetrical (Ciobanu et al., Reference Ciobanu, Slattery, Cook, Wade and Ehrig2021; Cook et al., Reference Cook, Ciobanu, Slattery, Wade and Ehrig2021) and symmetrical modules (Cook et al., Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019). The identity of the 7-, 9-, and 11-symmetrical layer stacks is shown for clogauite in the new set of images in the present contribution (Figs 3 and 4).
Concordant with the concept of mixed layer compounds, the SAED patterns for clogauite display two brightest reflections about the middle of d* and are described by the following two modulations:
(1) q = γ⋅${\rm c}_{{\rm sub}}^\ast$
 (q ≈ homoatomic interval; calculated γ = 1.75 for all polytypes, c sub ≈ 3d); and
(q ≈ homoatomic interval; calculated γ = 1.75 for all polytypes, c sub ≈ 3d); and(2) qF = γF⋅${\rm c}_{{\rm sub}}^\ast$
 ; qF = (i/N)⋅d* = i⋅d N*, i = S + L;
; qF = (i/N)⋅d* = i⋅d N*, i = S + L;
where S and L = number of longer and shorter modules with symmetrical M (M = Pb and Bi) and Te arrangements, γF = 0.1667 for all polytypes (Fig. 5).
Based on the relaxed structures, the d interval is 1.955, 1.953 and 1.954 Å for the 12H, 24H and 36H polytypes, respectively.
Density functional theory calculations combined with a STEM simulation study of structures in the aleksite series for homologues with an even number in the compositional range between n = 0 and n = 12 (Yao et al., Reference Yao, Ciobanu, Cook and Ehrig2023) shows a and c values within 1.5% of experimental data and both a and the interlayer distance dsub (the equivalent notation used here is d) decreasing as the PbS content increases. The study also showed simulated electron diffraction patterns that have two brightest reflections at the centre of d sub*, and are described by monotonic decrease of the two displacive modulations as described above, with γF = 0.2–0.059 and γ = 1.8 to 1.588 for the compositional range. Importantly, the linear relationship between γ and d sub allows prediction of any theoretical phases in the series. The study of Yao et al. (Reference Yao, Ciobanu, Cook and Ehrig2023) demonstrated the probable upper compositional limit of the aleksite series as n = 398 (Pb398Bi4Te4S400) but also the strong likelihood that additional members will be discovered and that at least some may exist as multiple polytypes.
The relationships between γ and d sub for the two Bi-chalcogenide series discussed here show that isostructural phases share the same γ values, but with d values slightly lower for aleksite relative to corresponding tetradymite compounds (Yao et al., Reference Yao, Ciobanu, Cook and Ehrig2023, Reference Yao, Ciobanu, Cook, Ehrig, Dima and Steinle-Neumann2024), e.g. clogauite and tsumoite (BiTe) both have γ = 1.75 but their d values are ~1.953–1.955 Å and 1.996 Å, respectively.
The results outlined above validate the crystal-structural formula for aleksite series as: S(MpXp +1).L(Mp +1Xp +2), where M = Pb and Bi, and X = Te and S, p 2, and S and L are the number of short and long modules with symmetrical M–X arrangement, respectively (Cook et al., Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019; Yao et al., Reference Yao, Ciobanu, Cook and Ehrig2023).
The alternative model of homology using modules of fixed size nPbTe.mBi2Te3 introduced by Shelimova et al. (Reference Shelimova, Karpinskii, Svechnikova, Avilov, Kretova and Zemskovet2004) and adopted by Kuribayashi et al. (Reference Kuribayashi, Nagase, Nozaki, Ishibashi, Shimada, Shimizu and Momma2019) does not depict the displacive modularity introduced by the layer arrangements, even though it may be conceptually useful to depict chemical variation within the aleksite series. For example, clogauite-12H would have m = 2 and n = 1, so three building modules instead of two (5- and 7-atom layers). The displacive modulation qF along c* shows there are two and not three modules, i.e. there are two divisions between the two brightest reflections by the middle of the d* interval. This mixed-layer compounds model allows prediction of the series that is checked by the correspondence between the number of layers (N), building modules (incremental blocks with an uneven number of atoms), characteristics of electron diffraction patterns, and indeed the ab initio study of Yao et al. (Reference Yao, Ciobanu, Cook and Ehrig2023).
Summary
Bismuth-Pb-chalcogenides of the informally named aleksite series, PbnBi4Te4Sn +2 (Cook et al., Reference Cook, Ciobanu, Stanley, Paar and Sundblad2007a) are a modular series derived from tetradymite (Bi2Te2S). Cook et al. (Reference Cook, Ciobanu, Liu, Slattery, Wade, Mills and Stanley2019) gave an overview of named, unnamed and predicted species in the aleksite series. The same paper introduced a homology for the series, where the phase now named as clogauite is the n = 1 homologue member, aleksite is n = 2, saddlebackite is n = 4 and hitachiite, n = 10. Multiple polytypes are a feature of the series, including two for aleksite (21R, 42R) and three for saddlebackite (9H, 18H, 54H), all supported by published data, as well as the approximate unit cell dimensions of predicted and inadequately characterised series members.
The three clogauite structures discussed here can be regarded as polytypes because they have the same chemistry but differ in terms of the stacking sequences, concordant with Hatert et al. (Reference Hatert, Mills, Pasero, Miyawaki and Bosi2023). Each chemically distinct species within the aleksite series is a polysome or homologue, whereas phases with the same chemistry but different stacking sequences, like clogauite, not affecting their chemistry – these are polytypes. The modularity of the three polytypes is recognised on their electron diffractions, atomic-scale images, and STEM simulations. Best fits for the cell dimensions are obtained from the DFT calculations. The qF modulation depicts the number of building modules by the divisions between the two brightest reflections in the middle of d interval.
Acknowledgements
The authors acknowledge Microscopy Australia for instrument access. Comments from two anonymous reviewers assisted us to improve clarity and expression.
Supplementary materials
Crystallographic information file (cif) data files for clogauite-12H, -24H and -36H can be found at https://doi.org/10.1180/mgm.2024.46
Competing interests
The authors declare none.