Introduction
During the last few years, there has been an increased interest in developing a rational explanation for the rather considerable variation in such bulk properties of sea ice as its strength, density, thermal conductivity, latent heat of melting, and coefficient of thermal expansion. Of these properties, sea ice strength has received by far the most attention for practical reasons. The first published investigation of sea-ice strength that was accompanied with sufficient temperature and salinity control to permit an analysis was made by Reference ButkovichButkovich (1956). He performed in-place cantilever, ring-tensile, small beam flexural, and unconfined compression tests. Reference Weeks and AndersonWeeks and Anderson (1958) studied the variation in flexural strength of a large number of in-place cantilever beams from thin, relatively high salinity sea ice. In a concurrent paper, Reference Weeks and AndersonAnderson and Weeks (1958) attempted to explain the strength relations of young sea ice on the basis of the ice-brine geometry, as revealed by the study of thin sections, and the hypothesis that the strength of sea ice is equal to σ p (1−λ)/k, where σ p is the strength of so-called “pure” ice (ice with no brine pockets or air bubbles), measured by a similar testing procedure, k is a stress-concentration factor introduced by the presence of brine pockets in the sea ice, and (1−λ) is the reduction in effective cross-sectional area of the sea ice as a result of brine inclusions. This work has been extended by Reference AssurAssur (1958), who pointed out that the ratio of stress concentration in pure ice to that in sea ice should be considered instead of the absolute magnitude of the stress concentration in sea ice. Assur also demonstrated the importance of considering the presence of solid salts in the sea ice when computing brine volume tables and focused attention on the possible influence of the solid salts on the strength of the ice. Basing his work on the chemical determinations of Reference RingerRinger (1906) and Reference Thompson and NelsonThompson and Nelson (1956), Assur calculated a phase diagram for the freezing of standard sea-water and analyzed the variation of ring-tensile-strength data from a number of localities in both polar regions in the light of this phase diagram. His main hypotheses concerning the “entire spectrum” of strength relations in sea ice are shown in his figure 3 (Reference AssurAssur, 1958, p. 111) and may he summarized as follows:
-
(a) At high temperatures (above −8.2° C.), the strength of sea ice significantly decreases with an increase in
where v is the volume of the brine.
-
(b) At temperatures between −8.2° C. and −22.9° C., the presence of solid Na2SO4.10H2O increases the strength of the ice by one-third.
-
(c) At temperatures below −22.9° C., the presence of solid NaCl.2H2O causes sea ice to give strength values two or more times higher than fresh-water ice, if identical test procedures are used. This increase in strength is dependent upon the amount of solid salt in the ice.
-
(d) There is a strength hysteresis between normal one-season sea ice and old perennial pack ice, as the result of an increase in the SO4/Cl ratio in the ice caused by differential drainage of chloride-rich brine during periods when the ice temperature is between −8.2° C. and −22.9° C.
Reference AssurAssur (1958) has also discussed a number of alternative hypotheses. Unfortunately, the field data presently available are insufficient to indicate clearly which of these hypotheses best describes the strength variation of natural sea ice.
In addition, Reference ButkovichButkovich (1959[b]) has observed an appreciable difference between ring-tensile tests of sea ice of equivalent temperatures and salinities at Thule, Greenland, and Hopedale, Labrador. Two explanations which could be advanced to account for these differences are:
-
(a) The strength of sea ice of a given composition is strongly dependent upon the treatment and thermal history of the sample.
-
(b) The different thermal histories at Hopedale and Thule have produced significant changes in the ion ratios in the ice, thereby causing a change in the crystallization temperatures of the various solid salts.
These problems could possibly be resolved by more extensive field testing. However, since the sea ice at a given field site at a specific time will usually have a rather restricted salinity and temperature range, tests at a large number of different field sites would be required to study a complete spectrum of temperatures and salinities. Therefore, it was decided to produce argificially an ice that is structurally similar to natural sea ice, but with a simple composition that makes the variation of physical properties with temperature and composition more amenable to study. The freezing of NaCI–H2O solutions was chosen since NaCl.2H20 is the major salt found in natural sea ice and the phase diagram NaCI–H2O has a simple eutectic point at −21.2° C. Above the eutectic temperature, there is no solid salt in the ice; below this temperature, all the NaCl is solid as the phase NaCl.2H2O. If the resulting ice is structurally similar to natural sea ice, it can then be tested to resolve some of the problems and theories as to the causes of the strength variation in sea ice.
Experimentation
Method of growing salt iceFootnote *
An open-top cylindrical steel tank with a height and diameter of approximately go cm. was modified by attaching an outlet to the bottom. The outlet was connected to a pressure release in order to prevent pressure build-up under the accreting ice. The inside of the tank was coated with a suitable corrosion preventing paint. A 1.5 cm. thick layer of sealed-cell foam rubber was cemented around the upper 30 cm. of the tank to minimize stresses in the ice due to expansion. The outer surfaces of the tank were wrapped with a 2.5 cm. layer of glass wool, and a series of heat tapes were stitched to the wool. A 15 cm. thick layer of glass wool was placed on top of this and covered with a layer of tar paper. Two additional heat tapes were placed in a coil on the underside of the tank and the tank was placed on a 15 cm. layer of insulating glass foam bricks. After installation of the tank in the cold room, the heat tapes were connected to a bank of “Powerstats” set at very low power to balance out lateral heat loss from the tank. The arrangement of heating and insulating elements effectively allowed one-dimensional cooling in the tank and simulated the heat flow conditions found on an ocean or a lake. A schematic diagram of this arrangement is shown in Figure 1.

Fig. 1. Schematic diagram of the freezing tank
A series of thermocouples installed on a vertical wooden rod was placed in the tank near its center so that temperatures were measured at 5 and 1 cm. above the initial water surface and 0, 5, 10, 15, 20, 30, 40, 60, and 80 cm. below the surface. During a freezing run, the air, ice and water temperatures were read twice daily. During all freezing runs, a continuous record of the general cold-room temperature (−20° C.) was maintained. As soon as the initial ice skim formed, a large table fan was used to blow cold air across the ice surface. The position and setting of this fan remained unchanged for all the runs. This breeze prevented air-temperature stragification and caused the upper ice surface temperature to approach the temperature of the cold room more closely. A freezing run normally took
Ice thicknesses were measured using a hollow thin brass tube with a cross-bar at the end. A Nichrome heating element encased in glass fiber was placed inside the tube. This tube was then allowed to freeze into the ice with the cross-bar well below the lower ice surface. To measure the ice thickness a current was passed through the heating element until the brass tube melted free from the surrounding ice, the tube was raised until the cross-bar hit the lower ice surface, and the ice thickness determined.
When the ice of a given run had reached a thickness of 35 to 38 cm., a rectangle 20×30 cm. was marked on the ice surface in the middle of the tank. The ice surrounding this rectangle was then cut into 7.6 cm. diameter vertical cores using a modified SIPRE corer Reference Bader(Bader, 1957). One core was immediately cut into a series of 2 cm. horizontal layers so that the vertical salinity distribution in the ice could be determined. The other cores were immediately placed in storage at a temperature below the NaCl–H2O eutectic point. This effectively prevented brine drainage from the ice. Approximately 20 cores were obtained. The rectangular center block was then cut free using a handsaw and placed in storage for thin-section studies. Salinities of the ice and water samples were determined by allowing the samples to come to thermal equilibrium at +20° C. and titrating the resulting solutions using a standard Mohr titration (Reference VogelVogel, 1952, p. 904). When the sampling was completed, a wooden insulated cover was placed over the top of the tank and several immersion heaters were inserted through holes in the cover. As soon as the remaining scrap ice had melted, the tank was drained, rinsed, and refilled with fresh salt solution in preparation for another run.
Strength test procedures
There are many types of tests which have been or could be used to study the variation of sea-ice strength. The ring-tensile test procedure as described by Reference ButkovichButkovich (1958) was chosen for several reasons. To characterize adequately the temperature dependence of the strength of ice of a relatively constant salinity, tests should be made at a minimum of five different temperatures: three above and at least two below the eutectic point. Since tests on apparently identical specimens of sea ice always show a large scatter (Reference ButkovichButkovich; 1956, Reference Butkovich1959[b]), a minimum of ten tests should be performed at any given temperature and ice salinity to characterize the strength distribution. This requires at least 50 strength tests on ice from a single freezing run. Because of the limited size of the ice sample formed in the tank, only a small-scale ice strength test would satisfy these requirements. Reference AssurAssur (1958) and Reference ButkovichButkovich (1956, Reference Butkovich1959[b]) have based their conclusions regarding the strength variation in natural sea ice almost entirely on ring-tensile tests; similar test procedures would facilitate a direct comparison. In addition, since recent theoretical attempts to explain the variation in sea-ice strength (Reference Anderson and WeeksAnderson and Weeks, 1958; Reference AssurAssur, 1958) are concerned with failures in tension, the test used should approximate this condition. Also, ring-tensile test samples are relatively easy to prepare and the tests are rapid and simple to perform.
The samples were prepared for testing in the following manner. The stored cores were measured roughly and marked into 6 cm. segments, noting the position of each segment below the upper surface of the ice sheet. The cores were cut along these marked lines with a handsaw., and the length of each segment was measured in three different places to eliminate possible errors resulting from an irregular surface. The samples were weighed on a triple-beam balance and their densities computed. A
The ring-tensile tests were performed using a Carver Hydraulic Press. The total load was determined with a Baldwin SR–4 (2,000 pound capacity) load cell which was attached to a recording potentiometer. The current input to the load cell was adjusted so that a full scale deflection of the potentiometer equaled 1,000 pounds. The theory for the ring-tensile test was developed by Reference Ripperger and DavidsRipperger and Davids (1947) and its application to the testing of ice has been discussed by Reference ButkovichButkovich (1958). The co-axially drilled cylinder is subjected to compression normal to its axis and the failure plane is directly beneath and parallel to the direction of application of the load.
The ring-tensile strength α can then be computed from

where P is the load at failure, l is the average length of the sample and r o is the outer radius of the sample, in this case 3.8 cm. The stress concentration factor K is determined by the ratio r i /r 0 where r i is the radius of the co-axial hole. Holes of different sizes have been used by various investigators and the effect of this change on strength results for glacier ice has been studied by Reference ButkovichButkovich (1959[a]) who concluded that no difference in ring-tensile strength resulted between holes of less than 2.5 cm. in diameter. The author used the
Since the ring-tensile test is designed specifically for testing a truly elastic material, the load was applied at a rate greater than 1 kg./cm.2 sec. This rate is apparently high enough to minimize any plastic yielding Reference Jellinek(Jellinek, 1958). Within the limit of this approximation, the ring tests should give the tensile strength of a brittle substance.
Ring-tensile tests give values that are consistently higher than tests made either in flexure or in direct tension. Although there is a large scatter in the test values from a given group of ring-tensile tests, ring tests apparently give more consistent results than small-beam flexural-strength tests, which are the only other small-sample tests that have been used extensively on sea ice (Assur, personal communication). The lack of direct tensile-test procedures is probably due to the difficulty of producing a firm bond between sea ice and metal at warm temperatures, where there is an appreciable amount of brine in the ice.
It is important to emphasize that the strength values presented in this paper should not be used directly in plate equations for the purpose of predicting trafficability criteria.
Bulk Properties of Salt Ice
Phase Relations
In natural sea ice, the phase relations are quite complex with varying amounts of brine, solid salt mixtures, and ice coexisting at different temperatures below the freezing point. Only in the narrow range between the initial freezing point of sea-water (c. −1.8° C.) and −2.2° C. where CaCO3.6H2O begins to crystallize can sea ice be considered as a true brine-ice system. As the temperature is lowered, the amount of brine in the ice decreases and the amount of solid salt increases. Even at −54° C., there is still a small amount of brine remaining in the ice Reference Assur(Assur, 1958).
NaCl ice offers a rather simplified model of natural sea ice and effectively allows one to test the strength variation of the two extreme cases of natural sea ice; an ice-brine system and an ice-solid salt system. The dividing temperature between these two systems is the eutectic temperature of −21.2° C. The phase diagram for the high H2O portion of the system NaCI −H2O is shown in Figure 2 Reference Landolt and Börnstein(Landolt and Börnstein, 1936).

Fig. 2. A portion of the phase diagram NaCl–H2O
The brine content by volume for air-free NaCl ice at temperatures above −21.2° C. was computed by using the following relations. In m grams of salt ice of salinity S i parts per thousand (‰), there are n grams of brine of salinity S b parts per thousand (Reference MalmgrenMalmgren, 1927, p 67).
The value of S b in equilibrium with ice is fixed at any given temperature by the relations shown on the NaCl–H2O phase diagram. NaCl brine tables were used in determining the relation between the freezing point and concentration of the brine. Since there are also m (1−S i /S b ) grams of ice at a given temperature, the brine content by volume v in parts per thousand of brine is

where ρ i and ρ b are the densities of the pure ice and brine respectively at the given temperatures. The variation of ρ i with temperature was computed using a coefficient of cubical expansion of 1.6 × 10–4/° C. (Reference ButkovichButkovich, 1955). The v relation was programmed for a digital computer and brine volume tables were generated in the ice salinity range of 0 to 30‰ at temperatures of −5°, −10°, and −20° C. All strength tests at temperatures higher than the eutectic were conducted at these three temperatures. The brine volume of a 1‰ salinity ice as a function of ice temperature is given in Figure 3. A good approximation of the brine volume of salt ice of any salinity can be obtained from this figure simply by multiplying the values for 1‰ by the observed salinity of the ice. The error caused by using this figure instead of the more accurate values used in this paper is 3.3 per cent for a 20‰ salt ice at −5° C. Considering the large scatter in the ring-tensile results, the error introduced in the final analysis by using the condensed brine volume table would not be appreciable for most purposes. This 3 per cent error can probably also be considered as a reasonable estimate of the maximum error resulting from the use of the table prepared by Reference AssurAssur (1958) for the brine volume of natural sea ice.

Fig. 3. Volume of brine and NaCl.2H2O in NaCl ice as a function of temperature
At temperatures below −21.2° C., where NaCl.2H2O crystallizes, a different relation must be used to compute the fraction of NaCl.2H2O by volume existing in the ice. Since titration gives the salinity of the ice in parts per thousand of NaCl by weight, this figure must be converted to the volume of NaCl.2H2O, v(NaCl.2H2O) per kilogram of ice using the relation

Therefore, the parts per thousand by volume of solid salt in the ice, V(NaCl.2H2O) is given by the equation

where S i is the salinity of the ice in grams of NaCl per kilogram of solution and M and ρ are the gram molecular weights and densities in g./cm.3 of the substances specified in the parentheses. A density of 1.630 g./cm.3 was used for ρ(NaCl.2H20) at all temperatures (Reference Adams and GibsonAdams and Gibson, 1930), since neither the coefficient of thermal expansion nor the structure of this compound appears to be known. The NaCl.2H2O volume in a 1‰ ice as a function of temperature is given in Figure 3.
Density and air content
The density of air-free salt ice as a function of temperature and salinity at temperatures above the eutectic point is presented in Figure 4. These values were computed using the relationship


Fig. 4. Density of an air-free NaCl ice as a function of temperature and salinity
Examination of Figure 4 shows that lower salinity ice goes through a density minimum above the eutectic point as the temperature decreases. This minimum is the result of the density decrease associated with the water-ice phase transition opposing the general density increase of both the ice and brine with decreasing temperature. That similar relations should exist in natural sea ice has been shown by Zubov (Reference Zubov1945, p. 360) and in more detail by Reference AndersonAnderson (1960). There is also a slight discontinuity in the density at −21.1° C., caused by the crystallization of ice and NaCl.2H2O at the eutectic point. At temperatures below the eutectic point, the density of salt ice slowly increases and was computed from

These values are also shown in Figure 4.
The proportion of the sample by volume that is air was then determined using the relation

where ρ i(o) is the observed density of the salt ice in g./cm.3 and ρ i(t) is the theoretical density of air-free salt ice with a salinity, temperature and internal pressure identical to that of the sample.
As discussed earlier, the observed densities ρ i(o) of the samples were obtained by weighing a segment of the cylindrical ice core. The length of this segment was measured accurately, but the diameter of the core was assumed to equal the inside diameter of the corer (7.62 cm.). Although the core could not have a diameter greater than 7.62 cm. it could easily have a diameter less than 7.62 cm. as a result of uneven drilling or gouges in the core, i.e. the computed density can be less, but should not be more, than the real density. That this is occasionally not the case can be seen by comparing the computed densities with the theoretical densities for air-free salt ice. In several cases, the measured densities are higher than the theoretical densities for the air-free ice. These anomalous values apparently result from slush formed during the coring process freezing to the ice core.
Strength Results
Seven different freezing runs were completed on solutions in the system NaCl–H2O. The initial compositions of the solutions and the average salinity of the resulting salt ice in each run are as follows: Runs I and VII, solution 0‰ NaCl, ice 0‰ NaCl; Run II, solution 4.46‰ NaCl, ice 1.73‰ NaCl; Run III, solution 9.77‰ NaCl, ice 2.83‰ NaCl; Run IV, solution 20.54‰, NaCl, ice 5.16‰ NaCl; Run V, solution 29.51‰ NaCl, ice 7.52‰ NaCl and Run VI, solution 70.13‰ NaCl, ice 15.73‰ NaCl. These solution compositions were chosen to simulate the salinities that would be expected in normal lake and sea-water, and the intermediate salinities characteristic of bodies of brackish water such as the Black and Baltic Seas. In addition, Run VI provides information on higher salinity ice, thereby establishing some control for extrapolating existing field data to higher salinities.
Strength of fresh-water ice
Both of the “pure” ice freezing runs used Lake Michigan tap water. The resulting ice from both Runs I and VII was coarsely crystalline with the majority of the c-axes normal to the plane of the freezing surface. The ice produced in both runs was extremely clear and contained no visible flaws or air bubbles. This is in contrast with natural fresh-water ice, which may contain a large number of small cracks and air bubbles.
The ring-tensile strengths and standard deviations of the ice from Runs I and VII are plotted against test temperature in Figure 5. A least-squares straight line to all the data σ = 23.94−0.27T indicates a slight positive slope with a temperature coefficient of 0.0113. The main factor contributing to this slope is the appreciable decrease in the σ values at −5° C. If these −5° C. values are disregarded, the least squares equation is σ = 28.02−0.11T with a temperature coefficient of 0.0039 indicating that the ring-tensile strength is essentially temperature independent in the range T = −10° to −35° C. It can be seen that Runs I and VII show similar trends; a relative independence of strength of temperature in the range −10° to −35° C. and a slightly lower strength value at −5° C. There is, however, an appreciable and consistent difference between the σ values from the different runs. An explanation of these differences is presented in the discusson of the effects of short-term cooling. The grand average of Run I is 32.15±10.95 kg./cm.2, while the average for Run VII is 24.53±6.18 kg /cm.2. The overall average for both runs is 27.56±9.18 kg./cm.2. The strength values at a given temperature of all the fresh-water ice tests are characterized by a very large scatter, which gives a natural variability (standard deviation divided by the arithmetic average) of 0.31 and 0.24 for Runs I and VII respectively.

Fig. 5. Ring-tensile strength of fresh-water ice as a function of temperature
Previous measurements of the tensile strength of ice are quite rare. Table I presents a summary of recent values from the literature. Of these, only Reference AssurAssur (1958) mentions the results of ring-tensile tests on lake ice, but without giving detailed data. In view of the facts that, in other types of ice, ring-tensile tests consistently yield higher values than either flexural or direct tension tests Reference Butkovich(Butkovich, 1958) and that other investigators appear to find that the tensile and flexural strength of lake and argificial ice lies in the range 12 to 20 kg./cm.2 at temperatures between 0° and −40° C., Assur’s originally reported value of somewhat above 15 kg./cm.2 appears to be too low. During later tests Assur has found average values more consistently above 20 kg./cm.2, which compare favorably with the present results.
Table I. Comparison of Tensile and Flexural Strength Values for Fresh-Water Ice

It is interesting to note that the author’s results are quite similar to the ring-tensile strengths obtained by Reference ButkovichButkovich (1959[a]) on glacier ice from the TUTO tunnel, Thule, Greenland. The ice studied by Butkovich was generally equi-granular with an average grain diameter in the range of 5 to 7 mm. Although many of these samples had a rather strong preferred orientation with the c-axes vertical, Butkovich found no difference between the ring-tensile strengths of samples from vertical and horizontal cores.
Strength of NaCl ice as a function of brine volume
Anderson and Reference Anderson and WeeksWeeks (1958) discussed two different specific models of the ice-brine geometry in attempting to account for the strength variation observed in sea ice. These models were based on observed changes in the shapes of the brine pockets as a function of temperature and can be described briefly as constant-width and cylindrical brine pocket models. If these models were to hold, the strength σ should be a linear function f l of v and
Test results were grouped according to their test temperatures (−5°, −10° and −20° C.) and plotted against various brine volume parameters. This grouping was used to nullify any temperature influence on the strength of the ice portion of the brine-ice system. Therefore, observed strength variations should be the result only of the variable brine volume and of changes in the geometry of the brine pockets.
A plot of σ against


where n is the number of tests (Reference GouldenGoulden, 1952, p. 457). The t-numbers, in all cases, are insignificant, indicating that the presently available data do not permit a choice between the different brine volume exponents. However, to facilitate comparison with previous work on natural sea ice, it was decided to utilize plots of σ vs

Fig. 6. Ring-tensile strength of NaCl ice vs
Figure 16 shows the average strength values for each test group plotted against the average value of
Strength of NaCl.2H2O ice as a function of the relative volume of solid salt
Among the more interesting hypotheses in Assur’s paper Reference Assur(1958) are: (1) that the presence of solid salt, in particular NaCl.2H2O, reinforces the brine pockets, causing the strength of cold sea ice to become more than twice the strength of fresh-water ice; and (2) that the strength of this ice may be dependent on both the amount of solid salt in the ice and the ice temperature. The larger the amount of solid salt, the higher the strength. To test these hypotheses, a number of ring-tensile tests were performed on ice containing solid NaCl.2H2O. The ring-tensile strengths of these samples at −25°, −30° and −35° C. are plotted against the volume of the solid NaCl.2H2O in Figures 7 and 8. The variation in the amount of solid salt in these samples is considerably greater than would ever be found in natural sea ice. No correlation was found between V(NaCl.2H2O) and the strength of the ice in the salinity range studied. The strength values also apparently are not temperature dependent.

Fig. 7. Ring-tensile strength of NaCl.2H2O ice vs V(NaCl.2H2O), T = −25° C.

Fig. 8. Ring-tensile strength of NaCl.2H2O ice vs V(NaCl.2H2O), T =−30° C. and −35° C.
Even if there is no correlation between σ and V(NaCl.2H2O), the average strength of the NaCl.2H2O ice might still be considerably greater than the strength of’ fresh water ice. It is clear that this is not the case. The V(NaCl.2H2O) = 0 intercept for −25°, −30° and −35° C. samples combined is 28.8±4.17 kg./cm.2, which is comparable to the average value for the strength of fresh-water ice, 27.58±9.18 kg./cm.2, obtained by the present author. It is concluded that, within the temperature and salinity range studied in this paper, the ring-tensile strength of NaCl.2H2O ice is:
-
(a) essentially independent of temperature and V(NaCl.2H2O), and
-
(b) comparable to the strength of fresh water ice.
These observations can he explained if we assume that, when the ice−NaCl.2H2O eutectic mixture crystallizes in a brine pocket, the former brine pocket has either the same or a greater strength than the ice matrix. The failure, therefore, presumably occurs in the ice matrix, causing the ring-tensile strength of the aggregate to be similar to the ring-tensile strength of fresh-water ice. It is, of course, probable that large volumes of NaCl.2H2O in the ice will cause a systematic shift in the strength of the aggregate. Otherwise, it would be necessary to suppose that the properties of pure ice and pure NaCl.2H2O are similar. Although no data are available on the strength characteristics of NaCl.2H2O, such a coincidence is considered highly improbable.
Effect of thermal history on salt ice strength
A number of alternate hypotheses have been advanced to explain apparently anomalous strength variations between sea ice from different test sites and with different thermal histories. The first of these requires a change in the bulk chemistry of the sea ice and is based on the field observation Reference Zubov(Zubov, 1945) that, as sea ice ages, the chloride/sulfate ratio is decreased by differential drainage of NaCl-rich brine from the ice. The crystallization temperature of Na2SO4.10H2O is −8.7° C. from a sea-water brine and only −1.2° C. from a Na2SO4–H2O solution. Reference AssurAssur (1958) has noted that this change would be reflected in the volumes of brine and solid salt in the ice and might be at least partly responsible for the differences between the strength characteristics of young sea ice and perennial pack ice. This hypothesis will be referred to as the “compositional effect”.
Other hypothetical explanations for strength variations are concerned only with the physical state of the ice—solid salt—brine system and do not require changes in the bulk chemistry. For example, when a sample of ice is heated, there might be a measurable lag between the time it arrives at the higher temperature and the time that the equilibrium amount of icebrine—solid salt is achieved. The sample would, therefore, retain its strength of the lower temperature for several hours after reaching the higher temperature, and then slowly weaken. This possible effect will be referred to as “phase hysteresis” since it is a kinetic phenomenon associated with the metastable persistence of an unstable phase.
A third hypothesis is that the geometry of the brine pockets and the distribution of solid salt in the ice are a function of the specific thermal path by which the ice sample approached the test temperature. If so, ice tested after being subjected to a warming cycle might not give the same strength values as ice tested after being subjected to a cooling cycle. This effect will be referred to as “geometric hysteresis”.
The other important factors which may influence sea-ice strength are probably related to the specific thermal history of the ice sheet during its nucleation and growth. Among these might be such factors as initial grain orientation, grain size, the geometry of the sub-plates that compose the single crystals of sea ice, and the initial shapes of the brine pockets. All of the ice used in the studies reported in this paper was grown under identical thermal conditions, therefore it is assumed that these factors, if important in controlling the strength of the ice, are constant for the present freezing runs.
Although the “compositional effect” could be studied in the laboratory, it would necessitate aging the ice for long periods under carefully controlled conditions. Therefore, experimentation was concentrated on studies of “phase” and “geometric hysteresis”.
Phase hysteresis. To test for the presence of NaCl.2H2O phase hysteresis, 60 ring tensile samples from Run IV were stored at −25° C. (below the eutectic point of the NaCl–H2O system). First ten of these samples were tested at −25° C. Then a dummy sample with a thermocouple frozen into it was warmed from −25° to −10° C. and the change in temperature with time was measured. It was found that the ice sample reached thermal equilibrium at −10° C. in 3 hr. The remaining 50 samples were then moved from −25° to −10° C. and allowed to reach thermal equilibrium. Ring-tensile tests were then performed on the first group of ten samples. Similar tests were made at about 1, 3, 24, and 48 hr. intervals after the time of thermal equilibrium (t eq = 0). These results are shown in Fig. 9. The correlation coefficient and t–number for the fitted curve are 0.090 and 0.166 respectively. It is obvious that, in the samples studied, the achievement of thermal equilibrium is accompanied by the achievement of tensile strength equilibrium and that there is no evidence of a phase hysteresis.

Fig. 9. Study of phase hysteresis in NaCl ice, Tt= −10° C.
A proof of an absence of phase hysteresis in NaCl.2H2O ice does not, of course, rule out the possibility of phase hysteresis in Na2SO4.10H2O ice. However, even if sea-water were initially frozen in a closed system, the maximum amount of Na,SO4.10H2O present at −34°C. would be 8.88 g. for 922 g. of ice or 9.63‰ by weight Reference Assur(Assur, 1958). If differential brine drainage were to proceed at maximum efficiency and remove all other ions, this value is still well below the solubility of Na2SO4.10H2O in water at its eutectic point (38 ‰ by weight).
Geometric hysteresis. To study geometric hysteresis, 60 ring-tensile samples from Run IV were subjected to different thermal histories. One group of to samples was tested at −20° C. immediately after being removed from the freezing tank. Since the air temperature in the freezing room was regulated at −20° C., these samples had never been below the eutectic temperature. Two other groups of samples were stored at −25° C. for varying periods of time then moved to −20° C. and tested after being allowed to reach thermal equilibrium. The remaining samples, after being at −25° C., were cycled between −10° and −20° C. until testing was completed. These data are presented in Figure 10. As can be seen, there is no correlation between the ring tensile strength at −20° C. and the specific thermal path that the samples followed before reaching the test temperature. There is, therefore, no measurable geometric hysteresis in salt ice, and consequently it should be permissible to group tests on natural sea ice, regardless of their thermal history, provided, of course, that the different test groups have similar bulk chemistries.

Fig. 10. Study of geometric hysteresis in NaCl ice, Run V, Tt= −20° C., cycled to −10° C.
Four series of tests were made to study the effects of thermal cycles on ice tested at temperatures below the eutectic point. Samples from Runs II and III were stored and tested at −25° C. and cycled to −10° C. Samples from Run VI were stored and tested at −30° C. and cycled to both −20° and −10° C. In all these samples, there was no doubt that NaCl.2H2O had crystallized prior to testing, since this crystallization is accompanied by a pronounced sample color change from grey to chalky white. A typical test series is shown in Figure 11. It is concluded that:
-
(a) The strength of the initial group of uncycled samples is significantly higher than that of the cycled samples.
-
(b) This decrease in strength usually occurs after the first cycle and is not affected by further cycles.

Fig. 11. Study of geometric hysteresis in NaCl.2H2O ice, Run VI, Tt = −30° C., cycled to −20° C.
When first noted, it was believed that this strength decrease resulted from brine drainage at the higher temperatures. However, checks of the sealed polyethylene bags that contained the samples during the cycling process revealed no evidence of brine drainage. This observation is supported by the lack of change in the average salinities of the groups of samples as a function of the number of cycles to a higher temperature (Fig. 12). When the second group of samples was pulsed, visual examination revealed that there had been an appreciable redistribution of the brine in the sample during the high temperature portion of the cycle. This change is not evident when examining the samples at temperatures above the eutectic temperature. However, at sub-eutectic temperatures, the redistribution of brine can be seen because of the chalky color of the NaCl.2H2O. No quantitative measurements have been made of this redistribution, but most of the brine apparently shifted to the lower portion of the sample.

Fig. 12. Average test group salinity vs number of cycles to a higher temperature
In ring-tensile tests, failure is forced on a predetermined small volume. If the brine in this volume is drained away during a heating cycle, then when the sample is returned to the sub-eutectic temperature, the brine pockets will be filled with air instead of the eutectic mixture of NaCl.2H2O and ice. The ice should then have a strength corresponding to a temperature higher than the eutectic point.
It has been shown that the ring-tensile strength of salt ice (σ) is approximately a function of

and the strength decrease Δσ b produced by the volume of brine present in the ice during the high temperature portion of the thermal cycle (vmax ) is obtained as

If it is assumed that the loss in brine volume (Δv) and the corresponding increase in the air content of the salt ice, as the result of thermal cycling, are proportional to the volume of brine present in the ice at the high temperature portion of the thermal cycle (vmax ), then
and
where Δσ is the strength decrease due to cycling.
If these assumptions are valid, a plot of log Δσ vs log v max should be a straight line with a slope of 0.5. The slope of the line in Figure 13 is 0.43 and is not significantly different from 0.5 at the 0.95 probability level.

Fig. 13. Log (Δσ), the strength loss due to cycling, vs log v max the volume of brine present in the ice during the high temperature portion of the thermal cycle
This phenomenon, which will be called the “brine redistribution effect”, has obvious implications for planning optimum testing procedures for natural sea ice. The best procedure, of course, is to test the sea ice immediately after removal from the ice sheet at the in situ temperature. If this is not possible, samples of NaCl ice should be stored at temperatures below the eutectic point, and samples of sea ice below the NaCl.2H2O crystallization temperature (−22.9° C.). If storage is necessary and low temperatures are unavailable, brine redistribution can possibly be minimized by rotating the samples every few hours and by not drilling the co-axial hole until shortly before the ring-tensile tests are performed.
It is also of interest to note that the brine redistribution effect, while clearly evident in ice tested at sub-eutectic temperatures, is not apparent in ice tested at temperatures above the eutectic point (see Fig. 10). This appears to indicate that, while there is a large strength difference between a volume filled with air and one filled with the NaCl.2H2O–ice eutectic mixture, there is no appreciable strength difference between a volume filled with air and one filled with brine.
Effect of short-term cooling on the strength offresh-water and NaCl.2H2O ice. As was noted earlier, there is a consistent difference between the ring-tensile strengths measured from the two fresh-water ice freezing runs. Since the ice from both runs is apparently quite similar in grain size and crystal orientation, it is reasonable to hypothesize that these differences are the result of changes in treatment.Footnote * Examination of the data shows that there are two main types of testing procedures for the fresh ice. The samples in the first group were stored for over two months at −25° C. before being tested, while samples in the second group were not subjected to prolonged storage, but quickly brought from the growth tank to the test temperature and tested after one day. To compare these strength values, it is necessary to reduce them to a common temperature (−10° C.) by using a relation suggested by Assur (personal communication, 1960).

where T t is the test temperature in °C., σ is the observed ring-tensile strength at temperature T t and σ a is the adjusted ring-tensile strength. This correction is rather small with a temperature coefficient of 0.00667 and is in agreement with both the results of the present study and the work of Reference ButkovichButkovich (1954). The standard deviations are adjusted, using the same ratio. The average strength and the standard error of the average
The significance of the difference can be tested by computing the statistic
which in this case is equal to 4.46. Since there are 129 degrees of freedom, the critical t-number for a significant difference at the 99 per cent level is 2.62. Therefore, we can conclude that there is a difference between the two groups of data. The cause of this difference appears to be the change in the testing procedure. However, since the samples in Group 1 are from Run I, and the samples in Group 2 are from Run VII, it is also possible that the strength differences are the result of some basic change in the strength of the ice from the different runs. Unfortunately, different sample groups from the same fresh-ice freezing run were not subjected to different aging histories.
The correlation between short-term cooling and strength decrease can be tested by studying the strength variation of NaCl.2H2O ice. As shown earlier, the strength of NaCl.2H2O ice is independent of the amount of NaCl.2H2O present in the ice, and is comparable to the strength of freshwater ice. This was interpreted as indicating that the strength of NaCl.2H2O ice is controlled by the strength of the ice matrix. Therefore, if the strength of fresh-water ice is affected by short-term cooling, the strength of NaCl.2H2O ice should also be affected. To test this, strength values of NaCl.2H2O ice were corrected to −10° C., using equation (10). This correction accounts only for the change in strength of the fresh ice component and ignores the presence of the brine pockets. These tests can also be separated into two groups. The first group was subjected to rapid cooling by 5° to 10° C. after storage, while the samples in group 2 were either tested at the storage temperature or after being warmed 5°. The averages and standard errors of the group averages are 21.99±[1.22] and 27.37±[1.23] kg./cm.2 If the weighted averages and standard errors are computed from the whole population instead of from the group averages, values of 22.30±[0.75] and 26.49±[0.72] kg./cm.2 are obtained. Similarly to those for fresh-water ice, the standard errors based on the group means are larger than those based on the individual test values, indicating that the group averages probably still contain hidden effects. The computed t-number is 4.03 as compared with the required t-number of 2.63 for a difference at the 99 per cent. level of significance. Therefore, it can be concluded that there is a statistically significant difference between the two sample groups, both in NaCl.2H2O ice and fresh-water ice.
This strength drop is probably caused by thermal shock, which produces small defects in the sample that do not heal in a day. Also, in NaCl.2H2O ice, when samples are moved from the temperature of the freezing tank to a sub-eutectic test temperature, the new eutectic mixture occupies 7.2 per cent more volume than the original brine pocket at the eutectic temperature. This sudden volume change will probably produce cracks in the pure-ice matrix and cause a strength decrease. In addition, once the eutectic mixture has formed, the larger thermal contraction of the fresh-ice component, as compared to the NaCl.2H2O inclusions, would produce strains and cracks in the ice matrix. If these factors are predominant, the NaCl.2H2O ice should exhibit a more pronounced strength decrease as a result of short term cooling than fresh ice. The sudden cooling reduces the strength of the fresh-water ice by 5.98±[1.34] kg./cm.2 and the NaCl.2H2O ice by 4.19±[1.04] kg./cm.2 or 20.2±[4.53] and 15.8±[3.93] per cent in relative terms. The computed t-number for the significance of the difference between the fresh-water and salt ice values is 0.73 and the required t-number is 3.03. Therefore, there is no significant difference between fresh and NaCl.2H2O ice in strength reduction produced by short-term cooling, indicating that the strength reduction is apparently the result of changes in the strength characteristics of the pure-ice part of the sample.
We can assume that the ring-tensile strength of fresh-water ice is 29.58±8.34 kg./cm.2 (52 tests) at −10° C., while the strength of NaCl.2H2O ice is 26.49±5.67 kg./cm.2 (62 tests) if the strength of its ice matrix is corrected to −10° C. The t-number indicates that this difference is significant at the 95 per cent level, but not at the 99 per cent level. Although a difference in strength is not proved, the statement that salt ice below the eutectic point has the same strength as fresh-water ice should be doubted. Since the average test temperature for the samples used in computing the average strength of NaCl.2H2O ice is −25.8° C., the strength value, when recalculated to this temperature, is 29.11±6.23 kg./cm.2.
Usually, when natural fresh-water ice is tested, there is an appreciable difference between the air temperature and the in situ ice temperature. The samples are removed from the ice sheet, allowed to come to equilibrium with the air temperature, and then immediately tested. This procedure will cause thermal shock in the test samples and probably partly accounts for the apparent discrepancy between the strength of natural fresh-water ice and Iaboratcry and glacier ice.
Effect of the volume of inclosed air on the strength of salt ice
Density determinations were made by a procedure similar to that used by all recent field investigators. A sample of ice is cut out and its dimensions and weight determined. Unfortunately, an analysis of the error involved shows that even if the diameter of the ice specimen is exactly that of the corer, an error of±0.5 mm. in measuring the length of the sample would produce an error of approximately 1.5 per cent. Also the external diameter of the core may deviate appreciably from the internal diameter of the corer due to grooving and gouging during coring and the formation of slush coatings after coring. These combined effects could easily produce an error greater than 2 per cent in any density measurements.
Unfortunately, such an error is of the same order of magnitude as the density decrease produced by the volume of air included in the ice. Figure 14 shows the volume of air in the ice plotted against the depth of the sample below the surface of the ice sheet for Run VI. The other freezing runs give similar results. In general, there is a slight increase in the volume of air in the ice with increasing depth. Such a result is quite reasonable, since the volume of brine in the in situ ice sample increases toward the lower portion of the sample. This higher brine volume facilitates brine drainage from the lower part of the ice core immediately after it is removed from the ice sheet, therefore, causing a higher volume of included air. There is a high scatter in the density values for a given ice. Much of this is undoubtedly the result of the error in the density determination. Figure 15 shows the average volume of air included in the ice of a given run plotted against the composition of the initial freezing solution. There does not appear to be a correlation. The effect of the total void volume—volume of air plus the volume of brine—on the ring-tensile strength of the salt ice was also studied. The conclusions are similar to those reached from considering only the volume of brine.

Fig. 14. Volume of air in the ice vs depth in the ice sheet, Run VI

Fig. 15. Average volume of air in the ice of a given run vs initial salinity of the freezing solution
It is suggested that a more accurate immersion method should be used for density measurements in the future. Such a study could perhaps resolve the question of the differences, if any, between the strength characteristics of ice containing brine pockets and air bubbles. As mentioned earlier, some of the data collected in this study appear to indicate that there is no major difference. This evidence is far from conclusive, however.
Conclusions
NaCl ice
The main conclusions reached in the present study may be summarized briefly, as follows:
-
The ring-tensile strength of fresh-water ice is essentially temperature independent in the temperature range −10° to −30° C. and shows a slight decrease at −5° C. The individual test groups show a large scatter. For the present, 29.6±8.5 kg./cm2 will be considered as the average strength of pure ice with no visible air bubbles or cracks at −10° C. This value is comparable to recent ring-tensile results from glacier ice (Reference ButkovichButkovich, 1959[a]).
-
The ring tensile strength of ice containing crystals of NaCl.2H2O is essentially independent of both the temperature of the sample and the volume of NaCl.2H2O present in the ice. This indicates that the brine pockets are reinforced and the failure occurs in the ice matrix. If the strength of the ice matrix is corrected to −10° C., the strength of NaCl.2H2O ice is 26.5±5.7 kg./cm.2. This corresponds to a value of 29.11±6.23 kg./cm.2 at the average test temperature of −25.8° C.
-
A t-test for the significance of the difference of means indicates that there is a difference between the strength of fresh-water ice and NaCl.2H2O ice at the 95 per cent level of significance but not at the 99 per cent level. Therefore, the statement that the strengths of fresh-water and NaCl.2H2O ice are identical should be doubted.
-
The strength of NaCl ice above the eutectic point decreases with an increase in the volume of brine in the ice and can be considered a unique function of the brine volume, independent of the individual temperature and salinity values. The presently available data do not permit a choice between the functions

When the average ring-tensile strengths of the different test groups are plotted against
for each group, the data can be adequately represented by the equation (Fig. 16).
(Fig. 16).
The intercepts (σ0) of the σ = f l (v k ) lines with the σ axis indicate the extrapolated strength of salt ice at the zero-brine condition. Following Reference AssurAssur (1958), we define σo as the basic strength of salt ice as determined by ring-tensile test. Since the test data do not allow a choice between the different powers of v, possible values of σ0, determined by linear extrapolation, vary from 19.4 to 24.7 kg./cm2 (Table II). To compare with Reference AssurAssur (1958), we will, for the remainder of this paper, use σ0=24.7±1.6 kg./cm2 as determined from the plot of
(Fig. 16).
-
A t-test for the significance of the difference of means indicates that there is a difference at the 0.99 level of significance between the average strength of fresh-water ice and σ0, the basic strength of salt ice as determined from Figure 16.
This indicates that the ratio of the stress concentration in salt ice to that in fresh water ice is 1.20. It should, of course, be noted that some uncertainty is introduced into the calculation of this ratio by the failure of the strength tests to indicate a unique value for the exponent of v. In any case, it may be concluded that the ratio is slightly greater than 1 in the range 1.1 to 1.5. It definitely is not 3, as initially suggested by Reference Anderson and WeeksAnderson and Weeks (1958). This is not meant to imply that the stress concentration factor for a small, isolated circular brine pocket would not be 3, but only that whatever stress concentration is introduced in sea ice by the presence of brine pockets is also largely present in the fresh-water ice studied in this paper.
Table II also gives value of v 0, the volume of brine in parts per thousand that would cause the ice to have a negligible ring-tensile strength. These values are determined from the intercepts of the σ=f l (v k ) curves with the v k axis. The v o intercept taken from the σ av against vav plot is 194‰, as compared with 152‰ computed by Reference Anderson and WeeksAnderson and Weeks (1958) from petrographic measurements.
-
No evidence was found to support the hypothesis that a phase hysteresis exists in NaCl ice.
-
No evidence was found for the existence of geometric hysteresis in NaCl ice tested at temperatures above the eutectic point. Therefore the strength of the sample can be considered independent of the specific thermal history immediately before testing. However, the strength of the ice tested at temperatures below the eutectic point was strongly dependent on whether or not the sample had been subjected to temperatures above the eutectic point. The sample groups that had been pulsed to warm temperatures gave strengths appreciably lower than those that were always kept below the eutectic temperature. The decrease in strength is proportional to the square root of the volume of brine existing in the ice during the warm portion of the thermal cycle. This phenomenon is termed the “brine redistribution effect”.
-
Short term cooling produces an appreciable decrease, approximately 20 per cent, in the tensile strength cf fresh and NaCl.2H2O ice. This decrease is believed to be the result of thermal shock, which produces microcracks in the ice.
Figure 17 summarizes the general conclusions of this study as to the strength variation of NaCl ice. To obtain the relative tensile strength of NaCl ice, the actual strength is divided by 24.7 kg./cm.2, the basic strength of salt ice as determined in this paper. Note that at temperatures between approximately −10° and −21.2° C., the ice strength is relatively insensitive to temperature changes, while at temperatures above −10° C., the strength decreases rapidly with rising temperature.
Table II. Comparison of Values for the Basic Strength of Salt Ice (σ0) and the Zero Strength Condition (v 0) as Determined from Plots of a Against Different Brine Volume Parameters


Fig. 16. Average ring-tensile strength vs average

Fig. 17. Relative ring-tensile strength of NaCl ice as a function of temperature and salinity
Sea ice
The results presented in this paper permit an experimental evaluation of certain aspects of the different hypotheses of Reference AssurAssur (1958) concerning the variation of the strength of natural sea ice. Points of interest are as follows:
-
The strength of fresh-water ice obtained in the laboratory and reported in this paper is considerably higher than the strength of natural fresh-water ice as assumed by Assur.
-
The slopes and intercepts of the
plots are apparently quite different in the temperature range where only ice and brine co-exist (temperatures above −8.7° C. for normal sea ice and −21.2° C. for NaCl ice).
Because of limited data, Reference AssurAssur (1958, Fig. 17, p. 131) calculated the value of v 0 his B 0, by substituting assumed petrographic data into his equation for an elliptical brine pocket model. The line σ0−v 0 was then fitted by least squares using only the data with
The strength tests on NaCl ice, however, indicate that
Figure 18 shows a plot of Assur’s data for normal sea ice (Reference AssurAssur, 1958, table 4, p. 129), tested in the temperature range of the ice-brine system (dots). Curve A is a least-squares fit of these tests
3. Assur has hypothesized that the crystallization of solid Na2SO4.10H2O in sea ice at temperatures between −8.7° and −22.9° C. causes the strength to become roughly one-third greater than would be expected if only brine were present in the ice. At temperatures below −22.9° C., the crystallization of NaCl.2H2O may cause an even greater increase in the strength of the ice.

Fig. 18. Measured tensile strength of sea ice vs the square root of the relative volume of brine (after Reference AssurAssur, 1958)
Figure 18 shows that sea-ice strengths determined in the temperature range of an icebrine—Na2SO4.10H2O system (crosses) appear to lie on the extension of Curve A. Curve B is a least squares fit of all the data tested at temperatures above −22.9° C.,
At temperatures below −22.9° C., where NaCl.2H2O crystallizes, the data presented by Assur are approximately 60 and 40 per cent higher than the values obtained from extrapolating curves A and B (Fig. 18). The average strength of sea ice containing brine is less than the strength of fresh-water ice and similar to the strength of NaCl.2H20 ice, as determined in this paper. Since the strength of salt ice does not seem to exceed the strength of lake ice even when all the brine has solidified, this suggests the hypothesis that the crystallization of NaCl.2H2O in natural sea ice affects the ice strength in a manner initially suggested by Assur for Na,SO4.10H2O. The solid salt reinforces the brine pockets, but does not cause an appreciable change in Young’s modulus oldie bulk sample, producing a discontinuity in the strength at −22.9° C. This reinforcement would be independent of the amount of precipitated NaCl.2H2O, provided that a certain critical amount has been precipitated. At temperatures below −22.9° C., the ring-tensile strength should continue to increase as a linear function of
Figure 19 shows a possible interpretation of the relative tensile strength (σ/σ0) of sea ice as a function cf temperature and salinity, if curve A (Fig. 18) is assumed to be the correct curve for the

Fig. 19. Tentative diagram showing the relative ring-tensile strength of sea ice as a function of temperature and salinity. Assuming curve A (Fig. 18) for the
Another possibility is that the crystallization of NaCl.2H2O increases the strength of sea ice to the strength of NaCl.2H2O ice, and, after a certain amount of NaCl.2H2O has crystallized, the strength does not vary with changes in the remaining volume of brine. In this case, the lower temperature curves in Figures 19 and 20 (T < −22.9° C.) would be similar to the relations shown in Figure 17 at temperatures below −21.2° C. Because of the extremely high scatter in ring-tensile tests made on sea ice at temperatures below the NaCl.2H2O crystallization point, these two interpretations may be difficult to resolve from field tests.

Fig. 20. Tentative diagram showing the relative ring-tensile strength of sea ice as a function of temperature and salinity. Assuming curve B (Fig. 18) for the
Petrographic measurements under controlled thermal conditions have been made on a large number of thin sections of NaCl ice in order to determine the specific relations between brine-pocket geometry, ring-tensile strength, and the conditions prevailing during the growth of the ice sheet. Also, a large number of additional ring-tensile tests have been completed, using ice obtained from freezing solutions in the systems Na2SO4–H2O and Na2SO4 NaCl–H2O. The results of these studies will appear later.
Acknowledgements
This paper was written as part of an investigation supported by the Snow and Ice Basic Research Branch; Snow, Ice and Permafrost Research Establishment, U.S. Army Corps of Engineers. The experimental work was carried out in the SIPRE laboratories, Wilmette, Illinois. W. F. Moll, G. Walker and R. Klaub assisted the author during the experimentation. T. R. Butkovich, C. C. Langway, J. Bender and Dr. H. Bader provided the author with many valuable suggestions. In particular, the author would like to thank Dr. A. Assur for his stimulating discussions of problems relating to sea-ice strength and for critically reading and helping to clarify many points in the final manuscript.


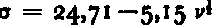 . The σ–axis intercept of this line is comparable to the a values determined for fresh ice indicating that there is little, if any, difference in stress concentration between sea and lake ice as a result of the presence of brine pockets. The strength of ice containing NaCl.2H
. The σ–axis intercept of this line is comparable to the a values determined for fresh ice indicating that there is little, if any, difference in stress concentration between sea and lake ice as a result of the presence of brine pockets. The strength of ice containing NaCl.2H



















