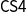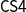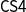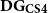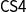A dual-context sequent calculus for the constructive modal logic S4

Abstract

The proof theory of the constructive modal logic S4 (hereafter $\mathsf{CS4}$ ) has been settled since the beginning of this century by means of either standard natural deduction and sequent calculi or by the reconstruction of modal logic through hypothetical and categorical judgments à la Martin-Löf, an approach carried out by using a special kind of sequents, which keeps two separated contexts representing ordinary and enhanced hypotheses, intuitively interpreted as true and valid assumptions. These so-called dual-context sequents, originated in linear logic, are used to define a natural deduction system handling judgments of validity, truth, and possibility, resulting in a formalism equivalent to an axiomatic system for $\mathsf{CS4}$ . However, this proof-theoretical study of $\mathsf{CS4}$ lacks, to the best of our knowledge, its third fundamental constituent, namely a sequent calculus. In this paper, we define such a dual-context formalism, called ${\bf DG_{CS4}}$ , and provide detailed proofs of the admissibility for the ordinary cut rule as well as the elimination of a second cut rule, which manipulates enhanced hypotheses. Furthermore, we make available a formal verification of the equivalence of this proposal with the previously defined axiomatic and dual-context natural deduction systems for $\mathsf{CS4}$ , using the Coq proof-assistant.

1. Introduction

Modal logics, whose origin can be traced back to Aristotle’s philosophical investigations about the truth of a proposition, have today several applications in different areas gained from distinct interpretations of the $\Box$ and $\Diamond$ modalities, dissimilar from the original readings as necessity and possibility. For instance, various type systems for concurrent and distributed computations (López et al. 2005; Murphy VII et al. 2004) employ modalities and a modal lambda calculus has been proposed to model information flow in computer networks (Borghuis and Feijs 2000). In Artificial Intelligence (AI), they are useful to model ontologies or knowledge structures, as well as for verifying agent-based computer systems, or in Philosophy, in the representation of concrete cases in modal argumentation theory, where the $\Box$ operator usually represents the argument attack relation (Boella et al. 2006; Grossi 2011).

The most widely studied modal logics are those based on classical reasoning where the duality principle $\Box A \leftrightarrow \neg \Diamond\neg A$ holds. When this principle is rejected, we land on the realm of non-classical modal logics. Although it is worth noting that there are non-classical logics where this duality principle still holds, like Lukasiewicz description logics (see Bobillo et al. 2015). However, to be more precise certain choices have to be made. For instance, the intuitionistic modal logics Fischer-Servi (1977), Plotkin and Stirling (1986) and Simpson (1994), are designed in order to obtain classical modal logics by adding the excluded middle axiom, and the constructive modal logics Alechina et al. (2001), Bierman and de Paiva (2000), and Wijesekera (1990) reject the $\Diamond$ -distributivity axioms: $\Diamond (A\lor B) \to \Diamond A \lor \Diamond B$ and $\neg\Diamond\bot$ . This last family has proved its relevance in computer science applications, for instance in concurrent and distributed programming (Moody 2004), hardware verification (Fairtlough and Mendler 1997) and programming languages semantics (Kobayashi 1997).

The proof theory of modal logics has developed mainly in two directions: on one hand Labeled Deduction Systems (Gabbay 2014; Negri 2011; Viganò 2000) which internalize the semantical approach within the syntax by means of relational atoms and labeled formulas corresponding to the forcing relation of the Kripke semantics and that are required to obey the usual features of traditional systems; on the other hand the search for pure, that is label-free, natural deduction or sequent calculi to capture modal logics has lead to the development of sophisticated formalisms like higher-arity or display calculi based on generalizations of Gentzen’s ordinary sequents: nested sequents, (tree-)hypersequents, etc. (see Indrzejczak 2010 for natural deduction modal systems and Poggiolesi 2010 for an overview of modal sequent calculi systems). In the case of the constructive modal logic $\mathsf{S4,}$ its proof theory, by means of ordinary sequent systems, is well established (Bierman and de Paiva 2000). Moreover, an alternative approach, having important applications in computer science (Davies and Pfenning 2001; Moody 2004), based on the judgmental reconstruction of modal logic was proposed in Pfenning and Davies (2001), an approach that follows the constructive philosophy of Martin-Löf (1996) by means of hypothetical and categorical judgments. This aim is realized by means of dual-context sequents, originated in linear logic (Barber and Plotkin 1997), of the form $\Delta\mid\Gamma\vdash A$ distinguishing between ordinary hypotheses belonging to $\Gamma$ and enhanced hypotheses contained in $\Delta$ . These qualifiers can be interpreted in different ways, for instance as propositional and necessary (of the form $\Box A$ ) hypotheses. However, as we will see, this intuitive interpretation is not enforced by the syntax. Dual-context systems have been further studied in several works. For instance, Kavvos (2020) discusses natural deduction systems and lambda calculi for several logics including the necessity fragment of $\mathsf{S4}$ and the logic of provability $\mathsf{GL};$ Heilala and Pientka (2007a) present a focused sequent calculus capturing the normal natural deductions of $\mathsf{S4}$ and Nanevski et al. (2008) provides a contextual modal type theory which relativizes the notion of validity with respect to arbitrary contexts. Moreover, we ourselves (González-Huesca et al. 2019; González Huesca et al. 2020) have formally verified the equivalence of the natural deduction systems for constructive $\mathsf{S4}$ of Pfenning and Davies (2001) with their Hilbert-style counterparts by means of the state-of-the-art Coq proof-assistant, such equivalence was not discussed previously in detail, except for the necessity fragment in Kavvos (2020). Further, in Miranda-Perea et al. (2020) we define a sequent calculus suitable for human-guided interactive proof-search in the necessity fragment of $\mathsf{S4}$ . It is worth noting that here, following the lines of all the above mentioned works on dual-context systems for constructive $\mathsf{S4}$ , we deal only with the positive fragment of $\mathsf{S4}$ , that is neither the constant of falsity $\bot$ nor a negation operator are present.

In this paper, we contribute to the proof theory of constructive modal logics by presenting a cut-free dual-context sequent calculus for $\mathsf{CS4}$ , called ${\bf DG_{CS4}}$ , which features two sets of left rules, one for each context, and results equivalent to the judgmental reconstruction of modal logic with the advantage of not requiring the explicit use of the judgments of validity, truth, or possibility. To the best of our knowledge, the literature lacks of such formalism, whose conception is already mentioned in Pfenning and Davies (2001). We discuss in detail the cut admissibility and elimination of the two cut rules for this calculus, together with the equivalence with its axiomatic and natural deduction counterparts, thus completing the definition of the three styles of deductive systems for the case of $\mathsf{CS4}$ . As a companion, we provide a formal verification of the systems discussed in this paper and their equivalence, developed in the Coq proof-assistant, available in https://bitbucket.org/luglzhuesca/mlogic-formalverif/src/master/DCS4/ We leave the full mechanization of cut elimination as a future work, since it constitutes an independent challenge that requires considerable additional effort consisting in automatizing at least 361 cases for each cut theorem, obtained by all possible combinations of rules deriving the premises of the cut rule, in a way corresponding to the succinct case analysis provided in our proofs of theorems in Section 7 (see Pfenning 2000 for a related endeavor). It is not our intention to explain here the companion formal verification; nevertheless, within the paper we present some results required for this task. In particular, we give some definitions and structural rules as implemented in our Coq development and follow a train-of-thought that eases the understanding of the implementation when compared with the paper definitions and proofs.

The paper is organized as follows: an axiomatic system featuring single contexts is presented in Section 3. The original judgmental reconstruction of modal logic by means of a dual-context natural deduction system is exposed in Section 4. In Section 5, we define a judgment-free natural deduction system that will serve as a bridge for the equivalence with our sequent calculus ${\bf DG_{CS4}}$ , which will be introduced in Section 6. The cut admissibility and elimination theorems are detailed in Section 7. The equivalence of all systems in this paper will be proved in Section 8. We close the paper by giving some final remarks in Section 9.

Let us start by reviewing some important definitions about syntax.

2. Formulas and Contexts

We dedicate this brief section to set up the important syntactic notions that accompany the rest of the work, namely formulas and contexts.

Modal formulas are generated by the following grammar:

\begin{equation*} \begin{array}{rclrcl}A,B & :: =&p_n \mid A\land B \mid A\lor B \mid A\to B \mid \Box A \mid \Diamond A \end{array}\end{equation*}

where $p_n$ denotes an element taken from an infinite supply of propositional variables, indexed by a natural number. Let us observe that we consider neither negation nor the constant $\bot$ . Thus, we will be dealing with modal logic obtained from minimal propositional logic with all connectives, extended with the modal operators of necessity and possibility.

All systems in this work are presented in sequent style and therefore it is adequate to state precisely what kind of contexts we will use. Following the original paper introducing dual-context systems for modal logic (Pfenning and Davies 2001), contexts are implemented as finite lists of formulas built from the empty list, denoted here by $\cdot$ , and a constructor that generates a new list from a given one by adding a new element to its right-end. This choice is also the data structure employed for the development of companion formal verification. Finite lists are formally defined as follows:

\begin{equation*} \begin{array}{rclrcl}\mathsf{L} & ::= & \cdot \mid \mathsf{L},A \end{array}\end{equation*}

The operation $\mathsf{L},A$ is usually called snoc. Furthermore, the append operation of two lists $\mathsf{L}$ and $\mathsf{L}'$ , denoted with a semicolon $\mathsf{L};\;\mathsf{L'}$ , is recursively defined as $\mathsf{L};\;\cdot=\mathsf{L}$ and $\mathsf{L};\;(\mathsf{L'},A) = (\mathsf{L};\;\mathsf{L}'),A$ . These definitions allow us to prove several useful properties by induction on contexts.

Lemma 1 (Snoc lists properties). The following properties hold:

• For all $A,\,\mathsf{L}$ , if $A\in\mathsf{L}$ then there are $\mathsf{L}_1,\mathsf{L}_2$ such that $\mathsf{L}=\mathsf{L}_1,A;\;\mathsf{L}_2$ .

• For all $A,\,\mathsf{L}_1$ and $\mathsf{L}_2$ , if $A\in \mathsf{L}_1;\;\mathsf{L}_2$ then $A \in \mathsf{L}_1$ or $A \in \mathsf{L}_2$ .

• For all A and $\mathsf{L}_1$ , if $A\in \mathsf{L}_1$ then for any $\mathsf{L}_2$ , $A\in \mathsf{L}_1;\;\mathsf{L}_2$ .

• For all A and $\mathsf{L}_2$ , if $A\in \mathsf{L}_2$ then for any $\mathsf{L}_1$ , $A\in \mathsf{L}_1;\;\mathsf{L}_2$ .

• If $\mathsf{L}_1 ;\; \mathsf{L}_2 = \mathsf{L}_3,A$ then either $\mathsf{L}_2$ is the empty list and $\mathsf{L}_1 = \mathsf{L}_3,A$ or there exists a context $\mathsf{L}_4$ such that $\mathsf{L}_2 = \mathsf{L}_4,A$ .

• If $\mathsf{L}_1;\;\mathsf{L}_2 = \mathsf{L}_3,A;\;\mathsf{L}_4$ then $A\in\mathsf{L}_1$ or $A\in\mathsf{L}_2$ .

These properties are mandatory for the formal verification. However, its use will not be mentioned in the below proofs. Furthermore, throughout this article we use the Greek letters $\Gamma$ and $\Delta$ to denote finite lists of formulas, called contexts.

3. An Axiomatic System

The traditional manner of presenting and studying modal logics is through a Hilbert-style system. Here we consider a formulation inspired by the system given by Hakli and Negri (2012) and designed to derive consequences from hypotheses using single context sequents. This is the key feature of axiomatic systems for modal logic in order to validate the deduction theorem and ease the proofs of equivalence with the other styles of deductive systems.

The set $\mathcal{A}$ of axioms defining the modal logic $\mathsf{CS4}$ is

The system manipulates single sequents of the form $\Gamma\vdash_{\mathsf{H}} A$ . The relation of modal derivability between these sequents is defined inductively by the following rules:

Let us observe that the necessitation rule concedes us to introduce a $\Box$ operator only if the formula to be boxed is a theorem. This restriction solves the controversy around the validity of the deduction theorem. Moreover, the modus ponens rule (MP) is stated in a multiplicative (independent contexts) style. The reason is that this is the natural way to establish a correspondence of $\mathsf{H}$ with an ordinary axiomatic system, one that does not handle hypotheses explicitly. Let us also note that, due to the presence of axiom ${\Diamond \mathbb{T}}$ , there is no need for an inference rule involving the $\Diamond$ operator (though see Lemma 4 below).

The deduction theorem and other relevant admissible rules in $\mathsf{H}$ , required for the formal verification, are presented next. Their proofs are included in the formalization and our previous works (see González-Huesca et al. 2019; González Huesca et al. 2020).

Theorem (Deduction Theorem). The following rule is admissible:

Corollary 2 (Principle of substitution). The following rule is admissible:

Theorem (Principle of detachment). The following rule is admissible:

Since the contexts are lists, the above rules allow only the (dis)charge of the last assumption in the context, that is, the transfer of such formula to one or the other side of the turnstile symbol. Thus, we need to admit a rule that allows us to discharge an arbitrary hypothesis in the context.

Theorem (Generalized Deduction Theorem). The following rule is admissible:

Next we state some useful structural rules working on contexts.

Lemma 3 (Structural rules). The following rules are admissible:

We show now some admissible rules which simplify the derivation process of modal formulas, namely a rule for diamond introduction and a generalization of the necessitation rule when a context is non-empty but consists only of boxed formulas.

Lemma 4 (Modal introduction rules). The following rules are admissible:

where $\Gamma^\Box=[\Box A\mid A\in \Gamma]$ .

We close the presentation of system $\mathsf{H}$ with a derivation example using the formula ${\Box(A \to B) \to \Diamond (\Box A \to \Diamond B)}$ . This formula will also be derived in the further deductive systems of this paper, in order to compare the deduction facilities of each system.

Example 3.1. The sequent $\cdot\vdash_{\mathsf{H}} \Box(A \to B) \to \Diamond (\Box A \to \Diamond B)$ is derivable.

Let us next review the original judgmental reconstruction of modal logic.

4. Dual-Context Natural Deduction with Judgments

The main reference of the dual-context approach to $\mathsf{S4}$ is the natural deduction system introduced in Pfenning and Davies (2001). This system features a treatment of propositions analyzed judgmentally, following the work of Martin-Löf (Martin-Löf and Sambin 1984) where the sequents relate three basic judgments which describe knowledge without explicit use of possible worlds semantics. Instead, formulas are labeled with semantic judgments, which follow the intuition of Kripke’s worlds, but without any reference to any formal semantics. The A true judgment denotes how to verify A under hypothetical judgments; A valid represents, by means of categorical judgments, a proposition which does not depend on true hypotheses, which intuitively means that A is true in any particular world. Finally, A poss represents a possible truth, meaning that A must be assumed as unique ordinary hypothesis, perhaps together with any number of enhanced hypotheses, in order to get a conclusion. This can be understood intuitively as A being true in an unknown world, of which we only know this truth.

In previous works (González-Huesca et al. 2019; González Huesca et al. 2020; Miranda-Perea et al. 2020), we studied and implemented this system with two main differences with respect to its original formulation. On one hand, contexts contain ordinary and not labeled formulas. Instead, we use two disjoint lists in order to omit the judgments true and valid. For instance, the hypotheses $\Diamond A\, true,\, C\to \Box B\, valid,\, \Box\,E\, true,D\, valid$ are represented, according to Pfenning and Davies (2001) (p. 516), as a list where we put together and first all valid formulas, namely $C\to \Box B\, valid,\, D\, valid,\Diamond A\, true,\, \Box\,E\, true$ whereas here we represent them with two disjoint lists separated by a $\mid$ symbol, that is $C\to \Box B,D \,\mid\, \Diamond A,\Box\,E$ , meaning that the first (second) list contains only valid (true) formulas. This choice simplifies the Coq implementation. On the other hand, we are obliged to add the rule (TP), which explicitly transforms a judgment of truth A true to a judgment of possibility A poss. Such rule is only used tacitly in Pfenning and Davies (2001) but its statement and use are mandatory for our formal verification.

Here we denote the system as ${{{\mathsf{j}\mathsf{N}}}}$ , a dual-context $\mathsf{j}$ udgmental $\mathsf{N}$ atural deduction system. The sequents in ${{{\mathsf{j}\mathsf{N}}}}$ have the form $\Delta|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} J$ where $\Delta$ and $\Gamma$ are the contexts for enhanced and ordinary hypotheses, respectively, and the succedent J is a conclusion judgment, formally defined as:

\begin{equation*} \begin{array}{rclrcl}J & ::= & A\, true\mid A\, poss \end{array}\end{equation*}

It is worth noting that, as exemplified above, the third kind of judgment, namely A valid, vanishes due to the use of contexts as disjoint lists.

The system is defined by the following inference rules:

We have two starting rules corresponding to both kinds of hypotheses, stated in the most general way allowing us to infer any formula that belongs to a context. The rule for the introduction of necessity ( $\Box\, \text{I}$ ) exactly captures the definition of validity through a categorical judgment, while the rule of necessity elimination ( $\Box\, \text{E}$ ) behaves as a substitution or cut rule where the formula $\Box A$ is used as lemma A in the enhanced hypotheses in order to prove C. See Kavvos (2020), Section 2.2.2 for a discussion in this regard. The judgment $A\, poss$ is explained with a combination of enhanced and ordinary judgments by the rules ( $\Box$ E-Poss), (TP), ( $\Diamond$ I), and ( $\Diamond$ E). The second elimination rule for the $\Box$ operator is given in order to conclude a statement of possibility $C\, poss$ , this taking advantage of a lemma of the form $\Box A\, true$ , meaning that we can dispense with the enhanced hypothesis A. It is important to mention that there is no need to derive judgments of the form $A\, valid$ since, as discussed in Pfenning and Davies (2001), the validity of A is defined as unconditional or necessary truth, that is $A\, valid$ corresponds to $\Box A\, true$ and can be constructed by the rule $(\Box I$ ).

Let us show our example theorem in this system.

Example 4.1. A derivation of the sequent $\cdot\,|\,\cdot\vdash_{{{\mathsf{j}\mathsf{N}}}} \Box(A \to B) \to \Diamond (\Box A \to \Diamond B)\, true\quad$

The following lemmas resume some structural rules and generalizations. Again, these explicit rules are not present in Pfenning and Davies (2001) but are mentioned in other related works, for instance Bierman and de Paiva (2000). The corresponding proofs are available in our previous works (see González-Huesca et al. 2019; González Huesca et al. 2020).

Lemma 5 (Structural Rules). The following rules are admissible

• Weakening

  

• Context Weakening:

  

• Exchange:

  

• Context Exchange:

  

Lemma 6 (Generalized Implication Introduction). The following rule is admissible:

Lemma 7 (Inversion Introduction rules). The following rules are admissible

The inversion of $\Diamond$ -introduction is proved using rules (TP) and ( $\Diamond$ E). This admissible rule together with ( $\Diamond$ I) constitutes a transference principle allowing to go from a judgment of truth to a judgment of possibility and back. This principle collapses the judgment $A\, poss$ and permit us to define a system free of judgment annotations, as we discuss in Section 5. Let us now focus on another important transference principle.

4.1 Formula transference between contexts

Since a sequent has two contexts, it is a natural question to ask whether we can transfer one formula between contexts. These transference processes are not discussed in Pfenning and Davies (2001), Kavvos (2020), and although some of them are stated in Bierman and de Paiva (2000) (Theorem 7), they have not been given due attention. Let us present them now.

Proposition 8 (Transference from enhanced to ordinary). The following is an admissible rule

Proof. First, we prove the case for a judgment of truth. Assuming $\Delta,A\,;\;\Delta'|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} B\, true$ we get $\Delta;\;\Delta',A|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} B\, true$ by a context exchange rule. From this, together with the obvious $\Delta;\;\Delta'|\Gamma,\Box A\vdash_{{{\mathsf{j}\mathsf{N}}}} \Box A\, true$ , the $(\Box E)$ rule yields the desired $\Delta;\;\Delta'|\Gamma,\Box A\vdash_{{{\mathsf{j}\mathsf{N}}}} B\, true$ . We can use now this rule to prove the case for a judgment of possibility, using adequately rule ( $\Diamond\,$ I) and its inverse.

This transference is achieved by deleting A from the enhanced assumptions while adding $\Box A$ to the ordinary hypotheses. This behavior considerably simplifies a backward proof-search process. We can iterate the application of this rule in such a way that the context of enhanced formulas becomes empty. However, this option is not suitable for actual proof construction in ${{{\mathsf{j}\mathsf{N}}}}$ , although plays an important role in the desired equivalence proof with respect to the axiomatic system ${\mathsf{H}}$ .

As a corollary, we obtain a rule that allows for the direct discharge of enhanced hypotheses.

Corollary 9 (Implication introduction for enhanced hypotheses). The following rule is admissible:

Proof. Straightforward using (EnhToOrd) and $(\to I)$ .

The above rule seems to be important for some special interpretations of the conditional, as in the case of lax logic where the lax implication can be defined as $\Box A\to B$ (see Pfenning and Davies 2001, Section 7). Furthermore, the rule is invertible according to the following

Proposition 10 (Detachment for boxed formulas). The following rule is admissible:

Proof. By a weakening on the premise, we get $\Delta,A;\;\Delta'|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} \!\Box A \to\! B\, true$ . On the other hand, we have $\Delta,A;\;\Delta'|\cdot\vdash_{{{\mathsf{j}\mathsf{N}}}} A\, true$ by (EHyp), which implies $\Delta,A;\;\Delta'|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} \Box A\, true$ by rule $(\Box I)$ . Finally, rule $(\to E)$ yields the desired conclusion $\Delta,A;\;\Delta'|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} \!B\, true$ .

This proposition allows us to prove the inversion of the rule in Proposition 8, according to which the transference of a boxed formula from the ordinary to the enhanced context is achieved by moving it without the box, thus converting a boxed ordinary hypothesis into a pure propositional enhanced assumption.

Proposition 11 (Transference from ordinary to enhanced). The following rule is admissible

Proof. First, we prove the case for a judgment of truth. Assuming $\Delta|\Gamma,\Box A\,;\;\Gamma'\vdash_{{{\mathsf{j}\mathsf{N}}}} B\, true$ rule (Gen $\to I$ ) yields $\Delta|\Gamma;\;\Gamma'\vdash_{{{\mathsf{j}\mathsf{N}}}} \Box A\to B\, true$ , which by rule ( $\Box\,$ Det) allows us to conclude the desired $\Delta,A|\Gamma;\;\Gamma'\vdash_{{{\mathsf{j}\mathsf{N}}}} B\, true$ . We can use now this rule to prove the case for a judgment of possibility, using adequately rule ( $\Diamond\,$ I) and its inverse.

In addition to the above rules, we show next yet another transference principle, which allows transforming a formula in the enhanced context, from the premise to the conclusion, while adding a $\Box$ .

Proposition 12 (Transference from enhanced to enhanced).

Proof. Straightforward, using $(\Box E)$ and $(\Box E-Poss)$ .

It is easy to see that the above rule is invertible. As we will see in Section 6, the presented transference principles will be relevant for the definition of our sequent calculus. Moreover, by simple combinatorics there are in total twelve possible rules capturing transference principles, three of them are unsound as they do not respect the semantic intuition. The discussion of all these rules will be presented elsewhere.

The transference rules and their corollaries provide a useful tool that considerably simplifies the actual construction of proofs as the following version of our pet example shows.

Example 4.2. A derivation of the sequent $\cdot \,|\,\cdot\vdash_{{{\mathsf{j}\mathsf{N}}}} \Box(A \to B) \to \Diamond (\Box A \to \Diamond B)\, true$ obtained by using the implication introduction for enhanced formulas.

4.2 Substitution properties in ${{{\mathsf{j}\mathsf{N}}}}$

In this section, we show that System ${{{\mathsf{j}\mathsf{N}}}}$ enjoys distinct substitution or composition properties, ensuring that derivations are closed under composition, or from a more practical point of view, guarantee the correctness of proofs organized with help of an auxiliary lemma. Since the system makes a distinction between two kinds of hypotheses or conclusions, there are multiple substitution properties gained by following a combination of a specific hypothesis (either enhanced or ordinary) and a particular conclusion judgment (either ordinary or possible). The total number of combinations is eight, but only five are appropriate and already given in Pfenning and Davies (2001, Section 5.1) where the proofs, though not present, are mentioned to succeed by structural induction on a premise.

Lemma 13 (Substitution principles). The following rules are admissible:

Proof. Rules 1 and 3 are proved directly due to the power of transference rules, which avoid the need for structural induction. Rules 2 and 4 by induction on the right premise. Details can be found in González Huesca et al. (2020).

The above four substitution principles involve a lemma A for which the judgment $A\, true$ holds. The last option considers the weak case where the lemma A only verifies the judgment $A\, poss$ . Therefore, A can only be used as a unique ordinary hypothesis in the right premise.

Lemma 14 (Substitution of a possible lemma). The following rule is admissible:

Proof. A direct consequence of the rules $(\Diamond E)$ and $(\Diamond I)$ .

It is worth noting that the primitive elimination rules, ( $\Box$ E), ( $\Box$ E-Poss), and ( $\Diamond$ E) can be gained from some transference principles, namely rule (EnhToOrd) or rule ( $\Diamond\,$ I-Inv), and a particular instance of a substitution principle when the lemma is an explicit modal proposition.

This finishes our overview of the judgmental reconstruction of modal logic. Next, we define a judgment-free version of ${{\mathsf{j}\mathsf{N}}}$ needed to simplify our equivalence proofs.

5. A Dual-Context Natural Deduction System

Due to the use of judgments $A \;\;true$ and $ A \;\;poss$ in a sequent succedent, deriving a proof in the ${{{\mathsf{j}\mathsf{N}}}}$ system might be tedious and the derived proofs tend to be long. In order to address this issue, we present in this section a dual-context natural deduction system ${{{\mathsf{N}}}}$ , which is a simplified version of ${{{\mathsf{j}\mathsf{N}}}}$ of Section 4, where the succedent consists of an ordinary formula instead of judgment of truth or possibility. This system has been previously defined at least two times. In Bierman and de Paiva (2000) (Section 5), it is presented as a multi-context formulation of IS4 that comes out as an alternative addressing the difficulties in formulating the $\Box$ introduction rule for the standard natural deduction formulation of IS4 in sequent style. As already mentioned, the context separation is inspired by works on intuitionistic linear logic. Besides this, Heilala and Pientka (2007b) proposes NJ_IS4, as a system based on Pfenning and Davies (2001), which makes no judgmental distinction between truth and possibility, by internalizing the poss judgment using the $\Diamond$ operator, a process independently identified by us and easily explained as follows: as a consequence of the $\Diamond$ -introduction rule and its inverse (Lemma 7), in ${{{\mathsf{j}\mathsf{N}}}}$ the judgment $A \; Poss$ can be replaced by $\Diamond \; A \; True$ and vice-versa. This replacement generates sequents involving only judgments of truth. In particular, the rules, and in consequence any derivation, can be transformed in such a way that only judgments of truth occur in them. Hence, the true label becomes redundant and can be completely removed.

The set of inference patterns for ${{{\mathsf{N}}}}$ is obtained by applying the internalization process and adding the usual rules for conjunction and disjunction to ${{{\mathsf{j}\mathsf{N}}}}$ , yielding the following rules:

It is worth noting that the rule ( $\Box$ E-poss) in ${{{\mathsf{j}\mathsf{N}}}}$ becomes a particular case of ( $\Box $ E) so there is no rule to add in ${{{\mathsf{N}}}}$ . Regarding ( $\Diamond$ I) in ${{{\mathsf{j}\mathsf{N}}}}$ , once the internalization has been applied, it becomes trivial for its premise and conclusion are identical. On the other hand, the internalization applied to the rule (TP) of ${{{\mathsf{j}\mathsf{N}}}}$ yields the new ( $\Diamond $ I) rule in ${{{\mathsf{N}}}}$ .

We show next a derivation of our pet example in the current system.

Example 5.1. The following is a proof of $\cdot \,|\,\cdot\vdash_{{{\mathsf{N}}}} \Box(A \to B) \to \Diamond(\Box A \to \Diamond B)$ .

With respect to the structural rules and transference principles, they hold in ${{{\mathsf{N}}}}$ as well. For example, the properties of weakening and exchange in ${{{\mathsf{j}\mathsf{N}}}}$ (Lemma 5) have analogous proofs in ${{{\mathsf{N}}}}$ . Additionally, the transfer principles are also valid. We state them next.

Proposition 15 (Transference principles). The following rules are admissible.

Proof. Straightforward.

To conclude this section, we present the substitution rules that are admissible in ${{{\mathsf{N}}}}$ . Our starting point is the set of admissible rules in Lemma 13. After substituting $A\, poss$ with $\Diamond A\, true$ , (subst-2) becomes a particular case of (subst-1), and (subst-4) becomes a particular case of (subst-3) as well. Regarding (subst-5), it collapses as a particular instance of $\Diamond $ E. Thus, we are left with two substitution rules only.

Theorem (Substitution rules). The following rules are admissible:

Proof. Straightforward.

This finishes the discussion on axiomatic and natural deduction systems for $\mathsf{CS4}$ . We are now in position of presenting the promised sequent calculus.

6. A Dual-Context Sequent Calculus

We present now the main contribution of this paper, a cut-free dual-context sequent calculus for the full constructive modal logic $\mathsf{S4}$ , called ${\bf DG_{CS4}}$ . Related dual-context formalisms are the sequent calculi MJ_IS4 and MJ^F_IS4 in Heilala and Pientka (2007a) which are focused versions of the sequent calculus LJ_IS4 presented in the unpublished technical report Heilala and Pientka (2007b) and are inspired by the sequent calculus for the intuitionistic contextual modal logic of Nanevski et al. (2008). These systems consider the enhanced context only in a parametric way. To the best of our knowledge, a dual-context sequent calculus featuring left rules for both contexts has not been defined before, except for our previous related work (Miranda-Perea et al. 2020) which only considers the box modality together with alternative left rules for implication, which, while suitable for interactive proof-search, also invalidate cut elimination.

The inference rules of ${\bf DG_{CS4}}$ are:

• Initial sequents: allowing to conclude a hypothesis according to the context it belongs.

  

• Right rules

  
  The right rules for propositional connectives and the diamond operator are standard. In the case of a modal formula $\Box A$ , the right rule corresponds to the so-called necessitation rule and allows us to introduce the box operator on the right hand side of the turnstile, only in the absence of ordinary assumptions. This rule is the dual-context version of the right rule present in single context sequent calculi since the work of Curry (1950); Curry (1952) and used later by Ohnishi and Matsumoto (1957), where to introduce $\Box A$ we are required to derive A using boxed hypotheses only.

As announced the left rules come in two versions, one for each context.

• Left rules for the ordinary context.

  
  The rules for the propositional connectives are standard. The left rule ( $\Box L$ ) captures the transference principle between contexts (Proposition 8): if we prove B using the enhanced hypothesis A, we can also derive B using the ordinary hypothesis $\Box A$ . Observing that the enhanced context is parametric in the rule for the $\Diamond$ operator, we realize that this rule is essentially the same as the left rule for standard systems apparently introduced in Ohnishi and Matsumoto (1957). This rule shows that statements of possibility interact only with themselves. That is, a possibility statement $\Diamond A$ allows to conclude only another possibility formula $\Diamond C$ , this by proving it using A as unique ordinary hypothesis.

• Left rules for the enhanced context.

  
  As usual, the formula introducing an operator in the conclusion of a left or right rule is called the principal formula of such rule, whereas its immediate subformulas, present in the premises of the rule, are called the active formulas. The enhanced left rule for conjunction is modeled after the fact that the formula $\Box(A\land B)\leftrightarrow\Box A\land\Box B$ is a theorem of $\mathsf{S4}$ . Observe that for disjunction and implication the active formulas appear in the ordinary context, otherwise the rules would be unsound. For instance, we would be able to derive $\Box (A \lor B) \to \Box A \lor \Box B$ , which is invalid in all known semantics of $\mathsf{CS4}$ . The rule ( $\Box$ LE), introduced by us in Miranda-Perea et al. (2020), says that, with respect to backward proof-search, an enhanced boxed hypothesis can be safely unboxed. Finally, the rule ( $\Diamond$ LE) follows the same idea of rule ( $\Diamond$ L).

As we will show in Section 7, ${\bf DG_{CS4}}$ is a cut-free calculus. However, due to the double context, we have to consider a specialized cut rule, in analogy to the substitution properties presented in Proposition 5, where the cut formula belongs to the enhanced context. For technical reasons, we have to keep this rule as primitive, although later we present an elimination theorem.

• Enhanced cut:

  
  In conclusion, ${\bf DG_{CS4}}$ consists of nineteen rules: two kinds of initial sequents; six right rules; five left rules; five enhanced left rules together with the enhanced cut rule. Furthermore, we introduce now a cut rule for ordinary hypotheses, hereafter called ordinary cut.

• Ordinary cut

  
  This rule is not primitive and later we will show its admissibility.

The following is an example of a derivation in ${\bf DG_{CS4}}$ :

Example 6.1. The sequent $\cdot \, \mid \, \cdot \vdash_{{{\mathsf{N}}}}\Box (A \to B) \to \Diamond (\Box A \to \Diamond B)$ is derivable.

We present now further rules required to prove the admissibility of the ordinary cut. Several proofs require a complex inductive argument, namely a simultaneous and nested induction involving both formulas and derivations. In such proofs, we can appeal to an induction hypothesis either with at least one less complex formula or with a formula of equal complexity, usually exactly the same formula involved in the inductive step, but with at least one simpler derivation. In the below proofs, we use structural complexity measures, going from subformulas to formulas and from premises to conclusions in any analized rule of a derivation. In particular, in any given inductive step it is legal to appeal to the induction hypothesis with exactly the same formula as long as at least one derivation involved decreases in complexity. Of course, these inductive arguments can also be thought of as using a numerical measure of complexity such as the number of logical operators in a formula and the height of a derivation like in Negri et al. (2001), Theorem 2.4.3. Nevertheless, we prefer to use structural measures since they ease the mechanization of the results in this section, a task that is part of future work (for a similar enterprise see Pfenning 2000). That said, let us start by proving the usual version of the exchange structural rule.

Lemma 16 (Exchange). Let $\Delta,\Delta',\Gamma,\Gamma'$ be contexts and A,B,C be formulas. The following rules are admissible

Proof. We prove the rule (Exch), since the rule (EExch) is analogous. The proof is by a simultaneous and nested structural induction on the formulas A,B and the premise. The base cases and all inductive cases where A and B are not principal formulas are direct from the I.H. In the remaining cases, A (or B) is principal. Let us show two of these cases, first when $A=_{def} A_1\to A_2$ and the premise is obtained by rule $(\to L)$ . The situation is as follows:

The case is solved by the I.H. on $A_1\to A_2$ and the left premise and by the I.H. on $A_2$ and the right premise as follows:

Next we show the most interesting case, namely when the premise is derived by rule ( $\land$ L) where the principal formula is $A=_{def} A_1\land A_2$ . The situation is:

By the I.H. on $A_2$ and the premise, we get $\Delta|\Gamma,A_1,B,A_2;\;\Gamma'\vdash_{\mathcal{G}} C$ . From this, the I.H. on $A_1$ yields $\Delta|\Gamma,B,A_1,A_2;\;\Gamma'\vdash_{\mathcal{G}} C$ . Finally we apply $(\land L)$ to get $\Delta|\Gamma,B,A_1\land A_2;\;\Gamma'\vdash_{\mathcal{G}} C$ .

Next we prove some weakening rules allowing to add a formula or a full context in a derivation.

Lemma 17 (Weakening). Let $\Delta,\Delta',\Gamma,\Gamma'$ be contexts and A,C be formulas. The following rules are admissible

Proof. The rules (Weak) and (EWeak) are proved by structural induction on the premise. For the contextual versions (Ctx-Weak) and (ECtx-Weak), we proceed by induction on the context $\Gamma'$ . When $\Gamma'=\cdot$ (respectively $\Delta'=\cdot$ ), the rules become trivial. Finally, the inductive step is straightforward from the I.H. and the rule (Weak) (respectively (EWeak)).

The above exchange and weakening rules allow us to prove the invertibility of some left rules.

Proposition 18 (Rule inversion). The following rules are admissible:

Proof. Each rule is proved by structural induction on the premise.

Apart from these rules, let us observe that rule ( $\to$ LE) is trivially invertible on its right premise as well as rule ( $\lor$ LE) on both premises. Moreover, it is easy to see that the remaining rules of ${\bf DG_{CS4}}$ are non-invertible.

Let us now present a quite general exchange structural rule, one that is independent from the order imposed by having defined contexts as lists. Such rule is usually not mentioned but used tacitly appealing to a repeated use of the simple exchange rule. However, it is mandatory to define it explicitly for the sake of formal verification. Our approach uses a non-deterministic insertion predicate for finite lists à la Prolog, specified as follows: ${\sf Insert}\,A\;\mathsf{L}\;\mathsf{L'}$ holds if and only if $\mathsf{L}'$ is obtained by inserting A to $\mathsf{L}$ . An inductive definition is given by the following rules:

The insertion predicate preserves derivations in the following sense:

Lemma 19. If $\mathsf{Insert}\;A\;\Gamma\;\Gamma'$ and $\Delta|\Gamma,A\vdash_{\mathcal{G}} C$ then $\Delta|\Gamma'\vdash_{\mathcal{G}} C$ .

Proof. By induction on the predicate $\mathsf{Insert}\;A\;\Gamma\;\Gamma'$ . The proof is analogous to that for the next lemma.

Lemma 20. If $\mathsf{Insert}\;A\;\Delta\;\Delta'$ and $\Delta,A|\Gamma\vdash_{\mathcal{G}} C$ then $\Delta'|\Gamma\vdash_{\mathcal{G}} C$ .

Proof. By induction on the predicate ${\sf Insert}\;A\;\Delta\;\Delta'$ . The base case is trivial since what we need to prove is exactly the assumption $\Delta,A|\Gamma\vdash_{\mathcal{G}} C$ . Assume now that ${\sf Insert}\;A\;(\Delta,B)\;(\Delta',B)$ holds, since ${\sf Insert}\;A\;\Delta\;\Delta'$ , and that $\Delta,B,A|\Gamma\vdash_{\mathcal{G}} C$ . The following derivation solves the inductive step:

We define now a permutation predicate by the following rules, where $\mathsf{Perm}\,\Gamma\,\Gamma'$ holds if and only if $\Gamma'$ is a permutation of $\Gamma$ :

Next we state the admissibility of the mentioned general permutation rule that allows us to reason as if the list contexts were multisets. We need one rule for each context.

Proposition 21. The following rules are admissible:

Proof. Induction on the predicate $\mathsf{Perm}\,\Gamma\,\Gamma'$ , respectively $\mathsf{Perm}\,\Delta\,\Delta'$ , using Lemmas 19 and 20. We prove the first rule. The base case is trivial since what we need to show is exactly the assumption $\Delta|\cdot\vdash_{\mathcal{G}} C$ . Let us assume now that $\mathsf{Perm}\,(\Gamma,A)\;\Gamma''$ , where $\mathsf{Perm}\,\Gamma\;\Gamma'$ and $\mathsf{Insert}\, A\;\Gamma'\;\Gamma''$ , and that $\Delta|\Gamma,A\vdash_{\mathcal{G}} C$ . The inductive step is solved as follows:

As usual, from now on we will use these permutation rules tacitly, that is, without mentioning them.

Next we deal with some structural rules for contraction.

Proposition 22 (Admissibility of contraction). The following rules are admissible:

Proof. First we must prove the rule for enhanced contraction (EContr). This is done by a straightforward nested structural induction on the contracted formula A and on the premise. Next we prove the rule for ordinary contraction (Contr) in a similar way. The need to prove first the enhanced contraction rule becomes manifest here in the inductive case when $A=\Box B$ is introduced by rule $(\Box L)$ . The situation is:

This occurrence of (Contr) disappears in favor of an enhanced contraction on B as follows:

We can now generalize the contraction rules in order to delete duplicate contexts.

Proposition 23. The following rules are admissible:

Proof. To prove (Ctx-contr) we proceed by induction on $\Gamma$ . In the base case, the rule becomes trivial. The inductive step goes as follows:

The rule (ECtx-contr) is analogously proved by means of an induction on $\Delta$ using adequately $(\Box L)$ , (Contr) and $({\Box L)}^{inv}$ .

Due to the use of two contexts, there is yet another possibility for a formula to be repeated to the left of the turnstile, handled by the next rule, which appears as a primitive rule in the sequent calculus of Heilala and Pientka (2007b).

Proposition 24. The following specialized contraction rule is admissible:

Proof. By a simultaneous and nested structural induction on the premise $\Delta,A;\;\Delta'|\Gamma,A;\;\Gamma'\vdash_{\mathcal{G}} C$ and the contracted formula A. In some cases, we will need the inversion of a rule (Proposition 18). The base case, the inductive cases for right rules, the enhanced cut rule and for left rules where the contracted formula A is not principal are straightforward. Below we present some of the remaining cases, including those involving modalities.

• The premise is obtained by rule $(\lor L)$ . Let $A\equiv A_1\lor A_2$ . The situation is:

  
  The occurrence of (SContr) is eliminated in favor of an ordinary contraction on the enhanced context:
  

• The premise is obtained by rule $(\land LE)$ . Let $A\equiv A_1\land A_2$ . The situation is:

  
  The case is solved as follows, using the I.H. in both $A_1$ and $A_2$ :
  

• The premise is obtained by rule $(\Box L)$ . The situation is:

  
  The occurrence of (SContr) is replaced by an ordinary contraction in the enhanced context.
  

• The premise is obtained by rule $(\Box LE)$ . The situation is:

  
  The occurrence of (SContr) is replaced by an ordinary contraction in the enhanced context.
  

• The premise is obtained by rule $(\Diamond L)$ . The situation is:

  
  The occurrence of (SContr) vanishes using an adequate instance of the enhanced rule $(\Diamond LE)$ :
  

• The premise is obtained by rule $(\Diamond LE)$ . Is analogous to the previous subcase.

We have now everything we need for cut elimination.

7. Ordinary Cut Admissibility and Enhanced Cut Elimination

This section is devoted to prove the admissibility of the ordinary cut rule in ${\bf DG_{CS4}}$ as well as the eliminability of the enhanced cut rule. Since we need both approaches to verify that the two cut rules are dispensable, it is adequate to recall their differences: admissibility of a rule R in any deductive system $\mathbf{S}$ means that such rule is not primitive but can be simulated in $\mathbf{S}$ , whereas eliminability means that R is a primitive, but redundant, rule of $\mathbf{S}$ . That is, any derivation in $\mathbf{S}$ can be transformed into a derivation in $\mathbf{S}$ that does not have occurrences of R. For a detailed discussion about the relationship between admissibility and eliminability, see Section 1.8.1 in Indrzejczak (2021).

Theorem (Cut Admissibility). The cut rule is admissible:

Proof. The proof is by a simultaneous and triple nested structural induction on the cut formula A and both premises. Let $\mathcal{L}$ be the left premise $\Delta_1|\Gamma_1\vdash_{\mathcal{G}} A$ and $\mathcal{R}$ be the right premise $\Delta_2|\Gamma_2,A\vdash_{\mathcal{G}} B$ . In the base case either $\mathcal{L}$ or $\mathcal{R}$ is an initial sequent. The most interesting cases are when $\mathcal{L}$ is an instance of (Hyp) or (EHyp), for they require the use of the specialized contraction rule (Proposition 24). Let us present the case for (EHyp), which means that $A\in\Delta_1$ . The cut vanishes as follows:

Next we consider the inductive cases where at least one of the premises is derived by (ECut)

• $\mathcal{L}$ was derived by (Ecut). This case is analogous to the next one.

• $\mathcal{R}$ is derived by (Ecut). The cut is:

  
  This instance of (Cut) is shown admissible as follows:
  
  where the new ordinary cut is admissible due to the I.H., since its right premise, namely $\Delta_2,C|\Gamma_2,A\vdash_{\mathcal{G}} B$ , has a structurally simpler derivation than the right premise of the original cut.

To solve the remaining inductive cases, we make a case analysis according to whether the cut formula A is principal, meaning that A is the formula introduced by a left or right rule in order to obtain such premise, in both or only one of the premises. This suffices since the case where A is not principal in neither premise does not need to be treated separately (see the remark at the end of case (2) below). We present all cases involving modalities. The propositional cases are omitted since they are solved in an analogous way to the proof for a standard sequent calculus for intuitionistic logic.

1. (1) The cut formula A is principal in both premises $\mathcal{L}$ and $\mathcal{R}$ . There are two subcases.

2. (a) Subcase $A\equiv\Box C$ . The cut is as follows:

   
   This cut is eliminated in favor of an enhanced cut by the I.H. on C and the above premises:
   

3. (b) Subcase $A\equiv\Diamond C$ . The cut is:

   
   The cut is eliminated as follows by the I.H., in favor of a cut on C and the above premises:
   

This finishes the first case.

1. (2) The cut formula A is not principal in the right premise $\mathcal{R}$ . There are six subcases.

   1. (a) $\mathcal{R}$ is derived by $(\Box R)$ . The cut is:

      
      In this case, the cut vanishes in favor of an application of the rule $(\Box R)$ .
      

   2. (b) $\mathcal{R}$ is derived by $(\Diamond R)$ . The cut is:

      
      The cut is permuted above $(\Diamond R)$ as follows, by the I.H. on the above premises.
      

   3. (c) $\mathcal{R}$ is derived by $(\Box L)$ . The cut is:

      
      where $\Gamma_2=\Sigma,\Box C;\;\Sigma'$ . The cut is permuted above $(\Box L)$ by the I.H on the above premises as follows:
      

   4. (d) $\mathcal{R}$ is derived by $(\Box LE)$ . Is analogous to the previous subcase.

   5. (e) $\mathcal{R}$ is derived by $(\Diamond L)$ . Is analogous to the next subcase.

   6. (f) $\mathcal{R}$ is derived by $(\Diamond LE)$ . The cut is:

      
      where $\Diamond C\in \Delta_2$ . The cut vanishes as follows:
      

This finishes the second case. Let us observe that since the left premise $\mathcal{L}$ is parametric in the above six subcases, the general case where A is not principal in neither of the premises is already covered by the above six subcases.

1. (3) The cut formula A is not principal in the left premise. There are four subcases.

   1. (a) $\mathcal{L}$ is derived by $(\Box L)$ . The cut is:

      
      where $\Gamma_1=\Sigma,\Box C;\;\Sigma'$ . The cut is permuted above $(\Box L)$ as follows, by the I.H. on the above premises.
      

   2. (b) $\mathcal{L}$ is derived by $(\Box LE)$ . Is analogous to the previous subcase.

   3. (c) $\mathcal{L}$ is derived by $(\Diamond L)$ . W.l.o.g, we can assume that the cut formula A is principal in the right premise, since the opposite case has already been considered. Let $\Diamond C\in\Gamma_1$ and $A\equiv \Diamond D$ . The cut is:

      
      where the cut is permuted above $(\Diamond L)$ as follows, by the I.H. on the left premise above and a new right premise with the same structure of the above right derivation.
      

   4. (d) $\mathcal{L}$ is derived by $(\Diamond LE)$ . Is analogous to the previous subcase.

This finishes the third case and the proof of the admissibility of the ordinary cut rule.

Next we prove an elimination theorem for enhanced cuts. It is worth noting that due to technical reasons, we were not able to prove the admissibility of the (Ecut) rule in a similar way to the Cut Admissibility Theorem. Though the below proof is quite analogous.

Theorem (Enhanced cut elimination). Every derivation $\pi$ in ${\bf DG_{CS4}}$ can be transformed into a derivation $\widehat{\pi}$ with no occurrences of the rule (Ecut).

Proof. It suffices to consider a derivation $\pi$ with only one occurrence of (Ecut). Let $\mathcal{L}$ be the left premise $\Delta|\cdot\vdash_{\mathcal{G}} A$ and $\mathcal{R}$ be the right premise $\Delta,A|\Gamma\vdash_{\mathcal{G}} B$ of such cut. To construct $\widehat{\pi,}$ we proceed now as in the proof of the Cut Admissibility Theorem.

The base case of the nested induction does not pose a challenge: if $\mathcal{L}$ is an initial sequent, it can only be (EHyp), since $\Gamma$ is empty. Thus, the cut vanishes by an enhanced contraction on $\mathcal{R}$ . When $\mathcal{R}$ is an instance of (Hyp), the conclusion of cut is again an instance of (Hyp) and the enhanced cut is dispensable. The same happens when $\mathcal{R}$ is an instance of (EHyp) with $B\in \Gamma$ . The remaining subcase is when $B=A$ and the cut disappears by an application of context weakening (rule (Ctx-Weak)) on $\mathcal{L}$ . For the inductive cases, we omit again those for propositional connectives and present all cases involving modalities.

1. (1) The cut formula A is principal in both premises $\mathcal{L}$ and $\mathcal{R}$ . There are two subcases.

2. (a) Subcase $A\equiv\Box C$ . The cut is as follows:

   
   The cut is eliminated in favor of an enhanced cut using the I.H. on C and the above premises:
   

3. (b) Subcase $A\equiv\Diamond C$ . The cut is:

   
   This cut is eliminated as follows:
   
   where the enhanced cut is eliminable by the I.H., since it has a structurally simpler right premise. This finishes the first case.

4. (2) The cut formula A is not principal in the right premise $\mathcal{R}$ . There are six subcases.

   1. (a) $\mathcal{R}$ is derived by $(\Box R)$ . The cut is:

      
      This cut is permuted above $(\Box R)$ by the I.H. on the above premises:
      

   2. (b) $\mathcal{R}$ is derived by $(\Diamond R)$ . This subcase is analogous to the corresponding one for an ordinary cut.

   3. (c) $\mathcal{R}$ is derived by $(\Box L)$ . This subcase is analogous to the corresponding one for an ordinary cut.

   4. (d) $\mathcal{R}$ is derived by $(\Box LE)$ . This subcase is analogous to the corresponding one for an ordinary cut.

   5. (e) $\mathcal{R}$ is derived by $(\Diamond L)$ . Let $\Diamond C\in\Gamma$ . The cut is:

      
      This cut is permuted by the I.H on the premises:
      

   6. (f) $\mathcal{R}$ is derived by $(\Diamond LE)$ . Is analogous to the previous subcase.

This finishes the second case. Let us observe again, that since the left premise is parametric in all the above subcases, the case when A is not principal in neither premise is already covered here.

1. (3) The cut formula A is not principal in the left premise $\mathcal{L}$ . Since the ordinary context is empty in the left premise, we only have to consider two subcases.

2. a. $\mathcal{L}$ is derived by $(\Box LE)$ . Is analogous to the corresponding subcase for an ordinary cut.

3. b. $\mathcal{L}$ is derived by $(\Diamond LE)$ . W.l.o.g we can assume that the cut formula A is principal in the right premise, say $A\equiv \Diamond D$ , since the opposite case has already been considered. Let $\Diamond C\in\Delta$ . The situation is:

   
   This cut is eliminated as follows:
   
   where the (Ecut) is justified by the I.H. since the right premise is simpler. This finishes the third case and the whole proof.

Since, according to the Cut Admissibility and Enhanced Cut Elimination theorems, both cut rules are dispensable and by simple inspection we can verify that all formulas in a premise of a left or right inference rule also occur in the conclusion of the same rule we immediately gain the subformula property

Corollary 25 (Subformula property). Any formula occurring in a derivation of $\Delta|\Gamma\vdash_{\mathcal{G}} C$ is a subformula of $\Delta,\Gamma$ or C.

This ends our presentation of the sequent calculus ${\bf DG_{CS4}}$ . Let us exhibit next the equivalence of this formalism with the previously discussed systems for $\mathsf{CS4}$ .

8. Equivalence

In this section, we summarize the equivalence properties of ${{\bf DG_{CS4}}}$ with the previously discussed axiomatic and natural deduction, this way ensuring that our sequent calculus actually corresponds to $\mathsf{CS4}$ . Although a direct proof of equivalence between ${{{\mathsf{j}\mathsf{N}}}}$ and ${{\bf DG_{CS4}}}$ could be provided, for the sake of reuse our previous formal verification in Coq (González Huesca et al. 2020), we prefer to use systems $\mathsf{H}$ and ${{{\mathsf{N}}}}$ as a bridge. This way, we also confirm the equivalence between the axiomatic and the judgment-free natural deduction system for $\mathsf{CS4}$ . Since we provide the mechanization, we do not give here the proofs details.

The equivalence between the judgmental natural deduction system ${{{\mathsf{j}\mathsf{N}}}}$ and its axiomatic counterpart $\mathsf{H}$ is achieved by using translations in both directions. From axiomatic to natural deduction proofs, the translation simulates the original proof by ignoring the enhanced context, this is straightforward since the Hilbert-style system handles sequents already. If instead, a derivation in $\mathsf{H}$ was a sequence of formulas, we would need a mechanism to collect the assumptions in a given deduction to being able to construct a context in ${{{\mathsf{j}\mathsf{N}}}}$ , as it is done for example in von Plato (2014). This certainly would complicate the implementation. On the other direction, the idea is to follow Proposition 8 to empty the enhanced context, thus getting a context of ordinary assumptions which can be directly managed in $\mathsf{H}$ .

Theorem (Equivalence between axiomatic and judgmental natural deduction proofs).

1. (1) If $\Gamma\vdash_{\mathsf{H}} A$ then $\cdot\,|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} A\, true$ and if $\Gamma\vdash_{\mathsf{H}} \Diamond A$ then $\cdot\,|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} A\, poss$ .

2. (2) $\text{If }\Delta|\Gamma\vdash_{{{\mathsf{j}\mathsf{N}}}} J \text{ then } \Delta^\Box ;\;\Gamma\vdash_{\mathsf{H}} J^t$

where $J^t$ is defined as $(A\, true)^t=A$ and $(A\, poss)^t=\Diamond A$ .

Proof. Each implication is proved by structural induction on the premise. See González Huesca et al. (2020) for details.

The equivalence between ${{{\mathsf{N}}}}$ and $\mathsf{H}$ is proved following the same idea as above but the proofs are simpler since system ${{{\mathsf{N}}}}$ is free of judgments.

Theorem (Equivalence between axiomatic and natural deduction proofs).

Proof. Each implication is proved by structural induction on the premise.

Finally, the equivalence between the natural deduction system ${{{\mathsf{N}}}}$ and the sequent calculus ${{\bf DG_{CS4}}}$ is proved, again by a structural induction, showing that the rules of one system are admissible in the other.

Theorem (Equivalence between natural deduction and sequent calculus proofs).

Proof. Structural induction on the premises $\Delta\,|\Gamma\vdash_{{{\mathsf{N}}}} A$ and $\Delta|\Gamma\vdash_{\mathcal{G}} A$ , respectively.

Since we provide a formal verification of these equivalences, we do not give here further proof details. However, it is important to note that, considering that the cut admissibility and elimination theorems are not verified, the results here stated are mechanized using ${\bf DG_{CS4}}^{\boldsymbol{+}}$ , that is the version of ${\bf DG_{CS4}}$ where the ordinary cut rule is primitive. Of course, this is harmless for the here presented results. This finishes our exposition.

9. Final Remarks

This paper introduces a dual-context sequent calculus ${\bf DG_{CS4}}$ for the constructive modal logic $\mathsf{S4}$ , thus completing the three styles of deductive systems for this logic. Our calculus is related to the system LJ_IS4 of the unpublished technical report Heilala and Pientka (2007b) but features initial sequents and left rules for both contexts, thus generating a deterministic set of inference rules. The ordinary left rule ( $\Box$ L) for necessity is gained from a transference property between contexts (Section 4.1, Proposition 15) which, though previously stated in natural deduction (Bierman and de Paiva 2000, Theorem 7), has not been further exploited before. Moreover, the rule ( $\Box$ LE) comes from yet another transference principle (Proposition 12) which, although quite natural, in our best knowledge has not been mentioned before. Finally, the left rules for possibility are directly gained from the corresponding elimination rule in natural deduction. With respect to the cut reasoning patterns, in order to prove the admissibility of the ordinary cut we require to keep the enhanced cut as primitive and later prove that it is eliminable. This way, both inductive proofs succeed. In our opinion, this proving process provides an interesting example of the difference between the admissibility and the elimination of an inference rule.

To prove that ${\bf DG_{CS4}}$ exactly corresponds to $\mathsf{CS4}$ , we provide an equivalence chain that goes from the sequent calculus to the judgmental natural deduction system ${{{\mathsf{j}\mathsf{N}}}}$ passing through the judgment-free natural deduction system ${{{\mathsf{N}}}}$ and the axiomatic system $\mathsf{H}$ . This chain of equivalences has been formally verified using the Coq proof-assistant. With the purpose of providing a better understanding of our formal development, we presented several structural inference rules which may be considered redundant, but that facilitate the understanding of the Coq code.

As current and future lines of research, we mention the mechanization of our cut admissibility and elimination theorems, a non-trivial task that requires the programming of several tactics in Coq in order to automatize more than 360 subcases in each of the two theorems, as well as the development of proof-search procedures based on ${{\bf DG_{CS4}}}$ , following the lines of Heilala and Pientka (2007a). A further line of research refers to the extension of the dual-context approach to the classical version of $\mathsf{S4}$ to improve and simplify some existent proof-search procedures (Andrikonis 2012; Pliuškevičius and Pliuškevišienė 2008). We conjecture that these methods can be simplified with the dual-context approach since the left rules for necessity safely eliminate $\Box A$ in the premise, which certainly simplifies the backward proof-search procedure. Another interesting task consists in proving the equivalence of dual-context systems with the ordinary natural deduction and sequent calculus for $\mathsf{S4}$ given in Bierman and de Paiva (2000). This seems straightforward in the paper but a formal verification is challenging in the case of natural deduction since the rules for $\Box$ -introduction and $\Diamond$ -elimination schematically represent an infinite family of rules. As future work, we mention the use of dual-context systems in proof-search related to the work on multi-agent dialogues of Sticht (2018) and the study of the semantical aspects and tools that will allow us to obtain completeness theorems for the here presented systems but also equivalent labeled deduction systems.