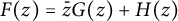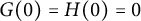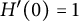Landau-type theorems for certain bounded bi-analytic functions and biharmonic mappings

Abstract

In this article, we establish three new versions of Landau-type theorems for bounded bi-analytic functions of the form $F(z)=\bar {z}G(z)+H(z)$, where G and H are analytic in the unit disk with $G(0)=H(0)=0$ and $H'(0)=1$. In particular, two of them are sharp, while the other one either generalizes or improves the corresponding result of Abdulhadi and Hajj. As consequences, several new sharp versions of Landau-type theorems for certain subclasses of bounded biharmonic mappings are proved.

1 Introduction and preliminaries

One of the open problems in classical complex analysis is to obtain the precise value of the Bloch constant for analytic functions in the unit disk. In [6], Chen et al. considered the analogous problem of estimating the Bloch constant for planar harmonic mappings. See also the work of Chen and Guathier [5] for planar harmonic and pluriharmonic mappings. Motivated by the work from [6], this topic was dealt by a number of authors with considerable improvements over the previously known Landau-type theorems. These will be indicated later in this section. In this article, we consider bi-analytic and biharmonic mappings and establish several new sharp versions of Landau-type theorems for these two classes of mappings.

1.1 Definitions and notations

A complex-valued function f is a bi-analytic (resp. harmonic) on a domain $D\subset \mathbb {C}$ if and only if f is twice continuously differentiable and satisfies the bi-analytic equation $f_{\bar {z}\bar {z}}(z)=0$ (resp. Laplacian equation $f_{z\overline {z}}(z)=0$ ) in D, where we use the common notations for its formal derivatives:

$$ \begin{align*} f_z=\frac{1}{2}(f_x - i f_y),~\mbox{ and }~f_{\overline{z}}=\frac{1}{2}(f_x + i f_y), \quad z=x+iy. \end{align*} $$

Note also that

$$ \begin{align*}\Delta f=4f_{z\overline{z}}=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}. \end{align*} $$

It is well-known that every bi-analytic function f in a simply connected domain D has the representation (cf. [1])

$$ \begin{align*} f(z)=\bar{z}g(z)+h(z), \end{align*} $$

where g and h are complex-valued analytic functions in D. Similarly, every harmonic function f in a simply connected domain D can be written as $f=h+\overline {g}$ with $f(0)=h(0)$ , where g and h are analytic on D (for details, see [11]).

A complex-valued function F is said to be biharmonic on a domain $D\subset \mathbb {C}$ if and only if F is four times continuously differentiable and satisfies the biharmonic equation $\Delta (\Delta f)=0$ in D. It is well-known (cf. [3]) that a biharmonic mapping F in a simply connected domain D has the following representation:

$$ \begin{align*} F(z)=|z|^2G(z)+H(z), \end{align*} $$

where G and H are harmonic in D.

A domain $D\subset \mathbb {C}$ is said to be starlike if and only if the line segment $[0,w]$ joining the origin $0$ to every other point $w\in D$ lies entirely in D.

Definition 1.1 (cf. [23–25])

A continuously differentiable function F on $\mathbb{D}=\{z: |z|<1\}$ is said to be fully starlike in $\mathbb{D}$ if it is sense-preserving, $F(0)= 0, F(z)\neq 0$ in $\mathbb{D}\backslash \{0\}$ and the curve $F(re^{it})$ is starlike with respect to the origin for each $r\in (0, 1)$ . The last condition is same as saying that

$$ \begin{align*} \frac{\partial\arg F(re^{it})}{\partial t} =\mathrm{Re}\bigg(\frac{z F_z(z)- \bar{z} F_{\bar z}(z)}{F(z)}\bigg)> 0 \end{align*} $$

for all $z = r\, e^{it}$ and $r\in (0, 1)$ .

For a complex-valued function f in D, its Jacobian $J_f(z)$ is given by $J_f(z)=|f_z(z)|^2-|f_{\overline {z}}(z)|^2$ . We say that a harmonic mapping f is locally univalent and sense-preserving if and only if its Jacobian $J_f(z)>0$ for $z\in D$ (cf. [16]). For continuously differentiable function f, let

$$ \begin{align*} \Lambda_{f}(z) =|f_{z}(z)|+|f_{\overline{z}}(z)| ~\mbox{ and }~ \lambda_{f}(z) =\big ||f_{z}(z)|-|f_{\overline{z}}(z)|\big |. \end{align*} $$

Throughout, ${\mathbb D}_{r}=\{z\in \mathbb {C}:\,|z|<r\}$ denotes the open disk about the origin so that ${\mathbb D}:= {\mathbb D}_1$ is the unit disk. For the convenience of the reader, let us fix some basic notations.

• • $\mathrm {Hol}({\mathbb D})=\{f:\, f \mbox { is analytic in } \mathbb {D}\}$ .

• • $\mathcal {B}_M=\{f \in \mathrm {Hol}({\mathbb D}):\, |f(z)|\leq M ~\mbox { in } {\mathbb D}\}.$

• • $\mathcal {A}_0=\{f \in \mathrm {Hol}({\mathbb D}):\, f(0) =0\}$ and $\mathcal {A}_1=\{f \in \mathrm {Hol}({\mathbb D}):\, f'(0) =1\}.$

• • $\mathcal {A}=\{f \in \mathrm {Hol}({\mathbb D}):\, f(0) =0=f'(0)-1\}:= \mathcal {A}_1 \cap \mathcal {A}_0.$

• • $\mathcal {H}=\{f:\, f \mbox { is harmonic in } \mathbb {D}\}.$

• • $\mathcal {H}_0=\{f\in \mathcal {H}:\, f(0) =0\}.$

• • $\mathcal {BH}_M=\{f\in \mathcal {H}:\, |f(z)|\leq M ~\mbox { in } {\mathbb D}\}.$

• • $\mathcal {BH}_M^0= \mathcal {BH}_M\cap \mathcal {H}_0.$

• • $\mathrm {Bi}\mathcal {H}=\{f:\, f \mbox { is biharmonic in } \mathbb {D}\}.$

• • $\mathrm {Bi}\mathcal {A}_0=\{f:\, f \mbox { is bi-analytic in } \mathbb {D} \mbox { with } f(0)=0\}.$

Definition 1.2 A function f in a family is said to belong to ${\mathcal S}(r;R)$ if it is univalent in ${\mathbb D}_r$ and the range $f(\mathbb {D}_r)$ contains a schlicht disk $\mathbb {D}_R$ .

1.2 Landau and Bloch theorems

The classical theorem of Landau states that if $f\in \mathcal {B}_M \cap \mathcal {A}$ for some $M>1$ , then $f\in {\mathcal S}(r;R)$ with $r=1/(M+\sqrt {M^2-1})$ and $R=Mr^2$ . This result is sharp, with the extremal function $f_0(z)=M z \frac {1-Mz}{M-z}$ .

The Bloch theorem asserts the existence of a positive constant number b such that if $f\in \mathcal {A}_1$ , then $f({\mathbb D})$ contains a schlicht disk of radius b, that is, a disk of radius b which is the univalent image of some subregion of the unit disk ${\mathbb D}$ . The supremum of all such constants b is called the Bloch constant (see [6, 13]).

In 2000, under a suitable restriction, Chen et al. [6] first established two non-sharp versions of Landau-type theorems for bounded harmonic mapping on the unit disk which we now recall with the help of our notation.

Theorem A [6, Theorem 3]

If $f\in \mathcal {BH}_M^0$ with the normalization $f_{\overline {z}}(0)=0$ and $f_z(0)=1$ , then $f\in {\mathcal S}(r_1;r_1/2)$ , where

$$ \begin{align*} r_1=\frac{\pi^2}{16 m M}\approx\frac{1}{11.105M}, \end{align*} $$

where $m\approx 6.85$ is the minimum of the function $(3-r^2)/(r(1-r^2))$ for $0<r<1$ .

Theorem B [6, Theorem 4]

If $f\in \mathcal {H}_0$ such that $\lambda _f(0)=1$ , and $\Lambda _f(z)\leq \Lambda $ for $z\in {\mathbb D}$ , then $f\in {\mathcal S}(r_2;r_2/2)$ , where $r_2=\frac {\pi }{4(1+\Lambda )}.$

Theorems A and B are not sharp. Better estimates were given in [12] and this topic was later dealt by a number of authors (cf. [5, 7, 9, 10, 14, 15, 18, 19]). In 2008, Abdulhadi and Muhanna established two versions of Landau-type theorems for certain bounded biharmonic mappings in [2]. For later developments on this topic, we refer to [8, 9, 17, 20, 22, 26]. In particular, sharp versions of Theorem B have been established in [15, 18, 19], and the corresponding sharp versions of Landau-type theorems for normalized bounded biharmonic mappings have also been established in [21].

Theorem C [21, Theorem 3.1]

Suppose that $\Lambda _1\geq 0$ and $\Lambda _2>1$ . Let $F\in \mathrm {Bi}\mathcal {H}$ and $F(z)=|z|^2G(z)+H(z)$ , where $G,H\in \mathcal {H}_0$ , $\lambda _{F}(0)=1,~\Lambda _{G}(z)\leq \Lambda _1$ and $\Lambda _{H}(z)<\Lambda _2$ for all $z\in {\mathbb D}$ . Then $F\in {\mathcal S}(r_3;R_3)$ , where $r_3$ is the unique root in $(0,\,1)$ of the equation

$$ \begin{align*} \Lambda_2\, \frac{1-\Lambda_2 r}{\Lambda_2-r}-3\Lambda_1 r^2=0, \end{align*} $$

and

$$ \begin{align*} R_3=\Lambda_2^2r_3+\left(\Lambda_2^3-\Lambda_2\right)\ln\left(1-\frac{r_3}{\Lambda_2}\right)-\Lambda_1 r_3^3. \end{align*} $$

This result is sharp.

Theorem D [21, Theorem 3.3]

Suppose that $\Lambda \geq 0$ . Let $F\in \mathrm {Bi}\mathcal {H}$ and $F(z)=|z|^2G(z)+H(z)$ , where $G,H\in \mathcal {H}_0$ , $\lambda _{F}(0)=1, \Lambda _{G}(z)\leq \Lambda $ and $\Lambda _H(z)\leq 1$ for all $z\in {\mathbb D}$ . Then $F\in {\mathcal S}(r_4;R_4)$ , where

$$ \begin{align*}r_4= \left \{ \begin{array}{rl} 1, &\mbox{ when } \displaystyle 0\leq\Lambda\leq\frac{1}{3}, \\ \displaystyle \frac{1}{\sqrt{3\Lambda}}, &\mbox{ when } \displaystyle \Lambda>\frac{1}{3}, \end{array} \right. \end{align*} $$

and $R_4=r_4-\Lambda r_4^{3}$ . This result is sharp.

However, the sharp version of Landau-type theorem for normalized bounded harmonic mappings or Theorem A for the case of the bound $M>1$ has not been established. In 2022, Abdulhadi and Hajj established the following non-sharp Landau-type theorem for certain bounded bi-analytic functions.

Theorem E [1]

Let $F\in \mathrm {Bi}\mathcal {A}_0$ and $F(z)=\bar {z}G(z)+H(z)$ , where $G, H\in \mathcal {A}\cap \mathcal {B}_M $ for some $M>0$ . Then, $F\in {\mathcal S}(r_5;R_5)$ , where

$$ \begin{align*} r_5=1-\sqrt{\frac{2M}{2M+1}} ~\mbox{ and }~ R_5=r_5-r_5^2-M\frac{r_5^2+r_5^3}{1-r_5}. \end{align*} $$

Theorem E is not sharp too.

1.3 Two natural question on Landau-type theorem

From the discussion above, a couple of natural questions arise.

Problem 1.3 Can we establish some sharp versions of Landau-type theorems for certain bounded bi-analytic functions?

Problem 1.4 Whether we can further generalize and/or improve Theorem E?

The article is organized as follows: In Section 2, we present statements of four theorems out of which one of them improves Theorem E. In addition, we provide several sharp versions of Landau-type theorems for certain bounded bi-analytic functions, which provide an affirmative answer to Problems 1.3 and 1.4. In particular, as consequence, we also obtain four sharp versions of Landau-type theorems for certain bounded biharmonic mappings. In Section 3, we state a couple of lemmas which are needed for the proofs of main results in Section 4.

2 Statement of main results and remarks

We first establish the following sharp version of Landau-type theorem for certain subclass of bounded bi-analytic functions.

Theorem 2.1 Suppose that $\Lambda _1\geq 0$ and $\Lambda _2>1$ . Let $F\in \mathrm {Bi}\mathcal {A}_0$ and $F(z)=\bar {z}G(z)+H(z)$ , where $G\in \mathcal {A}_0$ , $H\in \mathcal {A}$ , $|G'(z)|\leq \Lambda _1$ and $|H'(z)|<\Lambda _2$ for all $z\in {\mathbb D}$ . Then $F\in {\mathcal S}(\rho _1;\sigma _1)$ , where

(2.1) $$ \begin{align} \rho_1=\frac{2\Lambda_2}{\Lambda_2(2\Lambda_1+\Lambda_2)+\sqrt{\Lambda_2^2(2\Lambda_1+\Lambda_2)^2-8\Lambda_1\Lambda_2}}, \end{align} $$

and

(2.2) $$ \begin{align} \sigma_1=F_1(\rho_1), \quad F_1(z) = \Lambda_2^2 z-\Lambda_1|z|^2+\left(\Lambda_2^3-\Lambda_2\right)\ln\bigg(1-\frac{z}{\Lambda_2}\bigg). \end{align} $$

This result is sharp, with an extremal function given by $F_1(z)$ .

For the case $\Lambda _1\geq 0$ and $\Lambda _2=1$ , we will prove the following sharp version of Landau-type theorem for certain subclass of bounded bi-analytic functions.

Theorem 2.2 Suppose that $\Lambda \geq 0$ . Let $F\in \mathrm {Bi}\mathcal {A}_0$ and $F(z)=\bar {z}G(z)+H(z)$ , where $G\in \mathcal {A}_0$ , $H\in \mathcal {A}$ , $|G'(z)|\leq \Lambda $ , and $|H(z)|< 1$ or $|H'(z)|\leq 1$ for all $z\in {\mathbb D}$ . Then $F\in {\mathcal S}(\rho _2;\sigma _2)$ , where

$$ \begin{align*}\rho_2= \left \{ \begin{array}{rl} 1, &\mbox{ when } \displaystyle 0\leq\Lambda\leq\frac{1}{2},\\ \displaystyle \frac{1}{2\Lambda}, &\mbox{ when } \displaystyle \Lambda>\frac{1}{2}, \end{array}\right. \end{align*} $$

and $\sigma _2=\rho _2-\Lambda \rho _2^2$ . This result is sharp.

Remark 2.3 Note that $G\in \mathcal {A}_0$ implies that $G(z)=z G_1(z)$ with $G_1(z)$ being analytic in ${\mathbb D}$ . Thus, the bi-analytic function $F(z)=\bar {z}G(z)+H(z)$ reduces to the form $F(z)=|z|^2G_1(z)+H(z)$ which is clearly a biharmonic mappings. Hence, we conclude the following corollaries from Theorems 2.1 and 2.2.

Corollary 2.4 Suppose that $\Lambda _1\geq 0$ and $\Lambda _2>1$ . Let $F(z)=|z|^2G(z)+H(z)$ belong to $\mathrm {Bi}\mathcal {H}$ , where $G\in \mathrm {Hol}({\mathbb D})$ and $H\in \mathcal {A}$ .

1. (1) If $|G(z)+zG'(z)|\leq \Lambda _1$ , and $|H'(z)|<\Lambda _2$ for all $z\in {\mathbb D}$ , then $F\in {\mathcal S}(\rho _1;\sigma _1)$ where $\rho _1$ and $\sigma _1$ are given by (2.1) and (2.2), respectively. This result is sharp, with an extremal function $F_1(z)$ given by (2.2).

2. (2) If $|G(z)+zG'(z)|\leq \Lambda _1$ , and $|H(z)|< 1$ or $|H'(z)|\leq 1$ for all $z\in {\mathbb D}$ , then $F\in {\mathcal S}(\rho _2;\sigma _2)$ where $\rho _2$ and $\sigma _2$ are as in Theorem 2.2. This result is sharp, with an extremal function given by $F_2(z)=\Lambda _1 |z|^2+z$ .

If we replace the condition “ $|G(z)+zG'(z)|\leq \Lambda _1$ for all $z\in {\mathbb D}$ ” by the conditions “ $G(0)=0$ and $|G'(z)|\leq \Lambda _1$ for all $z\in {\mathbb D}$ ” in Corollary 2.4, then, by Theorems C and D, we have the following sharp versions of Landau-type theorems for the special subclasses of bounded biharmonic mappings.

Corollary 2.5 Suppose that $\Lambda _1\geq 0$ and $\Lambda _2>1$ . Let $F(z)=|z|^2G(z)+H(z)$ belong to $\mathrm {Bi}\mathcal {H}$ , where $G\in \mathrm {Hol}({\mathbb D})$ and $H\in \mathcal {A}$ .

1. (1) If $|G'(z)|\leq \Lambda _1$ , and $|H'(z)|<\Lambda _2$ for all $z\in {\mathbb D}$ , then $F\in {\mathcal S}(r_3;R_3)$ , where $r_3$ and $R_3$ are as in Theorem C. This result is sharp, with an extremal function given by

   $$ \begin{align*} F_0(z) =\Lambda_2^2 z-\Lambda_1|z|^2z+\left(\Lambda_2^3-\Lambda_2\right)\ln\bigg(1-\frac{z}{\Lambda_2}\bigg). \end{align*} $$

2. (2) If $|G'(z)|\leq \Lambda _1$ , and $|H(z)|< 1$ or $|H'(z)|\leq 1$ for all $z\in {\mathbb D}$ , then $F\in {\mathcal S}(r_4;R_4)$ , where $r_4$ and $R_4$ are as in Theorem D. This result is sharp, with an extremal function given by $F_2(z)=\Lambda _1 |z|^2+z$ .

Now, we improve Theorem E by establishing the following results.

Theorem 2.6 Let $F\in \mathrm {Bi}\mathcal {A}_0$ and $F(z)=\bar {z}G(z)+H(z)$ , where $G\in \mathcal {B}_{M_1}\cap \mathcal {A}$ and $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$ for some $M_1>0$ and $M_2>0$ . Then $F\in {\mathcal S}(\rho _3;\sigma _3)$ , where $\rho _3$ is the unique root in $(0,1)$ of the equation

(2.3) $$ \begin{align} 1-\Big(M_2-\frac{1}{M_2}\Big)\frac{2r-r^2}{(1-r)^2}-\Big(M_1-\frac{1}{M_1}\Big)\frac{(3-2r)r^2}{(1-r)^2}-2r=0, \end{align} $$

and

$$ \begin{align*} \sigma_3=\rho_3-\rho_3^2-\Big(M_2-\frac{1}{M_2}\Big)\frac{\rho_3^2}{1-\rho_3}-\Big(M_1-\frac{1}{M_1}\Big)\frac{\rho_3^3}{1-\rho_3}. \end{align*} $$

Remark 2.7 If we set $M_1=M_2=1$ in Theorem 2.6, then it is clear that $G(z)=z$ and $H(z)=z$ by Schwarz lemma. Thus, $\rho _3=\frac {1}{2}$ and $\sigma _3=\frac {1}{4}$ are sharp, with an extremal function $F_3(z)=|z|^2+z$ . Moreover, if we set $M_1=M_2=M$ in Theorem 2.6, then one can easily gets an improved version of Theorem E.

Furthermore, as with Remark 2.3, we easily have the following.

Corollary 2.8 Let $F(z)=|z|^2G(z)+H(z)$ belong to $\mathrm {Bi}\mathcal {H}$ , where $G\in \mathcal {B}_{M_1}\cap \mathcal {A}$ and $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$ for some $M_1>0$ and $M_2>0$ . Then $F\in {\mathcal S}(\rho _3;\sigma _3)$ , where $\rho _3$ and $\sigma _3$ are as in Theorem 2.6.

Remark 2.9 Again, if $M_1=M_2=1$ , then we have $\rho _3=\frac {1}{2}$ and $\sigma _3=\frac {1}{4}$ with an extremal function $F_3(z)=|z|^2+z$ .

Finally, we improve Theorem 2.6 by establishing the following theorem.

Theorem 2.10 Let $F\in \mathrm {Bi}\mathcal {A}_0$ and $F(z)=\bar {z}G(z)+H(z)$ , where $0\not \equiv G \in \mathcal {B}_{M_1}\cap \mathcal {A}$ and $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$ for some $M_1>0$ and $M_2>0$ . Then F is sense-preserving, univalent and fully starlike in the disk ${\mathbb D}_{\rho _3}$ , where $\rho _3$ is the unique root in $(0,\,1)$ of equation (2.3).

3 Key lemmas

In order to prove our main results, we need the following lemmas which play a key role in establishing the subsequent results in Section 4.

Lemma 3.1 Let $H\in \mathcal {A}_{1}$ and $|H'(z)|<\Lambda $ for all $z\in {\mathbb D}$ and for some $\Lambda>1$ .

1. (1) For all $z_1,z_2\in {\mathbb D}_r\, (0<r<1, z_1\neq z_2)$ , we have

   $$ \begin{align*} |H(z_1)-H(z_2)|=\bigg|\int_{\gamma }H'(z)\,dz\bigg|\geq\Lambda\, \frac{1-\Lambda r}{\Lambda-r}\, |z_1-z_2|, \end{align*} $$
   where $\gamma =[z_1,z_2]$ denotes the closed line segment joining $z_1$ and $z_2$ .

2. (2) For $z'\in \partial {\mathbb D}_r\, (0<r<1)$ with $w'=H(z')\in H(\partial {\mathbb D}_r)$ and $|w'|=\min \{|w|:\,w\in H (\partial {\mathbb D}_r)\}$ , set $\gamma _0=H^{-1}(\Gamma _0)$ and $\Gamma _0= [0,w'] $ denotes the closed line segment joining the origin and $w'$ . Then we have

   $$ \begin{align*} |H(z')| \geq\Lambda\int_{0}^{r}\frac{\frac{1}{\Lambda}-t}{1-\frac{t}{\Lambda}}\,dt=\Lambda^2 r+(\Lambda^3-\Lambda)\ln\left(1-\frac{r}{\Lambda}\right). \end{align*} $$

Proof Set $\omega (z)=H'(z)/\Lambda $ , $z\in {\mathbb D}$ . Then $\omega \in \mathcal {B}_1$ with $\alpha :=\omega (0)=\frac {H'(0)}{\Lambda }=\frac {1}{\Lambda }.$ Using Schwarz–Pick Lemma, we have

$$ \begin{align*} \frac{\frac{1}{\Lambda}-r}{1-\frac{r}{\Lambda}}= \frac{\alpha -r}{1-\alpha r} \leq \mathrm{Re}\, \omega(z) \leq |\omega(z)|\leq \frac{\alpha +r }{1+\alpha r} , \quad z\in {\mathbb D}_r. \end{align*} $$

(1) Fix $z_1,z_2\in {\mathbb D}_r\, (0<r<1)$ with $z_1\neq z_2$ , set $\theta _0=\arg (z_2-z_1)$ . Then

$$ \begin{align*} \hspace{1cm}|H(z_1)-H(z_2)|&= \bigg|\int_{\overline{\gamma }}H'(z)\,dz\bigg|=\left| \int_{\gamma}\Lambda\, \omega(z)e^{i\theta_0}\,|dz|\right|\\ &\geq \Lambda\int_{\gamma}\mathrm{Re}\, \omega(z)|dz|\\ &\geq \Lambda\, \int_{\gamma}\frac{\frac{1}{\Lambda}-r}{1-\frac{r}{\Lambda}}\,|dz|=\Lambda\, \frac{1-\Lambda r}{\Lambda-r}\, |z_1-z_2|. \end{align*} $$

(2) For $z'\in \partial {\mathbb D}_r\, (0<r<1)$ with $w'=H(z')\in H(\partial {\mathbb D}_r)$ , $|w'|=\min \{|w|:\,w\in F (\partial {\mathbb D}_r ) \}$ and $\Gamma _0=[0,w]$ , set $\gamma _0=H^{-1}(\Gamma _0)$ so that

$$ \begin{align*} \hspace{1.5cm}|H(z')|&=|w'|= \int_{\gamma_0}|H'(\zeta)|\,|d\zeta|=\Lambda\int_{\gamma_0}|\omega (\zeta)|\,|d\zeta|\\ &\geq \Lambda\int_{0}^{r} \frac{\frac{1}{\Lambda}-t}{1-\frac{t}{\Lambda}}dt=\Lambda^2 r+(\Lambda^3-\Lambda)\ln\left(1-\frac{r}{\Lambda}\right), \end{align*} $$

and the proof is complete.

Lemma 3.2 (Carlson lemma, [4])

If $F\in \mathcal {B}_{1}$ and $F(z)=\sum _{n=0}^{\infty }a_nz^{n}$ , then the following inequalities hold:

1. (a) $|a_{2n+1}|\leq 1-|a_0|^2-\cdots - |a_n|^2,\, n=0, 1, \ldots $ .

2. (b) $|a_{2n}|\leq 1-|a_0|^2-\cdots - |a_{n-1}|^2-\frac {|a_n|^2}{1+|a_0|},\, n=1, 2, \ldots $ .

These inequalities are sharp.

Lemma 3.3 If $f\in \mathcal {B}_M\cap \mathcal {A}_0$ for some $M>0$ and $f(z)=\sum _{n=1}^{\infty }a_nz^n$ , then

1. (a) $\displaystyle |a_{2n}|\leq M\left [1- \left (\frac {|a_1|^2+ \cdots + |a_n|^2}{M^2}\right )\right ],\, n=1, 2, \ldots $ .

2. (b) $\displaystyle |a_{2n+1 }|\leq M\left [1 - \left (\frac {|a_1|^2 + \cdots + |a_n|^2}{M^2}\right ) - \frac {|a_{n+1}|^2}{M(M+|a_1|)} \right ], \, n=1, 2, \ldots $ .

In particular, if $|a_1|=1$ , i.e., if $f\in \mathcal {B}_M\cap \mathcal {A}$ , then $M\geq 1$ and

$$ \begin{align*} |a_n|\leq M-\frac{1}{M} ~\mbox{ for } n=2, 3, \ldots. \end{align*} $$

These inequalities are sharp, with the extremal functions $f_n(z)$ , where

$$ \begin{align*} f_1(z)=z,\quad f_n(z)=Mz \frac{1-M z^{n-1}}{M-z^{n-1}}=z -\Big(M-\frac{1}{M}\Big)z^n -\sum\limits_{k=3}^\infty \frac{M^2-1}{M^{k-1}}z^{(n-1)(k-1)+1} \end{align*} $$

for $n=2,3,\ldots $ .

Proof Setting $g(z)=\frac {f(z)}{M z}$ for $z\in {\mathbb D}\backslash \{0\}$ , and $g(0)=\frac {a_1}{M}$ , shows that $g\in \mathcal {B}_1$ and

$$ \begin{align*} g(z)= \sum_{n=0}^{\infty}b_nz^{n}, \end{align*} $$

where $b_n= a_{n+1}/M$ for $n\geq 0$ . Note that $b_0=a_1/M$ . Applying Lemma 3.2 to the coefficients $b_n$ of g gives the desired inequality.

In particular, if $|a_1|=1$ , then we have $M\geq 1$ and it follows from (a) and (b) that

$$ \begin{align*} |a_{n}|\leq M\left (1- \frac{|a_1|^2}{M^2}\right ) =M-\frac{1}{M} ~\mbox{ for } n\geq 2,~ \end{align*} $$

and it is evident that equalities hold for all $n=2,3,\ldots $ for the functions

$$ \begin{align*} f_n(z)=Mz\frac{1-M z^{n-1}}{M-z^{n-1}}=z-\Big(M-\frac{1}{M}\Big)z^n-\sum\limits_{k=3}^\infty\frac{M^2-1}{M^{k-1}}z^{(n-1)(k-1)+1}, \end{align*} $$

and the proof is complete.

Lemma 3.4 Let $F(z)=\bar {z}G(z)+H(z)$ be a bi-analytic function of the unit disk ${\mathbb D}$ , where $G(z)=\sum \limits _{n=1}^\infty a_n z^n\not \equiv 0$ and $H(z)=z+\sum \limits _{n=2}^\infty b_n z^n$ are analytic in ${\mathbb D}$ , and satisfy the condition

(3.1) $$ \begin{align} \sum\limits_{n=2}^\infty n|b_n|r^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\leq 1, \end{align} $$

for some $r\in (0, 1)$ . Then $F(z)$ is sense-preserving, univalent and fully starlike in the disk ${\mathbb D}_r$ .

Proof We may use arguments similar to those in the proof of [23, Lemma 1]. For the sake of readability, we provide the details. Elementary computation gives

(3.2) $$ \begin{align} z F_z(z)-\bar{z}F_{\bar{z}}(z)-F(z) =\bar{z}\sum\limits_{n=1}^\infty (n-2)a_n z^n+\sum\limits_{n=2}^\infty (n-1)b_n z^n. \end{align} $$

Evidently, $J_{F}(0)=1$ . Now, we fix $r\in (0, 1]$ and find that

$$ \begin{align*} |F_z(z)|-|F_{\bar{z}}(z)|&= \Big|\bar{z}\sum\limits_{n=1}^\infty n a_n z^{n-1}+1+\sum\limits_{n=2}^\infty n b_n z^{n-1}\Big| -\Big|\sum\limits_{n=1}^\infty a_n z^n\Big|\\ &> 1-\sum\limits_{n=2}^\infty n|b_n|r^{n-1}-\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\geq 0, \end{align*} $$

and therefore, $J_{F}(z)= (|F_z(z)|+|F_{\bar {z}}(z)|)(|F_z(z)|-|F_{\bar {z}}(z)|)>0$ for $|z|<r$ .

Thus, F is sense-preserving in ${\mathbb D}_r$ . Finally, fix $r_0\in (0, r]$ and consider the circle $\partial {\mathbb D}_{r_0}=\{z:\,|z|=r_0\}$ . For $z\in \partial {\mathbb D}_{r_0}$ , it follows from $G(z)=\sum \limits _{n=1}^\infty a_n z^n\not \equiv 0$ , (3.1) and (3.2) that

$$ \begin{align*} |z F_z(z)-\bar{z}F_{\bar{z}}(z)-F(z)|&\leq \sum\limits_{n=1}^\infty |n-2|\,|a_n|\,|z|^{n+1}+\sum\limits_{n=2}^\infty (n-1)|b_n|\,|z|^n\\ &=|z| \Big(\sum\limits_{n=2}^\infty n|b_n|\,|z|^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|\,|z|^{n}\Big)\\ &\quad -|a_1|\,|z|^2-3\sum\limits_{n=2}^\infty |a_n|\,|z|^{n+1}-\sum\limits_{n=2}^\infty |b_n|\,|z|^{n}\\ &< |z|-\sum\limits_{n=2}^\infty |b_n|\,|z|^{n}-|\bar{z}|\sum\limits_{n=1}^\infty |a_n|\,|z|^{n}\\ &\leq |H(z)|-|\bar{z}G(z)|\leq |F(z)|, \end{align*} $$

which implies that

$$ \begin{align*} \bigg|\frac{z F_z(z)- \bar{z} F_{\bar z}(z)}{F(z)}-1\bigg|<1\quad\mbox{ for } |z|=r_0. \end{align*} $$

Thus, we obtain that F is univalent on $\partial {\mathbb D}_{r_0}$ , and it maps $\partial {\mathbb D}_{r_0}$ onto a starlike curve. Hence, by the sense-preserving property and the degree principle, we see that F is univalent in ${\mathbb D}_{r_0}$ . Since $r_0\in (0, r]$ is arbitrary, we conclude that F is univalent and fully starlike in ${\mathbb D}_r$ . The proof is complete.

4 Proofs of the main results

4.1 Proof of Theorem 2.1

By the assumption on $G\in \mathcal {A}_0$ , we have

(4.1) $$ \begin{align} |G(z)|=\bigg|\int_{[0,z]}G'(z)\, dz\bigg|\leq \int_{[0,z]}|G'(z)|\,|dz|\leq \Lambda_1 |z|,\ \ z\in {\mathbb D}. \end{align} $$

We first prove that F is univalent in the disk ${\mathbb D}_{\rho _1}$ . Choose, for all $z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _1$ , $z_1\neq z_2)$ , where $\rho _1$ is defined by (2.1). As $H'(0)=1$ , $|G'(z)|\leq \Lambda _1$ and $|H'(z)|<\Lambda _2$ for all $z\in {\mathbb D}$ , we obtain from Lemma 3.1 that

$$ \begin{align*} |F(z_2)-F(z_1)|&= \left|\int_{[z_1,z_2]}F_z(z)\,dz+F_{\bar{z}}(z)\,d\bar{z}\right| \, =\left|\int_{[z_1,z_2]}\left(\bar{z}G'(z)+H'(z)\right)dz+G(z)\,d\bar{z}\right|\nonumber\\ &\geq \bigg|\int_{[z_1,z_2]}H'(z)\,dz\bigg|-\bigg|\int_{[z_1,z_2]}\bar{z}G'(z)\,dz+G(z)\,d\bar{z}\bigg|\\ &\geq |z_1-z_2|\left(\Lambda_2 \frac{1-\Lambda_2 r}{\Lambda_2-r}-2\Lambda_1r\right)\nonumber\\ &= |z_1-z_2|\cdot\frac{2\Lambda_1r^2-\Lambda_2(2\Lambda_1+\Lambda_2)r+\Lambda_2}{\Lambda_2-r}\nonumber\\ &= |z_1-z_2|\frac{2\Lambda_1(r-\rho_1)(r-A)}{\Lambda_2-r},\nonumber \end{align*} $$

which is positive, if $r<\rho _1$ , where

$$\begin{align*} A=\frac{\Lambda_2(2\Lambda_1+\Lambda_2)+\sqrt{\Lambda_2^2(2\Lambda_1+\Lambda_2)^2-8\Lambda_1\Lambda_2}}{4\Lambda_1}. \end{align*}$$

This proves the univalency of F in the disk ${\mathbb D}_{\rho _1}$ .

Next, we prove that $F({\mathbb D}_{\rho _1}) \supseteq {\mathbb D}_{\sigma _1}$ , where $\sigma _1$ is defined by (2.2). First, we note that $F(0)=0$ , for $z'\in \partial {\mathbb D}_{\rho _1}$ with $w'=F(z')\in F(\partial {\mathbb D}_{\rho _1})$ and $|w'|=\min \{|w|:\,w\in F (\partial {\mathbb D}_{\rho _1} ) \}$ . By (4.1) and Lemma 3.1, we have that

$$ \begin{align*} |w'| = \big|\bar{z'}G(z')+H(z')\big|\geq |H(z')|-\Lambda_1 \rho_1^2 \geq h_0(\rho_1)=\sigma_1, \end{align*} $$

which implies that $F({\mathbb D}_{\rho _1})\supseteq {\mathbb D}_{\sigma _1}$ , where

(4.2) $$ \begin{align} h_0(x)=\Lambda_2^2x-\Lambda_1x^2+\left(\Lambda_2^3-\Lambda_2\right)\ln\left(1-\frac{x}{\Lambda_2}\right), \quad x\in [0, 1]. \end{align} $$

Now, we prove the sharpness of $\rho _1$ and $\sigma _1$ . To this end, we consider the bi-analytic function $F_1(z)$ which is given by (2.2). It is easy to verify that $F_1(z)$ satisfies the hypothesis of Theorem 2.1, and thus, we have that $F_1(z)$ is univalent in ${\mathbb D}_{\rho _1}$ , and $F_1({\mathbb D}_{\rho _1}) \supseteq {\mathbb D}_{\sigma _1}$ .

To show that the radius $\rho _1$ is sharp, we need to prove that $F_1(z)$ is not univalent in ${\mathbb D}_r$ for each $r\in (\rho _1, 1]$ . In fact for the real differentiable function $h_0(x)$ given above, we have

$$ \begin{align*} h_0'(x)=\frac{2\Lambda_1x^2-\Lambda_2(2\Lambda_1+\Lambda_2)x+\Lambda_2}{\Lambda_2-x}, \end{align*} $$

which is continuous and strictly decreasing on $[0, 1]$ with $h_0'(\rho _1)=0$ . It follows that $h_0'(x)=0$ for $x\in [0, 1]$ if and only if $x=\rho _1$ . So $h_0(x)$ is strictly increasing on $[0, \rho _1)$ and strictly decreasing on $[\rho _1, 1]$ . Since $h_0(0)=0$ , there is a unique real $\rho _1'\in (\rho _1, 1]$ such that $h_0(\rho _1')=0$ if $h_0(1)\leq 0$ , and

(4.3) $$ \begin{align} \sigma_1=\Lambda_2^2\rho_1+\left(\Lambda_2^3-\Lambda_2\right)\ln\left(1-\frac{\rho_1}{\Lambda_2}\right)-\Lambda_1\rho_1^2=h_0(\rho_1)>h_0(0)=0. \end{align} $$

For every fixed $r\in (\rho _1, 1]$ , set $x_1=\rho _1+\varepsilon $ , where

$$ \begin{align*} \varepsilon=\left\{ \begin{array}{lll} \displaystyle\min\left\{\frac{r-\rho_1}{2}, \frac{\rho_1'-\rho_1}{2}\right\}, && \mbox{ if } h_0(1)\leq 0,\\ \displaystyle \frac{r-\rho_1}{2}, && \mbox{ if } h_0(1)>0. \end{array} \right. \end{align*} $$

By the mean value theorem, there is a unique $\delta \in (0, \rho _1)$ such that $x_2:=\rho _1-\delta \in (0, \rho _1)$ and $h_0(x_1)=h_0(x_2)$ .

Let $z_1=x_1$ and $z_2=x_2$ . Then $z_1,\ z_2\in {\mathbb D}_r$ with $z_1\neq z_2$ and observe that

$$ \begin{align*} F_1(z_1)=F_1(x_1)=h_0(x_1)=h_0(x_2)=F_1(z_2). \end{align*} $$

Hence, $F_1$ is not univalent in the disk ${\mathbb D}_r$ for each $r\in (\rho _2, 1]$ , and thus, the radius $\rho _1$ is sharp.

Finally, note that $F_1(0)=0$ and picking up $z'=\rho _1\in \partial {\mathbb D}_{\rho _1}$ , by (2.2), (4.2), and (4.3), we have

$$ \begin{align*} |F_1(z')-F_1(0)|=|F_1(\rho_1)|=|h_0(\rho_1)|=h_0(\rho_1)=\sigma_1. \end{align*} $$

Hence, the radius $\sigma _1$ of the schlicht disk is also sharp.

4.2 Proof of Theorem 2.2

The assumption on H, namely, $H\in {\mathcal B}_1\cap {\mathcal A}$ , clearly gives that $H(z)\equiv z$ in ${\mathbb D}$ (by Schwarz’s lemma). Thus, F reduces to the form $F(z)=\bar {z} G(z)+z$ .

Now, we prove F is univalent in the disk ${\mathbb D}_{\rho _1}$ . To this end, for any $z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _2)$ with $z_1\neq z_2$ , by the condition $G(0)=0$ and $|G'(z)|\leq \Lambda $ for all $z\in {\mathbb D}$ , and (4.1), it follows that $|G(z)|\leq \Lambda |z|$ in ${\mathbb D}$ . Consequently,

$$ \begin{align*} |F(z_1)-F(z_2)|&\geq |z_1-z_2| -\bigg|\int_{[z_1,z_2]}\bar{z}G'(z)dz+G(z)d\bar{z}\bigg|\\ &\geq |z_1-z_2|(1-2\Lambda r)>0, \end{align*} $$

which proves the univalency of F in the disk ${\mathbb D}_{\rho _2}$ , where $\rho _2$ is given in the statement of the theorem.

Noticing that $F(0)=0$ , for any $z=\rho _2 e^{i\theta }\in \partial {\mathbb D}_{\rho _2}$ , we have

$$ \begin{align*} |F(z)|=|\bar{z} G(z)+z|\geq |z|-\rho_1|G(z)| \geq \rho_2-\Lambda \rho_2^2=\sigma_2. \end{align*} $$

Hence, $F({\mathbb D}_{\rho _2})$ contains a schlicht disk ${\mathbb D}_{\sigma _2}$ .

Finally, for $F_2(z)=\Lambda |z|^2+z$ , a direct computation verifies that $\rho _2$ and $\sigma _2$ are sharp. This completes the proof. $\Box $

4.3 Proof of Theorem 2.6

As $G\in \mathcal {B}_{M_1}\cap \mathcal {A}$ and $H\in \mathcal {B}_{M_2}\cap \mathcal {A}$ by assumption, we may write

$$ \begin{align*} G(z)=\sum\limits_{n=1}^\infty a_n z^n ~\mbox{ and }~ H(z)=\sum\limits_{n=1}^\infty b_n z^n, \end{align*} $$

where $a_1=b_1=1$ , and it follows from Lemma 3.3 that

(4.4) $$ \begin{align} |a_n|\leq M_1-\frac{1}{M_1}~\mbox{ and }~ |b_n|\leq M_2-\frac{1}{M_2} ~\mbox{ for all } n\geq 2. \end{align} $$

We first prove that F is univalent in the disk ${\mathbb D}_{\rho _3}$ , where $\rho _3$ is defined by (2.3). Indeed, for all $z_1,z_2\in {\mathbb D}_r\, (0<r<\rho _3$ , $z_1\neq z_2)$ , we see that (with $\gamma =[z_1,z_2]$ )

$$ \begin{align*} &\quad \ |F(z_2)-F(z_1)|=\left|\int_{\gamma}F_z(z)dz+F_{\bar{z}}(z)d\bar{z}\right|\nonumber\\ &\geq \bigg|\int_{\gamma}H'(0)dz\bigg|-\bigg|\int_{\gamma}(H'(z)-H'(0))dz\bigg| -\bigg|\int_{\gamma}\bar{z}G'(z)dz+G(z)d\bar{z}\bigg|\\\\ &\geq |z_1-z_2|\bigg[1-\sum\limits_{n=2}^\infty n|b_n|r^{n-1}-\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\bigg]\nonumber\\ &\geq |z_1-z_2|\bigg [1-\Big(M_2-\frac{1}{M_2}\Big)\sum\limits_{n=2}^\infty nr^{n-1}-\Big(M_1-\frac{1}{M_1}\Big)\sum\limits_{n=2}^\infty (n+1)r^{n}-2r\bigg ]\nonumber\\ &= |z_1-z_2|\Big [1-\Big(M_2-\frac{1}{M_2}\Big)\frac{2r-r^2}{(1-r)^2}-\Big(M_1-\frac{1}{M_1}\Big)\frac{(3-2r)r^2}{(1-r)^2}-2r\Big ]>0.\nonumber \end{align*} $$

This implies $F(z_1)\neq F(z_2)$ , which proves the univalency of F in the disk ${\mathbb D}_{\rho _3}$ .

Next, we prove that $F({\mathbb D}_{\rho _3}) \supseteq {\mathbb D}_{\sigma _3}$ , where $\sigma _3$ is as in the statement. Indeed, note that $F(0)=0$ and for any $z'\in \partial {\mathbb D}_{\rho _3}$ with $w'=F(z')\in F(\partial {\mathbb D}_{\rho _3})$ , it follows from (4.4) that

$$ \begin{align*} |w'|&= \big|\bar{z'}G(z')+H(z')\big|\geq |H(z')|-\rho_3 |G(z')|\\ &\geq |z'|-\sum\limits_{n=2}^\infty |b_n|\,|z'|^{n}-\rho_3\sum\limits_{n=1}^\infty |a_n|\,|z'|^{n}\\ &\geq \rho_3-\rho_3^2-\Big(M_2-\frac{1}{M_2}\Big)\frac{\rho_3^2}{1-\rho_3}-\Big(M_1-\frac{1}{M_1}\Big)\frac{\rho_3^3}{1-\rho_3}=\sigma_3, \end{align*} $$

which implies that $F({\mathbb D}_{\rho _3})\supseteq {\mathbb D}_{\sigma _3}$ . $\Box $

4.4 Proof of Theorem 2.10

We apply Lemmas 3.3 and 3.4. Now, by the assumption and the method of proof of Theorem 2.6, the inequalities in (4.4) hold, and thus, we have

$$ \begin{align*} &\quad \sum\limits_{n=2}^\infty n|b_n|r^{n-1}+\sum\limits_{n=1}^\infty (n+1)|a_n|r^{n}\\ &\leq \Big(M_2-\frac{1}{M_2}\Big)\sum\limits_{n=2}^\infty nr^{n-1}+\Big(M_1-\frac{1}{M_1}\Big)\sum\limits_{n=2}^\infty (n+1)r^{n}+2r\leq 1 \end{align*} $$

for $r\leq \rho _3$ . Hence, the desired conclusion of Theorem 2.10 follows from Lemma 3.4. $\Box $