In this paper we give a proof of the long-standing Upper-bound Conjecture for convex polytopes, which states that, for 1 ≤ j < d < v, the maximum possible number of j-faces of a d-polytope with v vertices is achieved by a cyclic polytope C(v, d).

It is well known that Cantor's ternary set C, constructed on [0, 1], has a difference set, D(C), equal to [0, 1]. If E ⊂ R we define Dk(E)(⊂ Rk-1), by Dk(E) = {(d1, d2, …, dk-1); di ≥ 0, and there is x ∈ E such that x + di ∈ E for all i, 1 ≤ i < k}. Thus D2(E) ≡ D(E) and Dk(E) tells us whether or not a particular set of k real numbers can be translated into E. We call Dk(E) the k-difference set of E. In this work we seek criteria for finding the Besicovitch dimension of Dk(E) (written dim Dk(E))) and in particular, conditions on certain classes of linear sets E that ensure that Dk(E) should contain an open interval in Rk-1.

Let G be a locally compact Abelian non-discrete group. Let M(G) be the convolution algebra of Radon measures on G. Let µ be an element of M(G) with its Lebesgue decomposition [1]

into absolutely continuous, purely discontinuous and continuous singular parts. The chief problem one encounters in the study of the invertibility of µ is with the case µs ≠ 0. As observed by Wiener and Pitt [2], the problem can be handled provided µs be “not too large”. In fact, Wiener and Pitt (loc. cit.) proved the following:

Let µ be a Radon measure on R (the real line) such that

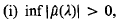
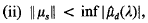
where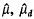are the Fourier transforms of µ, µd, and ≑µs≑ is the variational norm of µs. Then, µ has an inverse in M (R).

Erdös and Straus have conjectured that for every integer n > 1,

is soluble in positive integers x, y, z. Schinzel has conjectured that for every a > 0 if n > no(a),

is soluble in positive integers x, y, z.

A PV-number is defined to be an algebraic integer θ, of modulus greater than one, all of whose conjugates (excluding θ itself) lie inside the unit circle. Salem [1] has shown that the set S of PV-numbers forms a closed subset of the real line.

The stability equation of the asymptotic suction boundary layer profile, using a linear stability analysis, is transformed into a generalised hypergeometric equation. The solution of the stability problem may thus be written formally in terms of the relevant generalised hypergeometric functions. An asymptotic analysis is carried out on these functions for large values of the Reynolds number, and the asymptotic representation of the solutions shown to agree with that given by the usual Orr–Sommerfeld analysis.

The fluid mechanical problem with which we are concerned is the behaviour of fluid occupying the half-space x > 0 above a rotating disc which is coincident with the horizontal plane x = 0 and rotating about its axis which remains fixed. Studying rotationally symmetric solutions of this problem, von Kármán [1] (see also [2; p. 93]; [3; p. 133]) reduced it to the solution of two simultaneous equations in functions f(x), g(x) which may, with suitable normalisation, be written in the form

with the boundary conditions

A method of “inner and outer expansions” employed by Cox and Brenner (1967) is used to calculate the hydrodynamic force experienced by either of two identical small solid spheres, approaching each other, at low Reynolds number, with the same velocity along their line of centres, for the limiting case when the gap width between them tends to zero. Numerical results are compared with those furnished by the exact solution and an improved expression is then obtained for a similar problem arising from the motion of a small sphere towards an identical stationary sphere, in the limit of small gap widths.

A transversely isotropic elastic material can transmit three body waves in each direction, a quasi-longitudinal (QL) wave, a quasi-transverse (QT) wave, and a purely transverse wave. When the material is able to conduct heat the properties of small amplitude QL and QT waves are modified and we consider here the analysis of such thermo-elastic interactions in plane harmonic disturbances. The modified QL and QT waves are both found to exhibit frequency-dependent dispersion and damping of the kind known to affect dilatational waves in isotropic heat-conducting elastic materials, and in addition we show that the particle paths in the associated motions are ellipses with their axes inclined to the wave normal. This latter effect is peculiar to body waves travelling in anisotropic heat-conducting elastic materials and seems not to have been studied in detail hitherto. Numerical results referring to the propagation of plane harmonic body waves in a single crystal of zinc are presented and discussed.

Generating functions for the number of linearly independent invariants of a set of tensors under a given group of transformations are given by the theory of group representations. For the full and proper orthogonal groups these generating functions are in the form of definite integrals. The classical theory of algebraic invariants gives generating functions for the number of invariants of tensors under two-dimensional unimodular transformations, these generating functions being algebraic expressions. Because of a correspondence between the two-dimensional unimodular group and the three-dimensional proper orthogonal group, the corresponding generating functions are equivalent. The main result of this paper is an explicit demonstration of this equivalence. In addition, algebraic generating functions for the three-dimensional full orthogonal group are obtained and the use of the algebraic generating functions illustrated by applying them to a third order symmetric tensor.

1. If w(mod 2ω1, 2ω2) is an elliptic parameter for points of a normal elliptic curve C = 1Cn[n − 1], then it is well known that the sets of n points in which C is met by primes have a constant parameter sum k (mod 2ωl, 2ω2), and we may express this for convenience by saying that k is the prime parameter sum for the parametrisation of C by w. If we take the origin of w (the point for which w ≡ 0) to be one of the points of hyperosculation of C, then k ≡ 0, and we may say that w is a normal parameter for C. In the same way, if Γ is the Grassmannian image curve of the generators of a normal elliptic scroll 1R2n[n − 1], then a normal parametrisation of Γ defines a normal parameter w for the generators of 1R2n, such that n of the generators have parameter sum zero if and only if they belong to a linear line-complex not containing all the generators of 1R2n; or, in particular, if they all meet a space [n – 3] that is not met by every generator of the scroll. In this paper we are concerned in the first instance with the type of normal elliptic scroll 1R22m+1[2m] whose points can be represented by the unordered pairs (u1; u2) of values of an elliptic parameter u(mod 2ω1, 2ω2); and we establish a significant connection between any normal parametrisation of the generators of 1R2m+1 and an associated parametric representation (u1u2) of its points. We also add a brief note to indicate the lines along which this kind of connection can be extended to apply to a general normal elliptic scrollar variety 1Rkmk+1[mk] whose points can be represented by the unordered sets (u1, …, uk) of values of an elliptic parameter u.

A general convex body in Euclidean space can be approximated by smooth convex bodies, and many results, arising first in the differential geometry of smooth convex bodies, have been extended to yield corresponding results for general convex bodies. Although convex bodies can be approximated by convex polyhedra, very little of the rich theory of convex polyhedra has been extended to general convex bodies. In this paper, we extend the concept of the one-skeleton of a convex polytope to yield the concept of the one-skeleton of a general convex body. We investigate the connectivity properties of this one-skeleton, and we extend a result of Balinski [1], on paths in the one-skeleton of a convex polytope to the class of convex bodies.

All of our work takes place in Ed, d-dimensional Euclidean space, with unit ball B. Unless specifically noted to the contrary, all sets will be presumed to be closed and convex. If X is a subset of a sphere S with centre p, we will say X is spherically convex if X is contained in some open hemisphere of S and if the cone generated by X with vertex p is convex. The distance between two points x, y ε Ed will be denoted |x − y|. If K1K2 are two convex sets, ρ(K1, K2) will mean the usual Hausdorff distance between them.

It is natural to say that a set S in a metric space has infinite generalized Hausdorff dimension if there is no Hausdorff measure Λh with Λh(S) = 0. In this note we study such sets. We first need some definitions.

We say that h(x) is a Hausdorff measure function if it satisfies the conditions:

Let p be an odd prime and denote by [p] the field of p elements. Let C = C(n, p) be the set of points x = (x1 …, xn) of Zn (n ≥ 1) satisfying

In the present paper we consider the uniqueness of the solutions of the equations governing the motion of an incompressible second-order fluid in a bounded region. For such a fluid model the stress tensor S in a rectangular Cartesian coordinate system xi at a point xi of the fluid is determined from

where I is the unit tensor, p the hydrostatic pressure and μ, β, γ are material constants. The tensors A1 and A2 are the first and second Rivlin-Ericksen tensors which are defined in terms of the velocity field vi by