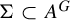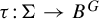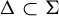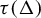On images of subshifts under embeddings of symbolic varieties

Abstract

We show that the image of a subshift X under various injective morphisms of symbolic algebraic varieties over monoid universes with algebraic variety alphabets is a subshift of finite type, respectively a sofic subshift, if and only if so is X. Similarly, let G be a countable monoid and let A, B be Artinian modules over a ring. We prove that for every closed subshift submodule $\Sigma \subset A^G$ and every injective G-equivariant uniformly continuous module homomorphism $\tau \colon \! \Sigma \to B^G$, a subshift $\Delta \subset \Sigma $ is of finite type, respectively sofic, if and only if so is the image $\tau (\Delta )$. Generalizations for admissible group cellular automata over admissible Artinian group structure alphabets are also obtained.

1 Introduction

The rich literature on injective and surjective morphisms of symbolic varieties and cellular automata admits a long history and substantial developments which date back to the works of Moore [20] and Myhill [21] on the well-known Garden of Eden theorem whose later generalization obtained in [11] gives a dynamical characterization of amenable groups [2]. Over group universes, various injective endomorphisms of symbolic varieties are surjective and thus bijective as motivated by Gottschalk’s surjunctivity conjecture [14] and the seminal paper of Gromov [15] (see also [3, 7, 8, 22, 24, 27]). Notable applications of the surjunctivity property, that is, injectivity $\implies $ surjectivity, include the well-known Kaplansky’s stable finiteness conjecture [17] on group rings (see [1, 3, 10, 13, 22, 25, 26]).

Over finite alphabets, bijective cellular automata over group universes are automorphisms (see e.g. [7, Theorem 1.3] for more general alphabets). However, when the universe is merely a monoid, we know many examples of injective non-surjective cellular automata (see [6] whenever the monoid universe contains a bicyclic submonoid) which provide us with interesting strict embeddings of subshifts. Hence, we find that it is natural to investigate the relations between subshifts, notably subshifts of finite type and sofic shifts, and their images under such embeddings, which constitutes the main motivation of the paper.

To state the results, we recall basic notions of symbolic dynamics. Fix a monoid G, called the universe, and two sets $A, B$ , the alphabets. The Bernoulli shift action of G on $A^G$ , respectively on $B^G$ , is defined by $(g, x) \mapsto g\star x$ where for all $g \in G$ and $x \in A^G$ , respectively $x \in B^G$ . We say that a subset $\Sigma \subset A^G$ is a subshift of $A^G$ if it is G-invariant. The sets $A^G$ , $B^G$ are equipped with the prodiscrete topology.

Associated with a given finite subset $D \subset G$ called a defining window, and a subset $P \subset A^D$ , we have a subshift of finite type $\Sigma (A^G; D,P)$ of $A^G$ which is closed with respect to the prodiscrete topology and is defined by

(1.1)

For sets $E \subset F$ and $\Delta \subset A^F$ , we denote the restriction of $\Delta $ to E by $\Delta _E = \{x\vert _E\colon \! x \in \Delta \}$ . Let $\Sigma \subset A^G$ be a subshift. Following the work of von Neumann [30], a map $\tau \colon \! \Sigma \to B^G$ is a cellular automaton if it admits a finite memory set $M \subset G$ and a local defining map $\mu \colon \! \Sigma _M \to B$ such that

$$ \begin{align*} (\tau(c))(g) = \mu((g\star c )\vert_M) \quad \text{for all } c \in \Sigma \text{ and } g \in G. \end{align*} $$

Equivalently, by an extension of the Curtis–Hedlund–Lyndon theorem (cf. [6, Theorem 4.6], see also [4, Theorem 1.1], [5, Theorem 1.9.1]), a map $\tau \colon \! \Sigma \to B^G$ is a cellular automaton if and only if it is G-equivariant and uniformly continuous with respect to the prodiscrete uniform structure.

Now let G be a monoid and let $X, Y$ be algebraic varieties over an algebraically closed field k, that is, reduced k-schemes of finite type [16]. We denote by $A=X(k)$ and $B=Y(k)$ the sets of k-points of X and Y. Note that we can identify X, Y with A, B respectively.

We say that a subshift $\Sigma \subset A^G$ is an algebraic subshift if for every finite subset $E \subset G$ , the restriction $\Sigma _E$ is a subvariety of $A^E$ . For an algebraic subshift $\Sigma \subset A^G$ , a map $\tau \colon \! \Sigma \to B^G$ is called an algebraic cellular automaton if there exists a finite memory subset $M \subset G$ and a local defining map which is a morphism of algebraic varieties $\mu \colon \! \Sigma _M \to B$ such that

$$ \begin{align*} \tau(x)(g) = \mu((g \star x)\vert_M) \quad \text{for all } x \in \Sigma \text{ and } g \in G. \end{align*} $$

Images of subshifts of finite type under cellular automata are called sofic subshifts [31]. When a sofic subshift is not of finite type, we say that it is strictly sofic. See [18, 31] for various examples of strictly sofic subshifts.

The first main result of the paper is the following theorem which asserts that the image $\tau (\Delta )$ of a subshift $\Delta $ under an injective algebraic cellular automaton $\tau $ is a subshift of finite type if and only if so is $\Delta $ . In particular, the image of a subshift of finite type under an injective algebraic cellular automaton cannot be strictly sofic.

More precisely, we will show in §5 the following.

Theorem A. Let G be a countable monoid and let $X, Y$ be algebraic varieties over an uncountable algebraically closed field k. Let $\Sigma \subset X(k)^G$ be a closed algebraic subshift. Suppose that $\tau \colon \! \Sigma \to Y(k)^G$ is an injective algebraic cellular automaton. Then a subshift $\Delta \subset X(k)^G$ contained in $\Sigma $ is of finite type, respectively sofic, if and only if so is the image subshift $\tau (\Delta ) \subset Y(k)^G$ .

Since the full shift is a subshift of finite type, we obtain as an immediate application of Theorem A as the following result.

Corollary A. Let G be a countable monoid and let $X,Y$ be algebraic varieties over an uncountable algebraically closed field k. Let $A=X(k)$ and $B=Y(k)$ . Suppose that $\tau \colon \! A^G \to B^G$ is an injective algebraic cellular automaton. Then $\tau (A^G)$ is a subshift of finite type of $B^G$ . $\Box $

Whenever $X=Y$ are finite and when G is moreover a group, Corollary A implies [12, Theorem 2.2]. Note also that [12, Theorem 2.2] is an extension of a result going back to Klaus Schmidt but only published in [29, Theorem 2] where the alphabet is a finite set and the universe is the free abelian group $\mathbb {Z}^d$ for some $d \geq 1$ .

The second goal of the paper is to establish a similar result to Theorem A for injective admissible group cellular automata over countable monoid universes and admissible Artinian group structure alphabets (see §6). Admissible group cellular automata were defined in [23] and are of particular interest since they always satisfy the pseudo-orbit tracing property which is also known as the shadowing property (see [23, 28] for more properties).

We formulate in the following a particular application of the general Theorem 8.4.

Theorem B. Let G be a countable monoid and let A, B be Artinian modules over a ring. Let $\Sigma \subset A^G$ be a closed subshift submodule, e.g. $\Sigma = A^G$ . Suppose that $\tau \colon \! \Sigma \to B^G$ is an injective cellular automaton which is also a module homomorphism. Then for every subshift $\Delta \subset A^G$ contained in $\Sigma $ , the subshift $\tau (\Delta ) \subset B^G$ is of finite type, respectively sofic, if and only if so is $\Delta $ .

The paper is organized as follows. Section 2 provides some basic lemmata and results on the induced local maps and subshifts of finite type. Section 3 presents a useful criterion (Theorem 3.1) for a subshift to be of finite type that we will apply frequently in the proof of the main results. In §4, we establish the left reversibility of injective morphisms of symbolic varieties. Section 5 contains the proof of Theorem A. Basic definitions and properties of admissible Artinian group structures and admissible group cellular automata are collected in §6. Then we formulate and prove a left reversibility result (Theorem 7.2) for injective admissible group cellular automata in §7. We establish in §8 the second main result of the paper (Theorem 8.4) from which we deduce a proof of Theorem B given in §9. Finally, in §10, we give another application of Theorem 8.4 to obtain an improvement on Theorem A in the case of injective morphisms of symbolic group varieties (Theorem 10.1).

2 Preliminaries

The set of non-negative integers is denoted by $\mathbb {N}$ . For subsets $E, F$ of a monoid G, we denote their product by

2.1 Subshifts of finite type

We have the following elementary observation which allows us to perform the base change of defining windows for subshifts of finite type.

Lemma 2.1. Let G be a monoid and let A be a set. Let $\Sigma = \Sigma (A^G; D,P)$ for some finite subset $D \subset G$ and some subset $P \subset A^D$ . Then for every subset $E \subset G$ such that $D \subset E$ , we have $\Sigma = \Sigma (A^G; E, \Sigma _E)$ .

Proof. See [23, Lemma 2.1], [9, Lemma 5.1] for the case when G is a group. The proof is similar when G is a monoid.

The following remark will be useful for the proof of our main results introduced in §1.

Lemma 2.2. Let G be a monoid and let A be a set. Suppose that $\Delta \subset A^G$ is a subshift. Let $F \subset G$ and $\Lambda = \Sigma (A^G; F, \Delta _F)$ . Then for every subset $E \subset F$ , we have $\Lambda _E= \Delta _E$ .

Proof. Observe first that $\Delta \subset \Lambda $ since every configuration $x \in \Delta $ satisfies trivially $(g\star x)\vert _F \subset \Delta _F$ for all $g \in G$ as $g \star x \in \Delta $ . It follows that $\Delta _E \subset \Lambda _E$ . However, since $ E \subset F$ by hypothesis, we find that

$$ \begin{align*} \begin{array}{r@{\,}ll}\Lambda_E & = (\Lambda_{F})_E & (\text{since } E \subset F) \\[2pt] & \subset (\Delta_{F})_E & (\text{as }\Lambda= \Sigma(A^G; F, \Delta_{F})) \\[2pt] & = \Delta_E & (\text{since } E \subset F) \\[2pt] & \subset \Lambda_E & (\text{since } \Delta \subset \Lambda). \end{array}\end{align*} $$

Consequently, we have $\Lambda _E= \Delta _E$ and the proof is complete.

2.2 Induced local maps

For the notation, let G be a monoid and let $A, B$ be sets. Let $\Sigma \subset A^G$ be a subshift and let $\tau \colon \! \Sigma \to B^G$ be a cellular automaton. Fix a memory set M and the corresponding local defining map $\mu \colon \! \Sigma _M \to B$ . For every finite subset $E \subset G$ , we denote by $\tau _E^+ \colon \! \Sigma _{ME} \to B^E$ the induced local map of $\tau $ defined by setting $\tau _E^+(x)(g) = \mu ((g \star y)\vert _M)$ for every $x \in \Sigma _{ME}$ , $g \in E$ , and $y \in \Sigma $ such that $y \vert _{ME}=x$ . Equivalently, we can define

$$ \begin{align*} \tau_E^+(x\vert_{ME})= \tau(x)\vert_E \quad \text{for all }x \in \Sigma. \end{align*} $$

We have the following auxiliary lemma for the induced maps of algebraic cellular automata.

Lemma 2.3. Let G be a monoid and let $X, Y$ be algebraic varieties over an algebraically closed field k. Let $A=X(k)$ , $B= Y(k)$ , and let $\Sigma \subset A^G$ be an algebraic subshift. Fix a memory set $M \subset G$ of an algebraic cellular automaton $\tau \colon \! \Sigma \to B^G$ . Then for every finite subset $E \subset G$ , the induced map $\tau _{E}^{+} \colon \! \Sigma _{M E} \to B^E$ is a morphism of k-algebraic varieties.

Proof. The lemma follows directly from the universal property of fibered products. The morphism $\tau _E^+$ is determined by the component morphisms $T_g\colon \! \Sigma _{ME} \to A^{\{g\}}$ , $g \in E$ , given by $T_g(x) = \mu ((g\star x)\vert _M)$ for all $x \in \Sigma _{ME}$ . It suffices to note that $T_g$ is the composition of the morphism $\Sigma _{Mg} \to B^{\{g\}}$ induced by the morphism $\mu $ and the canonical projection $\Sigma _{ME} \to \Sigma _{Mg}$ which is clearly algebraic.

3 A criterion for subshifts to be of finite type

In this section, we formulate a general technical criterion (Theorem 3.1) for subshifts to be of finite type that will be useful for the proof of the main results of the paper.

Let us first introduce the context and notation. Given a monoid G and two sets A, B, let $\Sigma \subset A^G$ and $\Gamma \subset B^G$ be two subshifts. Suppose that $\tau \colon \! \Sigma \to B^G$ and $\sigma \colon \! \Gamma \to A^G$ are cellular automata with a common memory set $M \subset G$ such that $1_G \in M$ .

Theorem 3.1. With the above notation, suppose that $\Gamma = \tau (\Sigma )$ and $\sigma \circ \tau $ is the identity map on $\Sigma $ . Assume in addition that $\Sigma = \Sigma (A^G; M, \Sigma _M)$ . Then one has $\Gamma = \Sigma (B^G; M^2, \Gamma _{M^2})$ . Thus, $\Gamma \subset B^G$ is a subshift of finite type.

Proof. Let us denote $\Lambda = \Sigma (B^G; M^2, \Gamma _{M^2})$ . Then $\Lambda $ is a subshift of finite type of $B^G$ and it is clear that $\Gamma \subset \Lambda $ .

Let $\mu _M \colon \! \Sigma _M \to B$ and $\eta _M \colon \! \Gamma _M \to A$ be respectively the local defining maps of $\tau $ and $\sigma $ associated with the memory set M. Note that since $1_G \in M$ , we have $M \subset M^2$ . It follows that $\Lambda _M= \Gamma _M$ by Lemma 2.2.

Consequently, we obtain a well-defined cellular automaton $\pi \colon \! \Lambda \to A^G$ which admits $\eta _M \colon \! \Lambda _M \to A$ as the local defining map associated with the finite memory set $M \subset G$ . Observe that $\pi \vert _{\Gamma } = \sigma $ since the cellular automata $\pi $ and $\sigma $ have the same local defining map and $\Gamma \subset \Lambda $ .

We claim that $\pi (\Lambda ) \subset \Sigma $ . Indeed, let $y \in \Lambda $ and let $g \in G$ . Since we have $\Lambda = \Sigma (B^G; M^2, \Gamma _{M^2})$ by definition, $(g \star y)\vert _{M^2} \in \Lambda _{M^2} = \Gamma _{M^2}$ . Therefore, $(g \star y)\vert _{M^2} = x\vert _{M^2}$ for some configuration $x \in \Gamma $ .

Since $\Gamma = \tau (\Sigma )$ by hypotheses, we can choose $z \in \Sigma $ such that $\tau (z)=x$ . We note that

$$ \begin{align*} \pi(\tau(z))=\sigma(\tau(z))=z \end{align*} $$

since $z \in \Sigma $ and since $\pi \circ \tau = \sigma \circ \tau $ acts as the identity map on $\Sigma $ . We can thus compute

(3.1) $$ \begin{align} (g \star \pi(y)) \vert_{M} & = \pi(g \star y)\vert_{M} = \pi_M^+((g\star y)\vert_{M^2}) \nonumber \\ & = \pi_M^+(x\vert_{M^2}) = \pi(x)\vert_M \nonumber \\ & = \pi(\tau(z))\vert_M= z\vert_M. \end{align} $$

Consequently, $(g \star \pi (y)) \vert _{M} = z\vert _M \in \Sigma _M$ for all $g \in G$ . Thus, it follows from the hypothesis $\Sigma = \Sigma (A^G; M, \Sigma _M)$ that $\pi (y) \in \Sigma $ for all $y \in \Lambda $ . Therefore, $\pi (\Lambda ) \subset \Sigma $ and the claim is proved.

Now let $y \in \Lambda $ and let $g \in G$ . Since $(g \star y)\vert _{M^2} \in \Lambda _{M^2} = \Gamma _{M^2}$ , we can find as above $x \in \Gamma $ and $z\in \Sigma $ such that $\tau (z)=x$ and $(g \star y)\vert _{M^2} = x\vert _{M^2}$ . In particular, $(g \star y)(1_G)=x(1_G)$ as $1_G \in M^2$ .

We have seen in (3.1) that $(g \star \pi (y)) \vert _{M} = z\vert _M$ . As $\pi (y) \in \Sigma $ , it makes sense to write and consider $\tau (\pi (y))$ that we can compute as follows:

$$ \begin{align*} \tau(\pi(y))(g) & = \mu_M ((g \star \pi(y))\vert_M) \\ & = \mu_M(z\vert_M) = \tau(z)(1_G) \\ & = x(1_G) = (g\star y)(1_G)\\ & = y(g). \end{align*} $$

Hence, we have $y= \tau (\sigma (y)) $ for all $y \in \Lambda $ . It follows that $y \in \tau (\Sigma ) = \Gamma $ and therefore $\Lambda \subset \Gamma $ . However, $\Gamma \subset \Sigma (A^G; M^2, \Gamma _{M^2})= \Lambda $ so we can conclude that

$$ \begin{align*} \Gamma = \Lambda= \Sigma(B^G; M^2, X_{M^2}). \end{align*} $$

In particular, $\Gamma $ is a subshift of finite type of $B^G$ . The proof is complete.

4 Left inverses of injective morphisms of symbolic varieties

In this section, we shall establish the following left reversibility result for injective algebraic cellular automata.

Theorem 4.1. Let G be a countable monoid. Let $X, Y$ be algebraic varieties over an uncountable algebraically closed field k and let $A=X(k)$ , $B=Y(k)$ . Let $\Sigma \subset A^G$ be a closed algebraic subshift and let $\Gamma = \tau (\Sigma )$ . Suppose that $\tau \colon \! \Sigma \to B^G$ is an injective algebraic cellular automaton. Then there exists a finite subset $N\subset G$ such that for every finite subset $E \subset G$ containing N, there exists a map $\eta _E \colon \! \Gamma _E \to A$ with $\eta _E(\tau (x)\vert _E)=x(1_G)$ for all $x\in \Sigma $ .

We begin with the following technical lemma from which Theorem 4.1 will follow without difficulty.

Lemma 4.2. Let the notation and hypotheses be as in Theorem 4.1. Then there exists $N\subset G$ finite and such that $\tau ^{-1}(x)(1_G)\in A$ depends uniquely on the restriction $x \vert _N$ for every configuration $x\in \Gamma $ .

Proof. Since $\tau \colon \! \Sigma \to B^G$ is an algebraic cellular automaton, it admits a local defining map $\mu \colon \! \Sigma _M \to B$ associated with a memory set $M \subset G$ such that $1_G \in M$ and such that $\mu $ is a k-morphism of algebraic varieties.

As G is countable, there exists an increasing sequence of finite subsets $(E_n)_{n \in \mathbb {N}}$ of G such that $G= \bigcup _{n \in \mathbb {N}} E_n$ and $M \subset E_0$ .

For every $n \in \mathbb {N}$ , we have a k-morphism $\tau _{E_n}^+ \colon \! \Sigma _{ME_n} \to B^{E_n}$ of algebraic varieties defined in §2.2. Then $\tau _{E_n}^+ $ induces a k-morphism of algebraic varieties:

For every finite subset $E \subset G$ , we denote respectively by $\Delta _E$ and $\Gamma _E$ the diagonal of $\Sigma _E \times _k \Sigma _E$ and $B^E \times _k B^E$ . Consider the canonical projections $\pi _{n} \colon \! \Sigma _{ME_n }\times _k \Sigma _{ME_n}\to \Sigma _{\{1_G\}} \times _k \Sigma _{\{1_G\}}$ . Since $\pi _n$ and $\Phi _n$ are clearly algebraic, we obtain a constructible subset of $\Sigma _{ME_n}\times _k \Sigma _{ME_n}$ given by

By construction, we note that the set of closed points of $V_n$ consists of the couples $(u,v)$ with $u,v \in \Sigma _{ME_n} $ such that $\tau _{E_n}^+(u)=\tau _{E_n}^+(v)$ and $u(1_G) \neq v(1_G)$ .

For the proof, we proceed by supposing on the contrary that there does not exist a finite subset N which satisfies the conclusion of the lemma.

Therefore, the sets $V_n$ are non-empty for all $n \in \mathbb {N}$ and we obtain a projective system $(V_n)_{n \in \mathbb {N} }$ of non-empty constructible subsets of the k-algebraic varieties $\Sigma _{ME_n}\times _k \Sigma _{ME_n}$ with transition maps $p_{m,n} : V_m \to V_n$ , for $m \geq n \geq 0$ , induced by the canonical projections $\Sigma _{ME_m }\times _k \Sigma _{ME_m} \to \Sigma _{ME_n }\times _k \Sigma _{ME_n}$ .

Since the field k is uncountable and algebraically closed, [7, Lemma B.2] (see also [9, Lemma 3.2]) implies that $\varprojlim _n V_n \neq \varnothing $ . However, since $\Sigma $ is closed in the prodiscrete topology by hypothesis, we infer from [23, Lemma 2.5] that $\varprojlim _n \Sigma _{E_n M} = \Sigma $ and hence

$$ \begin{align*} \varprojlim_n V_n \subset \varprojlim_n ( \Sigma_{E_n M} \times \Sigma_{E_n M} ) = \Sigma \times \Sigma. \end{align*} $$

Consequently, by the construction of the sets $V_n$ , we can find $x,y \in \Sigma $ such that $(x,y) \in \varprojlim _n V_n$ , and thus $\tau (x)= \tau (y)$ and $x(1_G) \neq y(1_G)$ . In particular, $x \neq y$ and as a result, the map $\tau $ is not injective, which is a contradiction. The proof is complete.

We are now in the position to give the proof of Theorem 4.1.

Proof of Theorem 4.1

Let $N \subset G$ be the finite subset given by Lemma 4.2. Then for every finite subset $E \subset G$ with $N \subset E$ , we obtain a well-defined map:

$$ \begin{align*} \eta_E \colon\! \Gamma_E \to A,\quad x \mapsto \tau^{-1}(y)(1_G), \end{align*} $$

where $y \in \Gamma $ is an arbitrary configuration such that $y\vert _E= x\vert _E$ and $\tau ^{-1}(y)$ denotes the unique element of $\Sigma $ whose image is y. Note that since $\tau $ is injective, $\tau ^{-1}(y)$ is well defined. Consequently, for $x \in \Sigma $ and $y= \tau (x)\vert _E$ , we can write $\tau ^{-1}(\tau (x))=x$ and thus

$$ \begin{align*} \eta_E(\tau(x)\vert_E)= \eta_E(y)= \tau^{-1}(\tau(x))(1_G)=x(1_G). \end{align*} $$

Hence, the proof is complete.

5 Images of injective morphisms of symbolic varieties

We shall establish in this section the following finiteness result on the images of injective algebraic cellular automata which is the first main result of the paper.

Theorem 5.1. Let G be a countable monoid and let $X, Y$ be algebraic varieties over an uncountable algebraically closed field k. Let $A= X(k)$ , $B=Y(k)$ , and let $\Sigma \subset A^G$ be a closed algebraic subshift. Suppose that $\tau \colon \! \Sigma \to B^G$ is an injective algebraic cellular automaton. Then for every subshift of finite type $\Delta \subset \Sigma $ of $A^G$ , the image $\tau (\Delta )\subset B^G$ is a subshift of finite type.

Proof. As G is countable, there exists an increasing sequence of finite subsets $(E_n)_{n \in \mathbb {N}}$ of G such that $G= \bigcup _{n \in \mathbb {N}} E_n$ and $1_G \subset E_0$ .

Let us fix an algebraic local defining map $\mu \colon \! \Sigma _M \to B$ of $\tau $ associated with a finite memory set $M\subset G$ such that $1_G \in M$ . As $\Delta $ is a subshift of finite type, it admits a defining window $D\subset G$ so that $\Delta = \Sigma (A^G; D, \Delta _D)$ (see Definition 1.1). We denote also $\Gamma = \tau (\Sigma )$ and $\Pi = \tau (\Delta )$ .

By Theorem 4.1, we can find a finite subset $N \subset G$ such that for every finite subset $E \subset G$ with $N \subset E$ , there exists a map $\eta _E \colon \! \Gamma _E \to A$ such that for every $x\in \Sigma $ , we have

(5.1) $$ \begin{align} \eta_E(\tau(x)\vert_E)=x(1_G). \end{align} $$

Up to enlarging M and N, we can suppose without loss of generality that $D \subset M=N$ . Hence, by Lemma 2.1, we can write

(5.2) $$ \begin{align} \Delta = \Sigma(A^G; M, \Delta_M). \end{align} $$

We define then it is clear that $\Omega \subset \Pi $ is a subshift of finite type of $B^G$ . In the following, we will show that $\Omega \subset \Pi $ and consequently $\tau (\Delta )=\Pi =\Omega $ will be a subshift of finite type.

Let us consider and the cellular automaton $\sigma \colon \! \Lambda \to A^G$ which admits M as a memory set and $\eta _M\colon \! \Gamma _M \to A$ as the local defining map. Note that $\Gamma _M= \Lambda _M$ since $1_G \in M$ (cf. the proof of Theorem 3.1).

We claim that $\sigma \circ \tau = \operatorname {\mathrm {Id}} \colon \! \Sigma \to \Sigma $ is the identity map on $\Sigma $ . Indeed, we infer from the G-equivariance of the cellular automata $\tau $ and $\sigma $ and from the property (5.1) that for all $x \in \Sigma $ and $g \in G$ , we have

(5.3) $$ \begin{align} \sigma(\tau(x))(g) & = \eta_M((g \star \tau(x))\vert_M) \nonumber \\ & = \eta_M(\tau(g \star x)\vert_M) \nonumber \\ & = (g \star x)(1_G) \nonumber \\ &= x(g). \end{align} $$

Since $g\in G$ is arbitrary, $\sigma (\tau (x))=x$ and the claim is thus proved. In particular, since $\Delta \subset \Sigma $ , the restriction $\sigma \circ \tau \vert _{\Delta } : \Delta \to A^G$ acts as the identity map on $\Delta $ .

Since $\Pi =\tau (\Delta )$ and $\Delta = \Sigma (A^G; M, \Delta _M)$ by definition, we infer from Theorem 3.1 applied to $\tau \vert _{\Delta } : \Delta \to B^G$ , $\sigma \vert _{\Pi }\colon \! \Pi \to A^G$ , and $\Delta $ that

$$ \begin{align*} \tau(\Delta) = \Pi = \Sigma(B^G; M^2, \Pi_{M^2}). \end{align*} $$

Therefore, the image $\tau (\Delta )$ is a subshift of finite type of $B^G$ . The proof is complete.

We prove below that the converse to Theorem 5.1 also holds. Moreover, we see that not only being a subshift of finite type but also soficity are preserved under injective morphisms of symbolic algebraic varieties. Theorem A in §1 is a consequence of the following result.

Theorem 5.2. Let G be a countable monoid. Let $X, Y$ be algebraic varieties over an uncountable algebraically closed field k. Suppose that $\tau \colon \! \Sigma \to Y(k)^G$ is an injective algebraic cellular automaton where $\Sigma \subset X(k)^G$ is a closed algebraic subshift. Then for every subshift $\Delta \subset X(k)^G$ such that $\Delta \subset \Sigma $ , the following hold:

1. (i) $\Delta $ is a subshift of finite type if and only if so is $\tau (\Delta )$ ;

2. (ii) $\Delta $ is a sofic subshift if and only if so is $\tau (\Delta )$ .

Proof. By Theorem 5.1, we know that if $\Delta \subset \Sigma $ is a subshift of finite type, then so is the image $\tau (\Delta )$ . This proves one of the two implications of (i). Now suppose that $\Pi =\tau (\Delta )$ is a subshift of finite type. We denote $A=X(k)$ , $B=Y(k)$ , and $\Gamma = \tau (\Sigma )$ . Then there exists a finite subset $F\subset G$ such that $\Pi = \Sigma (B^G; F, \Pi _F)$ . Let $\mu _M \colon \! \Sigma _M \to A$ be the local defining map of $\tau $ associated with a memory set $M\subset G$ such that $1_G \in M$ . Theorem 4.1 implies that there exists a finite subset $N \subset G$ such that for every finite subset $E \subset G$ containing N, we have a map $\eta _E \colon \! \Gamma _E \to A$ such that $ \eta _E(\tau (x)\vert _E)=x(1_G)$ for every $x\in \Sigma $ . By replacing M and N by $M \cup N \cup F$ , we can suppose without loss of generality that $F \subset M=N$ . We infer from Lemma 2.1 that

(5.4) $$ \begin{align} \Pi= \Sigma(A^G; M, \Pi_M). \end{align} $$

Let us define then $\Delta \subset Z$ . Moreover, we infer from Lemma 2.2 that $Z_M = \Sigma _M$ since $M \subset M^2$ as $1_G \in M$ .

Therefore, the local defining map $\mu _M$ determines a cellular automaton $\pi : Z \to A^G$ whose restriction to $\Delta $ coincides with $\tau $ , that is, $\pi \vert _{\Delta }= \tau $ .

Denote and consider the cellular automaton $\sigma \colon \! \Lambda \to A^G$ admitting $\eta _M \colon \! \Gamma _M \to A$ as a local defining map (note that $\Gamma _M=\Lambda _M$ by Lemma 2.2 as $M \subset M^2$ ).

Since $\sigma \circ \tau $ is the identity map on $\Sigma $ , as we have seen in the proof of (5.3) in Theorem 5.1, we have $\sigma (\Pi )=\sigma (\tau (\Delta ))= \Delta $ . However, since $\tau (\Delta )= \Pi $ and $\Delta \subset \Sigma $ , we deduce immediately that the restriction $\pi \circ \sigma \vert _\Pi = \tau \circ \sigma \vert _\Pi $ acts as the identity map on $\Pi $ .

Hence, it follows from Theorem 3.1 applied to the subshift of finite type $\Pi $ and the cellular automata $\sigma \vert _\Pi \colon \! \Pi \to A^G$ , $\tau \vert _\Delta : \Delta \to A^G$ that

$$ \begin{align*} \Delta = Z= \Sigma(A^G; M^2, \Delta_{M^2}), \end{align*} $$

so $\Delta $ is a subshift of finite type. The point (i) is proved.

For (ii), assume that $\Delta $ is sofic so $\Delta = \gamma (W)$ for some subshift of finite type W and some cellular automaton $\gamma $ . Since compositions of cellular automata are also cellular automata, we find that $\tau (\Delta )= \tau (\gamma (W))$ is a sofic subshift.

Conversely, suppose that $ \tau (\Delta ) \subset A^G$ is a sofic subshift. Then $\tau (\Delta )$ is the image of a subshift of finite type W under a cellular automaton $\gamma $ . Since $\Delta \subset \Sigma $ and $\sigma \circ \tau =\operatorname {\mathrm {Id}}_\Sigma $ , it follows that $\Delta = \sigma (\tau (\Delta )) = \sigma (\gamma (W))$ is a sofic subshift. The proof is complete.

6 Admissible group subshifts

In this section, we recall and formulate direct extensions to the case of monoid universes for the notion of admissible group subshifts introduced in [22] as well as their basic properties (see also [28]).

6.1 Admissible Artinian group structures

Definition 6.1. (cf. [22, 28])

Let A be a group. Suppose that for every $n\geq 1$ , $\mathcal {H}_n$ is a collection of subgroups of $A^n$ with the following properties:

1. (1) $ \{1_A\}, A \in \mathcal {H}_1$ , and $\Delta \in \mathcal {H}_2$ where $\Delta = \{(a,a) \in A^2 : a \in A \}$ is the diagonal subgroup of $A^2$ ;

2. (2) for $m \geq n \geq 1$ and for the projection $\pi : A^m \to A^n$ induced by any injection $\{1, \ldots , n\} \to \{ 1, \ldots , m\}$ , one has $\pi (H_m) \in \mathcal {H}_n$ and $\pi ^{-1}(H_n) \in \mathcal {H}_m$ for every $H_m \in \mathcal {H}_m$ and $H_n \in \mathcal {H}_n$ ;

3. (3) for each $n \geq 1$ and $H, K\in \mathcal {H}_n$ , one has $H \cap K \in \mathcal {H}_n$ ;

4. (4) for each $n \geq 1$ , every descending sequence $(H_k)_{k \geq 0}$ , where $H_k \in \mathcal {H}_n$ for every $k \geq 0$ , eventually stabilizes.

Let . We say that $(A, \mathcal {H})$ , or A if the context is clear, is an admissible Artinian group structure. For every $n \geq 1$ , elements of $\mathcal {H}_n$ are called admissible subgroups of $A^n$ .

Note that in our definition, we require the extra condition $\Delta \in \mathcal {H}_2$ in comparison to [22, Definition 9.1].

If E is a finite set, then $A^E$ admits an admissible Artinian structure induced by that of $A^{\{1, \ldots , |E|\}}$ via an arbitrary bijection $\{1, \ldots , |E|\} \to E$ .

Example 6.2. (Cf. [22, Examples 9.5, 9.7])

An algebraic group V over an algebraically closed field, respectively a compact Lie group W, respectively an Artinian (left or right) module M over a ring R, admits a canonical admissible Artinian structure given by all algebraic subgroups of $V^n$ , respectively by all closed subgroups of $W^n$ , respectively by all R-submodules of $M^n$ , for every $n \geq 1$ .

Definition 6.3. (Cf. [22])

Let $(A, \mathcal {H})$ be an admissible Artinian group structure. Let $m, n \geq 0$ and let $X, Y$ be respectively admissible subgroups of $A^m$ and $A^n$ . We say that a group homomorphism $\varphi : X \to Y$ is $\mathcal {H}$ -admissible (or simply admissible) if the graph is an admissible subgroup of $A^{m+n}$ .

In Definition 6.3, suppose that $\varphi : X \to Y $ is an admissible homomorphism. Then for all admissible subgroups $Z \subset X$ and $T \subset Y$ , the groups $\varphi (Z)$ , $\varphi ^{-1} (T)$ , and $Z \times T$ are admissible subgroups of $A^n$ , $A^m$ , and $A^{m+n}$ respectively. The identity map $\operatorname {\mathrm {Id}} : A \to A$ is an admissible homomorphism and more generally, one has for every $n \geq 2$ that

$$ \begin{align*} \Delta^{(n)} = \{ (a, \ldots, a) \in A^n : a \in A \} \in \mathcal{H}_n. \end{align*} $$

Suppose that $\psi : Y \to Z$ is an admissible homomorphism where Z is an $\mathcal {H}$ -admissible subgroup, then $\psi \circ \varphi : X \to Z$ is also an admissible homomorphism. Note also that for $p \geq q \geq 0$ , all the canonical projections $A^p \to A^q$ are admissible homomorphisms.

Example 6.4. With respect to the canonical admissible Artinian structures of algebraic groups, respectively of compact Lie groups, respectively of Artinian groups, and of R-modules respectively (see Example 6.2), one find that all homomorphisms of algebraic groups, respectively of compact Lie groups, respectively of Artinian groups, and morphisms of R-modules are admissible homomorphisms.

The following auxiliary result says that the fibered products of admissible homomorphisms are also admissible homomorphisms.

Lemma 6.5. Let A be an admissible Artinian group structure. Let $m , n \geq 1$ and let E be a finite set. Suppose that $\varphi _\alpha : A^m \to A^n$ is an admissible homomorphism for every $\alpha \in E$ . Then the fibered product morphism , for all $x \in A^m$ , is also an admissible homomorphism.

Proof. See [28, Lemma 5.7].

6.2 Admissible group subshifts

We recall the natural notion of admissible group subshifts introduced in [22]. However, we do not require the closedness property for subshifts in this paper.

Definition 6.6. Let G be a monoid and let A be an admissible Artinian group structure. A subshift $\Sigma \subset A^G$ is called an admissible group subshift if $\Sigma _E$ is an admissible subgroup of $A^E$ for every finite subset $E\subset G$ .

The following example gives a natural class of admissible group subshifts.

Example 6.7. Let G be a monoid and let A be an Artinian module over a ring R. Note that $A^G$ is an R-module with componentwise operations. Then every subshift $\Sigma \subset A^G$ , which is also an R-submodule, is automatically an admissible group subshift of $A^G$ with respect to the canonical admissible Artinian group structure on A (see Example 6.2).

6.3 Admissible group cellular automata

We extend the definition of admissible group cellular automata given [28, Definition 5.9] as follows.

Definition 6.8. Let G be a monoid and let A be an admissible Artinian group structure. Let $m, n \geq 1$ and let $\Sigma \subset (A^{m})^G$ , $\Lambda \subset (A^{n})^G$ be admissible group subshifts. A map $\tau \colon \! \Sigma \to \Lambda $ is called an admissible group cellular automaton if $\tau $ admits a finite memory set $M \subset G$ and an associated local defining map $\mu \colon \! \Sigma _M \to A^n$ which is an admissible homomorphism such that

$$ \begin{align*} \tau(x)(g) = \mu((g \star x)\vert_M) \quad \text{for all } x \in \Sigma, g \in G. \end{align*} $$

Observe that we no longer require admissible group cellular automata to extend to the full shift as in [28, Definition 5.9]. We have the following key technical result.

Lemma 6.9. Let G be a monoid and let A be an admissible Artinian group structure. Let $E \subset G$ be a finite subset and let $m, n \geq 1$ . Let $\Sigma \subset (A^m)^G$ be an admissible group subshift. Let $\tau \colon \! \Sigma \to (A^n)^G$ be an admissible group cellular automaton with a given memory set $M \subset G$ . Then the induced map $\tau _{E}^{+} \colon \! \Sigma _{M E} \to (A^n)^E$ defined by for all $c \in \Sigma _{ME}$ and $x \in \Sigma $ such that $x \vert _{ME}=c$ is an admissible homomorphism.

Proof. Using Lemma 6.5, the proof of the lemma is similar to the proof of [22, Lemma 9.20] in the case of group universes.

The following theorem provides us with the methods to produce many admissible group subshifts.

Theorem 6.10. Let G be a countable monoid and let A be an admissible Artinian group structure. Then the following hold for all $m, n \geq 1$ .

1. (i) If $D \subset G$ is a finite subset and $P \subset A^D$ is an admissible subgroup, then $\Sigma (A^G; D, P)$ is an admissible group subshift of $A^G$ .

2. (ii) If $\tau : (A^m)^G \to (A^n)^G$ is an admissible group cellular automaton and $\Sigma \subset (A^m)^G$ , $\Lambda \subset (A^n)^G$ are admissible group subshifts, then $\tau (\Sigma )$ , $\tau ^{-1}(\Lambda )$ are respectively admissible group subshifts of $(A^n)^G$ , $(A^m)^G$ .

Proof. See [28, Theorem 5.11].

7 Left inverses of injective admissible group cellular automata

We begin with the following auxiliary technical result on the left reversibility of injective admissible cellular automata on closed admissible group subshifts.

Lemma 7.1. Let G be a countable monoid. Let A be an admissible Artinian group structure and let $\Sigma \subset A^G$ be a closed admissible group subshift. Let $\tau \colon \! \Sigma \to A^G$ be an injective admissible group cellular automaton. Then there exists a finite subset $N\subset G$ such that

1. (P) for every $x\in \tau (A^G)$ , the element $\tau ^{-1}(x)(1_G)\in A$ depends uniquely on the restriction $x \vert _N$ .

Proof. Let us choose a finite memory set $M \subset G$ of $\tau $ such that $1_G \in M$ . Let $\mu \colon \! \Sigma _M \to A$ be the corresponding local defining map of $\tau $ .

Since G is countable, it admits an increasing sequence of finite subsets

$$ \begin{align*} M=E_0 \subset E_1 \subset \cdots \subset E_n \subset \cdots \end{align*} $$

such that $G=\bigcup _{n\in \mathbb {N}} E_n$ , that is, $(E_n)_{n \in \mathbb {N}}$ forms an exhaustion of the monoid G.

Let $\Gamma = \tau (A^G)$ . Note that since $\tau : A^G \to A^G$ is an injective group homomorphism, $\tau ^{-1} \colon \! \Gamma \to A^G$ is clearly a group homomorphism.

We proceed by assuming on the contrary that there does not exist a finite subset $N\subset G$ verifying the property $(P)$ . Consequently, there exist for every $n \geq 0$ , two configurations $x_n, y_n \in \Gamma $ such that we have

(7.1) $$ \begin{align} x_n\vert_{E_n}=y_n\vert_{E_n} \quad \text{and} \quad \tau^{-1}(x_n)(1_G)\neq \tau^{-1}(y_n)(1_G). \end{align} $$

We denote for every $n \geq 0$ . Let $e \in A$ be the neutral element. Then it follows that $z_n\vert _{E_n}=e^{E_n}$ . Since $\tau ^{-1}$ is a group homomorphism, we infer from (7.1) that $\tau ^{-1}(z_n)(1_G)\neq e$ .

Therefore, for , we find that

(7.2) $$ \begin{align} \tau_{E_n}^+(w_n)=z_n\vert_{E_n}= e^{E_n} \quad \text{and} \quad w_n(1_G) \neq e, \end{align} $$

where $\tau _{E_n}^+ \colon \! \Sigma _{E_n M } \to A^{E_n}$ is the admissible group homomorphism induced by the local defining map $\mu $ (see Lemma 6.9).

For every $n\in \mathbb {N}$ , we have an admissible subgroup of $\Sigma _{E_nM}$ defined by

Note that $e^{E_n M}, w_n \in U_n$ for each $n\in \mathbb {N}$ . Consider the canonical projection $\pi _{m,n} : A^{E_m M} \to A^{E_n M}$ . Then it is clear that $\pi _{k,n}(U_{k}) \subset \pi _{m,n}(U_m)$ for all $k \geq m \geq n \geq 0$ since

$$ \begin{align*} \pi_{k,n}(U_{k}) = \pi_{m,n}(\pi_{k,m}(U_{k})) \subset \pi_{m,n}(U_m). \end{align*} $$

Therefore, for every fixed $n\in \mathbb {N}$ , we have a decreasing sequence of admissible subgroups $(\pi _{m,n}(U_m))_{m \geq n}$ of $A^{E_n M}$ .

Since A is an admissible Artinian group structure, $(\pi _{nm}(U_m))_{m \geq n}$ must stabilize. It follows that we can choose the smallest $r(n) \in \mathbb {N}$ depending on n such that $r(n) \geq n$ and $\pi _{m,n}(U_m)= \pi _{r(n),n}(U_{r(n)})$ for all $m \geq r(n)$ .

For every $n \in \mathbb {N}$ , let us denote

(7.3)

Observe from our constructions that for all $m \geq n \geq 0$ , the projection $\pi _{m,n} : A^{E_m M} \to A^{E_n M}$ induces by restriction a well-defined group homomorphism $p_{m,n} : W_m \to W_n$ . Indeed, if $x \in W_m$ , then note that $x\in \pi _{k,m}(U_k)$ for $k = \max (r(m), r(n))$ . Hence, we find that

$$ \begin{align*} \pi_{m,n}(x) \in \pi_{m,n}(\pi_{k,m}(U_k)) = \pi_{k,n}(U_k)= W_n. \end{align*} $$

Claim. $p_{m,n} : W_m \to W_n$ is surjective for all $m\geq n \geq 0$ .

Indeed, let us fix $m \geq n \geq 0$ and $x\in W_n$ . Since $W_n=\tau _{k,n}(U_k)$ for $k= \max (r(m), r(n))$ , there exists $y\in U_k$ such that $p_{k,n}(y)=x$ . If we define $z = p_{k,m}(y) \in W_m$ , then we find that

$$ \begin{align*} p_{m,n}(z) = p_{m,n}(p_{k,m}(y)) = p_{k,n}(y)= x. \end{align*} $$

Hence, $W_n \subset p_{m,n}(W_n)$ and the claim is proved.

We construct a sequence $(u_n)_{n \in \mathbb {N}}$ with $u_n \in W_n$ and $p_{n+1,n}(u_{n+1})=u_n$ for all $n\in \mathbb {N}$ as follows. First, we define . We infer from (7.2) that $u_0(1_G) \neq e$ .

Suppose that we have constructed $u_n \in W_n$ for some $n\in \mathbb {N}$ . Since $p_{n+1,n}(W_{n+1})=W_n$ , we can find and fix $u_{n+1} \in W_{n+1}$ such that

$$ \begin{align*} \pi_{n+1,n}(u_{n+1})=p_{n+1,n}(u_{n+1})=u_n. \end{align*} $$

Hence, we obtain by induction the sequence $(u_n)_{n \in \mathbb {N}}$ with $u_n \in W_n$ and $u_{n+1}\vert _{E_nM}=u_n$ for all $n\in \mathbb {N}$ . Therefore, we can define $u \in A^G$ by setting $u\vert _{E_nM}= u_n \in W_n$ for every $n \in ~\mathbb {N}$ .

By construction, note that $u(1_G)= u_0(1_G) \neq e$ . Moreover, since we have $W_n \subset \Sigma _{M E_n}$ (see (7.3)) and $G= \bigcup _{n \in \mathbb {N}} E_n = \bigcup _{n \in \mathbb {N}}M E_n$ as $1_G \in M$ , we deduce that u belongs to the closure of $\Sigma $ in $A^G$ with respect to the prodiscrete topology. As $\Sigma $ is closed in $A^G$ , it follows that $u \in \Sigma $ .

However, we infer from the relation $W_n \subset U_n= \operatorname {\mathrm {Ker}} (\tau _{E_n}^+)$ that

$$ \begin{align*} \tau(u) \vert_{E_n} = \tau_{E_n}^+(u\vert_{M E_n})= \tau_{E_n}^+ (u_n) = e^{E_n}. \end{align*} $$

Therefore, $\tau (u)=e^G$ as $G= \bigcup _{n \in \mathbb {N}}M E_n$ . However, $\tau (e^G)=e^G$ while $u \neq e^G$ since $u(1_G)~\neq ~e$ , so we obtain a contradiction to the injectivity of $\tau $ . This proves the existence of a finite subset $N \subset G$ satisfying $(P)$ . The proof is complete.

We can now prove the following main result of the section.

Theorem 7.2. Let G be a countable monoid. Let A be an admissible Artinian group structure and let $\Sigma \subset A^G$ be a closed admissible group subshift. Let $\tau \colon \! \Sigma \to A^G$ be an injective admissible group cellular automaton. Let $\Gamma = \tau (\Sigma )$ , then there exists a finite subset $N\subset G$ such that

1. (K) for every finite subset $E \subset G$ containing N, there exists a group homomorphism $\eta _E \colon \! \Gamma _E \to A$ such that for every $x\in \Sigma $ :

   (7.4) $$ \begin{align} x(1_G)=\eta_E(\tau(x)\vert_E). \end{align} $$

Proof. We infer from Lemma 7.1 that there exists a finite subset $N \subset G$ such that for every $y \in \Gamma $ , the element $\tau ^{-1}(y)(1_G)\in A$ depends only on the restriction $y \vert _N$ . Consequently, we have the following well-defined map for every finite subset $E \subset G$ such that $N \subset E$ :

(7.5) $$ \begin{align} \eta_E \colon\! \Gamma_E \to A,\quad y \mapsto \tau^{-1}(z)(1_G), \end{align} $$

where $z \in \Gamma $ is any configuration extending $y \in \Gamma _E$ . Now for $x \in \Sigma $ , let $y= \tau (x)\vert _E$ then we deduce from (7.5) that

$$ \begin{align*} \eta_E(\tau(x)\vert_E)= \eta_E(y)= \tau^{-1}(\tau(x))(1_G)=x(1_G). \end{align*} $$

Hence, $\eta _E$ satisfies the relation (7.4). Observe that $\eta $ is clearly a group homomorphism since $\tau $ is an injective group homomorphism. The proof is complete.

8 Images of injective admissible group cellular automata

The first goal of the present section is to give a proof of the following result which says that the image of every subshift of finite type under an injective admissible group cellular automata must be a subshift of finite type.

Theorem 8.1. Let G be a countable monoid. Let A be an admissible Artinian group structure and let $\Sigma \subset A^G$ be a closed admissible group subshift. Let $\tau \colon \! \Sigma \to A^G$ be an injective admissible group cellular automaton. Suppose that $\Delta \subset A^G$ is a subshift of finite type such that $\Delta \subset \Sigma $ . Then $\tau (\Delta )$ is a subshift of finite type.

Proof. Let us denote $\Gamma = \tau (\Sigma )$ and $X= \tau (\Delta )$ . Let $\mu \colon \! \Sigma _M \to A$ be a local defining map of $\tau $ associated with a finite memory set $M\subset G$ such that $1_G \in M$ . Let $D\subset G$ be a defining window of $\Delta $ so that $\Delta = \Sigma (A^G; D, \Delta _D)$ .

By Theorem 7.2, we can find a finite subset $N \subset G$ such that for every finite subset $E \subset G$ containing N, we have a group homomorphism $\eta _E \colon \! \Gamma _E \to A$ such that for every $x\in \Sigma $ ,

(8.1) $$ \begin{align} x(1_G)=\eta_E(\tau(x)\vert_E). \end{align} $$

Therefore, together with Lemma 6.9, we can replace without loss of generality M and N by $(M \cup N)D$ . In particular, $D \subset M=N$ since $1_G \in M$ so that we have $\Delta = \Sigma (A^G; M, \Delta _M)$ by Lemma 2.1.

Let us denote and $Y= \Sigma (A^G; M^2, X_{M^2})$ . Consider the cellular automaton $\sigma \colon \! \Lambda \to A^G$ admitting $\eta _M\colon \! \Gamma _M \to A$ as a local defining map (note that $\Gamma _M=\Lambda _M$ as $M \subset M^2$ ). We deduce from the relation (8.1) and the G-equivariance of $\tau $ and $\sigma $ that for every $x \in \Sigma $ and every $g \in G$ , we have

$$ \begin{align*} \sigma(\tau(x))(g) & = \eta_M((g \star \tau(x))\vert_M) \\ & = \eta_M(\tau(g \star x)\vert_M) \\ & = (g \star x)(1_G) \\ &= x(g). \end{align*} $$

Consequently, $\sigma \circ \tau \colon \! \Sigma \to \Sigma $ is the identity map of $\Sigma $ . In particular, the restriction $\sigma \circ \tau \vert _\Delta $ is the identity map of $\Delta $ . We can then conclude from Theorem 3.1 that

$$ \begin{align*} X = Y= \Sigma(A^G; M^2, X_{M^2}) \end{align*} $$

is a subshift of finite type of $A^G$ . The proof is complete.

As an immediate application of Theorem 8.1, we obtain the following corollary.

Corollary 8.2. Let G be a countable monoid and let A be an admissible Artinian group structure. Let $\Sigma \subset A^G$ be an admissible group subshift of finite type. Then for every injective admissible group cellular automaton $\tau \colon \! \Sigma \to A^G$ , the image $\tau (\Sigma )$ is an admissible group subshift of finite type.

Proof. It follows from Theorem 8.1 that $\tau (\Sigma )$ is a subshift of finite type. Since $\Sigma $ is an admissible group subshift, we infer from Theorem 6.10 that $\tau (\Sigma )$ is an admissible group subshift of $A^G$ . The conclusion follows.

It turns out that the converse of Theorem 8.1 also holds as follows. The proof is similar to that of Theorem 5.2.

Theorem 8.3. Let G be a countable monoid. Let A be an admissible Artinian group structure and let $\Sigma \subset A^G$ be a closed admissible group subshift. Let $\tau \colon \! \Sigma \to A^G$ be an injective admissible group cellular automaton. Suppose that $\Delta \subset A^G$ is a subshift such that $\Delta \subset \Sigma $ and $\tau (\Delta )$ is a subshift of finite type. Then $\Delta $ is also a subshift of finite type.

Proof. We will proceed with several similar constructions and notation as in Theorem 8.1. Hence, we denote $\Gamma = \tau (\Sigma )$ and $X= \tau (\Delta )$ and note that $X \subset \Gamma $ since $\Delta \subset \Sigma $ by hypothesis.

Since X is a subshift of finite type by hypothesis, we can choose a finite defining window $D\subset G$ of X so that $X= \Sigma (A^G; D, X_D)$ . Let $\mu _M \colon \! \Sigma _M \to A$ be a local defining map of $\tau $ associated with a finite memory set $M\subset G$ such that $1_G \in M$ .

By Theorem 7.2, we can find a finite subset $N \subset G$ such that for every finite subset $E \subset G$ containing N, we have a group homomorphism $\eta _E \colon \! \Gamma _E \to A$ such that for every $x\in \Sigma $ , we have $x(1_G)=\eta _E(\tau (x)\vert _E)$ .

By replacing M and N by $(M \cup N)D$ , we can suppose without loss of generality that $D \subset M=N$ . Hence, by Lemma 2.1, we can write

(8.2) $$ \begin{align} X= \Sigma(A^G; M, X_M). \end{align} $$

Let us define then $\Delta \subset Z$ . Moreover, we infer from Lemma 2.2 that $Z_M = \Sigma _M$ since $M \subset M^2$ as $1_G \in M$ .

Therefore, the local defining map $\mu _M$ determines a cellular automaton $\pi : Z \to A^G$ whose restriction to $\Delta $ coincides with $\tau $ , that is, $\pi \vert _\Delta = \tau $ .

Denote and consider the cellular automaton $\sigma \colon \! \Lambda \to A^G$ admitting $\eta _M\colon \! \Gamma _M \to A$ as a local defining map (note that $\Gamma _M=\Lambda _M$ by Lemma 2.2 as $M \subset M^2$ ).

Since $\sigma \circ \tau $ is the identity map on $\Sigma $ , as we have seen in the proof of Theorem 8.1, we have $\sigma (X)=\sigma (\tau (\Delta ))= \Delta $ . However, since $\tau (\Delta )= X$ and $\Delta \subset \Sigma $ , we deduce immediately that the restriction $\pi \circ \sigma \vert _X= \tau \circ \sigma \vert _X$ acts as the identity map on X.

Hence, it follows from Theorem 3.1 applied to the subshift of finite type X and the cellular automata $\sigma \vert _X : X \to A^G$ , $\tau \vert _\Delta : \Delta \to A^G$ that

$$ \begin{align*} \Delta = Z= \Sigma(A^G; M^2, \Delta_{M^2}), \end{align*} $$

so $\Delta $ is a subshift of finite type. The proof is complete.

In parallel to Theorem 5.2, we can now establish the following general result from which we deduce easily Theorem B in §1.

Theorem 8.4. Let G be a countable monoid. Let A be an admissible Artinian group structure and let $\Sigma \subset A^G$ be a closed admissible group subshift. Let $\Delta \subset A^G$ be a subshift such that $\Delta \subset \Sigma $ . Suppose that $\tau \colon \! \Sigma \to A^G$ is an injective admissible group cellular automaton. Then the following hold:

1. (i) $\Delta $ is a subshift of finite type if and only if so is $\tau (\Delta )$ ;

2. (ii) $\Delta $ is a sofic subshift if and only if so is $\tau (\Delta )$ .

Proof. The point (i) results directly from the combination of Theorems 8.1 and 8.3. For (ii), suppose first that $\Delta $ is a sofic subshift. Then $\Delta $ is the image of a subshift of finite type X under a cellular automaton $\pi $ . Since the composition of two cellular automata is also a cellular automaton, it follows that $\tau (\Delta )= \tau (\pi (X))$ is also a sofic subshift.

Conversely, suppose that $ \tau (\Delta ) \subset A^G$ is a sofic subshift. Hence, $\tau (\Delta )$ is the image of a subshift of finite type Y under a cellular automaton $\pi $ . Let $\Gamma = \tau (\Sigma ) \subset A^G$ then, as in the proof of Theorem 8.1, there exists a cellular automaton $\sigma \colon \! \Gamma \to A^G$ such that $\sigma (\Gamma )=\Sigma $ and that $\sigma \circ \tau $ is the identity map of $\Sigma $ . Since $\Delta \subset \Sigma $ , it is clear that

$$ \begin{align*} \Delta = \sigma (\tau(\Delta)) = \sigma (\pi(Y)) \end{align*} $$

and we can again conclude that $\Delta $ is a sofic subshift. The proof is complete.

9 Proof of Theorem B

We can now deduce Theorem B from Theorem 8.4 using a general reduction step to the case of one alphabet as follows.

Proof of Theorem B

Let $M\subset G$ be a finite memory set of $\tau $ such that $1_G \in M$ and let $\mu \colon \! \Sigma _M \to B$ be the corresponding local defining map which is also a module homomorphism.

Let $\Delta \subset A^G$ be a subshift contained in $\Sigma $ . Since A and B are Artinian modules over a ring that we denote by R, the direct sum $S=A\oplus B$ is also an Artinian R-module.

For every subset $E \subset G$ , we denote by $\pi _E : S^E \to A^E$ the canonical projection. Let us consider the following subshifts $\Delta (S) \subset \Sigma (S)$ of $S^G$ :

It is clear that $\Sigma (S)$ is also a closed subshift submodule of $S^G$ since $\Sigma $ is a closed subshift submodule of $A^G$ . Moreover, we can verify without difficulty that $\Delta $ is a subshift of finite type, respectively a sofic subshift, if and only if so is the subshift $\Delta (S)$ . Note also that $\Sigma (S)_M = \pi _M^{-1}(\Sigma _M)$ .

We now define an R-module morphism $\mu _S \colon \! \Sigma (S)_M \to S$ as follows. Let $s \in \Sigma (S)_M \subset S^M$ , we define $x \in A^M$ and $y \in B^M$ by the direct sum decomposition $s(g)=(x(g),y(g)) \in A \oplus B$ for all $g \in M$ . Then we simply set . Using this formula, it is not hard to check that $\mu _S$ is a morphism of R-modules.

We denote by $\tau _S \colon \! \Sigma (S) \to S^G$ the cellular automaton which admits $\mu _S$ as a local defining map. Then $\tau $ is a homomorphism of R-modules and we deduce immediately from the construction that for $s=(x,y) \in \Sigma (S)$ where $x \in \Sigma $ and $y \in B^G$ , we have the following relation:

(9.1) $$ \begin{align} \tau_S(s)=(\tau(x), y). \end{align} $$

Consequently, $\tau _S(\Delta (S))= \pi _G^{-1}(\tau (\Delta ))$ and it follows that $\tau (\Delta )$ is a subshift of finite type, respectively a sofic subshift, if and only if so is $\tau _S(\Delta (S))$ .

Since $\tau $ is injective, we infer from (9.1) that $\tau _S$ is also injective. Therefore, with respect to the canonical admissible Artinian group structure of S as an Artinian module, Theorem 8.4 implies that the subshift $\tau _S(\Delta (S))\subset S^G$ is of finite type, respectively sofic, if and only if so is the subshift $\Delta (S)\subset S^G$ . Hence, the above discussions show that $\tau (\Delta )\subset A^G$ is a subshift of finite type, respectively sofic, if and only if so is $\Delta $ . The proof is complete.

10 Application on embeddings of symbolic group varieties

Given a monoid G and algebraic groups $X, Y$ over an algebraically closed field k (cf. [19]), let $A=X(k)$ and $B=Y(k)$ . Then following [23], a subshift $\Sigma \subset A^G$ is called a closed algebraic group subshift if it is closed and for every finite subset $E \subset G$ , the restriction $\Sigma _E$ is an algebraic subgroup of $A^E$ . Given a closed algebraic group subshift $\Sigma \subset A^G$ , a cellular automaton $\tau \colon \! \Sigma \to B^G$ is called an algebraic group cellular automaton if it admits a local defining map $\mu \colon \! \Sigma _M \to B$ for some finite memory $M \subset G$ such that $\mu $ is a k-homomorphism of algebraic groups.

As an another direct application of Theorem 8.4, we obtain the following extension of Theorem A in the case of algebraic group alphabets over any algebraically closed field (not necessarily uncountable).

Theorem 10.1. Let G be a countable monoid and let $X, Y$ be algebraic groups over an algebraically closed field k. Let $\Sigma \subset X(k)^G$ be a closed algebraic group subshift. Suppose that $\tau \colon \! \Sigma \to Y(k)^G$ is an injective algebraic group cellular automaton. Then for every subshift $\Delta \subset X(k)^G$ such that $\Delta \subset \Sigma $ , the subshift $\tau (\Delta ) \subset Y(k)^G$ is of finite type, respectively a sofic subshift, if and only if so is $\Delta $ .

Proof. It suffices to apply Theorem 8.4 after a reduction procedure described in the proof of Theorem B to reduce to the case when $X=Y$ . We only remark here that instead of taking the direct sum S of the two module alphabets, as in the proof of Theorem B, we simply consider the fibered product $S= X \times _k Y$ which is an algebraic group over k.

Note that by Remark 6.4, we find that $\tau $ is an admissible group cellular automata with respect to the admissible Artinian group structures associated with algebraic groups described in Example 6.2. Likewise, $\Sigma $ is a closed admissible group subshift of $X(k)^G$ . The proof is complete.