Long-term avalanche hazard assessment with a Bayesian depth-averaged propagation model

Abstract

While performing statistical–dynamical simulations for avalanche predetermination, a propagation model must reach a compromise between precise description of the avalanche flow and computation times. Crucial problems are the choice of appropriate distributions describing the variability of the different inputs/outputs and model identifiability. In this study, a depth-averaged propagation model is used within a hierarchical Bayesian framework. First, the joint posterior distribution is estimated using a sequential Metropolis–Hastings algorithm. Details for tuning the estimation algorithm are provided, as well as tests to check convergence. Of particular interest is the calibration of the two coefficients of a Voellmy friction law, with model identifiability ensured by prior information. Second, the point estimates are used to predict the joint distribution of different variables of interest for hazard mapping. Recent developments are employed to compute pressure distributions taking into account the rheology of snow. The different steps of the method are illustrated with a real case study, for which all possible decennial scenarios are simulated. It appears that the marginal distribution of impact pressures is strongly skewed, with possible high values for avalanches characterized by low Froude numbers. Model assumptions and results are discussed.

1. Introduction

In the avalanche field, a dichotomy between simple statistical relations (Lied and Bakkehøi, 1980; McClung and Lied, 1987; McClung, 2001; Keylock, 2005) and deterministic propagation models (Naaim, 1998; Bartelt and others 1999) has long existed. Recently, however, coupled statistical–dynamical approaches have been proposed to address the issue of avalanche predetermination (Barbolini and Keylock, 1999; Bozhinskiy and others, 2001; Meunier and others, 2001). They are based on a numerical model in which a constitutive law describes the behavior of snow in motion using different friction coefficients: one coefficient in the case of a Coulombian friction law, two in the case of the Voellmy friction law (Voellmy, 1955) or Perla’s friction law (Perla and others, 1980), more with more complex friction laws (Nishimura and Maeno, 1989; Harbitz and others, 1998; Salm, 2004). Probability distributions are chosen for the propagation model input variables, and fictitious avalanches are generated using Monte Carlo simulations to study the variability of the outputs.

A major difficulty is the choice of input distributions that appropriately represent the variability of the avalanche phenomenon at the studied site. This is sometimes overcome by calibrating simple parametric models using the available local data (Barbolini and Savi, 2001; Meunier and Ancey, 2004), but this can be difficult if correlations between the different input variables are to be taken into account. Moreover, the number of recorded variables is generally insufficient to perform the deterministic joint calibration of more than a single friction coefficient (Buser and Frutiger, 1980; Martinelli and others, 1980; Ancey and others, 2003). Only one friction coefficient is then calibrated with a classic statistical procedure (e.g. least-square minimization), while the other(s) is (are) set using expert considerations.

In environmental science, such a lack of local information is today often taken into account in a Bayesian framework (Krzysztofowicz, 1983; Berger, 1985; Kuczera and Parent, 1998; Kavetski and others, 2002; Berliner; 2003; Clark, 2005), for instance in association with complex numerical models (Oakley and O’Hagan, 2004; Karniadakis and Glimm, 2006). In the avalanche community, simple Bayesian computations have received some attention in the past (McClung and Tweedy, 1994; Harbitz and others, 2001). Interest in Bayesian methods for snow avalanche science has grown recently (Ancey, 2005; Straub and Grêt Regamey, 2006; Eckert and others, 2007b, in press), but their use remains relatively new in this field and is limited to simple propagation models. For instance, their utility for calibrating a friction law including more than one friction coefficient is not yet documented.

From a more practical point of view, mitigation against snow avalanches generally involves considering high-returnperiod avalanches to designate hazard zones and to design defense structures. For hazard zoning, two variables, runout distance and impact pressure, are usually studied, and a combination of two return periods derived from the marginal distributions of the two variables is generally retained (Salm and others, 1990). However, the pressure that must be taken into account is not a direct outcome of an avalanche propagation model. Its distribution must therefore be derived from other variables (Keylock and Barbolini, 2001), and an important question is how far pressure depends on the velocity and thickness of the incoming flow. Traditional engineering rules are based on hydrodynamics. They recommend considering the dynamic pressure in the free surface flow obtained by multiplying the kinetic energy by a constant drag coefficient. However, converging results from field data (Sovilla and others, 2008; Thibert and others, 2008) and small-scale experiments (Tiberghien, 2007) have shown strong variation of the drag coefficient with the flow parameters. In particular, it has been proved that a constant drag coefficient underestimates the impact pressure for avalanches characterized by low Froude numbers (e.g. dense snow avalanches close to their runout). A theoretical approach based on the definition of a viscous fluid equivalent to snow in motion has recently been developed to account for these observations (Naaim and others, 2008). It predicts high drag coefficients for viscous flows with low velocities, but to date it has not been implemented in a statistical–dynamical approach.

In a previous paper (Eckert and others, 2008a), we described a general Bayesian framework for computing return periods for avalanche hazard zoning. It allows local data to be used to perform on-site calibration of an avalanche propagation model and computation of design return periods. The possible correlations between input data are fully acknowledged, with a statistical formalism adapted to the input–output data structure. In the predictive phase, credible intervals are computed to give the decision-maker a fair quantification of the local state of knowledge. However, the propagation model is a simple sliding block with a Coulombian friction law. Its main advantages are the short computation times required and the easy calibration of its unique friction coefficient with the available release and runout positions. On the other hand, only the distribution of runout distances is then readily available for hazard assessment.

In this paper, we expand this preliminary approach by including a depth-averaged fluid propagation model with a Voellmy friction lawin the same Bayesian stochastic framework. Recent advances in impact pressure quantification are taken into account to compute realistic distributions of this crucial quantity for hazard mitigation. For the calibration step, we aim to show how a Metropolis–Hastings (MH) algorithm can be constructed and used to infer and identify the joint posterior distribution of the friction coefficients of a complex noninvertible avalanche model.

In the predictive phase, since there is a one-to-one mapping between a return period and an exceedance probability only for univariate variables (Ancey and others, 2004), we compute return periods for runout distances only. The main reason for this choice is that runout distance is the most ‘pessimistic’ variable in terms of hazard zoning (Eckert and others, 2007b). Indeed, the nominal runout distance must be exceeded for another variable (e.g impact pressure) to take a nonzero value. Nevertheless, we also aim to show that the joint distribution of the other model outputs at a given abscissa of the runout zone is an extremely valuable outcome for hazard mapping or defense structure design because it fully characterizes all the reference scenarios corresponding to the return period considered.

The paper is organized as follows: Section 2 presents the numerical avalanche model, how it is embedded in a stochastic framework, the details of its Bayesian calibration using an adapted MH algorithm, and how the point estimates obtained can be used to compute full reference scenarios. In section 3, the joint posterior distribution of the parameters of the stochastic avalanche model is computed for a case study from the French avalanche database. Practical details of the MH algorithm in action are also provided, as well as ways of checking convergence. In section 4, a Monte Carlo approach is used to obtain the return period for the case study associated with each runout distance. The joint distributions of the other variables of interest corresponding to a few return periods are studied. In particular, impact pressures taking snow rheology into account are computed for different sizes of obstacles. Section 5 discusses the results with special attention to model identifiability, modeling assumptions and possible further developments.

2. Materials and Methods

2.1. Snow avalanche numerical modeling

Snow avalanches are complex flows (e.g. Ancey, 2006; Pudasaini and Hutter, 2007). Their typical vertical stratification has been demonstrated through field measurements (Sovilla and others, 2001; Ancey and Meunier, 2004) on full-scale experimental sites. To be consistent with observations, avalanche flows can be modeled within the formal framework of continuum mechanics (Savage and Hutter, 1989) by different layers with different physical properties (Issler, 1998; Naaim, 1998; Zwinger, 2000). Such models are often used to back-calculate well-documented events. However, due to the time needed for one avalanche simulation, these models cannot be used within a probabilistic framework requiring at least a few hundred simulations.

Considering only the dense layer of the avalanche simplifies the problem, since the depth of the flow is then small compared to its length, allowing a shallow-water approximation of the mass and momentum conservation equations to be used. Although some physical processes (e.g. the formation of the powder part of the flow and vertical velocities in the dense flow) are thus ignored, a realistic representation of the avalanche can be obtained. Computation times are much more reasonable, allowing Monte Carlo simulations to be implemented (Barbolini and others, 2003).

In this paper, we therefore represent avalanche propagation with a fluid model based on depth-averaged Saint-Venant equations. We assume that the study site can be described by a curvilinear profile whose equation in a Cartesian frame is z = f ₁ (x), where z is the altitude and x the distance measured in Cartesian coordinates starting at the top of the path. The propagation model, noted G in Figure 1, is described by Naaim and others (2004). However, to facilitate the specification of the input conditions corresponding to each simulation and reduce computation times, we ignore snow incorporation and deposition here, so that mass is conserved. Variation in momentum corresponds to the difference between gravity g and a friction term, Fric, which is sometimes called the retarding acceleration (Gauer and others, 2009). The equations of mass and momentum conservation, in which v is the flow velocity, h is the flow depth, ϕ is the local slope and t is time, are

(1a)

(1b)

They are solved numerically using a finite volume scheme (Naaim, 1998). Even if they are expressed in a two-dimensional (2-D) frame, they in fact represent a one-dimensional (1-D) flow on the curvilinear profile (Greve and others, 1994; Gray and others, 1999; Pudasaini and Hutter, 2003).

Fig. 1. Direct acyclic graph of the stochastic avalanche model.

k _sv is the ratio between the stress normal to the slope and the stress parallel to the slope. It can be calculated from the Mohr–Coulomb plasticity model for quasi-static deformations (Savage and Hutter, 1989). For dense granular flows on rough surfaces, Silbert and others (2001) showed that the normal stress is equal to the stress along the slope. Even if it is not true in general, particularly during deposition (Pudasaini and others, 2007; Pudasaini and Kröner, 2008), Pouliquen and Forterre (2002) showed, using k _sv = 1, that, for depth-averaged equations, k _sv has no significant effect on the dynamics of the flow. α _sv is the shape of the vertical velocity profile. Observations of real snow flows showed a quasi-constant velocity over the whole core of the avalanche, and highly sheared vertical velocity profiles close to the bottom (Bouchet and others, 2004). This implies α _sv is very close to 1. We therefore set both α _sv and k _sv to 1 for the entire study.

A major problem is to specify a realistic friction term, Fric. The scarcity of measurements in real avalanche flows leaves the question open, but it seems reasonable to postulate that snow avalanches do not accelerate indefinitely on a quasi-constant slope. Since, with no erosion, the flow can reach an equilibrium speed only if friction increases with velocity, a constant friction term cannot be used in our model. Experimental approaches have supported this choice, showing using small-scale flows (Rognon and others, 2008) and shear cells (Casassa and others, 1989, 1991) the quasi-parabolic increase of friction with velocity. Although it continues to be debated in the avalanche community, the widely used Voellmy model (Voellmy, 1955) is therefore a good candidate. It associates a Coulombian term with a velocity square-dependent term, with two friction coefficients μ and ξ to be specified, so that

(2)

With this model, the limit velocity can be attained for constant slopes tan(ϕ) > μ. Traditionally (Salm and others, 1990), it is assumed that the coefficient μ summarizes snow properties as a function of altitude, exposure, etc., whereas ξ is assimilated to a morphological parameter representing the roughness of the path. However, this interpretation of the Voellmy equation continues to be discussed since it is based on expert considerations rather than on measurements. Its main advantage while fitting the model on a set of observed avalanches is that it reduces the number of unknown quantities. We therefore adopt this point of view: μ is modeled as a latent variable describing the random effects from one avalanche to another, and ξ as a parameter in the strict statistical sense of the term. ξ and μ_i , i ∊ [1, N], where N is the total number of observed avalanches, are estimated from the data.

2.2. Pressure computations

The dynamic pressure in the free surface flow is defined as ρ_Nv ², i.e. double the kinetic energy per unit volume. Impact pressure Pr can be expressed as

(3)

where ρ_N is the density of the flowing snow and Cx the drag coefficient. We compare the statistical distribution of the dynamic pressure in the free surface flow with the distributions of impact pressures obtained with both the experimental formulation of Sovilla and others (2008) and the semi-empirical formulation of Naaim and others (2008). For all computations, a constant density of 300 kg m⁻³ is assumed. The related uncertainty is not taken into account.

In the empirical formulation proposed by Sovilla and others (2008), the drag coefficient is expressed as

(4)

where the Froude number Fr is the ratio between inertial forces and gravity. The parameter pair (v ₁, v ₂) depends on the obstacle and the event considered (e.g. on the snow properties) and is fitted on various avalanche events from the Vallée de la Sionne test site in Switzerland. We use the values v ₁ = 5770 and v ₂ = 1.9, which correspond to the best-documented event.

Naaim and others (2008) used the framework of gradually variable shallow flows to define a macroscopic viscosity and a Reynolds number based on the mean velocity and on the obstacle-specific diameter. Assuming the Reynolds similarity, the drag coefficient formula obtained for simple fluids was extended to free surface flows of complex fluids. It is considered that the drag coefficient accounts for two different contributions. The first is determined by the shape of the obstacle. The second is related to the flow regime and is considered to be independent of the shape contribution.

The generalized Reynolds number Re represents the ratio between inertial and viscous forces. Assuming a quasi-permanent and uniform flow impacting an obstacle with a specific diameter d ₀ on a slope characterized by a slope angle ϕ, it can be written as

(5)

The formula is valid for a prismatic shape. For a cylindrical shape, the drag force is divided by 2. To investigate the influence of the size of the obstacle considered, we study two diameters: d ₀ = 0.25 m (e.g. a pylon) and d ₀ = 5 m (e.g. a small house or a defense structure such as a deflecting mound).

According to Naaim and others (2008), the variation of the drag coefficient can be expressed as

(6)

This semi-empirical formula was obtained by compiling existing data on the drag coefficient of Newtonian and non-Newtonian fluids. Low and moderate Reynolds numbers ranging from 0.1 to 200 were investigated, corresponding to the typical variation range of the equivalent Reynolds number in snow avalanche flows. For Re > 200, log ₁₀(Re) + 3 tends to zero and Equation (6) is no longer valid. This is not a real problem for pressure computations in dense snow avalanches since the drag coefficient then becomes constant. For a prismatic shape, Cx tends to 2 (Fig. 11a, shown further below).

Finally, with the formalism and friction model used, no steady and quasi-uniform flow is possible for slope angles lower than arctan(μ), because the avalanche is then in its decelerating phase. To compute the Reynolds number using Equation (5), the slope angle is therefore taken as the local slope angle ϕ(x) for avalanches that do not decelerate at abscissa x, and as arctan(μ), the last slope angle for which a steady flow was possible, for avalanches that decelerate at abscissa x. This can be rewritten as

(7)

2.3. French avalanche database, data transformation and stopping condition

The Enquête Permanente sur les Avalanches (EPA; permanent avalanche survey) is a database describing the avalanche events of ∼4000 determined paths in the French Alps and the Pyrenees since the beginning of the 20th century (Mougin, 1922; Bélanger and Cassayre, 2004). Avalanche counts are registered by local foresters as exhaustively as possible. A great deal of other quantitative and qualitative information is also collected. This unique database is particularly well designed for statistical–dynamical approaches and for more phenomenological large-scale studies relying on the entire database (Eckert and others, 2007a).

When using these data to calibrate a numerical avalanche model, the main difficulty is that not all the input variables needed are registered in the database. For example, for our propagation model, the length of the release zone, L _start, which we measure along the x axis, as well as the mean snow depth in the release zone, h _start, are necessary but not available. Following Meunier and others (2004), we evaluate the dimensions of the starting zone associated with the registered events using a deterministic transformation of the recorded deposit volume v _stop. However, the procedure chosen is highly speculative. A more realistic description of the release conditions, including the most recent developments concerning the size distribution of snow avalanches (McClung, 2009) could easily be included in our framework.

The three dimensions of the starting zone are assumed to have the same influence on the deposit volume, which implies dependencies to the power of 1/3 between v _stop and (h _start, L _start, l _start), respectively, the latter being the width of the release zone. Moreover, expert considerations are used to set the snow depth and the length of the starting zone associated with a very small and a very large avalanche. Under the assumption of a constant snow volume, this allows the relationship between the deposit volume and the mean snow depth in the release zone to be expressed as

(8)

and the relationship between the deposit volume and the length of the release zone as

(9)

A linear relationship between the snow depth and the length of the release zone then exists:

(10)

In addition, the width of the release zone can be evaluated using

(11)

where ϕ _start is the mean slope of the release zone between the abscissas x _start and x _start + L _start. Weighting by cos ϕ _start is necessary because of the projection of L _start on the release slope ϕ _start.

Our propagation model does not take into account the width of the release zone. When only L _start and h _start are used as input variables, roughly one-third of the variability of the deposit volumes is lost. An equivalent release volume depending on the mean release width can be computed as

(12)

Its variability from one avalanche to another represents the variability introduced in the propagation model more realistically than the variability of the observed deposit volumes.

Finally, when numerical avalanche propagation stops, the granular media are reorganized along the slope (e.g. Pudasaini and others, 2007). A stopping condition therefore has to be specified to distinguish these quasi-static motions from the avalanche flow. Here we assume any avalanche to be stopped as soon as the maximal propagated discharge is smaller than

(13)

This varying threshold is convenient for simulating avalanches of very different volumes. Very small avalanches are not immediately stopped, which occurs if the constant threshold chosen is too high; while, for very large avalanches, quasi-static reorganization is excluded, which is not the case if a low constant threshold is chosen.

2.4. Multivariate stochastic modeling

Stochastic modeling allows the variability of avalanche events on a given path to be described. Here we expose our assumptions concerning the distributions of the different input–output variables of the propagation model. The main characteristics of the obtained stochastic avalanche model are summarized in Figure 1 using a directed acyclic graph (Lauritzen, 1996). The relevance of the different probabilistic choices is discussed in section 5.4.

A distinction is made between avalanche frequency a and avalanche magnitude y. Avalanche frequency is a scalar discrete random variable corresponding to the number of avalanches recorded each winter and whose long-range mean is necessary for computing return periods. Avalanche magnitude is a random vector including all the correlated multivariate quantitative characteristics that vary from one event to another: runout distance, velocity and pressure profiles, snow volume, etc. The stochastic model is noted p(y, a|θ_M , θ_F ), indicating that the joint distribution p of the random variables y and a is indexed by the parameters (θ_M , θ_F ). Finally, the hypothesis of magnitude– frequency independence is made, considering that the number of avalanches per winter does not affect their quantitative characteristics. This classic hypothesis in avalanche modeling is fulfilled if the number of avalanches affecting the studied path each winter is not too high. It can be expressed as

(14)

Avalanche frequency is assumed to be an independent Poisson-distributed process (Eckert and others, 2007a), with its single parameter λ quantifying the mean annual avalanche number:

(15)

The magnitude model embeds the sliding block propagation model within several stochastic operators describing the variability of the different input–output quantities. McClung (2003) adopts a similar approach that describes avalanche events as a Poisson process with log-normal marks for avalanche masses.

The release abscissa x _start that corresponds to the beginning of the release zone is assumed to be purely random and beta-distributed (Meunier and others, 2001). A normalization is necessary, and the length of the release zone is used, so that

(16)

where x _max and x _min are the maximal and minimal abscissas of the release zone. x _max and x _min are assumed to be known. They can be estimated using simple topographical thresholds or the available data.

Given the normalized release abscissa, the mean release depth h _start is assumed to be gamma-distributed, with a parameterization reflecting the dependency of the snow depth on the release abscissa and a constant dispersion around the mean. For simplicity, the conditioning by x _max and x _min is dropped, which leads to

(17)

This model is chosen to represent the skewness of a hydrological variable such as snow depth (values much higher than the mean are plausible) as well as the possible variation of snow depth with altitude. Since a linear relation between the release depth and the length of the release zone exists (Equation (10)), there is no need to specify probability distributions for other input quantities.

Given the normalized release abscissa and the flow depth, the latent friction coefficient μ is assumed to be normally distributed, with four parameters characterizing its dependency on the release abscissa and mean release depth and with a constant dispersion around the mean. This can be written as

(18)

Small Gaussian differences between the observed runout distances and the latent computed runout distances x _stop are postulated, such as

(19)

These differences can result from numerical errors due to the imperfection of the propagation model, and/or from observation errors. The standard deviation σ _num is to be specified.

To sum up, the proposed frequency model has only one parameter, θ_F = λ. Conversely, the magnitude model is relatively complex, with ten parameters θ_M = (a ₁, a ₂, b ₁, b ₂, σ_h , c, d, e, σ, ξ) and, for each avalanche, the latent friction coefficient μ and the computed runout distance x _stop. The different input variables and μ are explicitly modeled as dependent variables to take into account possible correlations that may affect extreme events. The joint probability of the magnitude observations given parameters and latent variables is obtained by combining the different conditional distributions:

(20)

μ appears in the right-hand side term only indirectly, by constraining the deterministic propagation and x _stop.

Finally, we note , i ∊ [1, N] and a_t , t ∊ [1, T _obs], our datasets corresponding to the N avalanches registered on the studied site during T _obs years of observation. They are assumed to be mutually independent, which implies

(21a)

(21b)

For the magnitude model, this hypothesis is fulfilled if all avalanches that occur in a given winter are neither too numerous nor temporally too close, so that the quantitative characteristics of the first avalanche do not affect those of the next avalanches. For the frequency model, the physical independence of the number of avalanches occurring in two consecutive winters is clear.

2.5. Bayesian inference

Inference of the proposed stochastic model is performed under the Bayesian paradigm. Bayes’ theorem (Bayes, 1763) allows the observations to be combined with a prior distribution π(θ_M , λ) which encodes prior knowledge about the unknowns. The result of the computation is the joint posterior distribution of all parameters and latent variables p(θ_M , λ, μ, x _stop|data), where data denotes all observations .

Under the magnitude–frequency independence hypothesis, the frequency and the magnitude models can be inferred separately. For the frequency model, inference is analytically feasible as soon as a gamma prior,

(22)

is chosen for the parameter λ. The parameter pair (a_λ., b_λ ) represents the prior knowledge concerning avalanche occurrences. The posterior distribution is then still gamma-distributed, with the parameter pair verifying and .

For the magnitude model, inference is more cumbersome. Indeed, the probability of the latent variables given parameters and observations must be considered in Bayes’ theorem in addition to the prior and the probability of observations given parameters and latent variables, i.e.

(23)

The latent variable distribution is obtained by combining the distribution of the friction coefficient μ and the result of the deterministic propagation noted as the Dirac distribution δ():

(24)

In other words, x _stop must be equal to G(x _start, h _start, μ, ξ), otherwise a zero probability is assigned. This emphasizes that, even if our model has two latent variables, μ and, x _stop, they are deterministically linked.

2.6. Markov chain Monte Carlo methods and the Metropolis–Hastings algorithm

The normalizing constant in Equation (23) cannot be computed analytically, so recourse to a simulation-based estimation algorithm is necessary. A general exposition of the Markov chain Monte Carlo (MCMC) methods that can be used to obtain samples from p(θ_M , μ, x _stop |data, σ _num) can be found in various sources (Gilks and others, 1996; Robert, 1996; Brooks, 1998; Congdon, 2001; Parent and Bernier, 2007). Their principle is that, under few assumptions, there is a single stationary distribution for a Markov chain. Iterative MCMC algorithms have therefore been developed to construct chains in the space of model unknowns that converge to the target posterior distribution. Such procedures include the extremely general MH algorithm (Metropolis and others, 1953; Hastings, 1970), and the efficient but less general Gibbs sampler (Geman and Geman, 1984).

An initial state of the chain must be specified for all model unknowns, in our case (θ_M , μ, x _stop) ^(o) _. Then a burn-in period is needed to ensure that the chain has reached its so-called ergodic state. Finally, running enough iterations of the chain after the burn-in period reconstructs the target distribution. For example, each iteration k of the MH algorithm consists in the generation using an exploration function f ₂ of a candidate value for the unknowns (θ_M , μ, x _stop)^(C) = f ₂ (θ_M , μ, x _stop)^(k−1) and in a probabilistic acceptance–rejection rule deciding whether (θ_M , μ, x _stop)^(k) = (θ_M , μ, x _stop)^(C) or whether (θ_M , μ, x _stop)^(k) = (θ_M , μ, x _stop)^(k−1). The random feature in the acceptance–rejection rule is the key point: if the candidate is a posteriori more likely than the previous state of the chain, it is always accepted. In the opposite case, it is sometimes accepted, allowing the algorithm to leave the regions of high posterior probability where it mostly gravitates, and jump to regions of lower posterior probability. This way, the algorithm randomly browses the whole domain, looking for potential local second-order modes of the posterior distribution.

Convergence should occur for any symmetric exploration function that keeps the Markov chain homogeneous. However, the use of the MH algorithm is very subtle in practice because no general theoretical result concerning the rate of convergence is available. Moreover, for high-dimension parameter spaces, the posterior surface is likely to exhibit numerous modes and curvature ridges that may trap the algorithm and make it difficult to visit all regions according to their posterior probabilities. The choice of an appropriate exploration function is therefore the critical point in writing an algorithm that converges reasonably fast. A class of exploration functions is generally chosen and the strength of its jump is tuned to obtain the fastest convergence. Gelman and others (1995) showed that the main criterion to define a suitable value for the jump strength is the observed acceptance rate computed after a given number of iterations. A high acceptance rate means that candidates result from too small jumps around a main distribution mode, leading to numerous tiny moves. It then takes a long time to explore the whole posterior space. By contrast, a low observed acceptance rate implies that the jump values used are too high and that the chain is stuck. The observed acceptance rate must therefore stay around 0.23 for a number of unknowns greater than 5 and be ∼0.44 for a single parameter.

In addition to visual inspection, the convergence must be quantitatively checked (Brooks and Gelman, 1998; Brooks and Roberts, 1998), generally by launching many chains from different starting points of the parameter space. This allows verification that the different subsamples belong statistically to the same population by various parametric and nonparametric tests (Mengersen and others, 1999). For example, the Gelman–Rubin convergence diagnosis compares the variability of the generated parameters within and across the different sequences (Gelman, 1996). Further useful hints concerning exploration functions and convergence diagnosis for the MH algorithm are provided by F. Torre and others (http://www.cybergeo.presse.fr/).

Here a multivariate normal random-walk jump function has been used. This means that the candidate has been drawn from a multivariate normal distribution centered on the previous value of the chain. For strictly positive variance parameters, a logarithmic transformation has been used. The variance–covariance matrix of the jump function had to be tuned. To simplify this task, a sequential version of the MH algorithm has been implemented. This means that a diagonal variance–covariance matrix has been set for candidate proposals, and that for each iteration the credibility of the candidates for the different parameters has been evaluated separately. The target acceptance rate was 0.35–0.45 for all parameters except ξ. Since all avalanches must be propagated with the same value of ξ, the credibility of the different runouts obtained had to be evaluated simultaneously with regard to the data. ξ and all the latent variables μ, x _stop were therefore calibrated within the same acceptance–rejection rule, with a target acceptance rate of 0.25.

2.7. Computing reference scenarios using Monte Carlo simulations

For each unknown, a point estimate can be derived from the joint posterior probability distribution function (pdf) in addition to a credibility interval, which is the Bayesian counterpart for a confidence interval, but using the posterior pdf instead of the likelihood function. The posterior mean is the Bayesian estimator of the parameters of our model under the classic hypothesis of a quadratic loss function. and are then the posterior mean of the proposed models given and , respectively. These distributions quantify the randomness of the process studied given the data. The joint distribution includes the marginal distribution of some variables of interest for hazard zoning (runout distance, velocity, flow depth), and can also be used to compute the marginal distributions of Froude numbers , Reynolds numbers , drag coefficients , and impact pressures by combining the needed variables.

can easily be obtained because an explicit formulation of the model is available. However, for , a statistical–dynamical Monte Carlo approach is necessary to obtain the distribution of the outputs of the numerical avalanche propagation model given the distribution of its inputs. The specified conditional distributions must be used. Integration over the distribution of the latent friction coefficient μ must also be performed, which gives access to a sample of the distribution of the latent friction coefficient . This can be expressed as

(25)

To compute return periods, the expected annual frequency E[a|θ_F ] must be taken into account. With a Poisson frequency model, it is simply the unknown parameter λ. The return period , associated with the runout distance x _stop, is therefore estimated combining and , the estimated cumulative distribution function (cdf) of runout distances:

(26)

Practically speaking, if is the ordered sample obtained using Monte Carlo simulations, the empirical estimator for is simply k/n, where n is the sample size. For hazard zoning purposes, the inverse problem must be solved: the annual exceedance probability is known (e.g. 0.01 for the centennial event) and the associated runout distance quantile must be found. It is provided by the estimated inverse cdf of runout distances using

(27)

In the simulation set-up, the runout distance quantile corresponding to the return period T is then the th value of the ordered sample.

Using a Monte Carlo approach makes numerical errors unavoidable. A confidence interval for the non-exceedance probability associated with a given runout distance is

(28)

The confidence interval depends on the sample size, on the probability considered and on the quantile of the standard normal distribution corresponding to the desired confidence level α_c , usually 95%. It must be emphasized that such a confidence interval only accounts for the error due to a numerical evaluation. It allows checking that the sample size is large enough, but does not quantify other error sources (e.g. observation error, model error or estimation error). Their evaluation requires additional computational efforts to carry out sensitivity analyses and/or predictive simulations (section 5.5 for discussion).

Finally, the joint distribution of the exceedances summarizes the characteristics of all avalanche events at the abscissa . It can therefore be considered as the joint distribution of all the reference scenarios corresponding to the return period T. It can be obtained simply by considering only those events for which the runout distance exceeds . This partially counters the limitations of the return period for a multivariate hazard such as snow avalanches by giving the variation range to be considered at any abscissa.

3. Model Calibration on a Case Study

3.1. Case study presentation

The chosen case study is one of numerous paths of the French avalanche database. It is situated in the village of Bessans, Savoie department. It is only slightly channelized, and ends in the large flat valley of the Arc river. It is approximately 2300 m long from the top of the path to the Arc river, with a vertical drop of 1500 m (Fig. 2). The average slope is high, with several moderate changes of concavity along the slope profile. The slope remains predominantly above 30° during the first 1900 m of the path. The potential release zone is therefore long, so we chose x _max = 1900 m and x _min = 0_. Forty-one avalanches were recorded during T _obs = 44 years, with an empirical avalanche rate of 0.93 avalanches per year. However, only 26 of them were well enough documented to be used to calibrate the magnitude model. Therefore, N = 26, even if 41 events had to be used to compute the posterior distribution of the frequency model.

Fig. 2. Topography and available historical data for the case study. Bessans township, path EPA No. 13, Savoie, France.

The quantitative characteristics of the observed events are summarized in Table 1. Snow depths obtained from the deposit volumes range from 75 cm to 4 m, which seems plausible given the relatively large size of the studied avalanche site. Release zone lengths are ∼100–400 m. Release zone widths have a high residual variability, which is not taken into account for model calibration. Thus, the variability of the equivalent release volumes is significantly lower than the variability of the ‘true’ release volumes.

Table 1. Dataset descriptive statistics

The runout zone shows an irregular topography that constrains the empirical distribution of avalanche runout distances to be strongly multimodal. Figure 2 shows that most of the observed avalanches stopped on the gentle slopes at the end of the path between x = 1900 m and x = 2090 m. A few avalanches stopped earlier, between x = 1600 m and x = 1850 m, on average slopes that are situated above the last slope increase. An extreme event that stopped in the flat Arc valley was also registered, with a very large runout abscissa of 2208 m. This large variability of runout distances renders this case study a good test for the efficiency of our MH algorithm in calibrating the chosen avalanche propagation model.

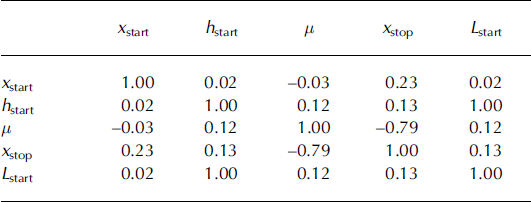
Empirical correlations between data are shown in Table 2. Although some of them are small, they are all significantly nonzero at the 95% significance level. The numerous correlation coefficients very close to 1 are due to the deterministic relationships used to estimate the nonobserved quantities. Correlations between the three dimensions (L _start, l _start, h _start) of the starting zone and the release abscissa x _start are slightly negative. For this path, the size of the avalanche decreases with the altitude of the beginning of the release zone. Correlations between (L _start, l _start, h _start) and the runout abscissa are also negative. The longest runouts therefore mainly correspond to avalanches released at relatively low altitudes. For example, the extreme event registered was released at 2000 m a.s.l., corresponding to x _start = 1518 m (Fig. 2).

Table 2. Dataset linear correlations

3.2. Prior distribution

The parameters were assumed a priori mutually independent, so that the joint prior distribution is simply

(29)

i.e. the product of the marginal distributions of the scalar parameters. This usual choice that facilitates prior elicitation is not very constraining since interparameter dependence is taken into account a posteriori. Moreover, the marginal prior distributions were assumed to belong to standard parametric families with their hyper-parameters to be specified.

Relatively informative marginal priors were used for the parameters c and σ (mean and variance of the latent friction coefficient μ), the release depth (parameter b ₁) and the friction coefficient ξ whose inverse controls the increase of friction with velocity and thus the limit velocity that can be reached by the flow. The choice of an informative prior for ξ has been made to ensure the model can be identified. For the other parameters, it was a modeling choice aimed at bringing more information into the analysis (see section 5.1 for discussion and sensitivity analysis).

The correlation parameters (b ₂, d, e) were assumed to be unknown a priori: the means of their marginal prior distributions were set to zero to let the data decide whether significant correlations between the different input variables of the propagation model exist. Vague priors (Bernardo and Smith, 1994) were also used for (a ₁, a ₂, λ), because prior knowledge was not available. The different marginal priors used are summarized in Table 3.

Table 3. Marginal prior distribution. U refers to the uniform distribution, N to the normal distribution and Gamma to the gamma distribution

3.3. Running the MH algorithm and assessing convergence

The numerical error σ _num for the discrepancy between observed and computed runout distances was set to 15 m. The 1-D random-walk jump functions shown in Table 4 were chosen for MH inference. They were tuned with respect to Gelman and others’ (1995) optimal acceptance rates to adapt the algorithm to the case study. After a burn-in period of 1000 iterations, 2000 iterations were performed and stored as a sample of the posterior distribution. Convergence was checked by launching different chains from different starting points of the parameter space and computing the Gelman–Rubin convergence diagnosis (see below). The total computations for one chain took ∼2 weeks on a recent standard PC. This very long time is related to the relative complexity of the propagation model used and to the fact that, at each iteration of the MH algorithm, N = 26 iterations of the propagation model had to be performed.

Table 4. Jump functions for the MH algorithm. logN refers to the log-normal distribution. Notations indicate, for example, that at each iteration k of the MH algorithm, the candidate value for the a ₁ parameter is drawn from a normal distribution centered on the value at the previous iteration

Table 5 shows the acceptance rates obtained for one chain. They are very close to the target optimal values discussed in section 2.6, i.e. 0.34–0.49 for the scalar parameters and 0.26 for the multidimensional jump corresponding to the friction coefficients. Figure 3 shows how well the two chains (for two parameters) mix during the ergodic phase. For the parameter a ₁ characterizing the distribution of release abscissas, the trajectories of the two chains show a stabilized variation domain as well as strong variability from one iteration to the other, and they mix well. This indicates that convergence is easily reached. For ξ, the chains are more autocorrelated, with lower variability from one iteration to the other and thus a lower level of mixing. This indicates that, for the friction coefficients, reaching convergence and obtaining a good approximation of the posterior pdf is more cumbersome and requires more iterations of the MH algorithm. A more quantitative check of the convergence is given in Table 6, which presents the Gelman–Rubin statistics for the different unknowns. It is not equal to 1 for all parameters. However, the highest value is 1.03, which indicates that the variability of the generated samples across the different sequences is <1.05 times the variability within the different sequences, even for the friction coefficients μ and ξ. This is in practice more than sufficient for considering that convergence has been reached and that a satisfactory numerical approximation of the joint posterior pdf is therefore available.

Table 5. Acceptance rates for the MH algorithm

Fig. 3. Two chains of the MH algorithm for two parameters, a ₁ and ξ. The algorithm is in its ergodic phase (burn-in period is not considered).

Table 6. Gelman and others’ (1995) convergence diagnosis

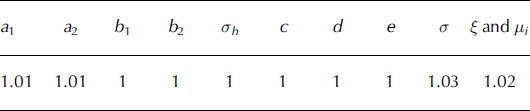
3.4. Posterior distribution

3.4.1. Model parameters

All marginal posterior distributions of the model’s parameters have a variance lower (sometimes much lower) than for the prior distributions (Fig. 4). This indicates that the information contained in the prior distribution has been updated. For instance, it shows that the data contained sufficient information to enable joint calibration of the two friction coefficients (see section 5.1 for discussion).

Fig. 4. Marginal prior and posterior distributions of model parameters. Poorly informative priors for parameters (a ₁, a ₂, λ) are not shown. Priors (in red) for the other parameters were obtained by expert elicitation.

All distributions are unimodal, making use of the point estimates in the predictive phase appropriate in this case. The posterior mean of the frequency parameter λ corresponds to the empirical annual avalanche rate, slightly less than one avalanche per year (Table 7). The posterior distributions of the dispersion parameter σ_h and of the friction coefficient ξ exhibit higher modal values than the corresponding marginal prior distributions (Fig. 4). This shows a higher variability of release depths around the model’s mean σ_h than was a priori assumed. It also shows a relatively low increase of friction with velocity ξ, indicating that higher limit velocities can be reached by the avalanches than was a priori assumed.

Table 7. Posterior distributions

Posterior correlations between release abscissas and release depths (parameter b ₂), release abscissas and Coulombian friction coefficients (parameter d), and release depths and Coulombian friction coefficients (parameter e) are not significantly nonzero at the 95% credibility level (Table 7). This indicates that, for this case study, the different input variables are nearly independent. However, whereas the credibility intervals for b ₂ and d are nearly centered on zero, this is not the case for e. This shows that relatively strong evidence exists in the data in favor of a positive correlation between release depths and Coulombian friction coefficients. This is related to the negative correlations observed in the data between (L _start, l _start, h _start) and the runout abscissa .

3.4.2. Latent variables

For each of the calibrated events, a marginal posterior distribution is obtained for the latent friction coefficient and for the latent runout distance. Most of these distributions are unimodal, bell-shaped and show a small dispersion. Figure 5 (a and c) show the posterior pdfs obtained for the 10 January 1936 avalanche.

Fig. 5. Marginal posterior distributions of latent variables. Left: the posterior distribution of the latent variables for one of the avalanches of the dataset: (a) friction coefficient and (c) runout distance. Right: histograms of the marginal posterior means for the full dataset: (b) friction coefficient and (d) runout distance.

For the whole dataset, the calibrated modal values for μ range from 0.16 to >0.6, with numerous values between 0.4 and 0.6 (Fig. 5b). In the avalanche literature, a 0.16 Coulombian friction coefficient is generally attributed to an extreme event involving very dry and cold snow. This statement is to some extent supported by the data since this value is found for the extreme event that has reached the longest runout by far ( ; Fig. 2). However, the corresponding snow volume was not exceptional (v _stop = 45000 m³), which somewhat contradicts Salm and others’ (1990) guidelines (see section 5.4.2). The modal values obtained for the other avalanches must be attributed to more ordinary events involving old wet snow or less cold dry snow. This is the case for the 10 January 1936 avalanche, with a posterior estimate of 0.57 for μ (Fig. 5a) and a runout distance .

The distributions obtained for each latent runout distance are discrete because of the 5 m discretization step used by the numerical avalanche model. However, they are all very close to their theoretical distribution, i.e. a Gaussian distribution centered on the observation and with a variance of (Fig. 5c). Propagation errors are therefore small for the whole dataset, with an empirical distribution that is unbiased and has a standard deviation close to the chosen value σ _num = 15 m (Fig. 5d). These results suggest that the probabilistic calibration of the past events has been successfully performed for this case study, even though the runout zone considered has a complex topography.

3.4.3. Posterior correlation

The result of Bayesian inference is the joint distribution of all unknowns rather than the analyzed marginal distributions up to this point. Given the large simulated sample, all interparameter linear correlation coefficients are nonzero at the 95% significance level. However, most of them are small, indicating that many parameter pairs are a posteriori nearly independent. This applies particularly to parameter pairs indexing distributions of different input variables (Fig. 6a) such as (a ₁, e), and parameter pairs including at least one variance parameter such as (b ₂, σ_h ). By contrast, parameter pairs indexing the mean of the distribution of the same input variable, i.e. (a ₁, a ₂), (b ₁, b ₂), (c, d), (c, e) and (d, e), show high (in absolute value) posterior correlations because of possible compensations (Fig. 6b), for instance −0.81 for (b ₁, b ₂) and −0.57 for (c, e).

Fig. 6. Three joint posterior distributions. Three unknown pairs are presented: (a) two parameters with no correlation; (b) two parameters with a high negative correlation; and (c) the two highly positively correlated friction coefficients for the 10 January 1936 avalanche.

Possible compensations to obtain the same runout distance also explain that a significant positive correlation exists between ξ and the Coulombian friction coefficient μ corresponding to the different calibrated events (e.g. 0.64 between ξ and the value of μ corresponding to the 10 January 1936 avalanche (Fig. 6c)). This is partially related to the difficulty of calibrating a Voellmy friction law using the available data (section 5.1), but is also a normal feature in a random-walk iterative search allowing several points of similar credibility in the parameter space to be reached.

4. Simulation of Reference Scenarios

4.1. Simulation set-up

For the predictive phase, 20 000 Monte Carlo simulations were performed. First, 20 000 values of the joint distribution of the input variables were sampled. This notation remembers that, in the predictive phase, all model parameters including ξ are fixed to their posterior estimates. The distribution of the release length L _start was obtained by computing the release length corresponding to each simulation using Equation (10). Then each set of input variables was propagated, which provides, using Equation (25), the joint distribution of the output variables . The notations v_xt and h_xt indicate that, for each simulation, a velocity and a flow depth are computed for each abscissa and each time-step. Note that the random noise σ _num is not considered in this predictive phase, so the runout distance distribution obtained is discrete with a 5 m discretization step.

Subsequently, the samples obtained were reworked to compute return periods and extract the distributions of friction coefficients, maximal velocities , and maximal flow depths at abscissas corresponding to different return periods. The associated distributions of Froude numbers, Reynolds numbers, drag coefficients and impact pressures were computed using these maximal values. The Froude numbers, Reynolds numbers and impact pressures considered are not rigorously maximal values, since maximal values for these quantities are not necessarily concomitant with maximal velocities and maximal flow depths. Nevertheless, tests were done to compare the values obtained with this simplified simulation set-up and the ‘true’ maximal values for a few events, showing very few differences. Moreover, recent experimental data concerning velocity and flow depth profiles in real avalanche flows (Sovilla and others, 2008) and avalanche simulations (Naaim and others, 2010) suggest that the Froude number is relatively constant in the avalanche body, so the distributions obtained with our simplified set-up may well be close to the distribution of the ‘real’ maxima of the different quantities at the abscissas considered. Total computations took approximately 5 days on a standard PC.

4.2. Distribution of input variables

Figure 7 shows the distribution of the ‘input’ variables of the propagation model given . Most avalanches are released in the upper part of the path, with release depths of 0.77–2.54 m at the 95% confidence level (Table 8). Corresponding release lengths range predominantly between 100 and 250 m. The distribution of the friction coefficient μ is slightly skewed to the left, but very close to a Gaussian distribution with a mean and a standard deviation . This comes from the low correlation between μ and the other input variables inferred on the data for this case study. The posterior correlation between μ and x _start and between μ and the release dimensions (h _start, L _start) is therefore very low (Table 9; see section 5.4.2 for discussion). Other a posteriori correlation coefficients are close to those obtained from the data. Given the large simulated sample, all these correlation coefficients, even the very small ones, are nonzero at the 95% significance level.

Fig. 7. Distribution of the input variables of the propagation model: (a) release abscissa, (b) release depth, (c) release length and (d) friction coefficient μ. Parameters of the magnitude model equal their posterior mean . Release lengths are derived from release depths using Equation (10).

Table 8. Distribution of model variables given

Table 9. Intervariable correlations (posterior mean)

4.3. Runout distances and return periods

Figure 8a shows the simulated runout distance distribution. It is strongly multimodal, with its main mode around x = 2000 m, a secondary mode around x = 1700 m and a tertiary mode around x = 900 m. This is in good agreement with the path’s complex geometry: the main mode corresponds to the gentle slopes at the bottom of the path, just before the arrival at the valley floor, where most of the observed avalanches have stopped. The secondary mode corresponds to the segment of the path where the slope decreases to ∼23° before increasing again to 40°, where a few of the observed avalanches have stopped. The third small mode in the middle of the path corresponds to a change in the path’s concavity that stops minor avalanches characterized by a very high level of friction. Due to their small size, such avalanches are not recorded in the French avalanche database.

Fig. 8. (a) Runout distance distribution and (b) return periods.

Table 10 confirms the fairly good agreement between the simulated sample and the data. For the median, the difference between observed and predicted samples is 45 m, and for the 90% quantile it is <30 m. Nevertheless, a systematic difference exists, with a lower exceedance probability associated with a given abscissa in the simulated sample than in the data. The simulated sample is also much more dispersed and skewed on the left than the dataset. These effects are presumably due to the absence of records of very small avalanches in the database, which causes the runout distance corresponding to a given exceedance probability to be overestimated with the empirical distribution. The simulated sample is thus arguably closer to reality. However, it is not possible to check this assumption since the basis on which certain small events were ignored in the past (threshold altitude or minimal deposit volume, etc.) is not precisely known.

Table 10. Comparison between data and simulated runout distances

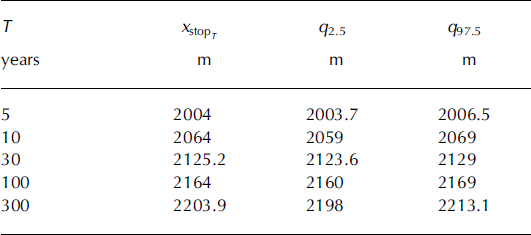
The abscissas corresponding to any return periods (e.g. the classic periods of 10, 30, 100 or 300 years) are obtained simply by considering the associated quantile of the runout distance distribution using Equation (27). Agreement between data and the one-to-one relationship between runout distance and return period derived from the simulated sample is quite good, except for the data corresponding to the highest recorded runout distance (Fig. 8b). This is because the empirical return period computed for this latter avalanche is highly unrealistic, as it necessarily nearly corresponds to the length of the observation period. The simulated sample gives a return period of 340 years for this event, which seems much more realistic and is consistent with the calibrated value of μ = 0.16.

Monte Carlo confidence intervals have been computed for a few return periods using Equation (28). Their width ranges from 5 to 10 m depending on the abscissa considered (Table 11). This indicates that the number of simulations performed is sufficient, even for evaluating runout distances corresponding to return periods >100 years. Indeed, such widths are within the order of magnitude of the discretization step of the numerical propagation, so better precision cannot be expected with a larger number of simulations. The variable width of the confidence interval is worth special mention. On a regular slope, it increases with the return period, since more and more simulations are required to precisely evaluate decreasing exceedance probabilities. Here, however, this is not the case, because of the irregular topography in the runout zone: when the local geometry constrains avalanches to stop because of a slope increase, the exceedance probability is precisely estimated, so the confidence interval is small (e.g. 3 m for T = 5 years and 5 m for T = 30 years). By contrast, when the local slope remains constant or increases, different runouts can be obtained for avalanches with very close dynamical properties, so the corresponding exceedance probability is harder to evaluate and the confidence interval is larger (e.g. 10 m for T = 10 years).

Table 11. Runout distance versus return period: posterior mean and Monte Carlo confidence interval

4.4. Coulombian friction coefficient

Figure 9 presents the distributions of μ_T , the Coulombian friction coefficient of the avalanches exceeding runout abscissas corresponding to return periods of T = 10, 30 and 100 years. Note that these distributions become more irregular as the return period increases because few avalanches obviously exceed high-return-period abscissas, thus increasing Monte Carlo error. With 20 000 simulations, there are slightly more than 200 centennial avalanches since the mean avalanche frequency is slightly lower than one event per year for the case study. The three distributions are skewed to the left, because avalanches that reach a high abscissa have predominantly low friction coefficients. This also explains why the mean of the distribution decreases with the return period, ranging from 0.314 for a 10 year return period to 0.2 for a 300 year return period. This confirms that the lowest calibrated value of 0.16 is due to an extreme avalanche, with a return period greater than 300 years. Finally, the standard deviation of μ_T remains constant whatever the return period and is approximately 0.07, little more than half the overall standard deviation .

Fig. 9. Distribution of the Coulombian friction coefficient versus return periods of (a) 10 years, (b) 30 years and (c) 100 years. Only the exceedances of the corresponding abscissa are retained (e.g. for T = 30 years, the abscissa has a 0.033 annual probability of being reached).

4.5. Flow velocities, flow depths and Froude numbers

Figure 10 presents the distribution of maximal velocities, maximal flow depths and Froude numbers at the abscissa corresponding to a return period of 10 years. Predicted maximal flow depths are nearly uniformly distributed between 0 and 3.5 m, but major decennial avalanches show flow depths up to 10 m. Corresponding maximal velocities range between 0 and 20 m s⁻¹,with a well-marked modal value close to 5 m s⁻¹,but a probability of 0.2 to observe maximal velocities higher than 10 m s⁻¹ (Table 12). This latter value is of practical interest since it corresponds to the probability of observing a dynamic pressure in the free-surface snow flow higher than the classic threshold of 30 kPa with the chosen mean snow density of 300 kg m⁻³. Finally, decennial avalanches are mainly associated with Froude numbers between 1 and 2.5, but much more dynamical flows are also possible, with Froude numbers >4. This is related to the slope at the 10 year abscissa, which is still significantly steep.

Fig. 10. Distribution of (a) velocity, (b) flow depth and (c) Froude number for a decennial avalanche.

Table 12. Maximal velocity versus return period

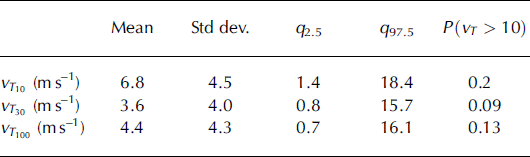
For higher return periods, a few avalanches still exhibit high velocities, flow depths and Froude numbers. However, these quantities globally decrease as the return period increases. For instance, most of the avalanches that exceed return period abscissas >30 years show low flow depths and low velocities (Table 12). The low velocities occur because the slope globally decreases with the abscissa, which decreases the dynamics of the flow and stops more and more avalanches. The low flow depths associated with high runouts are explained by the low friction coefficients of the avalanches reaching these high abscissas (Fig. 9), dry fluid flows being rather thin. Finally, for return periods of 30 and 100 years, the mean of the Froude number distribution is very close to 1, and few avalanches still show Froude numbers >3 (Table 13). Because of the slope profile, the mean and maximal values are slightly higher at the 100 year than at the 30 year return period abscissa.

Table 13. Froude number versus return period

4.6. Reynolds numbers and drag coefficients

Reynolds numbers can be derived from Froude numbers using Equation (5). The distribution obtained depends strongly on the diameter of the obstacle considered. With a small obstacle (d ₀ = 0.25 m), the distribution shows an exponential tail at a decennial abscissa (Fig. 11b), with a mean value around 10. However, for a few avalanches the Reynolds number given by Equation (5) is unrealistically high and had to be set at 200 to allow realistic drag coefficient and impact pressure computations. For a larger obstacle (d ₀ = 5 m), Reynolds numbers are much more dispersed, so for many avalanches they had to be set at 200 (Fig. 11c). As for Froude numbers, lower Reynolds numbers are observed at the 30 year return period abscissa than at the centennial abscissa because of the topography of the path (Table 14).

Fig. 11. Drag coefficient versus Reynolds number (a) and Reynolds number for a decennial avalanche for two sizes of obstacle, 0.25 m (b) and 5 m (c). The relationship between Reynolds number and drag coefficient is for a prismatic obstacle shape.

Table 14. Reynolds number versus return period

With Naaim and others’ (2008) formula, the Cx distribution is a direct consequence of the distribution of Reynolds numbers. With a large obstacle, the assumptions of hydrodynamics for a prismatic shape are nearly fulfilled at the decennial abscissa, with all values very close to 2 and maximal values not higher than 2.4 (Fig. 12c). For a small obstacle, this is not true, with drag coefficients ranging between 2 and 12 and with a modal value around 6 (Fig. 12b). With Sovilla and others’ (2008) formula (Fig. 12a), the results obtained are very close, which is not illogical since the experimental measurements were done on a pylon, which is in fact a small obstacle. The main drawback using this instead of Naaim and others’ (2008) formula is that drag coefficients <2 are generated for certain avalanches, which is unrealistic in the studied case of a prismatic obstacle.

Fig. 12. Drag coefficient for a decennial avalanche, evaluated with Savilla’s experimental formula (a) and Naaim’s semi-empirical formula for two sizes of obstacle, 0.25 m (b) and 5 m (c).

4.7. Impact pressures

At all the abscissas considered and whatever the formula used, the pressure distributions obtained are very strongly skewed to the right, with a modal value close to zero and an exponential tail because of the velocity square dependency (Fig. 13). Most of the avalanches are therefore characterized by low pressures in the runout zone, but very high values can be obtained for a few events. This is critical for hazard mitigation and indicates that, for the structural design of a defense structure or of an exposed building, very high impact pressures must be considered even if such events are very rare.

Fig. 13. Dynamic pressure in the free surface flow (a) versus impact pressure evaluated with Naaim’s formula (b) for a decennial avalanche.

The impact pressures computed using Naaim and others’ (2008) formula for a large obstacle are, at a decennial abscissa, close to the dynamic pressures in the free surface flow (Fig. 13a). This is not surprising given the values of the drag coefficient at this abscissa. The impact pressures computed for a small obstacle (Fig. 13b) or with Sovilla and others’ (2008) formula are much higher (e.g. nearly twice as high on average as using Naaim and others’ (2008) formula (Table 15)). With each formula, the probability of an event producing an impact pressure higher than the classic limit of 30 kPa is easily obtained: 0.21 for a large obstacle, which nearly corresponds to the probability of observing a maximal velocity higher than 10 m s⁻¹,but 0.48 for a small obstacle (Table 15). This indicates that at the decennial abscissa the classic threshold of 30 kPa is exceeded every 50 years on average for a large obstacle, but nearly every 20 years on average for a small obstacle.

Table 15. Impact pressure for a decennial avalanche

The differences between the formulas apply whatever the return period considered. For example, the probability of a centennial avalanche inflicting a pressure greater than 30 kPa is only 0.13 if the dynamic pressure in a free surface flow is studied, whereas it is 0.25 with Naaim and others’ (2008) formula for a small obstacle (Table 16). All these results indicate that a constant drag coefficient equal to 2 can possibly be used to compute impact pressures on a large obstacle, but that a much higher drag coefficient must be used for a smaller obstacle if one wants to use a constant value. However, given the large range of variation of the drag coefficient for a small obstacle, our results also suggest that it is much more reasonable to compute the Cx value to be used for a given reference event using the flow properties.

Table 16. Impact pressure for a centennial avalanche

5. Discussion

5.1. Identifiability, prior information and prior sensitivity

5.1.1. Identifiability of friction coefficients

A first option for a deterministic calibration of the two friction coefficients of a Voellmy friction law on a given study site is to fit a parameter pair (μ_i , ξ_i ) for each recorded event. Some data that are only measured on test sites (e.g. velocities) are then required (Blagovechshenskiy and others, 2002)). Another option is to use the same pair (μ, ξ) to fit all the events that have occurred on an avalanche path. However this is not possible because, for a given snow volume, various avalanche magnitudes can be observed due to variations in snow quality (temperature, density, humidity, etc.). Taking inspiration from traditional engineering practices (Salm and others, 1990) that continue to be debated, we choose an intermediate approach, having one latent friction coefficient μ_i , i ∊[1, N] and the parameter ξ to be estimated from the data.

Compared with having a parameter pair (μ_i , ξ_i ) for each event, our choice reduces the number of unknown quantities to be estimated. However, model identifiability is still not ensured. The critical question is whether the available release dimensions and positions , i ∊[1, N] are sufficiently constraining to be as informative as at least one runout distance, since N + 1 friction coefficients must be calibrated with N avalanche events. The answer to this question depends on the data available on a given path and on its topography. Correlations between release abscissas, release dimensions and runout distance are generally weak (see below), but may contain some information if the number of recorded events is sufficiently high. Reasonably complex runout zones with avalanches stopping both on flat regions and steep slopes are also relatively constraining for the ξ parameter, allowing only a small range of values to match all observations. By contrast, extremely regular runout zones are only very slightly constraining, giving an infinity of solutions (ξ, μ_i ), i ∊ [1, N] to the calibration problem.

An important consequence is that the likelihood function corresponding to our stochastic model cannot necessarily be maximized using Fischer, Neyman and Pearson’s traditional (frequentist) method, depending on the case study. Until the relations between data, topography and model identifiability are fully comprehended, which will require further research, our proposal to work under the Bayesian paradigm is a practical way to overcome the problem. At the cost of using an informative prior for ξ, it makes the model fully identifiable for any case study by restricting the research domain to a weighted range of possible values.

If there is little information on ξ in the case study because of a weak dataset and/or an overly simple path topography, the posterior distribution of all the is computed with respect to the variability of the prior distribution chosen, which is more satisfactory than imposing a constant fixed value for ξ. By contrast, if enough information exists in the data or in the path’s topography, the prior knowledge on ξ is updated. This is what happens in our example in which ξ′s posterior distribution has a much lower variance and a higher modal value than the prior distribution.

5.1.2. Prior subjectivity and sensitivity

Proposing an informative prior for ξ is technically easy in light of recent advances in elicitation (Craig and others, 1998; Kadane and Wolfson, 1998; O’Hagan, 1998; Parent and Bernier, 2003), and of the expert knowledge available concerning the link between ξ and the path’s roughness, altitude and exposure (Salm and others, 1990). The drawback is that it undeniably introduces subjectivity into the analysis. Indeed, encoding the partial knowledge of an unknown is historically the main argument against the Bayesian theory. It is denied as a matter of principle when probability is interpreted as an objective limit of frequencies rather than as a subjective bet that quantifies a probabilistic judgment.

However, using prior information is for us nothing more than a modeling choice, such as choosing an avalanche model and the stochastic operators describing the input–output variability (see sections 5.3 and 5.4). It has the advantage of bringing into the analysis extra-data information. As shown by the case study, it also favors a reasonably quick convergence of the MCMC algorithm by orienting the numerical search in regions of high presumed probability. While using our stochastic model, we therefore advocate using informative priors not only for ξ, but also for all other parameters for which knowledge is available except (b ₂, d, e). For these latter correlation parameters, vague priors must be preferred, so as to possibly infer weak correlations between the different variables.

The robustness of the results to the prior choice can easily be investigated through a sensitivity analysis using vague priors instead of informative ones for all parameters except ξ. This has been done for the case study, with results very close to those detailed in section 3. This indicates that there is enough information in the dataset studied for the sensitivity of the prior to be low. However, convergence took longer to reach because the algorithm did not as easily find the region of high posterior probability. The related increase in computation times is another argument in favor of informative priors for practical applications.

5.2. Advantages and disadvantages of the proposed MH algorithm

Beyond the question of the theoretical feasibility of inference, there remains the difficulty of its practical implementation. Like all MCMC methods, the MH algorithm has the advantage of being consistent with the direction of an avalanche model’s specification, i.e. the candidate values are generated for the input variables and the credibility of the outputs is evaluated after the propagation. Moreover, the MH algorithm is very general, unlike the Gibbs sampler (Geman and Geman, 1984). In theory, Bayesian inference using the MH algorithm and suitable informative priors should therefore be able to achieve the calibration of any avalanche propagation model. In practice, however, obtaining a good numerical approximation of the posterior pdf may be extremely tricky because of a too low convergence or numerical traps.

Even if convergence for the ξ parameter is difficult because of the high autocorrelation level of the MCMC chains, the algorithm proposed in this paper has proved its efficiency in the case study. One of its main advantages is that it is sequential, which reduces for each jump the difficulty of finding a new point of relatively high credibility in the parameter space. When the algorithm is tuned, this makes relatively high jump strengths correspond to the optimal acceptance rates, thus reducing the burn-in period (only 1000 iterations for the case study). The proposed algorithm may therefore be a good starting point for any avalanche practitioner or scientist willing to use their own depth-averaged propagation model within a Bayesian statistical framework. One must, though, keep in mind that the jump functions proposed in this paper are case-study specific, and, for a new case study, the strength of the different marginal jumps must be tuned again with respect to Gelman and others’ (1995) optimal acceptance rates, which can be difficult and time-consuming.

More generally, even if its sequential nature makes the proposed algorithm relatively efficient, computation times remain quite high, first to reach convergence (burn-in period) and then to obtain a good approximation of the posterior pdf. A first option to reduce these computation times would be to test even more efficient versions of the MH algorithm to explore more quickly the regions of high probability as soon as they are reached using adaptive jump strengths. A second option would be to abandon the MH algorithm and to use a noniterative numerical method such as importance sampling (Parent and Bernier, 2007, ch. 14), with an auxiliary distribution based on the inferential results from a much simpler statistical–dynamical model (Eckert and others, 2007b). This would not necessarily be technically easier given the large dimension of the parameter space.

5.3. Why a depth-averaged model with a Voellmy friction law?

5.3.1. Advantages and disadvantages

Many numerical avalanche models exist, with different levels of description, different friction laws and different simplifying hypotheses (e.g. Pudasaini and Hutter, 2007). Depth-averaged fluid descriptions of avalanche flows are now standard in many European countries as soon as numerical modeling is used for hazard zoning (Gruber and others, 1998; Hopf, 1998). They give access to space and time velocity, pressure and flow-depth profiles much closer to real avalanche flows than the single values provided by simpler block models. Even if it remains time-consuming, our stochastic model may therefore be useful for many practical configurations, as a reasonable compromise between a realistic description of the avalanche flow and computation times.

The search for physical realism would call for an even more complete 2-D avalanche model (Naaim, 1998; Pudasaini and Hutter, 2007) to possibly take into account several layers and/or the geometrical aspects of the flow. However, as stated in section 2.1, such models cannot for the moment be used in a statistical–dynamical setting because of the computation times needed for each simulation. This may become possible in the future with the continuous increase of PCs’ computational power. Methods for approximating the distribution of the outputs of a complex numerical code more rapidly than a standard Monte Carlo set-up, whose convergence rate is only , will also be required to reduce the number of iterations necessary to achieve the predictive simulations with sufficient precision (Skaggs and Barry, 1997).

Because of the complexity of snow flows and a lack of knowledge about snow rheology (Dent and Lang, 1980; Dent, 1993), the choice of one friction model remains a source of constant debate in the avalanche community. Since a Voellmy friction model implies the identifiability problems discussed in section 5.1, its choice can be questioned. Our justification is partly that the Voellmy model remains the most practised. In addition, as stated in section 2.1, it is consistent with the even stronger assumption of no erosion routine in the model. Both assumptions regarding the friction law and the erosion–deposition model could, however, be relaxed in later work within the same framework because of the generality of the MH algorithm pointed out in section 5.2.

5.3.2. Propagation model sensitivity

We have shown that our propagation model provides distributions of variables such as velocities and pressures that are not reliable enough with a simpler sliding block model. It can also be claimed that the runout distance distribution obtained with our statistical–dynamical fluid model is closer to reality than those obtained with simpler statistical–dynamical sliding block models, which allow more accurate estimation of return periods. To test this statement, the Voellmy fluid model discussed in this paper is compared in our case study with the statistical–dynamical sliding block model with a Coulombian friction law from Eckert and others (2007b), and with a similar stochastical–dynamical sliding block model with a Voellmy friction law (Fig. 14).

Fig. 14. Comparison with sliding block propagation models. The Voellmy fluid model of this paper is compared with the statistical–dynamical sliding block model with a Coulombian friction law from Eckert and others (2007b) and with a statistical–dynamical sliding block model with a Voellmy friction law.

Eckert and others (2007b) used 40 data to calibrate the Coulombian model. Here only the 26 used in this paper are considered, to compare the three models with similar information. With these data, the Coulombian model is clearly too pessimistic, with ‘small’ return periods associated with very high runout abscissas and an overestimation of high return periods. Eckert and others (2007b) obtained much more reasonable results. This shows that the Coulombian model needs a large calibration dataset to give accurate results. We believe this is because it has insufficient physical constraints (e.g. no increase of friction with velocity).

The two models with a Voellmy friction law show a more realistic and relatively similar one-to-one mapping between runout abscissa and return period for small return periods. Nevertheless, the runout distance distribution obtained with the Voellmy sliding block model looks too optimistic for high return periods, with, for example, a presumably far too high return period of ∼2200 years associated with the highest recorded event discussed earlier. As stated in section 4.3, the depth-averaged model presented proposes a 340 year return period for this event, which is much more credible. Moreover, the runout distance distribution is more regular with the fluid model than with the Voellmy sliding block model, with avalanches possibly stopping when the slope increases, which is not possible with a sliding block.

This short comparison suggests that an accurate fluid description of the avalanche flow can compensate a small data quantity, the model being less rough than a simple sliding block. The physical description of the flow thus adds information to the analysis, in the same spirit as prior knowledge balances information conveyed by the data in Bayes’ theorem.

The intermediate assumption of a depth-averaged fluid model with a Coulombian friction law could also have been tested, but at the cost of presumably unrealistic pressure and velocity distributions because of the absence of erosion in the propagation model. We therefore prefer to reserve this approach for further work including the erosion–deposition model described by Naaim and others (2004).

5.4. Stochastic modeling choices

5.4.1. Input variable description

We have modeled the latent friction coefficient with a conditional Gaussian mixture model. Since basal friction results from several perturbations on the same order of magnitude (avalanche size, snow quality, etc.) the central limit theorem suggests this is appropriate. The numerical/ observation errors were also assumed Gaussian for the same reason, with a zero mean because the propagation model and the observation process are supposed good enough to be unbiased.

The conditional gamma mixture model employed for release depths was based on the consideration that the amount of available snow increases with altitude (Durand and others, 2009). By contrast, the beta distribution used for the release abscissa had no real physical grounding, and it is probably too simple when the topography in the release zone shows substantial concavity changes. Furthermore, largely speculative operators have been used to transform the observed deposit volumes into release dimensions because of problems with collecting these data in the field.

A sensitivity analysis of the choice of distributions describing the input variables was performed with a simpler model (Eckert and others, 2007b). It showed the low sensitivity of runout distance distribution to the variability of the input quantities, but also that, as soon as any variability is neglected, high runout distance quantiles are underestimated. Our model can therefore be used in first approximation even if it is oversimplified, but more work is needed to find a stochastic structure that more satisfactorily models the entire random vector of input variables. Priority should be given to the most debatable assumptions regarding the distribution of release positions and dimensions. This includes the reparation along the path of available snow for mass incorporation during the flow.

5.4.2. Intervariable correlation

The proposed conditional model is designed to take into account all correlations between the input variables of the propagation model, using the (b ₂, d, e) parameters. Although it is a rough first attempt since only linear correlations are considered, this makes it better able to fit the variability of the data than independent standard distributions. From a more practical point of view, when the model is used for prediction, this should allow large avalanches that result from a combination of extreme constraining factors not to be underestimated.

For the case study, these correlations have been shown to be very small. For instance, the correlation between the friction coefficient μ and the avalanche size, in our model the initial depth h _start, has been found to be much lower than is assumed in traditional engineering practices (Salm and others, 1990). This may indicate that release conditions are quickly ‘forgotten’ by the flow, or, as stated in section 5.1, that the information conveyed by the data is too weak to infer this parameter from the data given the friction law chosen. More generally, it illustrates the usefulness of the proposed framework for inferring unobservable quantities in avalanche flows, which may be an interesting outcome for further developments.

5.5. Reference scenarios for avalanche hazard management

5.5.1. Multivariate reference scenarios and impact pressure distribution

The case study shows that there is an infinity of avalanches corresponding to the same return period. However, with the proposed approach, at least the joint distribution of all events corresponding to a given return period is obtained. Figures 9–13 give a complete picture of the decennial scenarios, from maximal velocities and flow depths to flow regimes and impact pressures. A few pertinent reference scenarios can be selected (e.g. those corresponding to the upper bound of the 95% confidence interval of the critical variables). Important information for hazard zoning is also provided, such as the link between the different variables of interest and the return period (Tables 12–16), as well as the probability of exceeding any threshold (Tables 12, 15 and 16).

To study the level of exposure of the elements at risk, the distributions of the impact pressures obtained are of particular interest. The case study shows that very high pressures remain possible for very high return periods, even if they seldom occur (Tables 15 and 16). It also shows that computation of the drag coefficient distribution is necessary to account for the high pressures exerted by avalanches characterized by low Froude numbers, especially on small obstacles such as pylons (Figs 11–13). Even if they are based on semi-empirical equations, these results are coherent with full-scale measurement (Sovilla and others, 2008).

5.5.2. Associated uncertainty

As shown in section 3, the estimation error related to the limited data quantity used for inference is clearly quantified in the Bayesian framework by the dispersion of the posterior distribution of model parameters θ. However, this source of uncertainty has not been considered for prediction in this paper: the reference scenarios were computed using the posterior mean of the model’s parameter, and only the Monte Carlo error was investigated. This has restricted the Bayesian computations to a powerful way of calibrating the parameters of a noninvertible and only partially identifiable propagation model. As illustrated with a sliding block model (Eckert and others, 2008a), the computation of credible intervals resulting from the lack of local data is, however, possible in the Bayesian framework using simulation sequences that reconstruct the predictive distribution of the return periods of interest. This could also be done for the depth-averaged model proposed here, at the cost of a significant additional computational effort. It would, for example, somewhat relax the debatable assumption of a constant ξ by sampling its posterior distribution with respect to the information conveyed by the data.

5.5.3. Validation

Of even greater concern is the problem of validating the reference scenarios obtained. In stochastic hydrology, the ‘true’ model is known because of asymptotic properties assuring the convergence of a sample of independent exceedances to a family of limit distributions (Coles, 2001). Sources of uncertainty are therefore essentially related to data (missing values, measurement errors, spatial extrapolation, etc.). By contrast, a stochastic snow avalanche model remains at least partly speculative, and is therefore highly questionable. For our case study, an extreme event was registered, allowing a qualitative check of the results obtained, at least for runout distances. In general, however, such an event is not available, and one cannot wait a few hundred years to see whether the proposed return periods are correct. Moreover, the number of recorded runout distances is usually so small that split-test approaches are not possible. Therefore other validation procedures must be employed. They include comparison between different modeling approaches (e.g. Barbolini and others, 2000), and comparison with naturalistic data from dendrochronology that may help to incorporate evidence of past extreme avalanches.

6. Conclusion and Outlook

A depth-averaged fluid propagation model has been used within a hierarchical Bayesian framework, thus implementing a statistical–dynamical approach with the actual standard in avalanche numerical modeling. Using a case study, the proposed sequential MH algorithm proved its ability to perform the joint calibration of a Voellmy friction law. Model identifiability was ensured by the choice of an informative prior for the friction coefficient ξ, and it was shown that this practical trick does not preclude capturing the information conveyed by the data as soon as it is valuable. In predictive simulation mode, it was demonstrated how the multivariate nature of avalanche hazard is acknowledged by the available joint distribution of all model outputs at any abscissa of the runout zone. For example, recent advances taking into account the particular rheology of snow have been used to compute realistic (i.e. compatible with the range measured on instrumented test sites) high-impact pressures for small obstacles.

This all shows that, even if the computations remain relatively complex and time-consuming, they are feasible on a real path and are worth the effort. We therefore believe that our Bayesian approach is a valuable framework for new developments in the field of avalanche dynamics. It allows different information sources (data, prior) and knowledge (deterministic modeling of avalanche propagation and stochastic modeling of the input variables), even if imperfect, to be brought together and exploited for operational risk assessment. From a more physical point of view, it is a consistent way to learn about unobservable parameters (e.g. correlation and friction coefficients).

We are fully aware that this approach, being relatively new, includes numerous subjective choices. Some of them, such as the operators used for transforming avalanche deposits into release dimensions, are very speculative and were made because of the weakness of available knowledge. Others, such as the choice of a Voellmy friction law, are more classical debates in the avalanche community. We made the modeling assumptions that we believed were the most sound, as an example of how all computations can be made, rather than with the objective of obtaining a definitive model that works in all situations. Most of our choices could easily be replaced by alternatives within the same framework, since it should be possible to adapt the proposed MH algorithm to any propagation model and many modeling assumptions.

Implementing the approach using various propagation models and friction laws on various datasets would improve our knowledge of avalanche flows (e.g. which variables are correlated, and which model structures and friction laws are best supported by the data). For this, the use of additional data such as velocity and pressure measurements acquired on test sites would be worthwhile. This would make identifiability problems less challenging and make it possible to infer additional parameters such as α _sv and k _sv in the depth-averaged equations, as well as the relations between velocity and pressure in real flows.

For practical applications, the reference scenarios obtained must be validated before the model can be routinely used for engineering purposes (Naaim and others, 2010). This will require greater sensitivity analysis and a comparison with other data sources on a selection of case studies. Research is also needed to reduce computation times, which could be done by improving the proposed calibration algorithm and implementing simulation methods that are more efficient than a Monte Carlo approximation.

Finally, as suggested in section 5.5.2, a direct continuation of the approach would be to perform Bayesian predictive simulations to take into account parameter uncertainty, especially concerning the friction coefficients. Another appealing outlook would be risk computations taking into account the elements at risk (Arnalds and others, 2004) to fully address the absence of one-to-one mapping between a multivariate hazard and a return period. This could be done using a combination of the Bayesian risk computations proposed by Eckert and others (2008b, 2009) with the hazard model described in this paper.

List of Symbols