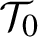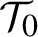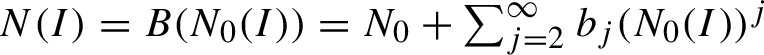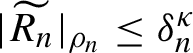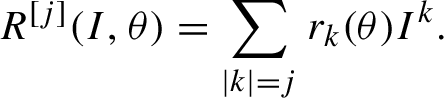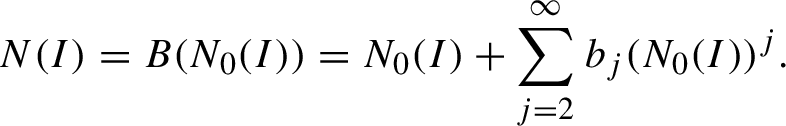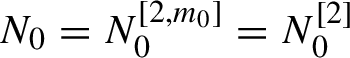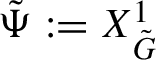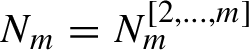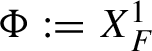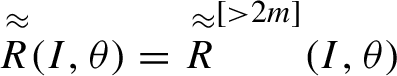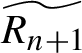1 Introduction
The goal of this paper is to study the convergence of the transformations of an analytic Hamiltonian system in a neighborhood of an invariant torus to the Birkhoff normal form. Here we assume that the frequency vector at the invariant torus is very resonant and, hence, already at the formal level, the existence of the Birkhoff normal form has obstructions. The main result, Theorem 1.1 below, will show that if the obstructions for the formal equivalence between the system and its Birkhoff normal form vanish and the normal form is convergent and has a particular form, then the system is analytically equivalent to its normal form. Hence, this result can be considered as a part of the rigidity program: identifying obstructions for a weak form of equivalence whose vanishing implies a stronger form of equivalence.
1.1 Classical theory of normal forms: existence and uniqueness
Consider an analytic function
where
![]() $\theta \in {\mathbb T}^d={\mathbb R}^d/{\mathbb Z}^d$
,
$\theta \in {\mathbb T}^d={\mathbb R}^d/{\mathbb Z}^d$
,
![]() $I\in ({\mathbb R}^d,0)$
,
$I\in ({\mathbb R}^d,0)$
,
![]() $\langle \cdot ,\cdot \rangle $
denotes the usual scalar product in
$\langle \cdot ,\cdot \rangle $
denotes the usual scalar product in
![]() ${\mathbb R}^d$
, and
${\mathbb R}^d$
, and
![]() $\lambda _0\in {\mathbb R}^d$
is a constant vector called the frequency vector. The Hamiltonian system associated to it is
$\lambda _0\in {\mathbb R}^d$
is a constant vector called the frequency vector. The Hamiltonian system associated to it is
![]() $ \dot I=\partial _{\theta } H(I,\theta ), \ \dot \theta =- \partial _{I}H(I,\theta ) $
. Note that we are assuming the standard symplectic form. In particular, the set
$ \dot I=\partial _{\theta } H(I,\theta ), \ \dot \theta =- \partial _{I}H(I,\theta ) $
. Note that we are assuming the standard symplectic form. In particular, the set
![]() $\mathcal T_0:=\{0\}\times {\mathbb T}^d $
is an invariant torus of this system. We say that
$\mathcal T_0:=\{0\}\times {\mathbb T}^d $
is an invariant torus of this system. We say that
![]() $H(I,\theta )$
has a Birkhoff normal form (BNF)
$H(I,\theta )$
has a Birkhoff normal form (BNF)
![]() $N(I)$
in a neighborhood of
$N(I)$
in a neighborhood of
![]() $\mathcal T_0$
if
$\mathcal T_0$
if
![]() $N(I)$
is a formal power series and there exists a formal symplectic transformation
$N(I)$
is a formal power series and there exists a formal symplectic transformation
![]() $\Psi (I,\theta )$
, tangent to the identity,
$\Psi (I,\theta )$
, tangent to the identity,
such that
in the sense of formal power series. Any canonical coordinate change
![]() $\Phi (I,\theta )$
as above is called a normalizing transformation. The following fundamental result is called the Birkhoff normal form [Reference Meyer, Hall and OffinMHO, Reference Siegel, Moser and KalmeSM71]. For
$\Phi (I,\theta )$
as above is called a normalizing transformation. The following fundamental result is called the Birkhoff normal form [Reference Meyer, Hall and OffinMHO, Reference Siegel, Moser and KalmeSM71]. For
![]() $H(I,\theta )$
as above, assume that
$H(I,\theta )$
as above, assume that
![]() $\lambda _0$
satisfies a Diophantine condition: there exist constants
$\lambda _0$
satisfies a Diophantine condition: there exist constants
![]() $(C,\tau )$
such that for all
$(C,\tau )$
such that for all
![]() $k\in {\mathbb Z}^d\setminus \{0\}$
, we have
$k\in {\mathbb Z}^d\setminus \{0\}$
, we have
Then
![]() $H(I,\theta )$
has a (formal) Birkhoff normal form. Moreover, if a normal form exists and
$H(I,\theta )$
has a (formal) Birkhoff normal form. Moreover, if a normal form exists and
![]() $\lambda _0$
is rationally independent, then the Birkhoff normal form is unique (up to trivial changes relabelling the actions). Note that the normalizing transformations are not unique, since composing
$\lambda _0$
is rationally independent, then the Birkhoff normal form is unique (up to trivial changes relabelling the actions). Note that the normalizing transformations are not unique, since composing
![]() $\Phi (I,\theta )$
with any transformation that preserves I gives a normalizing transformation.
$\Phi (I,\theta )$
with any transformation that preserves I gives a normalizing transformation.
The Birkhoff normal form is an important tool in the study of Hamiltonian systems. The assumption of existence and non-degeneracy of the normal form has strong dynamical consequences (see, e.g., [Reference Eliasson, Fayad and KrikorianEFK15, Theorem C]). The importance of the BNF becomes even stronger if the normal form is convergent and even more so if there exists an analytic normalizing transformation.
The standard way of constructing a BNF, which we will review in more detail later, is to proceed iteratively, devising transformations that normalize
![]() $H(I,\theta )$
up to the coefficients of order
$H(I,\theta )$
up to the coefficients of order
![]() $I^n$
. The normalization step involves solving differential equations with analytic conditions. The Diophantine conditions (1.2) can be somewhat weakened to subexponential growth (
$I^n$
. The normalization step involves solving differential equations with analytic conditions. The Diophantine conditions (1.2) can be somewhat weakened to subexponential growth (
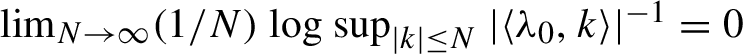 $ \lim _{N \to \infty }({1}/{N}) \log \mathop {\mathrm {sup}}_{|k| \le N } | \langle {\lambda }_0, k \rangle |^{-1} = 0$
).
$ \lim _{N \to \infty }({1}/{N}) \log \mathop {\mathrm {sup}}_{|k| \le N } | \langle {\lambda }_0, k \rangle |^{-1} = 0$
).
If
![]() ${\lambda }_0$
is resonant, one cannot guarantee the existence of the Birkhoff normal form even at the level of formal power series, since there may be some terms in the formal power series of H that cannot be eliminated by a canonical transformation. On the other hand, there are, of course, systems (e.g. the BNF itself, or changes of variables from it) for which one can construct a BNF even in the resonant case. Then one speaks of the Birkhoff–Gustavson normal form [Reference GustavsonGu66].
${\lambda }_0$
is resonant, one cannot guarantee the existence of the Birkhoff normal form even at the level of formal power series, since there may be some terms in the formal power series of H that cannot be eliminated by a canonical transformation. On the other hand, there are, of course, systems (e.g. the BNF itself, or changes of variables from it) for which one can construct a BNF even in the resonant case. Then one speaks of the Birkhoff–Gustavson normal form [Reference GustavsonGu66].
Analogous definitions and statements hold true for symplectic maps in a neighborhood of a fixed point. Even if the formal elimination procedures are very similar, the analysis is very different. Handy references for the classical theory of Birkhoff normal forms are [Reference Eliasson, Fayad and KrikorianEFK13, Reference Eliasson, Fayad and KrikorianEFK15, Reference Meyer, Hall and OffinMHO, Reference MurdockMu, Reference Siegel, Moser and KalmeSM71].
1.2 Generic divergence both of the Birkhoff normal form and the normalizing transformation
The BNF and the normalizing transformations are constructed as formal power series. The following natural questions are of great importance: the first one is whether the BNF converges for Hamiltonians in a certain class. The second is whether there is a convergent normalizing transformation.
Concerning the first question, Perez-Marco [Reference Pérez-MarcoPM] proved the following dichotomy: for any given non-resonant quadratic part, either the BNF is generically divergent or it always converges. The original proof was done in the setting of Hamiltonian systems having a non-resonant elliptic fixed point. The extension of this result to the case of the torus, which is not completely straightforward, has been worked out by Krikorian; see Theorem 1.1 in [Reference KrikorianKri].
Up to very recently it was unclear which of the possibilities is actually realized. Large progress has been made by Krikorian [Reference KrikorianKri], who proved that there exists a real analytic symplectic diffeomorphism f of a two-dimensional annulus such that
![]() $f({\mathbb T} \times \{0\})=({\mathbb T} \times \{0\})$
,
$f({\mathbb T} \times \{0\})=({\mathbb T} \times \{0\})$
,
![]() $f(\theta ,0)=(\theta +\omega _0,0)$
with
$f(\theta ,0)=(\theta +\omega _0,0)$
with
![]() $\omega _0$
Diophantine and having a non-degenerate divergent Birkhoff normal form. An analogous result in a neighborhood of an elliptic equilibrium was recently obtained by Fayad [Reference FayadF]. Combined with the aforementioned result of Perez-Marco, this implies that the Birkhoff normal form of an analytic Hamiltonian is ‘in general’ divergent.
$\omega _0$
Diophantine and having a non-degenerate divergent Birkhoff normal form. An analogous result in a neighborhood of an elliptic equilibrium was recently obtained by Fayad [Reference FayadF]. Combined with the aforementioned result of Perez-Marco, this implies that the Birkhoff normal form of an analytic Hamiltonian is ‘in general’ divergent.
Concerning the normalizing transformations, Poincaré proved that they are divergent for a generic Hamiltonian. Siegel proved the same statement in a neighborhood of an elliptic fixed point (in fact, for a larger class of Hamiltonians than just generic [Reference SiegelSi54]). This is implied by showing that the orbit structure of the map in any neighborhood is very different from that of the Birkhoff normal form (which is integrable). Analogous results for symplectic maps near an elliptic fixed point appear in [Reference RüssmannRü59]. Very different arguments showing divergence of normalizing transformations for generic systems appear in [Reference ZehnderZe73] and for some concrete polynomial mappings in [Reference MoserMo60].
1.3 Convergence of the transformations under the Diophantine conditions for some particularly simple BNF
There are classes of Hamiltonians for which we can guarantee the convergence of the normalizing transformation. The following influential rigidity result was proved independently by Bruno [Reference BrunoBr71] and Rüssmann [Reference RüssmannRü67]. Note that the main assumption is that the (in principle only formal) BNF is of a particular kind.
Consider an analytic Hamiltonian
![]() $H(I,\theta )$
whose frequency
$H(I,\theta )$
whose frequency
![]() ${\lambda }_0$
satisfies a Diophantine condition (1.2). Assume moreover that the Birkhoff normal form
${\lambda }_0$
satisfies a Diophantine condition (1.2). Assume moreover that the Birkhoff normal form
![]() $N(I)$
of
$N(I)$
of
![]() $H(I,\theta )$
is a formal function B of a single variable
$H(I,\theta )$
is a formal function B of a single variable
![]() $\Lambda _0:=\langle {\lambda } , I\rangle $
, that is,
$\Lambda _0:=\langle {\lambda } , I\rangle $
, that is,
Then there exists an analytic normalizing transformation and the BNF is, in fact, analytic.
We remark that Bruno proved the above result under a weaker condition on
![]() ${\lambda }_0$
than (1.2). For analogous statements in the case of invariant tori, see [Reference BrunoBr89]. Other modifications can be found in [Reference RüssmannRü02, Reference RüssmannRü04]. This result has been recently generalized to a much more general context by Eliasson, Fayad and Krikorian [Reference Eliasson, Fayad and KrikorianEFK13, Reference Eliasson, Fayad and KrikorianEFK15]. We stress that in all these works mentioned above,
${\lambda }_0$
than (1.2). For analogous statements in the case of invariant tori, see [Reference BrunoBr89]. Other modifications can be found in [Reference RüssmannRü02, Reference RüssmannRü04]. This result has been recently generalized to a much more general context by Eliasson, Fayad and Krikorian [Reference Eliasson, Fayad and KrikorianEFK13, Reference Eliasson, Fayad and KrikorianEFK15]. We stress that in all these works mentioned above,
![]() ${\lambda }_0$
is assumed to be non-zero and the crucial assumption is that
${\lambda }_0$
is assumed to be non-zero and the crucial assumption is that
![]() ${\lambda }_0$
satisfies a Diophantine-type condition and that the BNF is of a very simple form.
${\lambda }_0$
satisfies a Diophantine-type condition and that the BNF is of a very simple form.
1.4 ‘Sometimes’ convergence of the BNF implies convergence of a normalizing transformation
Our main result is close in spirit to the above works, but it does not rely on a Diophantine condition. In fact, we consider a special class of diffeomorphisms such that the frequency
![]() ${\lambda }_0$
is zero. Thus, the BNF is degenerate in the previous sense. But within this class of Hamiltonians we just use a standard non-degeneracy assumption on the quadratic part. Namely, we prove the following.
${\lambda }_0$
is zero. Thus, the BNF is degenerate in the previous sense. But within this class of Hamiltonians we just use a standard non-degeneracy assumption on the quadratic part. Namely, we prove the following.
Theorem 1.1. Assume the following.
-
(A1)
 $H(I,\theta )$
has a formal Birkhoff normal form
$H(I,\theta )$
has a formal Birkhoff normal form
 $N(I)$
that starts with quadratic terms in I, i.e. there exists a formal symplectic change of variables
$N(I)$
that starts with quadratic terms in I, i.e. there exists a formal symplectic change of variables
 $\Psi (I, \theta )$
, tangent to the identity, that is,
$\Psi (I, \theta )$
, tangent to the identity, that is,
 $ \Psi (I,\theta )=(I+\mathcal O^2(I),\phi +\mathcal O(I)) $
, such that in the sense of power series.
$ \Psi (I,\theta )=(I+\mathcal O^2(I),\phi +\mathcal O(I)) $
, such that in the sense of power series. $$ \begin{align*}H\circ \Psi (I,\theta) = N(I)=N_0(I)+ \mathcal O^3(I) \end{align*} $$
$$ \begin{align*}H\circ \Psi (I,\theta) = N(I)=N_0(I)+ \mathcal O^3(I) \end{align*} $$
-
(A2)
 $N_0(I)=I^{\rm tr} \Omega I$
(for some symmetric
$N_0(I)=I^{\rm tr} \Omega I$
(for some symmetric
 $\Omega $
) is non-degenerate:
$\Omega $
) is non-degenerate:
 $\det {\Omega } \neq 0$
.
$\det {\Omega } \neq 0$
. -
(A3)
 $N(I)=B(N_0(I))=N_0 + \sum _{j=2}^\infty b_j (N_0(I))^j$
, where B is an analytic function.
$N(I)=B(N_0(I))=N_0 + \sum _{j=2}^\infty b_j (N_0(I))^j$
, where B is an analytic function.
Then there exists an invertible analytic symplectic transformation
such that
Note that we start from a resonant torus, so that the existence of a BNF of the form we assume requires vanishing of (formal) obstructions. Hence, our main result can be reformulated as saying that the formal assumptions imply convergence of the normalizing transformation.
Similar rigidity statements have appeared in other contexts. In [Reference PoincaréPo92, Ch. 5], Poincaré studied the formal power series of canonical transformations that send a family of Hamiltonian systems into a family of integrable systems (in the sense of power series). In [Reference PoincaréPo92], it was shown that these formal power series do not exist unless there are some conditions (which are not met in the three-body problem for arbitrary masses). The non-existence of formal power series a fortiori implies the non-existence of analytic families of analytic transformations integrating the three-body problem.
The first author [Reference de la LlaveLl] proved a converse to the result in [Reference PoincaréPo92]: if the system satisfies a very specific and generic non-degeneracy condition, then existence of a formal power series that integrates the family of transformations in the sense of power series implies existence of a convergent one.
Assumption
![]() $A_3$
is there for technical purposes; see §3.3. Note that it is trivial for
$A_3$
is there for technical purposes; see §3.3. Note that it is trivial for
![]() $d=1$
. This assumption reminds us of that of Rüssmann in [Reference RüssmannRü02, Reference RüssmannRü04, Reference RüssmannRü67].
$d=1$
. This assumption reminds us of that of Rüssmann in [Reference RüssmannRü02, Reference RüssmannRü04, Reference RüssmannRü67].
The assumption that the Birkhoff normal form is a function of
![]() $N_0$
has been discussed in [Reference GallavottiGa] under the name of relative integrability. Two Hamiltonian dynamical systems are relatively integrable when one of them can be obtained from the other by a symplectic change of coordinates and a reparameterization of the time that only depends on the total energy. That is, the orbit structures of the two systems in an energy surface are equivalent up to a change of scale of time. The paper [Reference GallavottiGa] includes several arguments for why the notion of relative integrability is natural when discussing formal equivalence. In the present paper, however, the focus lies on the notion of equivalence under a symplectic change of variables. We show that, for a certain class of systems, equivalence in the sense of formal power series implies equivalence in the sense of analytic canonical changes of variables. Hence, our main result can be understood as a rigidity result. The class of systems for which this rigidity result holds can be succinctly described as the set of systems that are relatively integrable with respect to the main term.
$N_0$
has been discussed in [Reference GallavottiGa] under the name of relative integrability. Two Hamiltonian dynamical systems are relatively integrable when one of them can be obtained from the other by a symplectic change of coordinates and a reparameterization of the time that only depends on the total energy. That is, the orbit structures of the two systems in an energy surface are equivalent up to a change of scale of time. The paper [Reference GallavottiGa] includes several arguments for why the notion of relative integrability is natural when discussing formal equivalence. In the present paper, however, the focus lies on the notion of equivalence under a symplectic change of variables. We show that, for a certain class of systems, equivalence in the sense of formal power series implies equivalence in the sense of analytic canonical changes of variables. Hence, our main result can be understood as a rigidity result. The class of systems for which this rigidity result holds can be succinctly described as the set of systems that are relatively integrable with respect to the main term.
In the context of formal equivalence implying analytically convergent equivalence, it is natural to formulate the following conjecture.
Conjecture 1.2. Assume that an analytic Hamiltonian
![]() $H(I,\theta )$
as in (1.1) has a convergent BNF that satisfies the non-degeneracy assumption that the frequency map is a local diffeomorphism. Then there is a convergent normalizing transformation.
$H(I,\theta )$
as in (1.1) has a convergent BNF that satisfies the non-degeneracy assumption that the frequency map is a local diffeomorphism. Then there is a convergent normalizing transformation.
Note that the problems studied in [Reference BrunoBr71, Reference RüssmannRü67] do not satisfy the hypothesis of the conjecture, even though they satisfy the conclusion.
In the other direction, one can construct examples [Reference SaprykinaS] of analytic maps near a hyperbolic fixed point such that the Birkhoff normal form is quadratic (in the above notation,
![]() $N=\Lambda _0$
) with a non-resonant set of eigenvalues, and any normalizing transformation to the normal form diverges. In these examples, the eigenvalues form carefully chosen Liouville vectors. That is, the paper [Reference SaprykinaS] shows that, depending on the Diophantine conditions, quadratic normal forms may be rigid or not. The models in [Reference SaprykinaS] do not satisfy the hypothesis of the conjecture above.
$N=\Lambda _0$
) with a non-resonant set of eigenvalues, and any normalizing transformation to the normal form diverges. In these examples, the eigenvalues form carefully chosen Liouville vectors. That is, the paper [Reference SaprykinaS] shows that, depending on the Diophantine conditions, quadratic normal forms may be rigid or not. The models in [Reference SaprykinaS] do not satisfy the hypothesis of the conjecture above.
1.5 Overview of the proof
The standard method of obtaining the Birkhoff normal form is an iterative procedure in which we construct the transformations order by order: at the nth step of the procedure one computes the nth-order terms in the Taylor expansions, assuming that all the terms of lower orders are computed. It would appear natural to follow this scheme and try to estimate the transformations at each step of the recursive procedure. Unfortunately, this seems technically unfeasible. One of the main complications in any possible proof of convergence of the transformations is that even if the BNF is unique, the formal transformations
![]() $\Phi _N$
are very far from unique (since the BNF depends only on the actions, the
$\Phi _N$
are very far from unique (since the BNF depends only on the actions, the
![]() $\Phi _N$
can be composed with any canonical transformation which moves the angles but preserves the actions). So, an essential ingredient of any proof of convergence should be a specification of how to choose the normalizing transformations.
$\Phi _N$
can be composed with any canonical transformation which moves the angles but preserves the actions). So, an essential ingredient of any proof of convergence should be a specification of how to choose the normalizing transformations.
In this paper we use a quadratically convergent method in which we double the number of known coefficients at each step. Roughly—see more details in the next paragraphs—we will show that if the formal obstructions vanish we can choose a sequence of canonical transformations that proceed to converge quadratically: doubling the order of the BNF at every step of the construction. More importantly, there is a specific choice of the transformation that satisfies very explicit bounds. The bounds on the new transformation in terms of the remainder turn out to involve a loss of derivatives. Therefore, we need to implement a Nash–Moser scheme to estimate the important objects in a sequence of domains which decrease slowly.
Here is a short overview of the proof; the necessary notation is introduced in the next section. At the nth step of the iterative procedure we will start with a Hamiltonian of the form
where
![]() $N_n(I)$
is a polynomial in I of degree
$N_n(I)$
is a polynomial in I of degree
![]() $m_n=2^n+1$
and the remainder term
$m_n=2^n+1$
and the remainder term
![]() $\widetilde {R_n}$
is small in the following sense: for a certain domain-dependent norm, introduced in §2.1.1, for a certain small
$\widetilde {R_n}$
is small in the following sense: for a certain domain-dependent norm, introduced in §2.1.1, for a certain small
![]() ${\delta }_n$
(we assume that
${\delta }_n$
(we assume that
![]() ${\delta }_n \to 0$
with
${\delta }_n \to 0$
with
![]() $n\to \infty $
) and
$n\to \infty $
) and
![]() ${\kappa }>0$
, the remainder term satisfies
${\kappa }>0$
, the remainder term satisfies
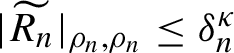 $|\widetilde {R_n}|_{\rho _n,\rho _n}\leq \delta _{n}^{\kappa } $
.
$|\widetilde {R_n}|_{\rho _n,\rho _n}\leq \delta _{n}^{\kappa } $
.
At this step we construct a symplectic change of coordinates
![]() $\Phi _n$
such that
$\Phi _n$
such that
 $$ \begin{align*}H_n\circ\Phi_n (I,\theta)=N_{n+1}(I)+ \widetilde{R_{n+1}}(I,\theta), \end{align*} $$
$$ \begin{align*}H_n\circ\Phi_n (I,\theta)=N_{n+1}(I)+ \widetilde{R_{n+1}}(I,\theta), \end{align*} $$
where
![]() $N_{n+1}$
has degree
$N_{n+1}$
has degree
![]() $m_{n+1}=2m_n-1$
and
$m_{n+1}=2m_n-1$
and
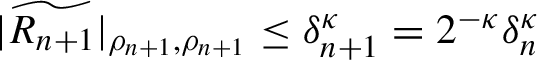 $|\widetilde {R_{n+1}}|_{\rho _{n+1},\rho _{n+1}}\leq \delta _{n+1}^{\kappa } =2^{-{\kappa }}\delta _{n}^{\kappa }$
.
$|\widetilde {R_{n+1}}|_{\rho _{n+1},\rho _{n+1}}\leq \delta _{n+1}^{\kappa } =2^{-{\kappa }}\delta _{n}^{\kappa }$
.
We construct
![]() $\Phi _n$
as a time-one map of the flow of a Hamiltonian vector field
$\Phi _n$
as a time-one map of the flow of a Hamiltonian vector field
![]() $F_n$
. The main ingredient consists in constructing and estimating the norm of
$F_n$
. The main ingredient consists in constructing and estimating the norm of
![]() $F_n$
(and thus
$F_n$
(and thus
![]() $\Phi _n$
), which is found as a solution of a certain homological equation (see (3.1) and in a simplified form (4.1)). In general, this equation may not have even a formal solution unless some constraints are met. However, the assumption of Theorem 1.1 implies that this equation does have a formal solution. The key observation in this paper is the following: if this homological equation has a formal solution, then it also has an analytic solution with tame estimates for it (in the sense of Nash–Moser theory). This statement is the content of Lemma 4.1. We note that the tame estimates use an argument different from the matching of powers.
$\Phi _n$
), which is found as a solution of a certain homological equation (see (3.1) and in a simplified form (4.1)). In general, this equation may not have even a formal solution unless some constraints are met. However, the assumption of Theorem 1.1 implies that this equation does have a formal solution. The key observation in this paper is the following: if this homological equation has a formal solution, then it also has an analytic solution with tame estimates for it (in the sense of Nash–Moser theory). This statement is the content of Lemma 4.1. We note that the tame estimates use an argument different from the matching of powers.
The procedure can be repeated, because the main assumption used to show the existence of solutions of the Newton equation is that there is a formal solution to all orders. This assumption is clearly preserved if we make any analytic change of variables. Once we know that the Newton procedure can be repeated infinitely often, the convergence is more or less standard.
2 Notation and a step of induction
2.1 Notation
2.1.1 Norms and majorants
Let
![]() ${\mathbb T}^d={\mathbb R}^d /{\mathbb Z}^d$
be a d-dimensional torus and, for
${\mathbb T}^d={\mathbb R}^d /{\mathbb Z}^d$
be a d-dimensional torus and, for
![]() ${\sigma }>0$
, consider its complex extension
${\sigma }>0$
, consider its complex extension
![]() ${\mathbb T}^d_{\sigma } =({\mathbb R}^d+(-{\sigma },{\sigma })\sqrt {-1} )/ {\mathbb Z}^d$
. Let
${\mathbb T}^d_{\sigma } =({\mathbb R}^d+(-{\sigma },{\sigma })\sqrt {-1} )/ {\mathbb Z}^d$
. Let
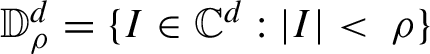 ${\mathbb D}^d_{\rho }=\{I\in {\mathbb C}^{d}: |I|<~\rho \}$
be a complex disk and define the ‘d-dimensional annulus’
${\mathbb D}^d_{\rho }=\{I\in {\mathbb C}^{d}: |I|<~\rho \}$
be a complex disk and define the ‘d-dimensional annulus’
 $$ \begin{align*}\mathbb A_{\rho,{\sigma} }:={\mathbb D}_{\rho}^d\times {\mathbb T}^d_{\sigma}. \end{align*} $$
$$ \begin{align*}\mathbb A_{\rho,{\sigma} }:={\mathbb D}_{\rho}^d\times {\mathbb T}^d_{\sigma}. \end{align*} $$
Let
![]() $\mathcal O(\mathbb A_{\rho ,{\sigma } })$
be the set of functions holomorphic in
$\mathcal O(\mathbb A_{\rho ,{\sigma } })$
be the set of functions holomorphic in
![]() $\mathbb A_{\rho ,{\sigma } }$
that are real symmetric, that is, such that
$\mathbb A_{\rho ,{\sigma } }$
that are real symmetric, that is, such that
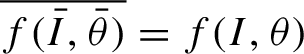 $\overline {f(\bar I,\bar \theta )}=f(I, \theta )$
(where the bar stands for the complex conjugate). We use supremum norms over
$\overline {f(\bar I,\bar \theta )}=f(I, \theta )$
(where the bar stands for the complex conjugate). We use supremum norms over
![]() $\mathbb A_{\rho ,{\sigma } }$
, denoted by
$\mathbb A_{\rho ,{\sigma } }$
, denoted by
![]() $\|f\|_{\rho ,{\sigma } }$
. In the same way, we define the set
$\|f\|_{\rho ,{\sigma } }$
. In the same way, we define the set
![]() $\mathcal O({\mathbb D}_{\rho })$
with the corresponding norm
$\mathcal O({\mathbb D}_{\rho })$
with the corresponding norm
![]() $\|f\|_{\rho }$
being the sup-norms over the disk
$\|f\|_{\rho }$
being the sup-norms over the disk
![]() ${\mathbb D}^d_{\rho }$
.
${\mathbb D}^d_{\rho }$
.
For a function
![]() $f\in \mathcal O(\mathbb A_{\rho ,{\sigma } })$
, consider its Taylor–Fourier representation in the powers of I:
$f\in \mathcal O(\mathbb A_{\rho ,{\sigma } })$
, consider its Taylor–Fourier representation in the powers of I:
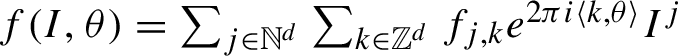 $ f(I,\theta )=\sum _{j\in {\mathbb N}^d} \sum _{k\in {\mathbb Z}^d} f_{j,k}e^{2\pi i \langle k,\theta \rangle } I^j $
. Consider a majorant for f of the form
$ f(I,\theta )=\sum _{j\in {\mathbb N}^d} \sum _{k\in {\mathbb Z}^d} f_{j,k}e^{2\pi i \langle k,\theta \rangle } I^j $
. Consider a majorant for f of the form
 $$ \begin{align*}\widehat{f}(I) = \sum_{j\in {\mathbb N}^d} \sum_{k\in {\mathbb Z}^d} |f_{j,k}| I^j e^{2\pi|k|{\sigma}}. \end{align*} $$
$$ \begin{align*}\widehat{f}(I) = \sum_{j\in {\mathbb N}^d} \sum_{k\in {\mathbb Z}^d} |f_{j,k}| I^j e^{2\pi|k|{\sigma}}. \end{align*} $$
We denote by
![]() $|f|_{\rho ,{\sigma } }$
the norm of the corresponding majorant
$|f|_{\rho ,{\sigma } }$
the norm of the corresponding majorant
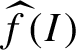 $\widehat {f}(I)$
:
$\widehat {f}(I)$
:
 $$ \begin{align*}|f|_{\rho,{\sigma} }=\|\widehat{f}\|_{\rho,{\sigma} }. \end{align*} $$
$$ \begin{align*}|f|_{\rho,{\sigma} }=\|\widehat{f}\|_{\rho,{\sigma} }. \end{align*} $$
Clearly,
![]() $\|f\|_{\rho ,{\sigma } } \leq |f|_{\rho ,{\sigma } }$
. Analogous notation
$\|f\|_{\rho ,{\sigma } } \leq |f|_{\rho ,{\sigma } }$
. Analogous notation
![]() $|f|_{\rho }$
corresponds to the norm
$|f|_{\rho }$
corresponds to the norm
![]() $\|f\|_{\rho }$
above.
$\|f\|_{\rho }$
above.
In what follows we will mostly have
![]() ${\sigma } =\rho $
.
${\sigma } =\rho $
.
2.1.2 Important constants for the iterative procedure
-
• Let
 $\rho _0=\mathop {\mbox {min}} \{1, \rho \}$
.
$\rho _0=\mathop {\mbox {min}} \{1, \rho \}$
. -
• The order of polynomials involved in the nth step of the iterative procedure is
 $$ \begin{align*}m_{n} =2^n +1. \end{align*} $$
$$ \begin{align*}m_{n} =2^n +1. \end{align*} $$
-
• The norm of the rest term
 $\widetilde {R_n}$
at the nth step will be estimated as
$\widetilde {R_n}$
at the nth step will be estimated as
 $|\widetilde {R_n}|_{\rho _n}\leq \delta _{n}^{\kappa } $
. Let
$|\widetilde {R_n}|_{\rho _n}\leq \delta _{n}^{\kappa } $
. Let  $$ \begin{align*} \begin{aligned} &\kappa = d + 6, \\ & b = 2^{-(\kappa + 3)}, \\ & \delta_{0}= \rho_{0} b 2^{-3} = \rho_{0} 2^{-(\kappa + 6)},\\ & \delta_{n+1}= 2^{-1} \delta_{n}. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\kappa = d + 6, \\ & b = 2^{-(\kappa + 3)}, \\ & \delta_{0}= \rho_{0} b 2^{-3} = \rho_{0} 2^{-(\kappa + 6)},\\ & \delta_{n+1}= 2^{-1} \delta_{n}. \end{aligned} \end{align*} $$
-
• Finally, let
and $$ \begin{align*}q_n=(2b)^{2^{-(n+1)}} \end{align*} $$
$$ \begin{align*}q_n=(2b)^{2^{-(n+1)}} \end{align*} $$
 $$ \begin{align*}\rho_{n+1}=(\rho_n-3{\delta}_n)q_n. \end{align*} $$
$$ \begin{align*}\rho_{n+1}=(\rho_n-3{\delta}_n)q_n. \end{align*} $$
2.1.3 Polynomials
In the iterative procedure we will work with polynomials in I whose coefficients depend on
![]() $\theta $
.
$\theta $
.
-
• Let
(2.1)where $$ \begin{align} N_0(I)=I^{\rm tr} \Omega I, \end{align} $$
$$ \begin{align} N_0(I)=I^{\rm tr} \Omega I, \end{align} $$
 $\Omega $
is a symmetric non-degenerate matrix:
$\Omega $
is a symmetric non-degenerate matrix:
 $\det {\Omega } \neq 0$
.
$\det {\Omega } \neq 0$
.
-
• An expression
 $M=f(\theta ) I^k $
(where k is a multi-index) is called a monomial.
$M=f(\theta ) I^k $
(where k is a multi-index) is called a monomial. -
• We will say that a monomial
 $M_{k,l}=I^ke^{2\pi i \langle l,\theta \rangle }$
is resonant if it satisfies
$M_{k,l}=I^ke^{2\pi i \langle l,\theta \rangle }$
is resonant if it satisfies
 $\{N_0, M\}=0$
.
$\{N_0, M\}=0$
. -
•
 $R^{[j]} (I,\theta )$
stands for a homogeneous polynomial in I of degree j with coefficients depending on
$R^{[j]} (I,\theta )$
stands for a homogeneous polynomial in I of degree j with coefficients depending on
 $\theta $
:
$\theta $
:  $$ \begin{align*}R^{[j]}(I,\theta)=\sum_{|k |=j} r_{k }(\theta ) I^{k }. \end{align*} $$
$$ \begin{align*}R^{[j]}(I,\theta)=\sum_{|k |=j} r_{k }(\theta ) I^{k }. \end{align*} $$
-
• We also use the notation
 $R^{[m,n]}$
to denote the range of degrees in I:
$R^{[m,n]}$
to denote the range of degrees in I:  $$ \begin{align*}R^{[m,n]} (I,\theta)=\sum_{j=m}^n R^{[j]} (I,\theta), \quad R^{[\geq m]} (I,\theta)=\sum_{j=m}^\infty R^{[j]} (I,\theta). \end{align*} $$
$$ \begin{align*}R^{[m,n]} (I,\theta)=\sum_{j=m}^n R^{[j]} (I,\theta), \quad R^{[\geq m]} (I,\theta)=\sum_{j=m}^\infty R^{[j]} (I,\theta). \end{align*} $$
Let
![]() $m_n$
be as above. The following functions will be of special importance.
$m_n$
be as above. The following functions will be of special importance.
-
• The normal form
 $N(I)$
is assumed to have the form (2.2)Denote
$N(I)$
is assumed to have the form (2.2)Denote $$ \begin{align} N(I) = B(N_0(I))= N_0(I) + \sum_{j=2}^\infty b_j (N_0(I))^j. \end{align} $$
(2.3)in particular, since
$$ \begin{align} N(I) = B(N_0(I))= N_0(I) + \sum_{j=2}^\infty b_j (N_0(I))^j. \end{align} $$
(2.3)in particular, since $$ \begin{align} N_n=N^{[2,m_n]}= (B(N_0))^{[2,m_n]}; \end{align} $$
$$ \begin{align} N_n=N^{[2,m_n]}= (B(N_0))^{[2,m_n]}; \end{align} $$
 $m_0=2$
,
$m_0=2$
,
 $N_0=N_0^{[2,m_0]}=N_0^{[2]}$
is quadratic.
$N_0=N_0^{[2,m_0]}=N_0^{[2]}$
is quadratic.
-
• The rest term at the nth inductive step is
 $\widetilde {R_n}(I, \theta )$
: (2.4)
$\widetilde {R_n}(I, \theta )$
: (2.4) $$ \begin{align} \widetilde{R_n}= \widetilde{R_n}^{ [>m_{n} ] }. \end{align} $$
$$ \begin{align} \widetilde{R_n}= \widetilde{R_n}^{ [>m_{n} ] }. \end{align} $$
-
• We will also need polynomials in I with
 $\theta $
-dependent coefficients:
$\theta $
-dependent coefficients:
 $R_n(I, \theta )$
and
$R_n(I, \theta )$
and
 $F_n(I, \theta )$
of the following degrees: (2.5)
$F_n(I, \theta )$
of the following degrees: (2.5) $$ \begin{align} R_n= R_n^{ [m_n+1,m_{n+1} ] }, \quad F_n=F_n^{[m_n, m_{n+1}-1]}. \end{align} $$
$$ \begin{align} R_n= R_n^{ [m_n+1,m_{n+1} ] }, \quad F_n=F_n^{[m_n, m_{n+1}-1]}. \end{align} $$
2.2 Base of induction: an equivalent problem
Lemma 2.1. Suppose that
 $$ \begin{align*}H(I,\theta)=N_0(I)+ \widetilde {R_0} (I,\theta) \in \mathcal O(\mathbb A_{\rho,{\sigma} }), \end{align*} $$
$$ \begin{align*}H(I,\theta)=N_0(I)+ \widetilde {R_0} (I,\theta) \in \mathcal O(\mathbb A_{\rho,{\sigma} }), \end{align*} $$
where
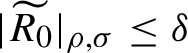 $|\widetilde {R_0}|_{\rho ,{\sigma } }\leq \delta $
, and there exists a formal (respectively, analytic) symplectic transformation
$|\widetilde {R_0}|_{\rho ,{\sigma } }\leq \delta $
, and there exists a formal (respectively, analytic) symplectic transformation
such that
 $$ \begin{align*}H\circ\Psi(I,\theta)= N(I)=N_0(I) + \sum_{j=2}^\infty b_j (N_0(I))^j. \end{align*} $$
$$ \begin{align*}H\circ\Psi(I,\theta)= N(I)=N_0(I) + \sum_{j=2}^\infty b_j (N_0(I))^j. \end{align*} $$
Then, for any
![]() $a> 0$
, there exist a Hamiltonian
$a> 0$
, there exist a Hamiltonian
![]() $\widehat H(I,\theta )$
and a formal (respectively, analytic) symplectic transformation
$\widehat H(I,\theta )$
and a formal (respectively, analytic) symplectic transformation
![]() $ \widehat {\Psi }(I,\theta )=(I+\mathcal O^2(I),\theta + \mathcal O(I)) $
such that
$ \widehat {\Psi }(I,\theta )=(I+\mathcal O^2(I),\theta + \mathcal O(I)) $
such that
 $$ \begin{align*}\widehat{H}\circ \widehat{\Psi}(I,\theta) =N_0(I)+ \widehat{R_0} (I,\theta) \in \mathcal O(\mathbb A_{({1}/{a}) \rho,{\sigma} }), \end{align*} $$
$$ \begin{align*}\widehat{H}\circ \widehat{\Psi}(I,\theta) =N_0(I)+ \widehat{R_0} (I,\theta) \in \mathcal O(\mathbb A_{({1}/{a}) \rho,{\sigma} }), \end{align*} $$
where
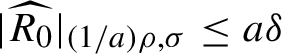 $| \widehat {R_0}|_{({1}/{a}) \rho ,{\sigma } }\leq a \delta $
, and
$| \widehat {R_0}|_{({1}/{a}) \rho ,{\sigma } }\leq a \delta $
, and
 $$ \begin{align*}N(I)=N_0(I) + \sum_{j=2}^\infty b_j a^{2(j-1)}(N_0(I))^j. \end{align*} $$
$$ \begin{align*}N(I)=N_0(I) + \sum_{j=2}^\infty b_j a^{2(j-1)}(N_0(I))^j. \end{align*} $$
Proof Define
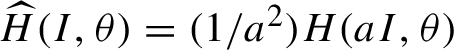 $\widehat H(I,\theta )=({1}/{a^2})H(aI,\theta )$
and
$\widehat H(I,\theta )=({1}/{a^2})H(aI,\theta )$
and
![]() $ \widehat {\Psi }(I,\theta )= (({1}/{a})\phi (aI,\theta ),\, \psi (aI,\theta ) ) $
. It can be verified directly that
$ \widehat {\Psi }(I,\theta )= (({1}/{a})\phi (aI,\theta ),\, \psi (aI,\theta ) ) $
. It can be verified directly that
![]() $\widehat {\Psi }$
is symplectic and tangent to the identity. Moreover,
$\widehat {\Psi }$
is symplectic and tangent to the identity. Moreover,
 $$ \begin{align*}\widehat{H} \circ \widehat{\Psi}(I,\theta)= \frac{1}{a^2} H(\phi(aI,\theta), \psi(aI,\theta)) = N_0(I) + \sum_{j=2}^\infty b_j a^{2(j-1)}(N_0(I))^j.\\[-48pt] \end{align*} $$
$$ \begin{align*}\widehat{H} \circ \widehat{\Psi}(I,\theta)= \frac{1}{a^2} H(\phi(aI,\theta), \psi(aI,\theta)) = N_0(I) + \sum_{j=2}^\infty b_j a^{2(j-1)}(N_0(I))^j.\\[-48pt] \end{align*} $$
2.3 Induction step
While the base of induction is given by formula (2.12), the step of the iterative procedure is provided by the following proposition.
Proposition 2.2. For a fixed
![]() $n> 0$
, let
$n> 0$
, let
![]() $m_n$
,
$m_n$
,
![]() $\rho _n$
, and
$\rho _n$
, and
![]() ${\delta }_n$
be as in §
2.1.2
above. Suppose that
${\delta }_n$
be as in §
2.1.2
above. Suppose that
![]() $H_n(I, \theta )$
is formally conjugated to the BNF of the form (2.2):
$H_n(I, \theta )$
is formally conjugated to the BNF of the form (2.2):
 $$ \begin{align*}N(I)=N_0(I) + \sum_{j=2}^{\infty} b_j (N_0(I))^j \end{align*} $$
$$ \begin{align*}N(I)=N_0(I) + \sum_{j=2}^{\infty} b_j (N_0(I))^j \end{align*} $$
and the normal form satisfies
 $$ \begin{align} |N^{[ m_n+j ]}|_{\rho_n}<{\delta}_n^{\kappa+1}, \quad j=0, \ldots, m_n; \end{align} $$
$$ \begin{align} |N^{[ m_n+j ]}|_{\rho_n}<{\delta}_n^{\kappa+1}, \quad j=0, \ldots, m_n; \end{align} $$
denoting
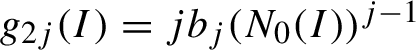 $ g_{2j}(I) = jb_j (N_0(I))^{j-1} $
, we assume that
$ g_{2j}(I) = jb_j (N_0(I))^{j-1} $
, we assume that
 $$ \begin{align} |g_j|_{\rho_n} \leq \frac1{4^j}, \quad j=1,\ldots ,m_n. \end{align} $$
$$ \begin{align} |g_j|_{\rho_n} \leq \frac1{4^j}, \quad j=1,\ldots ,m_n. \end{align} $$
Suppose that
where
![]() $N_n(I) = (B(N_0(I)))^{[2,m_n]} $
and
$N_n(I) = (B(N_0(I)))^{[2,m_n]} $
and
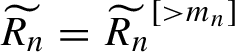 $\widetilde {R_n}= \widetilde {R_n}^{ [>m_{n} ] } $
satisfies
$\widetilde {R_n}= \widetilde {R_n}^{ [>m_{n} ] } $
satisfies
 $$ \begin{align*}|\widetilde {R_n} |_{\rho_n,\rho_n} \leq \delta_n^{\kappa}. \end{align*} $$
$$ \begin{align*}|\widetilde {R_n} |_{\rho_n,\rho_n} \leq \delta_n^{\kappa}. \end{align*} $$
Then there exists a symplectic change of coordinates
![]() $\Phi _n:(I', \theta ')\mapsto (I,\theta )$
,
$\Phi _n:(I', \theta ')\mapsto (I,\theta )$
,
given by a Hamiltonian
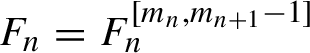 $F_n=F_n^{[m_{n},m_{n+1}-1]}$
such that
$F_n=F_n^{[m_{n},m_{n+1}-1]}$
such that
 $$ \begin{align} H_{n+1}(I', \theta'):=H_n \circ \Phi_n(I', \theta') = N_{n+1} (I') +\widetilde { R_{n+1} }(I', \theta'), \end{align} $$
$$ \begin{align} H_{n+1}(I', \theta'):=H_n \circ \Phi_n(I', \theta') = N_{n+1} (I') +\widetilde { R_{n+1} }(I', \theta'), \end{align} $$
where
![]() $N_{n+1}(I')=N^{[2,m_{n+1}]}(I')$
,
$N_{n+1}(I')=N^{[2,m_{n+1}]}(I')$
,
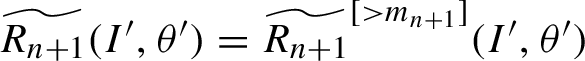 $\widetilde { R_{n+1}}(I',\theta ')=\widetilde {R_{n+1}}^{[>m_{n+1}]}(I',\theta ')$
, and
$\widetilde { R_{n+1}}(I',\theta ')=\widetilde {R_{n+1}}^{[>m_{n+1}]}(I',\theta ')$
, and
 $$ \begin{align} |\widetilde { R_{n+1}} |_{\rho_{n+1},\rho_{n+1}} \leq {\delta}_{n+1}^{\kappa}. \end{align} $$
$$ \begin{align} |\widetilde { R_{n+1}} |_{\rho_{n+1},\rho_{n+1}} \leq {\delta}_{n+1}^{\kappa}. \end{align} $$
Moreover,
![]() $\Phi _n(I', \theta ')=(U^{(n)}(I', \theta '), V^{(n)}(I', \theta '))$
satisfies
$\Phi _n(I', \theta ')=(U^{(n)}(I', \theta '), V^{(n)}(I', \theta '))$
satisfies
 $$ \begin{align} &\sum_{j=1}^d \|U_j^{(n)}(I^{\prime}, \theta^{\prime})-I^{\prime}_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}\nonumber\\ &\quad +\|V_j^{(n)}(I^{\prime}, \theta^{\prime})-\theta^{\prime}_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} < {\delta}_n \end{align} $$
$$ \begin{align} &\sum_{j=1}^d \|U_j^{(n)}(I^{\prime}, \theta^{\prime})-I^{\prime}_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}\nonumber\\ &\quad +\|V_j^{(n)}(I^{\prime}, \theta^{\prime})-\theta^{\prime}_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} < {\delta}_n \end{align} $$
and the inverse map,
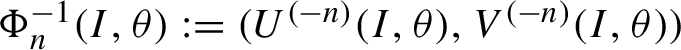 $\Phi _n^{-1}(I, \theta ):=(U^{(-n)}(I, \theta ),V^{(-n)}(I, \theta ))$
, satisfies
$\Phi _n^{-1}(I, \theta ):=(U^{(-n)}(I, \theta ),V^{(-n)}(I, \theta ))$
, satisfies
 $$ \begin{align} &\sum_{j=1}^d \| U_j^{(-n)}(I, \theta)-I_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}\nonumber\\ &\quad +\| V_j^{(-n)}(I, \theta)-\theta_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} < {\delta}_n. \end{align} $$
$$ \begin{align} &\sum_{j=1}^d \| U_j^{(-n)}(I, \theta)-I_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}\nonumber\\ &\quad +\| V_j^{(-n)}(I, \theta)-\theta_j \|_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} < {\delta}_n. \end{align} $$
The proof of this proposition constitutes the main technical tool of this paper. It implies Theorem 1.1 in a standard way. See, e.g., [Reference RüssmannRü67, pp. 61–63]. For convenience, we give a proof below.
2.4 Proof of Theorem 1.1
Lemma 2.1 permits us to assume without loss of generality that for the given Hamiltonian
![]() $ H_0(I,\theta ):=H(I,\theta ) = N_0(I)+\widetilde {R_0}(I,\theta ), $
$ H_0(I,\theta ):=H(I,\theta ) = N_0(I)+\widetilde {R_0}(I,\theta ), $
 $$ \begin{align} |\widetilde{R_0}|_{\rho_0,\rho_0}\leq \delta_{0}^{\kappa}. \end{align} $$
$$ \begin{align} |\widetilde{R_0}|_{\rho_0,\rho_0}\leq \delta_{0}^{\kappa}. \end{align} $$
Since the function B is analytic, the same lemma permits us to assume that (2.6) and (2.7) hold for each n.
The step of induction is provided by Proposition 2.2. Since
![]() $H_{n}$
is formally reducible to the normal form N, the same can be said about
$H_{n}$
is formally reducible to the normal form N, the same can be said about
![]() $H_{n+1}$
.
$H_{n+1}$
.
Repetition of this process leads to a sequence of transformations
Let us show that
![]() $T_n$
converges to the desired coordinate change
$T_n$
converges to the desired coordinate change
![]() $\Phi =T_\infty $
, analytic in the polydisk
$\Phi =T_\infty $
, analytic in the polydisk
![]() $\mathbb A_{\rho _\infty ,\rho _\infty }$
, where
$\mathbb A_{\rho _\infty ,\rho _\infty }$
, where
![]() $\rho _0 b < \rho _\infty < \rho _0$
. Indeed, with the notation of §2.1.2,
$\rho _0 b < \rho _\infty < \rho _0$
. Indeed, with the notation of §2.1.2,
 $$ \begin{align*}3 \sum_{k=0}^\infty {\delta}_k \leq 3\cdot 2{\delta}_0 < 3\cdot 2 \rho_0 b 2^{-3} <\rho_0 b. \end{align*} $$
$$ \begin{align*}3 \sum_{k=0}^\infty {\delta}_k \leq 3\cdot 2{\delta}_0 < 3\cdot 2 \rho_0 b 2^{-3} <\rho_0 b. \end{align*} $$
Then, for any n, we have
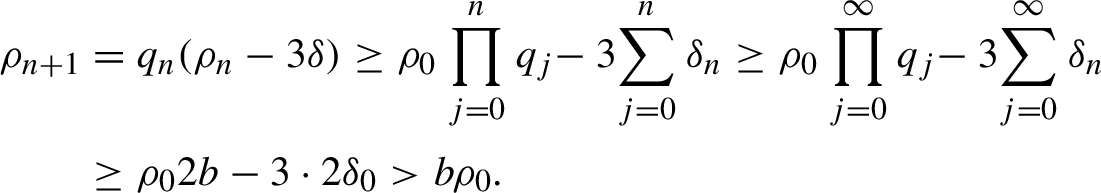 $$ \begin{align*}\rho_{n+1}&=q_n (\rho_{n} - 3{\delta}) \geq \rho_{0} \prod_{j=0}^n q_j \!- 3\!\sum_{j=0}^n {\delta}_n \geq \rho_{0} \prod_{j=0}^\infty q_j \!- 3\!\sum_{j=0}^\infty {\delta}_n \\ & \geq \rho_{0} 2b - 3\cdot 2{\delta}_0>b\rho_{0}. \end{align*} $$
$$ \begin{align*}\rho_{n+1}&=q_n (\rho_{n} - 3{\delta}) \geq \rho_{0} \prod_{j=0}^n q_j \!- 3\!\sum_{j=0}^n {\delta}_n \geq \rho_{0} \prod_{j=0}^\infty q_j \!- 3\!\sum_{j=0}^\infty {\delta}_n \\ & \geq \rho_{0} 2b - 3\cdot 2{\delta}_0>b\rho_{0}. \end{align*} $$
It is left to prove that
![]() $T_n$
converges to an analytic function
$T_n$
converges to an analytic function
![]() $T_\infty $
satisfying (1.3). Denote the variables involved in the nth step of the induction by
$T_\infty $
satisfying (1.3). Denote the variables involved in the nth step of the induction by
![]() $w_{n-1}=(I,\theta )$
and
$w_{n-1}=(I,\theta )$
and
![]() $w_{n}=(I',\theta ')$
, where
$w_{n}=(I',\theta ')$
, where
 $$ \begin{align*}w_{n}=\Phi_{n-1}^{-1} w_{n-1}. \end{align*} $$
$$ \begin{align*}w_{n}=\Phi_{n-1}^{-1} w_{n-1}. \end{align*} $$
In this notation,
Now, for
![]() $w_{n}=(I',\theta ')$
, we have
$w_{n}=(I',\theta ')$
, we have
Since
![]() $(\Phi _{n}(I',\theta ')-(I',\theta '))$
starts with the terms of degree
$(\Phi _{n}(I',\theta ')-(I',\theta '))$
starts with the terms of degree
![]() $2^n$
in
$2^n$
in
![]() $I'$
, for each j the expansion of
$I'$
, for each j the expansion of
![]() $(T_n(I',\theta ')-T_{n+j}(I',\theta '))$
starts with the terms of degree
$(T_n(I',\theta ')-T_{n+j}(I',\theta '))$
starts with the terms of degree
![]() $2^n$
in
$2^n$
in
![]() $I'$
. This implies that the sequence of maps
$I'$
. This implies that the sequence of maps
![]() $T_n$
formally converges, when
$T_n$
formally converges, when
![]() $n\to \infty $
, to a formal map
$n\to \infty $
, to a formal map
![]() $T_\infty $
such that (1.3) holds:
$T_\infty $
such that (1.3) holds:
We still need to show that
![]() $T_\infty $
is analytic. It is more convenient to prove that the maps
$T_\infty $
is analytic. It is more convenient to prove that the maps
 $$ \begin{align*}T_n^{-1}:=\Phi_{n-1}^{-1}\circ\cdots\circ\Phi_1^{-1}\circ\Phi_{0}^{-1} \end{align*} $$
$$ \begin{align*}T_n^{-1}:=\Phi_{n-1}^{-1}\circ\cdots\circ\Phi_1^{-1}\circ\Phi_{0}^{-1} \end{align*} $$
converge to an analytic map
![]() $T_\infty ^{-1}$
.
$T_\infty ^{-1}$
.
By Proposition 2.2, the map
 $$ \begin{align*}w_{n+1}=\Phi_n^{-1} w_n \end{align*} $$
$$ \begin{align*}w_{n+1}=\Phi_n^{-1} w_n \end{align*} $$
is analytic in
![]() $\mathbb A_{\rho _0 b/2,\rho _0 b/2}$
and, for all n, we have
$\mathbb A_{\rho _0 b/2,\rho _0 b/2}$
and, for all n, we have
 $$ \begin{align*}|\Phi_n^{-1} w_n- w_n|_{\rho_0 b/2,\rho_0 b/2}\leq {\delta}_n, \end{align*} $$
$$ \begin{align*}|\Phi_n^{-1} w_n- w_n|_{\rho_0 b/2,\rho_0 b/2}\leq {\delta}_n, \end{align*} $$
since
![]() $\rho _n-3{\delta }\geq \rho _{n+1}> \rho _0b$
for all n. Therefore, the map
$\rho _n-3{\delta }\geq \rho _{n+1}> \rho _0b$
for all n. Therefore, the map
![]() $T_n^{-1}$
such that
$T_n^{-1}$
such that
 $$ \begin{align*}w_{n}=T_n^{-1} w_0 \end{align*} $$
$$ \begin{align*}w_{n}=T_n^{-1} w_0 \end{align*} $$
is analytic in
![]() $\mathbb A_{\rho _0 b/4,\rho _0 b/4}$
and, for such
$\mathbb A_{\rho _0 b/4,\rho _0 b/4}$
and, for such
![]() $w_0$
, we have
$w_0$
, we have
 $$ \begin{align*}|T_n^{-1} w_0|\leq \sum_{j=0}^{n-1} |T_{j}^{-1}(w_j)-w_j| +|w_0|\leq \sum_{j=0}^{\infty}{\delta}_j +\rho_0b/4 \leq \rho_0b/2. \end{align*} $$
$$ \begin{align*}|T_n^{-1} w_0|\leq \sum_{j=0}^{n-1} |T_{j}^{-1}(w_j)-w_j| +|w_0|\leq \sum_{j=0}^{\infty}{\delta}_j +\rho_0b/4 \leq \rho_0b/2. \end{align*} $$
The estimate
 $$ \begin{align*}|T_{n+m}^{-1}(w_0)-T_n^{-1}(w_0)|_{\rho_0 b/4,\rho_0b/4}&\leq \sum_{j=n}^{n+m-1} |T_{j}^{-1}(w_j)- w_j)|_{\rho_0 b/4,\rho_0b/4}\\ &\leq \sum_{j=n}^{\infty}{\delta}_j =2^{1-n}{\delta}_0 \end{align*} $$
$$ \begin{align*}|T_{n+m}^{-1}(w_0)-T_n^{-1}(w_0)|_{\rho_0 b/4,\rho_0b/4}&\leq \sum_{j=n}^{n+m-1} |T_{j}^{-1}(w_j)- w_j)|_{\rho_0 b/4,\rho_0b/4}\\ &\leq \sum_{j=n}^{\infty}{\delta}_j =2^{1-n}{\delta}_0 \end{align*} $$
implies the convergence of the sequence of maps
![]() $T_n^{-1}$
to an analytic map
$T_n^{-1}$
to an analytic map
![]() $T_\infty ^{-1}$
in
$T_\infty ^{-1}$
in
![]() $\mathbb A_{\rho _0 b/4,\rho _0 b/4}$
. Since the formal inverse of
$\mathbb A_{\rho _0 b/4,\rho _0 b/4}$
. Since the formal inverse of
![]() $T_\infty ^{-1}$
is the series
$T_\infty ^{-1}$
is the series
![]() $T_{\infty }$
, the latter also defines an analytic function, providing the desired coordinate change. We set
$T_{\infty }$
, the latter also defines an analytic function, providing the desired coordinate change. We set
![]() $\Phi =T_\infty $
in the notation of Theorem 1.1.
$\Phi =T_\infty $
in the notation of Theorem 1.1.
![]() ${\kern288pt}\Box $
${\kern288pt}\Box $
3 Formal analysis
Here we start the proof of Proposition 2.2 by the formal analysis of the iterative procedure.
3.1 Iterative procedure
Given
![]() $H_n$
as in Proposition 2.2, we will construct
$H_n$
as in Proposition 2.2, we will construct
![]() $\Phi _n$
as the time-one map of the flow of a Hamiltonian
$\Phi _n$
as the time-one map of the flow of a Hamiltonian
![]() $F_n$
, that is,
$F_n$
, that is,
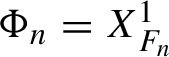 $\Phi _n = X_{F_n}^1$
, where
$\Phi _n = X_{F_n}^1$
, where
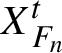 $X_{F_n}^t$
is the flow defined by
$X_{F_n}^t$
is the flow defined by
In this case,
![]() $\Phi _n$
is automatically symplectic.
$\Phi _n$
is automatically symplectic.
Notice that the normalizing transformation
![]() $\Phi _n$
, as well as the corresponding generating function
$\Phi _n$
, as well as the corresponding generating function
![]() $F_n$
, is not unique (one can compose with rotations in the angles which preserve the actions, for example). Clearly, the transformation that converges has to be very carefully chosen.
$F_n$
, is not unique (one can compose with rotations in the angles which preserve the actions, for example). Clearly, the transformation that converges has to be very carefully chosen.
In the following Lemma 3.1, we show that if a (formal) normalizing transformation exists, then there exists (another) normalizing transformation of a special kind. Namely, such that the corresponding generating function is a polynomial (in the sense of §2.1.3),
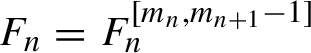 $F_n=F_n^{[m_n, m_{n+1}-1]}$
, and free from resonant monomials (see notation in §2.1.3).
$F_n=F_n^{[m_n, m_{n+1}-1]}$
, and free from resonant monomials (see notation in §2.1.3).
The idea of the proof is that we can always move the formal normalizing transformation by composing with some transformations that do not change the normal form. Therefore, we can ensure that the normalizing transformations belong to a space which is transversal to the space spanned by resonant monomials. Note that in the proof of Lemma 3.1, we use crucially the fact that the normal form is a function of
![]() $N_0$
so that the resonant terms are the same at all orders.
$N_0$
so that the resonant terms are the same at all orders.
There are some analogies between Lemma 3.1 and Proposition 2.6 in [Reference de la LlaveLl], but that result is significantly less delicate since there is an extra parameter that controls the smallness. In our case, the variable I controls both the smallness and the distance to the origin at the same time.
Let
![]() $\{\cdot , \cdot \}$
denote the standard Poisson bracket. Recall that for a differentiable function G, we have
$\{\cdot , \cdot \}$
denote the standard Poisson bracket. Recall that for a differentiable function G, we have
 $$ \begin{align*}\frac{d}{dt}G\circ X_F^t =\{ G,F\}\circ X_F^t. \end{align*} $$
$$ \begin{align*}\frac{d}{dt}G\circ X_F^t =\{ G,F\}\circ X_F^t. \end{align*} $$
Lemma 3.1. Suppose that for
![]() $H(I,\theta )$
, there exist
$H(I,\theta )$
, there exist
![]() $N_{2m}(I)=N_0 + B(N_0)$
with
$N_{2m}(I)=N_0 + B(N_0)$
with
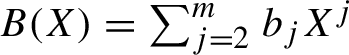 $B(X)=\sum _{j=2}^{m} b_j X^{j}$
,
$B(X)=\sum _{j=2}^{m} b_j X^{j}$
,
![]() $R(I,\theta )=R^{[> 2m]}(I,\theta )$
, and
$R(I,\theta )=R^{[> 2m]}(I,\theta )$
, and
![]() $G(I,\theta )=\mathcal O^2(I) $
such that
$G(I,\theta )=\mathcal O^2(I) $
such that
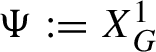 $\Psi :=X_G^1$
satisfies
$\Psi :=X_G^1$
satisfies
-
(1) Then there exists
 ${\tilde G}(I,\theta )$
, which is free from resonant monomials of order
${\tilde G}(I,\theta )$
, which is free from resonant monomials of order
 $< 2m$
, such that
$< 2m$
, such that
 $\tilde \Psi :=X_{\tilde G}^1$
normalizes H to the same normal form, that is, for some
$\tilde \Psi :=X_{\tilde G}^1$
normalizes H to the same normal form, that is, for some
 ${\tilde R}(I,\theta )=(\tilde R)^{[> 2m]}(I,\theta )$
, we have
${\tilde R}(I,\theta )=(\tilde R)^{[> 2m]}(I,\theta )$
, we have  $$ \begin{align*}H\circ {\tilde \Psi}(I,\theta)=N_{2m}(I)+{\tilde R} (I,\theta). \end{align*} $$
$$ \begin{align*}H\circ {\tilde \Psi}(I,\theta)=N_{2m}(I)+{\tilde R} (I,\theta). \end{align*} $$
-
(2) If, an addition to the previous assumption, we have that the original
 $H(I,\theta )$
has the form where
$H(I,\theta )$
has the form where $$ \begin{align*}H(I,\theta)= N_{m}(I)+ R^{[>m]}(I,\theta), \end{align*} $$
$$ \begin{align*}H(I,\theta)= N_{m}(I)+ R^{[>m]}(I,\theta), \end{align*} $$
 $N_{m}=N_{m}^{[2,\ldots , m]}$
, then there exists a polynomial
$N_{m}=N_{m}^{[2,\ldots , m]}$
, then there exists a polynomial
 $F=F^{[m, 2m-2]}$
, which is free from resonant monomials, such that
$F=F^{[m, 2m-2]}$
, which is free from resonant monomials, such that
 $\Phi :=X_{F}^1$
normalizes H to the same normal form, that is, for some
$\Phi :=X_{F}^1$
normalizes H to the same normal form, that is, for some
 ${{\overset{{\tiny\hskip2pt\approx}}{R}}}(I,\theta )={{\overset{{\tiny\hskip2pt\approx}}{R}}}^{[> 2m]}(I,\theta )$
, we have
${{\overset{{\tiny\hskip2pt\approx}}{R}}}(I,\theta )={{\overset{{\tiny\hskip2pt\approx}}{R}}}^{[> 2m]}(I,\theta )$
, we have  $$ \begin{align*}H\circ \Phi (I,\theta)=N_{2m}(I)+{{\overset{{\tiny\hskip2pt\approx}}{R}}}(I,\theta). \end{align*} $$
$$ \begin{align*}H\circ \Phi (I,\theta)=N_{2m}(I)+{{\overset{{\tiny\hskip2pt\approx}}{R}}}(I,\theta). \end{align*} $$
Proof (1) All the calculations below are made in the sense of formal Taylor–Fourier expressions. Suppose that
![]() $K(I,\theta )$
is such that
$K(I,\theta )$
is such that
![]() $\{N_0, K\}=0$
. Notice that in this case
$\{N_0, K\}=0$
. Notice that in this case
![]() $\{N_{2m}, K\}= B' (N_0)\{N_0, K\} =0$
. Use
$\{N_{2m}, K\}= B' (N_0)\{N_0, K\} =0$
. Use
![]() $K(I,\theta )$
as a Hamiltonian to define
$K(I,\theta )$
as a Hamiltonian to define
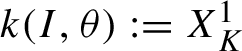 $k(I,\theta ):=X_{K}^1$
. Then, by the Taylor formula, we have
$k(I,\theta ):=X_{K}^1$
. Then, by the Taylor formula, we have
 $$ \begin{align*}\begin{aligned} H\circ \Psi \circ k &= (N_{2m}+R )\circ k= (N_{2m} + R )\circ X_{K}^t |_{t=1} = N_{2m} + R + \{(N_{2m}+R), K\} \\ &\quad + \tfrac12\{\{(N_{2m}+R), K \} ,K\}+ \cdots = N_{2m}+R_1, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} H\circ \Psi \circ k &= (N_{2m}+R )\circ k= (N_{2m} + R )\circ X_{K}^t |_{t=1} = N_{2m} + R + \{(N_{2m}+R), K\} \\ &\quad + \tfrac12\{\{(N_{2m}+R), K \} ,K\}+ \cdots = N_{2m}+R_1, \end{aligned} \end{align*} $$
where
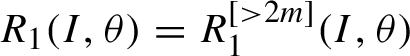 $R_1(I,\theta )=R_1^{[> 2m]}(I,\theta )$
.
$R_1(I,\theta )=R_1^{[> 2m]}(I,\theta )$
.
It is a classical fact that the composition
![]() $\Psi \circ k$
in the sense of formal power series is the time-one map of another Hamiltonian given by the Campbell–Baker–Dynkin formula (see [Reference DragtDragt, Appendix C] and [Reference de la Llave, Marco and MoriyónLlMM, Appendix]); here we denote it by the CBD formula. Note that in these references the usual notation for the Hamiltonian vector field defined by G is
$\Psi \circ k$
in the sense of formal power series is the time-one map of another Hamiltonian given by the Campbell–Baker–Dynkin formula (see [Reference DragtDragt, Appendix C] and [Reference de la Llave, Marco and MoriyónLlMM, Appendix]); here we denote it by the CBD formula. Note that in these references the usual notation for the Hamiltonian vector field defined by G is
![]() ${\mathcal L}_G$
, and
${\mathcal L}_G$
, and
![]() $\exp ({\mathcal L}_G)$
stands for its time-one map. In the present paper the same map is denoted by
$\exp ({\mathcal L}_G)$
stands for its time-one map. In the present paper the same map is denoted by
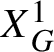 $X_G^1$
. Now suppose that
$X_G^1$
. Now suppose that
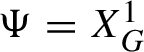 $\Psi = X_G^1$
and
$\Psi = X_G^1$
and
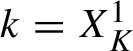 $ k = X_K^1$
. The CBD formula implies that the composition of these maps satisfies
$ k = X_K^1$
. The CBD formula implies that the composition of these maps satisfies
 $$ \begin{align*} & \tilde \Psi :=\Psi \circ k = X_{\tilde G}^1 \quad \text{where}\\ & {\tilde G} = G + K + \frac{1}{2}\{G, K\} + \frac{1}{12}\{G, \{G, K\}\} - \frac{1}{12}\{K, \{K, G\}\} + \cdots. \end{align*} $$
$$ \begin{align*} & \tilde \Psi :=\Psi \circ k = X_{\tilde G}^1 \quad \text{where}\\ & {\tilde G} = G + K + \frac{1}{2}\{G, K\} + \frac{1}{12}\{G, \{G, K\}\} - \frac{1}{12}\{K, \{K, G\}\} + \cdots. \end{align*} $$
The last sum is to be understood in the sense of formal power series in I.
To prove Lemma 3.1, we use the CBD formula and choose K recursively (order by order in I) so that
![]() ${\tilde G} $
has no resonant terms up to order
${\tilde G} $
has no resonant terms up to order
![]() $2m$
. At each step of the recursion we choose
$2m$
. At each step of the recursion we choose
![]() $(-K(I,\theta ))$
to be equal to the lowest order resonant term of G and set
$(-K(I,\theta ))$
to be equal to the lowest order resonant term of G and set
![]() ${\tilde G} $
to be the new G. As we saw above, the map
${\tilde G} $
to be the new G. As we saw above, the map
![]() $\tilde \Psi =\Psi \circ K$
, used as a normalization map, brings H to the same normal form as
$\tilde \Psi =\Psi \circ K$
, used as a normalization map, brings H to the same normal form as
![]() $\Psi $
did. But its generating Hamiltonian
$\Psi $
did. But its generating Hamiltonian
![]() ${\tilde G} $
has no lower order resonant monomials. Iterating this procedure, we get a normalization with the desired property.
${\tilde G} $
has no lower order resonant monomials. Iterating this procedure, we get a normalization with the desired property.
(2) Since we can normalize
![]() $H=N_{m}+R^{[>m]} $
to
$H=N_{m}+R^{[>m]} $
to
![]() $N_{2m}$
with the help of the generating function
$N_{2m}$
with the help of the generating function
![]() $G=\mathcal O^2(I)$
, then, by (1), we can also achieve the normalization using the transformation
$G=\mathcal O^2(I)$
, then, by (1), we can also achieve the normalization using the transformation
![]() $\tilde \Psi $
generated by a resonance-free Hamiltonian
$\tilde \Psi $
generated by a resonance-free Hamiltonian
![]() $\tilde G $
. Note that
$\tilde G $
. Note that
![]() $\tilde G =\mathcal O^2(I)$
.
$\tilde G =\mathcal O^2(I)$
.
By the Taylor formula for power series, we have
 $$ \begin{align*} \begin{aligned} H\circ \tilde \Psi & = (N_{m}+R^{[>m]} ) \circ {\tilde \Psi} = (N_{m} + R^{[>m]} )\circ {X}_{\tilde G}^t |_{t=1} = N_{m} + R^{[>m]} \\ &\quad+ \{(N_{m}+R^{[>m]}), \tilde G\} + \tfrac12\{ \{(N_{m}+R^{[>m]}), \tilde G \}, \tilde G \}+ \cdots = N_{2m}+R_1. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} H\circ \tilde \Psi & = (N_{m}+R^{[>m]} ) \circ {\tilde \Psi} = (N_{m} + R^{[>m]} )\circ {X}_{\tilde G}^t |_{t=1} = N_{m} + R^{[>m]} \\ &\quad+ \{(N_{m}+R^{[>m]}), \tilde G\} + \tfrac12\{ \{(N_{m}+R^{[>m]}), \tilde G \}, \tilde G \}+ \cdots = N_{2m}+R_1. \end{aligned} \end{align*} $$
Since
![]() $\tilde G $
is resonance-free, any monomial P in
$\tilde G $
is resonance-free, any monomial P in
![]() $\tilde G $
gives a non-zero impact
$\tilde G $
gives a non-zero impact
![]() $\{N_0, P\} $
to the sum above, whose order in I is strictly larger than the order of P. By comparing the orders of the coefficients in I, we see that the lowest possible order of a monomial in
$\{N_0, P\} $
to the sum above, whose order in I is strictly larger than the order of P. By comparing the orders of the coefficients in I, we see that the lowest possible order of a monomial in
![]() $\{N_{0}, \tilde G\} $
is the same as that in
$\{N_{0}, \tilde G\} $
is the same as that in
![]() $R^{[>m]}$
and hence
$R^{[>m]}$
and hence
![]() $\tilde G=\tilde G^{[\geq m]}$
. Finally, notice that the reduced generating function
$\tilde G=\tilde G^{[\geq m]}$
. Finally, notice that the reduced generating function
![]() $F:=\tilde G^{[m, 2m-2]}$
produces the same normal form.
$F:=\tilde G^{[m, 2m-2]}$
produces the same normal form.
The following lemma introduces the notation used in the proof of the main theorem (Theorem 1.1). Here we use the results of Lemma 3.1 to relate the conjugating function to the solutions of the homological equation (3.1) below.
Lemma 3.2. Adopt the notation for the degrees of polynomials from §
2.1.3
(in particular,
![]() $N_n=N^{[2,m_n]}$
as in
2.3
, and
$N_n=N^{[2,m_n]}$
as in
2.3
, and
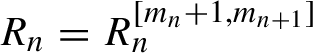 $R_n=R_n^{ [m_n+1,m_{n+1} ] }$
). Let
$R_n=R_n^{ [m_n+1,m_{n+1} ] }$
). Let
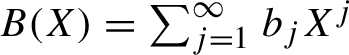 $B(X)=\sum _{j=1}^{\infty } b_j X^{j}$
. Suppose that
$B(X)=\sum _{j=1}^{\infty } b_j X^{j}$
. Suppose that
![]() $H_n$
has the form
$H_n$
has the form
 $$ \begin{align*}H_n= N_n +\widetilde{ R_n} = N_n + R_n +\widetilde{ R_n}^{[>m_{n+1}]}, \end{align*} $$
$$ \begin{align*}H_n= N_n +\widetilde{ R_n} = N_n + R_n +\widetilde{ R_n}^{[>m_{n+1}]}, \end{align*} $$
where
![]() $N_{n}(I)=N_0 + B(N_0)^{[4,m_n]}$
.
$N_{n}(I)=N_0 + B(N_0)^{[4,m_n]}$
.
Suppose that there exists
![]() $G(I,\theta )=\mathcal O^2(I) $
such that
$G(I,\theta )=\mathcal O^2(I) $
such that
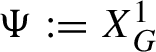 $\Psi :=X_G^1$
satisfies
$\Psi :=X_G^1$
satisfies
Then there exists a polynomial (in I)
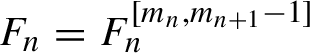 $F_n=F_n^{ [m_n,m_{n+1}-1] }$
with the following properties: the time-one map
$F_n=F_n^{ [m_n,m_{n+1}-1] }$
with the following properties: the time-one map
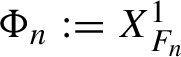 $\Phi _n:= X_{F_n}^1$
satisfies
$\Phi _n:= X_{F_n}^1$
satisfies
 $$ \begin{align*}H_{n+1}:=H_n \circ \Phi_n = N_{n+1} + \widetilde{ R_{n+1}}, \end{align*} $$
$$ \begin{align*}H_{n+1}:=H_n \circ \Phi_n = N_{n+1} + \widetilde{ R_{n+1}}, \end{align*} $$
![]() $F_n$
satisfies
$F_n$
satisfies
and
 $$ \begin{align*}\widetilde{ R_{n+1}}:= A_n+B_n +C_n, \end{align*} $$
$$ \begin{align*}\widetilde{ R_{n+1}}:= A_n+B_n +C_n, \end{align*} $$
where
 $$ \begin{align} A_n:= \widetilde{R_n}^{[>m_{n+1}]}\circ \Phi_n, \quad B_n:=\int_0^1\{ (1-t) \{N_n, F_n \}+R_n,F_n\}\circ {X}_{F_n}^t dt, \end{align} $$
$$ \begin{align} A_n:= \widetilde{R_n}^{[>m_{n+1}]}\circ \Phi_n, \quad B_n:=\int_0^1\{ (1-t) \{N_n, F_n \}+R_n,F_n\}\circ {X}_{F_n}^t dt, \end{align} $$
Notice that the expressions for
![]() $A_n$
,
$A_n$
,
![]() $B_n$
,
$B_n$
,
![]() $C_n$
start with terms of order
$C_n$
start with terms of order
![]() $m_{n+1}+1$
and, hence,
$m_{n+1}+1$
and, hence,
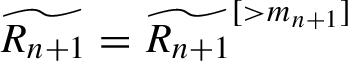 $\widetilde { R_{n+1}}=\widetilde { R_{n+1}}^{[>m_{n+1}]}$
, as needed.
$\widetilde { R_{n+1}}=\widetilde { R_{n+1}}^{[>m_{n+1}]}$
, as needed.
Proof Let
![]() $m=m_n=2^n+1$
. Then
$m=m_n=2^n+1$
. Then
![]() $m_{n+1}= 2m-1$
. With the notation for the degrees of polynomials from §2.1.3, Lemma 3.1 implies that there exists a polynomial
$m_{n+1}= 2m-1$
. With the notation for the degrees of polynomials from §2.1.3, Lemma 3.1 implies that there exists a polynomial
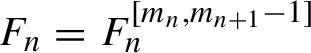 $F_n=F_n^{ [m_n,m_{n+1}-1] }$
such that
$F_n=F_n^{ [m_n,m_{n+1}-1] }$
such that
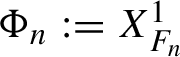 $\Phi _n:= X_{F_n}^1$
satisfies
$\Phi _n:= X_{F_n}^1$
satisfies
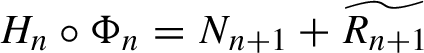 $H_n \circ \Phi _n = N_{n+1} +\widetilde {R_{n+1}}$
. By the Taylor formula, we have
$H_n \circ \Phi _n = N_{n+1} +\widetilde {R_{n+1}}$
. By the Taylor formula, we have
 $$ \begin{align} H_n \circ \Phi_n =&\ (N_n + R_n +\widetilde{ R_n}^{[>m_{n+1}]})\circ {X}_{F_n}^t |_{t=1} = N_n + \{N_n, F_n\} + R_n\nonumber \\ &+ \int_0^1\{ (1-t) \{N_n, F_n \}+R_n,F_n\}\circ {X}_{F_n}^t \, dt + \widetilde{R_n}^{[>m_{n+1}]}\circ \Phi_n\nonumber \\ =&\ N_{n+1} +\widetilde{R_{n+1}}. \end{align} $$
$$ \begin{align} H_n \circ \Phi_n =&\ (N_n + R_n +\widetilde{ R_n}^{[>m_{n+1}]})\circ {X}_{F_n}^t |_{t=1} = N_n + \{N_n, F_n\} + R_n\nonumber \\ &+ \int_0^1\{ (1-t) \{N_n, F_n \}+R_n,F_n\}\circ {X}_{F_n}^t \, dt + \widetilde{R_n}^{[>m_{n+1}]}\circ \Phi_n\nonumber \\ =&\ N_{n+1} +\widetilde{R_{n+1}}. \end{align} $$
Notice that by extracting all the terms of orders
![]() $m_n+1,\ldots ,m_{n+1} $
from the equation above, one gets the cohomological equation (3.1).
$m_n+1,\ldots ,m_{n+1} $
from the equation above, one gets the cohomological equation (3.1).
3.2 Homological equation order by order
Here we rewrite equation (3.1) as a (finite) set of equations for each degree of I. Equations corresponding to degrees
![]() $m_n+1,\ldots , m_{n+1}$
will formally determine
$m_n+1,\ldots , m_{n+1}$
will formally determine
![]() $F_n$
(they are written out explicitly in (3.5)). The rest of the equations define
$F_n$
(they are written out explicitly in (3.5)). The rest of the equations define
![]() $C_n$
(which is a part of the new remainder term). Equating coefficients with the same homogeneous degree in I in both sides of (3.4), we obtain for the degrees from
$C_n$
(which is a part of the new remainder term). Equating coefficients with the same homogeneous degree in I in both sides of (3.4), we obtain for the degrees from
![]() $m_n+1$
to
$m_n+1$
to
![]() $m_{n+1}$
the following recursive formula (we write m instead of
$m_{n+1}$
the following recursive formula (we write m instead of
![]() $m_n$
for typographic reasons):
$m_n$
for typographic reasons):
 $$ \begin{align} \begin{aligned} &\{N_0, F^{[m]} \}+R^{[m+1]} =N^{ [m+1] }, \\ &\{N_0, F^{[m+1]} \} + \{N^{[3]}, F^{[m]} \}+ R^{[m+2]}= N^{[m+2]}, \\ &\{N_0, F^{[m+2]} \} + \{N^{[4]}, F^{[m]} \}+ \{N^{[3]}, F^{[m+1]} \}+ R^{[m+3]}= N^{[m+3]}, \\ &\cdots \\ &\{N_0, F^{[2m-2]} \}+ \sum_{j=0}^{m-3}\{N^{[m-j]}, F^{[m+j]} \} + R^{[2m-1]}=N^{[2m-1]}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\{N_0, F^{[m]} \}+R^{[m+1]} =N^{ [m+1] }, \\ &\{N_0, F^{[m+1]} \} + \{N^{[3]}, F^{[m]} \}+ R^{[m+2]}= N^{[m+2]}, \\ &\{N_0, F^{[m+2]} \} + \{N^{[4]}, F^{[m]} \}+ \{N^{[3]}, F^{[m+1]} \}+ R^{[m+3]}= N^{[m+3]}, \\ &\cdots \\ &\{N_0, F^{[2m-2]} \}+ \sum_{j=0}^{m-3}\{N^{[m-j]}, F^{[m+j]} \} + R^{[2m-1]}=N^{[2m-1]}. \end{aligned} \end{align} $$
Recall that
![]() $2m_n-1=m_{n+1}$
; see §2.1.2. From the formal solvability we know that each of these equations has a formal solution
$2m_n-1=m_{n+1}$
; see §2.1.2. From the formal solvability we know that each of these equations has a formal solution
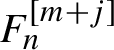 $F_n^{[m+j]}$
. Of course, such a solution is not unique. We will make the solution unique by prescribing the condition
$F_n^{[m+j]}$
. Of course, such a solution is not unique. We will make the solution unique by prescribing the condition
 $$ \begin{align*}\int_{{\mathbb T}^d} F_n^{[m+j]}(I,\theta) =0. \end{align*} $$
$$ \begin{align*}\int_{{\mathbb T}^d} F_n^{[m+j]}(I,\theta) =0. \end{align*} $$
As we will see, this normalization will allow us to get the estimates needed for the proof of the convergence. The sum of the terms of orders
![]() $m_{n+1}+1, \ldots , m_{n+1}+m_n-2$
(that is,
$m_{n+1}+1, \ldots , m_{n+1}+m_n-2$
(that is,
![]() $2m_{n}, \ldots , 3m_n-3$
) that appear in equation (4.1) is denoted by
$2m_{n}, \ldots , 3m_n-3$
) that appear in equation (4.1) is denoted by
![]() $C_n$
. In the notation
$C_n$
. In the notation
![]() $m=m_n$
, we have
$m=m_n$
, we have
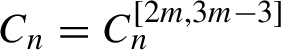 $C_n=C_n^{[2m, 3m-3]}$
. The terms of the uniform degree satisfy
$C_n=C_n^{[2m, 3m-3]}$
. The terms of the uniform degree satisfy
 $$ \begin{align} \begin{aligned} &C_n^{[2m]}=\{N_{[3]}, F^{[2m-2]} \}+ \{N_{[4]}, F^{[2m-3]} \} + \cdots + \{N_{[m]}, F^{[m+1]} \}, \\ &C_n^{[2m+1]}=\{N_{[4]}, F^{[2m-2]} \}+ \{N_{[5]}, F^{[2m-3]} \} + \cdots + \{N_{[m]}, F^{[m+2]} \}, \\ &\cdots \\ &C_n^{[3m-3]}=\{N_{[m]}, F^{[2m-2]} \}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &C_n^{[2m]}=\{N_{[3]}, F^{[2m-2]} \}+ \{N_{[4]}, F^{[2m-3]} \} + \cdots + \{N_{[m]}, F^{[m+1]} \}, \\ &C_n^{[2m+1]}=\{N_{[4]}, F^{[2m-2]} \}+ \{N_{[5]}, F^{[2m-3]} \} + \cdots + \{N_{[m]}, F^{[m+2]} \}, \\ &\cdots \\ &C_n^{[3m-3]}=\{N_{[m]}, F^{[2m-2]} \}. \end{aligned} \end{align} $$
This can be written more compactly as
 $$ \begin{align} C_n= \sum_{k=1}^{m-2} \{F^{[2m-1-k]}, \sum_{j=k+2}^{m}N^{[k+j]} \}. \end{align} $$
$$ \begin{align} C_n= \sum_{k=1}^{m-2} \{F^{[2m-1-k]}, \sum_{j=k+2}^{m}N^{[k+j]} \}. \end{align} $$
This should be viewed as a definition of the remainder term
![]() $C_n$
.
$C_n$
.
3.3 An important simplification
In the case when the normal form is an analytic function of
![]() $N_0(I)$
as in (2.2), we have an important simplification. Denote
$N_0(I)$
as in (2.2), we have an important simplification. Denote
 $$ \begin{align} g_{2j}(I):= j b_{j} (N_0(I))^{j-1} \text{ and } g_{2j+1}(I)\equiv 0. \end{align} $$
$$ \begin{align} g_{2j}(I):= j b_{j} (N_0(I))^{j-1} \text{ and } g_{2j+1}(I)\equiv 0. \end{align} $$
Then, for
![]() $j\in {\mathbb N}$
, we have
$j\in {\mathbb N}$
, we have
 $$ \begin{align} \begin{aligned} &\{N^{[2j]}, F\} = \{b_{j} (N_0)^{j}, F\}= j b_{j} (N_0)^{j-1} \{ N_0, F \}= g_{2j}(I) \{ N_0, F \}, \\ &\{N^{[2j+1]}, F\}= g_{2j+1}(I) \{ N_0, F \}\equiv 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\{N^{[2j]}, F\} = \{b_{j} (N_0)^{j}, F\}= j b_{j} (N_0)^{j-1} \{ N_0, F \}= g_{2j}(I) \{ N_0, F \}, \\ &\{N^{[2j+1]}, F\}= g_{2j+1}(I) \{ N_0, F \}\equiv 0. \end{aligned} \end{align} $$
We formulate this as a lemma.
Lemma 3.3. If the normal form is an analytic function of
![]() $N_0(I)$
as in (2.2), then equation (3.5) is equivalent to
$N_0(I)$
as in (2.2), then equation (3.5) is equivalent to
 $$ \begin{align} \begin{aligned} &\{N_0, F^{[m]} \}+R^{[m+1]} =N^{ [m+1] }, \\ &\{N_0, F^{[m+1]} \} + g_{3}(I)\{N_0, F^{[m]} \}+ R^{[m+2]}= N^{[m+2]}, \\ &\{N_0, F^{[m+2]} \} + g_{4}(I) \{N_0, F^{[m]} \}+ g_{3}(I)\{N_0, F^{[m+1]} \}+ R^{[m+3]}= N^{[m+3]}, \\ &\cdots \\ &\{N_0, F^{[2m-2]} \}+ \sum_{j=0}^{m-3}g_{m-j}(I)\{N_0, F^{[m+j]} \} + R^{[2m-1]}=N^{[2m-1]}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\{N_0, F^{[m]} \}+R^{[m+1]} =N^{ [m+1] }, \\ &\{N_0, F^{[m+1]} \} + g_{3}(I)\{N_0, F^{[m]} \}+ R^{[m+2]}= N^{[m+2]}, \\ &\{N_0, F^{[m+2]} \} + g_{4}(I) \{N_0, F^{[m]} \}+ g_{3}(I)\{N_0, F^{[m+1]} \}+ R^{[m+3]}= N^{[m+3]}, \\ &\cdots \\ &\{N_0, F^{[2m-2]} \}+ \sum_{j=0}^{m-3}g_{m-j}(I)\{N_0, F^{[m+j]} \} + R^{[2m-1]}=N^{[2m-1]}, \end{aligned} \end{align} $$
and
 $$ \begin{align} C_n= \sum_{k=1}^{m-2} \bigg(\{F^{[2m-1-k]}, \, N_0 \} \cdot \sum_{j=k+2}^{m} g_j \bigg). \end{align} $$
$$ \begin{align} C_n= \sum_{k=1}^{m-2} \bigg(\{F^{[2m-1-k]}, \, N_0 \} \cdot \sum_{j=k+2}^{m} g_j \bigg). \end{align} $$
3.4 Homological equations in majorants
Here we study a simple recursive formula and estimate its terms. Later it will provide an important estimate of
![]() $|\{N_0, F^{j} \}|_{\rho _n,\rho _n}$
. Here is the idea: suppose that in the lemma above for some
$|\{N_0, F^{j} \}|_{\rho _n,\rho _n}$
. Here is the idea: suppose that in the lemma above for some
![]() ${\epsilon }>0$
, for all
${\epsilon }>0$
, for all
![]() $j=0,\ldots ,m$
, we have
$j=0,\ldots ,m$
, we have
 $$ \begin{align*}P_j:=|R^{[m+j]}|_{\rho_n,\rho_n} + |N^{ [m+j] }|_{\rho_n,\rho_n}\leq {\epsilon}, \quad |g_{j}|_{\rho_n}\leq 1/4^j.\end{align*} $$
$$ \begin{align*}P_j:=|R^{[m+j]}|_{\rho_n,\rho_n} + |N^{ [m+j] }|_{\rho_n,\rho_n}\leq {\epsilon}, \quad |g_{j}|_{\rho_n}\leq 1/4^j.\end{align*} $$
Define
![]() $S_j$
by the relations (3.12) below. Then, by Lemma 3.3, for all
$S_j$
by the relations (3.12) below. Then, by Lemma 3.3, for all
![]() $j=0,\ldots ,m$
, we have
$j=0,\ldots ,m$
, we have
 $$ \begin{align*}|\{N_0, F^{j} \}|_{\rho_n,\rho_n}\leq S_j. \end{align*} $$
$$ \begin{align*}|\{N_0, F^{j} \}|_{\rho_n,\rho_n}\leq S_j. \end{align*} $$
Lemma 3.4. Given
![]() $ {\epsilon }>0$
, suppose that for all
$ {\epsilon }>0$
, suppose that for all
![]() $j=1, \ldots ,m-1$
, the numbers
$j=1, \ldots ,m-1$
, the numbers
![]() $P_j$
satisfy
$P_j$
satisfy
Let
![]() $S_j$
be defined recursively by the equations
$S_j$
be defined recursively by the equations
 $$ \begin{align} \begin{aligned} &S_{1} = P_{1}, \\ &S_{2} = P_{2} + \tfrac14 S_{1} , \\ &S_{3} = P_{3} + \frac14 S_{2}+ \frac1{4^2} S_{1}, \\ &S_{4} = P_{4} + \frac14 S_{3}+ \frac1{4^2} S_{2}+ \frac1{4^3} S_{1}, \\ &\cdots \\ &S_{m-1} = P_{m-1} + \sum_{j=1}^{m-1} \frac1{4^j} S_{m-1-j}.\\ \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &S_{1} = P_{1}, \\ &S_{2} = P_{2} + \tfrac14 S_{1} , \\ &S_{3} = P_{3} + \frac14 S_{2}+ \frac1{4^2} S_{1}, \\ &S_{4} = P_{4} + \frac14 S_{3}+ \frac1{4^2} S_{2}+ \frac1{4^3} S_{1}, \\ &\cdots \\ &S_{m-1} = P_{m-1} + \sum_{j=1}^{m-1} \frac1{4^j} S_{m-1-j}.\\ \end{aligned} \end{align} $$
Then, for each j, we have
Proof By the formula for
![]() $S^{[j]}$
above,
$S^{[j]}$
above,
 $$ \begin{align*}S_j \leq P_j + \tfrac14 S_{j-1} + \tfrac14 (S_{j-1} -P_{j-1} ) = P_j+ 2 \tfrac14 S_{j-1} \leq P_j+ S_{j-1}/2. \end{align*} $$
$$ \begin{align*}S_j \leq P_j + \tfrac14 S_{j-1} + \tfrac14 (S_{j-1} -P_{j-1} ) = P_j+ 2 \tfrac14 S_{j-1} \leq P_j+ S_{j-1}/2. \end{align*} $$
This implies that
 $$ \begin{align*}S_j \leq \sum_{k=0}^{j-1} 2^{-k} P_{j-k} \leq {\epsilon} \sum_{k=0}^{j-1}2^{-k} < 2 {\epsilon}.\\[-44pt] \end{align*} $$
$$ \begin{align*}S_j \leq \sum_{k=0}^{j-1} 2^{-k} P_{j-k} \leq {\epsilon} \sum_{k=0}^{j-1}2^{-k} < 2 {\epsilon}.\\[-44pt] \end{align*} $$
4 Formal solution provides analytic one with estimates
In this section we study a homological equation (4.1) below with an analytic right-hand side
![]() $Q(I,\theta )$
. Assuming that it has a formal solution, we will find an analytic one and estimate it in terms of the right-hand side. Similar procedures appear in [Reference de la LlaveLl].
$Q(I,\theta )$
. Assuming that it has a formal solution, we will find an analytic one and estimate it in terms of the right-hand side. Similar procedures appear in [Reference de la LlaveLl].
Lemma 4.1. Let
![]() $N_0(I)=I^{\rm tr}{\Omega } I$
, where
$N_0(I)=I^{\rm tr}{\Omega } I$
, where
![]() ${\Omega }$
is a symmetric matrix with
${\Omega }$
is a symmetric matrix with
![]() $\det {\Omega }\neq 0$
, and let
$\det {\Omega }\neq 0$
, and let
![]() $Q(I,\theta )$
be analytic in an annulus
$Q(I,\theta )$
be analytic in an annulus
![]() $\mathbb A_{\rho ,\sigma }$
for some
$\mathbb A_{\rho ,\sigma }$
for some
![]() $\rho $
,
$\rho $
,
![]() $\sigma>0$
. Suppose that the following equation has a formal solution
$\sigma>0$
. Suppose that the following equation has a formal solution
![]() $\widetilde F (I,\theta )$
:
$\widetilde F (I,\theta )$
:
Then equation (4.1) has an analytic solution
![]() $F(I,\theta )$
, defined in
$F(I,\theta )$
, defined in
![]() $\mathbb A_{\rho ,\sigma }$
, and, for any
$\mathbb A_{\rho ,\sigma }$
, and, for any
![]() $0<{\delta } <\rho $
,
$0<{\delta } <\rho $
,
![]() $0<\gamma <\sigma $
, we have
$0<\gamma <\sigma $
, we have
 $$ \begin{align*}|F |_{\rho -{\delta}, \sigma-\gamma} \leq c(d,{\Omega}) \frac{1}{{\delta} \gamma^d} | Q |_{\rho, \sigma}, \end{align*} $$
$$ \begin{align*}|F |_{\rho -{\delta}, \sigma-\gamma} \leq c(d,{\Omega}) \frac{1}{{\delta} \gamma^d} | Q |_{\rho, \sigma}, \end{align*} $$
where
![]() $c(d,{\Omega })$
is a constant only depending on d and
$c(d,{\Omega })$
is a constant only depending on d and
![]() ${\Omega }$
.
${\Omega }$
.
Moreover, if
![]() $Q(I,\theta )$
is a homogeneous polynomial in I with coefficients depending on
$Q(I,\theta )$
is a homogeneous polynomial in I with coefficients depending on
![]() $\theta $
, then so is
$\theta $
, then so is
![]() $F(I,\theta )$
.
$F(I,\theta )$
.
Proof Expanding F formally into a Fourier series:
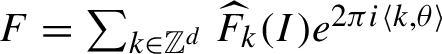 $F=\sum _{k\in {\mathbb Z}^d} \widehat {F}_k(I) e^{2\pi i\langle k,\theta \rangle }$
, we get
$F=\sum _{k\in {\mathbb Z}^d} \widehat {F}_k(I) e^{2\pi i\langle k,\theta \rangle }$
, we get
 $$ \begin{align*}\{N_0,F\} = \sum_{j=1}^d F_{\theta_j} (N_0)_{I_j} = 2\pi i \sum_{k\in {\mathbb Z}^d} \langle k, 2{\Omega} I\rangle \widehat{F}_k (I) e^{2\pi i \langle k,\theta\rangle}. \end{align*} $$
$$ \begin{align*}\{N_0,F\} = \sum_{j=1}^d F_{\theta_j} (N_0)_{I_j} = 2\pi i \sum_{k\in {\mathbb Z}^d} \langle k, 2{\Omega} I\rangle \widehat{F}_k (I) e^{2\pi i \langle k,\theta\rangle}. \end{align*} $$
Recall that
![]() ${\Omega }$
is symmetric, so
${\Omega }$
is symmetric, so
![]() $\langle k, {\Omega } I\rangle =\langle {\Omega } k, I\rangle $
. Expressing
$\langle k, {\Omega } I\rangle =\langle {\Omega } k, I\rangle $
. Expressing
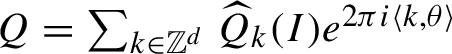 $Q=\sum _{k\in {\mathbb Z}^d} \widehat {Q}_k(I) e^{2\pi i \langle k,\theta \rangle }$
, we can rewrite equation (4.1) as a series of equations indexed by k:
$Q=\sum _{k\in {\mathbb Z}^d} \widehat {Q}_k(I) e^{2\pi i \langle k,\theta \rangle }$
, we can rewrite equation (4.1) as a series of equations indexed by k:
If
![]() $\langle k, {\Omega } I\rangle \neq 0$
, we can express
$\langle k, {\Omega } I\rangle \neq 0$
, we can express
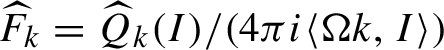 $\widehat {F}_k = \widehat {Q}_k(I)/ (4\pi i \langle {\Omega } k, I\rangle )$
.
$\widehat {F}_k = \widehat {Q}_k(I)/ (4\pi i \langle {\Omega } k, I\rangle )$
.
Since we have assumed existence of a formal solution of the homological equation (4.1) (and, hence, a solution of (4.2) for each k), we have
Hence, for
![]() $\langle {\Omega } k, I\rangle =0$
, the equation is satisfied for any value of
$\langle {\Omega } k, I\rangle =0$
, the equation is satisfied for any value of
![]() $\widehat {F}_k(I)$
. We define
$\widehat {F}_k(I)$
. We define
![]() $\widehat {F}_k$
at these points by continuity. A way to do it is the following. Differentiate equation (4.2) in the direction of
$\widehat {F}_k$
at these points by continuity. A way to do it is the following. Differentiate equation (4.2) in the direction of
![]() ${\Omega } k$
:
${\Omega } k$
:
where, for a vector
![]() $v\in {\mathbb R}^d$
, we denote
$v\in {\mathbb R}^d$
, we denote
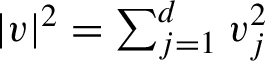 $|v|^2=\sum _{j=1}^d v_j^2$
. For
$|v|^2=\sum _{j=1}^d v_j^2$
. For
![]() $\langle {\Omega } k, I\rangle =0$
, define
$\langle {\Omega } k, I\rangle =0$
, define
 $\widehat {F}_k(I)= \langle {\Omega } k , \nabla \widehat Q_k(I)\rangle /(4\pi i |{\Omega } k|^2)$
. Summing up, we have defined a continuous function
$\widehat {F}_k(I)= \langle {\Omega } k , \nabla \widehat Q_k(I)\rangle /(4\pi i |{\Omega } k|^2)$
. Summing up, we have defined a continuous function
![]() $\widehat {F}_k(I) $
by
$\widehat {F}_k(I) $
by
 $$ \begin{align*}\widehat{F}_k (I) = \frac{1}{4\pi i} \begin{cases} \langle {\Omega} k, I\rangle^{-1} \widehat{Q}_k (I), \quad \langle {\Omega} k, I\rangle \neq 0, \\[3pt] \dfrac{1}{|{\Omega} k|^2}\langle {\Omega} k , \nabla \widehat{Q}_k(I)\rangle ,\ \ \langle {\Omega} k, I\rangle =0. \end{cases} \end{align*} $$
$$ \begin{align*}\widehat{F}_k (I) = \frac{1}{4\pi i} \begin{cases} \langle {\Omega} k, I\rangle^{-1} \widehat{Q}_k (I), \quad \langle {\Omega} k, I\rangle \neq 0, \\[3pt] \dfrac{1}{|{\Omega} k|^2}\langle {\Omega} k , \nabla \widehat{Q}_k(I)\rangle ,\ \ \langle {\Omega} k, I\rangle =0. \end{cases} \end{align*} $$
Moreover, since
![]() $\widehat {F}_k(I)$
is analytic in
$\widehat {F}_k(I)$
is analytic in
![]() ${\mathbb D}_\rho \setminus \{\langle {\Omega } k, I\rangle =0\}$
and bounded in
${\mathbb D}_\rho \setminus \{\langle {\Omega } k, I\rangle =0\}$
and bounded in
![]() ${\mathbb D}_\rho $
, it is analytic in
${\mathbb D}_\rho $
, it is analytic in
![]() ${\mathbb D}_{\rho }$
. Notice that if in equation (4.2)
${\mathbb D}_{\rho }$
. Notice that if in equation (4.2)
![]() $\widehat {Q}_k(I)$
is a homogeneous polynomial in I, then so is
$\widehat {Q}_k(I)$
is a homogeneous polynomial in I, then so is
![]() $\widehat {F}_k(I)$
.
$\widehat {F}_k(I)$
.
Now let us estimate the norm of the solution. Fix
![]() $0<{\delta }<\rho /2$
,
$0<{\delta }<\rho /2$
,
![]() $0<\gamma <\sigma $
. For each fixed
$0<\gamma <\sigma $
. For each fixed
![]() $k\in {\mathbb Z}^d$
, we will estimate the corresponding
$k\in {\mathbb Z}^d$
, we will estimate the corresponding
![]() $\widehat {F}_k(I)$
in two steps: first ‘
$\widehat {F}_k(I)$
in two steps: first ‘
![]() $\delta /2$
-close’ to the resonant plane
$\delta /2$
-close’ to the resonant plane
![]() $\langle {\Omega } k, I\rangle $
and then in the rest of
$\langle {\Omega } k, I\rangle $
and then in the rest of
![]() ${\mathbb D}_{\rho -{\delta }} $
.
${\mathbb D}_{\rho -{\delta }} $
.
For the first step, let
![]() $\Pi _{\delta }= \{\langle {\Omega } k,I\rangle =0 \} \cap {\mathbb D}_{\rho -{\delta }}$
be the part of the resonant plane falling into
$\Pi _{\delta }= \{\langle {\Omega } k,I\rangle =0 \} \cap {\mathbb D}_{\rho -{\delta }}$
be the part of the resonant plane falling into
![]() ${\mathbb D}_{\rho -{\delta }}$
. Notice that the orthogonal complement to this plane is formed by the vectors
${\mathbb D}_{\rho -{\delta }}$
. Notice that the orthogonal complement to this plane is formed by the vectors
![]() $\alpha e^{2 \pi i \phi } {\Omega } k $
,
$\alpha e^{2 \pi i \phi } {\Omega } k $
,
![]() $\alpha \geq 0$
,
$\alpha \geq 0$
,
![]() $\phi \in [0,1)$
. Let
$\phi \in [0,1)$
. Let
 $$ \begin{align*}\Delta=\bigg\{ I= \alpha \frac{{\Omega} k }{|{\Omega} k | } e^{2 \pi i \phi } \, \bigg| \, \alpha < {\delta} /2, \,\phi\in [0,1) \bigg\} \end{align*} $$
$$ \begin{align*}\Delta=\bigg\{ I= \alpha \frac{{\Omega} k }{|{\Omega} k | } e^{2 \pi i \phi } \, \bigg| \, \alpha < {\delta} /2, \,\phi\in [0,1) \bigg\} \end{align*} $$
be the complex disk of radius
![]() ${\delta } /2$
centered at zero and orthogonal to
${\delta } /2$
centered at zero and orthogonal to
![]() $\Pi _{\delta }$
. Note that the restrictions of
$\Pi _{\delta }$
. Note that the restrictions of
![]() $\widehat {Q}_k(I)$
and
$\widehat {Q}_k(I)$
and
![]() $\widehat {F}_k(I)$
to this disk are analytic. Consider the
$\widehat {F}_k(I)$
to this disk are analytic. Consider the
![]() ${{\delta }}/2$
-neighborhood
${{\delta }}/2$
-neighborhood
![]() $O_{\delta }$
of
$O_{\delta }$
of
![]() $\Pi _{\delta }$
:
$\Pi _{\delta }$
:
 $O_{\delta }=\bigcup _{I_0\in \Pi _{\delta }} (I_0+\Delta )$
. Then
$O_{\delta }=\bigcup _{I_0\in \Pi _{\delta }} (I_0+\Delta )$
. Then
![]() $O_{\delta }\subset {\mathbb D}_{\rho -{\delta }} $
.
$O_{\delta }\subset {\mathbb D}_{\rho -{\delta }} $
.
For each fixed
![]() $I\in O_{\delta }$
, there exists
$I\in O_{\delta }$
, there exists
![]() $I_0 \in \Pi _{\delta }$
such that
$I_0 \in \Pi _{\delta }$
such that
![]() $I\in I_0+\Delta $
. We can estimate
$I\in I_0+\Delta $
. We can estimate
![]() $|\widehat {F}_k (I)|$
by the maximum modulus principle on the disk
$|\widehat {F}_k (I)|$
by the maximum modulus principle on the disk
![]() $I_0+\Delta $
. Namely, for I lying on the boundary of this disk, we have
$I_0+\Delta $
. Namely, for I lying on the boundary of this disk, we have
![]() $|\langle {\Omega } k, I\rangle |= |\langle {\Omega } k, I_0\rangle + \langle {\Omega } k, {\delta } {\Omega } k/(2| {\Omega } k|) \rangle | = | {\Omega } k|{\delta }/2$
. Hence, for such I, we have
$|\langle {\Omega } k, I\rangle |= |\langle {\Omega } k, I_0\rangle + \langle {\Omega } k, {\delta } {\Omega } k/(2| {\Omega } k|) \rangle | = | {\Omega } k|{\delta }/2$
. Hence, for such I, we have
 $$ \begin{align*}|\widehat{F}_k (I)| \leq \frac{2 | \widehat{Q}_k |_\rho }{4\pi{\delta} |{\Omega} k|}< \frac{ | \widehat{Q}_k |_\rho }{{\delta} |{\Omega} k|}. \end{align*} $$
$$ \begin{align*}|\widehat{F}_k (I)| \leq \frac{2 | \widehat{Q}_k |_\rho }{4\pi{\delta} |{\Omega} k|}< \frac{ | \widehat{Q}_k |_\rho }{{\delta} |{\Omega} k|}. \end{align*} $$
As the second step in this estimate, consider
![]() $I\in {\mathbb D}_{\rho -{\delta }}\setminus O_{\delta } $
. Here
$I\in {\mathbb D}_{\rho -{\delta }}\setminus O_{\delta } $
. Here
![]() $|\langle {\Omega } k, I\rangle | \geq |{\Omega } k| {\delta } / 2$
, so
$|\langle {\Omega } k, I\rangle | \geq |{\Omega } k| {\delta } / 2$
, so
![]() $|\widehat {F}_k (I)| $
satisfies the same estimate as above.
$|\widehat {F}_k (I)| $
satisfies the same estimate as above.
By Cauchy estimates, we have
 $$ \begin{align*}|\widehat{Q}_k |_{\rho} \leq | Q |_{\rho,\sigma}e^{-|k|\sigma}. \end{align*} $$
$$ \begin{align*}|\widehat{Q}_k |_{\rho} \leq | Q |_{\rho,\sigma}e^{-|k|\sigma}. \end{align*} $$
Since det
![]() $\, {\Omega }\neq 0$
, there exists a constant
$\, {\Omega }\neq 0$
, there exists a constant
![]() $c({\Omega })$
such that
$c({\Omega })$
such that
![]() $|{\Omega } k|\geq |k|/c({\Omega })$
for all k. Then
$|{\Omega } k|\geq |k|/c({\Omega })$
for all k. Then
 $$ \begin{align*}\begin{aligned} |\widehat{F}_k |_{\rho-{\delta}} \leq \frac1{{\delta} |{\Omega} k|} | \widehat{Q}_k |_{\rho} \leq c({\Omega}) \frac{e^{-\sigma |k|}} {{\delta} |k|} | Q |_{\rho,\sigma}. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} |\widehat{F}_k |_{\rho-{\delta}} \leq \frac1{{\delta} |{\Omega} k|} | \widehat{Q}_k |_{\rho} \leq c({\Omega}) \frac{e^{-\sigma |k|}} {{\delta} |k|} | Q |_{\rho,\sigma}. \end{aligned} \end{align*} $$
Finally, for small
![]() ${\delta }$
and
${\delta }$
and
![]() $\gamma $
, we have
$\gamma $
, we have
 $$ \begin{align*}\begin{aligned} |F |_{\rho-{\delta},\sigma-\gamma}\leq & \sum_{k\in {\mathbb Z}^d \setminus \{0\}} e^{(\sigma-\gamma) |k|} |\widehat{F}_k |_{\rho-{\delta} } \leq \frac{c({\Omega})}{{\delta} } \sum_{k\in{\mathbb Z}^d \setminus \{0\}} \frac{e^{-\gamma |k|} }{|k|} | Q |_{\rho,\sigma}\\ \leq &\frac{c(d,{\Omega})}{{\delta} \gamma^d } | Q |_{\rho,\sigma}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} |F |_{\rho-{\delta},\sigma-\gamma}\leq & \sum_{k\in {\mathbb Z}^d \setminus \{0\}} e^{(\sigma-\gamma) |k|} |\widehat{F}_k |_{\rho-{\delta} } \leq \frac{c({\Omega})}{{\delta} } \sum_{k\in{\mathbb Z}^d \setminus \{0\}} \frac{e^{-\gamma |k|} }{|k|} | Q |_{\rho,\sigma}\\ \leq &\frac{c(d,{\Omega})}{{\delta} \gamma^d } | Q |_{\rho,\sigma}, \end{aligned} \end{align*} $$
where
![]() $c(d,{\Omega })$
is a constant only depending on d and
$c(d,{\Omega })$
is a constant only depending on d and
![]() ${\Omega }$
. The estimates above are very wasteful, but they are enough for our purposes.
${\Omega }$
. The estimates above are very wasteful, but they are enough for our purposes.
5 Proof of Proposition 2.2
Here we summarize the preparatory work to complete the proof of Proposition 2.2. Let us return to the original problem. For a fixed n, let the necessary constants be as in §2.1.2,
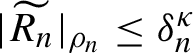 $|\widetilde {R_n} |_{\rho _n } \leq {\delta }_n^\kappa $
, and let
$|\widetilde {R_n} |_{\rho _n } \leq {\delta }_n^\kappa $
, and let
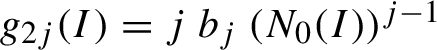 $ g_{2j}(I)=j\, b_{j} \, (N_0(I))^{j-1}$
as in (3.8).
$ g_{2j}(I)=j\, b_{j} \, (N_0(I))^{j-1}$
as in (3.8).
5.1 Estimate of
 $|\{N_0,F_n \}|_{\rho _n, \rho _n}$
and
$|\{N_0,F_n \}|_{\rho _n, \rho _n}$
and
 $|C_n |_{\rho _n, \rho _n }$
$|C_n |_{\rho _n, \rho _n }$
For
![]() $j=1, \ldots ,m_n-1$
, denote
$j=1, \ldots ,m_n-1$
, denote
 $$ \begin{align*}P_{j}:= |N^{[m_n+j]}|_{\rho_0 } +|R^{[m_n+j]} |_{\rho_n }. \end{align*} $$
$$ \begin{align*}P_{j}:= |N^{[m_n+j]}|_{\rho_0 } +|R^{[m_n+j]} |_{\rho_n }. \end{align*} $$
By the choice of
![]() $\rho _0$
, see §2.1.2, for all
$\rho _0$
, see §2.1.2, for all
![]() $j=1, \ldots , m_n-1$
, we have
$j=1, \ldots , m_n-1$
, we have
 $$ \begin{align*} |g_{j}(I) |_{\rho_0} \leq 4^{-j},\quad |N^{[m_n+j]}|_{\rho_0 } \leq {\delta}_n^\kappa. \end{align*} $$
$$ \begin{align*} |g_{j}(I) |_{\rho_0} \leq 4^{-j},\quad |N^{[m_n+j]}|_{\rho_0 } \leq {\delta}_n^\kappa. \end{align*} $$
Since, for
![]() $j=1, \ldots ,m_n-1$
, we have
$j=1, \ldots ,m_n-1$
, we have
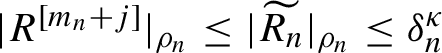 $|R^{[m_n+j]} |_{\rho _n } \leq |\widetilde {R_n} |_{\rho _n } \leq {\delta }_n^\kappa $
, for these values of j, we get
$|R^{[m_n+j]} |_{\rho _n } \leq |\widetilde {R_n} |_{\rho _n } \leq {\delta }_n^\kappa $
, for these values of j, we get
Let
![]() $S_j$
be defined by (3.12). By Lemma 3.4, for
$S_j$
be defined by (3.12). By Lemma 3.4, for
![]() $j=1,\ldots , m-1$
, we have
$j=1,\ldots , m-1$
, we have
![]() $S_j \leq 2{\epsilon } $
. Equations (3.10) imply that for
$S_j \leq 2{\epsilon } $
. Equations (3.10) imply that for
![]() $j=1,\ldots , m-1$
, we have
$j=1,\ldots , m-1$
, we have
 $$ \begin{align} | \{N_0, F_n^{[m+j-1]} \} |_{\rho_n,\rho_n} \leq S_j\leq 2{\epsilon} =4{\delta}_n^\kappa. \end{align} $$
$$ \begin{align} | \{N_0, F_n^{[m+j-1]} \} |_{\rho_n,\rho_n} \leq S_j\leq 2{\epsilon} =4{\delta}_n^\kappa. \end{align} $$
By linearity,
 $$ \begin{align*}| \{N_0, F_n \} |_{\rho_n,\rho_n} \leq \sum_{j=1}^{m_n-1} | \{N_0, F_n^{[m_n+j-1]} \} |_{\rho_n,\rho_n} \leq 4m_n {\delta}_n^\kappa \leq 4{\delta}_n^{\kappa - 1}. \end{align*} $$
$$ \begin{align*}| \{N_0, F_n \} |_{\rho_n,\rho_n} \leq \sum_{j=1}^{m_n-1} | \{N_0, F_n^{[m_n+j-1]} \} |_{\rho_n,\rho_n} \leq 4m_n {\delta}_n^\kappa \leq 4{\delta}_n^{\kappa - 1}. \end{align*} $$
The latter estimate follows from the definition of
![]() $m_n$
and
$m_n$
and
![]() ${\delta }_n$
; see §2.1.2.
${\delta }_n$
; see §2.1.2.
Moreover, by (3.11),
 $$ \begin{align*}\begin{aligned} |C_n |_{\rho_n} &= \sum_{k=1}^{m-2} \bigg(S_{m-k} \,\sum_{j=k+2}^{m} G_j \bigg) \leq \sum_{k=1}^{m-2} \bigg(S_{m-k} \,\sum_{j=k+2}^{\infty} 4^{-j} \bigg) \\ &\leq \frac{1}{3} \sum_{k=1}^{m-2} 4^{-(k+1)} S_{m-k} \leq \frac{1}{2} {\epsilon}={\delta}_n^\kappa. \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} |C_n |_{\rho_n} &= \sum_{k=1}^{m-2} \bigg(S_{m-k} \,\sum_{j=k+2}^{m} G_j \bigg) \leq \sum_{k=1}^{m-2} \bigg(S_{m-k} \,\sum_{j=k+2}^{\infty} 4^{-j} \bigg) \\ &\leq \frac{1}{3} \sum_{k=1}^{m-2} 4^{-(k+1)} S_{m-k} \leq \frac{1}{2} {\epsilon}={\delta}_n^\kappa. \end{aligned} \end{align*} $$
Hence,
5.2 Estimates for
 $F_n$
$F_n$
Consider equation (5.1). Lemma 4.1 with
![]() $\rho =\sigma =\rho _n$
,
$\rho =\sigma =\rho _n$
,
![]() ${\delta }=\gamma ={\delta }_n$
, and
${\delta }=\gamma ={\delta }_n$
, and
![]() $| Q |_{\rho , \sigma } \leq 4{\delta }_n^\kappa $
implies that
$| Q |_{\rho , \sigma } \leq 4{\delta }_n^\kappa $
implies that
 $$ \begin{align*}| F_n^{[m+j-1]} |_{\rho_n-{\delta}_n, \rho_n-{\delta}_n} \leq 4c(d,{\Omega}) {\delta}_n^{\kappa - d-1}. \end{align*} $$
$$ \begin{align*}| F_n^{[m+j-1]} |_{\rho_n-{\delta}_n, \rho_n-{\delta}_n} \leq 4c(d,{\Omega}) {\delta}_n^{\kappa - d-1}. \end{align*} $$
Since
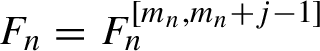 $F_n=F_n^{[m_n, m_n+j-1]} $
, where
$F_n=F_n^{[m_n, m_n+j-1]} $
, where
![]() $m_n\leq {\delta }_n^{-1}$
, we get
$m_n\leq {\delta }_n^{-1}$
, we get
 $$ \begin{align} | F_n |_{\rho_n - {\delta}_n , \rho_n-{\delta}_n} \leq \sum_{j=1}^{m_n-1} | F_n^{[m+j-1]} |_{\rho_n-{\delta}_n , \rho_n-{\delta}_n} \leq m_n \, 4c(d,{\Omega}) {\delta}_n^{\kappa - d-1} \leq {\delta}_n^{\kappa - d-3} \leq {\delta}_n^{3}. \end{align} $$
$$ \begin{align} | F_n |_{\rho_n - {\delta}_n , \rho_n-{\delta}_n} \leq \sum_{j=1}^{m_n-1} | F_n^{[m+j-1]} |_{\rho_n-{\delta}_n , \rho_n-{\delta}_n} \leq m_n \, 4c(d,{\Omega}) {\delta}_n^{\kappa - d-1} \leq {\delta}_n^{\kappa - d-3} \leq {\delta}_n^{3}. \end{align} $$
The latter estimate follows from the definition of
![]() $\kappa $
; see §2.1.2.
$\kappa $
; see §2.1.2.
5.3 Estimates for
 $\Phi _n$
$\Phi _n$
Here we prove that with
![]() $F_n$
as above, estimates (2.10) and (2.11) hold true. Indeed, the coordinate change
$F_n$
as above, estimates (2.10) and (2.11) hold true. Indeed, the coordinate change
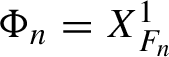 $\Phi _n = X_{F_n}^1$
is the time-one map of the flow
$\Phi _n = X_{F_n}^1$
is the time-one map of the flow
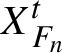 $X_{F_n}^t$
defined by the equations
$X_{F_n}^t$
defined by the equations
By (5.3) and Cauchy estimates, we get
 $$ \begin{align} | \partial_I F_n |_{\rho_n - 2{\delta}_n , \rho_n-{\delta}_n} \leq {\delta}_n^{2}, \quad | \partial_\theta F_n |_{\rho_n - {\delta}_n , \rho_n-2{\delta}_n} \leq {\delta}_n^{2}. \end{align} $$
$$ \begin{align} | \partial_I F_n |_{\rho_n - 2{\delta}_n , \rho_n-{\delta}_n} \leq {\delta}_n^{2}, \quad | \partial_\theta F_n |_{\rho_n - {\delta}_n , \rho_n-2{\delta}_n} \leq {\delta}_n^{2}. \end{align} $$
Then, for any
![]() $t\leq 1$
,
$t\leq 1$
,
 $$ \begin{align} |X_{F_n}^t (I,\theta)- (I,\theta)|_{\rho_n - 3\delta_n , \rho_n- 3 \delta_n} \leq t \, \delta_n^{-1} | F_n |_{\rho_n - 2\delta_n , \rho_n-2\delta_n} \leq \delta_n^{2}, \nonumber \\ X_{F_n}^t :\mathbb A_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} \mapsto \mathbb A_{\rho_n-2{\delta}_n,\rho_n-2{\delta}_n}.\qquad\qquad\quad \end{align} $$
$$ \begin{align} |X_{F_n}^t (I,\theta)- (I,\theta)|_{\rho_n - 3\delta_n , \rho_n- 3 \delta_n} \leq t \, \delta_n^{-1} | F_n |_{\rho_n - 2\delta_n , \rho_n-2\delta_n} \leq \delta_n^{2}, \nonumber \\ X_{F_n}^t :\mathbb A_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} \mapsto \mathbb A_{\rho_n-2{\delta}_n,\rho_n-2{\delta}_n}.\qquad\qquad\quad \end{align} $$
In particular, since
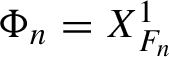 $ \Phi _n = X_{F_n}^1$
, we get the desired formulas (2.10) and (2.11).
$ \Phi _n = X_{F_n}^1$
, we get the desired formulas (2.10) and (2.11).
5.4 Estimate of the new remainder
 $\widetilde {R_{n+1}}$
$\widetilde {R_{n+1}}$
Lemma 5.1. For
![]() $F_n$
constructed above, the estimate (2.9) holds:
$F_n$
constructed above, the estimate (2.9) holds:
 $$ \begin{align*}|\widetilde {R_{n+1}} |_{\rho_n - 3{\delta}_n , \rho_n-3{\delta}_n} < 4 {\delta}_{n}^\kappa. \end{align*} $$
$$ \begin{align*}|\widetilde {R_{n+1}} |_{\rho_n - 3{\delta}_n , \rho_n-3{\delta}_n} < 4 {\delta}_{n}^\kappa. \end{align*} $$
Proof By Lemma 3.2,
 $$ \begin{align*}\widetilde {R_{n+1}}= A_n+B_n+C_n, \end{align*} $$
$$ \begin{align*}\widetilde {R_{n+1}}= A_n+B_n+C_n, \end{align*} $$
where
![]() $A_n$
,
$A_n$
,
![]() $B_n$
, and
$B_n$
, and
![]() $C_n$
are defined by (3.2) and (3.3).
$C_n$
are defined by (3.2) and (3.3).
Estimate of
![]() $A_n$
: Using (5.5), we get
$A_n$
: Using (5.5), we get
 $$ \begin{align*}| \widetilde {R_{n}}^{[>m_{n+1}]}\circ \Phi_n |_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} \leq |\widetilde {R_{n}} |_{\rho_n-2\rho_n,\rho_n-2{\delta}_n} \leq {\delta}_n^\kappa. \end{align*} $$
$$ \begin{align*}| \widetilde {R_{n}}^{[>m_{n+1}]}\circ \Phi_n |_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n} \leq |\widetilde {R_{n}} |_{\rho_n-2\rho_n,\rho_n-2{\delta}_n} \leq {\delta}_n^\kappa. \end{align*} $$
Estimate of
![]() $C_n$
: We showed in §5.1 that
$C_n$
: We showed in §5.1 that
Estimate of
![]() $B_n$
: By (5.4),
$B_n$
: By (5.4),
![]() $ | \partial _I F_n |_{\rho _n - 2{\delta }_n , \rho _n-{\delta }_n} \leq {\delta }_n^{2}$
and
$ | \partial _I F_n |_{\rho _n - 2{\delta }_n , \rho _n-{\delta }_n} \leq {\delta }_n^{2}$
and
![]() $ | \partial _\theta F_n |_{\rho _n - {\delta }_n , \rho _n-2{\delta }_n} \leq {\delta }_n^{2}. $
By (2.9),
$ | \partial _\theta F_n |_{\rho _n - {\delta }_n , \rho _n-2{\delta }_n} \leq {\delta }_n^{2}. $
By (2.9),
 $$ \begin{align*}|R_{n} |_{\rho_n,\rho_n} \leq |\widetilde {R_{n}} |_{\rho_n, \rho_n} \leq {\delta}_n^\kappa. \end{align*} $$
$$ \begin{align*}|R_{n} |_{\rho_n,\rho_n} \leq |\widetilde {R_{n}} |_{\rho_n, \rho_n} \leq {\delta}_n^\kappa. \end{align*} $$
This implies, using Cauchy estimates, that
Notice that, by formulas (3.1) and (3.3), we have
![]() $ \{ N_n, F_n \} = R_{n} +N_{n} - N_{n-1} +C_n$
.
$ \{ N_n, F_n \} = R_{n} +N_{n} - N_{n-1} +C_n$
.
By (2.6),
 $$ \begin{align*}|N_{n} - N_{n-1}|_{\rho_0,\rho_0} =\sum_{j=1}^{m_n}N^{[m_n+j]}\leq m_n {\delta}_n^{\kappa+1}\leq {\delta}_n^{\kappa} \end{align*} $$
$$ \begin{align*}|N_{n} - N_{n-1}|_{\rho_0,\rho_0} =\sum_{j=1}^{m_n}N^{[m_n+j]}\leq m_n {\delta}_n^{\kappa+1}\leq {\delta}_n^{\kappa} \end{align*} $$
and therefore
Combining the above estimates, we get
Since, by (5.5), for any
![]() $t\leq 1$
we have
$t\leq 1$
we have
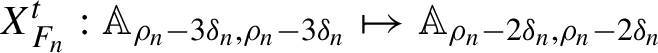 $X_{F_n}^t :\mathbb A_{\rho _n-3{\delta }_n,\rho _n-3{\delta }_n} \mapsto \mathbb A_{\rho _n-2{\delta }_n,\rho _n-2{\delta }_n} $
, we obtain
$X_{F_n}^t :\mathbb A_{\rho _n-3{\delta }_n,\rho _n-3{\delta }_n} \mapsto \mathbb A_{\rho _n-2{\delta }_n,\rho _n-2{\delta }_n} $
, we obtain
 $$ \begin{align*} &| \{ \{ N_n, F_n \} +R_n,F_n\} \circ {X}_{F_n}^t |_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}\\ &\quad\leq | \{ \{ N_n, F_n \} +R_n,F_n\} |_{\rho_n-2{\delta}_n,\rho_n-2{\delta}_n} \leq 2 {\delta}_n^\kappa.\\[-36pt] \end{align*} $$
$$ \begin{align*} &| \{ \{ N_n, F_n \} +R_n,F_n\} \circ {X}_{F_n}^t |_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}\\ &\quad\leq | \{ \{ N_n, F_n \} +R_n,F_n\} |_{\rho_n-2{\delta}_n,\rho_n-2{\delta}_n} \leq 2 {\delta}_n^\kappa.\\[-36pt] \end{align*} $$
Here we get the desired estimate for the remainder term. We have proved above that
 $$ \begin{align*}|\widetilde {R_{n+1}} |_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}< 4 {\delta}_{n}^{{\kappa}}. \end{align*} $$
$$ \begin{align*}|\widetilde {R_{n+1}} |_{\rho_n-3{\delta}_n,\rho_n-3{\delta}_n}< 4 {\delta}_{n}^{{\kappa}}. \end{align*} $$
Recall that
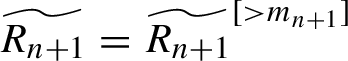 $\widetilde {R_{n+1}}=\widetilde {R_{n+1}}^{[>m_{n+1}]}$
. By Lemma 5.2 proved below, this implies the desired estimate
$\widetilde {R_{n+1}}=\widetilde {R_{n+1}}^{[>m_{n+1}]}$
. By Lemma 5.2 proved below, this implies the desired estimate
 $$ \begin{align*}|\widetilde {R_{n+1}} |_{\rho_{n+1},\rho_{n+1}}< {\delta}_{n+1}^{{\kappa}}. \end{align*} $$
$$ \begin{align*}|\widetilde {R_{n+1}} |_{\rho_{n+1},\rho_{n+1}}< {\delta}_{n+1}^{{\kappa}}. \end{align*} $$
This finishes the proof of Proposition 2.2 and hence Theorem 1.1 (as explained in the introduction).
![]() ${\kern304pt}\Box $
${\kern304pt}\Box $
Lemma 5.2. Suppose that the constants
![]() ${\kappa }$
, b,
${\kappa }$
, b,
![]() ${\delta }_n$
,
${\delta }_n$
,
![]() $q_n$
,
$q_n$
,
![]() $\rho _n$
are defined in §
2.1.2
, an analytic function
$\rho _n$
are defined in §
2.1.2
, an analytic function
![]() $G(I,\theta )$
satisfies
$G(I,\theta )$
satisfies
![]() $G=G^{[>m_{n+1}]}$
, and
$G=G^{[>m_{n+1}]}$
, and
Then
Proof By the definition of
![]() ${\kappa }$
in §2.1.2, we have
${\kappa }$
in §2.1.2, we have
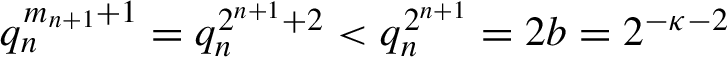 $q_n^{m_{n+1}+1}=q_{n}^{2^{n+1}+2} < q_{n}^{2^{n+1}} = 2b= 2^{-{\kappa }-2}$
. Also, recall that
$q_n^{m_{n+1}+1}=q_{n}^{2^{n+1}+2} < q_{n}^{2^{n+1}} = 2b= 2^{-{\kappa }-2}$
. Also, recall that
![]() ${\delta }_{n+1}=2^{-1}{\delta }_{n}$
.
${\delta }_{n+1}=2^{-1}{\delta }_{n}$
.
Since G starts with terms of degree
![]() $m_{n+1}=2^{n+1}+2$
, we have
$m_{n+1}=2^{n+1}+2$
, we have
 $$ \begin{align*}|G |_{q_n(\rho_n-3{\delta}_n),q_n(\rho_n-3{\delta}_n)}< q_n^{2^{n+1}+2} \,4 {\delta}_{n}^{{\kappa}} \leq 2^{-{\kappa}-2} \, 4 {\delta}_n^{{\kappa}} \leq {\delta}_{n+1}^{{\kappa}}.\\[-34pt] \end{align*} $$
$$ \begin{align*}|G |_{q_n(\rho_n-3{\delta}_n),q_n(\rho_n-3{\delta}_n)}< q_n^{2^{n+1}+2} \,4 {\delta}_{n}^{{\kappa}} \leq 2^{-{\kappa}-2} \, 4 {\delta}_n^{{\kappa}} \leq {\delta}_{n+1}^{{\kappa}}.\\[-34pt] \end{align*} $$
Acknowledgements
R. de la Llave was supported in part by NSF, DMS 1800241. M. Saprykina was supported in part by the Swedish Research Council, VR 2015-04012.