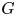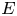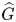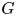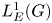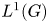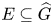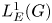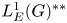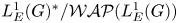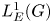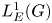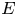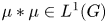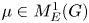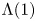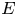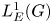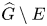Arens regularity of ideals of the group algebra of a compact Abelian group

Abstract

Let $G$ be a compact Abelian group and $E$ a subset of the group $\widehat {G}$ of continuous characters of $G$. We study Arens regularity-related properties of the ideals $L_E^1(G)$ of $L^1(G)$ that are made of functions whose Fourier transform is supported on $E\subseteq \widehat {G}$. Arens regularity of $L_E^1(G)$, the centre of $L_E^1(G)^{\ast \ast }$ and the size of $L_E^1(G)^\ast /\mathcal {WAP}(L_E^1(G))$ are studied. We establish general conditions for the regularity of $L_E^1(G)$ and deduce from them that $L_E^1(G)$ is not strongly Arens irregular if $E$ is a small-2 set (i.e. $\mu \ast \mu \in L^1(G)$ for every $\mu \in M_E^1(G)$), which is not a $\Lambda (1)$-set, and it is extremely non-Arens regular if $E$ is not a small-2 set. We deduce also that $L_E^1(G)$ is not Arens regular when $\widehat {G}\setminus E$ is a Lust-Piquard set.

1. Introduction

It has long been known, since the work of Arens [1] in the fifties, that the bidual $\mathscr {A}^{\ast \ast }$ of a Banach algebra $\mathscr {A}$ can be turned into a Banach algebra containing $\mathscr {A}$ as a subalgebra. Two different multiplications can actually be introduced on $\mathscr {A}^{\ast \ast }$ to this effect. But, while both these multiplications are defined following completely symmetric and absolutely natural rules, they can be essentially different. The left multiplication operator defined by one of them is always weak$^\ast$-continuous but may fail to be so for the other, with the situation reversed for the right multiplication operator.

The subset of $\mathscr {A}^{\ast \ast }$ made of those elements that produce weak$^\ast$-continuous multiplication operators from both sides is usually referred to as the topological centre of $\mathscr {A}^{\ast \ast }$, in symbols $\mathcal {Z}(\mathscr {A}^{\ast \ast })$ and it always contains $\mathscr {A}$. When the centre is as large as possible, i.e. when $\mathscr {A}^{\ast \ast }=\mathcal {Z}(\mathscr {A}^{\ast \ast })$, we say that $\mathscr {A}$ is Arens regular, this is the case, for instance, of $C^\ast$-algebras. Following Dales and Lau [4], we say that $\mathscr {A}$ is strongly Arens irregular (SAI for short) when $\mathcal {Z}(\mathscr {A}^{\ast \ast })$ is as small as possible, i.e. when $\mathcal {Z}(\mathscr {A}^{\ast \ast })=\mathscr {A}$. This is the case for the group algebra $L^1(G)$ discussed below.

Facing the problem from a different point of view, Pym [22] considered the space $\mathscr {WAP(A)}$ of weakly almost periodic functionals on $\mathscr {A}$. This is the precise subspace of $\mathscr {A}^*$ on which the two Arens-multiplications agree. So, $\mathscr {A}$ is Arens regular precisely when $\mathscr {A}^* =\mathscr {WAP(A)}$, i.e. when the quotient $\mathscr {A}^*/ \mathscr {WAP(A)}$ is trivial.

When the quotient $\mathscr {A}^*/\mathscr {WAP(A)}$ contains a closed subspace isomorphic to $\mathscr {A}^\ast$, and so it is as large as possible, we say that $\mathscr {A}$ is extremely non-Arens regular (ENAR for short). Extreme non-Arens regularity was first studied in the context of Fourier algebras with a slightly different definition, see the papers by Granirer [11] and Hu [14].

Işik et al. [15] proved that the group algebra $L^1(G)$ of a compact group is always SAI. Shortly afterwards, Lau and Losert [17] proved the same fact for every locally compact group. Bouziad and Filali [3] proved that $L^1(G)$ is ENAR for locally compact groups whose compact covering number is not smaller than their local character (i.e. when $G$, topologically speaking, looks more discrete than compact) and compact metrizable groups. The group algebra $L^1(G)$ was shown to be ENAR for every infinite locally compact group in [8].

In this paper, we work with ideals of $L^1(G)$ with $G$ a compact Abelian group. To describe these ideals, it is necessary to resort to duality. We denote by $\widehat {G}$ the group of all continuous homomorphisms into the multiplicative group of unimodular complex numbers, known as continuous characters. For $\mu \in M(G)$, the Fourier–Stieltjes transform of $\mu$ is the bounded function $\widehat {\mu }\colon \widehat {G}\to \mathbb {C}$ given by

\[ \widehat{\mu}(\gamma)= \int_G \langle-x, \gamma \rangle\,{\rm d}\mu (x). \]

In terms of the duality between $M(G)$ and $C(G)$, for every $\gamma \in \widehat {G}$,

\[ \widehat{\mu}(\gamma)= \langle {\check{\mu},\gamma}\rangle , \]

where for a measure $\mu \in M(G)$, we denote by $\check \mu$ the measure in $M(G)$ defined by

\[ \langle \check \mu , \phi \rangle=\langle \mu , \check \phi \rangle = \int _G \phi ({-}x)\,{\rm d}\mu(x) \qquad (\phi \in C(G)). \]

If $f\in L^1(G)$ this definition produces the function $\check f (x) = f(-x)\ (x \in G)$.

If $\mathcal {X}$ is a linear subspace of $M(G)$ and $E \subset \widehat G$, we denote by $\mathcal {X}_E$ the subspace of $\mathcal {X}$,

\[ \mathcal{X}_E = \{\mu \in \mathcal{X}: \widehat{\mu}(\gamma) =0\ \text{for}\ \gamma \in \widehat{G}\setminus E \rbrace. \]

Most prominent in our work will be the ideal $M_E(G)$ of $M(G)$ and its subspace the ideal $L_E^1(G)$ of $L^1(G)$.

1.1. Summary of results

In this paper, we address the Arens regularity properties of the ideals of $L^1(G)$ when $G$ is a compact Abelian group. These ideals are always of the form $L_E^1(G)$ for some subset $E$ of $\widehat {G}$, see e.g. [13, Theorem 38.7]. We relate the Arens regularity of $L_E^1(G)$ with the size of the subspace of $L_E^1(G)^\ast$ made of restrictions to $L_E^1(G)$ of convolutions of the form $\check {\mu } \ast \phi$ with $\mu \in M_E(G)$ and $\phi \in L^\infty (G)$.

As mentioned earlier, it is known that $L_E^1(G)$ is SAI and ENAR when $E=\widehat {G}$. On the contrary, if $E$ is finite, $L_E^1(G)$ has finite dimension and so is reflexive, and is thus Arens regular. One may therefore expect that the regularity properties of $L_E^1(G)$ improve as $E$ decreases in size. This is evidenced by the result of Ülger [26], the paper that inspired this work: if $E$ is a Riesz set, i.e. all measures on $G$ with Fourier–Stieltjes transforms supported in $E$ are absolutely continuous, then $L_E^1(G)$ is Arens regular. As an example, $L_\mathbb {N}^1(\mathbb {T})$ is Arens regular, $\mathbb {N}$ being a Riesz subset of $\mathbb {Z}$ by the F. and M. Riesz theorem.

The absolute continuity (with respect to Haar measure) of measures in $M_E(G)\ast M_E(G)$ turns out to be important in this discussion. When $M_E(G)\ast M_E(G)\subseteq L_E^1(G)$ (such a set is said to be small-2), $L_E^1(G)^{\ast \ast }$ has a large centre and so $L_E^1(G)$ cannot be SAI, unless it is reflexive, see corollary 5.6. We do not know whether $L^1_E(G)$ can be Arens regular when $E$ is not Riesz (the main question in [26]). But, we are able to prove that regularity of $L^1_E(G)$ forces $E$ to be small-2 (see corollary 5.2).

Another type of sets giving non-Arens regularity is provided by complements of Lust-Piquard sets (see below for the definition). For example, $L_{\mathbb {Z}\setminus E}^1(\mathbb {T})$ is not Arens regular when $E\subseteq \mathbb {Z}$ is the Lust-Piquard set consisting of the primes in the coset $5\mathbb {Z}+2$, see [20, Theorem 4].

Examples of $L_E^1(G)$ being SAI are provided by sets $E$ in the coset ring of $\widehat {G}$. In particular all maximal ideals of $L^1(G)$ happen to be SAI.

2. Arens regularity

In this section, we provide formal definitions for the concepts related to Arens regularity discussed in this paper.

Let $\mathscr {A}$ be a commutative Banach algebra and let $\mathscr {A}^\ast$ and $\mathscr {A}^{\ast \ast }$ be its first and second Banach duals, respectively. The multiplication of $\mathscr {A}$ can be extended naturally to $\mathscr {A}^{\ast \ast }$ in two different ways. These multiplications arise as particular cases of the abstract approach of Arens [1, 2] and can be formalized through the following three steps. For $u, v$ in $\mathscr {A}$, $\varphi$ in $\mathscr {A}^*$ and $m,n \in \mathscr {A}^{**},$ we define $\phi \cdot u, u \cdot \phi$, $m\cdot \phi, \phi \cdot m \in \mathscr {A}^*$ and $m \,\square \, n, m \diamondsuit n \in \mathscr {A}^{**}$ as follows:

\begin{align*} \langle \phi \cdot u, v\rangle& = \langle \phi, uv\rangle,\quad \langle u \cdot \phi, v\rangle= \langle \phi, vu\rangle \\ \langle m \cdot \phi, u \rangle & = \langle m, \phi \cdot u \rangle,\quad \langle \phi \cdot m, u\rangle = \langle m, u \cdot \phi \rangle\\ \langle m\,\square\, n, \phi \rangle & = \langle m\ , n \cdot \phi \rangle,\quad \langle m \diamondsuit n, \phi \rangle = \langle n, \phi \cdot m \rangle. \end{align*}

When $\,\square \,$ and $\diamondsuit$ coincide on $\mathscr {A}^{**}$, $\mathscr {A}$ is said to be Arens regular.

For any $m \in \mathscr {A}^{\ast \ast }$ the mapping $n\mapsto n\,\square \, m$ is weak$^*$–weak$^*$ continuous on $\mathscr {A}^{\ast \ast }$. However, the mapping $n\mapsto m\,\square \, n$ need not to be weak$^*$–weak$^*$ continuous. The situation is reversed for $\diamondsuit$. The left topological centre of $\mathscr {A}^{\ast \ast }$ is then defined as

\[ \mathcal{Z}(\mathscr{A}^{{\ast}{\ast}})= \{m \in \mathscr{A}^{{\ast}{\ast}}:n\mapsto m\,\square\, n\ \text{is weak}^{*}\text{--weak} ^{*}\ \text{continuous on }\mathscr{A}^{{\ast}{\ast}}\}. \]

Since we are assuming that $\mathscr {A}$ is commutative, it is easy to see that

\[ \mathcal{Z}(\mathscr{A}^{{\ast}{\ast}})=\left\{m \in \mathscr{A}^{{\ast}{\ast}}: m \,\square\, n = n\,\square\, m=m \diamondsuit n \ \text{for all }\ n \in \mathscr{A}^{{\ast}{\ast}}\right\}. \]

The algebra $\mathscr {A}$ is therefore Arens regular if and only if $\mathcal {Z}(\mathscr {A}^{\ast \ast }) = \mathscr {A}^{\ast \ast }$. Observe that $\mathscr {A}$ is always contained in $\mathcal {Z}(\mathscr {A}^{**})$. Sometimes, the elements of the centre stop here.

Definition 2.1 A commutative Banach algebra $\mathscr {A}$ is strongly Arens irregular (SAI for short) when $\mathcal {Z}(\mathscr {A}^{\ast \ast }) = \mathscr {A}$.

In [22], Pym considered the space $\mathscr {WAP(A)}$ of weakly almost periodic functionals on $\mathscr {A}$, this is the set of all $\varphi \in \mathscr {A}^*$ such that the linear map

\[ \mathscr{A} \to \mathscr{A}^*: a \mapsto a \cdot \varphi \]

is weakly compact. The functionals $\varphi \in \mathscr {WAP(A)}$ satisfy Grothendieck's double limit criterion

\[ \lim_n \lim_m \langle \varphi, a_n b_m\rangle= \lim_m \lim_n \langle \varphi, a_n b_m\rangle \]

for any pair of bounded sequences $(a_n)_n, (b_m)_m$ in $\mathscr {A}$ for which both the iterated limits exist. From this property, one may deduce that

\[ \langle {m\,\square\, n,\phi}\rangle = \langle {m\diamondsuit n,\phi}\rangle \quad\text{for every}\quad m,n\in \mathscr{A}^{{\ast}{\ast}} \]

if and only if $\phi \in \mathscr {WAP(A)}$. So, $\mathscr {A}$ is Arens regular when $\mathscr {A}^* =\mathscr {WAP(A)}$, i.e. when the quotient $\mathscr {A}^*/\mathscr {WAP(A)}$ is trivial. This is the motivation for the following definition.

Definition 2.2 A Banach algebra $\mathscr {A}$ is extremely non-Arens regular (ENAR for short) when $\mathscr {A}^*/ \mathscr {WAP(A)}$ contains a closed subspace isomorphic to $\mathscr {A}^\ast$.

The term extreme non-Arens regularity was coined by Granirer [11] to characterize a slightly more general behaviour: $\mathscr {A}$ is ENAR if the quotient space ${{\mathscr {A}^*}/{\mathscr {WAP(A)} }}$ contains a closed linear subspace which has $\mathscr {A}^*$ as a quotient, i.e. as a continuous linear image.

We have adopted here this simpler definition that is still enough to capture the extreme behaviour of many of the Banach algebras that harmonic analysis associates with a locally compact group. Clearly, ENAR in the sense of definition 2.2 implies ENAR in the sense of Granirer, but we do not know whether the two definitions are actually the same. See [5–7].

3. The structure of $L^1(G)^{\ast \ast }$ and $L_E^1(G)^{\ast \ast }$

We summarize here the structure of $L_E^1(G)^{\ast \ast }$ where $G$ is a compact Abelian group and $E\subseteq \widehat {G}$. Notation will be additive and the identities of both $G$ and $\widehat {G}$ will be denoted by 0. All the facts mentioned here are well-known when $E=\widehat {G}$, see e.g. [15]. No new insight is needed for them to hold for arbitrary $E\subseteq \widehat {G}$ but having them stated beforehand will simplify our proofs.

A good deal of the structure of $L^1(G)^{\ast \ast }$ is determined by the presence of right identities. These can be obtained as accumulation points in $L^1(G)^{\ast \ast }$ of bounded approximate identities of $L^1(G)$, which are always available (see e.g. [16, §1.3]). The first use of right identities is to bring measures on $G$ into elements of $L^1(G)^{\ast \ast }$.

For each $\mu \in M_E(G)$, one considers the convolution operator:

\[ C_\mu \colon L^1(G) \to L_E^1(G)\quad \text{given by}\ C_\mu(u) = \mu \ast u, \; u\in L^1(G). \]

Its double adjoint $C_\mu ^{\ast \ast }$ then maps $L^1(G)^{\ast \ast }$ into $L_E^1(G)^{\ast \ast }$. When necessary we will use $i\colon L_E^1(G)\to L^1(G)$ to denote the inclusion map, then $i^\ast \colon L^\infty (G)\to L_E^1(G)^\ast$ will be the restriction map and $i^{\ast \ast }\colon L_E^1(G)^{\ast \ast }\to L^1(G)^{\ast \ast }$ will be an embedding of Banach algebras. We will normally omit mentioning $i$ and $i^{\ast \ast }$ and see $L_E^1(G)^{\ast \ast }$ as an ideal of $L^1(G)^{\ast \ast }$.

With these notations, if $\mu \in M_E(G)$ and $\phi \in L^\infty (G)$ are given, a straightforward computation shows, that if $e$ is a right identity in $L^1(G)^{\ast \ast }$, then

(3.1)\begin{equation} C^{{\ast}{\ast}}_\mu(e)\cdot i^\ast(\phi)= i^\ast\left(\check{\mu} \ast \phi \right). \end{equation}

The lifting map

\[ J_e\colon M_E(G) \to L_E^1(G)^{{\ast}{\ast}} \quad\text{given by }J_e( \mu)= C_\mu^{**}(e), \]

turns out to be an algebra isomorphism onto $e \,\square \, i^{\ast \ast }(L_E^1(G)^{{\ast \ast }})$.

The algebra $L_E^1(G)$ can be seen both as an ideal in $M_E(G)$ and as an ideal in $L_E^1(G)^{\ast \ast }$ and, in that sense, it is left invariant by $J_e$, i.e.

(3.2)\begin{equation} J_e(f)=C_f^{{\ast}{\ast}} (e)=f \quad \text{for all}\ f\in L_E^1(G). \end{equation}

The canonical quotient map $R_E: L_E^1(G)^{{\ast \ast }}\to M_E(G)$, defined, for each $m\in L_E^1(G)^{\ast \ast }$, by $R_E(m) ={\left. m \vphantom {\big |} \right |_{C(G)} }$ is then a left inverse for $J_e$ and the composition $J_e \circ R_E$ is a projection. Regardless of the right identity $e$, $\ker R_E$ can always be identified with $i^\ast (C(G))^\perp$, the annihilator of the subspace $i^\ast \left (C(G)\right )$ in $L_E^1(G)^{\ast \ast }$. The projection $J_e\circ R_E$ therefore induces the decomposition

(3.3)\begin{equation} L_E^1(G)^{{\ast}{\ast}}= J_e(M_E(G))\oplus i^\ast\left(C(G)\right)^{{\perp}}. \end{equation}

So, for a given right identity $e$ of $L_E^1(G)^{\ast \ast }$, an element $m \in L_E^1(G)^{\ast \ast }$, may be uniquely decomposed as

(3.4)\begin{equation} m= C_\mu^{{\ast}{\ast}}(e)+r, \end{equation}

where $\mu \in M_E(G)$ and $r \in i^\ast (C(G))^\perp$.

The above decomposition becomes handier if one observes that the elements of $i^\ast \left (C(G)\right )^{\perp }$ are left annihilators of $L_E^1(G)^{\ast \ast }$. Indeed, for $r\in i^\ast \left (C(G)\right )^{\perp }$, if $m\in L_E^1(G)^{\ast \ast }$ is such that $m=\sigma \left (L_E^1(G)^{\ast \ast },L_E^1(G)^\ast \right )-\lim _\alpha u_\alpha$, with $u_\alpha \in L_E^1(G)$, and $\phi \in L^\infty (G)$, then

(3.5)\begin{align} \langle {m\,\square\, r,i^\ast(\phi)}\rangle & =\langle {i^{{\ast}{\ast}}\left(m\,\square\, r\right),\phi}\rangle \nonumber\\ & =\lim_\alpha \langle {u_\alpha,i^{{\ast}{\ast}}(r)\cdot\phi}\rangle \nonumber\\ & =\lim_\alpha \langle {r,i^\ast\left({\!\check u_\alpha\!}\;\ast \phi\right)}\rangle {=}0, \end{align}

where the last identity follows from ${\!\check u_\alpha \!}\;\ast \phi \in C(G)$.

Next, as we see, left annihilators can actually be used to characterize Arens regularity. We first need a definition.

Definition 3.1 Let $G$ be a compact Abelian group, $E \subseteq \widehat { G}$ and put

\[ S=i^\ast(C(G))^\perp \,\square\, L^1_E(G)^{**}. \]

Note that for any fixed right identity $e\in L^1(G)^{\ast \ast }$, the set $S$ is given by

\[ S=\left\{ r\,\square\, C_\mu^{{\ast}{\ast}}(e)\colon r\in i^\ast(C(G))^\perp \text{ and }\mu \in M_E(G)\right\}. \]

Observe as well that, $S\cap L_E^1(G)=\{0\}$. To see this, one can fix a right identity $e\in L^1(G)^{\ast \ast }$ and a bounded approximate identity $(u_\alpha )_\alpha$ in $L^1(G)$. Then, if $r\,\square \, C_\mu ^{\ast \ast }(e)\in S\cap L_E^1(G)$, we have that

\[ r\,\square\, C_\mu^{{\ast}{\ast}}(e)= \lim_\alpha u_\alpha\ast \left(r\,\square\, C_\mu^{{\ast}{\ast}}(e)\right)=0. \]

Theorem 3.2 Let $G$ be a compact Abelian group and let $E \subseteq \widehat { G}$. Then, $L^1_E(G)$ is Arens regular if and only if $S=\{0\}$.

Proof. Since $S\neq \{0\}$ immediately implies that $L_E^1(G)^{{\ast \ast }}$ is not commutative, by the preceding paragraph, we only need to show that $S=\{0\}$ implies that $L^1_E(G)$ is Arens regular.

Assume $S=\{0\}$ and fix a right identity $e$ in $L^1_E(G)^{**}$ and let $C_{\mu _1}^{\ast \ast }(e) +s_1$ and $C_{\mu _2}^{\ast \ast }(e)+s_2$ be arbitrary in $L_E^1(G)^{\ast \ast }$, with $s_1,s_2\in i^\ast (C(G))^\perp$ and $\mu _1,\mu _2\in M_E(G)$. Then,

\begin{align*} \left(C_{\mu_1}^{{\ast}{\ast}}(e)+s_1\right)\,\square\, \left(C_{\mu_2}^{{\ast}{\ast}}(e)+s_2\right)& =C_{\mu_1\ast\mu_2}^{{\ast}{\ast}}(e)\\ & = C_{\mu_2\ast\mu_1}^{{\ast}{\ast}}(e)\\ & = \left(C_{\mu_2}^{{\ast}{\ast}}(e)+s_2\right)\,\square\, \left(C_{\mu_1}^{{\ast}{\ast}}(e)+s_1\right), \end{align*}

and so $L^1_E(G)^{**}$ is commutative, i.e. $L^1_E(G)$ is Arens regular.

We wish to record the following lemma, a restatement of Theorem 3.3(v) of [15], for later use.

Lemma 3.3 Let $G$ be a compact Abelian group. Consider $E \subseteq \widehat {G}$ and $\mu \in M_E(G)$. If for every pair $e$ and $f$ of right identities in $L^1(G)^{\ast \ast }$, $C_\mu ^{\ast \ast }(e)=C_\mu ^{\ast \ast }(f)$, then $\mu \in L^1(G)$.

Proof. Suppose that $\mu \in M_E(G)$ but $\mu \notin L^1(G)$, we can then find $\phi \in L^\infty (G)$ such that $\check {\mu }\ast \phi$ is not continuous, see [13, Theorem 35.13]. By Lemma 2.3 of [15] we can find two different right identities $f_1, f_2\in L^1(G)^{\ast \ast }$ such that $\langle {f_1,\check {\mu }\ast \phi }\rangle {>}\neq \langle {f_2,\check {\mu }\ast \phi }\rangle$. Since

\[ \langle {C_\mu^{{\ast}{\ast}}(f_i),\phi}\rangle {=}\langle {f_i, \check{\mu}\ast \phi}\rangle ,\ i=1,2, \]

we deduce that $C_\mu ^{\ast \ast }(f_1)\neq C_\mu ^{\ast \ast }(f_2)$, a contradiction with our hypotheses.

4. Special subsets of $\widehat {G}$

We describe here the sets $E\subseteq \widehat {G}$ that lead to the concrete ideals $L_E^1(G)$ that will appear later in the paper.

We first recall that an invariant mean $M$ on $L^\infty (G)$ is a linear functional on $L^\infty (G)$ such that $\langle M, 1\rangle = \Vert M\Vert = 1$ and, for each $\phi \in L^\infty (G)$ and each $x \in G$, $\langle M, L_x \phi \rangle = \langle M, \phi \rangle$ where $L_x$ is the translation operator by $x$. An invariant mean that is always available is the one produced by Haar measure: $\phi \mapsto \int \phi (x)\,{\rm d}x$. If $G$ is compact, $L^\infty (G)$ always has other invariant means [23] but all them have the same effect on some functions. We say then that a function $\phi \in L^\infty (G)$ has a unique invariant mean if $\langle M ,\phi \rangle = \int \phi (x)\,{\rm d}x$ for every invariant mean $M$ on $L^\infty (G)$.

Definition 4.1 Let $G$ be a compact Abelian group and $E \subset \widehat G$. We say that $E$ is a

1. (i) Sidon set, if every $f \in C_E(G)$ has an absolutely convergent Fourier series.

2. (ii) $\Lambda (p)$-set, $p>0$, if there are $0< q< p$ and $C>0$ such that $\lVert f \rVert _p\leq C \lVert f \rVert _q$, for every trigonometric polynomial, $f=\sum _{k=1}^n c_{k} \chi _k$, with $\chi _1, \ldots, \chi _n \in E$.

3. (iii) Rosenthal set, if $L^\infty _E(G) = C_E(G)$.

4. (iv) Lust-Piquard set, if $\gamma \phi$ has a unique invariant mean for every $\phi \in L^\infty _E(G)$ and every $\gamma \in \widehat G$. We say in this case that $\phi$ is totally ergodic.

5. (v) Riesz set, if $M_E(G) = L^1_E(G)$.

6. (vi) Small-2 set, if $\mu \ast \mu \in L^1_E(G)$ for every $\mu \in M_E(G)$.

As pointed out to us by the referee, with the identity $2\mu \ast \nu =(\mu +\nu )^2-\mu ^2-\nu ^2$, one quickly checks that $\mu \ast \nu \in L^1_E(G)$ for every $\mu, \nu \in M_E(G)$ if and only if $\mu \ast \mu \in L^1_E(G)$ for every $\mu \in M_E(G)$ (i.e. if $E\subseteq \widehat G$ is a small-2 set).

Sidon sets are Rosenthal, see, e.g. [9, Corollary 6.2.5], and Rosenthal sets are Lust-Piquard (as continuous functions always have a unique invariant mean). Lust-Piquard sets are in turn always Riesz (see [18]) and Riesz sets are, obviously, small-2.

On the contrary, Sidon sets are $\Lambda (p)$ for every $p>0$ and $\Lambda (p)$ sets are $\Lambda (q)$ for every $q< p$ [13, Section 37]. It is a result of Hare [12] that a $\Lambda (p)$ is always a $\Lambda (q)$ set for some $q>p$. The following is a consequence that is important in our context.

Theorem 4.2 (Corollary in [12])

Let $G$ be a compact Abelian group and let $E\subset \widehat {G}$. The Banach space $L_E^1(G)$ is reflexive if and only if $E$ is a $\Lambda (1)$ set.

It follows from this Corollary that $\Lambda (1)$-sets are necessarily Riesz. For, if $\mu \in M_E(G)\setminus L_E^1(G)$ then $J_e(\mu )\in e\,\square \, L_E^1(G)^{{\ast \ast }}\setminus L_E^1(G)$, since $J_e$ is an isomorphism that fixes $L_E^1(G)$.

The preceding remarks are summarized in figure 1.

Figure 1. Relations between properties of $E\subset \widehat {G}$, $G$ compact and Abelian.

To the authors’ knowledge, it is still unknown whether small-2 sets are Riesz. As already mentioned by Ülger in [26, p. 273], this is a long-standing open problem that goes back to Glicksberg [10]. It might therefore happen that the classes defined in items (v)–(vi) above are actually the same.

Since $L_E^1(G)$ is Arens regular when $E$ is Riesz (see [26] or corollary 6.3) we will not be interested in $L_E^1(G)$ for $E$ in any class contained in that Riesz sets. However, sets $E$ whose complement $\widehat {G}\setminus E$ belongs to such a class will be of interest in § 7.2, especially after one learns that the union of a Riesz set and Lust-Piquard set is Riesz [19], and hence that complements of Lust-Piquard sets are never Riesz.

We turn now our attention to small-2 sets.

5. Small-2 sets

We start with the following result of Ülger which reveals the relevance of non-small-2 sets in the analysis of Arens regularity.

Theorem 5.1 (Theorem 2.2 of [25])

Let $\mathscr {A}$ be a commutative, semisimple, weakly sequentially complete and completely continuous Banach algebra, then an element $m \in \mathscr {A}^{\ast \ast }$ is in the centre of $\mathscr {A}$ if and only if $m \,\square \, \mathscr {A}^{\ast \ast }\subseteq \mathscr {A}$ and $\mathscr {A}^{\ast \ast } \,\square \, m \subseteq \mathscr {A}$.

Corollary 5.2 Let $G$ be a compact Abelian group and assume that $E\subseteq \widehat {G}$ is not a small-2 set. For every pair $\mu _1,\mu _2\in M_E(G)$ such that $\mu _1\ast \mu _2\notin L_E^1(G)$ and every right identity $e$ of $L^1(G)^{\ast \ast }$, we have that neither $C_{\mu _1}^{{\ast \ast }}(e)$ nor $C_{\mu _2}^{{\ast \ast }}(e)$ is in $\mathcal {Z}( L^1_E(G) ^{**})$.

Proof. Let $\mu _1, \mu _2 \in M (G)$ such that $\mu _1\ast \mu _2 \notin L^1_E(G)$. Towards a contradiction, assume that $C_{\mu _1}^{{\ast \ast }}(e) \in \mathcal {Z}( L^1_E(G) ^{**})$. By theorem 5.1:

\[ C_{\mu_1\ast \mu_2}^{{\ast{\ast}}}(e) =C_{\mu_1}^{{\ast{\ast}}}(e) \,\square\, C_{\mu_2}^{{\ast{\ast}}}(e) \in L^1_E(G). \]

Since $R_E$ is a left inverse of $J_e$, this is a contradiction.

Remark 5.3 With corollary 5.2, the last trivial implication

\[ E\;\text{is Riesz} \Longrightarrow E\;\text{is small-2} \]

in figure 1 may now be split into two non-trivial implications:

\[ E\ \text{is Riesz} \Longrightarrow L_E^1(G)\ \text{is Arens regular} \Longrightarrow E\ \text{is small-2}. \]

We shall further see in §7 that $L_E^1(G)$ is even ENAR when $E$ is not a small-2 set.

We proceed now to find non-trivial elements in the centre of $L_E^1(G)^{\ast \ast }$, when $E$ is a small-2 set. Recall that the set $S$ was defined in §3 as $S=i^\ast (C(G))^\perp \,\square \, L^1_E(G)^{**}$.

Theorem 5.4 Let $G$ be a compact Abelian group and let $E \subseteq \widehat {G}$ be a small 2-set. Then, $S\subseteq \mathcal {Z}(L_E^1(G)^{\ast \ast })$.

Proof. We first fix a right identity $e\in L^1(G)^{\ast \ast }$.

Let $r \in i^\ast (C(G))^\perp$ and $\mu \in M_E(G)$. Put $p= r\,\square \, C_\mu ^{\ast \ast }(e)$. If $q=C_\sigma ^{\ast \ast }(e)+s\in L_E^1(G)^{\ast \ast }$, with $s\in i^\ast (C(G))^\perp$ and $\sigma \in M_E(G)$, then $q\,\square \, p=0$, as $r$ is a left annihilator, (3.5). Since $s$ is also left annihilator and $C_\mu ^{\ast \ast }(e)\,\square \, C_\sigma ^{\ast \ast }(e) \in \mathcal {Z}(L_E^1(G)^{\ast \ast })$, for $\mu \ast \sigma \in L_E^1(G)$ since $E$ is a small-2 set, one gets:

\[ p\,\square\, q= r\,\square\, C_\mu^{{\ast}{\ast}}(e)\,\square\, C_\sigma^{{\ast}{\ast}}(e)=r\,\square\, C_{\mu\ast\sigma}^{{\ast}{\ast}}(e)=0. \]

Hence, $p\in \mathcal {Z}(L_E^1(G)^{\ast \ast })$, as needed.

We choose to express the main consequence of this theorem in two equivalent ways.

Corollary 5.5 Let $G$ be a compact Abelian group and let $E \subseteq \widehat {G}$ be a small-2 set. Then, $L^1_E(G)$ is SAI if and only if it is reflexive.

Corollary 5.6 Let $G$ be a compact Abelian group and let $E \subseteq \widehat {G}$. If $E$ is a small 2-set that is not $\Lambda (1)$, then $L_E^1(G)$ is not SAI.

Proof. Suppose that $E$ is small-2 set with $L^1_E(G)$ SAI. Since $S\cap L_E^1(G)=\{0\}$ (see the remarks after definition 3.1), theorem 5.4 implies that $S$ must be trivial. Theorem 3.2 implies then that $L^1_E(G)$ is Arens regular, and so it must be reflexive, i.e. $E$ must be $\Lambda (1)$ (theorem 4.2).

6. The role of $M_{-E}(G)\ast L^\infty (G)$

Many Arens regularity properties of $L_E^1(G)^{\ast \ast }$ can be described through the size of the subset $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right )$.

We begin with the following observation.

Lemma 6.1 Let $G$ be a compact Abelian group and let $E \subseteq \widehat G$. Then,

\[ i^\ast\left(M_{{-}E}(G)\ast L^\infty(G)\right) \subseteq \overline{i^*(C(G)) }\quad \text{if and only if }\quad i^*(C(G))^\perp{\subseteq} \mathcal{Z}(L^1_E(G)^{**}). \]

Proof. Assume first that $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right ) \subseteq \overline {i^*(C(G))}$ and let $r \in i^*(C(G))^\perp$. Then, for each $\mu \in M_E(G)$ and $\phi \in L^\infty (G)$, $i^\ast \left (\check \mu \ast \phi \right )\in \overline {i^*(C(G))}$ and we have, by (3.1), that

(6.1)\begin{equation} \langle {r\,\square\, C^{**}_\mu (e) , \phi}\rangle {=} \langle r , i^\ast(\check \mu \ast \phi)\rangle = 0. \end{equation}

Thus, if $m\in L_E^1(G)^{\ast \ast }$ is decomposed as in (3.4) $m=C_\mu ^{\ast \ast }(e)+s$, with $e$ being some right identity in $L^1(G)^{\ast \ast }$, $\mu \in M_E(G)$ and $s\in i^\ast (C(G))^\perp$, we have, using that elements of $i^\ast (C(G))^\perp$ are left annihilators of $L_E^1(G)^{\ast \ast }$, (3.5), that

\[ r\,\square\, m=r\,\square\, C^{**}_\mu (e) =0=m\,\square\, r. \]

Hence, $r\in \mathcal {Z}\left (L_E^1(G)^{\ast \ast }\right )$.

For the converse, assume that $i^\ast (C(G))^\perp \subseteq \mathcal {Z}(L_E^1(G)^{\ast \ast })$ and let $\mu \in M_{-E}(G)$ and $\phi \in L^\infty (G)$. Then, for each $r \in i^*(C(G))^\perp$, we have

\[ \langle { r, i^*(\check \mu \ast \phi)}\rangle {=} \langle {r \,\square\, C^{{\ast{\ast}}}_\mu (e), \phi}\rangle {=} \langle { C^{{\ast}{\ast}}_\mu(e)\,\square\, r, \phi}\rangle {=}0, \]

where the last equalities follow from $r$ being in the centre of $L_E^1(G)^{\ast \ast }$ (by hypothesis) and a left annihilator in $L_E^1(G)^{\ast \ast }$. Hence, $i^*(\check \mu \ast \phi ) \in i^*(C(G))^{\perp \perp }= \overline {i^*(C(G))}$.

Theorem 6.2 Let $G$ be a compact Abelian group and let $E \subseteq \widehat G$. Then$:$

1. (i) $L^1_E(G)$ is Arens regular if and only if $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right ) \subseteq \overline {i^\ast (C(G))}.$

2. (ii) $L^1_E(G)$ is SAI if and only if the linear span of $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right )$ is dense in $L_E^1(G)^\ast$.

Proof. We start with statement (i). Assume that $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right ) \subseteq \overline {i^\ast (C(G))}$. Lemma 6.1 then shows that $\overline {i^\ast (C(G))}^\perp$ is contained in $\mathcal {Z}\left (L_E^1(G)^{\ast \ast }\right )$.

Let $e$ be a right identity in $L_E^1(G)^{\ast \ast }$. If $m_1=C_{\mu _1}^{\ast \ast }(e)+r_1$ and $m_2=C_{\mu _2}^{\ast \ast }(e)+r_2$ are two arbitrary elements of $L_E^1(G)^{\ast \ast }$, decomposed following (3.4), and we use that $r_1$ and $r_2$ are left annihilators, (3.5):

\[ m_1\,\square\, m_2=C_{\mu_1\ast \mu_2}^{{\ast}{\ast}}(e)=C_{\mu_2\ast \mu_1}^{{\ast}{\ast}} (e)=m_2\,\square\, m_1, \]

proving that $L_E^1(G)$ is Arens regular.

Lemma 6.1 proves the converse statement.

We now prove statement (ii). Assume first that the linear span of $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right )$ is dense in $L_E^1(G)^\ast$ and let $m\in \mathcal {Z}\left (L^1_E(G)^{{\ast \ast }}\right )$. Pick a right identity $e\in L^1(G)^{\ast \ast }$ and let $m=C_\mu ^{\ast \ast }(e) +r$ be a decomposition of $m$ following (3.4).

Take $\nu \in M_E(G)$ and $\phi \in L^\infty (G)$, then $\langle {m,i^\ast (\check {\nu }\ast \phi )}\rangle =\langle {m\,\square \, C_\nu ^{\ast \ast }(e),\phi }\rangle$. Since $m$ is in the centre, and $r$ is a left annihilator, (3.5):

\begin{align*} \langle {m,i^\ast\left(\check{\nu}\ast \phi\right)}\rangle & =\langle { C_\nu^{{\ast}{\ast}}(e)\,\square\, \left(C_\mu^{{\ast}{\ast}}(e)+r\right),\phi}\rangle \\ & =\langle {C_\mu^{{\ast}{\ast}}(e), i^\ast\left(\check{\nu}\ast \phi\right)}\rangle . \end{align*}

Since the linear span of $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right )$ is dense in $L_E^1(G)^\ast$, it follows that $m=C_\mu ^{\ast \ast }(e)$ and this for every right identity $e$. It follows from lemma 3.3 that $\mu \in L_E^1(G)$ and we conclude that $L_E^1(G)$ is SAI.

Assume now that $L_E^1(G)$ is SAI. Let $r \in L_E^1(G)^{\ast \ast }$ be such that $r\in \left ( i^\ast (M_{-E}(G)\ast L^\infty (G))\right )^\perp$. Then, if $m=C_\mu ^{\ast \ast }(e)+s\in L_E^1(G)^{\ast \ast }$, with $\mu \in M_E(G)$ and $s\in i^\ast (C(G))^\perp$, and $\phi \in L^\infty (G)$:

\[ \langle {r\,\square\, m,i^\ast(\phi)}\rangle {=}\langle {r,i^\ast(\check{\mu}\ast \phi)}\rangle {=}0. \]

This means that $r\,\square \, m=0$ and, hence, that $r\in \mathcal {Z}\left (L_E^1(G)^{\ast \ast }\right )$. Since $L_E^1(G)$ is SAI, $L_E^1(G)\cap i^\ast (C(G))^\perp =\{0\}$ and $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right )^\perp \subseteq i^\ast (C(G))^\perp$, we conclude that $r=0$. Having shown that $i^\ast \left (M_{-E}(G)\ast L^\infty (G)\right )^{\perp }=\{0\}$, the denseness of the linear span of $i^\ast (M_{-E}(G)\ast L^\infty (G))$ in $L_E^1(G)^\ast$ is a simple consequence of the Hahn–Banach theorem.

Theorem 6.2 immediately implies Ülger's theorem.

Corollary 6.3 ([26])

Let $G$ be a compact Abelian group and let $E \subseteq \widehat G$. If $E$ is a Riesz set, then $L^1_E(G)$ is Arens regular.

Proof. Simply apply (i) of theorem 6.2, taking into account that $L^1(G)\ast L^\infty (G)\subseteq C(G)$.

Note that corollary 6.3 also follows from theorem 3.2 since $S$ is trivial when $E$ is a Riesz set.

7. The irregular side

The easy way to show that $L_E^1(G)$ is SAI is to require the presence of a bounded approximate identity. By [16, Corollary 5.6.2], this happens if and only if $E \in \Omega _{\widehat G}$, where $\Omega _{\widehat G}$ denotes the Boolean ring generated by the left cosets of subgroups of $\widehat G$, known as the coset ring of $\widehat G$. This is a consequence of P. J. Cohen's theorem to the effect that for a subset $E$ of $\widehat G$, ${\bf 1}_E$ is in $B(\widehat G)$, the Fourier–Stieltjes algebra on $\widehat G$, if and only if $E \in \Omega _{\widehat G}$ (see [24, Theorem 3.1.3] for an exposition of this result).

With these facts in mind, it is an immediate consequence of statement (ii) of theorem 6.2 that $L_E^1(G)$ is SAI if $E\in \Omega _{\widehat {G}}$. It is enough to observe that for $\mu \in M(G)$ with $\widehat {\mu }= \large {\mathbf {1}}_E$, one has that $i^\ast (\mu \ast \phi )=i^\ast (\phi )$.

Corollary 7.1 Let $G$ be a compact Abelian group and let $E \in \Omega _{\widehat G}$. Then, $L^1_E(G)$ is SAI. In particular, $L^1_{\widehat {G}\setminus F}$ is SAI if $F$ is finite.

7.1. $L_E^1(G)$ is ENAR if $E$ is not a small-2 set

Under conditions similar to those of theorem 5.1 we see that the set $\mathcal {WAP}(\mathscr {A})$ can be as small as possible. For this we need to produce approximations of triangles in $\mathscr {A}$ that are $\ell ^1$-sets, as done in [6]. We recall here the main concepts and results developed in that study. To avoid further technicalities, we will restrict ourselves to the countable case.

Definition 7.2 Let $\mathscr {A}$ be a Banach algebra. Consider two sequences in $\mathscr {A}$, $A= \{a_n : n \in \mathbb {N}\}$ and $B= \{b_n : n\in \mathbb {N} \}$. Then:

1. (i) The sets

   \[ T^{u}_{AB}=\left\{a_n b_m \colon n,m\in \mathbb{N},\; n\leq m\right\}\quad \text{and} \quad T^{l}_{AB}=\left\{a_n b_m \colon n, m \in \mathbb{N}, m\leq n\right\} \]
   are called, respectively, the upper and lower triangles defined by $A$ and $B$.

2. (ii) A set $X \subseteq \mathscr {A}$ is said to approximate segments in $T^{u}_{AB}$, if it can be enumerated as

   \[ X=\left\{x_{nm} \colon n,\, m\in \mathbb{N}, \; n\leq m\right\}, \]
   and for each $n\in \mathbb {N}$
   \[ \lim_{m}\lVert x_{nm} - a_n b_m \rVert = 0. \]

3. (iii) A set $X \subseteq \mathscr {A}$ is said to approximate segments in $T^{l}_{AB}$, if it can be enumerated as

   \[ X=\left\{x_{nm} \colon n,\, m \in \mathbb{N},\;m\leq n\right\}, \]
   and for each $m\in \mathbb {N}$,
   \[ \lim_{n}\lVert x_{nm} - a_nb_m \rVert= 0. \]

4. (iv) A double indexed subset $X=\{x_{nm} : n,\, m\in \mathbb {N}\}$ is vertically injective if the identity $x_{nm} = x_{n^\prime m^\prime }$ implies $m = m^\prime$. If $x_{nm} = x_{n^\prime m^\prime }$ implies $n = n^\prime$ we say that $X$ is horizontally injective.

Definition 7.3 Let $E$ be a normed space. A bounded sequence $B$ is an $\ell ^1$-base in $E$, with constant $K>0$, when, for every choice of scalars, $z_1, \ldots, z_p$ and of elements $a_1, \ldots, a_p\in B$, the following inequality holds:

\[ \left\lVert \sum_{n=1} ^{p} z_n a_{n} \right\rVert \geq K \sum_{n=1} ^{p}|z_n| . \]

Theorem 7.4 (Corollary 3.10 of [6])

Let $\mathscr {A}$ be a Banach algebra. Suppose that $\mathscr {A}$ contains two bounded sequences $A$ and $B$ and two disjoint sets $X_1$ and $X_2$ with the following properties$:$

1. (i) $X=X_1\cup X_2$ is an $\ell ^1$-base in $\mathscr {A}$.

2. (ii) $X_1$ and $X_2$ approximate segments in $T_{AB}^{u}$ and $T_{AB}^{l}$, respectively.

3. (iii) $X_1$ is vertically injective and $X_2$ is horizontally injective.

Then, there is a bounded linear map of $\mathscr {A}^\ast /\mathcal {WAP}(\mathscr {A})$ onto $\ell ^\infty$. If, in addition, $\mathscr {A}$ is separable, then $\mathscr {A}$ is ENAR.

Theorem 7.5 Let $\mathscr {A}$ be a commutative weakly sequentially complete Banach algebra that is an ideal in $\mathscr {A}^{\ast \ast }$. If $\mathscr {A}$ contains a sequential multiplier bounded approximate identity (MBAI) $(e_n)_n$ and there are $p,q \in \mathscr {A}^{\ast \ast }$ such that $(e_n \,\square \, p\,\square \, q)_n$ does not converge weakly, then $\mathscr {A}^\ast /\mathcal {WAP}(\mathscr {A})$ is not separable. If $\mathscr {A}$ is in addition separable, then $\mathscr {A}$ is ENAR.

Proof. We start by observing that the sequence $(e_n\,\square \, p\,\square \, q)_n$ cannot have weakly Cauchy subsequences. If $(e_{n(k)}\,\square \, p\,\square \, q)_k$ was such, weak sequential completeness of $\mathscr {A}$ would produce $a\in \mathscr {A}$ such that, in the $\sigma (\mathscr {A}, \mathscr {A}^\ast )$-topology, $\lim _k e_{n(k)}\,\square \, p\,\square \, q=a$. Now, for any subnet $(e_{n(\beta )}\,\square \, p\,\square \, q)_\beta$ of the sequence $(e_n\,\square \, p\,\square \, q)_n$, we have that, in the $\sigma (\mathscr {A}, \mathscr {A}^\ast )$-topology, which on $A$ coincides with the $\sigma (\mathscr {A}^{\ast \ast },\mathscr {A}^\ast )$:

\begin{align*} \lim_\beta e_{n(\beta)} \,\square\, p\,\square\, q & =\lim_\beta \lim_k e_{n(k)}\left( e_{n(\beta)} \,\square\, p\,\square\, q\right)\\ & \quad\ (\text{multiplication by}\ e_{n(\beta)} \text{is weak}^\ast\text{-continuous)}\\ & =\lim_\beta e_{n(\beta)} \left(\lim_k e_{n(k)}\,\square\, p\,\square\, q\right) \\ & =\lim_{\beta} e_{n(\beta)} a=a, \end{align*}

showing that $a$ is the only accumulation point of $(e_n\,\square \, p\,\square \, q)$ and, hence that the sequence $(e_n\,\square \, p\,\square \, q)$ is convergent. Since this goes against our assumption, we can invoke Rosenthal's theorem to deduce that there is a subsequence of $(e_n\,\square \, p\,\square \, q)_n$ that is an $\ell ^1$-base. We denote this $\ell ^1$-base again as $(e_n\,\square \, p\,\square \, q)_n$.

Now put

\begin{align*} A& =\left\{e_{2n} \,\square\, p \colon n\in \mathbb{N}\right\}, \quad \text{ and }\\ B& =\left\{ e_{2n+1} \,\square\, q \colon n\in \mathbb{N}\right\} \end{align*}

and define, for each $m,n \in \mathbb {N}$, $x_{nm}= e_{2m+1} \,\square \, (p \,\square \, q)$, if $m < n$ and $x_{nm}= e_{2n} \,\square \, (p \,\square \, q)$, if $n < m$. If we let

\begin{align*} X_1 & =\{x_{nm}: m,n \in \mathbb{N}, n< m\} {\text{ and }}\\ X_2& =\{x_{nm}: m,n \in \mathbb{N}, m< n\}. \end{align*}

Then, we have

\begin{align*} & \lim_{m } \left\lVert x_{nm}-(e_{2n}\,\square\, p)(e_{2m+1}\,\square\, q) \right\rVert\\ & \quad= \lim_{m} \left\lVert e_{2n} \,\square\, (p \,\square\, q) -(e_{2n} \,\square\, p) (e_{2m+1} \,\square\, q) \right\rVert\\ & \quad= \lim_{m} \left\lVert e_{2n} \,\square\, (p \,\square\, q) -e_{2m+1} \,\square\,(e_{2n} \,\square\, (p \,\square\, q) ) \right\rVert =0. \end{align*}

for each $n \in \mathbb {N}$. A symmetric computation yields, for each $m \in \mathbb {N}$:

\begin{align*} & \lim_{n } \left\lVert x_{nm}-(e_{2n}\,\square\, p)(e_{2m+1}\,\square\, q) \right\rVert\\& \quad =\lim_{n}\left\lVert e_{2m+1} \,\square\, (p \,\square\, q) -(e_{2n}\,\square\, p)(e_{2m+1}\,\square\, q) \right\rVert=0. \end{align*}

The sets $X_1, X_2$ therefore approximate the segments in $T^{u}_{AB}$ and $T^{l}_{AB},$ respectively.

Since $(e_n \,\square \, (p \,\square \, q))$ is an $\ell ^1$-base, we have that $e_n \,\square \, (p \,\square \, q)\neq e_{n^\prime } \,\square \, (p \,\square \, q)$ when $n \neq n^\prime$ and, hence, $X_1$ is vertically injective and $X_2$ is horizontally injective.

Theorem 7.4 can then be applied to deduce that $\mathscr {A}$ is ENAR.

While $L^1(G)$ always has bounded approximate identities whose accumulation points in $L^1(G)^{\ast \ast }$ are right identities, $L_E^1(G)$ may well fail to have any. Approximate identities that are bounded in the multiplier norm (MBAIs) are however always available. This is proved in [27, Proposition 1]. Since our $G$ is Abelian, the proof of this result is simple and follows from Plancherel's theorem. We include the proof for convenience.

Lemma 7.6 Let $G$ be a compact Abelian group and $E \subset \widehat {G}$. Then, $L^1_E(G)$ contains a net $(e_\alpha )_{\alpha \in \Lambda }$ with the following properties$:$

1. (i) If $u\in L_E^1(G)$, then $\lim _\alpha \lVert e_\alpha \ast u-u \rVert =0$, so that $(e_\alpha )_{\alpha \in \Lambda }$ is an approximate identity.

2. (ii) If $u\in L_E^1(G)$, then $\lVert e_\alpha \ast u \rVert \leq \lVert u \rVert$ for every $\alpha \in \Lambda$, so that $(e_\alpha )_{\alpha \in \Lambda }$ is an MBAI.

3. (iii) For every $\mu \in M_E(G)$, $\lim _\alpha e_\alpha \ast \mu =\mu$ in $\sigma ( M(G) ,C(G) )$.

Proof. Let $(u_\alpha )_\alpha$ be an approximate identity that is made of continuous functions of norm 1 (see e.g. [16, § 1.3]). By Plancherel's theorem, $(\widehat u_\alpha ) \subseteq \ell ^2(\widehat G)$. So $(\widehat u_\alpha \cdot \large {\mathbf {1}}_E) \subseteq \ell ^2(\widehat G)$. Let now $(e_\alpha )$ be a net in $L^2( G)$ such that

\[ \widehat e_\alpha=\widehat u_\alpha \cdot 1_E \quad (\alpha \in I). \]

Then, for each $\mu \in M_E(G)$, we have

\[ (e_\alpha \ast \mu) \widehat{}= \widehat e_\alpha \cdot \widehat\mu = \widehat u_\alpha \cdot 1_E \cdot \widehat\mu=(u_\alpha \ast \mu)~\widehat{}. \]

Thus, by the uniqueness theorem, $e_\alpha \ast \mu = u_\alpha \ast \mu$ for each $\alpha \in I$. From this all the assertions of the lemma follow easily.

Corollary 7.7 Let $G$ be a metrizable compact Abelian group. If $E \subset \widehat {G}$ is not a small-2 set, then $L^1_E(G)$ is ENAR.

Proof. The algebra $L_E^1(G)$ is commutative, weakly sequentially complete and has a sequential MBAI $(e_n)$, as shown in lemma 7.6. By (iii) of lemma 7.6, $(e_n\,\square \, C_\mu ^{\ast \ast }(e))_n=(e_n\ast \mu )_n$, $\mu \in M_E(G)$, can only converge (weakly) to $\mu.$ By weak sequential completeness, this implies that the sequence $(e_n\,\square \, C_\mu ^{\ast \ast }(e))_n$ cannot be weakly convergent unless $\mu \in L_E^1 (G)$. But, since $E$ is not small-2, one can find a measure $\mu \in M_E(G)$ such that $\mu ^2 \notin L_E^1 (G)$ so that the sequence $(e_n\,\square \, C_{\mu }^{\ast \ast }(e)\,\square \, C_{\mu }^{\ast \ast }(e))_n$ does not converge weakly. Apply now theorem 7.5.

7.2. Complements of Lust-Piquard sets

Certain thin subsets of $\widehat {G}$ have a complement $E$ that may not be very large, but is large enough to ensure that $L_E^1(G)$ is not Arens regular. Complements of Lust-Piquard sets can be regarded as such.

Lemma 7.8 Let $G$ be a compact metrizable Abelian group. If $\widehat {G} \setminus E$ is a Lust-Piquard set, then for each measure $\mu \in M_E(G) \setminus L^1(G)$, there exists $\phi \in L^\infty (G)$ such that $i^* (\check \mu \ast \phi ) \notin \overline { i^*(C(G))}$.

Proof. Notice first that, by [18, Proposition 2], there exists $\phi \in L^\infty (G)$ such that $\check \mu \ast \phi$ is not totally ergodic. Fix such a $\phi \in L^\infty (G)$. Towards a contradiction, assume that there is a sequence $(\psi _n)$ in $C(G)$ such that

\[ \lim_n i^*(\psi_n) = i^*(\check \mu \ast \phi). \]

Then, since the restriction mapping $i^\ast$ is a quotient map, one can find (see, e.g. [21, Theorem 1.7.7]) a sequence $(\xi _n)$ in $L^\infty (G)$ and $\xi \in L^\infty (G)$ such that, for each $n\in \mathbb {N} , i^*(\psi _n) = i^*(\xi _n)$, and $\lim _n \xi _n = \xi$. The equality $i^\ast (\psi _n) = i^*(\xi _n)$ entails that $\psi _n - \xi _n \in L^\infty _{- \widehat {G}\setminus E}(G)$, so that ($-\widehat {G}\setminus E$ is a Lust-Piquard set) $\psi _n - \xi _n$ is totally ergodic. Since $\psi _n$ is continuous, hence totally ergodic, we deduce that $\xi _n$ is totally ergodic for each $n \in \mathbb {N}$. Thus, $\xi$ is totally ergodic. Indeed, for $\gamma \in \widehat G$, $\lim _n\widehat {\xi _n}(-\gamma )=\widehat {\xi }(-\gamma )$, so for each invariant mean $M$, we have, using that, by total ergodicity, $\langle M,\gamma \xi _n\rangle =\widehat {\xi _n}(-\gamma )$:

\[ \langle M , \gamma \xi \rangle = \lim_n \langle M , \gamma \xi _n \rangle =\lim_n \hat \xi_n (-\gamma) =\hat \xi (-\gamma), \]

so $\xi$ is totally ergodic. On the contrary, $i^*(\check \mu \ast \phi ) = i^*(\xi )$ and, hence, $\check \mu \ast \phi - \xi \in L^\infty _{- \widehat {G}\setminus E}(G)$. So $\check \mu \ast \phi - \xi$ is totally ergodic, and, therefore, $\check \mu \ast \phi$ is totally ergodic, a contradiction. We conclude that $i^\ast (\check {\mu }\ast \phi )\notin \overline {i^\ast \left (C(G)\right )}$.

With the aid of lemma 7.8, the elements of $\mathcal {Z}(L_E^1(G)^{\ast \ast })$ can be confined when $\widehat {G}\setminus E$ is a Lust-Piquard set.

Proposition 7.9 Let $G$ be a compact metrizable Abelian group and let $E \subset \widehat {G}$ such that $\widehat {G} \setminus E$ is a Lust-Piquard set. Fix a right identity $e \in L^1(G)^{\ast \ast }$. Then,

\[ \mathcal{Z}(L^1_E(G)^{**})\subseteq \bigl\{C_u^{{\ast}{\ast}}(e)+r \colon u \in L_E^1(G), r \in \overline{i^\ast(C(G))}^\perp\bigr\}. \]

Proof. Let $p= C_\mu ^{\ast \ast }(e)+r \in L^1_E(G)^{\ast \ast }$ be an arbitrary element of $L_E^1(G)^{\ast \ast }$ with $\mu \in M_E(G)$ and $r\in i^\ast (C(G))^\perp$.

Assume that $\mu \in M_E(G)\setminus L^1_E(G)$. By lemma 7.8, there exists $\phi \in L^\infty (G)$ such that $\check \mu \ast \phi \notin \overline {i^*(C(G))}$. So there exists $s \in \overline {i^*(C(G))}^\perp$ such that $\langle s , i^*(\check \mu \ast \phi )\rangle \neq 0$. As in (6.1),

\[ 0\neq \langle {s,i^\ast(\check{\mu}\ast \phi)}\rangle {>} =\langle {s\,\square\, C_\mu^{{\ast}{\ast}}(e),\phi}\rangle {>} =\langle {s\,\square\, p,\phi}\rangle {>}, \]

showing that $p\notin \mathcal {Z}(L^1_E(G)^{{\ast \ast }})$ because $p\,\square \, s=0$.

The preceding proposition 7.9 yields the following result.

Corollary 7.10 Let $G$ be a compact metrizable Abelian group. If $E \subseteq \widehat {G}$ is such that $\widehat {G} \setminus E$ is a Lust-Piquard set, then $L^1_E(G)$ is not Arens regular.

We close the paper observing that, contrarily to what the previous corollary might suggest, the regularity properties of $L_E^1(G)$ do not determine those of $L^1_{\widehat {G}\setminus E}(G)$.

Example 7.11 $L_E^1(G)$ and $L_{\widehat {G}\setminus E}^1(G)$ can be both SAI and regular.

If $E\in \Omega _{\widehat {G}}$, then $\widehat {G}\setminus E \in \Omega _{\widehat {G}}$, then both $L_E^1(G)$ and $L_{\widehat {G}\setminus E}^1(G)$ are SAI by corollary 7.1.

If on the other hand we consider $E=\mathbb {N}\subseteq \mathbb {Z}$ the classical case of a Riesz set, then $\widehat {G}\setminus E=-\mathbb {N}$ is also a Riesz set so that $L_E^1(G)$ and $L_{\widehat {G}\setminus E}^1(G)$ are both Arens regular by corollary 6.3.

Remark 7.12 In our forthcoming paper, we shall deal with more general Banach algebras of the same type dealt with in this paper. Our study will include the group algebra of a non-Abelian compact group and the Fourier algebra of an amenable discrete group.