Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T14:15:27.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Mathematical modelling of respiratory syncytial virus (RSV): vaccination strategies and budget applications

Published online by Cambridge University Press:  15 December 2009

L. ACEDO ,
J. DÍEZ-DOMINGO ,
J.-A. MORAÑO  and
R.-J. VILLANUEVA
L. ACEDO*
Affiliation:
Instituto de Matemática Multidisciplinar, Universidad Politécnica de Valencia, Valencia, Spain
J. DÍEZ-DOMINGO
Affiliation:
Centro Superior de Investigación en Salud Pública (CSISP), Valencia, Spain
J.-A. MORAÑO
Affiliation:
Instituto de Matemática Multidisciplinar, Universidad Politécnica de Valencia, Valencia, Spain
R.-J. VILLANUEVA
Affiliation:
Instituto de Matemática Multidisciplinar, Universidad Politécnica de Valencia, Valencia, Spain
*
*Author for correspondence: Dr L. Acedo, Instituto de Matemática Multidisciplinar, Universidad Politécnica de Valencia, 46022, Valencia, Spain. (Email: [email protected])
Rights & Permissions [Opens in a new window]

Summary

We propose an age-structured mathematical model for respiratory syncytial virus in which children aged <1 year are especially considered. Real data on hospitalized children in the Spanish region of Valencia were used in order to determine some seasonal parameters of the model. Weekly predictions of the number of children aged <1 year that will be hospitalized in the following years in Valencia are presented using this model. Results are applied to estimate the regional cost of paediatric hospitalizations and to perform a cost-effectiveness analysis of possible vaccination strategies.

Keywords

Cost-effectiveness studyrespiratory syncytial virusvaccine policy development
Type
Original Papers
Information
Epidemiology & Infection , Volume 138 , Issue 6 , June 2010 , pp. 853 - 860
Copyright
Copyright © Cambridge University Press 2009

INTRODUCTION

Respiratory syncytial virus (RSV) is the most important respiratory virus in young children, and the major cause of hospitalizations, especially for bronchiolitis and pneumonia, in infants [Reference Hall, Feigin, Cherry, Demmler and Kaplan1]. Its impact on health services is increasing as the incidence of hospitalization in children for bronchiolitis increases [Reference Langley2]. It is only recently that the impact of RSV on adults has been studied, as up to 18% of the pneumonia hospitalizations in patients aged >65 years are due to RSV [Reference Han, Alexander and Anderson3].

In Spain, there are 15 000–20 000 visits to primary care due to RSV each year. In the Spanish region of Valencia, 1280 children aged <5 years are hospitalized each year as a consequence of RSV bronchiolitis [Reference Díez Domingo4]. The average hospitalization time is about 6 days. The cost of paediatric hospitalization for the Valencian Health Service is about €3·5 million per year.

RSV is the cause of annual seasonal epidemics with minor variations each year and its coincident occurrence with other widespread viral infections such as influenza or rotavirus, produces a high number of hospitalizations overstretching the health service. Moreover, it is easily transmitted and nosocomial infections are frequent [Reference Hall5].

Therefore, research on RSV and other viruses and the development of strategies to control epidemics are important from both the sanitary and economic point of view. Another problem is the study of vaccines to protect individuals at an early age, when the immune system is not completely developed. In this context it is important to note that the most seriously ill cases are not due to the RSV infection but are related to an anomalous immune response of the child [Reference Crowe6].

Mathematical models have been shown to be a powerful tool to analyse the epidemiology of infectious illnesses, to understand their behaviour, to predict their social impact and to discover how external factors change the impact of disease. In the case of RSV, the building of a reliable model is a priority objective to predict the medical care requirements needed in the following seasons.

Mathematical models for RSV have been developed previously. For example, SIRS (susceptible–infectious–recovered–susceptible) and MSEIRS (maternally derived immunity–susceptible–latent–infectious–recovered–susceptible) mathematical models with four possible re-infections were studied and applied with data from The Gambia, Singapore, Florida and Finland by Weber et al. [Reference Weber, Weber and Milligan7]. White et al. [Reference White8] presented a nested RSV model, stochastic simulations and fitting with data from several countries. Moreover, in an earlier paper, White et al. [Reference White9] considered the two types, A and B, of RSV and developed a SIRS model where re-infection by either type of RSV virus is possible, fitting the model with data from England & Wales and Finland.

Further, a PIV-vectored vaccine is already under development and clinical studies have been carried out recently [Reference Tang10, 11]. This vaccine might be available in the near future and, consequently, planning of vaccination strategies is urgently required. In this paper we consider a newborn vaccination strategy for Valencia in terms of the estimated cost of the vaccine, the average cost of hospitalization of RSV children that develop acute symptoms (in this case the average hospitalization time is ~6 days [Reference Díez Domingo4]) and parent work loss. To the best of our knowledge, vaccination strategies for RSV have not been studied and the imminence of the application of PIV-vectored vaccines demands such a study. A previous work on the cost-effectiveness of immunoprophylaxis with palivizumab has been recently reviewed [Reference Wang12].

Taking into account that RSV is an illness for which the most affected individuals (i.e. most hospitalizations) in the Spanish region of Valencia are children aged <1 year required the development of an adequate demographic model. We used a model with two age groups: G 1 corresponding to children aged <1 year and G 2 for the rest of the population. Birth and mortality rates as well as the transition rate from G 1 to G 2 were obtained from real statistical data.

The evolution of infected individuals is predicted by means of Weber et al.'s SIRS [Reference Weber, Weber and Milligan7] generalized to take into account two age groups and numerically integrated by standard numerical methods [Reference Wolfram13].

In the following sections we discuss the age-structured SIRS model estimating some demographic parameters from data from the Instituto Valenciano de Estadística (Statistical Service of the Spanish region of Valencia) [14]. Data corresponding to hospitalizations of children aged <1 year are presented and a Nelder–Mead procedure for model fitting is developed. A cost-effectiveness analysis is performed for a vaccination scenario in the region of Valencia, Spain. Finally, conclusions are given.

METHODS

The Spanish region of Valencia [15] is located in eastern Mediterranean Spain, with an area of 23 255 km2 and a population of 4 202 607 inhabitants (2001), composed of three provinces, Castellón (north), Alicante (south) and Valencia (middle).

Following [16, section 6·1, pp. 634–635], we introduced an age-structured SIRS model with two age groups: i=1 corresponds to children aged 0–1 year and i=2 corresponds to the rest of the population. This is justified because the disease is more acute in children aged <1 year, as confirmed by hospitalization data. For each age group we have three subpopulations according to the state of the individuals with respect to the disease:

  • • Susceptibles, S i(t) (i=1, 2): the proportion of those at risk of contracting the disease.

  • • Infectives, I i(t) (i=1, 2): the proportion of those infected and capable of transmitting the disease.

  • • Recovered, R i(t) (i=1, 2): the proportion of those recovered from the disease that are temporarily immune to re-infection.

Note that S i(t), I i(t) and R i(t), respectively, correspond to the fraction of susceptible, infected and recovered of age group G i (i=1, 2) and

0\les S_{i} \lpar t\rpar \comma I_{i} \lpar t\rpar \comma R_{i} \lpar t\rpar \les 1.

The age-structured model is then defined by the following system of differential equations:

(1)
S_{\hskip -1pt \setnum{1}} ^\prime \lpar t\rpar \equals \mu \minus \lsqb \hskip1pt \beta \lpar t\rpar \lpar I_{\setnum{1}} \lpar t\rpar \plus I_{\setnum{2}} \lpar t\rpar \rpar \plus c_{\setnum{1}} \plus d_{\setnum{1}} \rsqb S_{\setnum{1}} \lpar t\rpar \plus \gamma _{\setnum{1}} R_{\setnum{1}} \lpar t\rpar \comma
(2)
S_{\hskip -1pt \setnum{2}} ^\prime\lpar t\rpar \equals c_{\setnum{1}} S_{\setnum{1}} \lpar t\rpar \minus \lsqb \beta \lpar t\rpar \lpar I_{\setnum{1}} \lpar t\rpar \plus I_{\setnum{2}} \lpar t\rpar \rpar \plus d_{\setnum{2}} \rsqb S_{\setnum{2}} \lpar t\rpar \plus \gamma _{\setnum{2}} R_{\setnum{2}} \lpar t\rpar \comma
(3)
I_{\hskip -1pt \setnum{1}} ^\prime \lpar t\rpar \equals \beta \lpar t\rpar \lpar I_{\setnum{1}} \lpar t\rpar \plus I_{\setnum{2}} \lpar t\rpar \rpar S_{\setnum{1}} \lpar t\rpar \minus \lsqb \nu _{\setnum{1}} \plus c_{\setnum{1}} \plus d_{\setnum{1}} \rsqb I_{\setnum{1}} \lpar t\rpar \comma \hfill
(4)
I_{\hskip -1pt \setnum{2}} ^\prime \lpar t\rpar \equals c_{\setnum{1}} I_{\setnum{1}} \lpar t\rpar \plus \beta \lpar t\rpar \lpar I_{\setnum{1}} \lpar t\rpar \plus I_{\setnum{2}} \lpar t\rpar \rpar S_{\setnum{2}} \lpar t\rpar \minus \lsqb \nu _{\setnum{2}} \plus d_{\setnum{2}} \rsqb I_{\setnum{2}} \lpar t\rpar \comma
(5)
R_{\hskip -1pt \setnum{1}} ^\prime \lpar t\rpar \equals \nu _{\setnum{1}} I_{\setnum{1}} \lpar t\rpar \minus \lsqb \gamma _{\setnum{1}} \plus c_{\setnum{1}} \plus d_{\setnum{1}} \rsqb R_{\setnum{1}} \lpar t\rpar \comma \hfill
(6)
R_{\hskip -1pt \setnum{2}} ^\prime \lpar t\rpar \equals c_{\setnum{1}} R_{\setnum{1}} \lpar t\rpar \plus \nu _{\setnum{2}} I_{\setnum{2}} \lpar t\rpar \minus \lsqb \gamma _{\setnum{2}} \plus d_{\setnum{2}} \rsqb R{}_{\setnum{2}}\lpar t\rpar \comma \hfill

with the initial condition

(7)
S_{\setnum{1}} \lpar 0\rpar \equals S_{\setnum{1}}^{\setnum{0}} \comma I_{\setnum{1}} \lpar 0\rpar \equals I_{\setnum{1}}^{\setnum{0}} \comma R_{\setnum{1}} \lpar 0\rpar \equals R_{\setnum{1}}^{\setnum{0}} \comma \hfill
(8)
S_{\setnum{2}} \lpar 0\rpar \equals S_{\setnum{2}}^{\setnum{0}} \comma I_{\setnum{2}} \lpar 0\rpar \equals I_{\setnum{2}}^{\setnum{0}} \comma R_{\setnum{2}} \lpar 0\rpar \equals R_{\setnum{2}}^{\setnum{0}} \comma \hfill

where

  • • μ is the birth rate;

  • • β(t)=b 0+b 1 cos(2πt+ϕ), is the disease transmission rate, expressed as such in order to represent the seasonality of this disease. This type of function is also considered in other studies where seasonality is relevant [Reference Weber, Weber and Milligan7, Reference Grenfell, Bolker, Kleczkowski and Mollison17];

  • • c 1, is the transition rate from age groups G 1 to G 2;

  • • di (i=1, 2), is the death rate for each age group;

  • • γi, where 1/γi (i=1, 2) is the average time an individual of age group G i remains immune against re-infection,

  • • νi, where 1/νi (i=1, 2) is the average time to recover from the illness for an individual of age group G i.

It should be noted that this model assumes some simplifying hypotheses:

  1. (i) Primary and secondary infections have the same rate of recovery and infectivity but this is not the case in real clinical situations [Reference Hall5].

  2. (ii) The mixing between the different age groups is homogeneous.

  3. (iii) There is no maternal antibody protection.

It would be possible to generalize further the model in equations (1)–(6) to take into account that the strength of successive re-infections is progressively smaller. However, there is no reliable data for these clinical parameters for the different age groups. Heterogeneity could also be included by modulating the transmission rate, β(t), with a contact matrix C ij (i, j=1, 2). But this would increase the number of parameters to fit and therefore, create an additional difficulty in obtaining reliable fitted parameters in an acceptable time. For these reasons, we decided to study the simpler model, taking into account that the cost-effectiveness of the vaccination programme could be slightly different in a more general model.

Maternal antibody protection has already been studied in the context of RSV models by Weber et al. [Reference Weber, Weber and Milligan7], but there were no noticeable changes in respect of the simpler SIRS model without early antibody protection. On the other hand, we performed CHAID (χ2 automatic interaction detection) analysis with data of hospitalized children in the Spanish region of Valencia, obtaining an average duration of 23 days for the maternal antibody protection period, and this can be considered as a perturbation of the simpler SIRS model.

Estimating parameters

Numerical values can be assigned to most of the above parameters. For instance, γi, and νi (i=1, 2) can be obtained from [Reference Hall, Feigin, Cherry, Demmler and Kaplan1, Reference Weber, Weber and Milligan7], the average time to recover from RSV is 10 days and the average time to lose immunity is 200 days, both independent of the age group. Then,

(9)
\gamma _{\setnum{1}} \equals \gamma _{\setnum{2}} \equals {{365} \over {200}}\comma \hfill
(10)
\nu _{\setnum{1}} \equals \nu _{\setnum{2}} \equals {{365} \over {10}}\comma \hfill

If we denote by N i the fraction of persons in age group G i (i=1, 2) (in respect of the total population) the evolution equations for the fraction of individuals in each group is given by:

(11)
N\hskip1pt ^\prime _ {\hskip-1pt\setnum{1}} \equals \mu \lpar N_{\setnum{1}} \plus N_{\setnum{2}} \rpar \minus d_{\setnum{1}} N_{\setnum{1}} \minus c_{\setnum{1}} N_{\setnum{1}} \comma \hfill
(12)
N\hskip1pt ^\prime _{\hskip-1pt\setnum{2}} \equals c_{\setnum{1}} N_{\setnum{1}} \minus d_{\setnum{2}} N_{\setnum{2}} \comma \hfill
(13)
N_{\setnum{1}} \plus N_{\setnum{2}} \equals 1.\hfill

Using demographic data of the Spanish region of Valencia for the period 2001–2004 [14], where hospitalization data are available, we obtain:

  • • the mean population, 4 252 386 inhabitants;

  • • the mean fraction of both subpopulations, N 1=0·01038 and N 2=0·98962;

  • • the mean birth rate, μ=0·0107497;

  • • the mean death rate for each age group, d 1=0·0006796 and d 2=0·00912862.

Under the assumption of constant population for each age group (N 1′=N 2′=0) and equation (11), we find a simple relation for the transition rate from age group G 1 to age group G 2:

(14)
c_{\setnum{1}} \equals {\mu \over {N_{\setnum{1}} }} \minus d_{\setnum{1}} \equals 1{\cdot}03495.\hfill

By adding equations (11)–(13) we also find the following relation:

(15)
\mu \equals d_{\setnum{1}} N_{\setnum{1}} \plus d_{\setnum{2}} N_{\setnum{2}}.\hfill

Finally, we choose a new d 2 to satisfy equation (15), i.e. d 2*=0·0108554, which is different from the real value of d 2=0·00912862 because the population is not really constant in the 4-year interval considered. Nevertheless, the difference is sufficiently small (~7200 dead persons) to be ignored in our study.

Hence, as can be seen, only parameters b 0, b 1 and ϕ remain unknown, i.e. parameters dependent upon the seasonality.

Source RSV data

From CMBD (basic minimum dataset) database of the Spanish region of Valencia we obtained hospitalization data on RSV-related illness (bronchiolitis, infection, pneumonia, etc.) of children aged <1 year during the period January 2001 to December 2004. After processing the data we obtained the weekly number of hospitalizations of children in age group G 1 caused by a RSV-related infection as shown in Figure 1.

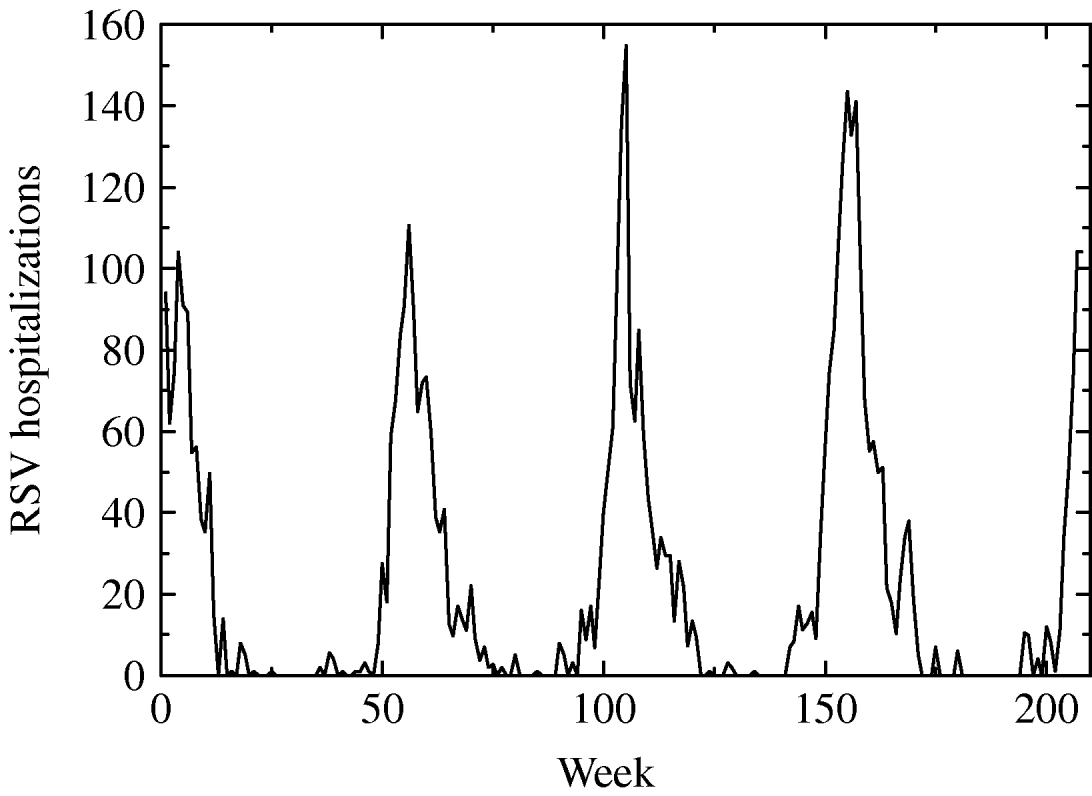
Fig. 1. Weekly hospitalizations for respiratory syncytial virus (RSV) infection from January 2001 to December 2004 of children aged <1 year in the region of Valencia.

It should be noted that data refer to hospitalizations, not to infected people. This means that only a proportion of infected are hospitalized and this proportion or scale, designated s, should be estimated in the model data fitting.

RESULTS

Model fitting

In order to fit the data for hospitalized children aged <1 year we numerically integrated the system of differential equations in equations (1)–(5) for different sets of unknown parameters: b 0, b 1, ϕ and the scale parameter s of the proportion of infected in G 1 that are hospitalized.

Additionally, the initial condition data are also unknown. We have considered throughout all the simulations that 1% of children in age group G 1 are infected at 1 January 1999 and the rest of individuals are susceptible.

The procedure for fitting the model is as follows: we solve numerically the system of differential equations in equation (1)–(5) with the aforementioned initial values. After a period of 2 years of transient evolution the solution becomes periodic. This numerical solution is optimized by mean of the Nelder–Mead algorithm [Reference Nelder and Mead18, Reference Press19], that does not need the computation of any derivative or gradient, which is impossible to know in this case.

The values of b 0, b 1, ϕ and s that minimize the function for the region of Valencia are:

(16)
b_{\setnum{0}} \equals 69{\cdot}52\comma \hfill
(17)
b_{\setnum{1}} \equals 14{\cdot}31\comma \hfill
(18)
\phi \equals 5{\cdot}997\comma \hfill
(19)
s \equals 0{\cdot}0219. \hfill

For the different health districts where the fitting procedure was performed we obtained very similar values. This supports the reliability of the fitting procedure because the parameters b 0, b 1 and ϕ are known to depend only on the climatological conditions of the countries where the RSV epidemic has been studied [Reference White8, Reference White9].

The parameter s is especially interesting because it provides information about the proportion of infected children that have to be hospitalized as a consequence of the infection. According to the data in equation (Reference Press19), we found that 2·19% of infected children are hospitalized by a disease derived from RSV infection.

The graphical representations of this model fitting can be seen in Figure 2.

Fig. 2. Model fitting from January 2001 to December 2004. The points are data of weekly hospitalizations of children aged <1 year and the continuous line the scaled solution of the system of differential equations for infected children aged <1 year, s*I 1(t). The dashed line corresponds to the fitting with γ1=γ2=1·59.

The average time of recovery from RSV illness (ν1=ν2=365/10) is a well-known value [Reference Hall, Feigin, Cherry, Demmler and Kaplan1, Reference Weber, Weber and Milligan7]. It can also be obtained and compared with the statistical analysis of hospitalization data.

On the other hand, a larger uncertainty is found in the average time of immunity following RSV infection, 1/γ. Weber et al. [Reference Weber, Weber and Milligan7] reported the value γ=1·8 corresponding to an average of 200 days of immunity. This value was contrasted by a sensibility analysis. Similar values have been proposed by White et al. [Reference White8]. In order to verify that the fitting of RSV hospitalization data to a SIRS model requires and immunity period compatible with the values suggested in the literature we performed a more detailed sensibility analysis. We considered that the value of γ is in the range 1·0<γ<2·5. A Nelder–Mead optimization algorithm was applied to obtain the best values of γ, the seasonal parameters b 0, b 1, ϕ and the scale factor s. The best fit is obtained with the values:

(20)
b_{\setnum{0}} \equals 71{\cdot}99\comma \hfill
(21)
b_{\setnum{1}} \equals 13{\cdot}11\comma \hfill
(22)
\phi \equals 6{\cdot}065\comma \hfill
(23)
s \equals 0{\cdot}0233\comma \hfill
(24)
\gamma \equals 1{\cdot}59\comma \hfill

These values are very similar to those obtained in equations (16)–(19) with the assumption γ=1·8 and confirm that a SIRS model approach to the spread of RSV disease implies an immunity time after infection of ~200 days. In Figure 2 we also compared this with a second fitting; however, the difference was minimal.

Vaccination strategies

We next developed a cost-effectiveness analysis for a newborn vaccination strategy for RSV. The effect of the vaccine is to remove a fraction p of newborns from the S 1 state and place them on a new vaccinated V state until they reach the age of the next age group. The box diagram for the model is plotted in Figure 3.

Fig. 3. Box diagram of a respiratory syncytial virus model with two age groups and newborn vaccination.

The reason that V state individuals evolve to the S 2 state instead of S 1 is the large immunization period, which is at least equal to the immunization of children recovered from the disease (γ=365/200 days). Moreover, the children should receive additional booster doses during the first year of life and, consequently, their immunization is prolonged.

Figure 4 plots the evolution of the total number of infected children aged <1 year in the region of Valencia after implementation of the vaccination programme immediately after the beginning of the fifth year. A total of 85% is vaccinated. It can be seen that the number of infected children decays to <1000 just 2 years after commencement of vaccination.

Fig. 4. Prediction of the model for the total number of infected children in the region of Valencia. Vaccination of 85% of newborn children begins after the fifth year.

The total cost of RSV healthcare is calculated as follows:

  • • Hospitalization cost: Taking into account an average of 6·28 hospitalization days for every acutely infected child [Reference Díez Domingo4] and €500 per day and child hospitalized.

  • • Vaccination cost: We calculated the number of children vaccinated during a year and an estimated cost of €100 per dose. Three doses are planned during the first year of life.

  • • Parent work loss: We take into account that for every hospitalized child parents lose d=6·28 days of work (average hospitalization of RSV-infected children). In the case of infected children we assume that they develop milder symptoms but, nevertheless, parents lose d days of work. This is a social parameter difficult to determine. We simulated cost-effectiveness for d=2, 3, 4. The mean labour cost in Spain is €75·21 per day [20].

The results for the costs of hospitalization, vaccination and parent work loss are plotted in Figures 5 and 6.

Fig. 5. Vaccination cost (—) and hospitalization cost (……) vs. the fraction of vaccinated newborn children.

Fig. 6. Costs for parent work loss. Taking into account d=6·28 days of work loss on average for hospitalized children and d=4 (—), d=3 (- - -) and d=2 (……) days of work loss for infected children that do not need hospitalization.

The global result for the cost-effectiveness analysis is plotted in Figure 7 for d=2, 3 or 4 days of parent work loss in the case of children that do not develop sufficiently acute symptoms to become hospitalized. A reduction of €2 million of total cost is predicted for an estimate of 4 days of parent work loss on average for infected children. Moreover, we have not taken into account the long-term effects of RSV infections. In particular, there is an accord among paediatricians regarding a connection between RSV at early ages and asthma episodes of children and adolescents. This has been confirmed by recent studies in mice [Reference Jafri21]. Therefore, even assuming that parents only lose four working days in caring for children who develop mild symptoms of RSV, a positive balance for the implementation of the vaccine is obtained.

Fig. 7. Total cost (hospitalization+parent work loss+vaccination) related to respiratory syncytial virus infections as a function of the fraction of vaccinated newborn children. Days of parent work loss: d=4 (—), d=3 (- - -) and d=2 (……).

DISCUSSION

In this paper we have presented an age-structured model for RSV that fits well with the data of hospitalized children aged <1 year in the region of Valencia. A Nelder–Mead method [Reference Nelder and Mead18] has been implemented in order to estimate the parameters which determine the seasonality and also the fraction of infected children that become hospitalized as a consequence of the RSV infection.

We used data of children aged <1 year hospitalized as a consequence of RSV infection in the period 2001–2004.

Independently of the health district considered, we have obtained very similar parameters for the variation of the infection rate with time in the SIR model: β(t)=b 0+b 1 cos(2πt+ϕ). This is unsurprising as it is expected that these parameters depend only on the climatological conditions of the country [Reference White8, Reference White9]. The climate in Valencia is Mediterranean with an average temperature around 18°C and minimum temperatures in January (the month in which the highest number of child hospitalizations due to RSV is observed). Moreover, the absence of mountain ranges, except for the Iberian Mountains in the northwest where population density is small, implies no significant climatic changes between the coast and the interior of the region. The study of these correlations is an interesting problem in itself and must be treated by means of statistical analysis. Sociodemographic factors, e.g. the opening and closing of schools, could be a secondary source for the outbreak of RSV. However, this is apparently not as important as climate because in Valencia schools open in September and the seasonal outbreak normally occurs at the end of November.

We have developed a model for newborn vaccinations with two booster doses during the first year of life. Assuming a cost of €300 per vaccination a positive balance for the implementation of the proposed vaccination strategy is obtained even with the cautious assumption that parents only lose 4 working days in the case of an infected child that does not become hospitalized. We must take into account that these results are obtained with a simple extension of a recently proposed SIRS model [Reference Weber, Weber and Milligan7] and should be considered as a first-order approximation. However, we are also aware that a mean-field network approach replicates the results discussed in our paper even with a continuous Forster–McKendrick population model [Reference Hethcote16], which is more realistic than the two age groups proposed in our paper.

Another possible alternative is the MSEIRS model with re-infections [Reference Weber, Weber and Milligan7]; however, taking into account that the vaccine is expected to prevent infections during the first year of life similar results to the model proposed in our paper are expected.

On the other hand, although the cosine function to simulate the seasonal strength of the infection rate, β(t), is the most widely used, other alternatives utilized in relation to climatological factors are probably more realistic. Nevertheless, there is no general agreement on which factors are relevant in unleashing the most acute episodes of the epidemic during the winter season: humidity, temperature or even ultraviolet B radiation has been linked with the propagation of RSV virus [Reference Novotni and Weber22–Reference Welliver24]. Further research on these factors in the region of Valencia could also provide better information on the epidemic propagation and the outcome of vaccination programmes. We are currently performing this statistical correlation analysis.

A more general model including heterogeneity of contacts in individuals, variable strength of re-infection, a more realistic model for β(t) based upon climatological factors and maternal antibody protection is currently under study and will be published elsewhere.

DECLARATION OF INTEREST

None.

References

REFERENCES

1.Hall, CB. Respiratory syncytial virus and human metapneumovirus. In: Feigin, RD, Cherry, JD, Demmler, GJ, Kaplan, SL, eds. Textbook of Pediatric Infectious Diseases, 5th edn, Philadelphia, PA: Saunders, 2004, pp. 2315–2341.Google Scholar
2.Langley, JM, et al. Increasing incidence of hospitalization for bronchiolitis among Canadian children 1980–2000. Journal of Infectious Diseases 2003; 188: 1764–1767.CrossRefGoogle ScholarPubMed
3.Han, L, Alexander, J, Anderson, L. Respiratory syncytial virus pneumonia among the elderly: An assessment of disease burden. Journal of Infectious Diseases 1999; 179: 25–30.CrossRefGoogle ScholarPubMed
4.Díez Domingo, J, et al. Incidence and costs of hospitalizations for bronchiolitis and respiratory syncytial virus (RSV) infections in the Autonomous Community of Valencia, Spain [in Spanish]. Anales de Pediatría 2006; 65-4: 325–330.Google Scholar
5.Hall, CB. Nosocomial respiratory syncytial virus infections: the ‘cold war’ has not ended. Clinical Infectious Diseases 2000; 31: 590–596.Google Scholar
6.Crowe, JE. Respiratory syncytial virus vaccine development. Vaccine 2002; 20: 532–537.Google Scholar
7.Weber, A, Weber, M, Milligan, P. Modeling epidemics caused by respiratory syncytial virus (RSV). Mathematical Biosciences 2001; 172: 95–113.CrossRefGoogle ScholarPubMed
8.White, LJ, et al. Understanding the transmission dynamics of respiratory syncytial virus using multiple time series and nested models. Mathematical Biosciences 2007; 209: 222–239.Google Scholar
9.White, LJ, et al. The transmission dynamics of groups A and B human respiratory syncytial virus (hRSV) in England & Wales and Finland: seasonality and cross-protection. Epidemiology and Infection 2005; 133: 279–289.Google Scholar
10.Tang, RS, et al. Development of a PIV-vectored RSV vaccine: preclinical evaluation of safety, toxicity, and enhanced disease and initial clinical testing in healthy adults. Vaccine 2008; 26: 6373–6382.Google Scholar
11.ClinicalTrials.gov. A study to evaluate the safety, tolerability, immunogenicity and vaccine-like viral shedding of MEDI-534, against respiratory syncytial virus (RSV) and parainfluenza virus type 3 (PIV3), in healthy 6 to <24 month-old children an in 2 month old infants (http://www.clinicaltrials.gov/ct2/show/NCT00686075?term=RSV+VACCINE&rank=3). Accessed 23 July 2009.Google Scholar
12.Wang, D, et al. Immunoprophylaxis against respiratory syncytial virus (RSV) with palivizumab in children: a systematic review and economic evaluation. Health Technology Assessment 2008; 12: 36 (http://www.hta.ac.uk).CrossRefGoogle ScholarPubMed
13.Wolfram, S. The Mathematica Book, 5th edn.Wolfram Media, 2003.Google Scholar
14.Instituto Valenciano de Estadística. (http://www.ive.es). Accessed 3 August 2007.Google Scholar
15.Valencia (autonomous community). (http://en.wikipedia.org/wiki/Valencian/_Community). Accessed 3 August 2007.Google Scholar
16.Hethcote, HW. The mathematics of infectious diseases. SIAM Review 2000; 42-4: 599–653.Google Scholar
17.Grenfell, B, Bolker, B, Kleczkowski, A. Seasonality, demography and the dynamics of measles in developed countries. In: Mollison, D, ed. Epidemic Models – Their Structure and Relation to Data. Cambridge University, 1995, pp. 248–268.Google Scholar
18.Nelder, JA, Mead, R. A simplex method for function minimization. Computer Journal 1964; 7: 308–313.CrossRefGoogle Scholar
19.Press, WH, et al. Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, 1986.Google Scholar
20.Encuesta Trimestral de Coste Laboral, Instituto Nacional de Empleo, Spain. (http://www.ine.esc).Google Scholar
21.Jafri, HS, et al. Respiratory syncytial virus induces pneumonia, cytokine response, airway obstruction and chronic inflammatory infiltrates associated with long-term airway hyperresponsiveness in mice. Journal of Infectious Diseases 2004; 189: 1856–65.CrossRefGoogle ScholarPubMed
22.Novotni, D, Weber, A. A Stochastic method for solving inverse problems in epidemic modeling. In: Proceedings of the International Conference on Mathematics and Engineering Techniques in Medicine and Biological Sciences (METMBS), Las Vegas, 2003. (http://cg.cs.uni-bonn.de/project-pages/symbolicanalysis/documents/NovotniWeber2003a.pdf)Google Scholar
23.Meerhoff, TJ, et al. Variation of the respiratory syncytial virus and the relation with meteorological factors in different winter seasons. Pediatric Infectious Disease Journal 2009: 28: 860–866.Google Scholar
24.Welliver, RC. Temperature, humidity, and ultraviolet B radiation predict community respiratory syncytial virus activity. Pediatric Infectious Disease Journal 2007; 26: S29–S35.CrossRefGoogle ScholarPubMed
Figure 0

Fig. 1. Weekly hospitalizations for respiratory syncytial virus (RSV) infection from January 2001 to December 2004 of children aged <1 year in the region of Valencia.

Figure 1

Fig. 2. Model fitting from January 2001 to December 2004. The points are data of weekly hospitalizations of children aged <1 year and the continuous line the scaled solution of the system of differential equations for infected children aged <1 year, s*I1(t). The dashed line corresponds to the fitting with γ1=γ2=1·59.

Figure 2

Fig. 3. Box diagram of a respiratory syncytial virus model with two age groups and newborn vaccination.

Figure 3

Fig. 4. Prediction of the model for the total number of infected children in the region of Valencia. Vaccination of 85% of newborn children begins after the fifth year.

Figure 4

Fig. 5. Vaccination cost (—) and hospitalization cost (……) vs. the fraction of vaccinated newborn children.

Figure 5

Fig. 6. Costs for parent work loss. Taking into account d=6·28 days of work loss on average for hospitalized children and d=4 (—), d=3 (- - -) and d=2 (……) days of work loss for infected children that do not need hospitalization.

Figure 6

Fig. 7. Total cost (hospitalization+parent work loss+vaccination) related to respiratory syncytial virus infections as a function of the fraction of vaccinated newborn children. Days of parent work loss: d=4 (—), d=3 (- - -) and d=2 (……).