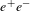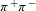1 Introduction
In the presence of strong electromagnetic fields, vacuum can be unstable and if a certain field strength is exceeded, electron–positron pair creation can occur[Reference Schwinger1, Reference Greiner, Muller and Rafelski2]. This characteristic critical field strength is the Schwinger field
![]() ${\mathcal{E}}_{ce}=(m_{e}c^{2})/e\unicode[STIX]{x1D706}_{ce}\simeq 1.3\times 10^{18}~\text{V}~\text{m}^{-2}$
, where
${\mathcal{E}}_{ce}=(m_{e}c^{2})/e\unicode[STIX]{x1D706}_{ce}\simeq 1.3\times 10^{18}~\text{V}~\text{m}^{-2}$
, where
![]() $m_{e}$
is the electron mass,
$m_{e}$
is the electron mass,
![]() $c$
the speed of light and
$c$
the speed of light and
![]() $\unicode[STIX]{x1D706}_{ce}=\hbar /(m_{e}c)$
is the Compton wavelength. However, as demonstrated by Schwinger[Reference Schwinger1], in order to observe pair creation, the invariant quantities
$\unicode[STIX]{x1D706}_{ce}=\hbar /(m_{e}c)$
is the Compton wavelength. However, as demonstrated by Schwinger[Reference Schwinger1], in order to observe pair creation, the invariant quantities
![]() ${\mathcal{F}}=\frac{1}{4}F_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}F^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}=-\frac{1}{2}(\vec{{\mathcal{E}}}^{2}-c^{2}\vec{{\mathcal{B}}}^{2})$
,
${\mathcal{F}}=\frac{1}{4}F_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}F^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}=-\frac{1}{2}(\vec{{\mathcal{E}}}^{2}-c^{2}\vec{{\mathcal{B}}}^{2})$
,
![]() ${\mathcal{G}}=\frac{1}{4}F_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\tilde{F}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}=c\vec{{\mathcal{E}}}\cdot \vec{{\mathcal{B}}}$
must be such that
${\mathcal{G}}=\frac{1}{4}F_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}\tilde{F}^{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}=c\vec{{\mathcal{E}}}\cdot \vec{{\mathcal{B}}}$
must be such that
![]() $\sqrt{{\mathcal{F}}^{2}+{\mathcal{G}}^{2}}-{\mathcal{F}}>0$
, where
$\sqrt{{\mathcal{F}}^{2}+{\mathcal{G}}^{2}}-{\mathcal{F}}>0$
, where
![]() $F_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}$
and
$F_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}$
and
![]() $\tilde{F}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}=\frac{1}{2}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}F^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
are the electromagnetic field tensor and its dual, respectively. These requirements can be satisfied at an area close to the antinodes of a standing wave or at the region of a focused laser beam. As the critical field strength corresponds to focal laser intensities of the order of
$\tilde{F}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}}=\frac{1}{2}\unicode[STIX]{x1D716}_{\unicode[STIX]{x1D707}\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}F^{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}$
are the electromagnetic field tensor and its dual, respectively. These requirements can be satisfied at an area close to the antinodes of a standing wave or at the region of a focused laser beam. As the critical field strength corresponds to focal laser intensities of the order of
![]() $10^{29}~\text{W}~\text{cm}^{-2}$
, the main question that arises, is whether an experimental verification of the phenomenon is possible. The rapid development of ultra-intense laser facilities has rekindled the interest in proposing a possible experimental setup as seen in various works[Reference DiPiazza3–Reference Tsohantjis, Moustaizis and Ploumistakis11]. Theoretical treatment of pair creation in an oscillating pure electric field and based on the atom ionization theory, was demonstrated in Brezin and Itzykson[Reference Brezin and Itzykson12] and Popov’s works[Reference Popov13–Reference Popov19]. The characteristic parameter of those treatments is the relativistic invariant parameter
$10^{29}~\text{W}~\text{cm}^{-2}$
, the main question that arises, is whether an experimental verification of the phenomenon is possible. The rapid development of ultra-intense laser facilities has rekindled the interest in proposing a possible experimental setup as seen in various works[Reference DiPiazza3–Reference Tsohantjis, Moustaizis and Ploumistakis11]. Theoretical treatment of pair creation in an oscillating pure electric field and based on the atom ionization theory, was demonstrated in Brezin and Itzykson[Reference Brezin and Itzykson12] and Popov’s works[Reference Popov13–Reference Popov19]. The characteristic parameter of those treatments is the relativistic invariant parameter
![]() $\unicode[STIX]{x1D6FE}=mc\unicode[STIX]{x1D714}/e{\mathcal{E}}=\hbar \unicode[STIX]{x1D714}{\mathcal{E}}_{c}/mc^{2}{\mathcal{E}}$
, which is analogous to the Keldysh parameter. In particular, Popov[Reference Popov13–Reference Popov19] applied the imaginary time method for the case of oscillating electric field such as the one realized at the antinodes of an electromagnetic standing wave formed by two coherent counterpropagating laser beams and for which
$\unicode[STIX]{x1D6FE}=mc\unicode[STIX]{x1D714}/e{\mathcal{E}}=\hbar \unicode[STIX]{x1D714}{\mathcal{E}}_{c}/mc^{2}{\mathcal{E}}$
, which is analogous to the Keldysh parameter. In particular, Popov[Reference Popov13–Reference Popov19] applied the imaginary time method for the case of oscillating electric field such as the one realized at the antinodes of an electromagnetic standing wave formed by two coherent counterpropagating laser beams and for which
![]() ${\mathcal{E}}\ll {\mathcal{E}}_{c}$
and
${\mathcal{E}}\ll {\mathcal{E}}_{c}$
and
![]() $\hbar \unicode[STIX]{x1D714}\ll mc^{2}$
, distinguishing two important regimes
$\hbar \unicode[STIX]{x1D714}\ll mc^{2}$
, distinguishing two important regimes
![]() $\unicode[STIX]{x1D6FE}\ll 1$
and
$\unicode[STIX]{x1D6FE}\ll 1$
and
![]() $\unicode[STIX]{x1D6FE}\gg 1$
. For
$\unicode[STIX]{x1D6FE}\gg 1$
. For
![]() $\unicode[STIX]{x1D6FE}\ll 1$
(high electric field strength and low frequency) the adiabatic non-perturbative tunneling mechanism dominates and the probability density is expressed as
$\unicode[STIX]{x1D6FE}\ll 1$
(high electric field strength and low frequency) the adiabatic non-perturbative tunneling mechanism dominates and the probability density is expressed as
![]() $W\propto \exp (-\unicode[STIX]{x1D70B}({\mathcal{E}}_{c}/{\mathcal{E}}))$
. For the case of
$W\propto \exp (-\unicode[STIX]{x1D70B}({\mathcal{E}}_{c}/{\mathcal{E}}))$
. For the case of
![]() $\unicode[STIX]{x1D6FE}\gg 1$
(low electric field strength and high frequency) respectively, the multiphoton mechanism is dominant and
$\unicode[STIX]{x1D6FE}\gg 1$
(low electric field strength and high frequency) respectively, the multiphoton mechanism is dominant and
![]() $W\propto ({\mathcal{E}}_{c}/{\mathcal{E}})^{-2n_{0}}$
(
$W\propto ({\mathcal{E}}_{c}/{\mathcal{E}})^{-2n_{0}}$
(
![]() $n_{0}=2mc^{2}/\hbar \unicode[STIX]{x1D714}$
is the multiphoton order threshold). Additionally in Ref. [Reference Popov, Mur, Narozhnyi and Popruzhenko20] the imaginary time method was further analyzed and applied for the cases of a constant electric field and time homogeneous electric field for a single or multiple laser pulses. Also, important work in pair production has been carried out concerning the interaction of a high intensity polarized laser beam in vacuum as seen in Refs. [Reference Narozhny, Bulanov, Mur and Popov21–Reference Fedotov23], leading to observation of pair production at laser intensities lower than the critical one. Along these lines, interaction of two circularly polarized counterpropagating laser pulses[Reference Bulanov, Narozhny, Mur and Popov24] was shown that pair creation can become experimentally observable for laser beam intensities one or two orders of magnitude lower than that of a single pulse. Finally in Refs. [Reference Narozhny and Fedotov22, Reference Bulanov, Chen, Schroeder, Esarey, Leemans, Bulanov, Esirkepov, Kando, Koga, Zhidkov, Chen, Mur, Narozhny, Popov, R. Thomas and Korn25, Reference Bulanov, Mur, Narozhny, Nees and Popov26] the collision of multiple electromagnetic pulses is proposed as yet an another possible experimental scheme, where lower threshold is required for pair observation. In the ultra-relativistic regime
$n_{0}=2mc^{2}/\hbar \unicode[STIX]{x1D714}$
is the multiphoton order threshold). Additionally in Ref. [Reference Popov, Mur, Narozhnyi and Popruzhenko20] the imaginary time method was further analyzed and applied for the cases of a constant electric field and time homogeneous electric field for a single or multiple laser pulses. Also, important work in pair production has been carried out concerning the interaction of a high intensity polarized laser beam in vacuum as seen in Refs. [Reference Narozhny, Bulanov, Mur and Popov21–Reference Fedotov23], leading to observation of pair production at laser intensities lower than the critical one. Along these lines, interaction of two circularly polarized counterpropagating laser pulses[Reference Bulanov, Narozhny, Mur and Popov24] was shown that pair creation can become experimentally observable for laser beam intensities one or two orders of magnitude lower than that of a single pulse. Finally in Refs. [Reference Narozhny and Fedotov22, Reference Bulanov, Chen, Schroeder, Esarey, Leemans, Bulanov, Esirkepov, Kando, Koga, Zhidkov, Chen, Mur, Narozhny, Popov, R. Thomas and Korn25, Reference Bulanov, Mur, Narozhny, Nees and Popov26] the collision of multiple electromagnetic pulses is proposed as yet an another possible experimental scheme, where lower threshold is required for pair observation. In the ultra-relativistic regime
![]() $\unicode[STIX]{x1D709}\gg 1\;(\unicode[STIX]{x1D709}=1/\unicode[STIX]{x1D6FE})$
recollision process of an electron–positron pair produced by the interaction of a high energy photon with an intense laser pulse allows relevant high energy physics effects[Reference Meuren, Hatsagortsyan, Keitel and Di Piazza27]. The concept of the E144 experiment[Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg28] and the agreement with theory is mentioned in Ref. [Reference Narozhny and Fedotov22] as a unique opportunity for future experiments, in order to investigate unexplored nonlinear vacuum effects, using laser intensities to 2–4 order higher than the laser intensity used for the first experimental verification of
$\unicode[STIX]{x1D709}\gg 1\;(\unicode[STIX]{x1D709}=1/\unicode[STIX]{x1D6FE})$
recollision process of an electron–positron pair produced by the interaction of a high energy photon with an intense laser pulse allows relevant high energy physics effects[Reference Meuren, Hatsagortsyan, Keitel and Di Piazza27]. The concept of the E144 experiment[Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg28] and the agreement with theory is mentioned in Ref. [Reference Narozhny and Fedotov22] as a unique opportunity for future experiments, in order to investigate unexplored nonlinear vacuum effects, using laser intensities to 2–4 order higher than the laser intensity used for the first experimental verification of
![]() $e^{-}e^{+}$
pair creation accomplished at SLAC[Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg28]. The experiment consisted of two stages. At first a high energy electron beam interacted with a laser beam via nonlinear Compton scattering producing high energy
$e^{-}e^{+}$
pair creation accomplished at SLAC[Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg28]. The experiment consisted of two stages. At first a high energy electron beam interacted with a laser beam via nonlinear Compton scattering producing high energy
![]() $\unicode[STIX]{x1D6FE}$
photons. These high energy photons then interact with low energy laser photons and electron–positron pairs are created through Breit–Wheeler process[Reference Breit and Wheeler29].
$\unicode[STIX]{x1D6FE}$
photons. These high energy photons then interact with low energy laser photons and electron–positron pairs are created through Breit–Wheeler process[Reference Breit and Wheeler29].
![]() $175\pm 13$
positrons were measured in 21962 laser pulses for a
$175\pm 13$
positrons were measured in 21962 laser pulses for a
![]() $n=5.1\pm 0.2$
(see Ref. [Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg28]) multiphoton order process, a result that is in very good agreement with the theory[Reference Kaberidis, Tsohantjis and Moustaizis30].
$n=5.1\pm 0.2$
(see Ref. [Reference Burke, Field, Horton-Smith, Spencer, Walz, Berridge, Bugg, Shmakov, Weidemann, Bula, McDonald, Prebys, Bamber, Boege, Koffas, Kotseroglou, Melissinos, Meyerhofer, Reis and Ragg28]) multiphoton order process, a result that is in very good agreement with the theory[Reference Kaberidis, Tsohantjis and Moustaizis30].
Based on Popov’s treatment we are going to present our numerical estimates for pair creation efficiency on an E144 like experimental setup that can be realized in the near future by high intensity laser facilities[Reference Perry and Mourou31–39].
Continuing with the presentation of Popov’s theory the probability density is given by Refs. [Reference Popov13–Reference Popov19]
where
![]() $w_{n}$
is the
$w_{n}$
is the
![]() $n$
th multiphoton order probability per Compton volume given by
$n$
th multiphoton order probability per Compton volume given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle w_{n}=\frac{(2s+1)}{2\unicode[STIX]{x1D70B}^{2}V_{c}}\frac{\hslash \unicode[STIX]{x1D714}}{mc^{2}}\left(\frac{n-n_{0}}{\unicode[STIX]{x1D6E5}_{2}}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad J_{n}\exp \left(-\frac{2mc^{2}}{\hslash \unicode[STIX]{x1D714}}f-\frac{2f_{1}}{\unicode[STIX]{x1D6E5}_{1}}(n-n_{0})\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle w_{n}=\frac{(2s+1)}{2\unicode[STIX]{x1D70B}^{2}V_{c}}\frac{\hslash \unicode[STIX]{x1D714}}{mc^{2}}\left(\frac{n-n_{0}}{\unicode[STIX]{x1D6E5}_{2}}\right)^{1/2}\nonumber\\ \displaystyle & & \displaystyle \quad J_{n}\exp \left(-\frac{2mc^{2}}{\hslash \unicode[STIX]{x1D714}}f-\frac{2f_{1}}{\unicode[STIX]{x1D6E5}_{1}}(n-n_{0})\right).\end{eqnarray}$$
In the above relation,
![]() $s$
is a factor that is equal to
$s$
is a factor that is equal to
![]() $0$
for the case of bosons and
$0$
for the case of bosons and
![]() $1/2$
for the case of fermions,
$1/2$
for the case of fermions,
![]() $m_{e}=9.1093\times 10^{-31}~\text{kg}\;(0.5~\text{MeV}~c^{-2})$
for electrons or
$m_{e}=9.1093\times 10^{-31}~\text{kg}\;(0.5~\text{MeV}~c^{-2})$
for electrons or
![]() $m_{\unicode[STIX]{x1D70B}}=2.488\times 10^{-28}~\text{kg}\;(139.570~\text{MeV}~c^{-2})$
for pions,
$m_{\unicode[STIX]{x1D70B}}=2.488\times 10^{-28}~\text{kg}\;(139.570~\text{MeV}~c^{-2})$
for pions,
![]() $V_{c}=\hslash ^{4}/m_{e,\unicode[STIX]{x1D70B}}^{4}c^{5}$
is the electron or pion 4-Compton volume,
$V_{c}=\hslash ^{4}/m_{e,\unicode[STIX]{x1D70B}}^{4}c^{5}$
is the electron or pion 4-Compton volume,
![]() $7.4\times 10^{-59}$
and
$7.4\times 10^{-59}$
and
![]() $2.16\times 10^{-143}~\text{m}^{3}~\text{s}$
, respectively,
$2.16\times 10^{-143}~\text{m}^{3}~\text{s}$
, respectively,
 $$\begin{eqnarray}\displaystyle & & \displaystyle n_{0}=mc^{2}\unicode[STIX]{x1D6E5}/\hslash \unicode[STIX]{x1D714},\quad \unicode[STIX]{x1D6E5}=\frac{4}{\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})}E(\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})),\nonumber\\ \displaystyle & & \displaystyle \quad \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})=1/\sqrt{1+\unicode[STIX]{x1D6FE}^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle n_{0}=mc^{2}\unicode[STIX]{x1D6E5}/\hslash \unicode[STIX]{x1D714},\quad \unicode[STIX]{x1D6E5}=\frac{4}{\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})}E(\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})),\nonumber\\ \displaystyle & & \displaystyle \quad \unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})=1/\sqrt{1+\unicode[STIX]{x1D6FE}^{2}},\end{eqnarray}$$
where
![]() $n_{0}$
is the threshold multiphoton order for pair production to take place and
$n_{0}$
is the threshold multiphoton order for pair production to take place and
![]() $\unicode[STIX]{x1D6E5}$
expresses the effective energy gap width between the continua and
$\unicode[STIX]{x1D6E5}$
expresses the effective energy gap width between the continua and
![]() $E(.)$
is the complete elliptic integral of the second kind. The functions
$E(.)$
is the complete elliptic integral of the second kind. The functions
![]() $\unicode[STIX]{x1D6E5}_{1}$
,
$\unicode[STIX]{x1D6E5}_{1}$
,
![]() $\unicode[STIX]{x1D6E5}_{2}$
,
$\unicode[STIX]{x1D6E5}_{2}$
,
![]() $J_{n}$
,
$J_{n}$
,
![]() $l$
,
$l$
,
![]() $\unicode[STIX]{x1D709}_{n}$
,
$\unicode[STIX]{x1D709}_{n}$
,
![]() $f$
,
$f$
,
![]() $f_{1}$
,
$f_{1}$
,
![]() $f_{2}$
are respectively given by
$f_{2}$
are respectively given by
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{n}=\int _{0}^{1}e^{l(n-n_{0})x^{2}}[1+\unicode[STIX]{x1D70E}(-1)^{n}\cos \unicode[STIX]{x1D709}_{n}x]\,dx, & \displaystyle \nonumber\\ \displaystyle & \displaystyle l=2\left(\frac{f_{1}}{\unicode[STIX]{x1D6E5}_{1}}-\frac{f_{2}}{\unicode[STIX]{x1D6E5}_{2}}\right),\quad x=\frac{p_{\Vert }}{p}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D709}_{n}=2\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})\sqrt{\frac{(n-n_{0})mc^{2}}{\hslash \unicode[STIX]{x1D714}}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f=\frac{\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}}{1+\sqrt{1+\unicode[STIX]{x1D6FE}^{2}}},\quad f_{1}=\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})/2=(1/\unicode[STIX]{x1D6FE})f_{2}, & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{n}=\int _{0}^{1}e^{l(n-n_{0})x^{2}}[1+\unicode[STIX]{x1D70E}(-1)^{n}\cos \unicode[STIX]{x1D709}_{n}x]\,dx, & \displaystyle \nonumber\\ \displaystyle & \displaystyle l=2\left(\frac{f_{1}}{\unicode[STIX]{x1D6E5}_{1}}-\frac{f_{2}}{\unicode[STIX]{x1D6E5}_{2}}\right),\quad x=\frac{p_{\Vert }}{p}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D709}_{n}=2\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})\sqrt{\frac{(n-n_{0})mc^{2}}{\hslash \unicode[STIX]{x1D714}}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f=\frac{\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}}{1+\sqrt{1+\unicode[STIX]{x1D6FE}^{2}}},\quad f_{1}=\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D713}(\unicode[STIX]{x1D6FE})/2=(1/\unicode[STIX]{x1D6FE})f_{2}, & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $K(.)$
is the complete elliptic integrals of the first kind and
$K(.)$
is the complete elliptic integrals of the first kind and
![]() $\unicode[STIX]{x1D70E}=1$
for electrons and
$\unicode[STIX]{x1D70E}=1$
for electrons and
![]() $-1$
for mesons (pions)[Reference Popov13–Reference Popov19] and
$-1$
for mesons (pions)[Reference Popov13–Reference Popov19] and
![]() $p_{\Vert }$
is the parallel to the electric field component of the momentum
$p_{\Vert }$
is the parallel to the electric field component of the momentum
![]() $p$
of the created particle.
$p$
of the created particle.
For the sake of introduction completeness the simplified asymptotic formulas for
![]() $e^{-}e^{+}$
pair creation will be presented even though they will not be used in our estimates. For the two regions of
$e^{-}e^{+}$
pair creation will be presented even though they will not be used in our estimates. For the two regions of
![]() $\unicode[STIX]{x1D6FE}$
that we have mentioned Equation (2) can be simplified. In the case
$\unicode[STIX]{x1D6FE}$
that we have mentioned Equation (2) can be simplified. In the case
![]() $\unicode[STIX]{x1D6FE}\ll 1$
the spectrum of
$\unicode[STIX]{x1D6FE}\ll 1$
the spectrum of
![]() $n\hbar \unicode[STIX]{x1D714}$
of the
$n\hbar \unicode[STIX]{x1D714}$
of the
![]() $n$
-photon processes is practically continuous giving the non-perturbative result[Reference Popov13–Reference Popov19, Reference Ringwald40]
$n$
-photon processes is practically continuous giving the non-perturbative result[Reference Popov13–Reference Popov19, Reference Ringwald40]
 $$\begin{eqnarray}\displaystyle w_{P} & \simeq & \displaystyle \frac{1}{2^{3/2}\unicode[STIX]{x1D70B}^{4}V_{c}}\left({\mathcal{E}}/{\mathcal{E}}_{c}\right)^{5/2}\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(-\unicode[STIX]{x1D70B}({\mathcal{E}}_{c}/{\mathcal{E}})\left(1-\frac{1}{8}\unicode[STIX]{x1D6FE}^{2}+O(\unicode[STIX]{x1D6FE}^{4})\right)\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle w_{P} & \simeq & \displaystyle \frac{1}{2^{3/2}\unicode[STIX]{x1D70B}^{4}V_{c}}\left({\mathcal{E}}/{\mathcal{E}}_{c}\right)^{5/2}\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(-\unicode[STIX]{x1D70B}({\mathcal{E}}_{c}/{\mathcal{E}})\left(1-\frac{1}{8}\unicode[STIX]{x1D6FE}^{2}+O(\unicode[STIX]{x1D6FE}^{4})\right)\right),\nonumber\end{eqnarray}$$
while the number of pairs created is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle N(\unicode[STIX]{x1D70F})=2^{-3/2}n_{0}^{4}\left({\mathcal{E}}/{\mathcal{E}}_{c}\right)^{5/2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \exp \left(-\frac{\unicode[STIX]{x1D70B}{\mathcal{E}}_{c}}{{\mathcal{E}}}\left(1-\frac{1}{2\left(n_{0}\frac{{\mathcal{E}}}{{\mathcal{E}}_{c}}\right)^{2}}\right)\right)(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}/2\unicode[STIX]{x1D70B}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle N(\unicode[STIX]{x1D70F})=2^{-3/2}n_{0}^{4}\left({\mathcal{E}}/{\mathcal{E}}_{c}\right)^{5/2}\nonumber\\ \displaystyle & & \displaystyle \quad \times \exp \left(-\frac{\unicode[STIX]{x1D70B}{\mathcal{E}}_{c}}{{\mathcal{E}}}\left(1-\frac{1}{2\left(n_{0}\frac{{\mathcal{E}}}{{\mathcal{E}}_{c}}\right)^{2}}\right)\right)(\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}/2\unicode[STIX]{x1D70B}),\end{eqnarray}$$
![]() $\unicode[STIX]{x1D70F}$
being the pulse duration. However in the typical multiphoton (and of perturbative nature) case
$\unicode[STIX]{x1D70F}$
being the pulse duration. However in the typical multiphoton (and of perturbative nature) case
![]() $\unicode[STIX]{x1D6FE}\gg 1$
,
$\unicode[STIX]{x1D6FE}\gg 1$
,
where
and Equation (1) yields the estimates[Reference Popov13–Reference Popov19, Reference Ringwald40]
In the following section (Section 2) the numerical estimates on the pair creation efficiency for electron and pion pairs will be presented, using the full formula that describes the whole range of
![]() $~\unicode[STIX]{x1D6FE}$
instead of the simplified ones [Equations (5) and (8)]. The reason for this choice is that the full formula can provide better estimations concerning the efficiency of the created pairs, especially around the area of
$~\unicode[STIX]{x1D6FE}$
instead of the simplified ones [Equations (5) and (8)]. The reason for this choice is that the full formula can provide better estimations concerning the efficiency of the created pairs, especially around the area of
![]() $\unicode[STIX]{x1D6FE}=1$
. The simplified formulas are asymptotic at this area and as we will discuss later do not allow us to observe crossing points between the curves that depict the created pair number versus electric field strength for different electron beam energies. These crossing points cannot be approached using the asymptotic formulas, as they are observed close to the area of
$\unicode[STIX]{x1D6FE}=1$
. The simplified formulas are asymptotic at this area and as we will discuss later do not allow us to observe crossing points between the curves that depict the created pair number versus electric field strength for different electron beam energies. These crossing points cannot be approached using the asymptotic formulas, as they are observed close to the area of
![]() $\unicode[STIX]{x1D6FE}=1.$
Their existence shows that for electric field strength values above the range where the crossing points are, higher multiphoton orders can result to higher creation efficiency. Our aim is to support and emphasize on the advantages of using such schemes to observe pair creation as they can provide satisfactory results. Also our results will show the dependence of efficiency on having an odd or even multiphoton order. In Section 3 our investigation will be extended to study the possible utilization of the proposed scheme to pions pair creation from vacuum by using ultra-intense lasers. This section will be concluded by a proposed mechanism that will enable us to select the type of the created particles. The latter is a quite interesting topic as there is an argument on wether we can reach to the point of creating mesons (pions on our case), or all the available energy will be consumed by the electron–positron pair creation process that requires lower critical electric field strength. The importance of pion creation is that it is closely related to muon creation. Laser generated muons can be applicable as a complementary to the accelerator source[Reference Ishida, Nagamine, Matsuzaki and Kawamura42, Reference Ishida, Nagamine, Matsuzaki and Kawamura43] in muon catalyzed fusion processes and neutrino factories[Reference Choubey, Gandhi, Goswami, Berg, Fernow, Gallardo, Gupta, Kirk, Simos, Souchlas, Ellis, Kyberd, Benedetto, Fernandez-Martinez, Efthymiopoulos, Garoby, Gilardoni, Martini, Prior, Indumathi, Sinha, Ballett, Pascoli, Bross, Geer, Johnstone, Kopp, Mokhov, Morfin, Neuffer, Parke, Popovic, Strait, Striganov, Blondel, Dufour, Laing, Soler, Lindner, Schwetz, Alekou, Apollonio, Aslaninejad, Bontoiu, Dornan, Eccleston, Kurup, Long, Pasternak, Pozimski, Bogacz, Morozov, Roblin, Bhattacharya, Majumdar, Mori, Planche, Zisman, Cline, Stratakis, Ding, Coloma, Donini, Gavela, Lopez Pavon, Maltoni, Bromberg, Bonesini, Hart, Kudenko, Mondal, Antusch, Blennow, Ota, Abrams, Ankenbrandt, Beard, Cummings, Flanagan, Johnson, Roberts, Yoshikawa, Migliozzi, Palladino, de Gouvea, Graves, Kuno, Peltoniemi, Blackmore, Cobb, Witte, Mezzetto, Rigolin, McDonald, Coney, Hanson, Snopok, Tortora, Andreopoulos, Bennett, Brooks, Caretta, Davenne, Densham, Edgecock, Kelliher, Loveridge, McFarland, Machida, Prior, Rees, Rogers, Thomason, Booth, Skoro, Karadzhov, Matev, Tsenov, Samulyak, Mishra, Petti, Dracos, Yasuda, Agarwalla, Cervera-Villanueva, Gomez-Cadenas, Hernandez, Li, Martin-Albo, Huber, Back, Barker, Harrison, Meloni, Tang and Winter44]. To enrich our study, one case that should be examined is the creation of pions from electron–positron collisions as seen in Ref. [Reference Müller, Hatsagortsyan and Keitel45] and to what extent this phenomenon contributes to the total rate of the pion creation.
$\unicode[STIX]{x1D6FE}=1.$
Their existence shows that for electric field strength values above the range where the crossing points are, higher multiphoton orders can result to higher creation efficiency. Our aim is to support and emphasize on the advantages of using such schemes to observe pair creation as they can provide satisfactory results. Also our results will show the dependence of efficiency on having an odd or even multiphoton order. In Section 3 our investigation will be extended to study the possible utilization of the proposed scheme to pions pair creation from vacuum by using ultra-intense lasers. This section will be concluded by a proposed mechanism that will enable us to select the type of the created particles. The latter is a quite interesting topic as there is an argument on wether we can reach to the point of creating mesons (pions on our case), or all the available energy will be consumed by the electron–positron pair creation process that requires lower critical electric field strength. The importance of pion creation is that it is closely related to muon creation. Laser generated muons can be applicable as a complementary to the accelerator source[Reference Ishida, Nagamine, Matsuzaki and Kawamura42, Reference Ishida, Nagamine, Matsuzaki and Kawamura43] in muon catalyzed fusion processes and neutrino factories[Reference Choubey, Gandhi, Goswami, Berg, Fernow, Gallardo, Gupta, Kirk, Simos, Souchlas, Ellis, Kyberd, Benedetto, Fernandez-Martinez, Efthymiopoulos, Garoby, Gilardoni, Martini, Prior, Indumathi, Sinha, Ballett, Pascoli, Bross, Geer, Johnstone, Kopp, Mokhov, Morfin, Neuffer, Parke, Popovic, Strait, Striganov, Blondel, Dufour, Laing, Soler, Lindner, Schwetz, Alekou, Apollonio, Aslaninejad, Bontoiu, Dornan, Eccleston, Kurup, Long, Pasternak, Pozimski, Bogacz, Morozov, Roblin, Bhattacharya, Majumdar, Mori, Planche, Zisman, Cline, Stratakis, Ding, Coloma, Donini, Gavela, Lopez Pavon, Maltoni, Bromberg, Bonesini, Hart, Kudenko, Mondal, Antusch, Blennow, Ota, Abrams, Ankenbrandt, Beard, Cummings, Flanagan, Johnson, Roberts, Yoshikawa, Migliozzi, Palladino, de Gouvea, Graves, Kuno, Peltoniemi, Blackmore, Cobb, Witte, Mezzetto, Rigolin, McDonald, Coney, Hanson, Snopok, Tortora, Andreopoulos, Bennett, Brooks, Caretta, Davenne, Densham, Edgecock, Kelliher, Loveridge, McFarland, Machida, Prior, Rees, Rogers, Thomason, Booth, Skoro, Karadzhov, Matev, Tsenov, Samulyak, Mishra, Petti, Dracos, Yasuda, Agarwalla, Cervera-Villanueva, Gomez-Cadenas, Hernandez, Li, Martin-Albo, Huber, Back, Barker, Harrison, Meloni, Tang and Winter44]. To enrich our study, one case that should be examined is the creation of pions from electron–positron collisions as seen in Ref. [Reference Müller, Hatsagortsyan and Keitel45] and to what extent this phenomenon contributes to the total rate of the pion creation.
For the numerical estimates of created pairs, to be presented, it is adequate to use Equation (2) for the case of
![]() $n=n_{0}+1$
, as this term will give the maximum contribution. Thus for the given particle mass and for a specific range of electric field strength
$n=n_{0}+1$
, as this term will give the maximum contribution. Thus for the given particle mass and for a specific range of electric field strength
![]() ${\mathcal{E}}$
we evaluate the multiphoton order
${\mathcal{E}}$
we evaluate the multiphoton order
![]() $n_{0}$
according to Equation (3). Then for
$n_{0}$
according to Equation (3). Then for
![]() $n=n_{0}+1$
we estimate
$n=n_{0}+1$
we estimate
![]() $w_{n}$
[Reference Popov13–Reference Popov18]. To avoid numerical evaluation discontinuities, when using Equations (2) and (4), we round
$w_{n}$
[Reference Popov13–Reference Popov18]. To avoid numerical evaluation discontinuities, when using Equations (2) and (4), we round
![]() $n_{0}+1$
up to the closest integral value which we denote by
$n_{0}+1$
up to the closest integral value which we denote by
![]() $[n_{0}+1]$
. Consequently as
$[n_{0}+1]$
. Consequently as
![]() ${\mathcal{E}}$
increases,
${\mathcal{E}}$
increases,
![]() $[n_{0}+1]$
, takes even and odd values and thus because of the term
$[n_{0}+1]$
, takes even and odd values and thus because of the term
![]() $1+\unicode[STIX]{x1D70E}(-1)^{[n_{0}+1]}\cos \unicode[STIX]{x1D709}_{n}x$
in
$1+\unicode[STIX]{x1D70E}(-1)^{[n_{0}+1]}\cos \unicode[STIX]{x1D709}_{n}x$
in
![]() $J_{n}$
,
$J_{n}$
,
![]() $w_{n}$
oscillates accordingly, as can be seen in all figures below. Note that this oscillation is present both in the creation of fermions (
$w_{n}$
oscillates accordingly, as can be seen in all figures below. Note that this oscillation is present both in the creation of fermions (
![]() $\unicode[STIX]{x1D70E}=-1$
) and bosons (
$\unicode[STIX]{x1D70E}=-1$
) and bosons (
![]() $\unicode[STIX]{x1D70E}=1$
). However, as expected, this oscillation is strongly manifested when we attempt to observe created pairs with
$\unicode[STIX]{x1D70E}=1$
). However, as expected, this oscillation is strongly manifested when we attempt to observe created pairs with
![]() $p_{\Vert }=0$
. In this case
$p_{\Vert }=0$
. In this case
![]() $w_{n}\propto$
$w_{n}\propto$
![]() $1+\unicode[STIX]{x1D70E}(-1)^{n}$
giving the known selection rule: fermions (with
$1+\unicode[STIX]{x1D70E}(-1)^{n}$
giving the known selection rule: fermions (with
![]() $p_{\Vert }=0$
) are created by odd harmonics while bosons (with
$p_{\Vert }=0$
) are created by odd harmonics while bosons (with
![]() $p_{\Vert }=0$
) by even ones.
$p_{\Vert }=0$
) by even ones.
Since
![]() $e^{+}-e^{-}$
and
$e^{+}-e^{-}$
and
![]() $\unicode[STIX]{x1D70B}^{+}-\unicode[STIX]{x1D70B}^{-}$
pair creation occur for different particle masses and electric field strength ranges, probabilities and pair number creations are obviously estimated separately.
$\unicode[STIX]{x1D70B}^{+}-\unicode[STIX]{x1D70B}^{-}$
pair creation occur for different particle masses and electric field strength ranges, probabilities and pair number creations are obviously estimated separately.
As mentioned above, our aim is to apply and investigate numerically Popov’s theory to an E144 like experimental setup. However it is worth commenting on the efficiency of other physical mechanisms that one can implement in such a setup. In particular, if we choose to implement the Breit–Wheeler mechanism via nonlinear Compton scattering, taking also into account radiation losses during electron–photon collision, the efficiency is lower than that of Popov’s theory due to low cross-section of the above events.
An interesting scheme is proposed at the recent work of Ref. [Reference Pike, Mackenroth, Hill and Rose46]. Experimental verification of
![]() $e^{+}e^{-}$
pair creation is examined through a two-stage process. At first a high energy electron beam interacts with a solid target producing gamma photons. At the second stage gamma photons collide with x-ray photons originated from laser heated hohlraum leading to
$e^{+}e^{-}$
pair creation is examined through a two-stage process. At first a high energy electron beam interacts with a solid target producing gamma photons. At the second stage gamma photons collide with x-ray photons originated from laser heated hohlraum leading to
![]() $e^{+}e^{-}$
pairs through the Breit–Wheeler mechanism. Even though this setup is not similar to the one proposed in our work, it is a perfect example of an optimized Breit–Wheeler process.
$e^{+}e^{-}$
pairs through the Breit–Wheeler mechanism. Even though this setup is not similar to the one proposed in our work, it is a perfect example of an optimized Breit–Wheeler process.
We modeled the two step scheme (1st step: electron beam–laser beam interaction, 2nd step: high energy photon–laser interaction) with the parameters used in Ref. [Reference Pike, Mackenroth, Hill and Rose46], obtaining analogous results to those presented. Afterward our intention is to examine that scheme using parameters that were selected for our scheme. According to the calculations presented in Ref. [Reference Pike, Mackenroth, Hill and Rose46] and also those carried out on our behalf, the estimated efficiency is up to
![]() $10^{4}$
–
$10^{4}$
–
![]() $10^{5}$
at best, for an electron beam of
$10^{5}$
at best, for an electron beam of
![]() $10^{9}$
electrons and hohlraum temperature
$10^{9}$
electrons and hohlraum temperature
![]() ${\sim}300~\text{keV}$
. If we implement the parameters used in our scheme, pair creation efficiency is expected to be lower, leading to
${\sim}300~\text{keV}$
. If we implement the parameters used in our scheme, pair creation efficiency is expected to be lower, leading to
![]() $10^{2}$
–
$10^{2}$
–
![]() $10^{3}$
pairs. This result indicates the possible contribution of Breit–Wheeler mechanism to our scheme. It is quite lower than the one estimated from the Popov’s theory.
$10^{3}$
pairs. This result indicates the possible contribution of Breit–Wheeler mechanism to our scheme. It is quite lower than the one estimated from the Popov’s theory.
The proposed scheme in Ref. [Reference Pike, Mackenroth, Hill and Rose46] is a well thought setup as it can be very efficient in terms of photon population of both gamma and x-ray photons. However it will require an NIF like facility in order to achieve the required electron number and hohlraum heating in the maximum temperatures presented. A scheme that would require a Petawatt laser facility like the one described in this paper, would lower the whole cost.
2 Pair creation using an E144 analogous scheme:
 $e^{+}e^{-}$
case
$e^{+}e^{-}$
case
Consider an experimental configuration where on the first step a high focal intensity (for the ELI system values of
![]() $I\sim 10^{24}~\text{W}~\text{cm}^{-2}$
can be achieved) ultra-short (
$I\sim 10^{24}~\text{W}~\text{cm}^{-2}$
can be achieved) ultra-short (
![]() $\unicode[STIX]{x1D70F}\sim 150~\text{fs}$
) laser beam of
$\unicode[STIX]{x1D70F}\sim 150~\text{fs}$
) laser beam of
![]() $\hbar \unicode[STIX]{x1D714}=1~\text{eV}$
, is used to produce and accelerate an electron beam (of charge
$\hbar \unicode[STIX]{x1D714}=1~\text{eV}$
, is used to produce and accelerate an electron beam (of charge
![]() ${\sim}1~\text{nC}$
) to reach the relativistic energy regime of some GeV (theoretical estimates for the ELI system allow up to 100 GeV[36]) as is described in Refs. [Reference Malka, Faure, Glinec, Pukhov and Rousseau47–Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick50]. On the second step this electron beam collides head on with the same focused laser beam (so that the effect of the magnetic field is negligible and
${\sim}1~\text{nC}$
) to reach the relativistic energy regime of some GeV (theoretical estimates for the ELI system allow up to 100 GeV[36]) as is described in Refs. [Reference Malka, Faure, Glinec, Pukhov and Rousseau47–Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick50]. On the second step this electron beam collides head on with the same focused laser beam (so that the effect of the magnetic field is negligible and
![]() ${\mathcal{F}}<0$
). In the electron’s frame of reference the photons have energy
${\mathcal{F}}<0$
). In the electron’s frame of reference the photons have energy
![]() $\hbar \unicode[STIX]{x1D714}^{\ast }=\unicode[STIX]{x1D6FE}_{L}\hbar \unicode[STIX]{x1D714}$
where
$\hbar \unicode[STIX]{x1D714}^{\ast }=\unicode[STIX]{x1D6FE}_{L}\hbar \unicode[STIX]{x1D714}$
where
![]() $\unicode[STIX]{x1D6FE}_{L}=E_{e\text{-}\text{beam}}/mc^{2}$
is the Lorentz factor and the electric field strength is
$\unicode[STIX]{x1D6FE}_{L}=E_{e\text{-}\text{beam}}/mc^{2}$
is the Lorentz factor and the electric field strength is
![]() ${\mathcal{E}}^{\ast }=\unicode[STIX]{x1D6FE}_{L}{\mathcal{E}}$
. This configuration is analogous to the E144 experiment (see also Ref. [Reference Ploumistakis, Moustaizis and Tsohantjis8]).
${\mathcal{E}}^{\ast }=\unicode[STIX]{x1D6FE}_{L}{\mathcal{E}}$
. This configuration is analogous to the E144 experiment (see also Ref. [Reference Ploumistakis, Moustaizis and Tsohantjis8]).
In Figure 1, we present the log plot of the
![]() $[n_{0}+1]$
th multiphoton order probability density [Equation (2)], as a function of
$[n_{0}+1]$
th multiphoton order probability density [Equation (2)], as a function of
![]() ${\mathcal{E}}^{\ast }$
, for the case of
${\mathcal{E}}^{\ast }$
, for the case of
![]() $E_{e\text{-}\text{beam}}=10~\text{GeV}$
. In this case
$E_{e\text{-}\text{beam}}=10~\text{GeV}$
. In this case
![]() $\unicode[STIX]{x1D6FE}_{L}=2\times 10^{4}$
and we have taken values of
$\unicode[STIX]{x1D6FE}_{L}=2\times 10^{4}$
and we have taken values of
![]() ${\mathcal{E}}^{\ast }$
between
${\mathcal{E}}^{\ast }$
between
![]() $2\times 10^{16}{-}4\times 10^{17}~\text{V}~\text{m}^{-1}$
, which in turn via Equation (3)
$2\times 10^{16}{-}4\times 10^{17}~\text{V}~\text{m}^{-1}$
, which in turn via Equation (3)
![]() $[n_{0}+1]$
takes values between 185 and 245. As expected the oscillation between even and odd values of
$[n_{0}+1]$
takes values between 185 and 245. As expected the oscillation between even and odd values of
![]() $[n_{0}+1]$
is explicitly shown with the upper dashes corresponding to odd and the lower dashes to even ones.
$[n_{0}+1]$
is explicitly shown with the upper dashes corresponding to odd and the lower dashes to even ones.

Figure 1. Pair creation probability per unit volume and unit time
![]() $w_{n}$
as a function of electric field strength
$w_{n}$
as a function of electric field strength
![]() ${\mathcal{E}}^{\ast }$
for
${\mathcal{E}}^{\ast }$
for
![]() $E_{e\text{-}\text{beam}}=$
10 GeV. Vertical straight line represents the electric field strength that corresponds to
$E_{e\text{-}\text{beam}}=$
10 GeV. Vertical straight line represents the electric field strength that corresponds to
![]() $\unicode[STIX]{x1D6FE}=1$
,
$\unicode[STIX]{x1D6FE}=1$
,
![]() $({\mathcal{E}}^{\ast }=5.46\times 10^{16}~\text{V}~\text{m}^{-1})$
.
$({\mathcal{E}}^{\ast }=5.46\times 10^{16}~\text{V}~\text{m}^{-1})$
.
In Figure 2, we present the log plot of the number of pairs
![]() $N_{n}=Vw_{n}$
as a function of
$N_{n}=Vw_{n}$
as a function of
![]() ${\mathcal{E}}^{\ast }$
, corresponding to Figure 1. For a typical interaction 4-volume, taken to be
${\mathcal{E}}^{\ast }$
, corresponding to Figure 1. For a typical interaction 4-volume, taken to be
![]() $V=10\unicode[STIX]{x1D706}^{3}\unicode[STIX]{x1D70F}\sim 10^{-48}~\text{m}^{3}~\text{s}$
,
$V=10\unicode[STIX]{x1D706}^{3}\unicode[STIX]{x1D70F}\sim 10^{-48}~\text{m}^{3}~\text{s}$
,
![]() $\unicode[STIX]{x1D706}$
being the laser beam wavelength and
$\unicode[STIX]{x1D706}$
being the laser beam wavelength and
![]() $\unicode[STIX]{x1D70F}$
the pulse duration, (see also Ref. [Reference Ploumistakis, Moustaizis and Tsohantjis8]),
$\unicode[STIX]{x1D70F}$
the pulse duration, (see also Ref. [Reference Ploumistakis, Moustaizis and Tsohantjis8]),
![]() $N_{n}$
varies from 5 to 120 pairs per laser shot. The case
$N_{n}$
varies from 5 to 120 pairs per laser shot. The case
![]() $\unicode[STIX]{x1D6FE}\sim 1$
corresponding to
$\unicode[STIX]{x1D6FE}\sim 1$
corresponding to
![]() ${\mathcal{E}}^{\ast }\sim 5\times 10^{16}~\text{V}~\text{m}^{-1}$
,
${\mathcal{E}}^{\ast }\sim 5\times 10^{16}~\text{V}~\text{m}^{-1}$
,
![]() $n_{0}\sim 57$
, is not shown here as it leads to very low number of pairs (per laser shot).
$n_{0}\sim 57$
, is not shown here as it leads to very low number of pairs (per laser shot).

Figure 2. Pair number
![]() $N_{n}$
as a function of electric field strength
$N_{n}$
as a function of electric field strength
![]() ${\mathcal{E}}^{\ast }$
for
${\mathcal{E}}^{\ast }$
for
![]() $E_{e\text{-}\text{beam}}=10~\text{GeV}$
. The case
$E_{e\text{-}\text{beam}}=10~\text{GeV}$
. The case
![]() $\unicode[STIX]{x1D6FE}\sim 1$
corresponding to
$\unicode[STIX]{x1D6FE}\sim 1$
corresponding to
![]() ${\mathcal{E}}^{\ast }\sim 5\times 10^{16}~\text{V}~\text{m}^{-1}$
, is not shown here as it leads to very low number of pairs (per laser shot).
${\mathcal{E}}^{\ast }\sim 5\times 10^{16}~\text{V}~\text{m}^{-1}$
, is not shown here as it leads to very low number of pairs (per laser shot).
However in Figure 3, the log plot of
![]() $N_{n}$
as a function of
$N_{n}$
as a function of
![]() ${\mathcal{E}}^{\ast }$
for the case of
${\mathcal{E}}^{\ast }$
for the case of
![]() $E_{e\text{-}\text{beam}}=100~\text{GeV}$
(
$E_{e\text{-}\text{beam}}=100~\text{GeV}$
(
![]() $\unicode[STIX]{x1D6FE}_{L}=2\times 10^{5}$
) is presented showing clearly the region of
$\unicode[STIX]{x1D6FE}_{L}=2\times 10^{5}$
) is presented showing clearly the region of
![]() $\unicode[STIX]{x1D6FE}\sim 1$
corresponding to
$\unicode[STIX]{x1D6FE}\sim 1$
corresponding to
![]() ${\mathcal{E}}^{\ast }\sim 5.46\times 10^{17}~\text{V}~\text{m}^{-1}$
,
${\mathcal{E}}^{\ast }\sim 5.46\times 10^{17}~\text{V}~\text{m}^{-1}$
,
![]() $n_{0}\sim 5$
giving approximately 100 pairs (per laser shot and the same interaction 4-volume). The region in the curve left of the value
$n_{0}\sim 5$
giving approximately 100 pairs (per laser shot and the same interaction 4-volume). The region in the curve left of the value
![]() ${\mathcal{E}}^{\ast }\sim 5\times 10^{17}~\text{V}~\text{m}^{-1}$
corresponds to
${\mathcal{E}}^{\ast }\sim 5\times 10^{17}~\text{V}~\text{m}^{-1}$
corresponds to
![]() $\unicode[STIX]{x1D6FE}\succ 1$
(typical multiphoton) and the right region to
$\unicode[STIX]{x1D6FE}\succ 1$
(typical multiphoton) and the right region to
![]() $\unicode[STIX]{x1D6FE}\prec 1$
(field effect).
$\unicode[STIX]{x1D6FE}\prec 1$
(field effect).

Figure 3. Pair number
![]() $N_{n}$
as a function of electric field strength
$N_{n}$
as a function of electric field strength
![]() ${\mathcal{E}}^{\ast }$
for
${\mathcal{E}}^{\ast }$
for
![]() $E_{e\text{-}\text{beam}}=100~\text{GeV}$
. Vertical straight line represents the electric field strength that corresponds to
$E_{e\text{-}\text{beam}}=100~\text{GeV}$
. Vertical straight line represents the electric field strength that corresponds to
![]() $\unicode[STIX]{x1D6FE}=1$
, (
$\unicode[STIX]{x1D6FE}=1$
, (
![]() ${\mathcal{E}}^{\ast }=5.46\times 10^{17}~\text{V}~\text{m}^{-1}$
).
${\mathcal{E}}^{\ast }=5.46\times 10^{17}~\text{V}~\text{m}^{-1}$
).
In Figure 4, the dependence of created pair number
![]() $N_{n}$
from
$N_{n}$
from
![]() ${\mathcal{E}}^{\ast }$
is presented, for three cases
${\mathcal{E}}^{\ast }$
is presented, for three cases
![]() $E_{e\text{-}\text{beam}}=50~\text{GeV}\;(\unicode[STIX]{x1D6FE}_{L}=1\times 10^{5})$
(a curve),
$E_{e\text{-}\text{beam}}=50~\text{GeV}\;(\unicode[STIX]{x1D6FE}_{L}=1\times 10^{5})$
(a curve),
![]() $100~\text{GeV}$
(
$100~\text{GeV}$
(
![]() $\unicode[STIX]{x1D6FE}_{L}=2\times 10^{5}$
) (b curve) and 200 GeV (
$\unicode[STIX]{x1D6FE}_{L}=2\times 10^{5}$
) (b curve) and 200 GeV (
![]() $\unicode[STIX]{x1D6FE}_{L}=4\times 10^{5}$
) (c curve). The 200 GeV case might be achievable in the future[39]. Here the existence of crossing points between the curves is demonstrated as expected, due to the multiphoton nature of the process (i.e., for a range of
$\unicode[STIX]{x1D6FE}_{L}=4\times 10^{5}$
) (c curve). The 200 GeV case might be achievable in the future[39]. Here the existence of crossing points between the curves is demonstrated as expected, due to the multiphoton nature of the process (i.e., for a range of
![]() ${\mathcal{E}}^{\ast }$
values, the pair creation efficiency is equal for different beam photon energies
${\mathcal{E}}^{\ast }$
values, the pair creation efficiency is equal for different beam photon energies
![]() $\hbar \unicode[STIX]{x1D714}^{\ast }$
). In fact crossing points appear (i) between the 50 GeV and the 100 GeV curves, at
$\hbar \unicode[STIX]{x1D714}^{\ast }$
). In fact crossing points appear (i) between the 50 GeV and the 100 GeV curves, at
![]() ${\mathcal{E}}^{\ast }\sim 4.9\times 10^{17}~\text{V}~\text{m}^{-1}$
and
${\mathcal{E}}^{\ast }\sim 4.9\times 10^{17}~\text{V}~\text{m}^{-1}$
and
![]() $N_{n}\sim 10$
pairs, (ii) between the 200 GeV and the 100 GeV curves, at
$N_{n}\sim 10$
pairs, (ii) between the 200 GeV and the 100 GeV curves, at
![]() ${\mathcal{E}}^{\ast }\sim 5.1\times 10^{17}~\text{V}~\text{m}^{-1}$
and
${\mathcal{E}}^{\ast }\sim 5.1\times 10^{17}~\text{V}~\text{m}^{-1}$
and
![]() $N_{n}\sim 100$
pairs, (iii) between the 50 GeV and the 200 GeV curves, at
$N_{n}\sim 100$
pairs, (iii) between the 50 GeV and the 200 GeV curves, at
![]() ${\mathcal{E}}^{\ast }\sim 5\times 10^{17}~\text{V}~\text{m}^{-1}$
and
${\mathcal{E}}^{\ast }\sim 5\times 10^{17}~\text{V}~\text{m}^{-1}$
and
![]() $N_{n}\sim 100$
pairs. For the 50 GeV top curve
$N_{n}\sim 100$
pairs. For the 50 GeV top curve
![]() $n_{0}$
ranges from 12 to 50 for the
$n_{0}$
ranges from 12 to 50 for the
![]() ${\mathcal{E}}^{\ast }$
values shown, for the 100 GeV middle curve
${\mathcal{E}}^{\ast }$
values shown, for the 100 GeV middle curve
![]() $n_{0}$
ranges from 6 to 14 for the
$n_{0}$
ranges from 6 to 14 for the
![]() ${\mathcal{E}}^{\ast }$
values shown and for the 200 GeV bottom curve
${\mathcal{E}}^{\ast }$
values shown and for the 200 GeV bottom curve
![]() $n_{0}$
ranges from 3 to 5 for the
$n_{0}$
ranges from 3 to 5 for the
![]() ${\mathcal{E}}^{\ast }$
values shown. Thus the higher the beam energy
${\mathcal{E}}^{\ast }$
values shown. Thus the higher the beam energy
![]() $E_{e\text{-}\text{beam}}$
, the lower the number of the created pairs and multiphoton order
$E_{e\text{-}\text{beam}}$
, the lower the number of the created pairs and multiphoton order
![]() $n_{0}$
for fixed common range of
$n_{0}$
for fixed common range of
![]() ${\mathcal{E}}^{\ast }$
values. In fact the higher the
${\mathcal{E}}^{\ast }$
values. In fact the higher the
![]() $E_{e\text{-}\text{beam}}$
becomes, pair creation process tends to become an almost single photon one.
$E_{e\text{-}\text{beam}}$
becomes, pair creation process tends to become an almost single photon one.

Figure 4. Electron–positron pair number
![]() $N_{n}$
as a function of electric field strength
$N_{n}$
as a function of electric field strength
![]() ${\mathcal{E}}^{\ast }$
for
${\mathcal{E}}^{\ast }$
for
![]() $E_{e\text{-}\text{beam}}=(\text{a})~50$
, (b) 100 and (c) 200 GeV. Vertical straight line represents the electric field strength that corresponds to
$E_{e\text{-}\text{beam}}=(\text{a})~50$
, (b) 100 and (c) 200 GeV. Vertical straight line represents the electric field strength that corresponds to
![]() $\unicode[STIX]{x1D6FE}=1$
,
$\unicode[STIX]{x1D6FE}=1$
,
![]() $({\mathcal{E}}^{\ast }=5.46\times 10^{17}~\text{V}~\text{m}^{-1})$
.
$({\mathcal{E}}^{\ast }=5.46\times 10^{17}~\text{V}~\text{m}^{-1})$
.
3 Pair creation using an E144 analogous scheme:
 $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
case
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
case
In this section pion pair creation is examined by considering the same setup as before. Pions are particles of
![]() $139.570~\text{MeV}~c^{-2}$
mass and of the same charge with electrons. The critical field strength for
$139.570~\text{MeV}~c^{-2}$
mass and of the same charge with electrons. The critical field strength for
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
production is
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
production is
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D70B}}=(m_{\unicode[STIX]{x1D70B}}c^{2})/e\unicode[STIX]{x1D706}_{c\unicode[STIX]{x1D70B}}=1.041\times 10^{23}~\text{V}~\text{m}^{-1}$
(
${\mathcal{E}}_{c\unicode[STIX]{x1D70B}}=(m_{\unicode[STIX]{x1D70B}}c^{2})/e\unicode[STIX]{x1D706}_{c\unicode[STIX]{x1D70B}}=1.041\times 10^{23}~\text{V}~\text{m}^{-1}$
(
![]() $\unicode[STIX]{x1D706}_{c\unicode[STIX]{x1D70B}}=11.7\times 10^{-15}~\text{m}$
) and the corresponding critical laser intensity is of the order of
$\unicode[STIX]{x1D706}_{c\unicode[STIX]{x1D70B}}=11.7\times 10^{-15}~\text{m}$
) and the corresponding critical laser intensity is of the order of
![]() $10^{43}~\text{W}~\text{m}^{-2}$
. To achieve these values, an XFEL laser beam of
$10^{43}~\text{W}~\text{m}^{-2}$
. To achieve these values, an XFEL laser beam of
![]() $\hbar \unicode[STIX]{x1D714}=100~\text{eV}$
, can be used to produce and accelerate an electron beam (as is described in Refs. [Reference Malka, Faure, Glinec, Pukhov and Rousseau47–Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick50]) which collides head on with the same focused XFEL laser beam. Again in the electron’s frame of reference, photon energy will transform to
$\hbar \unicode[STIX]{x1D714}=100~\text{eV}$
, can be used to produce and accelerate an electron beam (as is described in Refs. [Reference Malka, Faure, Glinec, Pukhov and Rousseau47–Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick50]) which collides head on with the same focused XFEL laser beam. Again in the electron’s frame of reference, photon energy will transform to
![]() $\hbar \unicode[STIX]{x1D714}^{\ast }=\unicode[STIX]{x1D6FE}_{L}\hbar \unicode[STIX]{x1D714}$
where the Lorentz factor is
$\hbar \unicode[STIX]{x1D714}^{\ast }=\unicode[STIX]{x1D6FE}_{L}\hbar \unicode[STIX]{x1D714}$
where the Lorentz factor is
![]() $\unicode[STIX]{x1D6FE}_{L}=E_{e\text{-}\text{beam}}/mc^{2}$
. The choice of an XFEL is justified by the fact of the high power density needed which cannot be provided by typical lasers.
$\unicode[STIX]{x1D6FE}_{L}=E_{e\text{-}\text{beam}}/mc^{2}$
. The choice of an XFEL is justified by the fact of the high power density needed which cannot be provided by typical lasers.
In Figure 5, the results for
![]() $N_{n}$
(analogous to that of Figure 4 for
$N_{n}$
(analogous to that of Figure 4 for
![]() $e^{+}e^{-}$
production) are presented, for
$e^{+}e^{-}$
production) are presented, for
![]() $E_{e\text{-}\text{beam}}=0.1~\text{GeV}$
(
$E_{e\text{-}\text{beam}}=0.1~\text{GeV}$
(
![]() $\unicode[STIX]{x1D6FE}_{L}=20$
, top curve), 1 GeV (
$\unicode[STIX]{x1D6FE}_{L}=20$
, top curve), 1 GeV (
![]() $\unicode[STIX]{x1D6FE}_{L}=2\times 10^{3}$
, middle curve), 10 GeV (
$\unicode[STIX]{x1D6FE}_{L}=2\times 10^{3}$
, middle curve), 10 GeV (
![]() $\unicode[STIX]{x1D6FE}_{L}=2\times 10^{4}$
, bottom curve) and for the selected range of values of
$\unicode[STIX]{x1D6FE}_{L}=2\times 10^{4}$
, bottom curve) and for the selected range of values of
![]() ${\mathcal{E}}^{\ast }$
shown. These numerical estimates have again been extracted using Equations (2)–(4) and for an interaction 4-volume
${\mathcal{E}}^{\ast }$
shown. These numerical estimates have again been extracted using Equations (2)–(4) and for an interaction 4-volume
![]() $V=10\unicode[STIX]{x1D706}^{3}\unicode[STIX]{x1D70F}\sim 10^{-46}~\text{m}^{3}\text{s}$
(with
$V=10\unicode[STIX]{x1D706}^{3}\unicode[STIX]{x1D70F}\sim 10^{-46}~\text{m}^{3}\text{s}$
(with
![]() $\unicode[STIX]{x1D706}\sim 10^{-8}~\text{m}$
,
$\unicode[STIX]{x1D706}\sim 10^{-8}~\text{m}$
,
![]() $\unicode[STIX]{x1D70F}\sim 0.1~\text{fs}$
see also Ref. [Reference Mourou and Tajima41]). For the top curve the range of threshold multiphoton orders
$\unicode[STIX]{x1D70F}\sim 0.1~\text{fs}$
see also Ref. [Reference Mourou and Tajima41]). For the top curve the range of threshold multiphoton orders
![]() $n_{0}$
is approximately from
$n_{0}$
is approximately from
![]() $10^{8}$
to
$10^{8}$
to
![]() $10^{9}$
, for the middle curve from
$10^{9}$
, for the middle curve from
![]() $10^{6}$
to
$10^{6}$
to
![]() $10^{7}$
and for the bottom curve from
$10^{7}$
and for the bottom curve from
![]() $300$
to
$300$
to
![]() $2000$
. Note that in all three cases
$2000$
. Note that in all three cases
![]() $\unicode[STIX]{x1D6FE}<1$
which, consistently with the high multiphoton orders, means that in order to have measurable
$\unicode[STIX]{x1D6FE}<1$
which, consistently with the high multiphoton orders, means that in order to have measurable
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair numbers, we have to focus in the field effect regime. Incidentally the crossing points appear for values of
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair numbers, we have to focus in the field effect regime. Incidentally the crossing points appear for values of
![]() ${\mathcal{E}}^{\ast }$
quite lower from
${\mathcal{E}}^{\ast }$
quite lower from
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
and of extremely low pair production efficiency.
${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
and of extremely low pair production efficiency.

Figure 5. Pion pair number
![]() $N_{n}$
as a function of electric field strength
$N_{n}$
as a function of electric field strength
![]() ${\mathcal{E}}^{\ast }$
for
${\mathcal{E}}^{\ast }$
for
![]() $E_{e\text{-}\text{beam}}=$
energies of (a) 0.1, (b) 1 and (c) 10 GeV. Vertical straight line represents the electric field strength that corresponds to
$E_{e\text{-}\text{beam}}=$
energies of (a) 0.1, (b) 1 and (c) 10 GeV. Vertical straight line represents the electric field strength that corresponds to
![]() $\unicode[STIX]{x1D6FE}=1$
,
$\unicode[STIX]{x1D6FE}=1$
,
![]() $({\mathcal{E}}^{\ast }=1.12\times 10^{21}~\text{V}~\text{m}^{-1})$
.
$({\mathcal{E}}^{\ast }=1.12\times 10^{21}~\text{V}~\text{m}^{-1})$
.
From the above analysis it is expected that according to the imaginary time method, adequate number of pion pairs can be detected in the field effect region of
![]() $\unicode[STIX]{x1D6FE}<1$
and for high multiphoton threshold orders.
$\unicode[STIX]{x1D6FE}<1$
and for high multiphoton threshold orders.
4 Conclusions
In this paper, we presented numerical estimates for
![]() $e^{+}e^{-}$
and
$e^{+}e^{-}$
and
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation by implementing the imaginary type method. Also a setup that could be used to experimentally produce electrons or pions was described based on the same principles as E144 experiment. The efficiency of
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation by implementing the imaginary type method. Also a setup that could be used to experimentally produce electrons or pions was described based on the same principles as E144 experiment. The efficiency of
![]() $e^{+}e^{-}$
and
$e^{+}e^{-}$
and
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation presented can be considered satisfactory for an experimental verification given the recent developments of high intensity laser facilities such as ELI or laser systems such as those investigated in IZEST project[Reference Quinn, Wheeler, Miquel, Zamfir and Sergeev51]. The choice of the specific interaction volumes used, aims mainly at obtaining reasonable estimates on the created pairs number without having to go to the diffraction limit of the laser beam.
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation presented can be considered satisfactory for an experimental verification given the recent developments of high intensity laser facilities such as ELI or laser systems such as those investigated in IZEST project[Reference Quinn, Wheeler, Miquel, Zamfir and Sergeev51]. The choice of the specific interaction volumes used, aims mainly at obtaining reasonable estimates on the created pairs number without having to go to the diffraction limit of the laser beam.
The crucial question that now arises is what occurs as far as the efficiency of pion pair detection concerns, near the critical pion field
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
where both
${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
where both
![]() $e^{+}e^{-}$
and
$e^{+}e^{-}$
and
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
are present. In particular, as dictated by energy conservation and the uncertainty principle, there is exactly one
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
are present. In particular, as dictated by energy conservation and the uncertainty principle, there is exactly one
![]() $e^{+}e^{-}$
pair produced at
$e^{+}e^{-}$
pair produced at
![]() ${\mathcal{E}}_{ce}$
and at the electron’s 4-Compton volume
${\mathcal{E}}_{ce}$
and at the electron’s 4-Compton volume
![]() $\unicode[STIX]{x1D706}_{ce}^{3}\times \unicode[STIX]{x1D706}_{ce}/c=7.4\times 10^{-59}~\text{m}^{3}~\text{s}$
while exceeding
$\unicode[STIX]{x1D706}_{ce}^{3}\times \unicode[STIX]{x1D706}_{ce}/c=7.4\times 10^{-59}~\text{m}^{3}~\text{s}$
while exceeding
![]() ${\mathcal{E}}_{ce}$
, as we approach
${\mathcal{E}}_{ce}$
, as we approach
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
, the number of
${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
, the number of
![]() $e^{+}e^{-}$
pairs created, in a typical interaction volume (say close to the laser diffraction limit), remains constant (that is why the plots in Figures 1–4, terminate at
$e^{+}e^{-}$
pairs created, in a typical interaction volume (say close to the laser diffraction limit), remains constant (that is why the plots in Figures 1–4, terminate at
![]() ${\mathcal{E}}^{\ast }={\mathcal{E}}_{ce}$
). However these
${\mathcal{E}}^{\ast }={\mathcal{E}}_{ce}$
). However these
![]() $e^{+}e^{-}$
pairs acquire spacial momentum as they are accelerated by the laser electric field within this small interaction volume, thus absorbing energy from the electric field. Consequently, approaching
$e^{+}e^{-}$
pairs acquire spacial momentum as they are accelerated by the laser electric field within this small interaction volume, thus absorbing energy from the electric field. Consequently, approaching
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D70B}}>{\mathcal{E}}_{ce}$
, we must examine whether there should be enough energy left for efficient pion pair production.
${\mathcal{E}}_{c\unicode[STIX]{x1D70B}}>{\mathcal{E}}_{ce}$
, we must examine whether there should be enough energy left for efficient pion pair production.
The resolution to this problem is to attempt to establish a kind of selection or better tunability process between the generation of
![]() $e^{+}e^{-}$
and
$e^{+}e^{-}$
and
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
by minimizing the number of the produced
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
by minimizing the number of the produced
![]() $e^{+}e^{-}$
pairs and improve the number of
$e^{+}e^{-}$
pairs and improve the number of
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs. As we have seen in the previous sections critical importance is the multiphoton order of the pair production. Low multiphoton orders achievable from higher energy electron beams are less efficient, for fixed laser parameters (see Figures 4 and 5). Thus in order to sufficiently detect pion pairs one can choose laser parameters and electron beam energy such that
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs. As we have seen in the previous sections critical importance is the multiphoton order of the pair production. Low multiphoton orders achievable from higher energy electron beams are less efficient, for fixed laser parameters (see Figures 4 and 5). Thus in order to sufficiently detect pion pairs one can choose laser parameters and electron beam energy such that
![]() $e^{+}e^{-}$
pair creation will be of low multiphoton order while
$e^{+}e^{-}$
pair creation will be of low multiphoton order while
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation of high one. Specifically, consider an electric field laser pulse profile and electron beam energy such that, on the electrons’ frame of reference,
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation of high one. Specifically, consider an electric field laser pulse profile and electron beam energy such that, on the electrons’ frame of reference,
![]() ${\mathcal{E}}^{\ast }$
increases from zero to
${\mathcal{E}}^{\ast }$
increases from zero to
![]() ${\mathcal{E}}_{ce}$
, then peaks at values close to
${\mathcal{E}}_{ce}$
, then peaks at values close to
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D70B}}$
and then gradually drops to zero. At
${\mathcal{E}}_{c\unicode[STIX]{x1D70B}}$
and then gradually drops to zero. At
![]() ${\mathcal{E}}_{ce}$
the number of
${\mathcal{E}}_{ce}$
the number of
![]() $e^{+}e^{-}$
pairs produced must be low so that small amount of energy will be absorbed to accelerate them while the field still increases to reach
$e^{+}e^{-}$
pairs produced must be low so that small amount of energy will be absorbed to accelerate them while the field still increases to reach
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
. This can occur for low multiphoton order
${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
. This can occur for low multiphoton order
![]() $e^{+}e^{-}$
pair creation. Approaching
$e^{+}e^{-}$
pair creation. Approaching
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
,
${\mathcal{E}}_{c\unicode[STIX]{x1D707}}$
,
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs are created and for high efficiency this can be achieved for high multiphoton order
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs are created and for high efficiency this can be achieved for high multiphoton order
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation.
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pair creation.
A specific numerical example of the above argument can be as follows. Consider a laser pulse of
![]() $I\sim 10^{24}~\text{W}~\text{cm}^{-2}$
, that peaks at
$I\sim 10^{24}~\text{W}~\text{cm}^{-2}$
, that peaks at
![]() $E=2\times 10^{15}~\text{V}~\text{m}^{-1}$
, and photon energy
$E=2\times 10^{15}~\text{V}~\text{m}^{-1}$
, and photon energy
![]() $\hbar \unicode[STIX]{x1D714}=3~\text{eV}$
. It collides with an electron beam of
$\hbar \unicode[STIX]{x1D714}=3~\text{eV}$
. It collides with an electron beam of
![]() $E_{e\text{-}\text{beam}}=200~\text{GeV}\;(\unicode[STIX]{x1D6FE}_{L}=4\times 10^{5})$
. When
$E_{e\text{-}\text{beam}}=200~\text{GeV}\;(\unicode[STIX]{x1D6FE}_{L}=4\times 10^{5})$
. When
![]() $E\sim 10^{12}~\text{V}~\text{m}^{-1}$
,
$E\sim 10^{12}~\text{V}~\text{m}^{-1}$
,
![]() $E^{\ast }\sim 10^{17}~\text{V}~\text{m}^{-1}$
and
$E^{\ast }\sim 10^{17}~\text{V}~\text{m}^{-1}$
and
![]() $\hbar \unicode[STIX]{x1D714}^{\ast }=1200~\text{keV}$
. From Equations (2)–(4) and for an interaction 4-volume
$\hbar \unicode[STIX]{x1D714}^{\ast }=1200~\text{keV}$
. From Equations (2)–(4) and for an interaction 4-volume
![]() $V=10\unicode[STIX]{x1D706}^{3}\unicode[STIX]{x1D70F}\sim 10^{-51}~\text{m}^{3}~\text{s}$
,
$V=10\unicode[STIX]{x1D706}^{3}\unicode[STIX]{x1D70F}\sim 10^{-51}~\text{m}^{3}~\text{s}$
,
![]() $e^{+}e^{-}$
pair creation efficiency is of the order of
$e^{+}e^{-}$
pair creation efficiency is of the order of
![]() $10^{3}$
pairs and the corresponding threshold multiphoton order is
$10^{3}$
pairs and the corresponding threshold multiphoton order is
![]() $n_{0}\sim 5$
, respectively. As the electric field strength
$n_{0}\sim 5$
, respectively. As the electric field strength
![]() ${\mathcal{E}}^{\ast }$
increases, it reaches its peak near
${\mathcal{E}}^{\ast }$
increases, it reaches its peak near
![]() ${\mathcal{E}}_{c\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FE}_{L}\times 10^{17}~\text{V}~\text{m}^{-1}\sim 10^{22}~\text{V}~\text{m}^{-1}$
the created
${\mathcal{E}}_{c\unicode[STIX]{x1D707}}=\unicode[STIX]{x1D6FE}_{L}\times 10^{17}~\text{V}~\text{m}^{-1}\sim 10^{22}~\text{V}~\text{m}^{-1}$
the created
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs are estimated to reach up to
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs are estimated to reach up to
![]() $10^{2}$
pairs with a threshold multiphoton order of
$10^{2}$
pairs with a threshold multiphoton order of
![]() $n_{0}=10^{4}$
. These investigations confirm the tunability (selectivity) between the
$n_{0}=10^{4}$
. These investigations confirm the tunability (selectivity) between the
![]() $e^{+}e^{-}$
pair creation and the
$e^{+}e^{-}$
pair creation and the
![]() $\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs and their experimental observation during ultra-high intensity laser pulses with high energy electron beam such as proposed by ELI[36, Reference Gerstner52], ORION[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett37, Reference Danson, Bett, Cann, Duffield, Edwards, Egan, Elsmere, Girling, Goldsack, Harvey, Hillier, Hoarty, Hopps, James, Norman, Oades, Parker, Roberts, Treadwell and Winter38] and IZEST – ICAN project[Reference Mourou, Brocklesby, Tajima and Limpert53]. The use of the new high energy, high average power, high efficiency (up to 30%) fiber CPA laser (ICAN project) and the physical decay of the pions to muons allow to propose an alternative to accelerators high quality muon source installed in future laser facilities, with important applications such as the study of muonic molecules formation in relatively high quantity for muon catalyzed fusion[Reference Ishida, Nagamine, Matsuzaki and Kawamura42, Reference Ishida, Nagamine, Matsuzaki and Kawamura43] and the neutrino factory[Reference Choubey, Gandhi, Goswami, Berg, Fernow, Gallardo, Gupta, Kirk, Simos, Souchlas, Ellis, Kyberd, Benedetto, Fernandez-Martinez, Efthymiopoulos, Garoby, Gilardoni, Martini, Prior, Indumathi, Sinha, Ballett, Pascoli, Bross, Geer, Johnstone, Kopp, Mokhov, Morfin, Neuffer, Parke, Popovic, Strait, Striganov, Blondel, Dufour, Laing, Soler, Lindner, Schwetz, Alekou, Apollonio, Aslaninejad, Bontoiu, Dornan, Eccleston, Kurup, Long, Pasternak, Pozimski, Bogacz, Morozov, Roblin, Bhattacharya, Majumdar, Mori, Planche, Zisman, Cline, Stratakis, Ding, Coloma, Donini, Gavela, Lopez Pavon, Maltoni, Bromberg, Bonesini, Hart, Kudenko, Mondal, Antusch, Blennow, Ota, Abrams, Ankenbrandt, Beard, Cummings, Flanagan, Johnson, Roberts, Yoshikawa, Migliozzi, Palladino, de Gouvea, Graves, Kuno, Peltoniemi, Blackmore, Cobb, Witte, Mezzetto, Rigolin, McDonald, Coney, Hanson, Snopok, Tortora, Andreopoulos, Bennett, Brooks, Caretta, Davenne, Densham, Edgecock, Kelliher, Loveridge, McFarland, Machida, Prior, Rees, Rogers, Thomason, Booth, Skoro, Karadzhov, Matev, Tsenov, Samulyak, Mishra, Petti, Dracos, Yasuda, Agarwalla, Cervera-Villanueva, Gomez-Cadenas, Hernandez, Li, Martin-Albo, Huber, Back, Barker, Harrison, Meloni, Tang and Winter44] due to muon decay to neutrino.
$\unicode[STIX]{x1D70B}^{+}\unicode[STIX]{x1D70B}^{-}$
pairs and their experimental observation during ultra-high intensity laser pulses with high energy electron beam such as proposed by ELI[36, Reference Gerstner52], ORION[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett37, Reference Danson, Bett, Cann, Duffield, Edwards, Egan, Elsmere, Girling, Goldsack, Harvey, Hillier, Hoarty, Hopps, James, Norman, Oades, Parker, Roberts, Treadwell and Winter38] and IZEST – ICAN project[Reference Mourou, Brocklesby, Tajima and Limpert53]. The use of the new high energy, high average power, high efficiency (up to 30%) fiber CPA laser (ICAN project) and the physical decay of the pions to muons allow to propose an alternative to accelerators high quality muon source installed in future laser facilities, with important applications such as the study of muonic molecules formation in relatively high quantity for muon catalyzed fusion[Reference Ishida, Nagamine, Matsuzaki and Kawamura42, Reference Ishida, Nagamine, Matsuzaki and Kawamura43] and the neutrino factory[Reference Choubey, Gandhi, Goswami, Berg, Fernow, Gallardo, Gupta, Kirk, Simos, Souchlas, Ellis, Kyberd, Benedetto, Fernandez-Martinez, Efthymiopoulos, Garoby, Gilardoni, Martini, Prior, Indumathi, Sinha, Ballett, Pascoli, Bross, Geer, Johnstone, Kopp, Mokhov, Morfin, Neuffer, Parke, Popovic, Strait, Striganov, Blondel, Dufour, Laing, Soler, Lindner, Schwetz, Alekou, Apollonio, Aslaninejad, Bontoiu, Dornan, Eccleston, Kurup, Long, Pasternak, Pozimski, Bogacz, Morozov, Roblin, Bhattacharya, Majumdar, Mori, Planche, Zisman, Cline, Stratakis, Ding, Coloma, Donini, Gavela, Lopez Pavon, Maltoni, Bromberg, Bonesini, Hart, Kudenko, Mondal, Antusch, Blennow, Ota, Abrams, Ankenbrandt, Beard, Cummings, Flanagan, Johnson, Roberts, Yoshikawa, Migliozzi, Palladino, de Gouvea, Graves, Kuno, Peltoniemi, Blackmore, Cobb, Witte, Mezzetto, Rigolin, McDonald, Coney, Hanson, Snopok, Tortora, Andreopoulos, Bennett, Brooks, Caretta, Davenne, Densham, Edgecock, Kelliher, Loveridge, McFarland, Machida, Prior, Rees, Rogers, Thomason, Booth, Skoro, Karadzhov, Matev, Tsenov, Samulyak, Mishra, Petti, Dracos, Yasuda, Agarwalla, Cervera-Villanueva, Gomez-Cadenas, Hernandez, Li, Martin-Albo, Huber, Back, Barker, Harrison, Meloni, Tang and Winter44] due to muon decay to neutrino.
Finally it should be noted that this work was solely based on applying and quantitatively investigating Popov’s imaginary time method[Reference Popov13–Reference Popov19] for
![]() $e^{+}-e^{-}$
and
$e^{+}-e^{-}$
and
![]() $\unicode[STIX]{x1D70B}^{+}-\unicode[STIX]{x1D70B}^{-}$
pair creation from vacuum in the presence of ultra-high electric field. This is a purely multiphoton method where photon absorption from vacuum (here studied in the laboratory frame and in the electron beam frame) is a direct absorption. As such we showed that higher order multiphoton pair generation is more efficient than low order one. For high intensity laser beam interaction with a high energy electron beam, QED secondary processes could be developed, as presented in Refs. [Reference Sokolov, Naumova, Nees and Mourou54, Reference Bulanov, Schroeder, Esarey and Leemans55]. These processes include recollision of the generated
$\unicode[STIX]{x1D70B}^{+}-\unicode[STIX]{x1D70B}^{-}$
pair creation from vacuum in the presence of ultra-high electric field. This is a purely multiphoton method where photon absorption from vacuum (here studied in the laboratory frame and in the electron beam frame) is a direct absorption. As such we showed that higher order multiphoton pair generation is more efficient than low order one. For high intensity laser beam interaction with a high energy electron beam, QED secondary processes could be developed, as presented in Refs. [Reference Sokolov, Naumova, Nees and Mourou54, Reference Bulanov, Schroeder, Esarey and Leemans55]. These processes include recollision of the generated
![]() $e^{+}-e^{-}$
pairs with the high energy photons, radiation reaction effects, photon–photon interaction of the multiphoton Breit–Wheeler mechanism, for which extensive investigations have been reported elsewhere[Reference Sokolov, Naumova, Nees and Mourou54–Reference Bell and Kirk58], and are beyond the scope of the present work.
$e^{+}-e^{-}$
pairs with the high energy photons, radiation reaction effects, photon–photon interaction of the multiphoton Breit–Wheeler mechanism, for which extensive investigations have been reported elsewhere[Reference Sokolov, Naumova, Nees and Mourou54–Reference Bell and Kirk58], and are beyond the scope of the present work.