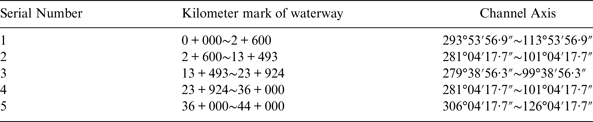1. INTRODUCTION
Safety is a major priority of waterway transportation. In order to avoid traffic collisions in navigable waterways, ships are required to maintain a safe zone between each other that is known as the ship domain. In the last decades, the modelling of ship domains has drawn increasing attention. This was motivated by waterway safety analysis aimed at gaining a higher level of understanding of how ship collisions occur, what are the most possible waterway navigation environments that may lead to collisions, and which ones are the most significant collision contributing factors. The developed domain models could generally be employed for assessment of ship collision risks, design and capacity analysis of inland navigable waterway channels and offshore waterway facilities and development of intelligent ship traffic control strategies. Countermeasures could then be identified to effectively enhance waterway transportation safety (Deng, Reference Deng2009; Wang, Reference Wang2012).
The first ship domain model was developed by Fujii and Tanaka (Reference Fujii and Tanaka1971) to deal with the safe navigation of ships in open waters off Japan. In this model, the ship domain is represented by an ellipse with semi-major and semi-minor axle lengths set as 8 and 3·2 times or 6 and 1·6 times the ship length. With an ellipse-shaped ship domain defined for each ship, this gives guide distances to keep ships safe distances apart, giving a trigger for ship officers to take appropriate action to avoid a collision. Goodwin and Kemp (Reference Goodwin and Kemp1975; Reference Goodwin and Kemp1977) proposed a sector-shaped domain model to investigate the maritime traffic in southern North Sea waters based on data generated by a radar simulator from collision experiments. In the Goodwin and Kemp model, the ship domain is defined as the area of three circular sectors with 112·5°, 112·5°, and 135° degrees of centre angles and 0·7 mile, 0·85 mile, and 0·45 mile radii in reference to the centre of gravity of the ship. Benefiting from this and the Fujii model, Tak and Spaans (Reference Tak and Spaans1977) introduced a new model that still creates an elliptical-shaped ship domain in which the position of the ship was moved backward and the ship's head was turned to port by an angle, making the area starboard, port and astern in proportion to the three circular sectors of the Goodwin (Reference Goodwin1977) model. In order to handle the difference in ship behaviours, Fujii (Reference Fujii1981) also constructed a long ovate domain model by modifying the elliptical-shaped domain model. Due to the fact that the boundary established by the three circular sectors in the Goodwin model with varying radii is not a smooth curve, it has significantly limited the model's practical applications. To overcome this limitation, Davis et al. (Reference Davis, Dove and Stockel1980; Reference Davis, Dove and Stockel1982) refined the model by using simulated data to create a circular ship domain area identical to the area established by the Goodwin model.
More recently, ship domain modelling has focused on addressing ship collision avoidance incorporating ship operators' behaviours. For instance, Bi (Reference Bi2000) and Bi et al. (Reference Bi, Jia and Wu2003) developed dynamic collision avoidance ship domain models that could help determine the ship domain boundary varying with the threshold of collision risks. Smierzchalski and Michalewicz (Reference Smierzchalski and Michalewicz2000) and Smierzchalski (Reference Smierzchalski2001) introduced a hexagon-shaped ship domain model in which the ship domain is determined by ship's speed and cycle parameters. The model is convenient for optimising the ship's path to avoid collisions using an evolutionary algorithm. Sun (Reference Sun2000) proposed a ship domain model to handle poor visibility from the perspective of collision avoidance and safety navigation. Guo (Reference Guo2001) analysed the boundary of the ship domain for crossing and overtaking situations by holistically considering ship dynamics, operator's psychological quality, and waterway condition. Kijima and Furukawa (Reference Kijima and Furukawa2001; Reference Kijima and Furukawa2003) constructed a new ship domain model that could establish an obstructed area and a visible area with which the visible area could be used for protection warning when the obstructed area is in violation. Pietrzykowski and Uriasz (Reference Pietrzykowski and Uriasz2004) proposed a polygon-shaped ship domain model for evaluating the ship collision risk using empirical discrete data obtained from different directions around ships. Further, Pietrzykowski and Uriasz (Reference Pietrzykowski and Uriasz2006; Reference Pietrzykowski and Uriasz2009) introduced a fuzzy domain model to effectively handle the navigation condition of a waterway to the level of safety required. Lisowski et al. (Reference Lisowski, Rak and Czechowigz2000), Zhu et al. (Reference Zhu, Xu and Lin2001), Pietrzykowski (Reference Pietrzykowski2008) and Wang et al. (Reference Wang, Tan and Liu2011) analysed the fuzzy boundary of ship domain based on Fuzzy Theory and Neural Networks. Wang et al. (Reference Wang, Meng and Xu2009), Wang (Reference Wang2010; Reference Wang2013), Liu (Reference Liu and Wang2014) and Xu (Reference Xu2014) proposed a quaternary ship domain model based on unified analytical framework to enhance the real world model operability.
While the development of ship domain models has been focusing on ship collision risk assessment and seeking countermeasures to achieve collision avoidance in open waters, efforts have also been made to ensure safe navigation of ships through restricted water channels. In this respect, Goldwell (Reference Goldwell1983) proposed a ship domain model applicable to restricted waters incorporating ship behaviours. Jia (Reference Jia1989) and Fan et al. (Reference Fan, Zhang, Zhou, Tan and Wang2013) proposed a variable ellipse-shaped ship domain model that maintained long and short axes proportional to the length and breadth of the ship to deal with situations of ship encounters in crowded water channels. Xu et al. (Reference Xu, Mou and Ji2004) introduced a three-dimensional domain model that could readily handle restrictions of waterway depth and vertical clearance. Chen and Guo (Reference Chen and Guo2008) proposed a ship domain model for ships using inland waterways with the vertical clearance restricted by bridge heights. For the domain of special purpose ships, Guo (Reference Guo2011) conducted research on the economical channel width for very large LNG carriers based on ship manoeuvring simulation and risk assessment criteria. Further, Wen et al. (Reference Wen, Yang and Xiao2013) defined the width of a moving safety zone around LNG carriers based on the probability of ship collisions and risk assessment criteria. The research showed that the width of moving safety zone around a LNG carrier was determined by the distribution of ship traffic flow, displacement and cruising speed.
1.1. Ship Domain Discussion
According to the literature reviewed, existing research ship domain methods can be divided into statistical methods, analytical expression and intelligent technology.
Before the 1980s, statistical analysis or cluster analysis methods were normally adopted in ship domain research. This obtained data from marine traffic investigation or experiments based on radar simulators, analysed the data based on probabilistic methods, and determined the shape and size of the ship domain of the research water area based on consideration of the traffic density, ships' size, speed and Collision Regulations (COLREGS). In this period, the research was based on qualitative methods that did not consider the human factors, environment and ship properties, and the models were quite different in shape and size.
In order to avoid the disadvantages of qualitative methods, experts and scholars used analytical expression to model the ship domain. This took the positions, speeds, directions and other characteristics of the own vessel and vessels around as input and the size of the ship domain as output, calculated the minimum distances to the vessels and barriers around for safe navigation based on shipping manoeuvring equations, steering model and deceleration model, and then determined the size of the ship domain in different directions. Compared with the domains determined by statistical methods, it quantified the boundary of ship domain based on consideration of the ship properties. However, analytical expression models could not meet the requirement of ship domains in complex environments in that they ignored the influence of human factors and the environment.
In recent years, experts and scholars have introduced intelligent technology to the investigation of marine traffic to reveal the relationship between ship domain, human factors and environment. These include neural networks, complex networks, cellular automatons, intelligent agents, etc. Existing research only constructed simple exercises on vessel parameters and empirical data, while human factors, navigation environment and other complex factors have not yet been considered.
1.2. Motivation and Study Objective
Although the ship domain models developed have greatly benefited safe operations of ships in both open waterways and restricted water channels, they also have some limitations. In particular, the shape and size considered for ship domain calculation were mainly based on data collected from numerical simulations associated with open waterways. Such data differs from ship operations in restricted water channels and real world circumstances. Also, the varying skill levels of ship operators in ship manoeuvring have not been readily incorporated into ship domain modelling. The inability to capture real world conditions of restricted waterways, ship shapes and sizes, and the operators' skills in the existing ship domain models will inevitably compromise the accuracy and precision of model analysis results (Zhou, Reference Zhou2012). This motivates developing new ship domain models using data more suited for restricted water channels and explicitly defining the shape and size of ship domains so that the refined models could be utilised to conduct waterway facility design and traffic operations analysis for restricted waterway channels.
The remainder of this paper is organised as follows. Section 2 briefly explains the characteristics of ship behaviours in restricted water channels and describes the proposed dynamic ship domain model. Section 3 elaborates on model application to restricted waterway channels of Tianjin Port, China. Section 4 compares the result of channel capacity estimation with other different methods. Finally, Section 5 summarises and concludes.
2. PROPOSED DYNAMIC SHIP DOMAIN MODEL
2.1. Typical Ship Navigation Movements in Restricted Waters
Generally, ship navigation behaviour aims to maintain the highest ship mobility while not compromising safety performance. Specifically, the ship behaviour may refer to proper navigation and manoeuvre of the ship for collision avoidance. In this context, the ship behaviour concerns not only the behaviour of a single ship. It deals with navigation actions of multiple ships within a certain range of the water channel to ensure waterway safety.
For restricted water channels, ship navigation behaviour can be mainly classified into four categories: i) navigating along the channel; ii) crossing the channel; iii) another flow joining; and iv) turning. As illustrated in Figure 1, navigating along the channel corresponds to ship movements along the main water channel direction entering into or departing from the inland waterway port. Crossing the channel refers to the ship crossing from one side of the restricted water channel at nearly a perpendicular angle to another side. Another flow joining involves two traffic flows at a certain angle arriving at the water channel and merging into one traffic flow under the navigation rules. Turning is related to ship turning motions in the wharf apron of a water channel, leading to a reduction in the channel capacity. Dynamic ship domain models are separately defined for these categories of navigation.

Figure 1. Illustration of typical ship navigation categories.
From the hydrodynamic perspective, the shape of domain for ships navigating along the channel is widely recognised as an ellipse, for which the most representative model is the Fujii Model. This paper sets the shape of the domain for ships navigating along the channel as an ellipse, and then constructs models for other ship navigation movements based on the ellipse model.
2.2. Domain Model for Ships Navigating Along the Channel
For ships navigating along the channel, ships are required to keep a minimum safe distance from ships travelling in the same longitudinal direction. This defines the major axis of the ship navigation domain. For a multi-lane water channel, ships in a lane need to keep a minimum safe clearance with other ships in adjacent travel lanes, which determines the minor axis of the ship domain.
Stopping visual range can be introduced to determine the major axis of ship domain for ships navigating along the channel. In road traffic engineering, stopping visual range refers to the minimum distance for a car to stop when the driver sees barriers or the preceding car stops. Stopping visual range consists of reaction distance, braking distance and safe distance.
Analogously, a ship should also keep a stopping visual range with the preceding ship when navigating along a channel. Therefore, the stopping visual range for a ship can be defined as:
 $$\eqalign{& S = S_0 + S_1 + S_2 \cr & S_1 = vt \cr & S_2 = v^2 /2a} $$
$$\eqalign{& S = S_0 + S_1 + S_2 \cr & S_1 = vt \cr & S_2 = v^2 /2a} $$where S is the stopping visual range for a ship, S 0 is the safe distance which is about a quarter of the ship length, S 1 is the reaction distance, S 2 is the braking distance, v is the initial speed of the ship, t is the response time of the ship operator and a is the braking rate of the ship behind.
If the navigation standard of the channel stipulates a safe distance for ships to keep from the ships in front or behind, the stipulated safe distance can be used as the major axis of ship domain for ships navigating along the channel.
The minor axis of ship domain for ships navigating along the channel can be determined according to the Guidelines for Design of Approach Channel, Code for Design of General Layout of Sea Ports or any other design guidelines for restricted water channels suited.
As shown in Figure 2, the longitudinal and transverse ship domains are respectively defined as follows
where A nav is the major axis, W nav is the minor axis, A is the width of track, and c is the safe reach width.

Figure 2. Dynamic ship domain for ships navigating along the channel.
With the ship domain model proposed as above, size-variant ship domains for ships navigating along the channel can be determined for individual ships in longitudinal and cross sectional directions on the basis of ship length and safe reach width. This will, in turn, help create safety clearance standards for overtaking manoeuvres as part of navigating along the channel in restricted waters. It will also assist in developing design specifications for restricted water channels to safely accommodate the projected ship traffic.
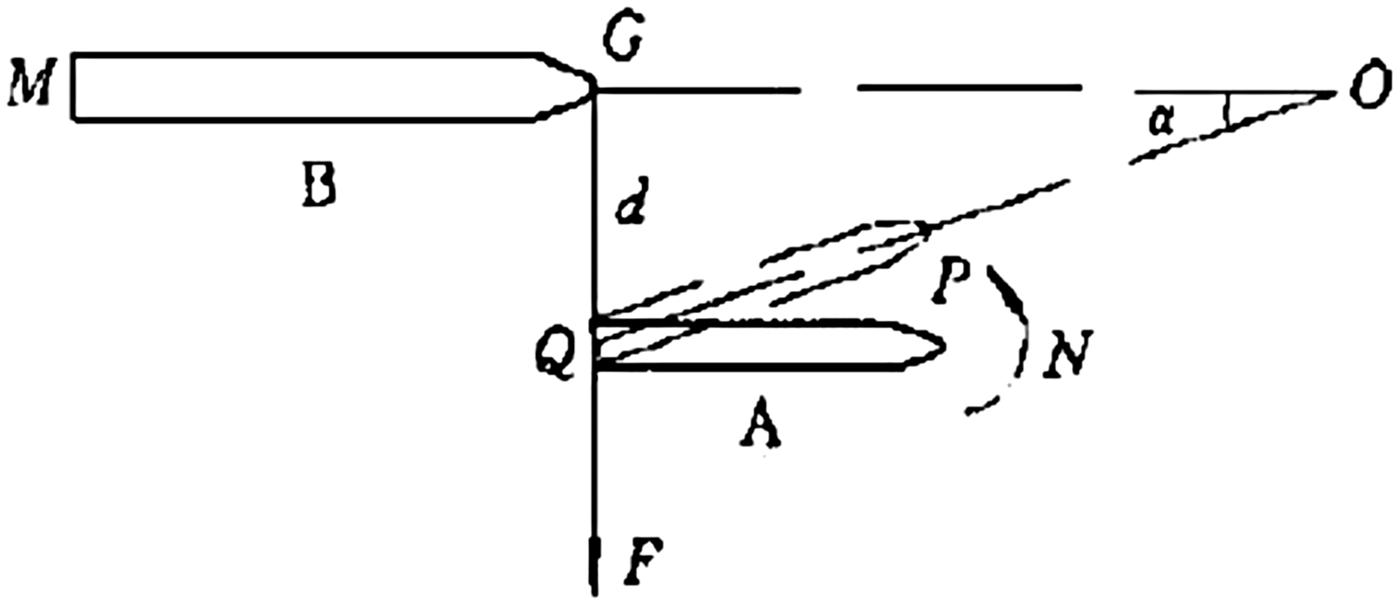
The minor axis of the ship domain for ships overtaking should consider interaction between ships. As shown in Figure 3, the transverse distance kept between ships should ensure that suction cannot affect navigation safety. The time ship A reaches the meeting-point (O) should be longer than ship B. As shown in Figure 4, the minor axis of the domain for ships overtaking can be calculated as follows
where T shipA is the time ship A reaches the meeting-point (O); T shipB is the time ship B reaches the meeting-point (O); L shipA is the length of ship A; L shipB is the length of ship B; V shipA is the speed of ship A; V shipB is the speed of ship B; d is the safe transverse distance; α is the included angle of the direction of ship A and ship B; and k is the speed ratio of ship A and ship B.

Figure 3. Suction between ships when overtaking.

Figure 4. Process of overtaking.
As a consequence, the longitudinal and cross sectional ship domains for ships overtaking are respectively defined as follows
2.3. Ship Domain Model for Crossing the Channel
For ship crossing navigation shown in Figure 5, the ship crossing domain is defined as the safe water region that another ship could not enter the ship's virtual domain illustrated as the red dotted line range (it is assumed to be the domain of the crossing ship navigating along the channel) when it is crossing the waterway. This indicates that the time for the ships navigating around the crossing ship to the junction of channels should be longer than the time that the crossing ship takes to cross the main channel.

Figure 5. Dynamic ship domain for crossing navigation.
The scale of the crossing domain can be determined as follows:
where A cro is the major axis, W cro is the minor axis, ![]() $D_{}^{{\rm in}} $ is the safe distance from the approaching ships,
$D_{}^{{\rm in}} $ is the safe distance from the approaching ships, ![]() $D_{}^{{\rm in}} $ is the safe distance from the departing ships, θ is the angle of main channel 1 and the major axis of the crossing domain,
$D_{}^{{\rm in}} $ is the safe distance from the departing ships, θ is the angle of main channel 1 and the major axis of the crossing domain, ![]() $A_{nav - 1} $ is the major axis of ship's navigation domain voyaging in main channel 1,
$A_{nav - 1} $ is the major axis of ship's navigation domain voyaging in main channel 1, ![]() $A_{nav - {\rm 2}} $ is the major axis of domain for crossing ship navigating along channel 2, D cro is the width of crossing channel 2, L cro is ship length, B cro is the ship width,
$A_{nav - {\rm 2}} $ is the major axis of domain for crossing ship navigating along channel 2, D cro is the width of crossing channel 2, L cro is ship length, B cro is the ship width, ![]() $V_{nav}^{in} $ is the in-flow ship cruising speed,
$V_{nav}^{in} $ is the in-flow ship cruising speed, ![]() $V_{nav}^{out} $ is the out-flow ship cruising speed, and W channel is the width of channel 1.
$V_{nav}^{out} $ is the out-flow ship cruising speed, and W channel is the width of channel 1.
The model considers the influence between crossing ships and ships navigating along the main channel where navigators must judge if crossing is safe. Meanwhile, the safe domains for ships cruising in the same direction in the main channel or crossing the channel could still be determined using the proposed domain model for ships navigating along the channel.
2.4. Ship Domain Model for “Another Flow Joining”
Where another channel joins a traffic flow, in general, “another flow joining” may be classified into two types. The first type does not need to go through the reverse traffic flow, while the second type needs to traverse through the reverse traffic flow.
As shown in Figures 6 and 7, the domain for another flow joining is defined as the safe water region that another ship could not enter the ship's virtual domain illustrated as the black dotted line range (it is assumed as the domain of the crossing ship navigating along the channel) when the flows merge. This means that the time that ships around the crossing ship navigating along the channel reach the junction of channels should be longer than the time that the ship takes to join the flow.

Figure 6. Type I dynamic ship domain for ships joining another flow without affecting reverse flow.

Figure 7. Type II dynamic ship domain for ships joining another flow affecting reverse flow.
As shown in Figure 6, the safe domain for ships joining another flow without the need to go through the reverse traffic flow can be determined as follows:
where ![]() $A_{join}^a $ is the major axis,
$A_{join}^a $ is the major axis, ![]() $W_{join}^a $ is the minor axis,
$W_{join}^a $ is the minor axis, ![]() $V_{nav}^{in} $ is the speed of ships joining the flow, T join is the time taken to join the flow,
$V_{nav}^{in} $ is the speed of ships joining the flow, T join is the time taken to join the flow, ![]() $A_{nav - 1} $ is the major axis of ship's domain for the ships in the main channel,
$A_{nav - 1} $ is the major axis of ship's domain for the ships in the main channel, ![]() $A_{nav - 2} $ is the major axis of the domain for the “joining” ship navigating along the main channel, L join is the length of joining ship, and ϕ is the steering angle.
$A_{nav - 2} $ is the major axis of the domain for the “joining” ship navigating along the main channel, L join is the length of joining ship, and ϕ is the steering angle.
Figure 7 presents the case when the ship joining another flow requires the ship to traverse through the reverse flow. The related safe domain can be determined as below:
where ![]() $A_{join}^b $ is the major axis,
$A_{join}^b $ is the major axis, ![]() $W_{join}^b $ is the minor axis,
$W_{join}^b $ is the minor axis, ![]() $V_{nav}^{in} $ is the speed of ships navigating in,
$V_{nav}^{in} $ is the speed of ships navigating in, ![]() $V_{nav}^{out} $ is the speed of ships navigating out, T join is the time of joining the flow,
$V_{nav}^{out} $ is the speed of ships navigating out, T join is the time of joining the flow, ![]() $A_{nav - 1} $ is the major axis of ship's domain for the ships voyaging in the main channel,
$A_{nav - 1} $ is the major axis of ship's domain for the ships voyaging in the main channel, ![]() $A_{nav - 2} $ is the major axis of domain for the joining ship navigating along the main channel, L join is the length of joining ship, and ϕ is the steering angle.
$A_{nav - 2} $ is the major axis of domain for the joining ship navigating along the main channel, L join is the length of joining ship, and ϕ is the steering angle.
The model addresses the influence between the joining ship and the ships navigating along the main channel, conforms to the conventional practice of restricted waterway dispatching and the standard that navigators judge whether joining the flow is safe. Moreover, the proposed model can handle cases with ships travelling from main channel to secondary channel or from secondary channel to main channel.
2.5. Ship Domain Model for Turning
For ships that are turning, the safe domain is the water area where other nearby ships cannot enter the ship's virtual domain (it is assumed as the domain of the crossing ship navigating along the channel) when it performs turning operations. This means that the time that ships navigating around the turning ship reach the turning operation waters should be longer than the time at which the turning ship finishes turning. Two types of ship operations may be considered for ships' turning, including turning affecting one-way traffic flow and turning affecting two-way traffic flow.
As seen in Figure 8, the ship turning affects one direction of the two-way water channel. The ship domain as illustrated by the red dotted area can be replaced by the rectangular area that encloses the dotted area and can then be determined by the following:
where ![]() $A_{turn}^a $ is the length of the ship turning domain,
$A_{turn}^a $ is the length of the ship turning domain, ![]() $W_{turn}^a $ is the width, L is the length of ship,
$W_{turn}^a $ is the width, L is the length of ship, ![]() $A_{nav - 1} $ is the major axis of the domain for the turning ship navigating along the channel. V is the speed of the other ship navigating in the channel, T turn is the time turning takes, and
$A_{nav - 1} $ is the major axis of the domain for the turning ship navigating along the channel. V is the speed of the other ship navigating in the channel, T turn is the time turning takes, and ![]() $W_{nav - 2} $ is the width of the domain for the turning ship navigating along the channel.
$W_{nav - 2} $ is the width of the domain for the turning ship navigating along the channel.

Figure 8. Type I dynamic domain for ship turning affecting one-way traffic.
Figure 9 illustrates ship turning affecting two-way traffic flow in the water channel. The safe domain can be determined as follows
where ![]() $A_{turn}^b $ is the major axis of turning domain,
$A_{turn}^b $ is the major axis of turning domain, ![]() $W_{turn}^b $ is the minor axis of turning domain, L is ship's length,
$W_{turn}^b $ is the minor axis of turning domain, L is ship's length, ![]() $A_{nav - 1} $ is the major axis of the domain for the turning ship navigating along the channel,
$A_{nav - 1} $ is the major axis of the domain for the turning ship navigating along the channel, ![]() $V_{nav}^{in} $ is the speed of ships navigating in,
$V_{nav}^{in} $ is the speed of ships navigating in, ![]() $V_{nav}^{out} $ is the speed of ships navigating out, T turn is the time taken in turning, and
$V_{nav}^{out} $ is the speed of ships navigating out, T turn is the time taken in turning, and ![]() $W_{nav - 2} $ is the width of the domain for the turning ship navigating along channel.
$W_{nav - 2} $ is the width of the domain for the turning ship navigating along channel.

Figure 9. Type II dynamic domain for ship turning affecting two-way traffic.
The model addresses the characteristic of ship turning and the influence between the turning ship and ships navigated along the main channel. This conforms to the current practice of inland waterway port dispatching and the standard that navigators used to judge whether turning is safe.
2.6. Security Zones for LNG Ships
The security and safety of LNG ships is particularly important. In addition to defining safe domains for LNG ships involving navigating along the channel, crossing the channel, “joining another flow”, and turning, security zones extending from the safe domains need to be determined for LNG ships. Figure 10 illustrates the security zone of a LNG ship in yellow. In the longitudinal direction, clearance distances that extend eight times the ship length from the front end and three times the ship length from the rear end need to be maintained. In the cross sectional direction, clearance distances of one ship length are required on each side of the ship (Liu and Yu, Reference Liu and Yu2011). The rectangular area enclosed by the longitudinal and cross sectional clearances is treated as the security zone of an LNG ship.

Figure 10. Security zone for an LNG ship.
The safe domain can be determined by the following equations:
where ![]() $A_{LNG} $ is the length of domain for LNG ship,
$A_{LNG} $ is the length of domain for LNG ship, ![]() $W_{LNG} $ is the width of domain for a LNG ship, L LNG is the length of a LNG ship,
$W_{LNG} $ is the width of domain for a LNG ship, L LNG is the length of a LNG ship, ![]() $W_{LNG} $ is the width of a LNG ship.
$W_{LNG} $ is the width of a LNG ship.
3. MODEL APPLICATION
The proposed dynamic ship domain models were applied in a computational study using the port of Tianjin, China. The coastal city Tianjin is one of the four municipalities equivalent to a province located in northern China. The port of Tianjin is the largest port in northern China and the main maritime gateway to Beijing. The port of Tianjin is comprised of river ports along Haihe River and deep-water seaports located on the western shore of the Bohai Bay, centred on the estuary of the Haihe River. This makes it ideal for applying the proposed dynamic ship domain models. Currently, the whole port of Tianjin occupies 121 km2 of land, with over 32 km of quay shoreline and 151 production berths. It handles 500 million tons of cargo and 13 million Twenty-Foot Equivalent Unit (TEU) of containers, making it the world's fourth largest port by throughput tonnage, and the ninth in container throughput (PSO, 2014).
3.1. Basic Information on the Restricted Water Channels
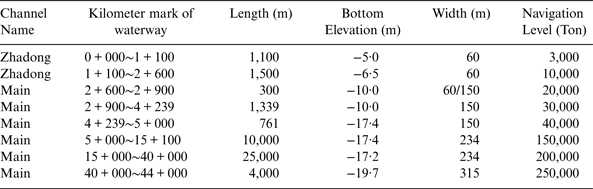
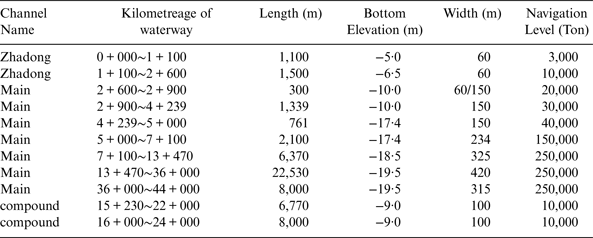
The waterway channels in the port of Tianjin contain the Main channel and the North channel. The Main channel is the main access of the port and the North channel is the access for ships navigating in or out of Beijiang and Dongjiang port areas. As shown in Figure 11, the Main channel is an approach channel for 250,000 dwt ships, which is about 44 km long. The North channel is an approach channel for 100,000 dwt ships, which is about 6·5 km in length and 390 m wide. The Main channel and North channel join at kilometre 9 + 000 of the Main channel, and the angle between Main channel and North channel is 29°. Tables 1 and 2 present technical data of the Main channel.

Figure 11. Diagram of port of Tianjin port waterway channels.
Table 1. The Axis of the Main Channel of Tianjin Port.

Table 2. The Geometric Design Parameters of the Main Channel of Tianjin Port.

3.2. Method for Calculating the Restricted Water Channel Capacity
Channel capacity refers to the number of vessels able to be navigated through the channel or a section of the channel in the unit time. This is the maximum traffic volume of the channel considering weather conditions, vessel size, vessel's behaviour, speed, safe distance and so on. The proposed dynamic ship domain models can be applied in a computational study of channel capacity.
According to space-time consumption theory (Hu, Reference Hu2001), the water channel capacity can be calculated by
where C ch is the water channel capacity, R ch is the space-time resource of the water channel, Rship is the space-time resource occupied by a single ship, and ![]() $Avail\_S$ and
$Avail\_S$ and ![]() $Avail\_T$ are the available space and time resources of the water channel.
$Avail\_T$ are the available space and time resources of the water channel.
The available space-time resource can be determined by the following factors: i) the space-time resource that a single ship consumes during navigation. A ship must keep a safe distance from other ships in the front or rear to ensure navigation safety; ii) the additional space-time resource in terms of the safe distance that a ship consumes during overtaking, crossing, joining, or turning; and iii) the number of accesses of the water channel.
Considering the relationship between space resource of the water channel and ship domains needed to maintain safety for sailing along the channel, crossing, joining another flow, and turning, the available space resource in Equation (22) can be determined by the following:
 $$\eqalign{Avail\_S & = \displaystyle{{Sing\_S} \over {\displaystyle{1 \over 4}\pi \cdot A_{nav} \cdot W_{nav}}} \cdot L_{ave} \cdot B_{ave} \cdot N\_ac - P_{cro} \cdot \displaystyle{\pi \over 4} \cdot A_{cro} \cdot W_{cro} \cr & - P_{\,join}^a \cdot \displaystyle{\pi \over 4} \cdot A_{\,join}^a \cdot W_{\,join}^a - P_{\,join}^b \cdot \displaystyle{\pi \over 4} \cdot A_{\,join}^b \cdot W_{\,join}^b - P_{turn}^a \cdot A_{turn}^a \cdot W_{turn}^a \cr & - P_{turn}^b \cdot \displaystyle{\pi \over 4} \cdot A_{turn}^b \cdot W_{turn}^b - P_{LNG} \cdot A_{LNG} \cdot W_{LNG}}$$
$$\eqalign{Avail\_S & = \displaystyle{{Sing\_S} \over {\displaystyle{1 \over 4}\pi \cdot A_{nav} \cdot W_{nav}}} \cdot L_{ave} \cdot B_{ave} \cdot N\_ac - P_{cro} \cdot \displaystyle{\pi \over 4} \cdot A_{cro} \cdot W_{cro} \cr & - P_{\,join}^a \cdot \displaystyle{\pi \over 4} \cdot A_{\,join}^a \cdot W_{\,join}^a - P_{\,join}^b \cdot \displaystyle{\pi \over 4} \cdot A_{\,join}^b \cdot W_{\,join}^b - P_{turn}^a \cdot A_{turn}^a \cdot W_{turn}^a \cr & - P_{turn}^b \cdot \displaystyle{\pi \over 4} \cdot A_{turn}^b \cdot W_{turn}^b - P_{LNG} \cdot A_{LNG} \cdot W_{LNG}}$$
where ![]() $Sing\_S$ is the space resource of a single access, which is the product of the length and width of the access.
$Sing\_S$ is the space resource of a single access, which is the product of the length and width of the access.![]() $N\_\kern1ptac$ is the number of the accesses of the water channel, L ave is the average ship length, P cro, P join, P turn are the probabilities of crossing, joining and turning, and the superscripts are the extents of influence to ship traffic along the water channel.
$N\_\kern1ptac$ is the number of the accesses of the water channel, L ave is the average ship length, P cro, P join, P turn are the probabilities of crossing, joining and turning, and the superscripts are the extents of influence to ship traffic along the water channel.
The time domain of a water channel can be described as the service time that a channel can provide except for impacts of geometric design and capacity, port operation condition, and conflict between ships. The available time resource in Equation (22) can be calculated as below:
where P port is the port operation efficiency, ![]() $Total\_T$ is the total time resource, T nature is the time resource consumed due to wind, fog, tide and other natural factors, T port is the time resource consumed because of the port operation condition limitations, and T conflict is the time resource consumed as a result of conflicts between ships.
$Total\_T$ is the total time resource, T nature is the time resource consumed due to wind, fog, tide and other natural factors, T port is the time resource consumed because of the port operation condition limitations, and T conflict is the time resource consumed as a result of conflicts between ships.
3.3. Input Data for Calculating the Water Channel Capacity
The following input values associated with the ship traffic flow, water channel geometrics, ship shape and size, and ship navigation behaviours were utilised for the capacity calculation.
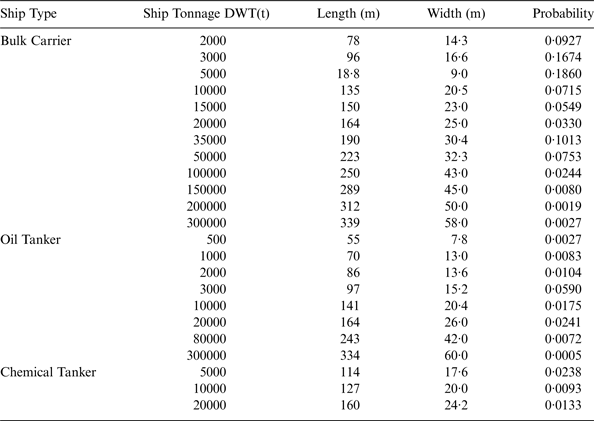
According to the data statistics from 2006 to 2008, the average time of ships turning from the North channel to the Main channel is about 12 minutes. The ships' scale and its probability are given in Table 3.
Table 3. The Ships' Sizes and Probability of Tianjin Port traffic.

The Probability Density Functions (PDFs) of ships’ speed entering into or exiting from the water channel are given as follows.
As shown in Figure 12, the PDF for ships' speed entering into the Main channel can be determined as below:
 $$f\,(v_{in} ) = \displaystyle{1 \over {2 \cdot 437\sqrt {2\pi}}} e^{ - \textstyle{{(V - 7\cdot871)^2} \over {2 \cdot (2\cdot437)^2}}} \quad (5 \le V \le 15)$$
$$f\,(v_{in} ) = \displaystyle{1 \over {2 \cdot 437\sqrt {2\pi}}} e^{ - \textstyle{{(V - 7\cdot871)^2} \over {2 \cdot (2\cdot437)^2}}} \quad (5 \le V \le 15)$$As shown in Figure 13, the PDF for ships' speed entering into the Main channel can be determined as below:
 $$f\,(v_{out} ) = \displaystyle{1 \over {2 \cdot 436\sqrt {2\pi}}} e^{ - \textstyle{{(V - 7 \cdot 902)^2} \over {2 \cdot (2 \cdot 436)^2}}} \quad (5 \le V \le 15)$$
$$f\,(v_{out} ) = \displaystyle{1 \over {2 \cdot 436\sqrt {2\pi}}} e^{ - \textstyle{{(V - 7 \cdot 902)^2} \over {2 \cdot (2 \cdot 436)^2}}} \quad (5 \le V \le 15)$$For different categories of ship navigation, the number and probability of ships involved with crossing, encountering, and turning were separately estimated. Since the Main channel and North channel were designed as enclosed passages, no ship crossing existed in practice. According to the navigation standard of the Main channel of Tianjin port, overtaking is prohibited and ships should keep at least six times of its length from the preceding ship. Also, there are no LNG ships sailing in the Main channel or North channel of Tianjin port. As such, the number and probability of ship-crossing navigation were set to zero. As related to the number and probability of ship encountering navigation, the PDFs of ship entering into or exiting from the water channel are given by:

Figure 12. Curve fitting of the ships' speed entering into Main channel.

Figure 13. Curve fitting of the ships' speed exiting from Main channel.
As shown in Figure 14, the PDF for ships entering into the Main channel can be determined as below:

Figure 14. Curve fitting of the ships entering into Main channel.
As shown in Figure 15, the PDF for ships exiting from the Main channel can be determined as below:

Figure 15. Curve fitting of the ships exiting from Main channel.
As shown in Figure 16, the PDF for ships exiting from the North channel can be determined as below:

Figure 16. Curve fitting of the ships exiting from North channel.
Encounter conflict means two traffic flows arriving at a confluence of waters at the same time, so the encounter conflict probability can be calculated as:
Consequently, the joint probability of ships encountering other ships for ships exiting from the North channel and entering into the Main channel can be calculated as:
The joint probability of ships encountering for ships exiting from the North channel and exiting from the Main channel can be computed as:
According to the ship turning statistics, the probability of turning which affects the traffic along the water channel was 0·001, and all such events affected the two-way traffic.
According to the statistics, except for the effect of wind, rain, visibility, storm tide, ocean current, port operation and human factor, the navigation time of Tianjin port is 305 days, where the one-way navigation time is 45 days. The port operation efficiency is 0·4.
3.4. Estimation of Water Channel Capacity
With the ship domain models proposed for restricted water channel capacity analysis and input data collected, the theoretical capacity of the main water channel of port of Tianjin was computed as below.
 $$\eqalign{ {C_{ch}} & = {R_{ch}}/{R_{ship}} = \displaystyle{{Avail\_S \cdot Avail\_T} \over {{L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}}} \cr & = \left(\displaystyle{{Sing\_S} \over {\displaystyle{\pi \over 4}{A_{nav}} \cdot {W_{nav}}}} \cdot {L_{ave}} \cdot {B_{ave}} \cdot N\_ac - P_{\,join}^a \cdot \displaystyle{\pi \over 4}A_{\,join}^a \cdot W_{\,join}^a - P_{\,join}^b \cdot \displaystyle{\pi \over 4}A_{\,join}^b \cdot W_{\,join}^b \right. \cr & - \left.P_{turn}^b \cdot \displaystyle{\pi \over 4}A_{turn}^b \cdot W_{turn}^b \right) \cdot {P_{\,port}} \cdot (Total\_T - {T_{nature}} - {T_{\,port}} - {T_{conflict}})/({L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}) \cr & = \left( {457600 - 5515 \cdot 8 - 5959 \cdot 2 - 2944 \cdot 1} \right) \times 0 \cdot 4 \times 7189 \cdot 7/\left( {137 \times 22 \times 4 \cdot 5} \right) \cr & = 93971 \; [ships/year] } $$
$$\eqalign{ {C_{ch}} & = {R_{ch}}/{R_{ship}} = \displaystyle{{Avail\_S \cdot Avail\_T} \over {{L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}}} \cr & = \left(\displaystyle{{Sing\_S} \over {\displaystyle{\pi \over 4}{A_{nav}} \cdot {W_{nav}}}} \cdot {L_{ave}} \cdot {B_{ave}} \cdot N\_ac - P_{\,join}^a \cdot \displaystyle{\pi \over 4}A_{\,join}^a \cdot W_{\,join}^a - P_{\,join}^b \cdot \displaystyle{\pi \over 4}A_{\,join}^b \cdot W_{\,join}^b \right. \cr & - \left.P_{turn}^b \cdot \displaystyle{\pi \over 4}A_{turn}^b \cdot W_{turn}^b \right) \cdot {P_{\,port}} \cdot (Total\_T - {T_{nature}} - {T_{\,port}} - {T_{conflict}})/({L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}) \cr & = \left( {457600 - 5515 \cdot 8 - 5959 \cdot 2 - 2944 \cdot 1} \right) \times 0 \cdot 4 \times 7189 \cdot 7/\left( {137 \times 22 \times 4 \cdot 5} \right) \cr & = 93971 \; [ships/year] } $$3.5. Forecast of Water Channel Capacity
In order to ease the traffic pressure of the Main channel of Tianjin Port, Tianjin Port Holdings Co., Ltd. started a channel broadening project in 2008. The channel broadening project was finished in 2012, and the geometric design parameters of the main channel of Tianjin Port after widening is shown in Table 4.
Table 4. The Design Parameters of the Main Channel of Tianjin Port after Broadening.

According to the ship turning statistics, the probability of turning affecting two-way traffic after the channel broadening project is 0·0002, the probability of turning affecting one-way traffic after the channel broadening project is 0·0008.
With the ship domain models proposed for restricted water channel capacity, the theoretical capacity of the Main channel of Tianjin Port can be forecast as below.
 $$\eqalign{ {C_{ch}} & = {R_{ch}}/{R_{ship}} = \displaystyle{{Avail\_S \cdot Avail\_T} \over {{L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}}} \cr & = \left(\displaystyle{{Sing\_S} \over {\displaystyle{\pi \over 4}{A_{nav}} \cdot {W_{nav}}}} \cdot {L_{ave}} \cdot {B_{ave}} \cdot N\_ac - P_{add - in}^a \cdot \displaystyle{\pi \over 4}A_{enc}^a \cdot W_{enc}^a - P_e^b \cdot \displaystyle{\pi \over 4}A_{enc}^b \cdot W_{enc}^b \right. \cr & - \left. P_{turn}^a \cdot A_{turn}^a \cdot W_{turn}^a - P_{turn}^b \cdot \displaystyle{\pi \over 4}A_{turn}^b \cdot W_{turn}^b \right) \cdot {P_{\,port}} \cdot (Total\_T - {T_{nature}} - {T_{\,port}} - {T_{conflict}}) \cr & /({L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}) \cr & = \left( {761389 - 5515 \cdot 8 - 5959 \cdot 2 - 501 \cdot 4 - 2355 \cdot 3} \right) \times 0 \cdot 4 \times 7189 \cdot 7/\left( {137 \times 22 \times 4 \cdot 5} \right) \cr & = 158405 \; [ships/year] } $$
$$\eqalign{ {C_{ch}} & = {R_{ch}}/{R_{ship}} = \displaystyle{{Avail\_S \cdot Avail\_T} \over {{L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}}} \cr & = \left(\displaystyle{{Sing\_S} \over {\displaystyle{\pi \over 4}{A_{nav}} \cdot {W_{nav}}}} \cdot {L_{ave}} \cdot {B_{ave}} \cdot N\_ac - P_{add - in}^a \cdot \displaystyle{\pi \over 4}A_{enc}^a \cdot W_{enc}^a - P_e^b \cdot \displaystyle{\pi \over 4}A_{enc}^b \cdot W_{enc}^b \right. \cr & - \left. P_{turn}^a \cdot A_{turn}^a \cdot W_{turn}^a - P_{turn}^b \cdot \displaystyle{\pi \over 4}A_{turn}^b \cdot W_{turn}^b \right) \cdot {P_{\,port}} \cdot (Total\_T - {T_{nature}} - {T_{\,port}} - {T_{conflict}}) \cr & /({L_{ave}} \cdot {B_{ave}} \cdot {T_{nav}}) \cr & = \left( {761389 - 5515 \cdot 8 - 5959 \cdot 2 - 501 \cdot 4 - 2355 \cdot 3} \right) \times 0 \cdot 4 \times 7189 \cdot 7/\left( {137 \times 22 \times 4 \cdot 5} \right) \cr & = 158405 \; [ships/year] } $$4. COMPARISON OF CHANNEL CAPACITY ESTIMATION USING DIFFERENT METHODS
4.1. Channel Capacity Estimation Methods
At present, channel capacity estimation methods contain empirical formulae based on ship manoeuvring, ship trials and computer simulation. Here, some common channel capacity estimation formulae are introduced to calculate the capacity of the main channel of Tianjin port, in order to validate the accuracy of the proposed model.
4.1.1. Calculation method based on Fujin model (Wu, Reference Wu1986)
This method is the most convenient and frequently used, which is constructed on considering the safe distance based on the Fujin domain.
where Cch is the water channel capacity, Rch is the space-time resource of the water channel, Rship is the space-time resource occupied by a single ship, Lch is the length of the channel, T is the time channel service, r is the major axis of ship domain, Vave is the average speed of the ships.
4.1.2. Calculation method based on features of different ship types (Liu et al., Reference Liu, Ai and Chen2006)
This method is constructed based on considering of the distribution of ship categories, ship scales and ship speeds from the Fujin domain. The formula is widely used in calculating the channel capacity of the downstream Yangtze River.
 $$C_{ch} = N\_ac \cdot \sum\limits_{i = 1}^n {\displaystyle{{r_i v_i} \over {l_i}}} (i = 1,2,3,4 \cdots )$$
$$C_{ch} = N\_ac \cdot \sum\limits_{i = 1}^n {\displaystyle{{r_i v_i} \over {l_i}}} (i = 1,2,3,4 \cdots )$$
where Cch is the water channel capacity, ![]() $N_{\_ac} $ is the number of the accesses of the channel, r i is the distribution of the ships of type i, v i is the average speed of the ships of type i, l i is the major axis of the ships of type i.
$N_{\_ac} $ is the number of the accesses of the channel, r i is the distribution of the ships of type i, v i is the average speed of the ships of type i, l i is the major axis of the ships of type i.
4.1.3. Calculation method on considering “afflux and gush” (Wen and Liu, Reference Wen and Liu2010)
This method is constructed based on considering traffic organisation of the port, which can reflect the influence of one-way navigation. The formula is widely used in calculating the channel capacity of a seaport.
where C ch is the water channel capacity, T sig is the time of one-way navigation per unit time, ![]() $C_{ch}^{in} $ is the capacity of the entrance access per unit time,
$C_{ch}^{in} $ is the capacity of the entrance access per unit time, ![]() $C_{ch}^{out} $ is the capacity of the exit access per unit time,
$C_{ch}^{out} $ is the capacity of the exit access per unit time, ![]() $C_{ch}^{sig} $ is the capacity of the channel while in a one-way situation per unit time.
$C_{ch}^{sig} $ is the capacity of the channel while in a one-way situation per unit time.
4.2. “Saturability” of Channel Capacity
Saturability of channel capacity is an important index to reflect the service level of the channel. Saturability of channel capacity is the ratio of the actual channel capacity and probable channel capacity (Li, Reference Li2008). Saturability of channel capacity can be calculated as below:
where, DS is the saturability of channel capacity, Ws is the actual channel capacity, Wm is the probable channel capacity.
According to the determination method of port channel capacity balance coefficient, the channel service level can be divided into five grades (Li, Reference Li2008) as shown in Table 5.
Table 5. Evaluation index of saturability of channel capacity.

4.3. Accuracy inspection of the result
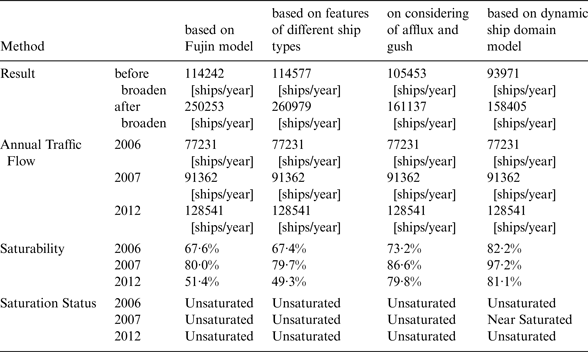
Calculation results for the above methods for Tianjin are shown in Table 6.
Table 6. The Calculation Result of Different Methods.

According to the conclusion of “Research on the Saturability and Navigation Risk of the Main Channel of Tianjin Port” (Tianjin Port Holdings Co., Ltd., 2007), the ship saturability of the Main channel of Tianjin port was approximately 80–90% in 2006, nearly at capacity.
However, in 2007, shipping volume increased 18·3% compared to 2006, and the channel capacity saturability was about 94·6% to 106·5%; the channel broadening project was badly needed and thus started in 2008.
After the channel broadening project was finished in 2012, the saturability of the channel capacity reduced but the vessel traffic volume increased rapidly again. The channel remains close to saturation even after the channel broadening project. Tianjin Port Holdings Co., Ltd has recently started a new project to further broaden and deepen the Main channel.
According to Table 6, it would appear that the proposed model was more accurate than earlier ones.
5. SUMMARY AND CONCLUSION
Developing adequate ship domain models has the potential to significantly benefit ship navigation safety that is collectively affected by the navigable waterway condition, the size and shape of the ship and operators' skills. The existing ship domain models developed over the last several decades mainly use constant values for the model input parameters, making them incapable of handling site-specific conditions. This study proposed dynamic ship domain models that explicitly considered restricted waterway conditions and ship types and sizes in an integrated manner. In particular, the proposed models could help determine ship domains for navigating along the channel, crossing, joining and turning in restricted water channels. In addition, security zones in excess of the ship domains for safe navigation were addressed for LNG ships. A computational experiment was conducted for model application using data on water channel design and ship traffic volumes associated with the Main channel of Port of Tianjin, China. Comparisons of results obtained between the proposed dynamic models with real ship traffic counts reveal that the proposed models could achieve a high degree of accuracy in estimating the capacity of restricted water channels.
The proposed dynamic ship domain models extended from the widely-used Fujii model taking account of ship behaviour and waterway conditions in restricted waters. From a practical point of view, the proposed dynamic ship domain models provided a heuristic methodology to determine ship safety domains for navigating along the channel, crossing, joining and turning in restricted waters that maintain the following characteristics:
• Addressing the characteristics of restricted waters by determining the values of input parameters according to the restricted water channel design specification and navigation standard;
• Considering different ship types and sizes ranging from general cargo ships to other special purpose ships, as well as differences in different grades of ships;
• Dealing with navigating along the channel, crossing, joining and turning that could help analyse ship conflicts between related categories of ship movements;
• Rigorously handling the influences of other ships on the specific ship conducting a certain category of navigation;
• Tackling the impacts of waterway traffic in a single direction or both directions for encountering and turning navigation;
• Performing refined analysis of ship turning navigation by considering different ways of berthing and unberthing;
• Capable of being used in simulation and evolution analysis of traffic flow, estimation of water channel capacity, and improvement in the efficiency of ship management entities;
• Applicable for analysing ship domains associated with open waters.
The model can also be used in forecasting channel capacity and optimising traffic organisation, which is quite important for channel construction and vessel traffic management.
In future work, in order to further enhance real world application, the proposed dynamic ship domain models should consider navigation risk and human factors.
ACKNOWLEDGMENT
This research was supported by the Chinese National Science Foundation (CNSF) under Grants No. 51179147 and No.51479156, along with an innovative research fund under “Fundamental Research Funds for the Central Universities” program of Wuhan University of Technology (No. 2013-YB-004).