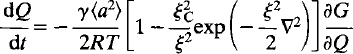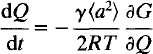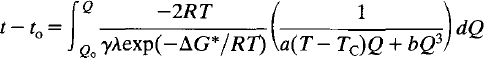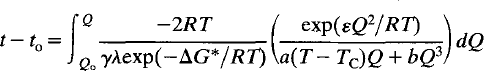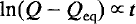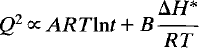Volume 53 - Issue 372 - September 1989
Petrology and Geochemistry
Carbonatite-related contact metasomatism in the Fen complex, Norway: effects and petrogenetic implications
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 395-414
-
- Article
- Export citation
The effect of organic acids on the dissolution of K-feldspar under conditions relevant to burial diagenesis
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 415-425
-
- Article
- Export citation
Mineralogy
Compositional relations in Li-micas from S.W. England and France: an ion- and electron-microprobe study
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 427-449
-
- Article
- Export citation
Niobian K–Ba–V titanates from micaceous kimberlite, Star mine, Orange Free State, South Africa
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 451-456
-
- Article
- Export citation
Holtite, (Si2.25Sb0.75)B [Al6(Al0.43Ta0.27□0.30) O15 (O,OH)2.25]: crystal structure and crystal chemistry
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 457-463
-
- Article
- Export citation
Mösbauer spectroscopic study of the decomposition mechanism of ankerite in CO2 atmosphere
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 465-471
-
- Article
- Export citation
Vochtenite, (Fe2+,Mg)Fe3+[UO2/PO4]4(OH). 12–13 H2O, a new uranyl phosphate mineral from Wheal Basset, Redruth, Cornwall, England
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 473-478
-
- Article
- Export citation
Curvature of gypsum crystals induced by growth in the presence of impurities
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 479-482
-
- Article
- Export citation
Time-dependent Landau theory for order/disorder processes in minerals
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 483-504
-
- Article
- Export citation
Short Communications
A naturally occurring alpha magnesium oxalate dihydrate from the northern Jordan Valley (Israel)
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 505-507
-
- Article
- Export citation
Queitite, a mineral new to Britain, from the Caldbeck Fells, Cumbria
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 508-509
-
- Article
- Export citation
Mineralogical Notes
Mineral nomenclature: fernandinite
-
- Published online by Cambridge University Press:
- 05 July 2018, p. 511
-
- Article
- Export citation
Book Reviews
E. G. Nisbet. The Young Earth: an Introduction to Archaean Geology. Boston and London (Unwin Hyman Ltd.), 1987. xviii + 402 pp. Price £18.95 paperback.
-
- Published online by Cambridge University Press:
- 05 July 2018, p. 513
-
- Article
- Export citation
R. G. Park and J. Tarney, Eds. Evolution of the Lewisian and Comparable Precambrian High Grade Terrains. London (Geological Society: Special Publication No. 27) and Oxford (Blackwell Scientific Publications), 1987. viii + 315 pp. Price £39.50.
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 513-514
-
- Article
- Export citation
M. Wilson. Igneous Petrogenesis: a Global Tectonic Approach. London (Unwin Hyman), 1989, xx + 466 pp. Price £50.00 (hardback); £24.95 (paper).
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 514-515
-
- Article
- Export citation
I. Parsons (ed.) Origins of Igneous Layering. Proceedings of the NATO Advanced Research Workshop, Narsarsuaq, South Greenland, 1986. NATO ASI, Series C, Vol. 196. Reidel (Dordrecht, Holland), 1987, xxiv + 666 pp. Price Dfl.280.00 (£98.00; $124.00).
-
- Published online by Cambridge University Press:
- 05 July 2018, p. 515
-
- Article
- Export citation
M. O'Donoghue. Gemstones. London (Chapman and Hall Ltd.), 1988. xiv + 372 pp. Price £37.50.
-
- Published online by Cambridge University Press:
- 05 July 2018, p. 515
-
- Article
- Export citation
H. M. Prichard, P. J. Potts, J. F. W. Bowles and S. J. Cribbs. Geo-Platinum 87. London and New York (Elsevier Science), 1988. xiii + 422 pp. Price £70.00.
-
- Published online by Cambridge University Press:
- 05 July 2018, p. 516
-
- Article
- Export citation
A. A. Hodgson. Alternatives to Asbestos and Asbestos. Crowthorne, Berkshire (Anjalena Publications Ltd.), 1987 (2nd Edition). ix + 284 pp. Price (post-free) UK £54.00, Europe £56.00, others £60.00.
-
- Published online by Cambridge University Press:
- 05 July 2018, pp. 516-517
-
- Article
- Export citation
S. K. Runcorn, G. Turner and M. M. Woolfson, eds. The Solar System: Chemistry as a key to its Origin. London (The Royal Society), 1988, xviii + 251 pp. Price £50.00.
-
- Published online by Cambridge University Press:
- 05 July 2018, p. 517
-
- Article
- Export citation

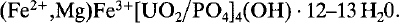
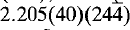 and
and  . Vochtenite is brown in colour with a bronzy lustre and is non-fluorescent. Mohs hardness is 2.5 and the density (calc.) = 3.663 g/cm
. Vochtenite is brown in colour with a bronzy lustre and is non-fluorescent. Mohs hardness is 2.5 and the density (calc.) = 3.663 g/cm