1. Introduction
Turbulent swirling flows are ubiquitous in both natural and technical flows. Their dynamics are governed by a variety of flow instabilities and modes (Gallaire & Chomaz Reference Gallaire and Chomaz2003). Among other mechanisms, Coriolis-driven inertial waves, also known as Kelvin waves, contribute significantly to the complex turbulent dynamics of swirling flows. These rotational modes occur in geophysics, for example in the Earth's atmosphere in the form of Rossby waves and geostrophic winds as well as in the Earth's oceans and lakes in the form of geostrophic currents (Greenspan Reference Greenspan1968). They are further hypothesized to occur in the liquid outer core of the Earth (Aldridge & Lumb Reference Aldridge and Lumb1987) and in tidal interactions of planets and stars (Ivanov & Papaloizou Reference Ivanov and Papaloizou2010). Inertial waves are also important in the context of vortex breakdown. The critical state theory says that the breakdown takes place if a supercritical-to-subcritical bifurcation occurs (Benjamin Reference Benjamin1962). In the subcritical state, standing vorticity waves are supported that ultimately leads to vortex breakdown. These vorticity waves can be identified as inertial waves (Wang & Rusak Reference Wang and Rusak1996; Renac, Sipp & Jacquin Reference Renac, Sipp and Jacquin2007). In gas turbines, inertial waves couple with velocity perturbations between stator–rotor stages of compressors or turbines, which play a significant role for noise generation and aeroelastic instabilities (Kerrebrock Reference Kerrebrock1977; Golubev & Atassi Reference Golubev and Atassi1998; Tam & Auriault Reference Tam and Auriault1998). Inertial waves are also suspected to trigger thermoacoustic instabilities in swirl-stabilized combustion systems. These instabilities are caused by a feedback between acoustic oscillations and heat release fluctuations. One mechanism that closes this feedback loop is related to azimuthal velocity or ‘swirl’ fluctuations originating at the swirler vanes of the mixing tube (Palies et al. Reference Palies, Schuller, Durox, Gicquel and Candel2011c). The cause and, particularly, the propagation mechanism of the swirl fluctuations downstream of the swirler are still an ongoing focus of research and will be the subject of this work.
In swirl-stabilized combustors, swirl fluctuations are generated via an acoustic-convective mode conversion process (Palies et al. Reference Palies, Durox, Schuller and Candel2011a). When a planar acoustic wave hits the swirl generator, the incoming pressure and velocity fluctuations interact with the trailing edge of the swirler vanes, leading to an oscillation of the Kutta condition that results in swirl fluctuations. This notion applies to both axial and radial swirl generators (Palies et al. Reference Palies, Durox, Schuller and Candel2011b). The generated swirl fluctuations propagate through the mixing tube before reaching the flame in the combustion chamber, ultimately leading to heat release fluctuations (Komarek & Polifke Reference Komarek and Polifke2010). The propagation velocity of the swirl fluctuations between the swirler and the flame is a very important quantity as it determines the time lag of the flame response and largely determines the stability of the entire combustion system (Juniper & Sujith Reference Juniper and Sujith2018).
Simple models for swirl fluctuations assume their phase and group velocity to be equal to the bulk velocity. However, it has been observed that the actual group velocity can deviate by approximately ![]() $50\,\%$ from the bulk velocity (Komarek & Polifke Reference Komarek and Polifke2010; Albayrak, Juniper & Polifke Reference Albayrak, Juniper and Polifke2019). More complex models based on linearized Euler or Navier–Stokes equations incorporate hydrodynamic waves such as inertial waves. These models have been demonstrated to be much more accurate with regard to propagation prediction (Albayrak, Bezgin & Polifke Reference Albayrak, Bezgin and Polifke2018; Albayrak et al. Reference Albayrak, Juniper and Polifke2019). The reason for the higher accuracy is that velocity fluctuations cannot be treated as passive scalars and the dispersive nature of the inertial wave is crucial to be accounted for. However, these linear models are based on simple flow fields under laminar conditions. Whether the inertial waves are still relevant and whether they are the governing mechanism for the swirl fluctuations under fully turbulent conditions remains unclear.
$50\,\%$ from the bulk velocity (Komarek & Polifke Reference Komarek and Polifke2010; Albayrak, Juniper & Polifke Reference Albayrak, Juniper and Polifke2019). More complex models based on linearized Euler or Navier–Stokes equations incorporate hydrodynamic waves such as inertial waves. These models have been demonstrated to be much more accurate with regard to propagation prediction (Albayrak, Bezgin & Polifke Reference Albayrak, Bezgin and Polifke2018; Albayrak et al. Reference Albayrak, Juniper and Polifke2019). The reason for the higher accuracy is that velocity fluctuations cannot be treated as passive scalars and the dispersive nature of the inertial wave is crucial to be accounted for. However, these linear models are based on simple flow fields under laminar conditions. Whether the inertial waves are still relevant and whether they are the governing mechanism for the swirl fluctuations under fully turbulent conditions remains unclear.
In the present study, swirl fluctuations are regarded as coherent fluctuations arising from coherent flow structures (Gallaire & Chomaz Reference Gallaire and Chomaz2003). In general, coherent structures are ‘organized’, quasi-deterministic motions in turbulent flows with very characteristic temporal scale and spatial shape (Hussain Reference Hussain1983). Under certain conditions, the fluctuations of these coherent structures can be described with the linearized Navier–Stokes equations, where the linearization is performed around the time-averaged (mean) flow field. The conditions are met if the energy gain of the coherent structure is primarily governed by the production through an energy exchange between the mean and the coherent field, while the energy loss to higher harmonics due to nonlinearities is small (Barkley Reference Barkley2006; Turton, Tuckerman & Barkley Reference Turton, Tuckerman and Barkley2015; Symon, Illingworth & Marusic Reference Symon, Illingworth and Marusic2021). Linearized mean field analysis is based on the conceptual separation of the turbulent flow field into large-scale coherent fluctuations and small-scale incoherent, stochastic fluctuations viewed as background turbulence. This notion was first proposed in the seminal work of Reynolds & Hussain (Reference Reynolds and Hussain1972), finding its formalization in the triple decomposition. Based on this concept, the linearized Navier–Stokes equations have been used in a multitude of different turbulent flow configurations. Numerous variants derived from this linear framework have been established such as resolvent analysis (RA), which will be used in this paper to model the swirl fluctuations.
In RA, the linearized Navier–Stokes equations are viewed as an input–output system, in which the resolvent operator acts as a transfer function that relates an arbitrary forcing of a linear, time-invariant system to its flow response in the frequency domain. A singular value decomposition of the resolvent operator under a given norm provides the optimal forcing and response modes (Farrell & Ioannou Reference Farrell and Ioannou2001; Sipp & Marquet Reference Sipp and Marquet2013). These response modes are supposed to represent self-sustaining, i.e. marginally or neutrally stable, coherent structures (when forced) in an otherwise globally stable flow (when not forced), which are either sustained through an intrinsic forcing due to the nonlinear turbulent term (McKeon & Sharma Reference McKeon and Sharma2010), or sustained through an external forcing (Jovanović & Bamieh Reference Jovanović and Bamieh2005). By that, coherent structures that are driven by resonant mechanisms, i.e. isolated eigenmodes, as well as pseudoresonant mechanisms, i.e. a superposition of a larger number of highly non-orthogonal eigenmodes, are found (Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). RA is distinguished between a local and global approach. The local RA is subject to the parallel flow assumption. Therefore, coherent structures are assumed to be periodic and the amplitude of the structures is assumed to stay constant in the main flow direction. Among others, the local RA was successfully used to identify coherent structures in turbulent channel flows (McKeon & Sharma Reference McKeon and Sharma2010; Morra et al. Reference Morra, Semeraro, Henningson and Cossu2019; Symon et al. Reference Symon, Illingworth and Marusic2021) and in the boundary layer of turbulent airfoil flows (Abreu et al. Reference Abreu, Tanarro, Cavalieri, Schlatter, Vinuesa, Hanifi and Henningson2021). In the global RA, no parallel flow assumption is made, making it possible to identify convective instabilities and coherent structures that grow and decay in space. This was demonstrated to work well, for example, for a backward-facing step (Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016), in turbulent jets (Schmidt et al. Reference Schmidt, Towne, Rigas, Colonius and Brès2018), turbulent jet flames (Casel et al. Reference Casel, Oberleithner, Zhang, Zirwes, Bockhorn, Trimis and Kaiser2022), turbulent swirling flows (Kaiser, Lesshafft & Oberleithner Reference Kaiser, Lesshafft and Oberleithner2019) and turbulent airfoil flows (Symon, Sipp & McKeon Reference Symon, Sipp and McKeon2019).
Apart from the modelling capabilities of RA, a major benefit of the linear framework unfolds when the complementary optimal forcing modes are considered. These can be exploited for a detailed analysis of the physical mechanisms driving the coherent structures (Pickering et al. Reference Pickering, Rigas, Nogueira, Cavalieri, Schmidt and Colonius2020), and for identifying regions of high receptivity and sensitivity (Brandt et al. Reference Brandt, Sipp, Pralits and Marquet2011; Sipp & Marquet Reference Sipp and Marquet2013; Qadri & Schmid Reference Qadri and Schmid2017).
Since the RA of turbulent flows is based on the nonlinearly modified mean flow, the mean–coherent and mean–incoherent interactions are implicitly accounted for. The coherent–incoherent interactions, however, are a priori not known. They are either assumed to be completely absorbed in the nonlinear forcing term, not requiring any closure of the equations, or taken (partially) into account with a turbulence model, which is usually based on a Boussinesq-like eddy viscosity. Several works have discussed the integration of such turbulence models and their importance for the validity of the linearized Navier–Stokes equations (Reau & Tumin Reference Reau and Tumin2002; Rukes, Paschereit & Oberleithner Reference Rukes, Paschereit and Oberleithner2016; Morra et al. Reference Morra, Semeraro, Henningson and Cossu2019; Pickering et al. Reference Pickering, Rigas, Schmidt, Sipp and Colonius2021; Kuhn et al. Reference Kuhn, Müller, Oberleithner, Knechtel and Soria2022; Symon et al. Reference Symon, Madhusudanan, Illingworth and Marusic2023; Fan et al. Reference Fan, Kozul, Li and Sandberg2024).
In the present work, the role of inertial waves in driving swirl fluctuations is investigated at fully turbulent conditions. For this, we consider a turbulent swirling pipe flow generated by a radial swirler as part of a swirl combustor. We conduct RA to model the spatio-temporal structure and propagation velocity of the swirl fluctuations. As such, the optimal frequency response of the swirling pipe flow in the mixing tube can be characterized and directly compared with an experimentally measured response of the system to acoustic forcing. In addition, we examine the physical mechanisms behind swirl fluctuations using RA. We compare the results with those from a simplified configuration to differentiate between inertial waves and shear-driven amplification mechanisms. Combining the linearized methods and the experimental data, the open questions pertaining to the validity of such a linear framework in turbulent conditions as well as the relevance and potential control opportunities of swirl fluctuations in turbulent swirling flows are discussed.
2. Set-up
In this section, a brief overview of the geometrical, numerical and experimental set-up is given. Numerical large-eddy simulation (LES) was used to generate a spatially well-resolved time-averaged mean velocity field that is required as an input for the linear model, which would not be fully accessible in an experimental rig otherwise. In the experimental set-up, the flow was acoustically excited and the time-averaged as well as fluctuating velocity field of the flow response was measured with time-resolved particle image velocimetry (PIV). The experimental measurements are used for validation of the time-averaged velocity fields of the LES and for validation of the linearly modelled flow response.
2.1. Geometrical set-up
The considered set-up is a modified generic swirl combustor consisting of a plenum, swirler and mixing tube. A cutaway view of the LES set-up is shown in figure 1(a) and a streamwise cut is shown in figure 1(b). The set-up consists of the straight end-section of the upstream plenum, the radial swirl generator and the mixing tube. The swirl generator was equipped with one central air inlet (indicated by the vertical dashed line) that creates a non-swirling axial jet. The swirler comprises eight radial-tangential air inlets (indicated by the horizontal dashed lines), which introduce the swirling flow with a geometric swirl number (Leuckel Reference Leuckel1967) of ![]() ${S}_{g} = 0.7$. The mixing tube has a diameter of
${S}_{g} = 0.7$. The mixing tube has a diameter of ![]() $D = 34$ mm and, with the extended exhaust tube, a length of
$D = 34$ mm and, with the extended exhaust tube, a length of ![]() $L = 7.5D$. The upstream plenum has a diameter and axial length of
$L = 7.5D$. The upstream plenum has a diameter and axial length of ![]() $4.4D$. The simulations and experiments were performed at isothermal (
$4.4D$. The simulations and experiments were performed at isothermal (![]() $T = 293$ K) and ambient pressure (
$T = 293$ K) and ambient pressure (![]() $p = 101\ 325$ Pa) operating conditions. The mass flow rate was
$p = 101\ 325$ Pa) operating conditions. The mass flow rate was ![]() $\dot {m} = 104\ {\rm kg}\ {\rm h}^{-1}$, corresponding to a bulk flow velocity of
$\dot {m} = 104\ {\rm kg}\ {\rm h}^{-1}$, corresponding to a bulk flow velocity of ![]() $U \approx 26\ {\rm m}\ {\rm s}^{-1}$. The Reynolds number of the swirling pipe flow in the mixing tube with respect to its diameter and bulk velocity was
$U \approx 26\ {\rm m}\ {\rm s}^{-1}$. The Reynolds number of the swirling pipe flow in the mixing tube with respect to its diameter and bulk velocity was ![]() $Re = UD/\nu \approx 58\ 000$, with
$Re = UD/\nu \approx 58\ 000$, with ![]() $\nu$ being the kinematic viscosity.
$\nu$ being the kinematic viscosity.

Figure 1. Large-eddy simulation set-up of the swirling pipe flow as (a) cutaway view and (b) streamwise cut with the origin of coordinates at the upstream end of the mixing tube (![]() $x=0$) and at the mixing tube centreline (
$x=0$) and at the mixing tube centreline (![]() $y=0$). The inlet and outlet of the simulation domain are at the leftmost and rightmost boundary, respectively.
$y=0$). The inlet and outlet of the simulation domain are at the leftmost and rightmost boundary, respectively.
2.2. Large-eddy simulation
The LES was conducted with the compressible AVBP code from CERFACS and IFPEN. The domain was discretized with approximately ![]() $31$ million triangular cells. Time stepping was performed using a two-step Taylor–Galerkin scheme (Colin & Rudgyard Reference Colin and Rudgyard2000), which is third-order accurate in space and time. Subgrid turbulence was accounted for by using the
$31$ million triangular cells. Time stepping was performed using a two-step Taylor–Galerkin scheme (Colin & Rudgyard Reference Colin and Rudgyard2000), which is third-order accurate in space and time. Subgrid turbulence was accounted for by using the ![]() $\sigma$-model (Nicoud et al. Reference Nicoud, Toda, Cabrit, Bose and Lee2011). At the inlet, a constant velocity profile with a mass flow rate of
$\sigma$-model (Nicoud et al. Reference Nicoud, Toda, Cabrit, Bose and Lee2011). At the inlet, a constant velocity profile with a mass flow rate of ![]() $\dot {m} = 104\ {\rm kg}\ {\rm h}^{-1}$ was set; at the outlet, a constant pressure of 101 325 Pa. Characteristic boundary conditions were applied at the inlet and outlet of the domain (Poinsot & Lele Reference Poinsot and Lele1992). The relaxation coefficient at the inlet was chosen as
$\dot {m} = 104\ {\rm kg}\ {\rm h}^{-1}$ was set; at the outlet, a constant pressure of 101 325 Pa. Characteristic boundary conditions were applied at the inlet and outlet of the domain (Poinsot & Lele Reference Poinsot and Lele1992). The relaxation coefficient at the inlet was chosen as ![]() $10^4$ to ensure a close adherence to the prescribed mass flow value. According to Selle, Nicoud & Poinsot (Reference Selle, Nicoud and Poinsot2004), this results in a reflection cutoff frequency for acoustic waves of approximately
$10^4$ to ensure a close adherence to the prescribed mass flow value. According to Selle, Nicoud & Poinsot (Reference Selle, Nicoud and Poinsot2004), this results in a reflection cutoff frequency for acoustic waves of approximately ![]() $800$ Hz. The relaxation coefficient at the outlet was set to
$800$ Hz. The relaxation coefficient at the outlet was set to ![]() $10^3$, resulting in an acoustically transmissive boundary condition with a cutoff frequency of approximately
$10^3$, resulting in an acoustically transmissive boundary condition with a cutoff frequency of approximately ![]() $80$ Hz. All walls were assumed to be no-slip and adiabatic. The Courant–Friedrichs–Lewy number was set to
$80$ Hz. All walls were assumed to be no-slip and adiabatic. The Courant–Friedrichs–Lewy number was set to ![]() $0.75$. The simulation was performed for a total time of
$0.75$. The simulation was performed for a total time of ![]() $0.03$ s, which corresponds to approximately four mixing tube flow-through times. The axisymmetric mean flow field was obtained by averaging along the temporal and the azimuthal direction. Only marginal changes of the numerical solution were found when repeating the simulation with an increased mesh resolution of
$0.03$ s, which corresponds to approximately four mixing tube flow-through times. The axisymmetric mean flow field was obtained by averaging along the temporal and the azimuthal direction. Only marginal changes of the numerical solution were found when repeating the simulation with an increased mesh resolution of ![]() $101$ million cells. The associated mean field changes had negligible effects on the optimal response and forcing modes of the RA.
$101$ million cells. The associated mean field changes had negligible effects on the optimal response and forcing modes of the RA.
2.3. Experimental measurements
For validation of the LES mean flow and the linear model, two experimental datasets are used. The primarily considered dataset of Bluemner, Paschereit & Oberleithner (Reference Bluemner, Paschereit and Oberleithner2019) has the exact same operating conditions and set-up as the LES, but with an added trombone section upstream of the plenum. The LES provides the time- and phase-averaged velocity fields of the axial and radial components in a streamwise section. Four loudspeakers located upstream of the plenum were used for acoustically exciting the flow at various frequencies and at a target amplitude of ![]() $10\,\%$ of the bulk velocity. This target amplitude ensures a sufficiently large but still linear flow response, which was cross-checked with prior microphone measurements. Two-dimensional (2-D), two-component, time-resolved PIV was performed for measuring the velocity fields. For this, the mixing tube was made of borosilicate glass for optical access and the light sheet was aligned with the mixing tube's centreline. The effective measurement region reached from
$10\,\%$ of the bulk velocity. This target amplitude ensures a sufficiently large but still linear flow response, which was cross-checked with prior microphone measurements. Two-dimensional (2-D), two-component, time-resolved PIV was performed for measuring the velocity fields. For this, the mixing tube was made of borosilicate glass for optical access and the light sheet was aligned with the mixing tube's centreline. The effective measurement region reached from ![]() $x/D \approx 1.35$ to
$x/D \approx 1.35$ to ![]() $x/D \approx 4$. The sampling frequency was
$x/D \approx 4$. The sampling frequency was ![]() $2027$ Hz with a measurement time of approximately
$2027$ Hz with a measurement time of approximately ![]() $1$ s. A second dataset of Müller et al. (Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022) is considered to obtain the time- and phase-averaged velocity fields of the azimuthal component in cross-wise sections, which were not recorded in the first dataset introduced above. The second dataset has a very similar set-up but with a shorter mixing tube length of
$1$ s. A second dataset of Müller et al. (Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022) is considered to obtain the time- and phase-averaged velocity fields of the azimuthal component in cross-wise sections, which were not recorded in the first dataset introduced above. The second dataset has a very similar set-up but with a shorter mixing tube length of ![]() $4.4D$ and a combustion chamber attached downstream. In the second experiment, the operating conditions were at a slightly lower mass flow rate with a bulk velocity of
$4.4D$ and a combustion chamber attached downstream. In the second experiment, the operating conditions were at a slightly lower mass flow rate with a bulk velocity of ![]() $U \approx 21\ {\rm m}\ {\rm s}^{-1}$, corresponding to a Reynolds number of
$U \approx 21\ {\rm m}\ {\rm s}^{-1}$, corresponding to a Reynolds number of ![]() $Re \approx 47\ 000$. For further details of both experimental set-ups, the reader is referred to the respective studies.
$Re \approx 47\ 000$. For further details of both experimental set-ups, the reader is referred to the respective studies.
2.4. Time-averaged flow field and validation of the LES
The time-averaged flow field is briefly characterized and the accuracy of the LES is evaluated with regard to the experimentally measured data. For the remainder of this paper, the velocity vector ![]() $\boldsymbol {u} = (u, v, w)^\mathrm {T}$ is defined by the components of axial, radial and azimuthal velocity, respectively. However, strictly speaking, we will show transverse instead of radial and out-of-plane instead of azimuthal velocities for the sake of visuals.
$\boldsymbol {u} = (u, v, w)^\mathrm {T}$ is defined by the components of axial, radial and azimuthal velocity, respectively. However, strictly speaking, we will show transverse instead of radial and out-of-plane instead of azimuthal velocities for the sake of visuals.
Figure 2 shows the contours of time-averaged velocity for all three components in the mixing tube of the LES, downstream of the central nozzle and the tangential swirler inlet (indicated by the dashed line between the black dots). At the central nozzle, a strong jet is evident for the axial component, introducing strong shear and velocity gradients. This jet joins with the tangentially and radially introduced flow from the swirler, as visible for the radial component. For the azimuthal component, a prominent region of very high swirl can be observed. Figure 3 compares the mean axial and azimuthal velocity profiles between LES and the two experiments for five different axial positions. The overall agreement is good. However, the LES overestimates the diffusive behaviour of the flow, as indicated by the increasingly homogeneous velocity profiles in the downstream direction. The azimuthal component reveals a region of nearly solid-body rotation for ![]() $|y/D| < 0.3$, which is almost fully developed at
$|y/D| < 0.3$, which is almost fully developed at ![]() $x/D = 2.2$.
$x/D = 2.2$.

Figure 2. Contours of the time-averaged LES flow field of the swirling pipe flow inside the mixing tube for (a) axial velocity, (b) radial velocity and (c) azimuthal velocity.

Figure 3. Profiles of the time-averaged LES flow field of the swirling pipe flow for (a) axial velocity and (b) azimuthal velocity compared against two experimental datasets (Bluemner et al. Reference Bluemner, Paschereit and Oberleithner2019; Müller et al. Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022) and plug flow with solid-body rotation. Grey shaded area indicates region of approximate solid-body rotation in the swirling pipe flow and coincides with the radial domain size of the plug flow with solid-body rotation.
The discrepancies between LES and experiment may be attributed to a mismatch of the pressure drop across the swirler. This pressure drop is critical since a false prediction can lead to an incorrect mass flow split between the central and tangential air inlet that disagrees with the experiment. Even slight errors in this mass flow split can have a large impact on the LES flow field inside the mixing tube. As mentioned in § 2.2, another LES for more than triple the mesh resolution was performed, but only marginal changes for the mean fields and negligible impact on the RA results were found. Due to these diminishing returns, we did not see any substantial benefit in further pursuing an exhaustive LES study.
3. Data analysis
The data obtained from the experiment and simulation are primarily analysed pertaining to the coherent structures that are associated with the swirl fluctuations. In particular, the experimental PIV data require a systematic post-processing to be accessible for inspection and physical interpretation.
The conceptual basis of the entire physics-based analysis is the triple decomposition. The flow field ![]() $\boldsymbol {q}(\boldsymbol {x},t) = [\boldsymbol {u}, p]^\mathrm {T}$, consisting of the velocity field
$\boldsymbol {q}(\boldsymbol {x},t) = [\boldsymbol {u}, p]^\mathrm {T}$, consisting of the velocity field ![]() $\boldsymbol {u} = (u, v, w)^\mathrm {T}$ and the pressure field
$\boldsymbol {u} = (u, v, w)^\mathrm {T}$ and the pressure field ![]() $p$, is decomposed according to (Reynolds & Hussain Reference Reynolds and Hussain1972)
$p$, is decomposed according to (Reynolds & Hussain Reference Reynolds and Hussain1972)
where ![]() $\boldsymbol {\overline {q}}$ is the time-averaged,
$\boldsymbol {\overline {q}}$ is the time-averaged, ![]() $\boldsymbol {\widetilde{q}}$ is the coherent-periodic fluctuation and
$\boldsymbol {\widetilde{q}}$ is the coherent-periodic fluctuation and ![]() $\boldsymbol {q''}$ is the remaining incoherent-stochastic fluctuation part. The time-averaged velocity field has already been discussed in § 2.4. The coherent part is going to be the main focus of interest in the following. The stochastic part will be relevant for the linear modelling in § 4.
$\boldsymbol {q''}$ is the remaining incoherent-stochastic fluctuation part. The time-averaged velocity field has already been discussed in § 2.4. The coherent part is going to be the main focus of interest in the following. The stochastic part will be relevant for the linear modelling in § 4.
3.1. Phase average
To extract the coherent fluctuation part, a phase-averaging procedure is conducted. The phase average of the velocity field ![]() $\langle \boldsymbol {u}(\boldsymbol {x},t) \rangle$ is defined by
$\langle \boldsymbol {u}(\boldsymbol {x},t) \rangle$ is defined by
 \begin{equation} \langle \boldsymbol{u}(\boldsymbol{x},t) \rangle = \lim_{N\to\infty} \frac{1}{N} \sum_{n=1}^{N} \boldsymbol{u}(\boldsymbol{x},t + n\tau) ,\end{equation}
\begin{equation} \langle \boldsymbol{u}(\boldsymbol{x},t) \rangle = \lim_{N\to\infty} \frac{1}{N} \sum_{n=1}^{N} \boldsymbol{u}(\boldsymbol{x},t + n\tau) ,\end{equation}
where ![]() $\tau$ is the characteristic period of the oscillation with the angular frequency
$\tau$ is the characteristic period of the oscillation with the angular frequency ![]() $\omega = 2{\rm \pi} /\tau$, in which the frequency is related to the instantaneous phase angle
$\omega = 2{\rm \pi} /\tau$, in which the frequency is related to the instantaneous phase angle ![]() $\varphi$ of the oscillation with
$\varphi$ of the oscillation with ![]() $\varphi \propto \omega t$. In practice, the phase-averaging in (3.2) cannot be computed continuously in
$\varphi \propto \omega t$. In practice, the phase-averaging in (3.2) cannot be computed continuously in ![]() $t$. Instead, the time signal is partitioned into segments, in which each segment corresponds to a phase angle bin. The loudspeaker input signal is used for a reference phase angle and a complete period of oscillation is divided into
$t$. Instead, the time signal is partitioned into segments, in which each segment corresponds to a phase angle bin. The loudspeaker input signal is used for a reference phase angle and a complete period of oscillation is divided into ![]() $N_\varphi = 16$ phase bins. The PIV snapshots are sorted to each of these phase bins
$N_\varphi = 16$ phase bins. The PIV snapshots are sorted to each of these phase bins ![]() $\varphi _j$ and averaged subsequently, yielding a phase-averaged field
$\varphi _j$ and averaged subsequently, yielding a phase-averaged field ![]() $\langle \boldsymbol {u} \rangle _j$ for each given phase angle bin. The coherent fluctuation is retrieved by
$\langle \boldsymbol {u} \rangle _j$ for each given phase angle bin. The coherent fluctuation is retrieved by
Finally, the coherent fluctuation is transformed into frequency space with
 \begin{equation} \skew2\hat{\boldsymbol{u}} = \frac{1}{N_\varphi} \sum_{j=1}^{N_\varphi} \boldsymbol{\widetilde{u}}_j \, \mathrm{e}^{-\mathrm{i}\varphi_j}. \end{equation}
\begin{equation} \skew2\hat{\boldsymbol{u}} = \frac{1}{N_\varphi} \sum_{j=1}^{N_\varphi} \boldsymbol{\widetilde{u}}_j \, \mathrm{e}^{-\mathrm{i}\varphi_j}. \end{equation}
This is done to filter out any higher harmonics and to obtain a defined spatial phase angle ![]() $\varphi _{\boldsymbol x} = \operatorname {atan2}({\rm Im}(\skew2\hat {\boldsymbol {u}}),{\rm Re}(\skew2\hat {\boldsymbol {u}}))$ required for computing the phase velocity in § 3.3.
$\varphi _{\boldsymbol x} = \operatorname {atan2}({\rm Im}(\skew2\hat {\boldsymbol {u}}),{\rm Re}(\skew2\hat {\boldsymbol {u}}))$ required for computing the phase velocity in § 3.3.
3.2. Separation of acoustic and hydrodynamic response
The acoustic forcing of the loudspeakers in the upstream part of the test rig triggers a general flow response that can be decomposed into an acoustic wave that travels at the speed of sound and a hydrodynamic wave that travels at typical convective time scales. For examination of the swirl fluctuations that travel at the order of the convective flow, we are only interested in the hydrodynamic part and we disregard the acoustic part. It has to be noted that an acoustic wave can be physically converted into a hydrodynamic wave as briefly described in § 1 with regard to the swirler, and that the distinction between acoustic and hydrodynamic response is a local property and therefore a function of space.
Due to the very low Mach number of ![]() $Ma < 0.1$ in the swirling pipe flow, the phase velocity of the hydrodynamic modes
$Ma < 0.1$ in the swirling pipe flow, the phase velocity of the hydrodynamic modes ![]() $c_{ph,h}$ is expected to be much lower than the phase velocity of the acoustics
$c_{ph,h}$ is expected to be much lower than the phase velocity of the acoustics ![]() $c_{ph,a}$, i.e.
$c_{ph,a}$, i.e. ![]() $c_{ph,h} \ll c_{ph,a}$. In turn, the axial wavenumber of the hydrodynamics
$c_{ph,h} \ll c_{ph,a}$. In turn, the axial wavenumber of the hydrodynamics ![]() $k_{x,{h}}$ is much greater than the axial wavenumber of the acoustics
$k_{x,{h}}$ is much greater than the axial wavenumber of the acoustics ![]() $k_{x,{a}}$, i.e.
$k_{x,{a}}$, i.e. ![]() $k_{x,{h}} \gg k_{x,{a}}$. This can be exploited when doing a spatial Fourier decomposition. Taking into account that the axial length of the swirling pipe flow's region of interest is significantly lower than the acoustic wavelengths, we can assume that the acoustics are largely contained in the wavenumber bin of
$k_{x,{h}} \gg k_{x,{a}}$. This can be exploited when doing a spatial Fourier decomposition. Taking into account that the axial length of the swirling pipe flow's region of interest is significantly lower than the acoustic wavelengths, we can assume that the acoustics are largely contained in the wavenumber bin of ![]() $k_x = 0$. This particular wavenumber is, thus, filtered in the spectral domain. Additionally, all negative wavenumbers
$k_x = 0$. This particular wavenumber is, thus, filtered in the spectral domain. Additionally, all negative wavenumbers ![]() $k_x < 0$ are filtered as well to discard all upstream travelling waves. The remaining spectral coefficients are inverse Fourier transformed to obtain the purely hydrodynamic part of the downstream travelling coherent fluctuations.
$k_x < 0$ are filtered as well to discard all upstream travelling waves. The remaining spectral coefficients are inverse Fourier transformed to obtain the purely hydrodynamic part of the downstream travelling coherent fluctuations.
3.3. Phase and group velocity
For fully characterizing the spatio-temporal structure of the coherent fluctuations associated with the swirl fluctuations, their propagation and dispersion needs to be examined. This is done by computing the phase and group velocity, reading
and
where we only consider the axial velocity component. For a given angular frequency ![]() $\omega = 2{\rm \pi} f$, the angular axial wavenumber
$\omega = 2{\rm \pi} f$, the angular axial wavenumber ![]() $k_x$ is in general a function of space, meaning that both phase and group velocity are local quantities. For simplicity, we will focus on the phase and group velocity on the centreline that is spatially averaged between
$k_x$ is in general a function of space, meaning that both phase and group velocity are local quantities. For simplicity, we will focus on the phase and group velocity on the centreline that is spatially averaged between ![]() $x/D = 1.3$ and
$x/D = 1.3$ and ![]() $2.2$. The axial wavenumber is computed with
$2.2$. The axial wavenumber is computed with ![]() $k_x = \overline {\partial \varphi _x(x,y=0) / \partial x}$, where
$k_x = \overline {\partial \varphi _x(x,y=0) / \partial x}$, where ![]() $\varphi _x$ is the axial phase angle of the axial component of the complex mode
$\varphi _x$ is the axial phase angle of the axial component of the complex mode ![]() $\hat {u}$, and the
$\hat {u}$, and the ![]() $\overline {({\cdot })}$ operator denotes the spatial average. To compute the group velocity, a power law is fitted to the axial wavenumber distribution and used to analytically calculate the group velocity according to (3.6).
$\overline {({\cdot })}$ operator denotes the spatial average. To compute the group velocity, a power law is fitted to the axial wavenumber distribution and used to analytically calculate the group velocity according to (3.6).
4. Linear modelling
The basis for modelling the coherent fluctuations are the linearized Navier–Stokes equations in cylindrical coordinates, which can be derived as follows. The incompressible Navier–Stokes equations are
where ![]() $\nu$ is the kinematic molecular viscosity and
$\nu$ is the kinematic molecular viscosity and ![]() $\rho$ is the density. Inserting the triple decomposition, (3.1), in (4.1), applying the phase average and subtracting the time average leads to the Navier–Stokes equations of the coherent fluctuation (Reynolds & Hussain Reference Reynolds and Hussain1972):
$\rho$ is the density. Inserting the triple decomposition, (3.1), in (4.1), applying the phase average and subtracting the time average leads to the Navier–Stokes equations of the coherent fluctuation (Reynolds & Hussain Reference Reynolds and Hussain1972):
where ![]() $\widetilde {\boldsymbol {u}''\boldsymbol {u}''}$ is the coherent component of the Reynolds stress tensor, which, according to (3.3), is defined as
$\widetilde {\boldsymbol {u}''\boldsymbol {u}''}$ is the coherent component of the Reynolds stress tensor, which, according to (3.3), is defined as ![]() $\widetilde {\boldsymbol {u}''\boldsymbol {u}''} = \langle {\boldsymbol {u}''\boldsymbol {u}''}\rangle - \overline {\boldsymbol {u}''\boldsymbol {u}''}$. Additionally,
$\widetilde {\boldsymbol {u}''\boldsymbol {u}''} = \langle {\boldsymbol {u}''\boldsymbol {u}''}\rangle - \overline {\boldsymbol {u}''\boldsymbol {u}''}$. Additionally, ![]() $(\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}} - \overline {\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}}})$ is the nonlinear term due to the interaction of the coherent structure with itself and its higher harmonics, and
$(\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}} - \overline {\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}}})$ is the nonlinear term due to the interaction of the coherent structure with itself and its higher harmonics, and ![]() $\boldsymbol {g}$ is an additionally introduced external forcing term. The term
$\boldsymbol {g}$ is an additionally introduced external forcing term. The term ![]() $\widetilde {\boldsymbol {u}''\boldsymbol {u}''}$ on the right-hand side of (4.2a) is a new unknown term, which is related to the classical turbulence closure problem encountered in Reynolds-averaged Navier–Stokes equations. In contrast to linearized analyses under laminar conditions, this term is exclusive to the turbulent form of the linearized Navier–Stokes equations. Its treatment is described further below.
$\widetilde {\boldsymbol {u}''\boldsymbol {u}''}$ on the right-hand side of (4.2a) is a new unknown term, which is related to the classical turbulence closure problem encountered in Reynolds-averaged Navier–Stokes equations. In contrast to linearized analyses under laminar conditions, this term is exclusive to the turbulent form of the linearized Navier–Stokes equations. Its treatment is described further below.
4.1. Resolvent analysis
The linear model is based on a global RA, which is essentially an optimal response analysis of the forced linearized Navier–Stokes equations, accomplished by a singular value decomposition of the resolvent operator (Farrell & Ioannou Reference Farrell and Ioannou2001). The global RA allows us to examine the spatial evolution of an optimal perturbation in the frequency domain.
The starting point for deriving the global RA equations is the Navier–Stokes equations of the coherent fluctuation, (4.2). Assuming the azimuthal direction to be homogeneous and the mean flow to be axisymmetric, we substitute a normal mode ansatz into (4.2) with harmonic fluctuations in ![]() $\theta$ and
$\theta$ and ![]() $t$,
$t$,
in which ![]() $\skew2\hat {\boldsymbol {q}}$ is the complex amplitude function that describes the spatial mode shape,
$\skew2\hat {\boldsymbol {q}}$ is the complex amplitude function that describes the spatial mode shape, ![]() $\mathrm {c.c.}$ is the complex conjugate,
$\mathrm {c.c.}$ is the complex conjugate, ![]() $m \in \mathbb {Z}$ is the azimuthal wavenumber and
$m \in \mathbb {Z}$ is the azimuthal wavenumber and ![]() $\omega \in \mathbb {R}$ is the angular frequency. The nonlinear terms and the external forcing are not set to zero, and both terms are lumped into a general forcing term
$\omega \in \mathbb {R}$ is the angular frequency. The nonlinear terms and the external forcing are not set to zero, and both terms are lumped into a general forcing term
The general forcing term can then be interpreted as being intrinsic due to turbulence (McKeon & Sharma Reference McKeon and Sharma2010), being external due to an external excitation (Jovanović & Bamieh Reference Jovanović and Bamieh2005), or both. The resulting Navier–Stokes equations in the spectral domain then read
where ![]() $\boldsymbol{\mathsf{B}}$ is a restriction operator and
$\boldsymbol{\mathsf{B}}$ is a restriction operator and ![]() $\boldsymbol {\mathcal {L}}$ is the 2-D linearized Navier–Stokes operator. Both expressions are given in Appendix B.
$\boldsymbol {\mathcal {L}}$ is the 2-D linearized Navier–Stokes operator. Both expressions are given in Appendix B.
The unknown term of the coherent Reynolds stress tensor on the right-hand side of (4.5) is separated ad hoc into a purely dissipative, energy-draining and a residual energy-donating part (Kuhn et al. Reference Kuhn, Müller, Oberleithner, Knechtel and Soria2022). The latter is absorbed in the remaining forcing term and the former, dissipative part is modelled by a Boussinesq-like eddy viscosity approach (Reau & Tumin Reference Reau and Tumin2002) in the form of
where ![]() $\overline {\boldsymbol{\mathsf{S}}} = 1/2 (\boldsymbol {\nabla } + \nabla ^\mathrm {T}) \overline {\boldsymbol {u}}$ and
$\overline {\boldsymbol{\mathsf{S}}} = 1/2 (\boldsymbol {\nabla } + \nabla ^\mathrm {T}) \overline {\boldsymbol {u}}$ and ![]() $\widetilde {\boldsymbol{\mathsf{S}}} = 1/2 (\boldsymbol {\nabla } + \nabla ^\mathrm {T}) \widetilde {\boldsymbol {u}}$ are the mean and coherent strain rate tensor, respectively,
$\widetilde {\boldsymbol{\mathsf{S}}} = 1/2 (\boldsymbol {\nabla } + \nabla ^\mathrm {T}) \widetilde {\boldsymbol {u}}$ are the mean and coherent strain rate tensor, respectively, ![]() $\overline {\nu }_{t}$ and
$\overline {\nu }_{t}$ and ![]() $\widetilde {\nu }_{t}$ are the mean and coherent eddy viscosity, respectively,
$\widetilde {\nu }_{t}$ are the mean and coherent eddy viscosity, respectively, ![]() $\widetilde {k}$ is the coherent kinetic energy and
$\widetilde {k}$ is the coherent kinetic energy and ![]() $\boldsymbol{\mathsf{I}}$ is the identity tensor. We assume a frozen eddy viscosity (
$\boldsymbol{\mathsf{I}}$ is the identity tensor. We assume a frozen eddy viscosity (![]() $\widetilde {\nu }_{t} = 0$) and neglect fluctuations of the turbulent kinetic energy (
$\widetilde {\nu }_{t} = 0$) and neglect fluctuations of the turbulent kinetic energy (![]() $\widetilde {k} = 0$), and extract the mean eddy viscosity from the mean Reynolds stresses (Tammisola & Juniper Reference Tammisola and Juniper2016) via a least-squares fit (Ivanova, Noll & Aigner Reference Ivanova, Noll and Aigner2013):
$\widetilde {k} = 0$), and extract the mean eddy viscosity from the mean Reynolds stresses (Tammisola & Juniper Reference Tammisola and Juniper2016) via a least-squares fit (Ivanova, Noll & Aigner Reference Ivanova, Noll and Aigner2013):
where ![]() $\langle {\cdot } , {\cdot } \rangle _{F}$ is the Frobenius inner product,
$\langle {\cdot } , {\cdot } \rangle _{F}$ is the Frobenius inner product, ![]() $\overline {\boldsymbol {u}'' \boldsymbol {u}''}$ is the Reynolds stress tensor and
$\overline {\boldsymbol {u}'' \boldsymbol {u}''}$ is the Reynolds stress tensor and ![]() $k''$ is the turbulent kinetic energy, both of the incoherent, stochastic part. To include the turbulence model, the molecular viscosity
$k''$ is the turbulent kinetic energy, both of the incoherent, stochastic part. To include the turbulence model, the molecular viscosity ![]() $\nu$ is then substituted by an effective viscosity
$\nu$ is then substituted by an effective viscosity ![]() $\nu _{eff} = \nu + \overline {\nu }_{t}$ within the linearized Navier–Stokes operator
$\nu _{eff} = \nu + \overline {\nu }_{t}$ within the linearized Navier–Stokes operator ![]() $\boldsymbol {\mathcal {L}}$ of (4.5). Figure 4 shows the eddy viscosity obtained from the LES and normalized with the molecular viscosity. Subsequently, (4.5) are discretized and recast as an input–output problem (Sipp & Marquet Reference Sipp and Marquet2013),
$\boldsymbol {\mathcal {L}}$ of (4.5). Figure 4 shows the eddy viscosity obtained from the LES and normalized with the molecular viscosity. Subsequently, (4.5) are discretized and recast as an input–output problem (Sipp & Marquet Reference Sipp and Marquet2013),
where ![]() $\boldsymbol {\mathcal {R}} = \boldsymbol{\mathsf{P}}^\mathrm {T}(- \mathrm {i}\omega \boldsymbol{\mathsf{B}} - \boldsymbol {\mathcal {L}})^{-1}\boldsymbol{\mathsf{P}}$ is a linear operator acting as a transfer function in the spectral domain that relates the input forcing
$\boldsymbol {\mathcal {R}} = \boldsymbol{\mathsf{P}}^\mathrm {T}(- \mathrm {i}\omega \boldsymbol{\mathsf{B}} - \boldsymbol {\mathcal {L}})^{-1}\boldsymbol{\mathsf{P}}$ is a linear operator acting as a transfer function in the spectral domain that relates the input forcing ![]() $\,\skew2\hat{\boldsymbol{f}}$ to the output response
$\,\skew2\hat{\boldsymbol{f}}$ to the output response ![]() $\skew2\hat {\boldsymbol {u}}$. The transfer function
$\skew2\hat {\boldsymbol {u}}$. The transfer function ![]() $\boldsymbol {\mathcal {R}}$ is called the resolvent operator. Here,
$\boldsymbol {\mathcal {R}}$ is called the resolvent operator. Here, ![]() $\boldsymbol{\mathsf{P}}^\mathrm {T}$ is a restriction operator and
$\boldsymbol{\mathsf{P}}^\mathrm {T}$ is a restriction operator and ![]() $\boldsymbol{\mathsf{P}}$ is a prolongation operator that are required to exclude the continuity equation and the pressure term from the forcing. The restriction operator can, furthermore, be used to restrict the forcing to a subset of the spatial domain. The full expressions of these operators are given in Appendix B.
$\boldsymbol{\mathsf{P}}$ is a prolongation operator that are required to exclude the continuity equation and the pressure term from the forcing. The restriction operator can, furthermore, be used to restrict the forcing to a subset of the spatial domain. The full expressions of these operators are given in Appendix B.

Figure 4. Eddy viscosity normalized with kinematic molecular viscosity.
One way to put (4.8) into effect is to conduct an input–output analysis. As such, the forcing ![]() $\,\skew2\hat{\boldsymbol{f}}$ needs to be known explicitly. In the present case, there are two approaches for specifying the forcing structure. The ‘upstream approach’ would specify the acoustic forcing upstream of the swirler that requires to include the complete swirler geometry. This would be formally simple, but numerically expensive since the full compressible three-dimensional linearized equations would need to be considered. The ‘downstream approach’ would specify the resulting forcing downstream of the swirler, in which the forcing is assumed to be the result of an acoustic-convective mode conversion process caused by the interaction of the acoustic wave with the swirler. This would be numerically much more viable, although formally difficult due to uncertainties related to the assumptions of how the mode conversion process takes place (e.g. the proposed actuator disk model as in Palies et al. Reference Palies, Durox, Schuller and Candel2011a).
$\,\skew2\hat{\boldsymbol{f}}$ needs to be known explicitly. In the present case, there are two approaches for specifying the forcing structure. The ‘upstream approach’ would specify the acoustic forcing upstream of the swirler that requires to include the complete swirler geometry. This would be formally simple, but numerically expensive since the full compressible three-dimensional linearized equations would need to be considered. The ‘downstream approach’ would specify the resulting forcing downstream of the swirler, in which the forcing is assumed to be the result of an acoustic-convective mode conversion process caused by the interaction of the acoustic wave with the swirler. This would be numerically much more viable, although formally difficult due to uncertainties related to the assumptions of how the mode conversion process takes place (e.g. the proposed actuator disk model as in Palies et al. Reference Palies, Durox, Schuller and Candel2011a).
An alternative way to put (4.8) into effect is to conduct an RA, in which the resolvent operator ![]() $\boldsymbol {\mathcal {R}}$ itself is directly analysed. In the RA, (4.8) is treated as an optimization problem, searching for the largest possible, marginally (or neutrally) stable flow response to any forcing (in an energy norm sense) of an otherwise globally stable eigenvalue spectrum (Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). We will still presume any forcing to be hydrodynamic in the sense that the acoustic excitation has generated significant hydrodynamic fluctuations through an acoustic-convective mode conversion process inside the swirler as suggested in Palies et al. (Reference Palies, Durox, Schuller and Candel2011a). However, the exact forcing structure does not need to be known in contrast to the input–output analysis. The parameter to maximize is the gain function
$\boldsymbol {\mathcal {R}}$ itself is directly analysed. In the RA, (4.8) is treated as an optimization problem, searching for the largest possible, marginally (or neutrally) stable flow response to any forcing (in an energy norm sense) of an otherwise globally stable eigenvalue spectrum (Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). We will still presume any forcing to be hydrodynamic in the sense that the acoustic excitation has generated significant hydrodynamic fluctuations through an acoustic-convective mode conversion process inside the swirler as suggested in Palies et al. (Reference Palies, Durox, Schuller and Candel2011a). However, the exact forcing structure does not need to be known in contrast to the input–output analysis. The parameter to maximize is the gain function ![]() $\sigma ^2$ defined as
$\sigma ^2$ defined as
which can be rearranged to yield a singular value decomposition of the resolvent operator (Farrell & Ioannou Reference Farrell and Ioannou2001; Sipp & Marquet Reference Sipp and Marquet2013). Here, ![]() $\langle {\cdot },{\cdot }\rangle$ is the norm-inducing
$\langle {\cdot },{\cdot }\rangle$ is the norm-inducing ![]() $L^2$ inner product in complex vector space defined as
$L^2$ inner product in complex vector space defined as ![]() $\langle \boldsymbol {a} , \boldsymbol {b} \rangle = \int _V \boldsymbol {a}^* \boldsymbol{\cdot} \boldsymbol {b}\, \mathrm {d}V$,
$\langle \boldsymbol {a} , \boldsymbol {b} \rangle = \int _V \boldsymbol {a}^* \boldsymbol{\cdot} \boldsymbol {b}\, \mathrm {d}V$, ![]() $({\cdot })^*$ denoting complex conjugation. The right singular vectors form an orthonormal basis of optimal forcing modes
$({\cdot })^*$ denoting complex conjugation. The right singular vectors form an orthonormal basis of optimal forcing modes ![]() $\hat {\boldsymbol {\varPhi }}_j$. The left singular vectors are the orthonormal optimal response modes
$\hat {\boldsymbol {\varPhi }}_j$. The left singular vectors are the orthonormal optimal response modes ![]() $\hat {\boldsymbol {\varPsi }}_j$ that satisfy
$\hat {\boldsymbol {\varPsi }}_j$ that satisfy ![]() $\skew2\hat {\boldsymbol {u}} = \sum _j \hat {\boldsymbol {\varPsi }}_j \sigma _j \langle \hat {\boldsymbol {\varPhi }}_j , \,\skew2\hat{\boldsymbol{f}} \rangle$. The inner product
$\skew2\hat {\boldsymbol {u}} = \sum _j \hat {\boldsymbol {\varPsi }}_j \sigma _j \langle \hat {\boldsymbol {\varPhi }}_j , \,\skew2\hat{\boldsymbol{f}} \rangle$. The inner product ![]() $\langle \hat {\boldsymbol {\varPhi }}_j , \,\skew2\hat{\boldsymbol{f}} \rangle$ is the projection of the actual forcing
$\langle \hat {\boldsymbol {\varPhi }}_j , \,\skew2\hat{\boldsymbol{f}} \rangle$ is the projection of the actual forcing ![]() $\,\skew2\hat{\boldsymbol{f}}$ onto the optimal forcing modes
$\,\skew2\hat{\boldsymbol{f}}$ onto the optimal forcing modes ![]() $\hat {\boldsymbol {\varPhi }}_j$. We consider two different types of forcings, namely volume forcing and boundary forcing. The volume forcing allows the forcing to act on the entire domain. The boundary forcing allows the forcing only to act at certain boundaries of the domain. In the present case, we will consider the boundary forcing to act at the tangential air inlet only (see figure 1b). The squared singular values quantify the optimal gain function,
$\hat {\boldsymbol {\varPhi }}_j$. We consider two different types of forcings, namely volume forcing and boundary forcing. The volume forcing allows the forcing to act on the entire domain. The boundary forcing allows the forcing only to act at certain boundaries of the domain. In the present case, we will consider the boundary forcing to act at the tangential air inlet only (see figure 1b). The squared singular values quantify the optimal gain function, ![]() $\sigma _j^2$. They are ranked with respect to their magnitude. The gain magnitude is a measure for the importance of the related optimal forcing and response modes. As a result, if the leading optimal gain,
$\sigma _j^2$. They are ranked with respect to their magnitude. The gain magnitude is a measure for the importance of the related optimal forcing and response modes. As a result, if the leading optimal gain, ![]() $\sigma _1^2$, is of significantly higher magnitude than all remaining gains and if the forcing
$\sigma _1^2$, is of significantly higher magnitude than all remaining gains and if the forcing ![]() $\,\skew2\hat{\boldsymbol{f}}$ does not show any preference in projection towards the suboptimal forcing modes
$\,\skew2\hat{\boldsymbol{f}}$ does not show any preference in projection towards the suboptimal forcing modes ![]() $\hat {\boldsymbol {\varPhi }}_{j>1}$, the resolvent is low-rank, and the leading mode governs most of the response dynamics and all remaining suboptimal modes can be neglected (Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016). The spatial shape of the Fourier mode
$\hat {\boldsymbol {\varPhi }}_{j>1}$, the resolvent is low-rank, and the leading mode governs most of the response dynamics and all remaining suboptimal modes can be neglected (Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016). The spatial shape of the Fourier mode ![]() $\skew2\hat {\boldsymbol {u}}$ is then well approximated by
$\skew2\hat {\boldsymbol {u}}$ is then well approximated by
4.1.1. Numerical implementation
To solve the singular value problem, the resolvent operator defined in (4.8) must be formed by integrating the linearized equations in the computational domain. This is done by the in-house linearized flow solver FELiCS (Kaiser et al. Reference Kaiser, Demange, Müller, Knechtel and Oberleithner2023a), which uses the finite element package FEniCS (Alnaes et al. Reference Alnaes, Blechta, Hake, Johansson, Kehlet, Logg, Richardson, Ring, Rognes and Wells2015). Second-order continuous Galerkin elements are applied for both velocity and pressure. The singular value problem is solved using ARPACK (Lehoucq, Sorensen & Yang Reference Lehoucq, Sorensen and Yang1998). The RA domain comprises the mixing tube downstream of the swirl generator with the outlet at ![]() $x/D=4$. The mean field is assumed to be axisymmetric such that the computations can be performed on a 2-D domain. Section 7.1 will briefly discuss why this assumption is justified. Homogeneous Dirichlet conditions for the velocity and homogeneous Neumann conditions for the pressure are imposed at all walls and, in the case of volume forcing, at the inlet. For boundary forcing, homogeneous Neumann conditions are set for both velocity and pressure at the inlet. At the outlet, stress-free conditions are used. On the axis, compatibility conditions are required for the limit
$x/D=4$. The mean field is assumed to be axisymmetric such that the computations can be performed on a 2-D domain. Section 7.1 will briefly discuss why this assumption is justified. Homogeneous Dirichlet conditions for the velocity and homogeneous Neumann conditions for the pressure are imposed at all walls and, in the case of volume forcing, at the inlet. For boundary forcing, homogeneous Neumann conditions are set for both velocity and pressure at the inlet. At the outlet, stress-free conditions are used. On the axis, compatibility conditions are required for the limit ![]() $r \to 0$ (Khorrami, Malik & Ash Reference Khorrami, Malik and Ash1989), in which homogeneous Dirichlet conditions are set for the radial and azimuthal velocity, and homogeneous Neumann conditions are set for the axial velocity and pressure. At the walls, homogeneous Dirichlet conditions are set for the velocity vector and homogeneous Neumann conditions for the pressure. As we are interested in the response to planar acoustic forcing, only axisymmetric modes with
$r \to 0$ (Khorrami, Malik & Ash Reference Khorrami, Malik and Ash1989), in which homogeneous Dirichlet conditions are set for the radial and azimuthal velocity, and homogeneous Neumann conditions are set for the axial velocity and pressure. At the walls, homogeneous Dirichlet conditions are set for the velocity vector and homogeneous Neumann conditions for the pressure. As we are interested in the response to planar acoustic forcing, only axisymmetric modes with ![]() $m=0$ are considered. A mesh convergence study showed that the domain is sufficiently discretized with approximately 20 000 elements.
$m=0$ are considered. A mesh convergence study showed that the domain is sufficiently discretized with approximately 20 000 elements.
5. Inertial waves in a plug flow with solid-body rotation
In this section, we introduce ‘canonical’ inertial waves under the simplified conditions of a plug flow with solid-body rotation through the lens of a global RA. The simplified case is selected to demonstrate the basic properties of inertial waves in an isolated fashion, in the absence of any other dominant modal or non-modal mechanism, posing the simplest configuration that supports inertial waves. Furthermore, the capability of RA to model inertial waves is demonstrated.
The considered set-up is sketched in figure 5, consisting of a circular pipe. To ensure similarity of the base flows between the plug flow with solid-body rotation and the swirling pipe flow, we introduce a new set of non-dimensional parameters referenced with respect to ![]() $x/D = 2.2$ in the swirling pipe flow where the solid-body rotation is virtually fully developed: the effective Reynolds number
$x/D = 2.2$ in the swirling pipe flow where the solid-body rotation is virtually fully developed: the effective Reynolds number ![]() $Re_{\delta,{eff}} = U\delta /(\nu + \overline {\nu }_{t}) \approx 500$ and the simplified swirl number
$Re_{\delta,{eff}} = U\delta /(\nu + \overline {\nu }_{t}) \approx 500$ and the simplified swirl number ![]() $S = \varOmega \delta / U \approx 2.5$. The characteristic length scale
$S = \varOmega \delta / U \approx 2.5$. The characteristic length scale ![]() $\delta = 0.6 D$ is the radial width of the approximate region of solid-body rotation,
$\delta = 0.6 D$ is the radial width of the approximate region of solid-body rotation, ![]() $\overline {\nu }_{t} = 100\nu$ is the area-weighted average eddy viscosity and
$\overline {\nu }_{t} = 100\nu$ is the area-weighted average eddy viscosity and ![]() $\varOmega = 3200\ {\rm s}^{-1}$ is the angular frequency of the solid-body rotation around the centreline. All of these parameters are adopted in the rotating plug flow case with the plug flow velocity set to the swirling pipe flow's bulk velocity
$\varOmega = 3200\ {\rm s}^{-1}$ is the angular frequency of the solid-body rotation around the centreline. All of these parameters are adopted in the rotating plug flow case with the plug flow velocity set to the swirling pipe flow's bulk velocity ![]() $\overline {u} = U$, the azimuthal velocity set to
$\overline {u} = U$, the azimuthal velocity set to ![]() $\overline {w} = \varOmega r$, the pipe diameter set to
$\overline {w} = \varOmega r$, the pipe diameter set to ![]() $\delta$ and the walls set as slip walls. A large axial domain length of
$\delta$ and the walls set as slip walls. A large axial domain length of ![]() $L/\delta \approx 42$ is considered and the same boundary conditions for inlet, outlet and axis as described in § 4.1.1 are used.
$L/\delta \approx 42$ is considered and the same boundary conditions for inlet, outlet and axis as described in § 4.1.1 are used.

Figure 5. Set-up of the plug flow with solid-body rotation.
5.1. Global resolvent analysis and phenomenological interpretation of inertial waves
Figure 6 displays the resolvent gain distribution as a function of non-dimensional frequency ![]() $f^* = f\delta /U$. Shown are the two leading modes that correspond to two different branches we will designate as S1 and F1.
$f^* = f\delta /U$. Shown are the two leading modes that correspond to two different branches we will designate as S1 and F1.

Figure 6. Resolvent gain distribution for the global RA in the plug flow with solid-body rotation.
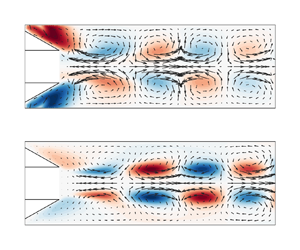
Figure 7 shows the spatial shape of the optimal response mode for the two leading optimal response modes at the non-dimensional frequency ![]() $f^* = 0.16$ at an arbitrary phase angle. The figure illustrates the existence of two modes that are distinguished from each other by their large difference in wavelength. The short wavelength mode we will designate as a slow-travelling wave belonging to the ‘S branch’, whereas the long wavelength mode we will designate as a fast-travelling wave belonging to the ‘F branch’. Furthermore, a number is designated to every mode on each branch separately with respect to the resolvent gain rank in ascending order, i.e. S1 for the leading mode on the S branch and F1 for the leading mode on the F branch. For both S1 and F1 modes, the vectors indicate the axial and radial fluctuations. Since the modes are axisymmetric distributions with
$f^* = 0.16$ at an arbitrary phase angle. The figure illustrates the existence of two modes that are distinguished from each other by their large difference in wavelength. The short wavelength mode we will designate as a slow-travelling wave belonging to the ‘S branch’, whereas the long wavelength mode we will designate as a fast-travelling wave belonging to the ‘F branch’. Furthermore, a number is designated to every mode on each branch separately with respect to the resolvent gain rank in ascending order, i.e. S1 for the leading mode on the S branch and F1 for the leading mode on the F branch. For both S1 and F1 modes, the vectors indicate the axial and radial fluctuations. Since the modes are axisymmetric distributions with ![]() $m=0$, the vectors indicate the presence of vortex rings whose axes of rotation are the azimuthal coordinate curves (i.e. curves with
$m=0$, the vectors indicate the presence of vortex rings whose axes of rotation are the azimuthal coordinate curves (i.e. curves with ![]() $x=\textrm {const.}$,
$x=\textrm {const.}$, ![]() $r=\textrm {const.}$) that alternate in the clockwise and counter-clockwise directions. The contours of azimuthal fluctuation
$r=\textrm {const.}$) that alternate in the clockwise and counter-clockwise directions. The contours of azimuthal fluctuation ![]() $\hat {w}$ reveal an additional rotational motion that is superposed to these vortex rings whose axis of rotation is the axial centreline (i.e.
$\hat {w}$ reveal an additional rotational motion that is superposed to these vortex rings whose axis of rotation is the axial centreline (i.e. ![]() $r=0$). Thus, the vortex rings are additionally spinning around the centreline, alternating in the clockwise and counter-clockwise directions. This spinning is induced by the Coriolis force because of the radial displacement of the fluid. Due to spatial quadrature of the imaginary counterpart (not shown in figure 7), the vortices are, furthermore, convected downstream.
$r=0$). Thus, the vortex rings are additionally spinning around the centreline, alternating in the clockwise and counter-clockwise directions. This spinning is induced by the Coriolis force because of the radial displacement of the fluid. Due to spatial quadrature of the imaginary counterpart (not shown in figure 7), the vortices are, furthermore, convected downstream.

Figure 7. Optimal response modes in the plug flow with solid-body rotation at ![]() $f^*=0.16$ for the (a) slow-travelling inertial wave S1 and (b) fast-travelling inertial wave F1, with vector arrows indicating axial and radial fluctuations and contours indicating the respective velocity fluctuations.
$f^*=0.16$ for the (a) slow-travelling inertial wave S1 and (b) fast-travelling inertial wave F1, with vector arrows indicating axial and radial fluctuations and contours indicating the respective velocity fluctuations.
At low frequencies, the slow-travelling wave S1 has a higher gain than the fast-travelling wave F1 (see figure 6). With increasing frequency, the gain of S1 decreases sharply and falls below the gain of F1, which remains almost constant. However, it should be noted that the gain curves depend on the domain length considered. This makes it difficult to draw conclusions about which mode actually dominates the dynamics. This is attributed to the arbitrary domain truncation in the axial direction, although the parallel flow is supposed to be infinite in the ![]() $x$-direction. The shorter the domain, the lower the gain of F1 becomes compared with S1 due to the larger wavelengths of F1 being increasingly more constricted. This applies especially to F1 structures at low frequencies. In other words, when the flow is homogeneous in the
$x$-direction. The shorter the domain, the lower the gain of F1 becomes compared with S1 due to the larger wavelengths of F1 being increasingly more constricted. This applies especially to F1 structures at low frequencies. In other words, when the flow is homogeneous in the ![]() $x$-direction and the domain is arbitrarily truncated in this direction, this leads to ambiguous results concerning which mode dominates. Notwithstanding, this does not diminish the capability of the global RA to model the leading inertial wave. Moreover, the domain truncation will be less of a problem for the swirling pipe flow case, where the flow is highly non-parallel and physically meaningful boundary conditions exist.
$x$-direction and the domain is arbitrarily truncated in this direction, this leads to ambiguous results concerning which mode dominates. Notwithstanding, this does not diminish the capability of the global RA to model the leading inertial wave. Moreover, the domain truncation will be less of a problem for the swirling pipe flow case, where the flow is highly non-parallel and physically meaningful boundary conditions exist.
Figure 8 displays the magnitude of the S1 and F1 response modes for the axial, radial and azimuthal velocity components. Comparing the mode shapes of the slow- and fast-travelling modes, it can be observed that the mode shapes are very similar. For S1 (and thus, F1), the axial component peaks on the centreline and exhibits additional subpeaks at the walls. The radial and azimuthal components peak in between the centreline and the walls. The axial fluctuations have the highest amplitudes, followed by the azimuthal and radial fluctuations. The displayed mode shapes are very characteristic for axisymmetric inertial waves (Albayrak et al. Reference Albayrak, Juniper and Polifke2019).

Figure 8. Optimal response modes in the plug flow with solid-body rotation at ![]() $f^*=0.16$ identified as inertial waves of the (a) slow-travelling branch S1 and (b) fast-travelling branch F1.
$f^*=0.16$ identified as inertial waves of the (a) slow-travelling branch S1 and (b) fast-travelling branch F1.
The propagation behaviour of the two leading optimal response modes S1 and F1 is presented in figures 9(a) and 9(b). The distribution of each mode's non-dimensional phase velocity ![]() $c_{ph}^* = c_{ph}/U = 2{\rm \pi} f^*/k_x^*$ in figure 9(a) demonstrates the existence of slow- and fast-travelling modes for the entire frequency range. The figure further shows that the S1 and F1 are modes with a phase velocity lower and higher than the bulk velocity, respectively. For both branches, the phase velocity is almost constant for the entire frequency range and very weakly converging towards
$c_{ph}^* = c_{ph}/U = 2{\rm \pi} f^*/k_x^*$ in figure 9(a) demonstrates the existence of slow- and fast-travelling modes for the entire frequency range. The figure further shows that the S1 and F1 are modes with a phase velocity lower and higher than the bulk velocity, respectively. For both branches, the phase velocity is almost constant for the entire frequency range and very weakly converging towards ![]() $c_{ph}^* \to 1$ with increasing frequency. Since all modes are only weakly dispersive, the group velocity in figure 9(b) has very comparable trends as the phase velocity.
$c_{ph}^* \to 1$ with increasing frequency. Since all modes are only weakly dispersive, the group velocity in figure 9(b) has very comparable trends as the phase velocity.

Figure 9. Propagation of leading optimal response modes in the plug flow with solid-body rotation on the centreline (![]() $y/D = 0$) characterized by (a) phase velocity over frequency and (b) group velocity over frequency.
$y/D = 0$) characterized by (a) phase velocity over frequency and (b) group velocity over frequency.
All of these observed features such as two-branch structure, dispersion relation and spatial mode shape clearly indicate that the rotating plug flow supports inertial waves (Gallaire & Chomaz Reference Gallaire and Chomaz2003; Albayrak et al. Reference Albayrak, Juniper and Polifke2019). The RA models these inertial waves as forced convective modes. The conclusion that we have only inertial wave modes in this type of flow can be further corroborated when conducting a linear stability analysis. It provides an alternative view on how to model and interpret these coherent structures. We decide here against a detailed global stability analysis since the spectrum is globally stable and the convective amplifier behaviour is better captured by a local spatial stability analysis. The results of this stability analysis are discussed in Appendix A. It reveals that the inertial waves of S1 and F1 can also be viewed as convectively stable eigenmodes that belong to a larger family of inertial waves on the S and F branch. In the local stability framework, the S1 and F1 are the modes with the smallest spatial decay rate and thus can be expected to be the most dominant response when forced. The results of the stability analysis also agree very well with the observations in Albayrak et al. (Reference Albayrak, Juniper and Polifke2019), further demonstrating that inertial waves are the only modes present in this type of flow.
6. Swirl fluctuations and inertial waves in the swirling pipe flow of a mixing tube
In this section, a global RA is applied to the swirling pipe flow with the aim to identify the coherent structures behind the swirl fluctuations and the contribution of inertial waves in the mixing tube set-up. The results are validated with experimentally measured phase-averaged velocity fields. A special focus is put on the correct prediction of the propagation speeds.
6.1. Global resolvent analysis and comparison with experimental measurements
In the following, the results from the global RA in the swirling pipe flow are presented and compared with the phase-averaged fields from the experiment and the global RA of the rotating plug flow case. Figure 10 shows, from top to bottom, the modelled coherent fluctuations of the flow response at ![]() $f^* = 0.16$ based on the leading optimal response mode from the global RA for (a) the plug flow with solid-body rotation (S1) and (b) the swirling pipe flow, and (c) the measured flow response for the acoustically excited flow in the experiment. On the left, the coherent axial velocity fluctuation for a fixed phase angle is shown. On the right, the magnitude of the coherent azimuthal fluctuation is shown for the three measured cross-sections.
$f^* = 0.16$ based on the leading optimal response mode from the global RA for (a) the plug flow with solid-body rotation (S1) and (b) the swirling pipe flow, and (c) the measured flow response for the acoustically excited flow in the experiment. On the left, the coherent axial velocity fluctuation for a fixed phase angle is shown. On the right, the magnitude of the coherent azimuthal fluctuation is shown for the three measured cross-sections.

Figure 10. Flow response at ![]() $f^*=0.16$ obtained by the (a) volume-forced RA of the plug flow with solid-body rotation (S1), (b) boundary-forced RA of the swirling pipe flow, (c) phase average from the acoustically excited experiments (Bluemner et al. Reference Bluemner, Paschereit and Oberleithner2019; Müller et al. Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022); first column, axial velocity fluctuation at arbitrary phase angle; remaining columns, magnitude of azimuthal velocity fluctuation.
$f^*=0.16$ obtained by the (a) volume-forced RA of the plug flow with solid-body rotation (S1), (b) boundary-forced RA of the swirling pipe flow, (c) phase average from the acoustically excited experiments (Bluemner et al. Reference Bluemner, Paschereit and Oberleithner2019; Müller et al. Reference Müller, Lückoff, Kaiser, Paschereit and Oberleithner2022); first column, axial velocity fluctuation at arbitrary phase angle; remaining columns, magnitude of azimuthal velocity fluctuation.
The leading mode of the RA for the swirling pipe flow case (figure 10b) originates at the swirler and shows a five-peak structure from wall to wall for the axial component and a four-peak structure from wall to wall in the azimuthal component. The axial response mode predicted from the RA agrees very well with the experimental measurement shown in figure 10(c). Comparing the magnitude of the azimuthal response, also a close correspondence can be seen. Deviations are noticeable close to the wall where fluctuations are very strong and more pronounced in the experiment than in the RA. Most importantly, both the global RA and the experiments reveal only a single branch of waves that will be shown to be travelling slower than the centreline velocity further below. The global RA of the swirling pipe flow does not detect any fast-travelling waves in the subleading response modes, and the phase-averaged fields from the experiment only reveal short wavelengths as well.
The coherent fluctuations of the swirling pipe flow are now compared with the coherent fluctuations of the plug flow with solid-body rotation. Figure 10(a) shows the leading S1 inertial wave of the plug flow with solid-body rotation at equal Reynolds number, swirl number and frequency. Evidently, the axial wavelength is very similar to the swirling pipe flow configuration. The rotating plug flow case features a three-peak structure from wall to wall for the axial component and a two-peak structure from wall to wall in the azimuthal component. Since the swirling pipe mean flow is not homogeneous in the ![]() $x$-direction, and has large axial and radial velocity gradients in contrast to the rotating plug flow case, the coherent structure is exposed to larger changes throughout the swirling pipe flow and the radial distribution of the mode is altered including additional peaks close to the wall.
$x$-direction, and has large axial and radial velocity gradients in contrast to the rotating plug flow case, the coherent structure is exposed to larger changes throughout the swirling pipe flow and the radial distribution of the mode is altered including additional peaks close to the wall.
Figure 11 shows the magnitude of the spatial modes for the slow-travelling mode S1 to further corroborate the similarities between the three considered cases. Within the region of solid-body rotation (![]() $|y/D < 0.3|$), the overall peak distribution of the modes is very similar among all three cases. In the experiment, additional peaks in the wall region occur that the RA is also able to capture. With regard to the magnitude ratios among the three velocity components, the rotating plug flow predicts slightly different values compared with the RA of the swirling pipe flow. In the swirling pipe flow, the relative magnitude of radial and azimuthal fluctuations is larger in relation to the axial fluctuation. This agrees well with the experiment for the azimuthal component. For the axial component, the RA of the swirling pipe flow underestimates the relative magnitude compared with the experiment. Notwithstanding, the large similarities between both RA results and the experiment clearly suggest that the coherent structure of the swirling pipe flow closely resembles a typical slow-travelling inertial wave.
$|y/D < 0.3|$), the overall peak distribution of the modes is very similar among all three cases. In the experiment, additional peaks in the wall region occur that the RA is also able to capture. With regard to the magnitude ratios among the three velocity components, the rotating plug flow predicts slightly different values compared with the RA of the swirling pipe flow. In the swirling pipe flow, the relative magnitude of radial and azimuthal fluctuations is larger in relation to the axial fluctuation. This agrees well with the experiment for the azimuthal component. For the axial component, the RA of the swirling pipe flow underestimates the relative magnitude compared with the experiment. Notwithstanding, the large similarities between both RA results and the experiment clearly suggest that the coherent structure of the swirling pipe flow closely resembles a typical slow-travelling inertial wave.

Figure 11. Optimal response modes in the swirling pipe flow at ![]() $x/D = 2.2$ and
$x/D = 2.2$ and ![]() $f^*=0.16$, identified as inertial waves of the slow-travelling branch S1, compared with optimal response mode in the plug flow with solid-body rotation and with experiment.
$f^*=0.16$, identified as inertial waves of the slow-travelling branch S1, compared with optimal response mode in the plug flow with solid-body rotation and with experiment.
At last, we analyse the spatio-temporal structure of the inertial-wave-driven coherent structures by examining their propagation through the mixing tube. Figure 12 compares the phase and group velocity on the centreline for the RA-based swirling pipe flow modes with the rotating plug flow modes as well as the experimental measurements spatially averaged between ![]() $x/D = 1.3$ and
$x/D = 1.3$ and ![]() $2.2$. The phase and group velocity are normalized with the centreline velocity that is likewise averaged between
$2.2$. The phase and group velocity are normalized with the centreline velocity that is likewise averaged between ![]() $x/D = 1.3$ and
$x/D = 1.3$ and ![]() $2.2$. Both phase and group velocity of RA and experiment agree very well. Moreover, the phase and group velocity are evidently lower than one and close to the velocity values of the rotating pipe flow's S1 branch, in major contrast to the velocity values of the F1 branch that are larger than one (see figure 9). This demonstrates that in the RA as well as the experiment, only inertial waves of the S branch are found.
$2.2$. Both phase and group velocity of RA and experiment agree very well. Moreover, the phase and group velocity are evidently lower than one and close to the velocity values of the rotating pipe flow's S1 branch, in major contrast to the velocity values of the F1 branch that are larger than one (see figure 9). This demonstrates that in the RA as well as the experiment, only inertial waves of the S branch are found.

Figure 12. Propagation of the inertial waves in the swirling pipe flow on the centreline (![]() $y/D = 0$) characterized by (a) phase velocity (black curve shows power law fit) and (b) group velocity, both averaged between
$y/D = 0$) characterized by (a) phase velocity (black curve shows power law fit) and (b) group velocity, both averaged between ![]() $x/D = 1.3$ and
$x/D = 1.3$ and ![]() $2.2$.
$2.2$.
In summary, we observe that the flow response measured in the forced experiments consists only of slow-travelling inertial waves and no evidence for the existence of fast-travelling waves are found. Likewise, the global RA selects the S branch and reproduces the measured response fairly well regarding mode shape, amplitude distribution and propagation velocity. The remaining deviations might be rooted in the fact that the RA predicts the optimally forced structures, while the experiments show the response to a specific acoustic forcing.
7. Physical mechanisms of amplification
This section is dedicated to reveal the physical mechanisms that are linked with the inertial-wave-driven swirl fluctuations observed in the swirling pipe flow. First, the role and interpretation of boundary and volume forcing in RA is discussed. Second, the coherent structures associated with the inertial waves are examined on a phenomenological level, and the interplay and coupling between forcing and response is investigated. Third, the coherent kinetic energy budgets are considered to uncover where and how the coherent structures associated with the inertial waves are gaining energy. All of these discussions concerning the swirling pipe flow case are conducted in juxtaposition to the rotating plug flow case to highlight where the ‘classical’ inertial wave mechanism is at work and where alterations occur.
7.1. Role of boundary, volume and optimal forcing
In § 6, RA was conducted assuming an optimal boundary forcing at the swirler. Boundary forcing can be interpreted as a periodic perturbation that is introduced upstream at a particular boundary from where its convective evolution is tracked throughout the domain. This means that perturbations are coming from outside into the domain, which aligns with our assumption that the hydrodynamic fluctuations are generated inside the swirler through an acoustic-convective mode conversion process (Palies et al. Reference Palies, Durox, Schuller and Candel2011a). By that, the convective amplification and decay of a locally introduced perturbation is considered. Although this optimal boundary forcing does not necessarily correspond to a physically realizable forcing, the dominance of one particular linear mechanism over all remaining ones in the swirling pipe flow still leads to a very similar response mode when the non-optimal true forcing is present. This dominance is indeed at hand in the swirling pipe flow case and it can be determined by considering the gain distribution of the volume-forced RA (see § 4.1 and Beneddine et al. Reference Beneddine, Sipp, Arnault, Dandois and Lesshafft2016).
Figure 13 displays the gain distribution for the first three most amplified modes of the volume-forced RA. There is a sufficiently large gain separation between the leading and the subleading modes. Thus, the actual forcing structure to trigger the leading response mode is only secondary since the actual response is directly proportional to the square root of the gain value, ![]() $\sigma$, as stated in (4.10). In other words, the response is not sensitive to the structure of the actually applied forcing and is heavily dominated by the leading optimal response mode, even though the forcing may not be optimal or may not even act in the entire domain. This explains why the response with arbitrary boundary forcing at the swirler leads to a very similar result compared with the response with volume forcing (which has not been shown yet for brevity). The gain separation, resulting in the system being virtually agnostic to the actual forcing structure, further demonstrates that the flow inside the swirler (and the associated mode conversion process) does not need to be included in the linearized model and why the 2-D-based RA excluding the swirler is justified.
$\sigma$, as stated in (4.10). In other words, the response is not sensitive to the structure of the actually applied forcing and is heavily dominated by the leading optimal response mode, even though the forcing may not be optimal or may not even act in the entire domain. This explains why the response with arbitrary boundary forcing at the swirler leads to a very similar result compared with the response with volume forcing (which has not been shown yet for brevity). The gain separation, resulting in the system being virtually agnostic to the actual forcing structure, further demonstrates that the flow inside the swirler (and the associated mode conversion process) does not need to be included in the linearized model and why the 2-D-based RA excluding the swirler is justified.

Figure 13. Resolvent gain distribution for volume-forced RA in the swirling pipe flow.
On a physics level, the large gain separation is equivalent to an amplification mechanism being significantly more dominant than any other in the flow (Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). In the swirling pipe flow, this mechanism is associated with the S branch of the inertial wave mode. The acoustic forcing, which is non-optimal, may excite a number of different response modes. However, due to its apparently high receptivity, only the S branch inertial wave is significantly amplified. This explains why the optimal response of the RA is a good representation of the actual response to acoustic forcing measured in the experiment.
7.2. Forcing–response coupling and driving of the inertial wave
The interplay and coupling of forcing and response of the coherent structures associated with the inertial waves is considered next to understand what drives these structures.
Figure 14(a) shows the optimal forcing and response modes at ![]() $f^* = 0.16$ for an arbitrary phase angle for the plug flow with solid-body rotation. The vectors indicate axial and radial fluctuations, and the contours represent azimuthal fluctuations. Evidently, the modes are highly similar. This is the effect of a very weak convective-type non-normality, which leads to a weak spatial separation and virtually zero phase shift of forcing and response (Chomaz Reference Chomaz2005; Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). In simple terms, the response has to be directly triggered by the forcing since no convective instability mechanism amplifies the fluctuations.
$f^* = 0.16$ for an arbitrary phase angle for the plug flow with solid-body rotation. The vectors indicate axial and radial fluctuations, and the contours represent azimuthal fluctuations. Evidently, the modes are highly similar. This is the effect of a very weak convective-type non-normality, which leads to a weak spatial separation and virtually zero phase shift of forcing and response (Chomaz Reference Chomaz2005; Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018). In simple terms, the response has to be directly triggered by the forcing since no convective instability mechanism amplifies the fluctuations.

Figure 14. Optimal forcing and response modes at ![]() $f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow, with vector arrows indicating axial and radial fluctuations and contours indicating azimuthal fluctuations.
$f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow, with vector arrows indicating axial and radial fluctuations and contours indicating azimuthal fluctuations.
Figure 14(b) displays the optimal forcing and response modes for the volume-forced RA in the swirling pipe flow. The picture is qualitatively similar to the rotating plug flow case with virtually zero phase shift between the modes. However, the location of highest magnitude in forcing and response is spatially strongly separated, in contrast to the rotating plug flow case where it roughly coincides. This spatial separation indicates a stronger convective-type non-normality than in the rotating plug flow (Chomaz Reference Chomaz2005). The forcing in the swirling pipe flow case resides mainly close to the swirler and is the strongest in the azimuthal component. In the downstream direction, the forcing becomes weaker, shifts towards the centreline and aligns with the region of approximate solid-body rotation, ![]() $\lvert y/D \rvert < 0.3$. For the response, the largest amplitudes are reached further downstream and are also mainly present in the region of approximate solid-body rotation. This is different to the boundary forcing case, where high amplitudes also occur close to the walls (see figure 10b).
$\lvert y/D \rvert < 0.3$. For the response, the largest amplitudes are reached further downstream and are also mainly present in the region of approximate solid-body rotation. This is different to the boundary forcing case, where high amplitudes also occur close to the walls (see figure 10b).
Overall, the structure of the optimal forcing and response modes in the swirling pipe flow show that inertial waves are most effectively amplified by azimuthal, i.e. swirl, fluctuations at the swirler outlet. This explains why the RA using boundary forcing agrees so well with the measured flow response, and more generally why inertial waves are actually very effective in propagating swirl fluctuations, since the strong optimal forcing close to the swirler indicates a high receptivity (Sipp & Marquet Reference Sipp and Marquet2013).
7.3. Structural sensitivity of the resolvent gain
The coupling between forcing and response is now examined quantitatively by considering the structural sensitivity tensor ![]() $\boldsymbol{\mathsf{S}}$ of the gain
$\boldsymbol{\mathsf{S}}$ of the gain ![]() $\sigma ^2$ with regard to small perturbations of the 2-D linearized Navier–Stokes operator
$\sigma ^2$ with regard to small perturbations of the 2-D linearized Navier–Stokes operator ![]() $\boldsymbol {\mathcal {L}}$, which is defined by (Qadri & Schmid Reference Qadri and Schmid2017)
$\boldsymbol {\mathcal {L}}$, which is defined by (Qadri & Schmid Reference Qadri and Schmid2017)
where ![]() $\otimes$ denotes the dyadic product defined by
$\otimes$ denotes the dyadic product defined by ![]() $\boldsymbol {a} \otimes \boldsymbol {b} = \boldsymbol {a} \boldsymbol {b}^\mathrm {T}$. The structural sensitivity quantifies the effect of a localized perturbation of the linearized Navier–Stokes operator
$\boldsymbol {a} \otimes \boldsymbol {b} = \boldsymbol {a} \boldsymbol {b}^\mathrm {T}$. The structural sensitivity quantifies the effect of a localized perturbation of the linearized Navier–Stokes operator ![]() $\boldsymbol {\mathcal {L}}$ contained in the resolvent operator
$\boldsymbol {\mathcal {L}}$ contained in the resolvent operator ![]() $\boldsymbol {\mathcal {R}}$ that leads to a drift of the resolvent gain
$\boldsymbol {\mathcal {R}}$ that leads to a drift of the resolvent gain ![]() $\sigma ^2$. In other words, the structural sensitivity identifies the coupling between forcing and response that causes this drift. A larger drift means the stronger the coupling must be. The structural sensitivity provides a
$\sigma ^2$. In other words, the structural sensitivity identifies the coupling between forcing and response that causes this drift. A larger drift means the stronger the coupling must be. The structural sensitivity provides a ![]() $3 \times 3$ tensor that reveals how each component of the optimal forcing mode couples with each component of the optimal response mode.
$3 \times 3$ tensor that reveals how each component of the optimal forcing mode couples with each component of the optimal response mode.
Figure 15(a) shows each component of the structural sensitivity tensor of the rotating plug flow case at ![]() $f^* = 0.16$ that characterizes the forcing–response coupling. The forcing contribution is ordered row by row and the response contribution is ordered column by column (first row, axial forcing; second row, radial forcing, etc.; first column, axial response, etc.). Note the individual colour map range for each of the sensitivity components and the normalization with the maximum component value of the sensitivity tensor in the displayed domain extents. Evidently, the most dominant forcing-response coupling occurs between axial forcing and axial response,
$f^* = 0.16$ that characterizes the forcing–response coupling. The forcing contribution is ordered row by row and the response contribution is ordered column by column (first row, axial forcing; second row, radial forcing, etc.; first column, axial response, etc.). Note the individual colour map range for each of the sensitivity components and the normalization with the maximum component value of the sensitivity tensor in the displayed domain extents. Evidently, the most dominant forcing-response coupling occurs between axial forcing and axial response, ![]() ${\mathsf{S}}_{xx}$: a forcing in the momentum equation in the
${\mathsf{S}}_{xx}$: a forcing in the momentum equation in the ![]() $x$-direction leads to a response in the velocity fluctuation of the
$x$-direction leads to a response in the velocity fluctuation of the ![]() $x$-component. Essentially, these are the axial fluctuations of the aforementioned inertial wave's vortex rings that are driven through an axial forcing in the centreline region. Another direct coupling occurs between azimuthal forcing and response (
$x$-component. Essentially, these are the axial fluctuations of the aforementioned inertial wave's vortex rings that are driven through an axial forcing in the centreline region. Another direct coupling occurs between azimuthal forcing and response (![]() ${\mathsf{S}}_{\theta \theta }$), as already observed in figure 14(a). This direct coupling as well as the cross-coupling terms
${\mathsf{S}}_{\theta \theta }$), as already observed in figure 14(a). This direct coupling as well as the cross-coupling terms ![]() ${\mathsf{S}}_{x\theta }$ and
${\mathsf{S}}_{x\theta }$ and ![]() ${\mathsf{S}}_{\theta x}$ are approximately one order of magnitude lower than
${\mathsf{S}}_{\theta x}$ are approximately one order of magnitude lower than ![]() ${\mathsf{S}}_{xx}$. The remaining components such as
${\mathsf{S}}_{xx}$. The remaining components such as ![]() ${\mathsf{S}}_{xr}$,
${\mathsf{S}}_{xr}$, ![]() ${\mathsf{S}}_{rx}$,
${\mathsf{S}}_{rx}$, ![]() ${\mathsf{S}}_{r\theta }$ and
${\mathsf{S}}_{r\theta }$ and ![]() ${\mathsf{S}}_{\theta r}$ are lower but not necessarily negligible. The former two describe a coupling between axial forcing and radial response (and vice versa) whereas the latter two describe a coupling between radial forcing and azimuthal response (and vice versa). Figure 15(b) displays the structural sensitivity for the swirling pipe flow. The general picture is very similar. The strongest coupling occurs again in
${\mathsf{S}}_{\theta r}$ are lower but not necessarily negligible. The former two describe a coupling between axial forcing and radial response (and vice versa) whereas the latter two describe a coupling between radial forcing and azimuthal response (and vice versa). Figure 15(b) displays the structural sensitivity for the swirling pipe flow. The general picture is very similar. The strongest coupling occurs again in ![]() ${\mathsf{S}}_{xx}$, followed by an
${\mathsf{S}}_{xx}$, followed by an ![]() ${\mathsf{S}}_{\theta \theta }$ and
${\mathsf{S}}_{\theta \theta }$ and ![]() ${\mathsf{S}}_{x\theta }$ as well as
${\mathsf{S}}_{x\theta }$ as well as ![]() ${\mathsf{S}}_{\theta x}$. The relative magnitudes of these components are of the same order of magnitude as in the rotating plug flow. However, the other cross-couplings
${\mathsf{S}}_{\theta x}$. The relative magnitudes of these components are of the same order of magnitude as in the rotating plug flow. However, the other cross-couplings ![]() ${\mathsf{S}}_{xr}$,
${\mathsf{S}}_{xr}$, ![]() ${\mathsf{S}}_{rx}$,
${\mathsf{S}}_{rx}$, ![]() ${\mathsf{S}}_{r\theta }$ and
${\mathsf{S}}_{r\theta }$ and ![]() ${\mathsf{S}}_{\theta r}$ are significantly increased by more than one order of magnitude. This indicates a fundamental difference in the physical mechanisms behind the forcing–response couplings in the swirling pipe flow, which are further explored in the following.
${\mathsf{S}}_{\theta r}$ are significantly increased by more than one order of magnitude. This indicates a fundamental difference in the physical mechanisms behind the forcing–response couplings in the swirling pipe flow, which are further explored in the following.

Figure 15. Forcing–response coupling at ![]() $f^* = 0.16$ quantified with the structural sensitivity tensor
$f^* = 0.16$ quantified with the structural sensitivity tensor ![]() $\boldsymbol{\mathsf{S}}$ of the resolvent gain for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.
$\boldsymbol{\mathsf{S}}$ of the resolvent gain for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.
A large value of ![]() ${\mathsf{S}}_{xx}$ is equivalent to a large sensitivity of the resolvent gain with respect to changes of the linear operator component
${\mathsf{S}}_{xx}$ is equivalent to a large sensitivity of the resolvent gain with respect to changes of the linear operator component ![]() $\mathcal {L}_{xx}$, per definition (see (7.1) and Qadri & Schmid Reference Qadri and Schmid2017). This component is mainly governed by convective and dissipative terms (see (B1a)). This implies that small changes to the convective and dissipative terms have a large impact on the resolvent gain. This also applies to the other main diagonal elements
$\mathcal {L}_{xx}$, per definition (see (7.1) and Qadri & Schmid Reference Qadri and Schmid2017). This component is mainly governed by convective and dissipative terms (see (B1a)). This implies that small changes to the convective and dissipative terms have a large impact on the resolvent gain. This also applies to the other main diagonal elements ![]() $\mathcal {L}_{rr}$ and
$\mathcal {L}_{rr}$ and ![]() $\mathcal {L}_{\theta \theta }$ which also contain convective and dissipative terms. Likewise, the off-diagonal elements of the sensitivity tensor are largely influenced by the corresponding off-diagonal elements of
$\mathcal {L}_{\theta \theta }$ which also contain convective and dissipative terms. Likewise, the off-diagonal elements of the sensitivity tensor are largely influenced by the corresponding off-diagonal elements of ![]() $\boldsymbol {\mathcal {L}}$ that contain terms associated with the production of fluctuations. For example,
$\boldsymbol {\mathcal {L}}$ that contain terms associated with the production of fluctuations. For example, ![]() ${\mathsf{S}}_{\theta r}$ quantifies the sensitivity of
${\mathsf{S}}_{\theta r}$ quantifies the sensitivity of ![]() $\mathcal {L}_{\theta r}$ that contains the Coriolis term
$\mathcal {L}_{\theta r}$ that contains the Coriolis term ![]() $(\overline {w}/r) \hat {v}$ and the strain rate term
$(\overline {w}/r) \hat {v}$ and the strain rate term ![]() $(\partial \overline {w}/\partial r) \hat {v}$ responsible for the production of inertial waves.
$(\partial \overline {w}/\partial r) \hat {v}$ responsible for the production of inertial waves.
The influence of selected terms in ![]() $\boldsymbol {\mathcal {L}}$ on the structural sensitivity
$\boldsymbol {\mathcal {L}}$ on the structural sensitivity ![]() $\boldsymbol{\mathsf{S}}$ is now further corroborated by comparing their magnitudes between rotating plug flow and swirling pipe flow. In the rotating plug flow in figure 16(a), the axial convection term contained in
$\boldsymbol{\mathsf{S}}$ is now further corroborated by comparing their magnitudes between rotating plug flow and swirling pipe flow. In the rotating plug flow in figure 16(a), the axial convection term contained in ![]() $\mathcal {L}_{xx}$ is much more dominant than the radial-azimuthal strain rate plus Coriolis term contained in
$\mathcal {L}_{xx}$ is much more dominant than the radial-azimuthal strain rate plus Coriolis term contained in ![]() $\mathcal {L}_{\theta r}$. This explains the strong sensitivity in
$\mathcal {L}_{\theta r}$. This explains the strong sensitivity in ![]() ${\mathsf{S}}_{xx}$. Moreover, since there is no axial-radial strain rate in
${\mathsf{S}}_{xx}$. Moreover, since there is no axial-radial strain rate in ![]() $\mathcal {L}_{xr}$, this term is zero. When examining the same terms for the swirling pipe flow case in figure 16(b), the balance between these individual terms is significantly different. The Coriolis and radial-azimuthal strain rate term are of the same order of magnitude as the convection term. Additionally, the axial-radial strain rate term is not zero any longer, and large in the region where the jets of the central hole and tangential swirler merge. The significant increase of shear and Coriolis effects in the swirling pipe flow explain the large increase in the off-diagonal sensitivity components observed in figure 15(b). The strong shear being mainly located in the upstream region also explains why many of the sensitivity components peak in that region.
$\mathcal {L}_{xr}$, this term is zero. When examining the same terms for the swirling pipe flow case in figure 16(b), the balance between these individual terms is significantly different. The Coriolis and radial-azimuthal strain rate term are of the same order of magnitude as the convection term. Additionally, the axial-radial strain rate term is not zero any longer, and large in the region where the jets of the central hole and tangential swirler merge. The significant increase of shear and Coriolis effects in the swirling pipe flow explain the large increase in the off-diagonal sensitivity components observed in figure 15(b). The strong shear being mainly located in the upstream region also explains why many of the sensitivity components peak in that region.

Figure 16. Momentum terms for axial convection in ![]() $\mathcal {L}_{xx}$ (left), axial-radial strain rate in
$\mathcal {L}_{xx}$ (left), axial-radial strain rate in ![]() $\mathcal {L}_{xr}$ (mid), and radial-azimuthal strain rate plus Coriolis effect in
$\mathcal {L}_{xr}$ (mid), and radial-azimuthal strain rate plus Coriolis effect in ![]() $\mathcal {L}_{\theta r}$ (right) at
$\mathcal {L}_{\theta r}$ (right) at ![]() $f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.
$f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.
Thus, the coherent fluctuations of the plug flow with solid-body rotation and swirling pipe flow largely share similar coupling mechanisms, further demonstrating that the identified response modes of the swirling pipe flow are indeed inertial waves. However, the shear in the swirling pipe flow case, caused by the merging of central and radial jet, increases the component-type non-normality (Marquet et al. Reference Marquet, Lombardi, Chomaz, Sipp and Jacquin2009; Symon et al. Reference Symon, Rosenberg, Dawson and McKeon2018) and intensifies the inertial wave amplification significantly compared with the rotating plug flow case.
7.4. Energy budgets
At last, we examine parts of the coherent kinetic energy budget terms to reveal how and where the inertial wave gains energy. For this, the energy source terms of the energy budgets are considered, namely the production term and the additional source term due to the forcing on the right-hand side of (4.5). These terms are readily obtained by contracting the momentum equations of the spectral linearized Navier–Stokes equations, (4.5), with the complex-conjugated spectral response mode ![]() $\skew2\hat {\boldsymbol {u}}^*$ and only retaining the real part (Symon et al. Reference Symon, Illingworth and Marusic2021). The production term is then given by
$\skew2\hat {\boldsymbol {u}}^*$ and only retaining the real part (Symon et al. Reference Symon, Illingworth and Marusic2021). The production term is then given by
It quantifies the energy transfer from the mean field to the coherent field due to linear amplification mechanisms. The energy forcing term is given by
which quantifies the energy gain due to intrinsic (turbulent) and external forcing (see § 4.1). The full expressions are provided in Appendix C.
Figure 17(a) shows the energy production ![]() $\mathcal {P}$ and energy forcing terms
$\mathcal {P}$ and energy forcing terms ![]() $\mathcal {F}$ normalized with their summated maximum value
$\mathcal {F}$ normalized with their summated maximum value ![]() $(\mathcal {P} + \mathcal {F})_{max}$ for the rotating plug flow at
$(\mathcal {P} + \mathcal {F})_{max}$ for the rotating plug flow at ![]() $f^* = 0.16$. The production peaks in the centre of the solid-body region and consists essentially of the production due to the Coriolis force,
$f^* = 0.16$. The production peaks in the centre of the solid-body region and consists essentially of the production due to the Coriolis force, ![]() $\hat {w}^*\hat {v} (\overline {w}/r)$. Evidently, the production is just a very small fraction of the total energy gain and the energy forcing term is the main contributor (note the different ranges of the colour bars). Therefore, the forcing is vital for sustaining the inertial wave. This is in line with the results of the sensitivity tensor, in which a Coriolis term is active but comparably low, leading to a low forcing–response coupling.
$\hat {w}^*\hat {v} (\overline {w}/r)$. Evidently, the production is just a very small fraction of the total energy gain and the energy forcing term is the main contributor (note the different ranges of the colour bars). Therefore, the forcing is vital for sustaining the inertial wave. This is in line with the results of the sensitivity tensor, in which a Coriolis term is active but comparably low, leading to a low forcing–response coupling.

Figure 17. Coherent kinetic energy production and energy forcing term at ![]() $f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.
$f^* = 0.16$ for the (a) plug flow with solid-body rotation and (b) swirling pipe flow.
For the swirling pipe flow, shown in figure 17(b), the contributions are switched. The energy gain from production is increased significantly due to the strong shear at ![]() $x/D \approx 1$ where the jets from the central hole and the swirler merge. The forcing distribution shows that fluctuations are initially triggered close to the swirler. From there, they first pass through the region of high shear where they are strongly amplified. Downstream, the perturbations are convected as inertial waves as they pass through the region of solid-body rotation. The amount of energy added by the forcing is comparably low. Thus, in the swirling pipe flow case, the forcing inside the mixing tube is secondary in triggering and driving the inertial waves.
$x/D \approx 1$ where the jets from the central hole and the swirler merge. The forcing distribution shows that fluctuations are initially triggered close to the swirler. From there, they first pass through the region of high shear where they are strongly amplified. Downstream, the perturbations are convected as inertial waves as they pass through the region of solid-body rotation. The amount of energy added by the forcing is comparably low. Thus, in the swirling pipe flow case, the forcing inside the mixing tube is secondary in triggering and driving the inertial waves.
In summary, the coherent structures of the plug flow with solid-body rotation and the swirling pipe flow share similar coupling mechanisms. The mode selection process in the swirling pipe flow is primarily governed by the immediate region close to the swirler where the optimal forcing and, thus, receptivity (Sipp & Marquet Reference Sipp and Marquet2013) of the inertial waves is high. However, whereas in the rotating plug flow case the forcing is essential for sustaining inertial waves, in the swirling pipe flow case, the shear-driven production is mainly responsible for providing energy. The lower magnitude of the energy forcing term is related to a smaller projection of the response mode onto the forcing mode per definition (see (7.3)) that suggests an increased component-type non-normality due to the additional shear (Chomaz Reference Chomaz2005; Symon et al. Reference Symon, Illingworth and Marusic2021).
8. Summary and discussion
In this study, the role of inertial waves in driving swirl fluctuations in a turbulent swirling pipe flow was investigated. RA was conducted based on the turbulent mean field taken from a LES. In addition, experimental measurements of the same set-up with an acoustically excited flow were conducted and the flow response was extracted with a phase-averaging procedure. Comparing the modelled RA response with the measured response, a very similar spatio-temporal structure, i.e. mode shape and wave propagation, was identified, especially in the centreline region where solid-body rotation occurs that acts as a wave guide for the inertial waves (Gallaire & Chomaz Reference Gallaire and Chomaz2003). Differences were mainly detected regarding the relative magnitude ratios of the three velocity components, which is probably related to a discrepancy between the actual forcing in the experiment and the optimal forcing of the RA.
As a ‘canonical’ case for comparison with the swirling pipe flow, a plug flow with solid-body rotation was considered. In this rotating plug flow, inertial waves occur in an isolated fashion and, thus, can be fully characterized in the absence of any other physical mechanism. We observe very weak convective-type non-normality for the rotating plug flow case, with the leading RA response modes being very similar to the least decaying linear stability eigenmodes of the slow- and fast-travelling branch (see Appendix A for this discussion). Comparing the rotating plug flow to the swirling pipe flow case, the most dominant modes of both cases share many similarities and the swirling pipe flow modes are, therefore, verified to be inertial waves. However, in contrast to the rotating plug flow case, the strong shear in some parts of the swirling pipe flow is identified to significantly contribute to the amplification of the inertial waves due to a stronger component-type non-normality. Moreover, in the swirling pipe flow case only slow-travelling branch waves are found to occur both in the experiment and RA.
The origin of the swirl fluctuations at the swirler, the high receptivity to swirl fluctuations closely downstream and the strong amplification due to the shear spatially coincide. This spatial concurrence is responsible for the preferred selection of the inertial waves over any other coherent structure, which makes the inertial waves particularly dangerous for thermoacoustics. This is not necessarily the case for every type of swirler/mixing tube configuration. The underlying mechanisms that feed the inertial wave may be fundamentally different compared with other cases with less shear and, thus, lower spatial amplification. For example, annular swirling flows that comprise swirlers without a central hole but with a centrebody along the axis feature much less shear. These types of flow probably resemble the rotating plug flow case much more and the annular swirling flows select swirl fluctuations that travel faster than the bulk velocity (Palies et al. Reference Palies, Durox, Schuller and Candel2011b,Reference Palies, Schuller, Durox, Gicquel and Candelc), which indicates inertial waves of the fast-travelling branch type. Therefore, the fundamental difference of annular swirling flows with weak shear and swirling flows with strong shear may be the root for the preferred selection of the slow-travelling branch in the present swirling pipe flow case.
The high receptivity close to the swirler has important implications for flow control. It suggests that inertial waves can be effectively manipulated by active flow control with harmonic excitation in this region (Sipp & Marquet Reference Sipp and Marquet2013). The proximity to the walls would help in implementing devices such as zero-net-mass-flux actuators or fluidic oscillators. Furthermore, the strong coupling of the forcing in the ![]() $x$-direction with the response in the
$x$-direction with the response in the ![]() $x$-direction demonstrates a high sensitivity to changes of the linear operator, which translates to changes or modifications in the underlying mean flow (Brandt et al. Reference Brandt, Sipp, Pralits and Marquet2011; Qadri & Schmid Reference Qadri and Schmid2017). In other words, minimizing the shear in the mean flow could drastically reduce the amplitude of the inertial waves. The minimization could be facilitated by a shape optimization of the central hole or swirler geometry.
$x$-direction demonstrates a high sensitivity to changes of the linear operator, which translates to changes or modifications in the underlying mean flow (Brandt et al. Reference Brandt, Sipp, Pralits and Marquet2011; Qadri & Schmid Reference Qadri and Schmid2017). In other words, minimizing the shear in the mean flow could drastically reduce the amplitude of the inertial waves. The minimization could be facilitated by a shape optimization of the central hole or swirler geometry.
9. Conclusion
In conclusion, this study has successfully identified and modelled the spatio-temporal structure of inertial-wave-driven swirl fluctuations in a fully turbulent swirling pipe flow using RA. The findings highlight the significance of these structures in the context of swirling pipe flows and their relevance for thermoacoustic stability analysis using a linearized mean field approach. The developed model represents a crucial step in understanding the dynamics of swirl fluctuations and their potential impact on combustion stability.
One noteworthy aspect for future research is the transition to an input–output analysis, which holds promise for improving the agreement between the modelled and measured responses by incorporating an actual, physically realizable forcing as an input parameter. Additionally, the behaviour of the inertial-wave-driven swirl fluctuations as they exit the mixing tube and enter the combustion chamber remains an open question, including their distortion and changes in propagation speed, which warrants further investigation. In a further step, the swirl fluctuations can be coupled with a flame model by introducing a linearized reaction model (Kaiser et al. Reference Kaiser, Varillon, Polifke, Zhang, Zirwes, Bockhorn and Oberleithner2023b). This links hydrodynamic fluctuations with heat release fluctuations, making it possible to assemble a flame transfer function purely based on time-averaged fields.
The study's resolvent framework reveals valuable insights into flow and thermoacoustic stability. Due to the high shear and increased component-type non-normality of the system, the amplification is larger than for inertial wave-driven swirl fluctuations that are only governed by the Coriolis term. Furthermore, the increased convective-type non-normality results in a spatial separation of the forcing and response modes, resulting in a high receptivity and sensitivity near the swirler. This proximity to the swirler emphasizes the relevance of swirl fluctuations in combustor flows and their critical role in thermoacoustic interactions. However, the high receptivity and sensitivity also offer opportunities for manipulation and flow control of inertial waves. The study suggests that shape optimization could effectively reduce shear by altering the mean flow, thereby mitigating a significant contributor to inertial wave amplification. Furthermore, periodic actuation near the swirler, owing to its high receptivity, could be employed in closed-loop control to directly reduce inertial wave amplitudes at critical thermoacoustic frequencies. Thus, this research not only advances our understanding of inertial waves in swirling pipe flows but also provides practical implications for improving flow stability and control in combustion systems.
Acknowledgements
The authors express their gratitude to CERFACS and IFPEN for the permission to use the AVBP code for the LES, and the authors thank W. Polifke and G. Varillon for the fruitful discussions about the manuscript.
Funding
The funding from the Research Association for Combustion Engines (FVV) within project numbers 1358 and 1421 and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within project numbers 429772199 and 441269395 is gratefully acknowledged.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Local linear stability analysis
A.1. Governing equations, normal mode ansatz and numerical implementation
Within the local linear stability analysis (LSA), the mean flow is assumed to be weakly non-parallel in the streamwise direction and a normal mode ansatz for the perturbation with harmonic fluctuations in ![]() $x$,
$x$, ![]() $\theta$ and
$\theta$ and ![]() $t$ is substituted in (4.2),
$t$ is substituted in (4.2),
with the same naming convention as in § 4.1 and ![]() $\alpha \in \mathbb {C}$ being the complex axial wavenumber, where
$\alpha \in \mathbb {C}$ being the complex axial wavenumber, where ![]() ${\rm Re}(\alpha ) = k_x$ is the angular axial wavenumber and
${\rm Re}(\alpha ) = k_x$ is the angular axial wavenumber and ![]() $-{\rm Im}(\alpha )$ is the spatial growth rate. Cancelling the nonlinear term
$-{\rm Im}(\alpha )$ is the spatial growth rate. Cancelling the nonlinear term ![]() $(\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}} - \overline {\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}}} )$, linearizing around the mean flow and disallowing external forcing leads to the linearized Navier–Stokes equations in the spectral domain:
$(\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}} - \overline {\boldsymbol {\widetilde {u}}\,\boldsymbol {\widetilde {u}}} )$, linearizing around the mean flow and disallowing external forcing leads to the linearized Navier–Stokes equations in the spectral domain:
where ![]() $\boldsymbol{\mathsf{B}}_1$ and
$\boldsymbol{\mathsf{B}}_1$ and ![]() $\boldsymbol{\mathsf{B}}_2$ are restriction operators and
$\boldsymbol{\mathsf{B}}_2$ are restriction operators and ![]() $\boldsymbol {\mathcal {L}}_1$ is the one-dimensional (spatial) linearized Navier–Stokes operator, which are all given in Appendix B.
$\boldsymbol {\mathcal {L}}_1$ is the one-dimensional (spatial) linearized Navier–Stokes operator, which are all given in Appendix B.
For the unknown term of the coherent Reynolds stress tensor on the right-hand side of (A2), the same eddy viscosity model is used as for the RA described in § 4.1. Then, the equations can be discretized and recast as a quadratic eigenvalue problem. Reducing the quadratic eigenvalue problem to a linear eigenvalue problem via a companion matrix method (Khorrami et al. Reference Khorrami, Malik and Ash1989) leads to the generalized eigenvalue problem of the form
where ![]() $\boldsymbol{\mathsf{B}}^\#$ is the augmented restriction operator,
$\boldsymbol{\mathsf{B}}^\#$ is the augmented restriction operator, ![]() $\boldsymbol {\mathcal {L}}_1^\#$ is the augmented one-dimensional linearized Navier–Stokes operator and
$\boldsymbol {\mathcal {L}}_1^\#$ is the augmented one-dimensional linearized Navier–Stokes operator and ![]() $\skew2\hat {\boldsymbol {q}}^\#$ is the augmented eigenvector. The full expressions for the operators and the augmented eigenvector are given in Appendix B.
$\skew2\hat {\boldsymbol {q}}^\#$ is the augmented eigenvector. The full expressions for the operators and the augmented eigenvector are given in Appendix B.
Equation (A3) is solved numerically using a Chebyshev spectral collocation method according to Khorrami et al. (Reference Khorrami, Malik and Ash1989), to which the reader is referred for a detailed description of the numerical procedure. A number of 200 Chebyshev points is used to ensure converged physical eigenmodes. On the axis, compatibility conditions are required for the limit ![]() $r \to 0$, in which homogeneous Dirichlet conditions are set for the radial and azimuthal velocity, and the axial velocity and pressure are required to be finite. At the walls, homogeneous Dirichlet conditions are set for the velocity vector and homogeneous Neumann conditions for the pressure. As we are interested in the response to planar acoustic forcing, only axisymmetric modes with
$r \to 0$, in which homogeneous Dirichlet conditions are set for the radial and azimuthal velocity, and the axial velocity and pressure are required to be finite. At the walls, homogeneous Dirichlet conditions are set for the velocity vector and homogeneous Neumann conditions for the pressure. As we are interested in the response to planar acoustic forcing, only axisymmetric modes with ![]() $m=0$ are considered. The eigenvalue problem is implemented and solved with the standard EIG routine in MATLAB. Since the local LSA is based on the weakly non-parallel flow assumption, the eigenvalue problem is solved separately and independently for each axial position.
$m=0$ are considered. The eigenvalue problem is implemented and solved with the standard EIG routine in MATLAB. Since the local LSA is based on the weakly non-parallel flow assumption, the eigenvalue problem is solved separately and independently for each axial position.
A.2. Local linear stability analysis of plug flow with solid-body rotation
Figure 18(a) shows the eigenmode spectrum for the non-dimensional frequency ![]() $f^*= f\delta /U = 0.16$. Displayed is the non-dimensional spatial growth rate
$f^*= f\delta /U = 0.16$. Displayed is the non-dimensional spatial growth rate ![]() $\gamma ^* = -{\rm Im}(\alpha \delta )$ over non-dimensional phase velocity
$\gamma ^* = -{\rm Im}(\alpha \delta )$ over non-dimensional phase velocity ![]() $c_{ph}^* = c_{ph}/U = 2{\rm \pi} f^*/k_x^*$ with
$c_{ph}^* = c_{ph}/U = 2{\rm \pi} f^*/k_x^*$ with ![]() $k_x^* = k_x \delta$ being the non-dimensional axial wavenumber. The entire spectrum consists of convectively, asymptotically stable, decaying modes with
$k_x^* = k_x \delta$ being the non-dimensional axial wavenumber. The entire spectrum consists of convectively, asymptotically stable, decaying modes with ![]() $\gamma ^* < 0$. A two-branch structure can be identified, dividing the spectrum into slow- (S) and fast- (F) travelling modes, similar to the global RA results. For
$\gamma ^* < 0$. A two-branch structure can be identified, dividing the spectrum into slow- (S) and fast- (F) travelling modes, similar to the global RA results. For ![]() $\gamma ^* \to 0$, the slow- and fast-travelling modes have a phase velocity that is lower and higher than the plug flow velocity, respectively. A number is designated to every eigenmode on each branch separately, such that every number denotes the mode order of least decaying modes in ascending order, e.g. S1 for the least decaying mode on the S branch and so on. Without loss of generality, we focus only on the three least decaying modes on each branch in the following, as highlighted in figure 18(a).
$\gamma ^* \to 0$, the slow- and fast-travelling modes have a phase velocity that is lower and higher than the plug flow velocity, respectively. A number is designated to every eigenmode on each branch separately, such that every number denotes the mode order of least decaying modes in ascending order, e.g. S1 for the least decaying mode on the S branch and so on. Without loss of generality, we focus only on the three least decaying modes on each branch in the following, as highlighted in figure 18(a).

Figure 18. Eigenvalue spectrum of the plug flow with solid-body rotation characterized by (a) growth rate over phase velocity at ![]() $f^*=0.16$, (b) growth rate over frequency, (c) phase velocity over frequency and (d) group velocity over frequency.
$f^*=0.16$, (b) growth rate over frequency, (c) phase velocity over frequency and (d) group velocity over frequency.
The change of growth rate over a range of frequencies is examined in figure 18(b). The growth rate is virtually constant for each branch, with S1 being the exception becoming less damped for higher frequencies. Comparing the slow modes with the fast modes of the same mode number (i.e. S1 to F1 and so on), the F modes are always less damped. Overall, the F1 mode is the most dominant, as its decay rate, i.e. magnitude of the negative growth rate, is the lowest. This is due to the fact that the F1 mode has the longest wavelength and is therefore least affected by viscous effects.
The propagation behaviour of each mode is presented in figures 18(c) and 18(d). The distribution of each mode's phase velocity in figure 18(c) demonstrates the separation in slow- and fast-travelling waves for the S and F branch, respectively. For each mode branch, the phase velocity is almost constant for the entire frequency range. The leading modes S1 and F1 are the slowest and fastest modes, respectively. The group velocity in figure 18(d) has very comparable trends as the phase velocity.
Figure 19(a) displays the magnitude of the S1 to S3 eigenmodes for the axial, radial and azimuthal velocity components. Likewise, figure 19(b) displays the F1 to F3 eigenmodes. Similar to the global RA results, the mode shapes of the slow- and fast-travelling modes are almost identical. For S1 (and thus, F1), the axial component peaks on the centreline and exhibits additional subpeaks at the walls. The radial and azimuthal components peak in between the centreline and the walls. With increasing mode number, the number of peaks from centreline to wall increases by one.

Figure 19. Eigenmodes in the plug flow with solid-body rotation at ![]() $f^*=0.16$ identified as inertial waves of the (a) slow-travelling branch (S1, S2, S3) and (b) fast-travelling branch (F1, F2, F3), compared with optimal response mode from global RA (RA S1 and RA F1).
$f^*=0.16$ identified as inertial waves of the (a) slow-travelling branch (S1, S2, S3) and (b) fast-travelling branch (F1, F2, F3), compared with optimal response mode from global RA (RA S1 and RA F1).
Furthermore, figures 18(c,d) and 19 compare the results of the global RA with the results of the spatial LSA. Overall, it can be observed that the RA results are in very good agreement with the LSA results. This finding demonstrates that the global RA and local LSA reproduce the same type of coherent structure.
The presented results from the spatial local LSA also agree very well with the observations in Albayrak et al. (Reference Albayrak, Juniper and Polifke2019), in which a temporal local LSA was performed to investigate inertial waves in a uniform axial plug flow with solid-body rotation in a cylindrical annulus with slip walls. The Reynolds number was ![]() $Re = 18\,000$ and the swirl number was
$Re = 18\,000$ and the swirl number was ![]() $S = 1.6$, based on the hydraulic diameter and plug flow velocity. It was found that the inertial waves can be divided into two families of waves, in which one family contains waves propagating slower and the other one those faster than the plug flow velocity. With increasing frequency and mode number, the phase velocity approaches the plug flow velocity. Furthermore, with increasing mode number, the decay rates increase and the number of magnitude peaks increases by one for each velocity component. All of these observations are in excellent agreement with the results of the present study, proving that we indeed pick up inertial waves in our set-up, both using spatial local LSA and global RA.
$S = 1.6$, based on the hydraulic diameter and plug flow velocity. It was found that the inertial waves can be divided into two families of waves, in which one family contains waves propagating slower and the other one those faster than the plug flow velocity. With increasing frequency and mode number, the phase velocity approaches the plug flow velocity. Furthermore, with increasing mode number, the decay rates increase and the number of magnitude peaks increases by one for each velocity component. All of these observations are in excellent agreement with the results of the present study, proving that we indeed pick up inertial waves in our set-up, both using spatial local LSA and global RA.
Appendix B. Linear operators of the resolvent and linear stability analysis
B.1. Resolvent analysis
For the global RA, the linearized Navier–Stokes equations in the spectral domain are
with the linear operators
 $$\begin{gather}
\boldsymbol{\mathcal{L}} = \begin{bmatrix} \mathcal{A} +
\dfrac{\partial \overline{u}}{\partial x} & \dfrac{\partial
\overline{u}}{ \partial r} & 0 & \dfrac{1}{\rho}
\dfrac{\partial}{\partial x} \\ \dfrac{\partial
\overline{v}}{\partial x} & \mathcal{A} + \dfrac{\partial
\overline{v}}{\partial r} + \dfrac{\nu}{r^2} &
-\dfrac{2\overline{w}}{r} + \dfrac{2\mathrm{i}m\nu}{r^2} &
\dfrac{1}{\rho} \dfrac{\partial}{\partial r} \\
\dfrac{\partial \overline{w}}{\partial x} & \dfrac{\partial
\overline{w}}{\partial r} + \dfrac{\overline{w}}{r} -
\dfrac{2\mathrm{i}m\nu}{r^2} & \mathcal{A} +
\dfrac{\overline{v}}{r} + \dfrac{\nu}{r^2} & \dfrac{1}{\rho}
\dfrac{\mathrm{i}m}{r} \\ \dfrac{\partial}{\partial x} &
\dfrac{\partial}{\partial r} \dfrac{1}{r} &
\dfrac{\mathrm{i}m}{r} & 0 \end{bmatrix} ,
\end{gather}$$
$$\begin{gather}
\boldsymbol{\mathcal{L}} = \begin{bmatrix} \mathcal{A} +
\dfrac{\partial \overline{u}}{\partial x} & \dfrac{\partial
\overline{u}}{ \partial r} & 0 & \dfrac{1}{\rho}
\dfrac{\partial}{\partial x} \\ \dfrac{\partial
\overline{v}}{\partial x} & \mathcal{A} + \dfrac{\partial
\overline{v}}{\partial r} + \dfrac{\nu}{r^2} &
-\dfrac{2\overline{w}}{r} + \dfrac{2\mathrm{i}m\nu}{r^2} &
\dfrac{1}{\rho} \dfrac{\partial}{\partial r} \\
\dfrac{\partial \overline{w}}{\partial x} & \dfrac{\partial
\overline{w}}{\partial r} + \dfrac{\overline{w}}{r} -
\dfrac{2\mathrm{i}m\nu}{r^2} & \mathcal{A} +
\dfrac{\overline{v}}{r} + \dfrac{\nu}{r^2} & \dfrac{1}{\rho}
\dfrac{\mathrm{i}m}{r} \\ \dfrac{\partial}{\partial x} &
\dfrac{\partial}{\partial r} \dfrac{1}{r} &
\dfrac{\mathrm{i}m}{r} & 0 \end{bmatrix} ,
\end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{B}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{B}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} \end{gather}$$and
The resolvent operator is defined by
with
 \begin{equation} \boldsymbol{\mathsf{P}} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix} . \end{equation}
\begin{equation} \boldsymbol{\mathsf{P}} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{bmatrix} . \end{equation}B.2. Linear stability analysis
The linearized Navier–Stokes equations of the local LSA in spectral domain read
with the linear operators
 $$\begin{gather}
\boldsymbol{\mathcal{L}}_1 = \begin{bmatrix} \mathcal{A}_1
& \dfrac{\partial \overline{u}}{ \partial r} & 0 & 0 \\ 0 &
\mathcal{A}_1 + \dfrac{\nu}{r^2} & -\dfrac{2\overline{w}}{r} +
\dfrac{2\mathrm{i}m\nu}{r^2} & \dfrac{1}{\rho}
\dfrac{\partial}{\partial r} \\ 0 & \dfrac{\partial
\overline{w}}{\partial r} + \dfrac{\overline{w}}{r} -
\dfrac{2\mathrm{i}m\nu}{r^2} & \mathcal{A}_1 +
\dfrac{\nu}{r^2} & \dfrac{1}{\rho} \dfrac{\mathrm{i}m}{r}
\\ 0 & \dfrac{\partial}{\partial r} + \dfrac{1}{r} &
\dfrac{\mathrm{i}m}{r} & 0 \end{bmatrix} ,
\end{gather}$$
$$\begin{gather}
\boldsymbol{\mathcal{L}}_1 = \begin{bmatrix} \mathcal{A}_1
& \dfrac{\partial \overline{u}}{ \partial r} & 0 & 0 \\ 0 &
\mathcal{A}_1 + \dfrac{\nu}{r^2} & -\dfrac{2\overline{w}}{r} +
\dfrac{2\mathrm{i}m\nu}{r^2} & \dfrac{1}{\rho}
\dfrac{\partial}{\partial r} \\ 0 & \dfrac{\partial
\overline{w}}{\partial r} + \dfrac{\overline{w}}{r} -
\dfrac{2\mathrm{i}m\nu}{r^2} & \mathcal{A}_1 +
\dfrac{\nu}{r^2} & \dfrac{1}{\rho} \dfrac{\mathrm{i}m}{r}
\\ 0 & \dfrac{\partial}{\partial r} + \dfrac{1}{r} &
\dfrac{\mathrm{i}m}{r} & 0 \end{bmatrix} ,
\end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{B}}_1 = \begin{bmatrix} \overline{u} & 0 & 0 & 1 \\ 0 & \overline{u} & 0 & 0 \\ 0 & 0 & \overline{u} & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} , \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{B}}_1 = \begin{bmatrix} \overline{u} & 0 & 0 & 1 \\ 0 & \overline{u} & 0 & 0 \\ 0 & 0 & \overline{u} & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} , \end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{B}}_2 = \begin{bmatrix} -\nu & 0 & 0 & 0 \\ 0 & -\nu & 0 & 0 \\ 0 & 0 & -\nu & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{B}}_2 = \begin{bmatrix} -\nu & 0 & 0 & 0 \\ 0 & -\nu & 0 & 0 \\ 0 & 0 & -\nu & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{gather}$$and
The linear eigenvalue problem of the reduced quadratic eigenvalue problem is
with the augmented eigenvector
and with the modified operators
 $$\begin{gather}
\boldsymbol{\mathcal{L}}_1^\# = \begin{bmatrix}
\mathcal{A}_1 & \dfrac{\partial \overline{u}}{ \partial r} & 0 &
0 & 0 & 0 & 0 \\ 0 & \mathcal{A}_1 + \dfrac{\nu}{r^2} &
-\dfrac{2\overline{w}}{r} + \dfrac{2\mathrm{i}m\nu}{r^2} &
\dfrac{1}{\rho} \dfrac{\partial}{\partial r} & 0 & 0 & 0 \\
0 & \dfrac{\partial \overline{w}}{\partial r} +
\dfrac{\overline{w}}{r} - \dfrac{2\mathrm{i}m\nu}{r^2} &
\mathcal{A}_1 + \dfrac{\nu}{r^2} & \dfrac{1}{\rho}
\dfrac{\mathrm{i}m}{r} & 0 & 0 & 0 \\ 0 & \dfrac{1}{r} +
\dfrac{\partial}{\partial r} & \dfrac{\mathrm{i}m}{r} & 0 &
0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0
& 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} ,
\end{gather}$$
$$\begin{gather}
\boldsymbol{\mathcal{L}}_1^\# = \begin{bmatrix}
\mathcal{A}_1 & \dfrac{\partial \overline{u}}{ \partial r} & 0 &
0 & 0 & 0 & 0 \\ 0 & \mathcal{A}_1 + \dfrac{\nu}{r^2} &
-\dfrac{2\overline{w}}{r} + \dfrac{2\mathrm{i}m\nu}{r^2} &
\dfrac{1}{\rho} \dfrac{\partial}{\partial r} & 0 & 0 & 0 \\
0 & \dfrac{\partial \overline{w}}{\partial r} +
\dfrac{\overline{w}}{r} - \dfrac{2\mathrm{i}m\nu}{r^2} &
\mathcal{A}_1 + \dfrac{\nu}{r^2} & \dfrac{1}{\rho}
\dfrac{\mathrm{i}m}{r} & 0 & 0 & 0 \\ 0 & \dfrac{1}{r} +
\dfrac{\partial}{\partial r} & \dfrac{\mathrm{i}m}{r} & 0 &
0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0
& 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{bmatrix} ,
\end{gather}$$ $$\begin{gather}\boldsymbol{\mathsf{B}}^\# = \begin{bmatrix} -\mathrm{i}\overline{u} & 0 & 0 & -\mathrm{i} & -\nu & 0 & 0\\ 0 & -\mathrm{i}\overline{u} & 0 & 0 & 0 & -\nu & 0 \\ 0 & 0 & -\mathrm{i}\overline{u} & 0 & 0 & 0 & -\nu \\ -\mathrm{i} & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \end{bmatrix} . \end{gather}$$
$$\begin{gather}\boldsymbol{\mathsf{B}}^\# = \begin{bmatrix} -\mathrm{i}\overline{u} & 0 & 0 & -\mathrm{i} & -\nu & 0 & 0\\ 0 & -\mathrm{i}\overline{u} & 0 & 0 & 0 & -\nu & 0 \\ 0 & 0 & -\mathrm{i}\overline{u} & 0 & 0 & 0 & -\nu \\ -\mathrm{i} & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \end{bmatrix} . \end{gather}$$Appendix C. Energy production and energy forcing term of the coherent kinetic energy budget equation
The explicit expression of the energy production term for ![]() $m=0$ is
$m=0$ is
The explicit expression of the energy forcing term is given by