Overthrusts due to easy-slip/poor-slip transitions at the bed: the mathematical singularity with non-linear isotropic viscosity

Abstract

There are several cases in which large overthrusts and sub-horizontal faults appear to have occurred in temperate or cold glaciers. As a contribution to solving the problem of their origin, the stress field when there is an abrupt change in the bottom boundary conditions is determined, assuming ice to be isotropic, third-power-law viscous. Deviatoric stresses vary with the distance r to the singularity as r^−1/4, and strain rates as r^−3/4. They are computed numerically to a multiplicative factor, which is determined by the conditions at a large distance, but not computed here. Although the apparent viscosity varies as r^1/2 times a function of the polar angle, the stress field around the singularity is not essentially different from that obtained assuming a constant viscosity. Some considerations on the apparition of faults follow, but at the scale of the microrelief the adopted model becomes oversimplified.

1. Introduction

This paper examines how a glacier or ice sheet reacts when there is a sharp change in the boundary conditions at the bed. In particular, is it possible that a fault originates at the point of discontinuity and that an overthrust ensues? (An overthrust is a thrust fault with a low dip and large net slip of the hanging wall.) Documented cases of overthrusts and faults in glaciers are reviewed below, but their mechanism remains a mystery.

The stress and strain-rate fields near an easy-slip/poor-slip transition (or the reverse) will be calculated, assuming the medium is perfectly continuous, without faults or thin shear layers. Contrary to former investigations, a realistic third-power law of viscosity will be adopted. Approximate solutions can be obtained by considering the main terms of these fields near the transition, which correspond to very simple conditions at the bed: no friction on one side, and no sliding on the other side. The possibility of faults or shear layers originating at the bed will then be addressed.

This study should also be relevant to another topic, the processes of glacial erosion and drift. Overthrusts should allow drift to rise within the ice sheet (Hutter and Olunloyo, 1981; Hambrey and others, 1999). Conversely, “downthrusts”, as I call the reverse of an overthrust, may allow basal ice to reach the bedrock. Also, as noted by Barcilon and McAyeal (1993), large deviatoric stresses near an easy-slip/poor-slip singularity might facilitate erosion. Glacial erosion is not dealt with in this paper, however. The role of such sharp transitions is probably marginal. Too many other circumstances, such as past changes in the climate and in the ice cover must be taken into account when tackling the huge and controversial topic of glacier erosion.

2. Field Observations and Adopted Rheology

2.1. Overthrusts in temperate glaciers

Several cases of large overthrusts in temperate glaciers are beyond doubt.

At Safuna, Cordillera Blanca, Peru, an overthrust of the glacier tongue that ends in the upper lake was inferred from ice discharge, and from the existence of a body of ice at the bottom of the lake. Boring in the glacier tongue confirmed this fact by crossing a major discontinuity. At depths of 135–138 m, the drill met a sheared zone, with a gap 20 cm thick through which the borehole lost its water (Lliboutry and others, 1977).

At Glaciar Torre, Fitz-Roy group, Patagonia, an overthrust of the upper part over the lower part was evident on aerial pictures: it had produced an arcuate frontal moraine crossing the latter (Lliboutry, 1993).

At Glacier des Bossons, Mont Blanc group, French Alps, E. E. Viollet-le-Duc observed and drew in 1873 the receding glacier tongue, discovering an old mass of dead ice on which it was lying. He believed that the dead ice had been left after the 1770 advance and that an overthrust occurred during the following 1835 advance. (Drawing reproduced in Lliboutry and others, 1977.)

At Mer de Glace, below the cog railway station of Montenvers, the bed was visited in late March 1962, thanks to a tunnel dug by Electricité de France for a hydroelectric subglacial catchment (Lliboutry, 1965, p.613; Vallon, 1967: pictures in Vivian, 1975, plates XXVI and XXIX). Ice there was very transparent, with only some isolated vertical ribbons of very large, centimetric, air bubbles. Some ice crystals were larger than a fist, and a few small water pockets of irregular shape, the size of a fig, were seen. It was certainly almost unstressed ice, moving very slowly. During these years the glacier surface there moved at a rate of > 20 m a⁻¹. Given the moderate thickness and surface slope, only sub-horizontal overthrusting can explain the difference in velocities between surface and bottom. (As a matter of fact, a fault 10 years old ran along the tunnel, but its throw was only 5–10 cm.) In a picture taken by P. Veyret in 1958 and published by Vivian (1969) a transverse cliff of ice is seen, which might be the front of an overthrust. As in Safuna or Glaciar Torre, the hypothesized overthrust was not due to a glacier advance: the surface of Mer de Glace below Montenvers sank by 61 m between 1944 and 1964.

Fig. 1. Infinite third-power viscous medium, with a cut and a zero shear stress along the half-plane φ = π. For z → ±∞ the state of stress is assumed to tend towards simple shear. Streamlines are drawn. The half-space 0 < φ < π may represent ice flowing over a free-slip/no-slip transition. Turning the figure upside down, the half-space −π < φ < 0 may represent ice flowing over a no-slip/free-slip transition. Therefore the solution calculated for the former problem is also valid for the latter, with some changes of sign.

Conversely, the advance of a temperate glacier seldom causes an overthrust. During the dramatic surge of Variegated Glacier, Alaska, U.S.A., by mid-1983 the surge front reached the terminal lobe, which was 40 m thick and moved at 0.1 m d⁻¹ or less. Although the surging part was moving at 20 m d⁻¹ or more, and was 90 m thick at the surge front, it did not overthrust the terminal lobe. The surge front was a ramp 200 m long, “including thrust faults, buckle folds, and longitudinally oriented crevasses” (Raymond and others, 1987).

2.2. Overthrusts in cold glaciers

Surging cold glaciers, unlike Variegated Glacier, often overthrust their lower part. This may be the case for Trapridge Glacier, Canada (Clarke and Blake, 1991), and is undoubtedly the case for Glaciar Grande del Nevado, central Argentinian Andes (Lliboutry 1998a).

At the very edge of polar ice sheets, outside fast ice streams, overthrusts allow the multiplication of so-called shear moraines (Bishop, 1957; Swinzow, 1962).

Coring to the bottom of the Greenland ice sheet (Greenland Ice Sheet Project 2 and Greenland Icecore Project) has revealed some shear layers of centimetric thickness, and undulations of decimetric wavelength below 500 m from the bottom. In the last 200 m, in ice deposited during the last interglacial (Eemian), some recumbent folds may cause perturbations in the ice stratigraphy (Alley and others, 1997; Gow and others, 1997; Johnsen and others, 1997). The vertical profiles of atmospheric δ ¹⁸O and CH₄ are quite different from those measured at Vostok, East Antarctica, where Eemian ice is distant from the bed. According to Johnsen and others (1997) , the stratigraphic sequence may be disturbed by folding, intrusions or both. This may suggest an overthrust in the bottom layers. However, the profiles for NH₄ ⁺, Ca²⁺, dust content, total gas content and ¹⁰Be do not confirm this perturbation of the sequence, and, for the time being, an overthrust must be considered an unproven hypothesis.

2.3. Faulting near surface or at shallow depth

Some unpublished fieldwork by the staff of Laboratoire de Glaciologie et Géophysique de l’Environnement, Grenoble, France, appearing in internal reports only, is of interest here. In 1970 a mechanical coring was carried out in the lowest part of the accumulation zone of Glacier de Saint-Sorlin, Grandes Rousses, French Alps, just below Col des Quirlies, where ice is temperate, the flow is mildly compressive and the firn was water-soaked at the time of boring. The corer was often jammed by the thrust of some faults which did not appear at the surface. For one, at 13 m depth, it was necessary to melt ice with a steam-jet borer for 3 days to recover the drill.

In 1973, a project began to study, by inclinometry, the strain in a temperate valley glacier, at the hectometric scale. The centre of Glacier duTacul (the upper part of the ablation zone of Mer de Glace) was chosen. The thickness there is 400 m, and the glacier width 800 m; the surface slope is quite uniform (about 6%) and there are no crevasses. Six vertical holes 130 m deep were bored, and electrical copper wires left in the boreholes. Vertical stretching of the glacier, of the order of 0.3% a⁻¹ at most, could not break them. Two years later, as expected, all the boreholes had closed. Three of them were redrilled with a hot-water jet. The nozzle followed the copper wires, but, surprisingly, the three wires were cut at about the same depth, 65–85 m. We thought that some sub-horizontal fault, or thin shear layer, was active at this depth, but could not explain its origin.

With smaller thicknesses and a compressive flow, faults dipping from the surface at 50–67° are often observed (Lliboutry, 1965 (p. 607–609), 2002; Goldthwait, 1973). They have also been observed on cold glaciers of Spitsbergen, Svalbard (Gripp, 1929). The most plausible explanation is that they are the outcrops of faults or shear layers originating at the not too distant bed. They should form along surfaces of maximum shear, which reach the free surface at about 45°. Larger dips should come from subsequent horizontal compression. The detailed and conclusive observations by Gripp (1929) on 20 glaciers of Spitsbergen, and by Philipp (1932) on 13 glaciers of the eastern Alps, are reported in Klebelsberg’s (1948–1949) and Shumskii’s (1955) textbooks, but not in recent ones in English.

2.4. Glacier ice rheology

Mechanical tests are done on ice samples of decimetric size, without shear bands or faults. To what extent they are pertinent to glacier ice deformation at the metric scale remains an open question (Colbeck and Evans, 1971; Tyulana, 1976). It will be assumed that they are pertinent to the hectometric or decametric scales considered in the first part of this paper.

Well below melting point (say, below −15°C), with a constant load, after a stage of decreasing transient creep, a constant strain rate is observed during some days (secondary creep). When the total strain since loading exceeds a critical value, about 1%, kinematic recrystallization (also called dynamic recrystallization, and syntectonic recrystallization by geologists) appears. Above −15°C, the critical strain for recrystallization is reached before the end of transient creep, and steady secondary creep cannot be observed (Duval, 1981). Recrystallization creep leads to the formation of a peculiar fabric, in which individual crystals are not oriented optimally for deformation, but which is very stable against perturbations in the stress regime (Duval, 1981; Azuma and Higashi, 1985). The c axes cluster into four maxima, and the rheology is macroscopically isotropic. This case is assumed in the mathematical model considered in this paper.

A material, whether it be a solid or a liquid in common language, is viscous when zero strain rates require zero deviatoric stresses and vice versa. In mechanics, pure viscosity also requires that the relationship between strain rates and deviatoric stresses (the rheology) be independent of time. This is more or less true for a real material that is flowing, because of transient creep following the continuous changes in load, and because of the possible development of a fabric. The former effect, which is very poorly known (see Lliboutry, 1987b, ch. 15), is ignored in this paper. The latter is introduced in the final discussion only.

Deviatoric stresses are denoted τ_ij, and strain rates (i, j = x, y, z or r, φ, y). A body (isotropic or not) is nth-power-law viscous when, if all the deviatoric stresses are multiplied by the same factor λ, all the strain rates are multiplied by λ ⁿ . The behaviour is isotropic when, at any point, the are proportional to the τ_ij. The factor of proportionality is practically independent of the mean pressure (first stress invariant), and must be a function only of the effective shear stress τ (or of the effective strain rate ). These invariants (when the frame of reference is changed) are defined like the length of a vector in a three-dimensional space (stresses and strain rates may be considered as vectors in a six-dimensional space):

(1)

For an isotropic viscous body we then have:

(2)

(no summation on repeated subscripts). The ratio η is the viscosity (often called apparent viscosity when it is a function of stress). For an isotropic power-law viscosity, B denoting a parameter which depends on temperature, but not on the stress:

(3)

Paterson (1994) uses A = B/2 and λ = 1/(2η). When n = 1 the viscosity is said to be Newtonian, even if the temperature, and hence η, are not uniform in the medium. Then B = 1/η

Correct values of B for macroscopically isotropic ice near melting temperature were obtained by Duval (1981) and Meyssonnier (1989). Measurements in situ, by inclinometry in boreholes or by the closure of tunnels, have been performed in temperate glaciers, where ice presents a typical four-maxima fabric (orientation of the c axes). This curious fabric was obtained in the laboratory by both Duval (1981) and Meyssonnier (1989). It does not modify the rheology consistently. For 0.2 < τ < 7 bar, the flow can always be described by an isotropic power-law viscosity, with n = 3.

The value of B depends on the temperature below melting point, being halved each time that this relative temperature lowers by 5.4 K. This temperature dependence is ignored in this paper. At the melting point, i.e. for temperate ice, B increases with the water content (Duval, 1977). The year will be used as unit of time throughout this paper (1 a = 3.1557 × 10⁷ s). The recommended value for temperate glaciers is B ≈ 430 kPa⁻³ a⁻¹, and when ice is dry and close to melting point B = 200 kPa⁻³ a⁻¹ (Lliboutry, 1987b, section 5.15). These values hold for pure ice. Some acid ions increase the value of B (Jones and Glen, 1969), whereas other impurities as found in Wisconsinan ice decrease it by a factor 2–3 (Dahl-Jensen and others, 1997). Therefore, in the case of polar ice sheets at least, the error in predicted strain rates may be important.

3. Stress and Velocity Fields

3.1. Historical

When the flow of cold ice sheets is modelled, two possible boundary conditions at the bed are considered (Lliboutry, 1987a, 1998b). Ice may be at a sub-freezing temperature and stick to the bedrock or the permafrost below, and the condition is a zero velocity, the shear stress against the bed, τ _b, (henceforth called the friction) resulting from the calculation and not determined in advance. Alternatively, the lower limit of the ice sheet may be at melting point and the ice sheet slips over its bed, the required local boundary condition being some sliding law that links τ _b and the sliding velocity U. At any transition between these two boundary conditions, whichever the value of n, the mechanics of continuous media yield an infinite stress.

For a numerical computation, the singularity has to be smoothed out. Hutter (1983, p. 141) assumes that the function τ _b(U) is continuous at the melting point. Although some sliding of ice at sub-freezing temperatures may be possible (Echelmeyer and Wang, 1987; Dash and others, 1995), the continuity of this function at the melting point does not follow (Shreve, 1984). Other workers (e.g. Herterich, 1987, who assumes isotropic third-power-law viscosity) use an artificial smoothing to obtain convergent algorithms.

Lestringant (1994) has tried to improve upon Herterich’s calculation. Contrary to the latter, he finds that no singularity exists at an ice-cap/ice-shelf transition. Lestringant attributes this discrepancy to his better calculation of the surface profile. In fact, the singularity disappears because Lestringant adopts a rheology that rules out infinite stresses, namely:

(4)

With this creep law, for a very large effective shear strain rate the effective shear stress tends towards a finite value (c ₁ + c ₂)(π/2), and thus all deviatoric stresses remain finite.

By using highly sophisticated mathematics, Barcilon and MacAyeal (1993) have rigorously dealt with the twodimensional no-slip/free slip transition, assuming isotropic and uniform linear viscosity. The surface profile that they find is questionable, however, because in fact ice viscosity is temperature- and stress-dependent. Consequently, the upper layers of the ice sheet should behave as an almost rigid plate, and this should smooth the predicted changes in the surface slope. As for the flow near the singularity, our approach below is simpler, yet more realistic because a power-law viscosity is used.

3.2. Simplest problem coping with the singularity

On the large scale considered, any microrelief of the bed is smoothed out. Near the singularity, the bed may be considered as a plane, which is taken as the xy-plane. Plane flow is assumed, with motion in the x direction and with variables independent of y. Cylindrical coordinates (r, φ, y) reduce to polar coordinates (r, φ), with φ = 0 corresponding to the positive x axis and φ = π/2 corresponding to the z axis.

The following approach will be adopted. It would be rigorous if ice rheology were linear, and if the boundary conditions were either a given force acting on the boundary, or a given velocity. The stress and velocity fields are considered as the sum of fields that correspond to two distinct problems, 1 and 2, the forces of gravity and the given forces or velocities at the boundaries being shared between both problems. Problem 1 is the simplest one that can cope with most of the singularity at the origin. Gravity forces are excluded from it. Problem 2 yields stresses and strain rates that are continuous and remain finite at the origin. In the case of transitions from easy slip upstream to limited slip (or no slip) downstream, problems 1 and 2 read as follows.

Problem 1

Gravity forces are zero. Ice is driven by forces that, at infinite distance from the origin, tend toward a simple shear. The boundary conditions on the bed are:

The bed is a streamline.

The normal stress on the bed (not the deviatoric one) is zero.

For φ = 0 the sliding velocity, U ₁, is zero. For φ = π the friction, τ _b1, is zero.

This abrupt change in the shear stress against the bed yields a singularity at the origin, where all deviatoric stresses become infinite. (Of course infinite values are a mathematical artifact of the model. What happens really in nature will be examined later, on a detailed scale.) Strain rates also become infinite at the origin. Nevertheless, U ₁ is continuous when crossing the origin: on the free-slip side it decreases progressively to zero.

The boundary conditions at the upper limit of the domain are such that the total work of the driving force on any boundary r = R, per unit width and unit time, is proportional to R, as would be the case in simple shear. The advantage of this choice will appear below.

Problem 2

Ice sheet subject to gravity, limited upwards by some free surface. The boundary conditions on the bed, besides the bed being a streamline, differ according to the global problem considered, but in any case they remain the same on both sides of the singularity. At an easy-slip/poor-slip transition, it is some uniform friction law relating the friction and the sliding velocity. Thus, when the boundary conditions are added for both problems, on one side of the bed the total friction will be larger than predicted by this law, and on the other side the total sliding velocity will be larger.

Unfortunately, since ice rheology is not linear, problems 1 and 2 cannot be solved separately in a rigorous way. At each point of the medium, the effective shear stress to be introduced in Equation (3) is the one corresponding to the sum of both deviatoric stress fields. Nevertheless, in the vicinity of the singularity, problem 2 yields much smaller deviatoric stresses than problem 1, which can be ignored. Our solution of the first problem will be approximate only, becoming asymptotically rigorous at the singularity.

3.3. Dependence of the stress and strain-rate fields on radius r

In the two-dimensional problem, the conservation of mass, hence of volume, is satisfied by introducing a stream function q, defined to an arbitrary additive constant. In polar coordinates, the velocities and strain rates read (Lliboutry, 1987b, p. 478; the signs have been changed to have a volumetric discharge per unit width between the bed and the streamline q = a constant equal to q, not to −q):

(5)

Stress equations (which express equilibrium, when inertia force and Coriolis force are negligible, as is always the case in glaciology) are satisfied by introducing an Airy’s stress function χ, also defined to an arbitrary additive constant. When body forces of gravity are zero, total stresses (for which von Kármán’s notations are used) read (Lliboutry, 1987b, p. 478):

(6)

In the two-dimensional problem the only non-zero strain rates are and , and the only non-zero deviatoric stresses are τ _rφ and τ _rr = (σ_r = −σ_φ )/2. It follows:

(7)

As is always done in continuum mechanics, we assume that stresses and strain rates are continuous functions of the space variables which can be indefinitely derived, except along some singular lines, like the bed in our case. Thus, for any fixed value of φ included in the open intervals]0, π[and] − π, 0[they are continuous functions of r that can be indefinitely derived, except at r = 0. We assume that this single singularity at the origin is regular. It means that stresses and strain rates can be expanded about the origin as:

(8)

the k being positive integers, and p being not necessarily an integer nor necessarily positive. The a_k are functions of φ which are indefinitely derivable within the mentioned open intervals. With this assumption or regularity, stress and strain-rate fields obeying all the equations and boundary conditions will be found. Therefore, if a non-regular singularity were possible, it would imply that the solution is not unique, contrary to what can be demonstrated when faults within the medium are excluded.

To obtain the form of Equation (8) for strain rates and for stresses, one must start from:

(9)

Then the prefactor before the Taylor expansion is r^{e +1} for the velocities, r^e for the strain rates and for , and r^s for the stresses. Now, problem 1 has been chosen such that the work per unit time and unit length along r = R is independent of R. This work is:

(10)

the C_k being functions of φ To be independent of r, the Taylor expansion must reduce to its first term, which is independent of r, and moreover we must have:

(11)

(note that the viscous dissipation of energy per unit width within a semicircle r < r ₁ is proportional to the power (e + s + 2) of r ₁, and thus vanishes with r ₁).

To obey Equation (3), e = ns is required. Thus:

(12)

The master functions q and χ can be written as follows (multiplicative factors K and BKⁿ, with K having the dimension of a stress, are introduced to make X(φ) and Q(φ) non-dimensional):

(13)

3.4. Boundary conditions for X(φ) and Q(φ)

Comparing Equations (6), (7) and (11) it is found (with primes denoting derivatives in φ):

(14)

The conditions at the bed will be written for a free-slip/no-slip transition. They are:

(15)

Another condition is needed to determine completely X and Q, because the multiplicative factor K has introduced one degree of freedom. Some non-null value of X or of Q must be arbitrarily fixed. (Recall that X and Q are dimensionless.) To find again notations used in the elastic problem equivalent to the linear viscous problem, this choice will be that on the no-slip side φ = 0 the shear stress is τ_rφ = Kr ^{−1/(n + 1)}, and thus X′(0) = −(n + 1)/n

The mechanical problem may be extended to the lower half-plane −π < φ < 0, keeping the same boundary conditions. Consequently, stresses and strain rates are continuous when crossing the no-slip half-plane φ = 0. The free-slip half-plane φ = π is a cut in the medium, and velocity changes sign when it is crossed. Q(φ) and X(φ) are then defined in the range −π < φ < π, Q is an even function and X an odd one. In the lower half-plane the streamlines are symmetrical about the x axis to the ones in the upper half-plane, but the flow is in the opposite direction, as sketched in Figure 1. Therefore, the solution for −π < φ < 0 corresponds to a no-slip/free-slip transition, and a single calculation is needed for both cases.

3.5. Solution for Newtonian viscosity

When n = 1, Equations (13) read:

(16)

From Equations (6) and (7) it follows:

(17)

The creep law (Equation (3)) reads:

(18)

Both X and Q obey the linear differential equation of fourth order:

(19)

With the boundary conditions above, the solution is found to be:

(20)

This solution might have been drawn from the equivalent problem in elasticity, by making Poisson’s ratio equal to 1/2, and replacing the elastic shear modulus by η∂/∂t. This equivalent elastic problem is the stress field at the tip of a crack, in the sliding mode of fracture (mode II), which occurs when the state of stress tends, for y infinite, towards a simple shear. It has been solved by methods that apply to linear problems only, and the results are given in several textbooks (e.g. Lliboutry, 1987b, p.308–310).

3.6. Solution for isotropic third-power-law viscosity

When n ≠ 1, the apparent viscosity η is:

(21)

where τ and γ are given by Equations (8). The two rheological equations corresponding to Equations (18) are no longer linear, and must be solved numerically. Only the case n = 3 is dealt with below:

(22)

To allow a computation by successive approximations it is convenient to use the two different expressions of η given by Equations (21):

(23)

(24)

At each successive step in the computation, the right-hand side is drawn from the previous approximation, and one has a linear differential equation of second order to solve. The conditions at the limits are:

(25)

As starting values, X(φ) for a Newtonian viscosity has been adopted, multiplied by 2/3 to obey X′(0) = −4/3:

(26)

The result of the computation is displayed in Figure 2.

Fig. 2. Functions Q(φ) and X(φ) when n = 3.

3.7. Longitudinal compression, streamlines and slip-lines

The inverse of the (apparent) viscosity, termed the (apparent) fluidity, is found to be:

(27)

F(φ) decreases from F(0) = 1 to a minimum near π/2 = 90°, F(90°) = 0.309; has a broad maximum around 150°, F(150°) = 0.578; and next decreases to F(180°) = 0.535. Lines of equal viscosity, obeying r = F ² × a constant, are given in Figure 3. For a given r, viscosity is lower against the no-slip side than against the free-slip side by a factor 0.535. It reaches a maximum over the singularity, where ice rotates much more than deforms and the effective shear stress is low. In part due to this fact, for a given r, the normal stress parallel to the bed, which is σ_φ when φ = 90° and σ _r when φ = 180°, is larger just above the singularity than on the free-slip bed by a factor 1.273. With linear, constant viscosity, it would be the reverse, with a factor 0.530.

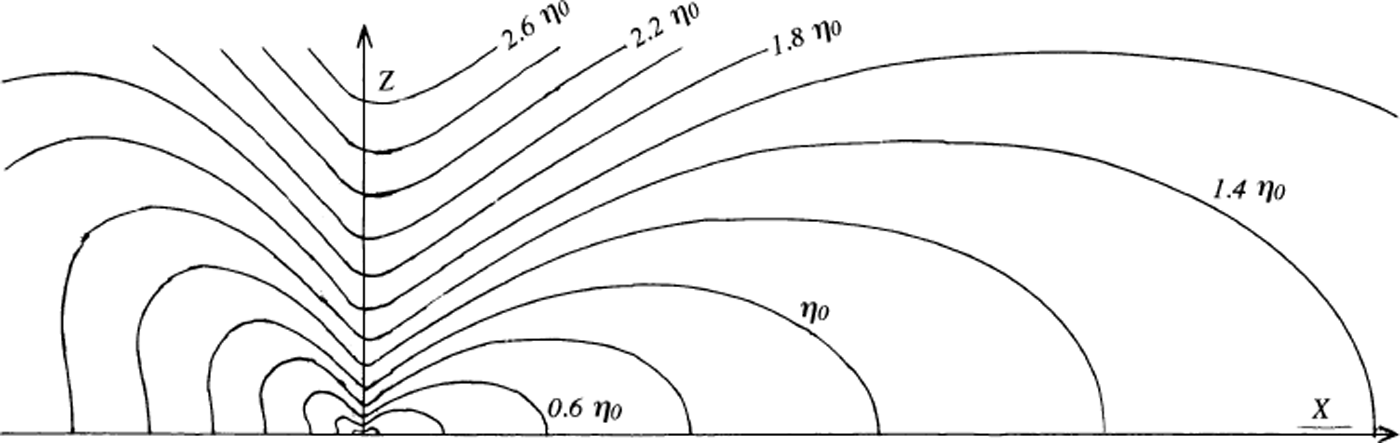
Fig. 3. Lines of equal apparent viscosity, for values in arithmetic progression. Since viscosity is proportional to K⁻², which has not been determined, the scale of the figure is arbitrary, and the unit of viscosity η₀ is not specified.

Streamlines are given by q(r, φ) = a constant, i.e. for any n:

(28)

Since streamlines are similar (more precisely, homothetic about the origin), a single one for n = 3 and a single one for n = 1 are displayed in Figure 4, both crossing the z axis at the same point. Near the origin they are almost identical, and some values of their slopes must be given to show the difference. The slope of a streamline is:

(29)

Since Q(0)= 0 and Q″(0) = 1, when φ is very small, Q ≈ φ ²/2. Comparing with Equation (29):

(30)

In the case n = 1 there is an inflexion point at φ = φ ₂ = arccos (−1/3) = 109.47°. This is exactly where Q′ = 0 and where the streamline is closest to the origin. The slope of the streamline there is 0.3536. Next, following ice flow, the slope lowers to 1/3 at φ = 90°. In the case n = 3, Q′ = 0 at φ = φ ₂ = 108.2°, and the slope of the streamline is then 0.329. The inflexion point is at φ = 101.6°, with a slope 0.332, and at φ = 90° the slope has lowered to 0.320.

Fig. 4. Streamline when n = 3, and direction of “sub-horizontal” slip-lines crossing it. Dashed line is the streamline when n = 1 crossing the z axis at the same point. The scale is not specified: all streamlines and slip-lines are homothetic about the origin. Above: values of the effective shear stress along the streamline, to factor K. In the plane problem, principal deviatoric stresses (normal ones and shear ones) equal it.

Significant differences appear at large distances from the origin, linked to the fact that with n = 3 the apparent viscosity is lower above the no-slip bed than above the free-slip bed. It is easily shown that far downstream y varies as x ^1/4 when n = 1, and faster, as x ^3/8 when n = 3. Far upstream y varies as |x| ^−1/2 when n = 1, and slower, as |x| ^−1/4, when n = 3.

From general theory, for a plane problem the effective shear stress is the absolute value of both principal deviatoric stresses, and it equals maximum shear stresses. These maximum shear stresses are found on planes at 45° from the principal directions, and they make an angle θ with the radius which is given by:

(31)

In particular, when n = 3, for φ → 0, from Equations (25), Q ≈ φ ²/2 and thus θ → 1 − φ/4. Equations (22) and (31) allow the intensity and direction of maximum shear stresses to be calculated. The one whose direction is the closest to that of the streamline is drawn in Figure 4. The variation of its intensity τ is also shown in this figure.

Slip-lines are tangent to a maximum shear stress at any point. They form two families, orthogonal to each other, which are referred to as sub-horizontal slip-lines or sub-vertical slip-lines, according to whether their angle with the bed remains smaller or larger than 45° (Fig. 5). When crossing the free-slip bed, they change family. The following description holds for the half-plane 0 < φ < 180°.

Fig. 5. Slip-lines in the complete space −180° < φ < 180^o.

Sub-horizontal slip-lines start from the free-slip bed at 45° forward, are tangent to a streamline at φ = φ ₂, and, far downstream, cross the streamlines at an angle 3φ/8. (With n = 1 it would be φ/4.) The no-slip bed (the half-straight line φ = 0) is a singular slip-line to be added to this family.

Sub-vertical slip-lines start from the free-slip bed at 45° backward, or from the no-slip bed perpendicularly to it. They tend to be parallel to φ = φ ₂ at a large distance from the bed. This family includes the half-straight lines φ = ±φ ₂. They form a single slip-line, with an infinite curvature at the origin. Because of this singularity, the two half-straight lines can be not perpendicular to the other slip-line reaching the origin, the no-slip bed φ = 0.

3.8. Estimation of the parameter K, and domain of validity of the solution above

The value of the multiplicative factor K must be inferred from the dynamics of the whole ice sheet, which is not modelled in the present study. Essential factors to be considered would be the temperature field (which modifies B), the ice discharge, and the friction law on the sliding side of the singularity. Another important parameter is the radius R up to which the solution above of problem 1 remains more or less valid for the global problem (1 + 2) (a lithostatic pressure having been added, however).

Rough estimations of K and R can be obtained by assuming that, at distance R from the singularity, the sliding velocity on the free-slip side and the friction on the no-slip side have the values commonly found in glaciers and ice sheets. The given solution of problem 1 yields:

(32)

For a temperate mountain glacier (B = 430 MPa⁻³ a⁻¹), a radius of validity R = 50 m is acceptable. It is found, for instance, with the realistic values U ≈ 17 m a⁻¹ and τ _b ≈ 0.10 MPa. For a cold ice sheet (B = 200 MPa⁻³ a⁻¹), an acceptable radius of validity is R = 500 m. It is found, for instance, with the realistic values U ≈ 10 m a⁻¹ and τ _b ≈ 0.05 MPa.

4. Processes at the Discontinuity that Keep Stresses Finite

4.1. Existence of a microrelief

The mathematical model yields infinite stresses and strain rates at r = 0, which cannot exist in nature. They may be avoided either because the discontinuity is blurred on a sufficiently detailed scale, or because other processes, not considered in the model, become important. These two possibilities will be examined successively.

The model assumes a plane bed. Recall that the concept of a friction on the bed and a corresponding sliding velocity is pertinent to a bed from which all the microrelief has been smoothed out. Sliding theories consider separately, on a finer scale, the flow of a bottom boundary layer on this microrelief. Therefore a no-friction condition is sound only if the bumps of the real bed are much smaller than R.

Consider cold ice sheets, where melting point is reached at the bottom, on the easy-slip side. A flat bed is possible if it consists of flattened sediments, as in the case of the fast ice streams flowing from West Antarctica into the Ross Ice Shelf (Engelhardt and Kamb, 1998). Only the upper 3 cm are deformed, and (according to the interpretation of raw data that they favour) account for only 17% of the sliding velocity. A free-slip/no-slip transition on flat sediments must come from a melting-point isotherm leaving the interface and entering the sediments with a very small dip. Consequently, over some distance there is a thin layer of frozen sediments, which should be caught and carried downstream as a moving bottom moraine (as geologists say) or a debris-rich bottom layer (as glaciologists say). This important case is excluded from the present study.

When the glacier bed consists of sound rock, the melting-point isotherm cuts many bumps of the microrelief. There should be a stripe of bed with intermingled temperate and cold patches. The temperature fluctuations caused by sliding modify their limits, but do not suppress them. When cold patches predominate, they should prevent any sliding on the temperate ones. When temperate patches predominate, they should enforce sliding by local faults on the cold ones. Coming back to the hectometric scale, the temperate–cold boundary is blurred and not well defined, but the boundary between slip and no-slip is sharp and well defined.

4.2. Faults and shear layers

When the flow is from a no-slip side to an easy-slip side, a fracture may start from the bed if the acting stress is large enough. It may be in the opening mode and perpendicular to the bed, producing a “bottom crack”, or in the sliding mode and at 45° from the bed, producing a normal fault. Fracture in the opening mode may always start, but the crack should extend upwards only if the superimposed lithostatic pressure is low enough. (A particular case is when the bottom crack reaches the surface, the sliding part goes downstream and the no-sliding one remains as a hanging glacier.)

A normal fault (or a reverse fault, in the case of a transition from easy slip to poor slip) may start from the bed at 45°, very close to the origin. It follows more or less a sub-horizontal slip-line, which at some distance from the bed becomes close to streamlines. This fact should allow the fracture to extend over a long distance from the origin as a thin shear layer, because the shear stress acting on it remains high for a long time. In this case, a strain-induced fabric that favours shear should form and make the process self-enforcing. The computed stress field would be modified, however.

The theoretical value of the acting shear stress at start given by our solution is not exact, because of the microrelief which provides locally, on its scale, higher deviatoric stresses. Therefore, when an overthrust is observed, the precise value of the stress at the point of departure cannot be reached, even if the global problem has been solved.

4.3. Necessity of a water input

The formation in the ice of a shear layer or a fault starting from the bed creates a gap at the ice–bed interface on one side. It must be infilled with water to balance the lithostatic pressure. A realistic possibility for an abrupt change in the conditions at the bottom is one side of the bed at melting temperature, the other one at sub-freezing temperatures. The required water must then come from the easy-slip side, and probably from upstream. This should have been the case during the quoted overthrusting and surge of Glaciar Grande del Nevado Plomo. Another possibility is, with all the bed at melting point, a subglacial water storage over some area that makes the friction drop almost to zero. This should have been the case for the quoted overthrusting of Glaciar Torre. A third possibility, not examined here, is when the abrupt discontinuity at the bed comes from a change in its nature: rock on one side, flat sediments on the other.

5. Conclusion

This theoretical paper is a contribution to the study of a poorly known process which deserves more attention in the field. The topic is of interest not only in glacial geology. Overthrusts in the tongues of glaciers may well invalidate many analyses of monitored advances and retreats.

I do not claim to have “explained” completely this well-proven process, which contradicts the usual assumption of a perfectly continuous medium. I have only removed a risk for investigators. The stress and strain-rate fields produced by an abrupt change from easy slip to poor slip (or no slip at all) with a realistic third-power viscosity might be quite different from the well-studied case of constant viscosity. For instance, in another problem, the flow over a perfectly smooth hemisphere, extrusion flow appears when n > 2 (Lliboutry, 1987b, section 13.5).

The mathematical singularity cannot be studied directly by the usual finite-element method. It has been shown that the stream function and the Airy stress function, from which strain rates and stresses can be drawn, are, respectively, q = BK ³ r ^2−3/4 Q(φ) and x = Kr ^2−1/4 X(φ). Deviatoric stresses vary as r ^−1/4. For a given φ, when r is 16 times smaller they are doubled, whereas with a constant viscosity they vary as r ^−1/2 and increase fourfold. This is the main change, since the solution becomes illusory because of the ignored microrelief and must not be used when r < R/16 or R/50.

Functions Q(φ) and X(φ) obey two coupled differential equations of second order, where the lefthand side is linear and involves a single function, while the righthand side is not linear (as when n = 1), but involves only the other function. Therefore this set is readily solved numerically, by successive approximations. Streamlines and slip-lines have been drawn. Their slopes differ from the linear viscous case, but, qualitatively, no essential differences appear.

The computed solution is no longer valid at the metric scale of the microrelief; moreover, in the case of cold ice sheets, frozen subglacial ground may be caught and dragged on the poor-slip side. Therefore, at this minute scale, just one essential fact has been pointed out: faulting or cracking may start from the sole of the glacier only if water at the overburden pressure is available to infill immediately the gap that appears. As for temperate glacier dynamics, subglacial hydraulics must be introduced to improve the model.