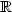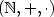Consider partial maps ∑* → $\mathbb R$ with a rational domain. We show that two families of such series are actually the same: the unambiguous rational series on the one hand, and the max-plus and min-plus rational series on the other hand. The decidability of equality was known to hold in both families with different proofs, so the above unifies the picture. We give an effective procedure to build an unambiguous automaton from a max-plus automaton and a min-plus one that recognize the same series.

We characterize conjugation classes of Christoffel words (equivalently of standard words) by the number of factors. We give several geometric proofs of classical results on these words and sturmian words.

It is known that the class of factorizing codes, i.e.,codes satisfying the factorization conjectureformulated by Schützenberger, isclosed under two operations:the classicalcomposition of codes and substitutionof codes.A natural question which arisesis whethera finite set Oof operations existssuch that each factorizingcode can be obtained by usingthe operations inO and starting with prefix or suffix codes.O is named herea complete setof operations (for factorizing codes).We show that composition and substitutionare not enough in order to obtaina completeset. Indeed, we exhibit a factorizing code over a two-letter alphabet A = {a,b}, precisely a 3-code, which cannot beobtained by decomposition or substitution.

It is shown that small fragments of the first-order theory of the subword order, the (partial) lexicographic path ordering on words, the homomorphism preorder, and the infix order are undecidable. This is in contrast to the decidability of the monadic second-order theory of the prefix order [M.O. Rabin, Trans. Amer. Math. Soc., 1969] and of the theory of the total lexicographic path ordering [P. Narendran and M. Rusinowitch, Lect. Notes Artificial Intelligence, 2000] and, in case of the subword and the lexicographic path order, improves upon a result by Comon & Treinen [H. Comon and R. Treinen, Lect. Notes Comp. Sci., 1994]. Our proofs rely on the undecidability of the positive ∑1-theory of $(\mathbb N,+,\cdot)$ 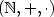[Y. Matiyasevich, Hilbert's Tenth Problem, 1993] and on Treinen's technique [R. Treinen, J. Symbolic Comput., 1992] that allows to reduce Post's correspondence problem to logical theories.

For both the edge deletion heuristic and the maximum-degree greedy heuristic, we studythe problem of recognizing those graphs for which that heuristic can approximate the size of a minimum vertex cover within a constant factor of r, where r is a fixed rational number. Our main results are that these problems are complete for the class of problems solvable via parallel access to NP. To achieve these main results, we also show that the restriction of the vertex cover problem to those graphs for which either of these heuristics can find an optimal solution remains NP-hard.