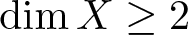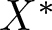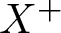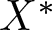Two dynamical approaches to the notion of exponential separation for random systems of delay differential equations

Abstract

This paper deals with the exponential separation of type II, an important concept for random systems of differential equations with delay, introduced in Mierczyński et al. [18]. Two different approaches to its existence are presented. The state space X will be a separable ordered Banach space with $\dim X\geq 2$, dual space $X^{*}$, and positive cone $X^+$ normal and reproducing. In both cases, appropriate cooperativity and irreducibility conditions are assumed to provide a family of generalized Floquet subspaces. If in addition $X^*$ is also separable, one obtains an exponential separation of type II. When this is not the case, but there is an Oseledets decomposition for the continuous semiflow, the same result holds. Detailed examples are given for all the situations, including also a case where the cone is not normal.

1. Introduction

This paper deals with the existence of principal Floquet subspaces and generalized exponential separation of type II for positive random dynamical systems generated by linear differential equations with finite delay. In particular, some previous results, obtained in Mierczyński et al. [18], are now completed and extended to random linear systems of delay differential equations. This reference introduced a new focusing condition motivated by the non-injectivity of the flow map defined by a linear delay differential equation, which is also of great interest in the vector case now considered. In addition to the construction method of the generalized exponential separation from the principal Floquet subspace given in [18] and now extended to the high-dimensional case, the present paper provides an alternative approach based on the Oseledets decomposition for the continuous time flow generated by the system of linear delay differential equations. This theorem was stated in Mierczyński et al. [19] as an adaptation of the semi-invertible Oseledets theorem proved in González-Tokman and Quas [8] and Lee [15].

The top finite Lyapunov exponent of a positive deterministic or random dynamical system is called the principal Lyapunov exponent if the associated invariant family of subspaces, where this Lyapunov exponent is reached, is one-dimensional and spanned by a positive vector. In this case, the invariant subspace is called the principal Floquet subspace. The exponential separation theory was initiated for positive discrete-time deterministic dynamical systems by Ruelle [31] and Poláčik and Tereščák [29, 30]. Subsequently, important contributions for discrete and continuous time flows were obtained by Húska and Poláčik [11], Húska [10], Húska et al. [12], Novo et al. [25], Mierczyński and Shen [20, 21], and Shen and Yi [33], among others. In particular, Novo et al. [25] introduced the exponential separation of type II, a version of the classical notion adapted to the study of deterministic delay differential equations. The importance of this concept for the study of linear and nonlinear nonautonomous functional differential equations with finite delay can be found in Novo et al. [26], Calzada et al. [6], and Obaya and Sanz [27, 28].

In the context of random dynamical systems, ${(\Omega,\mathfrak{F},\mathbb{P})}$ will denote a probability space with an ergodic measure $\mathbb{P}$, $\theta\colon\mathbb{R} \times \Omega \to\Omega$, $(t,{\omega}) \mapsto \theta_t{\omega}$ is a metric dynamical system, X is an ordered Banach space and $\Phi\colon \mathbb{R}^+ \times \Omega \times X \to \Omega\times X$, $(t, {\omega}, u) \mapsto (\theta_t{\omega},U_{\omega} (t)\,u)$ a measurable linear skew-product semiflow. The concept of generalized exponential separation (of type I) refers to a measurable decomposition $X=E_1({\omega}) \oplus F_1({\omega})$ for $\mathbb{P}$-a.e. ${\omega}\in\Omega$, where $E_1({\omega})= \text{span} \{w({\omega}) \}$ is the principal Floquet subspace, $F_1({\omega})$ is an invariant co-dimensional one closed vector subspace that does not admit any strictly positive vector, and $U_{\omega}(t)$ exhibits an exponential separation on the sum.

Arnold et al. [3] proved the existence of generalized exponential separation for discrete-time positive random dynamical systems generated by random families of positive matrices. Later, Mierczyński and Shen [22] provided the assumptions sufficient for a general random positive linear skew-product semiflows in order to admit a generalized principal Floquet subspace and generalized exponential separation. A wide range of applications of this theory, including random linear skew-product semiflow generated by cooperative families of ordinary differential equations and parabolic partial differential equations, can be found in Mierczyński and Shen [23, 24]. More recently, Mierczyński et al. [18] adapted the previous abstract theory to the case of a non-injective flow map. More precisely, assuming integrability, positivity, and a new focusing condition in the terms of the one in [22], a generalized exponential separation of type II is introduced. The main difference concerning this new focusing condition is that it implies the existence of a positive T > 0 such that for each $u \in X^+$ and ${\omega} \in \Omega$ then $U_{\omega} (T)\,u=0$ or $U_{\omega}(t)\,u$ is strictly positive. As a consequence of this dichotomy behaviour, concerning the measurable decomposition, now $F_1({\omega}) \cap X^+=\{u \in X^+ \colon U_{\omega}(T)\,u=0 \}$, that is, $F_1({\omega})$ can contain positive vectors. The present paper studies the applicability of this theory to the case of random systems of delay differential equations.

The paper is organized into five sections and X will denote a separable ordered Banach space with $\dim X\geq 2$, dual space $X^{*}$, and positive cone $X^+$ always reproducing and normal in most of the paper. Section 2 collects the main notions, assumptions, and results of [18] used throughout the paper. Assuming integrability, positivity, and a focusing condition, theorem 2.5 asserts that the semiflow Φ admits a generalized Floquet subspace $E_1({\omega})=\text{span}\{w({\omega})\}$. Moreover, theorem 2.5 (vii) provides the exponential convergence of the normalized trajectories of positive vectors to $w({\omega})$ in the forward and also in the pullback sense. In addition, when $X^*$ is also separable, theorem 2.9 concludes that Φ admits a generalized exponential separation of type II with measurable decomposition $X=E_1({\omega}) \oplus F_1({\omega})$. The previous properties of exponential convergence assure that the family of subspaces $E_1({\omega})$, $ F_1({\omega})$, and their associated projections can be calculated numerically in applications. This shows the interest of the applications of this part of the theory in the paper.

Section 3 assumes that Φ admits an Oseledets decomposition. As proved in [19, Theorem 3.4], this decomposition exists when Ω is a Lebesgue space and there is a $t_0 \gt 0$ such that $U_{\omega}(t_0)$ is a compact operator for all ${\omega} \in \Omega$. In particular, the separability of $X^*$ is not required. If the top Lyapunov exponent $\lambda_{\mathrm{top}} \gt -\infty$, then $X=E({\omega}) \oplus F({\omega})$, where $E(\omega) = \{u \in X:$ there exists an entire orbit passing through $({\omega},u)$ with $\lim_{t\to \pm \infty}\ln \|U_{\omega}(t)\,u\|/t = \lambda_{\mathrm{top}} \}$. and $F({\omega})=\{u\in X : \lim_{t \to \infty}\ln \|U_{\omega}(t)\,u\|/t \lt \lambda_{\mathrm{top}} \}$ for $\mathbb{P}$-a.e. ${\omega}\in\Omega$. Assuming that Φ admits a generalized Floquet subspace $E_1({\omega})=\text{span}\{w({\omega})\}$, theorem 3.8 proves that $E_1({\omega})=E({\omega})$ for $\mathbb{P}$-a.e. ${\omega}\in\Omega$ and then, the previous Oseledets decomposition provides a generalized exponential separation of type II.

Section 4 deals with systems of linear random delay differential equations of the form $z'(t)= A(\theta_t {\omega})\,z(t) + B(\theta_t {\omega})\,z(t-1)$, where A belongs to $L_1(\Omega)$ and B satisfies a L_q-integrability condition for some $1 \lt q \lt \infty$. Under these assumptions, as shown in [19], they induce measurable linear skew-product semidynamical systems $\Phi^{(L)}$ on $\Omega \times L$ for $L=\mathbb{R}^N\times L_p([-1,0],\mathbb{R}^N)$, $1/p+1/q=1$, and $\Phi^{(C)}$ on $\Omega \times C$ for $C=C([-1,0],\mathbb{R}^N)$. Following ideas from [24], appropriate cooperativity and irreducibility conditions on the systems are assumed to show that both $\Phi^{(L)}$ and $\Phi^{(C)}$ admit a family of generalized Floquet subspaces with principal Lyapunov exponent $\widetilde{\lambda}_1^{(L)}$ and $\widetilde{\lambda}_1^{(C)}$, respectively. In particular, the focusing condition needed for the exponential separation of type II allows the irreducibility condition to be expressed in terms of the matrix A + B, providing a simplified and weaker version of previous conditions of this type in terms of the matrix B. Since L is separable, an application of theorem 2.9 provides a generalized exponential separation of type II for $\Phi^{(L)}$ with $\widetilde{\lambda}_1^{(L)} \gt -\infty$. This result cannot be obtained for $\Phi^C$ in this way because C is not separable. However, the natural injection $J\colon C\rightarrow L$, introduced and discussed in [19], which in particular proves the norm-equivalence of the trajectories defined in both Banach spaces, allows us to deduce the result for $\Phi^C$ in theorem 4.8. For similar reasoning, see Froyland and Stancevic [7, Sect. 3] and González-Tokman and Quas [9, Appendix A] in the context of Perron–Frobenius operators, as well as Blumenthal and Punshon-Smith [5, Section 2.3] in the context of some fluid mechanics equations. For a more abstract setting, see Kryspin [14].

Finally, assuming that Ω is a Lebesgue space and by means of the results from the Oseledets theory obtained in §3, §5 shows the existence of an exponential separation of type II in some illustrative examples where the Banach space dual is not separable. More precisely, the above family of linear random delay systems, under two different L ₁-integrability conditions on B, induces measurable linear skew-product semidynamical systems $\Phi^{(\widehat{L})}$ on $\Omega \times \widehat{L}$ for the separable Banach space $\widehat{L}=\mathbb{R}^N\times L_1([-1,0],\mathbb{R}^N)$ and $\Phi^{(C)}$ on $\Omega \times C$ for $C=C([-1,0],\mathbb{R}^N)$. Then, with the same methods and assumptions of cooperativity and irreducibility of §4, both $\Phi^{(\widehat L)}$ and $\Phi^{(C)}$ admit a family of generalized Floquet subspaces. Lastly, conclusions of §3 provide a generalized exponential separation of type II for them with principal Lyapunov exponent $\widetilde{\lambda}_1^{(\widehat{L})} \gt -\infty$ and $\widetilde{\lambda}_1^{(C)} \gt -\infty$. The third case corresponds to the separable Banach space of absolutely continuous functions $AC=AC([-1,0],{\mathbb{R}}^N)$ with a Sobolev type norm which is not monotone and the cone is not normal, to show the applicability under a weaker condition on the positive cone. First we consider the same assumptions of the previous case for $\Phi^{(C)}$ to obtain a measurable linear skew-product semidynamical system $\Phi^{(AC)}$. Then, from the results for C, §3 and similar arguments to those of theorem 4.8, a family of generalized Floquet subspaces and an exponential separation of type II are obtained for AC.

2. A direct theory providing generalized exponential separation

A probability space is a triple ${(\Omega,\mathfrak{F},\mathbb{P})}$, where Ω is a set, $\mathfrak{F}$ is a σ-algebra of subsets of Ω, and $\mathbb{P}$ is a probability measure defined for all $F \in \mathfrak{F}$. We always assume that the measure $\mathbb{P}$ is complete. For a metric space S by $\mathfrak{B}(S)$, we denote the σ-algebra of Borel subsets of S.

A measurable dynamical system on the probability space ${(\Omega,\mathfrak{F},\mathbb{P})}$ is a $(\mathfrak{B}(\mathbb{R}) \otimes \mathfrak{F},\mathfrak{F})$-measurable mapping $\theta\colon\mathbb{R}\times \Omega\to \Omega$ such that

• • $\theta(0,{\omega})={\omega}$ for any ${\omega}\in\Omega$,

• • $\theta(t_1+t_2,w)=\theta(t_2,\theta(t_1,{\omega}))$ for any t ₁, $t_2\in\mathbb{R}$ and any ${\omega} \in\Omega$.

We write $\theta(t,{\omega})$ as $\theta_t{\omega}$. Also, we usually denote measurable dynamical systems by $({(\Omega,\mathfrak{F},\mathbb{P})},(\theta_{t})_{t \in \mathbb{R}})$ or simply by $(\theta_{t})_{t \in \mathbb{R}}$.

A metric dynamical system is a measurable dynamical system $({(\Omega,\mathfrak{F},\mathbb{P})},(\theta_{t})_{t \in \mathbb{R}})$ such that for each $t\in\mathbb{R}$ the mapping $\theta_t\colon \Omega\to\Omega$ is $\mathbb{P}$-preserving (i.e. $\mathbb{P}(\theta_t^{-1}(F))=\mathbb{P}(F)$ for any $F\in\mathfrak{F}$ and $t\in\mathbb{R}$). A subset $\Omega'\subset\Omega$ is invariant if $\theta_t(\Omega')=\Omega'$ for all $t\in\mathbb{R}$, and the metric dynamical system is said to be ergodic if for any invariant subset $F \in \mathfrak{F}$, either $\mathbb{P}(F) = 1$ or $\mathbb{P}(F) = 0$. Throughout the paper, we will assume that $\mathbb{P}$ is ergodic.

2.1. Measurable linear skew-product semidynamical systems

We consider a separable Banach space X with dual space $X^{*}$.

We write $\mathbb{R}^{+}$ for $[0, \infty)$. By a measurable linear skew-product semidynamical system or semiflow, $\Phi = ((U_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_t)_{t\in\mathbb{R}})$ on X covering a metric dynamical system $(\theta_{t})_{t \in \mathbb{R}}$ we understand a $(\mathfrak{B}(\mathbb{R}^{+}) \otimes \mathfrak{F} \otimes \mathfrak{B}(X), \mathfrak{B}(X))$-measurable mapping

\begin{equation*} [\mathbb{R}^{+} \times \Omega \times X \ni (t,{\omega},u) \mapsto U_{\omega}(t)\,u \in X ] \end{equation*}

satisfying

(2.1)\begin{equation} \begin{array}{lr} U_{\omega}(0) = \mathrm{Id}_{X} & \textrm{for\, each}\,{\omega} \in \Omega, \\ U_{\theta_{s}{\omega}}(t) \circ U_{\omega}(s)= U_{\omega}(t+s) & \textrm{for\, each} \,{\omega} \in \Omega \textrm{ and } t,\,s \in \mathbb{R}^{+}, \\ {\left[X \ni u \mapsto U_{\omega}(t)u \in X \right]} \in \mathcal{L}(X) & \textrm{for\, each}\,{\omega} \in \Omega \textrm{ and } t \in \mathbb{R}^{+}. \end{array} \end{equation}

Sometimes we write simply $\Phi = ((U_{\omega}(t)), (\theta_t))$. Eq. (2.1) is called the cocycle property.

For ${\omega} \in \Omega$, by an entire orbit of U_ω, we understand a mapping $v_{\omega} \colon \mathbb{R} \to X$ such that $v_{\omega}(s + t) = U_{\theta_{s}{\omega}}(t)\, v_{\omega}(s)$ for each $s \in \mathbb{R}$ and $t\geq 0$.

Next we introduce the dual of Φ in the case in which $X^{*}$ is separable. $\langle \cdot, \cdot \rangle$ will stand for the duality pairing: $\langle u, u^{*} \rangle$ is the action of a functional $u^{*} \in X^{*}$ on a vector $u \in X$. For ${\omega} \in \Omega$, $t \in \mathbb{R}^{+}$ and $u^{*} \in X^*$, we define $U^{*}_{\omega}(t)\,u^{*}$ by

\begin{equation*} \langle u, U^{*}_{\omega}(t)\,u^{*} \rangle = \langle U_{\theta_{-t}{\omega}}(t)\,u , u^{*} \rangle \qquad \text{for each}\, u \in X \end{equation*}

(in other words, $U^{*}_{\omega}(t)$ is the mapping dual to $U_{\theta_{-t}{\omega}}(t)$).

As explained in [22], since $X^*$ is separable, the mapping

\begin{equation*} [\mathbb{R}^{+} \times \Omega \times X^{*} \ni (t,{\omega},u^{*}) \mapsto U^{*}_{\omega}(t)\,u^{*} \in X^{*} ] \end{equation*}

is $(\mathfrak{B}(\mathbb{R}^{+}) \otimes \mathfrak{F} \otimes \mathfrak{B}(X^{*}), \mathfrak{B}(X^{*}))$-measurable. The measurable linear skew-product semidynamical system $\Phi^{*} = ((U^{*}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}},(\theta_{-t})_{t\in\mathbb{R}})$ on $X^{*}$ covering $(\theta_{-t})_{t \in \mathbb{R}}$ will be called the dual of Φ. The cocycle property for the dual takes the form

\begin{equation*} U^{*}_{\theta_{-t}{\omega}}(s) \circ U^{*}_{\omega}(t)= U^{*}_{\omega}(t+s) \qquad \textrm{for each} \,{\omega} \in \Omega \,\textrm{and}\, t,\,s \in \mathbb{R}^{+}. \end{equation*}

Let $\Omega_0 \in \mathfrak{F}$. A family $\{E({\omega})\}_{{\omega} \in \Omega_0}$ of l-dimensional vector subspaces of X is measurable if there are $(\mathfrak{F}, \mathfrak{B}(X))$-measurable functions $v_1, \dots, v_l \colon \Omega_0 \to X$ such that $(v_1({\omega}), \dots, v_l({\omega}))$ forms a basis of $E({\omega})$ for each ${\omega} \in \Omega_0$.

Let $\{E({\omega})\}_{{\omega} \in \Omega_0}$ be a family of l-dimensional vector subspaces of X, and let $\{F({\omega})\}_{{\omega} \in \Omega_0}$ be a family of l-codimensional closed vector subspaces of X, such that $E({\omega}) \oplus F({\omega}) = X$ for all ${\omega} \in \Omega_0$. We define the family of projections associated with the decomposition $E({\omega}) \oplus F({\omega}) = X$ as $\{P({\omega})\}_{{\omega} \in \Omega_0}$, where $P({\omega})$ is the linear projection of X onto $F({\omega})$ along $E({\omega})$, for each ${\omega} \in \Omega_0$.

The family of projections associated with the decomposition $E({\omega}) \oplus F({\omega}) = X$ is called strongly measurable if for each $u \in X$ the mapping $[\Omega_0 \ni {\omega} \mapsto P({\omega})u \in X ]$ is $(\mathfrak{F}, \mathfrak{B}(X))$-measurable.

We say that the decomposition $E({\omega}) \oplus F({\omega}) = X$, with $\{E({\omega})\}_{{\omega} \in \Omega_0}$ finite-dimensional, is invariant if Ω₀ is invariant, $U_{\omega}(t)E({\omega}) = E(\theta_{t}{\omega})$ and $U_{\omega}(t)F({\omega}) \subset F(\theta_{t}{\omega})$, for each $t \in \mathbb{R}^+$.

A strongly measurable family of projections associated with the invariant decomposition $E({\omega}) \oplus F({\omega}) = X$ is referred to as tempered if

\begin{equation*} \lim\limits_{t \to \pm\infty} \frac{\ln{\|P(\theta_{t}{\omega})\|}}{t} = 0 \qquad \mathbb{P}\text{-a.e. on}\ \Omega_0. \end{equation*}

Remark 2.1.

In the present paper, instead of the family $\{P({\omega})\}_{{\omega} \in \Omega_0}$ of projections onto $F({\omega})$ along $E({\omega})$, we usually employ the family $\{\widetilde{P}({\omega})\}_{{\omega} \in \Omega_0}$ of projections onto $E({\omega})$ along $F({\omega})$ which are related by $\widetilde{P}({\omega}) = \mathrm{Id}_X - P({\omega})$. It is straightforward that for the definition of strong measurability we can check the $(\mathfrak{F}, \mathfrak{B}(X))$-measurability of the mapping $[\Omega_0 \ni {\omega} \mapsto \widetilde{P}({\omega}) \, u \in X ]$ for each $u \in X$. Similarly, due to the inequalities $1 \le {\lVert\widetilde{P}({\omega}) \rVert} \le 1 + {\lVert P({\omega}) \rVert}$ and $1 \le {\lVert P({\omega}) \rVert} \le 1 + {\lVert\widetilde{P}({\omega}) \rVert}$, a strongly measurable family of projections associated is tempered if and only if

\begin{equation*} \lim\limits_{t \to \pm \infty} \frac{\ln{\lVert\widetilde{P}(\theta_{t}{\omega})\rVert}}{t} = 0 \qquad \mathbb{P}\text{-a.e.\ on}\, \Omega_0. \end{equation*}

2.2. Ordered Banach spaces

Let X be a Banach space with norm $\|\cdot\|$. We say that X is an ordered Banach space if there is a closed convex cone, that is, a nonempty closed subset $X^+\subset X$ satisfying

1. (O1) $X^++X^+\subset X^+$.

2. (O2) $\mathbb{R}^+ X^+\subset X^+$.

3. (O3) $X^+\cap (-X^+)=\{0\}$.

Then a partial ordering in X is defined by

\begin{equation*}\begin{array}{ll} u \leq v & \Longleftrightarrow \quad v -u\in X_+;\\ u \lt v & \Longleftrightarrow \quad v-u\in X_+\, \text{and}\, u\neq v. \end{array}\end{equation*}

The cone $X^+$ is said to be reproducing if $X^+ - X^+ = X$. The cone $X^+$ is said to be normal if the norm of the Banach space X is semimonotone, i.e. there is a positive constant k > 0 such that $0\leq u\leq v$ implies $\|u\|\leq k\,\|v\|$. In such a case, the Banach space can be renormed so that for any u, $v\in X$, $0\leq u\leq v$ implies $\|u\|\leq\|v\|$ (see Schaefer [32, V.3.1, p. 216]). Such a norm is called monotone.

For an ordered Banach space X denote by $(X^{*})^{+}$ the set of all $u^{*} \in X^{*}$ such that $\langle u, u^{*} \rangle \ge 0$ for all $u \in X^{+}$. The set $(X^{*})^{+}$ has the properties of a cone, except that $(X^{*})^{+} \cap (-(X^{*})^{+}) = \{0\}$ need not be satisfied (such sets are called wedges).

If $(X^{*})^{+}$ is a cone we call it the dual cone. This happens, for instance, when $X^{+}$ is total (that is, $X^{+}- X^{+}$ is dense in X, which in particular holds when $X^+$ is reproducing and this will be one of our hypothesis). Nonzero elements of $X^{+}$ (resp. of $(X^{*})^{+}$) are called positive.

2.3. Assumptions

Throughout the paper, we will assume that X is an ordered separable Banach space with $\dim X\geq 2$, dual space $X^{*}$ and positive cone $X^+$ normal and reproducing.

Let $\Phi = ((U_{\omega}(t)), (\theta_t))$ be a measurable linear skew-product semidynamical system on X covering an ergodic metric dynamical system $(\theta_{t})$ on ${(\Omega,\mathfrak{F},\mathbb{P})}$. We now list assumptions we will make at various points in the sequel.

1. (A1) (Integrability) The functions

   \begin{equation*} \bigl[\Omega \ni {\omega} \mapsto \sup\limits_{0 \le s \le 1} {ln^{+}{\|U_{\omega}(s)\|}} \in [0,\infty)\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}\,\, \text{and} \end{equation*}

   \begin{equation*} \bigl[\Omega \ni {\omega} \mapsto \sup\limits_{0 \le s \le 1}{ln^{+}{\|U_{\theta_{s}{\omega}}(1-s)\|}} \in [0,\infty)\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}. \end{equation*}

2. (A2) (Positivity) For any ${\omega} \in \Omega$, $t \ge 0$ and $u_1, u_2 \in X$ with $u_1 \le u_2$

   \begin{equation*} U_{\omega}(t)\,u_1 \le U_{\omega}(t)\,u_2. \end{equation*}

For a measurable linear skew-product semidynamical system Φ satisfying (A2), we say that an entire orbit v_ω of U_ω is positive if $v_{\omega}(t) \in X^{+} \setminus \{0\}$ for all $t \in \mathbb{R}$.

Next we introduce focusing condition (A3) in the following way.

1. (A3) (Focusing) (A2) is satisfied and there are $\mathbf e\in X^+$ with $\|\mathbf e\|=1$ and $U_{\omega}(1)\,\mathbf e\neq 0 $ for all ${\omega}\in\Omega$, and an $(\mathfrak{F},\mathfrak{B}(\mathbb{R}))$-measurable function $\varkappa\colon\Omega\to [1,\infty)$ with $ln^{+}\ln\varkappa\in L_1(\Omega,\mathfrak{F},\mathbb{P})$ such that for any ${\omega}\in\Omega$ and any nonzero $u\in X^+$

   • • $U_{\omega}(1)\,u=0$, or

   • • $U_{\omega}(1)\,u\neq 0$ and there is $\beta({\omega},u) \gt 0$ with the property that

     \begin{equation*} \beta({\omega},u)\,\mathbf e\leq U_{\omega}(1)\,u\leq \varkappa({\omega})\,\beta({\omega},u)\,\mathbf e. \end{equation*}

It should be remarked that our condition (A3) is weaker than condition (A3) in [22].

Remark 2.2.

Under (A3) for $u \in X^{+}$ the following dichotomy holds:

• • $U_{\omega}(t)\, u = 0$ for all $t \ge 1$, or

• • $U_{\omega}(t)\, u \gt 0$ for all $t \ge 1$.

When the dual space $X^*$ is separable, we consider the dual of Φ, as explained in §2.1, $\Phi^{*} = ((U^{*}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}},(\theta_{-t})_{t\in\mathbb{R}})$ on $X^{*}$ covering $(\theta_{-t})_{t \in \mathbb{R}}$, and the following assumptions for it.

1. (A1)* (Integrability) The functions

   \begin{equation*} \bigl[\Omega \ni {\omega} \mapsto \sup\limits_{0 \le s \le 1} {ln^{+}{\|U_{\omega}^*(s)\|}} \in [0,\infty)\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}\,\, \text{and} \end{equation*}

   \begin{equation*} \bigl[\Omega \ni {\omega} \mapsto \sup\limits_{0 \le s \le 1}{ln^{+}{\|U_{\theta_{s}{\omega}}^*(1-s)\|}} \in [0,\infty)\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}. \end{equation*}

2. (A2)* (Positivity) For any ${\omega} \in \Omega$, $t \ge 0$ and $u^{*}_1, u^{*}_2 \in X^*$ with $u^{*}_1 \le u^{*}_2$

   \begin{equation*} U^{*}_{\omega}(t)\,u^{*}_1 \le U^{*}_{\omega}(t)\,u^{*}_2. \end{equation*}

   Notice that in this case, as explained in [22], (A1)* follows from (A1) and (A2)* follows from (A2).

3. (A3)* (Focusing for $X^*$) (A2)* is satisfied and there are $\mathbf{e}^*\in (X^*)^+$ with $\langle \mathbf e,\mathbf e^*\rangle=1$ and $\| \mathbf e^*\|=1$ and an $(\mathfrak{F},\mathfrak{B}(\mathbb{R}))$-measurable function $\varkappa^*\colon \Omega\to[1,\infty)$ with $ln^{+}\ln\varkappa^*\in L_1(\Omega,\mathfrak{F},\mathbb{P})$ such that for any ${\omega}\in\Omega$ there holds $U_{\omega}^*(1)\, \mathbf e^* \ne 0$, and for any ${\omega}\in\Omega$ and any nonzero $u^*\in (X^*)^+$ there is $\beta^*({\omega},u^*) \gt 0$ with the property that

   \begin{equation*} \beta^*({\omega},u)\,U_{\omega}^*(1)\,\mathbf{e}^*\leq U_{\omega}^*(1)\,u^*\leq \varkappa^*({\omega})\,\beta^*({\omega},u^*)\,U^*_{\omega}(1)\,\mathbf e^*. \end{equation*}

Condition (A3)* follows from (A3), as proved in [18, Proposition 2.4],

Remark 2.3.

We can replace time 1 with some nonzero $T\in\mathbb{R}^+$ in (A1), (A3), and (A1)*, (A3)*.

2.4. Generalized exponential separation

In this subsection, we recall the definition and existence of a family of generalized principal Floquet subspaces, and of a generalized exponential separation of type II, introduced and proved in [18]. They are important for the cases in which the previous concepts given in [22] do not apply, as measurable linear skew-product semidynamical systems induced by delay differential equations.

Definition 2.4.

Let $\Phi = ((U_{\omega}(t)), (\theta_t))$ be a measurable linear skew-product semidynamical system on a Banach space X ordered by a normal reproducing cone $X^{+}$. A family of one-dimensional subspaces $\{E_1({\omega})\}_{{\omega} \in \widetilde{\Omega}}$ of X is called a family of generalized principal Floquet subspaces of Φ if $\widetilde{\Omega} \subset \Omega$ is invariant, $\mathbb{P}(\widetilde{\Omega}) = 1$, and

1. (i) $E_1({\omega}) = \text{span}{\{w({\omega})\}}$ with $w \colon \widetilde{\Omega} \to X^+ \setminus \{0\}$ being $(\mathfrak{F}, \mathfrak{B}(X))$-measurable,

2. (ii) $U_{\omega}(t) \,E_1({\omega}) = E_1(\theta_{t}{\omega})$, for any ${\omega} \in \widetilde{\Omega}$ and any t > 0,

3. (iii) there exists $\widetilde{\lambda} \in [-\infty, \infty)$ such that

   \begin{equation*} \widetilde{\lambda} = \lim_{t\to\infty} \frac{\ln{\|U_{\omega}(t)\,w({\omega})\|}}{t} \quad \text{for each}\, {\omega} \in \widetilde{\Omega}, \end{equation*}

4. (iv) for each ${\omega}\in\widetilde\Omega$ and each $ u\in X^+$ with $U_{\omega}(1)\,u\neq 0$

   (2.2)\begin{equation} \limsup_{t\to\infty} \frac{\ln{\|U_{\omega}(t)\,u\|}}{t} \le \widetilde{\lambda}. \end{equation}

$\widetilde{\lambda}$ is called the generalized principal Lyapunov exponent of Φ associated with the generalized principal Floquet subspaces $\{E_1({\omega})\}_{{\omega}\in\widetilde{\Omega}}$.

It should be remarked that a family of generalized principal Floquet subspaces need not be unique: take $U_{\omega}(t) = \mathrm{Id}_X$ for all $\omega \in \Omega$ and all $t \ge 0$; then for any nonzero $w \in X^{+}$ the assignment $E_1(\omega) = \text{span}{\{w\}}$ satisfies the definition. For conditions guaranteeing uniqueness, see theorem 2.5.

Under assumptions (A1) and (A3), (i)–(v) of the next theorem, proved in [18, Theorem 3.10], show the existence of an invariant set $\widetilde\Omega_1$ of full measure $\mathbb{P}(\widetilde\Omega_1)=1$, a family of generalized Floquet subspaces $\{E_1({\omega})\}_{{\omega} \in \widetilde\Omega_1}$, with $E_1({\omega}) = \text{span}\{w({\omega})\}$, and generalized principal Lyapunov exponent $\widetilde{\lambda}_1$. Notice that in [18], a standing assumption is that not only X but also its dual $X^{*}$ is a separable Banach space. However, the next result considers measurable linear skew-product semidynamical systems taking values in X only, so no assumptions on $X^{*}$ are needed.

Theorem 2.5.

Under assumptions (A1) and (A3), there is an invariant set $\bar\Omega_1$ and an $(\mathfrak{F},\mathfrak{B}(X))$-measurable function $w\colon\bar\Omega_1\to X^+,\,{\omega}\mapsto w({\omega})$, $\|w({\omega})\|=1$ for each ${\omega}\in \bar\Omega_1$, such that

1. (i) for each ${\omega}\in\bar\Omega_1$ and $t\geq 0$,

   \begin{equation*} w(\theta_t{\omega})=\frac{U_{\omega}(t)\,w({\omega})}{\|U_{\omega}(t)\,w({\omega})\|}; \end{equation*}

2. (ii) for each ${\omega}\in\bar\Omega_1$, the map $w_{\omega}\colon \mathbb{R}\to X^+$ defined by

   \begin{equation*} w_{\omega}(t) = \begin{cases} \frac{w(\theta_t{\omega})}{\|U_{\theta_t{\omega}}(-t) \, w(\theta_t{\omega})\|} & \quad \text{for}\ t\leq 0,\\ U_{\omega}(t)\,w({\omega})& \quad \text{for}\ t\geq 0; \end{cases} \end{equation*}

   is a positive entire orbit of U_ω, unique up to multiplication by a positive scalar;

3. (iii) there are an invariant set $\widetilde\Omega_1 \subset \bar\Omega_1$ with $\mathbb{P}(\widetilde\Omega_1) = 1$ and a $\widetilde\lambda_1 \in [-\infty,\infty)$ such that

   \begin{equation*} \widetilde\lambda_1 = \lim_{t\to\pm\infty} \frac{1}{t}\ln\|w_{\omega}(t)\| = \int_\Omega \ln\|w_{{\omega}'}(1)\|\,d\mathbb{P}({\omega}') \end{equation*}

   for each ${\omega} \in \widetilde\Omega_1$;

4. (iv) for each ${\omega} \in \widetilde\Omega_1$ and $u \in X^+$ with $U_{\omega}(1) \,u \neq 0$

   \begin{equation*} \lim_{t\to\infty} \frac{1}{t}\ln\|U_{\omega}(t)\,u\| = \widetilde\lambda_1; \end{equation*}

5. (v) for each ${\omega} \in \widetilde\Omega_1$ and $u \in X$

   \begin{equation*} \limsup_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}(t)\,u\|\leq \widetilde\lambda_1; \end{equation*}

   that is, $\{E_1({\omega})\}_{{\omega} \in \widetilde\Omega_1}$, with $E_1({\omega}) = \text{span}\{w({\omega})\}$, is a family of generalized principal Floquet subspaces, and $\widetilde\lambda_1$ is the generalized principal Lyapunov exponent;

6. (vi) for each ${\omega} \in \widetilde\Omega_1$,

   \begin{equation*} \lim_{t\to\infty} \frac{1}{t} \ln{\sup \{\, {\lVert U_{\omega}(t) \, u\rVert} : u \in X^{+} ,\,\|u\|\leq 1}\} = \widetilde{\lambda} _1; \end{equation*}

7. (vii) there exists σ > 0 such that, for any ${\omega} \in \widetilde{\Omega}_1$,

   \begin{equation*}\begin{array}{ll} &\!\!\!\!\!\!\!\!\!\!\limsup\limits_{t \to \infty} \frac{1}{t} \ln\Bigl(\sup{\Bigl\{ \Bigl\lVert \frac{U_{\theta_{-t}{\omega}}(t) u}{{\lVert U_{\theta_{-t}{\omega}}(t) u\rVert}} - w({\omega}) \Bigr\rVert : u \in X^{+}, U_{\theta_{-t}{\omega}}(1) u \ne 0} \Bigr\} \Bigr) \le -\sigma,\\ &\!\!\!\!\!\!\!\!\!\!\limsup\limits_{t \to \infty} \frac{1}{t} \ln\Bigl(\sup{\Bigl\{\, \Bigl\lVert \frac{U_{\omega}(t) \, u}{{\lVert U_{\omega}(t) \, u\rVert}} - w(\theta_{t}{\omega}) \Bigr\rVert : u \in X^{+},\, U_{\omega}(1) \, u \ne 0} \, \Bigr\} \Bigr) \le -\sigma. \end{array}\end{equation*}

Note that in view of the uniqueness of positive entire solutions stated in (ii), the family obtained of generalized principal Floquet subspaces is unique.

Proof. Parts (i)–(v) are [18, Theorem 3.10]. To prove part (vi), notice that in the proof of [18, Theorem. 3.10] on p. 6175 the inequality

\begin{equation*} {\lVert U_{\omega}(t) \, u\rVert} \le \frac{\varkappa({\omega}) \beta({\omega}, u)}{\beta({\omega}, w({\omega}))} \,{\lVert U_{\omega}(t) \, w({\omega})\rVert}, \quad t \ge 1, \end{equation*}

holds for all ${\omega} \in \widetilde{\Omega}_1$, where $\varkappa(\cdot)$ and $\beta(\cdot, \cdot)$ are as in (A3). For a fixed ${\omega} \in \widetilde{\Omega}_1$, since $U_{\omega}(1)$ is linear bounded, $\sup\{\, \beta({\omega}, u) : u \in X^{+},\,U_{\omega}(1) \, u \ne 0,\, \|u\|\leq 1 \,\} \lt \infty$. Consequently,

\begin{equation*}\begin{array}{l} \limsup\limits_{t\to\infty} \frac{1}{t} \ln{\sup \{\, {\lVert U_{\omega}(t)\,u\rVert} : u \in X^{+} \,\}} \\ \qquad = \limsup\limits_{t\to\infty} \frac{1}{t} \ln{\sup \{\, {\lVert U_{\omega}(t)\,u\rVert} : u \in X^{+},\, \|u\|\leq 1}\,\} \le \widetilde{\lambda}_1. \end{array}\end{equation*}

The other inequality is straightforward by theorem 2.5 (iv), and finally, part (vii) follows along the lines of the proof of [22, Proposition 5.5] (for a fairly similar reasoning, see p. 6173 below [18, Proposition 3.9]).

Definition 2.6.

Let $\Phi = ((U_{\omega}(t)), (\theta_t))$ be a measurable linear skew-product semidynamical system on a Banach space X ordered by a normal reproducing cone $X^{+}$. Φ is said to admit a generalized exponential separation of type II if there are a family of generalized principal Floquet subspaces $\{E_1({\omega})\}_{{\omega} \in \widetilde{\Omega}}$, and a family of one-codimensional closed vector subspaces $\{F_1({\omega})\}_{{\omega} \in \widetilde{\Omega}}$ of X, satisfying

1. (i) $F_1({\omega})\cap X^+=\{u\in X^+ : U_{\omega}(1)\,u=0\}$,

2. (ii) $X=E_1({\omega})\oplus F_1({\omega})$ for any ${\omega}\in\widetilde{\Omega}$, where the decomposition is invariant, and the family of projections associated with the decomposition is strongly measurable and tempered,

3. (iii) there exists $\widetilde{\sigma}\in (0,\infty]$ such that

   \begin{equation*} \lim_{t\to\infty}\frac{1}{t}\ln \frac{\|U_{\omega}(t)|_{F_1({\omega})}\|}{\|U_{\omega}(t)\,w({\omega})\|}=-\widetilde{\sigma} \end{equation*}

   for each ${\omega}\in\widetilde{\Omega}$.

It is said that $\{E_1(\cdot),F_1(\cdot),\widetilde{\sigma}\}$ generates a generalized exponential separation of type II.

Remark 2.7.

The following example shows that condition (i) in definition 2.6 does not follow from (ii) and (iii) and therefore cannot be removed because it is needed throughout the paper. Put Ω to be a singleton, $X = {\mathbb{R}}^2$with the standard cone, and

\begin{equation*} U(t) = \begin{pmatrix} 1 & e^t - 1 \\ 0 & e^t \end{pmatrix}, \textit{ i.e.} \,\, U(t) = e^{t A}, \text{ where}\,\, A = \begin{pmatrix} 0 & 1 \\ 0 & 1 \end{pmatrix}. \end{equation*}

As $e^t - 1 \ge 0$ for all $t \ge 0$, the dynamical system Φ is positive. Put $E_1 = \text{span}\{(1 \ 1)^{\top}\}$, and $F_1 = \text{span}\{(1 \ 0)^{\top}\}$.

The subspace E ₁ is a generalized principal Floquet subspace. Indeed, it is straightforward that properties (i) and (ii) in definition 2.4 are satisfied, with $w = \frac{1}{\sqrt{2}}(1 \ 1)^{\top}$. Further, one has

\begin{equation*} \lim\limits_{t \to \infty} \frac{\ln{{\lVert U(t) w\rVert}}}{t} = 1. \end{equation*}

Finally, for any nonzero $ \textit{v} \in \textit{X}$ we have either

\begin{equation*}\lim_{t\rightarrow\infty}\frac{\ln{\Arrowvert U(t)v\Arrowvert}}t=1\,\,(\text{if }\,v\not\in F_1)\quad\text{or}\quad\lim_{t\rightarrow\infty}\frac{\ln{\Arrowvert U(t)v\Arrowvert}}t=0\,\,(\text{if }\,v\in F_1).\end{equation*}

Therefore, E ₁ is a generalized principal Floquet subspace, and its associated generalized principal Lyapunov exponent $\widetilde{\lambda}$ equals 1.

Observe that (ii) and (iii) in definition 2.6 are satisfied, whereas, for example, $(1 \ 0)^{\top} \in F_1 \cap X^{+}$ but $U(1) (1 \ 0)^{\top} \ne 0$.

As stated in the introduction, sometimes a less general concept is used, namely, that of generalized exponential separation of type I. Then in definition 2.6(i), we would have just $F_1({\omega}) \cap X^+ = \{0\}$. Note that the only difference is that now $F_1({\omega})$ may contain those positive vectors u > 0 for which $U_{\omega}(1)\,u=0$. For a theory of generalized exponential separation of type I (called there generalized exponential separation), see the series of papers [22–24].

We include for completeness an example of a random semidynamical system, generated by a scalar linear random delay differential equation, which admits a generalized exponential separation of type II but not of type I. Recall that condition (i) in type I is $F_1(\omega)\cap X^+=\{0\}$. We claim that, in this case, $U_{\omega}(t)\,u\neq 0$ for each $t\in\mathbb{R}^+$ and $u\in X^+\setminus \{0\}$. Note that u can be written as $u=u_1+u_2$ with $u_1=\lambda_{\omega}(u)\,w({\omega})$ for each ${\omega}\in\widetilde{\Omega}$ with $\lambda_{\omega}(u) \gt 0$ and $u_2\in F_1({\omega})$. Then

\begin{equation*} \frac{{\lVert U_{\omega}(t)\,u\rVert}}{{\lVert U_{\omega}(t)\,w({\omega})\rVert}}=\frac{{\lVert\lambda(u)\,U_{\omega}(t)\,w({\omega})\rVert}}{{\lVert U_{\omega}(t)\,w({\omega})\rVert}} + \frac{{\lVert U_{\omega}(t)\,u_2\rVert}}{{\lVert U_{\omega}(t)\,w({\omega})\rVert}}=\lambda_{\omega}(u) + \frac{{\lVert U_{\omega}(t)\,u_2\rVert}}{{\lVert U_{\omega}(t)\,w({\omega})\rVert}}, \end{equation*}

which together with definition 2.6 (iii) shows that $U_{\omega}(t)\,u\neq 0$, as stated.

Example 2.8.

We put $\Omega=S^1=\mathbb{R}/\mathbb{Z}$ the unit circle and, as in [18, Section 5], we consider the separable Banach space $X=\mathbb{R}\times L_2([-1,0],\mathbb{R})$ with the norm

\begin{equation*}\|u\|_X=|u_1|+\|u_2\|_2=|u_1|+\left(\int_{-1}^0 |u_2(s)|^2\,ds\right)^{\!\!1/2}\, \text{for\, any}\, u=(u_1,u_2) \in X.\end{equation*}

Next, we take the 1-periodic function: $b_0(t)=0$ if $t\in[0,1/2)$ and $b_0(t)=1$ if $t\in [1/2,1)$. As usual, the equation $z'(t)=b_0(t)\,z(t-1)$ can be included in a family of the form $z'(t)=b(\theta_t\,{\omega})\,z(t-1)$, ${\omega}\in \Omega$, or equivalently $z'(t)=b(t+\varphi)\,z(t-1)$, $\varphi\in S^1=\mathbb{R}/\mathbb{Z}$. The initial value problem

(2.3)\begin{equation} \left\{\begin{array}{l} z'(t)=b(\theta_t\,{\omega})\,z(t-1),\\ z(t)=u_2(t),\quad t\in[-1,0),\\ z(0)=0, \end{array}\right. \end{equation}

with initial data $u_0=(0, u_2)$ given by the step function: $u_2(t)=1$ if $t\in[-1, -1/2)$ and $u_2(t)=0$ if $t\in[-1/2,0)$ induces a measurable linear skew-product semidynamical system on $S^1\times X$, which admits a generalized exponential separation of type II, as shown in [18, Theorem 5.8]. Finally, it is easy to check that $U_{\omega}(1)\,u_0= 0$ for ω corresponding to the original equation and then, as explained above, an exponential separation of type I cannot hold because $u_0\in X^+ \setminus \{0\}$.

The next theorem, proved in [18, Theorem 4.6] and included here for completeness, shows the existence of a generalized exponential separation of type II. We maintain the notation of theorem 2.5.

Theorem 2.9.

Assume that $X^*$ is separable. Under assumptions (A1) and (A3), let $\widetilde\lambda_1$ be the generalized principal Lyapunov exponent and assume that $\widetilde\lambda_1 \gt -\infty$. Then there is an invariant set $\widetilde\Omega_0\subset \widetilde \Omega_1$ of full measure $\mathbb{P}(\widetilde\Omega_0)=1$ such that

1. (i) The family $\{P({\omega})\}_{{\omega}\in\widetilde\Omega_0}$ of projections associated with invariant decomposition $ E_1({\omega})\oplus F_1({\omega})=X$ is strongly measurable and tempered.

2. (ii) $F_1({\omega})\cap X^+=\{u\in X^+ : U_{\omega}(1)\,u=0\}$ for any ${\omega}\in\widetilde\Omega_0$.

3. (iii) For any ${\omega}\in\widetilde\Omega_0$ and $u\in X\setminus F_1({\omega})$ with $U_{\omega}(1)\,u\neq 0$ there holds

   \begin{equation*} \lim_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}(t)\|=\lim_{t\to\infty}\frac{1}{t}\ln \|U_{\omega}(t)\,u\|=\widetilde{\lambda}_1.\end{equation*}

4. (iv) There exists $\widetilde\sigma\in(0,\infty]$ and $\widetilde\lambda_2=\widetilde\lambda_1-\widetilde\sigma$ such that

   \begin{equation*} \lim_{t\to\infty}\frac{1}{t}\ln \frac{\|U_{\omega}(t)|_{F_1({\omega})}\|}{\|U_{\omega}(t)\,w({\omega})\|}=-\widetilde{\sigma}\end{equation*}

   and

   \begin{equation*}\lim_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}(t)|_{F_1({\omega})}\|=\widetilde\lambda_2\end{equation*}

   for each ${\omega}\in\widetilde\Omega_0$.

That is, Φ admits a generalized exponential separation of type II.

3. Generalized exponential separation as a consequence of Oseledets decomposition

Let $\Phi = ((U_{\omega}(t)), (\theta_t))$ be a measurable linear skew-product semidynamical system on a separable Banach space X with $\dim{X} \ge 2$, covering a metric dynamical system $(\theta_{t})$. We always assume that (A1) is satisfied, that is, the functions $\bigl[\Omega \ni {\omega} \mapsto \sup\limits_{0 \le s \le 1} {ln^{+}{\|U_{\omega}(s)\|}} \in [0,\infty)\bigr]$ and $\bigl[\Omega \ni {\omega} \mapsto \sup\limits_{0 \le s \le 1} {ln^{+}{\|U_{\theta_{s}{\omega}}(1-s)\|}} \in [0,\infty)\bigr]$ belong to $L_1{(\Omega,\mathfrak{F},\mathbb{P})}$. It follows then from Kingman’s subadditive ergodic theorem that there exists $\lambda_{\mathrm{top}} \in [-\infty, \infty)$ such that

\begin{equation*} \lim\limits_{t \to \infty} \frac{\ln{{\lVert U_{\omega}(t)\rVert}}}{t} = \lambda_{\mathrm{top}} \end{equation*}

for $\mathbb{P}$-a.e. ${\omega} \in \Omega$. $\lambda_{\mathrm{top}}$ is called the top Lyapunov exponent.

Our starting point is the semi-invertible operator Oseledets-type theorem [19, Theorem 3.4], based on the results in [8]. We state here its parts used in the sequel.

Theorem 3.1.

Let ${(\Omega,\mathfrak{F},\mathbb{P})}$ be a Lebesgue space. Assume that $U_{\omega}(t_0)$ is compact for all ${\omega} \in \Omega$ and some $t_0\geq 1$. Let $\lambda_{\mathrm{top}} \gt -\infty$. Then there exist:

• • an invariant $\Omega' \subset \Omega$, with $\mathbb{P}(\Omega') = 1$,

• • an invariant measurable decomposition $X = E({\omega}) \oplus F({\omega})$, ${\omega} \in \Omega'$, such that the family of projections associated with it is tempered,

• • $\lambda_2 \in [- \infty, \lambda_{\mathrm{top}})$

with the properties that

1. (i) $E({\omega})$ has constant finite dimension, l, on $\Omega'$,

2. (ii) for each ${\omega} \in \Omega'$ and each t > 0, $U_{\omega}(t)|_{E({\omega})}$ is a linear isomorphism onto $E(\theta_{t}{\omega})$,

3. (iii) for any ${\omega} \in \Omega'$

   \begin{equation*} \lim_{t \to \infty} \frac{\ln{{\lVert U_{\omega}(t)|_{E({\omega})}\rVert}}}{t} = \lim_{t \to \infty} \frac{\ln{{\lVert(U_{\omega}(t)|_{E({\omega})})^{-1}\rVert}^{-1}}}{t} = \lambda_{\mathrm{top}}, \end{equation*}

4. (iv) for any ${\omega} \in \Omega'$

   \begin{equation*} \lim_{t \to \infty} \frac{\ln{{\lVert U_{\omega}(t)|_{F({\omega})}\rVert}}}{t} = \lambda_2. \end{equation*}

The measurable invariant decomposition satisfying the above is unique.

When $\dim{X} \lt \infty$ it is possible that $E({\omega}) = X$ for all ${\omega} \in \Omega'$. In that case, (iv) is vacuous.

Below, we apply some ideas from Blumenthal’s paper [4], elaborated later in Varzaneh and Riedel [34]. As in [16, Subsection 4.0.4], define the l-dimensional volume function $\text{vol} \colon X^l \to {\mathbb{R}}$ by the formula

(3.1)\begin{equation} \text{vol}(v_1, \ldots, v_l) := {\lVert v_l\rVert} \, \prod\limits_{i = 1}^{l - 1} \text{dist}(v_i, \text{span}{\{v_{i + 1}. \ldots, v_l\}}), \quad v_1, \ldots, v_l \in X. \end{equation}

Proposition 3.2.

Under the assumptions and notations of theorem 3.1, for any ${\omega} \in \Omega'$ and any basis $\{v_1, \ldots, v_l\}$ of $E({\omega})$ there holds

\begin{equation*} \lim_{n \to \infty} \frac{\ln{\text{vol}(U_{\omega}(n) \, v_1, \ldots, U_{\omega}(n) \, v_l)}}{n} = l \, \lambda_{\mathrm{top}}. \end{equation*}

Proof. See [34, Thm. 1.21(v)].

The following result is known as one of the Krein–Shmulyan theorems (see [1, Theorem 2.2]).

Lemma 3.3.

Let $X^{+}$ be a reproducing cone in a Banach space X with norm ${\lVert\cdot\rVert}$. Then there exists $K \ge 1$ with the property that for each $u \in X$ there are $u^{+}, u^{-} \in X^{+}$ such that $u = u^{+} - u^{-}$, ${\lVert u^{+}\rVert} \le K {\lVert u\rVert}$ and ${\lVert u^{-}\rVert} \le K {\lVert u\rVert}$.

Theorem 3.4.

Under the assumptions and notations of theorem 3.1, there holds $E({\omega}) \cap X^{+} \varsupsetneq \{0\}$ $\mathbb{P}$-a.e. on Ω.

Proof. It goes along the lines of the proof of Theorem 3.5 in [22].

From now on until the end of the present section we assume that, whenever we talk about generalized principal Floquet subspaces, the vectors $w({\omega}) \in X^{+} \setminus \{0\}$ spanning the one-dimensional subspace are chosen to be unit vectors.

Lemma 3.5.

Under the assumptions and notations of theorem 2.5, $\lambda_{\mathrm{top}} = \widetilde{\lambda}_1$.

Proof. The inequality $\widetilde{\lambda} _1\le \lambda_{\mathrm{top}}$ is straightforward. In order to prove the other one, observe that

\begin{align*} {\lVert U_{\omega}(t)\rVert} & = \sup\{\, \| U_{\omega}(t) (u^{+} - u^{-}) \|: {\lVert u^{+} - u^{-}\rVert} \le 1 \,\} \\ & \le 2\, K \sup\{\, \| U_{\omega}(t) \, u \| : u \in X^{+}, {\lVert u\rVert} \le 1 \,\}, \end{align*}

where $K \ge 1$ is a constant in lemma 3.3 and apply theorem 2.5(vi).

We should mention here that a similar result, [24, Proposition 2.2], was proved with the help of Baire’s theorem.

Lemma 3.6.

Under the assumptions and notations of theorems 2.5 and 3.1, $E_1({\omega}) \subset E({\omega})$ for $\mathbb{P}$-a.e. ${\omega} \in \Omega$.

Proof. It is sufficient to show that $w({\omega}) \in E({\omega})$ for $\mathbb{P}$-a.e. ${\omega} \in \Omega$. By theorem 3.4, $\mathbb{P}$-a.e. on Ω, for each $n \in {\mathbb{N}}$ we can find $u_n \in E(\theta_{-n}{\omega}) \cap X^{+}$, with ${\lVert u_n\rVert} = 1$. The invariance of E gives that $U_{\theta_{-n}{\omega}}(n) \, u_n/{\lVert U_{\theta_{-n}{\omega}}(n) \, u_n\rVert}$ belongs to $E({\omega})$. By theorem 2.5(vii), $U_{\theta_{-n}{\omega}}(n) \, u_n/{\lVert U_{\theta_{-n}{\omega}}(n) \, u_n\rVert}$ converges, as $n \to \infty$, to $w({\omega})$.

Theorem 3.7.

Under the assumptions and notations of theorems 2.5 and 3.1, the dimension l of $E({\omega})$ equals one.

Proof. Let $\widetilde{\Omega}_1$ be the invariant subset of Ω of theorem 2.5 and without loss of generality, assume that the set $\Omega'$ of theorem 3.1 is valid for theorem 3.4, that is, $E({\omega}) \cap X^{+} \varsupsetneq \{0\}$ for all ${\omega} \in \Omega'$.

Suppose to the contrary that $l \ge 2$. Fix ${\omega} \in \Omega' \cap \widetilde{\Omega}_1$ such that $E_1({\omega}) \subset E({\omega})$, and let $\{u_1, \ldots, u_{l - 1}, w({\omega}) \}$ be a basis of unit vectors for $E({\omega})$. We will look at the action of $U_{\omega}(n)$ on l-dimensional volume. We have, by (3.1),

(3.2)\begin{equation} \begin{array}{l} \text{vol}(U_{\omega}(n) \, u_1, \ldots, U_{\omega}(n) \, u_{l - 1}, U_{\omega}(n) \, w({\omega}) )\\ = {\lVert U_{\omega}(n) \, w({\omega})\rVert} \, \prod\limits_{i = 1}^{l - 1} \text{dist}(U_{\omega}(n) \, u_i, \text{span}{\{U_{\omega}(n) \, u_{i + 1}, \ldots, U_{\omega}(n) \, u_{l - 1}, U_{\omega}(n) \, w({\omega})\}}) \\ \qquad\qquad \le {\lVert U_{\omega}(n) \, w({\omega})\rVert} \, \prod\limits_{i = 1}^{l - 1} \text{dist}(U_{\omega}(n) \, u_i, E_1(\theta_{n}{\omega})) \end{array} \end{equation}

for all $n \in {\mathbb{N}}$.

By lemma 3.3, there is $K \ge 1$ such that for each u_i, $1 \le i \le l - 1$, one can find $u_{i}^{+}, u_{i}^{-} \in X^{+}$ with $u_{i} = u_{i}^{+} - u_{i}^{-}$, ${\lVert u_{i}^{+}\rVert} \le K$, ${\lVert u_{i}^{-}\rVert} \le K$.

It follows from theorem 2.5(vii) that for any $\rho \in (0, \sigma)$, one can find N ₀ such that for $n \ge N_0$ and $i \in \{1, \ldots, l - 1 \}$ there holds

\begin{equation*}\begin{array}{l} \Bigl\lVert U_{\omega}(n) \, u_{i}^{+} - {\lVert U_{\omega}(n) \, u_{i}^{+}\rVert} \, w(\theta_{n}{\omega}) \Bigr\rVert \le \exp(- n \rho) {\lVert U_{\omega}(n) \, u_{i}^{+}\rVert},\\ \Bigl\lVert U_{\omega}(n) \, u_{i}^{-} - {\lVert U_{\omega}(n) \, u_{i}^{-}\rVert} \, w(\theta_{n}{\omega}) \Bigr\rVert \le \exp(- n \rho) {\lVert U_{\omega}(n) \, u_{i}^{-}\rVert}, \end{array}\end{equation*}

consequently,

(3.3)\begin{equation} \begin{array}{l} \Bigl\lVert U_{\omega}(n) \, u_{i} - \bigl( {\lVert U_{\omega}(n) \, u_{i}^{+}\rVert} - {\lVert U_{\omega}(n) \, u_{i}^{-}\rVert} \bigr) \, w(\theta_{n}{\omega}) \Bigr\rVert \\ = \Bigl\lVert \bigl(U_{\omega}(n) \, u_{i}^{+} - {\lVert U_{\omega}(n) \, u_{i}^{+}\rVert} \, w(\theta_{n}{\omega}) \bigr) - \bigl( U_{\omega}(n) \, u_{i}^{-} - {\lVert U_{\omega}(n) \, u_{i}^{-}\rVert} \, w(\theta_{n}{\omega}) \bigr) \Bigr\rVert \\ \qquad \qquad \le \exp(- n \rho) \bigl( {\lVert U_{\omega}(n) \, u_{i}^{+}\rVert} + {\lVert U_{\omega}(n) \, u_{i}^{-}\rVert} \bigr). \end{array} \end{equation}

Pick some µ satisfying

\begin{equation*} \lambda_{\mathrm{top}} \lt \mu \lt \lambda_{\mathrm{top}} + \frac{l - 1}{l} \,\rho. \end{equation*}

There is N ₁ such that for $n \ge N_1$ and $i \in \{1, \ldots, l - 1 \}$, there holds

(3.4)\begin{equation} {\lVert U_{\omega}(n) \, u_{i}^{+}\rVert} \le \exp(n \mu) {\lVert u_{i}^{+}\rVert}, \quad {\lVert U_{\omega}(n) \, u_{i}^{-}\rVert} \le \exp(n \mu) {\lVert u_{i}^{-}\rVert}. \end{equation}

Gathering (3.3) and (3.4) we obtain, in view of lemma 3.3, the following:

\begin{equation*} \text{dist}(U_{\omega}(n) \, u_i, E_1(\theta_{n}{\omega})) \le 2 K \exp(n (\mu - \rho)), \quad 1 \le i \le l - 1, \end{equation*}

for $n \ge \max\{N_0, N_1\}$, which gives, via (3.2),

\begin{equation*}\begin{array}{l} \text{vol}(U_{\omega}(n) \, u_1, \ldots, U_{\omega}(n) \, u_{l - 1}, U_{\omega}(n) \, w({\omega})) \\ \qquad \qquad \le 2^{l-1} K^{l-1} \exp((l-1) n (\mu - \rho)) \, \exp(n \mu), \end{array}\end{equation*}

consequently,

\begin{equation*} \limsup\limits_{n \to \infty} \frac{\ln{\text{vol}(U_{\omega}(n) \, u_1, \ldots, U_{\omega}(n) \, u_{l - 1}, U_{\omega}(n) \, w({\omega}) )}}{n} \le l \mu - (l - 1) \rho, \end{equation*}

which contradicts proposition 3.2 and finishes the proof.

As a consequence, we can deduce the existence of a generalized exponential separation of type II as shown in the following theorem.

Theorem 3.8.

Let ${(\Omega,\mathfrak{F},\mathbb{P})}$ be a Lebesgue space, $\Phi = ((U_{\omega}(t)), (\theta_t))$ be a measurable linear skew-product semidynamical system on a separable Banach space X with $\dim{X} \ge 2$, positive cone $X^+$ normal and reproducing. Assume that (A1) and (A3) hold, $U_{\omega}(t_0)$ is compact for all ${\omega} \in \Omega$ and some $t_0\geq 1$, and moreover, $\lambda_{\mathrm{top}} \gt -\infty$. Then $((U_{\omega}(t)), (\theta_t))$ admits a generalized exponential separation of type II.

Proof. We claim that $F({\omega})$ of theorem 3.1 can serve as $F_1({\omega})$ in the definition of generalized exponential separation. Indeed, parts (ii) and (iii) in definition 2.6 are direct consequences of theorems 3.1 and 2.5 combined with theorem 3.7. In order to prove (i), let $u \in X^{+}$ be such that $U_{\omega}(1) \, u = 0$. Then, $\lim_{t \to \infty} \ln{{\lVert U_{\omega}(t) \, u\rVert}}/t = - \infty$, and hence, by the characterization given in theorem 3.1 (iii)–(iv), $u \in F({\omega}) = F_1({\omega})$. Finally, suppose to the contrary that there is a $u \in F({\omega}) \cap X^{+}$ such that $U_{\omega}(1) \, u \ne 0$. Then, by remark 2.2, $U_{\omega}(t) \, u \in X^{+} \setminus \{0\}$ for all $t \ge 1$. Hence, by theorem 2.5 (ii) and lemma 3.5, $\lim_{t \to \infty} \ln{{\lVert U_{\omega}(t) \, u\rVert}}/t = \lambda_{\mathrm{top}}$, which contradicts theorem 3.1 (iv), shows that definition 2.6 (i) holds and finishes the proof.

We should mention here that theorem 3.8 is new even in the case of generalized exponential separation of type I. Indeed, in [22, Theorem. 3.8] generalized exponential separation of type I was proved (with stipulating neither ${(\Omega,\mathfrak{F},\mathbb{P})}$ to be a Lebesgue space nor $\lambda_{\mathrm{top}} \gt - \infty$) under a much stronger assumption than (A3), namely, that $\ln{\varkappa}\in L_1(\Omega,\mathfrak{F},\mathbb{P})$ (such a property was called strong focusing). As both the Lebesgue property of ${(\Omega,\mathfrak{F},\mathbb{P})}$ and $\lambda_{\mathrm{top}} \gt - \infty$ are quite natural, the above theorem is, for all conceivable practical purposes, a strengthening of [22, Theorem 3.8].

4. Semiflows generated by linear random delay differential equations

This section is devoted to showing the applications of the theory of §2 to random dynamical systems generated by systems of linear random delay differential equations of the form

(4.1)\begin{equation} z'(t) = A(\theta_{t}{\omega}) \,z(t) + B(\theta_{t}{\omega}) \,z(t-1), \end{equation}

where $z(t) \in \mathbb{R}^N$, $N \ge 2$, $A({\omega})$, $B({\omega})$ are N × N real matrices:

\begin{equation*} A({\omega}) = \left(\begin{matrix} a_{11}({\omega})&a_{12}({\omega})&\cdots&a_{1N}({\omega}) \\ a_{21}({\omega})&a_{22}({\omega})&\cdots&a_{2N}({\omega}) \\ \vdots & \vdots & \ddots & \vdots \\ a_{N1}({\omega})&a_{N2}({\omega})&\cdots&a_{NN}({\omega}) \end{matrix}\right), \quad B({\omega}) = \left(\begin{matrix} b_{11}({\omega})&b_{12}({\omega})&\cdots&b_{1N}({\omega}) \\ b_{21}({\omega})&b_{22}({\omega})&\cdots&b_{2N}({\omega}) \\ \vdots & \vdots & \ddots & \vdots \\ b_{N1}({\omega})&b_{N2}({\omega})&\cdots&b_{NN}({\omega}) \end{matrix}\right), \end{equation*}

and $({(\Omega,\mathfrak{F},\mathbb{P})},(\theta_t)_{t \in \mathbb{R}})$ is an ergodic metric dynamical system, with $\mathbb{P}$ complete.

From now on, the Euclidean norm on $\mathbb{R}^N$ will be denoted by ${\lVert\cdot\rVert}$, $\mathbb{R}^{N \times N}$ will stand for the algebra of N × N real matrices with the operator or matricial norm induced by the Euclidean norm, i.e. ${\lVert A\rVert} := \sup\{{\lVert A\,u\rVert}: {\lVert u\rVert} \le 1\}$, for any $A \in \mathbb{R}^{N \times N}$. For $z = (z_1, \ldots, z_N) \in \mathbb{R}^N$ we write $z \gg 0$ if $z_i \gt 0$ for all $i \in \{1, 2, \ldots, N\}$.

For $1 \lt p \lt \infty$, let $L=\mathbb{R}^N\times L_p([-1,0],\mathbb{R}^N)$ be the separable Banach space with the norm

\begin{equation*} {\lVert u\rVert_{L}}={\lVert u_1\rVert}+{\lVert u_2\rVert}_p={\lVert u_1\rVert}+\left(\int_{-1}^0 {\lVert u_2(s)\rVert}^p\,ds\right)^{\!\!1/p} \end{equation*}

for any $u=(u_1,u_2)$ with $u_1\in\mathbb{R}^N$ and $u_2\in L_p([-1,0],\mathbb{R})$. The positive cone

\begin{equation*}L^+=\left\{u=(u_1,u_2)\in L: u_1 \geq 0 \,\text{and}\, u_2(s)\geq 0 \text{for Lebesgue-a.e.}~ s\in[0,1]\right\}\end{equation*}

is normal and reproducing, and the dual $L^*=\mathbb{R}^N\times L_q([-1,0],\mathbb{R})$ with $1/q+1/p=1$ is also separable.

We denote by C the Banach space $C([-1, 0], \mathbb{R}^N)$ of continuous $\mathbb{R}^N$-valued functions defined on $[-1,0]$, with the supremum norm (denoted by ${\lVert\cdot\rVert_{C}}$). The positive cone

\begin{equation*} C^{+} = \left\{\, u \in C : u(s) \geq 0 \,\text{for all}\, s \in [0,1] \,\right \} \end{equation*}

is normal and reproducing.

Further, by J we denote the linear mapping from C to L

(4.2)\begin{equation} \begin{array}{cccc} J\colon & C & \longrightarrow & L\\ & u & \mapsto & (u(0),u) , \end{array} \end{equation}

which belongs to $\mathcal{L}(C,L)$ and ${\lVert J\rVert}=2$.

Now we introduce the assumptions on the coefficients of the family (4.1):

1. (S1) (Measurability) $A, B \colon \Omega \to \mathbb{R}^{N \times N}$ are $(\mathfrak{F}, \mathfrak{B}(\mathbb{R}^{N \times N}))$-measurable.

2. (S2) (Summability) The $(\mathfrak{F}, \mathfrak{B}(\mathbb{R}))$-measurable functions a, $b\colon \Omega \to \mathbb{R}$ defined as $a({\omega}):={\lVert A({\omega})\rVert}$ and $b({\omega}):={\lVert B({\omega})\rVert}$ have the properties:

   \begin{equation*}\begin{array}{ll} & \bigl[\Omega \ni {\omega} \mapsto a({\omega}) \in \mathbb{R}\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}, \text{and} \\ & \Bigl[\Omega \ni {\omega} \mapsto ln^{+}{\int_{0}^{1}b^q(\theta_{s}{\omega}) \, ds} \in \mathbb{R} \, \Bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}. \end{array}\end{equation*}

As shown in [19, Remark 4.1], the following is sufficient for the fulfillment of the second condition in (S2):

\begin{equation*} \bigl[\Omega \ni {\omega} \mapsto b({\omega}) \in \mathbb{R}\bigr] \in L_q {(\Omega,\mathfrak{F},\mathbb{P})}. \end{equation*}

Remark 4.1.

Although the coefficients A and B are defined only $\mathbb{P}$-a.e. on Ω, we can put the value of $A({\omega})$ and $B({\omega})$ to be equal to 0 for ω in a set of null measure (see [19] for more details) to obtain

\begin{equation*}\begin{array}{ll} \bigl[\mathbb{R}\ni t\mapsto a(\theta_t{\omega})\in \mathbb{R}\bigr]&\in L_{1,\text{loc}}(\mathbb{R}),\\ \bigl[\mathbb{R}\ni t\mapsto b(\theta_t{\omega})\in \mathbb{R}\bigr]& \in L_{q,\text{loc}}(\mathbb{R})\subset L_{1,\text{loc}}(\mathbb{R}) , \end{array}\end{equation*}

for each ${\omega} \in \Omega$.

As a consequence, for a fixed ${\omega}\in\Omega$, we will denote by $U_{\omega}^{0}(\cdot)$ the fundamental matrix solution of the system of Carathéodory linear ordinary differential equations $z' = A(\theta_{t}{\omega})\,z$ and define

(4.3)\begin{equation} c({\omega}) := \sup\limits_{0 \le t_1 \le t_2 \le 1} {\lVert U^{0}_{\theta_{t_1}{\omega}}(t_2 - t_1)\rVert},\quad d({\omega}):=\biggl(\int_{-1}^0 \!b^q(\theta_{s+1}{\omega})\,ds\biggr)^{\!\!1/q}. \end{equation}

Notice that $c({\omega})\geq 1$, and as shown in [19, Lemma 4.2], we have

(4.4)\begin{equation} c({\omega}) \le \exp\biggl( \int_{0}^{1} a(\theta_{s}{\omega}) \, ds \biggr). \end{equation}

Under assumptions (S1) and (S2), it is shown in [19] that the family of systems (4.1) generate measurable linear skew-product semidynamical systems both on C and L. More precisely, for C, we consider the initial value problem of Carathéodory type

(4.5)\begin{equation} \begin{cases} z'(t) = A(\theta_{t}{\omega}) \,z(t) + B(\theta_{t}{\omega}) \,z(t-1), & t \in [0, \infty)\\ z(t) = u(t), & t \in [-1, 0], \end{cases} \end{equation}

where the initial datum u is assumed to belong to $C=C([-1,0],\mathbb{R}^N)$ and emphasize the dependence of the equation (resp. the initial value problem) on ${\omega} \in \Omega$ we will write (4.1) $_{\omega}$ (resp. (4.5) $_{\omega}$). As shown in [19], it has a unique solution denoted by $z(t,{\omega},u)$. Moreover, it can be checked that for each t and $r\geq 0$

(4.6)\begin{equation} z(t+r,{\omega},u)=z(t,\theta_r{\omega},z_r({\omega},u)), \end{equation}

where $z_r({\omega},u)\colon [-1,0]\to \mathbb{R}$ is defined by $s\mapsto z(r+s,{\omega},u)$, and $z_t({\omega},u)\in C$ for each $t\geq 0$, ${\omega}\in\Omega$ and $u\in C$. Therefore, we can define the linear operator

(4.7)\begin{equation} \begin{array}{lccc} U^{(C)}_{\omega}(t)\colon & C &\longrightarrow & C \\ & u & \mapsto & z_t({\omega},u). \end{array} \end{equation}

Analogously, concerning L we consider the initial value problem

(4.8)\begin{equation} \begin{cases} z'(t) = A(\theta_{t}{\omega}) \,z(t) + B(\theta_{t}{\omega})\, z(t-1), & t \in [0, \infty)\\ z(t) = u_2(t), & t \in [-1, 0),\\ z(0) = u_1, \end{cases} \end{equation}

with initial datum $u=(u_1,u_2)$ belonging to $L=\mathbb{R}^N\times L_p([-1,0],\mathbb{R}^N)$. Again, to emphasize the dependence of the initial value problem on ${\omega} \in \Omega$ we will write (4.8) $_{\omega}$. It has a unique solution denoted by $z(t,{\omega},u)$ and, as in C, we can define the linear operator

\begin{equation*} \begin{array}{lccc} U^{(L)}_{\omega}(t)\colon & L &\longrightarrow & L \\ & u & \mapsto & (z(t,{\omega},u),z_t({\omega},u)). \end{array} \end{equation*}

Finally, under assumptions (S1) and (S2), $\bigl((U^{(C)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+)}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ and $\bigl((U^{(L)}_{\omega}(t))_{{\omega} \in \Omega, t \in [0,\infty)}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ are measurable linear skew-product semiflows on C and L covering θ, as shown in [19, Proposition 4.4 and 4.14, resp]. Moreover, we can connect both semidynamical systems in the following way. By [19, Proposition 4.7], for $t\geq 1$ the linear operator

(4.9)\begin{equation} \begin{array}{lccc} U^{(L,C)}_{\omega}(t)\colon & L &\longrightarrow & C \\ & u & \mapsto & z_t({\omega},u) \end{array} \end{equation}

belongs to $ \mathcal{L}(L, C)$ and is a compact operator satisfying

(4.10)\begin{equation} U^{(L,C)}_{\omega}(t)= U_{\theta_{1}{\omega}}^{(C)}(t-1)\circ U_{\omega}^{(L,C)}(1). \end{equation}

Moreover, from [19, Corollary 4.8] we know that

(4.11)\begin{equation} U_{\omega}^{(L)}(t)=J\circ U_{\omega}^{(L,C)}(t), \quad U_{\omega}^{(C)}(t)=U_{\omega}^{(L,C)}(t)\circ J \end{equation}

for any $t\geq 1$ and any ${\omega}\in\Omega$.

For the rest of the section, the following assumptions will also be necessary.

1. (S3) (Cooperativity)

   1. (i) $a_{ij}({\omega})\geq 0$ for all i ≠ j, $i,j=1,2,\ldots, N$ and ${\omega}\in\Omega$.

   2. (ii) $b_{ij}({\omega})\geq 0$ for all $i,j=1,2,\ldots, N$ and ${\omega}\in\Omega$.

2. (S4) (Irreducibility) There is a $(\mathfrak{F}, \mathfrak{B}(\mathbb{R}))$-measurable function $\delta \colon \Omega \to (0,1]$, an invariant set $\widetilde\Omega_0$ of full measure $\mathbb{P}(\widetilde\Omega_0)=1$ and $M\in \mathbb{N}$ such that

   1. (i) for each ${\omega}\in\widetilde\Omega_0$ and $i\in \{1,2,\ldots,N\}$ there is a path $j_1, j_2,j_3,\ldots,j_N$ starting at $j_1=i$ such that $\{j_1,j_2,\ldots,j_N\}=\{1,2,\ldots, N\}$ and

      \begin{equation*} \int_0^M (a_{j_{l+1},j_l}(\theta_{s+t}{\omega})+b_{j_{l+1},j_l}(\theta_{s+t}{\omega}))\,ds \geq \delta(\theta_t{\omega}) \end{equation*}

      whenever $t\in\{k+(k-2)M:k=2,3,\dots,N\}$ and $l=1,2,\ldots, N-1$.

   2. (ii) $ln^{+} \ln (1/\delta)\in L_1{(\Omega,\mathfrak{F},\mathbb{P})}$.

3. (S5) (S4)(i) holds and condition (ii) is changed to

   1. (ii) $\ln (1/\delta)\in L_1{(\Omega,\mathfrak{F},\mathbb{P})}$.

Notice that (S5) implies (S4). Under assumptions (S1)–(S4), we will prove the existence of a family of generalized principal Floquet subspaces for the measurable linear skew-product semidynamical system $\bigl((U^{(L)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by (4.1). If, in addition, (S5) holds, then a generalized exponential separation of type II is obtained. In order to do that we first check the following results.

Proposition 4.2.

Assume (S1)–(S4) and let z(t) be a solution of (4.1) $_{\omega}$ satisfying $z(t)\geq 0$ for each $t\in[-1,\infty)$ and $\,\sup_{t\in[0,1]} {\lVert z(t)\rVert} \gt 0$. Then $z(t)\gg 0$ for each $t\geq N+(N-1)M$.

Proof. Let $t^*$ be the point of $[0,1]$ and j ₁ be the index in which the maximum is attained, that is, $c_1=z_{j_1}(t^*)\geq z_i(t)$ for each $i\in \{1,2,\ldots N\}$ and $t\in[0,1]$. Consider the path and the constant M given in (S4)(i), and denote

(4.12)\begin{equation} K_i({\omega})= \exp\bigg(-\int_0^{N+H}\!\!\!|a_{j_ij_i}(\theta_s{\omega})|\,ds \bigg),\, \text{for}\, i=1,2,\ldots,N \end{equation}

where $H=(N-1)M+1$. From $z'_{j_1}(t)\geq a_{j_1j_1} (\theta_{t}{\omega}) \,z_{j_1}(t)$, and using a comparison result for Carathéodory differential equations [35, Theorem 2], we deduce that

\begin{equation*}z_{j_1}(t)\geq \exp\bigg(\int_{t^*}^{t}\!\!\!a_{j_ij_i}(\theta_s{\omega})\,ds\bigg)z_{j_1}(t^*)\geq c_1K_1({\omega}) \,\text{for}\, t\in[1,N+H].\end{equation*}

Analogously, if $t\in[2+M,N+H]$, from

\begin{align*} z_{j_2}'(t) &\geq a_{j_2j_2}(\theta_t{\omega})\,z_{j_2}(t)+ a_{j_2j_1}(\theta_t{\omega}) z_{j_1}(t)+b_{j_2j_1}(\theta_t{\omega}) z_{j_1}(t-1) \\ & \geq a_{j_2j_2}(\theta_t{\omega})\,z_{j_2}(t)+ \left[a_{j_2j_1}(\theta_t{\omega}) +b_{j_2j_1}(\theta_t{\omega}) \right] c_1 K_1({\omega})\, \end{align*}

we obtain

\begin{align*} z_{j_2}(t)&\geq c_1K_1({\omega})K_2({\omega})\int_2^{t} \left[a_{j_2j_1} +b_{j_2j_1}\right](\theta_{s}{\omega}) \,ds\\ &\geq c_1 K_1({\omega})K_2({\omega})\int_0^{M}\left[a_{j_2j_1} +b_{j_2j_1}\right](\theta_{s+2}{\omega}) \,ds \end{align*}

and (S4)(i) provides

\begin{equation*} z_{j_2}(t)\geq c_1 K_1({\omega}) K_2({\omega})\,\delta(\theta_2{\omega})\,\text{for}\, t\in[2+M,N+H].\end{equation*}

Similarly,

\begin{equation*} z_{j_3}(t)\geq c_1 K_1({\omega}) K_2({\omega})K_3({\omega})\,\delta(\theta_2{\omega})\,\delta(\theta_{3+M}{\omega})\,\text{for}\, t\in[3+2\,M,N+H],\end{equation*}

and finally, in a recursive way we prove that for $k=2,3,\ldots N$

(4.13)\begin{equation} z_{j_k}(t)\geq c_1 \prod_{j=1}^{k} K_j({\omega})\prod_{j=2}^{k}\delta(\theta_{j+(j-2)M} {\omega})\ \,\text{for}\, t\in[k+(k-1)M,N+H], \end{equation}

which finishes the proof.

Theorem 4.3.

Consider the measurable linear skew-product semidynamical system $\bigl((U^{(L)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$. Under assumptions (S1)–(S4), conditions (A1) and (A3) hold for time $T=N+(N-1)M+1$.

Proof. As in [18, Proposition 5.7], concerning the first part of (A1) with T note that

\begin{equation*}\sup\limits_{0 \le s \le T} {ln^{+}{\|U^{(L)}_{\omega}(s)\|}}\leq \sum_{k=0}^{T-1}\sup\limits_{k\le s \le k+1} {ln^{+}{\|U^{(L)}_{\omega}(s)\|}}\end{equation*}

and from cocycle property (2.1)

\begin{align*} \sup\limits_{k\le s \le k+1} ln^{+}{\|U^{(L)}_{\omega}(s)\|}&=\sup\limits_{0 \le s \le 1} {ln^{+}{\|U^{(L)}_{\omega}(k+s)\|}} \\ &\leq \sup\limits_{0 \le s \le 1} \bigl(ln^{+}\|U^{(L)}_{\theta_s{\omega}}(k)\|+ ln^{+} \|U^{(L)}_{\omega}(s)\|\bigr). \end{align*}

Therefore,

\begin{equation*}\sup\limits_{0 \le s \le T} {ln^{+}{\|U^{(L)}_{\omega}(s)\|}}\leq T\,\sup\limits_{0 \le s \le 1} {ln^{+}{\|U^{(L)}_{\omega}(s)\|}}+ \sum_{k=1}^{T-1}\sup\limits_{0 \le s \le 1} {ln^{+}{\|U^{(L)}_{\theta_s{\omega}}(k)\|}}\end{equation*}

and we have to check that both terms belong to $L_1{(\Omega,\mathfrak{F},\mathbb{P})}$. As shown in [19, Proposition 4.6], ${\lVert U^{(L)}_{\omega}(t)\rVert}\leq 3\,c({\omega})\,(1+d({\omega}))$ for each $t\in[0,1]$ and ${\omega}\in\Omega$, where $c({\omega})$ and $d({\omega})$ are defined in (4.3) and $c({\omega})\geq 1$. Thus, from inequality (4.4) and [18, Lemma 5.6], we deduce that

\begin{equation*}\sup\limits_{0 \le s \le 1}{ln^{+}{\|U^{(L)}_{\omega}(s)\|}}\leq \ln 6 + ln^{+} c({\omega})+ ln^{+} d({\omega}) \leq \ln 6 + \int_{0}^{1} a(\theta_{s}{\omega}) \, ds + ln^{+} d({\omega}),\end{equation*}

which belongs to $L_1{(\Omega,\mathfrak{F},\mathbb{P})}$ because of the definition of d, (S1), (S2), Fubini’s theorem and the invariance of $\mathbb{P}$. We omit the proof of the second term, as well as that of the second part of (A1) because they are analogous. In addition, it is also immediate to check that (A2) follows from (S3).

We will finish by verifying that (A3) holds for time T. First we claim that for each ${\omega}\in\Omega$ and $u \in C^+$ with $U_{\omega}^{(C)}(T)\, u\neq 0$

(4.14)\begin{equation} \widetilde\beta({\omega},u)\,\widetilde{\mathbf{e}}\leq U_{\omega}^{(C)}(T)\,u\leq \varkappa({\omega})\,\widetilde \beta({\omega},u)\,\widetilde{\mathbf{e}} \end{equation}

where $\widetilde{\mathbf{e}}\in C^+$ is the constant unit function $\widetilde{\mathbf{e}}(s)=1$ for each $s\in[-1,0]$,

(4.15)\begin{align} \widetilde\beta({\omega},u)&={\lVert U_{\omega}^{(C)}(1)\,u\rVert_{C}}\,k_\delta({\omega}),\nonumber\\ \varkappa({\omega})&=k_\delta^{-1}({\omega})\,3^{T-1} \prod\limits_{j=0}^{T-2}c(\theta_{j+1}{\omega})(1+d(\theta_{j+1}{\omega})), \end{align}

(4.16)\begin{equation} k_\delta({\omega})=\prod_{j=1}^{N} K_j({\omega})\prod_{j=2}^{N}\delta(\theta_{j+(j-2)M} {\omega}), \end{equation}

and $K_j({\omega})$ are defined in (4.12) ( $N+H=T$). Notice that ${\lVert U_{\omega}^{(C)}(1)\,u\rVert_{C}}$ is strictly positive because of $U_{\omega}^{(C)}(T)\, u\neq 0$ and the cocycle property (2.1), so that $\widetilde\beta({\omega},u)$ is strictly positive. Moreover, since $(U_{\omega}^{(C)}(T)\,u)(s)= z(T+s,{\omega},u)$ for each $s\in[-1,0]$, the lower inequality of (4.14) follows from (4.13) with k = N and t = T and (4.16).

Concerning the upper inequality, we first claim that for each $n\geq 1$

(4.17)\begin{equation} {\lVert U_{\omega}^{(C)}(t)\,u\rVert_{C}}\leq 3^n \prod_{j=0}^{n-1}c(\theta_{j}{\omega})(1+d(\theta_{j}{\omega})) \,{\lVert u\rVert_{C}}\,\text{whenever}\, t\in[n-1,n].\end{equation}

From [19, Proposition 4.4], we deduce that

\begin{equation*} {\lVert U^{(C)}_{\omega}(t)\,u\rVert_{C}}\leq 3\,c({\omega})\,(1+d({\omega}))\,{\lVert u\rVert_{C}} \quad\text{for each}\, t\in[0,1] \text{and}\, {\omega}\in\Omega, \end{equation*}

which together with the cocycle property (2.1) yields

\begin{align*} {\lVert U_{\omega}^{(C)}(t)\,u\rVert_{C}}&={\lVert U_{\theta_1{\omega}}^{(C)}(t-1)\big(U_{\omega}^{(C)}(1)\,u\big)\rVert_{C}}\\ &\leq 3\,c(\theta_1{\omega})(1+d(\theta_1{\omega})\,3\,c({\omega})(1+d({\omega}))\,{\lVert u\rVert_{C}} \end{align*}

for each $t\in[1,2]$ and ${\omega}\in\Omega$. Thus (4.17) is easily checked in a recursive way.

Finally, from $U_{\omega}^{(C)}(T)\,u\leq {\lVert U_{\omega}^{(C)}(T)\,u\rVert_{C}}\, \widetilde{\mathbf{e}} $ and (4.17) for $t=T-1$, we obtain

\begin{align*} U_{\omega}^{(C)}(T)\,u&\leq{\lVert U_{\theta_1{\omega}}^{(C)}(T-1) (U_{\omega}^{(C)}(1)\,u)\rVert_{C}} \,\widetilde{\mathbf{e}} \\ & \leq \,{\lVert U_{\omega}^{(C)}(1)\,u)\rVert_{C}}\,3^{T-1} \prod\limits_{j=0}^{T-2}c(\theta_{j+1}{\omega})(1+d(\theta_{j+1}{\omega}))\,\widetilde{\mathbf{e}}\\ &=\varkappa({\omega})\,\widetilde\beta({\omega},u)\,\widetilde{\mathbf{e}}, \end{align*}

as claimed.

Next we will prove that for any $u\in L^+$ such that $U_{\omega}^{(L)}(T)\,u\not=0$

(4.18)\begin{equation} \beta({\omega},u)\,\mathbf e\leq U_{\omega}^{(L)}(T)\,u\leq \varkappa({\omega})\, \beta({\omega},u)\,\mathbf e, \end{equation}

where $\mathbf e=(1/(2\sqrt{N}))\,(\widetilde{\mathbf{e}}(0),\widetilde{\mathbf{e}})\in L^+$ is a unitary vector of L, i.e ${\lVert\mathbf e\rVert_{L}}=1$ and

(4.19)\begin{equation} \beta({\omega},u)=2\sqrt{N} \,{\lVert U_{\omega}^{(L,C)}(1)\,u\rVert_{C}}\, k_\delta({\omega}) \gt 0. \end{equation}

As shown in [19], the following relations hold

\begin{equation*} U^{(L)}_{\omega}(t) = J \circ U^{(L, C)}_{\omega}(t), \quad U^{(L, C)}_{\omega}(t)=U_{\theta_1{\omega}}^{(C)}(t-1)\circ U_{\omega}^{(L,C)}(1) \end{equation*}

for any $t \ge 1$ and any ${\omega} \in \Omega$, where J is the linear map defined in (4.2). Hence

\begin{equation*} U_{\omega}^{(L)}(T)\,u=(z(T,{\omega},u),z_T({\omega},u))=J\big( U_{\theta_1{\omega}}^{(C)}(T-1)(U_{\omega}^{(L,C)}(1)\,u)\big) \end{equation*}

and notice that $U_{\omega}^{(L,C)}(1)\,u=z_1({\omega},u)\in C$. Therefore, as in proposition 4.2,

\begin{equation*} z(T+s,{\omega},u)\geq {\lVert U_{\omega}^{(L,C)}(1)\,u\rVert_{C}} \,k_\delta({\omega})\, \widetilde{\mathbf{e}} \end{equation*}

for each $s\in[-1,0]$ and the lower inequality of (4.18) holds. Concerning the upper inequality, as above

\begin{equation*}z_T({\omega},u)\leq \,{\lVert U_{\omega}^{(L,C)}(1)\,u)\rVert_{C}}\,3^{T-1} \prod_{j=0}^{T-2}c(\theta_{j+1}{\omega})(1+d(\theta_{j+1}{\omega}))\,\widetilde{\mathbf{e}}\end{equation*}

from which the upper inequality of (4.18) can be easily checked.

In order to finish the proof we have to check that the $(\mathfrak{F},\mathfrak{B}(\mathbb{R}))$-measurable function $\varkappa$ defined by (4.15) satisfies $ln^{+}\ln\varkappa\in L_1{(\Omega,\mathfrak{F},\mathbb{P})}$. From (4.12) and the definition of $a({\omega})={\lVert A({\omega})\rVert}$ we deduce that there is a constant c ₀ such that

(4.20)\begin{equation} \Bigg(\prod_{j=1}^{N} K_j({\omega}))\Bigg)^{\!\!-1}\!\!\!= \exp\int_0^T \sum_{j=1}^N|a_{jj}(\theta_s{\omega})|\,ds\leq \exp\int_0^T c_0\,a(\theta_s{\omega}) \,ds. \end{equation}

Moreover, from (4.20), (4.4) and $\ln(1+x)\leq x$ if $x\geq 0$

\begin{equation*}ln^{+} \ln c(\theta_{j+1}{\omega})\leq \int_0^1 a(\theta_{j+1+s}{\omega})\,ds\, ,\quad ln^{+} \ln(1+d(\theta_{j+1}{\omega}))\leq ln^{+} d(\theta_{j+1}{\omega}),\end{equation*}

\begin{equation*} 0\leq ln^{+} \ln\Bigg(\prod_{j=1}^{N} K_j({\omega}))\Bigg)^{\!\!-1}\!\!\!\leq c_0 \int_0^T a(\theta_s{\omega}) \,ds, \end{equation*}

and we deduce from [18, Lemma 5.6] that there is an integer number n ₀ such that

\begin{align*} ln^{+} \ln\varkappa ({\omega})\leq & \, c_0 \int_0^T a(\theta_s{\omega})\,ds+ \sum_{j=0}^{T-2} \left[\int_0^1 a(\theta_{j+1+s} {\omega})\,ds+ \ln ^+d(\theta_{j+1}{\omega})\,\right] \\ &\quad + \sum_{j=2}^Nln^{+} \ln \left(1/\delta\right)(\theta_{j+(j-2)M}{\omega})+ ln^{+} \ln(3^{T-1})\,+\ln (n_0). \end{align*}

As before, from the definition of d, (S1), (S2), (S4)(ii), Fubini’s theorem and the invariance of $\mathbb{P}$ we conclude that $ln^{+} \ln \varkappa\in L_1{(\Omega,\mathfrak{F},\mathbb{P})}$ and (A3) holds for T, as stated.

As a consequence, from theorem 2.5 the existence of a family of generalized principal Floquet subspaces is obtained.

Theorem 4.4.

Under assumptions (S1)–(S4) there is a family of generalized principal Floquet subspaces for the measurable linear skew-product semidynamical system $\Phi ^{(L)}= ((U_{\omega}^{(L)}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_t)_{t\in\mathbb{R}})$ generated by (4.1), with generalized principal Lyapunov exponent $\widetilde{\lambda}^{(L)}_1$.

If we assume (S5) instead of (S4), the existence of a generalized exponential separation of type II is obtained, as claimed before.

Theorem 4.5.

Under assumptions (S1)–(S3) and (S5), the measurable linear skew-product semidynamical system $\Phi ^{(L)}= ((U_{\omega}^{(L)}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_t)_{t\in\mathbb{R}})$ generated by (4.1) admits a generalized exponential separation of type II with $\widetilde{\lambda}_1^{(L)} \gt - \infty$.

Proof. As $L=\mathbb{R}^N\times L_p([-1,0],\mathbb{R}^N)$ is an ordered separable Banach space with separable dual $L^*=\mathbb{R}^N\times L_q([-1,0],\mathbb{R}^N)$ and positive cone $L^+$ normal and reproducing, the claim follows from theorems 2.9, 4.3 and 4.4, once we check that $\widetilde\lambda_1^{(L)} \gt -\infty$.

Let $\mathbf e$ be the unitary vector of L defined for the focusing inequality (4.18). From proposition 4.2, we deduce that $U_{\omega}^{(L)}(T)\,\mathbf e\neq 0$ and hence $U_{\omega}^{(L)}(T)\,\mathbf e \geq \beta({\omega},\mathbf e)\,\mathbf e$ for each ${\omega}\in\Omega$. Thus, from the cocycle property (2.1), (A2), and the monotonicity of the norm, it is easy to check that

\begin{equation*} {\lVert U_{\omega}^{(L)}(n\,T)\,\mathbf e\rVert_{L}}\geq \prod_{k=0}^{n-1} \beta(\theta_{kT}{\omega},\mathbf e) \quad \text{for each}\, n\in\mathbb{N}, \end{equation*}

and therefore

\begin{equation*} \frac{\ln {\lVert U_{\omega}^{(L)}(n\,T)\,\mathbf e\rVert_{L}}}{nT}\geq \frac{1}{nT}\sum_{k=0}^{n-1} \ln \beta(\theta_{kT}{\omega},\mathbf e). \end{equation*}

Finally, note that the function $-\ln \beta(\cdot,\mathbf e)$ for β defined in (4.19) satisfies

\begin{equation*} 0\leq -\ln \beta({\omega},\mathbf e)\leq -\sum_{j=1}^N \ln K_j({\omega})+\sum_{j=2}^N\ln \left(1/\delta)(\theta_{j+(j-2)M}{\omega}\right)+ c_1 \end{equation*}

for some constant c ₁, and thus belongs to $L_1{(\Omega,\mathfrak{F},\mathbb{P})}$ from (4.20) and (S5). Then, an application of Birkhoff ergodic theorem gives that for $\mathbb{P}$-a.e. ${\omega}\in\Omega$, there holds

\begin{equation*} \lim_{n\to\infty}\frac{1}{n}\sum_{k=0}^{n-1} \ln \beta(\theta_{kT}{\omega},\mathbf e)=\int_\Omega \ln\beta(\theta_T{\omega}',\mathbf e)\,d\mathbb{P}({\omega}') \gt -\infty, \end{equation*}

hence

\begin{equation*} \limsup_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(L)}(t)\,\mathbf e\rVert_{L}}}{t} \gt -\infty, \end{equation*}

and (2.2) finishes the proof.

Lemma 4.6.

Let $U_{\omega}^{(L,C)}(1)$ be the compact linear operator defined in (4.9). Then the mapping

\begin{equation*} [\Omega\times L\ni ({\omega},u) \mapsto U_{\omega}^{(L,C)}(1)\,u \in C ] \text{is}(\mathfrak{F}\otimes\mathfrak{B}(L), \mathfrak{B}(C))\text{-measurable}. \end{equation*}

Proof. From [2, Lemma 4.51, pp. 153], it is enough to check that it is a Carathéodory function, i.e. for each fixed ${\omega}\in\Omega$, the map L → C, $u\mapsto U_{\omega}^{(L,C)}(1)\,u=z_1({\omega},u)$ is continuous, which is well known, and for each fixed $u\in L$, the map

(4.21)\begin{equation} [\Omega\ni {\omega} \mapsto U_{\omega}^{(L,C)}(1)\,u=z_1({\omega},u)\in C] \text{is} (\mathfrak{F}, \mathfrak{B}(C))\text{-measurable}. \end{equation}

In order to prove this, denoting by $u=(c,v)\in \mathbb{R}^N\times L_p([-1,0],\mathbb{R}^N)$, we can find a sequence of continuous functions $v_n\in C$ such that, $v_n(0)$ converges to c in $\mathbb{R}^N$ and v_n converges to v in $L_p([-1,0],\mathbb{R}^N)$ as $n \uparrow\infty$. Therefore, the measurability of the maps $[\Omega\ni {\omega} \mapsto z_1({\omega},v_n(0),v_n)=z_1({\omega},v_n)\in C]$ (see [19, Lemma 4.11]) for each $n\in\mathbb{N}$, the convergence of them to the map (4.21) as $n \uparrow\infty$ and [2, Corollary 4.29] show the measurability and finishes the proof.

Theorem 4.7.

Under assumptions (S1)–(S4), there is a family of generalized principal Floquet subspaces for the measurable linear skew-product semidynamical system $\Phi ^{(C)}= ((U_{\omega}^{(C)}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_t)_{t\in\mathbb{R}})$ generated by (4.1), with generalized principal Lyapunov exponent $\widetilde{\lambda}^{(C)}_1$ which coincide with $\widetilde{\lambda}^{(L)}_1$ of theorem 4.4.

Proof. Theorem 4.4 states the existence of a family $\{E_1^{(L)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ of generalized principal Floquet subspaces for $\Phi^{(L)}$. For ${\omega} \in \widetilde{\Omega}_1$, put $E_1^{(L)}({\omega}) := \text{span}\{w^{(L)}({\omega})\}$ with ${\lVert w^{(L)}({\omega})\rVert_{L}} = 1$. First notice that from (4.9) the function

\begin{equation*} U_{\theta_{-1}w}^{(L,C)}(1)w^{(L)}(\theta_{-1}{\omega}) =(z_1(\theta_{-1}{\omega},w^{(L)}(\theta_{-1}{\omega}))\in \ C, \end{equation*}

from (4.11), we deduce that

\begin{equation*} U_{\theta_{-1}{\omega}}^{(L)}(1)w^{(L)}(\theta_{-1}{\omega})=(z_1(\theta_{-1}{\omega},w^{(L)}(\theta_{-1}{\omega}))(0), z_1(\theta_{-1}{\omega},w^{(L)}(\theta_{-1}{\omega}))\in \mathbb{R}^N\times C, \end{equation*}

which is proportional to $w^{(L)}({\omega})$ because $U_{\theta_{-1}w}^{(L)}(1)E_1^{(L)}(\theta_{-1} w)=E_1^{(L)}({\omega})$, and hence, can be denoted by $w^{(L)}({\omega})=(w({\omega})(0),w({\omega}))\in \mathbb{R}^N\times C$. In particular, $w({\omega})$ is proportional to $U_{\theta_{-1}{\omega}}^{(L,C)}(1)w^{(L)}(\theta_{-1}{\omega})\neq 0$.

Next, we define $w^{(C)}({\omega}) := U_{\theta_{-1}{\omega}}^{(L,C)}(1) \, w^{(L)}(\theta_{-1}{\omega}) / {\lVert U_{\theta_{-1}{\omega}}^{(L,C)}(1) \, w^{(L)}(\theta_{-1}{\omega})\rVert_{C}} $, unitary and also proportional to $w({\omega})$. We consider the one-dimensional subspace of C defined by $E_1^{(C)}({\omega}):=\text{span}\{w^{(C)}({\omega})\}$ and we claim that $\{E_1^{(C)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ is a family of generalized principal Floquet subspaces of $\Phi^{(C)}$, i.e. conditions (i)–(iv) of definition 2.4 hold. First, it is easy to deduce from lemma 4.6 that $w^{(C)}\colon\widetilde\Omega_1\to C^+\setminus \{0\}$ is $(\mathfrak{F}, \mathfrak{B}(C))$-measurable and thus, (i) holds. Condition (ii), that is, the invariance of $\{E_1^{(C)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$, follows from $E_1^{(C)}({\omega}) = \text{span}\{w({\omega})\}$, $w^{(L)}({\omega})=(w({\omega})(0),w({\omega}))$ and the invariance of $\{E_1^{(L)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$. In order to check (iii), notice that from [19, Proposition 5.2(2)], we deduce that

(4.22)\begin{equation} \widetilde\lambda_1^{(L)}=\lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})\rVert_{L}}}{t}=\lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(L,C)}(t)\,w^{(L)}({\omega})\rVert_{C}}}{t}. \end{equation}

However, as stated in (4.11), $U_{\omega}^{(C)}(t)=U_{\omega}^{(L,C)}(t)\circ J$ for $t\geq 1$, then

(4.23)\begin{equation} \widetilde\lambda_1^{(L)}= \lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(C)}(t)\,w({\omega})\rVert_{C}}}{t}=\lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(C)}(t)\,w^{(C)}({\omega})\rVert_{C}}}{t}, \end{equation}

as needed, and in particular the generalized principal Lyapunov exponents of $\Phi^{(L)}$ and $\Phi^{(C)}$ coincide. Finally, for each ${\omega}\in\widetilde\Omega_1$ with $U_{\omega}^{(C)}(1)\,u\neq 0$ we know that $U_{\omega}^{(L)}(1)\,Ju\neq 0$. Then, as in [19, Proposition 5.2(1)], it can be shown that

(4.24)\begin{equation} \limsup_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(C)}(t)\,u\rVert_{C}}}{t}=\limsup_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(L)}(t)\,Ju\rVert_{L}}}{t}\leq \widetilde\lambda_1^{(L)}=\widetilde\lambda_1^{(C)}. \end{equation}

Therefore, (iv) holds and $\{E_1^{(C)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ is a family of generalized principal Floquet subspaces of $\Phi^{(C)}$, as claimed.

Although the dual space of $C=C([-1, 0], \mathbb{R}^N)$ is not a separable Banach space and thus, theorem 2.9 does not apply, we will show the existence of a generalized exponential separation of type II with $\widetilde{\lambda}_1^{(C)} \gt - \infty$ for the measurable linear skew-product semidynamical system $\Phi^{(C)}=\bigl((U^{(C)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$.

Theorem 4.8.

Under assumptions (S1)–(S3) and (S5), the measurable linear skew-product semidynamical system $\Phi^{(C)} = ((U_{\omega}^C(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_t)_{t\in\mathbb{R}})$ generated by (4.1) admits a generalized exponential separation of type II with $\widetilde{\lambda}_1^{(C)} \gt - \infty$.

Proof. In order to prove that $\Phi^{(C)}$ admits a generalized exponential separation of type II we need to check that the family $\{E_1^{(C)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ of theorem 4.7, defined by $E_1^{(C)}({\omega})=\text{span}\{w({\omega})\}$, satisfies conditions (i)–(iii) of definition 2.6.

First notice that from theorems 4.4 and 2.9, we know, among other things, that there are an invariant set $\widetilde\Omega_1$ of full measure $\mathbb{P}(\widetilde\Omega_1)=1$ and a family of generalized principal Floquet subspaces $\{E_1^{(L)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ with $E_1^{(L)}({\omega}) = \text{span}\{w^{(L)}({\omega})\}$ satisfying that the family of projections $\{P^{(L)}({\omega})\}_{{\omega}\in\widetilde\Omega_1}$, associated with the invariant decomposition $L=E_1^{(L)}({\omega})\oplus F_1^{(L)}({\omega})$, is strongly measurable and tempered, i.e.

(4.25)\begin{equation} \lim\limits_{t \to \pm\infty} \frac{\ln{\|P^{(L)}(\theta_{t}{\omega})\|}}{t} = 0 \qquad \mathbb{P}\text{-a.e. on}\, \widetilde\Omega_1, \end{equation}

and $F_1^{(L)}({\omega})\cap L^+=\{u\in L^+ : U_{\omega}^{(L)}(1)\,u=0\}$ for any ${\omega}\in\widetilde\Omega_1$. We also know that ${\lVert w^{(L)}({\omega})\rVert_{L}}=1$ for any ${\omega}\in\widetilde\Omega_1$. As in remark 2.1, the family of projections onto $E_1^{(L)}({\omega})$ will be denoted by $\{\widetilde P^{(L)}({\omega})\}_{{\omega}\in\widetilde\Omega_1}$ (remember that $\widetilde{P}^{(L)}({\omega}) = \mathrm{Id}_L - P^{(L)}({\omega})$). As $\widetilde{P}^{(L)}({\omega})$ is a projection on $\text{span}\{w^{(L)}({\omega})\}$, for each $\widehat u\in L$ we have $ \widetilde P^{(L)}({\omega})\,\widehat u=\lambda({\omega},\widehat u)\, w^{(L)}({\omega})$.

Next, for any $u\in C$, we know that $Ju=(u(0),u)\in L$ so that u can be decomposed as $u= \lambda({\omega},Ju)\,w({\omega})+ \bigl( u-\lambda({\omega},Ju)\,w({\omega}) \bigr)$, with $u-\lambda({\omega},Ju)\,w({\omega})\in C$. For ${\omega} \in \widetilde{\Omega}_1$, put $F_1^{(C)}({\omega}) := \{\, u \in C : J u \in F_1^{(L)}({\omega}) \,\}$. The closedness of $F_1^{(C)}({\omega})$ in C is a consequence of the continuity of J and the closedness of $F_1^{(L)}({\omega})$ in L.

We have thus obtained an invariant decomposition $C = E_1^{(C)}({\omega}) \oplus F_1^{(C)}({\omega})$. We claim that for any ${\omega} \in \widetilde{\Omega}_1$ there holds $F_1^{(C)}({\omega}) \cap C^+ = \{u\in C^+ : U_{\omega}^{(C)}(1)\,u=0 \}$. Indeed, let $u \in C^{+}$ be such that $J u \in F_1^{(L)}({\omega})$. Then, by (4.11) and the invariance of $F_1^{(L)}$, $J U_{\omega}^{(C)}(1)\, u = J U_{\omega}^{(L,C)}(1) J u = U_{\omega}^{(L)}(1) J u \in F_1^{(L)}(\theta_{1}{\omega})$. Further, it follows from (A2) and definition 2.6(i) for $\Phi^{(L)}$ that $J U_{\omega}^{(C)}(1)\, u = 0$. As J is injective, $U_{\omega}^{(C)}(1) \,u = 0$ holds. On the other hand, if $u \in C^{+}$ is such that $U_{\omega}^{(C)}(1)\, u = 0$, then, by (4.11), $0 = J U_{\omega}^{(L,C)}(1) J u = U_{\omega}^{(L)}(1) J u$, and, since $J u \in L^{+}$, again by definition 2.6(i) for $\Phi^{(L)}$, $J u \in F_1^{(L)}({\omega})$, that is, $u \in F_1^{(C)}({\omega})$, our claim is true and (i) of definition 2.6 holds for $\Phi^{(C)}$.

Next, in view of remark 2.1, we prove that the family $\{\widetilde P^{(C)}({\omega})\}_{{\omega}\in\widetilde\Omega_1}$ of projections onto $E_1^{(C)}({\omega})$, defined as $\widetilde{P}^{(C)}({\omega})\,u=\lambda({\omega},Ju)\,w({\omega})$ for each $u\in C$, is strongly measurable and tempered. Concerning the strong measurability, we have to check that for each $u \in C$ the mapping $[\widetilde \Omega_1 \ni {\omega} \mapsto \widetilde P^{(C)}({\omega})u \in C ]$ is $(\mathfrak{F}, \mathfrak{B}(C))$-measurable. Once we fix $u\in C$, the strong measurability of $\{\widetilde P^{(L)}({\omega})\}_{{\omega}\in\widetilde\Omega_1}$ together with $ \widetilde P^{(L)}({\omega})\, Ju=\lambda({\omega},Ju)\, w^{(L)}({\omega})$ and ${\lVert w^{(L)}({\omega})\rVert_{L}}=1$ show that $[\widetilde \Omega_1 \ni {\omega} \mapsto \lambda({\omega},Ju) \in \mathbb{R} ]$ is $(\mathfrak{F}, \mathfrak{B}(\mathbb{R}))$-measurable, and the result follows from the composition of the maps

\begin{equation*} \widetilde\Omega_1 \to \mathbb{R}\times C \to C,\quad {\omega} \mapsto (\lambda({\omega},Ju),w({\omega}))\mapsto \lambda({\omega},Ju)\,w({\omega}).\end{equation*}

In order to show that the family is tempered, first notice that from the definition of $\widetilde P^{(L)}$ and ${\lVert w^{(L)}({\omega})\rVert_{L}}=1$ we deduce that

\begin{equation*} {\lVert\widetilde P^{(L)}(\theta_t{\omega})\rVert} = \sup_{{\lVert\widehat u\rVert_{L}}\leq 1}{\lVert \widetilde P^{(L)}(\theta_t{\omega})\,\widehat u\rVert_{L}}= \sup_{{\lVert\widehat u\rVert_{L}}\leq 1} |\lambda(\theta_t{\omega},\widehat u)| \,\text{for any}\, {\omega}\in\widetilde\Omega_1. \end{equation*}

Therefore, from $\{Ju\in L : u\in C \,\text{and}\, {\lVert u\rVert_{C}}\leq 1\} \subset \{\widehat u\in L: {\lVert\widehat u\rVert_{L}}\leq 2\}$ it holds

\begin{align*} 1\leq {\lVert\widetilde P^{(C)}(\theta_t{\omega})\rVert} & =\sup_{{\lVert u\rVert_{C}}\leq 1}{\lVert \widetilde P^{(C)}(\theta_t{\omega})\,u\rVert_{C}}= \sup_{{\lVert u\rVert_{C}}\leq 1} |\lambda(\theta_t{\omega},Ju)\,|{\lVert w(\theta_t{\omega})\rVert_{C}}\\ &\leq \sup_{{\lVert\widehat u\rVert_{L}}\leq 2} |\lambda(\theta_t{\omega},\widehat u)| \,{\lVert w(\theta_t{\omega})\rVert_{C}}\leq 2 \,{\lVert\widetilde P^{(L)}(\theta_t{\omega})\rVert} \,{\lVert w(\theta_t{\omega})\rVert_{C}}, \end{align*}

and consequently,

\begin{equation*} 0\leq \lim\limits_{t \to \pm\infty} \frac{\ln{\|\widetilde P^{(C)}(\theta_{t}{\omega})\|}}{t}\leq \lim\limits_{t \to \pm\infty} \frac{\ln{\|\widetilde P^{(L)}(\theta_{t}{\omega})\|}}{t}+ \lim\limits_{t \to \pm\infty} \frac{\ln{{\lVert w(\theta_t{\omega})\rVert_{C}}}}{t}. \end{equation*}

Thus, because of (4.25), in order to prove that $\{\widetilde P^{(C)}({\omega})\}_{{\omega}\in\widetilde\Omega_1}$ is tempered, it is enough to check that

(4.26)\begin{equation} \lim\limits_{t \to \pm\infty} \frac{\ln{{\lVert w(\theta_t{\omega})\rVert_{C}}}}{t}=0. \end{equation}

From $U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})=\alpha(t,{\omega})\,w^{(L)}(\theta_t {\omega})$ and ${\lVert w^{(L)}(\theta_tw)\rVert_{L}}=1$, we obtain

\begin{equation*} w^{(L)}(\theta_t{\omega})=\frac{U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})}{{\lVert U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})\rVert_{L}}} \, , \,\text{and thus,}\, \,w(\theta_t{\omega})=\frac{U_{\omega}^{(L,C)}(t)\,w^{(L)}({\omega})}{{\lVert U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})\rVert_{L}}} \end{equation*}

for $t\geq 0$. Hence, $\ln{{\lVert w(\theta_t{\omega})\rVert_{C}}}= \ln{{\lVert U_{\omega}^{(L,C)}(t)\,w^{(L)}({\omega})\rVert_{C}}}-\ln {\lVert U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})\rVert_{L}}$ and (4.26) as t goes to $+\infty$ follows from (4.22). Concerning the limit as t goes to  $-\infty$, as in theorem 2.5 (see [18, Theorem 3.10] for the complete proof), we consider the negative semiorbit for $\Phi^{(L)}$ defined  as

(4.27)\begin{equation} w_{\omega}^{(L)}(s) =\frac{w^{(L)}(\theta_s{\omega})}{{\lVert U_{\theta_s{\omega}}^{(L)}(-s) \, w^{(L)}(\theta_s{\omega} )\rVert_{L}}} \quad \text{for} s\leq 0, \end{equation}

which satisfies $w_{\omega}^{(L)}(0)= w^{(L)}({\omega})$ and

(4.28)\begin{equation} \widetilde\lambda_1^{(L)} = \lim_{s\to- \infty} \frac{1}{s}\ln{\lVert w_{\omega}^{(L)}(s)\rVert_{L}} =-\lim_{s\to-\infty} \frac{\ln {\lVert U_{\theta_s {\omega}}^{(L)}(-s)\,w^{(L)}(\theta_s{\omega})\rVert_{L}}}{s}. \end{equation}

Then, as in [19, Theorem 5.6], denoting by $w_{\omega}(s)$ the second component of $w_{\omega}^{(L)}(s)$, which belongs to C, defines a negative semiorbit for $\Phi^{(C)}$, $J w_{\omega}(s)= w_{\omega}^{(L)}(s)$ and

(4.29)\begin{equation} \lim_{s\to-\infty}\frac{\ln{{\lVert w_{\omega}(s)\rVert_{C}}}}{s}=\widetilde\lambda_1^{(L)}. \end{equation}

Therefore, from (4.27), we deduce that

\begin{equation*} w(\theta_s{\omega})={\lVert U_{\theta_s {\omega}}^{(L)}(-s)\,w^{(L)}(\theta_s{\omega})\rVert_{L}}\,w_{\omega}(s) \quad \text{for each}\, s\leq 0, \end{equation*}

and $\ln{\lVert w(\theta_s{\omega})\rVert_{C}}= \ln{\lVert U_{\theta_s {\omega}}^{(L)}(-s)\,w^{(L)}(\theta_s{\omega})\rVert_{L}}+\ln {\lVert w_{\omega}(s)\rVert_{C}}$ holds. Thus from (4.28) and (4.29) the limit (4.26) holds as t goes to $-\infty$, $\{\widetilde P^{(C)}({\omega})\}_{{\omega}\in\widetilde\Omega_1}$ is tempered, as claimed, and (ii) of definition 2.6 holds.

Now we check that (iii) of this definition also holds, that is, there exists $\widetilde{\sigma}\in (0,\infty]$ such that

\begin{equation*} \lim_{t\to\infty}\frac{1}{t}\ln \frac{\|U_{\omega}^{(C)}(t)|_{F_1^{(C)}({\omega})}\|}{\|U_{\omega}^{(C)}(t)\,w({\omega})\|_C}=-\widetilde{\sigma} \quad \text{for each}\, {\omega}\in\widetilde\Omega_1.\end{equation*}

Again, from theorems 4.5 and 2.9, we know that there exists $\widetilde\sigma\in(0,\infty]$ such that $\widetilde\lambda^{(L)}_2=\widetilde\lambda^{(L)}_1-\widetilde\sigma$ and

\begin{equation*} \lim_{t\to\infty}\frac{1}{t}\ln \frac{\|U_{\omega}^{(L)}(t)|_{F_1^{(L)}({\omega})}\|}{\|U_{\omega}^{(L)}(t)\,w^{(L)}({\omega})\|_L}=-\widetilde{\sigma} \quad \text{and} \quad \lim_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(L)}(t)|_{F_1^{(L)}({\omega})}\|= \widetilde\lambda^{(L)}_2 \end{equation*}

for each ${\omega}\in\widetilde\Omega_1$, which together with (4.23) shows that it is enough to prove that

(4.30)\begin{equation} \lim_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(C)}(t)|_{F_1^{(C)}({\omega})}\| = \widetilde\lambda^{(L)}_2 \quad \text{for each}\, {\omega}\in\widetilde\Omega_1. \end{equation}

As in [19, Proposition 5.2(2)], it is easy to check that

(4.31)\begin{equation} \widetilde\lambda^{(L)}_2 =\lim_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(L)}(t)|_{F_1^{(L)}({\omega})}\| = \lim_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(L,C)}(t)|_{F_1^{(L)}({\omega})}\| \end{equation}

for each ${\omega}\in\widetilde\Omega_1$. Moreover, from (4.10) and the construction of $F^{(C)}_1({\omega})$, we obtain

(4.32)\begin{equation} U_{\omega}^{(L,C)}(1)\big(F_1^{(L)}({\omega})\big)\subset F_1^{(C)}(\theta_1{\omega}) \quad\text{and}\quad J(F_1^{(C)}({\omega}))\subset F_1^{(L)}({\omega}). \end{equation}

Thus, from (4.10), (4.11), (4.31) and (4.32), we deduce the following chain of inequalities

\begin{align*} \widetilde\lambda^{(L)}_2&=\lim\limits_{t\to\infty}\frac{1}{t+1}\ln\|U_{\theta_{-1}{\omega}}^{(L,C)}(t+1)|_{F_1^{(L)}(\theta_{-1}{\omega})}\| \\ &= \lim\limits_{t\to\infty}\frac{1}{t+1}\ln\|U_{\omega}^{(C)}(t)\circ U_{\theta_{-1}{\omega}}^{(L,C)}(1)|_{F_1^{(L)}(\theta_{-1}{\omega})}\|\\ & \leq \liminf\limits_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(C)}(t)|_{F_1^{(C)}({\omega})}\|\leq \limsup\limits_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(C)}(t)|_{F_1^{(C)}({\omega})}\| \\ & = \limsup\limits_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(L,C)}(t)\circ J|_{F_1^{(C)}({\omega})}\| \leq \lim\limits_{t\to\infty}\frac{1}{t}\ln\|U_{\omega}^{(L,C)}(t)|_{F_1^{(L)}({\omega})}\| = \widetilde\lambda^{(L)}_2, \end{align*}

which shows (4.30) and (iii) of definition 2.6 holds. Finally, from $\widetilde{\lambda}_1^{(L)} \gt - \infty$ and  (4.24), we deduce that $\widetilde{\lambda}_1^{(C)} \gt - \infty$, which finishes the proof.

5. Semiflows generated by linear random delay systems in a state space with not separable dual

This section deals with three cases in which the dual of the phase Banach space X is non-separable and ${(\Omega,\mathfrak{F},\mathbb{P})}$ is a Lebesgue space. In particular, we will apply the Oseledets theory of §3, more precisely theorem 3.8, to show the existence of a generalized exponential separation of type II.

5.1. Case 1

In this subsection, we briefly explain what happens for p = 1, that is, we consider the separable Banach space $\widehat{L}=\mathbb{R}^N\times L_1([-1,0],\mathbb{R}^N)$ with the norm

\begin{equation*} {\lVert u\rVert}_{\widehat{L}}={\lVert u_1\rVert}+{\lVert u_2\rVert}_{1}={\lVert u_1\rVert}+\int_{-1}^0 {\lVert u_2(s)\rVert} \, ds \end{equation*}

for any $u=(u_1,u_2)$ with $u_1\in \mathbb{R}^N$ and $u_2\in L_1([-1,0],\mathbb{R}^N)$. We maintain conditions (S1) and (S3)–(S5) and we change (S2) by

1. (S2a) The $(\mathfrak{F}, \mathfrak{B}(\mathbb{R}))$-measurable functions a, $b \colon \Omega \to \mathbb{R}$ defined as $a({\omega}) := {\lVert A({\omega})\rVert}$ and $b({\omega}):={\lVert B({\omega})\rVert}$ have the properties:

   \begin{equation*}\begin{array}{ll} & \bigl[\Omega \ni {\omega} \mapsto a({\omega}) \in \mathbb{R}\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}, \text{and}\\ &\bigl[\Omega \ni {\omega} \mapsto ln^{+} \text{ess\,sup}_{-1\le s\le 0} b(\theta_{s+1} {\omega}) \in \mathbb{R}\bigr] \in L_{1} {(\Omega,\mathfrak{F},\mathbb{P})}. \end{array}\end{equation*}

Remark 5.1.

Note that

\begin{equation*} \bigl[\Omega \ni {\omega} \mapsto b({\omega}) \in \mathbb{R}\bigr] \in L_{\infty} {(\Omega,\mathfrak{F},\mathbb{P})}\end{equation*}

is sufficient for the second part of the assumption (S2a). Moreover, under assumption (S2a), we can deduce that for $\mathbb{P}$-a.e. ${\omega} \in \Omega$

\begin{equation*} \bigl[\mathbb{R}\ni t\mapsto b(\theta_t{\omega})\in \mathbb{R}\bigr] \in L_{\infty,\text{loc}}(\mathbb{R}). \end{equation*}

Under assumptions (S1) and (S2a), the initial value problem (4.8) with initial datum $u=(u_1,u_2)\in \widehat{L}$ has a unique solution $z(\cdot,{\omega},u)$, and as before for L, we will denote $ U^{( \widehat{L})}_{\omega}(t)\colon \widehat{L} \longrightarrow \widehat{L}$, $u \mapsto (z(t,{\omega},u),z_t({\omega},u))$. If we change $d({\omega})$ in (4.3) by

(5.1)\begin{equation} \widehat{d}({\omega}):= \text{ess\,sup}_{{-1\le s\le 0}} b(\theta_{s+1} {\omega}), \end{equation}

it is not hard to check that Proposition 4.14 of [19] holds for the new fiber space $ \widehat{L}$, that is, $\Phi^{(\widehat{L})}=\bigl((U^{(\widehat{L})}_{\omega}(t))_{{\omega} \in \Omega, t \in {\mathbb{R}}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ is a measurable linear skew-product semiflow on $\widehat{L}$ covering θ. This result was already stated and used in [19, p. 2254].

Next we prove the existence of a family of generalized principal Floquet subspaces for this case.

Theorem 5.2.

Under assumptions (S1), (S2a), (S3), and (S4), there is a family of generalized principal Floquet subspaces for the measurable linear skew-product semidynamical system $\Phi^{(\widehat{L})}=\bigl((U^{(\widehat{L})}_{\omega}(t))_{{\omega} \in \Omega, t \in {\mathbb{R}}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by (4.1), with generalized principal Lyapunov exponent $\widetilde{\lambda}^{(\widehat{L})}_1$.

Proof. First note that from [19, Lemma 5.8], we have ${\lVert U^{(\widehat{L})}_{\omega}(t)\rVert}\leq 3\,c({\omega})\,(1+\widehat d({\omega}))$, where $\widehat{d}$ is defined in (5.1). In addition, proposition 4.2 remains true when (S2a) is assumed instead of (S2). Hence, as in theorem 4.3, we can deduce step by step that conditions (A1) and (A3) hold for time $T=N+(N-1)M+1$ for the semiflow  $\Phi^{(\widehat{L})}$. Finally, theorem 2.5 shows that a family of generalized principal Floquet subspaces of $\Phi^{(\widehat L)}$ is obtained, as claimed.

Finally, from §3, an exponential separation of type II for the measurable linear skew-product semidynamical system $\Phi^{(\widehat{L})}$ is obtained.

Theorem 5.3.

Assume (S1), (S2a), (S3), and (S5). Then the measurable linear skew-product semidynamical system $\Phi^{(\widehat{L})}=\bigl((U^{(\widehat{L})}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by (4.1) admits a generalized exponential separation of type II with $\widetilde{\lambda}_1^{(\widehat{L})} \gt - \infty$.

Proof. From theorem 3.8, it suffices to check that conditions (A1) and (A3) hold, the operator $U^{(\widehat{L})}_{\omega}(2)$ is compact and $\widetilde{\lambda}_1^{(\widehat{L})} \gt - \infty$. Since condition (S4) is weaker that (S5), from the previous theorem we know that (A1) and (A3) hold. Moreover, the compactness of the operator $U^{(\widehat{L})}_{\omega}(2)$ is shown in [19, Lemma 5.9(iii)]. Finally, from lemma 3.5, we deduce that $\widetilde{\lambda}_1^{(\widehat{L})}=\lambda_{\mathrm{top}}$, so it suffices to show that $\lambda_{\mathrm{top}} \gt -\infty$, which can be done via Birkhoff ergodic theorem as in theorem 4.5 and finishes the proof.

5.2. Case 2

In this subsection, we briefly explain what happens for the separable Banach space $C=C([-1,0],{\mathbb{R}}^N)$ with the usual sup-norm when we maintain conditions (S1) and (S3)–(S5) and we replace (S2) by

1. (S2b) The $(\mathfrak{F}, \mathfrak{B}(\mathbb{R}))$-measurable functions a, $b\colon \Omega \to \mathbb{R}$ defined as $a({\omega}):={\lVert A({\omega})\rVert}$ and $b({\omega}):={\lVert B({\omega})\rVert}$ have the properties:

   \begin{align*} & \bigl[\Omega \ni {\omega} \mapsto a({\omega}) \in \mathbb{R}\bigr] \in L_1{(\Omega,\mathfrak{F},\mathbb{P})}, \text{and}\\ & \Bigl[\Omega \ni {\omega} \mapsto ln^{+} \int_{-1}^0 \!b(\theta_{s+1}{\omega})\,ds \in \mathbb{R} \, \Bigr] \in L_{1} {(\Omega,\mathfrak{F},\mathbb{P})}. \end{align*}

Remark 5.4.

Note that

\begin{equation*} \bigl[\Omega \ni {\omega} \mapsto b({\omega}) \in \mathbb{R}\bigr] \in L_{1} {(\Omega,\mathfrak{F},\mathbb{P})}.\end{equation*}

is sufficient for the second part of the assumption (S2b). Moreover, under assumption (S2b), we can deduce that for $\mathbb{P}$-a.e. ${\omega} \in \Omega$

\begin{equation*}\bigl[\mathbb{R}\ni t\mapsto b(\theta_t{\omega})\in \mathbb{R}\bigr] \in L_{1,\text{loc}}(\mathbb{R}).\end{equation*}

As in §4, it can be checked that, under assumptions (S1), (S2b), for each $u\in C$ the initial value problem (4.5) has a unique Carathéodory type solution which will be denoted by $z(\cdot,{\omega},u)$. Moreover, the cocycle relation (4.6) is also satisfied and we will use the same notation $U^{(C)}_{\omega}(t)$ for the corresponding linear operator (4.7). Then, a measurable linear skew-product semidynamical system is also obtained, as shown in the next result.

Proposition 5.5.

Under (S1) and (S2b), $\bigl((U^{(C)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ is a measurable linear skew-product semiflow on C covering θ.

Proof. First of all in (4.3), we change d by

\begin{equation*} \widetilde{d}({\omega}):=\int_{-1}^0 \!b(\theta_{s+1}{\omega})\,ds. \end{equation*}

From this, it is not difficult to check that

(5.2)\begin{equation} {\lVert U^{(C)}_{\omega}(t)\,u\rVert_{C}}\leq c({\omega})\,(1+\widetilde{d}({\omega}))\,{\lVert u\rVert_{C}} \quad\text{for each}\, t\in[0,1] \,\text{and}\, {\omega}\in\Omega, \end{equation}

and together with the cocycle property (4.6) we deduce that $U^{(C)}_{\omega}(t)\in \mathcal{L}(C)$ for each $t\geq 0$ and ${\omega}\in\Omega$. The rest of the proof follows step by step the one of [19, Proposition 4.12].

Theorem 5.6.

Under assumptions (S1), (S2b), (S3), and (S4), there is a family of generalized principal Floquet subspaces for the measurable linear skew-product semidynamical system $\Phi^{(C)}=\bigl((U^{(C)}_{\omega}(t))_{{\omega} \in \Omega, t \in {\mathbb{R}}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by (4.1), with generalized principal Lyapunov exponent $\widetilde{\lambda}^{(C)}_1$.

Proof. First note that proposition 4.2 remains true when (S2b) is assumed instead of (S2). Hence, from (5.2), as in theorem 4.3, we can deduce that conditions (A1) and (A3) hold for time $T=N+(N-1)M+1$ for the semiflow  $\Phi^{(C)}$. Finally, as in case 1, theorem 2.5 finishes the proof.

Finally, once we check that $U_{\omega}^{(C)}(1)$ is a compact operator for each ${\omega}\in\Omega$, from §3 an exponential separation of type II for the measurable linear skew-product semidynamical system $\Phi^{(C)}$ is obtained.

Lemma 5.7.

Under (S1) and (S2b), the bounded operator $U^{(C)}_{\omega}(1)$ is compact for any ${\omega}\in\Omega$.

Proof. First notice that the equicontinuity of the set $\{U^{(C)}_{\omega}(1)\,u: {\lVert u\rVert}_C\le 1\}$ follows from (S1), (S2b), (5.2), and the inequality

\begin{align*} \lVert(U^{(C)}_{\omega}(1)u)(s_1) & -(U^{(C)}_{\omega}(1)u)(s_2)\rVert_{C} \\ &\le \int_{1+s_1}^{1+s_2} a(\theta_{s}{\omega}){\lVert z(s,{\omega},u)\rVert}\,ds+\int_{s_1}^{s_2} \ b(\theta_{s+1}{\omega}){\lVert u(s)\rVert}\,ds \\ &\leq c({\omega})(1+\widetilde{d}({\omega})){\lVert u\rVert}_{C} \int_{1+s_1}^{1+s_2} a(\theta_{s}{\omega})\,ds+ {\lVert u\rVert}_{C} \int_{s_1}^{s_2} b(\theta_{s+1}{\omega})\,ds. \end{align*}

whenever $-1\le s_1\le s_2 \le 0$. Therefore from $U^{(C)}_{\omega}(1)\in \mathcal{L}(C)$, the Ascoli–Arzelà theorem finishes the proof.

Theorem 5.8.

Assume (S1), (S2b), (S3), and (S5). Then the measurable linear skew-product semidynamical system $\Phi^{(C)}=\bigl((U^{(C)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by (4.1) admits a generalized exponential separation of type II with $\widetilde{\lambda}_1^{(C)} \gt - \infty$.

Proof. From theorem 3.8, it suffices to check that conditions (A1) and (A3) hold, the operator $U^{(C)}_{\omega}(1)$ is compact and $\widetilde{\lambda}_1^{(C)} \gt - \infty$. Since condition (S4) is weaker that (S5), from the previous theorem and lemma we know that (A1) and (A3) hold and $U^{(C)}_{\omega}(1)$ is compact. Finally, from lemma 3.5, we deduce that $\widetilde{\lambda}_1^{(C)}=\lambda_{\mathrm{top}}$, so it suffices to show that $\lambda_{\mathrm{top}} \gt -\infty$, which can be done via Birkhoff ergodic theorem as in theorem 4.5 and finishes the proof.

5.3. Case 3

In this subsection, we briefly explain what happens for the separable Banach space of absolutely continuous functions $AC=AC([-1,0],{\mathbb{R}}^N)$ with the Sobolev type norm

\begin{equation*} {\lVert u\rVert_{AC}}={\lVert u\rVert_{C}}+{\lVert u'\rVert}_1=\sup_{s\in[-1,0]} {\lVert u(s)\rVert}+\int_{-1}^0 {\lVert u'(s)\rVert}\,ds \quad \text{for any}\, u\in AC. \end{equation*}

We maintain conditions (S1), (S2b) and (S3)–(S5) of case 2. The problem now is that this norm is not monotone and the cone is not normal, so that we cannot directly apply the results of the previous sections. As before, under assumptions (S1) and (S2b), for each $u\in AC$, the initial value problem (4.5) has a unique Carathéodory-type solution which will be denoted by $z(\cdot,{\omega},u)$. Moreover, the cocycle relation (4.6) is also satisfied and we can define the linear operator $ U^{(AC)}_{\omega}(t)\colon AC \longrightarrow AC$, $u \mapsto z_t({\omega},u)$.

First we show that a measurable linear skew-product semidynamical system is also obtained. Then, although the cone is not normal, we will maintain definitions 2.4 and 2.6 without this assumption to prove, by using some of the results in case 2, the existence of a family of generalized principal Floquet subspaces and a generalized exponential separation of type II in this case. The conclusion of this subsection is that these measurable notions can appear and be used in some natural phase spaces even with weaker properties on the positive cone.

Proposition 5.9.

Under (S1) and (S2b), $\bigl((U^{(AC)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^{+}}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ is a measurable linear skew-product semiflow on AC covering θ.

Proof. From [17, Theorem 4.6], we deduce that $U^{(AC)}_{\omega}(t)\in \mathcal{L}(AC)$ for each $t\geq 0$ and ${\omega}\in\Omega$. In order to check the $(\mathfrak{B}(\mathbb{R}^{+}) \otimes \mathfrak{F} \otimes \mathfrak{B}(AC), \mathfrak{B}(AC))$-measurability of the mapping $[\mathbb{R}^{+} \times \Omega \times AC \ni (t,{\omega},u) \mapsto U^{(AC)}_{\omega}(t)\,u \in AC ]$, as shown in [2, Lemma 4.51, pp. 153], it is enough to check that it is a Carathéodory function, i.e. for each ${\omega}\in\Omega$, the map $\mathbb{R}^+\times AC\to AC$, $(t,u) \mapsto U_{\omega}^{(AC)}(t)\,u=z_t({\omega},u)$ is continuous, which follows from [17, Theorem 4.6], and for each $t\in \mathbb{R}^+$ and $u\in AC$

(5.3)\begin{equation} [\Omega\ni {\omega} \mapsto U_{\omega}^{(AC)}(t)\,u=z_t({\omega},u)\in AC] \text{is} (\mathfrak{F}, \mathfrak{B}(AC))\text{-measurable}. \end{equation}

Moreover, from the cocycle property (2.1), it is enough to check this property for each $t\in (0,1]$. First notice that $AC\simeq \mathbb{R}^N \times L_1([-1,0],\mathbb{R}^N)$ and then its dual space $(AC)^*\simeq \mathbb{R}^N\times L_\infty([-1,0],\mathbb{R}^N)$. Since AC is separable, from Pettis’ Theorem (see Hille and Phillips [13, Theorem 3.5.3 and Corollary 2 on pp. 72–73]) the weak and strong measurability notions are equivalent. Thus, to prove (5.3), it is enough to check that, for each $(v_1, v_2)\in \mathbb{R}^N\times L_\infty([-1,0],\mathbb{R}^N)$, $u\in AC$ and $t\in(0,1]$, the mapping

\begin{equation*} \bigl[\Omega\ni{\omega}\mapsto \big(\langle v_1,z(t,{\omega},u)\rangle + \langle v_2, (U_{\omega}^{(AC)}(t)\,u)'\rangle\big) \in \mathbb{R}\bigr] \text{is} (\mathfrak{F}, \mathfrak{B}(\mathbb{R}))\text{-measurable}, \end{equation*}

which follows from

\begin{align*} \langle v_2,(U_{\omega}^{(AC)}(t)\,u)'\rangle &=\int_{-1}^0 (v_2(\tau))^t z'(t+\tau,{\omega},u)\,d\tau \\ &=\int_{-1}^{-t} (v_2(\tau))^t\,u'(t+\tau)\, d\tau +\int_{0}^t (v_2(\tau-t))^t \, z'(\tau,{\omega},u)\,d\tau \\ &= \int_{-1}^{-t} (v_2(\tau))^t u'(t+\tau) d\tau +\int_0^t (v_2(\tau-t))^t A(\theta_{\tau}{\omega}) z(\tau,{\omega},u) d\tau \\ &\quad + \int_0^t (v_2(\tau-t))^t \, B(\theta_{\tau}{\omega})\,z(\tau-1,{\omega},u) \,d\tau \end{align*}

and similar arguments to those of [19, Lemmma 4.13].

In order to relate both semiflows $\Phi^{(AC)}$ and $\Phi^{(C)}$ (case 2), we define for each $t\geq 1$ the linear map

(5.4)\begin{equation} \begin{array}{lccc} U^{(C,AC)}_{\omega}(t)\colon & C &\longrightarrow & AC\\ [.1cm] & u & \mapsto & z_t({\omega},u). \end{array} \end{equation}

Proposition 5.10.

Under (S1) and (S2b), for any ${\omega}\in\Omega$, $U^{(C,AC)}_{\omega}(t)\in \mathcal{L}(C, AC)$ for each $t\geq 1$ and it is a compact operator for each $t\geq 2$.

Proof. First we check the result for t = 1 and each ${\omega}\in\Omega$. Take $u\in AC $; from the definition of the norm, proposition 5.5 and the delay differential equation (4.1), we deduce that

(5.5)\begin{align} {\lVert U^{(C,AC)}_{\omega}(1)\,u\rVert_{AC}} &= {\lVert z_1({\omega},u)\rVert_{C}}+\int_{-1}^0 {\lVert z'(1+s,{\omega},u)\rVert} \, ds \nonumber\\ & \leq {\lVert z_1({\omega},u)\rVert_{C}}\left(1 + \int_0^1 \!\!a(\theta_s{\omega}) \,ds\right) + \widetilde d({\omega}) \,{\lVert u\rVert_{C}} \nonumber\\ & \leq \left( c({\omega})(1+\widetilde{d}({\omega}))\left(1+ \int_0^1 \!\!a(\theta_s{\omega}) \,ds\right)+ \widetilde{d}({\omega})\right){\lVert u\rVert_{C}}\nonumber\\ &:=e({\omega}) \,{\lVert u\rVert_{C}} \end{align}

which shows that $U^{(C,AC)}_{\omega}(1)\in \mathcal{L}(C, AC)$. Next, from the cocycle property (4.6), we deduce that $U_{\omega}^{(C,AC)}(t)= U_{\theta_{t - 1} {\omega}}^{(C,AC)}(1) \circ U_{\omega}^{(C)}(t - 1) \in \mathcal{L}(C, AC)$ for each $t\geq 1$ and ${\omega}\in\Omega$. Moreover, from lemma 5.7, we know that $U_{\omega}^{(C)}(t)$ is compact for each ${\omega}\in\Omega$ and $t\geq 1$, so that the above composition proves the compactness of $U_{\omega}^{(C,AC)}(t)$ for each ${\omega}\in\Omega$ and $t\geq 2$, as claimed.

Corollary 5.11.

Under assumptions (S1) and (S2b), $U^{(AC)}_\omega(t)$ is a compact operator for any $t \ge 2$ and $\omega \in \Omega$.

Proof. It is a consequence of the continuity of the map $i\colon AC\to C$, $u\mapsto u$ and the previous result.

As a consequence, from [19, Theorem 3.4], we deduce that $\Phi^{(AC)}$ also admits an Oseledets decomposition and the next theorem shows the coincidence of the Lyapunov exponents for both semiflows $\Phi^{(AC)}$ and $\Phi^{(C)}$ (case 2). We refer the reader to [19] for all definitions and also the corresponding results for $\Phi^{(C)}$ and $\Phi^{(L)}$ that were proved in that paper. First we need the following lemma.

Lemma 5.12.

Assume (S1), (S2b) and consider the function e defined in (5.5). Then for $\mathbb{P}$-a.e. ${\omega}\in\Omega$

\begin{equation*} \limsup_{t\to\infty} \frac{\ln e(\theta_t {\omega})}{t}\leq 0.\end{equation*}

Proof. As in [19, Lemma 5.1], it is enough to check that $ln^{+}{e} \in L^1{(\Omega,\mathfrak{F},\mathbb{P})}$. From [18, Lemma 5.6] and inequality (4.4), we deduce that there is an integer number n ₀ such that

\begin{equation*} ln^{+} e({\omega}) \leq 2 \int_0^1 a(\theta_s{\omega})\,ds + 2\,ln^{+}\widetilde{d}({\omega}) + \ln n_0 \end{equation*}

and the claim follows from (S2b), Fubini’s theorem and the invariance of $\mathbb{P}$.

Theorem 5.13.

Under assumptions (S1) and (S2b), the sets of Lyapunov exponents for $\Phi^{(AC)}$ and $\Phi^{(C)}$ coincides.

Proof. Let $\lambda^{(C)}$ be a Lyapunov exponent for $\Phi^{(C)}$ and nonzero $u\in C$. First notice that for each $t\geq 0$ we have $U_\omega^{(C,AC)}(t+1){}u=U_{\theta_t\omega}^{(C,AC)}(1)(U_\omega^{(C)}(t){}u)\in AC$. Thus, from (5.5) we deduce that

\begin{equation*} {\lVert U_{\omega}^{(C)}(t+1)\,u\rVert_{C}}\leq {\lVert U_{\omega}^{(C,AC)}(t+1)\,u\rVert_{AC}}\leq e(\theta_t{\omega}) \, {\lVert U^{(C)}_{\omega}(t) \, u\rVert_{C}}.\end{equation*}

Therefore, from the definition of $\lambda^{(C)}$ and lemma 5.12, we deduce that

\begin{align*} \lambda^{(C)}&=\lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(C)}(t+1)\,u\rVert_{C}}}{t+1} \leq \lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(C,AC)}(t+1)\,u\rVert_{AC}}}{t+1} \\ &\leq \limsup_{t \to \infty}\frac{\ln e(\theta_{t}\omega)}{t} + \lim_{t \to \infty} \frac{\ln{{\lVert U^{(C)}_{\omega}(t) \,u\rVert_{C}}}}{t}\leq \lambda^{(C)}, \end{align*}

That is,

\begin{equation*} \lambda^{(C)}= \lim_{t\to\infty} \frac{\ln {\lVert U_{\omega}^{(C,AC)}(t+1)\,u\rVert_{AC}}}{t+1}= \lim_{t\to\infty} \frac{\ln {\lVert U_{\theta_1{\omega}}^{(AC)}(t)\, U_{\omega}^{C}(1)\,u\rVert_{AC}}}{t}\, \end{equation*}

is a Lyapunov exponent for $\Phi^{(AC)}$ and nonzero $ U_{\omega}^{C}(1)\,u\in AC$. When $u\in AC$, the above inequalities show that each Lyapunov exponent for $\Phi^{(AC)}$ and nonzero $u\in AC$ is a Lyapunov exponent for $\Phi^{(C)}$, which finishes the proof.

Lemma 5.14.

Let $U_{\omega}^{(C,AC)}(1)$ be the linear operator defined in (5.4). Then the mapping

\begin{equation*}[\Omega\times C\ni ({\omega},u) \mapsto U_{\omega}^{(C,AC)}(1)\,u \in AC ] \text{is}(\mathfrak{F}\otimes\mathfrak{B}(C), \mathfrak{B}(AC))\text{-measurable}.\end{equation*}

Proof. As in lemma 4.6, it is enough to check that it is a Carathéodory function, i.e. for each fixed ${\omega}\in\Omega$, the map C → AC, $u\mapsto U_{\omega}^{(C,AC)}(1)\,u$ is continuous, which follows from proposition 5.10, and for each fixed $u\in C$, the map

(5.6)\begin{equation} [\Omega\ni {\omega} \mapsto U_{\omega}^{(C,AC)}(1)\,u=z_1({\omega},u)\in AC] \,\text{is}\, (\mathfrak{F}, \mathfrak{B}(AC))\text{-measurable}. \end{equation}

In order to prove this, we take a sequence of functions $u_n\in AC$ converging to $u\in C$ as $n \uparrow\infty$. Thus, the measurability of the maps $[\Omega\ni {\omega} \mapsto z_1({\omega},u_n)\in AC]$ for each $n\in\mathbb{N}$, shown in (5.3), the convergence of them to the map (5.6) as $n \uparrow\infty$ and [2, Corollary 4.29] show the measurability, which finishes the proof.

Theorem 5.15.

Under assumptions (S1), (S2b), (S3), and (S4), there is a family of generalized principal Floquet subspaces for the measurable linear skew-product semidynamical system $\Phi^{(AC)}=\bigl((U^{(AC)}_{\omega}(t))_{{\omega} \in \Omega, t \in {\mathbb{R}}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by (4.1), with generalized principal Lyapunov exponent $\widetilde{\lambda}^{(AC)}_1=\widetilde{\lambda}^{(C)}_1 \gt -\infty$.

Proof. Theorem 5.6 states the existence of a family $\{E_1^{(C)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ of generalized principal Floquet subspaces for $\Phi^{(C)}$ with generalized principal Lyapunov exponent $\widetilde{\lambda}^{(C)}_1$. For ${\omega} \in \widetilde{\Omega}_1$, put $E_1^{(C)}({\omega}) := \text{span}\{w^{(C)}({\omega})\}$ with ${\lVert w^{(C)}({\omega})\rVert_{C}} = 1$. First notice that from (5.4)

\begin{equation*} U_{\theta_{-1}w}^{(C,AC)}(1)\,w^{(C)}(\theta_{-1}{\omega}) =z_1(\theta_{-1}{\omega} ,w^{(C)}(\theta_{-1}{\omega})) \quad \text{belongs to}\, AC \end{equation*}

and is proportional to $w^{(C)}({\omega})$ because $U_{\theta_{-1}w}^{(C)}(1)E_1^{(C)}(\theta_{-1} w)=E_1^{(C)}({\omega})$. Next, we define $w^{(AC)}({\omega}) := U_{\theta_{-1}{\omega}}^{(AC)}(1) \, w^{(C)}(\theta_{-1}{\omega}) / {\lVert U_{\theta_{-1}{\omega}}^{(AC)}(1) \, w^{(C)}(\theta_{-1}{\omega})\rVert_{AC}} $, unitary and proportional to $w^{(C)}({\omega})$. Then $E_1^{(AC)}({\omega}):=\text{span}\{w^{(AC)}({\omega})\}=E_1^{(C)}({\omega})$ is a one-dimensional subspace of AC and we claim that $\{E_1^{(AC)}({\omega})\}_{{\omega} \in \widetilde\Omega_1}$ is a family of generalized principal Floquet subspaces for $\Phi^{(AC)}$, i.e. conditions (i)–(iv) of definition 2.4 are satisfied. First of all, from lemma 5.14 it is easy to check that $w^{(AC)}\colon\widetilde\Omega_1\to AC^+\setminus \{0\}$ is $(\mathfrak{F}, \mathfrak{B}(AC))$-measurable and thus, (i) holds. Condition (ii) follows from $U_{\omega}^{(AC)}(t)\,E_1^{(AC)}({\omega})=U_{\omega}^{C}(t)\,E_1^{(C)}({\omega})=E_1^{(C)}(\theta_t{\omega})$. From theorem 5.13, we deduce conditions (iii)–(iv) and the coincidence of the generalized Lyapunov exponents because both $w^{(C)}({\omega})$ and $w^{(AC)}({\omega})$ belong to AC.

Finally, once we have checked that $\widetilde\lambda_1^{(AC)} \gt -\infty$ and $U^{(AC)}_\omega(2)$ is a compact operator, from theorem 3.1 and the previous theorem an exponential separation of type II for the measurable linear skew-product semidynamical system $\Phi^{(AC)}$ is obtained.

Theorem 5.16.

Assume (S1), (S2b), (S3), and (S5). Then the measurable linear skew-product semidynamical system $\Phi^{(AC)}=\bigl((U^{(AC)}_{\omega}(t))_{{\omega} \in \Omega, t \in \mathbb{R}^+}, (\theta_{t})_{t \in \mathbb{R}}\bigr)$ generated by system (4.1) admits a generalized exponential separation of type II with $\widetilde{\lambda}_1^{(AC)} \gt - \infty$.

Proof. From theorem 3.1, we obtain a measurable decomposition of AC. In addition, from the previous theorem the first term is the one-dimensional subspace $E_1^{(AC)}({\omega})$ with $\lambda_{\mathrm{top}}=\widetilde{\lambda}^{(AC)}_1 \gt -\infty$. Then, we denote $AC=E_1^{(AC)}({\omega})\oplus F_1^{(AC)}({\omega})$ where $F_1^{(AC)}({\omega})= AC\cap F_1^{(C)}({\omega})$ for $\mathbb{P}$-a.e. ${\omega}\in\Omega$. Properties (i) and (ii) of definition 2.6 are immediate and finally (iii) is deduced from theorem 5.8 following the arguments of theorem 4.8.