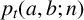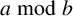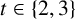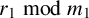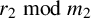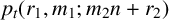1. Introduction and statement of results
A partition
![]() $\lambda $
, which is a nonincreasing sequence of positive integers summing to some integer n, can be represented visually by a collection of boxes arranged in left-justified rows. The row lengths are arranged in nonincreasing order and correspond to the size of each part of
$\lambda $
, which is a nonincreasing sequence of positive integers summing to some integer n, can be represented visually by a collection of boxes arranged in left-justified rows. The row lengths are arranged in nonincreasing order and correspond to the size of each part of
![]() $\lambda $
. Such a presentation is called the Ferrers–Young diagram for
$\lambda $
. Such a presentation is called the Ferrers–Young diagram for
![]() $\lambda $
. In such a diagram, we may refer to the cells by their place in this array; we will denote the cell in row i and column j by
$\lambda $
. In such a diagram, we may refer to the cells by their place in this array; we will denote the cell in row i and column j by
![]() $(i,j)$
.
$(i,j)$
.
We define the hook of
![]() $(i,j)$
to be the collection of cells
$(i,j)$
to be the collection of cells
![]() $(a,b)$
such that
$(a,b)$
such that
![]() $a=i$
and
$a=i$
and
![]() $b \geq j$
or
$b \geq j$
or
![]() $a \geq i$
and
$a \geq i$
and
![]() $b=j$
. The length of such a hook is the cardinality of this set, which we will denote by
$b=j$
. The length of such a hook is the cardinality of this set, which we will denote by
![]() $h(i,j)$
. We will call a hook a t-hook if its length is divisible by t. For example, the hook lengths
$h(i,j)$
. We will call a hook a t-hook if its length is divisible by t. For example, the hook lengths
![]() $h(i,j)$
for the partition
$h(i,j)$
for the partition
![]() $3+2+1$
are labelled in their respective cells as
$3+2+1$
are labelled in their respective cells as

A study of hook numbers enriches many areas where partitions naturally arise. For instance, recall that the partitions of n parametrise the irreducible complex representations of the symmetric group on n letters. Moreover, the degree of such a representation
![]() $\rho _{\lambda }\colon S_n \to \text {GL}(V_{\lambda })$
is given by the Frame–Thrall–Robinson hook length formula: if
$\rho _{\lambda }\colon S_n \to \text {GL}(V_{\lambda })$
is given by the Frame–Thrall–Robinson hook length formula: if
![]() $\lambda $
is a partition of n and
$\lambda $
is a partition of n and
![]() $p_{\lambda }$
is an irreducible complex representation of
$p_{\lambda }$
is an irreducible complex representation of
![]() $S_n$
as above, then
$S_n$
as above, then
 $$ \begin{align*} \dim(V_{\lambda})= \frac{n!}{\prod_{h(i,j) \in \mathcal{H}(\lambda)}h(i,j)}, \end{align*} $$
$$ \begin{align*} \dim(V_{\lambda})= \frac{n!}{\prod_{h(i,j) \in \mathcal{H}(\lambda)}h(i,j)}, \end{align*} $$
where
![]() $\mathcal {H}(\lambda )$
is the multiset of hook lengths of cells in the Ferrers–Young diagram for
$\mathcal {H}(\lambda )$
is the multiset of hook lengths of cells in the Ferrers–Young diagram for
![]() $\lambda $
[Reference Frame, de B. Robinson and Thrall4].
$\lambda $
[Reference Frame, de B. Robinson and Thrall4].
Further, recall the famous q-series identities of Euler and Jacobi:
 $$ \begin{align*} q \prod_{n=1}^\infty (1-q^{24n}) &= q-q^{25}-q^{49}+q^{121}+q^{169}-\cdots \\ q \prod_{n=1}^\infty (1-q^{8n})^3 &= q-3q^9+5q^{25}-7q^{49}+11q^{121}-\cdots{.} \end{align*} $$
$$ \begin{align*} q \prod_{n=1}^\infty (1-q^{24n}) &= q-q^{25}-q^{49}+q^{121}+q^{169}-\cdots \\ q \prod_{n=1}^\infty (1-q^{8n})^3 &= q-3q^9+5q^{25}-7q^{49}+11q^{121}-\cdots{.} \end{align*} $$
These identities appear as specialisations of the Nekrasov–Okounkov hook length formula, which is derived by taking a z-deformation of the generating function for the partition function. In particular, for any complex number z,
 $$ \begin{align*}\prod_{n=1}^\infty(1-q^n)^{z-1} = \sum_{\lambda} q^{|\lambda|} \prod_{h(i,j) \in \mathcal{H}(\lambda)} \bigg(1-\frac{z}{h(i,j)^2}\bigg).\end{align*} $$
$$ \begin{align*}\prod_{n=1}^\infty(1-q^n)^{z-1} = \sum_{\lambda} q^{|\lambda|} \prod_{h(i,j) \in \mathcal{H}(\lambda)} \bigg(1-\frac{z}{h(i,j)^2}\bigg).\end{align*} $$
This result, in which hook lengths appear prominently, constitutes a significant generalisation of many new and classical number-theoretic results on q-series.
We are motivated to explore the number of t-hooks across all partitions of size n in an attempt to obtain an analogue of Dirichlet’s theorem on primes in arithmetic progressions. There has been recent work on the distribution of partitions where the number of t-hooks lie in a fixed progression and it turns out that, unlike Dirichlet’s theorem, equidistribution does not hold in general. Going beyond unequal distribution, there are situations where such counts are identically zero. For example, Table 1 shows results of [Reference Bringmann, Craig, Males and Ono1] for congruence classes of the number of 2-hooks mod 3 for selected integers n.
Table 1 2-Hooks modulo 3.

This example highlights one of the more striking instances of the unequal distribution of t-hooks that has been observed in recent work (see [Reference Bringmann, Craig, Males and Ono1, Reference Craig and Pun3]). In particular, these results construct arithmetic progressions where these counts are identically zero. The existing proofs make use of the theory of theta functions to find exact formulae for the asymptotic behaviour of the number of t-hooks in a particular arithmetic progression. In this note, however, we argue the following result directly by appealing to the combinatorial study of hook lengths through abaci.
Theorem 1.1 [Reference Bringmann, Craig, Males and Ono1, Theorem 1.3]
Let
![]() $({\cdot }/{\ell })$
denote the Legendre symbol and
$({\cdot }/{\ell })$
denote the Legendre symbol and
![]() $\mathrm {ord}_\ell (n)$
the
$\mathrm {ord}_\ell (n)$
the
![]() $\ell $
-adic valuation of n. Then the following statements hold.
$\ell $
-adic valuation of n. Then the following statements hold.
-
(1) If
 $\ell $
is an odd prime and
$\ell $
is an odd prime and
 $a_1,a_2$
are integers for which
$a_1,a_2$
are integers for which
 $({-16a_1+8a_2+1}/{\ell })=-1$
, then
$({-16a_1+8a_2+1}/{\ell })=-1$
, then
 $ p_2(a_1,\ell ;\ell k+a_2)=0. $
$ p_2(a_1,\ell ;\ell k+a_2)=0. $
-
(2) If
 $\ell \equiv 2 \bmod {3}$
is prime and
$\ell \equiv 2 \bmod {3}$
is prime and
 $a_1,a_2$
are integers for which
$a_1,a_2$
are integers for which
 $\mathrm {ord}_{\ell }(-9a_1 \kern-1pt +\kern-1pt 3a_2 \kern-1pt +\kern-1pt 1)=1$
, then
$\mathrm {ord}_{\ell }(-9a_1 \kern-1pt +\kern-1pt 3a_2 \kern-1pt +\kern-1pt 1)=1$
, then
 $ p_3(a_1,\ell ^2;\ell ^2 k+a_2)=0. $
$ p_3(a_1,\ell ^2;\ell ^2 k+a_2)=0. $
Example 1.2. Let
![]() $\ell = 5$
,
$\ell = 5$
,
![]() $a_1=1$
and
$a_1=1$
and
![]() $a_2=1$
. Observe that
$a_2=1$
. Observe that
![]() $( {-16a_1+8a_2+1}/{5}) = -1$
and
$( {-16a_1+8a_2+1}/{5}) = -1$
and
![]() $\mathrm {ord}_{5}(-9a_1+3a_2+1)=1$
. Thus, if
$\mathrm {ord}_{5}(-9a_1+3a_2+1)=1$
. Thus, if
![]() $n \equiv 1 \bmod {5}$
, we have
$n \equiv 1 \bmod {5}$
, we have
![]() $p_2(1,5,n)=0$
; that is, there does not exist a partition
$p_2(1,5,n)=0$
; that is, there does not exist a partition
![]() $\lambda $
of n where the number of
$\lambda $
of n where the number of
![]() $2$
-hooks of
$2$
-hooks of
![]() $\lambda $
is equivalent to 1 mod 5. Likewise, if
$\lambda $
is equivalent to 1 mod 5. Likewise, if
![]() $n \equiv 1 \bmod {25},$
then
$n \equiv 1 \bmod {25},$
then
![]() $p_3(1,25;n)=0$
.
$p_3(1,25;n)=0$
.
In the following sections, we make use of a well-known bijection between integer partitions and their decompositions into t-cores and t-quotients. We are then able to approach the theorem directly using the theory of abaci and a naturally appearing positive definite binary quadratic form intimately related to the problem.
2. Nuts and bolts
2.1. Cores and quotients
Fix an integer t. A partition which does not contain any t-hooks is called a t-core. We may construct a t-core
![]() $\tilde {\lambda }$
from an arbitrary partition
$\tilde {\lambda }$
from an arbitrary partition
![]() $\lambda $
by removing rim t-hooks from the Ferrers–Young diagram of
$\lambda $
by removing rim t-hooks from the Ferrers–Young diagram of
![]() $\lambda $
. Moreover, this t-core is unique. To this end, [Reference Garvan, Kim and Stanton5] describes an algorithm for finding both the core and quotient of a partition by systematically removing rim-hooks from
$\lambda $
. Moreover, this t-core is unique. To this end, [Reference Garvan, Kim and Stanton5] describes an algorithm for finding both the core and quotient of a partition by systematically removing rim-hooks from
![]() $\lambda $
to build a t-quotient and arrive at the t-core of a partition.
$\lambda $
to build a t-quotient and arrive at the t-core of a partition.
The following is a well-known bijection which identifies a partition with its t-core and a t-tuple of partitions called its t-quotient. In particular, let P denote the space of all partitions,
![]() $c_t(P)$
all t-core partitions and
$c_t(P)$
all t-core partitions and
![]() $q_t(P)$
the space of t-quotients, which is isomorphic to the direct product of t copies of P. With this notation, there is a bijection
$q_t(P)$
the space of t-quotients, which is isomorphic to the direct product of t copies of P. With this notation, there is a bijection
![]() $\varphi : P \to c_t(P) \times q_t(P)$
given by
$\varphi : P \to c_t(P) \times q_t(P)$
given by
In particular,
 $$ \begin{align} |\lambda|=|\tilde{\lambda}|+ t \cdot \sum_{i=0}^{t-1}|\lambda_i|. \end{align} $$
$$ \begin{align} |\lambda|=|\tilde{\lambda}|+ t \cdot \sum_{i=0}^{t-1}|\lambda_i|. \end{align} $$
This decomposition is classical and gives rise to the fact that for a given partition
![]() $\lambda $
, the size of its corresponding t-quotient given by
$\lambda $
, the size of its corresponding t-quotient given by
![]() $\sum _{i=0}^{t-1}|\lambda _i|$
is a count of the number of t-hooks contained in
$\sum _{i=0}^{t-1}|\lambda _i|$
is a count of the number of t-hooks contained in
![]() $\lambda $
(for example, see [Reference Olsson8, Theorem 3.3]). To make full use of the content of this bijection, we will revisit this result in the context of abaci theory.
$\lambda $
(for example, see [Reference Olsson8, Theorem 3.3]). To make full use of the content of this bijection, we will revisit this result in the context of abaci theory.
2.2. Abaci
We may encode the data of a partition
![]() $\lambda $
of n in an abacus. To do this, let
$\lambda $
of n in an abacus. To do this, let
![]() $\lambda = \{\lambda _1 \geq \lambda _2 \geq \cdots \lambda _s> 0\}$
. For
$\lambda = \{\lambda _1 \geq \lambda _2 \geq \cdots \lambda _s> 0\}$
. For
![]() $1\leq i \leq s$
, define the ith structure number
$1\leq i \leq s$
, define the ith structure number
![]() $B_i$
by
$B_i$
by
![]() ${B_i = \lambda _i - i + s}$
; that is, the structure number
${B_i = \lambda _i - i + s}$
; that is, the structure number
![]() $B_i$
is the hook number of the entry in the ith row and first column of the Young diagram.
$B_i$
is the hook number of the entry in the ith row and first column of the Young diagram.
Now, create an abacus with t vertical runners labelled
![]() $0$
through
$0$
through
![]() $t-1$
, each infinitely long. We will place beads on the runners in accordance with the structure numbers. In particular, the
$t-1$
, each infinitely long. We will place beads on the runners in accordance with the structure numbers. In particular, the
![]() $B_i$
are positive integers and thus there exist (by Euclidean division) unique integers
$B_i$
are positive integers and thus there exist (by Euclidean division) unique integers
![]() $r_i$
and
$r_i$
and
![]() $c_i$
such that
$c_i$
such that
We place a bead representing
![]() $B_i$
in the row and column position
$B_i$
in the row and column position
![]() $(r_i,c_i)$
on the abacus.
$(r_i,c_i)$
on the abacus.
For example, consider the partition
![]() $\lambda = (5, 3, 2, 1)$
. We find
$\lambda = (5, 3, 2, 1)$
. We find
![]() $B_1=\lambda _1 -1 + 4 = 5-1+4 = 8$
. Likewise,
$B_1=\lambda _1 -1 + 4 = 5-1+4 = 8$
. Likewise,
![]() $B_2=5$
,
$B_2=5$
,
![]() $B_3=3$
and
$B_3=3$
and
![]() $B_4=1$
. The corresponding abacus with
$B_4=1$
. The corresponding abacus with
![]() ${t=3}$
is
${t=3}$
is
 $$ \begin{align*}\begin{array}{c|ccc} 1& \cdot & \circ & \cdot \\ 2& \circ & \cdot & \circ \\ 3& \cdot & \cdot & \circ \\ \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{c|ccc} 1& \cdot & \circ & \cdot \\ 2& \circ & \cdot & \circ \\ 3& \cdot & \cdot & \circ \\ \end{array}\end{align*} $$
Conversely, given an abacus with beads in positions
![]() $\{(r_i,c_i)\}$
, we can construct a decreasing sequence
$\{(r_i,c_i)\}$
, we can construct a decreasing sequence
![]() $B_1 \geq \cdots \geq B_k$
by defining
$B_1 \geq \cdots \geq B_k$
by defining
![]() $B_i=t(r_i-1)+c_i$
. Then we can find a corresponding partition by setting
$B_i=t(r_i-1)+c_i$
. Then we can find a corresponding partition by setting
![]() $\lambda _i=B_i+i-s$
.
$\lambda _i=B_i+i-s$
.
Lemma 2.1. Removing a t-hook from a partition
![]() $\lambda $
is equivalent to sliding a bead up one row on the abacus representing
$\lambda $
is equivalent to sliding a bead up one row on the abacus representing
![]() $\lambda $
.
$\lambda $
.
Proof. Let
![]() $\{B_1,B_2,\ldots ,B_k\}$
be a set of structure numbers for the partition
$\{B_1,B_2,\ldots ,B_k\}$
be a set of structure numbers for the partition
![]() $\lambda $
. Removing a rim t-hook T from
$\lambda $
. Removing a rim t-hook T from
![]() $\lambda $
is equivalent to subtracting t from some structure number
$\lambda $
is equivalent to subtracting t from some structure number
![]() $B_\ell $
, resulting in the set of structure numbers
$B_\ell $
, resulting in the set of structure numbers
![]() $\{B_1,\ldots ,B_{\ell -1},B_{\ell }-t,B_{\ell +1},\ldots ,B_k\}$
for
$\{B_1,\ldots ,B_{\ell -1},B_{\ell }-t,B_{\ell +1},\ldots ,B_k\}$
for
![]() $\lambda \setminus T$
[Reference James and Kerber7, Lemma 2.7.13].
$\lambda \setminus T$
[Reference James and Kerber7, Lemma 2.7.13].
By construction, the bead position on the abacus for
![]() $B_{\ell }$
is given by
$B_{\ell }$
is given by
![]() $(r_{\ell },c_{\ell })$
, where
$(r_{\ell },c_{\ell })$
, where
![]() $B_{\ell }=t(r_{\ell }-1)+c_{\ell }$
. Then
$B_{\ell }=t(r_{\ell }-1)+c_{\ell }$
. Then
and so removing a t-hook has the effect of sliding a bead up one row on the abacus.
Since rows in the abacus representing the partition
![]() $\lambda $
are labelled with nonnegative integers, and sliding a bead upward on the abacus fixes the column while subtracting one from the row number, the process of removing t-hooks can only be done finitely many times before arriving at an abacus representing the t-core of
$\lambda $
are labelled with nonnegative integers, and sliding a bead upward on the abacus fixes the column while subtracting one from the row number, the process of removing t-hooks can only be done finitely many times before arriving at an abacus representing the t-core of
![]() $\lambda $
.
$\lambda $
.
Furthermore, since removing a t-hook corresponds to sliding a bead upward on the abacus, an abacus representing a t-core partition has no gaps between beads in any column, and any nonempty column has a bead in the first row [Reference Ono and Sze9, Theorem 4]. Following this observation, we may restate (2.1) in terms of the t-hooks contained in
![]() $\lambda $
.
$\lambda $
.
Corollary 2.2. Let
![]() $h_t(\lambda )$
denote the number of t-hooks contained in
$h_t(\lambda )$
denote the number of t-hooks contained in
![]() $\lambda $
and let
$\lambda $
and let
![]() $\tilde {\lambda }$
denote its t-core. Then
$\tilde {\lambda }$
denote its t-core. Then
![]() $|\lambda | = |\tilde {\lambda }| + t \cdot h_t(\lambda ).$
$|\lambda | = |\tilde {\lambda }| + t \cdot h_t(\lambda ).$
We may thus denote the abaci of t-cores by t-tuples of nonnegative integers, indicating the number of beads in each column. However, there are multiple abaci which represent a single t-core partition.
Lemma 2.3 [Reference Ono and Sze9, Lemma 1]
The two abaci
represent the same t-core partition.
By repeatedly applying the above lemma, we may find a unique abacus representation for a given t-core containing zero beads in the first column. Thus, a tuple
![]() $(0, a_1, \ldots , a_{t-1})$
uniquely represents a t-core.
$(0, a_1, \ldots , a_{t-1})$
uniquely represents a t-core.
2.3. Structure theorem for 2- and 3-cores
We now specialise to the cases where t is two or three. Using the theory of abaci, we are able to completely classify
![]() $2$
- and
$2$
- and
![]() $3$
-core partitions by looking at the divisors of
$3$
-core partitions by looking at the divisors of
![]() $8n+1$
and
$8n+1$
and
![]() $3n+1$
, respectively.
$3n+1$
, respectively.
Theorem 2.4. Let
![]() $c_t(n)$
denote the number of t-core partitions of n.
$c_t(n)$
denote the number of t-core partitions of n.
-
(1) We have
 $c_2(n) = 1$
if
$c_2(n) = 1$
if
 $8n+1$
is an odd square, and 0 otherwise.
$8n+1$
is an odd square, and 0 otherwise. -
(2) We have
 $c_3(n) = \sum _{d \mid 3n+1} ({d}/{3}).$
In particular,
$c_3(n) = \sum _{d \mid 3n+1} ({d}/{3}).$
In particular,
 $c_3(n)\neq 0$
if and only if for all primes
$c_3(n)\neq 0$
if and only if for all primes
 $p \equiv 2 \bmod {3}$
,
$p \equiv 2 \bmod {3}$
,
 $\mathrm { ord}_p(3n+1)$
is even.
$\mathrm { ord}_p(3n+1)$
is even.
Remark 2.5. The equality in (1) is classical by considering the self-conjugate partitions arising from triangular numbers. The equality in (2) was first proven in [Reference Granville and Ono6] by comparing coefficients of closely related modular forms.
Sketch of Proof. The case
![]() $t=2$
. First, we show that n is a triangular number if and only if
$t=2$
. First, we show that n is a triangular number if and only if
![]() $8n+1$
is an odd square. A triangular number has the form
$8n+1$
is an odd square. A triangular number has the form
![]() $n={k(k+1)}/{2}$
for some integer k. Then
$n={k(k+1)}/{2}$
for some integer k. Then
Certainly, if n is a triangular number, we have a partition
![]() $\lambda $
where the the parts are given by
$\lambda $
where the the parts are given by
![]() $\lambda _i = k-i+1$
for
$\lambda _i = k-i+1$
for
![]() $1 \leq i \leq k$
, where
$1 \leq i \leq k$
, where
![]() $n=k(k+1)/2$
. We can check that this partition is indeed a 2-core by simply noting every hook is symmetric, so the hook length is of the form
$n=k(k+1)/2$
. We can check that this partition is indeed a 2-core by simply noting every hook is symmetric, so the hook length is of the form
![]() $2k+1$
for suitable k.
$2k+1$
for suitable k.
Now suppose
![]() $\lambda $
is a 2-core partition of n. Then some abacus
$\lambda $
is a 2-core partition of n. Then some abacus
![]() $\mathfrak {A}=(0,a)$
uniquely represents
$\mathfrak {A}=(0,a)$
uniquely represents
![]() $\lambda $
and has the shape
$\lambda $
and has the shape
 $$ \begin{align*}\begin{array}{c|cc} 1& \cdot & \circ \\ \vdots & \vdots &\vdots \\ a& \cdot & \circ \\ \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{c|cc} 1& \cdot & \circ \\ \vdots & \vdots &\vdots \\ a& \cdot & \circ \\ \end{array}\end{align*} $$
Note that
![]() $B_i = 2(a-i)+1, 1\leq i \leq a$
, and that a is the number of parts of the partition. Then recalling
$B_i = 2(a-i)+1, 1\leq i \leq a$
, and that a is the number of parts of the partition. Then recalling
![]() $\lambda _i = B_i+i-a$
, we have
$\lambda _i = B_i+i-a$
, we have
![]() $\lambda _i = 2(a-i)+1+i-a = (a-i)+1$
, and
$\lambda _i = 2(a-i)+1+i-a = (a-i)+1$
, and
 $$ \begin{align*} n = \sum_{i=1}^a \lambda_i = \sum_{k=1}^a k = \frac{k(k+1)}{2}. \end{align*} $$
$$ \begin{align*} n = \sum_{i=1}^a \lambda_i = \sum_{k=1}^a k = \frac{k(k+1)}{2}. \end{align*} $$
The case
![]() $t=3$
. Every 3-core partition can be uniquely represented by an abacus of the form
$t=3$
. Every 3-core partition can be uniquely represented by an abacus of the form
![]() $\mathfrak {A}=(0,a,b)$
for some nonnegative integers a and b. Working backwards, we obtain an expression for n in terms of the structure numbers determined by this abacus:
$\mathfrak {A}=(0,a,b)$
for some nonnegative integers a and b. Working backwards, we obtain an expression for n in terms of the structure numbers determined by this abacus:
 $$ \begin{align*} n &= \sum_{i = 1}^{a+b} \lambda_i \\ &= \sum_{i = 1}^{a+b} B_i + \sum_{i = 1}^{a+b} i - \sum_{i = 1}^{a+b} (a+b) \\ &= \sum_{i = 1}^{a+b} B_i + \frac{(a+b)(a+b+1)}{2} - (a+b)^2. \end{align*} $$
$$ \begin{align*} n &= \sum_{i = 1}^{a+b} \lambda_i \\ &= \sum_{i = 1}^{a+b} B_i + \sum_{i = 1}^{a+b} i - \sum_{i = 1}^{a+b} (a+b) \\ &= \sum_{i = 1}^{a+b} B_i + \frac{(a+b)(a+b+1)}{2} - (a+b)^2. \end{align*} $$
Now, we need only compute the structure numbers. We may do this by considering the beads in column one and column two separately. We have
 $$ \begin{align*} \sum_{i = 1}^{a+b} B_i &= \sum_{i = 1}^{a} (3(i-1)+1) + \sum_{j = 1}^{b} (3(\,j-1)+2) \\ &=3\cdot\frac{a(a+1)}{2} -2a + 3\cdot\frac{b(b+1)}{2} - b. \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^{a+b} B_i &= \sum_{i = 1}^{a} (3(i-1)+1) + \sum_{j = 1}^{b} (3(\,j-1)+2) \\ &=3\cdot\frac{a(a+1)}{2} -2a + 3\cdot\frac{b(b+1)}{2} - b. \end{align*} $$
Combining with the above and simplifying, we ultimately arrive at
Define
![]() $x := -a+2b+1$
,
$x := -a+2b+1$
,
![]() $y := a+b+1$
. Then
$y := a+b+1$
. Then
We now have an expression for
![]() $3n+1$
in terms of a positive definite binary quadratic form with discriminant
$3n+1$
in terms of a positive definite binary quadratic form with discriminant
![]() $D=-3$
. The ring of integers of the imaginary quadratic number field
$D=-3$
. The ring of integers of the imaginary quadratic number field
![]() $K=\mathbb {Q}(\sqrt {-3})$
is given by
$K=\mathbb {Q}(\sqrt {-3})$
is given by
![]() $\mathbb {Z}[\omega ]$
, where
$\mathbb {Z}[\omega ]$
, where
![]() $\omega = {(1+\sqrt {-3})}/{2}$
. The norm on
$\omega = {(1+\sqrt {-3})}/{2}$
. The norm on
![]() $\mathbb {Z}[\omega ]$
simplifies to
$\mathbb {Z}[\omega ]$
simplifies to
![]() $N(\alpha + \omega \beta ) = \alpha ^2-\alpha \beta +\beta ^2$
. The desired equality follows from constructing a correspondence between ideals in
$N(\alpha + \omega \beta ) = \alpha ^2-\alpha \beta +\beta ^2$
. The desired equality follows from constructing a correspondence between ideals in
![]() $\mathcal {O}_K$
with norm
$\mathcal {O}_K$
with norm
![]() $3n+1$
as in the proof of Theorem 4.1 in [Reference Brunat and Nath2].
$3n+1$
as in the proof of Theorem 4.1 in [Reference Brunat and Nath2].
In particular, every ideal of
![]() $\mathcal {O}_K$
is principal and factors uniquely into a product of finitely many (not necessarily distinct) prime ideals. Then given an integer prime p that divides
$\mathcal {O}_K$
is principal and factors uniquely into a product of finitely many (not necessarily distinct) prime ideals. Then given an integer prime p that divides
![]() $3n+1$
, it follows that p is either congruent to 1 or 2 mod 3. In the latter case, p is inert and the principal ideal
$3n+1$
, it follows that p is either congruent to 1 or 2 mod 3. In the latter case, p is inert and the principal ideal
![]() $(p)$
in
$(p)$
in
![]() $\mathcal {O}_K$
is prime with norm
$\mathcal {O}_K$
is prime with norm
![]() $p^2$
. Such p must have an even exponent in the prime factorisation of
$p^2$
. Such p must have an even exponent in the prime factorisation of
![]() $3n+1$
in
$3n+1$
in
![]() $\mathbb {Z}$
. To determine whether n admits a 3-core partition, we may compute the prime factorisation of
$\mathbb {Z}$
. To determine whether n admits a 3-core partition, we may compute the prime factorisation of
![]() $3n+1$
in
$3n+1$
in
![]() $\mathbb {Z}$
and check for even exponents on all primes p where
$\mathbb {Z}$
and check for even exponents on all primes p where
![]() $p \equiv 2 \bmod 3$
.
$p \equiv 2 \bmod 3$
.
3. Proof of Theorem 1.1
Suppose
![]() $\ell $
is an odd prime. Write
$\ell $
is an odd prime. Write
![]() $n = \ell m +a_2$
and suppose
$n = \ell m +a_2$
and suppose
![]() $\lambda \vdash n$
such that
$\lambda \vdash n$
such that
![]() $h_2(\lambda ) = \ell k +a_1$
, that is,
$h_2(\lambda ) = \ell k +a_1$
, that is,
![]() $h_2(\lambda ) \equiv a_1 \bmod {\ell }$
. Denote
$h_2(\lambda ) \equiv a_1 \bmod {\ell }$
. Denote
![]() $|\tilde {\lambda }|$
by
$|\tilde {\lambda }|$
by
![]() $\tilde {n}$
. Using Corollary 2.2, we may write
$\tilde {n}$
. Using Corollary 2.2, we may write
so
![]() $\tilde {n} = -2a_1 + a_2 + \ell (m-2k)$
. Then,
$\tilde {n} = -2a_1 + a_2 + \ell (m-2k)$
. Then,
Now,
![]() $8\tilde {n} + 1 \equiv -16a_1 + 8a_2 + 1 \bmod {\ell }$
. If
$8\tilde {n} + 1 \equiv -16a_1 + 8a_2 + 1 \bmod {\ell }$
. If
![]() $({-16a_1+8a_2+1}/{\ell })=-1$
, then
$({-16a_1+8a_2+1}/{\ell })=-1$
, then
![]() $8 \tilde {n} + 1$
cannot be an odd square. Since
$8 \tilde {n} + 1$
cannot be an odd square. Since
![]() $\tilde {\lambda }$
was assumed to be a 2-core, we have reached a contradiction. Thus, no such
$\tilde {\lambda }$
was assumed to be a 2-core, we have reached a contradiction. Thus, no such
![]() $\lambda $
can exist.
$\lambda $
can exist.
Next, suppose
![]() $\ell $
is a prime which is
$\ell $
is a prime which is
![]() $2 \bmod {3}$
. Write
$2 \bmod {3}$
. Write
![]() $n=\ell ^2m+a_2$
and suppose
$n=\ell ^2m+a_2$
and suppose
![]() $\lambda \vdash n $
such that
$\lambda \vdash n $
such that
![]() $h_3(\lambda )= \ell ^2 k +a_1$
or
$h_3(\lambda )= \ell ^2 k +a_1$
or
![]() $h_2(\lambda ) \equiv a_1 \bmod {\ell ^2}.$
We may write
$h_2(\lambda ) \equiv a_1 \bmod {\ell ^2}.$
We may write
so
![]() $\tilde {n} = - 3a_1 +a_2 + \ell ^2(m-3k)$
. Then
$\tilde {n} = - 3a_1 +a_2 + \ell ^2(m-3k)$
. Then
Now if
![]() $\text {ord}_\ell (-9a_1 + 3a_2 + 1)=1$
, then
$\text {ord}_\ell (-9a_1 + 3a_2 + 1)=1$
, then
![]() $\ell \mid -9a_1 + 3a_2 + 1$
but
$\ell \mid -9a_1 + 3a_2 + 1$
but
![]() $\ell ^2 \nmid -9a_1 + 3a_2 + 1$
. Since
$\ell ^2 \nmid -9a_1 + 3a_2 + 1$
. Since
![]() $\ell ^2 \mid \ell ^2(3n-9k)$
, we conclude that
$\ell ^2 \mid \ell ^2(3n-9k)$
, we conclude that
![]() $\ell $
divides
$\ell $
divides
![]() $3\tilde {N}+1$
but
$3\tilde {N}+1$
but
![]() $\ell ^2$
does not. Since
$\ell ^2$
does not. Since
![]() $\tilde {\lambda }$
was assumed to be a 3-core, we have reached a contradiction; therefore, no such
$\tilde {\lambda }$
was assumed to be a 3-core, we have reached a contradiction; therefore, no such
![]() $\lambda $
can exist.
$\lambda $
can exist.
![]() $\square $
$\square $
Acknowledgement
E.M. acknowledges the support of a UVa Dean’s Doctoral Fellowship.