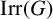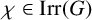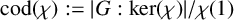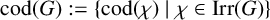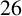ON THE CHARACTERISATION OF SPORADIC SIMPLE GROUPS BY CODEGREES

Abstract

Let G be a finite group and $\mathrm {Irr}(G)$ the set of all irreducible complex characters of G. Define the codegree of $\chi \in \mathrm {Irr}(G)$ as $\mathrm {cod}(\chi ):={|G:\mathrm {ker}(\chi ) |}/{\chi (1)}$ and denote by $\mathrm {cod}(G):=\{\mathrm {cod}(\chi ) \mid \chi \in \mathrm {Irr}(G)\}$ the codegree set of G. Let H be one of the $26$ sporadic simple groups. We show that H is determined up to isomorphism by cod$(H)$.

1 Introduction

Let G be a finite group and $\mathrm {Irr}(G)$ the set of all irreducible complex characters of G. For any $\chi \in \mathrm {Irr}(G),$ define the codegree of $\chi $ by $\mathrm {cod}(\chi ) := {|G:\mathrm {ker}(\chi )|}/{\chi (1)}.$ Then define the codegree set of G as $\mathrm {cod}(G) := \{\mathrm {cod}(\chi ) \mid \chi \in \mathrm {Irr}(G)\}.$ The concept of codegrees was originally considered in [7], where the codegree was defined as $\mathrm {cod}(\chi ) := {|G|}/{\chi (1)},$ and it was later modified to its current definition in [19] so that $\mathrm {cod}(\chi )$ is the same for G and $G/N$ when $N \leq \mathrm {ker}(\chi ).$

The codegree set of a group is closely related to the character degree set of a group, defined as $\mathrm {cd}(G) := \{\chi (1) \mid \chi \in \mathrm {Irr}(G)\}.$ The relationship between the character degree set and the group structure is an active area of research and many properties of group structure are largely determined by the character degree set. In 1990, Huppert made the following conjecture.

Huppert’s conjecture. Let H be a finite nonabelian simple group and G a finite group such that $\mathrm {cd}(H) = \mathrm {cd}(G).$ Then, $G \cong H \times A,$ where A is an abelian group.

Huppert’s conjecture has been verified for many cases, including alternating groups, sporadic groups and simple groups of Lie type with low rank, but it has yet to be verified for simple groups of Lie type with high rank. Recently, a similar conjecture related to codegrees was posed in [16] as Question 20.79.

Codegree version of Huppert’s conjecture. Let H be a finite nonabelian simple group and G a finite group such that $\mathrm {cod}(H) = \mathrm {cod}(G).$ Then, $G \cong H.$

This conjecture has been verified for $\mathrm {PSL}(2,q)$ , $\mathrm {PSL}(3,4), \mathrm {Alt}_7, \mathrm {J}_1$ , $^2B_2(2^{2f+1})$ , where $f \geq 1$ , $\mathrm {M}_{11}, \mathrm {M}_{12}, \mathrm {M}_{22}, \mathrm {M}_{23}$ and $\mathrm {PSL}(3,3)$ (see [1, 4, 10]). The conjecture has also been verified for ${\mbox {PSL}}(3,q)$ and ${\mbox {PSU}}(3,q)$ in [17] and ${}^2G_2(q)$ in [11]. Most of these results concern simple groups with fewer than $21$ character degrees [3]. We now provide a general proof verifying this conjecture for all the sporadic simple groups. The methods used may be generalised to simple groups of Lie type, giving promising results for characterising all simple groups by their codegree sets.

Theorem 1.1. Let H be a sporadic simple group and G a finite group. If $\mathrm {cod}(G)= \mathrm {cod}(H)$ , then $G \cong H$ .

Throughout the paper, we follow the notation used in Isaacs’ book [13] and the ATLAS of Finite Groups [8].

2 Preliminary results

We first reproduce several lemmas which will be used in later proofs.

Lemma 2.1 [18, Lemma 4.2].

Let S be a finite nonabelian simple group. Then there exists $\chi \in \mathrm {Irr}(S), \chi \ne 1_S$ , that extends to $\mathrm {Aut}(S)$ .

Lemma 2.2 [14, Theorem 4.3.34].

Let N be a minimal normal subgroup of G such that $N=S_1\times \cdots \times S_t$ , where $S_i \cong S$ is a nonabelian simple group for each $i=1,\ldots ,t$ . If $\chi \in \mathrm {Irr}(S)$ extends to $\mathrm {Aut}(S)$ , then $\chi \times \cdots \times \chi \in \mathrm {Irr}(N)$ extends to G.

Lemma 2.3 [10, Remark 2.6].

Let G be a finite group and H a finite nonabelian simple group with $\mathrm {cod}(G)=\mathrm {cod}(H)$ . Then, G is a perfect group.

Lemma 2.4 [12, Theorem C].

Let G be a finite group and S a finite nonabelian simple group such that $\mathrm {cod}(S) \subseteq \mathrm {cod}(G)$ . Then, $|S|$ divides $|G|$ .

Lemma 2.5. Let G be a finite group with $N \trianglelefteq G.$ Then, $\operatorname {cod}(G/N) \subseteq \operatorname {cod}(G)$ .

Proof. We can define $\operatorname {Irr}(G/N) = \{ \hat {\chi }(gN) = \chi (g) \mid \chi \in \operatorname {Irr}(G) \text { and } N \subseteq \operatorname {ker}(\chi )\}$ by [13, Lemma 2.22]. Take any $\hat {\chi } \in \mathrm {Irr}(G/N)$ . By definition, $\hat {\chi }(1) = \chi (1),$ so the denominators of $\mathrm {cod}(\hat {\chi })$ and $\mathrm {cod}(\chi )$ are equal. In addition, $\mathrm {ker}(\hat {\chi }) \cong \mathrm {ker}(\chi ) / N$ , so that $|\mathrm {ker}(\chi )| = |N| \cdot |\mathrm {ker}(\hat {\chi })|$ . Thus, $|G/N : \ker (\hat {\chi })| = {|G|/|N|}/{|\!\ker (\chi )|/|N|} = {|G|}/{|\!\ker (\chi )|},$ so that $\mathrm {cod}(\hat {\chi }) = \mathrm {cod}(\chi )$ and $\mathrm {cod}(G/N) \subseteq \mathrm {cod}(G).$

Lemma 2.6. Let G be a finite group with normal subgroups N and M such that $N\leq M$ . Then, $\mathrm {cod}(G/M)\subseteq \mathrm {cod}(G/N)$ .

Proof. By the third isomorphism theorem, $G / M \cong (G/N)/(M/N)$ is a quotient of $G / N$ , and by Lemma 2.5, $\mathrm {cod}(G / M) \subseteq \mathrm {cod}(G / N)$ .

Lemma 2.7. Let G and H be finite groups such that $\mathrm {cod} (G) \subseteq \mathrm {cod} (H)$ . Then there are at least $|\mathrm {cod} (G)|$ elements in $\mathrm {cod} (H)$ which divide $|G|$ .

Proof. For each $x\in \mathrm {cod}(G)$ , it is clear that x divides $|G|$ . The lemma follows.

3 Main results

Theorem 3.1. Let H be a sporadic simple group and G a finite group with $\mathrm {cod}(G)=\mathrm {cod}(H)$ . If N is a maximal normal subgroup of G, then $G/N \cong H$ .

Proof. By Lemma 2.3, G is perfect. Thus, $G/N$ is a nonabelian simple group. By Lemma 2.6, $\mathrm {cod}(G/N) \subseteq \mathrm {cod}(G)=\mathrm {cod}(H)$ . We will prove that this cannot occur unless $G/N \cong H.$ We can easily check that $\mathrm {cod}(K) \not \subseteq \mathrm {cod}(H)$ for any two non-isomorphic sporadic groups H and K. Thus, $G/N$ must belong to one of the $17$ infinite families of nonabelian simple groups.

Now, we work with each sporadic group in turn, computationally proving there are no possible exceptions. To do this, we use the code file available at https://github.com/zachslonim/Characterizing-Sporadic-Groups-by-Codegrees. All the code referenced in this paper is written in Julia [5] and each file contains comments providing further detail. In addition, we invite readers to contact the authors with any questions. We walk through what the code does in detail for one example here, namely, the Suzuki group, $\mathrm {Suz}.$ This group has order $448345497600.$ Using the order formulae for the $17$ infinite families of nonabelian simple groups [6], we first deduce which simple groups have order dividing $448345497600.$ In this case, we get the following list:

$$ \begin{align*} &\mathrm{A}_5, \mathrm{A}_6, \mathrm{A}_7, \mathrm{A}_8, \mathrm{A}_9, \mathrm{A}_{10}, \mathrm{A}_{11}, \mathrm{A}_{12}, \mathrm{A}_{13}, \mathrm{PSL}_2(7), \mathrm{PSL}_2(11), \mathrm{PSL}_2(13), \mathrm{PSL}_2(25), \\ &\mathrm{PSL}_2(27), \mathrm{PSL}_2(64), \mathrm{PSL}_3(3), \mathrm{PSL}_3(4), \mathrm{PSL}_3(9), \mathrm{PSL}_4(2), \mathrm{PSL}_4(3), \mathrm{O}_5(2)', \\ &\mathrm{O}_5(3), \mathrm{O}_7(2), \mathrm{O}_8^+(2), \mathrm{G}_2(2)', \mathrm{G}_2(3), \mathrm{G}_2(4), \mathrm{PSU}_3(3), ^2\mathrm{B}_2(8), ^2\mathrm{F}_4(2)'. \end{align*} $$

By Lemma 2.4, if a simple group K has $\mathrm {cod}(K)\subseteq \mathrm {cod}(\mathrm {Suz}),$ then it must belong to the above list. By Lemma 2.7, there must be at least $|\mathrm {cod}(K)|$ elements in $\mathrm {cod}(\mathrm {Suz})$ which divide $|K|.$ Then, from [2], any nonabelian simple group has $|\mathrm {cod}(K)|>3.$ Hence, if $\mathrm {cod}(K)\subseteq \mathrm {cod}(\mathrm {Suz}),$ then there are at least four elements of $\mathrm {cod}(\mathrm {Suz})$ that divide the order of $K.$ So, for each of the groups in the list above, we count the number of codegrees of $\mathrm {Suz}$ that divide the order of the group. We find that there are less than $4$ such codegrees in every case except for when $K=\mathrm {O}_8^+(2)$ which has order divisible by $5$ of the codegrees of $\mathrm {Suz}.$ However, [3] shows that $|\mathrm {cod}(\mathrm {O}_8^+(2))|> 20,$ so we would require that $|\mathrm {O}_8^+(2)|$ is divisible by at least $20$ of the codegrees of $\mathrm {Suz},$ which is a contradiction. Thus, if $\mathrm {cod}(K)\subseteq \mathrm {Suz}$ for some simple group $K,$ the only possibility is $K\cong \mathrm {Suz}.$

We repeat this process for all of the other sporadic simple groups. For each sporadic group $H,$ we first check which nonabelian simple groups K satisfy $|K|$ divides $|H|.$ These lists are given in Table 1. Second, we check which of these possibilities have order divisible by more than three codegrees of $H.$ We find two more groups H such that the number of codegrees of H dividing $|K|$ is more than three. These are $H\cong \mathrm {Fi}_{23}$ with $K\cong \mathrm {O}_8^+(3)$ and $H\cong \mathrm {Ru}$ with $K\cong \mathrm {G}_2(4)$ . In both cases, there are four such codegrees. Again, however, [3] shows that $|\mathrm {cod}(K)|\geq 18$ in both cases, which is a contradiction. Hence, for any sporadic group $H,$ if $\mathrm {cod}(K)\subseteq H$ for some simple group $K,\, \mathrm{then}\ K\cong H.$

Table 1 Possible simple groups K whose orders divide the order of the sporadic group G.

As $G/N$ is simple and $\mathrm {cod}(G/N)\subseteq H,$ we see that $G/N\cong H.$

Proof of Theorem 1.1.

Let G be a minimal counterexample and N a maximal normal subgroup of G. By Lemma 2.3, G is perfect, and by Theorem 3.1, $G/N \cong H$ . In particular, $N \neq 1$ as $G \not \cong H$ .

Step 1: N is a minimal normal subgroup of G.

Suppose L is a nontrivial normal subgroup of G with $L < N$ . By Lemma 2.6, $\mathrm {cod}(G/N) \subseteq \mathrm {cod}(G/L) \subseteq \mathrm {cod}(G)$ . However, $\mathrm {cod}(G/N)=\mathrm {cod}(H)=\mathrm {cod}(G)$ so equality must occur in each inclusion. Thus, $\mathrm {cod}(G/L)=\mathrm {cod}(H)$ which implies that $G/L \cong H,$ since G is a minimal counterexample. This is a contradiction since we also have $G/N\cong H,$ but $L < N$ .

Step 2: N is the only nontrivial, proper normal subgroup of G.

Assume U is another proper nontrivial normal subgroup of G. If N is included in U, then $U=N$ or $U=G$ since $G/N$ is simple, which is a contradiction. Then, $N\cap U=1$ and $G=N\times U$ . Since U is also a maximal normal subgroup of G, we have $N\cong U\cong H$ . Choose $\psi _1\in \operatorname {Irr}(N)$ and $\psi _2\in \operatorname {Irr}(U)$ such that $\operatorname {cod}(\psi _1)=\operatorname {cod}(\psi _2)=\max (\operatorname {cod}(H))$ . Set $\chi =\psi _1\cdot \psi _2\in \operatorname {Irr}(G)$ . Then, $\operatorname {cod}(\chi )=(\max (\operatorname {cod}(H)))^2\notin \operatorname {cod}(G)$ , which is a contradiction.

Step 3: For each nontrivial $\chi \in \mathrm {Irr}(G|N):=\mathrm {Irr}(G)-\mathrm {Irr}(G/N)$ , the character $\chi $ is faithful.

By [13, Lemma 2.22], $\mathrm {Irr}(G/N) = \{\chi \in \mathrm {Irr}(G) \mid N \leq \mathrm {ker}(\chi )\}.$ By the definition of $\mathrm {Irr}(G|N)$ , it follows that if $\chi \in \mathrm {Irr}(G|N),$ then $N \not \leq \mathrm {ker}(\chi ).$ Since N is the unique nontrivial, proper, normal subgroup of G, $\mathrm {ker}(\chi ) = G$ or $\mathrm {ker}(\chi ) = 1$ . Therefore, $\mathrm {ker}(\chi ) = 1$ for all nontrivial $\chi \in \mathrm {Irr}(G|N).$

Step 4: N is an elementary abelian group.

Suppose that N is not abelian. Since N is a minimal normal subgroup, by [9, Theorem 4.3A(iii)], $N=S^n$ , where S is a nonabelian simple group and $n\in \mathbb {Z}^+$ . By Lemmas 2.1 and 2.2, there is a nontrivial character $\chi \in \mathrm {Irr}(N)$ which extends to some $\psi \in \mathrm {Irr}(G).$ Now, ker $(\psi )=1$ by Step 3, so cod $(\psi )=|G|/\psi (1)=|G/N|\cdot |N|/\chi (1).$ This contradicts the fact that $|G/N|$ is divisible by cod $(\psi )$ , as $\chi (1)<|N|$ , so N must be abelian. Now to show that N is elementary abelian, let a prime p divide $|N|.$ Then, N has a p-Sylow subgroup K, and K is the unique p-Sylow subgroup of N since N is abelian, so K is characteristic in N. Thus, K is a normal subgroup of $G,$ so $K=N$ as N is minimal, so $|N|=p^n.$ Now, take the subgroup $N^p=\{n^p \mid n\in N\}$ of N which is proper by Cauchy’s theorem. Since $N^p$ is characteristic in $N,$ it must be normal in $G,$ so $N^p$ is trivial by the uniqueness of $N.$ Therefore, every element of N has order p, so N is elementary abelian.

Step 5: $\mathbf {C}_G(N) = N.$

First, note that since N is normal, $\mathbf {C}_G(N) \trianglelefteq G.$ Additionally, since N is abelian by Step 4, $N \leq \mathbf {C}_G(N),$ so by the maximality of $N,$ we must have $\mathbf {C}_G(N) = N$ or $\mathbf {C}_G(N) = G.$ If $\mathbf {C}_G(N) = N,$ we are done.

If not, then $\mathbf {C}_G(N) = G.$ Therefore, N must be in the centre of $G.$ Since N is the unique minimal normal subgroup of G by Step 2, $|N|$ must be prime. For, if not, there always exists a proper nontrivial subgroup K of $N,$ and K is normal since it is contained in $\mathbf {Z}(G),$ contradicting the minimality of $N.$ Moreover, since G is perfect, $\mathbf {Z}(G) = N,$ and N is isomorphic to a subgroup of the Schur multiplier of $G/N$ [13, Corollary 11.20].

If H is isomorphic to any of $\mathrm {M}_{11},\mathrm {M}_{23},\mathrm {M}_{24}, \mathrm {J}_1,\mathrm {J}_4,\mathrm {Co}_2,\mathrm {Co}_3,\mathrm {Fi}_{22},\mathrm {Fi}_{23}$ , He, HN, Ly, Th or M, then by [8], the Schur multiplier of H is trivial, so $N=1,$ which is a contradiction.

If H is isomorphic to $\mathrm {Co}_1,$ then $G \cong 2.\mathrm {Co}_1$ by [8]. However, $2.\mathrm {Co}_1$ has a character degree of $24,$ which gives a codegree of $2^{19}\cdot 3^8 \cdot 5^4 \cdot 7^2 \cdot 11 \cdot 13 \cdot 23 \in \mathrm {cod}(G),$ which is a contradiction, since $2^{19}\cdot 3^8 \cdot 5^4 \cdot 7^2 \cdot 11 \cdot 13 \cdot 23 \notin \mathrm {cod}(H).$ If H is isomorphic to $\mathrm {Fi}_{22},$ then $G \cong 2.\mathrm {Fi}_{22}$ or $G \cong 3.\mathrm {Fi}_{22}$ by [8]. If $G \cong 2.\mathrm {Fi}_{22},$ then $2^{13}\cdot 3^9 \cdot 5^2 \cdot 7 \cdot 13 \in \mathrm {cod}(G),$ which is a contradiction. If $G \cong 3.\mathrm {Fi}_{22},$ then $2^{17}\cdot 3^7 \cdot 5^2 \cdot 6 \cdot 11 \in \mathrm {cod}(G),$ which is a contradiction.

Similarly, for any sporadic simple group H with nontrivial Schur multiplier, we use [8] to reach a contradiction as above, by finding an element of $\mathrm {cod}(G)$ that is not in $\mathrm {cod}(H).$ Thus, $\mathbf {C}_G(N) = N.$

Step 6: Let $\lambda $ be a nontrivial character in $\mathrm {Irr}(N)$ and $\vartheta \in \mathrm {Irr}(I_G(\lambda )|\lambda ),$ the set of irreducible constituents of $\lambda ^{I_G(\lambda )},$ where $I_G(\lambda )$ is the inertia group of $\lambda\ in\ G.$ Then, ${|I_G(\lambda )|}/{\vartheta (1)} \in \mathrm {cod}(G).$ Also, $\vartheta (1)$ divides $|I_G(\lambda )/N|$ and $|N|$ divides $|G/N|.$ Lastly, $I_G(\lambda ) < G,$ that is, $\lambda $ is not G-invariant.

Let $\lambda $ be a nontrivial character in $\operatorname {Irr}(N)$ and $\vartheta \in \operatorname {Irr}(I_G(\lambda )|\lambda )$ . Let $\chi $ be an irreducible constituent of $\vartheta ^G.$ By [13, Corollary 5.4], $\chi \in \operatorname {Irr}(G)$ , and by [13, Definition 5.1], $\chi (1) = ({|G|}/{|I_G(\lambda )|}) \cdot \vartheta (1)$ . Moreover, $\operatorname {ker}(\chi ) = 1$ by Step 2, and thus $\operatorname {cod}(\chi ) = {|G|}/{\chi (1)} = {|I_G(\lambda )|}/{\vartheta (1)}$ , so ${|I_G(\lambda )|}/{\vartheta (1)} \in \mathrm {cod}(G)$ . Now, since N is abelian, $\lambda (1) = 1$ , so $\vartheta (1) = \vartheta (1)/\lambda (1)$ which divides ${|I_G(\lambda )|}/{|N|}$ , so $|N|$ divides ${|I_G(\lambda )|}/{\vartheta (1)}$ . Moreover, $\operatorname {cod}(G) = \operatorname {cod}(G/N)$ and all elements in $\operatorname {cod}(G/N)$ divide $|G/N|$ , so $|N|$ divides $|G/N|$ .

Next, we show $I_G(\lambda )$ is a proper subgroup of G. To reach a contradiction, assume $I_G(\lambda ) = G$ . Then, $\operatorname {ker}(\lambda ) \unlhd G$ . From Step 2, $\operatorname {ker}(\lambda ) = 1,$ and from Step 4, N is a cyclic group of prime order. Thus, by the normaliser-centraliser theorem, $G / N= \mathbf {N}_{G}(N) / \mathbf {C}_{G}(N) \leq \operatorname {Aut}(N)$ and so $G / N$ is abelian, which is a contradiction.

Step 7: Final contradiction.

From Step 4, N is an elementary abelian group of order $p^n$ for some prime p and integer $n\geq 1$ . By the normaliser-centraliser theorem, $H \cong G/N = \mathbf {N}_G(N)/\mathbf {C}_G(N) \leq \mathrm {Aut}(N)$ and $n>1$ . Note that in general, $\mathrm {Aut}(N)=\mathrm {GL}(n,p)$ . By Step 6, $|N|$ divides $|G/N|,$ so we only need to consider primes p such that $p^2$ divides $|H|$ .

We proceed computationally for each sporadic group separately. To do this, we use the code file https://github.com/zachslonim/Characterizing-Sporadic-Groups-by-Codegrees. Again, we explain here the computational steps for the Suzuki group, $\mathrm {Suz}.$ This group has order $448345497600=2^{13}\cdot 3^7\cdot 4^2 \cdot 7\cdot 11\cdot 13$ , so the possibilities for p and $n>1$ such that $p^n$ divides $|\mathrm {Suz}|$ are

$$ \begin{align*} 2^2, 2^3, 2^4, 2^5, 2^6, 2^7, 2^8, 2^9, 2^{10}, 2^{12}, 2^{12}, 2^{13}, 3^2, 3^3, 3^4, 3^5, 3^6, 3^7, 4^2. \end{align*} $$

For each of these possible $p^n,$ we compute the order of $\mathrm {GL}(n,p)$ using the well-known order formula:

$$ \begin{align*} |\mathrm{GL}(n,p)|=\prod_{i=0}^{n-1}(p^n-p^i). \end{align*} $$

Then, we check which values of p and n satisfy the fact that $|\mathrm {Suz}|$ divides $|\mathrm {GL}(n,p)|.$ In this case, we get only two exceptions, namely $ 2^{12} \text { and } 2^{13}.$

For each sporadic group H, we follow a similar procedure to check computationally which possibilities of $(p,n)$ satisfy $p^n$ divides $|H|$ and $|H|$ divides $|\mathrm {GL}(n,p)|$ . We summarise these in Table 2. If a sporadic group is missing, this means there are no possible exceptions. In other words, Table 2 gives all groups H and pairs $(p,n)$ such that $p^n$ divides $|H|$ and $|H|$ divides $|\mathrm {GL}(n,p)|$ .

Finally, in each of these seven cases, we refer to [15], which gives the minimum degree of a faithful representation of the group H over a finite field of characteristic p. We reproduce the relevant results in Table 2. We note that $H\lesssim \mathrm {GL}(n, p)$ implies that we can embed H into $\mathrm {GL}(n, p),$ giving a degree n faithful representation of H over a field of characteristic $p.$ However, in each row of the table, any possible values of $p,n$ contradict the minimum degree of such a faithful representation. Thus, we reach a contradiction for any sporadic simple group $H.$ Therefore, $N=1$ and $G \cong H$ .

Table 2 Sporadic groups and $p,n$ pairs such that $p^n$ divides $|H|$ and $|H|$ divides $|\mathrm {GL}(n,p)|$ .