Dynamic simultaneous localization and mapping based on object tracking in occluded environment

Abstract

In practical applications, many robots equipped with embedded devices have limited computing capabilities. These limitations often hinder the performance of existing dynamic SLAM algorithms, especially when faced with occlusions or processor constraints. Such challenges lead to subpar positioning accuracy and efficiency. This paper introduces a novel lightweight dynamic SLAM algorithm designed primarily to mitigate the interference caused by moving object occlusions. Our proposed approach combines a deep learning object detection algorithm with a Kalman filter. This combination offers prior information about dynamic objects for each SLAM algorithm frame. Leveraging geometric techniques like RANSAC and the epipolar constraint, our method filters out dynamic feature points, focuses on static feature points for pose determination, and enhances the SLAM algorithm’s robustness in dynamic environments. We conducted experimental validations on the TUM public dataset, which demonstrated that our approach elevates positioning accuracy by approximately 54% and boosts the running speed by 75.47% in dynamic scenes.

1. Introduction

Simultaneous localization and mapping (SLAM) is pivotal for robots aiming to achieve self-localization, tracking, and mapping in unfamiliar settings, as depicted in Fig 1. SLAM technology has entrenched its importance in sectors like intelligent robotics, virtual reality, and autonomous driving [1, 2]. Visual SLAM in static environments has made considerable advancements, and its methods can be classified into feature-based and direct approaches, depending on the pose estimation principles.

Figure 1. Several application scenarios of SLAM1.

Feature-based SLAM methods identify prominent feature points within images and assign them unique descriptors. ORB-SLAM3 [3] stands as a prime example, showcasing the robustness and precision of these methods in feature matching. However, in environments with low texture, the scarcity of feature points can lead to mismatch issues or even loss of tracking. Additionally, despite their importance, the computation of descriptors is expensive and might impede real-time performance.

Direct methods operate on the presumption of photometric consistency between consecutive frames. They employ pixel intensities for feature point matching and determine pose using pixel gradients and orientations [4]. Methods such as SVO [5] and LSD-SLAM [6] serve as prime examples of this approach. By avoiding computing descriptors, they achieve greater computational efficiency, leading to rapid real-time responses. Yet, their performance may degrade with changing lighting conditions or variations in photometric properties.

Practically, static environments are rarely encountered. Dynamic objects, which can cause inconsistent motion of feature points, complicate the scene. Such dynamic objects encompass not just freely moving objects but also entities exhibiting relative motion to a supposedly static backdrop, for example, the water jet in the field of view of a firefighting robot, the excavator arm within the viewpoint of an autonomous driving excavator, or other large obstacles that appear in the field of view. These moving objects can detrimentally affect the accuracy of SLAM systems [7, 8]. Feature-based SLAM algorithms, which lean heavily on feature points, might deduce incorrect pose changes when these dynamic points interfere.

Addressing the SLAM challenge in dynamic settings generally takes one of two routes: geometric or deep learning-based methods. Geometric methods capitalize on the intrinsic differences between dynamic and static points, determining their three-dimensional spatial positions and motion alterations, for example, using epipolar constraint or probabilistic methods to eliminate a small portion of dynamic interference points, such as the RANSAC [9, 10] algorithm. However, this method is only suitable for cases where the number of dynamic points is small. If dynamic points constitute over 50% of the total, this method may have adverse effects.

Deep learning methods primarily use object detection or semantic segmentation algorithms to recognize dynamic objects in images, providing prior information about dynamic points for SLAM. Object detection algorithms focus on estimating the approximate locations of target objects, usually represented by bounding boxes. Meanwhile, semantic segmentation goes a step further, providing a detailed pixel-by-pixel classification of these entities.

This paper focuses on the challenges posed by moving objects in dynamic SLAM. We introduce a novel approach that combines a lightweight object detection algorithm with geometric techniques, including Kalman filtering, RANSAC, and epipolar constraints. This approach aims to eliminate dynamic feature points, enhancing both the positioning accuracy and computational efficiency of dynamic SLAM.

The organization of the subsequent sections of the paper is as follows: section 2 provides an overview of the research status both domestically and internationally, section 3 presents the overall framework and specific algorithms of the proposed approach, section 4 validates the proposed algorithms through experiments, and finally, section 5 concludes the paper.

2. Related work

Machine learning and deep learning, gaining tremendous momentum in recent years, have introduced novel techniques into the domain of SLAM, most notably in dynamic SLAM. For traditional static SLAM algorithms, combining deep learning can enable end-to-end feature point extraction or camera pose estimation, which can save the cost of feature point extraction, feature matching, and pose computation. Furthermore, deep learning is also used to address SLAM problems in dynamic scenes by pre-training deep learning algorithms to detect specific targets and provide prior information about the target’s position in SLAM, helping to understand complex dynamic scenes. This can assist SLAM algorithms in accurately removing dynamic object features, thereby improving the robustness of SLAM algorithms in dynamic scenes [11].

Usually, object detection or semantic segmentation algorithms are used to obtain prior information, so based on this, deep learning methods can be divided into two categories. The difference is that the object detection algorithms provide approximate object positions, while the semantic segmentation algorithms provide pixel-level segmentation results of the target object

Berta Bescos et al. proposed DynaSLAM [12] in 2018, which is based on ORBSLAM2 and Mask-RCNN algorithm. When obtaining new image frames, DynaSLAM uses a semantic segmentation algorithm to directly remove regions with obvious dynamic objects, such as “people, animals, and vehicles," and then perform lightweight tracking on the remaining regions. Moving objects are segmented and judged using multi-geometry methods, and the static background is repaired. However, due to the possibility of non-existent static scenes or invalid depth information in historical frames’ dynamic regions, this method may result in cracks in the generated static map.

Chao Yu et al. proposed DSSLAM [13], which uses ORBSLAM2 as the base framework and SegNet algorithm as the semantic segmentation algorithm. When dynamic objects are segmented, the corresponding feature points are set as potential dynamic points, and a two-step strategy is used to determine if the point is a dynamic point: first, each feature point in the segmentation area is filtered, and if the feature point is too close to the edge of the segmentation area or the pixel difference in the surrounding $3\times 3$ image block is too large, it is deleted. Then Random Sample Consensus(RANSAC) is combined to calculate the most suitable fundamental matrix with the maximum number of inliers. The point is judged as a dynamic point based on epipolar line distance. The authors combine the dynamic/static status of feature points with the dynamic/static status of segmented objects. If a certain point is determined as a dynamic point, the entire segmented area will be considered as a dynamic object. If the number of dynamic points on a dynamic object is greater than a certain threshold, all feature points on the dynamic object will be deleted.

Fangwei Zhong et al. proposed a Detect-SLAM based on the object detection algorithm [14], which utilizes prior information provided by the object detection algorithm to extract features from moving objects and only uses static features for subsequent tracking processes and map construction. To improve the efficiency of the algorithm, the authors only detect dynamic objects in keyframes and classify all feature points in other ordinary frames based on motion probability, greatly improving the real-time performance of the algorithm.

Fethi Demim et al [15–19] proposed a series of methods based on the Smooth Variable Structure Filter (SVSF) to solve the dynamic slam problem. Their hypothesis is that a feature that is moving with an important velocity is considered that is out of date and it cannot maintain much useful information.

Kenye L et al [20] utilized deep neural networks, or DNN-based object detection modules, to acquire bounding boxes. Subsequently, they employ a depth-first search algorithm on the detected semantics to generate a lower-resolution binary mask image. This process effectively represents the segmentation of the foreground from the static background.

Scona et al. proposed a surface element-based RGBD-SLAM algorithm called StaticFusion [21], which can estimate camera poses and segment static objects in the current frame at near real-time speed, and construct dense maps using information from historical static objects. However, this algorithm heavily relies on static features during initialization, and if there are too many dynamic objects in the scene during the initialization stage, it may cause initialization failure of the system.

MaskFusion [22], postulated by Runz et al., is an object-level RGBD-SLAM system for dynamic environments. Grounded in the Mask-RCNN algorithm, it segments and tracks objects in RGBD images. Unlike traditional SLAM algorithms that primarily focus on static scenes, MaskFusion seamlessly integrates dynamic object pose tracking while preserving the static scene’s integrity. Despite its innovative approach, the algorithm grapples with certain limitations: Mask-RCNN’s slow segmentation speed, potential pose output delays, and a drop in real-time efficiency when dynamic objects are predominant.

In 2020, Facil et al. proposed VDO-SLAM [23], which integrates the camera and IMU and uses the YOLOv3 algorithm as the object detector to identify dynamic objects in the scene, achieving tracking and map updating of dynamic objects. The core idea is to use a multi-sensor fusion approach that combines geometric methods with deep learning methods to achieve high-precision calculation of camera poses in dynamic scenes, which also plays an important role in navigation tasks for robots.

Although the above-mentioned dynamic SLAM algorithms based on semantic segmentation algorithms have high accuracy, they consume a large number of resources during algorithm execution and require superior hardware configurations. In practical application environments, especially outdoor environments, most of the embedded devices have limited computing capabilities, these dynamic SLAM algorithms based on semantic segmentation cannot run in real-time. The algorithm proposed in this paper significantly improves algorithm efficiency while ensuring accuracy comparable to dynamic SLAM algorithms based on object detection algorithms. It not only enables the algorithm to be deployed on embedded devices with limited computing capabilities but also provides the possibility for the algorithm to ensure real-time performance while expanding subsequent functions.

3. Dynamic SLAM based on object tracking in occluded environment

3.1. Algorithm framework and SLAM system implementation principle

The algorithm proposed in this paper is mainly designed for outdoor scenarios in practical applications, such as firefighting robots, remote-controlled construction machinery, etc. The system utilizes a distributed architecture. At the operational end, devices such as the Raspberry Pi, characterized by limited computational capabilities, manage the pan-tilt camera’s direction adjustments and image acquisition. The SLAM algorithm is deployed on a high-performance server at the remote control end. The operation end and remote control end communicate through a ROS system via 5G network or local area network. The specific algorithm flow is shown in Fig 2.

Figure 2. Schematic diagram of the improved algorithm system.

The main framework of the algorithm proposed in this paper is based on OV2SLAM [24], which is a lightweight SLAM system with stronger real-time performance compared to the classical feature-based ORBSLAM2, as shown in Fig. 2. The entire SLAM system framework consists of five threads, including the dynamic object tracking thread, visual front-end thread, mapping thread, state optimization thread, and loop detection thread.

In the algorithm, when the images captured by the operation terminal arrive at the control terminal, they are simultaneously input into the visual front-end thread and the dynamic object tracking thread. The dynamic object tracking thread implements object tracking using YOLOv5s and Kalman filter fusion. This thread is trained on the COCO dataset and self-built engineering dataset to accurately recognize potential dynamic objects in the images. It combines IOU matching with the predicted values from the Kalman filter to achieve tracking of the two-dimensional position of dynamic objects. The results are used to update the Kalman filter and generate outputs.

The visual front-end thread only extracts FAST [25] corners and uses sparse LK optical flow [26] to track these feature points. This approach, compared to matching and tracking feature points using corners and descriptors, saves the computational cost of descriptor extraction, making the system more lightweight and faster. During the system initialization stage, the same strategy as ORBSLAM2 [27] is adopted. In the monocular case, the essential matrix is computed using the method of epipolar geometry from the first two frames, followed by triangulation to obtain 3D points. In the case of stereo vision, after matching the FAST corners in both left and right images using optical flow, 3D points are directly computed.

During the local map tracking stage, the system focuses on the current keyframe and its immediately covisible keyframes, creating a compact local map. This approach prioritizes real-time performance, albeit at the expense of tracking accuracy. Subsequently, bounding box data of likely dynamic objects, sourced from the target tracking thread, allows for the categorization of FAST corners within the current keyframe. These corners are deemed potential dynamic or static based on their location relative to the bounding box, with those inside considered dynamic and those outside as static. A motion consistency check, leveraging static points for reference, is then conducted on these potential dynamic points. This process distinguishes true static from dynamic points, integrating the former into the existing static point collection. Conversely, dynamic points undergo a deletion of their historical data, including 2D coordinates, connections to local map points, and covisibility links.

In the loop detection thread, unlike the offline training dictionary using DBOW in ORBSLAM2, the algorithm adopts the strategy of iBowLCD [28] to build the dictionary online. During the mapping and tracking process, the dictionary is incrementally updated, and candidate keyframes are verified using kNN-BF matching, EM-RANSAC, and P3P-RANSAC. The hypothesis pose of the current keyframe is optimized using motion-only bundle adjustment (BA). Finally, the optimization thread performs bundle adjustment (BA) only on the current keyframe and map points affected by loop closure, which significantly reduces the optimization scope compared to the full BA used in ORBSLAM2, thereby improving real-time performance.

3.2. The object tracking based on YOLOv5s and Kalman filtering

The object tracking thread is based on the YOLOv5s algorithm and Kalman filter, which provides prior information about potential dynamic objects for the SLAM thread.

The Yolov5s algorithm is the algorithm with the smallest depth and the smallest width of the feature map in the Yolov5 series. Compared to its predecessor YOLOv4, YOLOv5 slightly falls behind in performance, but it has shorter training time and smaller model size, resulting in significant improvements in flexibility and inference speed. In batched inference, YOLOv5s can even achieve an inference speed of up to 140FPS, making it the current state-of-the-art in the field of object detection. In terms of data augmentation, YOLOv5 uses three types of data augmentation through data loaders, including scaling, color space adjustment, and mosaic augmentation. For anchor box selection, YOLOv4 uses the clustering method, while YOLOv5 uses adaptive anchor box calculation. In terms of loss calculation, YOLOv5 still uses BCEloss for class loss and confidence loss, the same as YOLOv4. However, for localization loss, YOLOv5 uses GIOU LOSS instead of CIOU LOSS used in YOLOv4, resulting in slightly lower performance compared to CIOU LOSS.

The proposed object tracking algorithm in this paper integrates YOLOv5s and Kalman filter, as shown in Algorithm 1. In robot motion or engineering machinery motion, due to the vibration of the machine itself or uneven ground, it often leads to severe image jitter or too fast motion speed, which can result in the camera’s capture rate not keeping up. As a result, the collected images may appear blurred, and the object detection algorithm may not accurately recognize the target objects or even fail to detect them directly. At this time, using a Kalman filter to provide a predicted position of the existing target object can effectively solve the problem of short-term failure of the object detection algorithm.

Algorithm 1 Object Tracking Based on YOLOv5s and Kalman Filter

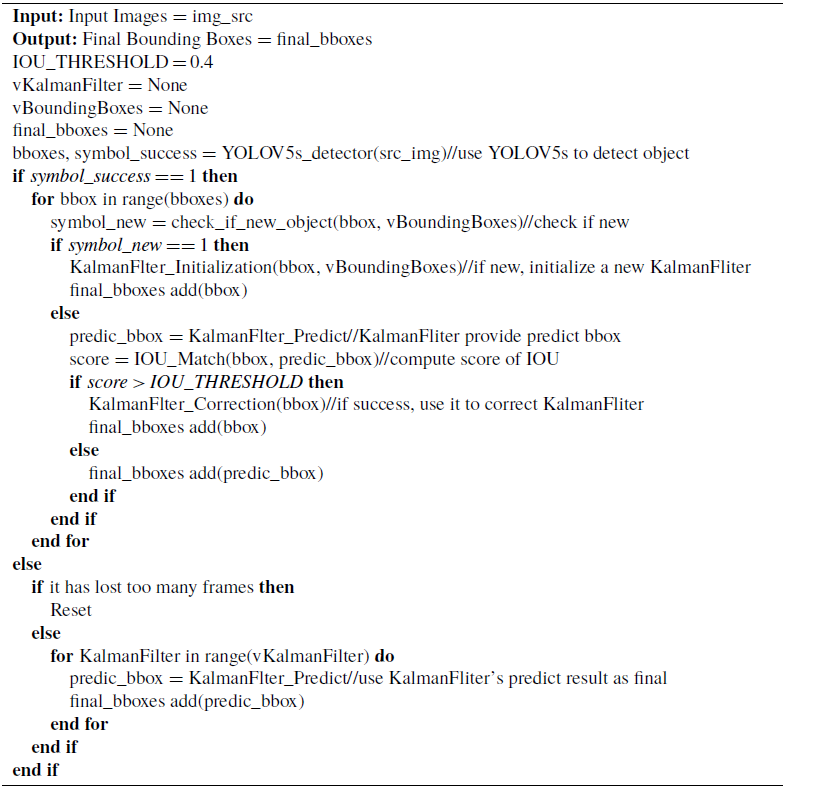
The objects that are maintained and predicted by the Kalman filter are the bounding boxes of dynamic objects, and the state vector is composed of $x=\left [ cx,cy,w,h,dx,dy,dw,dh \right ] ^T$ , where $cx$ and $cy$ represent the horizontal and vertical coordinates of the center point of the target bounding box, respectively, and $w$ and $h$ represent the width and height of the target bounding box, respectively. $dx$ , $dy$ , $dw$ , and $dh$ represent the differential quantities of the aforementioned state variables. The state equation is

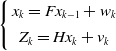(1) \begin{equation} \left \{\begin{array}{c} x_{k}=F x_{k-1}+w_{k} \\[4pt] Z_{k}=H x_{k}+v_{k} \end{array}\right . \end{equation}

where $x_{k}$ is the state estimate at k moment, $Z_{k}$ is the observation vector. $w_{k}$ is the process noise, and $v_{k}$ is the measurement noise.

More specifically, $ F = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1& 0& 0& 0& 1& 0& 0& 0 \\[4pt] 0& 1& 0& 0& 0& 1& 0& 0 \\[4pt] 0& 0& 1& 0& 0& 0& 1& 0 \\[4pt] 0& 0& 0& 1& 0& 0& 0& 1 \\[4pt] 0& 0& 0& 0& 1& 0& 0& 0 \\[4pt] 0& 0& 0& 0& 0& 1& 0& 0 \\[4pt] 0& 0& 0& 0& 0& 0& 1& 0 \\[4pt] 0& 0& 0& 0& 0& 0& 0& 1 \end{array} \right ]$ , $Z = \left [ \begin{array}{c} cx \\[4pt] cy \\[4pt] w \\[4pt] h \end{array} \right ]$ , and $H = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1& 0& 0& 0& 0& 0& 0& 0 \\[4pt] 0& 1& 0& 0& 0& 0& 0& 0 \\[4pt] 0& 0& 1& 0& 0& 0& 0& 0 \\[4pt] 0& 0& 0& 1& 0& 0& 0& 0 \end{array} \right ]$ .

For each frame of the image, the Kalman filter provides a predicted value based on the Kalman prediction formula (2):

(2) \begin{equation} \left \{\begin{array}{c} \hat{x}_{t}^{-}=F \hat{x}_{t-1} \\[7pt] P_{t}^{-}=F P_{t-1} F^{T}+Q \end{array}\right . \end{equation}

where $\hat{x}_{t}^{-}$ is the prior state estimate, $F$ is the state matrix, $P_{t}^{-}$ is the prior state covariance, and $Q$ is the state noise covariance.

If the object detection algorithm fails to output the two-dimensional position information of dynamic objects due to issues such as image blur, the predicted values provided by the Kalman filter are directly used as the final result.

If the object detection algorithm is able to function properly and output the two-dimensional bounding box of the detected targets, then an Intersection over Union (IOU) matching is performed between this two-dimensional position information and the bounding boxes provided by all the Kalman filters, as follows:

(3) \begin{equation} IOU=\frac{A\cap B}{A\cup B} \end{equation}

where $A$ and $B$ are two bounding boxes for comparison, and $IOU$ presents the IOU score.

If $IOU \gt 0.4$ , it is considered a successful match, and the object is considered an existing object. The bounding box with the highest IOU matching result is taken as the tracking result, and the corresponding Kalman filter is updated using the updated as

(4) \begin{equation} \left \{\begin{array}{c} K_t=P_t^-H^T\big(HP_t^-H^T+R\big)^{-1} \\[6pt] \hat{x}_{t}=\hat{x}_{t}^{-}+K_t\big(z_t-H\hat{x}_{t}^{-}\big) \\[6pt] P_t=(I-K_tH)P_t^- \end{array}\right . \end{equation}

where $K_t$ is the Kalman gain, $H$ is the observation matrix, $R$ is the observation noise covariance, $\hat{x}_{t}$ is the posterior state estimate, $z_t$ is the observation vector, and $P_t$ is the posterior state covariance matrix.

On the contrary, if there is no successful match, the object is considered as a newly appearing target. Then, a Kalman filter is initialized to continuously track this target in the subsequent process, and the initialization data is provided by the object detection algorithm. In addition, due to the fixed position of the “excavator arm” in special engineering scenarios, that is, when the object label is “Arm," the initial position is preset as

\begin{equation*} X_{arm} = \left [ \begin {array}{cccccccc} 0.75*col& 0.5*row& 0.3*col& 0.5*row& 0& 0& 0& 0 \end {array} \right ]^T \end{equation*}

At the same time, the objects are continuously tracked in each frame. If tracking fails for 12 consecutive frames, the target is considered lost, and the corresponding Kalman filter is destructed. Similarly, the target is considered lost if the center point coordinates move out of the frame or if the width and height become negative. In these cases, the Kalman filter corresponding to the lost target is destructed.

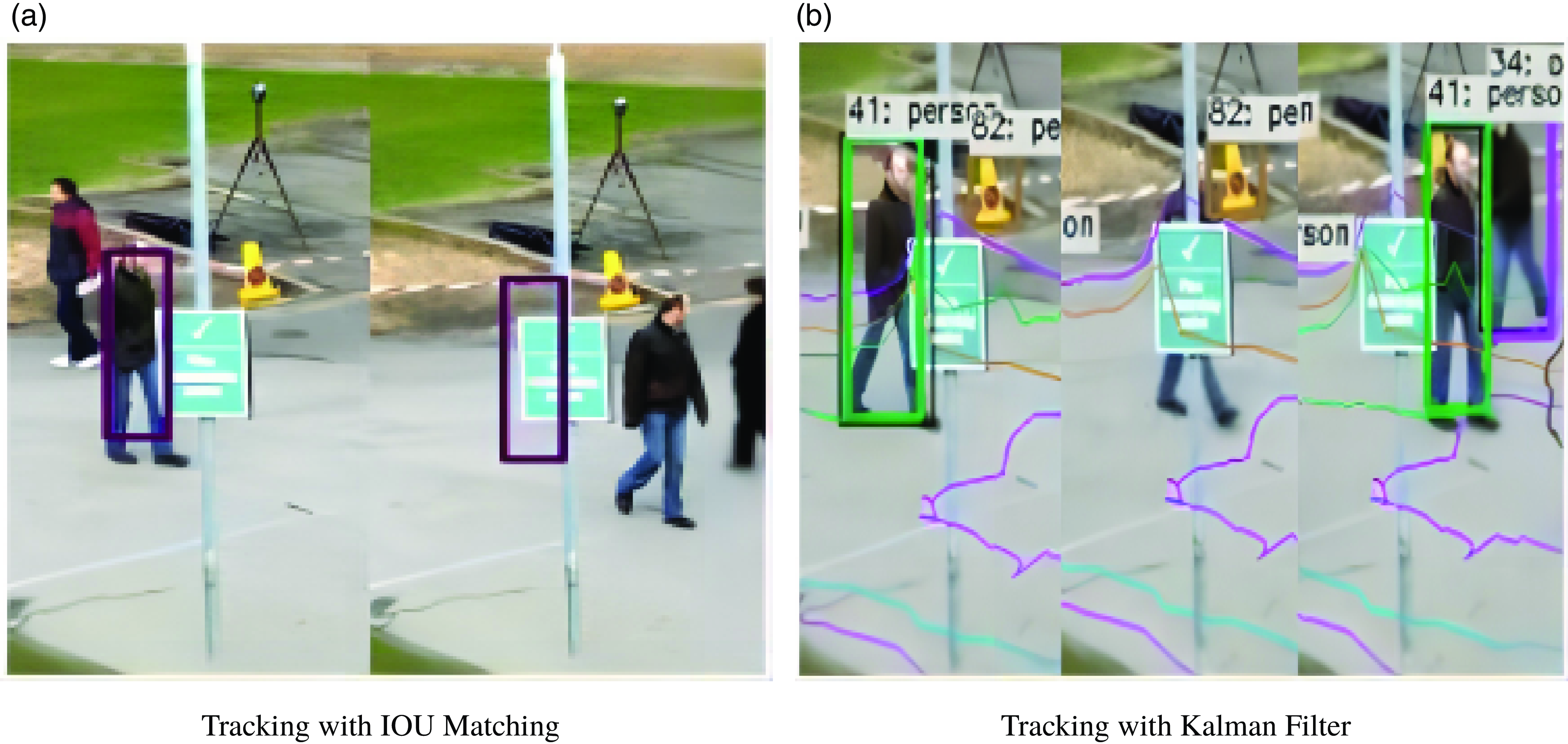
Figure 3. Comparison of different tracking results.

Figure 3(a) shows the results of using IOU matching. The purple rectangular boxes represent the stored tracked targets’ bounding boxes. In the experiment, when a person is occluded for a long time and reappears, the bounding box provided by YOLO cannot be matched with the stored bounding box information using IOU matching, resulting in tracking loss. The person walking out of the occluded area will be treated as a new target. Fig 3(b) shows the experimental results of tracking the bounding box position using the Kalman filter. The Kalman filter predicts the next frame’s position based on the movement of the bounding box. When the target is occluded, the predicted bounding box position does not stay in place but follows the past movement trend to predict the next frame’s position. When the target walks out of the occluded area, IOU matching can be successful, and the target can be re-tracked after a short period of loss.

3.3. Motion consistency detection

The use of rectangle information provided by the dynamic object tracking thread can categorize the feature points in the SLAM into two types: static feature points and potential dynamic feature points. Static points, due to their stable spatial positions, can ensure good pose estimation accuracy in SLAM. On the other hand, dynamic points are moving with respect to the camera and their spatial positions in the local map change over time. Using these dynamic points for pose estimation may introduce errors. However, blindly removing potential dynamic feature points is not desirable, as there may be a significant number of static points among them. If the static points outside the rectangle are not sufficient to support pose estimation, it may result in tracking failure of the entire SLAM system. Therefore, it is necessary to accurately classify static and dynamic points from these potential dynamic feature points, and make the most use of these static points whenever possible.

First, for the static points already determined outside the rectangle, epipolar geometry constraints are applied using equation (6), and the most fitting essential matrix is obtained using the RANSAC algorithm $E$ :

(5) \begin{equation} x_2^Tt^\wedge Rx_1=0 \end{equation}

(6) \begin{equation} E=t^\wedge R \end{equation}

where $E$ is the essential matrix, $t$ is the translation matrix and $R$ is the rotation matrix. Calculating the essential matrix requires the use of the eight-point algorithm [29]:

For each pair of matched 2D image points $x_1=\left ( \begin{array}{c@{\quad}c@{\quad}c} u_1&v_1&1 \end{array}\right )^T$ and $x_2=\left ( \begin{array}{c@{\quad}c@{\quad}c} u_2&v_2&1 \end{array}\right )^T$ , the epipolar geometry can be obtained through the following equation:

(7) \begin{equation} \left (\begin{array}{c@{\quad}c@{\quad}c} u_2&v_2&1 \end{array}\right ) \left (\begin{array}{c@{\quad}c@{\quad}c} e_1&e_2&e_3 \\[4pt] e_4&e_5&e_6 \\[4pt] e_7&e_8&e_9 \end{array}\right ) \left (\begin{array}{c} u_1 \\[4pt] v_1 \\[4pt] 1 \end{array}\right )=0 \end{equation}

where $E= \left (\begin{array}{c@{\quad}c@{\quad}c} e_1&e_2&e_3 \\[4pt] e_4&e_5&e_6 \\[4pt] e_7&e_8&e_9 \end{array}\right )$ is the sought-after essential matrix. Expanding the equation yields:

(8) \begin{equation} e_1u_1u_2+e_2u_1v_1+e_3u_1+e_4u_2v_1+e_5v_1v_2+e_6v_1+e_7u_2+e_8v_2+e_9=0 \end{equation}

Let $\vec{e} =\left (\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} e_1&e_2&e_3&e_4&e_5&e_6&e_7&e_8&e_9 \end{array}\right )^T$ , the equation can be further transformed into:

(9) \begin{equation} \left (\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} u_1u_2&u_2v_1&u_2&u_1v_2&v_1v_2&v_2&u_1&v_1&1 \end{array}\right)\vec{e}=0 \end{equation}

Due to scale equivalence, the degrees of freedom can be reduced by 1, and only 8 pairs of such matching points are needed to solve for the essential matrix.

To obtain the most fitting essential matrix using the RANSAC algorithm:

Algorithm 2 Object Tracking Based on YOLOv5s and Kalman Filter

After obtaining the essential matrix $E$ , the distance from points to the epipolar line can be calculated to determine if they are dynamic points. As shown in Fig 4, point $P$ is the 3D point triangulated from the previous frame’s point $P_1$ . Ideally, the projection of the static point $P$ onto the current frame $P_2$ should lie on its epipolar line. However, due to disturbances and errors, the actual projection point $P_2^{\prime }$ may deviate from the epipolar line by a certain distance. If the distance between $P_2^{\prime }$ and the epipolar line is too large, we have reason to believe that point $P$ is a dynamic point.

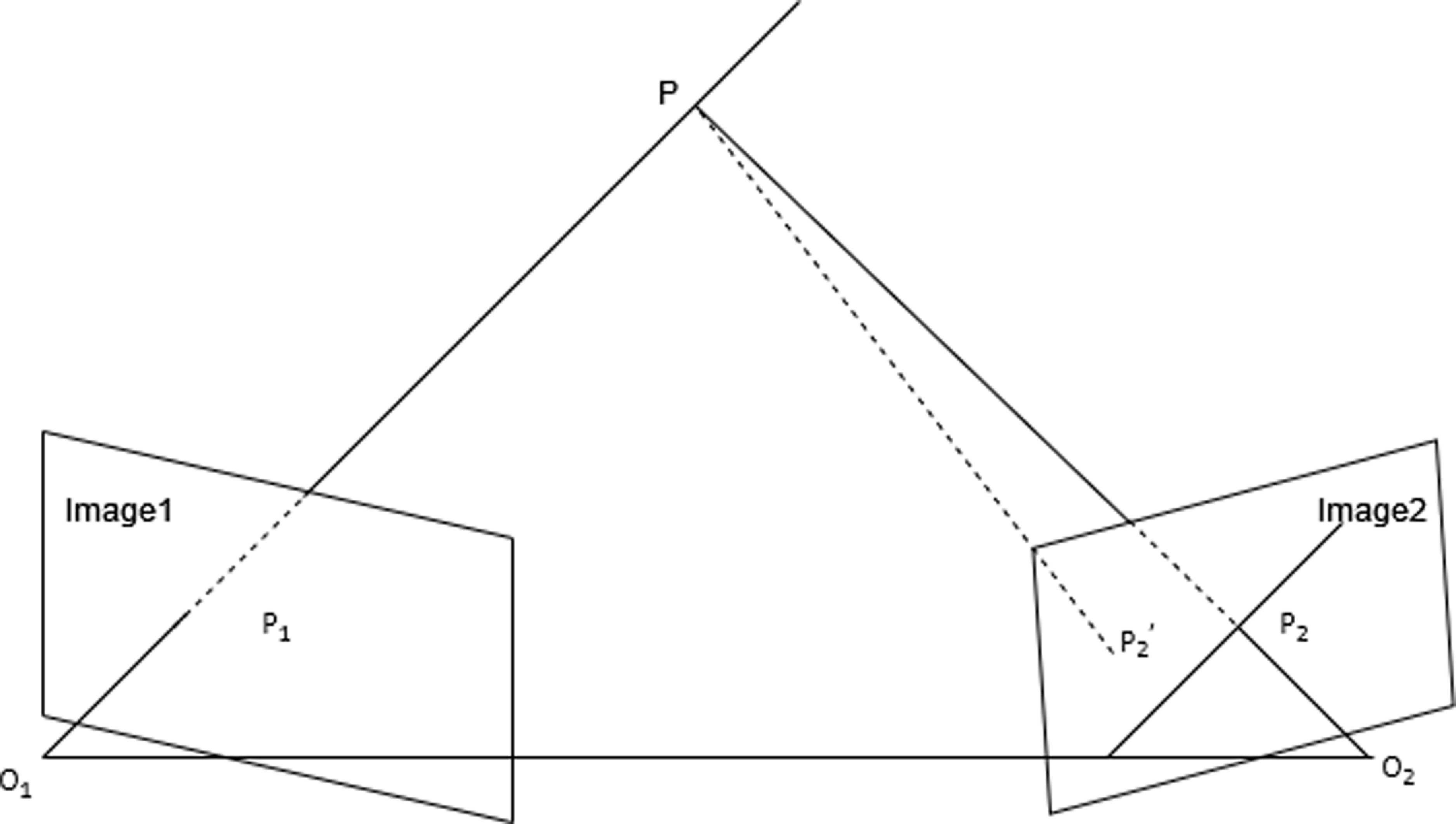
Figure 4. Epipolar line distance of reprojected points.

The distance $D$ from the keypoints of the current frame to the epipolar line can be calculated as

(10) \begin{equation} D=\frac{\left | x_2^TFx_1 \right | }{\sqrt{\left \| X \right \|^2+\left \| Y \right \| ^2 } } \end{equation}

where $x_1$ and $x_2$ are a pair of matched points, $F$ is the fundamental matrix, $X$ and $Y$ are the normal vectors of the epipolar lines. If the calculated distance $D$ is greater than the threshold $D_{th}$ , the point is considered as a dynamic point. If it is smaller than the threshold $D_{th}$ , the point is considered as a static point. Dynamic points are removed, and static points are merged.

4. Experimental analysis

4.1. TUM dataset

In order to verify the robustness of the proposed algorithm for trajectory estimation in dynamic scenes, experiments were conducted using the TUM public dataset. The TUM dataset, provided and researched by the Technical University of Munich, includes ground truth trajectories obtained from a precise motion capture system. This dataset is widely recognized among the SLAM community and is commonly used as a benchmark for evaluating SLAM algorithms. Due to the focus of this article on the dynamic SLAM problem, the experiment does not consider datasets that do not contain or only contain a small number of dynamic targets in the scene. The dataset sequences used in this study include the following six sequences: sitting_static, sitting_xyz, sitting_halfsphere, walking_static, walking_xyz, and walking_halfsphere. The “sitting” related sequences represent low dynamic scenes, where people in the frame are simply sitting and talking without much movement. The “walking” related sequences represent high-dynamic scenes, where two people in the frame are walking back and forth. The “static” related sequences represent scenes where the camera position remains relatively unchanged, and the “xyz” related sequences represent scenes where the camera position moves along the xyz axis. The “half-sphere” related sequences represent scenes where the camera position moves along the surface of a sphere and rotates. For convenience, in the following text, “fr3” is used to represent freiburg3, “s” is used for sitting, “w” is used for walking, and “half” is used for half-sphere.

The proposed algorithm in this paper was run on the computer with an Intel i5-10300 CPU, GTX-1050Ti GPU, 16 GB RAM, and 4 GB VRAM. The operating system used was Ubuntu 18.04 with ROS (Robot Operating System) version melodic.

4.2. Pose error experiment

The evaluation metric used in this paper to assess the accuracy of SLAM pose estimation is the Absolute Trajectory Error (ATE), which is calculated as

(11) \begin{equation} ATE_{all}=\sqrt{\frac{1}{N}\sum _{i=1}^{N}\left \| log\left(T_{gt,i}^{-1},T_{esti,i}\right)^\vee \right \| _2^2 } \end{equation}

where $T_{gt,i}^{-1}$ and $T_{esti,i}$ represent the ground truth trajectory and the estimated trajectory that needs to be evaluated, respectively. ATE represents the coordinate error between the trajectory points of the tested SLAM system and the ground truth trajectory, reflecting the alignment or overlap between the estimated trajectory and the ground truth trajectory. ATE is a direct method for evaluating the accuracy of the SLAM trajectory, providing a quantitative measure of the alignment between the estimated trajectory and the ground truth trajectory.

The algorithm proposed in this paper is a target detection-based SLAM algorithm, and the comparative algorithms include the DynaSLAM algorithm based on semantic segmentation and the static SLAM algorithm ov2slam. Since the TUM dataset does not provide stereo data, single-camera datasets were used for experiments. Pose error analysis was performed using the evo tool, which compares the SLAM trajectory with the ground truth poses provided by the TUM dataset. Each algorithm was run 10 times on each TUM sequence, and the average value of ATE was recorded. The experimental results are shown in the Figs. 5–7 and Table I.

Figure 5. Trajectory error plot.

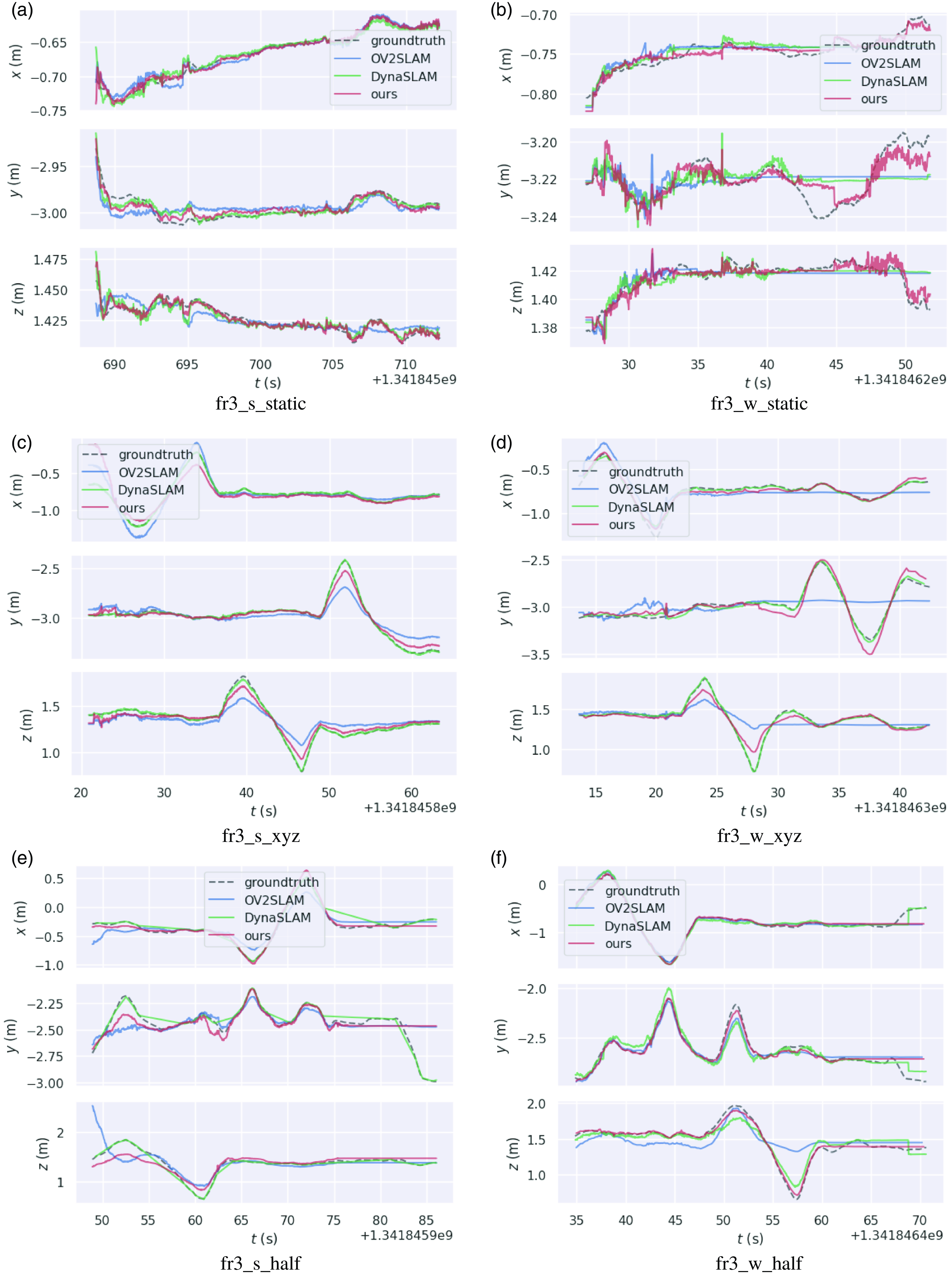
Figure 6. XYZ axis error plot.

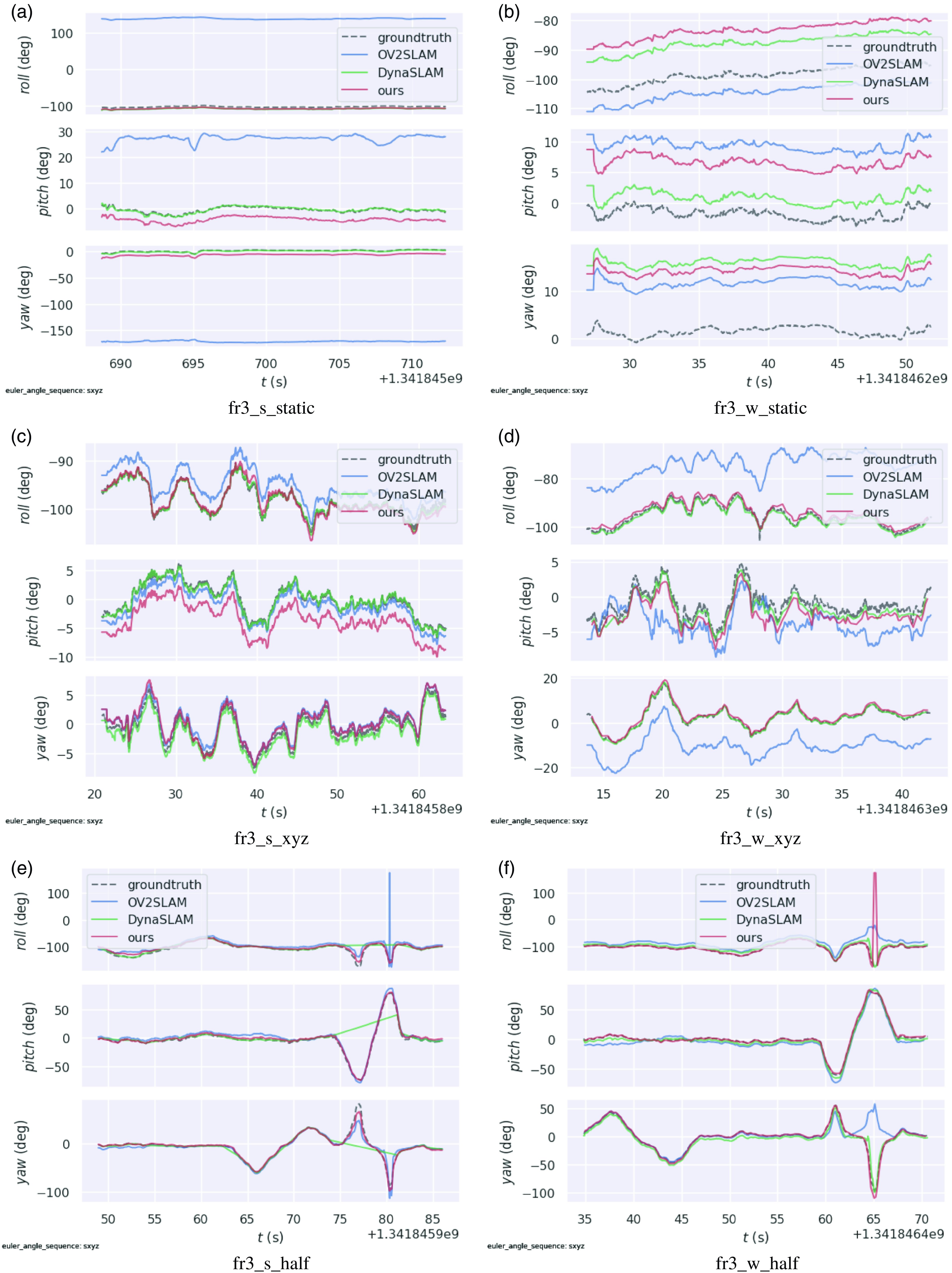
Figure 7. Euler angle error plot.

Table I. Absolute trajectory error (ATE) analysis comparison.

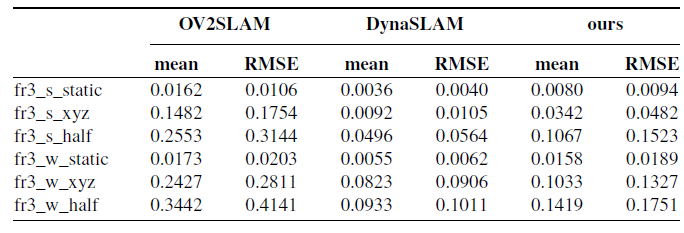
From the analysis in Table I, it can be observed that for low dynamic scenes (sitting), as shown in Fig 5(a) and Fig 5(b), the motion of people in the scene is minimal, resulting in a small number of dynamic feature points. Therefore, simple geometric methods such as epipolar geometry and RANSAC can be used to remove these few dynamic points, resulting in good performance. This leads to the fact that the improved algorithm in this chapter, compared to the original OV2SLAM algorithm, does not show significant improvement, and fails to fully reflect the importance of capturing prior information on dynamic objects using YOLO.

In high-dynamic scenes (walking), the performance of the original OV2SLAM algorithm using only simple geometric methods starts to degrade, as people in the scene are moving more freely, resulting in more dynamic feature points. However, with the prior information on dynamic objects provided by YOLO, the improved algorithm shows better performance in such dynamic scenes, as shown in Fig 5(d) to Fig 5(f). In the fr3_w_xyz sequence, the improved algorithm achieves a 52.79% improvement in pose accuracy compared to the original OV2SLAM algorithm. In the fr3_w_half sequence, the improvement is 57.71%.

It is worth noting that in fr3_w_xyz, the two persons in the scene appear simultaneously in several frames and occupy over 70% of the image. In the improved algorithm, the potential points within the bounding box are not processed in the current frame. However, the static points used for pose estimation outside the bounding box are not sufficient to support subsequent computations, resulting in temporary tracking failures in a few frames, which leads to suboptimal performance in fr3_w_xyz.

In contrast, DynaSLAM uses a pixel-level semantic segmentation algorithm that can determine dynamic points in the current frame, resulting in higher pose estimation accuracy. Compared to the improved algorithm, DynaSLAM achieves an increase of 31.72% and 42.26% in accuracy on fr3_w_xyz and fr3_w_half sequences, respectively.

4.3. Algorithm time analysis

The advantage of the algorithm proposed in this paper is its lightweight nature, which allows it to run smoothly on embedded devices with limited computing capabilities. This makes the algorithm suitable for a wider range of practical applications in real-world scenarios.

The algorithm’s runtime was tested on the fr3_w_half sequence by conducting 10 experiments and averaging the results. A comparison was made with DynaSLAM, and the time taken for various stages, including feature point extraction (which includes descriptor computation for DynaSLAM), dynamic object detection, and per-frame tracking, was recorded. The experimental results are presented in Table II.

Table II. Running time of different stage(ms).

In terms of feature point extraction, DynaSLAM uses the same strategy as ORBSLAM2, which involves extracting both corner points and computing descriptors. In contrast, our algorithm only extracts FAST corner points, resulting in a 61.39% reduction in runtime for the feature point extraction stage. For dynamic object detection, DynaSLAM utilizes the Mask-RCNN algorithm, which is resource-intensive and not real-time, with a detection time of 165.1883 ms per frame. On the other hand, our algorithm employs a lightweight object detection algorithm, yolov5s, which only takes 22.1885 ms per frame for detection, resulting in an 86.57% reduction in runtime for dynamic object detection. Due to the dynamic object detection being typically implemented in a separate thread that is asynchronous with the SLAM thread, in DynaSLAM, on average, one priori information from the dynamic object detection thread is obtained for every 4 frames. In contrast, our algorithm can obtain priori information from dynamic object detection for every 2 frames on average. Additionally, since we use a Kalman filter to estimate the position of the dynamic object bounding box, even if the current frame does not have prior information from the object detection algorithm, the Kalman filter can provide an estimated value for the dynamic object bounding box to ensure that priori information is available for every frame. As for the tracking thread, DynaSLAM inherits from ORBSLAM2 and computes the pose after descriptor matching, while our algorithm inherits from ov2slam and utilizes optical flow, eliminating the need for descriptor matching and reducing runtime by 84.94%. In terms of total runtime, considering only feature point extraction and per-frame tracking, our method reduces runtime by 75.47% compared to DynaSLAM.

5. Conclusion

This paper proposes a lightweight dynamic SLAM algorithm that utilizes optical flow and object tracking to save system resources. By combining geometric and object detection methods to exclude dynamic points, the algorithm is able to robustly operate in dynamic scenes. Experimental results show that the improved algorithm achieves a 52.79% increase in pose accuracy compared to the original OV2SLAM algorithm on dynamic datasets, and sacrifices an average of about 35% accuracy compared to DynaSLAM and other SLAM algorithms based on semantic segmentation algorithms, in exchange for speed. Our algorithm achieves an overall speed improvement of 75.47% and can run in real-time even on embedded devices with limited computing capabilities. However, there are limitations in this algorithm, such as the requirement of 2 frames to differentiate dynamic points. If there are too many dynamic objects in the scene, all feature points on dynamic objects may be labeled as potential dynamic points, which do not participate in the pose calculation of the current frame. This may result in poor tracking performance or even tracking failure when the number of static points involved in the tracking process is too low. Future work will address this issue by optimizing potential dynamic point selection steps or adding more features (such as line features [30]), in order to incorporate these points into the attitude calculation process as early as possible. In addition, it is also possible to consider enhancing object detection techniques and combining multi-sensor fusion techniques or SVSF method, etc to enhance the robustness of SLAM to dynamic environments.