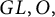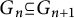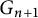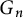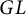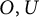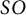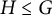1 Introduction
Let
![]() ${\mathbb F}$
be a local field of positive characteristic different from 2. Let
${\mathbb F}$
be a local field of positive characteristic different from 2. Let
![]() ${\mathbb K}$
be either equal to
${\mathbb K}$
be either equal to
![]() ${\mathbb F}$
or an extension of it of degree 2. Let V be a vector space of dimension n over
${\mathbb F}$
or an extension of it of degree 2. Let V be a vector space of dimension n over
![]() ${\mathbb K}$
. Let
${\mathbb K}$
. Let
![]() $W:=V\oplus {\mathbb K} v_{n+1}$
be an (
$W:=V\oplus {\mathbb K} v_{n+1}$
be an (
![]() $n+1$
)-dimensional vector space containing it. Assume that we have a nondegenerate Hermitian (symmetric in the case
$n+1$
)-dimensional vector space containing it. Assume that we have a nondegenerate Hermitian (symmetric in the case
![]() ${\mathbb K}={\mathbb F}$
) form on W, with respect to which V is orthogonal to
${\mathbb K}={\mathbb F}$
) form on W, with respect to which V is orthogonal to
![]() $v_{n+1}$
. Note that this implies, in particular, that
$v_{n+1}$
. Note that this implies, in particular, that
![]() $\left \langle v_{n+1},v_{n+1}\right\rangle\neq 0$
. We will denote G to be either the group
$\left \langle v_{n+1},v_{n+1}\right\rangle\neq 0$
. We will denote G to be either the group
![]() $O$
or
$O$
or
![]() $SO$
in the case
$SO$
in the case
![]() ${\mathbb K}={\mathbb F}$
or U in the case
${\mathbb K}={\mathbb F}$
or U in the case
![]() ${\mathbb K}\neq {\mathbb F}$
. Consider the group
${\mathbb K}\neq {\mathbb F}$
. Consider the group
![]() $G(V)$
as a subgroup of
$G(V)$
as a subgroup of
![]() $G(W)$
.
$G(W)$
.
The following theorem is among the main theorems proved in this paper.
Theorem 1.1 Let
![]() $\pi $
and
$\pi $
and
![]() $\rho $
be irreducible smooth representations of
$\rho $
be irreducible smooth representations of
![]() $G(W)$
and
$G(W)$
and
![]() $G(V)$
, respectively. Then
$G(V)$
, respectively. Then
Let us define an anti-involution
![]() $\sigma $
of
$\sigma $
of
![]() $G(W)$
for all three families of classical groups:
$G(W)$
for all three families of classical groups:
In the case of
![]() $O$
, define
$O$
, define
![]() $\sigma : g\mapsto g^{-1}$
.
$\sigma : g\mapsto g^{-1}$
.
In the case of
![]() $SO$
, choose
$SO$
, choose
![]() $T\in G(V)$
of order 2 with
$T\in G(V)$
of order 2 with
![]() $\det T = (-1)^{\lfloor {\frac {n+1}{2}}\rfloor }$
: One may choose such an element by taking a basis of V with respect to which the symmetric form is diagonal, and in this basis, take a diagonal matrix of
$\det T = (-1)^{\lfloor {\frac {n+1}{2}}\rfloor }$
: One may choose such an element by taking a basis of V with respect to which the symmetric form is diagonal, and in this basis, take a diagonal matrix of
![]() $\pm 1$
with the appropriate parity of
$\pm 1$
with the appropriate parity of
![]() $-1$
entries. Define
$-1$
entries. Define
![]() $\sigma : g\mapsto Tg^{-1}T$
.
$\sigma : g\mapsto Tg^{-1}T$
.
In the case of U, choose a basis of W for which the Hermitian product of all pairs lies in
![]() ${\mathbb F}$
(for example, by choosing a basis that diagonalizes the Hermitian form). Then we have an involution
${\mathbb F}$
(for example, by choosing a basis that diagonalizes the Hermitian form). Then we have an involution
![]() $T:v\mapsto \bar {v}$
(writing v as a vector in this basis). Define an anti-involution of
$T:v\mapsto \bar {v}$
(writing v as a vector in this basis). Define an anti-involution of
![]() $G(W)$
by
$G(W)$
by
![]() $\sigma : g\mapsto Tg^{-1}T$
.
$\sigma : g\mapsto Tg^{-1}T$
.
Consider the action of
![]() $G(V)$
on
$G(V)$
on
![]() $G(W)$
by conjugation. The following theorem implies Theorem 1.1 using the Gelfand–Kazhdan criterion.
$G(W)$
by conjugation. The following theorem implies Theorem 1.1 using the Gelfand–Kazhdan criterion.
Theorem 1.2 Any
![]() $G(V)$
-invariant distribution on
$G(V)$
-invariant distribution on
![]() $G(W)$
is also invariant under
$G(W)$
is also invariant under
![]() $\sigma $
.
$\sigma $
.
The proof of this implication in zero characteristic is given in [Reference Sun12, Appendix B], [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Section 1], and [Reference Waldspurger14], and the same proofs apply verbatim in arbitrary odd characteristic.
We also prove another theorem which we shall now describe, given in [Reference Sun12] for characteristic 0. One may also look there for more extensive explanations about the basic notations and definitions used. This theorem will be related to the uniqueness of Fourier–Jacobi models, and will regard all the previous families of classical groups, as well as
![]() $Sp$
.
$Sp$
.
Let A be a finite-dimensional commutative involutive algebra over
![]() ${\mathbb F}$
, and let V be a finitely generated A-module. Let
${\mathbb F}$
, and let V be a finitely generated A-module. Let
![]() $\epsilon = \pm 1$
, and let
$\epsilon = \pm 1$
, and let
![]() $\tau $
be the involution of A. Assume that V is equipped with a nondegenerate
$\tau $
be the involution of A. Assume that V is equipped with a nondegenerate
![]() $\epsilon $
-Hermitian form, i.e., a nondegenerate
$\epsilon $
-Hermitian form, i.e., a nondegenerate
![]() ${\mathbb F}$
-bilinear map
${\mathbb F}$
-bilinear map
![]() $\langle\cdot , \cdot\rangle:V\times V\to A$
satisfying A-linearity in the first argument, and
$\langle\cdot , \cdot\rangle:V\times V\to A$
satisfying A-linearity in the first argument, and
![]() $\langle v, u\rangle= \epsilon \langle u, v\rangle^\tau $
. Denote by S the group of all A-module automorphisms of V which preserve this form. It is a finite product of general linear groups, unitary groups, orthogonal groups, and symplectic groups. Denote by
$\langle v, u\rangle= \epsilon \langle u, v\rangle^\tau $
. Denote by S the group of all A-module automorphisms of V which preserve this form. It is a finite product of general linear groups, unitary groups, orthogonal groups, and symplectic groups. Denote by
![]() $A^{\tau = -\epsilon }$
the subset of A of elements a satisfying
$A^{\tau = -\epsilon }$
the subset of A of elements a satisfying
![]() $a^\tau = -\epsilon a$
. Let H be the Heisenberg group defined as
$a^\tau = -\epsilon a$
. Let H be the Heisenberg group defined as
![]() $\{(v, t)|v\in V, t\in A^{\tau = -\epsilon }\}$
with multiplication
$\{(v, t)|v\in V, t\in A^{\tau = -\epsilon }\}$
with multiplication
 $$ \begin{align*}(v,t)(v',t') = \left(v + v', t + t' + \frac{\langle v, v'\rangle}{2} - \frac{\langle v', v\rangle}{2}\right)\!.\end{align*} $$
$$ \begin{align*}(v,t)(v',t') = \left(v + v', t + t' + \frac{\langle v, v'\rangle}{2} - \frac{\langle v', v\rangle}{2}\right)\!.\end{align*} $$
We have a natural action of S on H. Denote by
![]() $J:=H\rtimes S$
the semidirect product of H and S with respect to this action. We prove in this paper the following theorem.
$J:=H\rtimes S$
the semidirect product of H and S with respect to this action. We prove in this paper the following theorem.
Theorem 1.3 Let
![]() $\pi $
and
$\pi $
and
![]() $\rho $
be irreducible smooth representations of J and S, respectively. Then
$\rho $
be irreducible smooth representations of J and S, respectively. Then
Again, we shall use the method of Gelfand and Kazhdan. Choose an
![]() ${\mathbb F}$
-linear involution
${\mathbb F}$
-linear involution
![]() $\sigma $
of V such that
$\sigma $
of V such that
![]() $\langle\sigma u, \sigma v\rangle = \langle v, u\rangle$
. To see that it is always possible, write G as a product of unitary, orthogonal, symplectic, and general linear groups with the corresponding orthogonal decomposition of V over
$\langle\sigma u, \sigma v\rangle = \langle v, u\rangle$
. To see that it is always possible, write G as a product of unitary, orthogonal, symplectic, and general linear groups with the corresponding orthogonal decomposition of V over
![]() ${\mathbb F}$
. In each of these cases, we are able to construct such an involution, and we can take the product of these involutions as
${\mathbb F}$
. In each of these cases, we are able to construct such an involution, and we can take the product of these involutions as
![]() $\sigma $
. The involution
$\sigma $
. The involution
![]() $\sigma $
extends to an anti-involution of H by
$\sigma $
extends to an anti-involution of H by
![]() $(v, t)\mapsto (-\sigma v, t)$
, which together with the anti-involution
$(v, t)\mapsto (-\sigma v, t)$
, which together with the anti-involution
![]() $g\mapsto \sigma g^{-1}\sigma $
of S gives an anti-involution of J (which we shall also call
$g\mapsto \sigma g^{-1}\sigma $
of S gives an anti-involution of J (which we shall also call
![]() $\sigma $
). Let S act on J by conjugation. The following theorem implies Theorem 1.3 using the Gelfand–Kazhdan criterion.
$\sigma $
). Let S act on J by conjugation. The following theorem implies Theorem 1.3 using the Gelfand–Kazhdan criterion.
Theorem 1.4 Any S-invariant distribution on J is also invariant under
![]() $\sigma $
.
$\sigma $
.
The implication is proved in [Reference Sun12, Appendix B] in zero characteristic, and the same proof applies verbatim in arbitrary odd characteristic.
Sections 3–8 are dedicated to the simultaneous proof of Theorems 1.2 and 1.4.
Remark 1.5 One could ask whether an analog of Theorem 1.1 holds for the subgroup
![]() $SU$
of Hermitian operators with determinant
$SU$
of Hermitian operators with determinant
![]() $1$
. However, the answer turns out to be negative even for the most simple case of
$1$
. However, the answer turns out to be negative even for the most simple case of
![]() $\dim V = 1$
. In this case,
$\dim V = 1$
. In this case,
![]() $SU(V) = \{1\}$
, while
$SU(V) = \{1\}$
, while
![]() $SU(W)$
is noncommutative, showing that the two groups do not satisfy a multiplicity one property.
$SU(W)$
is noncommutative, showing that the two groups do not satisfy a multiplicity one property.
Remark 1.6 The assumption of
![]() ${\mathbb F}$
having positive characteristic is not used anywhere in this paper, and is given mainly to distinguish the work in this paper from the already existing proofs of the discussed theorems when the characteristic of
${\mathbb F}$
having positive characteristic is not used anywhere in this paper, and is given mainly to distinguish the work in this paper from the already existing proofs of the discussed theorems when the characteristic of
![]() ${\mathbb F}$
is 0.
${\mathbb F}$
is 0.
1.1 Corollaries of the main theorems
There are corollaries of Theorems 1.1 and 1.3 which were shown over characteristic 0, and the proofs of implication still apply over positive characteristic. We list them here with references.
An analog of the following theorem appears in [Reference Sun12] as Theorem B, and its implication from the analog of Theorem 1.3 is shown in Appendix A of the same.
Theorem 1.7 Let G denote one of the groups
![]() $GL(n), U(n)$
, and
$GL(n), U(n)$
, and
![]() $Sp(2n)$
(note that
$Sp(2n)$
(note that
![]() $U(n)$
is dependent on the choice of a Hermitian form), regarded as a subgroup of
$U(n)$
is dependent on the choice of a Hermitian form), regarded as a subgroup of
![]() $Sp(2n)$
as usual. Let
$Sp(2n)$
as usual. Let
![]() ${\widetilde {G}}$
be the double cover of G induced by the metaplectic cover
${\widetilde {G}}$
be the double cover of G induced by the metaplectic cover
![]() $\widetilde {Sp}(2n)$
of
$\widetilde {Sp}(2n)$
of
![]() $Sp(2n)$
. Denote by
$Sp(2n)$
. Denote by
![]() $\omega _\psi $
the smooth oscillator representation of
$\omega _\psi $
the smooth oscillator representation of
![]() $\widetilde {Sp}(2n)$
corresponding to a nontrivial character
$\widetilde {Sp}(2n)$
corresponding to a nontrivial character
![]() $\psi $
of
$\psi $
of
![]() ${\mathbb F}$
. Then, for any irreducible smooth representation
${\mathbb F}$
. Then, for any irreducible smooth representation
![]() $\pi $
of G, and for any genuine irreducible smooth representation
$\pi $
of G, and for any genuine irreducible smooth representation
![]() $\pi '$
of
$\pi '$
of
![]() ${\widetilde {G}}$
, one has that
${\widetilde {G}}$
, one has that
An analog of the following theorem appears in [Reference Chen and Sun7], along with its implication from the analog of the above theorem (see [Reference Chen and Sun7] for the definitions and notation used).
Theorem 1.8 (Uniqueness of Rankin–Selberg models)
For all irreducible smooth representations
![]() $\pi $
of
$\pi $
of
![]() $GL(n)$
and
$GL(n)$
and
![]() $\sigma $
of
$\sigma $
of
![]() $GL(r)$
, and for all generic characters
$GL(r)$
, and for all generic characters
![]() $\chi $
of the rth Rankin–Selberg subgroup
$\chi $
of the rth Rankin–Selberg subgroup
![]() $R_r$
of
$R_r$
of
![]() $GL(n)$
, one has that
$GL(n)$
, one has that
Analogs of the following two theorems appear in [Reference Gan, Gross and Prasad8, Chapters 12–16], along with their implications from the analogs of Theorems 1.1 and 1.3 and the multiplicity one property for
![]() $GL(n+1), GL(n)$
, which is proved for positive characteristic in [Reference Mezer9, Theorem 1.2] and in [Reference Aizenbud, Avni and Gourevitch1].
$GL(n+1), GL(n)$
, which is proved for positive characteristic in [Reference Mezer9, Theorem 1.2] and in [Reference Aizenbud, Avni and Gourevitch1].
Theorem 1.9 (Uniqueness of Bessel models)
Let V be a linear space with a symmetric or Hermitian (including the case
![]() ${\mathbb K}={\mathbb F}\times {\mathbb F}$
) form. Denote the respective orthogonal or unitary group
${\mathbb K}={\mathbb F}\times {\mathbb F}$
) form. Denote the respective orthogonal or unitary group
![]() $G(V)$
. Let W be a subspace of odd codimension on which the form is nondegenerate and so that
$G(V)$
. Let W be a subspace of odd codimension on which the form is nondegenerate and so that
![]() $W^\perp $
is split. Let H be the Bessel group corresponding to W, considered as a subgroup of
$W^\perp $
is split. Let H be the Bessel group corresponding to W, considered as a subgroup of
![]() $G(V)\times G(W)$
, and let
$G(V)\times G(W)$
, and let
![]() $\nu $
be a generic character of H. Then, for any irreducible smooth representations
$\nu $
be a generic character of H. Then, for any irreducible smooth representations
![]() $\pi $
of
$\pi $
of
![]() $G(V)$
and
$G(V)$
and
![]() $\pi '$
of
$\pi '$
of
![]() $G(W)$
, one has
$G(W)$
, one has
Theorem 1.10 (Uniqueness of Fourier–Jacobi models)
Let V be a linear space with a skew-symmetric or skew-Hermitian (including the case
![]() ${\mathbb K}={\mathbb F}\times {\mathbb F}$
) form. Denote the respective symplectic or unitary group
${\mathbb K}={\mathbb F}\times {\mathbb F}$
) form. Denote the respective symplectic or unitary group
![]() $G(V)$
. Let W be a subspace of even codimension on which the form is nondegenerate and so that
$G(V)$
. Let W be a subspace of even codimension on which the form is nondegenerate and so that
![]() $W^\perp $
is split. Let H be the Fourier–Jacobi group corresponding to W, considered as a subgroup of
$W^\perp $
is split. Let H be the Fourier–Jacobi group corresponding to W, considered as a subgroup of
![]() $G(V)\times G(W)$
. Let
$G(V)\times G(W)$
. Let
![]() $\widetilde {H}$
be its appropriate double cover, and let
$\widetilde {H}$
be its appropriate double cover, and let
![]() $\nu $
be the representation of
$\nu $
be the representation of
![]() $\widetilde {H}$
constructed in [Reference Gan, Gross and Prasad8, Chapter 12] (depending on some choices of characters). Take either
$\widetilde {H}$
constructed in [Reference Gan, Gross and Prasad8, Chapter 12] (depending on some choices of characters). Take either
![]() $\pi $
to be an irreducible smooth representations of
$\pi $
to be an irreducible smooth representations of
![]() ${\widetilde {G}}(V)$
(an appropriate double cover of
${\widetilde {G}}(V)$
(an appropriate double cover of
![]() $G(V)$
) and
$G(V)$
) and
![]() $\pi '$
to be such a representation of
$\pi '$
to be such a representation of
![]() $G(W)$
, or the other way around, i.e.,
$G(W)$
, or the other way around, i.e.,
![]() $\pi $
to be an irreducible smooth representation of
$\pi $
to be an irreducible smooth representation of
![]() $G(V)$
and
$G(V)$
and
![]() $\pi '$
to be such a representation of an appropriate
$\pi '$
to be such a representation of an appropriate
![]() ${\widetilde {G}}(W)$
. Then one has
${\widetilde {G}}(W)$
. Then one has
1.2 Comparison with previous works
In [Reference Mezer9], the proof of a multiplicity one theorem for
![]() $GL_n$
in characteristic 0 is extended to include also positive odd characteristic. The premise of this paper is to use these methods to extend the proof of additional multiplicity one theorems from characteristic 0 to positive odd characteristic. The proofs for characteristic 0 on which we base this paper are given in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14]. Let us give an overview of the methods and steps of this paper, explaining which ones are taken from [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14], which ones were introduced in [Reference Mezer9], and which ones are new to this paper.
$GL_n$
in characteristic 0 is extended to include also positive odd characteristic. The premise of this paper is to use these methods to extend the proof of additional multiplicity one theorems from characteristic 0 to positive odd characteristic. The proofs for characteristic 0 on which we base this paper are given in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14]. Let us give an overview of the methods and steps of this paper, explaining which ones are taken from [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14], which ones were introduced in [Reference Mezer9], and which ones are new to this paper.
In Section 3, we give reformulations of the problems in a way identical to the ones given in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14].
In Section 4, we use a certain analog of the Harish–Chandra descent method for positive characteristic, that gives weaker results than in the zero characteristic case. The entirety of this method as used in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14] fails over positive characteristic fields, due to nonseparable extensions, and in fact, this is the crucial point in which these proofs fail for a positive characteristic.
In Section 5, we pass from the group to its Lie algebra using Cayley transform. The difference from the analogous linearization in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14] is that, in these papers, linearization is done after using the method of Harish–Chandra descent to restrict the possible support to the unipotent cone, whereas we only have a weaker restriction on the support.
In Section 6, we adapt the main new ideas of [Reference Mezer9] to the unitary, orthogonal, and symplectic settings, introducing a new family
![]() $\rho $
of automorphisms playing the same role as
$\rho $
of automorphisms playing the same role as
![]() $\rho $
in [Reference Mezer9].
$\rho $
in [Reference Mezer9].
Section 7 uses the method of stratification to reduce the problem to a problem on a single orbit. The contents of this section are completely analogous to what is done in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14], only without the restriction of nilpotency, which is not truly needed, as was the case in [Reference Mezer9].
In Section 8, we solve the previous problem on a single orbit by repeating the arguments and ideas used in [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Sun12, Reference Waldspurger14], sometimes giving slight generalizations of them.
The archimedean version of Theorems 1.1 and 1.4 can be found in [Reference Sun and Zhu13]. Special cases of Theorems 1.1 and 1.2 can be found in [Reference Aizenbud, Gourevitch and Sayag4].
2 Preliminaries and notation
Most of this section is borrowed from the preliminaries sections of [Reference Aizenbud and Gourevitch2, Reference Aizenbud, Gourevitch, Rallis and Schiffmann3], and also of [Reference Mezer9] (which was also mostly borrowed from the previous two).
Let us now introduce a uniform notation for all the groups
![]() $O,SO,U$
, and
$O,SO,U$
, and
![]() $Sp$
. Note that the case
$Sp$
. Note that the case
![]() $G=Sp$
was not included in Theorems 1.1 and 1.2, but it will be relevant for Theorems 1.3 and 1.4. Let
$G=Sp$
was not included in Theorems 1.1 and 1.2, but it will be relevant for Theorems 1.3 and 1.4. Let
![]() ${\mathbb F}$
be a local field of characteristic different from 2. Let
${\mathbb F}$
be a local field of characteristic different from 2. Let
![]() ${\mathbb K}$
be a field which is either equal to
${\mathbb K}$
be a field which is either equal to
![]() ${\mathbb F}$
or a quadratic field extension of it. Let
${\mathbb F}$
or a quadratic field extension of it. Let
![]() $\lambda \mapsto \bar {\lambda }$
be either the nontrivial automorphism of
$\lambda \mapsto \bar {\lambda }$
be either the nontrivial automorphism of
![]() ${\mathbb K}/{\mathbb F}$
or the identity automorphism if
${\mathbb K}/{\mathbb F}$
or the identity automorphism if
![]() ${\mathbb K} = {\mathbb F}$
. Let V be a
${\mathbb K} = {\mathbb F}$
. Let V be a
![]() ${\mathbb K}$
-linear space of dimension n. Assume that we have on V a nondegenerate sesquilinear form B which is either symmetric, Hermitian, or symplectic (in the Hermitian case
${\mathbb K}$
-linear space of dimension n. Assume that we have on V a nondegenerate sesquilinear form B which is either symmetric, Hermitian, or symplectic (in the Hermitian case
![]() ${\mathbb K}\neq {\mathbb F}$
and in the other cases
${\mathbb K}\neq {\mathbb F}$
and in the other cases
![]() ${\mathbb K} = {\mathbb F}$
). Denote by
${\mathbb K} = {\mathbb F}$
). Denote by
![]() $G=G(V)$
one of the groups
$G=G(V)$
one of the groups
![]() $O(V), SO(V), U(V)$
, or
$O(V), SO(V), U(V)$
, or
![]() $Sp(V)$
. Denote by
$Sp(V)$
. Denote by
![]() $\mathfrak {g}=\mathfrak {g}(V)$
the Lie algebra of G, which is either
$\mathfrak {g}=\mathfrak {g}(V)$
the Lie algebra of G, which is either
![]() $\mathfrak {o}(V)$
,
$\mathfrak {o}(V)$
,
![]() $\mathfrak {u}(V)$
, or
$\mathfrak {u}(V)$
, or
![]() $\mathfrak {sp}(V)$
, i.e., linear transformations A satisfying
$\mathfrak {sp}(V)$
, i.e., linear transformations A satisfying
![]() $A^*=-A$
with respect to the symmetric, Hermitian, or symplectic form. In the
$A^*=-A$
with respect to the symmetric, Hermitian, or symplectic form. In the
![]() $O, SO, U$
cases, assume that we have
$O, SO, U$
cases, assume that we have
![]() $W\supseteq V$
of dimension
$W\supseteq V$
of dimension
![]() $n+1$
with an extension of
$n+1$
with an extension of
![]() $\langle\cdot , \cdot\rangle$
to a form on W of the same type. In these cases, we have also
$\langle\cdot , \cdot\rangle$
to a form on W of the same type. In these cases, we have also
![]() $G(W)$
, and we may consider G as a subgroup of it.
$G(W)$
, and we may consider G as a subgroup of it.
Let
![]() ${\widetilde {G}}$
denote the subgroup of
${\widetilde {G}}$
denote the subgroup of
![]() $\operatorname {Aut}_{\mathbb F}(V)\times \{\pm 1\}$
consisting of all
$\operatorname {Aut}_{\mathbb F}(V)\times \{\pm 1\}$
consisting of all
![]() $(T, \delta )$
such that
$(T, \delta )$
such that
![]() $\langle Tu, Tv\rangle= \langle u, v\rangle$
if
$\langle Tu, Tv\rangle= \langle u, v\rangle$
if
![]() $\delta = 1$
and
$\delta = 1$
and
![]() $\langle Tu, Tv\rangle= \langle v, u\rangle$
if
$\langle Tu, Tv\rangle= \langle v, u\rangle$
if
![]() $\delta = -1$
. In the case that
$\delta = -1$
. In the case that
![]() $G = SO$
, we also require that
$G = SO$
, we also require that
![]() $\det T = \delta ^ {\lfloor {\frac {n+1}{2}}\rfloor }$
. This group contains G as a subgroup of index
$\det T = \delta ^ {\lfloor {\frac {n+1}{2}}\rfloor }$
. This group contains G as a subgroup of index
![]() $2$
. Denote by
$2$
. Denote by
![]() $\chi : {\widetilde {G}} \to {\pm 1}$
the character
$\chi : {\widetilde {G}} \to {\pm 1}$
the character
![]() $(T, \delta )\mapsto \delta $
. We have natural actions of G on
$(T, \delta )\mapsto \delta $
. We have natural actions of G on
![]() $G(W), G, \mathfrak {g}, V$
(by conjugation on all but V, on which we let G act in the usual way). This action extends to an action of
$G(W), G, \mathfrak {g}, V$
(by conjugation on all but V, on which we let G act in the usual way). This action extends to an action of
![]() ${\widetilde {G}}$
by
${\widetilde {G}}$
by
![]() $(T, \delta ).A := TA^\delta T^{-1}$
on
$(T, \delta ).A := TA^\delta T^{-1}$
on
![]() $G(W)$
and G, by
$G(W)$
and G, by
![]() $(T, \delta ).A := \delta TAT^{-1}$
on
$(T, \delta ).A := \delta TAT^{-1}$
on
![]() $\mathfrak {g}$
, and by
$\mathfrak {g}$
, and by
![]() $(T, \delta ).v := \delta Tv$
on V.
$(T, \delta ).v := \delta Tv$
on V.
Notation 2.1 Let
![]() $\Delta :G \to {\mathbb K}[x]$
be the characteristic polynomial map. We shall also consider it as a map from
$\Delta :G \to {\mathbb K}[x]$
be the characteristic polynomial map. We shall also consider it as a map from
![]() $G\times V$
, by first projecting onto G.
$G\times V$
, by first projecting onto G.
We shall use the standard terminology of l-spaces introduced in [Reference Bernstein and Zelevinsky6, Section 1]. We denote by
![]() ${\mathcal S}(Z)$
the space of Schwartz functions on an l-space Z, and by
${\mathcal S}(Z)$
the space of Schwartz functions on an l-space Z, and by
![]() ${\mathcal S}^*(Z)$
the space of distributions on Z equipped with the weak topology.
${\mathcal S}^*(Z)$
the space of distributions on Z equipped with the weak topology.
Notation 2.2 (Fourier transform)
Let W be a finite-dimensional vector space over
![]() ${\mathbb F}$
with a nondegenerate bilinear form B on W. We denote by
${\mathbb F}$
with a nondegenerate bilinear form B on W. We denote by
![]() ${\mathcal {F}}_B:{\mathcal S}^*(W) \to {\mathcal S}^*(W)$
the Fourier transform defined using B and the self-dual Haar measure on W. If W is clear from the context, we sometimes omit it from the notation and denote
${\mathcal {F}}_B:{\mathcal S}^*(W) \to {\mathcal S}^*(W)$
the Fourier transform defined using B and the self-dual Haar measure on W. If W is clear from the context, we sometimes omit it from the notation and denote
![]() ${\mathcal {F}}={\mathcal {F}}_W$
.
${\mathcal {F}}={\mathcal {F}}_W$
.
Remark 2.3 In the Hermitian case, we take for Fourier transform the
![]() ${\mathbb F}$
-bilinear form given by taking the trace of the Hermitian form.
${\mathbb F}$
-bilinear form given by taking the trace of the Hermitian form.
Theorem 2.4 (Localization principle; see [Reference Bernstein5, Section 1.4])
Let
![]() $q:Z \to T$
be a continuous map of l-spaces. We can consider
$q:Z \to T$
be a continuous map of l-spaces. We can consider
![]() ${\mathcal S} ^*(Z)$
as an
${\mathcal S} ^*(Z)$
as an
![]() ${\mathcal S}(T)$
-module. Denote
${\mathcal S}(T)$
-module. Denote
![]() $Z_t:= q^{-1}(t)$
. For any M which is a closed
$Z_t:= q^{-1}(t)$
. For any M which is a closed
![]() ${\mathcal S}(T)$
-submodule of
${\mathcal S}(T)$
-submodule of
![]() ${\mathcal S}^*(Z)$
,
${\mathcal S}^*(Z)$
,
Informally, it means that, in order to prove a certain property of distributions on Z, it is enough to prove that distributions on every fiber
![]() $Z_t$
have this property.
$Z_t$
have this property.
Corollary 2.5 Let
![]() $q:Z \to T$
be a continuous map of l-spaces. Let an l-group H act on Z preserving the fibers of q. Let
$q:Z \to T$
be a continuous map of l-spaces. Let an l-group H act on Z preserving the fibers of q. Let
![]() $\mu $
be a character of H. Suppose that, for any
$\mu $
be a character of H. Suppose that, for any
![]() $t\in T$
,
$t\in T$
,
![]() ${\mathcal S}^*(q^{-1}(t))^{H,\mu }=0$
. Then
${\mathcal S}^*(q^{-1}(t))^{H,\mu }=0$
. Then
![]() ${\mathcal S}^*(Z)^{H,\mu }=0$
.
${\mathcal S}^*(Z)^{H,\mu }=0$
.
Corollary 2.6 Let
![]() $H_i \subset \widetilde {H}_i$
be l-groups acting on l-spaces
$H_i \subset \widetilde {H}_i$
be l-groups acting on l-spaces
![]() $Z_i$
, for
$Z_i$
, for
![]() $i=1, \ldots , k$
. Suppose that
$i=1, \ldots , k$
. Suppose that
![]() ${\mathcal S}^*(Z_i)^{H_i}={\mathcal S}^*(Z_i)^{\widetilde {H}_i}$
for all i. Then
${\mathcal S}^*(Z_i)^{H_i}={\mathcal S}^*(Z_i)^{\widetilde {H}_i}$
for all i. Then
![]() ${\mathcal S}^*(\prod Z_i)^{\prod H_i}={\mathcal S}^*(\prod Z_i)^{\prod \widetilde {H}_i}$
.
${\mathcal S}^*(\prod Z_i)^{\prod H_i}={\mathcal S}^*(\prod Z_i)^{\prod \widetilde {H}_i}$
.
Theorem 2.7 (Frobenius descent [Reference Bernstein5, Section 1.5])
Let H be a unimodular l-group acting on two l-spaces E and Z, with the action on Z being transitive. Suppose that we have an H-equivariant map
![]() $\varphi :E \to Z$
. Let
$\varphi :E \to Z$
. Let
![]() $x\in Z$
be a point with a unimodular stabilizer in H. Denote by F the fiber of x with respect to
$x\in Z$
be a point with a unimodular stabilizer in H. Denote by F the fiber of x with respect to
![]() $\varphi $
. Then, for any character
$\varphi $
. Then, for any character
![]() $\mu $
of H, the following holds:
$\mu $
of H, the following holds:
-
(i) There exists a canonical isomorphism
 $\mathrm {Fr}: {\mathcal S}^*(E)^{H,\mu } \to {\mathcal S}^*(F)^{\mathrm {Stab}_H(x),\mu }$
.
$\mathrm {Fr}: {\mathcal S}^*(E)^{H,\mu } \to {\mathcal S}^*(F)^{\mathrm {Stab}_H(x),\mu }$
. -
(ii) For any distribution
 $\xi \in {\mathcal S}^*(E)^{H,\mu }$
,
$\xi \in {\mathcal S}^*(E)^{H,\mu }$
,
 $\mathrm {Supp}(\mathrm {Fr}(\xi ))=\mathrm {Supp}(\xi )\cap F$
.
$\mathrm {Supp}(\mathrm {Fr}(\xi ))=\mathrm {Supp}(\xi )\cap F$
. -
(iii) Frobenius descent commutes with Fourier transform.
To formulate (iii) explicitly, let W be a finite-dimensional linear space over
![]() ${\mathbb F}$
with a nondegenerate bilinear form B, and suppose that H acts on W linearly preserving B. Then, for any
${\mathbb F}$
with a nondegenerate bilinear form B, and suppose that H acts on W linearly preserving B. Then, for any
![]() $\xi \in {\mathcal S}^*(Z\times W)^{H,\mu }$
, we have
$\xi \in {\mathcal S}^*(Z\times W)^{H,\mu }$
, we have
![]() ${\mathcal {F}}_{B}(\mathrm {Fr}(\xi ))=\mathrm {Fr}({\mathcal {F}}_{B}(\xi ))$
, where
${\mathcal {F}}_{B}(\mathrm {Fr}(\xi ))=\mathrm {Fr}({\mathcal {F}}_{B}(\xi ))$
, where
![]() $\mathrm {Fr}$
is taken with respect to the projection
$\mathrm {Fr}$
is taken with respect to the projection
![]() $Z \times W \to Z$
.
$Z \times W \to Z$
.
Remark 2.8 Let Z be an l-space, and let
![]() $Q\subset Z$
be a closed subset. We may identify
$Q\subset Z$
be a closed subset. We may identify
![]() ${\mathcal S}^*(Q)$
with the space of all distributions on Z supported on Q. In particular, we can restrict a distribution
${\mathcal S}^*(Q)$
with the space of all distributions on Z supported on Q. In particular, we can restrict a distribution
![]() $\xi $
to any open subset of the support of
$\xi $
to any open subset of the support of
![]() $\xi $
.
$\xi $
.
Definition 2.9 An element
![]() $A \in \mathrm {gl}(V)$
is said to be regular if its minimal polynomial is equal to its characteristic polynomial. In case that this polynomial f of A is a power of an irreducible polynomial, we call A a minimal regular element.
$A \in \mathrm {gl}(V)$
is said to be regular if its minimal polynomial is equal to its characteristic polynomial. In case that this polynomial f of A is a power of an irreducible polynomial, we call A a minimal regular element.
Theorem 2.10 (Rational canonical form)
Any element
![]() $A\in \mathrm {gl}(V)$
can be represented as a direct sum of minimal regular elements. Moreover, the isomorphism classes of these elements are uniquely determined by the conjugacy class of A inside
$A\in \mathrm {gl}(V)$
can be represented as a direct sum of minimal regular elements. Moreover, the isomorphism classes of these elements are uniquely determined by the conjugacy class of A inside
![]() $GL(V)$
and vice versa.
$GL(V)$
and vice versa.
This form is called the rational canonical form of A.
Definition 2.11 For any polynomial f given by
![]() $f(x)=\sum _{i=0}^n a_i x^i$
, define
$f(x)=\sum _{i=0}^n a_i x^i$
, define
 $$ \begin{align*}f^*(x)=\sum_{i=0}^n (-1)^i \bar{a_i} x^i,\end{align*} $$
$$ \begin{align*}f^*(x)=\sum_{i=0}^n (-1)^i \bar{a_i} x^i,\end{align*} $$
 $$ \begin{align*}f^\dagger(x)=\sum_{i=0}^n \overline{a_{n-i}} x^i.\end{align*} $$
$$ \begin{align*}f^\dagger(x)=\sum_{i=0}^n \overline{a_{n-i}} x^i.\end{align*} $$
Remark 2.12 For any
![]() $A\in \mathfrak {g}$
(resp.
$A\in \mathfrak {g}$
(resp.
![]() $A\in G(V)$
), we have
$A\in G(V)$
), we have
![]() $f(A)^* = f^*(A)$
(resp.
$f(A)^* = f^*(A)$
(resp.
![]() $f(A)^\dagger =A^{-n}f^\dagger (A)$
).
$f(A)^\dagger =A^{-n}f^\dagger (A)$
).
Lemma 2.13 Let
![]() $A\in \mathfrak {g}$
(
$A\in \mathfrak {g}$
(
![]() $A\in G$
). Let
$A\in G$
). Let
![]() $\left (f_i\right )_{i\in I}$
be the different irreducible factors in the characteristic polynomial of A. Let
$\left (f_i\right )_{i\in I}$
be the different irreducible factors in the characteristic polynomial of A. Let
![]() $\left (V_i\right )_{i\in I}$
be the generalized eigenspace associated with each. Take
$\left (V_i\right )_{i\in I}$
be the generalized eigenspace associated with each. Take
![]() $i,j \in I$
, not necessarily different. If
$i,j \in I$
, not necessarily different. If
![]() $f_i^*\neq \pm f_j$
(resp.
$f_i^*\neq \pm f_j$
(resp.
![]() $f_i^\dagger \nmid f_j$
), then
$f_i^\dagger \nmid f_j$
), then
![]() $V_i\perp V_j$
.
$V_i\perp V_j$
.
Proof We give the proof in the
![]() $A\in \mathfrak {g}$
case (the
$A\in \mathfrak {g}$
case (the
![]() $A\in G$
case is analogous). Take
$A\in G$
case is analogous). Take
![]() $u\in V_i, v\in V_j$
. Then, for k large enough,
$u\in V_i, v\in V_j$
. Then, for k large enough,
Thus,
![]() $V_i \perp f_i^*(A)^k V_j$
, but if
$V_i \perp f_i^*(A)^k V_j$
, but if
![]() $f_i^* \neq \pm f_j$
, then they are coprime to each other, and so
$f_i^* \neq \pm f_j$
, then they are coprime to each other, and so
![]() $f_i^*(A)^k V_j=V_j$
.▪
$f_i^*(A)^k V_j=V_j$
.▪
Definition 2.14
-
(1) An operator
 $A\in \mathfrak {g}$
will be called a simple split operator (or block) if the following conditions hold:
$A\in \mathfrak {g}$
will be called a simple split operator (or block) if the following conditions hold:-
• There is a possibly nonorthogonal decomposition
 $V=V'\oplus \overline {V^{\prime *}}$
.
$V=V'\oplus \overline {V^{\prime *}}$
. -
•
 $V'$
and
$V'$
and
 $\overline {V^{\prime *}}$
are isotropic, and the sesquilinear form B induces the natural pairing between them.
$\overline {V^{\prime *}}$
are isotropic, and the sesquilinear form B induces the natural pairing between them. -
• The action of A on
 $V'\oplus \overline {V^{\prime *}}$
decomposes as
$V'\oplus \overline {V^{\prime *}}$
decomposes as
 $A'\oplus A"$
.
$A'\oplus A"$
. -
•
 $\langle A'u,v\rangle=\langle u,-A"v\rangle$
for any
$\langle A'u,v\rangle=\langle u,-A"v\rangle$
for any
 $u\in V', v\in \overline {V^{\prime *}}$
.
$u\in V', v\in \overline {V^{\prime *}}$
. -
•
 $A'$
(and so also
$A'$
(and so also
 $A"$
) is a minimal regular operator (see Definition 2.9).
$A"$
) is a minimal regular operator (see Definition 2.9). -
• The irreducible factor f of the minimal polynomial of
 $A'$
is not equal to
$A'$
is not equal to
 $f^*$
.
$f^*$
.
-
-
(2) An operator
 $A\in \mathfrak {g}$
will be called a simple nonsplit operator (or block) if:
$A\in \mathfrak {g}$
will be called a simple nonsplit operator (or block) if:-
• It is a minimal regular operator.
-
• Its characteristic polynomial is not equal to
 $x^d$
with d even if
$x^d$
with d even if
 $\mathfrak {g} = \mathfrak {o}$
, and it is not equal to
$\mathfrak {g} = \mathfrak {o}$
, and it is not equal to
 $x^d$
with d odd if
$x^d$
with d odd if
 $\mathfrak {g} = \mathfrak {sp}$
.
$\mathfrak {g} = \mathfrak {sp}$
.
-
-
(3) An operator
 $A\in \mathfrak {o}$
will be called a simple even nilpotent operator (or block) if the following conditions hold:
$A\in \mathfrak {o}$
will be called a simple even nilpotent operator (or block) if the following conditions hold:-
• Its minimal polynomial is
 $x^d$
for some even d.
$x^d$
for some even d. -
• V has a basis of the form
 $e, Ae, \dots , A^{d-1}e, f, Af, \dots , A^{d-1}f$
.
$e, Ae, \dots , A^{d-1}e, f, Af, \dots , A^{d-1}f$
. -
• For all
 $i, j$
we have
$i, j$
we have
 $\langle A^ie, A^je\rangle = \langle A^if, A^jf\rangle = 0$
.
$\langle A^ie, A^je\rangle = \langle A^if, A^jf\rangle = 0$
. -
• For all
 $i, j$
we have
$i, j$
we have
 $\langle A^ie, A^jf\rangle = \begin {cases} (-1)^{j}, & \mathrm {if}\ i + j = d - 1,\\ 0, & \mathrm {otherwise.} \end {cases} $
$\langle A^ie, A^jf\rangle = \begin {cases} (-1)^{j}, & \mathrm {if}\ i + j = d - 1,\\ 0, & \mathrm {otherwise.} \end {cases} $
-
-
(4) An operator
 $A\in \mathfrak {sp}$
will be called a simple odd nilpotent operator (or block) if the following conditions hold:
$A\in \mathfrak {sp}$
will be called a simple odd nilpotent operator (or block) if the following conditions hold:-
• Its minimal polynomial is
 $x^d$
for some odd d.
$x^d$
for some odd d. -
• V has a basis of the form
 $e, Ae, \dots , A^{d-1}e, f, Af, \dots , A^{d-1}f$
.
$e, Ae, \dots , A^{d-1}e, f, Af, \dots , A^{d-1}f$
. -
• For all
 $i, j$
we have
$i, j$
we have
 $\langle A^ie, A^je\rangle = \langle A^if, A^jf\rangle = 0$
.
$\langle A^ie, A^je\rangle = \langle A^if, A^jf\rangle = 0$
. -
• For all
 $i, j$
we have
$i, j$
we have
 $\langle A^ie, A^jf\rangle = \begin {cases} (-1)^{j}, & \mathrm {if}\ i + j = d - 1,\\ 0, & \mathrm {otherwise.} \end {cases} $
$\langle A^ie, A^jf\rangle = \begin {cases} (-1)^{j}, & \mathrm {if}\ i + j = d - 1,\\ 0, & \mathrm {otherwise.} \end {cases} $
-
The following useful proposition will be proved in Appendix A.
Proposition 2.15 Each
![]() $A\in \mathfrak {u}$
decomposes as an orthogonal sum of simple split blocks and simple nonsplit blocks. Each
$A\in \mathfrak {u}$
decomposes as an orthogonal sum of simple split blocks and simple nonsplit blocks. Each
![]() $A\in \mathfrak {o}$
decomposes as an orthogonal sum of simple split blocks, simple nonsplit blocks, and simple even nilpotent blocks. Each
$A\in \mathfrak {o}$
decomposes as an orthogonal sum of simple split blocks, simple nonsplit blocks, and simple even nilpotent blocks. Each
![]() $A\in \mathfrak {sp}$
decomposes as an orthogonal sum of simple split blocks, simple nonsplit blocks, and simple odd nilpotent blocks.
$A\in \mathfrak {sp}$
decomposes as an orthogonal sum of simple split blocks, simple nonsplit blocks, and simple odd nilpotent blocks.
Remark 2.16 The contents of Proposition 2.15 are contained in known papers and books such as [Reference Springer and Steinberg11, Reference Wall15]. However, for clarity and completeness, we formulated only the propositions we need and give short proofs of them in Appendix A.
Proposition 2.17 [Reference Mezer9, Appendix A]
Let V be a linear space of finite dimension n over a field
![]() ${\mathbb K}$
,
${\mathbb K}$
,
![]() $A\in \mathrm {gl} (V)$
,
$A\in \mathrm {gl} (V)$
,
![]() $v\in V$
, and
$v\in V$
, and
![]() $\phi \in V^*$
. The following are equivalent.
$\phi \in V^*$
. The following are equivalent.
-
(1)
 $\forall k\geq 0,\ \phi A^k v=0$
.
$\forall k\geq 0,\ \phi A^k v=0$
. -
(2) For all
 $\lambda \in {\mathbb K}$
,
$\lambda \in {\mathbb K}$
,
 $\mathrm {ch}(A+\lambda v\otimes \phi )=\mathrm {ch}(A)$
.
$\mathrm {ch}(A+\lambda v\otimes \phi )=\mathrm {ch}(A)$
. -
(3) There exists
 $\lambda \in {\mathbb F} ^ \times $
such that
$\lambda \in {\mathbb F} ^ \times $
such that
 $\mathrm {ch}(A+\lambda v\otimes \phi )=\mathrm {ch}(A)$
.
$\mathrm {ch}(A+\lambda v\otimes \phi )=\mathrm {ch}(A)$
. -
(4)
 $\frac {\partial }{\partial \lambda }\mathrm {ch}(A+\lambda v\otimes \phi )|_{\lambda =0}=0.$
$\frac {\partial }{\partial \lambda }\mathrm {ch}(A+\lambda v\otimes \phi )|_{\lambda =0}=0.$
Let V be a vector space over a local field
![]() ${\mathbb F}$
of characteristic different from
${\mathbb F}$
of characteristic different from
![]() $2$
. Let
$2$
. Let
![]() $\operatorname {GL}(V)$
act on
$\operatorname {GL}(V)$
act on
![]() $\mathfrak {gl}(V) \times V \times V^*$
by conjugation, and the natural actions on
$\mathfrak {gl}(V) \times V \times V^*$
by conjugation, and the natural actions on
![]() $V, V^*$
. Consider also the transposition involution, which involves a choice of an isomorphism
$V, V^*$
. Consider also the transposition involution, which involves a choice of an isomorphism
![]() $t:V\to V^*$
, and sends
$t:V\to V^*$
, and sends
![]() $(A, v, \phi )$
to
$(A, v, \phi )$
to
![]() $A^t, \phi ^t, v^t$
. As immediate corollaries of [Reference Mezer9, Theorem 3.1] (and of the proof that it implies Theorem 1.1 of the same paper), we have the following theorems.
$A^t, \phi ^t, v^t$
. As immediate corollaries of [Reference Mezer9, Theorem 3.1] (and of the proof that it implies Theorem 1.1 of the same paper), we have the following theorems.
Theorem 2.18 Any
![]() $\operatorname {GL}(V)$
-invariant distribution on
$\operatorname {GL}(V)$
-invariant distribution on
![]() $GL(V) \times V \times V^*$
is also invariant to transposition.
$GL(V) \times V \times V^*$
is also invariant to transposition.
Theorem 2.19 Any
![]() $\operatorname {GL}(V)$
-invariant distribution on
$\operatorname {GL}(V)$
-invariant distribution on
![]() $\mathfrak {gl}(V) \times V \times V^*$
is also invariant to transposition.
$\mathfrak {gl}(V) \times V \times V^*$
is also invariant to transposition.
3 Reformulations of the problem
Let
![]() $V, G, {\widetilde {G}}, \chi $
be as in Section 2. Both Theorems 1.2 and 1.4 follow from the following theorem.
$V, G, {\widetilde {G}}, \chi $
be as in Section 2. Both Theorems 1.2 and 1.4 follow from the following theorem.
Theorem 3.1 Any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $G\times V$
is 0.
$G\times V$
is 0.
Proof that Theorem 3.1 implies Theorem 1.2
This proof is the same as the proof of [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Proposition 5.1]. Use the notations given in the introduction (e.g.,
![]() $V,W,G(V),{\widetilde {G}}(V)$
). We actually prove that Theorem 3.1 for W implies Theorem 1.2 for V. The idea is to consider the set
$V,W,G(V),{\widetilde {G}}(V)$
). We actually prove that Theorem 3.1 for W implies Theorem 1.2 for V. The idea is to consider the set
and use Frobenius descent (Theorem 2.7) on the projection
![]() $G(W)\times Y \to Y$
. The group
$G(W)\times Y \to Y$
. The group
![]() ${\widetilde {G}}(W)$
acts on Y with centralizer
${\widetilde {G}}(W)$
acts on Y with centralizer
![]() ${\widetilde {G}}(V)$
. The fiber of the projection is
${\widetilde {G}}(V)$
. The fiber of the projection is
![]() $G(W)$
. So we get a bijection between
$G(W)$
. So we get a bijection between
![]() $({\widetilde {G}}(V), \chi )$
-equivariant distributions on
$({\widetilde {G}}(V), \chi )$
-equivariant distributions on
![]() $G(W)$
and
$G(W)$
and
![]() $({\widetilde {G}}(W), \chi )$
-equivariant distributions on
$({\widetilde {G}}(W), \chi )$
-equivariant distributions on
![]() $G(W)\times Y$
. The latter of which has no nonzero elements by the assumption on W. Thus, any
$G(W)\times Y$
. The latter of which has no nonzero elements by the assumption on W. Thus, any
![]() $({\widetilde {G}}(V), \chi )$
-equivariant distribution on
$({\widetilde {G}}(V), \chi )$
-equivariant distribution on
![]() $G(W)$
is 0, which immediately implies Theorem 1.2.▪
$G(W)$
is 0, which immediately implies Theorem 1.2.▪
Proof that Theorem 3.1 implies Theorem 1.4
The group S in the formulation of Theorem 1.4 decomposes as a product of groups of types
![]() $O, SO, U, Sp$
, with
$O, SO, U, Sp$
, with
![]() $\sigma $
a product of appropriate anti-involutions. By Corollary 2.5 of the localization principle, it follows that Theorem 3.1 implies an analogous claim for S, which can be seen to easily imply Theorem 1.4.▪
$\sigma $
a product of appropriate anti-involutions. By Corollary 2.5 of the localization principle, it follows that Theorem 3.1 implies an analogous claim for S, which can be seen to easily imply Theorem 1.4.▪
The proof of the theorem is by induction on
![]() $\dim V$
, proving simultaneously the following theorem.
$\dim V$
, proving simultaneously the following theorem.
Theorem 3.2 Any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g}\times V$
is 0.
$\mathfrak {g}\times V$
is 0.
For
![]() $n=0$
, Theorems 3.1 and 3.2 are trivial.
$n=0$
, Theorems 3.1 and 3.2 are trivial.
Remark 3.3 In [Reference Waldspurger14], the needed induction basis was
![]() $n=1,n=2$
, as the proof given there used the triviality of the center of G (up to
$n=1,n=2$
, as the proof given there used the triviality of the center of G (up to
![]() $\pm 1$
). However, we do not use this fact and so the trivial case
$\pm 1$
). However, we do not use this fact and so the trivial case
![]() $n=0$
suffices for us as a basis for the induction.
$n=0$
suffices for us as a basis for the induction.
Theorem 3.2 (along with Theorem 3.1) is proved in the end of Section 7.
4 Harish–Chandra descent
In this section, we use the technique of Harish–Chandra descent to restrict the support of an equivariant distribution as discussed in Theorems 3.1 and 3.2. For the course of this section assume that Theorems 3.1 and 3.2 hold for all smaller dimensions, over all finite field extensions of
![]() ${\mathbb K}$
.
${\mathbb K}$
.
Let
![]() $(A, v)$
be a point in the support of a
$(A, v)$
be a point in the support of a
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution either on
$({\widetilde {G}}, \chi )$
-equivariant distribution either on
![]() $G\times V$
(the group case) or on
$G\times V$
(the group case) or on
![]() $\mathfrak {g}\times V$
(the Lie-algebra case). Let
$\mathfrak {g}\times V$
(the Lie-algebra case). Let
![]() $g(X)$
be the characteristic polynomial of A. Consider also the characteristic polynomial map
$g(X)$
be the characteristic polynomial of A. Consider also the characteristic polynomial map
![]() $\Delta :G\times V \to {\mathbb K}[x]$
(or
$\Delta :G\times V \to {\mathbb K}[x]$
(or
![]() $\Delta :\mathfrak {g}\times V \to {\mathbb K}[x]$
in the Lie algebra case). Note that
$\Delta :\mathfrak {g}\times V \to {\mathbb K}[x]$
in the Lie algebra case). Note that
![]() $g\mid g^\dagger $
in the group case, and
$g\mid g^\dagger $
in the group case, and
![]() $g=\pm g^*$
in the Lie algebra case (recall Definition 2.11 of
$g=\pm g^*$
in the Lie algebra case (recall Definition 2.11 of
![]() $g^\dagger $
and
$g^\dagger $
and
![]() $g^*$
).
$g^*$
).
Theorem 4.1 Unless we are in the group case and
![]() $G = SO$
, the polynomial g cannot be factorized into two coprime factors
$G = SO$
, the polynomial g cannot be factorized into two coprime factors
![]() $g_1, g_2$
satisfying
$g_1, g_2$
satisfying
![]() $g_1\mid g_1^\dagger $
and
$g_1\mid g_1^\dagger $
and
![]() $g_2\mid g_2^\dagger $
(resp.
$g_2\mid g_2^\dagger $
(resp.
![]() $g_1 = \pm g_1^*$
and
$g_1 = \pm g_1^*$
and
![]() $g_2 = \pm g_2^*$
in the Lie algebra case). In the case
$g_2 = \pm g_2^*$
in the Lie algebra case). In the case
![]() $G=SO$
, it is still true that it is impossible for g to be divisible by both
$G=SO$
, it is still true that it is impossible for g to be divisible by both
![]() $x-1$
and
$x-1$
and
![]() $x+1$
.
$x+1$
.
Proof We give the proof for the group case and for the Lie algebra case simultaneously. By the localization principle (Corollary 2.5), it is enough to show that there is no
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution
$({\widetilde {G}}, \chi )$
-equivariant distribution
![]() $\xi $
on any of the fibers of
$\xi $
on any of the fibers of
![]() $\Delta $
which is above a polynomial not satisfying the condition we gave on g. Let F be such a fiber lying above a polynomial
$\Delta $
which is above a polynomial not satisfying the condition we gave on g. Let F be such a fiber lying above a polynomial
![]() $g(x) = g_1(x)g_2(x)$
with
$g(x) = g_1(x)g_2(x)$
with
![]() $g_1, g_2$
coprime and of positive degree, satisfying
$g_1, g_2$
coprime and of positive degree, satisfying
![]() $g_1\mid g_1^\dagger $
and
$g_1\mid g_1^\dagger $
and
![]() $g_2\mid g_2^\dagger $
(
$g_2\mid g_2^\dagger $
(
![]() $g_1 = \pm g_1^*$
and
$g_1 = \pm g_1^*$
and
![]() $g_2 = \pm g_2^*$
in the Lie algebra case). If we are in the group case and
$g_2 = \pm g_2^*$
in the Lie algebra case). If we are in the group case and
![]() $G=SO$
, we further assume that
$G=SO$
, we further assume that
![]() $g_1(x) = (x-1)^k$
for some
$g_1(x) = (x-1)^k$
for some
![]() $k>0$
. Let
$k>0$
. Let
![]() $d_1, d_2$
be the degrees of
$d_1, d_2$
be the degrees of
![]() $g_1, g_2$
. Given A with characteristic polynomial
$g_1, g_2$
. Given A with characteristic polynomial
![]() $g(x)$
, one may consider
$g(x)$
, one may consider
![]() $V_1, V_2$
, its generalized eigenspaces associated with
$V_1, V_2$
, its generalized eigenspaces associated with
![]() $g_1(x), g_2(x)$
, respectively. By Lemma 2.13,
$g_1(x), g_2(x)$
, respectively. By Lemma 2.13,
![]() $V_1, V_2$
are perpendicular to each other. Consider
$V_1, V_2$
are perpendicular to each other. Consider
to be the space of decompositions of V as an orthogonal sum
![]() $V_1\oplus V_2$
to subspaces of dimensions
$V_1\oplus V_2$
to subspaces of dimensions
![]() $d_1, d_2$
. There is a natural
$d_1, d_2$
. There is a natural
![]() ${\widetilde {G}}$
-equivariant map
${\widetilde {G}}$
-equivariant map
![]() $\rho : F\to \Lambda $
. Consider the stratification on
$\rho : F\to \Lambda $
. Consider the stratification on
![]() $\Lambda $
given by G-orbits. Note that these are the same as
$\Lambda $
given by G-orbits. Note that these are the same as
![]() ${\widetilde {G}}$
-orbits. To show that this is indeed a stratification, we must show that there are finitely many G-orbits. Recall that there are finitely many isomorphism classes of sesquilinear forms of the same type as B (symmetric, Hermitian, or symplectic) on a
${\widetilde {G}}$
-orbits. To show that this is indeed a stratification, we must show that there are finitely many G-orbits. Recall that there are finitely many isomorphism classes of sesquilinear forms of the same type as B (symmetric, Hermitian, or symplectic) on a
![]() ${\mathbb K}$
-vector space of a given dimension. If two elements in
${\mathbb K}$
-vector space of a given dimension. If two elements in
![]() $\Lambda $
share the isomorphism classes of the restrictions of B to
$\Lambda $
share the isomorphism classes of the restrictions of B to
![]() $V_1, V_2$
, then these isomorphisms can be extended orthogonally to an element of G (in the case
$V_1, V_2$
, then these isomorphisms can be extended orthogonally to an element of G (in the case
![]() $G=SO$
, it will only be an element of
$G=SO$
, it will only be an element of
![]() $O$
. However, it is enough to prove that there are finitely many
$O$
. However, it is enough to prove that there are finitely many
![]() $O$
orbits). This implies that the two elements we had in
$O$
orbits). This implies that the two elements we had in
![]() $\Lambda $
are in the same G-orbit (
$\Lambda $
are in the same G-orbit (
![]() $O$
-orbit if
$O$
-orbit if
![]() $G=SO$
). It follows that there are indeed finitely many G-orbits, and so partition into orbits is a stratification.
$G=SO$
). It follows that there are indeed finitely many G-orbits, and so partition into orbits is a stratification.
Let S be the union of strata intersecting
![]() $\rho ({\mathrm {supp}}(\xi ))$
, and let
$\rho ({\mathrm {supp}}(\xi ))$
, and let
![]() $\Omega $
be a stratum of the largest dimension in it (we assume by contradiction that
$\Omega $
be a stratum of the largest dimension in it (we assume by contradiction that
![]() $\xi \neq 0$
, i.e., S is nonempty). It is open in S, and so we may restrict
$\xi \neq 0$
, i.e., S is nonempty). It is open in S, and so we may restrict
![]() $\xi $
to
$\xi $
to
![]() $\rho ^{-1}(\Omega )$
. Since
$\rho ^{-1}(\Omega )$
. Since
![]() $\Omega {\subseteq } S$
, this restriction is not the zero distribution.
$\Omega {\subseteq } S$
, this restriction is not the zero distribution.
For the following, assume that we are not in the groups case where
![]() $G=SO$
. The action of
$G=SO$
. The action of
![]() ${\widetilde {G}}$
on
${\widetilde {G}}$
on
![]() $\Omega $
is transitive by definition, and the stabilizer of a point in
$\Omega $
is transitive by definition, and the stabilizer of a point in
![]() $\Omega $
(call it H) is a subgroup of index
$\Omega $
(call it H) is a subgroup of index
![]() $2$
of
$2$
of
![]() ${\widetilde {G}}(V_1) \times {\widetilde {G}}(V_2)$
, which is a unimodular group (thus, it is also unimodular). H also contains
${\widetilde {G}}(V_1) \times {\widetilde {G}}(V_2)$
, which is a unimodular group (thus, it is also unimodular). H also contains
![]() $G(V_1)\times G(V_2)$
as a subgroup of index
$G(V_1)\times G(V_2)$
as a subgroup of index
![]() $2$
. Using Frobenius descent (Theorem 2.7) on
$2$
. Using Frobenius descent (Theorem 2.7) on
![]() $\xi $
, we get an
$\xi $
, we get an
![]() $(H, \chi )$
-equivariant distribution on the fiber, which is a closed subspace of
$(H, \chi )$
-equivariant distribution on the fiber, which is a closed subspace of
![]() $(G(V_1)\times V_1) \times (G(V_2)\times V_2)$
. In particular, this distribution is
$(G(V_1)\times V_1) \times (G(V_2)\times V_2)$
. In particular, this distribution is
![]() $G(V_1)\times G(V_2)$
-invariant. Hence, this distribution is
$G(V_1)\times G(V_2)$
-invariant. Hence, this distribution is
![]() ${\widetilde {G}}(V_1)\times {\widetilde {G}}(V_2)$
-invariant by the induction hypothesis and Corollary 2.6 to the Localization Principle. In particular, it is also H-invariant; thus, it is 0, in contradiction to our assumption.
${\widetilde {G}}(V_1)\times {\widetilde {G}}(V_2)$
-invariant by the induction hypothesis and Corollary 2.6 to the Localization Principle. In particular, it is also H-invariant; thus, it is 0, in contradiction to our assumption.
In the case
![]() $G=SO$
, we have a similar situation. The action of
$G=SO$
, we have a similar situation. The action of
![]() ${\widetilde {SO}}(V)$
on
${\widetilde {SO}}(V)$
on
![]() $\Omega $
is transitive, and the stabilizer of a point in
$\Omega $
is transitive, and the stabilizer of a point in
![]() $\Omega $
, which we will call H, is a unimodular subgroup of index
$\Omega $
, which we will call H, is a unimodular subgroup of index
![]() $4$
inside
$4$
inside
![]() ${\widetilde {O}}(V_1)\times {\widetilde {O}}(V_2)$
. This group H contains
${\widetilde {O}}(V_1)\times {\widetilde {O}}(V_2)$
. This group H contains
![]() $SO(V_1)\times SO(V_2)$
as a subgroup of index
$SO(V_1)\times SO(V_2)$
as a subgroup of index
![]() $4$
, on which the character
$4$
, on which the character
![]() $\chi $
is trivial. Since the determinant of an operator acting on
$\chi $
is trivial. Since the determinant of an operator acting on
![]() $V_1$
with characteristic polynomial
$V_1$
with characteristic polynomial
![]() $g_1(x)=(x-1)^k$
and on
$g_1(x)=(x-1)^k$
and on
![]() $V_2$
with characteristic polynomial
$V_2$
with characteristic polynomial
![]() $g_2(x)$
is 1, we get that
$g_2(x)$
is 1, we get that
![]() $g_2(0) = (-1)^{\dim V_2}$
. If
$g_2(0) = (-1)^{\dim V_2}$
. If
![]() $\dim V_2$
was odd, it would imply that
$\dim V_2$
was odd, it would imply that
![]() $g_2^\dagger = -g_2$
, and in particular
$g_2^\dagger = -g_2$
, and in particular
![]() $g_2(1) = 0$
. By assumption, this is not the case, and so we have that
$g_2(1) = 0$
. By assumption, this is not the case, and so we have that
![]() $\dim V_2$
must be even. It follows that
$\dim V_2$
must be even. It follows that
Take elements
![]() $(g_1, -1) \in {\widetilde {SO}}(V_1)\setminus SO(V_1)$
and
$(g_1, -1) \in {\widetilde {SO}}(V_1)\setminus SO(V_1)$
and
![]() $(g_2, -1)\in {\widetilde {SO}}(V_2)\setminus SO(V_2)$
. From the above, it follows that
$(g_2, -1)\in {\widetilde {SO}}(V_2)\setminus SO(V_2)$
. From the above, it follows that
![]() $\gamma :=(g_1\oplus g_2, -1)$
is an element of
$\gamma :=(g_1\oplus g_2, -1)$
is an element of
![]() $({\widetilde {SO}}(V_1)\times {\widetilde {SO}}(V_2))\cap H$
, on which
$({\widetilde {SO}}(V_1)\times {\widetilde {SO}}(V_2))\cap H$
, on which
![]() $\chi $
gives
$\chi $
gives
![]() $-1$
. The fiber of
$-1$
. The fiber of
![]() $\rho $
above
$\rho $
above
![]() $(V_1, V_2)$
is
$(V_1, V_2)$
is
![]() $SO(V_1)\times SO(V_2)$
, because any element in it acts with characteristic polynomial
$SO(V_1)\times SO(V_2)$
, because any element in it acts with characteristic polynomial
![]() $(x-1)^k$
on
$(x-1)^k$
on
![]() $V_1$
, and thus has determinant
$V_1$
, and thus has determinant
![]() $1$
when restricted to it. It follows that the restriction to
$1$
when restricted to it. It follows that the restriction to
![]() $V_2$
also has determinant
$V_2$
also has determinant
![]() $1$
. As before, we get that any
$1$
. As before, we get that any
![]() $(H,\chi )$
-equivariant distribution on
$(H,\chi )$
-equivariant distribution on
![]() $SO(V_1)\times SO(V_2)$
is invariant to
$SO(V_1)\times SO(V_2)$
is invariant to
![]() ${\widetilde {SO}}(V_1)\times {\widetilde {SO}}(V_2)$
(using the localization principle and the induction hypothesis). In particular, it is
${\widetilde {SO}}(V_1)\times {\widetilde {SO}}(V_2)$
(using the localization principle and the induction hypothesis). In particular, it is
![]() $\gamma $
-invariant, and thus it is
$\gamma $
-invariant, and thus it is
![]() $0$
, since
$0$
, since
![]() $\chi (\gamma )=-1$
. Using Frobenius descent, we get that this implies
$\chi (\gamma )=-1$
. Using Frobenius descent, we get that this implies
![]() $\xi = 0$
, giving a contradiction.▪
$\xi = 0$
, giving a contradiction.▪
We give the following theorem only in the Lie algebra case as this is what will be used. However, it also holds in the group case, with the same proof.
Theorem 4.2 Assume that we are in the Lie algebra case. The polynomial g must be a power of an irreducible polynomial.
Proof Again, we use the localization principle. Let F be the fiber above a polynomial of the form
![]() $g(x) = g_1(x)g_2(x)$
with
$g(x) = g_1(x)g_2(x)$
with
![]() $g_2 = \pm g_1^*$
, and the two are coprime to each other. (By Theorem 4.1, it is enough to consider this case.) Given A with characteristic polynomial
$g_2 = \pm g_1^*$
, and the two are coprime to each other. (By Theorem 4.1, it is enough to consider this case.) Given A with characteristic polynomial
![]() $g(x)$
, one may consider
$g(x)$
, one may consider
![]() $V_1, V_2$
, its generalized eigenspaces associated with
$V_1, V_2$
, its generalized eigenspaces associated with
![]() $g_1(x), g_2(x)$
, respectively. By Lemma 2.13,
$g_1(x), g_2(x)$
, respectively. By Lemma 2.13,
![]() $V_1, V_2$
are both isotropic. Consider
$V_1, V_2$
are both isotropic. Consider
There is a natural
![]() ${\widetilde {G}}$
-equivariant map
${\widetilde {G}}$
-equivariant map
![]() $\rho : F\to \Lambda $
.
$\rho : F\to \Lambda $
.
To see that G acts transitively on
![]() $\Lambda $
, take
$\Lambda $
, take
![]() $(V_1, V_2), (V_1', V_2')\in \Lambda $
. Choose arbitrary bases
$(V_1, V_2), (V_1', V_2')\in \Lambda $
. Choose arbitrary bases
![]() $E_1, E_1'$
of
$E_1, E_1'$
of
![]() $V_1, V_1'$
. We may take
$V_1, V_1'$
. We may take
![]() $E_2$
to be the basis of
$E_2$
to be the basis of
![]() $V_2$
dual to
$V_2$
dual to
![]() $E_1$
with respect to the pairing between
$E_1$
with respect to the pairing between
![]() $V_1, V_2$
induced by B. Similarly, we may take
$V_1, V_2$
induced by B. Similarly, we may take
![]() $E_2'$
. The linear transformation which sends
$E_2'$
. The linear transformation which sends
![]() $E_1$
to
$E_1$
to
![]() $E_1'$
and
$E_1'$
and
![]() $E_2$
to
$E_2$
to
![]() $E_2'$
preserves B, and thus it is an element of G. So the actions of both G and
$E_2'$
preserves B, and thus it is an element of G. So the actions of both G and
![]() ${\widetilde {G}}$
on
${\widetilde {G}}$
on
![]() $\Lambda $
are transitive, and the stabilizer inside
$\Lambda $
are transitive, and the stabilizer inside
![]() ${\widetilde {G}}$
of a point in
${\widetilde {G}}$
of a point in
![]() $\Lambda $
is isomorphic to
$\Lambda $
is isomorphic to
![]() $\widetilde {\operatorname {GL}}(V_1)$
, which is a unimodular group. Using Frobenius descent (Theorem 2.7) on
$\widetilde {\operatorname {GL}}(V_1)$
, which is a unimodular group. Using Frobenius descent (Theorem 2.7) on
![]() $\xi $
, we get a
$\xi $
, we get a
![]() $(\widetilde {\operatorname {GL}}(V_1), \chi )$
-equivariant distribution on the fiber, which is isomorphic to
$(\widetilde {\operatorname {GL}}(V_1), \chi )$
-equivariant distribution on the fiber, which is isomorphic to
By Theorem 2.19, this distribution must be equal to
![]() $0$
, and so is the original one.▪
$0$
, and so is the original one.▪
We formulate the next theorem only for the Lie algebra case, and
![]() $\mathfrak {g}=\mathfrak {sp}$
, although again it is also true for all the other cases.
$\mathfrak {g}=\mathfrak {sp}$
, although again it is also true for all the other cases.
Theorem 4.3 Consider the Lie algebra case of
![]() $\mathfrak {g} = \mathfrak {sp}$
. In this case, the irreducible factor of g is either linear or inseparable.
$\mathfrak {g} = \mathfrak {sp}$
. In this case, the irreducible factor of g is either linear or inseparable.
Proof Again, we use the localization principle. Let F be the fiber above a polynomial
![]() $g(x) = f(x)^s$
with f irreducible, separable, of degree
$g(x) = f(x)^s$
with f irreducible, separable, of degree
![]() $d> 1$
, and satisfying
$d> 1$
, and satisfying
![]() $f^* \neq \pm f$
. Given A with characteristic polynomial
$f^* \neq \pm f$
. Given A with characteristic polynomial
![]() $g(x)$
, we may consider its additive Jordan decomposition into semisimple and unipotent parts,
$g(x)$
, we may consider its additive Jordan decomposition into semisimple and unipotent parts,
![]() $A_s$
and
$A_s$
and
![]() $A_u$
(that is in virtue of the characteristic polynomial being separable). Let
$A_u$
(that is in virtue of the characteristic polynomial being separable). Let
![]() $F_s$
be the space of possible
$F_s$
be the space of possible
![]() $A_s$
’s, that is the space of semisimple elements of
$A_s$
’s, that is the space of semisimple elements of
![]() $\mathfrak {g}$
with characteristic polynomial
$\mathfrak {g}$
with characteristic polynomial
![]() $g(x)$
. We have a
$g(x)$
. We have a
![]() ${\widetilde {G}}$
-equivariant map
${\widetilde {G}}$
-equivariant map
![]() $\theta : F\to F_s$
. By [Reference Springer and Steinberg11],
$\theta : F\to F_s$
. By [Reference Springer and Steinberg11],
![]() $F_s$
is a disjoint union of finitely many G-orbits, all of the same dimension. By [Reference Mœglin, Vignéras and Waldspurger10, Chapter 4, Proposition 1.2], for each point
$F_s$
is a disjoint union of finitely many G-orbits, all of the same dimension. By [Reference Mœglin, Vignéras and Waldspurger10, Chapter 4, Proposition 1.2], for each point
![]() $A\in F_s$
, there is an element in
$A\in F_s$
, there is an element in
![]() ${\widetilde {G}}\setminus G$
which centralizes it (see the details of this implication in Lemma 8.5). Thus, G-orbits in
${\widetilde {G}}\setminus G$
which centralizes it (see the details of this implication in Lemma 8.5). Thus, G-orbits in
![]() $F_s$
are
$F_s$
are
![]() ${\widetilde {G}}$
-invariant. So it is enough to show that, for any orbit
${\widetilde {G}}$
-invariant. So it is enough to show that, for any orbit
![]() $\mathfrak {O}{\subseteq } F_s$
, any
$\mathfrak {O}{\subseteq } F_s$
, any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\theta ^{-1}(\mathfrak {O})$
is
$\theta ^{-1}(\mathfrak {O})$
is
![]() $0$
. By Frobenius descent, this is equivalent to showing that, for some
$0$
. By Frobenius descent, this is equivalent to showing that, for some
![]() $A\in \mathfrak {O}$
, any
$A\in \mathfrak {O}$
, any
![]() $({\widetilde {G}}_A, \chi )$
-equivariant distribution on
$({\widetilde {G}}_A, \chi )$
-equivariant distribution on
![]() $\theta ^{-1}(A)$
is
$\theta ^{-1}(A)$
is
![]() $0$
(
$0$
(
![]() ${\widetilde {G}}_A$
being the stabilizer of A in
${\widetilde {G}}_A$
being the stabilizer of A in
![]() ${\widetilde {G}}$
).
${\widetilde {G}}$
).
In order to prove this, let us describe the stabilizer of a point A in
![]() $F_s$
. Let
$F_s$
. Let
![]() $m:={\mathbb F}[T] / f(T)$
. We define an
$m:={\mathbb F}[T] / f(T)$
. We define an
![]() ${\mathbb F}$
-linear involution of m by
${\mathbb F}$
-linear involution of m by
![]() $\sigma :h(T)\mapsto h^*(T) = h(-T)$
(that is the same as saying
$\sigma :h(T)\mapsto h^*(T) = h(-T)$
(that is the same as saying
![]() $T\mapsto -T$
). Let
$T\mapsto -T$
). Let
![]() $m_0$
be the fixed subfield of this involution. It is a subfield of m of index
$m_0$
be the fixed subfield of this involution. It is a subfield of m of index
![]() $2$
. Fix a nonzero
$2$
. Fix a nonzero
![]() ${\mathbb F}$
-linear functional
${\mathbb F}$
-linear functional
![]() $\ell :m\to {\mathbb F}$
which satisfies that
$\ell :m\to {\mathbb F}$
which satisfies that
![]() $\ell (\sigma h) = \ell (h)$
for all
$\ell (\sigma h) = \ell (h)$
for all
![]() $h\in {\mathbb F}$
. Any other
$h\in {\mathbb F}$
. Any other
![]() ${\mathbb F}$
-linear functional can be written as
${\mathbb F}$
-linear functional can be written as
![]() $h\mapsto \ell (\lambda h)$
for some unique
$h\mapsto \ell (\lambda h)$
for some unique
![]() $\lambda \in m$
. Being semisimple,
$\lambda \in m$
. Being semisimple,
![]() $f(A)$
must be equal 0. Thus, V can be given the structure of a linear space over m, by
$f(A)$
must be equal 0. Thus, V can be given the structure of a linear space over m, by
![]() $hv:=h(A)v$
. Given
$hv:=h(A)v$
. Given
![]() $v, v'\in V$
, the map
$v, v'\in V$
, the map
![]() $h\mapsto \langle h(A)v, v'\rangle $
is an
$h\mapsto \langle h(A)v, v'\rangle $
is an
![]() ${\mathbb F}$
-linear functional
${\mathbb F}$
-linear functional
![]() $m\to {\mathbb F}$
, and so can be written as
$m\to {\mathbb F}$
, and so can be written as
![]() $\langle h(A)v, v'\rangle = \ell (S(v, v')h)$
for some
$\langle h(A)v, v'\rangle = \ell (S(v, v')h)$
for some
![]() $S(v, v')\in m$
. One may check that
$S(v, v')\in m$
. One may check that
![]() $S(v, v')$
is m-sesquilinear (with respect to
$S(v, v')$
is m-sesquilinear (with respect to
![]() $\sigma $
) considering V as a linear space over m by
$\sigma $
) considering V as a linear space over m by
![]() $h\cdot v:=h(A)v$
. The form S is also nondegenerate, and satisfies
$h\cdot v:=h(A)v$
. The form S is also nondegenerate, and satisfies
![]() $S(v',v) = -\sigma S(v, v')$
. Fix
$S(v',v) = -\sigma S(v, v')$
. Fix
![]() $a\in m$
such that
$a\in m$
such that
![]() $\sigma a = -a$
(e.g.,
$\sigma a = -a$
(e.g.,
![]() $a = T\in {\mathbb F}[T] / f(T)$
). Then it follows from the above that
$a = T\in {\mathbb F}[T] / f(T)$
). Then it follows from the above that
![]() $aS(\cdot , \cdot )$
is a nondegenerate Hermitian form on
$aS(\cdot , \cdot )$
is a nondegenerate Hermitian form on
![]() $V_m$
(with respect to the involution
$V_m$
(with respect to the involution
![]() $\sigma $
), where
$\sigma $
), where
![]() $V_m$
is V as a linear space over m. To say that a linear automorphism of V commutes with A is to say that it is m linear, and for such an automorphism to say that it is in
$V_m$
is V as a linear space over m. To say that a linear automorphism of V commutes with A is to say that it is m linear, and for such an automorphism to say that it is in
![]() $G(V)$
is to say that it preserves
$G(V)$
is to say that it preserves
![]() $aS$
. Thus, we have that the centralizer of A in
$aS$
. Thus, we have that the centralizer of A in
![]() $G(V)$
can be described as
$G(V)$
can be described as
![]() $U(V_m)$
. Moreover, the stabilizer of A in
$U(V_m)$
. Moreover, the stabilizer of A in
![]() ${\widetilde {G}}(V)$
can be described as
${\widetilde {G}}(V)$
can be described as
![]() ${\widetilde {U}}(V_m)$
. Moreover, the centralizer of A inside
${\widetilde {U}}(V_m)$
. Moreover, the centralizer of A inside
![]() $\mathfrak {g}(v)$
can be described as
$\mathfrak {g}(v)$
can be described as
![]() $\mathfrak {u}(V_m)$
.
$\mathfrak {u}(V_m)$
.
Recall that we need to show that any
![]() $({\widetilde {U}}(V_m), \chi )$
-equivariant distribution on
$({\widetilde {U}}(V_m), \chi )$
-equivariant distribution on
![]() $\theta ^{-1}(A)$
is
$\theta ^{-1}(A)$
is
![]() $0$
. The space
$0$
. The space
![]() $\theta ^{-1}(A)$
is identified with
$\theta ^{-1}(A)$
is identified with
![]() $\mathfrak {u}_n(V_m)\times V_m$
,
$\mathfrak {u}_n(V_m)\times V_m$
,
![]() $\mathfrak {u}_n(V_m)$
being the space of nilpotent elements in
$\mathfrak {u}_n(V_m)$
being the space of nilpotent elements in
![]() $\mathfrak {u}(V_m)$
. This in turn is a closed subspace of
$\mathfrak {u}(V_m)$
. This in turn is a closed subspace of
![]() $\mathfrak {u}(V_m)\times V$
. Thus, our claim follows from the fact that any
$\mathfrak {u}(V_m)\times V$
. Thus, our claim follows from the fact that any
![]() $({\widetilde {U}}(V_m), \chi )$
-equivariant distribution on
$({\widetilde {U}}(V_m), \chi )$
-equivariant distribution on
![]() $\mathfrak {u}(V_m)$
is
$\mathfrak {u}(V_m)$
is
![]() $0$
, which follows from our induction hypothesis of Theorem 3.1, as
$0$
, which follows from our induction hypothesis of Theorem 3.1, as
![]() $\dim V_m < n$
.▪
$\dim V_m < n$
.▪
5 Separation of
 $1,-1$
as eigenvalues, and passage to the Lie algebra
$1,-1$
as eigenvalues, and passage to the Lie algebra
In this section, we pass from the group case to the Lie algebra case, showing that Theorem 3.2 implies Theorem 3.1.
Definition 5.1 Let
![]() $G_{(1)}$
be the open subset of G consisting of elements of which
$G_{(1)}$
be the open subset of G consisting of elements of which
![]() $1$
is not an eigenvalue. Similarly, define
$1$
is not an eigenvalue. Similarly, define
![]() $G_{(-1)}$
to be the open subset of elements of which
$G_{(-1)}$
to be the open subset of elements of which
![]() $-1$
is not an eigenvalue. Define also
$-1$
is not an eigenvalue. Define also
![]() $\Xi :=G \setminus (G_{(1)} \cup G_{(-1)})$
, i.e., elements of which both
$\Xi :=G \setminus (G_{(1)} \cup G_{(-1)})$
, i.e., elements of which both
![]() $1,-1$
are eigenvalues.
$1,-1$
are eigenvalues.
The following proposition is an immediate corollary of Theorem 4.1.
Proposition 5.2 To prove Theorem 3.1, it is enough to show that any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $G_{(\pm 1)} \times V$
is 0.
$G_{(\pm 1)} \times V$
is 0.
Definition 5.3 (Cayley transform)
Define
![]() $C_1:G_{(1)}(V)\to \mathfrak {g}$
by
$C_1:G_{(1)}(V)\to \mathfrak {g}$
by
![]() $C_1(A)=\frac {I+A}{I-A}$
. Similarly, define
$C_1(A)=\frac {I+A}{I-A}$
. Similarly, define
![]() $C_{-1}:G_{(-1)}(V)\to \mathfrak {g}$
by
$C_{-1}:G_{(-1)}(V)\to \mathfrak {g}$
by
![]() $C_{-1}(A)=\frac {I-A}{I+A}$
.
$C_{-1}(A)=\frac {I-A}{I+A}$
.
This definition makes sense since, for
![]() $A\in G_{(1)}(V)$
,
$A\in G_{(1)}(V)$
,
and similarly for
![]() $C_{-1}$
.
$C_{-1}$
.
Definition 5.4 Let
![]() $\mathfrak {g}_0$
be the subspace of
$\mathfrak {g}_0$
be the subspace of
![]() $\mathfrak {g}$
not having
$\mathfrak {g}$
not having
![]() $\pm 1$
as eigenvalues.
$\pm 1$
as eigenvalues.
Proposition 5.5 The maps
![]() $C_{\pm 1}$
are
$C_{\pm 1}$
are
![]() ${\widetilde {G}}$
-homeomorphisms from
${\widetilde {G}}$
-homeomorphisms from
![]() $G_{(\pm 1)}(V)$
(respectively) to
$G_{(\pm 1)}(V)$
(respectively) to
![]() $\mathfrak {g}_0$
, unless we are in the case
$\mathfrak {g}_0$
, unless we are in the case
![]() $G=SO$
, considering
$G=SO$
, considering
![]() $C_1$
, and
$C_1$
, and
![]() $\dim V$
is even. In this case,
$\dim V$
is even. In this case,
![]() $SO_{(1)}(V)=\emptyset $
.
$SO_{(1)}(V)=\emptyset $
.
Proof First, exclude the case
![]() $G=SO$
. We will give the proof for
$G=SO$
. We will give the proof for
![]() $C_1$
. The proof for
$C_1$
. The proof for
![]() $C_{-1}$
is similar. First, notice that indeed
$C_{-1}$
is similar. First, notice that indeed
![]() $C_1(A)$
does not have
$C_1(A)$
does not have
![]() $\pm 1$
as eigenvalues. If it did have, then
$\pm 1$
as eigenvalues. If it did have, then
![]() $(I+A)v=\pm (I-A)v$
, which leads to either
$(I+A)v=\pm (I-A)v$
, which leads to either
![]() $v=0$
or
$v=0$
or
![]() $Av=0$
, and A is invertible. Second, we construct an inverse,
$Av=0$
, and A is invertible. Second, we construct an inverse,
![]() $B \mapsto \frac {B-I}{B+I}$
: One can see that the inverse map is indeed into
$B \mapsto \frac {B-I}{B+I}$
: One can see that the inverse map is indeed into
![]() $G_{(1)}$
, as
$G_{(1)}$
, as
 $$ \begin{align*}\left(\frac{B-I}{B+I}\right)^*=\frac{B^*-I}{B^*+I}=\frac{-B-I}{-B+I}=\frac{B+I}{B-I}=\left(\frac{B-I}{B+I}\right)^{-1}\end{align*} $$
$$ \begin{align*}\left(\frac{B-I}{B+I}\right)^*=\frac{B^*-I}{B^*+I}=\frac{-B-I}{-B+I}=\frac{B+I}{B-I}=\left(\frac{B-I}{B+I}\right)^{-1}\end{align*} $$
and also
![]() $\frac {B-I}{B+I}$
cannot have
$\frac {B-I}{B+I}$
cannot have
![]() $1$
as an eigenvalue, as then
$1$
as an eigenvalue, as then
![]() $(B-I)v=(B+I)v$
, and hence
$(B-I)v=(B+I)v$
, and hence
![]() $v=0$
. To see that we indeed constructed an inverse map,
$v=0$
. To see that we indeed constructed an inverse map,
 $$ \begin{align*}\frac{I+\frac{B-I}{B+I}}{I-\frac{B-I}{B+I}}=\frac{B+I+B-I}{B+I-(B-I)}=\frac{2B}{2I}=B,\end{align*} $$
$$ \begin{align*}\frac{I+\frac{B-I}{B+I}}{I-\frac{B-I}{B+I}}=\frac{B+I+B-I}{B+I-(B-I)}=\frac{2B}{2I}=B,\end{align*} $$
 $$ \begin{align*}\frac{\frac{I+A}{I-A}-I}{\frac{I+A}{I-A}+I}=\frac{I+A-(I-A)}{I+A+I-A}=\frac{2A}{2I}=A.\end{align*} $$
$$ \begin{align*}\frac{\frac{I+A}{I-A}-I}{\frac{I+A}{I-A}+I}=\frac{I+A-(I-A)}{I+A+I-A}=\frac{2A}{2I}=A.\end{align*} $$
There are similar arguments for
![]() $C_{-1}$
showing it is a
$C_{-1}$
showing it is a
![]() ${\widetilde {G}}$
-isomorphism to
${\widetilde {G}}$
-isomorphism to
![]() $\mathfrak {g}_0$
.
$\mathfrak {g}_0$
.
For the case
![]() $G=SO$
, it simply holds that
$G=SO$
, it simply holds that
![]() $SO_{(-1)} = O_{(-1)}$
,
$SO_{(-1)} = O_{(-1)}$
,
![]() $SO_{(1)} = O_{(1)}$
when
$SO_{(1)} = O_{(1)}$
when
![]() $\dim V$
is even, and
$\dim V$
is even, and
![]() $SO_{(1)} = \emptyset $
when
$SO_{(1)} = \emptyset $
when
![]() $\dim V$
is odd.▪
$\dim V$
is odd.▪
Proposition 5.6 To prove Theorem 3.1, it suffices to show that any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g}_0 \times V$
is 0.
$\mathfrak {g}_0 \times V$
is 0.
Proof Use
![]() $C_{\pm 1}$
.▪
$C_{\pm 1}$
.▪
Proof Take
![]() $\xi $
to be a
$\xi $
to be a
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g}_0 \times V$
. Assume by contradiction that it is not
$\mathfrak {g}_0 \times V$
. Assume by contradiction that it is not
![]() $0$
, and let
$0$
, and let
![]() $(A_0,v_0)$
be a point in its support. Let
$(A_0,v_0)$
be a point in its support. Let
![]() $t=\det ((A_0-I)(A_0+I))\neq 0$
. One can choose
$t=\det ((A_0-I)(A_0+I))\neq 0$
. One can choose
![]() $f\in {\mathcal S}({\mathbb K})$
s.t.
$f\in {\mathcal S}({\mathbb K})$
s.t.
![]() $f(t)\neq 0,f(0)=0$
. Note that
$f(t)\neq 0,f(0)=0$
. Note that
![]() $\mathfrak {g}_0$
is an open subset of
$\mathfrak {g}_0$
is an open subset of
![]() $\mathfrak {g}$
, and
$\mathfrak {g}$
, and
![]() $g(A):=f(\det ((A-I)(A+I)))$
is a locally constant function, compactly supported inside
$g(A):=f(\det ((A-I)(A+I)))$
is a locally constant function, compactly supported inside
![]() $\mathfrak {g}_0$
. Thus, we can extend
$\mathfrak {g}_0$
. Thus, we can extend
![]() $g\cdot \xi $
to a
$g\cdot \xi $
to a
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g}\times V$
with
$\mathfrak {g}\times V$
with
![]() $(A_0,v_0)$
in its support. In particular, this distribution is not 0, which creates a contradiction to our assumption.▪
$(A_0,v_0)$
in its support. In particular, this distribution is not 0, which creates a contradiction to our assumption.▪
6 An important lemma and automorphisms
Lemma 6.1 Any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g} \times V$
is supported on
$\mathfrak {g} \times V$
is supported on
![]() $\mathfrak {g}\times \Gamma $
, where
$\mathfrak {g}\times \Gamma $
, where
![]() $\Gamma :=\{v\in V | \langle v,v\rangle =0\}$
.
$\Gamma :=\{v\in V | \langle v,v\rangle =0\}$
.
Proof We do not consider in the following the case
![]() $\mathfrak {g}=\mathfrak {sp}$
, as in this case
$\mathfrak {g}=\mathfrak {sp}$
, as in this case
![]() $\Gamma =V$
and there is nothing to prove. This proof is the same as the proof of [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Proposition 5.2]. The idea is to consider the map
$\Gamma =V$
and there is nothing to prove. This proof is the same as the proof of [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Proposition 5.2]. The idea is to consider the map
![]() $\mathfrak {g}\times V\to {\mathbb K}$
given by
$\mathfrak {g}\times V\to {\mathbb K}$
given by
![]() $(A,v)\mapsto \langle v,v\rangle$
, and apply the localization principle (Corollary 2.5) to it to restrict to a fiber. Then apply Frobenius descent (Theorem 2.7) on the projection on the second coordinate, to reach a point where it is enough to show that any
$(A,v)\mapsto \langle v,v\rangle$
, and apply the localization principle (Corollary 2.5) to it to restrict to a fiber. Then apply Frobenius descent (Theorem 2.7) on the projection on the second coordinate, to reach a point where it is enough to show that any
![]() $({\widetilde {G}}(V'), \chi )$
-equivariant distribution on
$({\widetilde {G}}(V'), \chi )$
-equivariant distribution on
![]() $\mathfrak {g}(V')$
is 0, for some subspace
$\mathfrak {g}(V')$
is 0, for some subspace
![]() $V'{\subseteq } V$
of codimension 1. We have a decomposition
$V'{\subseteq } V$
of codimension 1. We have a decomposition
![]() $\mathfrak {g} = \mathfrak {g}(V')\oplus V'\oplus E$
, with E being either a zero- or one-dimensional vector space over
$\mathfrak {g} = \mathfrak {g}(V')\oplus V'\oplus E$
, with E being either a zero- or one-dimensional vector space over
![]() ${\mathbb F}$
with trivial
${\mathbb F}$
with trivial
![]() ${\widetilde {G}}(V')$
-action, and so we can use the induction hypothesis to finish.▪
${\widetilde {G}}(V')$
-action, and so we can use the induction hypothesis to finish.▪
Denote by
![]() $\phi _v$
the linear transformation
$\phi _v$
the linear transformation
![]() $u\mapsto \langle u,v\rangle v$
.
$u\mapsto \langle u,v\rangle v$
.
The following definition will be relevant for the cases of
![]() $\mathfrak {u}$
and
$\mathfrak {u}$
and
![]() $\mathfrak {sp}$
.
$\mathfrak {sp}$
.
Definition 6.2 For any
![]() $\lambda \in {\mathbb K}$
, requiring
$\lambda \in {\mathbb K}$
, requiring
![]() $\bar {\lambda }=-\lambda $
if
$\bar {\lambda }=-\lambda $
if
![]() $\mathfrak {g} = \mathfrak {u}$
, we define an automorphism of
$\mathfrak {g} = \mathfrak {u}$
, we define an automorphism of
![]() $\mathfrak {g}$
by
$\mathfrak {g}$
by
![]() $\nu _{\lambda }(A,v):= (A + \lambda \phi _v, v)$
. This is an automorphism of
$\nu _{\lambda }(A,v):= (A + \lambda \phi _v, v)$
. This is an automorphism of
![]() $\mathfrak {g}$
as a space with a
$\mathfrak {g}$
as a space with a
![]() ${\widetilde {G}}$
action.
${\widetilde {G}}$
action.
The following definition will be relevant only for case of
![]() $\mathfrak {o}$
.
$\mathfrak {o}$
.
Definition 6.3 For any
![]() $\lambda \in {\mathbb F}$
, define an automorphism of
$\lambda \in {\mathbb F}$
, define an automorphism of
![]() $\mathfrak {g}\times V$
by
$\mathfrak {g}\times V$
by
This is an automorphism of
![]() $\mathfrak {g}\times V$
as a space with a
$\mathfrak {g}\times V$
as a space with a
![]() ${\widetilde {G}}$
action.
${\widetilde {G}}$
action.
Fix a fiber F of
![]() $\Delta :\mathfrak {g}\times V\to {\mathbb K}[x]$
at a polynomial f. Recall that we must have
$\Delta :\mathfrak {g}\times V\to {\mathbb K}[x]$
at a polynomial f. Recall that we must have
![]() $f^*(x)=(-1)^n f(x)$
. Choose a polynomial
$f^*(x)=(-1)^n f(x)$
. Choose a polynomial
![]() $g\in {\mathbb K}[x]$
coprime to f that also satisfies
$g\in {\mathbb K}[x]$
coprime to f that also satisfies
![]() $g^*(x) = g(x) \mod f(x)$
. Then we can define the following definition.
$g^*(x) = g(x) \mod f(x)$
. Then we can define the following definition.
Definition 6.4 Define an automorphism of F by
![]() $\rho _g(A,v)=(A,g(A)v)$
.
$\rho _g(A,v)=(A,g(A)v)$
.
To show that it is invertible, notice that there is an “inverse” polynomial
![]() $g^{-1}$
such that
$g^{-1}$
such that
![]() $gg^{-1}=1\mod f$
. It also satisfies
$gg^{-1}=1\mod f$
. It also satisfies
![]() $(g^{-1})^*(x)= g^{-1}(x) \mod f(x)$
, as for some polynomial a,
$(g^{-1})^*(x)= g^{-1}(x) \mod f(x)$
, as for some polynomial a,
 $$ \begin{align*} 1&=((g^{-1}g +af))^*(x)=(g^{-1})^*(x)g^*(x)+a^*(x)f^*(x)\\ &=(g^{-1})^*(x)g^*(x) + (-1)^n a^*(x)f(x). \end{align*} $$
$$ \begin{align*} 1&=((g^{-1}g +af))^*(x)=(g^{-1})^*(x)g^*(x)+a^*(x)f^*(x)\\ &=(g^{-1})^*(x)g^*(x) + (-1)^n a^*(x)f(x). \end{align*} $$
The last being equal to
![]() $(g^{-1})^*(x)g(x)$
modulo
$(g^{-1})^*(x)g(x)$
modulo
![]() $f(x)$
. This implies that we have
$f(x)$
. This implies that we have
![]() $\rho _{g^{-1}}$
which is inverse to
$\rho _{g^{-1}}$
which is inverse to
![]() $\rho _g$
. To show that
$\rho _g$
. To show that
![]() $\rho _h$
commutes with the action of
$\rho _h$
commutes with the action of
![]() ${\widetilde {G}}$
, the only nontrivial part is to show that it commutes with the action of an element
${\widetilde {G}}$
, the only nontrivial part is to show that it commutes with the action of an element
![]() $x\in {\widetilde {G}} \setminus G$
. Consider x as an element of
$x\in {\widetilde {G}} \setminus G$
. Consider x as an element of
![]() $\operatorname {End}_{\mathbb F}(V)$
satisfying
$\operatorname {End}_{\mathbb F}(V)$
satisfying
![]() $\langle xu, xw\rangle = \langle w,u\rangle$
for any
$\langle xu, xw\rangle = \langle w,u\rangle$
for any
![]() $u,w\in V$
. In particular, x satisfies
$u,w\in V$
. In particular, x satisfies
![]() $axu = x\bar {a}u$
for any
$axu = x\bar {a}u$
for any
![]() $a\in {\mathbb K}, u\in V$
. To show commutation, we need to show that
$a\in {\mathbb K}, u\in V$
. To show commutation, we need to show that
![]() $-xg(A)v=g(-xAx^{-1})(-xv)$
. This is true as
$-xg(A)v=g(-xAx^{-1})(-xv)$
. This is true as
For the last equation, we used the condition imposed on g, and the fact that
![]() $f(A)=0$
.
$f(A)=0$
.
Thus, we get that
![]() $\rho _g$
is a
$\rho _g$
is a
![]() ${\widetilde {G}}$
-automorphism of F.
${\widetilde {G}}$
-automorphism of F.
In the case
![]() $\mathfrak {g}=\mathfrak {sp}$
, we give the following lemma by using the automorphisms
$\mathfrak {g}=\mathfrak {sp}$
, we give the following lemma by using the automorphisms
![]() $\nu _\lambda $
to amplify the restriction of Theorem 4.3.
$\nu _\lambda $
to amplify the restriction of Theorem 4.3.
Lemma 6.5 Assume that
![]() $\mathfrak {g} = \mathfrak {sp}$
. Then any
$\mathfrak {g} = \mathfrak {sp}$
. Then any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g} \times V$
is supported on
$\mathfrak {g} \times V$
is supported on
![]() $\mathfrak {g}\times \Gamma _1$
, where
$\mathfrak {g}\times \Gamma _1$
, where
![]() $\Gamma _1:=\{v\in V | \langle Av,v\rangle =0\}$
.
$\Gamma _1:=\{v\in V | \langle Av,v\rangle =0\}$
.
Proof Given
![]() $A\in \operatorname {End}(V)$
, write the characteristic polynomial of A as
$A\in \operatorname {End}(V)$
, write the characteristic polynomial of A as
with the convention that
![]() $c_0(A) = 1$
. Let
$c_0(A) = 1$
. Let
![]() $(A, v)$
be a point in the support of a
$(A, v)$
be a point in the support of a
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g} \times V$
. From Theorem 4.3, we deduce that we have
$\mathfrak {g} \times V$
. From Theorem 4.3, we deduce that we have
![]() $c_1(A) = n\alpha $
and
$c_1(A) = n\alpha $
and
![]() $c_2(A) = \binom {n}{2}\alpha ^2$
for some
$c_2(A) = \binom {n}{2}\alpha ^2$
for some
![]() $\alpha \in {\mathbb F}$
(if the characteristic polynomial is a power of a linear polynomial this is clear, and if it is a power of an inseparable polynomial, then we indeed have
$\alpha \in {\mathbb F}$
(if the characteristic polynomial is a power of a linear polynomial this is clear, and if it is a power of an inseparable polynomial, then we indeed have
![]() $c_1(A) = c_2(A) = 0$
). Note that using this condition,
$c_1(A) = c_2(A) = 0$
). Note that using this condition,
![]() $c_1(A)$
determines uniquely
$c_1(A)$
determines uniquely
![]() $c_2(A)$
. Now, we may translate by
$c_2(A)$
. Now, we may translate by
![]() $\nu _\lambda $
and then apply the above condition to get
$\nu _\lambda $
and then apply the above condition to get
![]() $c_1(A + \lambda \phi _v) = n\beta , c_2(A + \lambda \phi _v) = \binom {n}{2}\beta ^2$
. However, by [Reference Mezer9, Theorem A.2], we have
$c_1(A + \lambda \phi _v) = n\beta , c_2(A + \lambda \phi _v) = \binom {n}{2}\beta ^2$
. However, by [Reference Mezer9, Theorem A.2], we have
and
Since
![]() $\langle v,v\rangle = 0$
, this is saying that
$\langle v,v\rangle = 0$
, this is saying that
![]() $c_1(A + \lambda \phi _v) = c_1(A)$
, and hence
$c_1(A + \lambda \phi _v) = c_1(A)$
, and hence
![]() $\beta = \alpha $
and so also
$\beta = \alpha $
and so also
![]() $c_2(A + \lambda \phi _v) = c_2(A)$
, and from the second equation
$c_2(A + \lambda \phi _v) = c_2(A)$
, and from the second equation
![]() $c_2(A + \lambda \phi _v) = c_2(A) - \langle Av,v\rangle $
. Thus,
$c_2(A + \lambda \phi _v) = c_2(A) - \langle Av,v\rangle $
. Thus,
![]() $\langle Av, v\rangle = 0$
.▪
$\langle Av, v\rangle = 0$
.▪
Definition 6.6 For any
![]() $A\in \mathfrak {g}$
, denote
$A\in \mathfrak {g}$
, denote
Denote also
Proposition 6.7 Any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g}\times V$
is supported on R.
$\mathfrak {g}\times V$
is supported on R.
Proof By the localization principle (Corollary 2.5), it is enough to show that any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on a fiber F of
$({\widetilde {G}}, \chi )$
-equivariant distribution on a fiber F of
![]() $\Delta $
at a polynomial f is supported on
$\Delta $
at a polynomial f is supported on
![]() $R\cap F$
(note that R is
$R\cap F$
(note that R is
![]() ${\widetilde {G}}$
-invariant). Let
${\widetilde {G}}$
-invariant). Let
![]() $\xi $
be such a distribution, and let
$\xi $
be such a distribution, and let
![]() $(A,v)$
be a point in
$(A,v)$
be a point in
![]() $\mathrm {supp}(\xi )$
. Let us start with the case of
$\mathrm {supp}(\xi )$
. Let us start with the case of
![]() $\mathfrak {u}$
.
$\mathfrak {u}$
.
Choose
![]() $\omega \in {\mathbb K}^\times $
with
$\omega \in {\mathbb K}^\times $
with
![]() $\bar {\omega }=-\omega $
. Let
$\bar {\omega }=-\omega $
. Let
![]() $g\in {\mathbb F}[x]$
and consider
$g\in {\mathbb F}[x]$
and consider
![]() $g_1(x)=g(x^2)$
and
$g_1(x)=g(x^2)$
and
![]() $g_2(x)=\omega x g(x^2)$
. They satisfy
$g_2(x)=\omega x g(x^2)$
. They satisfy
![]() $\overline {g_1}(-x)=g_1(x),\overline {g_2}(-x)=g_2(x)$
. Choose g such that
$\overline {g_1}(-x)=g_1(x),\overline {g_2}(-x)=g_2(x)$
. Choose g such that
![]() $g_1$
will be coprime to f. We can apply
$g_1$
will be coprime to f. We can apply
![]() $\rho _{g_1}$
to
$\rho _{g_1}$
to
![]() $\xi $
and extend back to
$\xi $
and extend back to
![]() $\mathfrak {g}\times V$
to get that by Lemma 6.1,
$\mathfrak {g}\times V$
to get that by Lemma 6.1,
![]() $\langle g_1(A)v,g_1(A)v\rangle =0$
. We know this for a Zariski dense subset of polynomials
$\langle g_1(A)v,g_1(A)v\rangle =0$
. We know this for a Zariski dense subset of polynomials
![]() $g\in {\mathbb F}[x]$
, and so for all
$g\in {\mathbb F}[x]$
, and so for all
![]() $g\in {\mathbb F}[x]$
. The same goes for
$g\in {\mathbb F}[x]$
. The same goes for
![]() $g_2$
. So, in particular,
$g_2$
. So, in particular,
 $$ \begin{align*} \langle A^{2k+1}v,v\rangle =&\omega^{-1}\langle \omega A^{2k+1}v, v\rangle =\frac{\omega^{-1}}{2}(\langle (\omega A^{2k+1}+I)v,(\omega A^{2k+1}+I)v\rangle\\ &-\langle\omega A^{2k+1}v,\omega A^{2k+1}v\rangle -\langle v,v\rangle)=0. \end{align*} $$
$$ \begin{align*} \langle A^{2k+1}v,v\rangle =&\omega^{-1}\langle \omega A^{2k+1}v, v\rangle =\frac{\omega^{-1}}{2}(\langle (\omega A^{2k+1}+I)v,(\omega A^{2k+1}+I)v\rangle\\ &-\langle\omega A^{2k+1}v,\omega A^{2k+1}v\rangle -\langle v,v\rangle)=0. \end{align*} $$
Note that indeed it follows from
![]() $A^* = -A$
that
$A^* = -A$
that
![]() $\langle A^{2k}v, v\rangle = \langle v, A^{2k}v\rangle$
and that
$\langle A^{2k}v, v\rangle = \langle v, A^{2k}v\rangle$
and that
![]() $\langle \omega A^{2k+1}v,v\rangle = \langle v,\omega A^{2k+1}v\rangle$
.
$\langle \omega A^{2k+1}v,v\rangle = \langle v,\omega A^{2k+1}v\rangle$
.
Now, for the case of
![]() $\mathfrak {o}$
, we still have
$\mathfrak {o}$
, we still have
![]() $g_1$
, and the same proof as before shows that
$g_1$
, and the same proof as before shows that
![]() $\langle A^{2k}v,v\rangle =0$
. However, it is always true that
$\langle A^{2k}v,v\rangle =0$
. However, it is always true that
and hence
![]() $\langle A^{2k+1}v,v\rangle =0$
.
$\langle A^{2k+1}v,v\rangle =0$
.
For the case of
![]() $\mathfrak {sp}$
, we use the same technique but to the condition imposed from Lemma 6.5. This way we get that for a Zariski dense subset of
$\mathfrak {sp}$
, we use the same technique but to the condition imposed from Lemma 6.5. This way we get that for a Zariski dense subset of
![]() ${\mathbb F}[x]$
(and thus for all
${\mathbb F}[x]$
(and thus for all
![]() $g\in {\mathbb F}[x]$
) that
$g\in {\mathbb F}[x]$
) that
![]() $\langle Ag(A^2)v, g(A^2)v\rangle = 0$
. From this, we are able to get
$\langle Ag(A^2)v, g(A^2)v\rangle = 0$
. From this, we are able to get
 $$ \begin{align*} \langle A^{2k+1}v,v\rangle =&\frac{1}{2}(\langle A(A^{2k}+I)v,(A^{2k}+I)v\rangle \\ &-\langle A\cdot A^{2k}v,A^{2k}v\rangle -\langle Av,v\rangle )=0. \end{align*} $$
$$ \begin{align*} \langle A^{2k+1}v,v\rangle =&\frac{1}{2}(\langle A(A^{2k}+I)v,(A^{2k}+I)v\rangle \\ &-\langle A\cdot A^{2k}v,A^{2k}v\rangle -\langle Av,v\rangle )=0. \end{align*} $$
Moreover, it is always true that
and hence
![]() $\langle A^{2k}v,v\rangle = 0$
.▪
$\langle A^{2k}v,v\rangle = 0$
.▪
Lemma 6.8 Given
![]() $(A,v)\in R$
, we have:
$(A,v)\in R$
, we have:
-
(i) For any
 $\lambda \in {\mathbb K}$
for which
$\lambda \in {\mathbb K}$
for which
 $\nu _\lambda $
is defined,
$\nu _\lambda $
is defined,
 $\Delta (\nu _\lambda (A,v))=\Delta (A,v)$
.
$\Delta (\nu _\lambda (A,v))=\Delta (A,v)$
. -
(ii) For any
 $\lambda \in {\mathbb F}$
,
$\lambda \in {\mathbb F}$
,
 $\Delta (\mu _\lambda (A,v))=\Delta (A,v)$
.
$\Delta (\mu _\lambda (A,v))=\Delta (A,v)$
.
Proof For
![]() $\Delta (\nu _\lambda (A,v))$
, this follows directly from Proposition 2.17. For
$\Delta (\nu _\lambda (A,v))$
, this follows directly from Proposition 2.17. For
![]() $\Delta (\mu _\lambda (A,v))$
, this also follows from Proposition 2.17, but with an iterative use.
$\Delta (\mu _\lambda (A,v))$
, this also follows from Proposition 2.17, but with an iterative use.
Since
![]() $\langle A^k Av, v\rangle =0$
for all
$\langle A^k Av, v\rangle =0$
for all
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $\Delta (A)=\Delta (A+A\phi _v)$
. To prove that we also have
$\Delta (A)=\Delta (A+A\phi _v)$
. To prove that we also have
![]() $\Delta (A+A\phi _v)=\Delta (A+A\phi _v+\phi _v A)$
, we must check that
$\Delta (A+A\phi _v)=\Delta (A+A\phi _v+\phi _v A)$
, we must check that
![]() $\langle (A+A\phi _v)^k v, A^* v\rangle =0$
for all
$\langle (A+A\phi _v)^k v, A^* v\rangle =0$
for all
![]() $k\geq 0$
. Now, for any
$k\geq 0$
. Now, for any
![]() $k\geq 0$
, we have
$k\geq 0$
, we have
![]() $\phi _v A^k v = \langle A^k v, v\rangle v = 0$
, so
$\phi _v A^k v = \langle A^k v, v\rangle v = 0$
, so
▪
7 Stratification
For any
![]() $g\in {\mathbb K} [x]$
which is a power of an irreducible polynomial, let
$g\in {\mathbb K} [x]$
which is a power of an irreducible polynomial, let
![]() $Y_g$
be the subspace of
$Y_g$
be the subspace of
![]() $\mathfrak {g}$
consisting of elements with characteristic polynomial g. By the localization principle (Corollary 2.5), the previous reformulations, and Theorem 4.2, it is enough to prove that any
$\mathfrak {g}$
consisting of elements with characteristic polynomial g. By the localization principle (Corollary 2.5), the previous reformulations, and Theorem 4.2, it is enough to prove that any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\Delta ^{-1}(g)=Y_g\times V$
is
$\Delta ^{-1}(g)=Y_g\times V$
is
![]() $0$
, for any g as above. Let us fix g and prove this claim for it.
$0$
, for any g as above. Let us fix g and prove this claim for it.
We proceed similarly to [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Reference Mezer9]. The strategy will be to stratify
![]() $Y_g$
and restrict stratum by stratum the possible support for a
$Y_g$
and restrict stratum by stratum the possible support for a
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution (note that
$({\widetilde {G}}, \chi )$
-equivariant distribution (note that
![]() $Y_g$
is a union of finitely many
$Y_g$
is a union of finitely many
![]() ${\widetilde {G}}$
orbits). For the unitary case, choose
${\widetilde {G}}$
orbits). For the unitary case, choose
![]() $\omega \in {\mathbb K}$
s.t.
$\omega \in {\mathbb K}$
s.t.
![]() $\bar {\omega }=-\omega $
(in the symplectic case denote
$\bar {\omega }=-\omega $
(in the symplectic case denote
![]() $\omega = 1$
). For
$\omega = 1$
). For
![]() $\lambda \in {\mathbb F}$
, denote by
$\lambda \in {\mathbb F}$
, denote by
![]() $\eta _\lambda $
either
$\eta _\lambda $
either
![]() $\nu _{\lambda \omega }$
or
$\nu _{\lambda \omega }$
or
![]() $\mu _\lambda $
, depending on which case we are in.
$\mu _\lambda $
, depending on which case we are in.
Notation 7.1 Denote by
![]() $P_i(g)$
the union of all
$P_i(g)$
the union of all
![]() ${\widetilde {G}}$
-orbits of
${\widetilde {G}}$
-orbits of
![]() $Y_g$
of dimension at most i, and let
$Y_g$
of dimension at most i, and let
![]() $R_i(g):=R\cap (P_i(g) \times V)$
. Moreover, for any open
$R_i(g):=R\cap (P_i(g) \times V)$
. Moreover, for any open
![]() ${\widetilde {G}}$
-orbit
${\widetilde {G}}$
-orbit
![]() $O$
of
$O$
of
![]() $P_i(g)$
, set
$P_i(g)$
, set
Note that
![]() $P_i(g)$
are Zariski closed inside
$P_i(g)$
are Zariski closed inside
![]() $Y_g$
,
$Y_g$
,
![]() $P_k(g)=Y_g$
for k big enough, and
$P_k(g)=Y_g$
for k big enough, and
![]() $P_{-1}(g)=\emptyset $
.
$P_{-1}(g)=\emptyset $
.
We denote by
![]() ${\mathcal {F}}_V$
the Fourier transform on V with respect to the nondegenerate
${\mathcal {F}}_V$
the Fourier transform on V with respect to the nondegenerate
![]() ${\mathbb F}$
-bilinear form
${\mathbb F}$
-bilinear form
![]() $(u,v)\mapsto \operatorname {tr}_{{\mathbb K}/{\mathbb F}}(\langle u,v\rangle)$
. It will also be used to denote the partial Fourier transform on V when applied to
$(u,v)\mapsto \operatorname {tr}_{{\mathbb K}/{\mathbb F}}(\langle u,v\rangle)$
. It will also be used to denote the partial Fourier transform on V when applied to
![]() $X\times V$
for some space X. In the cases of
$X\times V$
for some space X. In the cases of
![]() $\mathfrak {g} = \mathfrak {o}$
and
$\mathfrak {g} = \mathfrak {o}$
and
![]() $\mathfrak {g} = \mathfrak {u}$
,
$\mathfrak {g} = \mathfrak {u}$
,
![]() ${\mathcal {F}}_V$
commutes with the action of
${\mathcal {F}}_V$
commutes with the action of
![]() ${\widetilde {G}}$
. In the case of
${\widetilde {G}}$
. In the case of
![]() $\mathfrak {g} = \mathfrak {sp}$
, it is not true. Instead, the action on
$\mathfrak {g} = \mathfrak {sp}$
, it is not true. Instead, the action on
![]() ${\widetilde {G}}$
after applying
${\widetilde {G}}$
after applying
![]() ${\mathcal {F}}_V$
is compatible with the action of
${\mathcal {F}}_V$
is compatible with the action of
![]() ${\widetilde {G}}$
on V by
${\widetilde {G}}$
on V by
![]() $(g, \delta ).v:= gv$
(recall that the usual action of
$(g, \delta ).v:= gv$
(recall that the usual action of
![]() ${\widetilde {G}}$
on V is by
${\widetilde {G}}$
on V is by
![]() $(g, \delta ).v:= \delta gv$
). Since
$(g, \delta ).v:= \delta gv$
). Since
![]() $-1\in Sp$
, we still have that Fourier transform maps
$-1\in Sp$
, we still have that Fourier transform maps
![]() ${\mathcal S}^*(X\times V)^{H, \tau }$
into itself for any
${\mathcal S}^*(X\times V)^{H, \tau }$
into itself for any
![]() $X{\subseteq } \mathfrak {sp}$
, any subgroup H of
$X{\subseteq } \mathfrak {sp}$
, any subgroup H of
![]() ${\widetilde {Sp}}$
containing
${\widetilde {Sp}}$
containing
![]() $-1$
, and any
$-1$
, and any
![]() $\tau \in \{1, \chi \}$
.
$\tau \in \{1, \chi \}$
.
Claim 7.2 Let
![]() $g\in {\mathbb K}[x]$
be a polynomial which is a power of an irreducible polynomial f satisfying
$g\in {\mathbb K}[x]$
be a polynomial which is a power of an irreducible polynomial f satisfying
![]() $f = \pm f^*$
. Let
$f = \pm f^*$
. Let
![]() $O$
be an open
$O$
be an open
![]() ${\widetilde {G}}$
-orbit of
${\widetilde {G}}$
-orbit of
![]() $P_i(g)$
. Suppose that
$P_i(g)$
. Suppose that
![]() $\xi $
is a
$\xi $
is a
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $O\times V$
such that
$O\times V$
such that
and
Then
![]() $\xi =0$
.
$\xi =0$
.
This claim will be proved in the next section.
Let us now show how it implies the main theorems. Recall that Theorem 3.2, which states that any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\mathfrak {g}\times V$
is 0, implies Theorems 1.2 and 1.4. This is by virtue of Theorem 5.7 and what is shown in Section 3.
$\mathfrak {g}\times V$
is 0, implies Theorems 1.2 and 1.4. This is by virtue of Theorem 5.7 and what is shown in Section 3.
Proof of Theorem 3.2
We prove the following claim by downward induction—any
![]() $({\widetilde {G}}, \chi )$
-equivariant distribution on
$({\widetilde {G}}, \chi )$
-equivariant distribution on
![]() $\Delta ^{-1}(g)$
is supported inside
$\Delta ^{-1}(g)$
is supported inside
![]() $R_i(g)$
. This claim for i big enough follows from Proposition 6.7, and the claim for
$R_i(g)$
. This claim for i big enough follows from Proposition 6.7, and the claim for
![]() $i=-1$
implies Theorem 3.2 by the localization principle (Corollary 2.5) and Proposition 4.2, as already explained in the top of this section. For the induction step, take such a distribution
$i=-1$
implies Theorem 3.2 by the localization principle (Corollary 2.5) and Proposition 4.2, as already explained in the top of this section. For the induction step, take such a distribution
![]() $\xi $
. As
$\xi $
. As
![]() $P_i(g)\setminus P_{i-1}(g)$
is a disjoint union of open orbits, it is enough to show that the restriction of
$P_i(g)\setminus P_{i-1}(g)$
is a disjoint union of open orbits, it is enough to show that the restriction of
![]() $\xi $
to any
$\xi $
to any
![]() $O\times V$
, where
$O\times V$
, where
![]() $O$
is an open orbit of
$O$
is an open orbit of
![]() $P_i(g)$
, is zero. Let
$P_i(g)$
, is zero. Let
![]() $\zeta =\xi |_{O\times V}$
be such a restriction. By the induction hypothesis applied to
$\zeta =\xi |_{O\times V}$
be such a restriction. By the induction hypothesis applied to
![]() $\eta _{\lambda }(\xi )$
, we know that
$\eta _{\lambda }(\xi )$
, we know that
![]() $\mathrm {supp}(\zeta ) {\subseteq } {\widetilde {O}}$
and similarly
$\mathrm {supp}(\zeta ) {\subseteq } {\widetilde {O}}$
and similarly
![]() $\mathrm {supp}({\mathcal {F}}_{V}(\zeta )) {\subseteq } {\widetilde {O}}$
. Hence, by Claim 7.2,
$\mathrm {supp}({\mathcal {F}}_{V}(\zeta )) {\subseteq } {\widetilde {O}}$
. Hence, by Claim 7.2,
![]() $\zeta =0$
.▪
$\zeta =0$
.▪
8 Handling a single stratum—proof of Claim 7.2
8.1 Nice operators
This subsection closely follows [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Section 6] and [Reference Mezer9, Section 4.3], but we give it here for completeness.
Notation 8.1 For
![]() $A\in \mathrm {gl}(V)$
, set, in the cases
$A\in \mathrm {gl}(V)$
, set, in the cases
![]() $\mathfrak {g} = \mathfrak {u}, \mathfrak {sp}$
,
$\mathfrak {g} = \mathfrak {u}, \mathfrak {sp}$
,
In the case
![]() $\mathfrak {g} = \mathfrak {o}$
, set
$\mathfrak {g} = \mathfrak {o}$
, set
Here,
![]() $[B,C]:=BC-CB$
is the Lie bracket, and
$[B,C]:=BC-CB$
is the Lie bracket, and
![]() $[A,\mathfrak {g} (V)]=\{[A,B]|B\in \mathfrak {g} (V)\}$
.
$[A,\mathfrak {g} (V)]=\{[A,B]|B\in \mathfrak {g} (V)\}$
.
Proposition 8.2 If
![]() $(A,v)\in {\widetilde {O}}$
, then
$(A,v)\in {\widetilde {O}}$
, then
![]() $v\in Q_A$
.
$v\in Q_A$
.
Proof Consider a point
![]() $(A,v)\in {\widetilde {O}}$
. The Zariski tangent space to
$(A,v)\in {\widetilde {O}}$
. The Zariski tangent space to
![]() $O$
at A is
$O$
at A is
![]() $[A,\mathfrak {g} (V)]$
. Denote by
$[A,\mathfrak {g} (V)]$
. Denote by
![]() $A_\lambda $
the operator
$A_\lambda $
the operator
![]() $A+\lambda \omega \phi _v$
in the unitary case,
$A+\lambda \omega \phi _v$
in the unitary case,
![]() $A+\lambda \phi _v$
in the symplectic case, or
$A+\lambda \phi _v$
in the symplectic case, or
![]() $A + \lambda (A \phi _v + \phi _v A)$
in the orthogonal case. Since
$A + \lambda (A \phi _v + \phi _v A)$
in the orthogonal case. Since
![]() $A_\lambda $
is contained in
$A_\lambda $
is contained in
![]() $O$
for
$O$
for
![]() $\lambda $
small enough (as
$\lambda $
small enough (as
![]() $\eta _{\lambda }$
keeps A inside
$\eta _{\lambda }$
keeps A inside
![]() $P_i(g)$
, in which
$P_i(g)$
, in which
![]() $O$
is open), we get that
$O$
is open), we get that
![]() $\phi _v\in [A,\mathfrak {g} (V)]$
(or
$\phi _v\in [A,\mathfrak {g} (V)]$
(or
![]() $A\phi _v + \phi _v A \in [A, \mathfrak {g}(V)]$
in the orthogonal case).▪
$A\phi _v + \phi _v A \in [A, \mathfrak {g}(V)]$
in the orthogonal case).▪
Theorem 8.3 Unless we are in the case
![]() $\mathfrak {g} = \mathfrak {o}$
and the characteristic polynomial of A is equal to
$\mathfrak {g} = \mathfrak {o}$
and the characteristic polynomial of A is equal to
![]() $x^n$
, we have
$x^n$
, we have
![]() $Q_A {\subseteq } R_A$
. In this case, we still have
$Q_A {\subseteq } R_A$
. In this case, we still have
![]() $\langle A^{k}v, v\rangle =0$
for any
$\langle A^{k}v, v\rangle =0$
for any
![]() $v\in Q_A$
and
$v\in Q_A$
and
![]() $k\geq 1$
.
$k\geq 1$
.
Proof For the unitary and symplectic cases: Assume that
![]() $\phi _v= [A,B]$
, for some
$\phi _v= [A,B]$
, for some
![]() $B \in G$
. Then
$B \in G$
. Then
For the orthogonal case: Assume that
![]() $A\phi _v + \phi _v A = [A,B]$
, for some
$A\phi _v + \phi _v A = [A,B]$
, for some
![]() $B \in G$
. Then
$B \in G$
. Then
 $$ \begin{align*} \begin{split} {\operatorname{tr}} A^k A\phi_v & ={\operatorname{tr}} A^k \phi_v A = \frac{{\operatorname{tr}} (A^{k+1}\phi_v + A^k \phi_v A)}{2} = \frac{{\operatorname{tr}} A^{k}(AB - BA)}{2}=\frac{{\operatorname{tr}}[A, A^{k+1}B]}{2}\\ &=0. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} {\operatorname{tr}} A^k A\phi_v & ={\operatorname{tr}} A^k \phi_v A = \frac{{\operatorname{tr}} (A^{k+1}\phi_v + A^k \phi_v A)}{2} = \frac{{\operatorname{tr}} A^{k}(AB - BA)}{2}=\frac{{\operatorname{tr}}[A, A^{k+1}B]}{2}\\ &=0. \end{split} \end{align*} $$
Now,
![]() ${\operatorname {tr}} A^k A\phi _v=\langle A^{k+1}v, v\rangle $
, so we know for any
${\operatorname {tr}} A^k A\phi _v=\langle A^{k+1}v, v\rangle $
, so we know for any
![]() $k\geq 1$
that
$k\geq 1$
that
![]() $\langle A^{k}v, v\rangle =0$
. If the characteristic polynomial g (which is a power of an irreducible polynomial) is not a power of x, then there is a polynomial
$\langle A^{k}v, v\rangle =0$
. If the characteristic polynomial g (which is a power of an irreducible polynomial) is not a power of x, then there is a polynomial
![]() $h(A)$
s.t.
$h(A)$
s.t.
![]() $Ah(A) = \operatorname {Id}$
. This implies that
$Ah(A) = \operatorname {Id}$
. This implies that
![]() $\langle v, v\rangle =\langle Ah(A)v, v\rangle = 0$
, and so
$\langle v, v\rangle =\langle Ah(A)v, v\rangle = 0$
, and so
![]() $v\in R_A$
.▪
$v\in R_A$
.▪
Notation 8.4 Let
![]() $A \in \mathfrak {g}$
. We denote by
$A \in \mathfrak {g}$
. We denote by
![]() $C_A$
the stabilizer of A in G and by
$C_A$
the stabilizer of A in G and by
![]() ${\widetilde {C}}_A$
the stabilizer of A in
${\widetilde {C}}_A$
the stabilizer of A in
![]() ${\widetilde {G}}$
.
${\widetilde {G}}$
.
Lemma 8.5 For any
![]() $A\in \mathfrak {g}$
,
$A\in \mathfrak {g}$
,
![]() ${\widetilde {C}}_A\neq C_A$
.
${\widetilde {C}}_A\neq C_A$
.
Proof We give here the proof for all cases except
![]() $G=SO$
. The proof for
$G=SO$
. The proof for
![]() $G=SO$
is given in Appendix B. By [Reference Mœglin, Vignéras and Waldspurger10, Chapter 4, Proposition 1.2], There exists an
$G=SO$
is given in Appendix B. By [Reference Mœglin, Vignéras and Waldspurger10, Chapter 4, Proposition 1.2], There exists an
![]() ${\mathbb F}$
-linear map
${\mathbb F}$
-linear map
![]() $T:V\to V$
which satisfies
$T:V\to V$
which satisfies
![]() $TAT^{-1} = -A$
, such that, for any
$TAT^{-1} = -A$
, such that, for any
![]() $u,v\in V$
, we have that
$u,v\in V$
, we have that
![]() $\langle Tu, Tv\rangle = \langle v, u\rangle$
(this condition implies that
$\langle Tu, Tv\rangle = \langle v, u\rangle$
(this condition implies that
![]() $s\lambda u = \overline {\lambda u}$
). Consider
$s\lambda u = \overline {\lambda u}$
). Consider
![]() $s=(T,-1)$
as an element of
$s=(T,-1)$
as an element of
![]() ${\widetilde {G}}$
. Then
${\widetilde {G}}$
. Then
![]() $s.A= -TAT^{-1} = A$
. Thus,
$s.A= -TAT^{-1} = A$
. Thus,
![]() $s\in {\widetilde {C}}(A)\setminus C_A$
.▪
$s\in {\widetilde {C}}(A)\setminus C_A$
.▪
Thus, the
![]() ${\widetilde {G}}$
-orbit of A is equal to its G-orbit. It is known that
${\widetilde {G}}$
-orbit of A is equal to its G-orbit. It is known that
![]() $C_A$
is unimodular, and hence
$C_A$
is unimodular, and hence
![]() ${\widetilde {C}}_A$
is also unimodular. Claim 7.2 follows now from Frobenius descent (Theorem 2.7), Proposition 8.2, and the following proposition.
${\widetilde {C}}_A$
is also unimodular. Claim 7.2 follows now from Frobenius descent (Theorem 2.7), Proposition 8.2, and the following proposition.
Proposition 8.6 Let
![]() $A \in \mathfrak {g}$
. Let
$A \in \mathfrak {g}$
. Let
![]() $\eta \in {\mathcal S}^*(V)^{C_A}$
. Suppose that both
$\eta \in {\mathcal S}^*(V)^{C_A}$
. Suppose that both
![]() $\eta $
and
$\eta $
and
![]() ${\mathcal {F}}_{V}(\eta )$
are supported in
${\mathcal {F}}_{V}(\eta )$
are supported in
![]() $Q_A$
. Then
$Q_A$
. Then
![]() $\eta \in {\mathcal S}^*(V)^{{\widetilde {C}}_A}$
.
$\eta \in {\mathcal S}^*(V)^{{\widetilde {C}}_A}$
.
Definition 8.7 Call an element
![]() $A\in \mathfrak {g}$
“nice” if the previous proposition holds for A. Namely, A is “nice” if any distribution
$A\in \mathfrak {g}$
“nice” if the previous proposition holds for A. Namely, A is “nice” if any distribution
![]() $\eta \in {\mathcal S}^*(V)^{C_A}$
such that both
$\eta \in {\mathcal S}^*(V)^{C_A}$
such that both
![]() $\eta $
and
$\eta $
and
![]() ${\mathcal {F}}(\eta )$
are supported in
${\mathcal {F}}(\eta )$
are supported in
![]() $Q_A$
is also
$Q_A$
is also
![]() ${\widetilde {C}}_A$
-invariant.
${\widetilde {C}}_A$
-invariant.
Lemma 8.8 Let
![]() $A_1 \in \mathfrak {g}(V_1)$
and
$A_1 \in \mathfrak {g}(V_1)$
and
![]() $A_2 \in \mathfrak {g}(V_2)$
be nice. Then
$A_2 \in \mathfrak {g}(V_2)$
be nice. Then
![]() $A_1 \oplus A_2 \in \mathfrak {g}(V_1\oplus V_2)$
is nice.
$A_1 \oplus A_2 \in \mathfrak {g}(V_1\oplus V_2)$
is nice.
Proof See the proof of [Reference Aizenbud, Gourevitch, Rallis and Schiffmann3, Lemma 6.3].▪
8.2 A “simple” operator is nice
Using the classification of Proposition 2.15, we need to check that simple nonsplit, simple even nilpotent, and simple odd nilpotent blocks are nice (recall that we assumed the characteristic polynomial of our original operator to be a power of an irreducible polynomial, and thus we need not check simple split operators). Let A be a block of one of these types. Let
![]() $s = (T, -1)$
be an element of
$s = (T, -1)$
be an element of
![]() ${\widetilde {C}}_A$
with
${\widetilde {C}}_A$
with
![]() $\chi (s)=-1$
. We have
$\chi (s)=-1$
. We have
![]() $A = s.A = -TAT^{-1}$
, and so
$A = s.A = -TAT^{-1}$
, and so
![]() $TA = -AT$
. We need to prove the following claim for each of the possible block types.
$TA = -AT$
. We need to prove the following claim for each of the possible block types.
Claim 8.9 Let
![]() $\xi $
be a
$\xi $
be a
![]() $C_A$
-invariant distribution on V, such that both
$C_A$
-invariant distribution on V, such that both
![]() $\xi $
and
$\xi $
and
![]() ${\mathcal {F}}(\xi )$
are supported on
${\mathcal {F}}(\xi )$
are supported on
![]() $Q_A$
. Then
$Q_A$
. Then
![]() $\xi $
is also s-invariant.
$\xi $
is also s-invariant.
We shall prove this claim in the following subsections. This claim implies Claim 7.2.
8.2.1 Simple nonsplit blocks
Assume that A is a simple nonsplit block with minimal polynomial
![]() $f^d$
, f irreducible, and
$f^d$
, f irreducible, and
![]() $f^*=\pm f$
. If we are in the case
$f^*=\pm f$
. If we are in the case
![]() $\mathfrak {g} = \mathfrak {o}$
, assume also that
$\mathfrak {g} = \mathfrak {o}$
, assume also that
![]() $f(x)\neq x$
. We know by Proposition 8.3 that
$f(x)\neq x$
. We know by Proposition 8.3 that
![]() $Q_A{\subseteq } R_A$
. Consider the self-dual increasing filtration
$Q_A{\subseteq } R_A$
. Consider the self-dual increasing filtration
![]() $V^i=\ker f(A)^i$
. One can easily see that
$V^i=\ker f(A)^i$
. One can easily see that
![]() $R_A=V^{\lfloor {d/2}\rfloor }$
. The fact that
$R_A=V^{\lfloor {d/2}\rfloor }$
. The fact that
![]() ${\mathcal {F}}(\xi )$
is supported on
${\mathcal {F}}(\xi )$
is supported on
![]() $V^{\lfloor {d/2}\rfloor }$
means that
$V^{\lfloor {d/2}\rfloor }$
means that
![]() $\xi $
is invariant to shifts by
$\xi $
is invariant to shifts by
![]() $(V^{\lfloor {d/2}\rfloor })^{\perp }=V^{\lceil {d/2}\rceil }$
. Now, consider two cases:
$(V^{\lfloor {d/2}\rfloor })^{\perp }=V^{\lceil {d/2}\rceil }$
. Now, consider two cases:
-
(1) d is odd. Then
 $V^{\lfloor {d/2}\rfloor }\subsetneq V^{\lceil {d/2}\rceil }$
. Choosing a vector
$V^{\lfloor {d/2}\rfloor }\subsetneq V^{\lceil {d/2}\rceil }$
. Choosing a vector
 $v\in V^{\lceil {d/2}\rceil }\setminus V^{\lfloor {d/2}\rfloor }$
, we get that
$v\in V^{\lceil {d/2}\rceil }\setminus V^{\lfloor {d/2}\rfloor }$
, we get that
 $\xi $
is the same as
$\xi $
is the same as
 $\xi $
shifted by v, and that it is supported on
$\xi $
shifted by v, and that it is supported on
 $V^{\lfloor {d/2}\rfloor }\cap (v+V^{\lfloor {d/2}\rfloor })=\emptyset $
, and thus
$V^{\lfloor {d/2}\rfloor }\cap (v+V^{\lfloor {d/2}\rfloor })=\emptyset $
, and thus
 $\xi =0$
.
$\xi =0$
. -
(2) d is even. Then
 $V^{\lfloor {d/2}\rfloor }= V^{\lceil {d/2}\rceil }=V^{d/2}$
. Thus,
$V^{\lfloor {d/2}\rfloor }= V^{\lceil {d/2}\rceil }=V^{d/2}$
. Thus,
 $\xi $
is the extension by 0 of
$\xi $
is the extension by 0 of
 $\xi |_{V^{d/2}}$
, which is a shift invariant distribution on
$\xi |_{V^{d/2}}$
, which is a shift invariant distribution on
 $V^{d/2}$
. Thus, it is a multiple of the Lebesgue measure on
$V^{d/2}$
. Thus, it is a multiple of the Lebesgue measure on
 $V^{d/2}$
. So it is left to check that if the Lebesgue measure
$V^{d/2}$
. So it is left to check that if the Lebesgue measure
 $\zeta $
on
$\zeta $
on
 $V^{d/2}$
is
$V^{d/2}$
is
 $C_A$
invariant it is also s-invariant. For this, first check that
$C_A$
invariant it is also s-invariant. For this, first check that
 $V^{d/2}$
is T-invariant (and so s invariant):
$V^{d/2}$
is T-invariant (and so s invariant):  $$ \begin{align*} \begin{split} TV^{d/2} &=Tf(A)^{d/2}V= \bar{f}(TAT^{-1})^{d/2}TV = \bar{f}(-A)^{d/2}V = f(A)^{d/2}V=V^{d/2}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} TV^{d/2} &=Tf(A)^{d/2}V= \bar{f}(TAT^{-1})^{d/2}TV = \bar{f}(-A)^{d/2}V = f(A)^{d/2}V=V^{d/2}. \end{split} \end{align*} $$
So s multiplies
 $\zeta $
by a constant c, which is positive, because s preserves the positivity of the Lebesgue measure. Since
$\zeta $
by a constant c, which is positive, because s preserves the positivity of the Lebesgue measure. Since
 $s^2\in C_A$
, we have by assumption
$s^2\in C_A$
, we have by assumption
 $s^2\zeta =\zeta $
. So unless
$s^2\zeta =\zeta $
. So unless
 $\zeta =0$
,
$\zeta =0$
,
 $c^2=1$
, hence by positivity
$c^2=1$
, hence by positivity
 $c=1$
, and we are done.
$c=1$
, and we are done.
8.2.2 Simple nonsplit nilpotent blocks in the orthogonal case
Note that a simple nonsplit nilpotent block is such that V has a basis of the form
![]() $e, Ae, \dots , A^{d-1}e$
, the minimal polynomial of A is equal to
$e, Ae, \dots , A^{d-1}e$
, the minimal polynomial of A is equal to
![]() $x^d$
, and for some nonzero constant
$x^d$
, and for some nonzero constant
![]() $c\in {\mathbb F}$
,
$c\in {\mathbb F}$
,
 $$ \begin{align*}\langle A^i e, A^j e\rangle = \begin{cases} (-1)^j c, & i + j = d-1,\\ 0, & \mathrm{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}\langle A^i e, A^j e\rangle = \begin{cases} (-1)^j c, & i + j = d-1,\\ 0, & \mathrm{otherwise.} \end{cases} \end{align*} $$
Note that this implies that d must be odd. Let A be such a block. Denote
 $$ \begin{align*} V_1:= & {\operatorname{Span}}(e, \dots, A^{(d-3)/{2}}e),\\ V_2:= & {\operatorname{Span}}(A^{(d-1)/{2}}e),\\ V_3:= & A^{(d+1)/{2}}V = {\operatorname{Span}}(A^{(d+1)/{2}}e, \dots, A^{d-1}e). \end{align*} $$
$$ \begin{align*} V_1:= & {\operatorname{Span}}(e, \dots, A^{(d-3)/{2}}e),\\ V_2:= & {\operatorname{Span}}(A^{(d-1)/{2}}e),\\ V_3:= & A^{(d+1)/{2}}V = {\operatorname{Span}}(A^{(d+1)/{2}}e, \dots, A^{d-1}e). \end{align*} $$
Then, by Theorem 8.3,
![]() $Q_A{\subseteq } V_2\oplus V_3$
. So
$Q_A{\subseteq } V_2\oplus V_3$
. So
![]() $\xi $
is supported on
$\xi $
is supported on
![]() $V_2\oplus V_3$
, and is invariant to shifts by
$V_2\oplus V_3$
, and is invariant to shifts by
![]() $(V_2\oplus V_3)^\perp = V_3$
. So it is of the form
$(V_2\oplus V_3)^\perp = V_3$
. So it is of the form
![]() $\delta _1 \otimes R \otimes dv_3$
, where
$\delta _1 \otimes R \otimes dv_3$
, where
![]() $dv_3$
is the Lebesgue measure on
$dv_3$
is the Lebesgue measure on
![]() $V_3$
,
$V_3$
,
![]() $\delta _1$
is the Dirac measure at
$\delta _1$
is the Dirac measure at
![]() $0$
on
$0$
on
![]() $V_1$
, and R is some distribution on
$V_1$
, and R is some distribution on
![]() $V_2$
. Since it is enough to prove our claim for any valid choice of
$V_2$
. Since it is enough to prove our claim for any valid choice of
![]() $s = (T, -1)\in {\widetilde {C}}_A$
, we may simply take
$s = (T, -1)\in {\widetilde {C}}_A$
, we may simply take
![]() $T(A^i e) = (-1)^{(d+1) / 2 + i} A^i e$
. Then s acts on V by
$T(A^i e) = (-1)^{(d+1) / 2 + i} A^i e$
. Then s acts on V by
![]() $A^i e\mapsto (-1)^{(d-1) / 2 + i} A^i e$
. The spaces
$A^i e\mapsto (-1)^{(d-1) / 2 + i} A^i e$
. The spaces
![]() $V_1, V_2, V_3$
are s invariant, and s acts on
$V_1, V_2, V_3$
are s invariant, and s acts on
![]() $V_2$
by identity. It is also clear that
$V_2$
by identity. It is also clear that
![]() $dv_3, \delta _1$
are s-invariant. Thus,
$dv_3, \delta _1$
are s-invariant. Thus,
![]() $\xi $
is s invariant, and we are done.
$\xi $
is s invariant, and we are done.
8.2.3 Simple even nilpotent blocks
Let
![]() $A\in \mathfrak {o}$
be a simple even nilpotent block. Denote
$A\in \mathfrak {o}$
be a simple even nilpotent block. Denote
and
Denote also
and
Let
![]() $P:V\to V$
be defined by
$P:V\to V$
be defined by
![]() $P A^i e = A^i f, P A^i f = A^i e$
. So
$P A^i e = A^i f, P A^i f = A^i e$
. So
![]() $PA = AP$
. For any two vectors
$PA = AP$
. For any two vectors
![]() $u,w\in V$
, define the linear operator
$u,w\in V$
, define the linear operator
![]() $\phi _{u,w}v := \langle v, w\rangle u$
. For any
$\phi _{u,w}v := \langle v, w\rangle u$
. For any
![]() $X\in \operatorname {End}(V)$
, denote by
$X\in \operatorname {End}(V)$
, denote by
![]() $X|_E$
the linear operator from E to itself which sends
$X|_E$
the linear operator from E to itself which sends
![]() $v\in E$
to
$v\in E$
to
![]() $u_E$
, where
$u_E$
, where
![]() $Xv = u_E + u_F$
and we have
$Xv = u_E + u_F$
and we have
![]() $u_E\in E, u_F\in F$
. Let
$u_E\in E, u_F\in F$
. Let
![]() $v\in Q_A$
. By definition, we have
$v\in Q_A$
. By definition, we have
![]() $A\phi _{v, v} + \phi _{v, v}A = [A, B]$
for some
$A\phi _{v, v} + \phi _{v, v}A = [A, B]$
for some
![]() $B\in \mathfrak {g}$
. We have
$B\in \mathfrak {g}$
. We have
 $$ \begin{align*} (P(A\phi_{v, v} + \phi_{v, v}A))|_E =& (P[A, B])|_E = (PAB - PBA)|_E = (APB - PBA)|_E \\ =& [A|_E, (PB)|_E]. \end{align*} $$
$$ \begin{align*} (P(A\phi_{v, v} + \phi_{v, v}A))|_E =& (P[A, B])|_E = (PAB - PBA)|_E = (APB - PBA)|_E \\ =& [A|_E, (PB)|_E]. \end{align*} $$
The last equation following from the fact that A preserves E and F. From this, it follows that, for any
![]() $k\geq 0$
,
$k\geq 0$
,
 $$ \begin{align*} {\operatorname{tr}}((P(A\phi_{v, v} + \phi_{v, v}A)A^k)|_E) = &{\operatorname{tr}}([A|_E, (PB)|_E] (A|_E)^k) \\ =& {\operatorname{tr}}([A|_E, (PB)|_E(A|_E)^k]) = 0. \end{align*} $$
$$ \begin{align*} {\operatorname{tr}}((P(A\phi_{v, v} + \phi_{v, v}A)A^k)|_E) = &{\operatorname{tr}}([A|_E, (PB)|_E] (A|_E)^k) \\ =& {\operatorname{tr}}([A|_E, (PB)|_E(A|_E)^k]) = 0. \end{align*} $$
However,
 $$ \begin{align*} {\operatorname{tr}}((PA\phi_{v, v}A^k)|_E) = &{\operatorname{tr}}((AP\phi_{v, v}A^k)|_E)= {\operatorname{tr}}(A|_E(P\phi_{v,v}A^k)|_E) \\=& {\operatorname{tr}}((P\phi_{v,v}A^k)|_E A|_E) = {\operatorname{tr}}((P\phi_{v, v}A^{k+1})|_E). \end{align*} $$
$$ \begin{align*} {\operatorname{tr}}((PA\phi_{v, v}A^k)|_E) = &{\operatorname{tr}}((AP\phi_{v, v}A^k)|_E)= {\operatorname{tr}}(A|_E(P\phi_{v,v}A^k)|_E) \\=& {\operatorname{tr}}((P\phi_{v,v}A^k)|_E A|_E) = {\operatorname{tr}}((P\phi_{v, v}A^{k+1})|_E). \end{align*} $$
So this expression is equal to half of the left-hand side of the previous equation, and so
However,
where
![]() $v = v_E + v_F$
,
$v = v_E + v_F$
,
![]() $v_E\in E, v_F\in F$
. Thus, for any
$v_E\in E, v_F\in F$
. Thus, for any
![]() $k\geq 1$
, we have
$k\geq 1$
, we have
![]() $\langle A^k Pv_F, v_F\rangle = 0$
. Similarly,
$\langle A^k Pv_F, v_F\rangle = 0$
. Similarly,
![]() $\langle A^k Pv_E, v_E\rangle = 0$
. This implies
$\langle A^k Pv_E, v_E\rangle = 0$
. This implies
![]() $v\in E_2\oplus F_2$
. Thus, if
$v\in E_2\oplus F_2$
. Thus, if
![]() $\xi $
is a distribution as in the statement of Claim 8.9, it must be supported on
$\xi $
is a distribution as in the statement of Claim 8.9, it must be supported on
![]() $E_2\oplus F_2$
and invariant to translations by
$E_2\oplus F_2$
and invariant to translations by
![]() $(E_2\oplus F_2)^\perp = E_2\oplus F_2$
. Thus, it is equal to a multiple of the Lebesgue measure on
$(E_2\oplus F_2)^\perp = E_2\oplus F_2$
. Thus, it is equal to a multiple of the Lebesgue measure on
![]() $E_2\oplus F_2$
. As it is enough to prove the claim for any specific choice of
$E_2\oplus F_2$
. As it is enough to prove the claim for any specific choice of
![]() $s=(T, -1)\in {\widetilde {C}}_A$
, we can choose T to be
$s=(T, -1)\in {\widetilde {C}}_A$
, we can choose T to be
For this choice, s acts by
![]() $A^i e\mapsto (-1)^{i+1} A^i e, A^i f \mapsto (-1)^i A^i f$
, and so fixes
$A^i e\mapsto (-1)^{i+1} A^i e, A^i f \mapsto (-1)^i A^i f$
, and so fixes
![]() $\xi $
as desired.
$\xi $
as desired.
8.2.4 Simple odd nilpotent blocks
Let
![]() $A\in \mathfrak {sp}$
be a simple odd nilpotent block. Denote
$A\in \mathfrak {sp}$
be a simple odd nilpotent block. Denote
and
Denote also
 $$ \begin{align*} E_1:=&{\operatorname{Span}}(e, Ae, \dots, A^{\frac{d-3}{2}}e),\\ E_2:=&{\operatorname{Span}}(A^{\frac{d-1}{2}}e),\\ E_3:=&{\operatorname{Span}}(A^{\frac{d+1}{2}}e, \dots, A^{d-1}e), \end{align*} $$
$$ \begin{align*} E_1:=&{\operatorname{Span}}(e, Ae, \dots, A^{\frac{d-3}{2}}e),\\ E_2:=&{\operatorname{Span}}(A^{\frac{d-1}{2}}e),\\ E_3:=&{\operatorname{Span}}(A^{\frac{d+1}{2}}e, \dots, A^{d-1}e), \end{align*} $$
and
 $$ \begin{align*} F_1:=&{\operatorname{Span}}(f, Af, \dots, A^{\frac{d-3}{2}}f),\\ F_2:=&{\operatorname{Span}}(A^{\frac{d-1}{2}}f),\\ F_3:=&{\operatorname{Span}}(A^{\frac{d+1}{2}}f, \dots, A^{d-1}f). \end{align*} $$
$$ \begin{align*} F_1:=&{\operatorname{Span}}(f, Af, \dots, A^{\frac{d-3}{2}}f),\\ F_2:=&{\operatorname{Span}}(A^{\frac{d-1}{2}}f),\\ F_3:=&{\operatorname{Span}}(A^{\frac{d+1}{2}}f, \dots, A^{d-1}f). \end{align*} $$
The following is done similarly to the previous case, of simple even nilpotent blocks. Let
![]() $P:V\to V$
be defined by
$P:V\to V$
be defined by
![]() $P A^i e = A^i f, P A^i f = A^i e$
. So
$P A^i e = A^i f, P A^i f = A^i e$
. So
![]() $PA = AP$
. For any two vectors
$PA = AP$
. For any two vectors
![]() $u,w\in V$
, define the linear operator
$u,w\in V$
, define the linear operator
![]() $\phi _{u,w}v := \langle v, w\rangle u$
. For any
$\phi _{u,w}v := \langle v, w\rangle u$
. For any
![]() $X\in \operatorname {End}(V)$
, denote by
$X\in \operatorname {End}(V)$
, denote by
![]() $X|_E$
the linear operator from E to itself which sends
$X|_E$
the linear operator from E to itself which sends
![]() $v\in E$
to
$v\in E$
to
![]() $u_E$
, where
$u_E$
, where
![]() $Xv = u_E + u_F$
and we have
$Xv = u_E + u_F$
and we have
![]() $u_E\in E, u_F\in F$
. Let
$u_E\in E, u_F\in F$
. Let
![]() $v\in Q_A$
. By definition, we have
$v\in Q_A$
. By definition, we have
![]() $\phi _{v, v}= [A, B]$
for some
$\phi _{v, v}= [A, B]$
for some
![]() $B\in \mathfrak {g}$
. We have
$B\in \mathfrak {g}$
. We have
 $$ \begin{align*} (P\phi_{v, v})|_E =& (P[A, B])|_E = (PAB - PBA)|_E = (APB - PBA)|_E \\ =& [A|_E, (PB)|_E]. \end{align*} $$
$$ \begin{align*} (P\phi_{v, v})|_E =& (P[A, B])|_E = (PAB - PBA)|_E = (APB - PBA)|_E \\ =& [A|_E, (PB)|_E]. \end{align*} $$
From this, it follows that, for any
![]() $k\geq 0$
,
$k\geq 0$
,
 $$ \begin{align*} {\operatorname{tr}}((P\phi_{v, v}A^k)|_E) = &{\operatorname{tr}}([A|_E, (PB)|_E] (A|_E)^k) \\ =& {\operatorname{tr}}([A|_E, (PB)|_E(A|_E)^k]) = 0. \end{align*} $$
$$ \begin{align*} {\operatorname{tr}}((P\phi_{v, v}A^k)|_E) = &{\operatorname{tr}}([A|_E, (PB)|_E] (A|_E)^k) \\ =& {\operatorname{tr}}([A|_E, (PB)|_E(A|_E)^k]) = 0. \end{align*} $$
However,
where
![]() $v = v_E + v_F$
,
$v = v_E + v_F$
,
![]() $v_E\in E, v_F\in F$
. Thus, for any
$v_E\in E, v_F\in F$
. Thus, for any
![]() $k\geq 0$
, we have
$k\geq 0$
, we have
![]() $\langle A^k Pv_F, v_F\rangle = 0$
. Similarly,
$\langle A^k Pv_F, v_F\rangle = 0$
. Similarly,
![]() $\langle A^k Pv_E, v_E\rangle = 0$
. This implies
$\langle A^k Pv_E, v_E\rangle = 0$
. This implies
![]() $v\in E_3\oplus F_3$
. Thus, if
$v\in E_3\oplus F_3$
. Thus, if
![]() $\xi $
is an equivariant distribution as in the statement of Claim 8.9, it must be supported on
$\xi $
is an equivariant distribution as in the statement of Claim 8.9, it must be supported on
![]() $E_3\oplus F_3$
and invariant to translations by
$E_3\oplus F_3$
and invariant to translations by
![]() $(E_3\oplus F_3)^\perp = E_2\oplus E_3\oplus F_2\oplus F_3$
. This clearly implies that
$(E_3\oplus F_3)^\perp = E_2\oplus E_3\oplus F_2\oplus F_3$
. This clearly implies that
![]() $\xi = 0$
.
$\xi = 0$
.
A Conjugacy classes and “simple” elements in the orthogonal and unitary groups
Our goal in this appendix is to prove Proposition 2.15. We will focus on the classification of G-conjugacy classes inside
![]() $\mathfrak {g}$
, although most of the work, if not all of it, applies also for conjugacy classes in
$\mathfrak {g}$
, although most of the work, if not all of it, applies also for conjugacy classes in
![]() $G(V)$
. The classification will be in three parts. The first is, using Lemma 2.13, to separate the different nonrelated eigenvalues, the second is to separate the different sizes of rational (or Jordan) blocks, and the third is to separate blocks of the same size one from the other.
$G(V)$
. The classification will be in three parts. The first is, using Lemma 2.13, to separate the different nonrelated eigenvalues, the second is to separate the different sizes of rational (or Jordan) blocks, and the third is to separate blocks of the same size one from the other.
A.1 Separating nonrelated eigenvalues
Recall Definition 2.11.
Lemma 2.13 has the following corollary, using also Theorem 2.10.
Corollary A.1 Any
![]() $A\in \mathfrak {g}$
splits to a direct orthogonal sum of block of two types:
$A\in \mathfrak {g}$
splits to a direct orthogonal sum of block of two types:
-
(A) simple split blocks;
-
(B) blocks of which the characteristic polynomial is
 $f^d$
, and f is irreducible and satisfies
$f^d$
, and f is irreducible and satisfies
 $f^*=\pm f$
.
$f^*=\pm f$
.
Now, we continue with the classification of blocks of Type (B).
A.2 Classifying blocks of Type (B)
Let
![]() $A\in \mathfrak {g}(V)$
be a block of Type (B), with minimal polynomial
$A\in \mathfrak {g}(V)$
be a block of Type (B), with minimal polynomial
![]() $f^d$
, f irreducible and satisfying
$f^d$
, f irreducible and satisfying
![]() $f=\pm f^*$
.
$f=\pm f^*$
.
Definition A.2 An operator
![]() $X\in \mathfrak {g}(W)$
(for some W) which is of Type (X) will be called homogeneous if, for any
$X\in \mathfrak {g}(W)$
(for some W) which is of Type (X) will be called homogeneous if, for any
![]() $0\leq j\leq d$
, we have
$0\leq j\leq d$
, we have
![]() $f(X)^j V=\ker f(X)^{d-j}$
. That is equivalent to saying that the rational canonical form of X consists of blocks all of the same size.
$f(X)^j V=\ker f(X)^{d-j}$
. That is equivalent to saying that the rational canonical form of X consists of blocks all of the same size.
We dedicate this subsection to proving the following proposition.
Proposition A.3
V can be decomposed as an orthogonal sum
![]() $V=\bigoplus _{i=1}^d U_i$
, and accordingly
$V=\bigoplus _{i=1}^d U_i$
, and accordingly
![]() $A=\bigoplus _{i=1}^d A_i$
, such that each
$A=\bigoplus _{i=1}^d A_i$
, such that each
![]() $A_i$
is homogeneous.
$A_i$
is homogeneous.
Consider the decreasing filtration
![]() $f(A)^i V$
of V, and the increasing filtration
$f(A)^i V$
of V, and the increasing filtration
![]() $V_i=\ker f(A)^i$
. We have
$V_i=\ker f(A)^i$
. We have
![]() $f(A)^i V\subseteq V_{d-i}$
, and
$f(A)^i V\subseteq V_{d-i}$
, and
![]() $V_i^{\perp }=f(A)^i V$
. Let m be the minimal integer so that
$V_i^{\perp }=f(A)^i V$
. Let m be the minimal integer so that
![]() $V_m \subsetneq f(A)V$
. For any
$V_m \subsetneq f(A)V$
. For any
![]() $0\leq i\leq m-1$
, we have
$0\leq i\leq m-1$
, we have
![]() $f(A)^i V_m=V_{m-i}$
.
$f(A)^i V_m=V_{m-i}$
.
Lemma A.4 For any
![]() $0\leq i\leq d$
,
$0\leq i\leq d$
,
![]() $V_i^\perp = f(A)^i V$
.
$V_i^\perp = f(A)^i V$
.
Proof Obviously,
![]() $f(A)^i V {\subseteq } V_i^\perp $
. However,
$f(A)^i V {\subseteq } V_i^\perp $
. However,
Thus, we have
![]() $V_i^\perp = f(A)^i V$
.▪
$V_i^\perp = f(A)^i V$
.▪
Lemma A.5 The form B on V induces a nondegenerate pairing of
![]() $f(A)^i V_m / f(A)^{i+1} V_{m+1}$
with
$f(A)^i V_m / f(A)^{i+1} V_{m+1}$
with
![]() $f(A)^{m-i-1}V_m / f(A)^{m-i} V_{m+1}$
.
$f(A)^{m-i-1}V_m / f(A)^{m-i} V_{m+1}$
.
Proof Let
![]() $v\in f(A)^i V_m=V_{m-i}$
, and assume that
$v\in f(A)^i V_m=V_{m-i}$
, and assume that
![]() $v\perp f(A)^{m-i-1}V_m=V_{i+1}$
. Then
$v\perp f(A)^{m-i-1}V_m=V_{i+1}$
. Then
![]() $v\in V_{i+1}^{\perp }\cap V_{m-i}=f(A)^{i+1}V\cap V_{m-i}=f(A)^{i+1}V_{m+1}$
. The other direction is symmetric.▪
$v\in V_{i+1}^{\perp }\cap V_{m-i}=f(A)^{i+1}V\cap V_{m-i}=f(A)^{i+1}V_{m+1}$
. The other direction is symmetric.▪
Proof of Proposition A.3
One can naturally give
![]() $V_m / f(A)V_{m+1}$
the structure of a vector space over the field
$V_m / f(A)V_{m+1}$
the structure of a vector space over the field
![]() $L:={\mathbb K}[A] / f(A)$
. Choose
$L:={\mathbb K}[A] / f(A)$
. Choose
![]() $e_1,\dots , e_k \in V_m$
which are the lifts of a basis of
$e_1,\dots , e_k \in V_m$
which are the lifts of a basis of
![]() $V_m / f(A)V_{m+1}$
over L, and let
$V_m / f(A)V_{m+1}$
over L, and let
![]() $U_m:={\operatorname {Span}}(A^i e_j){\subseteq } V_m$
. We claim that, for any relation of the form
$U_m:={\operatorname {Span}}(A^i e_j){\subseteq } V_m$
. We claim that, for any relation of the form
![]() $h_1(A)e_1 + \cdots + h_k(A)e_k + f(A)^r v = 0$
, with
$h_1(A)e_1 + \cdots + h_k(A)e_k + f(A)^r v = 0$
, with
![]() $v\in V$
, all the polynomials
$v\in V$
, all the polynomials
![]() $h_i$
are divisible by
$h_i$
are divisible by
![]() $f(A)^{\min (m,r)}$
. To see this, assume otherwise, and rewrite this relation as
$f(A)^{\min (m,r)}$
. To see this, assume otherwise, and rewrite this relation as
![]() $f(A)^\ell (f(A)^{r-\ell }v + \sum _{i=1}^k \widetilde h_i(A)e_i) = 0$
, where at least one of the polynomials
$f(A)^\ell (f(A)^{r-\ell }v + \sum _{i=1}^k \widetilde h_i(A)e_i) = 0$
, where at least one of the polynomials
![]() $\widetilde {h}_i(A)$
is not divisible by
$\widetilde {h}_i(A)$
is not divisible by
![]() $f(A)$
. Since
$f(A)$
. Since
![]() $\ell < m$
, we have
$\ell < m$
, we have
![]() $\sum _{i=1}^k \widetilde h_i(A)e_i\in V_\ell + f(A)V = f(A)V$
, and thus
$\sum _{i=1}^k \widetilde h_i(A)e_i\in V_\ell + f(A)V = f(A)V$
, and thus
![]() $\sum _{i=1}^k \widetilde h_i(A)e_i$
is a nontrivial relation in
$\sum _{i=1}^k \widetilde h_i(A)e_i$
is a nontrivial relation in
![]() $V_m / f(A)V_{m+1}$
over L, which is a contradiction. From this claim, it follows that the map
$V_m / f(A)V_{m+1}$
over L, which is a contradiction. From this claim, it follows that the map
![]() $f(A)^i U_m/f(A)^{i+1} U_m \to f(A)^i V_m / f(A)^{i+1} V_{m+1}$
is an isomorphism. Thus, the form B on V induces a nondegenerate pairing of
$f(A)^i U_m/f(A)^{i+1} U_m \to f(A)^i V_m / f(A)^{i+1} V_{m+1}$
is an isomorphism. Thus, the form B on V induces a nondegenerate pairing of
![]() $f(A)^i U_m / f(A)^{i+1} U_{m+1}$
with
$f(A)^i U_m / f(A)^{i+1} U_{m+1}$
with
![]() $f(A)^{m-i-1} U_m / f(A)^{m-i} U_{m+1}$
. In particular, its restriction to
$f(A)^{m-i-1} U_m / f(A)^{m-i} U_{m+1}$
. In particular, its restriction to
![]() $U_m$
is nondegenerate. So
$U_m$
is nondegenerate. So
![]() $U_m$
splits as an A-invariant orthogonal direct summand of V. The restriction of A to
$U_m$
splits as an A-invariant orthogonal direct summand of V. The restriction of A to
![]() $U_m$
is a homogeneous block because
$U_m$
is a homogeneous block because
Because of the choice of m,
![]() $\dim U_m>0$
. Furthermore, on
$\dim U_m>0$
. Furthermore, on
![]() $V':=U_m^{\perp }$
, the minimal
$V':=U_m^{\perp }$
, the minimal
![]() $m'$
s.t.
$m'$
s.t.
![]() $V^{\prime }_{m'}\subsetneq f(A)V'$
is bigger than m. So, by induction, we are done.▪
$V^{\prime }_{m'}\subsetneq f(A)V'$
is bigger than m. So, by induction, we are done.▪
A.3 Decomposing homogeneous blocks to simple nonsplit blocks
Lemma A.6 Given a nonzero symmetric, Hermitian, or skew-Hermitian form on a vector space V, there is a non-isotropic vector.
Proof Assume that
![]() $\langle v, v\rangle =0$
holds for any V. Then
$\langle v, v\rangle =0$
holds for any V. Then
Thus, the form is skew-symmetric, which contradicts our assumptions.▪
Corollary A.7 Any homogeneous operator decomposes as the direct orthogonal sum of simple nonsplit blocks, unless it is in the
![]() $\mathfrak {o}$
case and its minimal polynomial is
$\mathfrak {o}$
case and its minimal polynomial is
![]() $x^d$
for some even d, or it is in the
$x^d$
for some even d, or it is in the
![]() $\mathfrak {sp}$
case and its minimal polynomial is
$\mathfrak {sp}$
case and its minimal polynomial is
![]() $x^d$
for some odd d. In these cases, it decomposes as the direct sum of simple even nilpotent blocks (resp. simple odd nilpotent blocks).
$x^d$
for some odd d. In these cases, it decomposes as the direct sum of simple even nilpotent blocks (resp. simple odd nilpotent blocks).
Proof Assume that we are neither in the symplectic case nor in the even nilpotent orthogonal case which was excluded. Define a nondegenerate sesquilinear form on
![]() $U:=V/f(A)V$
by
$U:=V/f(A)V$
by
![]() $\langle u,v\rangle_U:=\langle f(A)^{d-1}u,v\rangle_V$
. If we are in the unitary case, then it is either Hermitian or skew-Hermitian, depending on whether
$\langle u,v\rangle_U:=\langle f(A)^{d-1}u,v\rangle_V$
. If we are in the unitary case, then it is either Hermitian or skew-Hermitian, depending on whether
![]() $(f^{d-1})^*=f^{d-1}$
(
$(f^{d-1})^*=f^{d-1}$
(
![]() $f^{d-1}$
is of even degree), or
$f^{d-1}$
is of even degree), or
![]() $(f^{d-1})^*=-f^{d-1}$
(
$(f^{d-1})^*=-f^{d-1}$
(
![]() $f^{d-1}$
is of odd degree). If we are in the orthogonal case,
$f^{d-1}$
is of odd degree). If we are in the orthogonal case,
![]() $(f^{d-1})^*=f^{d-1}$
, and so this bilinear form is symmetric. So there is a nonisotopic vector in U, which means that there is a vector
$(f^{d-1})^*=f^{d-1}$
, and so this bilinear form is symmetric. So there is a nonisotopic vector in U, which means that there is a vector
![]() $v\in V$
such that
$v\in V$
such that
![]() $\langle f(A)^{d-1}v,v\rangle =\lambda \neq 0$
. Let
$\langle f(A)^{d-1}v,v\rangle =\lambda \neq 0$
. Let
![]() $V_0={\operatorname {Span}}(v, Av, A^2v,\dots )$
. It is an A-invariant space, to which the restriction of the form B is nondegenerate. It is also generated by one vector (v). By induction, we are done.
$V_0={\operatorname {Span}}(v, Av, A^2v,\dots )$
. It is an A-invariant space, to which the restriction of the form B is nondegenerate. It is also generated by one vector (v). By induction, we are done.
In the symplectic case which is not the case excluded, we have a similar proof. Again, define a bilinear form on
![]() $U:=V/f(A)V$
. If the minimal polynomial is
$U:=V/f(A)V$
. If the minimal polynomial is
![]() $x^d$
for d even, define as before
$x^d$
for d even, define as before
![]() $\langle u,v\rangle_U:=\langle A^{d-1}u,v\rangle$
, and it will be a symmetric form. Otherwise, A is invertible and we set
$\langle u,v\rangle_U:=\langle A^{d-1}u,v\rangle$
, and it will be a symmetric form. Otherwise, A is invertible and we set
![]() $\langle u,v\rangle_U:=\langle Af(A)^{d-1}u,v\rangle$
. Again this bilinear form is symmetric. The rest of the proof follows the same, with noticing that
$\langle u,v\rangle_U:=\langle Af(A)^{d-1}u,v\rangle$
. Again this bilinear form is symmetric. The rest of the proof follows the same, with noticing that
![]() $\langle Af(A)^{d-1}v,v\rangle\neq 0$
implies that
$\langle Af(A)^{d-1}v,v\rangle\neq 0$
implies that
![]() $V_0\cap V_0^\perp = 0$
for
$V_0\cap V_0^\perp = 0$
for
![]() $V_0={\operatorname {Span}}(v, Av, A^2v,\dots )$
.
$V_0={\operatorname {Span}}(v, Av, A^2v,\dots )$
.
In the orthogonal case, if the minimal polynomial is
![]() $x^d$
for d even (resp. the symplectic case and d odd), the bilinear form
$x^d$
for d even (resp. the symplectic case and d odd), the bilinear form
![]() $\langle u, v\rangle_U:=\langle A^{d-1}u, v\rangle$
on U is skew-symmetric. Take
$\langle u, v\rangle_U:=\langle A^{d-1}u, v\rangle$
on U is skew-symmetric. Take
![]() $u_1, u_2\in U$
s.t.
$u_1, u_2\in U$
s.t.
![]() $\langle u_1, u_2\rangle_U=1$
. Lift them to
$\langle u_1, u_2\rangle_U=1$
. Lift them to
![]() $v_1, v_2 \in V$
, and Take
$v_1, v_2 \in V$
, and Take
![]() $V_0 = {\operatorname {Span}}(v_1, Av_1, A^2v_1, \dots ) \oplus {\operatorname {Span}}(v_2, Av_2, A^2v_2, \dots )$
(note that this sum is indeed direct).
$V_0 = {\operatorname {Span}}(v_1, Av_1, A^2v_1, \dots ) \oplus {\operatorname {Span}}(v_2, Av_2, A^2v_2, \dots )$
(note that this sum is indeed direct).
![]() $V_0$
is A-invariant, and
$V_0$
is A-invariant, and
![]() $V_0^\perp \cap V_0=0$
. Now, we are left to show that
$V_0^\perp \cap V_0=0$
. Now, we are left to show that
![]() $V_0$
is a simple even nilpotent block (resp. simple odd nilpotent block). The first step is to show that we can alter the lifts of
$V_0$
is a simple even nilpotent block (resp. simple odd nilpotent block). The first step is to show that we can alter the lifts of
![]() $u_1, u_2$
to
$u_1, u_2$
to
![]() $v_1, v_2$
(from
$v_1, v_2$
(from
![]() $V_0 / AV_0$
to
$V_0 / AV_0$
to
![]() $V_0$
) such that
$V_0$
) such that
![]() $\langle A^j v_1, v_1\rangle = 0$
for all j. (We will show it for
$\langle A^j v_1, v_1\rangle = 0$
for all j. (We will show it for
![]() $v_1$
, but it is exactly the same for
$v_1$
, but it is exactly the same for
![]() $v_2$
.) For odd (resp. even) j, this holds automatically. We assume for the following that
$v_2$
.) For odd (resp. even) j, this holds automatically. We assume for the following that
![]() $v_2$
is any lift of
$v_2$
is any lift of
![]() $u_2$
(the important property is that
$u_2$
(the important property is that
![]() $\langle A^{d-1}v_1, v_2\rangle = 1$
). If m is the minimal integer such that
$\langle A^{d-1}v_1, v_2\rangle = 1$
). If m is the minimal integer such that
![]() $\langle A^{d-m}v_1, v_1\rangle\neq 0$
, we can add a multiple of
$\langle A^{d-m}v_1, v_1\rangle\neq 0$
, we can add a multiple of
![]() $A^{m-1}v_2$
to
$A^{m-1}v_2$
to
![]() $v_1$
to fix that, as
$v_1$
to fix that, as
 $$ \begin{align*} \begin{split} & \langle A^{d-m}(v_1 + \lambda A^{m-1}v_2), v_1 + \lambda A^{m-1}v_2\rangle \\ = & \langle A^{d-m}v_1, v_1\rangle + 2\lambda\langle A^{d-1}v_2, v_1\rangle - \lambda ^ 2\langle A^{d+m-2}v_2, v_2\rangle \\ = & \langle A^{d-m}v_1, v_1\rangle - 2\lambda, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} & \langle A^{d-m}(v_1 + \lambda A^{m-1}v_2), v_1 + \lambda A^{m-1}v_2\rangle \\ = & \langle A^{d-m}v_1, v_1\rangle + 2\lambda\langle A^{d-1}v_2, v_1\rangle - \lambda ^ 2\langle A^{d+m-2}v_2, v_2\rangle \\ = & \langle A^{d-m}v_1, v_1\rangle - 2\lambda, \end{split} \end{align*} $$
for any
![]() $i<m$
, and
$i<m$
, and
Notice that m must be even and
![]() $m\geq 2$
. So, by applying this consecutively, we may change the lift of
$m\geq 2$
. So, by applying this consecutively, we may change the lift of
![]() $v_1$
(and similarly
$v_1$
(and similarly
![]() $v_2$
) in the desired way (notice that indeed we changed it only by vectors in
$v_2$
) in the desired way (notice that indeed we changed it only by vectors in
![]() $AV_0$
). Now, all that is left is to again change
$AV_0$
). Now, all that is left is to again change
![]() $v_1, v_2$
so that
$v_1, v_2$
so that
![]() $\langle A^kv_1, v_2\rangle = 0$
for any
$\langle A^kv_1, v_2\rangle = 0$
for any
![]() $k < d - 1$
. For this, simply choose a vector
$k < d - 1$
. For this, simply choose a vector
![]() $\tilde {v}_2$
which is orthogonal to
$\tilde {v}_2$
which is orthogonal to
![]() $v_1, Av_1, A^2v_1, \dots , A^{d-2}v_1, v_2, Av_2, \dots , A^{d-1}v_2$
and such that
$v_1, Av_1, A^2v_1, \dots , A^{d-2}v_1, v_2, Av_2, \dots , A^{d-1}v_2$
and such that
![]() $\langle A^{d-1}v_1, v_2\rangle = 1$
. Note that the vector
$\langle A^{d-1}v_1, v_2\rangle = 1$
. Note that the vector
![]() $v_2 - \tilde {v}_2$
is perpendicular to the subspace
$v_2 - \tilde {v}_2$
is perpendicular to the subspace
![]() $V_2:={\operatorname {Span}}(v_2, Av_2, \dots , A^{d-1}v_2)$
, and so
$V_2:={\operatorname {Span}}(v_2, Av_2, \dots , A^{d-1}v_2)$
, and so
![]() $v_2 - \tilde {v}_2\in V_2^\perp = V_2$
. This implies that, for all
$v_2 - \tilde {v}_2\in V_2^\perp = V_2$
. This implies that, for all
![]() $k\geq 0$
,
$k\geq 0$
,
![]() $\langle A^k \tilde {v}_2, \tilde {v}_2\rangle = 0$
. Moreover,
$\langle A^k \tilde {v}_2, \tilde {v}_2\rangle = 0$
. Moreover,
![]() $v_2 - \tilde {v}_2$
is perpendicular to
$v_2 - \tilde {v}_2$
is perpendicular to
![]() $A^{d-1}V_0$
, and so
$A^{d-1}V_0$
, and so
![]() $v_2 - \tilde {v}_2\in AV_2$
. Thus, we can replace
$v_2 - \tilde {v}_2\in AV_2$
. Thus, we can replace
![]() $v_2$
with
$v_2$
with
![]() $\tilde {v}_2$
, and all of the needed conditions will be satisfied.▪
$\tilde {v}_2$
, and all of the needed conditions will be satisfied.▪
The above immediately implies Proposition 2.15.
B On the centralizers in
 $\widetilde {\operatorname {SO}}$
$\widetilde {\operatorname {SO}}$
In this appendix, we prove Theorem 8.5 for the case of
![]() $G = \operatorname {SO}(V)$
. We need to show that there exists an element
$G = \operatorname {SO}(V)$
. We need to show that there exists an element
![]() $T\in \operatorname {O}(V)$
such that
$T\in \operatorname {O}(V)$
such that
![]() $TAT^{-1} = -A$
and
$TAT^{-1} = -A$
and
![]() $\det T = (-1)^{\lfloor {\frac {n+1}{2}}\rfloor }$
. Assume the decomposition of Proposition 2.15. It is enough to prove Theorem 8.5 for each of the blocks, as then taking the direct sum of the elements
$\det T = (-1)^{\lfloor {\frac {n+1}{2}}\rfloor }$
. Assume the decomposition of Proposition 2.15. It is enough to prove Theorem 8.5 for each of the blocks, as then taking the direct sum of the elements
![]() $T_i$
found gives an element
$T_i$
found gives an element
![]() $T\in \operatorname {O}(V)$
with
$T\in \operatorname {O}(V)$
with
![]() $TAT^{-1} = -A$
. If all of the dimensions of the blocks
$TAT^{-1} = -A$
. If all of the dimensions of the blocks
![]() $n_i$
are even, then
$n_i$
are even, then
![]() $\det (\bigoplus T_i) = \prod \det T_i = (-1)^{\sum n_i / 2} = (-1) ^ {n / 2}$
. Otherwise, there is an odd block, and by replacing
$\det (\bigoplus T_i) = \prod \det T_i = (-1)^{\sum n_i / 2} = (-1) ^ {n / 2}$
. Otherwise, there is an odd block, and by replacing
![]() $T_i$
by
$T_i$
by
![]() $-T_i$
if needed, we can control the sign of the determinant to be as we wish. Now, we need to check each of the simple block types.
$-T_i$
if needed, we can control the sign of the determinant to be as we wish. Now, we need to check each of the simple block types.
B.1 Simple split blocks
We have
![]() $V = V'\oplus V^{\prime *}$
, with the natural symmetric bilinear form coming from the pairing.
$V = V'\oplus V^{\prime *}$
, with the natural symmetric bilinear form coming from the pairing.
 $A = \begin {bmatrix} A'&0\\0&-A^{\prime *} \end {bmatrix}$
. By the well-known theorem claiming that any square matrix (over any field and of any dimension) is conjugate to its transpose, there is an isomorphism
$A = \begin {bmatrix} A'&0\\0&-A^{\prime *} \end {bmatrix}$
. By the well-known theorem claiming that any square matrix (over any field and of any dimension) is conjugate to its transpose, there is an isomorphism
![]() $B: V^{\prime *}\to V'$
such that
$B: V^{\prime *}\to V'$
such that
![]() $BA^{\prime *}B^{-1} = A'$
. Taking
$BA^{\prime *}B^{-1} = A'$
. Taking
 $T = \begin {bmatrix} 0&B\\ (B^*)^{-1}&0\end {bmatrix}\in \operatorname {O}(V)$
, we get
$T = \begin {bmatrix} 0&B\\ (B^*)^{-1}&0\end {bmatrix}\in \operatorname {O}(V)$
, we get
 $$ \begin{align*} TAT^{-1} &= \begin{bmatrix} 0&B\\ (B^*)^{-1}&0\end{bmatrix} \begin{bmatrix} A'&0\\ 0&-A^{\prime *} \end{bmatrix}\begin{bmatrix} 0&B^*\\ B^{-1}&0\end{bmatrix} = \begin{bmatrix} 0&-BA^{\prime *}\\ (B^*)^{-1}A'&0\end{bmatrix} \begin{bmatrix} 0&B^*\\ B^{-1}&0\end{bmatrix} \\[6pt] &=\begin{bmatrix} -BA^{\prime *}B^{-1}&0\\ 0&(B^*)^{-1}A'B^*\end{bmatrix}= \begin{bmatrix} -A'&0\\ 0&A^{\prime *}\end{bmatrix} = -A. \end{align*} $$
$$ \begin{align*} TAT^{-1} &= \begin{bmatrix} 0&B\\ (B^*)^{-1}&0\end{bmatrix} \begin{bmatrix} A'&0\\ 0&-A^{\prime *} \end{bmatrix}\begin{bmatrix} 0&B^*\\ B^{-1}&0\end{bmatrix} = \begin{bmatrix} 0&-BA^{\prime *}\\ (B^*)^{-1}A'&0\end{bmatrix} \begin{bmatrix} 0&B^*\\ B^{-1}&0\end{bmatrix} \\[6pt] &=\begin{bmatrix} -BA^{\prime *}B^{-1}&0\\ 0&(B^*)^{-1}A'B^*\end{bmatrix}= \begin{bmatrix} -A'&0\\ 0&A^{\prime *}\end{bmatrix} = -A. \end{align*} $$
Furthermore,
![]() $\det T = (-1)^{\dim V'} = (-1)^{\dim V/2}$
.
$\det T = (-1)^{\dim V'} = (-1)^{\dim V/2}$
.
B.2 Simple nonsplit blocks
We have
![]() $V = {\operatorname {Span}}(e, Ae, A^2e, \dots )$
for some
$V = {\operatorname {Span}}(e, Ae, A^2e, \dots )$
for some
![]() $e\in V$
. Define
$e\in V$
. Define
![]() $T:V\to V$
by
$T:V\to V$
by
![]() $T(g(A)e) = g(-A)e$
. It is well defined since g is well defined modulo
$T(g(A)e) = g(-A)e$
. It is well defined since g is well defined modulo
![]() $f(A)^d$
, and
$f(A)^d$
, and
![]() $f(-A)=\pm f(A)$
. T is an element of
$f(-A)=\pm f(A)$
. T is an element of
![]() $\operatorname {O}(V)$
, as
$\operatorname {O}(V)$
, as
Clearly,
![]() $TAT^{-1} = -A$
. Moreover,
$TAT^{-1} = -A$
. Moreover,
![]() $\det T = (-1)^{\lfloor {n/2}\rfloor }$
, which is what we wanted in the nonnilpotent case (where n is even), and in the nilpotent case (where n is odd), we may replace T by
$\det T = (-1)^{\lfloor {n/2}\rfloor }$
, which is what we wanted in the nonnilpotent case (where n is even), and in the nilpotent case (where n is odd), we may replace T by
![]() $-T$
if needed, in order to achieve the desired sign of the determinant of T.
$-T$
if needed, in order to achieve the desired sign of the determinant of T.
B.3 Simple even nilpotent blocks
We can choose
![]() $T(A^ie) = (-1)^iA^ie$
and
$T(A^ie) = (-1)^iA^ie$
and
![]() $T(A^if) = (-1)^{i+1}A^if$
. It clearly satisfies
$T(A^if) = (-1)^{i+1}A^if$
. It clearly satisfies
![]() $TAT^{-1} = -A$
and
$TAT^{-1} = -A$
and
![]() $T\in \operatorname {O}(V)$
. It only remains to note that
$T\in \operatorname {O}(V)$
. It only remains to note that
![]() $\det T = (-1) ^{\dim V / 2}$
, which is exactly what we wanted.
$\det T = (-1) ^{\dim V / 2}$
, which is exactly what we wanted.
Acknowledgment
I would like to deeply thank my advisor, Dmitry Gourevitch, for helping me with my work on this paper, for exposing me to this fascinating area of mathematics, and for the guidance and support along the way. I would also like to thank him for the exceptional willingness to help. I would also like to thank Guy Henniart for fruitful discussions he had with my advisor.