The seasonality of population data has been of great interest in demographic studies. Seasonality depends mainly on the climatic conditions, and hence, the findings may vary from study to study. Commonly, the studies are based on monthly data. A central role is played by the population at risk. In a study of seasonal variation in the number of births or deaths, the population at risk is the product of the size of the population and the length of the month. For short periods, the population can be assumed to be constant, and therefore, the population at risk is proportional to the lengths of the months. Hence, for studies of monthly birth and death data, one must analyze the number of cases per day.
If one studies the seasonal variation in multiple maternities or in the occurrence of an innate disease, the population at risk is the total number of confinements. Hence, the number of multiple maternities in a given month must be compared with the monthly number of all maternities. Therefore, one has to consider the monthly rate of the multiple maternities. If one considers the monthly rates, the monthly number of birth data is eliminated and one has the possibility of obtaining an unaffected seasonality measure of the multiple maternities.
When seasonal models are applied, special attention should be paid to how well the model fits the data. A poor fit can erroneously result in a statement that the seasonality is slight, although the observed seasonal fluctuations are marked.
To our knowledge, Neefe (Reference Neefe1877) was the first to analyze detailed statistics concerning the seasonality of multiple births. He presented data from Denmark (1855–1869) and from the towns of Hamburg and Oldenburg. For Denmark, he considered the total dataset and, in addition, detailed statistics for urban and rural data, and legitimate and illegitimate maternities. Later, Weinberg (Reference Weinberg1901) published multiple maternity data for Denmark (1855–1894) and for Switzerland (1876–1890). While Weinberg's Denmark data were for a longer period than Neefe's data, they were not as detailed. In the 1920s, Cristalli (Reference Cristalli1924) analyzed seasonal data concerning multiple maternities in the city of Naples (Italy) for the period 1914–1921. All of these demographic data will be scrutinized in this study.
Our research team has shown a continuous interest in seasonality of twin and other demographic data, first presented by Eriksson (Reference Eriksson1973), and later analyzed by Eriksson and Fellman (Reference Eriksson and Fellman1999, Reference Eriksson and Fellman2000) and Fellman and Eriksson (Reference Fellman and Eriksson1999a).
Materials and Methods
Materials
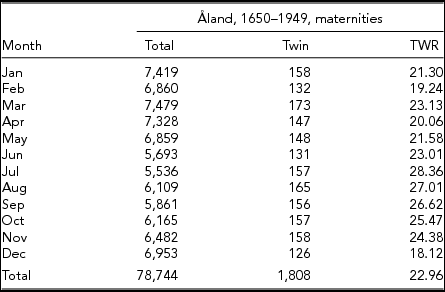
The data considered in this study are presented in the appendix and comprise the following: Neefe's Danish data in Table A1, Weinberg's data from Denmark in Table A2 and from Switzerland in Table A3, Cristalli's data from Naples (Italy) in Table A4, and Eriksson's twinning data from the Åland Islands (Finland) in Table A5. In all datasets, with the exception of Eriksson (Reference Eriksson1973), the authors consider multiple maternities instead of twin maternities. Table A3 differs from the others because the data are means for a 15-year period. In our tables, we have included the rates of multiple maternities (MURs).
Chi-Squared Tests
Fellman and Eriksson (Reference Fellman and Eriksson2009) tested the seasonality
of births and deaths by chi-squared tests. Let Ni
be the observed
number of births in month number i and let ki
be
the length of the month in days. Furthermore, let N =
∑12
i = 1
Ni
be
the total number of births and let k =
∑12
i = 1
ki
be
the length of the year. The expected number of births in month number i is
![]() ${\hat{N}_i} = {k_i}\frac{N}{k}$
. The chi-squared test is
${\hat{N}_i} = {k_i}\frac{N}{k}$
. The chi-squared test is
 $$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({N_i} - {{\hat{N}}_i})}^2}}}{{{{\hat{N}}_i}}}}
\end{equation}$$
$$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({N_i} - {{\hat{N}}_i})}^2}}}{{{{\hat{N}}_i}}}}
\end{equation}$$
with 11 degrees of freedom. Obviously, a similar test holds for deaths.
For twin and other multiple maternities, we have to modify the test. Let
ni
be the number of twin maternities in month number
i and let n be the total number of twin maternities. The mean
twinning rate (TWR) is
![]() $r = \frac{n}{N}$
and the expected number of twin maternities in month number
i is
$r = \frac{n}{N}$
and the expected number of twin maternities in month number
i is
![]() ${\hat{n}_i} = r{N_i}$
. Hence, the chi-squared test is
${\hat{n}_i} = r{N_i}$
. Hence, the chi-squared test is
 $$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({n_i} - {{\hat{n}}_i})}^2}}}{{{{\hat{n}}_i}}}}
\end{equation}$$
$$\begin{equation}
{\chi ^2} = \sum\limits_{i = 1}^{12} {\frac{{{{({n_i} - {{\hat{n}}_i})}^2}}}{{{{\hat{n}}_i}}}}
\end{equation}$$
with 11 degrees of freedom.
The critical values for chi-squared tests with 11 degrees of freedom are χ 2 = 19.68 for p < .05, χ 2 = 24.73 for p < .01, and χ 2 = 31.26 for p < .001.
Sinusoidal Model Building
St. Leger (Reference Leger1976) assumed that the pattern of the seasonal variation is sine-shaped, and he estimated the sine curve by a maximum likelihood approach. Fellman and Eriksson (Reference Fellman and Eriksson1999a) considered a regression approach, and this will be used in this study. Consider the sinusoidal model
The equation can be written as
 $$\begin{eqnarray}
E({Y_i}) &=& C + A\sin ({t_i} + \alpha) \nonumber\\
&=& C + A\cos ({t_i})\sin (\alpha) + A\sin ({t_i})\cos (\alpha) \nonumber\\
&=& \;C + {B_1}\cos ({t_i}) + {B_2}\sin ({t_i}),
\end{eqnarray}$$
$$\begin{eqnarray}
E({Y_i}) &=& C + A\sin ({t_i} + \alpha) \nonumber\\
&=& C + A\cos ({t_i})\sin (\alpha) + A\sin ({t_i})\cos (\alpha) \nonumber\\
&=& \;C + {B_1}\cos ({t_i}) + {B_2}\sin ({t_i}),
\end{eqnarray}$$
where Yi is the observed rate for month number i, and ti is an angle created from the time (in months) and B1 = Asin(α) and B2 = Acos(α).
The parameter estimation is based on the simplified model:
The intercept and the parameters B 1 and B 2 are estimated by ordinary least squares (OLS) for the monthly data, and the initial parameters can be calculated by the equations
and
Fellman and Eriksson (Reference Fellman and Eriksson2002) presented without
argumentations or proofs that
![]() ${\rm{Var}}(\hat{A}) \approx {\rm{Var}}({\hat{B}_1}) \approx {\rm{Var}}({\hat{B}_2})$
.
${\rm{Var}}(\hat{A}) \approx {\rm{Var}}({\hat{B}_1}) \approx {\rm{Var}}({\hat{B}_2})$
.
This assumption underestimates
![]() ${\rm{Var}}(\hat{A})$
and overestimates the significance of the sinusoidal model. In the following,
we try to improve the valuation of the
${\rm{Var}}(\hat{A})$
and overestimates the significance of the sinusoidal model. In the following,
we try to improve the valuation of the
![]() ${SE}_{\hat{A}}$
.
${SE}_{\hat{A}}$
.
 $$\begin{eqnarray*}
{\rm{Var}}(\hat{A}) &=& E({\hat{A}^2}) - {\left({E(\hat{A})} \right)^2} = E\left({\hat{B}_1^2 + \hat{B}_2^2} \right) - {\left({E(\hat{A})} \right)^2}\\
&=& {\rm{Var}}({\hat{B}_1}) + {\left({E({{\hat{B}}_1})} \right)^2} + {\rm{Var}}({\hat{B}_2})\\
&&\quad +\, {\left({E({{\hat{B}}_2})} \right)^2} - {\left({E(\hat{A})} \right)^2} \\
&\approx & {\rm{Var}}({\hat{B}_1}) + \hat{B}_1^2 + {\rm{Var}}({\hat{B}_2}) + \hat{B}_2^2 - {\left({E(\hat{A})} \right)^2} \\
&\approx & {\rm{Var}}({\hat{B}_1}) + {\rm{Var}}({\hat{B}_2}) + {\hat{A}^2} - {\left({E(\hat{A})} \right)^2}\\
&\approx & {\rm{Var}}({\hat{B}_1}) + {\rm{Var}}({\hat{B}_2}).
\end{eqnarray*}$$
$$\begin{eqnarray*}
{\rm{Var}}(\hat{A}) &=& E({\hat{A}^2}) - {\left({E(\hat{A})} \right)^2} = E\left({\hat{B}_1^2 + \hat{B}_2^2} \right) - {\left({E(\hat{A})} \right)^2}\\
&=& {\rm{Var}}({\hat{B}_1}) + {\left({E({{\hat{B}}_1})} \right)^2} + {\rm{Var}}({\hat{B}_2})\\
&&\quad +\, {\left({E({{\hat{B}}_2})} \right)^2} - {\left({E(\hat{A})} \right)^2} \\
&\approx & {\rm{Var}}({\hat{B}_1}) + \hat{B}_1^2 + {\rm{Var}}({\hat{B}_2}) + \hat{B}_2^2 - {\left({E(\hat{A})} \right)^2} \\
&\approx & {\rm{Var}}({\hat{B}_1}) + {\rm{Var}}({\hat{B}_2}) + {\hat{A}^2} - {\left({E(\hat{A})} \right)^2}\\
&\approx & {\rm{Var}}({\hat{B}_1}) + {\rm{Var}}({\hat{B}_2}).
\end{eqnarray*}$$
Hence,
On account of the fact that the angle α and the amplitude A have
to be estimated from formulae (6) and (7), statistically non-significant estimates
![]() ${\hat{B}_1}$
and
${\hat{B}_1}$
and
![]() ${\hat{B}_2}$
cannot be ignored. Therefore, Fellman and Eriksson (Reference Fellman and Eriksson2002) recommended full pairs of trigonometric terms. Another argument for
this is that
${\hat{B}_2}$
cannot be ignored. Therefore, Fellman and Eriksson (Reference Fellman and Eriksson2002) recommended full pairs of trigonometric terms. Another argument for
this is that
![]() $\hat{A}$
may differ significantly from zero, but the angle
$\hat{A}$
may differ significantly from zero, but the angle
![]() $\hat{\alpha }$
may be such that
$\hat{\alpha }$
may be such that
![]() ${\hat{B}_1}$
or
${\hat{B}_1}$
or
![]() ${\hat{B}_2}$
is close to zero and consequently assumed non-significant. The geometric
interpretation is that when one fits the model to the data one focuses on the initial model in
(2), and consequently, the amplitude
A and the angle α are of interest. From this, it
follows that the parameter tests for significance should be applied to
${\hat{B}_2}$
is close to zero and consequently assumed non-significant. The geometric
interpretation is that when one fits the model to the data one focuses on the initial model in
(2), and consequently, the amplitude
A and the angle α are of interest. From this, it
follows that the parameter tests for significance should be applied to
![]() ${\hat{A}}$
and
${\hat{A}}$
and
![]() ${\hat{\alpha}}$
, but not to
${\hat{\alpha}}$
, but not to
![]() ${\hat{B}_1}$
or
${\hat{B}_1}$
or
![]() ${\hat{B}_2}$
. These assumptions indicate that the intercept C is an
estimate of the mean annual level of the rate of multiple maternities. The association between
the intercept C and the total MUR can be seen later in Table 2. The amplitude A can be used as a measure of the
seasonality (the model varies between C + A and
C − A). Finally, the adjusted coefficient of
determination,
${\hat{B}_2}$
. These assumptions indicate that the intercept C is an
estimate of the mean annual level of the rate of multiple maternities. The association between
the intercept C and the total MUR can be seen later in Table 2. The amplitude A can be used as a measure of the
seasonality (the model varies between C + A and
C − A). Finally, the adjusted coefficient of
determination,
![]() ${\bar{R}^2}$
, is a measure of the goodness of fit, and one has to pay special attention to
how well the model fits the data. If the goodness of fit is poor, the non-significant results
obtained can erroneously lead to the statement that the seasonality is slight, although the
observed seasonal fluctuations are marked. Fellman and Eriksson (Reference Fellman and Eriksson2002) noted this discrepancy and suggested the use of more general
trigonometric regression models. In this study, we consider only sinusoidal models and use the
adjusted coefficient of determination,
${\bar{R}^2}$
, is a measure of the goodness of fit, and one has to pay special attention to
how well the model fits the data. If the goodness of fit is poor, the non-significant results
obtained can erroneously lead to the statement that the seasonality is slight, although the
observed seasonal fluctuations are marked. Fellman and Eriksson (Reference Fellman and Eriksson2002) noted this discrepancy and suggested the use of more general
trigonometric regression models. In this study, we consider only sinusoidal models and use the
adjusted coefficient of determination,
![]() ${\bar{R}^2}$
, as a measure of the goodness of fit. In Table 1, the estimates are included for all datasets. The significance of the model
can also be checked by comparing
${\bar{R}^2}$
, as a measure of the goodness of fit. In Table 1, the estimates are included for all datasets. The significance of the model
can also be checked by comparing
![]() ${\hat{A}}$
, which is always positive, and
${\hat{A}}$
, which is always positive, and
![]() $S{E_{\hat{A}}}$
. Although
$S{E_{\hat{A}}}$
. Although
![]() ${\hat{A}}$
is by no means normally distributed, it can be considered approximately
normal and
${\hat{A}}$
is by no means normally distributed, it can be considered approximately
normal and
![]() $t = \frac{{\hat{A} - 0}}{{S{E_{\hat{A}}}}}$
should be greater than two in order that a significant deviation from zero
can be considered.
$t = \frac{{\hat{A} - 0}}{{S{E_{\hat{A}}}}}$
should be greater than two in order that a significant deviation from zero
can be considered.
TABLE 1 Collection of Chi-Squared, Standard Deviations (SDs) Measuring the
Strength of Seasonality and the Adjusted Coefficient of Determination
![]() ${\bar{R}^2}$
Measuring the Goodness of Fit for Sinusoidal Models for the MURs for
Different Datasets
${\bar{R}^2}$
Measuring the Goodness of Fit for Sinusoidal Models for the MURs for
Different Datasets

Goodness of fit for the Danish legitimate dataset is (0.672), the Åland
dataset is (0.630), the dataset for Denmark is (1855–1894) (0.577), and the
total Danish dataset is (1855–1869) (0.535). The estimates for the Switzerland
data are based on 15 annual means and are not comparable to the other estimates. This is
discussed in the text. For the rest of the data, the adjusted coefficients of
determination
![]() ${\bar{R}^2}$
are below 0.500, which we consider the limit for an acceptable strength
of seasonality.
${\bar{R}^2}$
are below 0.500, which we consider the limit for an acceptable strength
of seasonality.
Results
In Table A1, we present the Danish data according to Neefe (Reference Neefe1877). We follow Neefe and present his data for rural and urban, legitimate and illegitimate, and total data. In the table, we have included all maternities, multiple maternities, and the monthly rates of multiple maternities (MURs). In Figure 1a, we present the MURs of the subsets for urban and rural data and in Figure 1b the subsets for legitimate and illegitimate data. The figures also include the total dataset and the seasonal models. The figures indicate that the seasonality is strongest for the illegitimate data, followed by the urban data. For the other datasets, the seasonality is rather similar. These findings are supported by the standard deviations given in Table 1. Also included in Table 1 are chi-squared tests for the strength of the seasonality. The obtained chi-squared test results indicate that seasonality is significant for all datasets. In Figure 1a and b, we have included the sinusoidal models for the datasets. The inclusion of these models describes the general seasonal pattern of these datasets. The obtained models are discussed below.

FIGURE 1 Comparison between the MURs for the total dataset, the urban and rural subdata (a) and the legitimate and illegitimate subdata (b) in Denmark in 1855–1869 (Neefe, Reference Neefe1877). The corresponding sinusoidal models are included.
Weinberg's Danish data for the total and multiple maternities are presented in Table A2 and his data for Switzerland in Table A3 (Weinberg, Reference Weinberg1901). In Table A4, we present the data for Naples according to Cristalli (Reference Cristalli1924). In fact, we identified a misprint in Cristalli's tables. This misprint is corrected in our analyses. In Figure 2, we include the data from Switzerland (1876–1890) and Naples (1914–1921). According to the chi-squared test results in Table 1, the Naples data show slight significant seasonality. The Switzerland data are means of 15 annual data, and therefore the chi-squared value should be multiplied by 15 in order to yield a value comparable with the Naples test result (15 × 2.74 = 41.1). Later, when we consider sinusoidal models, we return to the means of 15 annual data for Switzerland. The seasonality for Denmark for both the Neefe and Weinberg data is marked. Eriksson's data of twin maternities from the Åland Islands (Finland) are presented in Table A5. According to Table 1, the seasonality for Åland is remarkably strong. The analyses of the sinusoidal models are presented below.

FIGURE 2 Comparison between the MURs for Switzerland, 1876–1890 (Weinberg, Reference Weinberg1901) and Naples, 1914–1921 (Cristalli, Reference Cristalli1924). The corresponding sinusoidal models are included.
Sinusoidal Model Building
We built sinusoidal models for all datasets. Below, we analyze the results using the goodness of fit measured with the adjusted coefficient of determination. The Switzerland data result in a model that has the best goodness of fit. The model is
Hence,
![]() $SE({\hat{B}_1}) = 0.112$
,
$SE({\hat{B}_1}) = 0.112$
,
![]() $SE({\hat{B}_2}) = 0.112$
, and
$SE({\hat{B}_2}) = 0.112$
, and
![]() ${\bar{R}^2} = 0.824$
. The first parameter is almost significant and the second is significant. The
obtained estimates of the initial parameters are
${\bar{R}^2} = 0.824$
. The first parameter is almost significant and the second is significant. The
obtained estimates of the initial parameters are
![]() $\hat{A} = 0.818$
and
$\hat{A} = 0.818$
and
![]() $\hat{\alpha } = - 17.6^\circ$
. When we use
$\hat{\alpha } = - 17.6^\circ$
. When we use
![]() ${\bar{R}^2}$
as a measure of significance, the Switzerland data give the best goodness of
fit and the model is acceptable. However, the obtained value
${\bar{R}^2}$
as a measure of significance, the Switzerland data give the best goodness of
fit and the model is acceptable. However, the obtained value
![]() $\hat{A} = 0.818$
indicates that the seasonality is weak.
$\hat{A} = 0.818$
indicates that the seasonality is weak.
The obtained results for Åland are
where
Both parameter estimates are significant. The obtained estimates of the initial parameters
are
![]() $\hat{A} = {\rm{3}}{\rm{.679}}$
and
$\hat{A} = {\rm{3}}{\rm{.679}}$
and
![]() $\hat{\alpha } = {\rm{221}}{\rm{.9}}^\circ$
. According to the
$\hat{\alpha } = {\rm{221}}{\rm{.9}}^\circ$
. According to the
![]() ${\hat{A}}$
value, the seasonality is strong; in fact, the strongest among all datasets.
The seasonality of the Åland data is given in Figure 3.
${\hat{A}}$
value, the seasonality is strong; in fact, the strongest among all datasets.
The seasonality of the Åland data is given in Figure 3.

FIGURE 3 Comparison between twinning rates for Åland, 1750–1949 (Eriksson, Reference Eriksson1973), and multiple maternity for Denmark, 1855–1894 (Weinberg, Reference Weinberg1901) and Naples (Italy), 1914–1920 (Cristalli, Reference Cristalli1924). The sinusoidal models are illustrated with dashed lines. For details, see the text.
For Denmark (1855–1894), the obtained results are
where
![]() ${\rm{Var}}({\hat{B}_1})\! =\! 0.164639$
,
${\rm{Var}}({\hat{B}_1})\! =\! 0.164639$
,
![]() ${\rm{Var}}({\hat{B}_2}) \!=\! 0.164295$
,
${\rm{Var}}({\hat{B}_2}) \!=\! 0.164295$
,
![]() $\hat{A} \!=\! 0.678564$
,
$\hat{A} \!=\! 0.678564$
,
![]() $\hat{\alpha } = - 15.6^\circ$
and
$\hat{\alpha } = - 15.6^\circ$
and
![]() ${\bar{R}^2} = 0.577$
. Only the second parameter estimate is significant, but as pointed out above,
both terms should be included in the model. Furthermore, the Neefe data for urban, legitimate,
and total data in Denmark (1855–1869) yields acceptable goodness of fit. The
obtained model for Denmark is
${\bar{R}^2} = 0.577$
. Only the second parameter estimate is significant, but as pointed out above,
both terms should be included in the model. Furthermore, the Neefe data for urban, legitimate,
and total data in Denmark (1855–1869) yields acceptable goodness of fit. The
obtained model for Denmark is
where
![]() ${\rm{Var}}({\hat{B}_1}) = 0.234818$
,
${\rm{Var}}({\hat{B}_1}) = 0.234818$
,
![]() ${\rm{Var}}({\hat{B}_2}) = {\rm{0}}{\rm{.234327}}$
,
${\rm{Var}}({\hat{B}_2}) = {\rm{0}}{\rm{.234327}}$
,
![]() $\hat{A} = 0.898$
,
$\hat{A} = 0.898$
,
![]() $\hat{\alpha } = - 5.5^\circ$
, and the adjusted coefficient of determination,
$\hat{\alpha } = - 5.5^\circ$
, and the adjusted coefficient of determination,
![]() ${\bar{R}^2} = 0.535.$
${\bar{R}^2} = 0.535.$
For the rest of the datasets, the model-building results yield low adjusted coefficients of
determination (
![]() ${\bar{R}^2} < 0.500$
), and we assume that the goodness of fit is so slight that the corresponding
models should not be discussed. The estimates of the parameters and their standard errors
(SEs) for all datasets are given in Table
2.
${\bar{R}^2} < 0.500$
), and we assume that the goodness of fit is so slight that the corresponding
models should not be discussed. The estimates of the parameters and their standard errors
(SEs) for all datasets are given in Table
2.
TABLE 2 Test Results of the Sinusoidal Models

The population data resulting in R 2 > 0.500 are discussed in the text. The rate of MUR is the overall rate of multiple maternities, and the association between MUR and the intercept C can be analyzed in the table (the α is about 30° per month).
a The negative value is a consequence of a very bad fit with too many regressors.
Considering the periods 1855–1869 and 1870–1894, we can compare the temporal changes in the MURs for Denmark. In Figure 4, one can observe similar seasonal models for the MURs, but also a decrease on average of about 1.08 per 1,000. In Figure 3, we present the Åland data, the Weinberg dataset for Denmark (1855–1894), and the Naples data relative to the corresponding sinusoidal models. The variable seasonality strength is apparent.

FIGURE 4 Comparison in seasonality in Denmark in 1855–1869 and 1870–1894. The corresponding sinusoidal models are included.
Discussion
Fellman and Eriksson (Reference Fellman and Eriksson1999b) used Walter and Elwood's (Reference Walter and Elwood1975) sinusoidal model to evaluate the seasonal variation in the twinning rate in Denmark, Switzerland, England, and Wales. Fellman and Eriksson (Reference Fellman and Eriksson1999b) studied the secular changes in the seasonal patterns of births in Sweden, Norway, and Iceland. They introduced a modified Walter–Elwood model and investigated the temporal variations in the Walter–Elwood theta and quarters with high and low numbers of births per day. Fellman and Eriksson (Reference Fellman and Eriksson2002) studied the temporal changes in births and death using trigonometric regression models. The trigonometric regression models are generalizations of the sinusoidal model. They are used when the general pattern of the graphs is too complicated for a sinusoidal model. That study was based on data from Italy, France, Germany, Denmark, Norway, Scotland, Sweden, and Iceland. Special attention was paid to data from Iceland. Eriksson et al. (Reference Eriksson, Fellman, Jorde and Pitkänen2008) considered the seasonality in births and deaths on the Åland Islands. Finally, Fellman and Eriksson (Reference Fellman and Eriksson2009) considered births for the Åland Islands and its sub-regions and introduced a new measure of the strength of the seasonality.
Conclusions
When seasonality is studied, one must decide whether one seeks the strength of the seasonality
or whether one seeks a seasonality model. When seasonal models are applied, one pays special
attention to how well the model fits the data. In this study, we used the test of the amplitude
![]() $\hat{A}$
and the adjusted coefficient of determination
$\hat{A}$
and the adjusted coefficient of determination
![]() ${\bar{R}^2}$
as measures of goodness of fit (cf. Table
2). If goodness of fit is poor, the non-significant results obtained can erroneously
lead to a statement that the seasonality is slight, although the observed seasonal fluctuations
are marked (cf. Switzerland and Naples). Under such circumstances, the use of more general
trigonometric regression models could be considered.
${\bar{R}^2}$
as measures of goodness of fit (cf. Table
2). If goodness of fit is poor, the non-significant results obtained can erroneously
lead to a statement that the seasonality is slight, although the observed seasonal fluctuations
are marked (cf. Switzerland and Naples). Under such circumstances, the use of more general
trigonometric regression models could be considered.
Appendix
TABLE A1 Multiple Maternity Statistics for Denmark, 1855–1869, including the Rate of Multiple Maternities (MUR)

TABLE A2 Twinning Statistics for Denmark (1855–1894) according to Weinberg (Reference Weinberg1901)
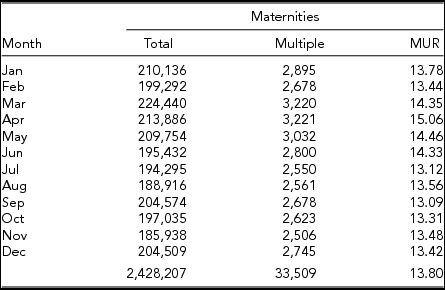
TABLE A3 Seasonal Data for Total Maternities, Multiple Maternities, and MURs for Switzerland (1876–1890) According to Weinberg (Reference Weinberg1901)

TABLE A4 Seasonal Data for Total Maternities, Multiple Maternities, and MURs for the City of Naples (Italy) (1914–1921) According to Cristalli (Reference Cristalli1924)
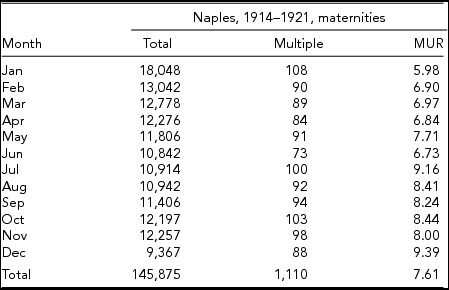
TABLE A5 Seasonal Data for Total Maternities, Twin Maternities and TWRs for the Åland Islands (1650–1949) According to Eriksson (Reference Eriksson1973)