Introduction
For the estimate of snow-and ice-mass changes, most mountain-glacier energy-balance models require accurate information on the surface-cover albedo and temperature. These surface-radiative parameters are, in most cases, measured in a few “representative” areas and are then extrapolated over the entire basin. Often, however, the introduction of a nominal albedo value for snow, ice and bare-ground covers is responsible for the poor performance of net shortwave-radiation models (Reference Dozier,Dozier, 1987). The use of nominal surface-temperature information for the unglaciated parts of a basin is even more hazardous. It has been indicated, however, that an accurate distributed assessment of surface albedo and surface emittance would increase the quality of the radiative-transfer analysis (Reference Munro, and Young,Munro and Young, 1982; Reference Oerlemans,Oerlemans, 1986; Reference Oerlemans, and Hoogendoorn,Oerlemans and Hoogendoorn, 1989). A remotely sensed method of assessing radiative-transfer processes which considers separately a series of distinctive zones in the drainage basin provides this improvement (Reference Gratton,Gratton, 1991; Reference Gratton,, Howarth. and GagnonGratton and others, 1993).
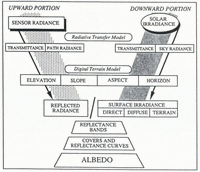
The accuracy of these surface-radiative parameters is, however, linked to the precision of the models for computing the different components of irradiance in a mountainous terrain. While elaborate models have been proposed, which account for the effects of topography on incoming direct, diffuse and atmospheric-emitted radiation, more attention needs to be given to terrain shortwave and longwave irradiance.
The terrain shortwave-irradiance component is often considered insignificant in the ablation process and is dismissed in many analyses of the shortwave-radiation balance. In certain basin sectors, however, the high reflectance of snow and ice surfaces in particular wavelengths, in addition to the topographic shadowing effects, may result in a large part of the total spectral irradiance coming from the neighbouring terrain. In this case, the reliability of the computed glacial surface-cover reflectance and albedo from satellite imagery will be dependent on the accuracy of the terrain-irradiance calculations.
Recently, an in situ radiation-exchange analysis pointed out the effects of longwave terrain irradiance on the spatial distribution of snow-and ice-surface net radiation (Reference Mountain,Mountain, 1990). It is suggested that the mapping of this component through the use of satellite-measured surface-brightness temperatures, as presented in this paper, could further contribute to this investigation.
In the first part of this study, a Landsat-5 Thematic Mapper (TM) image acquired at 1813 h GMT (1113 h local time, solar azimuth ~147° and zenith angle ~48°) and digital elevation data are used to investigate the importance of terrain-reflected radiation in the computation of surface albedo and net shortwave radiation. In the second part, the proportion of terrain-emitted radiation in the context of total longwave irradiance is evaluated based on surface-brightness temperature values extracted from the TM thermal band (band 6). The emphasis in this paper is to present the results in map form and provide interpretations of the patterns that are displayed within the glacier basin.
Study Area
The study area is the Athabasca Glacier basin (~52.2° N, ~117.3°W), one of the most important outlet glacier basins of the Columbia Icefield in the Canadian Rocky Mountains. It borders Banff and Jasper National Parks in the Province of Alberta, Canada (Fig. 1).
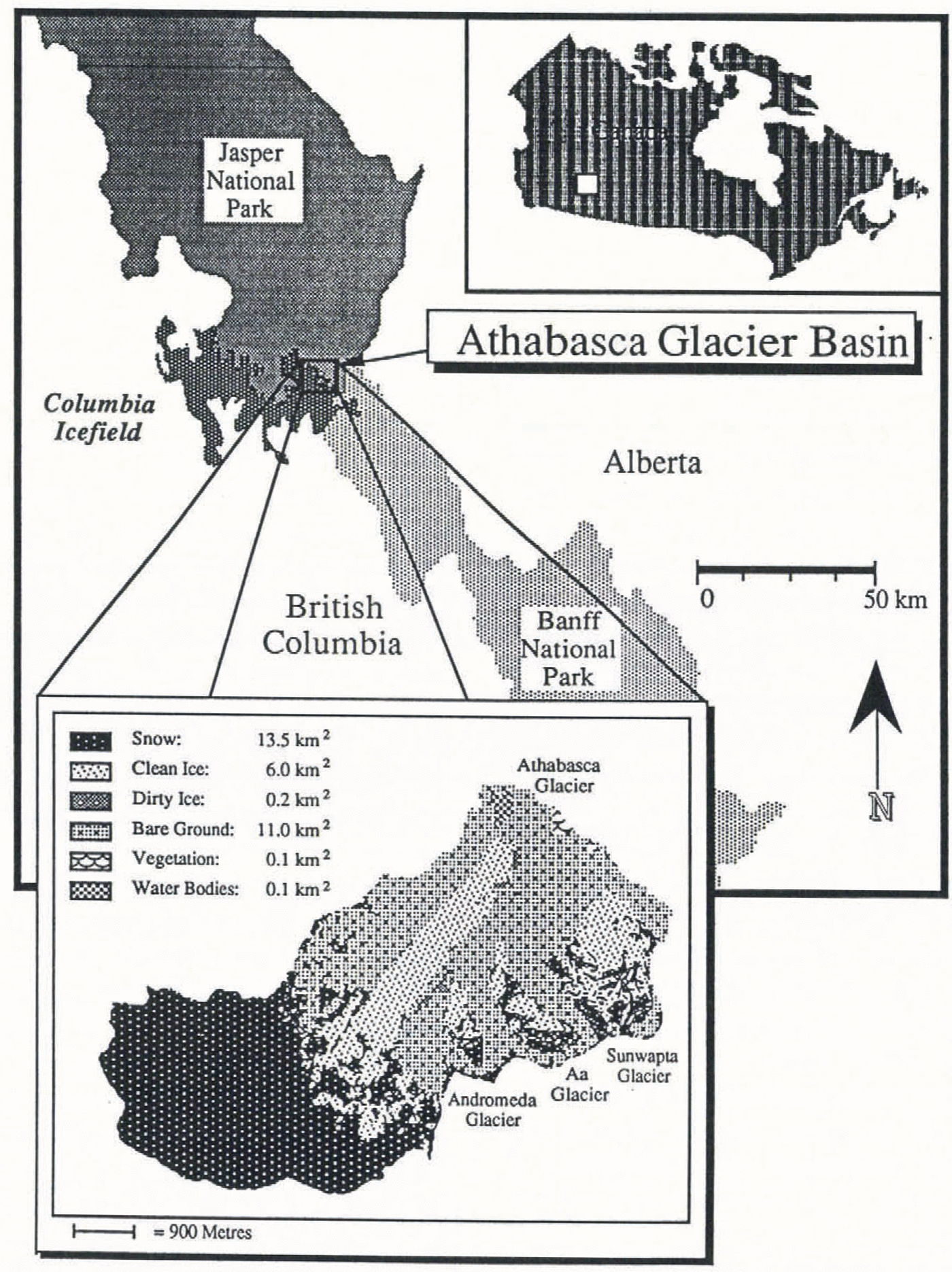
Fig. 1. Regional setting and surface-cover map of the Athabasca Glacier basin.
While the average altitude of the basin is around 2700 m, the summit is found close to 3500 m and the snout is at 1930 m. Of the 31.1 km2 drainage basin more than 65% is glacier-covered. Athabasca Glacier occupies 16.1 km2 (1.5 km2 of debris on ice). Three other glaciers on the southeast side of the basin occupy a total of 4.2 km2: Sunwapta Glacier, 2.5 km2 (0.04 km2 of debris on ice); Aa Glacier, 1.1 km2 (0.1 km2 of debris on ice); and Andromeda Glacier, 0.6 km2. The remaining 10.8 km2 is unglacierized. Most of the glacier-free area, except for high ridges, is rid of its snow layer by September. The surface cover on the northwest slope is mostly bare rock, while the great bulk of the fairly coarse moraine debris is on the lower southeast side and proglacial part of the basin.
Athabasca Glacier is a valley glacier. It descends from the rim of the ice field in a series of three icefalls over a distance of 2 km. At the beginning of September, the transient snow-line is found at the base of the highest icefall around 2500 m. The elevation of the ice surface at the base of the lowest icefall is approximately 2300 m. The remaining 3.6 km of the tongue slopes gently between 2° and 5° with an average width of 1.1 km, which varies only slightly over the total length. At the terminus, where it meets a rock outcrop, the slope increases to about 10°. The clean-ice ablation area is bordered by two bands, about 100 m wide, of thick (> 5 cm) debris-covered ice.
The other three glaciers in the basin are of the cirque type. The least encased of the three is Sunwapta Glacier; the others occupy deep U-shaped basins with high surrounding rocky ridges. Because of their topography, the glacier snowline in September is more fragmented and harder to pinpoint at a specific elevation but it is around 2700–2800 m. Andromeda and Aa Glaciers are tributaries of Athabasca Glacier. Neither is joined to the main glacier, although Andromeda Glacier, terminating in a steep icefall, contributes a small quantity of snow-and ice-avalanche debris on to the bordering debris-on-ice band.
Shortwave Radiation
The computation of surface-cover albedo from satellite imagery for the different parts of a glacier basin requires an investigation of all probable radiation components (Reference Gratton,, Howarth. and Marceau.Gratton and others, 1992). The investigation of each component starts from the irradiance values obtained from a radiative-transfer model. The spectrally based radiative-transfer model incorporated in the LOWTRAN-6 code (Reference Kneizys,Kneizys and others, 1983) was used, with information on the general atmospheric conditions acquired from radiosonde data. It provided total irradiance values for each of the six TM reflective spectral bands, as well as for the total shortwave spectrum (0.28–5.0 μm). Each total-irradiance value represents the sum of the direct and diffuse radiation for an unobstructed horizontal target and is more or less independent of the ground reflectance (Reference Proy,, D and Deschamps,Proy and others, 1989). In mountainous terrain, however, radiation modelling must highlight the influence of topography in the estimation of incoming radiation and in the computation of the surface spectral reflectance (Fig. 2). Elevation, slope, aspect and the enclosing topography factor become the building blocks on which direct and diffuse radiation components are adjusted. Furthermore, the total radiation reflected off the terrain is responsible for providing an additional component. In order to compute this shortwave terrain irradiance, it is important to have a certain a priori knowledge of the surface-cover distribution and its reflective behaviour. An automated procedure to provide the surface-cover information was developed (Reference Gratton,, Howarth. and Marceau.Gratton and others, 1990) and nominal reflectance values were assigned to each cover type (Reference Gratton,, Howarth., Marceau. and Blasco,Gratton, 1991). In this section, each irradiance component will be described; this will be followed by a general analysis of its distribution in the Athabasca Glacier basin at the time of the TM-image acquisition.

Fig. 2. Methodological steps used to calculate albedo.
Direct irradiance
Shortwave direct irradiance, in all spectral intervals received on inclined surfaces, varies according to: (1) the altitude of the surface which influences atmospheric attenuation, (2) the geometric arrangement between the position of the solar beam defined by the zenith and azimuth angles and the surface represented by the slope and aspect, and (3) the horizon profile and the projected shadow distribution which stops all direct radiation.
In the study basin, the computed direct radiation was the main component at the time of the TM-image acquisition, representing, on average, more than 87% of the total irradiance (Reference Gratton,, Howarth., Marceau. and Blasco,Gratton, 1991). Because of the basin’s general position, maximum values appear on the rocky northwest side of the valley. For snow and ice surfaces, maximum values are found in the upper northwest part of the accumulation zone. With respect to minimum values, more than 10% of the basin is under self or projected shadows and receives no direct radiation.
Diffuse irradiance
The shortwave diffuse irradiance results from the scattering of spectral components of the solar beam by atmospheric constituents. This component is a function of the proportion of sky hemisphere not obstructed by topography or the altitude of the surface. A sky-view factor computation must account for all components of the terrain, including the slope and aspect of the surface with respect to the horizon profile (Reference Dozier, and Marks,Dozier and Marks, 1987). Furthermore, the diffuse irradiance received on an inclined surface exhibits some anisotropic-radiation behaviour. While a consensus exists on the importance of treating isotropic and anisotropic diffuse radiation separately, different methods of estimating the value of each component have been proposed (Reference Temps, and Coulson,Temps and Coulson, 1977; Reference Hay,Hay, 1983; Reference Isard,Isard, 1986; Reference Proy,, D and Deschamps,Proy and others, 1989). The diffuse-irradiance anisotropy is estimated in relation to the position of the light source with respect to the surface, the wavelength and the local variations in atmospheric constituents. Most models account for the anisotropy of diffuse irradiance by concentrating on the regions of maximum intensity. In a mountainous environment a region is found in the direction normal to the Sun. This diffuse radiation is circum-solar and linked to the solar-incidence angle and the position of the Sun (Reference Dozier,Dozier, 1980). On the other hand, the isotropic part is solely a function of the sky-view factor. It is worthwhile noting that surfaces under projected shadows will not receive circum-solar anisotropic diffuse irradiance. These surfaces have to be identified when computing the diffuse irradiance.
For the Athabasca Glacier basin, on a clear late morning, the diffuse irradiance contributes about 11% of the total shortwave irradiance (Reference Gratton,, Howarth, and Marceau.Gratton, 1991). Being a function of the sky-view and circum-solar anisotropic scattering, the bulk of the maximum values for this component are found, as for the direct irradiance, on the northwest side of the valley but at lower altitudes. The minimum values, on the other hand, are found in the upper southeast, shadowed part of the basin. For snow and ice surfaces, the maximum diffuse irradiance is received along the centre line of the Athabasca Glacier ablation zone at generally lower altitudes and on certain northwest, Sun-facing snow surfaces on the ice field.
Terrain irradiance
The proportion of the total irradiance coming from the neighbouring terrain increases when a surface, sloping away from the Sun, is receiving low or no direct radiation while the neighbouring terrain receives large amounts of incoming radiation. This proportion increases even more if the surrounding surfaces, like snow and clean ice, have a high reflectance. In fact, because shadowed surfaces can receive approximately 10 times less total irradiance than surfaces in the Sun, the accurate assessment of total irradiance on a shadowed surface is largely dependent on the handling of the terrain-reflected radiation component. Three variables are required for the modelling of this irradiance: the neighbouring-terrain incoming radiation, the reflectance of the covers and the terrain geometry.
Overall, in the study basin, the terrain-irradiance component contributes approximately 2% on average to the total basin irradiance (Reference Gratton,, Howarth., Marceau. and Blasco,Gratton, 1991). However, in certain areas, particularly in the cirque-glacier basins, it provides a significant radiation addition which is approximately equivalent to the diffuse-irradiance component. Analysing the distribution of the proportion of terrain-reflected radiation in the Athabasca Glacier basin, compared with the sum of all incoming radiation fluxes, shows the importance of this component in an assessment of the total irradiance values in all parts of the basin (Fig. 3). Figure 3 also shows that, while the use of a priori nominal surface-cover reflectance values probably introduces some error into the computation of terrain irradiance, it is significantly lower than the error inserted into the total-irradiance analysis, particularly for shadowed areas, if this component were to be excluded. At the time of the TM-image acquisition, the large shadowed areas received, on average, about 20–25% of the total irradiance from the neighbouring terrain. Even some non-shadowed areas acquire around 10% of their incoming irradiance from this process.

Fig. 3. Map of the percentage of shortwave terrain irradiance over all incoming shortwave radiation for the Athabasca Glacier basin at the time of the TM-image acquisition.
The importance of accounting for terrain irradiance in most glacier basins will increase when larger areas are in shadow due to lower Sun elevation earlier and later in the day, or for glaciers at higher latitudes. Basin geomorphology plays an important role in these conditions. Moreover, the spectral distribution of the terrain-irradiance proportion is not constant over the spectrum because of the variable reflectance of surface covers found in glacier basins. Large valley sides covered with highly reflective snow and ice surfaces are bound to increase the contribution of terrain irradiance to total flux, particularly in the visible wavelengths.
Surface-cover reflectance and albedo
The Athabasca Glacier basin surface-cover spectral-reflectance values are acquired by computing the ratio of the sum of the spectral-irradiance components (direct, diffuse and of the terrain) to the measured TM-band radiances, corrected for the upward-path effects (Fig. 2). The upward-path radiance and transmittance values are also given by the LOWTRAN-6 code. Using the downward and upward components for each pixel, the reflectance values are calculated. The average reflectance values for each TM band, computed from a random sample of pixels for different surface covers, appear in Table 1. These values compare favourably with published values (Reference Hall,, Chang, and Siddalingaiah,Hall and others, 1988, Reference Hall,, Chang,, Foster, and Kovalick,1989; Reference Duguay,Duguay, 1989).
Table 1. Average reflectance and albedo values for the six surface covers

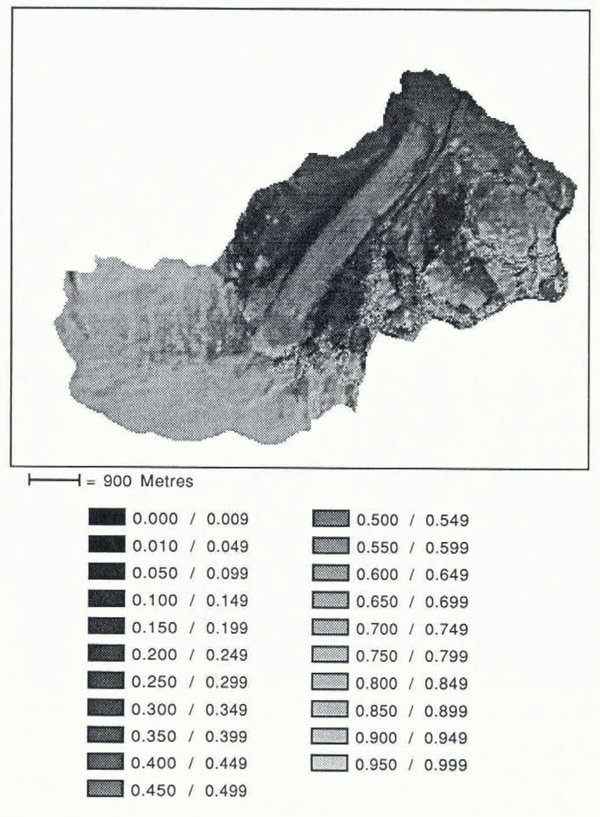
The albedo map is then derived from a proven weighting-function method which integrates the TM-band reflectance values according to the typical surface-cover reflective behaviours over a broad range of wavelengths (Reference Brest,Brest, 1987; Reference Duguay,Duguay, 1989; Reference Gratton,Gratton, 1991). This strategy must account for three factors: (1) the surface-cover spectral-reflectance pattern, (2) the spectral distribution of the total irradiance, and (3) the spectral band best representing a part of the spectrum.
In most cases, the reflective behaviour represented by a single band is valid only for part of the spectrum. This is because the surface reflectance is wavelength-dependent and very few surfaces are uniform reflectors of all shortwave radiation. Some well-defined segments of the spectral-reflectance curves of the glacier-basin surface covers are, however, found to match well with the six TM spectral bands. The albedo may be calculated, knowing the general reflectance pattern of the covers, even if the TM bands include only parts of this spectrum (Reference Pinker, and Ewing,Pinker and Ewing, 1985). Wavelength-dependent reflective behaviour is represented by a relatively uniform segment of each cover’s generalized spectral curve, which may be associated with a TM band that registers a similar reflectance pattern. The derived TM-band reflectance is then weighted by the proportion of the total shortwave-spectrum irradiance (0.28–5.0 μm) received in that particular spectral segment. The resulting value is the proportion of the total outgoing radiation, the sum of which, over all segments, represents the albedo of the surface cover (Fig. 4).

Fig. 4. Albedo map of the Athabasca Glacier basin.
The average albedo values for the Athabasca Glacier basin (Table 1) compare very well with average values measured in situ on an adjacent glacier, Peyto Glacier (personal communication from S. Reference Munro, and Young,Munro, 1991). Regionally, the average albedo of snow should be very similar. The close similarities between the average snow albedos found in the two basins give a good indication of the accuracy of the model.
Net shortwave-radiation balance
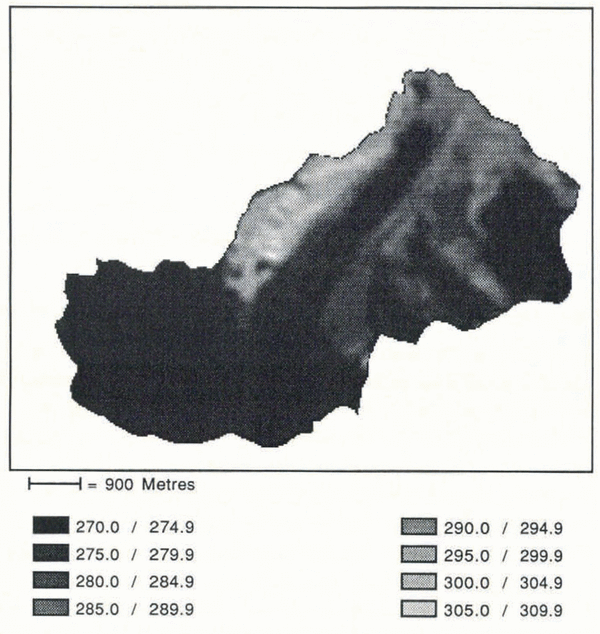
Establishing the net shortwave radiation for each pixel, using the sum of the irradiance components for incoming flux and the computed surface albedo for the outgoing flux at this time of day (18l3 h GMT), shows some distinctive patterns (Fig. 5). First, the large amount of absorbed radiation on the northwest rock face of the Athabasca Glacier valley certainly results in an increased surface temperature (Fig. 6) and, as described later, is a primary source of surface longwave emission. Over time, the radiation-exchange pattern in this area of Athabasca Glacier, plus the low albedo of the bordering debris-covered ice, probably enhanced, if not created, the large peripheral debris-covered channel. Secondly, the retreating snow-line and topographic setting of the Athabasca Glacier icefall area produces zones of higher radiation absorption when compared to the flatter parts at the base of the icefall. The highest net radiation values for the glacierized area of the basin appear, as one would expect, on the dirty-ice zones at the front of Athabasca Glacier.

Fig. 5. Net shortwave-radiation flux map of the Athabasca Glacier basin at the time of the TM-image acquisition (units in Wm−2).

Fig. 6. Surface-brightness temperature map of the Athabasca Glacier basin from the TM6 image (units in K).
Longwave Radiation
On mountain-glacier snow and ice covers, the incoming atmospheric and terrain longwave-radiation emission is often assumed to be almost balanced by the outgoing snow and ice emittance. However, under clear skies, this balance is partly a function of the distribution of the longwave terrain-irradiance component. The amount of emitted longwave radiation from the warm, unglacierized bare-ground surfaces bordering the glacier participates significantly in the snow-and ice-radiation load (Reference Gratton,, Howarth., Marceau. and Blasco,Gratton and Howarth, 1991).
Similar to diffuse irradiance, the atmospheric longwave emittance is computed on the basis of the proportion of sky hemisphere not obstructed by topography or the altitude of the surface. As with diffuse irradiance, the atmospheric-emitted irradiance may exhibit some anisotropic-radiation behaviour. Often, however, for the sake of simplicity, the longwave irradiance is considered isotropic and is modelled accordingly on an unobstructed horizontal surface.
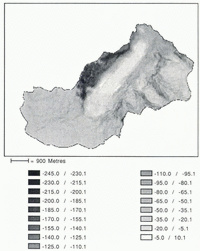
For terrain longwave irradiance, the most important variable to be included in the model is the surface temperature. Using TM6, the thermal band, direct measurements of surface-brightness temperature at the time of the satellite overpass may be acquired (Fig. 6).
To convert the surface-brightness temperature into thermodynamic values, information on the emissivity of surface covers is required. Many experimental and theoretical models have provided some values of emissivity for natural surface covers. The values used in our research are: 0.99 for snow (Reference Warren,Warren, 1982), 0.96 for clean and dirty ice (Reference Dozier,, Strahler, and ColwellDozier and Strahler, 1983), 0.915 for bare ground (Reference Dozier,Dozier and Strahler, 1983), 0.90 for vegetation (Reference Dozier,, Strahler, and ColwellDozier and Strahler, 1983) and 0.986 for water (Reference Wukelic,, Gibbons,, Martucci, and Foote,Wukelic and others, 1989).
Reference Bartolucci,, Chang,, Anuta, and Graves,Bartolucci and others (1988) and Reference Wukelic,, Gibbons,, Martucci, and Foote,Wukelic and others (1989) both stated that, in a clear-sky atmosphere, the TM-measured radiance provides an accurate assessment of the surface-brightness temperature. Reference Wukelic,, Gibbons,, Martucci, and Foote,Wukelic and others (1989) added that an atmospheric transmittance of ≥0.900 and a path radiance of ≥0.101 define the clear sky conditions in the TM6 spectral interval. Using LOWTRAN-6, the calculated atmospheric transmittance and path radiance from a basin of an average elevation of 2700 m for the time of the image acquisition were found to be 0.936 and 0.0735, respectively. In order to ensure the accuracy of the radiative-transfer model calculations, a comparison between image-derived and a known surface temperature was performed. Using the emissivity value of 0.99 for snow (Reference Warren,Warren, 1982), the average surface-temperature value for a random sample of 49 firn-line pixels was 273.86 Κ with a standard deviation of 0.42. The noise-equivalent temperature difference for TM6 is 0.5 deg, making the average measured temperature for melting snow very close to 273 K. From this, it was assumed that all surface-cover brightness temperatures measured with TM6 over the 120 m pixel were accurate. These temperature values were introduced into the computation of the amount of terrain-emitted radiation received on each individual target, taking into account the terrain geometry as was done for the terrain-reflected radiation.
With this model, it is possible to analyse the participation of terrain longwave irradiance in the total radiation balance. For example, the proportion of longwave terrain irradiance over all longwave fluxes in the upper part of the Athabasca Glacier ablation zone (just below the icefalls) and in the Aa Glacier accumulation zone was found to represent around 20% of the total incoming longwave radiation (Fig. 7). This tempering effect reduces the net loss to almost zero and is responsible for increased ablation in these areas, which otherwise would not occur. Furthermore, for all snow and ice covers, an average additional 6–7% of absorbed radiation is attributable to terrain longwave irradiance. Without the computation of terrain-emitted irradiance, the longwave deficit in many areas on clear days would be much higher, permitting snow and ice covers to absorb more shortwave radiation without melting.

Fig. 7. Map of the percentage of longwave terrain irradiance over all incoming longwave radiation for the Athabasca Glacier basin at the time of the TM-image acquisition.
The maximum values of the combined terrain and atmospheric longwave-radiation fluxes appear in the lower parts of the basin, while minimum values are found on high-elevation, steep, rocky surfaces (Reference Gratton,, Howarth. and GagnonGratton, 1991). On a clear day, most of the variance for the total longwave irradiance comes from the terrain component. In fact, for most surface covers, more than twice as much terrain irradiance comes from the neighbouring terrain in the longwave than in the shortwave part of the spectrum.
Using the information on surface temperature with the Stefan-Boltzman law, we obtain the amount of surface longwave-radiation emission and may calculate the net longwave-radiation values (Fig. 8). As expected, the spatial distribution of these values shows very few surfaces with a positive balance. On some snow and ice covers receiving high terrain irradiance, however, the incoming longwave radiation is found almost to balance the outgoing radiation. Without this terrain-irradiance component, most snow and ice covers could resist melt for much longer.

Fig. 8. Net longwave-radiation flux map of the Athabasca Glacier basin at the time of the TM-image acquisition (units in Wm−2).
Conclusions
Throughout this paper, special emphasis has been given to the importance of accurately modelling terrain irradiance in order to estimate values of total incoming radiation in all areas of the Athabasca Glacier basin in the Rocky Mountains of Canada. In fact, terrain irradiance participates in two key areas for establishing the net radiation load. First, estimates of the terrain-reflected radiation are required to calculate the total shortwave spectral irradiance in all parts of the glacier basin. In shadowed areas particularly, terrain irradiance represents an average of 20–25% of the total fluxes over all the shortwave spectrum. Detailed computation of all shortwave fluxes permits accurate surface-cover reflectance and albedo values to be derived from the satellite imagery. Secondly, assessment of the terrain-emitted radiation explains how, locally, the snow and ice covers have a very small longwave-radiation deficit. The computation of longwave terrain irradiance is made possible because the brightness-temperature values for surface covers on a clear day, available from TM6, correspond well to the expected surface-cover values. When the spatial distribution of the proportion of terrain longwave irradiance to the total longwave irradiance is compared with the net longwave-radiation values, the important participation of the terrain-emitted radiation in inducing snow-and-ice melt is recognized. Without this terrain-irradiance component, most snow and ice covers would experience much less melting.
Acknowledgements
Financial support for this research was provided to P.J. Howarth by the Natural Sciences and Engineering Research Council of Canada (NSERC), grant No. A0766. D. Gratton received postgraduate scholarships for his Ph.D. from NSERC and from the “Fond de concertation pour l’aide à la recherche” (FCAR) of the Province of Québec, Canada. D. Marceau received a postgraduate scholarship for her Ph.D. from the “Fond de concertation pour l’aide à la recherche” (FCAR) of the Province of Québec, Canada.