INTRODUCTION
Pneumonia and invasive pneumococcal diseases caused by Streptococcus pneumoniae (pneumococcus) are estimated to cause 1 million annual deaths worldwide with the greatest burden in developing countries [Reference Mulholland1]. The natural habitat of the bacteria is the human nasopharynx where carriage occurs in episodes of varying length. Disease is a rare event, arising when the bacteria spread from the nasopharynx and invade, for example the middle ear, lungs, blood, or meninges. Most episodes of pneumococcal carriage are asymptomatic and not observed. However, they are important as the source of transmission of bacteria to new hosts and thus indirectly as reservoir of serious pneumococcal diseases [Reference Bogaert, de Groot and Hermans2].
At the moment 91 different polysaccharide capsules of pneumococci are known. The capsule defines many biological characteristics of the bacterium and is the basis for classification of pneumococci into serotypes. Different serotypes often have different virulence and carriage properties [Reference Shouval3, Reference Smith4]. It is also assumed that different serotypes compete with each other in colonizing hosts [Reference Melegaro5]. Therefore, epidemiological analyses of pneumococcal carriage may need to address simultaneously individual serotypes and their interactions.
Transmission of pneumococci requires close contacts among individuals, typically children [Reference Bogaert, de Groot and Hermans2]. In particular, the household and day-care groups have been shown to be important contact groups for pneumococcal transmission [Reference Hendley6–Reference Leino10]. A proper analysis of transmission within such groups requires longitudinal data, i.e. repeated measurements of carriage in the same individuals over a period of time. Instead of actual event histories, which record times of acquisition and clearance, the analysis relies in practice on repeated measurements of carriage, taken at fixed time points. Interpretation of these types of longitudinal data in terms of episodes of carriage usually requires a model-based approach.
The epidemiological analysis of pneumococcal carriage has often been based on the idea of a binary process (carrier/non-carrier). Serotypes can be included as additional ‘marks’ on the events of acquisition, although analyses involving simultaneously more than one serotype have been rare. Auranen et al. [Reference Auranen11] studied the role of exposure and age on pneumococcal colonization by using three most prevalent serotypes in the data and assuming shared parameters across the serotypes. Cauchemez et al. [Reference Cauchemez12], studying 15 serotypes simultaneously, did not find differences between serotypes in the transmission rates within school classes. Recently Hoti et al. [Reference Hoti13] studied the dynamics of pneumococcal transmission in a day-care setting assuming shared parameters for all the studied serotypes. In these papers Bayesian estimation was used together with data augmentation to deal with incompletely observed data. Melegaro et al. [Reference Melegaro, Gay and Medley14] studied the role of age together with serotype-specific properties of current carriage and exposure using single serotype models and utilizing discretized transition probabilities.
While the frequency of pneumococcal carriage is highest in developing countries, most studies of transmission have been done for developed countries. In this study, we analysed longitudinal data about pneumococcal carriage in Bangladeshi families, collected with a 2- to 4-week sampling interval. Our main interest was describing parameters determining within-family transmission, including rates of within-family transmission and clearance of pneumococcal carriage. We analysed a number of serotypes jointly in a single model. This brings power to the statistical estimation and also makes it possible to take into account interactions between serotypes.
MATERIAL AND METHODS
Material
The data in the current study have been described in more detail previously [Reference Granat15, Reference Granat16]. Briefly, this was a longitudinal study of pneumococcal carriage in 99 infants (index children) born between May 2000 and April 2001, and followed for 1 year. The per-protocol sampling frequency was 2 weeks up to age 16 weeks of the index child and 4 weeks thereafter until age 1 year, with a total of 16 sampling rounds (Fig. 1b). Nasopharyngeal samples were taken at each sampling round (visit) from the index child and from those family members who were present and consented. The realized sampling times followed the per-protocol sampling quite well: the average (standard deviation) of the time intervals between consecutive visits during the scheduled 2-week sampling intervals was 18·3 (6·7) days and during the scheduled 4-week sampling intervals it was 32·0 (5·7) days. The realized shortest and longest time intervals between consecutive visits were 10 and 84 days, respectively.

Fig. 1. Compliance to sampling by visit together with the scheduled visiting scheme according to the protocol. (a) The proportion of samples of the maximum possible number by visit in different participant categories (index children, mothers, siblings, other family members). (b) The scheduled visits (v1–v16) according to the protocol.
All 99 index children and all 98 mothers, 152 siblings (43 aged <5 years, 109 aged between 5 and 18 years) and 115 other family members gave at least one sample during the follow-up. Hereafter, these individuals are referred to as study participants. In total 1459 samples were obtained from index children, 1378 from mothers, 1150 from siblings and 330 from other family members. The compliance of sampling was thus high in index children and mothers, with 92% and 88% of the maximum possible number of samples obtained, respectively. The compliance in participating siblings (47%) and other family members (18%) was lower. Figure 1a shows the percentage of samples obtained in different participant categories by visit.
Pneumococci were cultured, isolated and serotyped by standard methods as described previously [Reference Herva17]. The average point prevalence of pneumococcal carriage was moderate in the index children and siblings aged <5 years: 45% of samples were positive in both categories. The prevalence in study participants aged >18 years (7%) was clearly lower. The index children had their first pneumococcal carriage episode at an early age; half had been colonized at least once by age 2 months [Reference Granat15].
Exploratory analysis
According to the laboratory protocol, only the dominant serotype was searched for, and it is therefore assumed throughout the paper that an individual is always either a carrier of one of the pneumococcal serotypes or a non-carrier (Fig. 2). For each person, the follow-up period was defined as the period from the first sample to the last one in the individual. However, if there were >45 days between any two consecutive samples for an individual, the follow-up was discontinued for the time interval between the two samples. Episodes were defined as a series of consecutive samples of the same serotype in an individual. Each carriage episode was assumed to start midway between the first isolation of the type in the episode and the previous visit, and correspondingly to end midway between the last isolation in the episode and the following visit.

Fig. 2. The model graph. The model is illustrated for two serotypes, with three possible pairs of transitions between the different epidemiological states.
In the exploratory analysis, only the four most common serotypes in the episode data (6A, 19F, 15B/CFootnote †, 6B) were considered. Hereafter, these serotypes are referred to as target serotypes. Of these types there were 151 episodes in index children (34% among all in this group) and 131 (25%) in others. Family exposure was defined on the basis of carriage episodes in other family members. Specifically, a person was termed as exposed to a particular serotype at a given time, if any of the other family members had carried the type in question any time during the previous 30 days.
Based on episodes, Nelson–Aalen estimates of cumulative rates [Reference Nelson19, Reference Aalen20] were calculated to explore the dependence of acquisition on age group, serotype-specific exposure and current carriage (non-colonized/colonized) for an individual. Subsequently, estimates of constant crude hazards of acquisition were calculated, stratified by exposure and current carriage. Nelson–Aalen estimates of cumulative rates of clearance were also calculated, assuming that the four most common serotypes share the same rate. Two age groups were used: study participants aged <5 years, termed as children, and others, termed as adults.
The transmission model
A parametric transmission model was constructed to estimate serotype-specific parameters simultaneously. The same model structure as in the exploratory analysis was employed, allowing direct transitions from one carriage state to another (Fig. 2). The model is based on mass action law in assuming that the rate of acquisition of serotype s in a non-carrying child in family f is
where n f is the (fixed) size of family f and C(t)fs denotes the number of carriers of serotype s in family f at time t. In equation (1) the serotype-specific terms βs and κs represent family transmission parameters from a carrier to a susceptible and for the background rate (community force of infection), respectively. The rate of acquisition in a carrying child was specified as θαsf,child(t). The competition parameter θ, is the relative rate of acquisition in a carrying vs. non-carrying child, and has a similar interpretation to the ‘challenging strength’ as used in [Reference Melegaro5].
In contrast to previous studies [Reference Auranen11, Reference Cauchemez12, Reference Melegaro, Gay and Medley14], duration of pneumococcal carriage was assumed to follow a Weibull distribution. This is a two-parameter distribution with shape and scale parameters and probability density function τρ−τx τ−1exp(−(x/ρ)τ). The shape parameter was fixed (τ=2·0) but serotype-specific scale parameters, denoted by ρs, were assumed.
Regardless of the large overall number of samples, the absolute number of episodes is fairly small for all but the most common serotypes. Consequently, serotypes were grouped as follows. The four most common serotypes (6A, 19F, 15B/C, 6B) had their own individual rates of acquisition and clearance. For the next four most common serotypes (34, 10, 23F, 33) shared acquisition and clearance rates were assumed, but each episode was identified individually. The rest of the serotypes were pooled as one single class and thus the exact serotype identity was ignored for this class. The number of different carriage states is thus nine. In the model the same age classification of individuals as in the exploratory analysis was used.
A large number of serotype-specific parameters would obviously lead to identifiability problems, in particular in adults with only a few episodes per serotype. Therefore, all acquisition rates in adults were modelled through a common relative rate (η), relative to the corresponding rates in children. Similarly, all clearance rates in adults were modelled through a common relative rate (δ), relative to the corresponding rates in children.
To resolve the problem of unobserved acquisition and clearance times, Bayesian data augmentation was used to statistically impute histories of carriage within families (see Appendix). Regarding episodes, the difference from the exploratory analysis is that they were treated as random with respect to their number and exact location in time.
There were a large number of individuals that submitted only a few samples. To regulate this, persons fulfilling both of the following criteria were discarded from the transmission model: (1) those having no positive sample during the follow-up, (2) where the number of samples was less than half of the maximum (n=16). The number of these individuals (n=130), including mostly fathers (n=52) and grandmothers (n=24), was comparably large. However, in the current study children were the main focus of interest. Although the amount of exposure on children could be under-estimated due to ignoring part of the data, the impact of this is likely to be marginal because carriage in ignored individuals is relatively rare.
Model assessment
Predictive data were simulated from the transmission model using the posterior mean of the model parameters. In each of the simulations families excluding the index children were simulated for 2 years to obtain stationarity. The index children were then added to the families and the prevalence of pneumococcal carriage in index children was recorded at the true sampling times and compared with the actually observed values.
RESULTS
Exploratory analysis
Table 1 shows the serotype distribution separately in the samples and episodes for the eight most common serotypes in the data. Table 2 summarizes episodes for the exploratory analysis of acquisition for the four most common (target) serotypes. The data summaries are given in terms of episodes, which define the appropriate time at risk for acquisition of a specific serotype, and the number of acquisitions (new episodes) for the serotype in question. For analysis of acquisition, the episodes were stratified by exposure within the family and current state of carriage (non-colonized/colonized). Table 3 summarizes the data for the exploratory analysis of carriage clearance.
Table 1. Numbers of isolates and episodes. The numbers (percentages) are presented for four different participant categories: index children (newborns, n=99), siblings aged <5 years (n=43), older siblings (n=109) and other family members (>18 years, n=213)

* Other serotypes containing non-capsulated pneumococci.
Table 2. Serotype-specific numbers of acquisitions (no. acq.) with the time at risk for acquisition (Trisk), stratified by exposure within the family and current state of carriage in children (upper row numbers) and adults (lower row numbers). In children, serotype-specific crude acquisition rates (rate) were calculated, stratified by exposure

* The total number of new episodes of the serotype.
† The total follow-up time spent not carrying the serotype in question given as 10 000 days.
‡ Given per 10 000 days.
§ The ratio (i.e. the relative rate) of the rates with and without exposure.
Table 3. Number of clearances together with the time at risk (Trisk) and rate estimate (rate) for children (upper row numbers) and adults (lower row numbers) for the four most common serotypes

* Reported as per days.
Family exposure
The ratio of acquisition rates in children with and without exposure to the family varied between 4·8 and 10·5 for the four target serotypes (Table 2). The ratio of the total acquisition rates for these serotypes was 7·5 in children and 6·1 (=14·3/2·4) in adults, suggesting a significant effect of exposure on the rates of acquisition. Adjusting for a possible interaction between current carriage and acquisition, the effect of exposure in the non-colonized state only was effectively the same (children 8·5, adults 6·5). From the cumulative rate estimates (Fig. 3), showing the total rate for acquisition of any of the four target serotypes, the effect of exposure was similar: the rate (i.e. the slope) in exposed children (Fig. 3a, dashed line) was about tenfold compared to children with no family exposure (solid line). The effect of exposure was again similar in adults (Fig. 3b). The acquisition rates in both children and adults appear reasonably constant throughout the follow-up. In particular, the rates in adults appear proportional to those in children in all strata.

Fig. 3. Cumulative rate estimators, stratified by family exposure or current carriage state. Cumulative rates were determined by Nelson–Aalen estimators. Acquisition events are denoted as open symbols (○). (a) Cumulative rate of acquisition of the four target serotypes in children (aged <5 years), stratified by family exposure (yes/no). Rates were determined only from episodes of non-carriage. (b) Cumulative rate of acquisition of the four target types in adults (aged ⩾5 years), stratified by family exposure (yes/no). Rates were determined only from episodes of non-carriage. (c) Cumulative rate of acquisition of the four target serotypes in children without exposure to the family, stratified by current carriage state (non-colonized/colonized). Note the difference in the y scales
Age dependence
The estimated rate of acquisition for acquiring any of the four target serotypes without exposure was 8·2 (per 10 000 days) in children and 2·4 in adults, suggesting a significant effect of age on acquisition rates (Table 2). By comparing the cumulative acquisition rates (slopes) from the non-colonized state in non-exposed children and adults (Fig. 3a, b), a similar effect of age on the rate of acquisition as inferred above can be seen although the number of acquisitions in adults is small (note the difference in scales in the y axis).
Competition
According to the data shown in Table 2, the rate of acquisition for a child to acquire any of the four target serotypes with or without family exposure was 84·5 and 10·0 per 10 000 days, respectively, for transitions from a non-colonized state. For transitions from a colonized state the corresponding rate was 40·0 and 6·1 per 10 000 days, respectively, suggesting the presence of competition between serotypes. The same phenomenon can be inferred from Figure 3c, which shows the cumulative rates of acquisition in children stratified by the current carriage (non-colonized/colonized). The acquisition rate from the colonized state is 50% of that from the non-colonized state, and when ignoring the time interval, about 20–30 weeks of follow-up time when there are only a few acquisitions from the colonized state, the relative rate is about 0·8.
Clearance
The number of clearances (transitions to a non-carrying state) and the time at risk for clearance were calculated in order to investigate possible differences between serotypes in carriage clearance (Table 3). The crude estimates of clearance rates do not suggest any significant differences between the studied four serotypes. However, there appears to be some dependency in clearance rates on age, although the number of acquisitions is small in the adult age group.
The transmission model
Table 4 summarizes the posterior mean estimates of the model parameters, with 90% credible intervals (CIs). The results from the parametric model suggest that there are differences in the community acquisition rates between the serotypes analysed. For serotypes 6A and 19F the estimated mean sojourn time from the community for a susceptible child without exposure to the family was 1100 days, while for any serotype from the class (34, 10, 23F, 33) this was roughly double. The mean sojourn times of other serotypes were between these two values. The strikingly large estimate for the serotype class ‘Rest’ is due fact that in the model the community rate alone accounts for all acquisitions of the 47 serotypes in this class.
Table 4. Estimates of serotype-specific parameters in children (the posterior mean of the parameter and the 90% credible interval within parentheses)

* Per 1000 days.
† Based on estimated scale parameters (ρs) and the Weibull assumption with fixed-shape parameter (=2).
However, the differences between the community acquisition rates are masked when exposure to the family is present. For any of the studied serotypes the acquisition rate was about 12-fold when one other family member was carrying that particular serotype in a family of n=4 (i.e. mode of sampled family sizes). There were no significant differences in family transmission parameters between the studied serotypes. For a non-carrying child the mean acquisition time with one carrier in a family of n=4 ranged from 142 days (serotype 6B) to 108 days (serotype 15B/C). The common competition parameter (θ) for the eight most common serotypes was estimated as 0·83 (0·73–0·93). The proportionality describing adult susceptibility (η) was estimated as 0·46 (0·45–0·49).
The estimated mean duration of carriage episodes in children was between 44 (serotype 6B) and 62 (19F) days. Serotype 19F was found to be carried significantly longer than the other studied serotypes. No other significant differences between the serotypes were found. The adult clearance rate proportionality parameter (δ) was estimated as 1·13 (90% CI 1·15–1·18) suggesting a small but statistically significant difference between clearance rates in the studied age groups.
The model fit was assessed by comparing predictive data to the actual observations. Figure 4 presents samples of the predictive prevalence of overall pneumococcal carriage in the index children. The model is seen to fit well to the data.

Fig. 4. Posterior predictive analysis of the model indicating the model fit. Observations (◊) and 50 model predictions (dots) for prevalence of pneumococcal carriage in the index children.
DISCUSSION
In this paper we investigated transmission characteristics of pneumococcal serotypes, based on a 1-year follow-up of carriage in Bangladeshi infants and their family members. Based on a structured model of acquisition and clearance of carriage and state-of-the-art methods to deal with incompletely observed event times of acquisition and clearance, we were able to quantify serotype-specific parameters simultaneously. Serotypes that were common in the data were more often acquired from the community than rarer serotypes. In contrast, when conditioning acquisition rates on the presence of exposure within the family, there were no differences across serotypes in within-family transmission. The conditional acquisition rate in the presence of one carrier in a family of n=4 was roughly 12-fold compared to the community force of infection. Some differences were found between serotypes in the rate of carriage clearance, the more common serotypes being cleared at a slightly slower rate. In addition, the analysis provided evidence for between-serotype competition in that current pneumococcal carriage reduced acquisition of other serotypes.
The community force of infection was similar for the four most common serotypes in the data (6A, 19F, 15B/C, 6B), with about one acquisition from the community every 3 years per child (Table 4). In the group of the four next most common serotypes, any one of the serotypes (34, 10, 23F, 33) had a significantly lower community force of infection, with about double the waiting time for new acquisitions from the community. Although the overall rate of the group of remaining serotypes was about fivefold compared to the most common serotypes, this rate represents a total of 47 serotypes in the data. Consequently, individual serotypes within this group had on average a clearly lower community acquisition rate than the eight most common serotypes.
Simultaneous follow-up data regarding carriage in index children and their family members allowed estimation of conditional transmission rates within the family. Notably, the acquisition rate for a non-carrying child with a carrying family member was estimated to be similar across all studied serotypes (Table 4). This result applies to all eight serotypes that were treated separately. For the four most common serotypes, the conditional rate of acquisition with one carrier in the family was approximately 12-fold to the background rate (community force of infection) in a family of four members. Our data were collected from 17 different villages and therefore provided the option of using villages as contact groups instead of families. However, performing similar analysis to that in Table 3 the rate ratio of exposure vs. no exposure was close to 1 giving strong support to using family as the source of exposure in this analysis.
The model accommodated between-serotype competition in colonizing hosts through stratification of acquisition rates by current carriage (yes/no) in the individual. Current carriage in the child was found to reduce acquisition of other pneumococcal serotypes. Specifically, presence of between-serotype competition was quantified as a relative rate of acquisition of 0·83 (90% CI 0·68–0·94) in a carrying child compared to a non-carrying child. When the model was expanded with serotype-specific competition parameters, the estimates of other model parameters remained the same with wider credibility intervals, but there were no significant differences between the competition parameters. Detection of differences in competition across serotypes would thus require more extensive data. A further limitation of our analysis is that the data only recorded single carriage. It is unlikely that the model structure (Fig. 2) as employed in the current study fully corresponds to the actual mechanism of competition, which is likely to work through reduced rates for a carrier to acquire a secondary type. In this context the estimated magnitude of competition in our model might not have a straightforward interpretation.
The estimated mean duration of pneumococcal carriage varied between 44 and 62 days for all studied serotypes. All serotypes except one had similar mean durations of just above 6 weeks. Serotype 19F was estimated to be carried somewhat longer (mean 62 days), although the credible interval overlaps with those of the other serotypes. In the parametric model we estimated a higher clearance rate (1·21, 90% CI 1·13–1·27) for adults.
The effect of exposure has been noted previously as a risk factor for carriage and a higher acquisition rate has been shown for the family setting (see [Reference Hendley6, Reference Leino10, Reference Brimblecombe21]). On a qualitative level our results on the strong effect of exposure are consistent with results from a recent study of transmission in UK families [Reference Melegaro5]. In that study, significant differences in family transmission rates between serotypes were found. In the current study we did not find such differences. However, the method of Melegaro et al. [Reference Melegaro5] in using different models for different serotypes makes comprehensive comparisons of their results to other studies difficult. Our result of similar family transmission rates is parallel to a study of transmission rates within school classes where differences in conditional acquisition rates between two clusters of serotypes (vaccine and non-vaccine types) were not found [Reference Cauchemez12].
Our result on the lower susceptibility, i.e. lower rate of acquisition, in adults (mean 0·46, 90% CI 0·44–0·48) is supported by other studies (see [Reference Melegaro5–Reference Rosén7, Reference Hussain9–Reference Auranen11]). The overall effect of current carriage is consistent, at least on a qualitative level, with the results of other studies [Reference Melegaro5, Reference Granat16], while due to single serotype analysis done in [Reference Melegaro5], exact comparison is again difficult. This applies also to [Reference Granat16], where a slightly different model approach was applied to essentially the same data as ours.
In the current study, the eight most common serotypes covered only half of the episodes of 43 serotypes recovered from the index children (Table 1, [Reference Granat15]). The serotype distribution was thus skewed, which is a characteristic of most epidemiological studies of pneumococcal carriage. In the current analysis, the differences in serotype frequencies were largely attributed to differences in the community rate of acquisition. By contrast, the within-family rates were quite similar and therefore do not seem to account for varying serotype frequencies. It thus remains a question as to what maintains the skewed distribution of pneumococcal serotypes in the whole population. First, it is possible that even small differences in transmission characteristics would yield observable differences in the population prevalence across different serotypes. In fact, the estimated credible intervals of serotype-specific parameters do not hinder such behaviour. Moreover, our analysis did not allow serotype-specific estimates of rarer serotypes due to small number of episodes. These serotypes are likely to be different from the more common ones. Second, recent theoretical work on the joint dynamics of (pneumococcal) strains implies that differences across serotypes may exist even in the absence of differences in fitness (e.g. transmission characteristics) [Reference Lipsitch22]. Under such ‘ecological neutrality’, differences in prevalence could be present purely due to chance. Finally, it is known that pneumococcal carriage exhibits temporal and local microepidemics (see e.g. [Reference Hoti13]). This means that differences in abundance of serotypes reflect secular trends in any particular study.
Tabulation of crude rates of acquisition as well as non-parametric estimation of cumulative rates were used to guide in choosing the structure and parameterization of the actual transmission model. For example, the rates of acquisition in children (aged <5 years) and adults were found to be proportional in such exploratory analysis (Fig. 3). Another finding from the crude analysis was the lack of interaction between current carriage and the effect of exposure (Table 2). Comparison of results of the formal analysis to those from the data exploration also served as a way of performing model assessment. The magnitude of the estimated rates compared well with those from exploratory analysis. In particular, although the definition of exposure in the exploratory phase did not take into account the number of carriers in the family, the estimated relative rates due to exposure were similar.
Pneumococcal carriage was observed by repeated sampling of the state of carriage in the study participants, with a sampling interval ranging between 10 days to 12 weeks. The episodes of carriage were subsequently determined for the exploratory analysis in a way that did not require any specific pattern of within-sample intervals, although the minimum possible length of an episode was equal to the minimum sampling interval. The transmission model also accommodated shorter episodes due to statistical data augmentation, in agreement with the parametric assumptions of the rates of acquisition and clearance.
Under both phases of data analysis, estimation of clearance rates may suffer from too infrequent sampling, which does not allow sensitive detection of short episodes. Moreover, the observed prevalence of carriage remained stable at around 50% throughout the age range of 1–5 years. This means that it would be difficult to identify slight trends in age-specific rates even if they existed.
Exponential distribution has been widely used (e.g. [Reference Smith4, Reference Melegaro5, Reference Cauchemez12, Reference Högberg23]), although it may allow very short episodes, not directly supported by the observations. To achieve model-based augmentation of episodes, we therefore employed the Weibull distribution with a given shape parameter (τ=2, corresponding to a coefficient of variation of 0·52, compared to 1 of the exponential distribution). An alternative analysis with the exponential assumption (τ=1) resulted in almost similar estimates of mean durations. The mean durations in our study broadly correspond to those in [Reference Melegaro5], except for serotype 6B which was estimated to be carried for longer.
The break-off point of 5 years in modelling rates of acquisition and clearance was chosen because the point prevalence of pneumococcal carriage in the data remained at about 50% throughout this age range [Reference Granat15]. The same age range is routinely used to report morbidity and mortality in young children, and it is also often used in epidemiological studies of carriage (e.g. [Reference Melegaro5]). The assumption of a homogeneous rate of clearance, in particular in the age range ⩾5 years, is likely to be a crude simplification. However, a more stratified analysis was not possible with the available number of episodes in the data.
In summary, we have reported an analysis of a longitudinal dataset on pneumococcal transmission in a developed country setting. The main features of transmission were found to be similar to those in previous analyses in other settings. Most notably, the importance of close contacts within families was reinforced by the current study. However, the question remains as to what maintains the diversity of pneumococcal serotypes in the population. This question gains weight from the observation that at least the most common serotypes in the current study did not appear to differ notably in terms of their transmission characteristics. It should also to be noted that the serotypes analysed in the current study included only three types (6B, 19F, 23F) that are components of pneumococcal conjugate vaccines (PCV). These commonly carried types are generally known to be opportunistic pathogens. Whether similar transmission characteristics apply to other PCV types could not be determined in the current study. More detailed analyses of epidemiological data and the dynamics of transmission in a population are required.
APPENDIX
Likelihood
Assume that at time t each individual is either a non-carrier (i.e. has carriage state ‘0’) or carries one of the serotypes (1, …, n s). The transition probability to move from state r to state s≠r over time interval dt is
where I ir(t) is an indicator of individual i being state r at time t. Depending on the values of r and s(≠r) we define
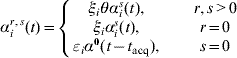
where ξi=1 for a child (aged <5 years), ξi=η for an adult. Analogously, in the case of clearance (s=0), εi is an age variable taking the values εi=1 for a child and εi=δ for an adult. The baseline rate of acquisition (αis(t)) is given by equation (1), and the rate of clearance α0(t−t acq) depends on the time of acquisition of the previous acquisition (serotype r) according to the Weibull rate. Denote by T ir,s the set of times at which individual i makes transitions from state r to state s during their family-specific follow-up time [t i0,t i1] and by ![]() the set of all n individuals' complete data. The likelihood of the complete data T n is now
the set of all n individuals' complete data. The likelihood of the complete data T n is now
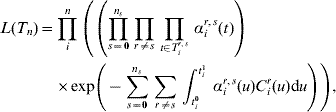
where C ir(u) denotes the number of carriers of serotype r in the family of individual i at time u.
Priors
The following non-informative normal priors were used: βs~N(0·01, 1002), κs~N(0·01, 1002), ρs~N(0·02, 1002), η~N(1, 1002) and δ~N(1, 1002), all restricted to positive values only. For competition parameter θ a uniform prior (0, 10) for the logarithm of θ was used. The possible maximum number of acquisitions of each study participant during the family-wise follow-up time was set to 50 (for more details, see [Reference Hoti13]).
Statistical inference
Combining the prior with the likelihood allows us to formulate the posterior distribution of the model parameters. Sampling from this distribution was done using a Markov Chain Monte Carlo algorithm, where the exact number of episodes and their location in time (set as T n above) were treated as additional model parameters.
ACKNOWLEDGEMENTS
This study is part of the research of the PneumoCarr Consortium funded by a grant from the Bill and Melinda Gates Foundation through the Grand Challenges in Global Health Initiative.
DECLARATION OF INTEREST
None.










