1 Introduction
A widespread principle in real algebraic geometry is to find and use algebraic certificates for geometric statements. For example, a sum of squares representation of a homogeneous polynomial
![]() $p\in {\mathbb R}[x_1,\ldots ,x_n]_{2d}$
of degree
$p\in {\mathbb R}[x_1,\ldots ,x_n]_{2d}$
of degree
![]() $2d$
is a finite sequence of polynomials
$2d$
is a finite sequence of polynomials
![]() $g_1,\dots ,g_r\in {\mathbb R}[x_1,\ldots ,x_n]_d$
such that
$g_1,\dots ,g_r\in {\mathbb R}[x_1,\ldots ,x_n]_d$
such that
and serves as an algebraic certificate of the geometric property that p takes only nonnegative values at real points:
![]() $p(x)\geq 0$
for all
$p(x)\geq 0$
for all
![]() $x\in {\mathbb R}^n$
. In an influential paper, Hilbert [Reference HilbertHil88] showed that the converse is true if (and only if)
$x\in {\mathbb R}^n$
. In an influential paper, Hilbert [Reference HilbertHil88] showed that the converse is true if (and only if)
![]() $2d=2$
, or
$2d=2$
, or
![]() $n=1$
, or
$n=1$
, or
![]() $(2d,n)=(4,3)$
. While in the first two cases this can be seen quite easily via linear algebra and the fundamental theorem of algebra, respectively, the proof for the case
$(2d,n)=(4,3)$
. While in the first two cases this can be seen quite easily via linear algebra and the fundamental theorem of algebra, respectively, the proof for the case
![]() $(2d,n)=(4,3)$
of ternary quartics is nontrivial. There have been several different new proofs of this statement in the last 20 years: via the Jacobian of the plane curve defined by p [Reference Powers, Reznick, Scheiderer and SottilePRSS04] relying on results of Coble [Reference CobleCob82], using elementary techniques [Reference Pfister and ScheidererPS12], and as a special case of more general results on varieties of minimal degree [Reference Blekherman, Smith and VelascoBSV16].
$(2d,n)=(4,3)$
of ternary quartics is nontrivial. There have been several different new proofs of this statement in the last 20 years: via the Jacobian of the plane curve defined by p [Reference Powers, Reznick, Scheiderer and SottilePRSS04] relying on results of Coble [Reference CobleCob82], using elementary techniques [Reference Pfister and ScheidererPS12], and as a special case of more general results on varieties of minimal degree [Reference Blekherman, Smith and VelascoBSV16].
Another instance, that has attracted a lot of attention recently, is the following. Let
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
be a homogeneous polynomial for which there are real symmetric (or complex Hermitian) matrices
$h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
be a homogeneous polynomial for which there are real symmetric (or complex Hermitian) matrices
![]() $A_0,\ldots ,A_n$
and
$A_0,\ldots ,A_n$
and
![]() $r\in {\mathbb Z}_{>0}$
such that
$r\in {\mathbb Z}_{>0}$
such that
and
![]() $e_0A_0+\cdots +e_nA_n$
is positive definite for some
$e_0A_0+\cdots +e_nA_n$
is positive definite for some
![]() $e\in {\mathbb R}^{n+1}$
. In this case, we say that
$e\in {\mathbb R}^{n+1}$
. In this case, we say that
![]() $h^r$
has a definite symmetric (or Hermitian) determinantal representation and it is a certificate that h is hyperbolic with respect to e in the sense that the univariate polynomial
$h^r$
has a definite symmetric (or Hermitian) determinantal representation and it is a certificate that h is hyperbolic with respect to e in the sense that the univariate polynomial
![]() $h(te-v)\in {\mathbb R}[t]$
has only real zeros for all
$h(te-v)\in {\mathbb R}[t]$
has only real zeros for all
![]() $v\in {\mathbb R}^{n+1}$
. The minimal polynomial of a Hermitian matrix has only real zeros. Lax [Reference LaxLax58] conjectured that for
$v\in {\mathbb R}^{n+1}$
. The minimal polynomial of a Hermitian matrix has only real zeros. Lax [Reference LaxLax58] conjectured that for
![]() $n=2$
and arbitrary
$n=2$
and arbitrary
![]() $d\in {\mathbb Z}_{>0}$
, the following strong converse is true: every hyperbolic polynomial
$d\in {\mathbb Z}_{>0}$
, the following strong converse is true: every hyperbolic polynomial
![]() $h\in {\mathbb R}[x_0,x_1,x_2]_d$
has a definite symmetric determinantal representation (up to multiplication with a nonzero scalar). This conjecture was solved to the affirmative by Helton and Vinnikov [Reference Helton and VinnikovHV07]. Furthermore, every hyperbolic
$h\in {\mathbb R}[x_0,x_1,x_2]_d$
has a definite symmetric determinantal representation (up to multiplication with a nonzero scalar). This conjecture was solved to the affirmative by Helton and Vinnikov [Reference Helton and VinnikovHV07]. Furthermore, every hyperbolic
![]() $h\in {\mathbb R}[x_0,x_1,x_2,x_3]_3$
has a definite Hermitian determinantal representation [Reference Buckley and KoširBK07], and for every quadratic hyperbolic polynomial
$h\in {\mathbb R}[x_0,x_1,x_2,x_3]_3$
has a definite Hermitian determinantal representation [Reference Buckley and KoširBK07], and for every quadratic hyperbolic polynomial
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_2$
, there is an
$h\in {\mathbb R}[x_0,\ldots ,x_n]_2$
, there is an
![]() $r\in {\mathbb Z}_{>0}$
such that
$r\in {\mathbb Z}_{>0}$
such that
![]() $h^r$
has definite symmetric (or Hermitian) determinantal representation [Reference Netzer and ThomNT12]. On the other hand, if
$h^r$
has definite symmetric (or Hermitian) determinantal representation [Reference Netzer and ThomNT12]. On the other hand, if
![]() $d\geq 4$
and
$d\geq 4$
and
![]() $n\geq 3$
or if
$n\geq 3$
or if
![]() $d\geq 3$
and
$d\geq 3$
and
![]() $n\geq 5$
, there are hyperbolic polynomials
$n\geq 5$
, there are hyperbolic polynomials
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
such that no power
$h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
such that no power
![]() $h^r$
has a definite symmetric (or Hermitian) determinantal representation (see [Reference BrändénBrä11, Reference KummerKum16b]; resp. [Reference SaundersonBKS+ar, Sau19]). The case
$h^r$
has a definite symmetric (or Hermitian) determinantal representation (see [Reference BrändénBrä11, Reference KummerKum16b]; resp. [Reference SaundersonBKS+ar, Sau19]). The case
![]() $(d,n)=(3,4)$
is open.
$(d,n)=(3,4)$
is open.
The condition of
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
being hyperbolic with respect to e can be phrased in geometric terms as follows: let
$h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
being hyperbolic with respect to e can be phrased in geometric terms as follows: let
![]() $X={\mathcal V}(h)\subset \mathbb {P}^n$
be the hypersurface defined by h. Then h is hyperbolic with respect to e if and only if the linear projection
$X={\mathcal V}(h)\subset \mathbb {P}^n$
be the hypersurface defined by h. Then h is hyperbolic with respect to e if and only if the linear projection
![]() $\pi _e\colon X\to \mathbb {P}^{n-1}$
with center e is real fibered in the sense that
$\pi _e\colon X\to \mathbb {P}^{n-1}$
with center e is real fibered in the sense that
![]() $\pi _e^{-1}(\mathbb {P}^{n-1}({\mathbb R}))\subset X({\mathbb R})$
. This leads to a natural generalization of hyperbolicity to arbitrary embedded varieties introduced in [Reference Shamovich and VinnikovSV18] and further studied in [Reference Kummer and ShamovichKS20]. A subvariety
$\pi _e^{-1}(\mathbb {P}^{n-1}({\mathbb R}))\subset X({\mathbb R})$
. This leads to a natural generalization of hyperbolicity to arbitrary embedded varieties introduced in [Reference Shamovich and VinnikovSV18] and further studied in [Reference Kummer and ShamovichKS20]. A subvariety
![]() $X\subset \mathbb {P}^n$
of dimension k is hyperbolic with respect to a linear subspace
$X\subset \mathbb {P}^n$
of dimension k is hyperbolic with respect to a linear subspace
![]() $E\subset \mathbb {P}^n$
of codimension
$E\subset \mathbb {P}^n$
of codimension
![]() $k+1$
if
$k+1$
if
![]() $X\cap E=\emptyset $
and the linear projection
$X\cap E=\emptyset $
and the linear projection
![]() $\pi _E\colon X\to \mathbb {P}^k$
with center E is real fibered. Furthermore, a polynomial
$\pi _E\colon X\to \mathbb {P}^k$
with center E is real fibered. Furthermore, a polynomial
![]() $p\in {\mathbb R}[x_1,\ldots ,x_n]_{2d}$
is nonnegative if and only if the double cover
$p\in {\mathbb R}[x_1,\ldots ,x_n]_{2d}$
is nonnegative if and only if the double cover
![]() $X\to \mathbb {P}^n$
ramified along the zero set of p is real fibered, where X is defined as the zero set of
$X\to \mathbb {P}^n$
ramified along the zero set of p is real fibered, where X is defined as the zero set of
![]() $y^2-p$
in a suitable weighted projective space. Thus, both abovementioned geometric properties of polynomials, being nonnegative and being hyperbolic, can be seen as special instances of real-fibered morphisms.
$y^2-p$
in a suitable weighted projective space. Thus, both abovementioned geometric properties of polynomials, being nonnegative and being hyperbolic, can be seen as special instances of real-fibered morphisms.
Let
![]() $f\colon X\to Y$
be a morphism of schemes. A coherent sheaf
$f\colon X\to Y$
be a morphism of schemes. A coherent sheaf
![]() ${\mathcal F}$
on X is called f-Ulrich if there is a natural number
${\mathcal F}$
on X is called f-Ulrich if there is a natural number
![]() $r>0$
such that
$r>0$
such that
![]() $f_*{\mathcal F}\cong {\mathcal O}_Y^r$
. If
$f_*{\mathcal F}\cong {\mathcal O}_Y^r$
. If
![]() $X\subset \mathbb {P}^n$
is a closed subscheme, then one defines a coherent sheaf
$X\subset \mathbb {P}^n$
is a closed subscheme, then one defines a coherent sheaf
![]() ${\mathcal F}$
on X to be an Ulrich sheaf per se if it is
${\mathcal F}$
on X to be an Ulrich sheaf per se if it is
![]() $\pi $
-Ulrich for any finite surjective linear projection
$\pi $
-Ulrich for any finite surjective linear projection
![]() $\pi \colon X\to \mathbb {P}^k$
. This is equivalent to
$\pi \colon X\to \mathbb {P}^k$
. This is equivalent to
![]() $H^i(X,{\mathcal F}(-j))=0$
for
$H^i(X,{\mathcal F}(-j))=0$
for
![]() $1\leq j\leq \dim (X)$
and all i. See [Reference BeauvilleBea18] for an introduction to Ulrich sheaves. The question of which subvarieties of
$1\leq j\leq \dim (X)$
and all i. See [Reference BeauvilleBea18] for an introduction to Ulrich sheaves. The question of which subvarieties of
![]() $\mathbb {P}^n$
carry an Ulrich sheaf is of particular interest in the context of Boij–Söderberg theory [Reference Eisenbud and SchreyerES11].
$\mathbb {P}^n$
carry an Ulrich sheaf is of particular interest in the context of Boij–Söderberg theory [Reference Eisenbud and SchreyerES11].
For real-fibered morphisms
![]() $f\colon X\to Y$
, positive f-Ulrich sheaves have been defined in [Reference Kummer and ShamovichKS20] and it was shown that a hypersurface in
$f\colon X\to Y$
, positive f-Ulrich sheaves have been defined in [Reference Kummer and ShamovichKS20] and it was shown that a hypersurface in
![]() $\mathbb {P}^n$
carries a positive Ulrich sheaf if and only if it is cut out by a polynomial with a definite determinantal representation. For subvarieties
$\mathbb {P}^n$
carries a positive Ulrich sheaf if and only if it is cut out by a polynomial with a definite determinantal representation. For subvarieties
![]() $X\subset \mathbb {P}^n$
of higher codimension supporting a positive Ulrich sheaf is equivalent to admitting some generalized type of determinantal representation, that was introduced in [Reference Shamovich and VinnikovSV18] and motivated by operator theory. The existence of such a determinantal representation for X implies that some power of the Chow form of X has a definite determinantal representation. On the other hand, we will show that a real-fibered double cover
$X\subset \mathbb {P}^n$
of higher codimension supporting a positive Ulrich sheaf is equivalent to admitting some generalized type of determinantal representation, that was introduced in [Reference Shamovich and VinnikovSV18] and motivated by operator theory. The existence of such a determinantal representation for X implies that some power of the Chow form of X has a definite determinantal representation. On the other hand, we will show that a real-fibered double cover
![]() $f\colon X\to \mathbb {P}^n$
, which is ramified along the zero set of a homogeneous polynomial p, admits a positive f-Ulrich sheaf if and only if p is a sum of squares. Therefore, the notion of positive Ulrich sheaves encapsulates both types of algebraic certificates for the abovementioned geometric properties of homogeneous polynomials, namely being a sum of squares and having a definite determinantal representation.
$f\colon X\to \mathbb {P}^n$
, which is ramified along the zero set of a homogeneous polynomial p, admits a positive f-Ulrich sheaf if and only if p is a sum of squares. Therefore, the notion of positive Ulrich sheaves encapsulates both types of algebraic certificates for the abovementioned geometric properties of homogeneous polynomials, namely being a sum of squares and having a definite determinantal representation.
The main result of this article is a criterion for a coherent sheaf to be a positive Ulrich sheaf, which implies all the abovementioned existence results on representations as sums of squares and determinantal representations, and more. It only comprises a positivity criterion that can be checked locally as well as a condition on the dimension of the space of global sections (but surprisingly not of the higher cohomology groups) of the coherent sheaf at hand.
To this end, after some preparations in Section 3, we characterize Ulrich sheaves in terms of a certain bilinear mapping and its behavior on the level of global sections in Section 4 (see, in particular, Theorem 4.6). In this part, we work over an arbitrary ground field and we believe that these results can be of independent interest.
After we review some facts on the codifferent sheaf in Section 5, that will be important later on, we focus on varieties over
![]() ${\mathbb R}$
. In Section 6, we recall some facts about real-fibered morphisms. We then define positive Ulrich sheaves in Section 7. Theorem 7.2 is the abovementioned convenient criterion for checking whether a sheaf is a positive Ulrich sheaf. In Section 8, we show that for a given polynomial having a determinantal or sum of squares representation is equivalent to the existence of a certain positive Ulrich sheaf. From this, the result on determinantal representations of quadratic hyperbolic polynomials from [Reference Netzer and ThomNT12] follows directly. In order to make our general theory also applicable to other cases of interest, we specialize to Ulrich sheaves of rank one on irreducible varieties in Section 9. Theorem 9.3 gives a convenient criterion for a Weil divisor giving rise to a positive Ulrich sheaf. Namely, under some mild assumptions, if
${\mathbb R}$
. In Section 6, we recall some facts about real-fibered morphisms. We then define positive Ulrich sheaves in Section 7. Theorem 7.2 is the abovementioned convenient criterion for checking whether a sheaf is a positive Ulrich sheaf. In Section 8, we show that for a given polynomial having a determinantal or sum of squares representation is equivalent to the existence of a certain positive Ulrich sheaf. From this, the result on determinantal representations of quadratic hyperbolic polynomials from [Reference Netzer and ThomNT12] follows directly. In order to make our general theory also applicable to other cases of interest, we specialize to Ulrich sheaves of rank one on irreducible varieties in Section 9. Theorem 9.3 gives a convenient criterion for a Weil divisor giving rise to a positive Ulrich sheaf. Namely, under some mild assumptions, if
![]() $f\colon X\to Y$
is a real-fibered morphism and D a Weil divisor on X such that
$f\colon X\to Y$
is a real-fibered morphism and D a Weil divisor on X such that
![]() $2D$
differs from the ramification divisor of f only by a principal divisor defined by a nonnegative rational function, then the sheaf associated with D is a positive f-Ulrich sheaf whenever its space of global sections has dimension
$2D$
differs from the ramification divisor of f only by a principal divisor defined by a nonnegative rational function, then the sheaf associated with D is a positive f-Ulrich sheaf whenever its space of global sections has dimension
![]() $\deg (f)$
. A particularly nice case is that of hyperbolic hypersurfaces: The existence of a definite determinantal representation is guaranteed by the existence of a certain interlacer, generalizing the construction for plane curves from [Reference Plaumann and VinzantPV13] (see Corollary 9.9).
$\deg (f)$
. A particularly nice case is that of hyperbolic hypersurfaces: The existence of a definite determinantal representation is guaranteed by the existence of a certain interlacer, generalizing the construction for plane curves from [Reference Plaumann and VinzantPV13] (see Corollary 9.9).
In Section 10, we apply our theory to the case of curves and show how it easily implies the Helton–Vinnikov theorem on plane hyperbolic curves [Reference Helton and VinnikovHV07] as well as its generalization to curves of higher codimension from [Reference Shamovich and VinnikovSV18] using the
![]() $2$
-divisibility of the Jacobian. Finally, in Section 11, we consider the anticanonical map on real del Pezzo surfaces in order to reprove Hilbert’s theorem on ternary quartics [Reference HilbertHil88] and the existence of a Hermitian determinantal representation on cubic hyperbolic surfaces [Reference Buckley and KoširBK07]. We further prove a new result on quartic del Pezzo surfaces in
$2$
-divisibility of the Jacobian. Finally, in Section 11, we consider the anticanonical map on real del Pezzo surfaces in order to reprove Hilbert’s theorem on ternary quartics [Reference HilbertHil88] and the existence of a Hermitian determinantal representation on cubic hyperbolic surfaces [Reference Buckley and KoširBK07]. We further prove a new result on quartic del Pezzo surfaces in
![]() $\mathbb {P}^4$
. Apart from our general theory, the only ingredients for this part are basic properties of (real) del Pezzo surfaces as well as the Riemann–Roch theorem.
$\mathbb {P}^4$
. Apart from our general theory, the only ingredients for this part are basic properties of (real) del Pezzo surfaces as well as the Riemann–Roch theorem.
2 Preliminaries and notation
For any scheme X and
![]() $p\in X$
, we denote by
$p\in X$
, we denote by
![]() $\kappa (p)$
the residue class field of X at p. If X is separated, reduced (but not necessarily irreducible), and of finite type over a field K, we say that X is a variety over K. For any coherent sheaf
$\kappa (p)$
the residue class field of X at p. If X is separated, reduced (but not necessarily irreducible), and of finite type over a field K, we say that X is a variety over K. For any coherent sheaf
![]() ${\mathcal F}$
on X, we denote by
${\mathcal F}$
on X, we denote by
![]() $\operatorname {rank}_p({\mathcal F})$
the dimension of the fiber of
$\operatorname {rank}_p({\mathcal F})$
the dimension of the fiber of
![]() ${\mathcal F}$
at p considered as
${\mathcal F}$
at p considered as
![]() $\kappa (p)$
-vector space. If X is irreducible with generic point
$\kappa (p)$
-vector space. If X is irreducible with generic point
![]() $\xi $
, we simply denote
$\xi $
, we simply denote
![]() $\operatorname {rank}({\mathcal F})=\operatorname {rank}_\xi ({\mathcal F})$
. If X is a scheme (over a field K) and L a field (extension of K), then we denote by
$\operatorname {rank}({\mathcal F})=\operatorname {rank}_\xi ({\mathcal F})$
. If X is a scheme (over a field K) and L a field (extension of K), then we denote by
![]() $X(L)$
the set of all morphisms
$X(L)$
the set of all morphisms
![]() $\operatorname {Spec}(L)\to X$
of schemes (over K). For a field K, we let
$\operatorname {Spec}(L)\to X$
of schemes (over K). For a field K, we let
![]() $\mathbb {P}^n_K=\textrm {Proj}(K[x_0,\ldots ,x_n])$
, and if the field is clear from the context, we omit the index and just write
$\mathbb {P}^n_K=\textrm {Proj}(K[x_0,\ldots ,x_n])$
, and if the field is clear from the context, we omit the index and just write
![]() $\mathbb {P}^n$
. We say that a scheme is Noetherian if it can be covered by a finite number of open affine subsets that are spectra of Noetherian rings.
$\mathbb {P}^n$
. We say that a scheme is Noetherian if it can be covered by a finite number of open affine subsets that are spectra of Noetherian rings.
3 Bilinear mappings on coherent sheaves
Definition 3.1 Let X be a scheme, and let
![]() ${\mathcal F}_1,{\mathcal F}_2$
, and
${\mathcal F}_1,{\mathcal F}_2$
, and
![]() ${\mathcal G}$
be coherent sheaves on X. A
${\mathcal G}$
be coherent sheaves on X. A
![]() ${\mathcal G}$
-valued pairing of
${\mathcal G}$
-valued pairing of
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
is a morphism of coherent sheaves
${\mathcal F}_2$
is a morphism of coherent sheaves
![]() $\varphi \colon {\mathcal F}_1 \otimes {\mathcal F}_2 \to {\mathcal G}$
. Let K be a field and
$\varphi \colon {\mathcal F}_1 \otimes {\mathcal F}_2 \to {\mathcal G}$
. Let K be a field and
![]() $\alpha \in X(K)$
, i.e., a morphism
$\alpha \in X(K)$
, i.e., a morphism
![]() $\alpha \colon \operatorname {Spec} (K) \to X$
. Then we get a bilinear map
$\alpha \colon \operatorname {Spec} (K) \to X$
. Then we get a bilinear map
![]() $\alpha ^* \varphi $
on
$\alpha ^* \varphi $
on
![]() $\alpha ^* {\mathcal F}_1 \times \alpha ^*{\mathcal F}_2$
with values in
$\alpha ^* {\mathcal F}_1 \times \alpha ^*{\mathcal F}_2$
with values in
![]() $\alpha ^* {\mathcal G}$
which are just finite-dimensional K-vector spaces. We say that
$\alpha ^* {\mathcal G}$
which are just finite-dimensional K-vector spaces. We say that
![]() $\varphi $
is nondegenerate at
$\varphi $
is nondegenerate at
![]() $\alpha \in X(K)$
if the map
$\alpha \in X(K)$
if the map
![]() ${\alpha ^* {\mathcal F}_1 \to \operatorname {Hom}_K( \alpha ^*{\mathcal F}_2, \alpha ^* {\mathcal G})} $
induced by
${\alpha ^* {\mathcal F}_1 \to \operatorname {Hom}_K( \alpha ^*{\mathcal F}_2, \alpha ^* {\mathcal G})} $
induced by
![]() $\alpha ^* \varphi $
is an isomorphism.
$\alpha ^* \varphi $
is an isomorphism.
For the rest of this section, unless stated otherwise, let X always be a geometrically integral scheme with generic point
![]() $\xi $
which is proper over a field K.
$\xi $
which is proper over a field K.
Lemma 3.1 Let
![]() ${\mathcal F}$
be a coherent sheaf on X which is generated by global sections. If there is a K-basis of
${\mathcal F}$
be a coherent sheaf on X which is generated by global sections. If there is a K-basis of
![]() $H^0(X,{\mathcal F})$
which is also a
$H^0(X,{\mathcal F})$
which is also a
![]() $\kappa (\xi )$
-basis of
$\kappa (\xi )$
-basis of
![]() ${\mathcal F}_\xi $
, then
${\mathcal F}_\xi $
, then
![]() ${\mathcal F}\cong {\mathcal O}_X^r$
, where
${\mathcal F}\cong {\mathcal O}_X^r$
, where
![]() $r=\dim H^0(X,{\mathcal F})$
.
$r=\dim H^0(X,{\mathcal F})$
.
Proof Let
![]() ${\mathcal K}$
be the kernel of the map
${\mathcal K}$
be the kernel of the map
![]() ${\mathcal O}_X^r\to {\mathcal F}$
that sends the unit vectors to the K-basis of
${\mathcal O}_X^r\to {\mathcal F}$
that sends the unit vectors to the K-basis of
![]() $H^0(X,{\mathcal F})$
. Since
$H^0(X,{\mathcal F})$
. Since
![]() ${\mathcal F}$
is generated by global sections, this map is surjective. We thus obtain the short exact sequence
${\mathcal F}$
is generated by global sections, this map is surjective. We thus obtain the short exact sequence
Passing to the stalk at
![]() $\xi $
gives
$\xi $
gives
![]() ${\mathcal K}_\xi =0$
by our assumption. Since
${\mathcal K}_\xi =0$
by our assumption. Since
![]() ${\mathcal K}$
is torsion-free as a subsheaf of
${\mathcal K}$
is torsion-free as a subsheaf of
![]() ${\mathcal O}_X^r$
, this implies that
${\mathcal O}_X^r$
, this implies that
![]() ${\mathcal K}=0$
and therefore
${\mathcal K}=0$
and therefore
![]() ${\mathcal O}_X^r\cong {\mathcal F}$
.
${\mathcal O}_X^r\cong {\mathcal F}$
.
Remark 3.2 Let
![]() $\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X} {\mathcal F}_2 \to {\mathcal O}_X$
be a pairing of the coherent sheaves
$\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X} {\mathcal F}_2 \to {\mathcal O}_X$
be a pairing of the coherent sheaves
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
. This induces a bilinear mapping
${\mathcal F}_2$
. This induces a bilinear mapping
where
![]() $V_i=H^0(X,{\mathcal F}_i)$
since
$V_i=H^0(X,{\mathcal F}_i)$
since
![]() $H^0(X,{\mathcal O}_X)=K$
.
$H^0(X,{\mathcal O}_X)=K$
.
Lemma 3.3 Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent sheaves on X, let
${\mathcal F}_2$
be coherent sheaves on X, let
![]() $V_i=H^0(X,{\mathcal F}_i)$
, and let
$V_i=H^0(X,{\mathcal F}_i)$
, and let
![]() $s_1,\ldots ,s_r$
be a basis of
$s_1,\ldots ,s_r$
be a basis of
![]() $V_1$
. Let
$V_1$
. Let
![]() $\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X}{\mathcal F}_2\to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
$\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X}{\mathcal F}_2\to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
![]() $V_1 \times V_2\to K$
is nondegenerate. Then the images of
$V_1 \times V_2\to K$
is nondegenerate. Then the images of
![]() $s_1,\ldots ,s_r$
in the
$s_1,\ldots ,s_r$
in the
![]() $\kappa (\xi )$
-vector space
$\kappa (\xi )$
-vector space
![]() $({\mathcal F}_1)_\xi $
are linearly independent.
$({\mathcal F}_1)_\xi $
are linearly independent.
Proof Since the bilinear mapping
![]() $V_1 \times V_2\to K$
is nondegenerate, there is a basis
$V_1 \times V_2\to K$
is nondegenerate, there is a basis
![]() $t_1,\ldots ,t_r\in V_2$
that is dual to
$t_1,\ldots ,t_r\in V_2$
that is dual to
![]() $s_1,\ldots ,s_r$
with respect to this bilinear mapping. Suppose
$s_1,\ldots ,s_r$
with respect to this bilinear mapping. Suppose
![]() $f_1,\ldots ,f_r\in \kappa (\xi )$
such that
$f_1,\ldots ,f_r\in \kappa (\xi )$
such that
Tensoring with
![]() $t_j$
and applying
$t_j$
and applying
![]() $\varphi $
yields
$\varphi $
yields
![]() $f_j\cdot \varphi (s_j\otimes t_j)=0$
and therefore
$f_j\cdot \varphi (s_j\otimes t_j)=0$
and therefore
![]() $f_j=0$
since
$f_j=0$
since
![]() $\varphi (s_j\otimes t_j)=1$
by assumption.
$\varphi (s_j\otimes t_j)=1$
by assumption.
Proposition 3.4 Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent sheaves on X, let
${\mathcal F}_2$
be coherent sheaves on X, let
![]() $V_i=H^0(X,{\mathcal F}_i)$
, and let
$V_i=H^0(X,{\mathcal F}_i)$
, and let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be generated by global sections. Let
${\mathcal F}_2$
be generated by global sections. Let
![]() $\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X} {\mathcal F}_2 \to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
$\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X} {\mathcal F}_2 \to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
![]() $V_1 \times V_2\to K$
is nondegenerate. Then:
$V_1 \times V_2\to K$
is nondegenerate. Then:
-
(a)
 ${\mathcal F}_i\cong {\mathcal O}_X^r$
, where
${\mathcal F}_i\cong {\mathcal O}_X^r$
, where
 $r=\dim V_i$
.
$r=\dim V_i$
. -
(b) The morphism
 ${\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal O}_X)$
corresponding to
${\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal O}_X)$
corresponding to
 $\varphi $
is an isomorphism.
$\varphi $
is an isomorphism.
Proof Let
![]() $s_1,\ldots ,s_r\in V_1$
be a basis of
$s_1,\ldots ,s_r\in V_1$
be a basis of
![]() $V_1$
. By assumption,
$V_1$
. By assumption,
![]() $s_1,\ldots ,s_r$
span the
$s_1,\ldots ,s_r$
span the
![]() $\kappa (\xi )$
-vector space
$\kappa (\xi )$
-vector space
![]() $({\mathcal F}_1)_\xi $
and, by Lemma 3.3, they are linearly independent. Thus, by Lemma 3.1, we have
$({\mathcal F}_1)_\xi $
and, by Lemma 3.3, they are linearly independent. Thus, by Lemma 3.1, we have
![]() ${\mathcal F}_1\cong {\mathcal O}_X^r$
. The same argument applies to
${\mathcal F}_1\cong {\mathcal O}_X^r$
. The same argument applies to
![]() ${\mathcal F}_2$
and part (b) then follows immediately from (a).
${\mathcal F}_2$
and part (b) then follows immediately from (a).
Lemma 3.5 Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent torsion-free sheaves on X. Assume that the image of
${\mathcal F}_2$
be coherent torsion-free sheaves on X. Assume that the image of
![]() $V_i=H^0(X,{\mathcal F}_i)$
spans the stalk
$V_i=H^0(X,{\mathcal F}_i)$
spans the stalk
![]() $({\mathcal F}_i)_\xi $
as
$({\mathcal F}_i)_\xi $
as
![]() $\kappa (\xi )$
-vector space. Furthermore, let
$\kappa (\xi )$
-vector space. Furthermore, let
![]() $\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X} {\mathcal F}_2 \to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
$\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X} {\mathcal F}_2 \to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
![]() $V_1 \times V_2\to K$
is nondegenerate. Then the corresponding morphism
$V_1 \times V_2\to K$
is nondegenerate. Then the corresponding morphism
![]() ${\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal O}_X)$
is injective.
${\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal O}_X)$
is injective.
Proof Let
![]() $s_1,\ldots ,s_r\in V_1$
be a basis of
$s_1,\ldots ,s_r\in V_1$
be a basis of
![]() $V_1$
, and let
$V_1$
, and let
![]() $t_1,\ldots ,t_r\in V_2$
be the dual basis with respect to the bilinear mapping
$t_1,\ldots ,t_r\in V_2$
be the dual basis with respect to the bilinear mapping
![]() $V_1 \times V_2\to K$
. Let
$V_1 \times V_2\to K$
. Let
![]() $U\subset X$
be some open affine subset,
$U\subset X$
be some open affine subset,
![]() $A={\mathcal O}_X(U)$
and
$A={\mathcal O}_X(U)$
and
![]() $M_i={\mathcal F}_i(U)$
. For any
$M_i={\mathcal F}_i(U)$
. For any
![]() $0\neq g\in M_1$
, there is
$0\neq g\in M_1$
, there is
![]() $0\neq a\in A$
such that
$0\neq a\in A$
such that
![]() $a\cdot g$
is in the submodule of
$a\cdot g$
is in the submodule of
![]() $M_1$
that is spanned by the restrictions
$M_1$
that is spanned by the restrictions
![]() $s_i|_U$
:
$s_i|_U$
:
for some
![]() $f_j\in A$
that are not all zero. Let, for instance,
$f_j\in A$
that are not all zero. Let, for instance,
![]() $f_i\neq 0$
, then
$f_i\neq 0$
, then
This shows that the map
![]() $M_1\to \operatorname {Hom}_A(M_2,A)$
induced by
$M_1\to \operatorname {Hom}_A(M_2,A)$
induced by
![]() $\varphi $
in injective.
$\varphi $
in injective.
Lemma 3.6 Let
![]() ${\mathcal F}$
be a coherent sheaf on X and
${\mathcal F}$
be a coherent sheaf on X and
![]() ${\mathcal G}$
a subsheaf with
${\mathcal G}$
a subsheaf with
![]() ${\mathcal G}_\xi ={\mathcal F}_\xi $
. Then the natural map
${\mathcal G}_\xi ={\mathcal F}_\xi $
. Then the natural map
![]() $\operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F},{\mathcal O}_X)\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal G},{\mathcal O}_X)$
is injective.
$\operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F},{\mathcal O}_X)\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal G},{\mathcal O}_X)$
is injective.
Proof Let
![]() $U\subset X$
be some open affine subset,
$U\subset X$
be some open affine subset,
![]() $A={\mathcal O}_X(U)$
,
$A={\mathcal O}_X(U)$
,
![]() $M={\mathcal F}(U)$
, and
$M={\mathcal F}(U)$
, and
![]() ${N={\mathcal G}(U)}$
. Consider a morphism
${N={\mathcal G}(U)}$
. Consider a morphism
![]() $\varphi \colon M\to A$
such that
$\varphi \colon M\to A$
such that
![]() $\varphi |_N=0$
. For every
$\varphi |_N=0$
. For every
![]() $g\in M$
, there is a nonzero
$g\in M$
, there is a nonzero
![]() $t\in A$
such that
$t\in A$
such that
![]() $t\cdot g\in N$
. Thus,
$t\cdot g\in N$
. Thus,
![]() $\varphi (t\cdot g)=t\cdot \varphi (g)=0$
, and therefore
$\varphi (t\cdot g)=t\cdot \varphi (g)=0$
, and therefore
![]() $\varphi (g)=0$
. This shows that
$\varphi (g)=0$
. This shows that
![]() $\varphi =0$
.
$\varphi =0$
.
Theorem 3.7 Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent torsion-free sheaves on X, and let
${\mathcal F}_2$
be coherent torsion-free sheaves on X, and let
![]() ${V_i=H^0(X,{\mathcal F}_i)}$
. Let
${V_i=H^0(X,{\mathcal F}_i)}$
. Let
![]() $\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X}{\mathcal F}_2\to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
$\varphi \colon {\mathcal F}_1\otimes _{{\mathcal O}_X}{\mathcal F}_2\to {\mathcal O}_X$
be a pairing such that the induced bilinear mapping
![]() $V_1 \times V_2\to K$
is nondegenerate. If
$V_1 \times V_2\to K$
is nondegenerate. If
![]() $\dim V_1 \geq \operatorname {rank} {\mathcal F}_1$
, then
$\dim V_1 \geq \operatorname {rank} {\mathcal F}_1$
, then
![]() ${\mathcal F}_1\cong {\mathcal O}_X^r$
and
${\mathcal F}_1\cong {\mathcal O}_X^r$
and
![]() $r=\dim V_1 = \operatorname {rank} {\mathcal F}_1$
. Furthermore,
$r=\dim V_1 = \operatorname {rank} {\mathcal F}_1$
. Furthermore,
![]() ${\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal O}_X)$
is an isomorphism.
${\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal O}_X)$
is an isomorphism.
Proof By Proposition 3.4(a), it suffices to show that
![]() ${\mathcal F}_i$
is generated by global sections. Let
${\mathcal F}_i$
is generated by global sections. Let
![]() ${\mathcal G}_i$
be the subsheaf of
${\mathcal G}_i$
be the subsheaf of
![]() ${\mathcal F}_i$
generated by its global sections
${\mathcal F}_i$
generated by its global sections
![]() $V_i$
. We get the commutative diagram
$V_i$
. We get the commutative diagram
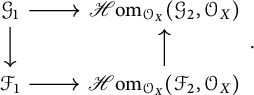
The homomorphism
![]() ${\mathcal G}_1 \to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal G}_2,{\mathcal O}_X)$
is an isomorphism by Proposition 3.4(b). By Lemma 3.3 and the condition on the dimension it follows that the image of
${\mathcal G}_1 \to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal G}_2,{\mathcal O}_X)$
is an isomorphism by Proposition 3.4(b). By Lemma 3.3 and the condition on the dimension it follows that the image of
![]() $V_i=H^0(X,{\mathcal F}_i)$
spans the stalk
$V_i=H^0(X,{\mathcal F}_i)$
spans the stalk
![]() $({\mathcal F}_i)_\xi $
as
$({\mathcal F}_i)_\xi $
as
![]() $\kappa (\xi )$
-vector space and that
$\kappa (\xi )$
-vector space and that
![]() $({\mathcal G}_i)_\xi =({\mathcal F}_i)_\xi $
. Thus, the bottom and right maps in the diagram are also injective by Lemmas 3.5 and 3.6, respectively. This implies that
$({\mathcal G}_i)_\xi =({\mathcal F}_i)_\xi $
. Thus, the bottom and right maps in the diagram are also injective by Lemmas 3.5 and 3.6, respectively. This implies that
![]() ${\mathcal G}_1={\mathcal F}_2$
, and therefore
${\mathcal G}_1={\mathcal F}_2$
, and therefore
![]() ${\mathcal F}_1$
is generated by global sections.
${\mathcal F}_1$
is generated by global sections.
Example 3.8 This example is to illustrate that the assumption in Theorem 3.7 of being nondegenerate on global sections is crucial. Let
![]() $X={\mathbb {P}^1}$
and
$X={\mathbb {P}^1}$
and
![]() $\xi $
the generic point of
$\xi $
the generic point of
![]() ${\mathbb {P}^1}$
. Consider the coherent torsion-free sheaf
${\mathbb {P}^1}$
. Consider the coherent torsion-free sheaf
![]() ${\mathcal F}={\mathcal O}_{\mathbb {P}^1}(1)\oplus {\mathcal O}_{\mathbb {P}^1}(-1)$
on
${\mathcal F}={\mathcal O}_{\mathbb {P}^1}(1)\oplus {\mathcal O}_{\mathbb {P}^1}(-1)$
on
![]() ${\mathbb {P}^1}$
. We have
${\mathbb {P}^1}$
. We have
![]() $\dim H^0({\mathbb {P}^1},{\mathcal F}) = 2 = \operatorname {rank}_\xi {\mathcal F}$
. On
$\dim H^0({\mathbb {P}^1},{\mathcal F}) = 2 = \operatorname {rank}_\xi {\mathcal F}$
. On
![]() ${\mathcal F}$
, we define the pairing
${\mathcal F}$
, we define the pairing
![]() $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to {\mathcal O}_X$
that sends
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to {\mathcal O}_X$
that sends
![]() $(a,b)\otimes (c,d)$
to
$(a,b)\otimes (c,d)$
to
![]() $ad+bc$
which is nondegenerate at
$ad+bc$
which is nondegenerate at
![]() $\xi $
. But the induced bilinear form on the global sections of
$\xi $
. But the induced bilinear form on the global sections of
![]() ${\mathcal F}$
is identically zero and
${\mathcal F}$
is identically zero and
![]() ${\mathcal F}\not \cong {\mathcal O}_{\mathbb {P}^1}^2$
.
${\mathcal F}\not \cong {\mathcal O}_{\mathbb {P}^1}^2$
.
4 Ulrich sheaves
Definition 4.1 Let
![]() $f\colon X\to Y$
be a morphism of schemes. A coherent sheaf
$f\colon X\to Y$
be a morphism of schemes. A coherent sheaf
![]() ${\mathcal F}$
on X is f-Ulrich if
${\mathcal F}$
on X is f-Ulrich if
![]() $f_*{\mathcal F}\cong {\mathcal O}_Y^r$
for some natural number r.
$f_*{\mathcal F}\cong {\mathcal O}_Y^r$
for some natural number r.
Remark 4.1 Let
![]() $f_i\colon X_i\to Y$
be finitely many morphisms of schemes. Let X be the disjoint union of the
$f_i\colon X_i\to Y$
be finitely many morphisms of schemes. Let X be the disjoint union of the
![]() $X_i$
and
$X_i$
and
![]() $f\colon X\to Y$
the morphism induced by the
$f\colon X\to Y$
the morphism induced by the
![]() $f_i$
. A coherent sheaf
$f_i$
. A coherent sheaf
![]() ${\mathcal F}$
on X is f-Ulrich if and only if
${\mathcal F}$
on X is f-Ulrich if and only if
![]() ${\mathcal F}|_{X_i}$
is
${\mathcal F}|_{X_i}$
is
![]() $f_i$
-Ulrich for all i. Thus, we can usually restrict to the case when X is connected.
$f_i$
-Ulrich for all i. Thus, we can usually restrict to the case when X is connected.
A case of particular interest is when X is an embedded projective variety.
Proposition 4.2 [Reference Eisenbud, Schreyer and WeymanESW03, Proposition 2.1]
Let
![]() $X\subset \mathbb {P}^n$
be a closed subscheme, and let
$X\subset \mathbb {P}^n$
be a closed subscheme, and let
![]() $f\colon X\to \mathbb {P}^{k}$
be a finite surjective linear projection from a center that is disjoint from X. Let
$f\colon X\to \mathbb {P}^{k}$
be a finite surjective linear projection from a center that is disjoint from X. Let
![]() ${\mathcal F}$
be a coherent sheaf whose support is all of X. Then the following are equivalent:
${\mathcal F}$
be a coherent sheaf whose support is all of X. Then the following are equivalent:
-
(i)
 ${\mathcal F}$
is f-Ulrich.
${\mathcal F}$
is f-Ulrich. -
(ii)
 $H^i(X,{\mathcal F}(-i))=0$
for
$H^i(X,{\mathcal F}(-i))=0$
for
 $i>0$
and
$i>0$
and
 $H^i(X,{\mathcal F}(-i-1))=0$
for
$H^i(X,{\mathcal F}(-i-1))=0$
for
 $i<k$
.
$i<k$
. -
(iii)
 $H^i(X,{\mathcal F}(j))=0$
for all
$H^i(X,{\mathcal F}(j))=0$
for all
 $1\leq i\leq k-1$
,
$1\leq i\leq k-1$
,
 $j\in {\mathbb Z}$
;
$j\in {\mathbb Z}$
;
 $H^0(X,{\mathcal F}(j))=0$
for
$H^0(X,{\mathcal F}(j))=0$
for
 $j<0$
and
$j<0$
and
 $H^k(X,{\mathcal F}(j))=0$
for
$H^k(X,{\mathcal F}(j))=0$
for
 $j\geq -k$
.
$j\geq -k$
. -
(iv) The module
 $M=\oplus _{i\in {\mathbb Z}}H^0(X,{\mathcal F}(i))$
of twisted global sections is a Cohen–Macaulay module over the polynomial ring
$M=\oplus _{i\in {\mathbb Z}}H^0(X,{\mathcal F}(i))$
of twisted global sections is a Cohen–Macaulay module over the polynomial ring
 $S=K[x_0,\ldots ,x_n]$
of dimension
$S=K[x_0,\ldots ,x_n]$
of dimension
 $k+1$
whose minimal S-free resolution is linear.
$k+1$
whose minimal S-free resolution is linear.
If
![]() ${\mathcal F}$
as in Proposition 4.2 satisfies these equivalent conditions, then we say that
${\mathcal F}$
as in Proposition 4.2 satisfies these equivalent conditions, then we say that
![]() ${\mathcal F}$
is an Ulrich sheaf on X without specifying the finite surjective linear projection f as conditions (ii)–(iv) do not depend on the choice of f. A major open question in this context is the following.
${\mathcal F}$
is an Ulrich sheaf on X without specifying the finite surjective linear projection f as conditions (ii)–(iv) do not depend on the choice of f. A major open question in this context is the following.
Problem 4.3 [Reference Eisenbud, Schreyer and WeymanESW03, p. 543]
Is there an Ulrich sheaf on every closed subvariety
![]() ${X\subset \mathbb {P}^n}$
?
${X\subset \mathbb {P}^n}$
?
We now want to apply the results from Section 3 to give a criterion for a sheaf to be Ulrich. For this, we need a relative notion of nondegenerate bilinear mappings. Let
![]() $f\colon X \to Y$
be a finite morphism of Noetherian schemes. For any quasi-coherent sheaf
$f\colon X \to Y$
be a finite morphism of Noetherian schemes. For any quasi-coherent sheaf
![]() ${\mathcal G}$
on Y, we consider the sheaf
${\mathcal G}$
on Y, we consider the sheaf
![]() $\operatorname {{\mathscr Hom}}_{{\mathcal O}_Y}(f_* {\mathcal O}_X, {\mathcal G})$
. Since this is a quasi-coherent
$\operatorname {{\mathscr Hom}}_{{\mathcal O}_Y}(f_* {\mathcal O}_X, {\mathcal G})$
. Since this is a quasi-coherent
![]() $f_* {\mathcal O}_X$
-module, it corresponds to a quasi-coherent
$f_* {\mathcal O}_X$
-module, it corresponds to a quasi-coherent
![]() ${\mathcal O}_X$
-module which we will denote by
${\mathcal O}_X$
-module which we will denote by
![]() $f^! {\mathcal G}$
. We recall the following basic lemma (cf. [Reference HartshorneHar77, Chapter III Section 6, Exercise 6.10]).
$f^! {\mathcal G}$
. We recall the following basic lemma (cf. [Reference HartshorneHar77, Chapter III Section 6, Exercise 6.10]).
Lemma 4.4 Let
![]() $f\colon X \to Y$
be a finite morphism of Noetherian schemes. Let
$f\colon X \to Y$
be a finite morphism of Noetherian schemes. Let
![]() ${\mathcal F}$
be a coherent sheaf on X, and let
${\mathcal F}$
be a coherent sheaf on X, and let
![]() ${\mathcal G}$
be a quasi-coherent sheaf on Y. There is a natural isomorphism
${\mathcal G}$
be a quasi-coherent sheaf on Y. There is a natural isomorphism
of quasi-coherent
![]() $f_*{\mathcal O}_X$
-modules.
$f_*{\mathcal O}_X$
-modules.
Let
![]() $f\colon X \to Y$
be a finite morphism of Noetherian schemes. Let
$f\colon X \to Y$
be a finite morphism of Noetherian schemes. Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent sheaves on X and consider an
${\mathcal F}_2$
be coherent sheaves on X and consider an
![]() $f^! {\mathcal O}_Y$
-valued pairing, i.e., a morphism
$f^! {\mathcal O}_Y$
-valued pairing, i.e., a morphism
![]() ${\mathcal F}_1\otimes {\mathcal F}_2 \to f^! {\mathcal O}_Y$
of coherent
${\mathcal F}_1\otimes {\mathcal F}_2 \to f^! {\mathcal O}_Y$
of coherent
![]() ${\mathcal O}_X$
-modules. This corresponds to a morphism
${\mathcal O}_X$
-modules. This corresponds to a morphism
![]() ${{\mathcal F}_1 \to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2, f^! {\mathcal O}_Y)}$
. Lemma 4.4 tells us that this gives us a morphism
${{\mathcal F}_1 \to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2, f^! {\mathcal O}_Y)}$
. Lemma 4.4 tells us that this gives us a morphism
which corresponds to an
![]() ${\mathcal O}_Y$
-valued pairing on the pushforwards
${\mathcal O}_Y$
-valued pairing on the pushforwards
![]() $f_* {\mathcal F}_1$
and
$f_* {\mathcal F}_1$
and
![]() $f_*{\mathcal F}_2$
.
$f_*{\mathcal F}_2$
.
Remark 4.5 Let us explain here the affine case in more detail. To that end, let
![]() ${X=\operatorname {Spec}(B)}$
,
${X=\operatorname {Spec}(B)}$
,
![]() $Y=\operatorname {Spec}(A)$
, and
$Y=\operatorname {Spec}(A)$
, and
![]() $f\colon X\to Y$
be induced by the finite ring homomorphism
$f\colon X\to Y$
be induced by the finite ring homomorphism
![]() $f^\#\colon A\to B$
. Then
$f^\#\colon A\to B$
. Then
![]() $f^!{\mathcal O}_Y$
is the sheaf on X associated with the B-module
$f^!{\mathcal O}_Y$
is the sheaf on X associated with the B-module
![]() $\operatorname {Hom}_A(B,A)$
whose B-module structure is given by
$\operatorname {Hom}_A(B,A)$
whose B-module structure is given by
![]() $(b\cdot \varphi )(m)=\varphi (b\cdot m)$
for all
$(b\cdot \varphi )(m)=\varphi (b\cdot m)$
for all
![]() $b,m\in B$
. If
$b,m\in B$
. If
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
are the coherent sheaves associated with the B-modules
${\mathcal F}_2$
are the coherent sheaves associated with the B-modules
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, then a morphism
$M_2$
, then a morphism
![]() ${\mathcal F}_1 \otimes {\mathcal F}_2 \to f^! {\mathcal O}_Y$
of coherent
${\mathcal F}_1 \otimes {\mathcal F}_2 \to f^! {\mathcal O}_Y$
of coherent
![]() ${\mathcal O}_X$
-modules corresponds to a homomorphism
${\mathcal O}_X$
-modules corresponds to a homomorphism
![]() $\psi \colon M_1\otimes _B M_2\to \operatorname {Hom}_A(B,A)$
of B-modules. This gives rise to the following A-bilinear map on
$\psi \colon M_1\otimes _B M_2\to \operatorname {Hom}_A(B,A)$
of B-modules. This gives rise to the following A-bilinear map on
![]() $M_1\times M_2$
:
$M_1\times M_2$
:
This gives the
![]() ${\mathcal O}_Y$
-valued pairing of the pushforwards
${\mathcal O}_Y$
-valued pairing of the pushforwards
![]() $f_* {\mathcal F}_1$
and
$f_* {\mathcal F}_1$
and
![]() $f_*{\mathcal F}_2$
.
$f_*{\mathcal F}_2$
.
Definition 4.2 Let
![]() $f\colon X \to Y$
be a finite morphism of Noetherian schemes. Let
$f\colon X \to Y$
be a finite morphism of Noetherian schemes. Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent sheaves on X and consider an
${\mathcal F}_2$
be coherent sheaves on X and consider an
![]() $f^! {\mathcal O}_Y$
-valued pairing
$f^! {\mathcal O}_Y$
-valued pairing
![]() $\varphi \colon {\mathcal F}_1\otimes {\mathcal F}_2 \to f^! {\mathcal O}_Y$
. For a field K, we say that
$\varphi \colon {\mathcal F}_1\otimes {\mathcal F}_2 \to f^! {\mathcal O}_Y$
. For a field K, we say that
![]() $\varphi $
is nondegenerate at
$\varphi $
is nondegenerate at
![]() $\alpha \in Y(K)$
if the induced
$\alpha \in Y(K)$
if the induced
![]() ${\mathcal O}_Y$
-valued pairing of the pushforwards
${\mathcal O}_Y$
-valued pairing of the pushforwards
![]() $f_* {\mathcal F}_1$
and
$f_* {\mathcal F}_1$
and
![]() $f_*{\mathcal F}_2$
is nondegenerate at
$f_*{\mathcal F}_2$
is nondegenerate at
![]() $\alpha $
.
$\alpha $
.
Now, let Y be a geometrically irreducible variety which is proper over a field K. Let further
![]() $f\colon X\to Y$
be a finite surjective morphism and
$f\colon X\to Y$
be a finite surjective morphism and
![]() ${\mathcal F}_1$
,
${\mathcal F}_1$
,
![]() ${\mathcal F}_2$
coherent sheaves on X with a pairing
${\mathcal F}_2$
coherent sheaves on X with a pairing
![]() ${\mathcal F}_1\otimes {\mathcal F}_2\to f^! {\mathcal O}_Y$
. We have seen that this induces an
${\mathcal F}_1\otimes {\mathcal F}_2\to f^! {\mathcal O}_Y$
. We have seen that this induces an
![]() ${\mathcal O}_Y$
-valued pairing on the pushforwards which in turn induces a K-bilinear mapping
${\mathcal O}_Y$
-valued pairing on the pushforwards which in turn induces a K-bilinear mapping
Theorem 4.6 Let X be an equidimensional variety over a field K with irreducible components
![]() $X_1,\ldots ,X_s$
. Let
$X_1,\ldots ,X_s$
. Let
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
be coherent torsion-free sheaves on X, and let
${\mathcal F}_2$
be coherent torsion-free sheaves on X, and let
![]() $V_i=H^0(X,{\mathcal F}_i)$
. Let Y be a geometrically irreducible variety which is proper over K and
$V_i=H^0(X,{\mathcal F}_i)$
. Let Y be a geometrically irreducible variety which is proper over K and
![]() $f\colon X\to Y$
a finite surjective morphism. Assume that there is an
$f\colon X\to Y$
a finite surjective morphism. Assume that there is an
![]() $f^! {\mathcal O}_Y$
-valued pairing of
$f^! {\mathcal O}_Y$
-valued pairing of
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
such that the induced K-bilinear mapping
${\mathcal F}_2$
such that the induced K-bilinear mapping
![]() $V_1\times V_2\to K$
is nondegenerate. Then the following are equivalent:
$V_1\times V_2\to K$
is nondegenerate. Then the following are equivalent:
-
(i)
 $\dim V_1 \geq \sum _{i=1}^s \deg (f|_{X_i}) \cdot \operatorname {rank} ({\mathcal F}_1|_{X_i})$
.
$\dim V_1 \geq \sum _{i=1}^s \deg (f|_{X_i}) \cdot \operatorname {rank} ({\mathcal F}_1|_{X_i})$
. -
(ii)
 ${\mathcal F}_1$
is f-Ulrich.
${\mathcal F}_1$
is f-Ulrich.
Proof We will apply Theorem 3.7 to the coherent sheaves
![]() $f_*{\mathcal F}_1$
and
$f_*{\mathcal F}_1$
and
![]() $f_*{\mathcal F}_2$
. First, we need that the
$f_*{\mathcal F}_2$
. First, we need that the
![]() $f_*{\mathcal F}_i$
are torsion-free. This follows from the assumptions that f is finite and surjective, X is equidimensional and
$f_*{\mathcal F}_i$
are torsion-free. This follows from the assumptions that f is finite and surjective, X is equidimensional and
![]() ${\mathcal F}_i$
is torsion-free. Further, by [Reference KollárKol96, Chapter VI Section 2, Proposition 2.7], one has
${\mathcal F}_i$
is torsion-free. Further, by [Reference KollárKol96, Chapter VI Section 2, Proposition 2.7], one has
![]() $\operatorname {rank} (f_*{\mathcal F}_1)=\sum _{i=1}^s \deg (f|_{X_i}) \cdot \operatorname {rank} ({\mathcal F}_1|_{X_i})$
.
$\operatorname {rank} (f_*{\mathcal F}_1)=\sum _{i=1}^s \deg (f|_{X_i}) \cdot \operatorname {rank} ({\mathcal F}_1|_{X_i})$
.
Remark 4.7 Let
![]() $f\colon X\to Y$
as in Theorem 4.6. Assume that
$f\colon X\to Y$
as in Theorem 4.6. Assume that
![]() ${\mathcal F}_1$
is an f-Ulrich sheaf on X, and let
${\mathcal F}_1$
is an f-Ulrich sheaf on X, and let
![]() ${\mathcal F}_2=\operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F},f^!{\mathcal O}_Y)$
. Then we have a canonical map
${\mathcal F}_2=\operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F},f^!{\mathcal O}_Y)$
. Then we have a canonical map
![]() ${\mathcal F}_1\otimes {\mathcal F}_2\to f^!{\mathcal O}_Y$
which satisfies the assumptions of Theorem 4.6.
${\mathcal F}_1\otimes {\mathcal F}_2\to f^!{\mathcal O}_Y$
which satisfies the assumptions of Theorem 4.6.
Example 4.8 Let
![]() $X=\mathbb {P}^1$
and consider the natural morphism
$X=\mathbb {P}^1$
and consider the natural morphism
![]() $f\colon X\times X\to X^{(2)}$
, where
$f\colon X\times X\to X^{(2)}$
, where
![]() $X^{(2)}$
is the symmetric product. This corresponds to the inclusion
$X^{(2)}$
is the symmetric product. This corresponds to the inclusion
![]() $S^{\sigma }\subset S$
, where S is the bigraded ring
$S^{\sigma }\subset S$
, where S is the bigraded ring
![]() $K[x_0,x_1,y_0,y_1]$
and
$K[x_0,x_1,y_0,y_1]$
and
![]() $S^\sigma $
is the ring of invariants under the action of the automorphism
$S^\sigma $
is the ring of invariants under the action of the automorphism
![]() $\sigma \colon S\to S$
that interchanges
$\sigma \colon S\to S$
that interchanges
![]() $x_i$
and
$x_i$
and
![]() $y_i$
for
$y_i$
for
![]() $i=0,1$
. For every
$i=0,1$
. For every
![]() $f,g\in S$
, we have that
$f,g\in S$
, we have that
![]() $g\sigma (f)-\sigma (g)f$
is divisible by
$g\sigma (f)-\sigma (g)f$
is divisible by
![]() $x_0y_1-x_1y_0$
. Thus,
$x_0y_1-x_1y_0$
. Thus,
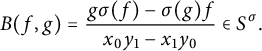 $$ \begin{align*} B(f,g)=\frac{g\sigma(f)-\sigma(g)f}{x_0y_1-x_1y_0}\in S^\sigma. \end{align*} $$
$$ \begin{align*} B(f,g)=\frac{g\sigma(f)-\sigma(g)f}{x_0y_1-x_1y_0}\in S^\sigma. \end{align*} $$
Since the denominator has bidegree
![]() $(1,1)$
, this defines a morphism
$(1,1)$
, this defines a morphism
of
![]() ${\mathcal O}_{X\times X}$
-modules that sends a section g to
${\mathcal O}_{X\times X}$
-modules that sends a section g to
![]() $B(f,g)$
. Thus, we get an
$B(f,g)$
. Thus, we get an
![]() $f^!{\mathcal O}_{X^{(2)}}$
-valued pairing of
$f^!{\mathcal O}_{X^{(2)}}$
-valued pairing of
![]() ${\mathcal F}_1={\mathcal O}_{X\times X}(1,0)$
and
${\mathcal F}_1={\mathcal O}_{X\times X}(1,0)$
and
![]() ${\mathcal F}_2={\mathcal O}_{X\times X}(0,1)$
. The induced K-bilinear mapping is given by the matrix
${\mathcal F}_2={\mathcal O}_{X\times X}(0,1)$
. The induced K-bilinear mapping is given by the matrix
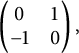 $$ \begin{align*} \begin{pmatrix} 0&1\\ -1&0 \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 0&1\\ -1&0 \end{pmatrix}, \end{align*} $$
so, in particular, nondegenerate. Thus, we can apply Theorem 4.6 to deduce that
![]() ${\mathcal F}_1$
and
${\mathcal F}_1$
and
![]() ${\mathcal F}_2$
are f-Ulrich.
${\mathcal F}_2$
are f-Ulrich.
5 The codifferent sheaf
In this section, we recall some properties of
![]() $f^!{\mathcal O}_Y$
and its relation to the codifferent sheaf. Most of the results should be well known, but for a lack of adequate references, we will include (at least partial) proofs here.
$f^!{\mathcal O}_Y$
and its relation to the codifferent sheaf. Most of the results should be well known, but for a lack of adequate references, we will include (at least partial) proofs here.
Lemma 5.1 Let
![]() $f\colon X\to Y$
be a finite morphism of Noetherian schemes.
$f\colon X\to Y$
be a finite morphism of Noetherian schemes.
-
(a) If f is flat and both X and Y are Gorenstein, then
 $f^!{\mathcal O}_Y$
is a line bundle.
$f^!{\mathcal O}_Y$
is a line bundle. -
(b) If Y is a smooth variety over K and X is Gorenstein, then
 $f^!{\mathcal O}_Y$
is a line bundle.
$f^!{\mathcal O}_Y$
is a line bundle.
Proof We first note that (b) is a special case of part (a) because, in this situation, the morphism f is automatically flat as Gorenstein implies Cohen–Macaulay. In order to prove part (a), note that for every
![]() $y \in Y$
, the canonical module of
$y \in Y$
, the canonical module of
![]() ${\mathcal O}_{Y,y}$
is
${\mathcal O}_{Y,y}$
is
![]() ${\mathcal O}_{Y,y}$
itself by [Reference Herzog and KunzHK71, Satz 5.9], and for every
${\mathcal O}_{Y,y}$
itself by [Reference Herzog and KunzHK71, Satz 5.9], and for every
![]() $x \in X$
, the canonical module of
$x \in X$
, the canonical module of
![]() ${\mathcal O}_{X,x}$
is
${\mathcal O}_{X,x}$
is
![]() $(f^! {\mathcal O}_Y)_x$
by [Reference Herzog and KunzHK71, Satz 5.12]. Thus, again by [Reference Herzog and KunzHK71, Satz 5.9],
$(f^! {\mathcal O}_Y)_x$
by [Reference Herzog and KunzHK71, Satz 5.12]. Thus, again by [Reference Herzog and KunzHK71, Satz 5.9],
![]() $f^! {\mathcal O}_Y$
is a line bundle on X if X is Gorenstein.
$f^! {\mathcal O}_Y$
is a line bundle on X if X is Gorenstein.
Remark 5.2 The preceding lemma implies that the sheaf
![]() $f^!{\mathcal O}_Y$
is a line bundle whenever
$f^!{\mathcal O}_Y$
is a line bundle whenever
![]() $f\colon X\to Y$
is a finite morphism of smooth varieties over a field K.
$f\colon X\to Y$
is a finite morphism of smooth varieties over a field K.
Definition 5.1 Let A be a Noetherian integral domain, and let
![]() $A\subset B$
be a finite ring extension such that for each minimal prime ideal
$A\subset B$
be a finite ring extension such that for each minimal prime ideal
![]() ${\mathfrak p}$
of B, we have
${\mathfrak p}$
of B, we have
![]() ${\mathfrak p}\cap A=(0)$
. Let K be the quotient field of A, and let L be the total quotient ring of B. Then L is a finite-dimensional K-vector space and we have the K-linear map
${\mathfrak p}\cap A=(0)$
. Let K be the quotient field of A, and let L be the total quotient ring of B. Then L is a finite-dimensional K-vector space and we have the K-linear map
![]() $\operatorname {tr}_{L/K}\colon L\to K$
that associates to every element
$\operatorname {tr}_{L/K}\colon L\to K$
that associates to every element
![]() $x\in L$
the trace of the K-linear map
$x\in L$
the trace of the K-linear map
![]() $L\to L,\, a\mapsto ax$
. The codifferent of the ring extension
$L\to L,\, a\mapsto ax$
. The codifferent of the ring extension
![]() $A\subset B$
is the B-module
$A\subset B$
is the B-module
Clearly, the map
is a homomorphism of B-modules.
Now, let Y be an integral Noetherian scheme and
![]() $f\colon X\to Y$
a finite morphism such the generic point of each irreducible component of X is mapped to the generic point of Y. Let
$f\colon X\to Y$
a finite morphism such the generic point of each irreducible component of X is mapped to the generic point of Y. Let
![]() ${\mathcal K}_X$
be the sheaf of total quotient rings of
${\mathcal K}_X$
be the sheaf of total quotient rings of
![]() ${\mathcal O}_X$
. By gluing the above, we define the quasi-coherent subsheaf
${\mathcal O}_X$
. By gluing the above, we define the quasi-coherent subsheaf
![]() $\Delta (X/Y)$
of
$\Delta (X/Y)$
of
![]() ${\mathcal K}_X$
and we obtain a morphism of
${\mathcal K}_X$
and we obtain a morphism of
![]() ${\mathcal O}_X$
-modules
${\mathcal O}_X$
-modules
![]() $\Delta (X/Y)\to f^!{\mathcal O}_Y$
. We call
$\Delta (X/Y)\to f^!{\mathcal O}_Y$
. We call
![]() $\Delta (X/Y)$
the codifferent sheaf of f.
$\Delta (X/Y)$
the codifferent sheaf of f.
Example 5.3 Let A be an integral domain and
![]() $K=\operatorname {Quot}(A)$
. Let
$K=\operatorname {Quot}(A)$
. Let
![]() $f\in A[t]$
be a monic polynomial over A which has only simple zeros in the algebraic closure of K, and let
$f\in A[t]$
be a monic polynomial over A which has only simple zeros in the algebraic closure of K, and let
![]() $B=A[t]/(f)$
. Then the codifferent
$B=A[t]/(f)$
. Then the codifferent
![]() $\Delta (B/A)$
is the fractional ideal generated by
$\Delta (B/A)$
is the fractional ideal generated by
![]() $\frac {1}{f'}$
in the total quotient ring of B. Here,
$\frac {1}{f'}$
in the total quotient ring of B. Here,
![]() $f'$
denotes the formal derivative of f. This follows from a lemma often attributed to Euler (see [Reference SerreSer79, III, Section 6]).
$f'$
denotes the formal derivative of f. This follows from a lemma often attributed to Euler (see [Reference SerreSer79, III, Section 6]).
Remark 5.4 In order to construct a pairing
![]() ${\mathcal F}_1\otimes {\mathcal F}_2\to f^!{\mathcal O}_Y$
, it thus suffices by the discussion in Definition 5.1 to construct a pairing
${\mathcal F}_1\otimes {\mathcal F}_2\to f^!{\mathcal O}_Y$
, it thus suffices by the discussion in Definition 5.1 to construct a pairing
![]() ${\mathcal F}_1\otimes {\mathcal F}_2\to {\mathcal K}_X$
whose image is contained in
${\mathcal F}_1\otimes {\mathcal F}_2\to {\mathcal K}_X$
whose image is contained in
![]() $\Delta (X/Y)$
.
$\Delta (X/Y)$
.
Lemma 5.5 Let X and Y be varieties over a field of characteristic zero, X equidimensional and Y irreducible. Then, for any finite surjective morphism
![]() $f\colon X\to Y$
, the map
$f\colon X\to Y$
, the map
![]() $\Delta (X/Y)\to f^!{\mathcal O}_Y$
is an isomorphism of
$\Delta (X/Y)\to f^!{\mathcal O}_Y$
is an isomorphism of
![]() ${\mathcal O}_X$
-modules.
${\mathcal O}_X$
-modules.
Proof We can reduce to the affine case: let
![]() $A\subset B$
be a finite ring extension such that A is an integral domain and
$A\subset B$
be a finite ring extension such that A is an integral domain and
![]() ${\mathfrak p}\cap A=(0)$
for all minimal prime ideals
${\mathfrak p}\cap A=(0)$
for all minimal prime ideals
![]() ${\mathfrak p}$
of B. Let E and F be the total quotient rings of A and B, respectively. Since
${\mathfrak p}$
of B. Let E and F be the total quotient rings of A and B, respectively. Since
![]() $B\otimes _A E$
is finite-dimensional as an E-vector space and reduced, it is a ring of the form
$B\otimes _A E$
is finite-dimensional as an E-vector space and reduced, it is a ring of the form
![]() $F_1\times \cdots \times F_r$
for some finite field extensions
$F_1\times \cdots \times F_r$
for some finite field extensions
![]() $F_i$
of E. Since no element of A is a zero divisor in B, we actually have that
$F_i$
of E. Since no element of A is a zero divisor in B, we actually have that
![]() $F=F_1\times \cdots \times F_r$
. Thus, we have an injective map
$F=F_1\times \cdots \times F_r$
. Thus, we have an injective map
![]() $\operatorname {Hom}_A(B,A)\to \operatorname {Hom}_E(F,E)$
that is given by tensoring with E. By definition, the preimage of
$\operatorname {Hom}_A(B,A)\to \operatorname {Hom}_E(F,E)$
that is given by tensoring with E. By definition, the preimage of
![]() $\operatorname {Hom}_A(B,A)$
under the map
$\operatorname {Hom}_A(B,A)$
under the map
is exactly
![]() $\Delta (B/A)$
. It thus suffices to show that
$\Delta (B/A)$
. It thus suffices to show that
![]() $\psi $
is an isomorphism because then the restriction of
$\psi $
is an isomorphism because then the restriction of
![]() $\psi $
to
$\psi $
to
![]() $\Delta (B/A)$
is the desired isomorphism
$\Delta (B/A)$
is the desired isomorphism
![]() $\Delta (B/A)\to \operatorname {Hom}_A(B,A)$
. The map
$\Delta (B/A)\to \operatorname {Hom}_A(B,A)$
. The map
![]() $\psi $
is the direct sum of the maps
$\psi $
is the direct sum of the maps
and thus it suffices to show that each
![]() $\psi _i$
is an isomorphism. We have that
$\psi _i$
is an isomorphism. We have that
![]() $\operatorname {tr}_{F_i/E}(1)$
is the dimension of
$\operatorname {tr}_{F_i/E}(1)$
is the dimension of
![]() $F_i$
as an E-vector space. Since we work over a field of characteristic zero, this shows that each
$F_i$
as an E-vector space. Since we work over a field of characteristic zero, this shows that each
![]() $\psi _i$
is a nonzero map. But since
$\psi _i$
is a nonzero map. But since
![]() $\operatorname {Hom}_E(F_i,E)$
is one-dimensional considered as a vector space over
$\operatorname {Hom}_E(F_i,E)$
is one-dimensional considered as a vector space over
![]() $F_i$
, this implies that
$F_i$
, this implies that
![]() $\psi _i$
is an isomorphism.
$\psi _i$
is an isomorphism.
Remark 5.6 Lemma 5.5 is no longer true over fields of positive characteristic because the trace
![]() $\operatorname {tr}_{L/K}$
is identically zero for inseparable field extensions
$\operatorname {tr}_{L/K}$
is identically zero for inseparable field extensions
![]() $K\subset L$
. This is one reason why we have not worked with the codifferent sheaf to begin with.
$K\subset L$
. This is one reason why we have not worked with the codifferent sheaf to begin with.
Proposition 5.7 Let
![]() $f\colon X\to Y$
be a finite surjective morphism of varieties over a field of characteristic zero. Let X be equidimensional and Gorenstein. Let Y be smooth and irreducible. Then
$f\colon X\to Y$
be a finite surjective morphism of varieties over a field of characteristic zero. Let X be equidimensional and Gorenstein. Let Y be smooth and irreducible. Then
![]() $\Delta (X/Y)$
is an invertible subsheaf of
$\Delta (X/Y)$
is an invertible subsheaf of
![]() ${\mathcal K}_X$
and thus
${\mathcal K}_X$
and thus
![]() $\Delta (X/Y)={\mathcal L}(R)$
for some Cartier divisor R on X. This Cartier divisor is effective and its support consists exactly of those points where f is ramified.
$\Delta (X/Y)={\mathcal L}(R)$
for some Cartier divisor R on X. This Cartier divisor is effective and its support consists exactly of those points where f is ramified.
Proof By Lemma 5.5,
![]() $\Delta (X/Y)$
is isomorphic to
$\Delta (X/Y)$
is isomorphic to
![]() $f^!{\mathcal O}_Y$
which is an invertible sheaf by Lemma 5.1. Thus,
$f^!{\mathcal O}_Y$
which is an invertible sheaf by Lemma 5.1. Thus,
![]() $\Delta (X/Y)$
is an invertible subsheaf of
$\Delta (X/Y)$
is an invertible subsheaf of
![]() ${\mathcal K}_X$
, and we can write
${\mathcal K}_X$
, and we can write
![]() $\Delta (X/Y)={\mathcal L}(R)$
for some Cartier divisor R on X. We first show that R is effective, which is equivalent to the constant
$\Delta (X/Y)={\mathcal L}(R)$
for some Cartier divisor R on X. We first show that R is effective, which is equivalent to the constant
![]() $1$
being a global section of
$1$
being a global section of
![]() $\Delta (X/Y)$
. This can be checked locally. We thus consider a finite ring extension
$\Delta (X/Y)$
. This can be checked locally. We thus consider a finite ring extension
![]() $A\subset B$
, where A is an integral domain. Furthermore, this ring extension is flat by the assumptions on X and Y. Thus, without loss of generality, we can assume that B is free as A-module. Therefore, the A-linear map
$A\subset B$
, where A is an integral domain. Furthermore, this ring extension is flat by the assumptions on X and Y. Thus, without loss of generality, we can assume that B is free as A-module. Therefore, the A-linear map
![]() $B\to B$
given by multiplication with an element
$B\to B$
given by multiplication with an element
![]() $b\in B$
can be represented by a matrix having entries in A. Using the notation of Definition 5.1, this shows that
$b\in B$
can be represented by a matrix having entries in A. Using the notation of Definition 5.1, this shows that
![]() $\operatorname {tr}_{L/K}(1\cdot B)\subset A$
. Thus, the constant
$\operatorname {tr}_{L/K}(1\cdot B)\subset A$
. Thus, the constant
![]() $1$
is a global section of
$1$
is a global section of
![]() $\Delta (X/Y)$
and R is effective. The image of
$\Delta (X/Y)$
and R is effective. The image of
![]() $1$
under the map
$1$
under the map
![]() $H^0(X,\Delta (X/Y))\to H^0(X,f^!{\mathcal O}_Y)$
is just the trace map and the subscheme associated with R is the zero set of this section. This consists exactly of the ramification points of f (see, for example, [Sta20, Tag 0BW9] or [Reference KummerKum16a, Remark 2.2.19]).
$H^0(X,\Delta (X/Y))\to H^0(X,f^!{\mathcal O}_Y)$
is just the trace map and the subscheme associated with R is the zero set of this section. This consists exactly of the ramification points of f (see, for example, [Sta20, Tag 0BW9] or [Reference KummerKum16a, Remark 2.2.19]).
Definition 5.2 In the situation of Proposition 5.7, we call the Cartier divisor R on X that corresponds to the invertible subsheaf
![]() $\Delta (X/Y)$
of
$\Delta (X/Y)$
of
![]() ${\mathcal K}_X$
the ramification divisor of f.
${\mathcal K}_X$
the ramification divisor of f.
Lemma 5.8 Let
![]() $f\colon X\to Y$
be a finite surjective morphism of varieties. Let X be equidimensional, and let Y be smooth and irreducible. Let
$f\colon X\to Y$
be a finite surjective morphism of varieties. Let X be equidimensional, and let Y be smooth and irreducible. Let
![]() $Z\subset X$
be of codimension at least two. Consider the open subset
$Z\subset X$
be of codimension at least two. Consider the open subset
![]() $V=X\setminus Z$
and its inclusion
$V=X\setminus Z$
and its inclusion
![]() $\iota \colon V\to X$
to X. Then
$\iota \colon V\to X$
to X. Then
![]() $\iota _*(\Delta |_V)=\Delta $
, where
$\iota _*(\Delta |_V)=\Delta $
, where
![]() $\Delta =\Delta (X/Y)$
.
$\Delta =\Delta (X/Y)$
.
Proof If we enlarge Z, then the statement becomes stronger, so we may assume that
![]() $Z=f^{-1}(Z')$
for some
$Z=f^{-1}(Z')$
for some
![]() $Z'\subset Y$
of codimension at least two. We write
$Z'\subset Y$
of codimension at least two. We write
![]() ${\mathcal D}=\iota _*(\Delta |_V)$
. Then
${\mathcal D}=\iota _*(\Delta |_V)$
. Then
![]() $\Delta $
is a subsheaf of
$\Delta $
is a subsheaf of
![]() ${\mathcal D}$
and we need to show equality. To that end, let
${\mathcal D}$
and we need to show equality. To that end, let
![]() $U\subset Y$
be an affine open subset and
$U\subset Y$
be an affine open subset and
![]() $W=f^{-1}(U)$
. Then we have the following:
$W=f^{-1}(U)$
. Then we have the following:
-
(1)
 ${\mathcal O}_X(W)\subset {\mathcal O}_X(W\setminus Z)$
and
${\mathcal O}_X(W)\subset {\mathcal O}_X(W\setminus Z)$
and -
(2)
 ${\mathcal O}_{Y}(U)={\mathcal O}_{Y}(U\setminus Z')$
.
${\mathcal O}_{Y}(U)={\mathcal O}_{Y}(U\setminus Z')$
.
Letting L be the total quotient ring of X and K the function field of Y, we get
and due to (1) and (2) the latter is contained in
Thus, we have
![]() ${\mathcal D}(W)=\Delta (W)$
. Since
${\mathcal D}(W)=\Delta (W)$
. Since
![]() $f\colon X\to Y$
is affine, the sets
$f\colon X\to Y$
is affine, the sets
![]() $W=f^{-1}(U)$
for
$W=f^{-1}(U)$
for
![]() ${U\subset Y}$
open and affine give an affine covering of X and thus
${U\subset Y}$
open and affine give an affine covering of X and thus
![]() ${\mathcal D}=\Delta $
.
${\mathcal D}=\Delta $
.
6 Real-fibered morphisms
In this section, we recall the notion of real-fibered morphisms, basic examples and some of their properties.
Definition 6.1 Let
![]() $f\colon X\to Y$
be a morphism of varieties over
$f\colon X\to Y$
be a morphism of varieties over
![]() ${\mathbb R}$
. If
${\mathbb R}$
. If
![]() $f^{-1}(Y({\mathbb R}))=X({\mathbb R})$
, then we say that f is real fibered.
$f^{-1}(Y({\mathbb R}))=X({\mathbb R})$
, then we say that f is real fibered.
Example 6.1 Let
![]() $p\in {\mathbb R}[x_0,\ldots ,x_n]_{2d}$
be a homogeneous polynomial of degree
$p\in {\mathbb R}[x_0,\ldots ,x_n]_{2d}$
be a homogeneous polynomial of degree
![]() $2d$
. Inside the weighted projective space
$2d$
. Inside the weighted projective space
![]() $\mathbb {P}(d,1,\ldots ,1)$
, we consider the hypersurface X defined by
$\mathbb {P}(d,1,\ldots ,1)$
, we consider the hypersurface X defined by
![]() $y^2=p(x_0,\ldots ,x_n)$
and the natural projection
$y^2=p(x_0,\ldots ,x_n)$
and the natural projection
![]() $\pi \colon X\to \mathbb {P}^n$
onto the x-coordinates. This is a double cover of
$\pi \colon X\to \mathbb {P}^n$
onto the x-coordinates. This is a double cover of
![]() $\mathbb {P}^n$
ramified at the hypersurface defined by
$\mathbb {P}^n$
ramified at the hypersurface defined by
![]() $p=0$
. Clearly
$p=0$
. Clearly
![]() $\pi $
is real fibered if and only if p is globally nonnegative, i.e.,
$\pi $
is real fibered if and only if p is globally nonnegative, i.e.,
![]() $p(x)\geq 0$
for all
$p(x)\geq 0$
for all
![]() $x\in {\mathbb R}^{n+1}$
.
$x\in {\mathbb R}^{n+1}$
.
Hyperbolic polynomials yield another class of examples.
Definition 6.2 Let
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
be a homogeneous polynomial of degree d, and let
$h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
be a homogeneous polynomial of degree d, and let
![]() $e\in {\mathbb R}^{n+1}$
. We say that h is hyperbolic with respect to e if the univariate polynomial
$e\in {\mathbb R}^{n+1}$
. We say that h is hyperbolic with respect to e if the univariate polynomial
![]() $h(te-v)\in {\mathbb R}[t]$
has only real zeros for all
$h(te-v)\in {\mathbb R}[t]$
has only real zeros for all
![]() $v\in {\mathbb R}^{n+1}$
. Note that this implies
$v\in {\mathbb R}^{n+1}$
. Note that this implies
![]() $h(e)\neq 0$
. A hypersurface
$h(e)\neq 0$
. A hypersurface
![]() $X\subset \mathbb {P}^n$
is called hyperbolic with respect to
$X\subset \mathbb {P}^n$
is called hyperbolic with respect to
![]() $[e]$
if its defining polynomial is hyperbolic with respect to e.
$[e]$
if its defining polynomial is hyperbolic with respect to e.

Figure 1: A plane quartic curve that is hyperbolic with respect to any point in the inner oval
Example 6.2 Let
![]() $X\subset \mathbb {P}^n$
be a hypersurface, and let
$X\subset \mathbb {P}^n$
be a hypersurface, and let
![]() $e\in \mathbb {P}^n$
be a point that does not lie on X. Then the linear projection
$e\in \mathbb {P}^n$
be a point that does not lie on X. Then the linear projection
![]() $\pi _e\colon X\to \mathbb {P}^{n-1}$
with center e is real-fibered if and only if X is hyperbolic with respect to e.
$\pi _e\colon X\to \mathbb {P}^{n-1}$
with center e is real-fibered if and only if X is hyperbolic with respect to e.
One can generalize this notion naturally to varieties of higher codimension.
Definition 6.3 Let
![]() $X\subset \mathbb {P}^n$
be a variety of pure dimension d, and let
$X\subset \mathbb {P}^n$
be a variety of pure dimension d, and let
![]() $E\subset \mathbb {P}^n$
be a linear subspace of codimension
$E\subset \mathbb {P}^n$
be a linear subspace of codimension
![]() $d+1$
which does not intersect X. We say that X is hyperbolic with respect to E if the linear projection
$d+1$
which does not intersect X. We say that X is hyperbolic with respect to E if the linear projection
![]() $\pi _E\colon X\to \mathbb {P}^{d}$
with center E is real-fibered.
$\pi _E\colon X\to \mathbb {P}^{d}$
with center E is real-fibered.
An important feature of real-fibered morphisms is the following.
Theorem 6.3 [Reference Kummer and ShamovichKS20, Theorem 2.19]
Let
![]() $f\colon X\to Y$
be a real-fibered morphism of smooth varieties over
$f\colon X\to Y$
be a real-fibered morphism of smooth varieties over
![]() ${\mathbb R}$
. Then the ramification divisor of f has no real point.
${\mathbb R}$
. Then the ramification divisor of f has no real point.
The following property of real-fibered morphisms will come in handy later when we want to construct positive semidefinite bilinear forms.
Proposition 6.4 Let Y be an irreducible smooth variety, and let X be an equidimensional variety over
![]() ${\mathbb R}$
. Let
${\mathbb R}$
. Let
![]() $f\colon X\to Y$
be a finite surjective real-fibered morphism. Let K and L be the total quotient rings of Y and X and
$f\colon X\to Y$
be a finite surjective real-fibered morphism. Let K and L be the total quotient rings of Y and X and
![]() $\operatorname {tr}_{L/K}\colon L\to K$
the trace map. If
$\operatorname {tr}_{L/K}\colon L\to K$
the trace map. If
![]() $g\in L$
is nonnegative on
$g\in L$
is nonnegative on
![]() $X({\mathbb R})$
(wherever it is defined), then
$X({\mathbb R})$
(wherever it is defined), then
![]() $\operatorname {tr}_{L/K}(g)$
is nonnegative on
$\operatorname {tr}_{L/K}(g)$
is nonnegative on
![]() $Y({\mathbb R})$
(wherever it is defined).
$Y({\mathbb R})$
(wherever it is defined).
Proof Assume that
![]() $g\in L$
is nonnegative on
$g\in L$
is nonnegative on
![]() $X({\mathbb R})$
(wherever it is defined). By generic freeness [Reference GrothendieckGro65, Lemma 6.9.2], there is a nonempty open affine subset
$X({\mathbb R})$
(wherever it is defined). By generic freeness [Reference GrothendieckGro65, Lemma 6.9.2], there is a nonempty open affine subset
![]() $U\subset Y$
such that
$U\subset Y$
such that
![]() $B={\mathcal O}_X(f^{-1}(U))$
is a free A-module, where
$B={\mathcal O}_X(f^{-1}(U))$
is a free A-module, where
![]() $A={\mathcal O}_Y(U)$
and such that
$A={\mathcal O}_Y(U)$
and such that
![]() $g\in B$
. By a version of the Artin–Lang theorem [Reference BeckerBec82, Lemma 1.5], the real points of U are dense in
$g\in B$
. By a version of the Artin–Lang theorem [Reference BeckerBec82, Lemma 1.5], the real points of U are dense in
![]() $Y({\mathbb R})$
with respect to the euclidean topology because Y is smooth. Thus, it suffices to show that
$Y({\mathbb R})$
with respect to the euclidean topology because Y is smooth. Thus, it suffices to show that
![]() $\operatorname {tr}_{L/K}(g)\in A$
is nonnegative on every real point p of U. Let
$\operatorname {tr}_{L/K}(g)\in A$
is nonnegative on every real point p of U. Let
![]() ${\mathfrak m}\subset A$
be the corresponding maximal ideal. Then
${\mathfrak m}\subset A$
be the corresponding maximal ideal. Then
![]() $C=B/{\mathfrak m} B$
is finite-dimensional as vector space over
$C=B/{\mathfrak m} B$
is finite-dimensional as vector space over
![]() ${\mathbb R}=A/{\mathfrak m}$
and
${\mathbb R}=A/{\mathfrak m}$
and
![]() $\operatorname {Spec}(C)$
consists only of real points because f is real fibered. Thus, letting
$\operatorname {Spec}(C)$
consists only of real points because f is real fibered. Thus, letting
![]() $\overline {g}\in C$
be the residue class of g and because g is nonnegative on
$\overline {g}\in C$
be the residue class of g and because g is nonnegative on
![]() $f^{-1}(p)$
, the quadratic form
$f^{-1}(p)$
, the quadratic form
is positive semidefinite by [Reference Pedersen, Roy and SzpirglasPRS93, Theorem 2.1]. Thus, in particular,
![]() $\operatorname {tr}_{C/{\mathbb R}}(\overline {g})\geq 0$
. Finally, by flatness, we have that
$\operatorname {tr}_{C/{\mathbb R}}(\overline {g})\geq 0$
. Finally, by flatness, we have that
![]() $\overline {\operatorname {tr}_{L/K}(g)}=\operatorname {tr}_{C/{\mathbb R}}(\overline {g})\geq 0$
.
$\overline {\operatorname {tr}_{L/K}(g)}=\operatorname {tr}_{C/{\mathbb R}}(\overline {g})\geq 0$
.
7 Positive semidefinite bilinear forms
The criterion for a coherent sheaf being Ulrich that we have seen in Section 4 very much relies on the induced bilinear form on global sections being nondegenerate. Verifying this condition might be hard in general. However, in this section, we show that when working over the real numbers, we have a more convenient criterion at hand, namely, positivity.
We first have to define Hermitian bilinear forms on sheaves. To this end, let X be a scheme, and let
![]() ${\mathcal F}_1,{\mathcal F}_2$
, and
${\mathcal F}_1,{\mathcal F}_2$
, and
![]() ${\mathcal G}$
be coherent sheaves on X. A
${\mathcal G}$
be coherent sheaves on X. A
![]() ${\mathcal G}$
-valued pairing
${\mathcal G}$
-valued pairing
![]() $\varphi \colon {\mathcal F}_1 \otimes {\mathcal F}_2 \to {\mathcal G}$
induces naturally the two morphisms
$\varphi \colon {\mathcal F}_1 \otimes {\mathcal F}_2 \to {\mathcal G}$
induces naturally the two morphisms
![]() $\varphi _1\colon {\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal G})$
and
$\varphi _1\colon {\mathcal F}_1\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_2,{\mathcal G})$
and
![]() $\varphi _2\colon {\mathcal F}_2\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_1,{\mathcal G})$
.
$\varphi _2\colon {\mathcal F}_2\to \operatorname {{\mathscr Hom}}_{{\mathcal O}_X}({\mathcal F}_1,{\mathcal G})$
.
Definition 7.1 Let X be a scheme, and let
![]() ${\mathcal F}$
and
${\mathcal F}$
and
![]() ${\mathcal G}$
be coherent sheaves on X. A
${\mathcal G}$
be coherent sheaves on X. A
![]() ${\mathcal G}$
-valued pairing
${\mathcal G}$
-valued pairing
![]() $\varphi \colon {\mathcal F} \otimes {\mathcal F} \to {\mathcal G}$
is symmetric if
$\varphi \colon {\mathcal F} \otimes {\mathcal F} \to {\mathcal G}$
is symmetric if
![]() $\varphi _1=\varphi _2$
.
$\varphi _1=\varphi _2$
.
Definition 7.2 Let X be a scheme over
![]() ${\mathbb R}$
. Denote by
${\mathbb R}$
. Denote by
![]() $X_{\mathbb C}=X\times _{\operatorname {Spec}({\mathbb R})} \operatorname {Spec}({\mathbb C})$
the base change to
$X_{\mathbb C}=X\times _{\operatorname {Spec}({\mathbb R})} \operatorname {Spec}({\mathbb C})$
the base change to
![]() ${\mathbb C}$
and
${\mathbb C}$
and
![]() $\pi \colon X_{\mathbb C}\to X$
the natural projection. Further, let
$\pi \colon X_{\mathbb C}\to X$
the natural projection. Further, let
![]() $\tau \colon X_{\mathbb C}\to X_{\mathbb C}$
be the automorphism induced by complex conjugation. Let
$\tau \colon X_{\mathbb C}\to X_{\mathbb C}$
be the automorphism induced by complex conjugation. Let
![]() ${\mathcal G}$
be a coherent sheaf on X, and let
${\mathcal G}$
be a coherent sheaf on X, and let
![]() ${\mathcal F}$
be a coherent sheaf on
${\mathcal F}$
be a coherent sheaf on
![]() $X_{\mathbb C}$
. A pairing
$X_{\mathbb C}$
. A pairing
![]() $\varphi \colon {\mathcal F} \otimes \tau ^*{\mathcal F} \to \pi ^*{\mathcal G}$
is Hermitian if
$\varphi \colon {\mathcal F} \otimes \tau ^*{\mathcal F} \to \pi ^*{\mathcal G}$
is Hermitian if
![]() $\varphi _1$
agrees with the pullback of
$\varphi _1$
agrees with the pullback of
![]() $\varphi _2$
via
$\varphi _2$
via
![]() $\tau $
.
$\tau $
.
From now on, in this section, X will always be a variety over
![]() ${\mathbb R}$
.
${\mathbb R}$
.
Definition 7.3 Let
![]() ${\mathcal F}$
be a coherent sheaf on X. Consider a symmetric bilinear form
${\mathcal F}$
be a coherent sheaf on X. Consider a symmetric bilinear form
![]() $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to {\mathcal O}_X$
. Let
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to {\mathcal O}_X$
. Let
![]() $\alpha \in X({\mathbb R})$
, i.e., a morphism
$\alpha \in X({\mathbb R})$
, i.e., a morphism
![]() $\alpha \colon \operatorname {Spec}({\mathbb R}) \to X$
. Then we get a symmetric bilinear form
$\alpha \colon \operatorname {Spec}({\mathbb R}) \to X$
. Then we get a symmetric bilinear form
![]() $\alpha ^* \varphi $
on the pullback
$\alpha ^* \varphi $
on the pullback
![]() $\alpha ^* {\mathcal F}$
which is just a finite-dimensional
$\alpha ^* {\mathcal F}$
which is just a finite-dimensional
![]() ${\mathbb R}$
-vector space. We say that
${\mathbb R}$
-vector space. We say that
![]() $\varphi $
is positive semidefinite at
$\varphi $
is positive semidefinite at
![]() $\alpha \in X({\mathbb R})$
if
$\alpha \in X({\mathbb R})$
if
![]() $\alpha ^* \varphi $
is positive semidefinite. We say that
$\alpha ^* \varphi $
is positive semidefinite. We say that
![]() $\varphi $
is positive semidefinite if it is positive semidefinite at every
$\varphi $
is positive semidefinite if it is positive semidefinite at every
![]() $\alpha \in X({\mathbb R})$
.
$\alpha \in X({\mathbb R})$
.
Analogously, let
![]() ${\mathcal F}$
be a coherent sheaf on
${\mathcal F}$
be a coherent sheaf on
![]() $X_{\mathbb C}$
and consider a Hermitian bilinear form
$X_{\mathbb C}$
and consider a Hermitian bilinear form
![]() $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} \overline {{\mathcal F}} \to {\mathcal O}_X$
. We can consider any
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} \overline {{\mathcal F}} \to {\mathcal O}_X$
. We can consider any
![]() $\alpha \in X({\mathbb R})$
also as a point of
$\alpha \in X({\mathbb R})$
also as a point of
![]() $X_{\mathbb C}$
that is fixed by the involution. Like this, we obtain a Hermitian bilinear form
$X_{\mathbb C}$
that is fixed by the involution. Like this, we obtain a Hermitian bilinear form
![]() $\alpha ^* \varphi $
on the pullback
$\alpha ^* \varphi $
on the pullback
![]() $\alpha ^* {\mathcal F}$
which is just a finite-dimensional
$\alpha ^* {\mathcal F}$
which is just a finite-dimensional
![]() ${\mathbb C}$
-vector space. We say that
${\mathbb C}$
-vector space. We say that
![]() $\varphi $
is positive semidefinite at
$\varphi $
is positive semidefinite at
![]() $\alpha \in X({\mathbb R})$
if
$\alpha \in X({\mathbb R})$
if
![]() $\alpha ^* \varphi $
is positive semidefinite. We say that
$\alpha ^* \varphi $
is positive semidefinite. We say that
![]() $\varphi $
is positive semidefinite if it is positive semidefinite at every
$\varphi $
is positive semidefinite if it is positive semidefinite at every
![]() $\alpha \in X({\mathbb R})$
.
$\alpha \in X({\mathbb R})$
.
A symmetric or Hermitian bilinear form on a coherent sheaf induces a symmetric or Hermitian bilinear form on the space of global sections. The next lemma shows how this behaves with respect to positivity.
Lemma 7.1 Let X be irreducible and proper over
![]() ${\mathbb R}$
with generic point
${\mathbb R}$
with generic point
![]() $\xi $
. Let
$\xi $
. Let
![]() $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to {\mathcal O}_X$
be a positive semidefinite symmetric bilinear form on the coherent sheaf
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to {\mathcal O}_X$
be a positive semidefinite symmetric bilinear form on the coherent sheaf
![]() ${\mathcal F}$
and
${\mathcal F}$
and
![]() $V=H^0(X,{\mathcal F})$
.
$V=H^0(X,{\mathcal F})$
.
-
(a) If
 $X({\mathbb R})\neq \emptyset $
, then the induced bilinear form
$X({\mathbb R})\neq \emptyset $
, then the induced bilinear form
 $V \times V\to {\mathbb R}$
is positive semidefinite.
$V \times V\to {\mathbb R}$
is positive semidefinite. -
(b) If
 $X({\mathbb R})$
is Zariski dense in X,
$X({\mathbb R})$
is Zariski dense in X,
 $\varphi $
is nondegenerate at
$\varphi $
is nondegenerate at
 $\xi $
and
$\xi $
and
 ${\mathcal F}$
is torsion-free, then the induced bilinear form
${\mathcal F}$
is torsion-free, then the induced bilinear form
 $V \times V\to {\mathbb R}$
is positive definite and thus in particular nondegenerate.
$V \times V\to {\mathbb R}$
is positive definite and thus in particular nondegenerate.
The corresponding statements for Hermitian bilinear forms hold true as well.
Proof For part (a), we observe that if
![]() $\varphi (s,s)=-1$
for some
$\varphi (s,s)=-1$
for some
![]() $s\in V$
, then
$s\in V$
, then
![]() $\varphi $
is not positive semidefinite at any point from
$\varphi $
is not positive semidefinite at any point from
![]() $X({\mathbb R})$
.
$X({\mathbb R})$
.
In order to show part (b), we first observe that since
![]() $X({\mathbb R})$
is Zariski dense in X, the field
$X({\mathbb R})$
is Zariski dense in X, the field
![]() $\kappa (\xi )$
has an ordering P. Consider a nonzero section
$\kappa (\xi )$
has an ordering P. Consider a nonzero section
![]() $s\in V$
. Since
$s\in V$
. Since
![]() $\varphi (s,s)\geq 0$
at all points in
$\varphi (s,s)\geq 0$
at all points in
![]() $X({\mathbb R})$
, Tarski’s principle implies that
$X({\mathbb R})$
, Tarski’s principle implies that
![]() $\varphi (s,s)$
is also nonnegative with respect to the ordering P when considered as an element of
$\varphi (s,s)$
is also nonnegative with respect to the ordering P when considered as an element of
![]() $\kappa (\xi )$
. Thus, the bilinear form induced by
$\kappa (\xi )$
. Thus, the bilinear form induced by
![]() $\varphi $
on the
$\varphi $
on the
![]() $\kappa (\xi )$
-vector subspace of
$\kappa (\xi )$
-vector subspace of
![]() ${\mathcal F}_\xi $
spanned by V is also positive semidefinite (with respect to P). But since
${\mathcal F}_\xi $
spanned by V is also positive semidefinite (with respect to P). But since
![]() $\varphi $
is nondegenerate at
$\varphi $
is nondegenerate at
![]() $\xi $
, it is even positive definite (with respect to P). Finally, because
$\xi $
, it is even positive definite (with respect to P). Finally, because
![]() ${\mathcal F}$
is torsion-free, the nonzero section s is mapped to a nonzero element in the stalk
${\mathcal F}$
is torsion-free, the nonzero section s is mapped to a nonzero element in the stalk
![]() ${\mathcal F}_\xi $
and therefore by positive definiteness
${\mathcal F}_\xi $
and therefore by positive definiteness
![]() $\varphi (s,s)\neq 0$
. This shows the claim.
$\varphi (s,s)\neq 0$
. This shows the claim.
Thus, if we assume positive semidefiniteness, we only need to assure that our bilinear form is nondegenerate at the generic point rather than on global sections.
Theorem 7.2 Let Y be a geometrically irreducible variety which is proper over
![]() ${\mathbb R}$
. Let
${\mathbb R}$
. Let
![]() $f\colon X\to Y$
be a finite surjective morphism, where X is an equidimensional variety over
$f\colon X\to Y$
be a finite surjective morphism, where X is an equidimensional variety over
![]() ${\mathbb R}$
with
${\mathbb R}$
with
![]() $X({\mathbb R})$
Zariski dense in X. Let
$X({\mathbb R})$
Zariski dense in X. Let
![]() $X_1,\ldots , X_s$
be the irreducible components of X. Let
$X_1,\ldots , X_s$
be the irreducible components of X. Let
![]() ${\mathcal F}$
be a coherent torsion-free sheaf on X, and let
${\mathcal F}$
be a coherent torsion-free sheaf on X, and let
![]() $V=H^0(X,{\mathcal F})$
. Let
$V=H^0(X,{\mathcal F})$
. Let
![]() $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to f^!{\mathcal O}_Y$
be a symmetric bilinear map which is nondegenerate at the generic point of each
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to f^!{\mathcal O}_Y$
be a symmetric bilinear map which is nondegenerate at the generic point of each
![]() $X_i$
. If the induced
$X_i$
. If the induced
![]() ${\mathcal O}_Y$
-valued bilinear form on
${\mathcal O}_Y$
-valued bilinear form on
![]() $f_*{\mathcal F}$
is positive semidefinite, then the following are equivalent:
$f_*{\mathcal F}$
is positive semidefinite, then the following are equivalent:
-
(i)
 $\dim V \geq \sum _{i=1}^s \deg (f|_{X_i})\cdot \operatorname {rank} ({\mathcal F}|_{X_i})$
.
$\dim V \geq \sum _{i=1}^s \deg (f|_{X_i})\cdot \operatorname {rank} ({\mathcal F}|_{X_i})$
. -
(ii)
 ${\mathcal F}$
is an f-Ulrich sheaf.
${\mathcal F}$
is an f-Ulrich sheaf.
Proof Combining Lemma 7.1 and Theorem 3.7, it remains to show that the induced symmetric
![]() ${\mathcal O}_Y$
-valued bilinear form on
${\mathcal O}_Y$
-valued bilinear form on
![]() $f_*{\mathcal F}$
is nondegenerate at the generic point of Y. But this follows from the assumption that
$f_*{\mathcal F}$
is nondegenerate at the generic point of Y. But this follows from the assumption that
![]() $\varphi $
is nondegenerate at the generic point of each
$\varphi $
is nondegenerate at the generic point of each
![]() $X_i$
by Lemma 7.3 whose easy proof we leave as an exercise.
$X_i$
by Lemma 7.3 whose easy proof we leave as an exercise.
Lemma 7.3 Let
![]() $A=K_1\times \cdots \times K_r$
be the direct product of fields
$A=K_1\times \cdots \times K_r$
be the direct product of fields
![]() $K_i$
each of which is a finite extension of the field K. Let M be a finitely generated A-module. Then
$K_i$
each of which is a finite extension of the field K. Let M be a finitely generated A-module. Then
![]() $M\cong V_1\times \cdots \times V_r$
, where each
$M\cong V_1\times \cdots \times V_r$
, where each
![]() $V_i$
is a finite-dimensional
$V_i$
is a finite-dimensional
![]() $K_i$
-vector space and the right-hand side is considered as an A-module in the obvious way. A homomorphism
$K_i$
-vector space and the right-hand side is considered as an A-module in the obvious way. A homomorphism
![]() ${\varphi \colon M\to \operatorname {Hom}_K(M,K)}$
of A-modules such that all induced maps
${\varphi \colon M\to \operatorname {Hom}_K(M,K)}$
of A-modules such that all induced maps
![]() $V_i\to \operatorname {Hom}_K(V_i,K)$
are isomorphisms is an isomorphism itself. In particular, the induced K-bilinear form
$V_i\to \operatorname {Hom}_K(V_i,K)$
are isomorphisms is an isomorphism itself. In particular, the induced K-bilinear form
![]() ${M\otimes _K M\to K}$
is nondegenerate.
${M\otimes _K M\to K}$
is nondegenerate.
In the same manner, we obtain the Hermitian version.
Theorem 7.4 Let Y be a geometrically irreducible variety which is proper over
![]() ${\mathbb R}$
. Let
${\mathbb R}$
. Let
![]() $f\colon X\to Y$
be a finite surjective morphism, where X is an equidimensional variety over
$f\colon X\to Y$
be a finite surjective morphism, where X is an equidimensional variety over
![]() ${\mathbb R}$
with
${\mathbb R}$
with
![]() $X({\mathbb R})$
Zariski dense in X. Let
$X({\mathbb R})$
Zariski dense in X. Let
![]() $X_1,\ldots , X_s$
be the irreducible components of
$X_1,\ldots , X_s$
be the irreducible components of
![]() $X_{\mathbb C}$
. Let
$X_{\mathbb C}$
. Let
![]() ${\mathcal F}$
be a coherent torsion-free sheaf on
${\mathcal F}$
be a coherent torsion-free sheaf on
![]() $X_{\mathbb C}$
, and let
$X_{\mathbb C}$
, and let
![]() $V=H^0(X,{\mathcal F})$
. Let
$V=H^0(X,{\mathcal F})$
. Let
![]() $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} \overline {{\mathcal F}} \to f^!{\mathcal O}_{Y_{\mathbb C}}$
be a Hermitian bilinear map which is nondegenerate at the generic point of each
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} \overline {{\mathcal F}} \to f^!{\mathcal O}_{Y_{\mathbb C}}$
be a Hermitian bilinear map which is nondegenerate at the generic point of each
![]() $X_i$
. If the induced
$X_i$
. If the induced
![]() ${\mathcal O}_{Y_{\mathbb C}}$
-valued Hermitian bilinear form on
${\mathcal O}_{Y_{\mathbb C}}$
-valued Hermitian bilinear form on
![]() $f_*{\mathcal F}$
is positive semidefinite, then the following are equivalent:
$f_*{\mathcal F}$
is positive semidefinite, then the following are equivalent:
-
(i)
 $\dim V \geq \sum _{i=1}^s \deg (f|_{X_i})\cdot \operatorname {rank} ({\mathcal F}|_{X_i})$
.
$\dim V \geq \sum _{i=1}^s \deg (f|_{X_i})\cdot \operatorname {rank} ({\mathcal F}|_{X_i})$
. -
(ii)
 ${\mathcal F}$
is an f-Ulrich sheaf.
${\mathcal F}$
is an f-Ulrich sheaf.
Definition 7.4 Let Y be a geometrically irreducible variety which is proper over
![]() ${\mathbb R}$
. Let
${\mathbb R}$
. Let
![]() $f\colon X\to Y$
be a finite surjective morphism, where X is an equidimensional variety over
$f\colon X\to Y$
be a finite surjective morphism, where X is an equidimensional variety over
![]() ${\mathbb R}$
with
${\mathbb R}$
with
![]() $X({\mathbb R})$
Zariski dense in X. Let
$X({\mathbb R})$
Zariski dense in X. Let
![]() $X_1,\ldots , X_s$
be the irreducible components of
$X_1,\ldots , X_s$
be the irreducible components of
![]() $X_{\mathbb C}$
.
$X_{\mathbb C}$
.
-
(a) Let
 ${\mathcal F}$
be an f-Ulrich sheaf on X. If there exists a symmetric bilinear map
${\mathcal F}$
be an f-Ulrich sheaf on X. If there exists a symmetric bilinear map
 $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to f^!{\mathcal O}_Y$
which is nondegenerate at the generic point of each
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} {\mathcal F} \to f^!{\mathcal O}_Y$
which is nondegenerate at the generic point of each
 $X_i$
such that the induced
$X_i$
such that the induced
 ${\mathcal O}_Y$
-valued bilinear form on
${\mathcal O}_Y$
-valued bilinear form on
 $f_*{\mathcal F}$
is positive semidefinite, then we say that
$f_*{\mathcal F}$
is positive semidefinite, then we say that
 ${\mathcal F}$
is a positive symmetric f-Ulrich sheaf.
${\mathcal F}$
is a positive symmetric f-Ulrich sheaf. -
(b) Let
 ${\mathcal F}$
be an f-Ulrich sheaf on
${\mathcal F}$
be an f-Ulrich sheaf on
 $X_{\mathbb C}$
. If there exists a Hermitian bilinear map
$X_{\mathbb C}$
. If there exists a Hermitian bilinear map
 $\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} \overline {{\mathcal F}} \to f^!{\mathcal O}_{Y_{\mathbb C}}$
which is nondegenerate at the generic point of each
$\varphi \colon {\mathcal F}\otimes _{{\mathcal O}_X} \overline {{\mathcal F}} \to f^!{\mathcal O}_{Y_{\mathbb C}}$
which is nondegenerate at the generic point of each
 $X_i$
such that the induced
$X_i$
such that the induced
 ${\mathcal O}_{Y_{\mathbb C}}$
-valued bilinear form on
${\mathcal O}_{Y_{\mathbb C}}$
-valued bilinear form on
 $f_*{\mathcal F}$
is positive semidefinite, then we say that
$f_*{\mathcal F}$
is positive semidefinite, then we say that
 ${\mathcal F}$
is a positive Hermitian f-Ulrich sheaf.
${\mathcal F}$
is a positive Hermitian f-Ulrich sheaf.
In order to check the positivity condition, the following lemma will be useful.
Lemma 7.5 Let Y be an irreducible smooth variety with
![]() $Y({\mathbb R})\neq \emptyset $
, and let X be an equidimensional variety over
$Y({\mathbb R})\neq \emptyset $
, and let X be an equidimensional variety over
![]() ${\mathbb R}$
. Let
${\mathbb R}$
. Let
![]() $f\colon X\to Y$
be a finite surjective real-fibered morphism. Let s be a global section of
$f\colon X\to Y$
be a finite surjective real-fibered morphism. Let s be a global section of
![]() ${\mathcal K}_X$
which is nonnegative on
${\mathcal K}_X$
which is nonnegative on
![]() $X({\mathbb R})$
, and let
$X({\mathbb R})$
, and let
![]() ${\mathcal D}$
be the subsheaf of
${\mathcal D}$
be the subsheaf of
![]() ${\mathcal K}_X$
given by
${\mathcal K}_X$
given by
![]() $s\cdot \Delta (X/Y)$
. Let
$s\cdot \Delta (X/Y)$
. Let
![]() ${\mathcal L}$
be a subsheaf of
${\mathcal L}$
be a subsheaf of
![]() ${\mathcal K}_X$
such that
${\mathcal K}_X$
such that
![]() ${\mathcal L}\cdot {\mathcal L}\subset {\mathcal D}$
. Then there is an
${\mathcal L}\cdot {\mathcal L}\subset {\mathcal D}$
. Then there is an
![]() $f^!{\mathcal O}_Y$
-valued symmetric bilinear form on
$f^!{\mathcal O}_Y$
-valued symmetric bilinear form on
![]() ${\mathcal L}$
such that the induced
${\mathcal L}$
such that the induced
![]() ${\mathcal O}_Y$
-valued bilinear form on
${\mathcal O}_Y$
-valued bilinear form on
![]() $f_*{\mathcal L}$
is positive semidefinite.
$f_*{\mathcal L}$
is positive semidefinite.
Proof By assumption, we can define the symmetric
![]() $\Delta (X/Y)$
-valued bilinear form on
$\Delta (X/Y)$
-valued bilinear form on
![]() ${\mathcal L}$
that maps a pair of sections
${\mathcal L}$
that maps a pair of sections
![]() $(g,h)$
to
$(g,h)$
to
![]() $\frac {g\cdot h}{s}$
. Thus the induced
$\frac {g\cdot h}{s}$
. Thus the induced
![]() ${\mathcal O}_Y$
-valued bilinear form maps
${\mathcal O}_Y$
-valued bilinear form maps
![]() $(g,g)$
to the trace of
$(g,g)$
to the trace of
![]() $\frac {g^2}{s}$
which is nonnegative by Proposition 6.4.
$\frac {g^2}{s}$
which is nonnegative by Proposition 6.4.
Remark 7.6 Let
![]() $\iota \colon X\hookrightarrow \mathbb {P}^n$
be an embedding of a k-dimensional projective variety, and let
$\iota \colon X\hookrightarrow \mathbb {P}^n$
be an embedding of a k-dimensional projective variety, and let
![]() ${\mathcal F}$
be an Ulrich sheaf on X, i.e.,
${\mathcal F}$
be an Ulrich sheaf on X, i.e.,
![]() ${\mathcal F}$
is
${\mathcal F}$
is
![]() $\pi $
-Ulrich for some finite surjective linear projection
$\pi $
-Ulrich for some finite surjective linear projection
![]() $\pi \colon X\to \mathbb {P}^k$
. One can show that
$\pi \colon X\to \mathbb {P}^k$
. One can show that
Thus, our notion of symmetry coincides with the one introduced in [Reference Eisenbud, Schreyer and WeymanESW03, Section 3.1]. In particular, the property of being symmetric does not depend on the choice of the linear projection
![]() $\pi $
but the positivity condition does, as the next example shows.
$\pi $
but the positivity condition does, as the next example shows.
Example 7.7 Let
![]() $Y=\mathbb {P}^1$
and
$Y=\mathbb {P}^1$
and
![]() $X={\mathcal V}(x_0^2-x_1^2-x_2^2)\subset \mathbb {P}^2$
. We let
$X={\mathcal V}(x_0^2-x_1^2-x_2^2)\subset \mathbb {P}^2$
. We let
![]() $f_i\colon X\to \mathbb {P}^1$
be the linear projection with center
$f_i\colon X\to \mathbb {P}^1$
be the linear projection with center
![]() $e_i$
, where
$e_i$
, where
![]() $e_1=[1\colon 0\colon 0]$
and
$e_1=[1\colon 0\colon 0]$
and
![]() $e_2=[0\colon 1\colon 0]$
. Note that
$e_2=[0\colon 1\colon 0]$
. Note that
![]() $f_1$
is real fibered but
$f_1$
is real fibered but
![]() $f_2$
is not. Let
$f_2$
is not. Let
![]() $P=[1\colon 1\colon 0]\in X$
(Weil divisor on X) and
$P=[1\colon 1\colon 0]\in X$
(Weil divisor on X) and
![]() ${\mathcal L}={\mathcal L}(P)$
the corresponding invertible subsheaf of
${\mathcal L}={\mathcal L}(P)$
the corresponding invertible subsheaf of
![]() ${\mathcal K}_X$
. A basis of the space of global sections V of
${\mathcal K}_X$
. A basis of the space of global sections V of
![]() ${\mathcal L}(P)$
is given by the two rational functions
${\mathcal L}(P)$
is given by the two rational functions
![]() $g_1=1$
and
$g_1=1$
and
![]() $g_2=\frac {x_0+x_1}{x_2}$
. The ramification divisor
$g_2=\frac {x_0+x_1}{x_2}$
. The ramification divisor
![]() $R_i$
of
$R_i$
of
![]() $f_i$
is given by
$f_i$
is given by
![]() $R_1=Q_0+\overline {Q_0}$
and
$R_1=Q_0+\overline {Q_0}$
and
![]() $R_2=Q_1+Q_2$
with
$R_2=Q_1+Q_2$
with
![]() $Q_0=[0\colon 1\colon \textrm {i}], Q_1=[1\colon 0\colon 1] \textrm { and } Q_2=[1\colon 0\colon -1]$
. Denoting by
$Q_0=[0\colon 1\colon \textrm {i}], Q_1=[1\colon 0\colon 1] \textrm { and } Q_2=[1\colon 0\colon -1]$
. Denoting by
![]() $\Delta _i$
the codifferent sheaf associated with
$\Delta _i$
the codifferent sheaf associated with
![]() $f_i$
, we thus get that
$f_i$
, we thus get that
defines a symmetric bilinear form
![]() ${\mathcal L}\otimes {\mathcal L}\to \Delta _1$
. Via the isomorphism
${\mathcal L}\otimes {\mathcal L}\to \Delta _1$
. Via the isomorphism
![]() $\Delta _1\cong f_1^!{\mathcal O}_{\mathbb {P}^1}$
, this induces an
$\Delta _1\cong f_1^!{\mathcal O}_{\mathbb {P}^1}$
, this induces an
![]() ${\mathcal O}_{\mathbb {P}^1}$
-valued bilinear form on
${\mathcal O}_{\mathbb {P}^1}$
-valued bilinear form on
![]() $(f_1)_*{\mathcal L}$
. With respect to the above basis of V, it is given by the matrix
$(f_1)_*{\mathcal L}$
. With respect to the above basis of V, it is given by the matrix
 $$ \begin{align*}\begin{pmatrix} 2 & 0\\0 &2 \end{pmatrix},\end{align*} $$
$$ \begin{align*}\begin{pmatrix} 2 & 0\\0 &2 \end{pmatrix},\end{align*} $$
which is positive definite. Thus,
![]() ${\mathcal L}$
is a positive symmetric
${\mathcal L}$
is a positive symmetric
![]() $f_1$
-Ulrich sheaf. On the other hand, via the isomorphism
$f_1$
-Ulrich sheaf. On the other hand, via the isomorphism
![]() $\Delta _1\to \Delta _2$
that is given by multiplication with
$\Delta _1\to \Delta _2$
that is given by multiplication with
![]() $\frac {x_0}{x_1}$
, we get from (7.1) and
$\frac {x_0}{x_1}$
, we get from (7.1) and
![]() $\Delta _2\cong f_2^!{\mathcal O}_{\mathbb {P}^1}$
an
$\Delta _2\cong f_2^!{\mathcal O}_{\mathbb {P}^1}$
an
![]() ${\mathcal O}_{\mathbb {P}^1}$
-valued bilinear form on
${\mathcal O}_{\mathbb {P}^1}$
-valued bilinear form on
![]() $(f_2)_*{\mathcal L}$
. With respect to the above basis of V, it is given by the matrix
$(f_2)_*{\mathcal L}$
. With respect to the above basis of V, it is given by the matrix
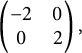 $$ \begin{align*}\begin{pmatrix} -2 &0 \\ 0& 2 \end{pmatrix}, \end{align*} $$
$$ \begin{align*}\begin{pmatrix} -2 &0 \\ 0& 2 \end{pmatrix}, \end{align*} $$
which is not positive semidefinite. Thus, although
![]() $f_1^!{\mathcal O}_{\mathbb {P}^1}\cong f_2^!{\mathcal O}_{\mathbb {P}^1}$
as abstract line bundles, for checking the positivity condition, we need to specify the morphism. Moreover, Proposition 9.2 will show that actually no nonzero symmetric
$f_1^!{\mathcal O}_{\mathbb {P}^1}\cong f_2^!{\mathcal O}_{\mathbb {P}^1}$
as abstract line bundles, for checking the positivity condition, we need to specify the morphism. Moreover, Proposition 9.2 will show that actually no nonzero symmetric
![]() $f_2^!{\mathcal O}_{\mathbb {P}^1}$
-valued bilinear form on
$f_2^!{\mathcal O}_{\mathbb {P}^1}$
-valued bilinear form on
![]() ${\mathcal L}$
will induce a positive semidefinite bilinear form on
${\mathcal L}$
will induce a positive semidefinite bilinear form on
![]() $(f_2)_*{\mathcal L}$
since
$(f_2)_*{\mathcal L}$
since
![]() $f_2$
is not real-fibered.
$f_2$
is not real-fibered.
Since, later on, we will focus on irreducible varieties, we close this section with an example for the reducible case. A systematic study of positive Ulrich sheaves on reducible hypersurfaces would be very interesting with regard to the so-called generalized Lax conjecture (see [Reference VinnikovVin12, Conjecture 3.3]). We think it would be particularly beneficial to understand how the main result of [Reference KummerKum17] fits into our context here.
Example 7.8 Let
![]() $l=x_0-x_1$
and
$l=x_0-x_1$
and
![]() $h=x_0^2-(x_1^2+x_2^2+x_3^2)$
. Let
$h=x_0^2-(x_1^2+x_2^2+x_3^2)$
. Let
![]() $X=X_1\cup X_2$
, where
$X=X_1\cup X_2$
, where
![]() $X_1={\mathcal V}(l)\subset \mathbb {P}^3$
and
$X_1={\mathcal V}(l)\subset \mathbb {P}^3$
and
![]() $X_2={\mathcal V}(h)\subset \mathbb {P}^3$
. The linear projection
$X_2={\mathcal V}(h)\subset \mathbb {P}^3$
. The linear projection
with center
![]() $e=[1\colon 0\colon 0\colon 0]$
is real-fibered, and we want to construct a positive symmetric f-Ulrich sheaf on X. The function field of
$e=[1\colon 0\colon 0\colon 0]$
is real-fibered, and we want to construct a positive symmetric f-Ulrich sheaf on X. The function field of
![]() $\mathbb {P}^2$
is
$\mathbb {P}^2$
is
![]() $K={\mathbb R}(\frac {x_2}{x_1},\frac {x_3}{x_1})$
and the total quotient ring of X is
$K={\mathbb R}(\frac {x_2}{x_1},\frac {x_3}{x_1})$
and the total quotient ring of X is
![]() $L=L_1\times L_2$
, where
$L=L_1\times L_2$
, where
![]() $L_i$
is the function field of
$L_i$
is the function field of
![]() $X_i$
for
$X_i$
for
![]() $i=1,2$
. We note that
$i=1,2$
. We note that
![]() ${\mathcal O}_X$
can be identified with the following subsheaf of
${\mathcal O}_X$
can be identified with the following subsheaf of
![]() ${\mathcal K}_X$
:
${\mathcal K}_X$
:
for
![]() $U\subset X$
. We further define the subsheaf
$U\subset X$
. We further define the subsheaf
![]() ${\mathcal P}$
of
${\mathcal P}$
of
![]() ${\mathcal K}_X$
via
${\mathcal K}_X$
via
for
![]() $U\subset X$
. Note that
$U\subset X$
. Note that
![]() ${\mathcal P}$
is a line bundle on X and
${\mathcal P}$
is a line bundle on X and
![]() ${\mathcal P}\cdot {\mathcal P}={\mathcal O}_X$
. Finally, let
${\mathcal P}\cdot {\mathcal P}={\mathcal O}_X$
. Finally, let
The coherent sheaf
![]() ${\mathcal E}$
is defined in such a way that
${\mathcal E}$
is defined in such a way that
![]() ${\mathcal E}\cdot {\mathcal E}\subset {\mathcal P}$
.
${\mathcal E}\cdot {\mathcal E}\subset {\mathcal P}$
.
Now, let
![]() $V_i\subset \mathbb {P}^2$
be the open affine set, where
$V_i\subset \mathbb {P}^2$
be the open affine set, where
![]() $x_i\neq 0$
and
$x_i\neq 0$
and
![]() $U_i=f^{-1}(V_i)$
for
$U_i=f^{-1}(V_i)$
for
![]() $i=1,2,3$
. By Example 5.3, the codifferent sheaf
$i=1,2,3$
. By Example 5.3, the codifferent sheaf
![]() $\Delta (X/\mathbb {P}^2)$
is the subsheaf of
$\Delta (X/\mathbb {P}^2)$
is the subsheaf of
![]() ${\mathcal K}_X$
generated by
${\mathcal K}_X$
generated by
![]() $\frac {x_i^2}{\textrm {D}_e(l\cdot h)}$
on
$\frac {x_i^2}{\textrm {D}_e(l\cdot h)}$
on
![]() $U_i$
for
$U_i$
for
![]() $i=1,2,3$
. As an element of
$i=1,2,3$
. As an element of
![]() $L_1\times L_2$
, this is
$L_1\times L_2$
, this is
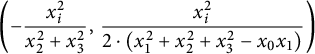 $$ \begin{align*} \left(-\frac{x_i^2}{x_2^2+x_3^2},\, \frac{x_i^2}{2\cdot(x_1^2+x_2^2+x_3^2-x_0x_1)}\right) \end{align*} $$
$$ \begin{align*} \left(-\frac{x_i^2}{x_2^2+x_3^2},\, \frac{x_i^2}{2\cdot(x_1^2+x_2^2+x_3^2-x_0x_1)}\right) \end{align*} $$
on
![]() $U_i$
for
$U_i$
for
![]() $i=1,2,3$
. Let
$i=1,2,3$
. Let
![]() ${\mathcal L}$
be the subsheaf of
${\mathcal L}$
be the subsheaf of
![]() ${\mathcal K}_X$
generated by
${\mathcal K}_X$
generated by
![]() $(\frac {x_i}{x_1},\frac {x_i}{x_1})$
on
$(\frac {x_i}{x_1},\frac {x_i}{x_1})$
on
![]() $U_i$
. Consider
$U_i$
. Consider
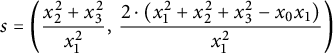 $$ \begin{align*} s=\left(\frac{x_2^2+x_3^2}{x_1^2},\, \frac{2\cdot(x_1^2+x_2^2+x_3^2-x_0x_1)}{x_1^2}\right) \end{align*} $$
$$ \begin{align*} s=\left(\frac{x_2^2+x_3^2}{x_1^2},\, \frac{2\cdot(x_1^2+x_2^2+x_3^2-x_0x_1)}{x_1^2}\right) \end{align*} $$
which is nonnegative on
![]() $X({\mathbb R})$
. We have
$X({\mathbb R})$
. We have
![]() ${\mathcal L}\cdot {\mathcal L}\subset s\cdot {\mathcal P}\cdot \Delta (X/\mathbb {P}^2)$
. Thus, we have
${\mathcal L}\cdot {\mathcal L}\subset s\cdot {\mathcal P}\cdot \Delta (X/\mathbb {P}^2)$
. Thus, we have
![]() ${\mathcal F}\cdot {\mathcal F}\subset s\cdot \Delta (X/\mathbb {P}^2)$
, where
${\mathcal F}\cdot {\mathcal F}\subset s\cdot \Delta (X/\mathbb {P}^2)$
, where
![]() ${\mathcal F}={\mathcal E}\cdot {\mathcal L}$
. This gives us an
${\mathcal F}={\mathcal E}\cdot {\mathcal L}$
. This gives us an
![]() $f^!{\mathcal O}_{\mathbb {P}^2}$
-valued symmetric bilinear form on
$f^!{\mathcal O}_{\mathbb {P}^2}$
-valued symmetric bilinear form on
![]() ${\mathcal L}$
such that the induced
${\mathcal L}$
such that the induced
![]() ${\mathcal O}_{\mathbb {P}^2}$
-valued bilinear form on
${\mathcal O}_{\mathbb {P}^2}$
-valued bilinear form on
![]() $f_*{\mathcal F}$
is positive semidefinite by Theorem 7.5. Here are linearly independent global sections of
$f_*{\mathcal F}$
is positive semidefinite by Theorem 7.5. Here are linearly independent global sections of
![]() ${\mathcal F}$
:
${\mathcal F}$
:
Thus,
![]() ${\mathcal F}$
is a positive symmetric f-Ulrich sheaf.
${\mathcal F}$
is a positive symmetric f-Ulrich sheaf.
8 Ulrich sheaves, determinantal representations, and sums of squares
The main reason why we are interested in Ulrich sheaves is because they correspond to certain determinantal representations. For the applications we consider in this article, we are interested in the following situation. Let
![]() $S={\mathbb R}[y,x_1,\ldots ,x_n]$
be the polynomial ring with the grading determined by letting
$S={\mathbb R}[y,x_1,\ldots ,x_n]$
be the polynomial ring with the grading determined by letting
![]() $\deg (y)=e$
and
$\deg (y)=e$
and
![]() $\deg (x_i)=1$
for
$\deg (x_i)=1$
for
![]() $i=1,\ldots ,n$
, let
$i=1,\ldots ,n$
, let
![]() $h\in S_{de}$
be an irreducible homogeneous element of degree
$h\in S_{de}$
be an irreducible homogeneous element of degree
![]() $d\cdot e$
, and let
$d\cdot e$
, and let
![]() $X={\mathcal V}(h)\subset \mathbb {P}(e,1,\ldots ,1)$
be the hypersurface in the weighted projective space corresponding to S. Assume
$X={\mathcal V}(h)\subset \mathbb {P}(e,1,\ldots ,1)$
be the hypersurface in the weighted projective space corresponding to S. Assume
![]() $h(1,0,\ldots ,0)=1$
. The following proposition and the subsequent remark are well known among experts. But since we are not aware of a reference for the precise statement that we need, we include a proof for the sake of completeness. The case
$h(1,0,\ldots ,0)=1$
. The following proposition and the subsequent remark are well known among experts. But since we are not aware of a reference for the precise statement that we need, we include a proof for the sake of completeness. The case
![]() $e=1$
is treated, for example, in [Reference BeauvilleBea00, Theorem A] and the proof for the general case works essentially in the same way.
$e=1$
is treated, for example, in [Reference BeauvilleBea00, Theorem A] and the proof for the general case works essentially in the same way.
Proposition 8.1 Let
![]() $f\colon X\to \mathbb {P}^{n-1}$
be the projection on the last coordinates, and let
$f\colon X\to \mathbb {P}^{n-1}$
be the projection on the last coordinates, and let
![]() ${\mathcal F}$
be an f-Ulrich sheaf on X with
${\mathcal F}$
be an f-Ulrich sheaf on X with
![]() $\operatorname {rank}({\mathcal F})=r$
. Then there is a square matrix A of size
$\operatorname {rank}({\mathcal F})=r$
. Then there is a square matrix A of size
![]() $d\cdot r$
whose entries are homogeneous polynomials in the
$d\cdot r$
whose entries are homogeneous polynomials in the
![]() $x_i$
of degree e such that
$x_i$
of degree e such that
![]() $h^r=\det (y\cdot I-A)$
. If
$h^r=\det (y\cdot I-A)$
. If
![]() ${\mathcal F}$
is a positive symmetric (resp. Hermitian) f-Ulrich sheaf, then A can be chosen to be symmetric (resp. Hermitian).
${\mathcal F}$
is a positive symmetric (resp. Hermitian) f-Ulrich sheaf, then A can be chosen to be symmetric (resp. Hermitian).
Proof Let
![]() ${\mathcal O}_X(1)$
be the pullback of
${\mathcal O}_X(1)$
be the pullback of
![]() ${\mathcal O}_{\mathbb {P}^{n-1}}(1)$
via f, and let
${\mathcal O}_{\mathbb {P}^{n-1}}(1)$
via f, and let
![]() $M=\oplus _{i\in {\mathbb Z}}H^0(X,{\mathcal F}(i))$
be the module of twisted global sections. Since
$M=\oplus _{i\in {\mathbb Z}}H^0(X,{\mathcal F}(i))$
be the module of twisted global sections. Since
![]() ${\mathcal F}$
is an f-Ulrich sheaf, we have that M considered as a module over
${\mathcal F}$
is an f-Ulrich sheaf, we have that M considered as a module over
![]() $R={\mathbb R}[x_1,\ldots ,x_n]\subset S$
is isomorphic to
$R={\mathbb R}[x_1,\ldots ,x_n]\subset S$
is isomorphic to
![]() $R^{d\cdot r}$
. Multiplication with y is an R-linear map, homogeneous of degree e, that can thus be represented by a square matrix A of size
$R^{d\cdot r}$
. Multiplication with y is an R-linear map, homogeneous of degree e, that can thus be represented by a square matrix A of size
![]() $d\cdot r$
whose entries are real homogeneous polynomials in the
$d\cdot r$
whose entries are real homogeneous polynomials in the
![]() $x_i$
of degree e and whose minimal polynomial is h. Thus,
$x_i$
of degree e and whose minimal polynomial is h. Thus,
![]() ${h^r=\det (y\cdot I-A)}$
. Further, a symmetric positive semidefinite bilinear form as in Theorem 7.2 yields a homomorphism of graded S-modules (of degree zero)
${h^r=\det (y\cdot I-A)}$
. Further, a symmetric positive semidefinite bilinear form as in Theorem 7.2 yields a homomorphism of graded S-modules (of degree zero)
which has the property that the induced R-bilinear form
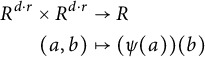 $$ \begin{align*} R^{d\cdot r}\times R^{d\cdot r}&\to R\\ (a,b)&\mapsto (\psi(a))(b) \end{align*} $$
$$ \begin{align*} R^{d\cdot r}\times R^{d\cdot r}&\to R\\ (a,b)&\mapsto (\psi(a))(b) \end{align*} $$
is symmetric, i.e.,
![]() $(\psi (a))(b)=(\psi (b))(a)$
. The degree zero part V of
$(\psi (a))(b)=(\psi (b))(a)$
. The degree zero part V of
![]() $M\cong _R R^{d\cdot r}$
is the space of global sections of
$M\cong _R R^{d\cdot r}$
is the space of global sections of
![]() ${\mathcal F}$
and the restriction of this symmetric bilinear form to V is thus positive definite by Lemma 7.1. We can therefore choose an orthonormal basis of V with respect to this bilinear form. Note that this will also be a basis of the R-module
${\mathcal F}$
and the restriction of this symmetric bilinear form to V is thus positive definite by Lemma 7.1. We can therefore choose an orthonormal basis of V with respect to this bilinear form. Note that this will also be a basis of the R-module
![]() $R^{d\cdot r}$
that is orthonormal with respect to
$R^{d\cdot r}$
that is orthonormal with respect to
![]() $\psi $
. Since
$\psi $
. Since
![]() $\psi $
is a homomorphism of S-modules, we have
$\psi $
is a homomorphism of S-modules, we have
![]() $(\psi (a))(y\cdot b)=(\psi (y\cdot a))(b)$
, so multiplication with y is self-adjoint with respect to our above defined symmetric bilinear form. Thus, we can choose the representing matrix A of the R-linear map given by multiplication with y to be symmetric. The Hermitian case follows analogously.
$(\psi (a))(y\cdot b)=(\psi (y\cdot a))(b)$
, so multiplication with y is self-adjoint with respect to our above defined symmetric bilinear form. Thus, we can choose the representing matrix A of the R-linear map given by multiplication with y to be symmetric. The Hermitian case follows analogously.
Remark 8.2 The converse of Proposition 8.1 is also true: if
![]() $h^r=\det (y\cdot I-A)$
, then the cokernel M of the map
$h^r=\det (y\cdot I-A)$
, then the cokernel M of the map
![]() $S^{d\cdot r}\to S^{d\cdot r}$
given by
$S^{d\cdot r}\to S^{d\cdot r}$
given by
![]() $y\cdot I-A$
is supported on X and M considered as R-module is just
$y\cdot I-A$
is supported on X and M considered as R-module is just
![]() $R^{d\cdot r}$
. If A is symmetric, then an isomorphism of M with
$R^{d\cdot r}$
. If A is symmetric, then an isomorphism of M with
![]() $\operatorname {Hom}_R(M,R)$
as S-modules is given by sending the standard basis of
$\operatorname {Hom}_R(M,R)$
as S-modules is given by sending the standard basis of
![]() $R^{d\cdot r}$
to its dual basis. We argue analogously in the Hermitian case.
$R^{d\cdot r}$
to its dual basis. We argue analogously in the Hermitian case.
A refined statement is true for possibly reducible subvarieties
![]() $X\subset \mathbb {P}^n$
that are not necessarily hypersurfaces (see [Reference Kummer and ShamovichKS20, Theorem 5.7]). These correspond to so-called determinantal representations of Livšic-type introduced in [Reference Shamovich and VinnikovSV18] which are closely related to determinantal representations of the Chow form of X (see also [Reference Eisenbud, Schreyer and WeymanESW03]. The main applications of this article, however, concern irreducible varieties only.
$X\subset \mathbb {P}^n$
that are not necessarily hypersurfaces (see [Reference Kummer and ShamovichKS20, Theorem 5.7]). These correspond to so-called determinantal representations of Livšic-type introduced in [Reference Shamovich and VinnikovSV18] which are closely related to determinantal representations of the Chow form of X (see also [Reference Eisenbud, Schreyer and WeymanESW03]. The main applications of this article, however, concern irreducible varieties only.
Example 8.3 The positive symmetric f-Ulrich sheaf on the reducible cubic hypersurface
![]() $X={\mathcal V}((x_0-x_1)\cdot (x_0^2-(x_1^2+x_2^2+x_3^2))\subset \mathbb {P}^3$
from Example 7.8 gives the following symmetric definite determinantal representation:
$X={\mathcal V}((x_0-x_1)\cdot (x_0^2-(x_1^2+x_2^2+x_3^2))\subset \mathbb {P}^3$
from Example 7.8 gives the following symmetric definite determinantal representation:
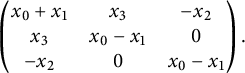 $$ \begin{align*} \begin{pmatrix} x_0+x_1& x_3 & -x_2\\ x_3& x_0-x_1 & 0\\ -x_2& 0& x_0-x_1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} x_0+x_1& x_3 & -x_2\\ x_3& x_0-x_1 & 0\\ -x_2& 0& x_0-x_1 \end{pmatrix}. \end{align*} $$
Now we consider again the situation of Example 6.1, when h is of the form
![]() ${y^2-p(x)}$
, where
${y^2-p(x)}$
, where
![]() $p\in {\mathbb R}[x_1,\ldots ,x_n]_{2e}$
is a globally nonnegative polynomial.
$p\in {\mathbb R}[x_1,\ldots ,x_n]_{2e}$
is a globally nonnegative polynomial.
Lemma 8.4 Let
![]() $p\in {\mathbb R}[x_1,\ldots ,x_n]_{2e}$
be a globally nonnegative polynomial which is not a square. Let
$p\in {\mathbb R}[x_1,\ldots ,x_n]_{2e}$
be a globally nonnegative polynomial which is not a square. Let
![]() $h=y^2-p(x)$
, where y has degree e. If
$h=y^2-p(x)$
, where y has degree e. If
![]() $h^r=\det (y\cdot I-A)$
for some
$h^r=\det (y\cdot I-A)$
for some
![]() $r\geq 1$
and a symmetric or Hermitian matrix A of size
$r\geq 1$
and a symmetric or Hermitian matrix A of size
![]() $2r$
whose entries are homogeneous of degree e, then p is a sum of
$2r$
whose entries are homogeneous of degree e, then p is a sum of
![]() $2r$
squares in the symmetric case and a sum of
$2r$
squares in the symmetric case and a sum of
![]() $4r-1$
squares in the Hermitian case.
$4r-1$
squares in the Hermitian case.
Proof Since p is not a square, we find that h is irreducible. Thus,
![]() ${h^r=\det (y\cdot I-A)}$
implies that h is the minimal polynomial of A, i.e.,
${h^r=\det (y\cdot I-A)}$
implies that h is the minimal polynomial of A, i.e.,
![]() $A^2=p\cdot I$
. Letting
$A^2=p\cdot I$
. Letting
![]() $a_i$
be the ith column of A, we then have
$a_i$
be the ith column of A, we then have
![]() $p=a_i^ta_i$
in the symmetric case and
$p=a_i^ta_i$
in the symmetric case and
![]() $p=a_i^t\overline {a_i}$
in the Hermitian case. Thus, p is a sum of
$p=a_i^t\overline {a_i}$
in the Hermitian case. Thus, p is a sum of
![]() $2r$
squares in the symmetric case and a sum of
$2r$
squares in the symmetric case and a sum of
![]() $4r-1$
squares in the Hermitian case.
$4r-1$
squares in the Hermitian case.
A converse of this last conclusion is given by the following lemma.
Lemma 8.5 Let
![]() $P=G_1^2+\cdots +G_n^2$
, where the
$P=G_1^2+\cdots +G_n^2$
, where the
![]() $G_i\in A$
are elements of some commutative ring A. There is a symmetric square matrix Q of some size
$G_i\in A$
are elements of some commutative ring A. There is a symmetric square matrix Q of some size
![]() $m\in {\mathbb N}$
whose entries are
$m\in {\mathbb N}$
whose entries are
![]() ${\mathbb Z}$
-linear combinations of the
${\mathbb Z}$
-linear combinations of the
![]() $G_i$
such that
$G_i$
such that
![]() $P\cdot I_m=Q^2$
.
$P\cdot I_m=Q^2$
.
Proof This follows from the basic properties of Clifford algebras. Recall that the Clifford algebra
![]() $Cl_{0,n}({\mathbb R})$
is generated by
$Cl_{0,n}({\mathbb R})$
is generated by
![]() $e_1,\ldots ,e_n$
satisfying
$e_1,\ldots ,e_n$
satisfying
![]() $e_i\cdot e_j=-e_j\cdot e_i$
if
$e_i\cdot e_j=-e_j\cdot e_i$
if
![]() $i\neq j$
and
$i\neq j$
and
![]() $e_i^2=-1$
. In particular, we have
$e_i^2=-1$
. In particular, we have
for all
![]() $x_k\in {\mathbb R}$
. For
$x_k\in {\mathbb R}$
. For
![]() $1\leq i\leq n$
, let
$1\leq i\leq n$
, let
![]() $A_i$
be the representing matrix of the map
$A_i$
be the representing matrix of the map
with respect to the basis
![]() $e_{i_1}\ldots e_{i_r}$
of
$e_{i_1}\ldots e_{i_r}$
of
![]() $Cl_{0,n}({\mathbb R})$
with
$Cl_{0,n}({\mathbb R})$
with
![]() $1\leq i_1<\cdots <i_r\leq n$
and
$1\leq i_1<\cdots <i_r\leq n$
and
![]() $r\geq 0$
. Then one immediately verifies that
$r\geq 0$
. Then one immediately verifies that
![]() $A_i$
is a matrix having only entries in
$A_i$
is a matrix having only entries in
![]() $\{0,\pm 1\}$
satisfying
$\{0,\pm 1\}$
satisfying
![]() $A_i^T=-A_i$
. It follows that
$A_i^T=-A_i$
. It follows that
for all
![]() $x_k\in {\mathbb R}$
, where
$x_k\in {\mathbb R}$
, where
![]() $S=x_1 A_1+\cdots +x_n A_n$
and N is the dimension of
$S=x_1 A_1+\cdots +x_n A_n$
and N is the dimension of
![]() $Cl_{0,n}({\mathbb R})$
. Now we can choose
$Cl_{0,n}({\mathbb R})$
. Now we can choose
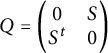 $$ \begin{align*} Q=\begin{pmatrix}0&S\\S^t&0 \end{pmatrix} \end{align*} $$
$$ \begin{align*} Q=\begin{pmatrix}0&S\\S^t&0 \end{pmatrix} \end{align*} $$
and we get
![]() $(x_1^2+\cdots +x_n^2)\cdot I_N=Q^2$
for all
$(x_1^2+\cdots +x_n^2)\cdot I_N=Q^2$
for all
![]() $x_k\in {\mathbb R}$
. Since the entries of the
$x_k\in {\mathbb R}$
. Since the entries of the
![]() $A_i$
are integers, the identity holds over every commutative ring.
$A_i$
are integers, the identity holds over every commutative ring.
Putting all this together, we get the following connection of sums of squares to Ulrich sheaves.
Theorem 8.6 Let
![]() $p\in {\mathbb R}[x_1,\ldots ,x_n]_{2e}$
be a homogeneous polynomial of degree
$p\in {\mathbb R}[x_1,\ldots ,x_n]_{2e}$
be a homogeneous polynomial of degree
![]() $2e$
which is not a square. Inside the weighted projective space
$2e$
which is not a square. Inside the weighted projective space
![]() $\mathbb {P}(e,1,\ldots ,1)$
, we consider the hypersurface X defined by
$\mathbb {P}(e,1,\ldots ,1)$
, we consider the hypersurface X defined by
![]() $y^2=p(x_0,\ldots ,x_n)$
and the natural projection
$y^2=p(x_0,\ldots ,x_n)$
and the natural projection
![]() $\pi \colon X\to \mathbb {P}^n$
onto the x-coordinates. Then p is a sum of squares of polynomials if and only if there is a positive symmetric (or Hermitian)
$\pi \colon X\to \mathbb {P}^n$
onto the x-coordinates. Then p is a sum of squares of polynomials if and only if there is a positive symmetric (or Hermitian)
![]() $\pi $
-Ulrich sheaf
$\pi $
-Ulrich sheaf
![]() ${\mathcal F}$
on X. In that case, if
${\mathcal F}$
on X. In that case, if
![]() $\operatorname {rank}({\mathcal F})=r$
then p is a sum of
$\operatorname {rank}({\mathcal F})=r$
then p is a sum of
![]() $2r$
squares in the symmetric case and a sum of
$2r$
squares in the symmetric case and a sum of
![]() $4r-1$
squares in the Hermitian case.
$4r-1$
squares in the Hermitian case.
Proof First assume that p is a sum of squares. By Lemma 8.5, there is a symmetric square matrix A of some size
![]() $m\in {\mathbb N}$
whose entries are homogeneous of degree e in the variables
$m\in {\mathbb N}$
whose entries are homogeneous of degree e in the variables
![]() $x_1,\ldots ,x_n$
such that
$x_1,\ldots ,x_n$
such that
![]() $p\cdot I_m=A^2$
. Because p is not a square, the polynomial
$p\cdot I_m=A^2$
. Because p is not a square, the polynomial
![]() $h=y^2-p$
is irreducible. Thus,
$h=y^2-p$
is irreducible. Thus,
![]() $A^2-p\cdot I_m=0$
shows that h is the minimal polynomial of A. This implies that
$A^2-p\cdot I_m=0$
shows that h is the minimal polynomial of A. This implies that
![]() $h^r=\det (y\cdot I-A)$
for some
$h^r=\det (y\cdot I-A)$
for some
![]() $r>0$
. Thus, there is a positive symmetric
$r>0$
. Thus, there is a positive symmetric
![]() $\pi $
-Ulrich sheaf on X by Remark 8.2.
$\pi $
-Ulrich sheaf on X by Remark 8.2.
Now assume that there is a positive symmetric (or Hermitian)
![]() $\pi $
-Ulrich sheaf
$\pi $
-Ulrich sheaf
![]() ${\mathcal F}$
on X. Then, by Proposition 8.1, there is a symmetric (resp. Hermitian) matrix A of size
${\mathcal F}$
on X. Then, by Proposition 8.1, there is a symmetric (resp. Hermitian) matrix A of size
![]() $2\cdot r$
whose entries are homogeneous polynomials in the
$2\cdot r$
whose entries are homogeneous polynomials in the
![]() $x_i$
of degree e such that
$x_i$
of degree e such that
![]() $h^r=\det (y\cdot I-A)$
. Now the claim follows from Lemma 8.4.
$h^r=\det (y\cdot I-A)$
. Now the claim follows from Lemma 8.4.
As a special case, we get the following result by Netzer and Thom [Reference Netzer and ThomNT12].
Corollary 8.7 Let
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_2$
be a quadratic hyperbolic polynomial. Then
$h\in {\mathbb R}[x_0,\ldots ,x_n]_2$
be a quadratic hyperbolic polynomial. Then
![]() $h^r$
has a definite symmetric determinantal representation for some
$h^r$
has a definite symmetric determinantal representation for some
![]() $r>0$
.
$r>0$
.
Proof If
![]() $X={\mathcal V}(h)$
is hyperbolic with respect to
$X={\mathcal V}(h)$
is hyperbolic with respect to
![]() $e\in \mathbb {P}^n$
, then the linear projection
$e\in \mathbb {P}^n$
, then the linear projection
![]() $\pi _e\colon X\to \mathbb {P}^{n-1}$
is a real-fibered double cover ramified along the zero set of a nonnegative quadratic polynomial p. Since p is a sum of squares, there is a positive symmetric
$\pi _e\colon X\to \mathbb {P}^{n-1}$
is a real-fibered double cover ramified along the zero set of a nonnegative quadratic polynomial p. Since p is a sum of squares, there is a positive symmetric
![]() $\pi _e$
-Ulrich sheaf on X by Theorem 8.6. Proposition 8.1 implies the claim.
$\pi _e$
-Ulrich sheaf on X by Theorem 8.6. Proposition 8.1 implies the claim.
Remark 8.8 Positive Ulrich sheaves on reciprocal linear spaces, i.e., the closure of the image of a linear space under coordinatewise inversion, were used in [Reference Kummer and VinzantKV19] to prove that a certain polynomial associated with a hyperplane arrangement, called the entropic discriminant, is a sum of squares. The relation of Ulrich sheaves and sums of squares used in [Reference Kummer and VinzantKV19] is a generalization of one direction of Theorem 8.6. Namely, let
![]() $f\colon X\to \mathbb {P}^n$
be a finite surjective real-fibered morphism such that
$f\colon X\to \mathbb {P}^n$
be a finite surjective real-fibered morphism such that
![]() $f_*{\mathcal O}_X$
is a sum of line bundles. Then, if there is a positive f-Ulrich sheaf, then the polynomial defining the branch locus of f is a sum of squares [Reference Kummer and VinzantKV19, Theorem 6.1].
$f_*{\mathcal O}_X$
is a sum of line bundles. Then, if there is a positive f-Ulrich sheaf, then the polynomial defining the branch locus of f is a sum of squares [Reference Kummer and VinzantKV19, Theorem 6.1].
9 Positive Ulrich sheaves of rank one on irreducible varieties
In this section, let
![]() $f\colon X\to Y$
always denote a finite surjective morphism of geometrically irreducible varieties which are proper over
$f\colon X\to Y$
always denote a finite surjective morphism of geometrically irreducible varieties which are proper over
![]() ${\mathbb R}$
. We assume that Y is smooth and has a real point. We further assume that the singular locus of X has codimension at least two. This allows us to speak about Weil divisors on X. For a given Weil divisor D on X, we denote by
${\mathbb R}$
. We assume that Y is smooth and has a real point. We further assume that the singular locus of X has codimension at least two. This allows us to speak about Weil divisors on X. For a given Weil divisor D on X, we denote by
![]() ${\mathcal L}(D)$
the subsheaf of
${\mathcal L}(D)$
the subsheaf of
![]() ${\mathcal K}_X$
consisting of all rational functions with pole and zero orders prescribed by D. We further denote
${\mathcal K}_X$
consisting of all rational functions with pole and zero orders prescribed by D. We further denote
![]() ${\ell (D)=\dim (\Gamma (X,{\mathcal L}(D)))}$
. Let
${\ell (D)=\dim (\Gamma (X,{\mathcal L}(D)))}$
. Let
![]() $Z\subset Y$
be a closed subset of codimension at least two such that
$Z\subset Y$
be a closed subset of codimension at least two such that
![]() $f^{-1}(Z)$
contains
$f^{-1}(Z)$
contains
![]() $X_{\mathrm {sing}}$
. Letting
$X_{\mathrm {sing}}$
. Letting
![]() $V=Y\setminus Z$
and
$V=Y\setminus Z$
and
![]() $U=f^{-1}(V)$
, the restriction
$U=f^{-1}(V)$
, the restriction
![]() $f|_U\colon U\to V$
is a finite surjective morphism of smooth irreducible varieties. Thus,
$f|_U\colon U\to V$
is a finite surjective morphism of smooth irreducible varieties. Thus,
![]() $\Delta (U/V)$
is invertible by Proposition 5.7 and thus corresponds to a Weil divisor R on U. Since
$\Delta (U/V)$
is invertible by Proposition 5.7 and thus corresponds to a Weil divisor R on U. Since
![]() $X\setminus U$
has codimension at least two, we can also consider R as a Weil divisor on X which we call the ramification divisor of f. Lemma 5.8 shows that the associated subsheaf
$X\setminus U$
has codimension at least two, we can also consider R as a Weil divisor on X which we call the ramification divisor of f. Lemma 5.8 shows that the associated subsheaf
![]() ${\mathcal L}(R)$
of
${\mathcal L}(R)$
of
![]() ${\mathcal K}_X$
is exactly
${\mathcal K}_X$
is exactly
![]() $\Delta (X/Y)$
. All this holds true for the complexification
$\Delta (X/Y)$
. All this holds true for the complexification
![]() $X_{\mathbb C}$
as well. Complex conjugation gives an involution
$X_{\mathbb C}$
as well. Complex conjugation gives an involution
![]() $\sigma \colon X_{\mathbb C}\to X_{\mathbb C}$
and for a Weil divisor D on
$\sigma \colon X_{\mathbb C}\to X_{\mathbb C}$
and for a Weil divisor D on
![]() $X_{\mathbb C}$
we denote
$X_{\mathbb C}$
we denote
![]() $\sigma (D)$
by
$\sigma (D)$
by
![]() $\overline {D}$
. We have
$\overline {D}$
. We have
![]() ${\mathcal L}(\overline {D})=\overline {{\mathcal L}(D)}$
as subsheaves of
${\mathcal L}(\overline {D})=\overline {{\mathcal L}(D)}$
as subsheaves of
![]() ${\mathcal K}_{X_{\mathbb C}}$
.
${\mathcal K}_{X_{\mathbb C}}$
.
Remark 9.1 If
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are Weil divisors on X, then we have
$D_2$
are Weil divisors on X, then we have
considered as subsheaves of
![]() ${\mathcal K}_X$
. But since
${\mathcal K}_X$
. But since
![]() ${\mathcal L}(D_i)$
is not necessarily an invertible sheaf, we do not have equality in general.
${\mathcal L}(D_i)$
is not necessarily an invertible sheaf, we do not have equality in general.
The relative notion of positive semidefiniteness introduced in Section 7 relates to the notion of being real fibered in the following way.
Proposition 9.2 [Reference Kummer and ShamovichKS20, Theorem 5.11]
The following are equivalent:
-
(i) There is a coherent sheaf
 ${\mathcal F}$
on X with
${\mathcal F}$
on X with
 $\operatorname {Supp}({\mathcal F})=X$
and a symmetric nonzero
$\operatorname {Supp}({\mathcal F})=X$
and a symmetric nonzero
 $f^!{\mathcal O}_Y$
-valued bilinear form on
$f^!{\mathcal O}_Y$
-valued bilinear form on
 ${\mathcal F}$
such that the induced bilinear form on
${\mathcal F}$
such that the induced bilinear form on
 $f_*{\mathcal F}$
is positive semidefinite.
$f_*{\mathcal F}$
is positive semidefinite. -
(ii) f is real fibered, i.e.,
 $f^{-1}(Y({\mathbb R}))=X({\mathbb R})$
.
$f^{-1}(Y({\mathbb R}))=X({\mathbb R})$
.
In this situation, we get the following convenient criterion for a Weil divisor to give rise to a positive Ulrich sheaf.
Theorem 9.3 Let
![]() $f\colon X\to Y$
be a real-fibered finite surjective morphism of geometrically irreducible varieties which are proper over
$f\colon X\to Y$
be a real-fibered finite surjective morphism of geometrically irreducible varieties which are proper over
![]() ${\mathbb R}$
. Let Y be smooth and have a real point. Further, let the singular locus of X have codimension at least two. Let R be the ramification divisor of f, and let s be a rational function on X which is nonnegative on
${\mathbb R}$
. Let Y be smooth and have a real point. Further, let the singular locus of X have codimension at least two. Let R be the ramification divisor of f, and let s be a rational function on X which is nonnegative on
![]() $X({\mathbb R})$
.
$X({\mathbb R})$
.
-
(1) If D is a Weil divisor on X such that
 $2D+(s)=R$
and
$2D+(s)=R$
and
 $\ell (D)\geq \deg (f)$
, then the sheaf
$\ell (D)\geq \deg (f)$
, then the sheaf
 ${\mathcal L}(D)$
on X is a positive symmetric f-Ulrich sheaf.
${\mathcal L}(D)$
on X is a positive symmetric f-Ulrich sheaf. -
(2) If D is a Weil divisor on
 $X_{\mathbb C}$
that satisfies
$X_{\mathbb C}$
that satisfies
 $D+\overline {D}+(s)=R$
and
$D+\overline {D}+(s)=R$
and
 $\ell (D)\geq \deg (f)$
, then the sheaf
$\ell (D)\geq \deg (f)$
, then the sheaf
 ${\mathcal L}(D)$
on
${\mathcal L}(D)$
on
 $X_{\mathbb C}$
is a positive Hermitian f-Ulrich sheaf.
$X_{\mathbb C}$
is a positive Hermitian f-Ulrich sheaf.
Proof Let
![]() ${\mathcal L}={\mathcal L}(D)$
be the subsheaf of
${\mathcal L}={\mathcal L}(D)$
be the subsheaf of
![]() ${\mathcal K}_X$
corresponding to D. By assumption, we can define the symmetric (resp. Hermitian)
${\mathcal K}_X$
corresponding to D. By assumption, we can define the symmetric (resp. Hermitian)
![]() $\Delta (X/Y)$
-valued bilinear form on
$\Delta (X/Y)$
-valued bilinear form on
![]() ${\mathcal L}$
that maps a pair of sections
${\mathcal L}$
that maps a pair of sections
![]() $(g,h)$
to the product
$(g,h)$
to the product
![]() $s\cdot g\cdot h$
. This is clearly nondegenerate at the generic point of X and it is positive semidefinite by Proposition 6.4. Then the claim follows from Theorems 7.2 and 7.4, respectively.
$s\cdot g\cdot h$
. This is clearly nondegenerate at the generic point of X and it is positive semidefinite by Proposition 6.4. Then the claim follows from Theorems 7.2 and 7.4, respectively.
Remark 9.4 Let D be a Weil divisor on X or
![]() $X_{\mathbb C}$
such that
$X_{\mathbb C}$
such that
![]() $2D$
or
$2D$
or
![]() $D+\overline {D}$
, respectively, is linearly equivalent to R, i.e., they differ only by a principal divisor
$D+\overline {D}$
, respectively, is linearly equivalent to R, i.e., they differ only by a principal divisor
![]() $(g)$
. The signs that g takes on real points of X (up to global scaling) do only depend on the divisor class of D. Indeed, if
$(g)$
. The signs that g takes on real points of X (up to global scaling) do only depend on the divisor class of D. Indeed, if
![]() $D'=D+(f)$
for some rational function f, then
$D'=D+(f)$
for some rational function f, then
![]() $2D'$
resp.
$2D'$
resp.
![]() $D'+\overline {D'}$
differs from R by
$D'+\overline {D'}$
differs from R by
![]() $g\cdot f^2$
or
$g\cdot f^2$
or
![]() $g\cdot f\overline {f}$
, respectively.
$g\cdot f\overline {f}$
, respectively.
Example 9.5 Let
![]() $L\subset \mathbb {P}^n$
be a linear subspace of dimension
$L\subset \mathbb {P}^n$
be a linear subspace of dimension
![]() $d<n$
that is not contained in any coordinate hyperplane. We denote by
$d<n$
that is not contained in any coordinate hyperplane. We denote by
![]() $L^{-1}$
its reciprocal, i.e., the (Zariski closure of the) image of L under the rational map
$L^{-1}$
its reciprocal, i.e., the (Zariski closure of the) image of L under the rational map
![]() $\mathbb {P}^n\dashrightarrow \mathbb {P}^n$
defined by coordinatewise inversion. It was shown by Varchenko [Reference VarchenkoVar95] that
$\mathbb {P}^n\dashrightarrow \mathbb {P}^n$
defined by coordinatewise inversion. It was shown by Varchenko [Reference VarchenkoVar95] that
![]() $L^{-1}$
is hyperbolic with respect to the orthogonal complement
$L^{-1}$
is hyperbolic with respect to the orthogonal complement
![]() $L^\perp $
of L. Further, it was shown in [Reference Kummer and VinzantKV19] that there is a symmetric positive f-Ulrich sheaf of rank one on
$L^\perp $
of L. Further, it was shown in [Reference Kummer and VinzantKV19] that there is a symmetric positive f-Ulrich sheaf of rank one on
![]() $L^{-1}$
, where
$L^{-1}$
, where
![]() $f\colon X\to \mathbb {P}^d$
is the linear projection from
$f\colon X\to \mathbb {P}^d$
is the linear projection from
![]() $L^\perp $
. We want to outline how this also follows from Theorem 9.3, at least for generic L. To this end, let L be the row span of a matrix
$L^\perp $
. We want to outline how this also follows from Theorem 9.3, at least for generic L. To this end, let L be the row span of a matrix
![]() $A=(a_{ij})$
of size
$A=(a_{ij})$
of size
![]() $(d+1)\times (n+1)$
and assume that every maximal minor of A is nonzero. Letting
$(d+1)\times (n+1)$
and assume that every maximal minor of A is nonzero. Letting
![]() $l_j=\sum _{i=1}^{d+1}a_{ij}x_i$
, for
$l_j=\sum _{i=1}^{d+1}a_{ij}x_i$
, for
![]() $j=1,\ldots ,n+1$
, we can describe
$j=1,\ldots ,n+1$
, we can describe
![]() $L^{-1}$
as the image of the rational map
$L^{-1}$
as the image of the rational map
Note that
![]() $\psi $
is defined in all points where at most one of the
$\psi $
is defined in all points where at most one of the
![]() $l_j$
vanishes. It follows from the proof of [Reference Sanyal, Sturmfels and VinzantSSV13, Corollary 5] and [Reference Sanyal, Sturmfels and VinzantSSV13, Remark 31] that the ramification divisor R of f on
$l_j$
vanishes. It follows from the proof of [Reference Sanyal, Sturmfels and VinzantSSV13, Corollary 5] and [Reference Sanyal, Sturmfels and VinzantSSV13, Remark 31] that the ramification divisor R of f on
![]() $L^{-1}$
is the proper transform under
$L^{-1}$
is the proper transform under
![]() $\psi $
of the zero set
$\psi $
of the zero set
![]() $Z\subset \mathbb {P}^d$
of
$Z\subset \mathbb {P}^d$
of
where the sum is taken over all
![]() $I\subset \{1,\ldots ,n+1\}$
of size
$I\subset \{1,\ldots ,n+1\}$
of size
![]() $n-d$
and
$n-d$
and
![]() $A_I$
denotes the submatrix of A obtained from erasing all columns indexed by I. Let
$A_I$
denotes the submatrix of A obtained from erasing all columns indexed by I. Let
![]() $H\subset \mathbb {P}^d$
be a generic hyperplane defined by a linear form G, and let D be the divisor on
$H\subset \mathbb {P}^d$
be a generic hyperplane defined by a linear form G, and let D be the divisor on
![]() $L^{-1}$
defined as the proper transform of H under
$L^{-1}$
defined as the proper transform of H under
![]() $\psi $
. On
$\psi $
. On
![]() $\mathbb {P}^d$
, we have
$\mathbb {P}^d$
, we have
![]() $2(n-d)H = Z + \left (\frac {P}{G^{2(n-d)}}\right )$
and our genericity assumption on A implies that P does not vanish entirely on any of the
$2(n-d)H = Z + \left (\frac {P}{G^{2(n-d)}}\right )$
and our genericity assumption on A implies that P does not vanish entirely on any of the
![]() ${\mathcal V}(l_i,l_j)\subset \mathbb {P}^d$
which comprise the locus where
${\mathcal V}(l_i,l_j)\subset \mathbb {P}^d$
which comprise the locus where
![]() $\psi $
is not regular. Therefore, we have
$\psi $
is not regular. Therefore, we have
![]() $2(n-d)D=R+\left (\frac {P}{G^{2(n-d)}}\right )$
as divisors on
$2(n-d)D=R+\left (\frac {P}{G^{2(n-d)}}\right )$
as divisors on
![]() $L^{-1}$
. Clearly, the rational function
$L^{-1}$
. Clearly, the rational function
![]() $\frac {P}{G^{2(n-d)}}$
is nonnegative and
$\frac {P}{G^{2(n-d)}}$
is nonnegative and
![]() $\ell ((n-d)\cdot D)$
equals
$\ell ((n-d)\cdot D)$
equals
![]() $\binom {n}{d}$
, the number of monomials of degree
$\binom {n}{d}$
, the number of monomials of degree
![]() $n-d$
in
$n-d$
in
![]() $d+1$
variables. Since this is also the degree of
$d+1$
variables. Since this is also the degree of
![]() $L^{-1}$
[Reference Proudfoot and SpeyerPS06], Theorem 9.3(1) implies that
$L^{-1}$
[Reference Proudfoot and SpeyerPS06], Theorem 9.3(1) implies that
![]() ${\mathcal L}((n-d)\cdot D)$
is a positive symmetric f-Ulrich sheaf on
${\mathcal L}((n-d)\cdot D)$
is a positive symmetric f-Ulrich sheaf on
![]() $L^{-1}$
.
$L^{-1}$
.
The previous example leads to the following question. Let
![]() $X\subset \mathbb {P}^n$
be an irreducible variety not contained in any coordinate hyperplane which is hyperbolic with respect to every linear subspace of codimension
$X\subset \mathbb {P}^n$
be an irreducible variety not contained in any coordinate hyperplane which is hyperbolic with respect to every linear subspace of codimension
![]() $\dim (X)+1$
all of whose Plücker coordinates are positive. Then the image
$\dim (X)+1$
all of whose Plücker coordinates are positive. Then the image
![]() $X^{-1}$
of X under coordinatewise inversion is hyperbolic with respect to all these subspaces as well [Reference Kummer and VinzantKV19, Proposition 1.4].
$X^{-1}$
of X under coordinatewise inversion is hyperbolic with respect to all these subspaces as well [Reference Kummer and VinzantKV19, Proposition 1.4].
Problem 9.6 Given a symmetric positive Ulrich bundle on a variety
![]() $X\subset \mathbb {P}^n$
as above. Does there exist one on
$X\subset \mathbb {P}^n$
as above. Does there exist one on
![]() $X^{-1}$
of the same rank as well?
$X^{-1}$
of the same rank as well?
Remark 9.7 Using [Reference KummerKum13, Proposition 3.3.8] one can show that the answer to Problem 9.6 is yes for hypersurfaces. It is also true for X a linear subspace by [Reference Kummer and VinzantKV19].
In the case of hypersurfaces, Theorem 9.3 has a geometric interpretation in terms of so-called interlacers.
Definition 9.1 Let
![]() $g,h\in {\mathbb R}[x_0,\ldots ,x_n]$
with
$g,h\in {\mathbb R}[x_0,\ldots ,x_n]$
with
![]() $d=\deg (g)+1=\deg (h)$
be hyperbolic with respect to e. If, for all
$d=\deg (g)+1=\deg (h)$
be hyperbolic with respect to e. If, for all
![]() $v\in {\mathbb R}^{n+1}$
, we have that
$v\in {\mathbb R}^{n+1}$
, we have that
where the
![]() $a_i$
and
$a_i$
and
![]() $b_i$
are the zeros of
$b_i$
are the zeros of
![]() $h(te-v)$
and
$h(te-v)$
and
![]() $g(te-v)$
, respectively, we say that g interlaces h, or that g is an interlacer of h. This definition carries over to hyperbolic hypersurfaces in the obvious way.
$g(te-v)$
, respectively, we say that g interlaces h, or that g is an interlacer of h. This definition carries over to hyperbolic hypersurfaces in the obvious way.
Figure 2: A cubic hyperbolic plane curve (blue) interlaced by a plane hyperbolic conic (red).
Example 9.8 If
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]$
is hyperbolic with respect to e, then the directional derivative
$h\in {\mathbb R}[x_0,\ldots ,x_n]$
is hyperbolic with respect to e, then the directional derivative
![]() $\textrm {D}_eh$
of h in direction e is an interlacer of h. This follows from Rolle’s theorem.
$\textrm {D}_eh$
of h in direction e is an interlacer of h. This follows from Rolle’s theorem.
Corollary 9.9 Let
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
be hyperbolic with respect to e, and let
$h\in {\mathbb R}[x_0,\ldots ,x_n]_d$
be hyperbolic with respect to e, and let
![]() $X={\mathcal V}(h)\subset \mathbb {P}^n$
be the corresponding hypersurface. Assume that the singular locus of X has dimension at most
$X={\mathcal V}(h)\subset \mathbb {P}^n$
be the corresponding hypersurface. Assume that the singular locus of X has dimension at most
![]() $n-3$
. Let g be an interlacer of h and denote by G the Weil divisor it defines on X.
$n-3$
. Let g be an interlacer of h and denote by G the Weil divisor it defines on X.
-
(1) Assume that
 $G=2D$
for some Weil divisor D on X. If the vector space of all
$G=2D$
for some Weil divisor D on X. If the vector space of all
 ${p\in {\mathbb R}[x_0,\ldots ,x_n]_{d-1}}$
that vanish on D has dimension at least d, then h has a definite symmetric determinantal representation.
${p\in {\mathbb R}[x_0,\ldots ,x_n]_{d-1}}$
that vanish on D has dimension at least d, then h has a definite symmetric determinantal representation. -
(2) Assume that
 $G=D+\overline {D}$
for some Weil divisor D on
$G=D+\overline {D}$
for some Weil divisor D on
 $X_{\mathbb C}$
. If the vector space of all
$X_{\mathbb C}$
. If the vector space of all
 $p\in {\mathbb C}[x_0,\ldots ,x_n]_{d-1}$
that vanish on D has dimension at least d, then h has a definite Hermitian determinantal representation.
$p\in {\mathbb C}[x_0,\ldots ,x_n]_{d-1}$
that vanish on D has dimension at least d, then h has a definite Hermitian determinantal representation.
Proof The ramification divisor of the linear projection with center e is the zero set of the directional derivative
![]() $\textrm {D}_eh$
on X. Since g is an interlacer, we have that the rational function
$\textrm {D}_eh$
on X. Since g is an interlacer, we have that the rational function
![]() $\frac {\textrm {D}_eh}{g}$
is nonnegative on
$\frac {\textrm {D}_eh}{g}$
is nonnegative on
![]() $X({\mathbb R})$
by [Reference Kummer, Plaumann and VinzantKPV15, Lemma 2.4]. Then the claim follows from Theorem 9.3 and Proposition 8.1 by our dimensional assumption.
$X({\mathbb R})$
by [Reference Kummer, Plaumann and VinzantKPV15, Lemma 2.4]. Then the claim follows from Theorem 9.3 and Proposition 8.1 by our dimensional assumption.
Remark 9.10 When
![]() $n=2$
, the case of plane curves, the dimensional condition in Corollary 9.9 is automatically satisfied by Riemann–Roch. If
$n=2$
, the case of plane curves, the dimensional condition in Corollary 9.9 is automatically satisfied by Riemann–Roch. If
![]() $g=\textrm {D}_eh$
, then
$g=\textrm {D}_eh$
, then
![]() $G=D+\overline {D}$
by Theorem 6.3. In that case, this recovers the result from [Reference Plaumann and VinzantPV13, Section 4]. Note that the proof in [Reference Plaumann and VinzantPV13] does not seem to generalize to higher dimensions as it uses Max Noether’s AF+BG theorem. It would be interesting to know when we actually need the dimensional condition in the case of higher-dimensional hypersurfaces.
$G=D+\overline {D}$
by Theorem 6.3. In that case, this recovers the result from [Reference Plaumann and VinzantPV13, Section 4]. Note that the proof in [Reference Plaumann and VinzantPV13] does not seem to generalize to higher dimensions as it uses Max Noether’s AF+BG theorem. It would be interesting to know when we actually need the dimensional condition in the case of higher-dimensional hypersurfaces.
Problem 9.11 Find hyperbolic hypersurfaces
![]() $X\subset \mathbb {P}^n$
for which there is an interlacer whose zero divisor on X is of the form
$X\subset \mathbb {P}^n$
for which there is an interlacer whose zero divisor on X is of the form
![]() $D+\overline {D}$
with
$D+\overline {D}$
with
![]() $\ell (D)<\deg (X)$
.
$\ell (D)<\deg (X)$
.
Example 9.12 Let
![]() $h\in {\mathbb R}[x_0,\ldots ,x_n]_n$
be the elementary symmetric polynomial of degree n in
$h\in {\mathbb R}[x_0,\ldots ,x_n]_n$
be the elementary symmetric polynomial of degree n in
![]() $x_0,\ldots ,x_n$
. It is hyperbolic with respect to every point in the positive orthant and
$x_0,\ldots ,x_n$
. It is hyperbolic with respect to every point in the positive orthant and
![]() $g=\frac {\partial }{\partial x_0}h$
is an interlacer. The zero divisor of g on the hypersurface
$g=\frac {\partial }{\partial x_0}h$
is an interlacer. The zero divisor of g on the hypersurface
![]() ${X={\mathcal V}(h)\subset \mathbb {P}^n}$
is of the form
${X={\mathcal V}(h)\subset \mathbb {P}^n}$
is of the form
![]() $2D$
, where
$2D$
, where
![]() $D=\sum _{1\leq i<j\leq n} L_{ij}$
. Here,
$D=\sum _{1\leq i<j\leq n} L_{ij}$
. Here,
![]() $L_{ij}$
is the linear subspace
$L_{ij}$
is the linear subspace
![]() ${\mathcal V}(x_i,x_j)\subset X$
. Each monomial
${\mathcal V}(x_i,x_j)\subset X$
. Each monomial
![]() $\frac {x_1\cdots x_n}{x_i}$
for
$\frac {x_1\cdots x_n}{x_i}$
for
![]() $1\leq i\leq n$
vanishes on D. Thus, by Corollary 9.9, the polynomial h has a definite symmetric determinantal representation. This was known before and follows, e.g., from the more general result that the bases generating polynomial of a regular matroid (in our case
$1\leq i\leq n$
vanishes on D. Thus, by Corollary 9.9, the polynomial h has a definite symmetric determinantal representation. This was known before and follows, e.g., from the more general result that the bases generating polynomial of a regular matroid (in our case
![]() $U_{n,n+1}$
) has a definite symmetric determinantal representation (see [Reference Choe, Oxley, Sokal and WagnerCOSW04, Section 8.2]).
$U_{n,n+1}$
) has a definite symmetric determinantal representation (see [Reference Choe, Oxley, Sokal and WagnerCOSW04, Section 8.2]).
10 Smooth curves
In this section, let
![]() $f\colon X\to Y$
be a real-fibered morphism between smooth irreducible curves that are projective over
$f\colon X\to Y$
be a real-fibered morphism between smooth irreducible curves that are projective over
![]() ${\mathbb R}$
with
${\mathbb R}$
with
![]() $Y({\mathbb R})$
Zariski dense in Y. Let R be the ramification divisor of f. We want to apply Theorem 9.3.
$Y({\mathbb R})$
Zariski dense in Y. Let R be the ramification divisor of f. We want to apply Theorem 9.3.
Lemma 10.1 There is a divisor M on X and a nonnegative s in the function field of X such that
![]() $R+(s)=2M$
.
$R+(s)=2M$
.
Proof The proof is a projective version of the proof of [Reference HanselkaHan17, Corollary 4.2]. By Theorem 6.3, we have that f is unramified at real points. Thus R, considered as a Weil divisor, is a sum of nonreal points. Therefore, the Weil divisor
![]() $R'$
that we obtain on the complexification
$R'$
that we obtain on the complexification
![]() $X_{\mathbb C}=X\times _{\mathbb R} {\mathbb C}$
of X is of the form
$X_{\mathbb C}=X\times _{\mathbb R} {\mathbb C}$
of X is of the form
![]() $R'=Q+\overline {Q}$
, where Q is some effective divisor and
$R'=Q+\overline {Q}$
, where Q is some effective divisor and
![]() $\overline {Q}$
its complex conjugate. Since the group
$\overline {Q}$
its complex conjugate. Since the group
![]() $\textrm {Pic}^0(X_{\mathbb C})$
is divisible, there is a g in the function field of
$\textrm {Pic}^0(X_{\mathbb C})$
is divisible, there is a g in the function field of
![]() $X_{\mathbb C}$
and a divisor N on
$X_{\mathbb C}$
and a divisor N on
![]() $X_{\mathbb C}$
such that
$X_{\mathbb C}$
such that
![]() $Q-nP=2N+(g)$
, where
$Q-nP=2N+(g)$
, where
![]() $n=\deg (Q)$
and P is any point on
$n=\deg (Q)$
and P is any point on
![]() $X_{\mathbb C}$
with
$X_{\mathbb C}$
with
![]() $P=\overline {P}$
. Thus
$P=\overline {P}$
. Thus
![]() $(Q-nP)+(\overline {Q-nP})=2(N+\overline {N})+(g\cdot \overline {g})$
which implies
$(Q-nP)+(\overline {Q-nP})=2(N+\overline {N})+(g\cdot \overline {g})$
which implies
Since
![]() $N+\overline {N}+nP$
is fixed by conjugation, it descends to a divisor M on X. The function
$N+\overline {N}+nP$
is fixed by conjugation, it descends to a divisor M on X. The function
![]() $s=g\cdot \overline {g}$
is a sum of two squares and thus nonnegative.
$s=g\cdot \overline {g}$
is a sum of two squares and thus nonnegative.
From this, we get the following theorem.
Theorem 10.2 Let X be a smooth irreducible curve that is projective over
![]() ${\mathbb R}$
. For every real fibered
${\mathbb R}$
. For every real fibered
![]() $f\colon X\to \mathbb {P}^1$
, there is a positive symmetric f-Ulrich line bundle.
$f\colon X\to \mathbb {P}^1$
, there is a positive symmetric f-Ulrich line bundle.
Proof Let M be the divisor from Lemma 10.1. By Theorem 9.3, we have to show that
![]() $\ell (M)\geq \deg (f)$
. By Hurwitz’s Theorem, we have that
$\ell (M)\geq \deg (f)$
. By Hurwitz’s Theorem, we have that
![]() $2g-2=\deg (R)-2\deg (f)$
, where g is the genus of X. Thus
$2g-2=\deg (R)-2\deg (f)$
, where g is the genus of X. Thus
![]() $\deg (M)=\deg (f)+g-1$
and by Riemann–Roch
$\deg (M)=\deg (f)+g-1$
and by Riemann–Roch
Corollary 10.3 [Reference Shamovich and VinnikovSV18, Theorem 7.2]
The Chow form of every hyperbolic curve
![]() $X\subset \mathbb {P}^n$
has a symmetric and definite determinantal representation.
$X\subset \mathbb {P}^n$
has a symmetric and definite determinantal representation.
Proof By [Reference Kummer and ShamovichKS20, Theorem 5.7] and [Reference Kummer and ShamovichKS20, Remark 4.4], it suffices to show that there is a positive Ulrich bundle of rank one on X. But this follows from the preceding theorem applied to the linear projection from an
![]() $n-2$
-space of hyperbolicity if X is smooth. Otherwise we can pass to the normalization of X.
$n-2$
-space of hyperbolicity if X is smooth. Otherwise we can pass to the normalization of X.
Corollary 10.4 (Helton–Vinnikov Theorem [Reference Helton and VinnikovHV07])
Every hyperbolic polynomial in three variables has a definite determinantal representation.
Example 10.5 If the target is not
![]() $\mathbb {P}^1$
as in Theorem 10.2, then there is, in general, no (positive symmetric) f-Ulrich sheaf on X. This fails already in the next easiest case, namely, when X and Y both have genus one. Indeed, let
$\mathbb {P}^1$
as in Theorem 10.2, then there is, in general, no (positive symmetric) f-Ulrich sheaf on X. This fails already in the next easiest case, namely, when X and Y both have genus one. Indeed, let
![]() $f\colon X\to Y$
be an unramified and real-fibered double cover of an elliptic curve Y. Such maps exist, see, for example, [Reference Kummer and SinnKS22, Lemma 6.5], and by Riemann–Hurwitz X is an elliptic curve as well. We claim that in this case there is actually no f-Ulrich sheaf at all. Indeed, there is a line bundle
$f\colon X\to Y$
be an unramified and real-fibered double cover of an elliptic curve Y. Such maps exist, see, for example, [Reference Kummer and SinnKS22, Lemma 6.5], and by Riemann–Hurwitz X is an elliptic curve as well. We claim that in this case there is actually no f-Ulrich sheaf at all. Indeed, there is a line bundle
![]() ${\mathcal L}$
on Y which is nontrivial and
${\mathcal L}$
on Y which is nontrivial and
![]() $2$
-torsion such that
$2$
-torsion such that
![]() $f_*{\mathcal O}_X={\mathcal O}_Y\oplus {\mathcal L}$
. Then we have
$f_*{\mathcal O}_X={\mathcal O}_Y\oplus {\mathcal L}$
. Then we have
![]() ${f^*{\mathcal L}={\mathcal O}_X}$
and the projection formula implies that
${f^*{\mathcal L}={\mathcal O}_X}$
and the projection formula implies that
![]() $f_*{\mathcal F}={\mathcal L}\otimes f_*{\mathcal F}$
for all coherent sheaves
$f_*{\mathcal F}={\mathcal L}\otimes f_*{\mathcal F}$
for all coherent sheaves
![]() ${\mathcal F}$
on X. This excludes
${\mathcal F}$
on X. This excludes
![]() $f_*{\mathcal F}={\mathcal O}_Y^r$
.
$f_*{\mathcal F}={\mathcal O}_Y^r$
.
11 del Pezzo surfaces
Recall that a del Pezzo surface is a smooth projective and geometrically irreducible surface whose anticanonical class is ample. We are interested in morphisms
![]() $f\colon X\to \mathbb {P}^2$
, where X is a del Pezzo surface and the pullback
$f\colon X\to \mathbb {P}^2$
, where X is a del Pezzo surface and the pullback
![]() $f^*{\mathcal O}_{\mathbb {P}^2}(1)$
is the anticanonical line bundle. It was shown in [Reference BeauvilleBea18, Proposition 4.1] that for such f there exist f-Ulrich line bundles. We will show that if f is real fibered, then there are even positive Hermitian f-Ulrich line bundles. An introduction to the classical theory of del Pezzo surfaces can be found, for example, in [Reference DolgachevDol12, Chapter 8] or [Reference Kollár, Smith and CortiKSC04, Section 3.5]. This section further relies on the classification of real del Pezzo surfaces due to Comessatti [Reference ComessattiCom12, Reference ComessattiCom28] (see also [Reference RussoRus02] for a survey in English).
$f^*{\mathcal O}_{\mathbb {P}^2}(1)$
is the anticanonical line bundle. It was shown in [Reference BeauvilleBea18, Proposition 4.1] that for such f there exist f-Ulrich line bundles. We will show that if f is real fibered, then there are even positive Hermitian f-Ulrich line bundles. An introduction to the classical theory of del Pezzo surfaces can be found, for example, in [Reference DolgachevDol12, Chapter 8] or [Reference Kollár, Smith and CortiKSC04, Section 3.5]. This section further relies on the classification of real del Pezzo surfaces due to Comessatti [Reference ComessattiCom12, Reference ComessattiCom28] (see also [Reference RussoRus02] for a survey in English).
Definition 11.1 The degree of a del Pezzo surface X is the self-intersection number
![]() $K_X.K_X$
of its canonical class
$K_X.K_X$
of its canonical class
![]() $K_X$
. A line on X is an irreducible curve
$K_X$
. A line on X is an irreducible curve
![]() $L\subset X$
such that
$L\subset X$
such that
![]() $L.L=L.K_X=-1$
.
$L.L=L.K_X=-1$
.
Remark 11.1 Note that if the anticanonical class
![]() $-K_X$
of a del Pezzo surface X is very ample, then a line L on X is mapped by the associated embedding to an actual line, i.e., a linear subspace of dimension one because
$-K_X$
of a del Pezzo surface X is very ample, then a line L on X is mapped by the associated embedding to an actual line, i.e., a linear subspace of dimension one because
![]() $L.K_X=-1$
.
$L.K_X=-1$
.
Example 11.2 These are examples of del Pezzo surfaces [Reference Kollár, Smith and CortiKSC04, Theorem 3.36(7)]:
-
(1) A smooth hypersurface of degree four in the weighted projective space
 $\mathbb {P}(2,1,1,1)$
is a del Pezzo surface of degree two.
$\mathbb {P}(2,1,1,1)$
is a del Pezzo surface of degree two. -
(2) A smooth cubic hypersurface in
 $\mathbb {P}^3$
is a del Pezzo surface of degree three.
$\mathbb {P}^3$
is a del Pezzo surface of degree three. -
(3) A smooth complete intersection of two quadrics in
 $\mathbb {P}^4$
is a del Pezzo surface of degree four.
$\mathbb {P}^4$
is a del Pezzo surface of degree four.
Furthermore, in case (1), the (complete) anticanonical linear system corresponds to the projection
![]() $\mathbb {P}(2,1,1,1)\dashrightarrow \mathbb {P}^2$
restricted to our surface. Moreover, in the cases (2) and (3), the embeddings of the surfaces to
$\mathbb {P}(2,1,1,1)\dashrightarrow \mathbb {P}^2$
restricted to our surface. Moreover, in the cases (2) and (3), the embeddings of the surfaces to
![]() $\mathbb {P}^3$
and
$\mathbb {P}^3$
and
![]() $\mathbb {P}^4$
, respectively, correspond to the (complete) anticanonical linear system. These statements are, for example, shown in the course of the proof of [Reference Kollár, Smith and CortiKSC04, Theorem 3.36].
$\mathbb {P}^4$
, respectively, correspond to the (complete) anticanonical linear system. These statements are, for example, shown in the course of the proof of [Reference Kollár, Smith and CortiKSC04, Theorem 3.36].
Remark 11.3 If X is a del Pezzo surface over an algebraically closed field, then X is isomorphic to either
![]() $\mathbb {P}^1\times \mathbb {P}^1$
or a blowup of
$\mathbb {P}^1\times \mathbb {P}^1$
or a blowup of
![]() $\mathbb {P}^2$
in
$\mathbb {P}^2$
in
![]() $n\leq 8$
points (see [Reference Kollár, Smith and CortiKSC04, Exercise 3.56] or [Reference DolgachevDol12, Corollary 8.1.17 and Proposition 8.1.25]. A straightforward calculation shows that the degree of X is eight in the former and
$n\leq 8$
points (see [Reference Kollár, Smith and CortiKSC04, Exercise 3.56] or [Reference DolgachevDol12, Corollary 8.1.17 and Proposition 8.1.25]. A straightforward calculation shows that the degree of X is eight in the former and
![]() $9-n$
in the latter case.
$9-n$
in the latter case.
Lemma 11.4 Let
![]() $X\subset \mathbb {P}^4$
be a smooth complete intersection of two quadrics in
$X\subset \mathbb {P}^4$
be a smooth complete intersection of two quadrics in
![]() $\mathbb {P}^4$
such that
$\mathbb {P}^4$
such that
![]() $X({\mathbb R})$
is homeomorphic to the disjoint union of two spheres. Then:
$X({\mathbb R})$
is homeomorphic to the disjoint union of two spheres. Then:
-
(1) X is contained in exactly five real singular quadrics.
-
(2) One of these five quadrics has signature
 $(2,2)$
, and the other four have signature
$(2,2)$
, and the other four have signature
 $(3,1)$
.
$(3,1)$
. -
(3) For exactly two of these singular quadrics, the linear projection from its vertex realizes X as a real-fibered double cover of a hyperbolic quadratic hypersurface
 $Q\subset \mathbb {P}^3$
.
$Q\subset \mathbb {P}^3$
.
Proof The complex pencil
![]() $\lambda q_0+\mu q_1$
contains five singular quadrics as the
$\lambda q_0+\mu q_1$
contains five singular quadrics as the
![]() $q_i$
can be represented by symmetric
$q_i$
can be represented by symmetric
![]() $5\times 5$
matrices. We will show that all of them are real. To this end, recall that by Remark 11.3, the complexification
$5\times 5$
matrices. We will show that all of them are real. To this end, recall that by Remark 11.3, the complexification
![]() $X_{\mathbb C}$
of X is isomorphic to the blowup of
$X_{\mathbb C}$
of X is isomorphic to the blowup of
![]() $\mathbb {P}^2$
at five points
$\mathbb {P}^2$
at five points
![]() $p_0,\ldots ,p_4$
. The 16 lines on
$p_0,\ldots ,p_4$
. The 16 lines on
![]() $X_{\mathbb C}$
correspond to the exceptional divisors
$X_{\mathbb C}$
correspond to the exceptional divisors
![]() $E_0,\ldots ,E_4$
, the lines
$E_0,\ldots ,E_4$
, the lines
![]() $l_{ij}$
through
$l_{ij}$
through
![]() $p_i$
and
$p_i$
and
![]() $p_j$
for
$p_j$
for
![]() $0\leq i<j\leq 4$
and the conic C through all five points
$0\leq i<j\leq 4$
and the conic C through all five points
![]() $p_0,\ldots ,p_4$
(see, for example, [Reference ManinMan86, Theorem 26.2]). After relabeling, if necessary, the complex conjugation on
$p_0,\ldots ,p_4$
(see, for example, [Reference ManinMan86, Theorem 26.2]). After relabeling, if necessary, the complex conjugation on
![]() $X_{\mathbb C}$
interchanges
$X_{\mathbb C}$
interchanges
![]() $E_0$
with C,
$E_0$
with C,
![]() $E_i$
with
$E_i$
with
![]() $l_{0i}$
for
$l_{0i}$
for
![]() $1\leq i\leq 4$
and
$1\leq i\leq 4$
and
![]() $l_{ij}$
with
$l_{ij}$
with
![]() $l_{kl}$
for
$l_{kl}$
for
![]() $\{i,j,k,l\}=\{1,2,3,4\}$
and
$\{i,j,k,l\}=\{1,2,3,4\}$
and
![]() $i<j$
,
$i<j$
,
![]() $k<l$
(see [Reference RussoRus02, Example 2, case
$k<l$
(see [Reference RussoRus02, Example 2, case
![]() $n=3$
]). We write
$n=3$
]). We write
(divisors on X) and note that all
![]() $A_i$
belong to the same linear system. Similarly, the divisors
$A_i$
belong to the same linear system. Similarly, the divisors
![]() $B_i=E_i+l_{0i}$
for
$B_i=E_i+l_{0i}$
for
![]() $1\leq i\leq 4$
on X are also linearly equivalent to each other. Note that we did write
$1\leq i\leq 4$
on X are also linearly equivalent to each other. Note that we did write
![]() $A_i=L_i+\overline {L_i}$
and
$A_i=L_i+\overline {L_i}$
and
![]() $B_i=L_i'+\overline {L_i'}$
for suitable lines
$B_i=L_i'+\overline {L_i'}$
for suitable lines
![]() $L_i$
and
$L_i$
and
![]() $L_i'$
on
$L_i'$
on
![]() $X_{\mathbb C}$
. Each of the two linear systems realize X as a conic bundle, i.e., define a morphism
$X_{\mathbb C}$
. Each of the two linear systems realize X as a conic bundle, i.e., define a morphism
![]() $X\to \mathbb {P}^1$
all of whose fibers are isomorphic to a plane conic curve [Reference RussoRus02, Example 2]. The four singular fibers of each bundle are exactly the
$X\to \mathbb {P}^1$
all of whose fibers are isomorphic to a plane conic curve [Reference RussoRus02, Example 2]. The four singular fibers of each bundle are exactly the
![]() $A_i$
and
$A_i$
and
![]() $B_i$
, respectively. Therefore, for each connected component S of
$B_i$
, respectively. Therefore, for each connected component S of
![]() $X({\mathbb R})$
, there are exactly two values for i and j such that
$X({\mathbb R})$
, there are exactly two values for i and j such that
![]() $L_i\cap \overline {L_i}$
resp.
$L_i\cap \overline {L_i}$
resp.
![]() $L_j'\cap \overline {L_j'}$
is a point on S. Our two conic bundle structures on X induce a map
$L_j'\cap \overline {L_j'}$
is a point on S. Our two conic bundle structures on X induce a map
![]() $X\to \mathbb {P}^1\times \mathbb {P}^1$
which is a double cover since
$X\to \mathbb {P}^1\times \mathbb {P}^1$
which is a double cover since
![]() $A_i\cdot B_j=2$
. Since
$A_i\cdot B_j=2$
. Since
![]() $A_i+B_j$
is an anticanonical divisor, this double cover is a linear projection of X to
$A_i+B_j$
is an anticanonical divisor, this double cover is a linear projection of X to
![]() $\mathbb {P}^3$
whose image is a hypersurface isomorphic to
$\mathbb {P}^3$
whose image is a hypersurface isomorphic to
![]() $\mathbb {P}^1\times \mathbb {P}^1$
, i.e., defined by a quadric with signature
$\mathbb {P}^1\times \mathbb {P}^1$
, i.e., defined by a quadric with signature
![]() $(2,2)$
. The cone over this quadric in
$(2,2)$
. The cone over this quadric in
![]() $\mathbb {P}^4$
is one of our singular quadrics. The four divisors
$\mathbb {P}^4$
is one of our singular quadrics. The four divisors
on
![]() $X_{\mathbb C}$
for
$X_{\mathbb C}$
for
![]() $1\leq j\leq 4$
also realize
$1\leq j\leq 4$
also realize
![]() $X_{\mathbb C}$
as a conic bundle
$X_{\mathbb C}$
as a conic bundle
![]() $X_{\mathbb C}\to \mathbb {P}^1_{\mathbb C}$
and, for each j, we consider the map
$X_{\mathbb C}\to \mathbb {P}^1_{\mathbb C}$
and, for each j, we consider the map
![]() $X_{\mathbb C}\to \mathbb {P}^1_{\mathbb C}\times \mathbb {P}^1_{\mathbb C}$
associated with
$X_{\mathbb C}\to \mathbb {P}^1_{\mathbb C}\times \mathbb {P}^1_{\mathbb C}$
associated with
![]() $D_j$
in the first coordinate and
$D_j$
in the first coordinate and
![]() $\overline {D_j}$
on the second. This corresponds to a morphism
$\overline {D_j}$
on the second. This corresponds to a morphism
![]() $f_j\colon X\to Q$
, where
$f_j\colon X\to Q$
, where
![]() $Q\subset \mathbb {P}^3$
is a hypersurface defined by a quadric of signature
$Q\subset \mathbb {P}^3$
is a hypersurface defined by a quadric of signature
![]() $(3,1)$
. Since
$(3,1)$
. Since
![]() $D_j\cdot \overline {D_j}=2$
, this is a double cover, and since
$D_j\cdot \overline {D_j}=2$
, this is a double cover, and since
![]() $D_j+\overline {D_j}$
is anticanonical, the maps
$D_j+\overline {D_j}$
is anticanonical, the maps
![]() $f_j$
correspond to linear projections of X. This shows
$f_j$
correspond to linear projections of X. This shows
![]() $(2)$
and
$(2)$
and
![]() $(3)$
. We have
$(3)$
. We have
Thus, in order to determine whether
![]() $f_i\colon X\to Q$
is real-fibered or not, we have to check whether the two intersection points
$f_i\colon X\to Q$
is real-fibered or not, we have to check whether the two intersection points
![]() $L_1\cap \overline {L_1}$
and
$L_1\cap \overline {L_1}$
and
![]() $L_i'\cap \overline {L_i'}$
lie on the same (not real fibered) or different connected components (real fibered) of
$L_i'\cap \overline {L_i'}$
lie on the same (not real fibered) or different connected components (real fibered) of
![]() $X({\mathbb R})$
. As noted above, both cases occur for exactly two values of j.
$X({\mathbb R})$
. As noted above, both cases occur for exactly two values of j.
With this preparation, we are able to determine for which del Pezzo surfaces X there is a real-fibered morphism
![]() $X\to \mathbb {P}^2$
whose corresponding linear system is anticanonical.
$X\to \mathbb {P}^2$
whose corresponding linear system is anticanonical.
Proposition 11.5 Let X be a real del Pezzo surface, and let K be a canonical divisor on X. There is a real-fibered morphism
![]() $f\colon X\to \mathbb {P}^2$
such that the pullback of a line is linearly equivalent to
$f\colon X\to \mathbb {P}^2$
such that the pullback of a line is linearly equivalent to
![]() $-K$
on X if and only if we have one of the following:
$-K$
on X if and only if we have one of the following:
-
(1) X is a quartic surface in
 $\mathbb {P}^4$
such that
$\mathbb {P}^4$
such that
 $X({\mathbb R})$
is homeomorphic to a disjoint union of two spheres.
$X({\mathbb R})$
is homeomorphic to a disjoint union of two spheres. -
(2) X is a cubic hypersurface in
 $\mathbb {P}^3$
such that
$\mathbb {P}^3$
such that
 $X({\mathbb R})$
is homeomorphic to a disjoint union of a sphere and a real projective plane.
$X({\mathbb R})$
is homeomorphic to a disjoint union of a sphere and a real projective plane. -
(3) X is a double cover of
 $\mathbb {P}^2$
branched along a smooth plane quartic curve C with
$\mathbb {P}^2$
branched along a smooth plane quartic curve C with
 $C({\mathbb R})=\emptyset $
so that
$C({\mathbb R})=\emptyset $
so that
 $X({\mathbb R})$
is homeomorphic to a disjoint union of two real projective planes.
$X({\mathbb R})$
is homeomorphic to a disjoint union of two real projective planes.
In particular, in each case,
![]() $X({\mathbb R})$
has two connected components.
$X({\mathbb R})$
has two connected components.
Proof Let
![]() $d=K.K$
. For
$d=K.K$
. For
![]() $d=2$
, the anticanonical map is a double cover of
$d=2$
, the anticanonical map is a double cover of
![]() $\mathbb {P}^2$
branched along a plane quartic curve C (see Example 11.2). This is real fibered if and only if
$\mathbb {P}^2$
branched along a plane quartic curve C (see Example 11.2). This is real fibered if and only if
![]() $C({\mathbb R})=\emptyset $
and
$C({\mathbb R})=\emptyset $
and
![]() $X({\mathbb R})$
is homeomorphic to a disjoint union of two real projective planes. In general, if there exists such a morphism f, then
$X({\mathbb R})$
is homeomorphic to a disjoint union of two real projective planes. In general, if there exists such a morphism f, then
![]() $X({\mathbb R})$
must be homeomorphic to the disjoint union of s spheres and r real projective planes such that
$X({\mathbb R})$
must be homeomorphic to the disjoint union of s spheres and r real projective planes such that
![]() $d=2s+r$
by [Reference Kummer and ShamovichKS20, Corollary 2.20]. Going through the classification of real del Pezzo surfaces in [Reference RussoRus02], we see that for
$d=2s+r$
by [Reference Kummer and ShamovichKS20, Corollary 2.20]. Going through the classification of real del Pezzo surfaces in [Reference RussoRus02], we see that for
![]() $d\neq 2$
this is only possible for a complete intersection of two quadrics in
$d\neq 2$
this is only possible for a complete intersection of two quadrics in
![]() $\mathbb {P}^4$
such that
$\mathbb {P}^4$
such that
![]() $X({\mathbb R})$
is homeomorphic to a disjoint union of two spheres (
$X({\mathbb R})$
is homeomorphic to a disjoint union of two spheres (
![]() $d=4$
) or a cubic hypersurface in
$d=4$
) or a cubic hypersurface in
![]() $\mathbb {P}^3$
such that
$\mathbb {P}^3$
such that
![]() $X({\mathbb R})$
is homeomorphic to a disjoint union of a sphere and a real projective plane (
$X({\mathbb R})$
is homeomorphic to a disjoint union of a sphere and a real projective plane (
![]() $d=3$
). This shows the “only if part.” It thus remains to show that the embedded surfaces in
$d=3$
). This shows the “only if part.” It thus remains to show that the embedded surfaces in
![]() $(1)$
and
$(1)$
and
![]() $(2)$
are hyperbolic as these embeddings correspond to the anticanonical linear system (see Example 11.2). The case
$(2)$
are hyperbolic as these embeddings correspond to the anticanonical linear system (see Example 11.2). The case
![]() $d=3$
is covered by [Reference VinnikovVin12, Proposition 2.2]. For the case
$d=3$
is covered by [Reference VinnikovVin12, Proposition 2.2]. For the case
![]() $d=4$
, we can compose a real-fibered linear projection
$d=4$
, we can compose a real-fibered linear projection
![]() $X\to Q$
from Lemma 11.4 to a hyperbolic hypersurface
$X\to Q$
from Lemma 11.4 to a hyperbolic hypersurface
![]() $Q\subset \mathbb {P}^3$
with the linear projection
$Q\subset \mathbb {P}^3$
with the linear projection
![]() $Q\to \mathbb {P}^2$
from a point with respect to which Q is hyperbolic.
$Q\to \mathbb {P}^2$
from a point with respect to which Q is hyperbolic.
Lemma 11.6 Let X be a del Pezzo surface, and let K be a canonical divisor on X. Let
![]() $f\colon X\to \mathbb {P}^2$
be a real-fibered morphism of degree d such that the pullback of a line is linearly equivalent to
$f\colon X\to \mathbb {P}^2$
be a real-fibered morphism of degree d such that the pullback of a line is linearly equivalent to
![]() $-K$
as constructed in the previous proposition.
$-K$
as constructed in the previous proposition.
-
(a) The ramification divisor R is linearly equivalent to
 $-2K$
.
$-2K$
. -
(b) Let g be a rational function on X whose principal divisor is
 $R+2K$
. Then g has constant sign on each of the two connected components of
$R+2K$
. Then g has constant sign on each of the two connected components of
 $X({\mathbb R})$
and these signs are not the same.
$X({\mathbb R})$
and these signs are not the same.
Proof The ramification divisor is linearly equivalent to the canonical divisor on X minus the pullback of the canonical divisor on
![]() $\mathbb {P}^2$
. As the latter is
$\mathbb {P}^2$
. As the latter is
![]() ${\mathcal O}_{\mathbb {P}^2}(-3)$
its pullback is
${\mathcal O}_{\mathbb {P}^2}(-3)$
its pullback is
![]() $3K$
. This shows (a).
$3K$
. This shows (a).
For
![]() $d=2$
, part (b) follows from the fact X is a double cover of
$d=2$
, part (b) follows from the fact X is a double cover of
![]() $\mathbb {P}^2$
of the form
$\mathbb {P}^2$
of the form
![]() ${y^2=p(x)}$
, where
${y^2=p(x)}$
, where
![]() $p\in {\mathbb R}[x_0,x_1,x_2]_4$
is a globally positive quartic curve. The ramification divisor is given as the zero locus of y, whereas
$p\in {\mathbb R}[x_0,x_1,x_2]_4$
is a globally positive quartic curve. The ramification divisor is given as the zero locus of y, whereas
![]() $-K$
is the zero set of a linear form
$-K$
is the zero set of a linear form
![]() $l\in {\mathbb R}[x_0,x_1,x_2]$
. Clearly,
$l\in {\mathbb R}[x_0,x_1,x_2]$
. Clearly,
![]() $\frac {y}{l^2}$
has the desired properties.
$\frac {y}{l^2}$
has the desired properties.
In the case
![]() $d=3$
, our surface X is the zero set of a hyperbolic polynomial h and our morphism f is the linear projection from a point
$d=3$
, our surface X is the zero set of a hyperbolic polynomial h and our morphism f is the linear projection from a point
![]() $e\in \mathbb {P}^3$
of hyperbolicity. Its ramification divisor is thus cut out by the interlacer
$e\in \mathbb {P}^3$
of hyperbolicity. Its ramification divisor is thus cut out by the interlacer
![]() $\textrm {D}_eh$
. Again
$\textrm {D}_eh$
. Again
![]() $-K$
is the zero set of a linear form
$-K$
is the zero set of a linear form
![]() $l\in {\mathbb R}[x_0,x_1,x_2]$
and
$l\in {\mathbb R}[x_0,x_1,x_2]$
and
![]() $\frac {\textrm {D}_eh}{l^2}$
has different sign on the two connected components of
$\frac {\textrm {D}_eh}{l^2}$
has different sign on the two connected components of
![]() $X({\mathbb R})$
.
$X({\mathbb R})$
.
In the case
![]() $d=4$
, we first note that by Lemma 11.4, we can assume (after a linear change of coordinates) that X is cut out by
$d=4$
, we first note that by Lemma 11.4, we can assume (after a linear change of coordinates) that X is cut out by
![]() $q_1=x_0^2-(x_1^2+x_2^2+x_3^2)$
and
$q_1=x_0^2-(x_1^2+x_2^2+x_3^2)$
and
![]() $q_2=x_4^2-p$
for some quadratic form
$q_2=x_4^2-p$
for some quadratic form
![]() $p\in {\mathbb R}[x_0,x_1,x_2,x_3]_2$
that is nonnegative on
$p\in {\mathbb R}[x_0,x_1,x_2,x_3]_2$
that is nonnegative on
![]() $Q={\mathcal V}(q_1)\subset \mathbb {P}^3$
. Our real-fibered morphism
$Q={\mathcal V}(q_1)\subset \mathbb {P}^3$
. Our real-fibered morphism
![]() $f\colon X\to \mathbb {P}^2$
is then the composition of the two linear projections
$f\colon X\to \mathbb {P}^2$
is then the composition of the two linear projections
![]() $X\to Q$
with center
$X\to Q$
with center
![]() $[0\colon 0\colon 0\colon 0\colon 1]$
and
$[0\colon 0\colon 0\colon 0\colon 1]$
and
![]() $Q\to \mathbb {P}^2$
with center
$Q\to \mathbb {P}^2$
with center
![]() $[1\colon 0\colon 0\colon 0]$
. Thus the ramification locus of f is cut out by
$[1\colon 0\colon 0\colon 0]$
. Thus the ramification locus of f is cut out by
![]() $x_0\cdot x_4$
. Again
$x_0\cdot x_4$
. Again
![]() $-K$
is the zero set of a linear form
$-K$
is the zero set of a linear form
![]() $l\in {\mathbb R}[x_0,x_1,x_2]$
and
$l\in {\mathbb R}[x_0,x_1,x_2]$
and
![]() $\frac {x_0\cdot x_4}{l^2}$
has different sign on the two connected components of
$\frac {x_0\cdot x_4}{l^2}$
has different sign on the two connected components of
![]() $X({\mathbb R})$
.
$X({\mathbb R})$
.
Let
![]() $X_4$
be a complete intersection of two quadrics in
$X_4$
be a complete intersection of two quadrics in
![]() $\mathbb {P}^4$
such that
$\mathbb {P}^4$
such that
![]() $X({\mathbb R})$
is homeomorphic to a disjoint union of two spheres. We fix a sequence of morphisms
$X({\mathbb R})$
is homeomorphic to a disjoint union of two spheres. We fix a sequence of morphisms
where each map
![]() $f_i\colon X_{i}\to X_{i+1}$
is the blowup of
$f_i\colon X_{i}\to X_{i+1}$
is the blowup of
![]() $X_i$
at a real point on a connected component of
$X_i$
at a real point on a connected component of
![]() $X_i({\mathbb R})$
that is homeomorphic to a sphere. Further, let
$X_i({\mathbb R})$
that is homeomorphic to a sphere. Further, let
![]() $E_i$
be the exceptional divisor of
$E_i$
be the exceptional divisor of
![]() $f_i$
. By the classification of real del Pezzo surfaces, we have that
$f_i$
. By the classification of real del Pezzo surfaces, we have that
![]() $X_3$
is a cubic hypersurface in
$X_3$
is a cubic hypersurface in
![]() $\mathbb {P}^3$
such that
$\mathbb {P}^3$
such that
![]() $X({\mathbb R})$
is homeomorphic to a disjoint union of a sphere and a real projective plane and
$X({\mathbb R})$
is homeomorphic to a disjoint union of a sphere and a real projective plane and
![]() $X_2$
is a double cover of
$X_2$
is a double cover of
![]() $\mathbb {P}^2$
branched along a smooth plane quartic curve C with
$\mathbb {P}^2$
branched along a smooth plane quartic curve C with
![]() $C({\mathbb R})=\emptyset $
so that
$C({\mathbb R})=\emptyset $
so that
![]() $X({\mathbb R})$
is homeomorphic to a disjoint union of two real projective planes. Conversely, every such real del Pezzo surface fits in such a sequence of blowups.
$X({\mathbb R})$
is homeomorphic to a disjoint union of two real projective planes. Conversely, every such real del Pezzo surface fits in such a sequence of blowups.
Lemma 11.7 Consider the cubic hypersurface
![]() $X_3\subset \mathbb {P}^3$
.
$X_3\subset \mathbb {P}^3$
.
-
(a) In addition to
 $E_3$
, there are two more real lines L and
$E_3$
, there are two more real lines L and
 $L'$
on
$L'$
on
 $X_3$
. These three lines lie on a common plane.
$X_3$
. These three lines lie on a common plane. -
(b) There are two different hyperplanes that contain L and are tangential to a real point on the connected component of
 $X_3({\mathbb R})$
that is homeomorphic to the sphere.
$X_3({\mathbb R})$
that is homeomorphic to the sphere. -
(c) The divisors
 $H_1$
and
$H_1$
and
 $H_2$
on
$H_2$
on
 $X_3$
that are defined as the intersections with the hyperplanes from part (b) are of the form
$X_3$
that are defined as the intersections with the hyperplanes from part (b) are of the form
 $H_i=L+L_i+\overline {L_i}$
for some nonreal lines
$H_i=L+L_i+\overline {L_i}$
for some nonreal lines
 $L_i$
on
$L_i$
on
 $(X_3)_{\mathbb C}$
.
$(X_3)_{\mathbb C}$
. -
(d) The lines
 $L_i$
and
$L_i$
and
 $\overline {L_i}$
are disjoint from
$\overline {L_i}$
are disjoint from
 $E_3$
. Furthermore,
$E_3$
. Furthermore,
 $L_1$
and
$L_1$
and
 $L_2$
are disjoint.
$L_2$
are disjoint. -
(e) Let f be a rational function on
 $X_3$
whose principal divisor is
$X_3$
whose principal divisor is
 $L_2+\overline {L_2}-L_1-\overline {L_1}$
. Then f has constant sign on each of the two connected components of
$L_2+\overline {L_2}-L_1-\overline {L_1}$
. Then f has constant sign on each of the two connected components of
 $X({\mathbb R})$
and these signs are not the same.
$X({\mathbb R})$
and these signs are not the same.
Proof The number of real lines on
![]() $X_3$
can be found, for example, in [Reference RussoRus02, p. 302]. As they all must lie in the component of
$X_3$
can be found, for example, in [Reference RussoRus02, p. 302]. As they all must lie in the component of
![]() $X({\mathbb R})$
that is homeomorphic to
$X({\mathbb R})$
that is homeomorphic to
![]() ${\mathbb R}\mathbb {P}^2$
, each two of them intersect in a point. Thus they all lie in a common plane
${\mathbb R}\mathbb {P}^2$
, each two of them intersect in a point. Thus they all lie in a common plane
![]() $H_0$
which proves (a).
$H_0$
which proves (a).
In the affine chart
![]() ${\mathbb R}^3=(\mathbb {P}^3\setminus H_0)({\mathbb R})$
, the connected component of
${\mathbb R}^3=(\mathbb {P}^3\setminus H_0)({\mathbb R})$
, the connected component of
![]() $X_3({\mathbb R})$
that is homeomorphic to a sphere is the boundary of a compact convex set
$X_3({\mathbb R})$
that is homeomorphic to a sphere is the boundary of a compact convex set
![]() $K\subset {\mathbb R}^3$
, namely, K is an affine slice of the hyperbolicity cone of the cubic that defines
$K\subset {\mathbb R}^3$
, namely, K is an affine slice of the hyperbolicity cone of the cubic that defines
![]() $X_3$
. The hyperplanes containing L correspond to a family of parallel affine hyperplanes in
$X_3$
. The hyperplanes containing L correspond to a family of parallel affine hyperplanes in
![]() ${\mathbb R}^3$
. Thus exactly two of them are tangent to K. This shows (b).
${\mathbb R}^3$
. Thus exactly two of them are tangent to K. This shows (b).
The zero divisors of these hyperplanes
![]() $H_i$
contain besides L a plane conic which has an isolated real point, namely, the point of tangency. Thus the conic is a complex conjugate pair of lines
$H_i$
contain besides L a plane conic which has an isolated real point, namely, the point of tangency. Thus the conic is a complex conjugate pair of lines
![]() $L_i$
and
$L_i$
and
![]() $\overline {L_i}$
which shows part (c).
$\overline {L_i}$
which shows part (c).
In order to show (d), assume for the sake of a contradiction that
![]() $L_i$
intersects
$L_i$
intersects
![]() $E_3$
. Since
$E_3$
. Since
![]() $L_i\subset H_i$
and
$L_i\subset H_i$
and
![]() $E_3\subset H_0$
, this intersection point must lie on
$E_3\subset H_0$
, this intersection point must lie on
![]() $E_3\cap H_0\cap H_i=E_3\cap L$
which implies that it is real. But the only real point of
$E_3\cap H_0\cap H_i=E_3\cap L$
which implies that it is real. But the only real point of
![]() $L_i$
lies on the spherical component of
$L_i$
lies on the spherical component of
![]() $X_3({\mathbb R})$
. An analogous argument shows that
$X_3({\mathbb R})$
. An analogous argument shows that
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are disjoint.
$L_2$
are disjoint.
Finally, let
![]() $l_i$
be the linear form that cuts out
$l_i$
be the linear form that cuts out
![]() $H_i$
. Then, by construction,
$H_i$
. Then, by construction,
![]() $p=l_1l_2$
is an interlacer of the polynomial defining
$p=l_1l_2$
is an interlacer of the polynomial defining
![]() $X_3$
. Thus the rational function
$X_3$
. Thus the rational function
![]() $f=\frac {p}{l_1^2}$
has constant sign on each of the two connected components of
$f=\frac {p}{l_1^2}$
has constant sign on each of the two connected components of
![]() $X({\mathbb R})$
and these signs are not the same. Clearly the principal divisor corresponding to f is
$X({\mathbb R})$
and these signs are not the same. Clearly the principal divisor corresponding to f is
![]() $L_2+\overline {L_2}-L_1-\overline {L_1}$
. Therefore, we have shown part (d).
$L_2+\overline {L_2}-L_1-\overline {L_1}$
. Therefore, we have shown part (d).

Figure 3: A cubic hyperbolic hypersurface with two planes that contain a line on the pseudoplane (red) and are tangent to the spherical component (yellow).
Theorem 11.8 Let X be a del Pezzo surface, and let
![]() $f\colon X\to \mathbb {P}^2$
be a real-fibered morphism of degree d such that the pullback of a line is the anticanonical divisor class
$f\colon X\to \mathbb {P}^2$
be a real-fibered morphism of degree d such that the pullback of a line is the anticanonical divisor class
![]() $-K$
. Then there is a positive Hermitian f-Ulrich line bundle.
$-K$
. Then there is a positive Hermitian f-Ulrich line bundle.
Proof We put X into a sequence of blowups as in (11.1). Since the lines
![]() $L_i$
and
$L_i$
and
![]() $\overline {L_i}$
on
$\overline {L_i}$
on
![]() $(X_3)_{\mathbb C}$
from Lemma 11.7 are disjoint from
$(X_3)_{\mathbb C}$
from Lemma 11.7 are disjoint from
![]() $E_3$
, they can be identified with some lines on
$E_3$
, they can be identified with some lines on
![]() $(X_4)_{\mathbb C}$
which we, by abuse of notation, also denote by
$(X_4)_{\mathbb C}$
which we, by abuse of notation, also denote by
![]() $L_i$
and
$L_i$
and
![]() $\overline {L_i}$
. The same we do for the proper transforms of
$\overline {L_i}$
. The same we do for the proper transforms of
![]() $L_i$
and
$L_i$
and
![]() $\overline {L_i}$
in
$\overline {L_i}$
in
![]() $(X_2)_{\mathbb C}$
. We want to apply part (b) of Theorem 9.3 to the divisor
$(X_2)_{\mathbb C}$
. We want to apply part (b) of Theorem 9.3 to the divisor
![]() $M=L_2-L_1-K$
, where K is a canonical divisor on X. Since X is birational to
$M=L_2-L_1-K$
, where K is a canonical divisor on X. Since X is birational to
![]() $X_3$
, the rational function f from part (e) of Lemma 11.7 is also a rational function on X and we have
$X_3$
, the rational function f from part (e) of Lemma 11.7 is also a rational function on X and we have
![]() $M+\overline {M}=(f)-2K$
. By Lemma 11.6, there is a rational function g on X such that
$M+\overline {M}=(f)-2K$
. By Lemma 11.6, there is a rational function g on X such that
![]() $(g)=R+2K$
, where R is the ramification divisor. Furthermore, we can choose g to have the same sign on each connected component of
$(g)=R+2K$
, where R is the ramification divisor. Furthermore, we can choose g to have the same sign on each connected component of
![]() $X({\mathbb R})$
as f. Thus
$X({\mathbb R})$
as f. Thus
![]() $M+\overline {M}=(\frac {f}{g})+R$
and
$M+\overline {M}=(\frac {f}{g})+R$
and
![]() $\frac {f}{g}$
is nonnegative. It thus remains to show that the dimension
$\frac {f}{g}$
is nonnegative. It thus remains to show that the dimension
![]() $\ell (M)$
of the space of global sections of
$\ell (M)$
of the space of global sections of
![]() ${\mathcal L}(M)$
is at least d. To this end, we invoke the theorem of Riemann–Roch for surfaces [Reference HartshorneHar77, Theorem 1.6]:
${\mathcal L}(M)$
is at least d. To this end, we invoke the theorem of Riemann–Roch for surfaces [Reference HartshorneHar77, Theorem 1.6]:
Now, since the intersection product of
![]() $(K-M)$
with the ample divisor
$(K-M)$
with the ample divisor
![]() $-K$
equals
$-K$
equals
![]() $-2d<0$
, it cannot be effective. Thus
$-2d<0$
, it cannot be effective. Thus
![]() $\ell (K-M)=0$
and the claim follows.
$\ell (K-M)=0$
and the claim follows.
We now apply Theorem 11.8 to the three cases from Proposition 11.5. The following consequence is originally due to Buckley and Koşir [Reference Buckley and KoširBK07].
Corollary 11.9 Every hyperbolic polynomial
![]() $h\in {\mathbb R}[x_0,x_1,x_2,x_3]$
of degree three has a definite Hermitian determinantal representation.
$h\in {\mathbb R}[x_0,x_1,x_2,x_3]$
of degree three has a definite Hermitian determinantal representation.
Proof First assume that the zero set of h is smooth. Then we are in case
![]() $(2)$
of Proposition 11.5 and the claim follows from Theorem 11.8 and Proposition 8.1. For the singular case, note that by [Reference NuijNui68], the set of all hyperbolic polynomials is the closure of the smooth ones. Furthermore, by [Reference Plaumann and VinzantPV13, Lemma 3.4], the set of hyperbolic polynomials with a definite Hermitian determinantal representation is closed.
$(2)$
of Proposition 11.5 and the claim follows from Theorem 11.8 and Proposition 8.1. For the singular case, note that by [Reference NuijNui68], the set of all hyperbolic polynomials is the closure of the smooth ones. Furthermore, by [Reference Plaumann and VinzantPV13, Lemma 3.4], the set of hyperbolic polynomials with a definite Hermitian determinantal representation is closed.
The following consequence is originally due to Hilbert [Reference HilbertHil88].
Corollary 11.10 Every nonnegative ternary quartic is a sum of three squares.
Proof First consider a nonnegative ternary quartic p with smooth zero set. The hypersurface defined by
![]() $y^2-p$
in
$y^2-p$
in
![]() $\mathbb {P}(2,1,1,1)$
is an instance of Proposition 11.5(3). Thus, the claim follows from Theorems 8.6 and 11.8. The general case now follows from a limit argument as the set of sums of squares is closed in
$\mathbb {P}(2,1,1,1)$
is an instance of Proposition 11.5(3). Thus, the claim follows from Theorems 8.6 and 11.8. The general case now follows from a limit argument as the set of sums of squares is closed in
![]() ${\mathbb R}[x_0,x_1,x_2]_4$
.
${\mathbb R}[x_0,x_1,x_2]_4$
.
Remark 11.11 A recent generalization of Hilbert’s result on nonnegative ternary quartics was established in [Reference Blekherman, Smith and VelascoBSV16]. Among others, they show that every quadratic polynomial
![]() $p\in {\mathbb R}[x_0,\ldots ,x_n]$
which is nonnegative on the real part of an irreducible variety
$p\in {\mathbb R}[x_0,\ldots ,x_n]$
which is nonnegative on the real part of an irreducible variety
![]() $X\subset \mathbb {P}^n$
with
$X\subset \mathbb {P}^n$
with
![]() $\deg (X)=\operatorname {codim}(X)+1$
and Zariski dense real part is a sum of squares modulo the ideal I of X. Analogously to Theorem 8.6, one can show that this is equivalent to the existence of a certain positive Ulrich sheaf. Namely, let Y be the zero set in
$\deg (X)=\operatorname {codim}(X)+1$
and Zariski dense real part is a sum of squares modulo the ideal I of X. Analogously to Theorem 8.6, one can show that this is equivalent to the existence of a certain positive Ulrich sheaf. Namely, let Y be the zero set in
![]() $\mathbb {P}^{n+1}$
of the ideal generated by I and the polynomial
$\mathbb {P}^{n+1}$
of the ideal generated by I and the polynomial
![]() $y^2-p$
. Let
$y^2-p$
. Let
![]() $f\colon Y\to X$
the natural projection. Analogously to Theorem 8.6, the polynomial p is a sum of squares modulo I if and only if there is a positive f-Ulrich sheaf. It would be interesting to construct these sheaves directly.
$f\colon Y\to X$
the natural projection. Analogously to Theorem 8.6, the polynomial p is a sum of squares modulo I if and only if there is a positive f-Ulrich sheaf. It would be interesting to construct these sheaves directly.
Corollary 11.12 The Chow form of a smooth hyperbolic surface in
![]() $\mathbb {P}^4$
of degree four, which is a complete intersection of two quadrics, has a definite Hermitian determinantal representation.
$\mathbb {P}^4$
of degree four, which is a complete intersection of two quadrics, has a definite Hermitian determinantal representation.
Proof Here, we are in case (1) of Proposition 11.5. The claim follows from Theorem 11.8 together with a straightforward adaption of the proof of [Reference Kummer and ShamovichKS20, Theorem 5.7] to the Hermitian case and [Reference Kummer and ShamovichKS20, Remark 4.4].
Remark 11.13 We have seen that every nonnegative polynomial
![]() $p\in {\mathbb R}[x_0,x_1,x_2]_4$
is a sum of squares and every hyperbolic polynomial
$p\in {\mathbb R}[x_0,x_1,x_2]_4$
is a sum of squares and every hyperbolic polynomial
![]() $h\in {\mathbb R}[x_0,x_1,x_2,x_3]_3$
has a definite Hermitian determinantal representation, i.e., the associated real-fibered morphisms admit a positive Ulrich sheaf. This is no longer true if we increase the degrees: not every nonnegative polynomial
$h\in {\mathbb R}[x_0,x_1,x_2,x_3]_3$
has a definite Hermitian determinantal representation, i.e., the associated real-fibered morphisms admit a positive Ulrich sheaf. This is no longer true if we increase the degrees: not every nonnegative polynomial
![]() $p\in {\mathbb R}[x_0,x_1,x_2]_6$
is a sum of squares [Reference HilbertHil88] and there are hyperbolic polynomials
$p\in {\mathbb R}[x_0,x_1,x_2]_6$
is a sum of squares [Reference HilbertHil88] and there are hyperbolic polynomials
![]() $h\in {\mathbb R}[x_0,x_1,x_2,x_3]_4$
such that no power
$h\in {\mathbb R}[x_0,x_1,x_2,x_3]_4$
such that no power
![]() $h^r$
has a definite determinantal representation, take, for example, the polynomial considered in [Reference KummerKum16b]. Double covers of
$h^r$
has a definite determinantal representation, take, for example, the polynomial considered in [Reference KummerKum16b]. Double covers of
![]() $\mathbb {P}^2$
ramified along plane sextic curves and quartic hypersurfaces in
$\mathbb {P}^2$
ramified along plane sextic curves and quartic hypersurfaces in
![]() $\mathbb {P}^3$
both belong to the class of K3 surfaces. So it would be very interesting to understand which real-fibered morphisms
$\mathbb {P}^3$
both belong to the class of K3 surfaces. So it would be very interesting to understand which real-fibered morphisms
![]() $X\to \mathbb {P}^2$
from a K3 surface X admit a positive Ulrich bundle. Note that (not necessarily positive) Ulrich sheaves of rank two on K3 surfaces have been constructed in [Reference Aprodu, Farkas and OrtegaAFO17]. Similarly, we cannot increase the dimensions: not every nonnegative polynomial
$X\to \mathbb {P}^2$
from a K3 surface X admit a positive Ulrich bundle. Note that (not necessarily positive) Ulrich sheaves of rank two on K3 surfaces have been constructed in [Reference Aprodu, Farkas and OrtegaAFO17]. Similarly, we cannot increase the dimensions: not every nonnegative polynomial
![]() $p\in {\mathbb R}[x_0,x_1,x_2,x_3]_4$
is a sum of squares [Reference HilbertHil88] and it is not known whether there are hyperbolic polynomials
$p\in {\mathbb R}[x_0,x_1,x_2,x_3]_4$
is a sum of squares [Reference HilbertHil88] and it is not known whether there are hyperbolic polynomials
![]() $h\in {\mathbb R}[x_0,x_1,x_2,x_3,x_4]_3$
such that no power
$h\in {\mathbb R}[x_0,x_1,x_2,x_3,x_4]_3$
such that no power
![]() $h^r$
has a definite determinantal representation (see [Reference SaundersonSau19, Section 5] for cubic hyperbolic hypersurfaces). Double covers of
$h^r$
has a definite determinantal representation (see [Reference SaundersonSau19, Section 5] for cubic hyperbolic hypersurfaces). Double covers of
![]() $\mathbb {P}^3$
ramified along quartic surfaces and cubic hypersurfaces in
$\mathbb {P}^3$
ramified along quartic surfaces and cubic hypersurfaces in
![]() $\mathbb {P}^4$
both belong to the class of Fano threefolds of index two. In [Reference BeauvilleBea18, Section 6], Ulrich sheaves of rank two on such threefolds have been constructed.
$\mathbb {P}^4$
both belong to the class of Fano threefolds of index two. In [Reference BeauvilleBea18, Section 6], Ulrich sheaves of rank two on such threefolds have been constructed.
Problem 11.14 Understand which finite surjective and real-fibered morphisms
![]() $X\to \mathbb {P}^n$
admit a positive Ulrich sheaf for X a K3 surface or a Fano threefold of index two. If such exist, what are their ranks? Are there hyperbolic cubic hypersurfaces in
$X\to \mathbb {P}^n$
admit a positive Ulrich sheaf for X a K3 surface or a Fano threefold of index two. If such exist, what are their ranks? Are there hyperbolic cubic hypersurfaces in
![]() $\mathbb {P}^4$
that do not carry a positive Ulrich sheaf?
$\mathbb {P}^4$
that do not carry a positive Ulrich sheaf?
We conclude this section with some examples.
Example 11.15 Let
![]() $h=x_0^3-x_0(2x_1^2+2x_2^2+x_3^2)+x_1^3+x_1x_2^2$
. The hypersurface
$h=x_0^3-x_0(2x_1^2+2x_2^2+x_3^2)+x_1^3+x_1x_2^2$
. The hypersurface
![]() ${X={\mathcal V}(h)\subset \mathbb {P}^3}$
is hyperbolic with respect to
${X={\mathcal V}(h)\subset \mathbb {P}^3}$
is hyperbolic with respect to
![]() $e=[1\colon 0\colon 0\colon 0]$
and contains the real line
$e=[1\colon 0\colon 0\colon 0]$
and contains the real line
![]() $L={\mathcal V}(x_0,x_1)$
. The hyperplanes
$L={\mathcal V}(x_0,x_1)$
. The hyperplanes
![]() $H_1={\mathcal V}(x_0)$
and
$H_1={\mathcal V}(x_0)$
and
![]() $H_2={\mathcal V}(x_0-x_1)$
contain L and are tangent to the hyperbolicity cone of h. The quadratic polynomial
$H_2={\mathcal V}(x_0-x_1)$
contain L and are tangent to the hyperbolicity cone of h. The quadratic polynomial
![]() $p=x_0(x_0-x_1)$
is an interlacer of h and its zero divisor on X is
$p=x_0(x_0-x_1)$
is an interlacer of h and its zero divisor on X is
where
![]() $L_1={\mathcal V}(x_0,x_1+\textrm {i}x_2)$
and
$L_1={\mathcal V}(x_0,x_1+\textrm {i}x_2)$
and
![]() $L_2={\mathcal V}(x_0-x_1,x_2+\textrm {i}x_3)$
. Thus, we have
$L_2={\mathcal V}(x_0-x_1,x_2+\textrm {i}x_3)$
. Thus, we have
![]() $D=M+\overline {M}$
with
$D=M+\overline {M}$
with
![]() $M=L+L_1+L_2$
. The space of all quadrics vanishing on
$M=L+L_1+L_2$
. The space of all quadrics vanishing on
![]() $L, L_1$
, and
$L, L_1$
, and
![]() $L_2$
is spanned by
$L_2$
is spanned by
The minimal free resolution over
![]() $S={\mathbb R}[x_0,x_1,x_2,x_3]$
of the ideal in
$S={\mathbb R}[x_0,x_1,x_2,x_3]$
of the ideal in
![]() $S/(h)$
generated by these quadrics has length one and is given by the matrix
$S/(h)$
generated by these quadrics has length one and is given by the matrix
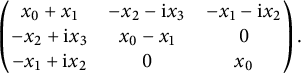 $$ \begin{align*} \begin{pmatrix}x_0+x_1& -x_2-\textrm{i}x_3& -x_1-\textrm{i}x_2\\ -x_2+\textrm{i}x_3& x_0-x_1& 0\\ -x_1+\textrm{i}x_2& 0& x_0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix}x_0+x_1& -x_2-\textrm{i}x_3& -x_1-\textrm{i}x_2\\ -x_2+\textrm{i}x_3& x_0-x_1& 0\\ -x_1+\textrm{i}x_2& 0& x_0 \end{pmatrix}. \end{align*} $$
This matrix is Hermitian and positive definite at e. Its determinant is indeed h.
Example 11.16 Consider the following nonnegative ternary quartic
and let
![]() $X\subset \mathbb {P}(2,1,1,1)$
be the corresponding double cover defined by
$X\subset \mathbb {P}(2,1,1,1)$
be the corresponding double cover defined by
![]() $y^2=p$
. On X, we have the two lines
$y^2=p$
. On X, we have the two lines
The principal divisor associated with the rational function
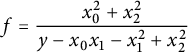 $$ \begin{align*} f=\frac{x_0^2+x_2^2}{y-x_0x_1-x_1^2+x_2^2} \end{align*} $$
$$ \begin{align*} f=\frac{x_0^2+x_2^2}{y-x_0x_1-x_1^2+x_2^2} \end{align*} $$
is
![]() $L_2-L_1+\overline {L_2}-\overline {L_1}$
. As
$L_2-L_1+\overline {L_2}-\overline {L_1}$
. As
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are both nonreal lines, this implies that f has constant sign on each of the two connected components of
$L_2$
are both nonreal lines, this implies that f has constant sign on each of the two connected components of
![]() $X({\mathbb R})$
. Evaluating f at points from the two different components, for example, at
$X({\mathbb R})$
. Evaluating f at points from the two different components, for example, at
shows that f changes sign. Letting K be a canonical divisor on X, we have for
![]() $M=L_2-L_1-K$
that
$M=L_2-L_1-K$
that
![]() $M+\overline {M}=(f)-2K$
as in the proof of Theorem 11.8. We can realize the divisor class of M by the ideal in
$M+\overline {M}=(f)-2K$
as in the proof of Theorem 11.8. We can realize the divisor class of M by the ideal in
![]() ${\mathbb R}[y,x_0,x_1,x_2]/(y^2-p)$
that is generated by
${\mathbb R}[y,x_0,x_1,x_2]/(y^2-p)$
that is generated by
![]() $y-x_0x_1-x_1^2+x_2^2$
and
$y-x_0x_1-x_1^2+x_2^2$
and
![]() $(x_0+\textrm {i}x_1)(x_0+\textrm {i}x_2)$
. The minimal free resolution over the ring
$(x_0+\textrm {i}x_1)(x_0+\textrm {i}x_2)$
. The minimal free resolution over the ring
![]() ${\mathbb R}[y,x_0,x_1,x_2]$
has length one and is given by the matrix
${\mathbb R}[y,x_0,x_1,x_2]$
has length one and is given by the matrix
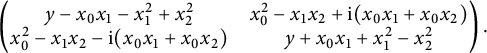 $$ \begin{align*} \begin{pmatrix} y-x_0x_1-x_1^2+x_2^2 & x_0^2-x_1x_2+\textrm{i}(x_0x_1+x_0x_2) \\ x_0^2-x_1x_2-\textrm{i}(x_0x_1+x_0x_2) & y+x_0x_1+x_1^2-x_2^2 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \begin{pmatrix} y-x_0x_1-x_1^2+x_2^2 & x_0^2-x_1x_2+\textrm{i}(x_0x_1+x_0x_2) \\ x_0^2-x_1x_2-\textrm{i}(x_0x_1+x_0x_2) & y+x_0x_1+x_1^2-x_2^2 \end{pmatrix}. \end{align*} $$
Indeed, we have that
![]() $A^2=p\cdot I$
. Therefore,
$A^2=p\cdot I$
. Therefore,
The key ingredient for this construction was the rational function f. One way to find it is to blow down a real line of X and then proceed as in Lemma 11.7.
Example 11.17 The del Pezzo surface
of degree four is hyperbolic with respect to the line E spanned by
![]() $[0\colon 0\colon 0\colon 1\colon 0]$
and
$[0\colon 0\colon 0\colon 1\colon 0]$
and
![]() $[0\colon 0\colon 0\colon 0\colon 1]$
. The rational function
$[0\colon 0\colon 0\colon 0\colon 1]$
. The rational function
![]() $\frac {(x_3-x_0)(x_4-x_0)}{x_0^2}$
has different signs on the two connected components of
$\frac {(x_3-x_0)(x_4-x_0)}{x_0^2}$
has different signs on the two connected components of
![]() $X({\mathbb R})$
. Its corresponding divisor is of the form
$X({\mathbb R})$
. Its corresponding divisor is of the form
![]() $M+\overline {M}+2K$
for a suitable divisor M on
$M+\overline {M}+2K$
for a suitable divisor M on
![]() $X_{\mathbb C}$
with
$X_{\mathbb C}$
with
![]() $\ell (M)=4$
. Thus,
$\ell (M)=4$
. Thus,
![]() ${\mathcal L}(M)$
is a positive Hermitian Ulrich line bundle by Theorem 9.3. As in [Reference Eisenbud, Schreyer and WeymanESW03, Theorem 0.3], we obtain from that the following determinantal representation of the Chow form of X, written in the Plücker coordinates:
${\mathcal L}(M)$
is a positive Hermitian Ulrich line bundle by Theorem 9.3. As in [Reference Eisenbud, Schreyer and WeymanESW03, Theorem 0.3], we obtain from that the following determinantal representation of the Chow form of X, written in the Plücker coordinates:
 $$\begin{align*}\begin{pmatrix} 2 x_{03}-2 x_{04}+2 x_{34}&\!\!\! 4 x_{01}-6 \textrm{i} x_{02}+4 x_{13}-6 \textrm{i} x_{23}&\!\!\! -2 x_{01}+2 \textrm{i} x_{02}-2 x_{14}+2 \textrm{i} x_{24}&\!\!\! -2 \textrm{i} x_{12}\\4 x_{01}+6 \textrm{i} x_{02}+4 x_{13}+6 \textrm{i} x_{23}&\!\!\! -2 x_{03}-2 x_{04}+2 x_{34}&\!\!\! 10 \textrm{i} x_{12}&\!\!\! 2 x_{01}-2 \textrm{i} x_{02}-2 x_{14}+2 \textrm{i} x_{24}\\-2 x_{01}-2 \textrm{i} x_{02}-2 x_{14}-2 \textrm{i} x_{24}&\!\!\! -10 \textrm{i} x_{12}&\!\!\! 2 x_{03}+2 x_{04}+2 x_{34}&\!\!\! -4 x_{01}+6 \textrm{i} x_{02}+4 x_{13}-6 \textrm{i} x_{23}\\2 \textrm{i} x_{12}&\!\!\! 2 x_{01}+2 \textrm{i} x_{02}-2 x_{14}-2 \textrm{i} x_{24}&\!\!\! - 4 x_{01}-6 \textrm{i} x_{02}+4 x_{13}+6 \textrm{i} x_{23}&\!\!\! -2 x_{03}+2 x_{04}+2 x_{34} \end{pmatrix}\kern-1pt.\end{align*}$$
$$\begin{align*}\begin{pmatrix} 2 x_{03}-2 x_{04}+2 x_{34}&\!\!\! 4 x_{01}-6 \textrm{i} x_{02}+4 x_{13}-6 \textrm{i} x_{23}&\!\!\! -2 x_{01}+2 \textrm{i} x_{02}-2 x_{14}+2 \textrm{i} x_{24}&\!\!\! -2 \textrm{i} x_{12}\\4 x_{01}+6 \textrm{i} x_{02}+4 x_{13}+6 \textrm{i} x_{23}&\!\!\! -2 x_{03}-2 x_{04}+2 x_{34}&\!\!\! 10 \textrm{i} x_{12}&\!\!\! 2 x_{01}-2 \textrm{i} x_{02}-2 x_{14}+2 \textrm{i} x_{24}\\-2 x_{01}-2 \textrm{i} x_{02}-2 x_{14}-2 \textrm{i} x_{24}&\!\!\! -10 \textrm{i} x_{12}&\!\!\! 2 x_{03}+2 x_{04}+2 x_{34}&\!\!\! -4 x_{01}+6 \textrm{i} x_{02}+4 x_{13}-6 \textrm{i} x_{23}\\2 \textrm{i} x_{12}&\!\!\! 2 x_{01}+2 \textrm{i} x_{02}-2 x_{14}-2 \textrm{i} x_{24}&\!\!\! - 4 x_{01}-6 \textrm{i} x_{02}+4 x_{13}+6 \textrm{i} x_{23}&\!\!\! -2 x_{03}+2 x_{04}+2 x_{34} \end{pmatrix}\kern-1pt.\end{align*}$$
We observe that it is Hermitian and positive definite at E.
Acknowledgment
We would like to thank Alejandro González Nevado for helpful comments on an earlier version of this paper.






